Solving Problems through Engineering Design: An Exploratory Study with Pre-Service Teachers
Abstract
:1. Introduction
2. Theoretical Framework
2.1. The Teaching and Learning of Mathematics: Current Trends
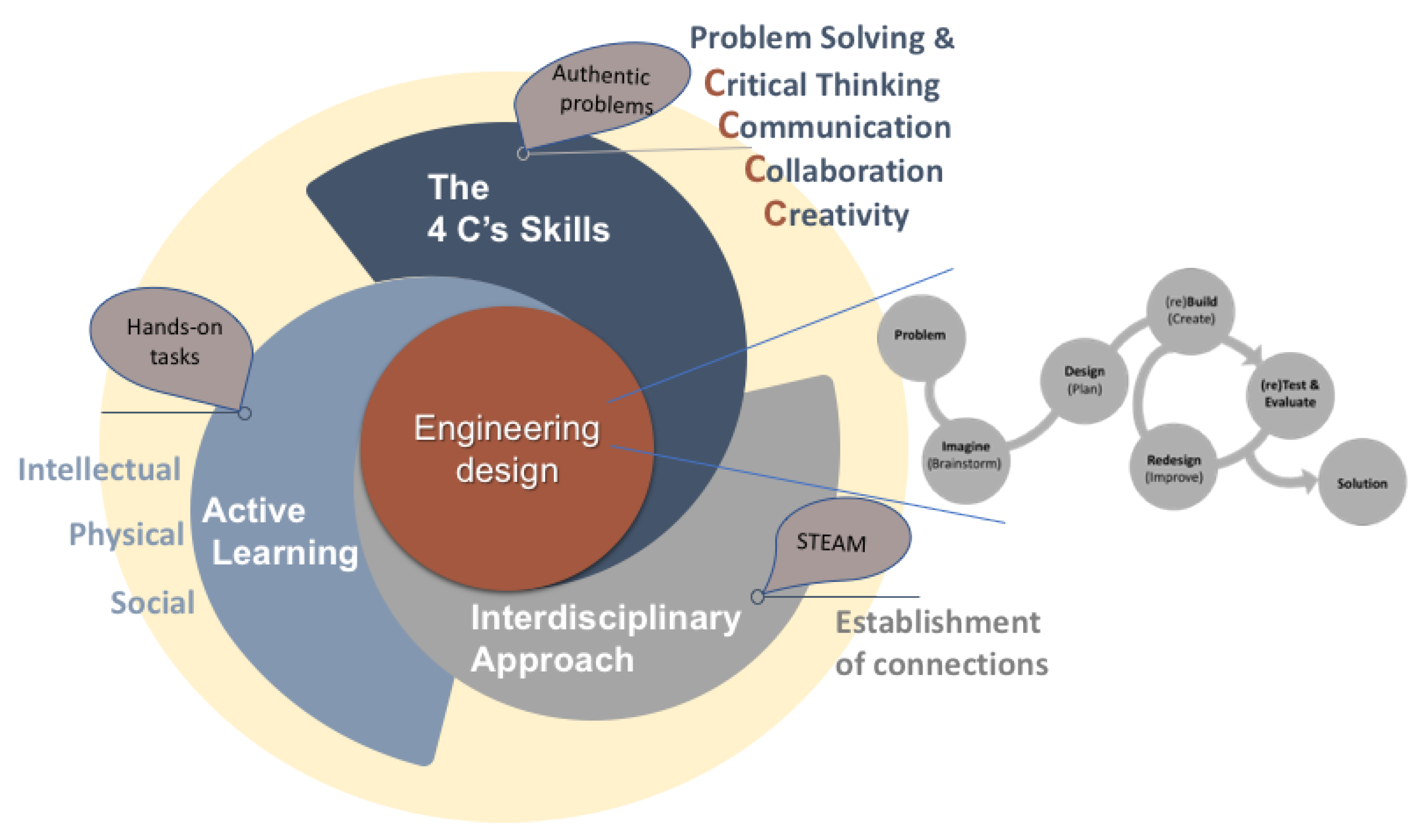
2.2. Perspectives about STEAM Integration
2.3. Engineering Design in STEAM Education
2.4. Summarizing
3. Method and Procedures
3.1. Context and Participants
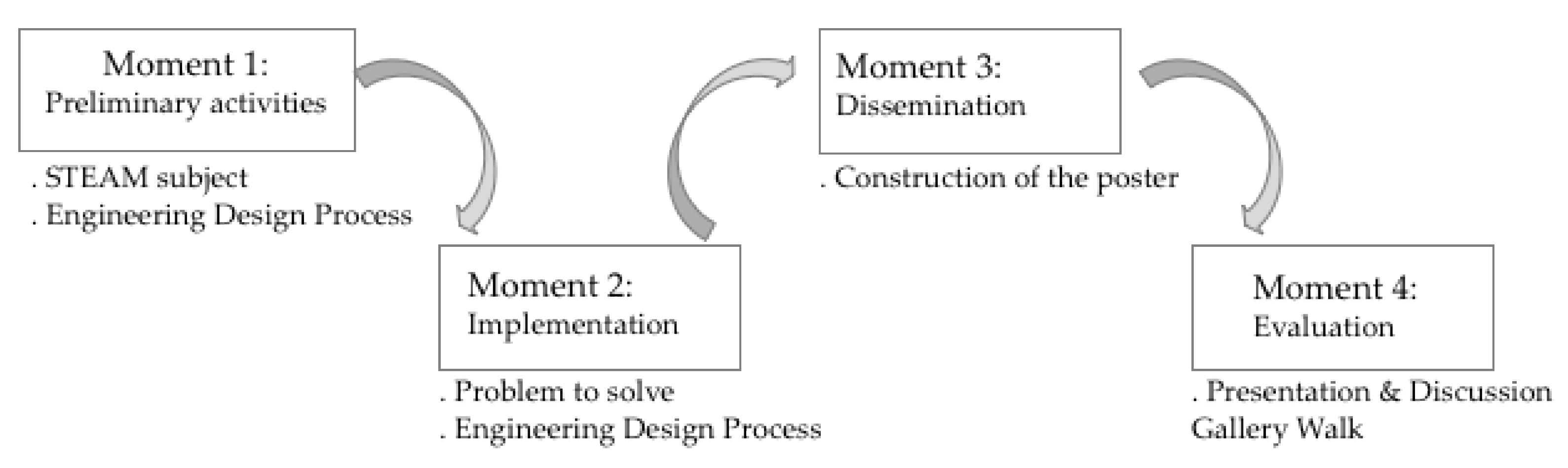
3.2. The Moments in the Didactical Experience
3.2.1. Moment 1—Preliminary Activities
3.2.2. Moment 2—Implementation
3.2.3. Moment 3—Dissemination
3.2.4. Moment 4—Evaluation
3.3. Data Collection and Analysis
4. Results from the Implementation of the Paper Table Problem
4.1. The Participants along the Engineering Design Cycle
4.1.1. Part 1. Exploring and Designing the Problem
4.1.2. Part 2. (Re)Building, (Re)Testing and (Re)Designing
4.1.3. Group Results
4.2. Participants’ Engagement in the Didactical Experience
4.2.1. Cognitive Engagement
4.2.2. Affective Engagement
4.2.3. Behavioral Engagement
5. Conclusions
6. Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- English, L.D.; King, D. STEM integration in sixth grade: Designing and constructing paper bridges. Int. J. Sci. Math. Educ. 2019, 17, 863–884. [Google Scholar] [CrossRef] [Green Version]
- Edwards, S. Active learning in the middle grades. Middle Sch. J. 2015, 46, 26–32. [Google Scholar] [CrossRef]
- Edwards, S.; Kemp, A.; Page, C. The middle school philosophy: Do we practice what we preach or do we preach something different? Curr. Issues Middle Level Educ. 2014, 19, 13–19. [Google Scholar]
- Nesin, G. Active Learning. In This We Believe in Action: Implementing Successful Middle Level Schools; Association for Middle Level Education: Westerville, OH, USA, 2012; pp. 17–27. [Google Scholar]
- Vale, I.; Barbosa, A. Movement & learning: The gallery walk strategy. In Improving Children’s Learning and Well-Being; Carvalho, G.S., Palhares, P., Azevedo, F., Parente, C., Eds.; UM-CIEC: Braga, Portugal, 2020; pp. 7–22. [Google Scholar]
- Fadel, C.; Bialik, M.; Trilling, B. Four-Dimensional Education: The Competencies Learners Need to Succeed. Center for Curriculum Redesign, 2008; Available online: https://curriculumredesign.org/our-work/four-dimensional-21st-century-education-learning-competencies-future-2030/ (accessed on 10 September 2022).
- World Economic Forum. New Vision for Education: Fostering Social and Emotional Learning through Technology. 2016. Available online: http://www3.weforum.org/docs/WEF_New_Vision_for_Education.pdf (accessed on 12 September 2022).
- Prince, M. Does Active Learning Work? A Review of the Research. J. Eng. Educ. 2004, 93, 223–231. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics. Principles to Actions: Ensuring Mathematical Success for All; NCTM: Reston, VA, USA, 2014; pp. 9–11. [Google Scholar]
- Hannaford, C. Smart Moves: Why Learning Is Not All in Your Head, 2nd ed.; Great River Books: Salt Lake City, UT, USA, 2005; pp. 15–16. [Google Scholar]
- Fredricks, J.A.; Blumenfeld, P.C.; Paris, A.H. School Engagement: Potential of the Concept, State of the Evidence. Rev. Educ. Res. 2004, 74, 59–109. [Google Scholar] [CrossRef] [Green Version]
- Kong, Q.P.; Wong, N.Y.; Lam, C.C. Student engagement in mathematics: Development of instrument and validation of construct. Math. Ed. Res. J. 2003, 15, 4–21. [Google Scholar] [CrossRef]
- Attard, C. Engagement with mathematics: What does it mean and what does it look like? APMC 2012, 17, 9–13. [Google Scholar]
- Leikin, R. Interplay between creativity and expertise in teaching and learning of mathematics. In Proceedings of the 40th Conference of the International Group for the Psychology of Mathematics Education, Szeged, Hungary, 3–7 August 2016; Csíkos, C., Rausch, A., Szitányi, J., Eds.; PME: Szeged, Hungary, 2016; Volume 1, pp. 19–34. [Google Scholar]
- Sullivan, P.; Clarke, D.; Clarke, B. Teaching with Tasks for Effective Mathematics Learning; Springer: New York, NY, USA, 2013; pp. 13–21. [Google Scholar]
- Vale, I.; Barbosa, A. Visualization—A pathway to mathematical challenging tasks. In Mathematical Challenge for All; Leikin, R., Christou, C., Karp, A., Pitta-Pantazi, D., R. Zazkis, R., Eds.; Springer International Publishing: Cham, Switzerland, 2022; in press. [Google Scholar]
- Vale, I.; Pimentel, T.; Barbosa, A. The power of seeing in problem solving and creativity: An issue under discussion. In Broadening the Scope of Research on Mathematical Problem Solving: A Focus on Technology, Creativity and Affect; Carreira, S., Amado, N., Jones, K., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 243–272. [Google Scholar]
- Fries, L.; Son, J.Y.; Givvin, K.B.; Sligler, J.W. Practicing Connections: A Framework to Guide Instructional Design for Developing Understanding in Complex Domains. Educ. Psychol. Rev. 2021, 33, 739–762. [Google Scholar] [CrossRef]
- Jurdak, M. Contrasting Perspectives and Performance of High School Students on Problem Solving in Real World Situated, and School Contexts. Educ. Stud. Math. 2006, 63, 283–301. [Google Scholar] [CrossRef]
- Palm, T. The Realism of Mathematical Schools Tasks—Features and Consequences. Ph.D. Thesis, Umea University, Umea, Sweden, 2002. [Google Scholar]
- OECD. Education at a Glance 2011: OECD Indicators; OECD Publishing: Paris, France, 2011. [Google Scholar]
- Vos, P. What Is ’Authentic’ in the Teaching and Learning of Mathematical Modelling? In Trends in Teaching and Learning of Mathematical Modelling: International Perspectives on the Teaching and Learning of Mathematical Modelling; Kaiser, G., Blum, W., Borromeo, R., Stillman, G., Eds.; Springer: Dordrecht, The Netherlands, 2011; Volume 1. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics. Principles and Standards for School Mathematics; NCTM: Reston, VA, USA, 2000. [Google Scholar]
- OECD. PISA 2018 Results. Combined Executive Summaries, Volume I, II & III. OECD, 2019. Available online: https://www.oecd.org/pisa/Combined_Executive_Summaries_PISA_2018.pdf (accessed on 25 July 2022).
- English, L.D. Advancing elementary and middle school STEM education. Int. J. Sci. Math. Educ. 2017, 15 (Suppl. S1), 5–24. [Google Scholar] [CrossRef] [Green Version]
- Quigley, C.F.; Herro, D.; Shekell, C.; Cian, H.; Jacques, L. Connected learning in STEAM classrooms: Opportunities for engaging youth in science and math classrooms. Int. J. Sci. Math. Educ. 2020, 18, 1441–1463. [Google Scholar] [CrossRef]
- Breiner, J.M.; Harkness, S.S.; Johnson, C.C.; Koehler, C.M. What Is STEM? A Discussion about Conceptions of STEM in Education and Partnerships. Sch. Sci. Math. 2012, 112, 3–11. [Google Scholar] [CrossRef]
- English, L.D. Learning while designing in a fourth-grade integrated STEM problem. Int. J. Techno Des. Educ. 2018, 29, 1011–1032. [Google Scholar] [CrossRef] [Green Version]
- Vasquez, J.; Sneider, C.; Comer, M. STEM lesson Essentials, Grades 3–8: Integrating Science, Technology, Engineering, and Mathematics; Heinemann: Portsmouth, NH, USA, 2013. [Google Scholar]
- Bybee, R. Advancing STEM education: A 2020 vision. Technol. Eng. Teach. 2010, 70, 30–35. [Google Scholar]
- Martín-Páez, T.; Aguilera, D.; Perales-Palacios, F.J.; Vílchez-González, J.M. What are we talking about when we talk about STEM education? A review of literature. Sci. Educ. 2019, 103, 799–822. [Google Scholar] [CrossRef]
- Thibaut, L.; Ceuppens, S.; De Loof, H.; De Meester, J.; Goovaerts, L.; Struyf, A.; Boeve-de Pauw, J.; Dehaene, W.; Deprez, J.; De Cock, M.; et al. Integrated STEM Education: A Systematic Review of Instructional Practices in Secondary Education. Eur. J. STEM Educ. 2018, 3, 1–12. [Google Scholar] [CrossRef]
- Hiebert, J.; Carpenter, T.P.; Fennema, E.; Fuson, K.C.; Wearne, D.; Murray, H.; Olivier, A.; Human, P. Making Sense: Teaching and Learning Mathematics with Understanding; Heinemann: Portsmouth, NH, USA, 1997. [Google Scholar]
- English, L.D. STEM: Challenges and Opportunities for Mathematics Education. In Proceedings of the 39th Conference of the International Group for the Psychology of Mathematics Education, Hobart, Australia, 13–18 July 2015; Beswick, K., Muir, T., Wells, J., Eds.; PME: Hobart, Australia, 2015; Volume 1, pp. 4–18. [Google Scholar]
- English, L.D.; King, D.T. STEM learning through engineering design: Fourth-grade students’ investigations in aerospace. Int. J. STEM Educ. 2015, 2, 14. [Google Scholar] [CrossRef]
- Honey, M.; Pearson, G.; Schweingruber, H. (Eds.) STEM Integration in K-12 Education: Status, Prospects, and an Agenda for Research; Academies Press: Washington, DC, USA, 2014. [Google Scholar]
- Bryan, L.A.; Moore, T.J.; Johnson, C.C.; Roehrig, G.H. Integrated STEM education. In STEM Roadmap: A Framework for Integration; Johnson, C., Peters-Burton, E., Moore, T., Eds.; Taylor & Francis: London, UK, 2015; pp. 23–37. [Google Scholar]
- Lucas, B.; Claxton, G.; Hanson, J. Thinking Like an Engineer: Implications for the Education System; Royal Academy of Engineers, 2014; Available online: www.raeng.org.uk/thinkinglikeanengineer (accessed on 31 August 2022).
- Kelley, T.R.; Knowles, J.G. A conceptual framework for integrated STEM education. Int. J. STEM Ed. 2016, 3, 11. [Google Scholar] [CrossRef] [Green Version]
- Cunningham, C.M. Engineering is elementary. Bridge 2009, 30, 11–17. [Google Scholar]
- Shahali, E.H.; Halim, L.; Rasul, M.S.; Osman, K.; Zulkifeli, M.A. STEM learning through engineering design: Impact on middle secondary students’ interest towards STEM. Eurasia J. Math. Sci. Techno Educ. 2017, 13, 1189–1211. [Google Scholar] [CrossRef]
- Fan, S.; Yu, K. How an integrative STEM curriculum can benefit students in engineering design practices. Int. J. Techno Des. Educ. 2017, 27, 107–129. [Google Scholar] [CrossRef]
- Wells, J.G. PIRPOSAL Model of Integrative STEM Education: Conceptual and Pedagogical Framework for Classroom Implementation. Techno Eng. Teach. 2016, 75, 12–19. [Google Scholar]
- Guzey, S.S.; Moore, T.J.; Harwell, M. Building up STEM: An analysis of teacher-developed engineering design-based STEM integration curricular materials. J. Pre-Coll. Eng. Educ. Res. 2016, 6, 2. [Google Scholar] [CrossRef] [Green Version]
- Education Department at WGBH. Design Squad Global Inventing Green 12-Week Club Guide. WGBH, 2019. Available online: https://pbskids.org/designsquad/pdf/parentseducators/DSG_Inventing_Green_Club_Guide_6_Week.pdf (accessed on 3 September 2022).
- Cunningham, C.M.; Hester, K. Engineering is Elementary: An Engineering and Technology Curriculum for Children. In Proceedings of the ASSE Annual Conference and Exposition, Honolulu, HI, USA, 1 January 2007; pp. 12.639.1–12.639.18. [Google Scholar]
- Kelly, G.J.; Cunningham, C.M. Epistemic tools in engineering design for K-12 education. Sci. Educ. 2019, 103, 1080–1111. [Google Scholar] [CrossRef]
- Mann, E.L.; Mann, R.L.; Strutz, M.L.; Duncan, D.; Yoon, S.Y. Integrating engineering into K-6 curriculum developing talent in the STEM disciplines. J. Adv. Acad. 2011, 22, 639–658. [Google Scholar]
- Carreira, S.; Baioa, A.M. Mathematical modelling with hands-on experimental tasks: On the student’s sense of credibility. ZDM Math. Educ. 2018, 50, 201–215. [Google Scholar] [CrossRef]
- Dougherty, D. The maker movement. Innovations 2012, 7, 11–14. [Google Scholar] [CrossRef]
- García-Molina, R. Ciência recreativa: Un recurso didáctico para enseñar deleitando. Rev. Eureka Enseñ Div. Ciencias 2011, 8, 370–392. [Google Scholar] [CrossRef]
- Erickson, F. Qualitative Methods in Research on Teaching. In Handbook of Research on Teaching; Wittrockk, M., Ed.; MacMillan: New York, NY, USA, 1986; pp. 119–161. [Google Scholar]
- Miles, M.B.; Huberman, A.M. Qualitative Data Analysis; Sage Publications: Thousand Oaks, CA, USA, 1994. [Google Scholar]
- Given, L.M. (Ed.) The SAGE Encyclopedia of Qualitative Research Methods; Sage Publications: Thousand Oaks, CA, USA, 2008; Volume 1–2. [Google Scholar]
- Yin, R.K. Case Study Research: Design and Methods; Sage Publications: Thousand Oaks, CA, USA, 2003. [Google Scholar]
- Bacharach, N.; Heck, T.; Dahlberg, K. Researching the use of co-teaching in the student teaching experience. In Moving forward and Broadening Perspectives: Coteaching in International Contexts; Murphy, C., Scantlebury, K., Eds.; Springer Publishing: New York, NY, USA, 2013. [Google Scholar]
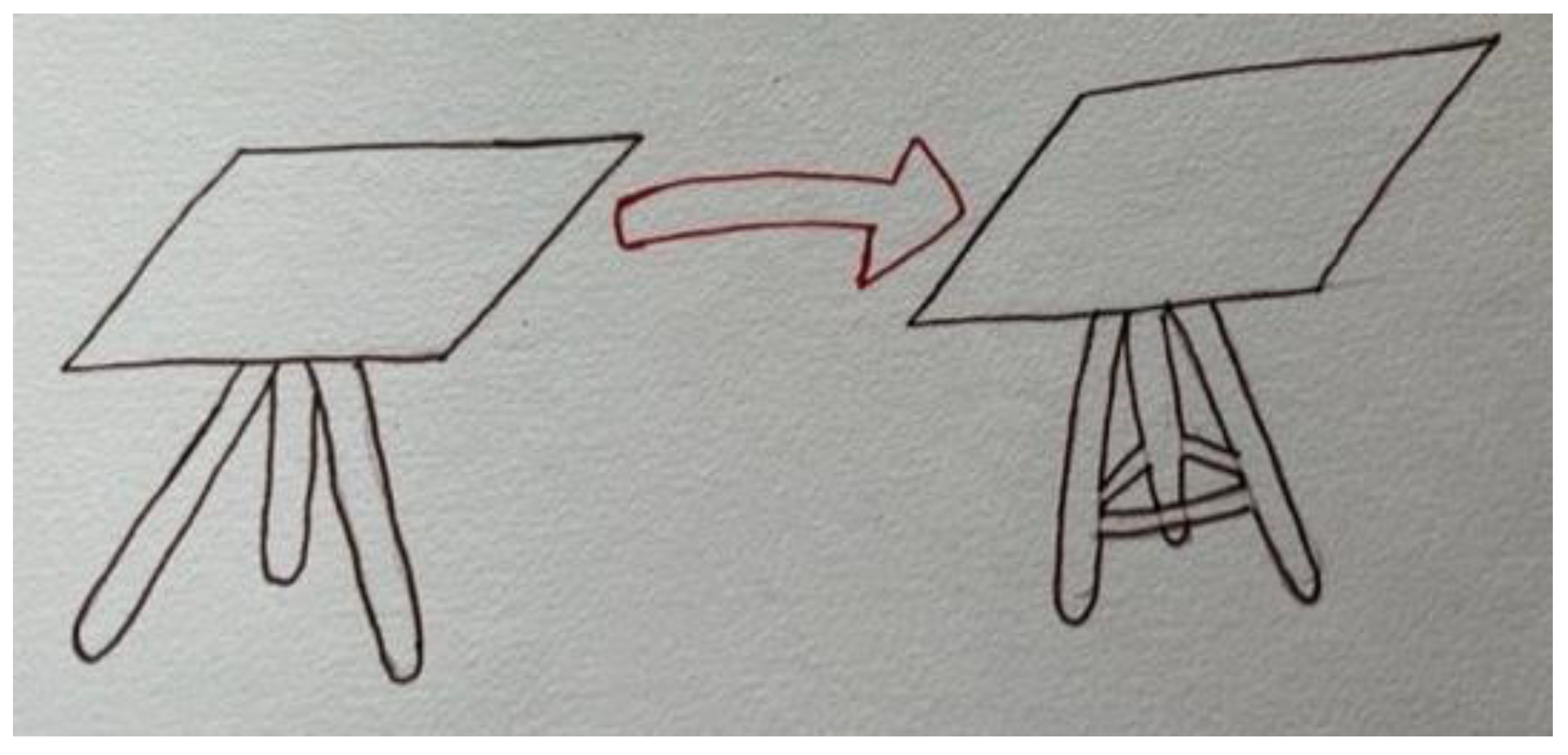
- Enderson, M.C.; Grant, M.R. Emerging engineers design a paper table. Math. Teach. Middle Sch. 2013, 18, 362–369. [Google Scholar] [CrossRef]
- Stoner, M.; Stuby, K.; Szczepanski, S. The engineering process in construction & design. Math. Teach. Middle Sch. 2013, 18, 333–338. [Google Scholar]
- Polya, G. How to Solve It? Princeton University Press: Princeton, NJ, USA, 1945; pp. 27–42. [Google Scholar]
- Vale, I.; Barbosa, A. Promoting mathematical knowledge and skills in a mathematical classroom using a gallery walk. Int. J. Res. Educ. Sci. 2021, 7, 1211–1225. [Google Scholar] [CrossRef]
- Creswell, J.W. Research Design: Qualitative, Quantitative and Mixed Methods Approaches, 3rd ed.; Sage Publications: Thousand Oaks, CA, USA, 2009. [Google Scholar]
- English, L.D.; King, D.; Hudson, P.; Dawes, L. The aerospace engineering challenge. Teach. Child. Math. 2014, 21, 122–126. [Google Scholar] [CrossRef]








| Levels of Engagement | Descriptors |
|---|---|
| Cognitive | Surface strategy (memorization; procedural knowledge; handling tests) Deep strategy (understanding; establish connections; justification) Reliance (pose questions; follow the teacher’s instructions) |
| Affective | Interest (joy; pleasure; sense of satisfaction; curiosity; excitement) Achievement orientation (effort to get good results; focus on finishing a task) Anxiety (nervous, worried; afraid of poor results) Frustration (uncomfortable; tired; dislike for the task) |
| Behavioral | Attentiveness (listen; take an active part in the discussion; make an effort; concentration) Diligence (effort to understand; try again; persistence) Time spent (on out-of-class learning) |
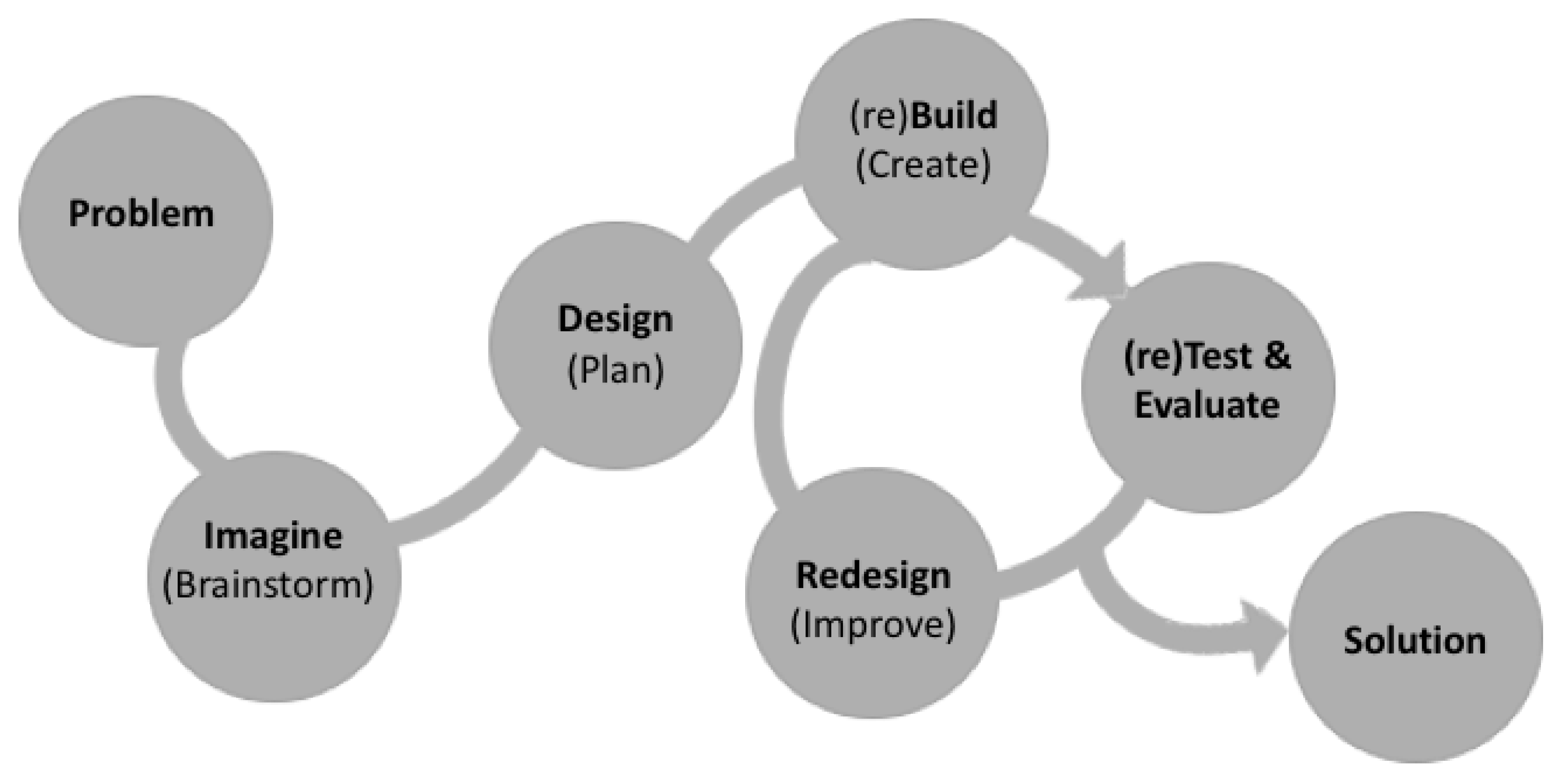
| Engineering Design Process | Problem Solving Process (Adapted from Polya [59]) | |
|---|---|---|
| The problem | Understand the problem | Did I understand the problem? What is asked? |
| Imagine (Brainstorm) | What do I need to know about the problem? Do I have enough information to solve the problem? | |
| Design (Plan) | Devise a plan | Collect all the available information. Do I know a related problem? Did I use all the conditions? Can I use know strategies, like look for a pattern; draw a Figure? |
| (re)Build (Create) | Carry out the plan | Carry out the previous plan. Select a strategy to solve the problem. Solve the problem |
| (re)Test & Evaluate | Look back | Examine the solution. Does the answer/solution make sense? Does the solution fit the conditions? Does it work? |
| Redesign (Improve) | Does the solution work? If not redesign it. Check each step. Can I find a simpler or better solution? | |
| Share the Solution | Share the solution. | |
| Design Process | Description |
|---|---|
| Identify the Problem | Can I build a table that supports a book, without breaking down? |
| Imagine | What kind of tables can I build? |
| Design (plan) | Choose one table type. Draw a sketch of the table. |
| (re)Build (create) | Did you follow the plan to create a model/prototype? |
| (re)Test & Evaluate | Did the table support the book? |
| Redesign (Improve) | Modify the table if it doesn’t fit the conditions or improve the model. Did you confirm the strength of the table legs? Did you build a table prototype? |
| Share Solutions | Communicate your product. Create a poster where you summarize the used process and the STEAM contents. |
| Engineering | Science | Mathematics | Art | Technology |
|---|---|---|---|---|
| Engage in the ED process. Identify and compare different basic types of tables (e.g., one, three, four legs), table support legs (e.g., triangular, cross, cylindrical) and discuss how these structures enhance stability and strength. Create, develop and communicate design ideas and processes. Build and share at least one paper table prototype that is able to hold a book for a minute. | Develop an understanding of the center of mass. Identify forces acting on different table types, including tension and compression. Understand how different table types support a book. Understand the resistance of the available materials. | Apply measurement skills and geometry concepts: polygons; solids; symmetries; … Identify the properties of polygons or solids correctly; … Apply spatial reasoning in working 2-D and 3-D shapes. Draw sketches using 2-D and 3-D representations. Use mathematical language correctly. Use problem solving strategies. | Show flexibility and divergent thinking. Show originality in design. Construct the artifact with aesthetic sense and perfection. | Look for types of tables in webpages. Consult webpages about tables’ resistance. |
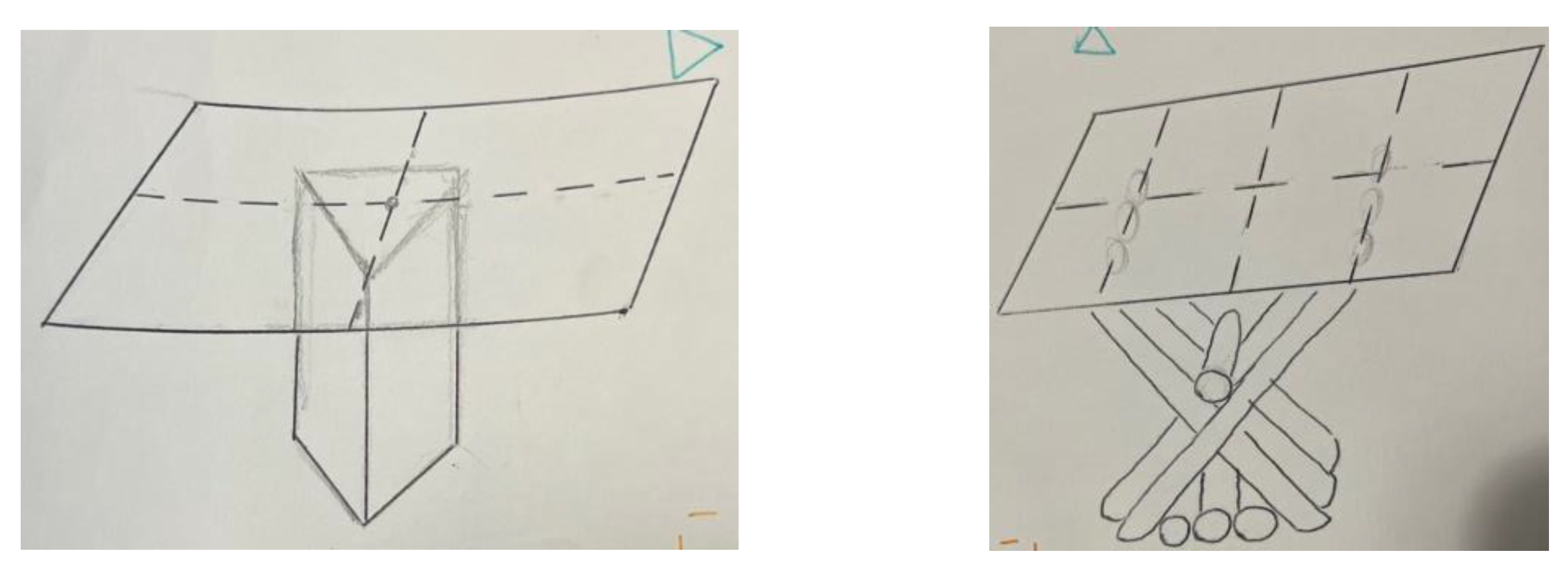
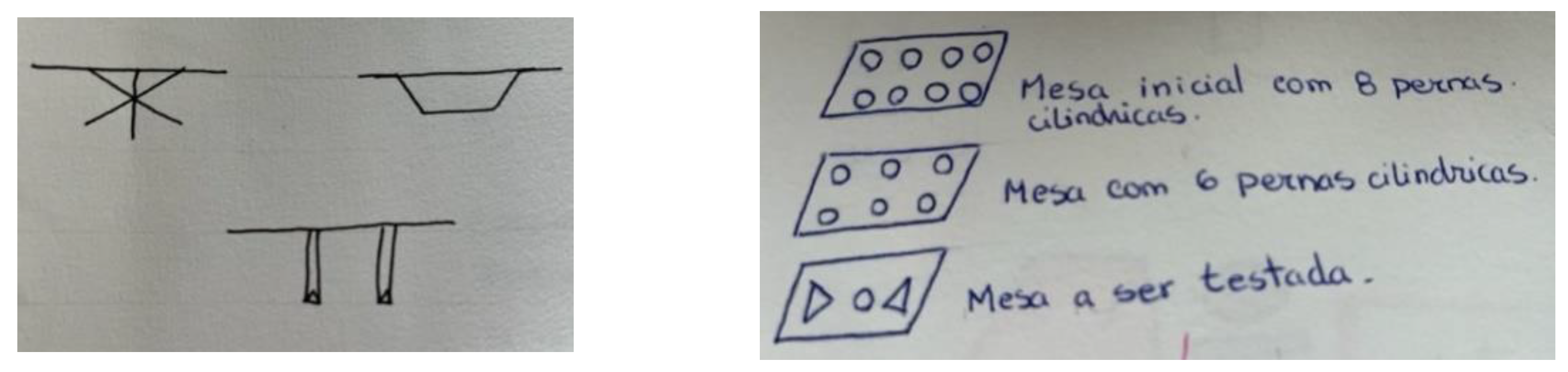
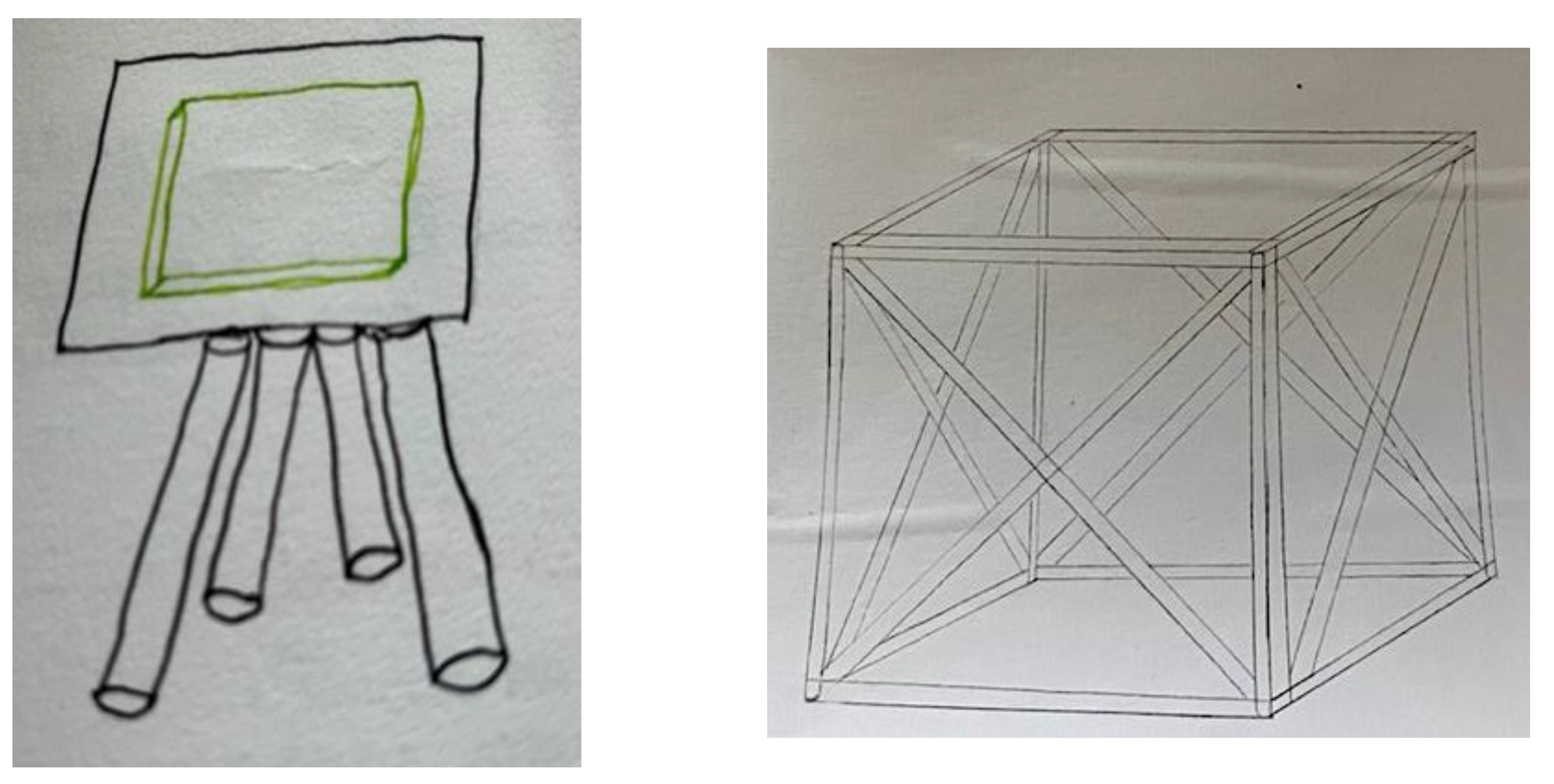
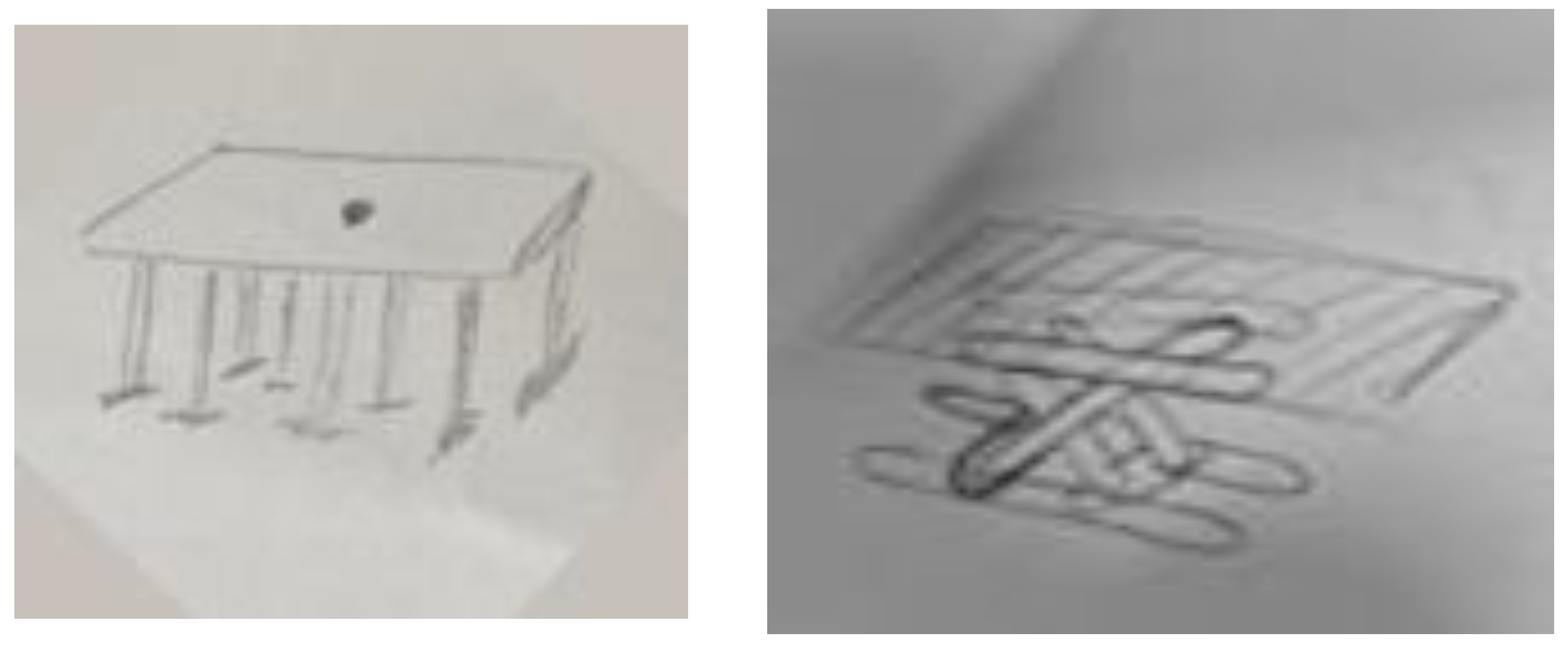
| Solids (38%) | Isolated/Simple Legs (46%) | Combined (16%) |
|---|---|---|
| Cubes | I-legs | Prism + legs |
| Triangular prisms | V-legs | Cilinder + square Indian tent |
| Square pyramids | X-legs | |
| Cylinder | Legs in triangle Indian tent | |
| Mixed solids | Legs in square Indian tent |
| Disciplinary Area | Contents and Actions for Building Paper Table |
|---|---|
| Science | Develop basic understandings of centers of mass and forces Contribute to justify the balance and resistance of the table and the materials used Contribute to understand how different tables support a load |
| Technology | Used spontaneously in the Imagine step, during brainstorming to discover types of tables |
| Engineering | Contribute to recognize basic table types (e.g., one foot; four feet) and table structures (e.g., triangulation of the table legs) Engage participants in its design model to address and solve the problem (arrive at a consensus, test and retest) Recognize how the structures constructed enhance stability and strength |
| Art | Contribute to creativity with the aesthetics features of the prototype of the table created (design, structure, design, overall look) Contribute to creativity with the aesthetics features in the elaboration and organization of the poster (e.g., disposition of the cycle and the sketches of the table, use of colors) |
| Mathematics | Contribute to solve an authentic hands-on problem, using problem solving strategies (e.g., guess and check; logical reasoning, simulation) Construct arguments in group’s design and criticize their peers’ designs Understand the effect of using some concepts (e.g., shapes; pyramids; prisms, cubes; symmetry; estimation and measurements; perpendicularity; angles; weight) Spatial reasoning in recognizing, drawing and working with different 2-D and 3-D shapes and their representations |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vale, I.; Barbosa, A.; Peixoto, A.; Fernandes, F. Solving Problems through Engineering Design: An Exploratory Study with Pre-Service Teachers. Educ. Sci. 2022, 12, 889. https://doi.org/10.3390/educsci12120889
Vale I, Barbosa A, Peixoto A, Fernandes F. Solving Problems through Engineering Design: An Exploratory Study with Pre-Service Teachers. Education Sciences. 2022; 12(12):889. https://doi.org/10.3390/educsci12120889
Chicago/Turabian StyleVale, Isabel, Ana Barbosa, Ana Peixoto, and Fátima Fernandes. 2022. "Solving Problems through Engineering Design: An Exploratory Study with Pre-Service Teachers" Education Sciences 12, no. 12: 889. https://doi.org/10.3390/educsci12120889
APA StyleVale, I., Barbosa, A., Peixoto, A., & Fernandes, F. (2022). Solving Problems through Engineering Design: An Exploratory Study with Pre-Service Teachers. Education Sciences, 12(12), 889. https://doi.org/10.3390/educsci12120889







