Assessing the Effectiveness of Differentiated Instructional Approaches for Teaching Math to Preschoolers with Different Levels of Executive Functions
Abstract
1. Introduction
1.1. Development of Cognitive Processes
1.2. Relationship between Children Mathematical Skills and Cognitive Processes
1.3. The Aim of the Present Study
- Children with a higher cognitive processes development level will perform better as a result of learning through the modeling approach; and
- Learning through the contextual approach will be most effective for children with a lower cognitive process development level.
2. Materials and Methods
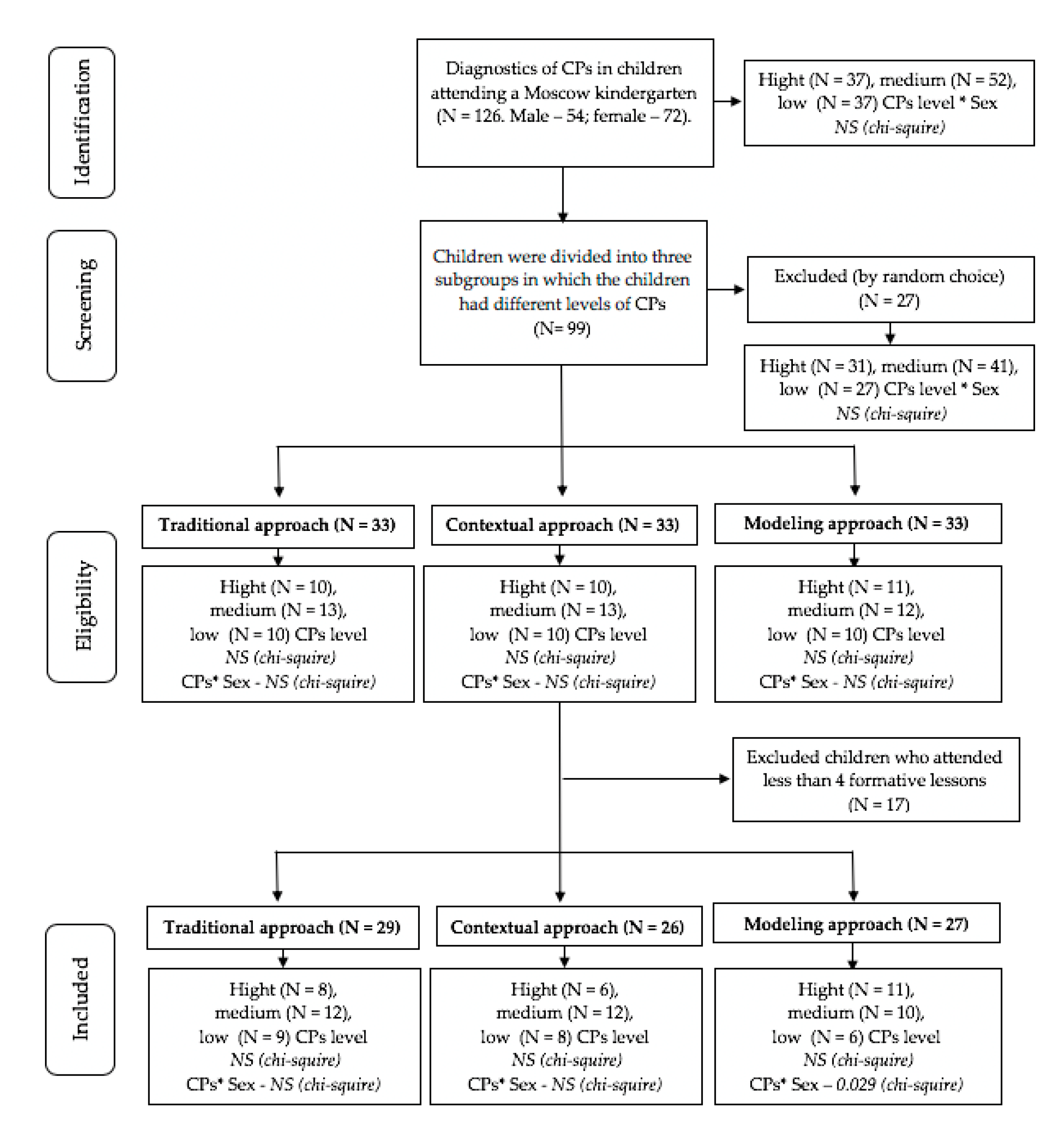
2.1. Participants
2.2. Instruments
2.3. Procedure
2.3.1. Pretest Math Assessment
2.3.2. Training Sessions
2.3.3. Post-Test Assessment
3. Results
3.1. Descriptive Statistics
3.2. Relation between Students’ Cognitive Processes Scores and Pre- to Post-Test Changes in Their Math Scores
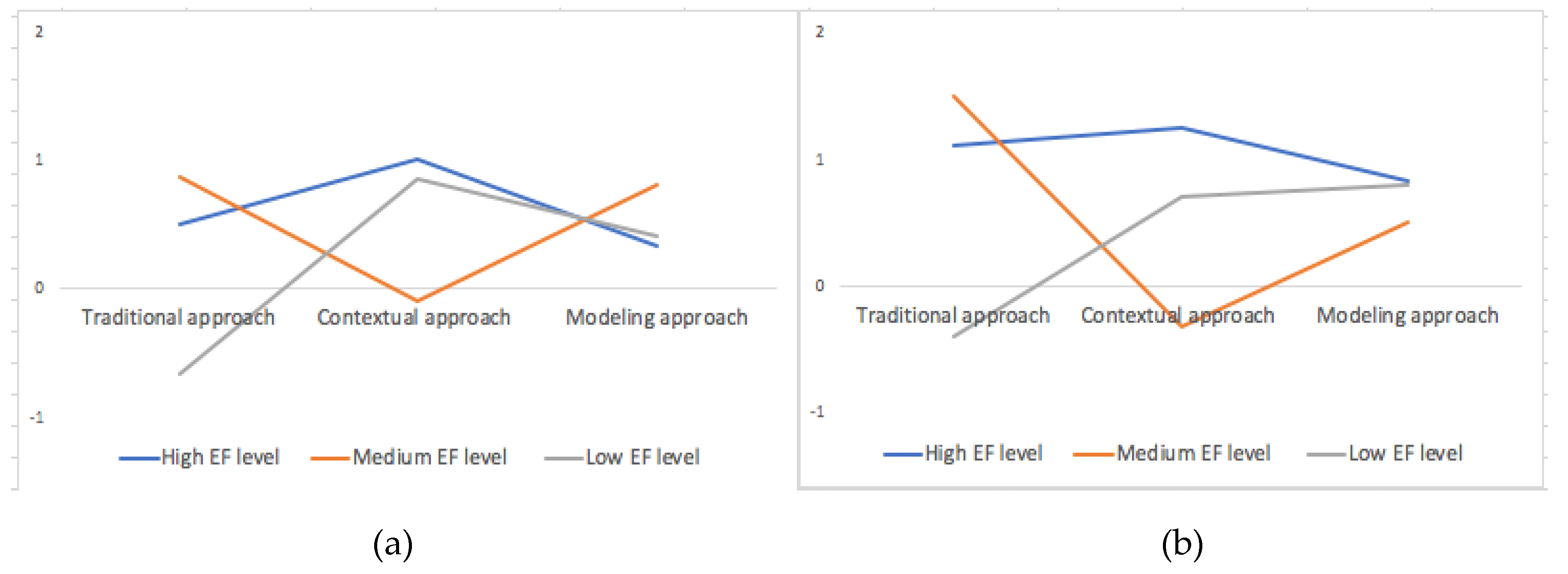
3.3. Analysis of the Effectiveness of Classes Types Depending on the Initial Level of CP
4. Discussion
Limitations
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B

References
- Willoughby, M.T.; Kupersmidt, J.B.; Voegler-Lee, M.E. Is preschool executive function causally related to academic achievement? Child Neuropsychol. 2012, 18, 79–91. [Google Scholar] [CrossRef] [PubMed]
- Best, J.R.; Miller, P.H. A developmental perspective on executive function. Child Dev. 2010, 81, 1641–1660. [Google Scholar] [CrossRef] [PubMed]
- Diamond, A.; Lee, K. Interventions shown to aid executive function development in children 4 to 12 years old. Science 2011, 333, 959–964. [Google Scholar] [CrossRef] [PubMed]
- McClelland, M.M.; Geldhof, J.; Cameron, C.E.; Wanless, S.B. Development and Self-Regulation. In Theory and Method: Handbook of Child Psychology and Developmental Science 2014, 7th ed.; Overton, W.F., Molenaar, P.C.M., Eds.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2014; Volume 1. [Google Scholar] [CrossRef]
- Schmitt, S.A.; McClelland, M.M.; Tominey, S.L.; Acock, A.C. Strengthening school readiness for Head Start children: Evaluation of a self-regulation intervention. Early Child. Res. Q. 2015, 30, 20–31. [Google Scholar] [CrossRef]
- Miyake, A.; Friedman, N.P.; Emerson, M.J.; Witzki, A.H.; Howerter, A.; Wager, T. The unity and diversity of executive functions and their contributions to complex “frontal lobe” tasks: A latent variable analysis. Cogn. Psychol. 2000, 41, 49–100. [Google Scholar] [CrossRef]
- Diamond, A. Executive functions. Annu. Rev. Psychol. 2012, 64, 135–154. [Google Scholar] [CrossRef]
- Friedman, N.P.; Miyake, A. Unity and diversity of executive functions: Individual differences as a window on cognitive structure. Cortex 2017, 86, 186–204. [Google Scholar] [CrossRef]
- Almazova, O.V.; Buhalenkova, D.A.; Veraksa, A.N.; Jakupova, V.A. The connection of the theory of consciousness and executive functions in senior preschool age. Psychol. Pedagog. 2018, 8, 293–311. [Google Scholar]
- Clements, D.H.; Sarama, J.; Germeroth, C. Learning executive function and early mathematics: Directions of causal relations. Early Child. Res. Q. 2016, 36, 79–90. [Google Scholar] [CrossRef]
- Best, J.R.; Miller, P.H.; Naglieri, J.A. Relations between executive function and academic achievement from ages 5 to 17 in a large, representative national sample. Learn. Individ. Differ. 2011, 21, 327–336. [Google Scholar] [CrossRef]
- Aben, B.; Stapert, S.; Blokland, A. About the distinction between working memory and short-term memory. Front. Psychol. 2012, 3, 1–9. [Google Scholar] [CrossRef]
- Cain, K. Individual differences in children’s memory and reading comprehension: An investigation of semantic and inhibitory deficits. Memory 2006, 14, 553–569. [Google Scholar] [CrossRef] [PubMed]
- Oakhill, J.V.; Cain, K.; Bryant, P.E. The dissociation of word reading and text comprehension: Evidence for component skills. Lang. Cogn. Process. 2003, 18, 443–468. [Google Scholar] [CrossRef]
- Bull, R.; Espy, K.A.; Wiebe, S.A. Short-term memory, working memory, and executive functioning in preschoolers: Longitudinal predictors of mathematical achievement at age 7 years. Dev. Neuropsychol. 2008, 33, 205–228. [Google Scholar] [CrossRef] [PubMed]
- Espy, K.A.; McDiarmid, M.M.; Cwik, M.F.; Stalets, M.M.; Hamby, A.; Senn, T.E. The Contribution of Executive Functions to Emergent Mathematic Skills in Preschool Children. Dev. Neuropsychol. 2004, 26, 465–486. [Google Scholar] [CrossRef] [PubMed]
- Bull, R.; Scerif, G. Executive functioning as a predictor of children’s mathematics ability: Inhibition, switching, and working memory. Dev. Neuropsychol. 2001, 19, 273–293. [Google Scholar] [CrossRef]
- Kyttala, M.; Aunio, P.; Lehto, J.E.; Van Luit, J.; Hautamaki, J. Visuospatial working memory and early numeracy. Educ. Child Psychol. 2003, 20, 65–76. [Google Scholar]
- Duncan, G.J.; Dowsett, C.J.; Claessens, A.; Magnusen, K.; Huston, A.C.; Klebanov, P.K.; Brooks-Gunn, J. School readiness and later achievement. Dev. Psychol. 2007, 43, 1428–1446. [Google Scholar] [CrossRef]
- Aunola, K.; Leskinen, E.; Lerkkanen, M.-K.; Nurmi, J.-E. Developmental dynamics of math performance from preschool to grade 2. J. Educ. Psychol. 2004, 96, 699–713. [Google Scholar] [CrossRef]
- Jarvis, H.L.; Gathercole, S.E. Verbal and nonverbal working memory and achievements on national curriculum tests at 7 and 14 years of age. Educ. Child Psychol. 2003, 20, 123–140. [Google Scholar]
- McLean, J.F.; Hitch, G.J. Working memory impairments in children with specific arithmetic learning difficulties. J. Exp. Child Psychol. 1999, 74, 240–260. [Google Scholar] [CrossRef] [PubMed]
- Swanson, H.L.; Sachse-Lee, C. Mathematical problem solving and working memory in children with learning disabilities: Both executive and phonological processes are important. J. Exp. Child Psychol. 2001, 79, 294–321. [Google Scholar] [CrossRef] [PubMed]
- Gathercole, S.E.; Pickering, S.J.; Knight, C.; Stegman, Z. Working memory skills and educational attainment: Evidence from National Curriculum assessments at 7 and 14 years of age. Appl. Cogn. Psychol. 2004, 18, 1–16. [Google Scholar] [CrossRef]
- Florit, E.; Roch, M.; Altoe, G.; Levorato, M.C. Listening comprehension in preschoolers: The role of memory. Br. J. Dev. Psychol. 2009, 27, 935–951. [Google Scholar] [CrossRef] [PubMed]
- Bruner, J. Processes of Cognitive Growth: Infancy (Heinz Werner Lectures); Clark University Press: Worcester, UK, 1968; pp. 19–54. [Google Scholar]
- Vygotskij, L.S. The Dynamics of the Mental Development of a Student in Connection with Learning. In Mental Development of Children in the Learning Process; Vygotskij, L.S., Ed.; GIS: Moscow, Russia, 1935; pp. 33–52. [Google Scholar]
- Gorev, P.M. Napravlenija sovershenstvovanija shkol’nogo matematicheskogo obrazovanija. [Directions of the modern math education at schools]. Math. Bull. Pedagog. Inst. Univ. Volga-Vyatka Reg. 2015, 17, 224–236. [Google Scholar]
- Veraksa, A.; Veraksa, N. Symbolic representation in early years learning: The acquisition of complex notions. Eur. Early Child. Educ. Res. J. 2016, 3, 1–16. [Google Scholar] [CrossRef]
- Venger, L.A.; D’jachenko, O.M.; Astas’kova, N.F.; Bardina, R.I. Program: Gifted Child; Novaja Shkola: Moscow, Russia, 1995. [Google Scholar]
- Venger, L.A. The Development of Spatial Modeling Abilities. In Development of the Ability for Visual and Spatial Modeling; Venger, L.A., Ed.; Doshkol’noe Vospitanie: Moscow, Russia, 1982; Volume 9, pp. 4–5. [Google Scholar]
- Zhujkova, T.P. Characterization of the Modeling Method in the Formation of Spatial Representations in Children of Preschool Age. In Proceedings of the Actual Problems of Pedagogy, the Second International Scientific Conference, Chita, Russia, 23 May 2012; Available online: https://moluch.ru/conf/ped/archive/59/2408/ (accessed on 12 March 2019).
- Galperin, P.J. A General View of the Doctrine of the So-Called Phased Formation of Mental Actions, Ideas and Concepts; Stepanova, M.A., Ed.; Moscow University Psychology Bulletin: Moscow, Russia, 1998; Volume 2, pp. 3–8. [Google Scholar]
- Talyzina, N.F. Knowledge Management; MSU: Moscow, Russia, 1984; p. 344. [Google Scholar]
- Korkman, M.; Kirk, U.; Kemp, S.L. NEPSY II. Administrative Manual; Psychological Corporation: San Antonio, TX, USA, 2007; p. 228. [Google Scholar]
- Zelazo, P.D. The Dimensional Change Card Sort (DCCS): A method of assessing executive function in children. Nat. Protoc. 2006, 1, 297–301. [Google Scholar] [CrossRef]
- Veraksa, A.N.; Almazova, O.V.; Bukhalenkova, D.A. Diagnostics of regulatory functions in senior preschool age: A battery of methods and norms. Natl. Psychol. J. 2020. Pre Print. [Google Scholar]
- Pogozhina, I.N. Specific Features of the Relationships between Operational Structures within Preschoolers’ Systems of Tough. Psychol. Russ. State Art 2018, 3, 183–194. [Google Scholar] [CrossRef]
- Clements, D.H.; Sarama, J. Learning Executive Function and Early Mathematics. In Mathematical Instruction for Perseverance Collected Papers; Kurose, C., Albert, N., Eds.; Spencer Foundation: Chicago, IL, USA, 2015; p. 20. [Google Scholar]
- Ramani, G.B.; Brownell, C.A. Preschoolers’ cooperative problem solving: Integrating play and problem solving. J. Early Child. Res. 2014, 12, 92–108. [Google Scholar] [CrossRef]
- Ramani, G.B.; Siegler, R.S. Promoting broad and stable improvements in low-income children’s numerical knowledge through playing number board games. Child Dev. 2008, 79, 375–394. [Google Scholar] [CrossRef] [PubMed]
- Salmina, N.G.; Forero Navas, I. Maths. Teacher Manual; Talyzina, N.F., Ed.; Didakt: Moscow, Russia, 1994; p. 128. [Google Scholar]
- El’konin, D.B. Action as a unit of development. Vopr. Psihol. 2004, 1, 35–49. [Google Scholar]
- El’konin, D.B. Play Psychology, 2nd ed.; VLADOS: Moscow, Russia, 1999; p. 360. [Google Scholar]
- Van Oers, B. Learning resources in the context of play. Promoting effective learning in early childhood. Eur. Early Child. Educ. Res. J. 2003, 11, 7–26. [Google Scholar] [CrossRef]
- Lillard, A. Pretend play skills and the child’s theory of mind. Child Dev. 1993, 64, 348–371. [Google Scholar] [CrossRef]
- Dubrovina, I.V. Psychological problems of education of children and schoolchildren in the conditions of the information society. Natl. Psychol. J. 2018, 1, 6–16. [Google Scholar] [CrossRef]

| Low CP Level (n = 37) | Medium CP Level (n = 52) | High CP Level (n = 37) | The Significance of Differences | |
|---|---|---|---|---|
| M ± SD | M ± SD | M ± SD | H-criterion p-value | |
| Verbal STM (SR) | 17.95 ± 4.5 | 19.00 ± 4.6 | 19.58 ± 4.6 | H = 2.933; p = 0.231 |
| Visual STM (MD Total) | 62 ± 13.7 | 75.71 ± 19.4 | 82 ± 18.6 | H = 21.83; p < 0.001 |
| Cognitive flexibility (DCCS) | 18.11 ± 2.2 | 18.9 ± 3.0 | 19.22 ± 2.8 | H = 14.448; p = 0.049 |
| Naming, uncorrected mistakes | 0.86 ± 1.5 | 0.52 ± 1.0 | 0.5 ± 0.8 | H = 0.469; p = 0.791 |
| Naming, corrected mistakes | 1.16 ± 1.2 | 0.85 ± 0.95 | 0.83 ± 0.73 | H = 1.083; p = 0.582 |
| Naming, time | 54.89 ± 14.6 | 47.29 ± 10.8 | 46.35 ± 9.5 | H = 9.23; p = 0.01 |
| Inhibition, uncorrected mistakes | 4.27 ± 7.05 | 4.88 ± 10.07 | 3.16 ± 6.9 | H = 5.585; p = 0.061 |
| Inhibition, corrected mistakes | 1.84 ± 1.7 | 2.13 ± 1.8 | 1.86 ± 1.5 | H = 0.533; p = 0.766 |
| Inhibition, time | 69.57 ± 17.5 | 61.62 ± 12.6 | 63.41 ± 17.2 | H = 6.28; p = 0.043 |
| Traditional Approach | Contextual Approach | Modeling Approach | ||
|---|---|---|---|---|
| High CP level | Frequency | 8 | 6 | 11 |
| % | 32% | 24% | 44% | |
| Average CP level | Frequency | 12 | 12 | 10 |
| % | 35% | 35% | 29% | |
| Low CP level | Frequency | 9 | 8 | 6 |
| % | 39% | 34% | 26% | |
| Chi-square = 4.672; p = 0.256 | ||||
| Traditional Approach | Contextual Approach | Modeling Approach | Kruskal–Wallis Criterion, Significance Level | |
|---|---|---|---|---|
| M ± SD | M ± SD | M ± SD | Chi-square = 2.852 | |
| Total pre-test score | 4.36 ± 2.6 | 3.4 ± 2.6 | 3.7 ± 2.7 | p = 0.240 |
| High CP Level (Mean Value, Standard Deviation) | Low CP Level (Mean Value, Standard Deviation) | Mann–Whitney Criterion, Significance Level | |
|---|---|---|---|
| M ± SD | M ± SD | ||
| Total pre-test score | 4.77 ± 2.4 | 3.15 ± 2.5 | U = 779.0 p = 0.008 |
| Score for the first part of the post-test | 5.23 ± 2.4 | 3.7 ± 2.7 | U = 206.5 p = 0.061 |
| Total score for the post-test | 7.31 ± 2.9 | 5.78 ± 3.3 | U = 218.0 p = 0.102 |
| Score for the first part of the delayed post-test | 5.33 ± 2.3 | 4.08 ± 3.3 | U = 245.5 p = 0.088 |
| Total score for the delayed post-test | 7.81 ± 2.7 | 6.28 ± 3.4 | U = 241.5 p = 0.077 |
| Study Approach | Score for the First Part of the First Final Test M ± SD | Score for the First Part of the Delayed Final Test M ± SD | Total Score of the First Final Test M ± SD | Total Score of the Delayed Final Test M ± SD | |
|---|---|---|---|---|---|
| High CP level | Traditional | 5.25 ± 1.75 | 5.75 ± 2.32 | 7 ± 1.93 | 8.13 ± 2.48 |
| Contextual | 5.0 ± 3.08 | 4.4 ± 2.61 | 7.4 ± 3.36 | 7.0 ± 2.92 | |
| Modeling | 5.31 ± 2.72 | 5.43 ± 2.41 | 7.46 ± 3.43 | 7.93 ± 3.05 | |
| Average CP level | Traditional | 5.7 ± 2.16 | 6.27 ± 2.24 | 7.2 ± 2.66 | 8.45 ± 2.98 |
| Contextual | 3.92 ± 2.99 | 4 ± 3.05 | 6.08 ± 2.99 | 6 ± 3.36 | |
| Modeling | 3.75 ± 3.2 | 4.36 ± 2.62 | 6 ± 3.81 | 6.55 ± 2.98 | |
| Low CP level | Traditional | 3.7 ± 2.93 | 3.6 ± 3.17 | 6 ± 3.64 | 6 ± 3.65 |
| Contextual | 3.89 ± 2.93 | 5.5 ± 3.34 | 6.11 ± 3.26 | 7.88 ± 3.52 | |
| Modeling | 3 ± 2.55 | 3.14 ± 2.193 | 4.2 ± 3.271 | 4.86 ± 2.41 |
| Teaching Approach | Differences in the First Final Test Scores with Similar Pre-Test Tasks | F Friedman Significance | Differences in the Delayed Final Test Scores of with Similar Pre-Test Tasks | F Friedman Significance | ||||
|---|---|---|---|---|---|---|---|---|
| High CP level | Medium CP level | Low CP level | High CP level | Medium CP level | Low CP level | |||
| M ± SD | M ± SD | M ± SD | F; p-Value | M ± SD | M ± SD | M ± SD | F; p-Value | |
| Traditional approach | 0.25 ± 2.05 | 0.7 ± 2.16 | 1.55 ± 2.96 | F = 2.000 p = 0.157 | 0.75 ± 2.25 | 1.1 ± 2.7 | 1.5 ± 3.4 | F = 1.190 p = 0.275 |
| Contextual approach | 0.2 ± 2.2 | 1.1 ± 2.79 | 0.01 ± 3.0 | F = 0.800 p = 0.371 | 0.8 ± 2.04 | 0.83 ± 2.7 | 2.1 ± 3.09 | F = 0.889 p = 0.376 |
| Modeling approach | 0.69 ± 2.8 | − 0.17 ± 2.79 | 0.6 ± 3.57 | F = 0.727 p = 0.394 | 0.92 ± 2.9 | 0.1 ± 2.02 | 1.15 ± 3.28 | F = 2.130 p = 0.144 |
| Total | 0.46 ± 2.4 | 0.57 ± 2.6 | 0.73 ± 3.04 | F = 3.276 p = 0.071 | 0.85 ± 5.53 | 0.72 ± 2.49 | 1.6 ± 3.16 | F = 4.126 p = 0.042 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veraksa, A.N.; Aslanova, M.S.; Bukhalenkova, D.A.; Veraksa, N.E.; Liutsko, L. Assessing the Effectiveness of Differentiated Instructional Approaches for Teaching Math to Preschoolers with Different Levels of Executive Functions. Educ. Sci. 2020, 10, 181. https://doi.org/10.3390/educsci10070181
Veraksa AN, Aslanova MS, Bukhalenkova DA, Veraksa NE, Liutsko L. Assessing the Effectiveness of Differentiated Instructional Approaches for Teaching Math to Preschoolers with Different Levels of Executive Functions. Education Sciences. 2020; 10(7):181. https://doi.org/10.3390/educsci10070181
Chicago/Turabian StyleVeraksa, Aleksander N., Margarita S. Aslanova, Daria A. Bukhalenkova, Nikolay E. Veraksa, and Liudmila Liutsko. 2020. "Assessing the Effectiveness of Differentiated Instructional Approaches for Teaching Math to Preschoolers with Different Levels of Executive Functions" Education Sciences 10, no. 7: 181. https://doi.org/10.3390/educsci10070181
APA StyleVeraksa, A. N., Aslanova, M. S., Bukhalenkova, D. A., Veraksa, N. E., & Liutsko, L. (2020). Assessing the Effectiveness of Differentiated Instructional Approaches for Teaching Math to Preschoolers with Different Levels of Executive Functions. Education Sciences, 10(7), 181. https://doi.org/10.3390/educsci10070181







