Abstract
The Traveling Salesman and Vehicle Routing Problems are integral parts of bachelor and master programs related to Operations Research/Management Science. This is due to their relevance in both practical applications and research. For students, it is essential to gain a deep understanding of the problems’ inherent complexity. For this, several tools are available online. A systematic classification of both the Traveling Salesman Problem (TSP) and Vehicle Routing Problem (VRP) teaching material is provided and discussed. This classification takes target groups as well as learning objectives into account. Recommended choices depending on the teaching context are provided. A special focus lies on interactive visualizations, which seem to be most useful for supporting students in their solution-oriented competencies. We observe that didactic visualization tools for vehicle routing are scarce. This is surprising since, in practice, this problem is prevalent.
1. Introduction
Vehicle routing is a core component of today’s logistics operations. The Traveling Salesman Problem (TSP) and its generalization, the Vehicle Routing Problem (VRP), aim at finding optimal routes for fleets of vehicles that have to visit customers. Seminal work goes back to, e.g., [1,2,3], while in [4], a state-of-the-art classification and review is provided.
While in TSP, only one vehicle is considered, VRPs deal with the multiple-vehicle case. Both the TSP and VRP are -hard combinatorial optimization problems. Special classes of the VRP include the periodic VRP (PVRP), the multi-depot VRP (MDVRP), the VRP with time windows (VRPTW), the capacitated VRP (CVRP), and the VRP with pickup and delivery locations (VRPPDP). These classes differ in the frequency customers with which have to be visited (PVRP), the number of available depots (MDVRP), customer requirements like time windows (VRPTW), vehicle capacities (CVRP), or specific origin and destination locations (VRPPDP). For a state-of-the-art classification and extensive review, readers are referred to [4].
Due to their great relevance in practice, routing problems are an integral part of bachelor and master programs related to Operations Research/Management Science ([5,6]). The authors of [5] observe that the TSP is such a classical problem in Operations Research that it can play a central role in an undergraduate course about integer programming. In academic literature, TSPs and VRPs have been studied for several decades ([4]). The combinatorial complexity of these problems demands a practical and comprehensible visualization for teaching purposes. This is emphasized by [5], who claim that nothing humbles a graduate student so quickly as a brutally difficult problem. Without any digital tools, only very small instances can be analyzed in the classroom. These are typically too small to give students the right impression of their computational complexity [5].
TSPs and, even more, VRPs are clearly in this category of problems. While several teaching tools for the TSP do exist, applications that support scholars in teaching VRPs are very rare. This is surprising, since carriers typically own more than one vehicle. Hence, the VRP can be considered the more practically relevant planning problem.
In our study, we review existing online applications that can be used to visualize routing problems suitable for teaching purposes. We elaborate on the necessity of convenient and simple tools that support students to gain a deep understanding of the problems’ inherent complexity. We show that, particularly for VRPs, there is a clear lack of available software for didactic visualization. We recommend the closing of this gap by interactive but simple visualization tools.
2. Basics of the Traveling Salesman Problem
The TSP is a cost- or distance-minimizing single-vehicle routing problem, where n locations have to be visited exactly once before the vehicle returns to its origin. In addition to being used for transportation logistics, the TSP can be the underlying model in job sequencing (e.g., [7]), order picking (e.g., [8]), clustering of data arrays (e.g., [9]), or computer wiring (e.g., [10]), amongst others.
While the TSP had already been mentioned in the 1930s, it became very popular in the 1950s and 1960s (e.g., [1,2,3]). The problem with a plethora of variants has been intensively researched ever since [11].
The TSP can be mathematically formulated on a complete graph with a set of V vertices and a set of A arcs. The costs of traversing arc are represented by . We are facing a symmetric TSP if equals for each pair of nodes. Otherwise, it is known as an asymmetric TSP. Although the symmetric TSP can be tackled with formulations of the asymmetric TSP, it is more efficient to separate these two cases by assuming symmetric or asymmetric (i.e., ) cost matrices, respectively. The decision variable becomes 1 if arc is used, and 0 otherwise. The asymmetric problem can be formulated as follows [12]:
The objective function (1) minimizes total cost by multiplying transportation costs or distances with the decision variable . Constraints (2) state that each vertex j is entered by exactly one arc, while Constraints (3) give that, in the solution, each vertex i can be left by exactly one arc. The connectivity constraints given in (4) eliminate subtours, where less than vertices are visited within a tour. These constraints can be replaced by algebraically equivalent subtour elimination constraints:
It should be noted that subtour elimination constraints are needed [12].
Constraints (5) indicate the binary property of the decision variables.
For the symmetric problem, where , is considered an edge with , which supports efficient solution approaches [12].
Over the last decades, a vast number of both exact and heuristic solution methods have been introduced. It is known that instances with more than 85,000 nodes can be solved to optimality by using well-established open-source code, e.g., Concorde TSP Solver (http://www.math.uwaterloo.ca/tsp/concorde.html). It is worth mentioning that Concorde provides an app available for smartphones and tablets (https://apps.apple.com/at/app/concorde-tsp/id498366515). The app includes several helpful features, including solution process visualizations. Due to its strict hardware requirements, the usability in the classroom might be limited. However, instructors might encourage students to download the app in order to assess their problem-solving capabilities. Concorde supports the QSopt linear programming solver, and the callable library includes over 700 functions that permit users to create specialized codes for TSP-like problems.
3. Basics of the Vehicle Routing Problem
The classical VRP, as the multi-vehicle generalization of the TSP, was first mentioned in [2]. It is known to be one of the most studied combinatorial optimization problems in transportation logistics. The VRP aims at finding optimal routes for a fleet of vehicles in order to serve all required customers. Vehicles start and end at a depot [13]. Note that a single-vehicle VRP corresponds to the TSP.
While a typical objective of the VRP is the minimization of transportation costs, other objectives can be the minimization of the number of vehicles used, balancing the routes regarding travel time and vehicle load, or the minimization of penalties linked to unfulfilled customer service [14]. A very common assumption is that load capacities are restricted, which is referred to as the capacitated VRP (CVRP). Other well-known extensions and variations are the VRP with multiple depots, the VRP with backhauls, the VRP with time windows, the VRP with pickup and delivery, and combinations of the above [4].
The following model mathematically formulates the CVRP. All vehicles start from a central depot (denoted as 0) and have the same limited capacity. All customers, of whom each has a given demand, have to be served. The objective of the CVRP is to minimize total travel cost [14].
The objective function (7) minimizes total transportation cost. Constraints (8) and (9) ensure that vehicles enter and leave nodes using exactly one arc per node. By this, it is guaranteed that each customer is served. The degree requirements, (10) and (11), determine that K vehicles leave the depot and return to it. Given this formulation, K vehicles have to be used, resulting in K routes. Other formulations, where less than K vehicles or routes are allowed, do exist. The capacity-cut Constraints (12) eliminate subtours, since is the minimum number of vehicles required to serve all customer demands of subset S with a fleet of vehicles with capacity C. Finally, Constraints (13) indicate the binary property of the decision variables.
The literature includees numerous exact and heuristic solution approaches for the CVRP. The interested reader is referred to a recent survey provided by [4].
4. Review of Existing Tools
Both the TSP and VRP are core components of quantitative-oriented academic bachelor and master courses on Operations Management all over the world [15]. The authors of [6] list the TSP and VRP among three central topics in their course on computational discrete optimization for senior-level undergraduate students.
The most prevalent field of application lies in transportation logistics. However, production planners also have to deal with the TSP or VRP. Optimization of drilling processes in semiconductor manufacturing, for instance, can be modeled as a TSP (e.g., [16]).
For teaching purposes, it is essential to transfer the problem’s inherent complexity into the classroom. Students have to understand the difficulties of combinatorial explosions. For TSP, it is known that for problems with n customers, there are possible sequences of visiting them. Thus, if a problem with three customers (1,2,3) and one depot (D) is to be solved, there are six different routes, i.e., (D-1-2-3-D), (D-1-3-2-D), (D-2-1-3-D), (D-2-3-1-D), (D-3-1-2-D), and (D-3-2-1-D). Obviously, a complete enumeration of all possible solutions is easy to perform. However, if the number of customers increases to 10, we are facing 3,628,800 possible tours. Thus, complete enumeration is not an option for larger problem sizes. Note that VRPs are even more complex, since not only the sequencing of customers, but also the assignment of customers to vehicles or tours has to be tackled. Typically, case studies, precomputed solutions, or optimization solvers are used for didactic purposes (e.g., [6,17]). The authos of [5] give suggestions for pedagogical devices, homework assignments and exams, PowerPoint® presentations, and a convenient package of AMPL (https://ampl.com/) models and scripts. They discuss scripts for visualization of the TSP solutions. In their paper, they place a special focus on these visualizations, which are intended to provide convenient ways for students to view and report their solutions. However, AMPL programming skills are required. The authors observe that Google (www.google.com) reports 115,000 hits for the search “edu traveling salesman problem”. An overview of key educational sites that are appropriate for third- or fourth-year students is provided. We observe that none of the websites listed as aiming at TSP visualization are accessible anymore.
However, in order to support students in handling the complexity, didactic visualization tools appear to be of great value [5]. In our study, we survey and categorize tools available online by the following classification: (i) Videos, puzzles, and games, (ii) solver-based applications, and (iii) interactive route generation.
4.1. Videos, Puzzles, and Games
DePuy [18] suggested the illustration of TSP to students using scenes from the 2014 movie Guardians of the Galaxy. One of the characters, Yondu Udonta, is equipped with a hover-dart. This dart is used by Yondu in self-defense against aliens. The authors refer to a scene where Yondu sends forth the dart in a TSP-like tour that enables it to meet, i.e., kill, each of the offending aliens and to return to Yondu in the most efficient way possible. They suggest the use of this within a student workshop to demonstrate the use of the TSP.
A chain-reaction puzzle available online is used by [19] as a precursor to a discussion of the TSP and its IP formulation. In Figure 1, we illustrate a possible 3 × 3 chain-reaction puzzle as it is used in [19]. Users should form a chain that visits every symbol once (starting from x), where each link in the chain connects two symbols that match either by shape or color. Moves are only allowed to adjacent cells. On the right, we show the solution: Numbers give the sequence of visiting cells.
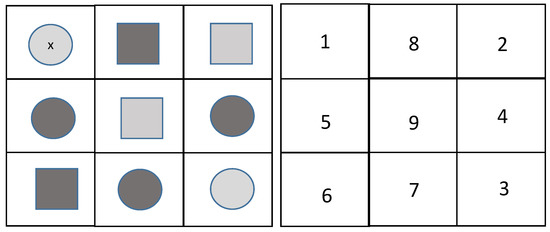
Figure 1.
Traveling Salesman Problem (TSP)-related chain-reaction puzzle as proposed in [19].
The authors explain that students can quickly see how the formulation increases in size as more moves are possible (as is the case with a TSP) and the dimensions of the puzzle board increase.
The proposed puzzle can be seen as a TSP that has to be solved on a sparse matrix, since many moves are forbidden. In the online application discussed by [19], it is not required to return to the depot. Thus, it does not have the full complexity of a TSP. This can, however, easily be adapted by adding a constraint indicating that the last move has to end at the starting point. We recommend the use of this or similar puzzles in bachelor courses, where the learning objective is that students capture the combinatorial explosion of routing (or related) problems.
For the VRP, suitable teaching material is scarce. The authors of [20] present an elaborate case study for teaching the CVRP in undergraduate- and graduate-level transportation and logistics or optimization courses. The objective of the case is to provide students with hands-on experience developing and applying solution techniques for a large unstructured VRP. The students are supposed to learn how to extend and implement VRP techniques learned in class for a problem of realistic size. Another VRP case study is presented by [21].
4.2. Solver-Based Applications
TSP Solve (https://tspsolve.com/), as well as TSP tools provided by Gurobi (http://examples.gurobi.com/traveling-salesman-problem) or Google (https://developers.google.com/optimization/routing/tsp), are examples of online applications for solving TSP based on given coordinates. Typically, users can select cities or points of interest on a map or are able to enter coordinates. For these, solutions are generated. An example is displayed in Figure 2.

Figure 2.
Visualization of a TSP solution (http://examples.gurobi.com/traveling-salesman-problem/).
The ArcGIS Network Analyst extension (https://desktop.arcgis.com/en/) can be used to solve several transportation-network-related problems, including routing problems. Data from real road networks can be generated. However, it should be noted that ArcGIS is proprietary and requires students to acquire profound knowledge on the software. Free and open-source geographical information systems are available, e.g., QGIS (http://plugins.qgis.org/plugins/TSP/).
These applications focus on supporting users in finding good routes rather than on teaching purposes. Users are provided with the solutions, but learning effects on solution methodology are not supported. Generally, Google OR Tools (https://developers.google.com/optimization/routing) is a specialized library providing sample codes for defining routing problems and calling provided solvers. This seems to be helpful in classes focusing on programming skills, but appears to be too sophisticated to deliver basics of routing problems.
A good source for TSP and VRP visualizations is Wolfram Demonstrations Project (http://demonstrations.wolfram.com/), which is a platform for publishing open-code free online interactive resources generated by the Wolfram programming language. According to the website, each demonstration is reviewed and edited by experts with respect to content, clarity, presentation, quality, and reliability. Demonstrations can be run directly from the site or downloaded to the desktop, which requires Wolfram-specific software. In the available repository, several TSP demonstrators and one VRP demonstrator are provided. Users have the possibility to add, remove, or drag nodes. Solutions based on various heuristic algorithms as well as optimal routes can be computed and displayed. The demonstrator provided by [22] enables one to directly compare the routes determined by different algorithms. These can be compared based on solution quality and computational time (see Figure 3). This might be too detailed for bachelor courses, but seems to be helpful tools in master courses, where the objective is to deliver a first experience in computational studies in the field of combinatorial optimization.
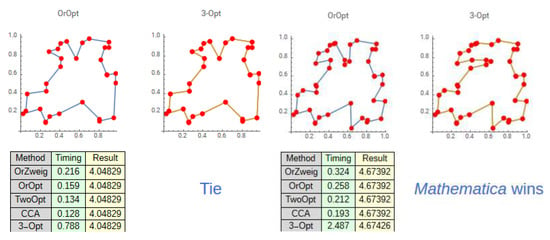
Figure 3.
A TSP demonstrator that enables the comparison of solutions generated by different algorithms [22].
A VRP spreadsheet solver is provided by [23]. The open-source tool solves VRPs and CVRPs with a maximum number of 200 customers. Graph-based solution visualization is supported. Special characteristics, such as pickup and delivery customers or time windows, can be considered as well. In total, 64 different variants are covered. In [23], applications in healthcare and the tourism sector are emphasized. For more details, exemplary illustrations, and video material, we refer to [23] and the author’s website (https://people.bath.ac.uk/ge277/vrp-spreadsheet-solver/). A guided tour on solving TSPs with spreadsheets is provided by [24], whereas the authors of [25] compare different spreadsheet solvers with other general-purpose optimization tools. Again, we recommend these tools for master courses, where students are supposed to gain first experience in computational optimization.
The Larry Snyder VRP solver (https://coral.ise.lehigh.edu/larry/software/vrp-solver/) applies a randomized version of the Clarke–Wright savings algorithm, including various improvement heuristics, such as the well-known two-opt operator. The software enables individual fine-tuning of the provided algorithm. Clearly, this feature is not necessarily required for introductory VRP visualizations, but offers interesting options for advanced users. Customer latitudes and longitudes as well as demands are taken from user-provided text files. Distances can be computed using two different metrics, namely euclidean or great-circle distances. Solutions are displayed in graphical form as well as in text form. While the application seems to be well suited for classroom usage, it might be seen as a drawback that the software has to be downloaded and text files have to be provided. Clearly, the target group includes advanced students with a basic knowledge of heuristics in the field of vehicle routing.
4.3. Interactive Route Generation
An interactive TSP game is provided by [26]. This game offers several features, including the generation of input data, manual generation of routes, and a comparison with exact and heuristic solutions. For the input data, the user can choose among different geographical regions (Africa, Italy, Germany) or an artificial grid. The number of nodes is limited to 50, and three types of distance metrics are available (euclidean, Manhattan, and maximum distance). Once a manual route has been created, the user can compare it to the optimal solution. Description of available algorithms as well as results of each calculation step (e.g., upper bounds and lower bounds) can be displayed. These features are supposed to support students in achieving a deep understanding of standard solution approaches. While the applications discussed in Section 4.1 and Section 4.2 basically focus on capturing the problem’s complexity, the tool provided by [26] appears to support academics in teaching solution methods. It should be mentioned that the solution of each calculation step can be visualized individually. An example is depicted in Figure 4.

Figure 4.
A TSP game that enables one to follow the solution approach step by step ([26]).
Another didactic and interactive TSP game is provided by the University of Vienna (https://prolog.univie.ac.at/tspGame/game.html). Up to 99 nodes can be scattered randomly on the plane. The user interface supports students in adding or removing nodes arbitrarily. Manually generated routes are automatically compared to the optimal solution. The percentage gap is constantly provided, such that the user can try to improve his or her solution towards the optimum. Edges can be repositioned or deleted, which permits an easy modification of the current route. The application automatically highlights edge crossovers, since these are obviously inefficient. By clicking on the marked crossing, this inefficiency is dissolved by connecting one of the crossed edges to an alternative node. For users who want to be guided towards the optimal solution, the “auto” feature is provided. By clicking it, the current route is incrementally improved until the optimal solution is reached. If desired, the optimal solution can be displayed at any point of the game. The user interface is displayed in Figure 5 (https://prolog.univie.ac.at/tspGame/game.html).
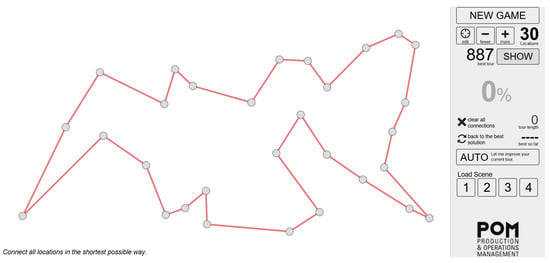
Figure 5.
A TSP game provided by the University of Vienna.
To the best of our knowledge, only very few didactic tools for the VRP exist. This is surprising since, in practice, VRP problems are clearly more relevant. In Figure 6, we display a VRP game, which is again provided by the University of Vienna (https://prolog.univie.ac.at/tspGame/vrp_en.html).

Figure 6.
A Vehicle Routing Problem (VRP) game provided by the University of Vienna.
This application focuses on a user-friendly visualization for introductory courses. Students are enabled to manually generate routes for a user-defined number of nodes and vehicles. Through this, they get used to the additional complexity of the VRP. Generally, the didactic visualization tools discussed in this section are recommended for bachelor courses, where the learning objective is to gain first insights on the problems’ inherent complexity.
5. Comparison and Recommendations
In this section, a comparison of visualization tools with regard to (i) the type of the routing problem, (ii) target group, and (iii) learning objective is provided. The aim is to help instructors to decide which tool is most appropriate for his or her class. Regarding the type of routing problem, the TSP and VRP are considered. For the target groups, we distinguish between bachelor and master students, while for the learning objectives, we classify according to the following.
- Complexity: This indicates whether the instructors aim at delivering basic knowledge on complexity theory. If this is the case, students are required to understand complexity classes, particularly -hardness. Furthermore, they will be able to quantify how computational time increases with problem size.
- Implementation: In order to apply these tools, knowledge on solution methods and their coding is required. Students have to acquire at least fundamental implementation skills and be able to conduct numerical analyses.
- Managerial: These courses aim at finding and delivering managerial insights. Students have to fully grasp settings of exemplary cases and analyze them such that meaningful insights can be extracted.
For this comparison, the following tools are considered:
- Chain-reaction puzzle ([19]);
- Case studies ([20,21]);
- TSP tools by Gurobi (http://examples.gurobi.com/traveling-salesman-problem) or Google (https://developers.google.com/optimization/routing/tsp);
- Wolfram Demonstration Project (http://demonstrations.wolfram.com/);
- VRP spreadsheet solver ([23]);
- Freeware solver by Larry Snyder (https://coral.ise.lehigh.edu/larry/software/vrp-solver/);
- Games by TU Munich ([26]) or University of Vienna (https://prolog.univie.ac.at/tspGame/game.html);
- Game by University of Vienna (https://prolog.univie.ac.at/tspGame/vrp_en.html).
In Table 1, these tools are classified according to the criteria listed above.

Table 1.
Comparison of tools according to routing problem (TSP, VRP), course level (Bachelor, Master), and learning objectives (Complexity, Math, Implementation, Managerial).
We observe that tools for both bachelor and master courses are available. However, regarding learning objectives, the portfolio is very limited. All tools can be used to deliver the problems’ inherent complexity, but only one of them (Cases) is suitable for classes, where students are expected to implement solution methods by themselves. Additionally, Cases is explicitly designed for classes where students are expected to discuss managerial insights. We found it surprising to observe that none of the tools require students to formulate the problems mathematically. Clearly, this observation will not hold for courses where TSP or VRP are starting points for even more complex optimization problems. For these courses, it will be necessary to deliver mathematical modeling skills in addition to the visualization tools analyzed here.
For courses where students are supposed to interactively generate routes by themselves, the last two (TSP game and VRP game) are recommended. These tools can be used in all common browsers and do not require set-up effort. Students can play these games without any knowledge on solution methodologies. Students are challenged to find attractive routes by themselves. This piques curiosity on systematic solution procedures.
In addition, Commercial, Snyder, and Wolfram can be used in an interactive way. However, they appear to be a bit less intuitive and user-friendly. Therefore, they require more effort in student instruction and set-up.
Cases and Spreadsheet are most appropriate for students’ projects with a time horizon of several weeks where they are supposed to understand and solve given problem settings.
We recommend Chain in bachelor classes where students are supposed to capture the combinatorial explosion of routing problems.
It can be observed that several tools provide the possibility to visualize different heuristic or exact methods. However, these features do not exist for the VRP. This is a gap worth closing, since, in practice, the VRP is the prevalent problem. An interactive tool that supports didactic visualization of simple VRP heuristics is supposed to be of great value in both bachelor and master courses. Students could, for example, build up initial tours and then improve it stepwise by applying provided local search operators. Clearly, this requires elaborate user interfaces. We hope our study encourages researchers to enhance available tools in this direction.
6. Conclusions
Sustainability goals and increased price pressure force logistics companies to improve their operations’ efficiency. In many cases, the underlying setting belongs to the class of routing problems, the two basic concepts of which are the TSP and VRP. In classes related to Operations Research/Management Science, solution-oriented competencies surrounding these routing problems are regularly required. In order to support students in gaining a deep understanding of the problems’ inherent complexity and appropriate solution methodologies, digital tools seem to be most useful.
We reviewed available online teaching material for the TSP and VRP. For this, we focused on interactive visualizations applicable for classroom purposes. However, videos, puzzles, and cases as well as solver-based applications were also discussed. A systematic classification regarding target groups and learning objectives was provided and discussed. We observed that tools for supporting academics in teaching VRP solution methods are scarce. This is surprising, since, in practice, the VRP is obviously the more relevant problem.
We found that none of the tools analyzed in our study require deep understanding of the underlying mathematical models. However, we concluded that fundamental solution competencies and modeling skills are essential for analyzing more complex but practically very relevant variants like the VRP with time windows, backhauls, or pickup and delivery problems.
We hope that our observations will encourage academics to develop and share online teaching material suitable for supporting students in understanding and solving the VRP and its variants.
Author Contributions
Conceptualization, M.G; methodology, M.G.; software, M.G. and V.K.; validation, M.G. and V.K.; formal analysis, M.G.; investigation, V.K. and M.G.; resources, V.K. and M.G.; writing—original draft preparation, M.G.; writing—review and editing, M.G.; visualization, M.G. and V.K.; supervision, M.G.; project administration, M.G.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dantzig, G.; Fulkerson, R.; Johnson, S. Solution of a Large-Scale Traveling-Salesman Problem. J. Oper. Res. Soc. Am. 1954, 2, 393–410. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Fulkerson, D.R.; Johnson, S.M. On a Linear-Programming, Combinatorial Approach to the Traveling-Salesman Problem. Oper. Res. 1959, 7, 58–66. [Google Scholar] [CrossRef]
- Miller, C.E.; Tucker, A.W.; Zemlin, R.A. Integer Programming Formulation of Traveling Salesman Problems. J. ACM 1960, 7, 326–329. [Google Scholar] [CrossRef]
- Braekers, K.; Ramaekers, K.; Nieuwenhuyse, I.V. The vehicle routing problem: State of the art classification and review. Comput. Ind. Eng. 2016, 99, 300–313. [Google Scholar] [CrossRef]
- Lee, J.; Raffensperger, J.F. Using AMPL for Teaching the TSP. INFORMS Trans. Educ. 2006, 7, 37–69. [Google Scholar] [CrossRef][Green Version]
- Alpers, A.; Trotter, L.E. Teaching Computational Discrete Optimization at the Undergraduate Level. INFORMS Trans. Educ. 2009, 9, 63–69. [Google Scholar] [CrossRef][Green Version]
- Ahmadi, E.; Goldengorin, B.; Süer, G.A.; Mosadegh, H. A hybrid method of 2-TSP and novel learning-based GA for job sequencing and tool switching problem. Appl. Soft Comput. 2018, 65, 214–229. [Google Scholar] [CrossRef]
- Ratliff, H.D.; Rosenthal, A.S. Order-Picking in a Rectangular Warehouse: A Solvable Case of the Traveling Salesman Problem. Oper. Res. 1983, 31, 507–521. [Google Scholar] [CrossRef]
- Lenstra, J.K. Technical Note—Clustering a Data Array and the Traveling-Salesman Problem. Oper. Res. 1974, 22, 413–414. [Google Scholar] [CrossRef]
- Hahsler, M.; Hornik, K. TSP-Infrastructure for the Traveling Salesperson Problem. J. Stat. Softw. 2007, 23, 1–21. [Google Scholar] [CrossRef]
- Laporte, G. Fifty Years of Vehicle Routing. Transp. Sci. 2009, 43, 408–416. [Google Scholar] [CrossRef]
- Ghiani, G.; Laporte, G.; Musmanno, R. (Eds.) Managing Freight Transport. In Introduction to Logistics Systems Management; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; Chapter 6; pp. 318–441. [Google Scholar]
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Irnich, S.; Toth, P.; Vigo, D. The Family of Vehicle Routing Problems. In Vehicle Routing: Problems, Methods, and Applications, 2nd ed.; Toth, P., Vigo, D., Eds.; Number 18 in MOS-SIAM Series on Optimization: Philadelphia, PA, USA, 2014; Chapter 1; pp. 1–23. [Google Scholar]
- Klug, V. Didactic Visualization of the Traveling Salesman Problem and the Vehicle Routing Problem in Teaching. Master’s Thesis, University of Vienna, Vienna, Austria, 2019. [Google Scholar]
- Aoyama, E.; Hirogaki, T.; Katayama, T.; Hashimoto, N. Optimizing drilling conditions in printed circuit board by considering hole quality: Optimization from viewpoint of drill-movement time. J. Mater. Process. Technol. 2004, 155-156, 1544–1550. [Google Scholar] [CrossRef]
- Pataki, G. Teaching Integer Programming Formulations Using the Traveling Salesman Problem. SIAM Rev. 2003, 45, 116–123. [Google Scholar] [CrossRef]
- Chlond, M.J. Puzzle—TSP at the Movies: Yondu’s Dart Problem. INFORMS Trans. Educ. 2016, 16, 110–111. [Google Scholar] [CrossRef][Green Version]
- DePuy, G.W. Puzzle—Chain-Reaction: A Puzzle to Demonstrate TSP Formulation. INFORMS Trans. Educ. 2009, 10, 41–44. [Google Scholar] [CrossRef][Green Version]
- Milburn, A.B.; Kirac, E.; Hadianniasar, M. Case Article—Growing Pains: A Case Study for Large-Scale Vehicle Routing. INFORMS Trans. Educ. 2017, 17, 75–80. [Google Scholar] [CrossRef][Green Version]
- Drake, M. Vehicle Routing at Otto’s Discount Brigade; Pearson: Upper Saddle River, NJ, USA, 2014. [Google Scholar]
- Wu, F. Comparing Algorithms for the Traveling Salesman Problem. Wolfram Demonstration Project. 2011. Available online: https://demonstrations.wolfram.com/ComparingAlgorithmsForTheTravelingSalesmanProblem/ (accessed on 19 June 2020).
- Erdoğan, G. An open source Spreadsheet Solver for Vehicle Routing Problems. Comput. Oper. Res. 2017, 84, 62–72. [Google Scholar] [CrossRef]
- Rasmussen, R. TSP in Spreadsheets—A Guided Tour. Int. Rev. Econ. Educ. 2011, 10, 94–116. [Google Scholar] [CrossRef]
- Rasmussen, R. TSP in spreadsheets—A fast and flexible tool. Omega 2011, 39, 51–63. [Google Scholar] [CrossRef]
- Lotz, W. Lösung und graphische Darstellung des Traveling Salesman Problems in einer Webapplikation. Bachelor’s Thesis, Technical University of Munich, Munich, Germany, July 2014. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).