Concept Mapping in Magnetism and Electrostatics: Core Concepts and Development over Time
Abstract
1. Introduction
1.1. Conceptual Change Theories
1.2. Concept Mapping
1.3. The Present Research
- (a)
- What are the central terms and common misconceptions across time, and how does terms’ centrality differ between the timepoints?
- (b)
- What are the underlying structural properties of the concept maps across the learning process?
- (c)
- Are there differences regarding different types of words used in the concept map?
- (d)
- How do the student concept maps compare to the expert maps?
2. Materials and Methods
2.1. Participants
2.2. Procedure
2.3. Statistical Analyses
3. Results
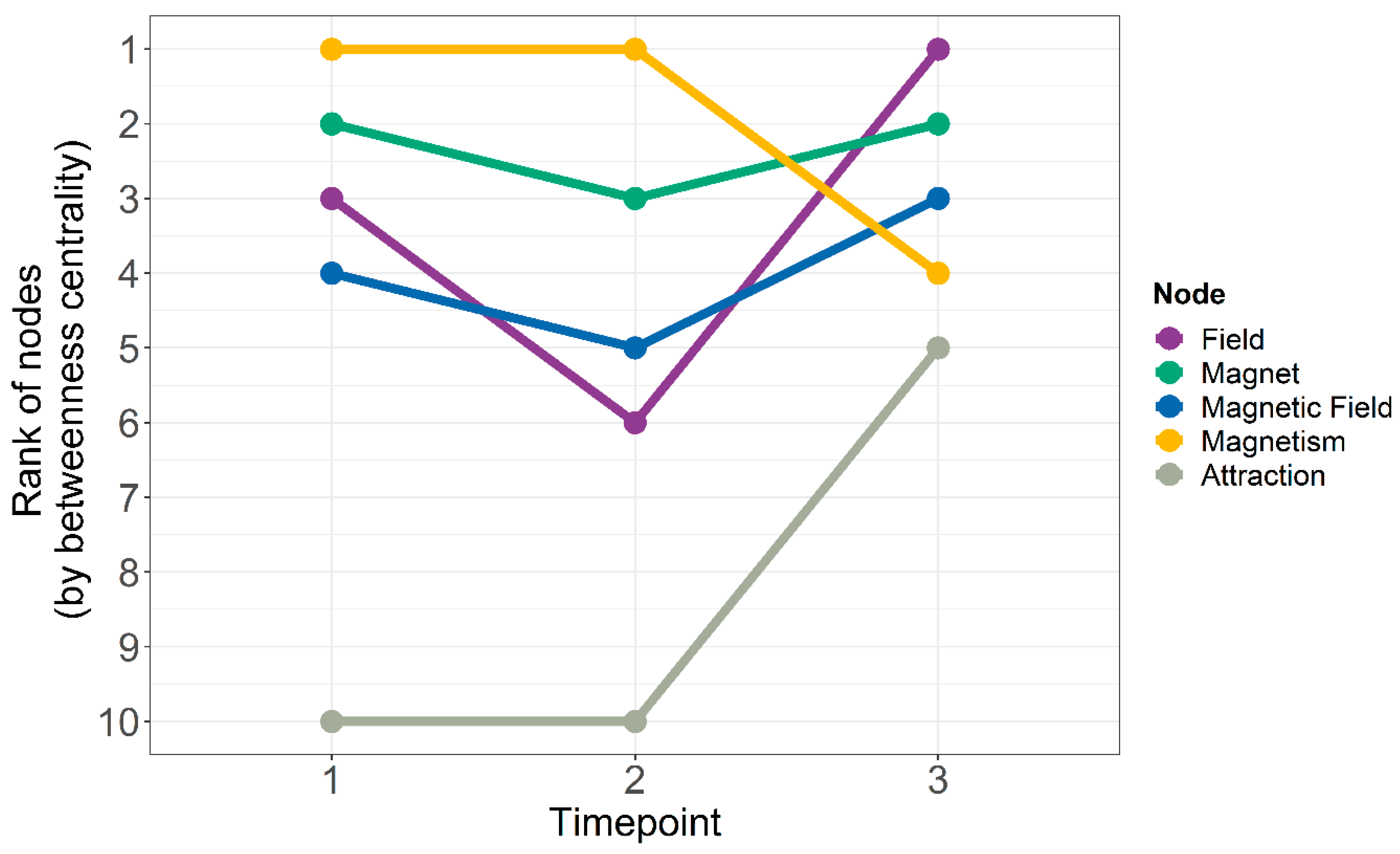
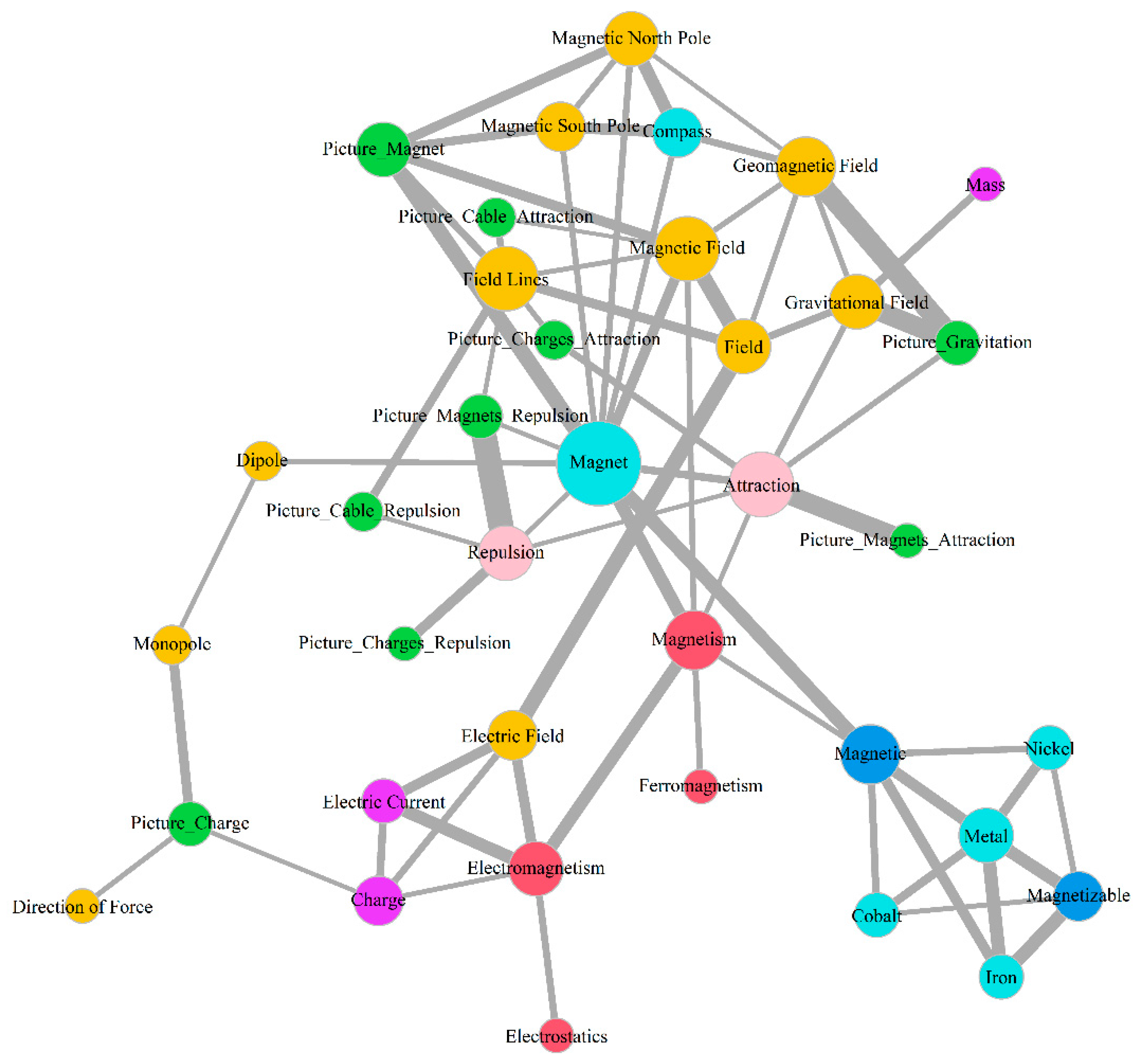
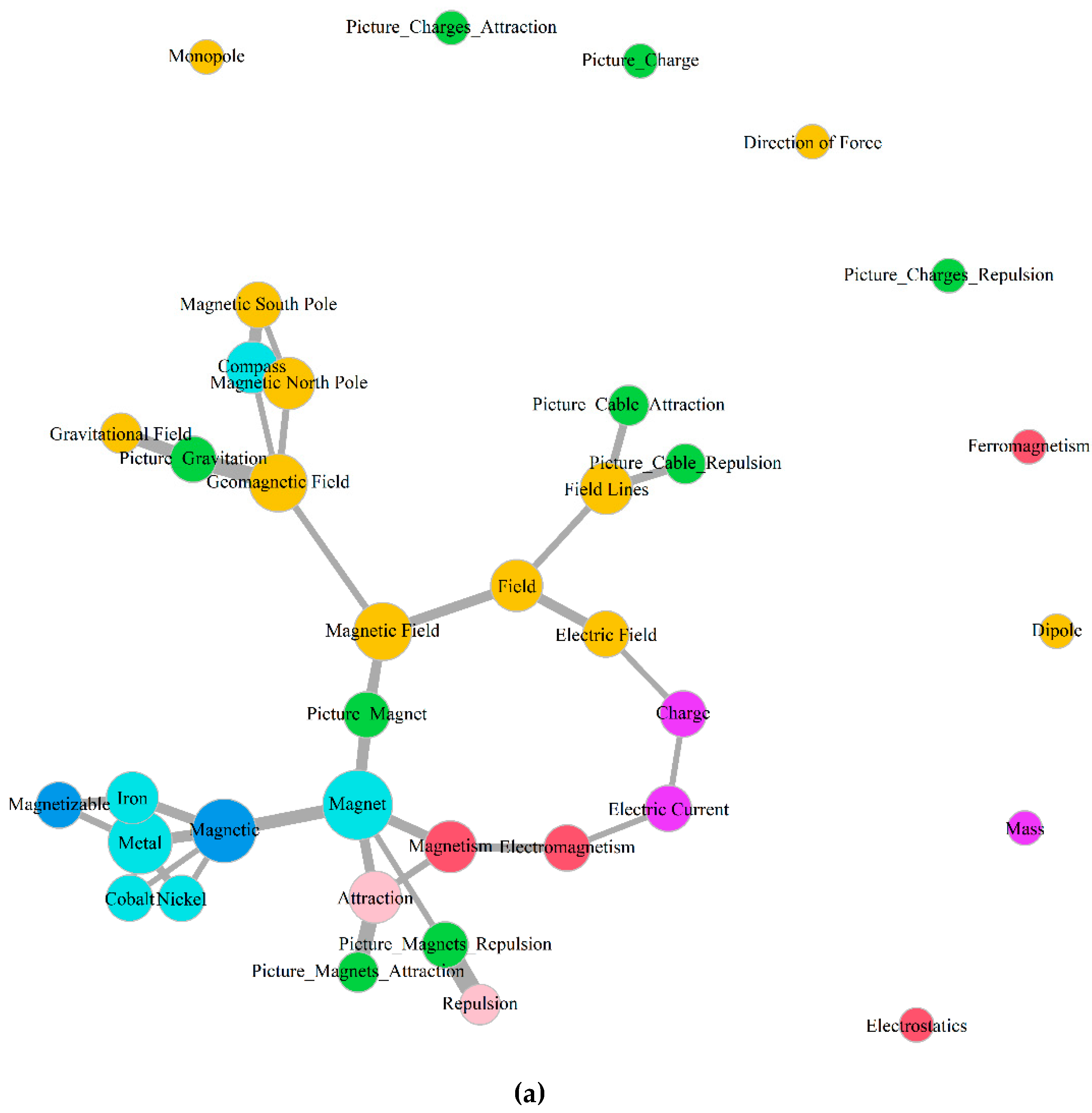
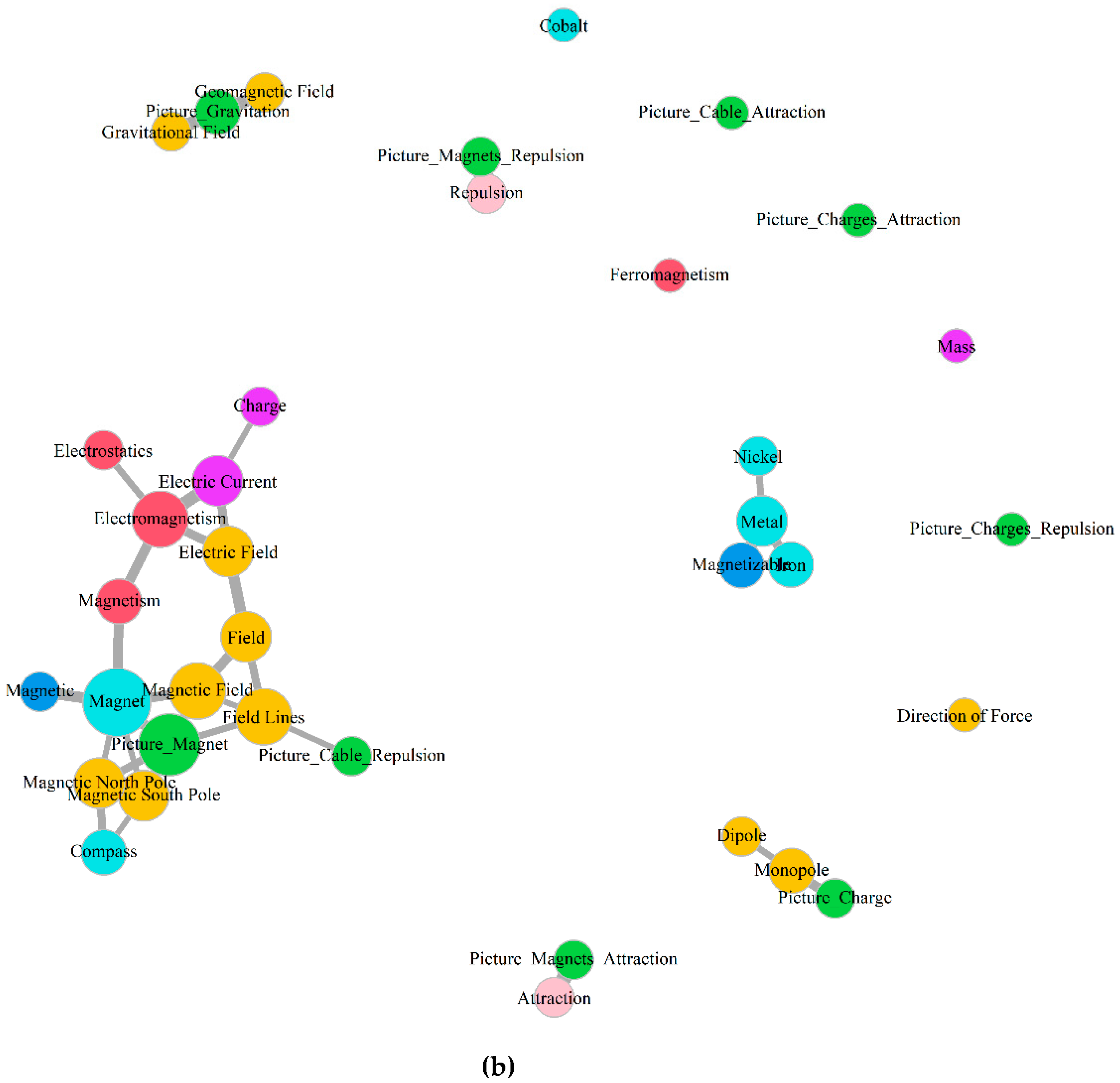
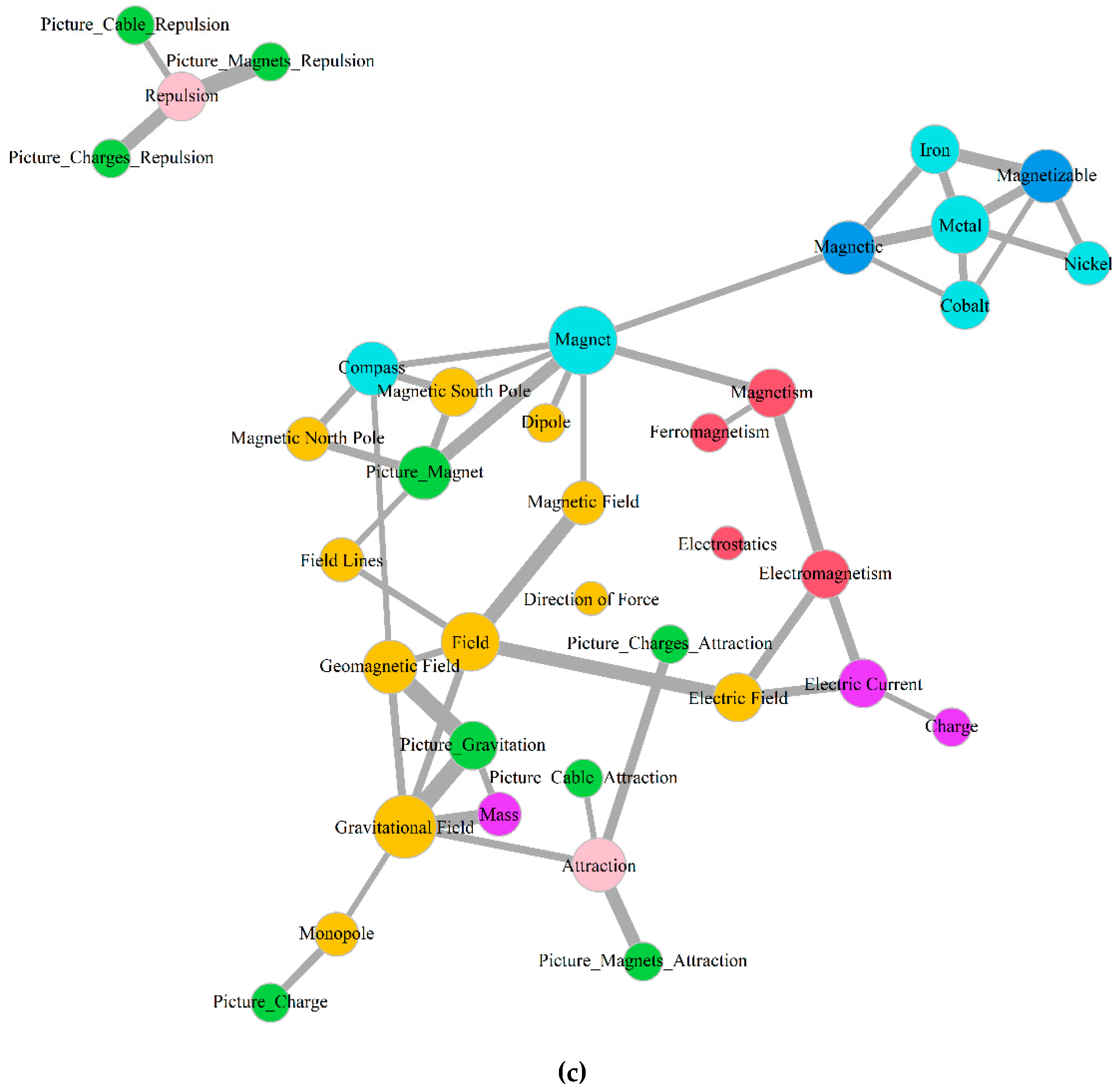
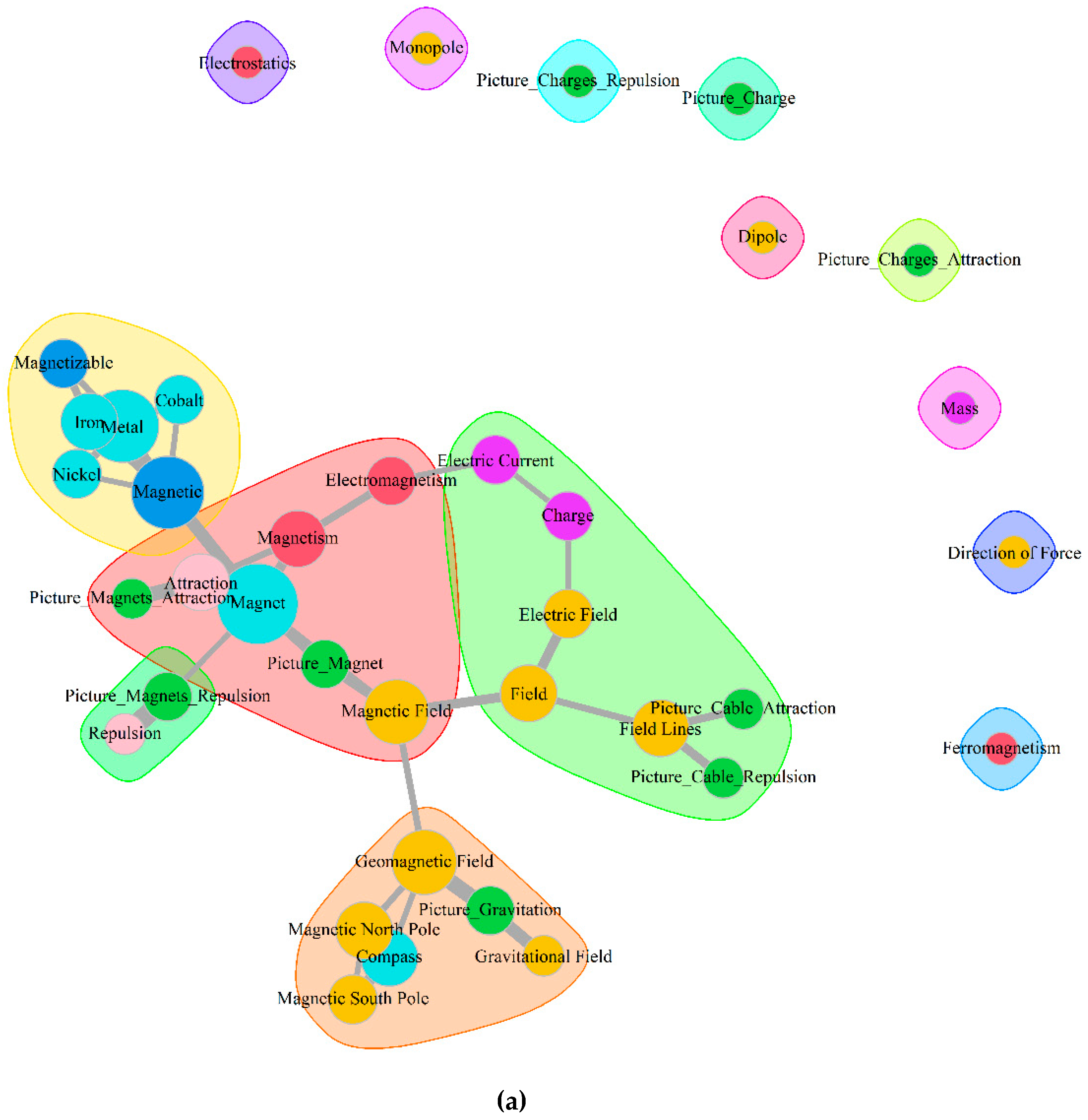
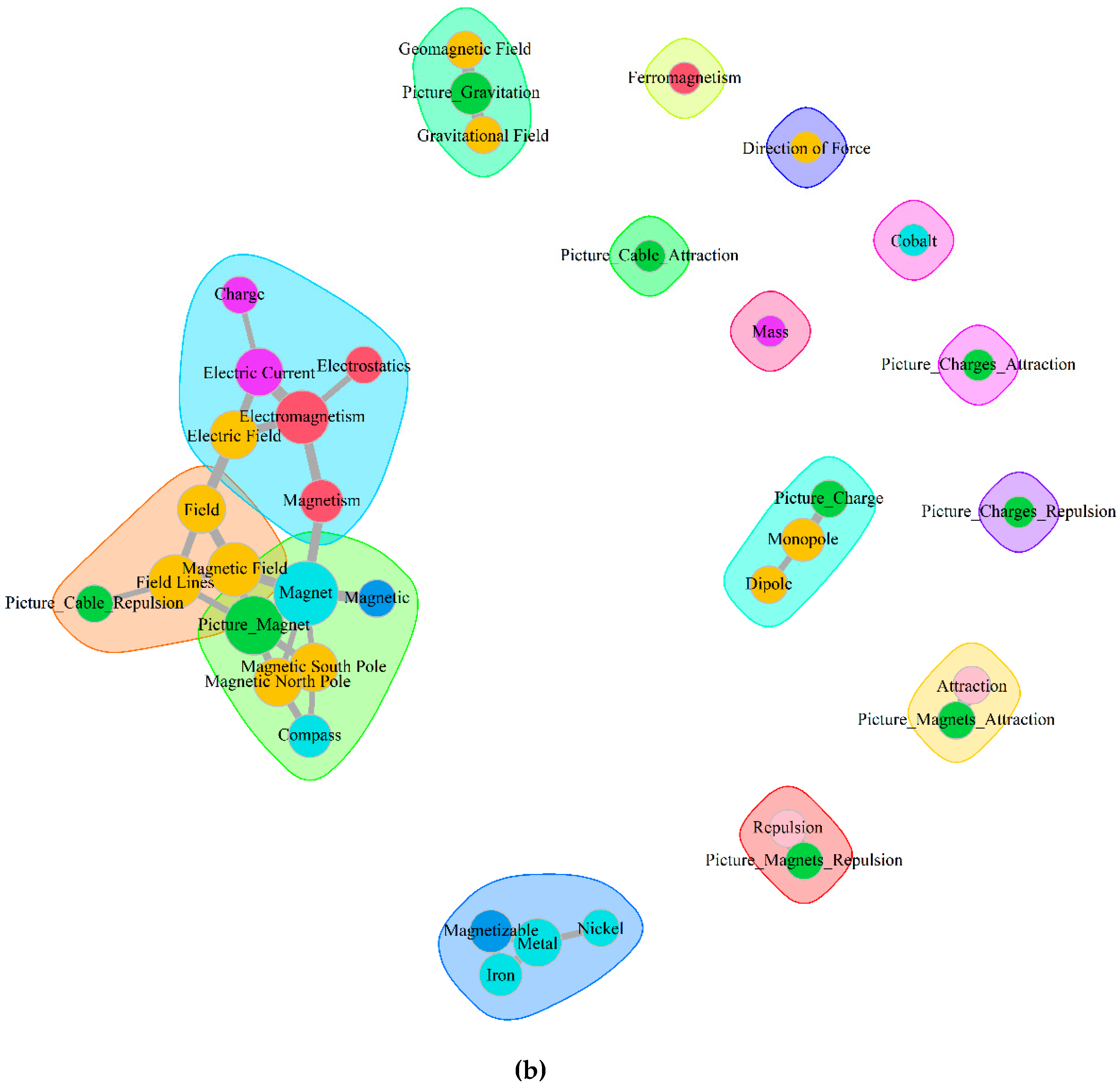
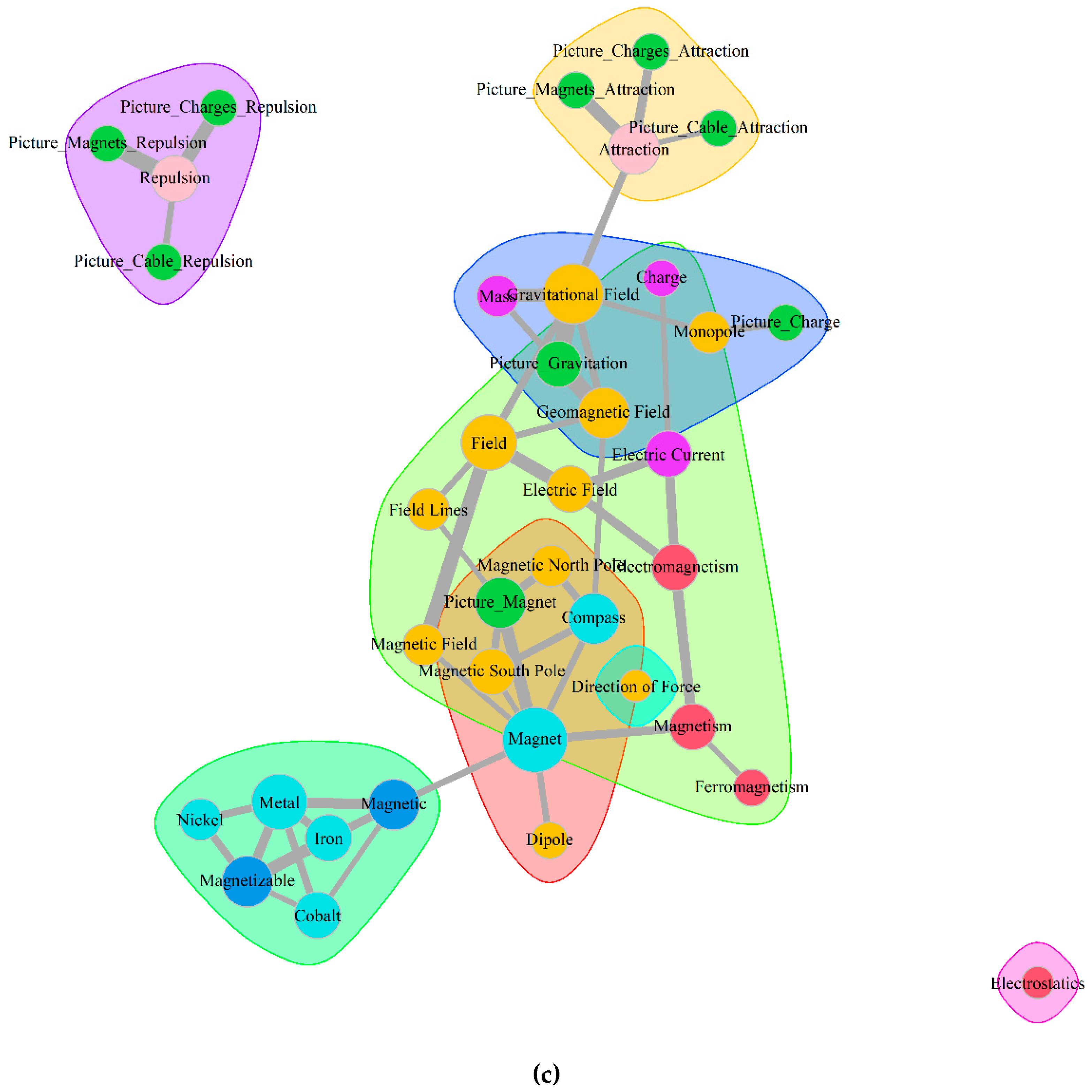
3.1. Development across Time
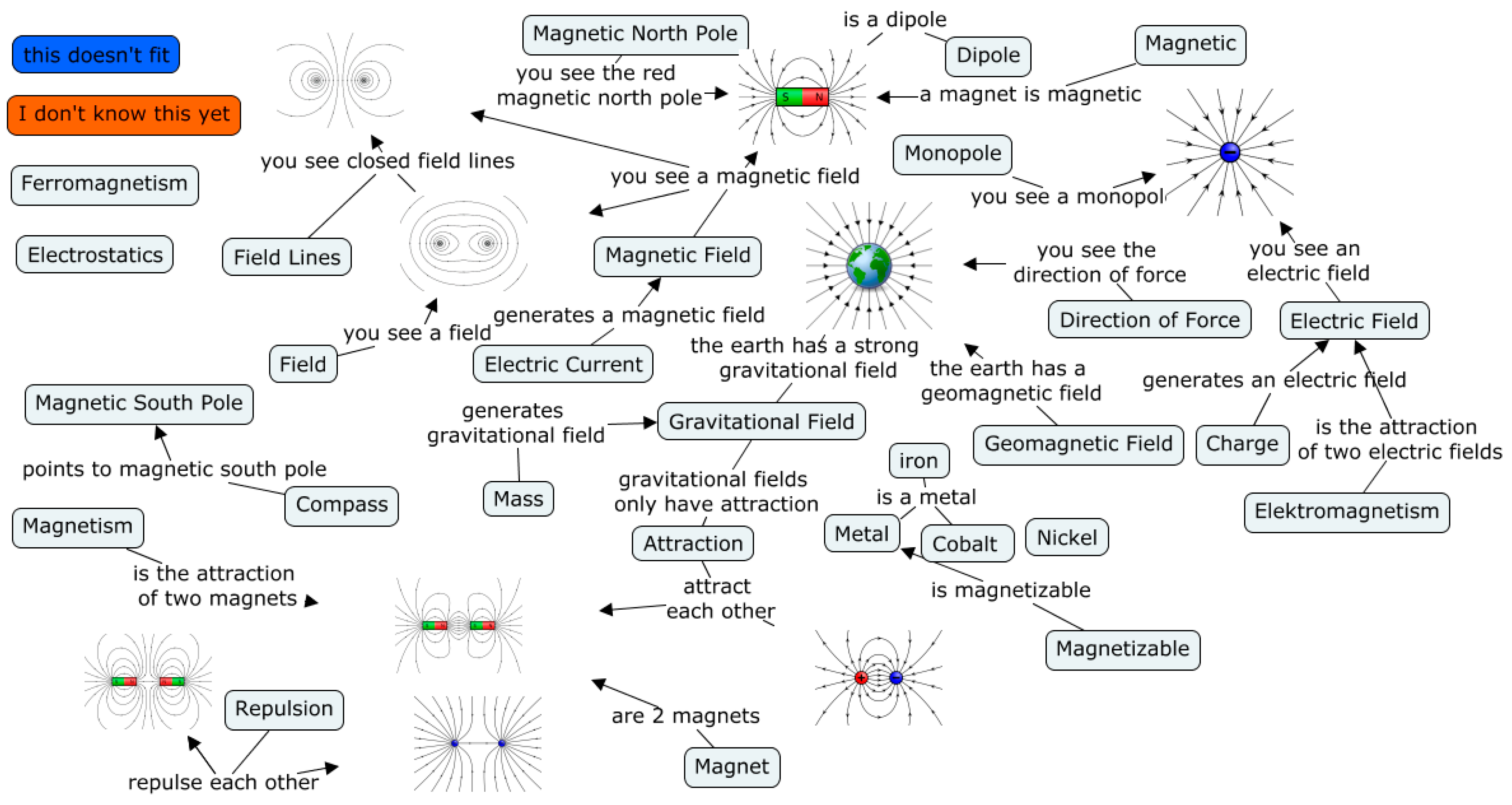
3.1.1. Special Nodes and Landmarks
3.1.2. Misconceptions
3.2. Aggregated Concept Maps
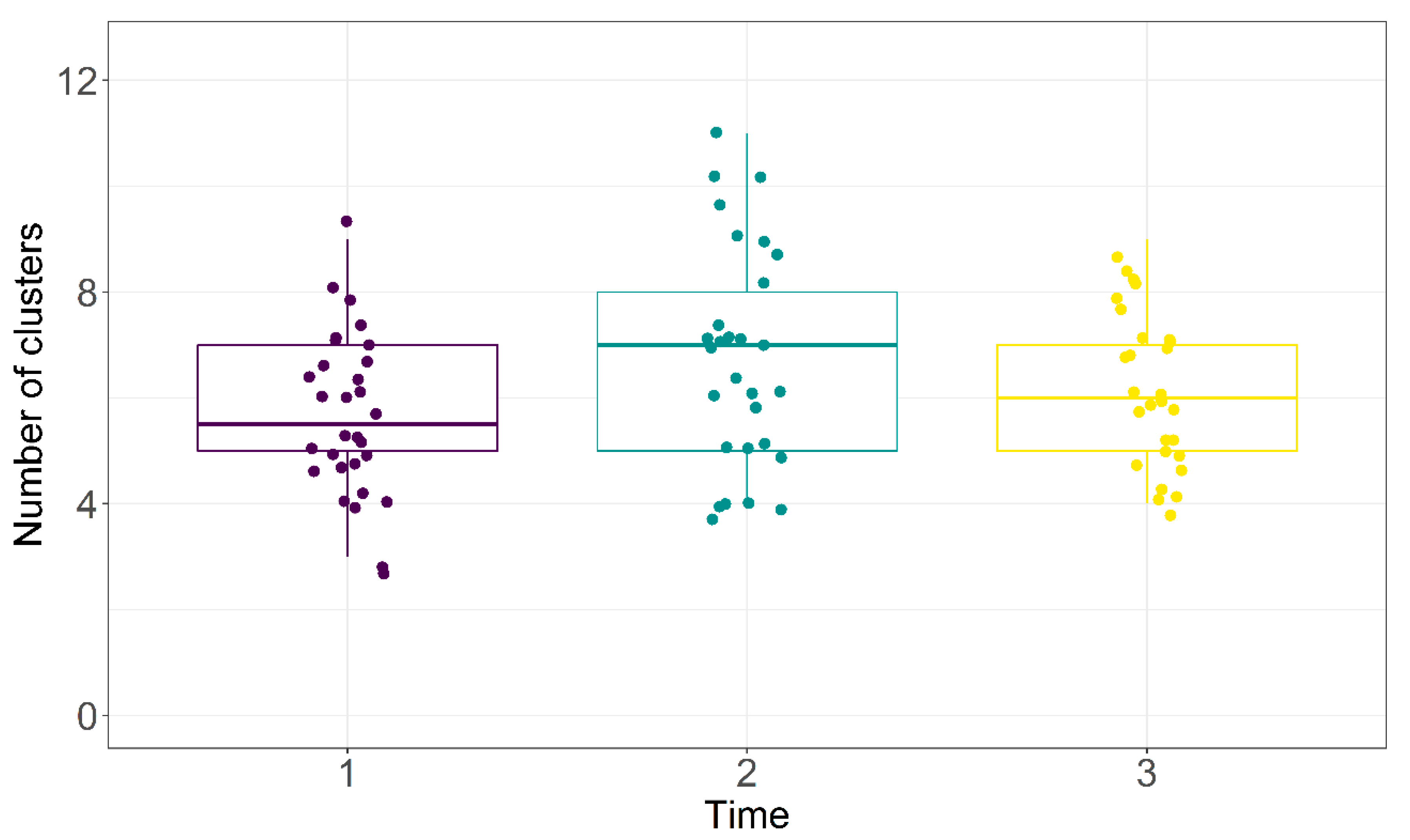
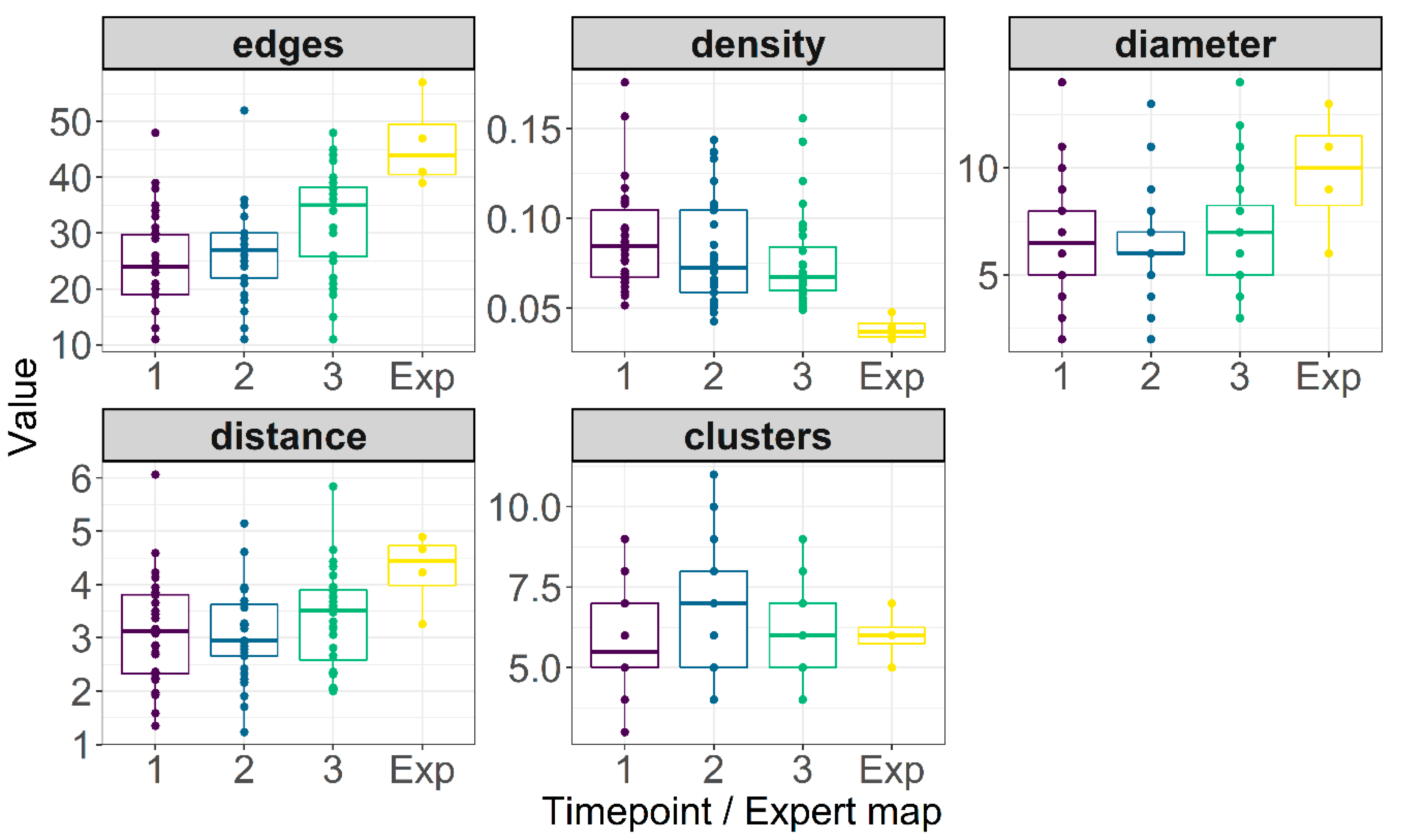
3.3. Clustering Structure
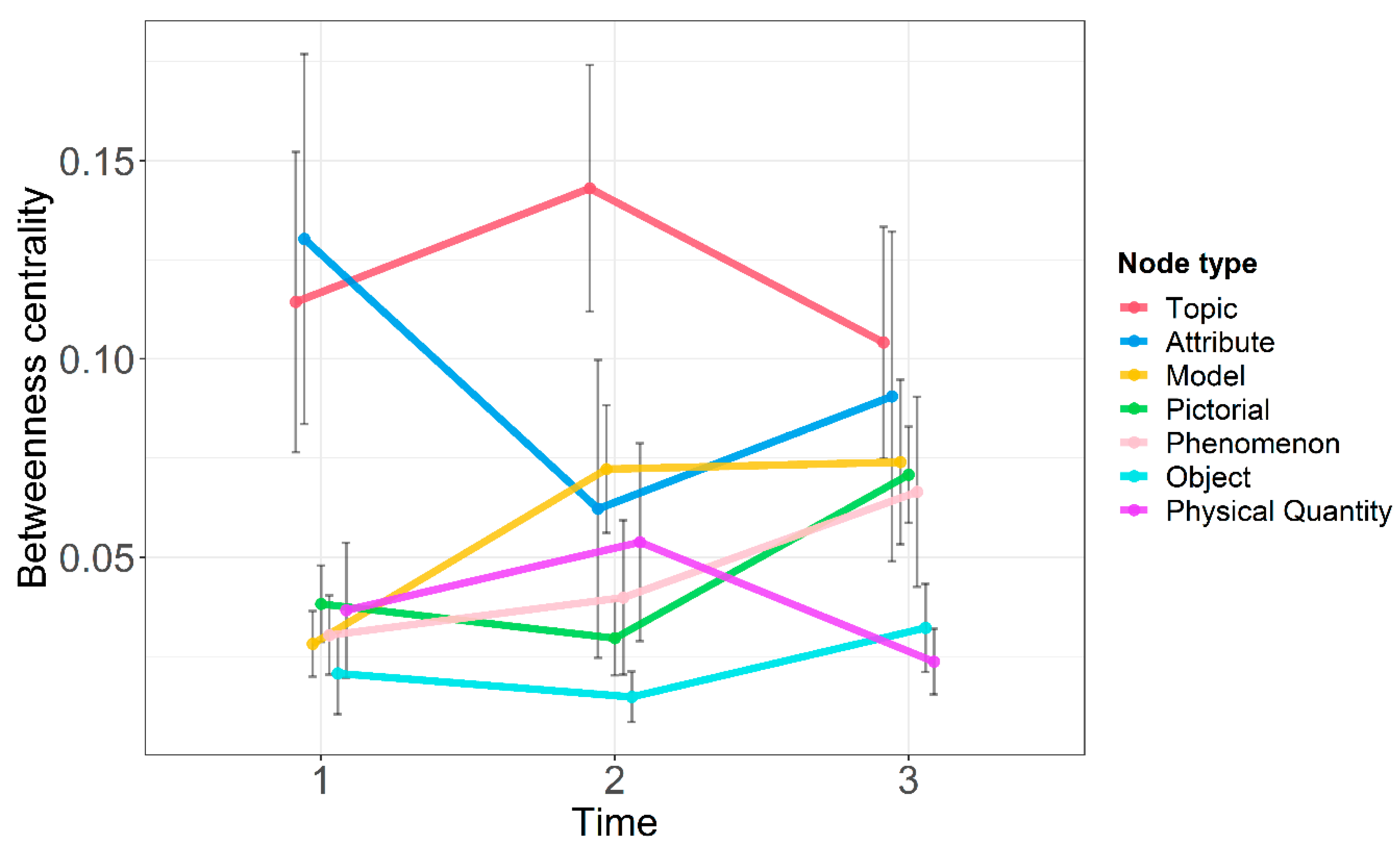
3.4. Different Node Types
3.5. Comparison with Experts
4. Discussion
4.1. Usage of Concept Mapping in Magnetism and Electrostatics in School
4.2. Limitations
4.3. Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
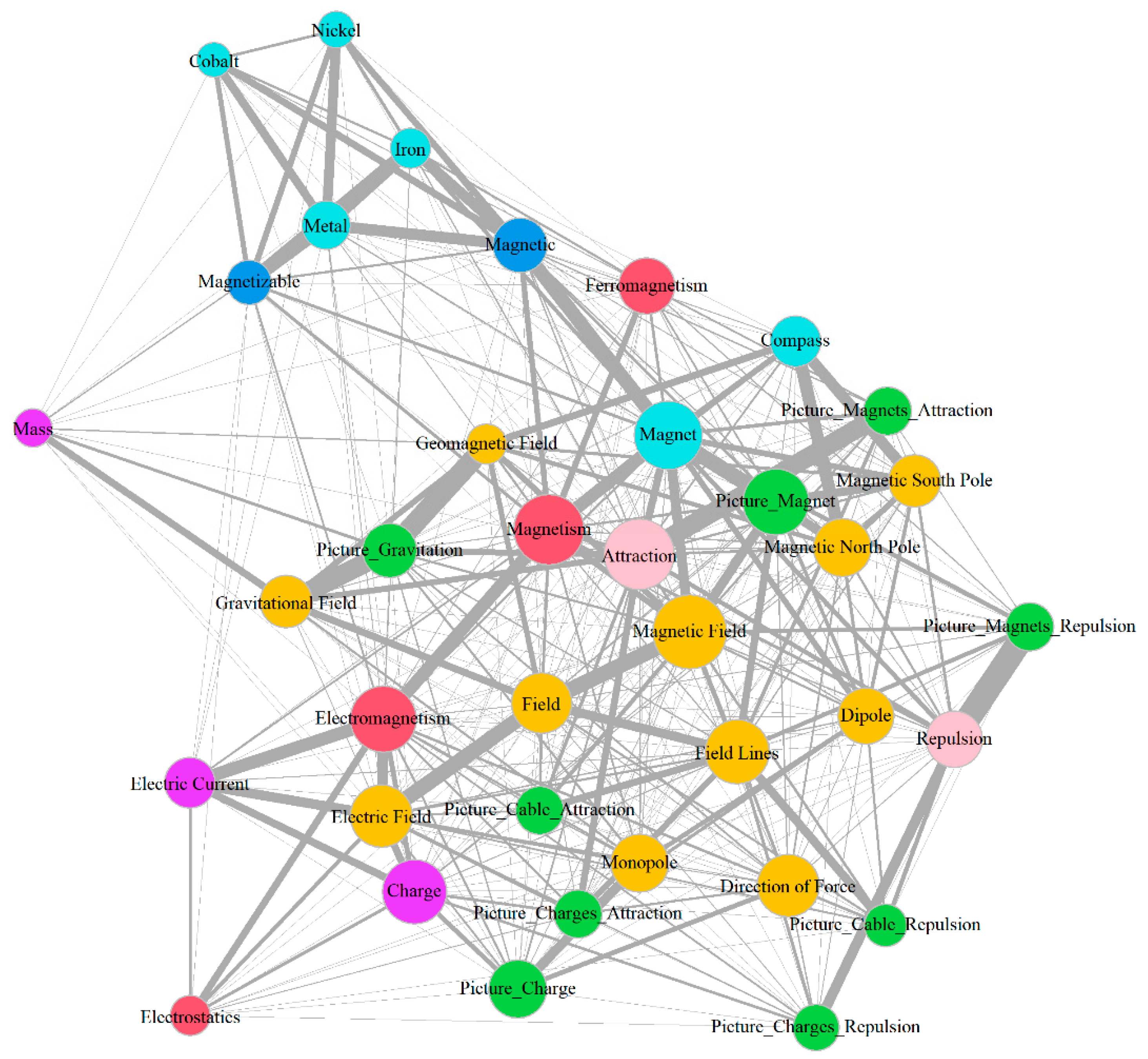
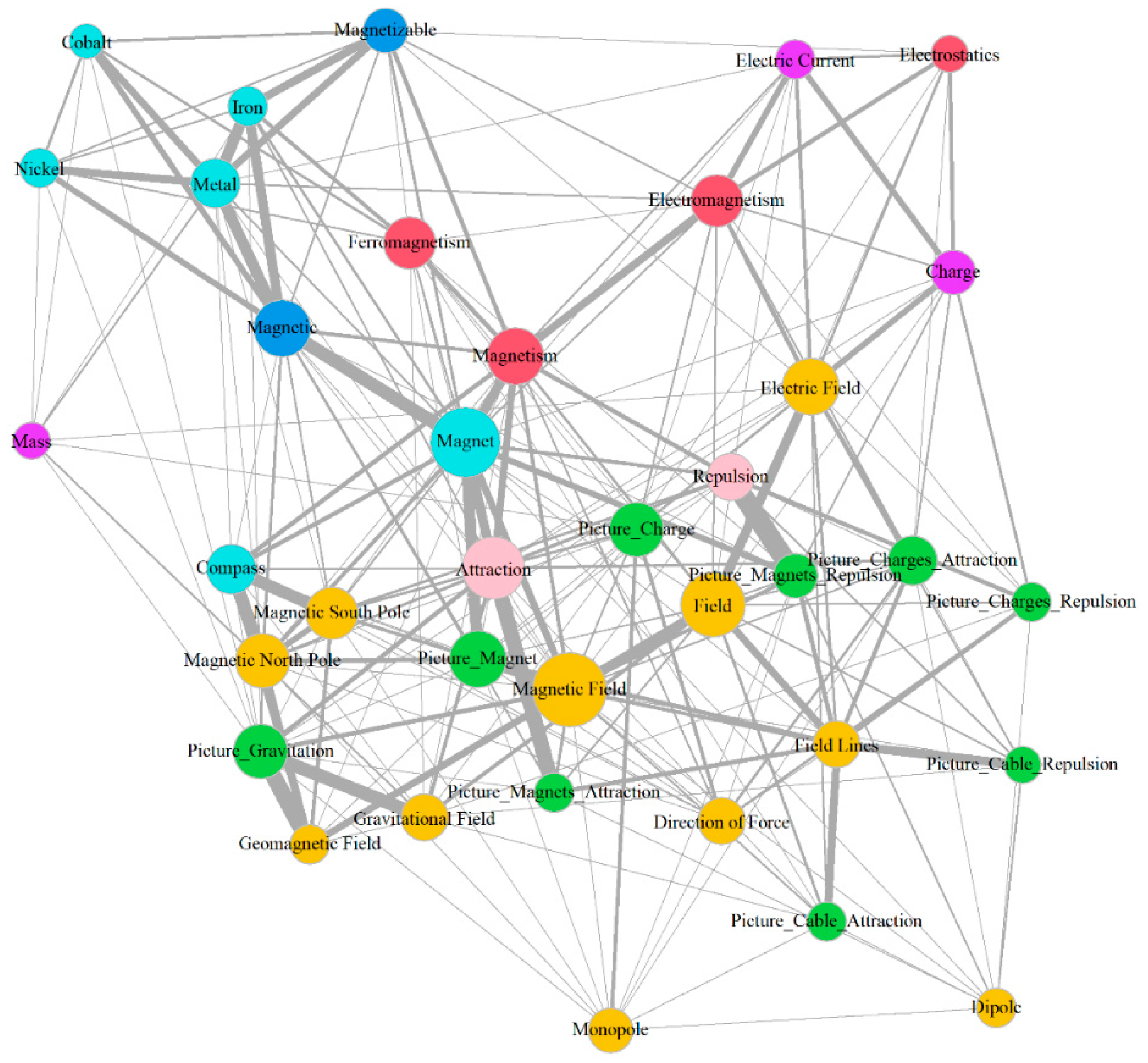
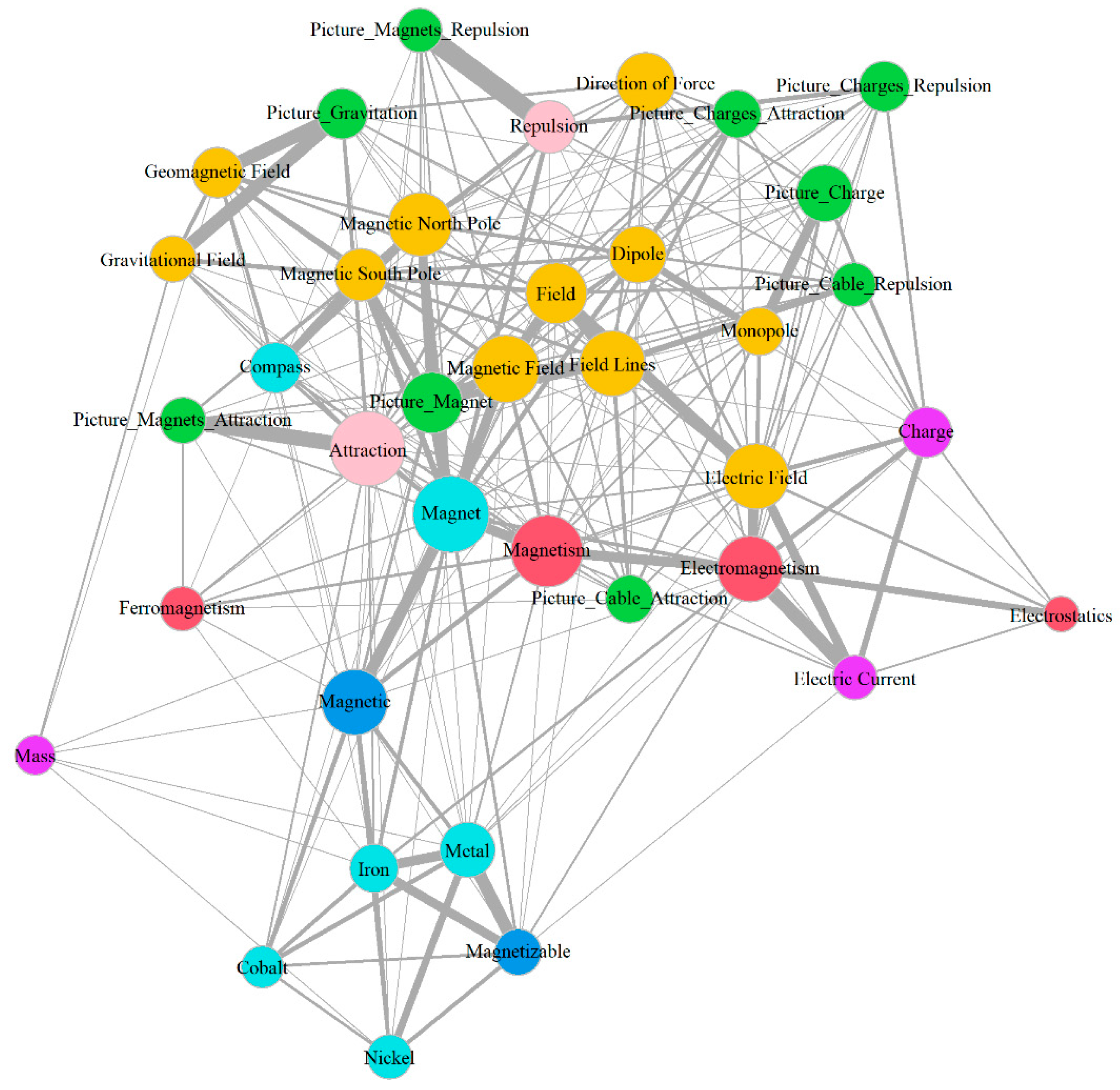
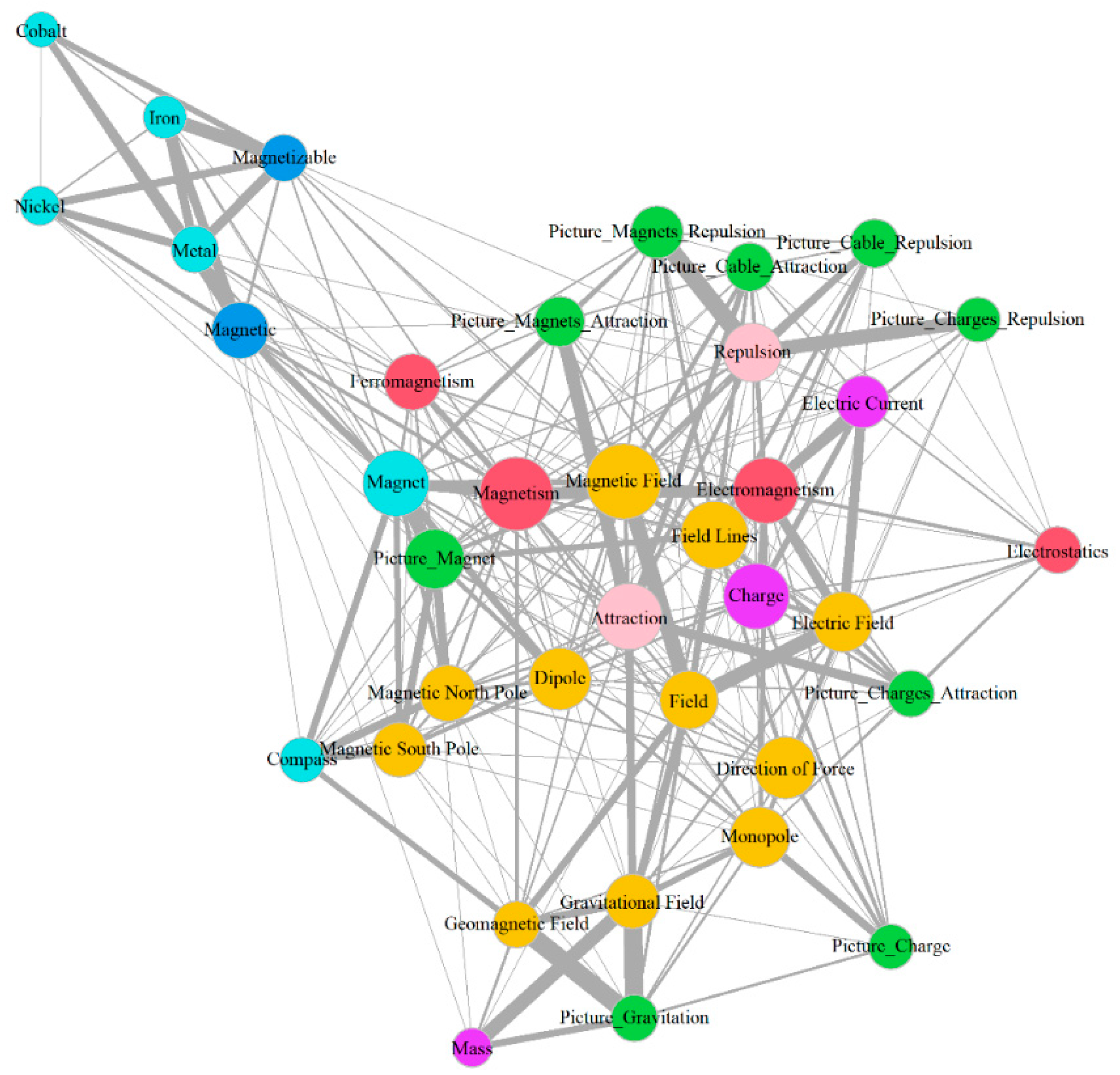
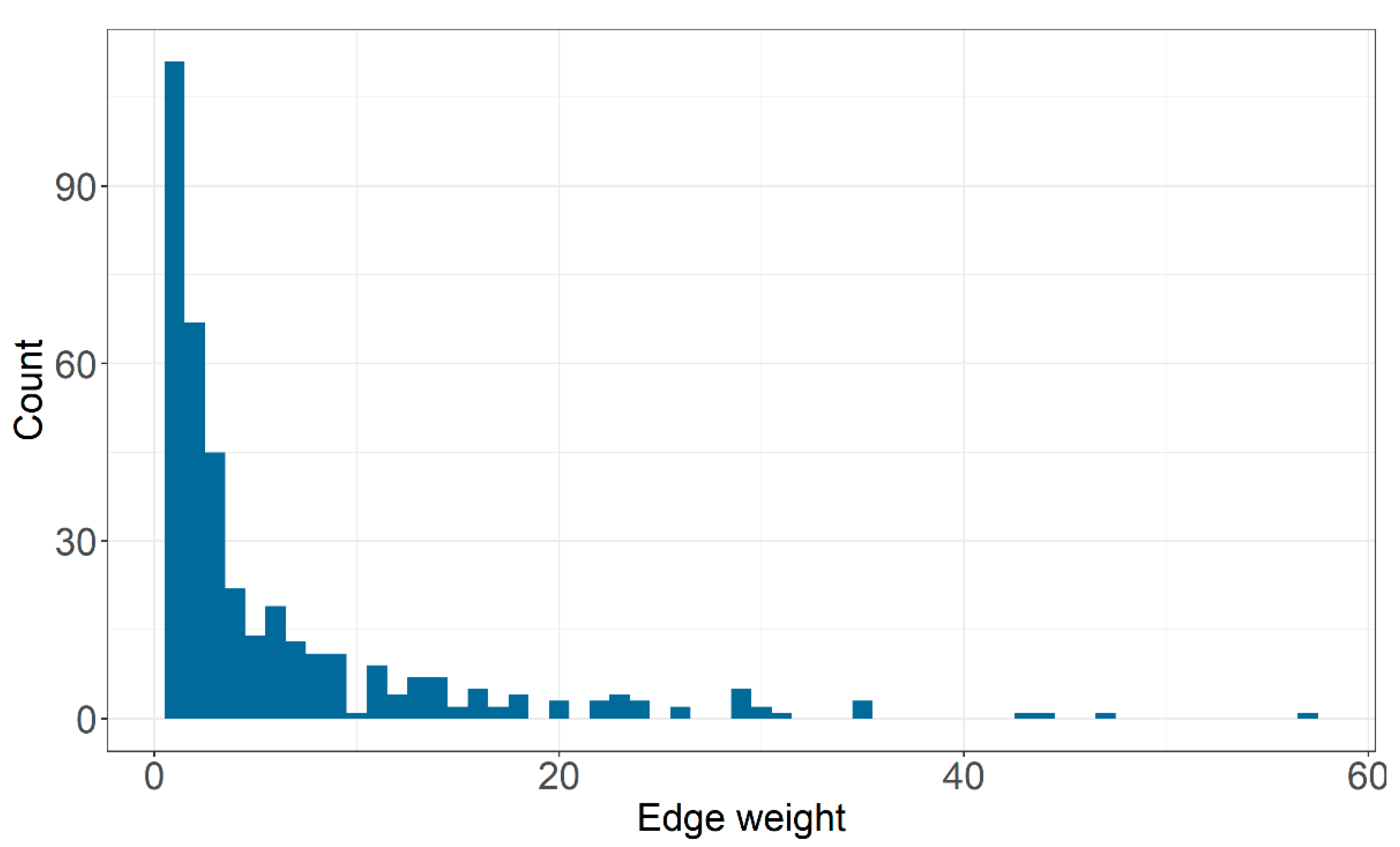
| Timepoint 1 | Timepoint 2 | Timepoint 3 | |
|---|---|---|---|
| Number of concept maps | 30 | 29 | 28 |
| Number of concepts | 24.9 (6.32) | 27.1 (6.20) | 30.4 (6.62) |
| CI95[22.6; 27.3] | CI95[24.8; 29.5] | CI95[27.8; 32.9] | |
| Number of edges | 25.1 (8.58) | 26.9 (8.21) | 32.5 (9.61) |
| CI95[21.9; 28.3] | CI95[23.8; 30.1] | CI95[28.7; 36.2] | |
| Density | 0.089 (0.0286) | 0.082 (0.0301) | 0.077 (0.0267) |
| CI95[0.078; 0.01] | CI95[0.07; 0.093] | CI95[0.067; 0.087] | |
| Mean distance | 3.13 (0.994) | 3.05 (0.849) | 3.36 (0.927) |
| CI95[2.76; 3.51] | CI95[2.73; 3.37] | CI95[3.00; 3.72] | |
| Diameter | 6.63 (2.47) | 6.41 (2.16) | 7.25 (2.61) |
| CI95[5.71; 7.56] | CI95[5.59; 7.24] | CI95[6.24; 8.26] | |
| Number of clusters | 5.67 (1.47) | 6.72 (2.07) | 6.18 (1.44) |
| CI95[5.12; 6.22] | CI95[5.94; 7.51] | CI95[5.62; 6.74] |
| Timepoint 1 | Timepoint 2 | Timepoint 3 | Expert Maps | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | D | PR | node | B | D | PR | node | B | D | PR | node | B | D | PR | node |
| 0.265 | 3.14 | 0.058 | Magnetism | 0.183 | 2.76 | 0.044 | Magnetism | 0.196 | 3.4 | 0.042 | Field | 0.289 | 6.75 | 0.024 | Magnet |
| 0.192 | 3.32 | 0.061 | Magnet | 0.166 | 3 | 0.049 | Ferromagnetism | 0.187 | 3.74 | 0.053 | Magnet | 0.24 | 5 | 0.037 | Electric Field |
| 0.171 | 2.71 | 0.053 | Field | 0.164 | 3.7 | 0.061 | Magnet | 0.158 | 2.92 | 0.04 | Magnetic Field | 0.234 | 4 | 0.031 | Ferromagnetism |
| 0.151 | 2.54 | 0.048 | Magnetic Field | 0.143 | 3.29 | 0.053 | Electromagnetism | 0.154 | 3.21 | 0.043 | Magnetism | 0.182 | 3.75 | 0.027 | Field |
| 0.13 | 2.79 | 0.054 | Magnetic | 0.119 | 2.38 | 0.042 | Magnetic Field | 0.12 | 2.85 | 0.042 | Attraction | 0.166 | 4 | 0.058 | Attraction |
| 0.127 | 2.33 | 0.044 | Picture_Magnet | 0.1 | 2.52 | 0.044 | Electric Field | 0.108 | 2.85 | 0.042 | Gravitational Field | 0.153 | 2.75 | 0.023 | Magnetism |
| 0.116 | 3.05 | 0.056 | Field Lines | 0.098 | 2.5 | 0.046 | Field | 0.104 | 3.13 | 0.043 | Electromagnetism | 0.152 | 2.25 | 0.013 | Compass |
| 0.114 | 2.33 | 0.041 | Electromagnetism | 0.086 | 2.38 | 0.044 | Field Lines | 0.097 | 2.67 | 0.041 | Picture_Magnet | 0.146 | 3.75 | 0.05 | Repulsion |
| 0.11 | 2.36 | 0.044 | Attraction | 0.076 | 2.36 | 0.043 | Attraction | 0.096 | 2.5 | 0.036 | Electric Field | 0.139 | 2 | 0.023 | Picture_Magnets_Attraction |
| 0.106 | 2.4 | 0.046 | Electric Field | 0.075 | 2.44 | 0.042 | Picture_Magnet | 0.091 | 2.29 | 0.042 | Magnetic | 0.137 | 2.25 | 0.019 | Dipole |
| 0.102 | 2.45 | 0.046 | Ferromagnetism | 0.072 | 2.35 | 0.039 | Dipole | 0.086 | 2.64 | 0.039 | Field Lines | 0.134 | 2.75 | 0.041 | Field Lines |
| 0.075 | 1.85 | 0.041 | Compass | 0.062 | 2.45 | 0.041 | Magnetic | 0.074 | 1.91 | 0.029 | Dipole | 0.119 | 2.25 | 0.017 | Geomagnetic Field |
| 0.056 | 2.29 | 0.047 | Metal | 0.055 | 1.72 | 0.038 | Gravitational Field | 0.071 | 2.37 | 0.039 | Picture_Gravitation | 0.119 | 2 | 0.026 | Picture_Charges_Repulsion |
| 0.051 | 1.92 | 0.039 | Magnetic North Pole | 0.054 | 1.83 | 0.034 | Charge | 0.067 | 2.62 | 0.042 | Repulsion | 0.117 | 3.25 | 0.047 | Magnetic Field |
| 0.051 | 1.75 | 0.036 | Magnetizable | 0.049 | 1.54 | 0.031 | Picture_Charges_Repulsion | 0.06 | 2.5 | 0.032 | Ferromagnetism | 0.112 | 4 | 0.033 | Magnetizable |
| 0.049 | 1.37 | 0.029 | Electric Current | 0.045 | 1.55 | 0.031 | Picture_Charge | 0.052 | 2.39 | 0.034 | Geomagnetic Field | 0.107 | 2.5 | 0.042 | Magnetic |
| 0.048 | 1.57 | 0.031 | Picture_Magnets_Attraction | 0.044 | 1.6 | 0.031 | Compass | 0.05 | 2.04 | 0.028 | Monopole | 0.098 | 1.75 | 0.021 | Picture_Magnet |
| 0.046 | 2.14 | 0.034 | Monopole | 0.04 | 1.93 | 0.038 | Repulsion | 0.049 | 2.04 | 0.037 | Magnetizable | 0.091 | 3 | 0.02 | Charge |
| 0.044 | 1.68 | 0.037 | Gravitational Field | 0.039 | 2.08 | 0.039 | Metal | 0.045 | 2.25 | 0.038 | Metal | 0.089 | 2.75 | 0.028 | Gravitational Field |
| 0.043 | 1.88 | 0.043 | Geomagnetic Field | 0.038 | 1.65 | 0.03 | Direction of Force | 0.035 | 1.79 | 0.03 | Picture_Magnets_Repulsion | 0.073 | 2.5 | 0.024 | Monopole |
| 0.039 | 1.82 | 0.035 | Electrostatics | 0.037 | 1.81 | 0.034 | Magnetizable | 0.035 | 1.56 | 0.026 | Picture_Charge | 0.067 | 2.75 | 0.025 | Electromagnetism |
| 0.038 | 1.89 | 0.042 | Picture_Gravitation | 0.035 | 1.5 | 0.03 | Picture_Cable_Repulsion | 0.034 | 2 | 0.028 | Magnetic South Pole | 0.038 | 2 | 0.018 | Electrostatics |
| 0.038 | 1.53 | 0.036 | Picture_Charges_Attraction | 0.03 | 1.85 | 0.034 | Magnetic South Pole | 0.033 | 1.63 | 0.025 | Direction of Force | 0.038 | 1.75 | 0.021 | Picture_Charges_Attraction |
| 0.037 | 1.8 | 0.04 | Picture_Magnets_Repulsion | 0.03 | 1.75 | 0.037 | Picture_Gravitation | 0.032 | 1.64 | 0.028 | Iron | 0.031 | 1.25 | 0.044 | Direction of Force |
| 0.037 | 1.63 | 0.035 | Charge | 0.028 | 1.96 | 0.036 | Magnetic North Pole | 0.031 | 1.68 | 0.027 | Picture_Magnets_Attraction | 0.029 | 2 | 0.04 | Electric Current |
| 0.035 | 1.67 | 0.035 | Direction of Force | 0.026 | 1.68 | 0.032 | Monopole | 0.03 | 1.61 | 0.027 | Compass | 0.023 | 1.5 | 0.022 | Picture_Magnets_Repulsion |
| 0.03 | 1.62 | 0.038 | Repulsion | 0.026 | 1.68 | 0.032 | Electric Current | 0.029 | 1.6 | 0.026 | Electric Current | 0.022 | 1.75 | 0.019 | Picture_Charge |
| 0.029 | 1.75 | 0.035 | Magnetic South Pole | 0.024 | 1.41 | 0.03 | Picture_Magnets_Attraction | 0.028 | 1.92 | 0.027 | Magnetic North Pole | 0.015 | 2 | 0.011 | Cobalt |
| 0.028 | 2 | 0.031 | Dipole | 0.022 | 1.74 | 0.038 | Geomagnetic Field | 0.026 | 1.6 | 0.031 | Picture_Cable_Attraction | 0.015 | 2 | 0.011 | Iron |
| 0.021 | 1.77 | 0.034 | Picture_Charges_Repulsion | 0.022 | 1.31 | 0.029 | Picture_Cable_Attraction | 0.024 | 1.48 | 0.023 | Picture_Charges_Attraction | 0.015 | 2 | 0.011 | Nickel |
| 0.021 | 1.56 | 0.034 | Picture_Charge | 0.019 | 1.33 | 0.027 | Picture_Charges_Attraction | 0.024 | 2.18 | 0.033 | Charge | 0.012 | 1.5 | 0.016 | Mass |
| 0.021 | 1.48 | 0.032 | Iron | 0.016 | 1.28 | 0.028 | Picture_Magnets_Repulsion | 0.022 | 1.5 | 0.029 | Picture_Cable_Repulsion | 0.005 | 2.75 | 0.025 | Metal |
| 0.013 | 1.5 | 0.028 | Picture_Cable_Attraction | 0.015 | 1.88 | 0.033 | Iron | 0.02 | 1.33 | 0.02 | Electrostatics | 0.003 | 2.25 | 0.057 | Magnetic North Pole |
| 0.006 | 1.4 | 0.029 | Picture_Cable_Repulsion | 0.013 | 1.62 | 0.025 | Cobalt | 0.015 | 1.3 | 0.022 | Picture_Charges_Repulsion | 0 | 1 | 0.021 | Picture_Gravitation |
| 0.004 | 1.47 | 0.028 | Cobalt | 0.003 | 1.25 | 0.025 | Electrostatics | 0.009 | 1.26 | 0.022 | Mass | - | - | - | Magnetic South Pole |
| 0.002 | 1.35 | 0.026 | Nickel | 0.001 | 1.47 | 0.024 | Nickel | 0.001 | 1.23 | 0.023 | Nickel | - | - | - | Picture_Cable_Attraction |
| 0.001 | 1.43 | 0.023 | Mass | 0 | 1.14 | 0.021 | Mass | 0 | 1.14 | 0.021 | Cobalt | - | - | - | Picture_Cable_Repulsion |
References
- Carey, S. Science education as conceptual change. J. Appl. Dev. Psychol. 2000, 21, 13–19. [Google Scholar] [CrossRef]
- Vosniadou, S.; Brewer, W.F. Mental models of the earth: A study of conceptual change in childhood. Cogn. Psychol. 1992, 24, 535–585. [Google Scholar] [CrossRef]
- Chi, M.T.; Slotta, J.D.; De Leeuw, N. From things to processes: A theory of conceptual change for learning science concepts. Learn. Instr. 1994, 4, 27–43. [Google Scholar] [CrossRef]
- Di Sessa, A.A.; Sherin, B.L. What changes in conceptual change? Int. J. Sci. Educ. 1998, 20, 1155–1191. [Google Scholar] [CrossRef]
- Duit, R.; Treagust, D.F. Conceptual change: A powerful framework for improving science teaching and learning. Int. J. Sci. Educ. 2003, 25, 671–688. [Google Scholar] [CrossRef]
- Chi, M.T. Two kinds and four sub-types of misconceived knowledge, ways to change it, and the learning outcomes. In International Handbook of Research on Conceptual Change, 2nd ed.; Vosniadou, S., Ed.; Routledge: New York, NY, USA, 2013; Volume 1, pp. 61–82. [Google Scholar] [CrossRef]
- Koponen, I.T.; Pehkonen, M. Coherent knowledge structures of physics represented as concept networks in teacher education. Sci. Educ. 2010, 19, 259–282. [Google Scholar] [CrossRef]
- Goldwater, M.B.; Schalk, L. Relational categories as a bridge between cognitive and educational research. Psychol. Bull. 2016, 142, 729–757. [Google Scholar] [CrossRef]
- Di Sessa, A.A. A Bird’s-Eye View on the “Pieces” vs. “Coherence” Controversy (From the Pieces Side of the Fence). In International Handbook of Research on Conceptual Change, 2nd ed.; Vosniadou, S., Ed.; Routledge: New York, NY, USA, 2013; Volume 1, pp. 31–48. [Google Scholar]
- Novak, J.D.; Gowin, D.B. Learning How to Learn, 1st ed.; Cambridge University Press: Cambridge, UK, 1984; pp. 15–54. [Google Scholar] [CrossRef]
- İngeç, Ş.K. Analysing concept maps as an assessment tool in teaching physics and comparison with the achievement tests. Int. J. Sci. Educ. 2009, 31, 1897–1915. [Google Scholar] [CrossRef]
- Wallace, J.D.; Mintzes, J.J. The concept map as a research tool: Exploring conceptual change in biology. J. Res. Sci. Teach. 1990, 27, 1033–1052. [Google Scholar] [CrossRef]
- Vosniadou, S. Capturing and modeling the process of conceptual change. Learn. Instr. 1994, 4, 45–69. [Google Scholar] [CrossRef]
- Di Sessa, A.A. Toward an epistemology of physics. Cogn. Instr. 1993, 10, 105–225. [Google Scholar] [CrossRef]
- Alexander, P.A. Positioning conceptual change within a model of domain literacy. In Perspectives on Conceptual Change: Multiple Ways to Understand Knowing and Learning in a Complex World, 1st ed.; Guzzetti, B., Hynd, C., Eds.; Erlbaum Associates: Mahwah, NJ, USA, 1998; pp. 55–76. [Google Scholar]
- Reif, F.; Heller, J.I. Knowledge structure and problem solving in physics. Educ. Psychol. 1982, 17, 102–127. [Google Scholar] [CrossRef]
- Kokkonen, T. Concepts and Concept Learning in Physics: The systemic view. Ph.D. Thesis, University of Helsinki, Helsinki, Finland, 22 November 2017. Available online: http://urn.fi/URN:ISBN:978-951-51-2782-2 (accessed on 24 April 2020).
- Chiou, G.; Anderson, R.O. A study of undergraduate physics students’ understanding of heat conduction based on mental model theory and an ontology-process analysis. Sci. Educ. 2010, 94, 825–854. [Google Scholar] [CrossRef]
- Koponen, I.T.; Huttunen, L. Concept development in learning physics: The case of electric current and voltage revisited. Sci. Educ. 2013, 22, 2227–2254. [Google Scholar] [CrossRef]
- Brown, D.E.; Hammer, D. Conceptual change in physics. In International Handbook of Research on Conceptual Change, 1st ed.; Vosniadou, S., Ed.; Routledge: New York, NY, USA, 2008; Volume 1, pp. 127–154. [Google Scholar]
- Slotta, J.D.; Chi, M.T.; Joram, E. Assessing students’ misclassifications of physics concepts: An ontological basis for conceptual change. Cogn. Instr. 1995, 13, 373–400. [Google Scholar] [CrossRef]
- Vosniadou, S.; Ioannides, C.; Dimitrakopoulou, A.; Papademetriou, E. Designing learning environments to promote conceptual change in science. Learn. Instr. 2001, 11, 381–419. [Google Scholar] [CrossRef]
- Montenegro, M.J. Identifying Student Mental Models from Their Response Pattern to A Physics Multiple-Choice Test. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2008. [Google Scholar]
- Frappart, S.; Raijmakers, M.; Frède, V. What do children know and understand about universal gravitation? Structural and developmental aspects. J. Exp. Child Psychol. 2014, 120, 17–38. [Google Scholar] [CrossRef]
- Edelsbrunner, P.A.; Schalk, L.; Schumacher, R.; Stern, E. Variable control and conceptual change: A large-scale quantitative study in elementary school. Learn. Individ. Differ. 2018, 66, 38–53. [Google Scholar] [CrossRef]
- Finkelstein, N. Learning physics in context: A study of student learning about electricity and magnetism. Int. J. Sci. Educ. 2005, 27, 1187–1209. [Google Scholar] [CrossRef]
- Törnkvist, S.; Pettersson, K.A.; Tranströmer, G. Confusion by representation: On student’s comprehension of the electric field concept. Am. J. Phys. 1993, 61, 335–338. [Google Scholar] [CrossRef]
- Cao, Y.; Brizuela, B.M. High school students’ representations and understandings of electric fields. Phys. Rev. Spec. Top. 2016, 12, 020102. [Google Scholar] [CrossRef]
- Maloney, D.P.; O’Kuma, T.L.; Hieggelke, C.J.; Van Heuvelen, A. Surveying students’ conceptual knowledge of electricity and magnetism. Am. J. Phys. 2001, 69, S12–S23. [Google Scholar] [CrossRef]
- Koponen, I.T.; Pehkonen, M. Physics concepts and laws as network-structures: Comparisons of structural features in experts’ and novices’ concept maps. In Concept Mapping: Connecting Educators, Proceedings of the 3rd International Conference on Concept Mapping, Tallinn, Estonia and Helsinki, Finland, 22–25 September 2008; Cañas, A.J., Reiska, P., Åhlberg, M.K., Novak, J.D., Eds.; Tallinn University: Tallinn, Estonia, 2008; Volume 2, pp. 540–547. [Google Scholar]
- Donald, J.G. Disciplinary Differences in Knowledge Validation. New Dir. Teach. Learn. 1995, 64, 7–17. [Google Scholar] [CrossRef]
- Novak, J.D.; Musonda, D. A twelve-year longitudinal study of science concept learning. Am. Educ. Res. J. 1991, 28, 117–153. [Google Scholar] [CrossRef]
- Ruiz-Primo, M.A.; Shavelson, R.J. Problems and issues in the use of concept maps in science assessment. J. Res. Sci. Teach. 1996, 33, 569–600. [Google Scholar] [CrossRef]
- Plötzner, R.; Beller, S.; Härder, J. Wissensvermittlung, tutoriell unterstützte Wissensanwendung und Wissensdiagnose mit Begriffsnetzen. In Wissen Sichtbar Machen. Wissensmanagement mit Mapping-Techniken, 1st ed.; Mandl, H., Fischer, F., Eds.; Hogrefe: Göttingen, Germany, 2000; Volume 1, pp. 180–198. [Google Scholar]
- Goldstone, R.L.; Kersten, A.; Carvalho, P.F. Concepts and categorization. In Handbook of Psychology, 2nd ed.; Weiner, I.B., Ed.; Wiley: Hoboken, NJ, USA, 2012; Volume 4. [Google Scholar]
- Liu, X.; Hinchey, M. The internal consistency of a concept mapping scoring scheme and its effect on prediction validity. Int. J. Sci. Educ. 1996, 18, 921–937. [Google Scholar] [CrossRef]
- Kinchin, I.M. Concept mapping in biology. J. Biol. Educ. 2000, 34, 61–68. [Google Scholar] [CrossRef]
- Nousiainen, M. Physics Concept Maps: Analysis on Coherent Knowledge Structures in Physics Teacher Education. Ph.D. Thsis, University of Helsinki, Helsinki, Finland, 26 October 2012. [Google Scholar]
- Schalk, L.; Edelsbrunner, P.A.; Deiglmayr, A.; Schumacher, R.; Stern, E. Improved application of the control-of-variables strategy as a collateral benefit of inquiry-based physics education in elementary school. Learn. Instr. 2019, 59, 34–45. [Google Scholar] [CrossRef]
- Hofer, S.I.; Schumacher, R.; Rubin, H.; Stern, E. Enhancing physics learning with cognitively activating instruction: A quasi-experimental classroom intervention study. J. Educ. Psychol. 2018, 110, 1175. [Google Scholar] [CrossRef]
- Ziegler, E.; Stern, E. Delayed benefits of learning elementary algebraic transformations through contrasted comparisons. Learn. Instr. 2014, 33, 131–146. [Google Scholar] [CrossRef]
- Chi, M.T.H.; De Leeuw, N.; Chiu, M.-H.; LaVancher, C. Eliciting self-explanations improves understanding. Cogn. Sci. 1994, 18, 439–477. [Google Scholar] [CrossRef]
- Rittle-Johnson, B. Promoting transfer: Effects of self-explanation and direct instruction. Child Dev. 2006, 77, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Cañas, A.J.; Hill, G.; Carff, R.; Suri, N.; Lott, J.; Gómez, G.; Eskridge, T.C.; Arroyo, M.; Carvajal, R. CmapTools: A knowledge modeling and sharing environment. In Concept Maps: Theory, Methodology, Technology, Proceedings of the First International Conference on Concept Mapping, Pamplona, Spain, 14–17 September 2004; Cañas, A.J., Novak, J.D., González, F.M., Eds.; Direcciónde Publicaciones de la Universidad Pública de Navarra: Navarra, Spain, 2004; Volume 1. [Google Scholar]
- VectorFieldPlot. Available online: https://commons.wikimedia.org/wiki/User:Geek3/VectorFieldPlot (accessed on 13 January 2020).
- Page, L.; Brin, S.; Motwani, R.; Winograd, T. The PageRank citation ranking: Bringing order to the web. Technical report. Stanford. InfoLab. 1999. Available online: http://ilpubs.stanford.edu:8090/422/1/1999-66.pdf (accessed on 24 April 2020).
- Brandes, U.; Delling, D.; Gaertler, M.; Gorke, R.; Hoefer, M.; Nikoloski, Z.; Wagner, D. On modularity clustering. IEEE T. Knowl. Data Eng. 2007, 20, 172–188. [Google Scholar] [CrossRef]
- Singmann, H.; Bolker, B.; Westfall, J.; Aust, F.; Ben-Shachar, M.S. Afex: Analysis of Factorial Experiments. R Package Version 0.25-1. Available online: https://CRAN.R-project.org/package=afex (accessed on 13 January 2020).
- Ashtiani, M. CINNA: Deciphering Central Informative Nodes in Network Analysis. R Package Version 1.1.53. 2019. Available online: https://CRAN.R-project.org/package=CINNA (accessed on 13 January 2020).
- Jalili, M. Centiserve: Find Graph Centrality Indices. R Package Version 1.0.0. 2017. Available online: https://CRAN.R-project.org/package=centiserve (accessed on 13 January 2020).
- Muehling, A. Comato: Analysis of Concept Maps and Concept Landscapes. R Package Version 1.1. 2018. Available online: https://CRAN.R-project.org/package=comato (accessed on 13 January 2020).
- Wei, T.; Simko, V. “Corrplot”: Visualization of a Correlation Matrix. R Package Version 0.84. 2017. Available online: https://github.com/taiyun/corrplot (accessed on 13 January 2020).
- Wickham, H.; François, R.; Henry, L.; Müller, K. Dplyr: A Grammar of Data Manipulation. R Package Version 0.8.3. 2019. Available online: https://CRAN.R-project.org/package=dplyr (accessed on 13 January 2020).
- Lenth, R. Emmeans: Estimated Marginal Means, aka Least-Squares Means. R Package Version 1.4.1. 2019. Available online: https://CRAN.R-project.org/package=emmeans (accessed on 13 January 2020).
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Csardi, G.; Nepusz, T. The igraph software package for complex network research. Int. J. Complex Syst. 2006, 1695, 1–9. [Google Scholar]
- Kuznetsova, A.; Brockhoff, P.B.; Christensen, R.H.B. lmerTest Package: Tests in Linear Mixed Effects Models. J. Stat. Softw. 2017, 82, 1–26. [Google Scholar] [CrossRef]
- Bache, S.M.; Wickham, H. Magrittr: A Forward-Pipe Operator for R. R Package Version 1.5. 2014. Available online: https://CRAN.R-project.org/package=magrittr (accessed on 13 January 2020).
- Meyer, D.; Buchta, C. Proxy: Distance and Similarity Measures. R Package Version 0.4-23. 2019. Available online: https://CRAN.R-project.org/package=proxy (accessed on 13 January 2020).
- Epskamp, S.; Cramer, A.O.J.; Waldorp, L.J.; Schmittmann, V.D.; Borsboom, D. qgraph: Network Visualizations of Relationships in Psychometric Data. J. Stat. Softw. 2012, 48, 1–18. [Google Scholar] [CrossRef]
- Nowosad, J. ‘CARTOColors’ Palettes. R Package Version 1.0.0. 2018. Available online: https://nowosad.github.io/rcartocolor (accessed on 13 January 2020).
- Wickham, H.; Bryan, J. readxl: Read Excel Files. R Package Version 1.3.1. 2019. Available online: https://CRAN.R-project.org/package=readxl (accessed on 13 January 2020).
- Koponen, I.T.; Nousiainen, M. Pre-Service Teachers’ Knowledge of Relational Structure of Physics Concepts: Finding Key Concepts of Electricity and Magnetism. Educ. Sci. 2019, 9, 18. [Google Scholar] [CrossRef]
- Koponen, I.T.; Nousiainen, M. Concept networks of students’ knowledge of relationships between physics concepts: Finding key concepts and their epistemic support. Appl. Netw. Sci. 2018, 3, 14. [Google Scholar] [CrossRef]
- Malone, J.; Dekkers, J. The concept map as an aid to instruction in science and mathematics. Sch. Sci. Math. 1984, 84, 220–231. [Google Scholar] [CrossRef]
- Nesbit, J.C.; Adesope, O.O. Learning with concept and knowledge maps: A meta-analysis. Rev. Educ. Res. 2006, 76, 413–448. [Google Scholar] [CrossRef]
- Yin, Y.; Vanides, J.; Ruiz-Primo, M.A.; Ayala, C.C.; Shavelson, R.J. Comparison of two concept-mapping techniques: Implications for scoring, interpretation, and use. J. Res. Sci. Teach. 2005, 42, 166–184. [Google Scholar] [CrossRef]
- Ritchhart, R.; Turner, T.; Hadar, L. Uncovering students’ thinking about thinking using concept maps. Metacogn. Learn. 2009, 4, 145–159. [Google Scholar] [CrossRef]
- Cutrer, W.B.; Castro, D.; Roy, K.M.; Turner, T.L. Use of an expert concept map as an advance organizer to improve understanding of respiratory failure. Med. Teach. 2011, 33, 1018–1026. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, E.; Stern, E. Consistent advantages of contrasted comparisons: Algebra learning under direct instruction. Learn. Instr. 2016, 41, 41–51. [Google Scholar] [CrossRef]
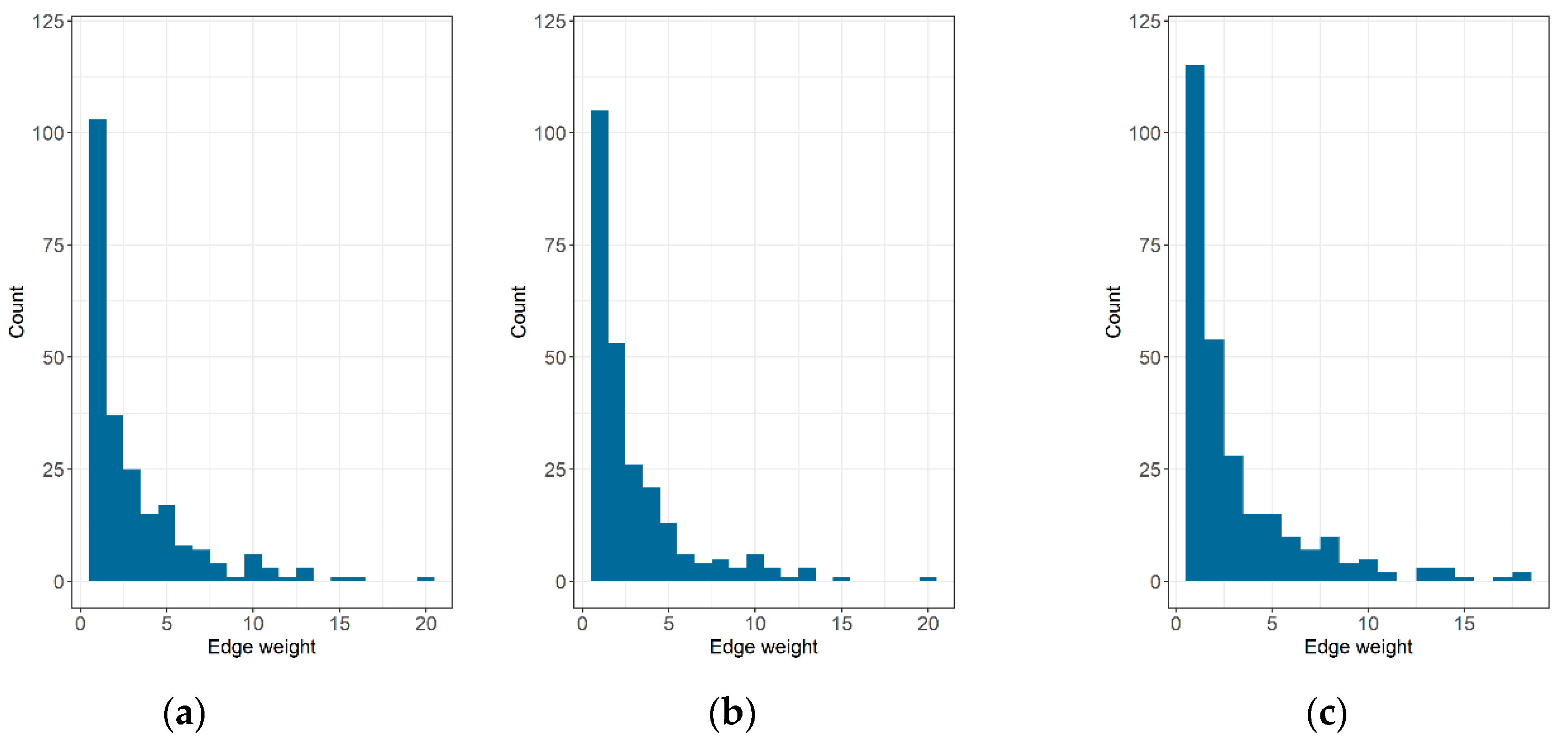
| Single Object Situations | Attraction Situations | Repulsion Situations |
|---|---|---|
Picture_Magnet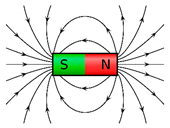 | Picture_Magnets_Attraction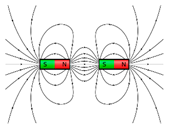 | Picture_Magnets_Repulsion |
Picture_Charge | Picture_Charges_Attraction | Picture_Charges_Repulsion |
Picture_Gravitation | Picture_Cable_Attraction | Picture_Cable_Repulsion |
| Timepoint 1 | Timepoint 2 | Timepoint 3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| B | D | PR | Node | B | D | PR | Node | B | D | PR | Node |
| 0.26 | 3.14 | 0.058 | Magne-tism | 0.18 | 2.76 | 0.044 | Magne-tism | 0.2 | 3.4 | 0.042 | Field |
| 0.19 | 3.32 | 0.061 | Magnet | 0.17 | 3.00 | 0.049 | Ferromag-netism | 0.19 | 3.74 | 0.053 | Magnet |
| 0.17 | 2.71 | 0.053 | Field | 0.16 | 3.7 | 0.061 | Magnet | 0.16 | 2.92 | 0.040 | Magnetic Field |
| 0.15 | 2.54 | 0.048 | Magnetic Field | 0.14 | 3.29 | 0.053 | Electromag-netism | 0.15 | 3.21 | 0.043 | Magne-tism |
| 0.13 | 2.79 | 0.054 | Magnetic | 0.12 | 2.38 | 0.042 | Magnetic Field | 0.12 | 2.85 | 0.042 | Attraction |
| Timepoint 1 | Timepoint 2 | Timepoint 3 | Total | |
|---|---|---|---|---|
| Picture_Magnets_Attraction—Attraction | 15 | 15 | 13 | 43 |
| Picture_Cable_Attraction—Attraction | 1 | 2 | 6 | 9 |
| Picture_Charges_Attraction—Attraction | 3 | 3 | 10 | 16 |
| Picture_Magnets_Repulsion—Repulsion | 20 | 20 | 17 | 57 |
| Picture_Cable_Repulsion—Repulsion | 2 | 2 | 7 | 11 |
| Picture_Charges_Repulsion—Repulsion | 5 | 5 | 14 | 24 |
| Charge—Electric Field | 6 | 5 | 5 | 16 |
| Electric Current—Magnetic Field | - | - | 1 | 1 |
| Mass—Gravitational Field | 2 | 2 | 14 | 18 |
| Electric Current—Charge | 6 | 6 | 6 | 18 |
| Students (Timepoint 3) | Experts | ||||||
|---|---|---|---|---|---|---|---|
| B | D | PR | Node | B | D | PR | Node |
| 0.2 | 3.4 | 0.042 | Field | 0.29 | 6.75 | 0.024 | Magnet |
| 0.19 | 3.74 | 0.053 | Magnet | 0.24 | 5.00 | 0.036 | Electric Field |
| 0.16 | 2.92 | 0.040 | Magnetic Field | 0.23 | 4.00 | 0.031 | Ferromagnetism |
| 0.15 | 3.21 | 0.043 | Magnetism | 0.18 | 3.75 | 0.027 | Field |
| 0.12 | 2.85 | 0.042 | Attraction | 0.17 | 4.00 | 0.058 | Attraction |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thurn, C.M.; Hänger, B.; Kokkonen, T. Concept Mapping in Magnetism and Electrostatics: Core Concepts and Development over Time. Educ. Sci. 2020, 10, 129. https://doi.org/10.3390/educsci10050129
Thurn CM, Hänger B, Kokkonen T. Concept Mapping in Magnetism and Electrostatics: Core Concepts and Development over Time. Education Sciences. 2020; 10(5):129. https://doi.org/10.3390/educsci10050129
Chicago/Turabian StyleThurn, Christian M., Brigitte Hänger, and Tommi Kokkonen. 2020. "Concept Mapping in Magnetism and Electrostatics: Core Concepts and Development over Time" Education Sciences 10, no. 5: 129. https://doi.org/10.3390/educsci10050129
APA StyleThurn, C. M., Hänger, B., & Kokkonen, T. (2020). Concept Mapping in Magnetism and Electrostatics: Core Concepts and Development over Time. Education Sciences, 10(5), 129. https://doi.org/10.3390/educsci10050129





