The Environmental Consequences of Growth: Empirical Evidence from the Republic of Kazakhstan
Abstract
1. Introduction
2. The Models and Methods
3. Data
4. The Results
5. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Akpan, Godwin Effiong, and Usenobong Friday Akpan. 2012. Electricity consumption, carbon emissions and economic growth in Nigeria. International Journal of Energy Economics and Policy 2: 292–306. [Google Scholar]
- Andreoni, James, and Arik Levinson. 2001. The simple analytics of the environmental Kuznets curve. Journal of Public Economics 80: 269–86. [Google Scholar] [CrossRef]
- Bacon, Robert W., Soma Bhattacharya, Richard Damania, Masami Kojima, and Kseniya Lvovsky. 2007. Growth and CO2 Emissions: How Do Different Countries Fare? Environment Department Papers 113. Available online: http://www3.imperial.ac.uk/pls/portallive/docs/1/34721711.PDF (accessed on 12 December 2017).
- Baek, Jungho. 2015. A panel cointegration analysis of CO2 emissions, nuclear energy and income in major nuclear generating countries. Applied Energy 145: 133–38. [Google Scholar] [CrossRef]
- Baek, Jungho. 2015. Environmental Kuznets curve for CO2 emissions: The case of Arctic countries. Energy Economics 50: 13–17. [Google Scholar] [CrossRef]
- Baek, Jungho. 2016. A new look at the FDI-income-energy-environment nexus: Dynamic panel data analysis of ASEAN. Energy Policy 91: 22–27. [Google Scholar] [CrossRef]
- Baek, Jungho, and Yoon Jung Choi. 2017. Does foreign direct investment harm the environment in developing countries? Dynamic panel analysis of Latin American countries. Economies 5: 39. [Google Scholar] [CrossRef]
- Baek, Jungho, and Hyun Seok Kim. 2011. Trade liberalization, economic growth, energy consumption and the environment: Time series evidence from G-20 countries. Journal of East Asian Economic Integration 15: 3–32. [Google Scholar] [CrossRef]
- Baek, Jungho, and Hyun Seok Kim. 2013. Is economic growth good or bad for the environment? Empirical evidence from Korea. Energy Economics 36: 744–49. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1979. Distributions of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Frankel, Jeffrey A., and Andrew K. Rose. 2005. Is trade good or bad for the environment: Sorting out the causality. Review of Economics and Statistic 87: 85–91. [Google Scholar] [CrossRef]
- Halicioglu, Ferda. 2009. An econometric study of CO2 emissions, energy consumption, income and foreign trade in Turkey. Energy Policy 37: 1156–64. [Google Scholar] [CrossRef]
- Harbaugh, William T., Arik Levinson, and David M. Wilson. 2002. Reexamining the empirical evidence for an environmental Kuznets curve. Review of Economics and Statistic 84: 541–51. [Google Scholar] [CrossRef]
- Heil, Mark T., and T.M. Selden. 2001. Carbon emissions and economic development: Future trajectories based on historical experience. Environment and Development Economics 6: 63–83. [Google Scholar] [CrossRef]
- Holtz-Eakin, D., and Thomas M. Selden. 1995. Stoking the fires? CO2 emissions and economic growth. Journal of Public Economics 57: 85–101. [Google Scholar] [CrossRef]
- Ibrahiem, Dalia M. 2016. Environmental Kuznets curve: An empirical analysis for carbon dioxide emissions in Egypt. International Journal of Green Economics 10: 136–50. [Google Scholar] [CrossRef]
- Itkonen, Juha V. A. 2012. Problems estimating the carbon Kuznets curve. Energy 39: 274–80. [Google Scholar] [CrossRef]
- Iwata, Hiroki, Keisuke Okada, and Sovannroeun Samreth. 2010. Empirical study on the environmental Kuznets curve for CO2 in France: The role of nuclear energy. Energy Policy 38: 4057–63. [Google Scholar] [CrossRef]
- Iwata, Hiroki, Keisuke Okada, and Sovannroeun Samreth. 2011. A note on the environmental Kuznets curve for CO2: A polled mean group approach. Applied Energy 88: 1986–96. [Google Scholar] [CrossRef]
- Jaforullah, Mohammad, and Alan King. 2017. The econometric consequences of an energy consumption variable in a model of CO2 emissions. Energy Economics 63: 84–91. [Google Scholar] [CrossRef]
- Jalil, Abdul, and Syed F. Mahmud. 2009. Environment Kuznets curve for CO2 Emissions: A cointegration analysis for China. Energy Policy 37: 5167–72. [Google Scholar] [CrossRef]
- John, Andrew, and Rowena A. Pecchenino. 1994. An overlapping generations model of growth and the environment. Economic Journal 104: 1393–410. [Google Scholar] [CrossRef]
- Kivyiro, Pendo, and Heli Arminen. 2014. Carbon dioxide emissions, energy consumption, economic growth, and foreign direct investment: Causality analysis for Sub-Saharan Africa. Energy 74: 595–606. [Google Scholar] [CrossRef]
- Liddle, Brantley. 2015. What are the carbon emissions elasticities for income and population? Bridging STIRPAT and EKC vis robust heterogeneous panel estimates. Global Environmental Change 31: 62–73. [Google Scholar] [CrossRef]
- List, John A., and Craig A. Gallet. 1999. The environmental Kuznets curve: Does one size fit all? Ecological Economics 31: 409–23. [Google Scholar] [CrossRef]
- Liu, Xuemei. 2005. Explaining the relationship between CO2 emissions and national Income: The role of energy consumption. Economics Letters 87: 325–28. [Google Scholar] [CrossRef]
- Lopez, Ramon. 1994. The environment as a factor of production: The effects of economic growth and trade liberalization. Journal of Environmental Economics and Management 27: 163–84. [Google Scholar] [CrossRef]
- Marsiglio, Simone, Alberto Ansuategi, and Maria C. Gallastegui. 2016. The environmental Kuznets curve and the structural change hypothesis. Environmental and Resource Economics 63: 265–88. [Google Scholar] [CrossRef]
- Martinez-Zarzoso, Inmaculada, and Aurelia Bengochea-Morancho. 2004. Pooled mean group estimation of an environmental Kuznets curve for CO2. Economics Letters 82: 121–26. [Google Scholar] [CrossRef]
- Mikayilov, Jeyhun, Vusal Shukurov, and Sabuhi Yusifov. 2017. The impact of economic growth and population on CO2 emissions from transport sector: Azerbaijan case. Academic Journal of Economic Society 3: 60–67. [Google Scholar]
- Mitic, Petar, M.Olja Ivanovic, and Aleksandar Zdravkovic. 2017. A cointegration analysis of real GDP and CO2 emissions in transitional countries. Sustainability 9: 568. [Google Scholar] [CrossRef]
- Moomaw, William R., and Gregory C. Unruh. 1997. Are environmental Kuznets curve misleading us? The case of CO2 emissions. Environment and Development Economics 2: 451–63. [Google Scholar] [CrossRef]
- Narayan, Paresh K. 2005. The saving and investment nexus for China: Evidence from cointegration tests. Applied Economics 37: 1979–90. [Google Scholar] [CrossRef]
- Panayotou, Theodore. 1993. Empirical Tests and Policy Analysis of Environmental Degradation at Different Stages of Economic Development. Geneva: ILO. [Google Scholar]
- Pao, Hsiao-Tien, and Chung-Ming Tsai. 2011. Multivariate Granger causality between CO2 emissions, energy consumption, FDI (foreign direct investment) and GDP (gross domestic product): Evidence from a panel of BRIC (Brazil, Russian Federation, India and China) countries. Energy 36: 685–93. [Google Scholar] [CrossRef]
- Pao, Hsiao-Tien, Hsiao-Cheng Yu, and Yeou-Herng Yang. 2011. Modeling the CO2 emissions, energy use and economic growth in Russia. Energy 36: 5094–100. [Google Scholar] [CrossRef]
- Perman, Roger, and David I. Stern. 2003. Evidence from panel unit root and cointegration tests that the environmental Kuznets curve does not exist. Australian Journal of Agricultural and Resource Economics 47: 325–47. [Google Scholar] [CrossRef]
- Perron, Pierre, and Timothy J. Vogelsang. 1992. Testing for a unit root in a time series with a changing mean: Corrections and extensions. Journal of Business and Economic Statistics 10: 467–70. [Google Scholar]
- Pesaran, M. Hashem, Yongcheol Shin, and Richard J. Smith. 2001. Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Roberts, Timmons J., and Peter Grimes. 1997. Carbon intensity and economic development 1962–1991: A brief exploration of the environmental Kuznets curve. World Development 25: 191–98. [Google Scholar] [CrossRef]
- Selden, Thomas, and Daqing Song. 1995. Neoclassical growth, the J curve for abatement, and the inverted U curve for pollution. Journal of Environmental Economics and Management 29: 162–68. [Google Scholar] [CrossRef]
- Shafik, Nemat, and Sushenjit Bandyopadhyay. 1992. Economic Growth and Environmental Quality: Time Series and Cross-Country Evidence. NBER Working Paper No. 904. Washington: World Bank Publications. [Google Scholar]
- Shahbaz, Muhammad, Mihai Mutascu, and Parvez Azim. 2013. Environmental Kuznets curve in Romania and the role of energy consumption. Energy Economics 18: 165–73. [Google Scholar] [CrossRef]
- Soytas, Ugur, and Ramazan Sari. 2009. Energy consumption, economic growth, and carbon emissions: Challenges faced by an EU candidate member. Ecological Economics 68: 1667–75. [Google Scholar] [CrossRef]
- Tamazian, Artur, and Bhaskara B. Rao. 2010. Do economic, financial and institutional developments matter for environmental degradation? Evidence from transitional economies. Energy Economics 32: 137–45. [Google Scholar] [CrossRef]
- Tutulmaz, Onur. 2015. Environmental Kuznets curve time series application for Turkey: Why controversial results exist for similar models? Renewable and Sustainable Energy Reviews 50: 73–81. [Google Scholar] [CrossRef]
- Yang, Xuechun, Feng Lou, Mingxing Sun, Renqing Wang, and Yutao Wang. 2017. Study of the relationship between greenhouse gas emissions and the economic growth of Russia based on the Environmental Kuznets curve. Applied Energy 193: 162–73. [Google Scholar] [CrossRef]
| 1 | It is worth discussing main theoretical explanations for the EKC hypothesis. One of the main theories explaining the ECK is that the shape of the EKC reflects changes in the demand for environment quality with growth, known as the income effect (Lopez 1994). That is, income growth driven by accumulation of production factors increases firms’ demand for pollution inputs. At the same time, demand for environmental quality rises with growth as the willingness to pay for a clean environment increases. An alternatively widely cited explanation for the EKC is the threshold effect (John and Pecchenino 1994; Selden and Song 1995). That is, since pollution could be unregulated entirely at the early stage of development, pollution at first tends to rise with growth. After some threshold has been reached and regulation is implemented, however, pollution tends to decline with growth. The increasing returns to abatement effect argues that as the scale of abatement increases, its efficiency tends to increase, which makes abatement more profitable and hence reduces pollution levels as more abatement is undertaken (Andreoni and Levinson 2001). Finally, the most recent explanation for the EKC is that growth tends to shift economic production system from high polluting industries to low polluting industries, known as the structural change effect (Marsiglio et al. 2016). |
| 2 | Another advantage of this method is that it has been proven to have superior small sample properties, which makes it a good choice for our sample of less than 30 annual observations compared to other cointegration methods (i.e., Johansen method). |
| 3 | The authors thank an anonymous referee for raising this issue discussed here. |
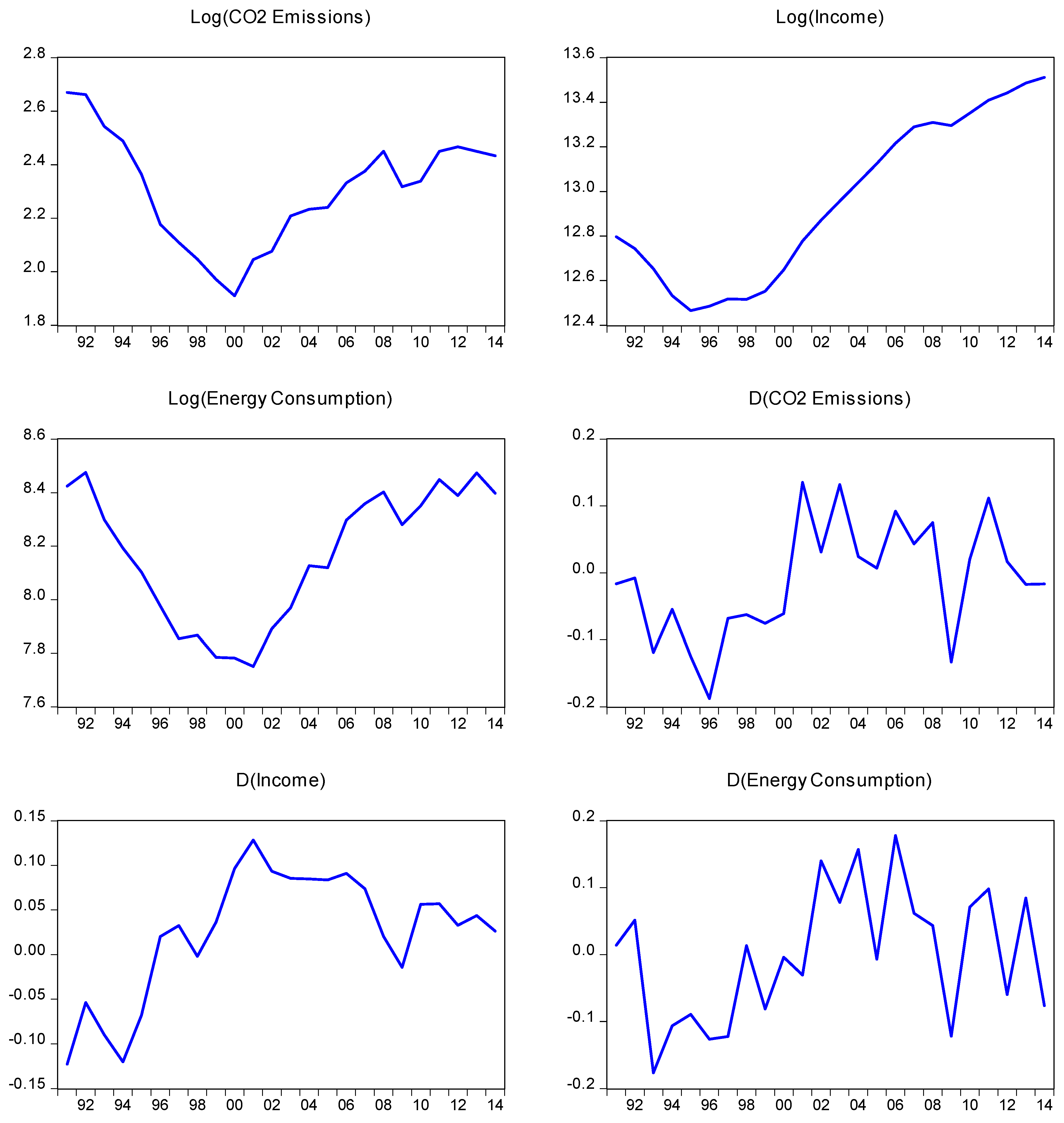
| 4 | It is worth mentioning that since Kazakhstan’s independence from the USSR in 1991, the collapse of demand for Kazakhstan’s heavy industry products has resulted in a sharp contraction of the economy during the 1990s. Since the beginning of economic reforms and opening up to the outside world in the early 2000s, however, Kazakhstan’s economy has grown sharply (except for the global financial crisis in 2009). As illustrated in Figure 1, therefore, CO2 emissions per capita, energy consumption per capita, and income per capita have persistently declined up to 2000 and have increased since then. |
| 5 | It should be pointed out that when there is no trend in ADF and PV tests, the unit root hypothesis for the two income variables cannot be rejected. With the time trend included, however, we can strongly reject the null for both variables. Thus, the best characterization of the two income variables seems to be as a trend-stationary process; that is, a process that is stationary about its time trend. |
| 6 | The Schwarz Bayesian Criterion (SBC) generally used for low small size of studies like this paper also identifies ARDL (1, 0, 0, 0) as the optimal model. |
| 7 | Among five cases of testing for cointegration, case III (unrestricted intercept and no trend) is used for the analysis. The associated 5% and 10% critical value bounds are (3.23, 4.35) and (2.72, 3.77), respectively, which are taken from Table CI (iii) Case III: unrestricted intercept and no trend on p. 300 of Pesaran et al. (2001). |
| 8 | In order to capture the effects of technological progress or enhanced environmental awareness on CO2 emissions, a time trend is included in estimating Equation (2). However, our findings are more conclusive when the F-test is applied to Equation (2) without a time trend. Further, a time trend is not statistically significant even at the 10% level. Hence, a time trend is excluded from the final model. |
| 9 | As a cross-check, we also perform the bounds t-test of H0: σ0 = 0 against H1: σ0 < 0. If the null is rejected using the upper critical value bounds tabulated by Pesaran et al. (2001, pp. 303–4), this would support cointegration relationship among the variables. In our case, the t-statistic on ct−1 in −4.58. When we look at Table CII(iii) (Case III: unrestricted intercept and no trend) on p. 303 of Pesaran et al. (2001), the associated 5% and 10% critical value bounds for the t-statistic are (−2.86, −3.78) and (−2.57, −3.46), respectively. Even at the 5% level, therefore, this result confirms our conclusion that there is a long-run relationship among the four variables. |
| 10 | Using different data from different sources perhaps results in such finding. In this paper, for example, CO2 emissions are taken from Statistical Yearbook published by Agency on Statistics of the Republic of Kazakhstan, whereas income and energy consumption are obtained from World Development Indicator (WDI) database. For this reason, we also re-estimate Equation (2) after collecting CO2 emissions from WDI. However, we obtain almost the same results. |
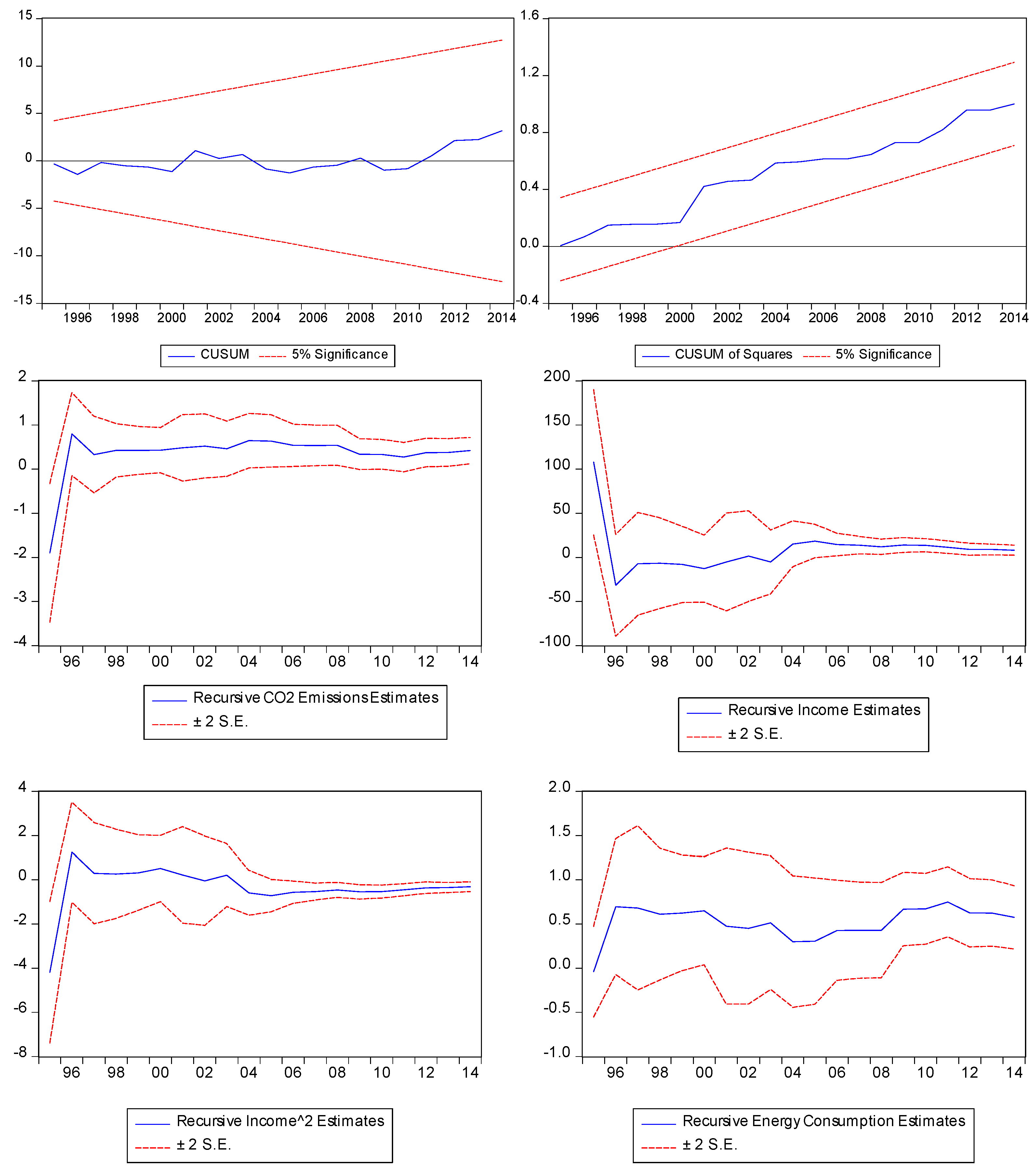
| 11 | It should be pointed out that, although we have a relatively small sample size, the regression fits reasonably well (adj. R2 = 0.67) and passes all the necessary diagnostic tests (Panel C in Table 3). Further, we also adopt other alternative cointegration methods such as Fully Modified Least Squares (FMOLS), Dynamic Least Squares (DOLS), and Canonical Cointegration Regression (CCR) for robustness check, although those methods require all the variables to be I(1) processes. We also find almost the same results as those reported in Table 3. Combined with our diagnostic results, therefore, this should somehow mitigate our concern with the relatively short period of dataset and strengthen the credibility of our findings. |
| Mean | Standard Deviation | Min | Max | |
|---|---|---|---|---|
| CO2 emissions | 10.249 | 2.099 | 6.756 | 14.435 |
| Income | 452,622.2 | 165,430.3 | 259,194.0 | 738,066.4 |
| Energy consumption | 3626.116 | 855.193 | 2324.548 | 4796.144 |
| Variable | ADF Test | |||
| Level | First Difference | |||
| CO2 emissions | −1.855 (0) | −3.574 ** (0) | ||
| Income | −3.730 ** (0) | |||
| (Income)2 | −3.777 ** (0) | |||
| Energy consumption | −1.913 (0) | −4.252 ** (1) | ||
| Variable | Perron-Vogelsang Test | |||
| Level | Time Break | First Difference | Time Break | |
| CO2 emissions | −2.929 (1) | 2003 | −6.569 ** (1) | 2000 |
| Income | −6.299 ** (1) | 2000 | ||
| (Income)2 | −6.259 ** (1) | 2000 | ||
| Energy consumption | −2.195 (1) | 2003 | −5.237 ** (1) | 2001 |
| Panel A: Short-Run Results | |||||
| ∆(income)t | ∆(income)t2 | ∆(energy consumption)t | ect−1 | ||
| 6.858 (2.208) ** | −0.268 (−2.256) ** | 0.619 (3.315) ** | −0.636 (−3.936) ** | ||
| Panel B: Long-Run Results | |||||
| incomet | incomet2 | energy consumptiont | Constant | ||
| 10.779 (1.689) * | −0.422 (−1.725) * | 0.973 (10.448) ** | −74.444 (−1.793) * | ||
| Panel C: Diagnostic Statistics | |||||
| F-statistic | LM | RESET | Normality | ARCH | Heteroskedasticity |
| 8.453 ** | 0.561 [0.454] | 0.829 [0.363] | 0.607 [0.738] | 0.236 [0.889] | 1.069 [0.397] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbota, A.; Baek, J. The Environmental Consequences of Growth: Empirical Evidence from the Republic of Kazakhstan. Economies 2018, 6, 19. https://doi.org/10.3390/economies6010019
Akbota A, Baek J. The Environmental Consequences of Growth: Empirical Evidence from the Republic of Kazakhstan. Economies. 2018; 6(1):19. https://doi.org/10.3390/economies6010019
Chicago/Turabian StyleAkbota, Amantay, and Jungho Baek. 2018. "The Environmental Consequences of Growth: Empirical Evidence from the Republic of Kazakhstan" Economies 6, no. 1: 19. https://doi.org/10.3390/economies6010019
APA StyleAkbota, A., & Baek, J. (2018). The Environmental Consequences of Growth: Empirical Evidence from the Republic of Kazakhstan. Economies, 6(1), 19. https://doi.org/10.3390/economies6010019






