Range-Based Localization of a Wireless Sensor Network for Internet of Things Using Received Signal Strength Indicator and the Most Valuable Player Algorithm

Abstract

The localization of the nodes in wireless sensor networks is essential in establishing effective communication among different devices connected, within the Internet of Things. This paper proposes a novel method to accurately determine the position and distance of the wireless sensors linked in a local network. The method utilizes the signal strength received at the target node to identify its location in the localized grid system. The Most Valuable Player Algorithm is used to solve the localization problem. Initially, the algorithm is implemented on four test cases with a varying number of sensor nodes to display its robustness under different network occupancies. Afterward, the study is extended to incorporate actual readings from both indoor and outdoor environments. The results display higher accuracy in the localization of unknown sensor nodes than previously reported.

1. Introduction

In the realm of networking and communication, wireless sensor networks (WSN) play a pivotal role in establishing connections among disparate devices situated at distant locations. Usually, hundreds of wireless sensors share a network to communicate useful information with each other. Therefore, WSNs are becoming crucial, supported by increasing trends of digitalization [1]. This lays down the cornerstone of the concept of the Internet of Things (IoT), which is considered to be the next step in a digital society, whereby, multi-purpose devices share a networking platform to communicate with each other in a common language [2,3]. Throughout a WSN, sensor nodes are continuously transmitting and receiving the information from the base station and are widely used in the secured networks serving military, healthcare, environment monitoring, and smart home systems [4]. These applications often require localizing the node by determining both the distance and coordinates from a known node or router. The purpose of ascertaining the location of a specific node location is to track the information route while managing and optimizing network latency. Therefore, the unavailability of localization data ends up in the deteriorated performance and control of WSN for a specific application.

In the process of localization, the position of the node with the unknown or consistently changing position (target node) is determined by utilizing the signals from nearby reference nodes, usually referred to as anchors. The localization technique aims to determine the coordinate vectors of the target node. Therefore, the localization technique is carried out in two steps: (i) Estimating the distance of the target node from the reference node; (ii) determining geographical coordinates using the estimated distance and known coordinates of anchors. In WSN, various methods are used to carry out localization including the range-free method and range-based method [5].

Hop count-based method [6] and the fingerprint algorithm [7] are examples of a range-free method. Usually, such methods are cost-effective as they utilize topological information but exhibit low accuracy. They skip the step of distance estimation as an intermediate step and directly determine the coordinates. The method used in [6] is easy to implement and relatively simple but the localization error increases with the distance. In the fingerprint algorithm, the data are recorded for the predefined and known locations and the unknown locations are estimated offline by matching the measured values with those recorded earlier for the known cases. Two indoor localization algorithms, namely Comparative Received Signal Strength (CRSS) Algorithm and vector algorithm, have been compared in [7]. The effects of operating frequency, number of access points, and map resolution have been investigated for both cases to conclude the superior performance of vector algorithm as CRSS suffers from ambiguity and needs more access points and higher frequency. A modified version of k-Nearest Neighbor algorithm has been proposed in [8] which uses the signal matching approach, on a single test case, to claim an increase in the accuracy of signal fingerprint positions.

Range-based methods, on the other hand, estimates the distance between the nodes. Global positioning system (GPS) [9], time difference of arrival (TDoA) [10,11], time of arrival (ToA) [12], acoustic energy [13], angle of arrival (AoA) [14], and received signal strength indicator (RSSI) [15] are the most common range-based methods used for distance estimation. For the line-of-sight (LoS) applications operating in the outdoors, GPS is the most widely used method despite being expensive, requiring more hardware, and consuming high power. Moreover, such applications are beyond the scope of WSNs under consideration in this study. TDoA-based distance estimation is sensitive to synchronism among the nodes of interest. Moreover, to ensure this synchronism, two signals transmitted at different speeds are required, making it an inefficient method in terms of both energy and cost. Similarly, for ToA, high-resolution clocks are required to determine the exact time of arrival. Moreover, it needs the exact speed of signal propagation. AoA is a directional distance estimation method and therefore, relies on the angle of the antenna receiving the incoming signal, resulting in increased cost of the hardware. In contrast to other methods, RSSI-based localization is independent of the antenna array, synchronization requirements, and any other extra hardware, and hence it is selected to carry out the localization of target nodes in this research work.

The signal strength received at a node depends on multiple factors including the power of the transmitted signal and the path terrain. However, this work will take into consideration the impact of path loss and the distance between two nodes [16]. The path loss is substantiated by reflection, diffraction, and scattering of the signal [17]. Moreover, the propagation path also incurs a certain loss in signal strength. RSSI is the measure of signal power received at any node and is measured in dBm. Many factors influence the RSSI [18,19,20] at a certain node including the relative movements of transmitter and/or receiver. It must be noted that even if devices stay static, the motion of objects in the propagation environment may also affect the RSSI at any instant [21,22]. The multivariate dependencies of RSSI inhibit the formation of a direct relationship with the distance of the nodes emanating signals. Therefore, an accurate and systematic methodology is required to determine both the distance and coordinates of unknown nodes. The localization of the target nodes is crucial in minimizing network latency by using the optimal path for a data package transfer throughout the network.

In this paper, a relatively new approach, Most Valuable Player Algorithm (MVPA), is applied to localize a sensor node given only RSSI. MVPA is a sports competition-based optimization algorithm, well-ranked in various benchmarking studies. In the past, it was used in energy-management systems and electromagnetic wave theory. However, despite its superior performance, it has not been used in sensor localization in a WSN so far. This work not only explains the flow of the proposed approach but also opens an avenue for future research of how it may be applied to other similar problems. It applies a two-fold technique to localize the target sensor node. First, the relationship between RSSI and distance from reference to target node is ascertained by developing a nonlinear regression model. In the second stage, MVPA is used to convert the distance data into (x, y) coordinates of a 2-dimensional plane. Four test cases with a different number of nodes reflecting variable network occupancy are studied. The results obtained using MVPA are compared with renowned classical techniques, whereby the proposed approach outperforms other techniques in terms of accuracy and parametric dependence. Mean square error sees a reduction by a factor of 10 for case 3, and case 4 when contrasted with the second-best performing algorithm, reflecting the superiority of MVPA. To demonstrate the improvement on a real-world example, the experimental set-up of [23] is reused followed by comparative discussion indicating higher coordinate estimation accuracy with MVPA than other contemporary algorithms. The remainder of this paper is organized as follows. The proposed approach is described in Section 2. The simulation tests along with the experimental study are combined in Section 3. Finally, conclusions are drawn in Section 4.

2. Proposed Approach

2.1. A. Description

Very often a WSN, consisting of several nodes, is dispersed in a geographical area. However, in some applications, the location (the x and y coordinates in 2d) of these nodes called target is needed. Along with these target nodes, usually, there are some reference nodes with known locations or coordinates. In this work, routers play the role of reference nodes while end device nodes play the role of target nodes. Therefore, the objective of the proposed approach is to find the location of target nodes ($x$ and $y$ coordinates) based on the distance estimation (estimated from RSSI) knowing the locations of the reference nodes.

The flowchart of the proposed approach is given in Figure 1. It starts by estimating the distances of different target nodes with respect to the reference nodes based on measured RSSI. Measurements are carried out with the loop-infinite option to cater to infinite packet transmission [23]. If $P_{t }$ represents the transmitted power and $P_L\left(d\right)$ denotes the path loss power at distance$d$ in dBm, then RSSI is given by:

$$RSSI=P_t-P_L\left(d\right)$$

(1)

Here, $P_L\left(d\right)$ can be represented by Log-Normal Shadowing Model (LNSM) in terms of path loss at a known point $d_0$, $P_L\left(d_0\right)$, path loss exponent,$n$, and zero-mean Gaussian random variable with $\sigma$ standard deviation, $X_{\sigma }$, as below:

$$P_L\left(d\right)=P_L\left(d_0\right)+10nlog\left(\frac{d}{d_0}\right)+X_{\sigma }$$

(2)

Combining (1) and (2) relates RSSI, in dBm with the distance between the nodes.

$$RSSI=P_t-P_L\left(d_0\right)+10nlog\left(\frac{d}{d_0}\right)+X_{\sigma }$$

(3)

The nonlinear regression model is used to estimate the distances from (3). Once all distances are obtained using regression, it is pertinent to use a systematic way to provide all distances to the algorithm. The matrix, named $DistanceRT$, combines all distances in a closed-form. Hence, it becomes easier for the algorithm to perform matrix operations making the approach speed efficient. All distances, denoted by, $d_{ij}$, between the reference node $i$ and the target node $j$, are restructured in a matrix as follows:

$$DistanceRT=\left[\begin{array}{cccc}{d}_{11}& d_{12}& \dots & d_{1n}\\ d_{21}& d_{22}& \dots & d_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ d_{m1}& d_{m1}& \dots & d_{mn}\end{array}\right]$$

(4)

In (4), $n$ is the number of target nodes and $m$ is the number of reference nodes.

After that, the MVPA is used to optimize the problem at hand. In other words, the MVPA is used to determine the location ($x$ and $y$ coordinates) of target nodes by minimizing the following objective function:

$$\begin{gathered} OF=\frac{1}{n\times m}\left\{\left|d_{11}-d_{11}^{\prime }\right|+\left|d_{12}-d_{12}^{\prime }\right|+\dots \left|d_{1n}-d_{1n}^{\prime }\right|+\left|d_{21}-d_{21}^{\prime }\right|+\left|d_{22}-d_{22}^{\prime }\right|+\dots +\left|d_{2n}-d_{2n}^{\prime }\right| \\ +\left|d_{m1}-d_{m1}^{\prime }\right|+\left|d_{m2}-d_{m2}^{\prime }\right|+\dots +\left|d_{mn}-d_{mn}^{\prime }\right|\right\} \end{gathered}$$

(5)

where $d_{ij}$ is the Euclidian distance between reference node $i$ and target node $j$ estimated using RSSI and $d_{ij}^{\prime }$ is the Euclidian distance between reference node $i$ and target node $j$ calculated using the MVPA and it is expressed as follows:

$$d_{ij}^{\prime }=\sqrt{{\left(x_i-x_j\right)}^2+{\left(y_i-y_j\right)}^2}$$

(6)

where $x_i \mathrm{and} y_i$ are the location of the target node $i$ to be calculated by the optimization process (i.e., design variables).

The objective function can be simplified in a more compact form as follows:

$$OF=\frac{1}{n\times m}{\displaystyle \sum }_{i=1}^m\left({\displaystyle \sum }_{\begin{array}{c}j=1\end{array}}^n\left|d_{ij}-d_{ij}^{\prime }\right|\right)$$

(7)

A matrix containing all possible connection distances, $d_{ij}^{\prime }$, of a specific WSN form a solution set. Several of such solutions form a single team and then similar teams compete together based on the objective function of (7), as detailed in Algorithm 1 in the next section. The number of teams, number of players, and number of fixtures are hyperparameters of the algorithm and are usually chosen during the execution phase of the algorithm by trial-and-error.

2.2. B. Most Valuable Player Algorithm (MVPA)

A. General description

MVPA is one of the newest modern optimization algorithms [24]. It is inspired by sports competitions. It is applied to various fields with always excellent results. In [24] it was applied to a set of mathematical functions and compared with 13 optimization algorithms in terms of overall success to find the global optimum and the number of functions evaluations; it was found to be the best one. In [25], a comparative study was carried out between modern optimization algorithms inspired by sports events including the MVPA. The MVPA was ranked first for unimodal problems and equally ranked first with two other algorithms for multimodal problems. In [26], it was applied in the field of electromagnetics. In [27] it was used for efficient energy management in a microgrid with intermittent renewable energy and storage sources. In [28] the MVPA was applied to solve the direction overcurrent relays coordination problem. In [29] a binary version of the MVPA was developed and implemented to optimize wind farm layouts considering obstacles. In [30] an improved version of the MVPA by doubling the training mechanism was proposed and compared with other optimization algorithms for engineering design problems. In [31] an enhanced version of the MVPA was proposed and applied to the optimal power flow problem.

The pseudocode of the MVPA used in this paper is given in Algorithm 1. The MVPA starts by generating a random population of players in a given search space (Line 3 in Algorithm 1). Then for a certain number of fixtures, these players will compete collectively (in teams to win the league championship) and individually to win the trophy of the best player called in some sports like basketball the Most Valuable Player (MVP). This competition (lines 5 to 15 in Algorithm 1) will improve the skills of the players until the optimization problem at hand is solved. In other words, the solutions are improved iteratively by minimizing the objective function of Equation (5). Other steps are added to the MVPA to improve its performance like the application of greediness and application of elitism in addition to the diversification of players. More details about the MVPA can be found in [24].

B. Context description

In the previous section, we have described the MVPA in its general form. The MVPA is used in this paper to solve the optimization problem of estimating the locations of target nodes formulated in the previous sections. To do so, some random locations (also called solutions and using the MVPA terminology called players and teams) are first generated in the initialization phase. Here it is worth mentioning that a solution is represented by a vector of $x_i$ and $y_i$ of all target nodes. Therefore, if there are $N$ target nodes any solution is represented by a vector of $2\times N$ values. For instance, if there are three target nodes a solution is represented as follows:

$$Solution=\left[x_1,x_2,x_3,y_1,y_2,y_3\right]$$

(8)

where: $\left(x_1,y_1\right), \left(x_2,y_2\right)$, and $\left(x_3,y_3\right)$ are the coordinates of target node #1, targe node #2, and targe node #3, respectively.

After that, these solutions move inside the search space of the problem in hand until the best locations are found (using the MVPA terminology this is achieved in the competition phase where the aim is to improve the solutions). Other numerical stages and phases are then performed on the solutions to improve them as aforesaid. This process is iterative, i.e., the process is repeated until a termination criterion is fulfilled (using the MVPA terminology the algorithm iterates MaxNFix times). In the end, the best solution called the MVP is given as the output. In our case, the best solution will be the best locations for all the target nodes.

Algorithm 1. MVPA pseudocode.
1	Inputs		ObjFunction (objective function), ProblemSize (dimension of the problem), PlayersSize (number of players), TeamsSize (number of teams) and MaxNFix (maximum number of fixtures)
2	Output		MVP (best solution)
3	Initialization
4	for fixture=1: MaxNFix
5	for i = 1:TeamsSize
6	${\mathrm{TEAM}}_{\mathrm{i}}=$ Select the team number i from the league’s teams
7	${\mathrm{TEAM}}_{\mathrm{j}}=$ Randomly select another team j from the league’s teams where j ≠ i
8	${\mathrm{TEAM}}_{\mathrm{i}}={\mathrm{TEAM}}_{\mathrm{i}}+\mathrm{rand}\times \left({\mathrm{FranchisePlayer}}_{\mathrm{i}}-{\mathrm{TEAM}}_{\mathrm{i}}\right)+2\times \mathrm{rand}\times \left(\mathrm{MVP}-{\mathrm{TEAM}}_{\mathrm{i}}\right)$
9			if ${\mathrm{TEAM}}_{\mathrm{i}}\mathrm{wins}$ against ${\mathrm{TEAM}}_{\mathrm{j}}$
10	${\mathrm{TEAM}}_{\mathrm{i}}={\mathrm{TEAM}}_{\mathrm{i}}+\mathrm{rand}\times \left({\mathrm{TEAM}}_{\mathrm{i}}-{\mathrm{FranchisePlayer}}_{\mathrm{j}}\right)$
11			else
12	${\mathrm{TEAM}}_{\mathrm{i}}={\mathrm{TEAM}}_{\mathrm{i}}+\mathrm{rand}\times \left({\mathrm{FranchisePlayer}}_{\mathrm{j}}-{\mathrm{TEAM}}_{\mathrm{i}}\right)$
13	end if
14	Check if there are players outside the search space
15	end for
16	Application of greediness
17	Application of elitism
18	Diversification
19	end for

3. Application and Results

To validate the proposed approach both simulation and actual test cases are investigated. Initially, four simulation-based cases are investigated and discussed. Then, the real-time experimental study is presented and discussed. Furthermore, a comparison study is carried out with the established metaheuristic techniques to proclaim the superior performance of the proposed technique. The comparisons are drawn with Biogeography-Based Optimization (BBO), Differential Evolution (DE), Particle Swarm Optimization (PSO), and Genetic Algorithm (GA). The four selected comparing algorithms are among the most well-known optimization metaheuristics. PSO is a population-based stochastic optimization method developed by Eberhart and Kennedy in 1995. It is inspired by the social behavior of bird flocking or fish schooling [32,33]. GA is the most famous global optimization method, and it is based on Darwin’s theory about evolution. DE was initially developed by Kenneth V. Price and R. Storn in 1995 while trying to solve the Chebyshev polynomial-fitting problem [34]. It stems from the genetic annealing algorithm which was also developed by Kenneth V. Price [35]. The BBO is an optimization algorithm inspired by biogeography [36].

Furthermore, a fifth optimization algorithm called Sequential Quadratic Programming (SQP) is also used for comparison. SQP is one of the most performant methods for the numerical solution of constrained nonlinear optimization problems. Unlike the other methods used in this paper (i.e., the metaheuristics) which are based on a random search, this method is deterministic and gives always the same results starting from the same point.

3.1. A. Simulation Study

3.1.1. Case 1: Illustrative Case

This first case is an illustrative one used to explain the developed approach rather than to assess its performance.

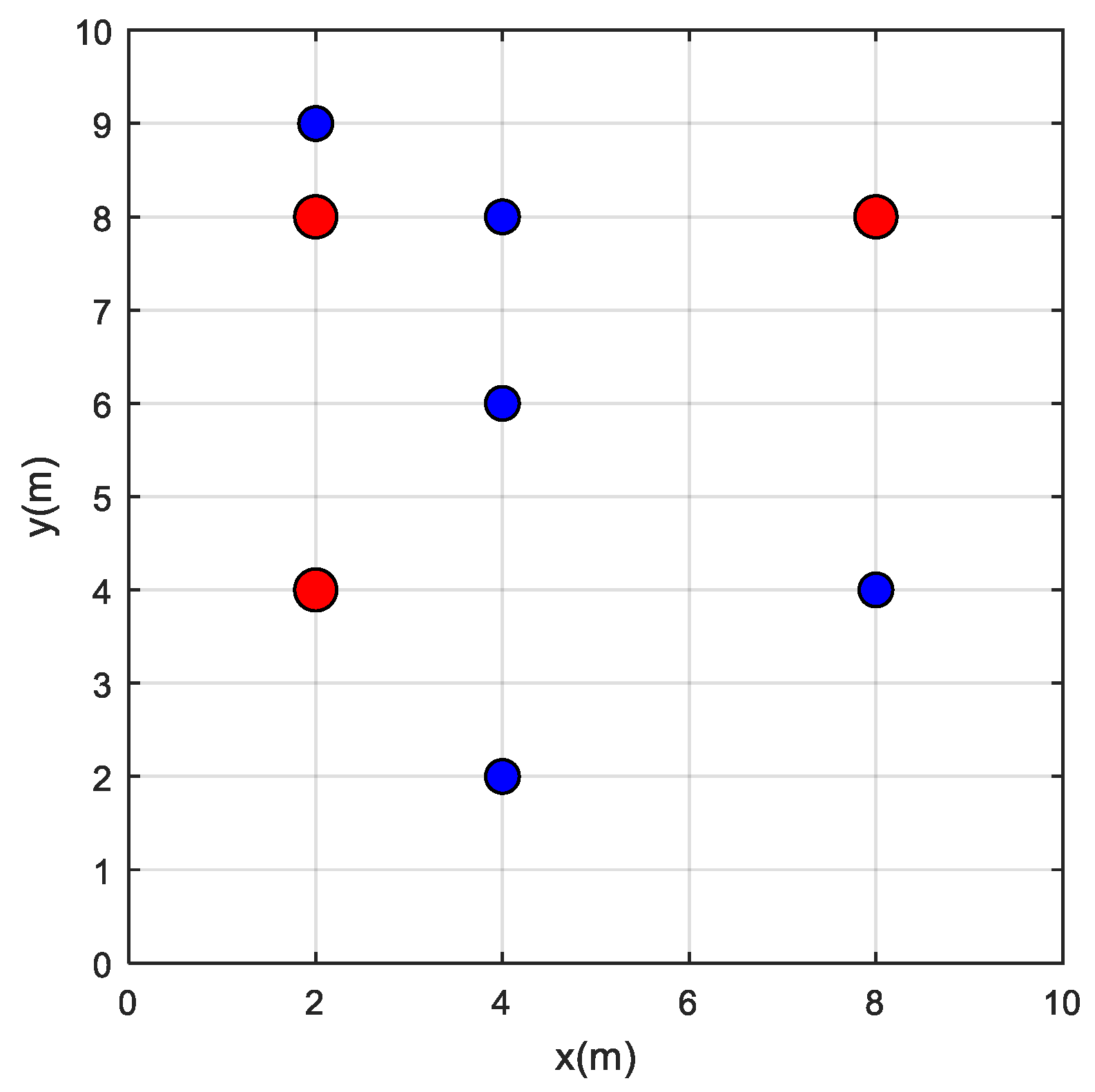
Let us assume that we have three reference nodes located at (2,4), (8,8), and (2,8) along with five target nodes located at (4,2), (8,4), (4,6), (4,8), and (2,9) as shown in Figure 2. Using the proposed approach first the distances between reference nodes and target nodes are estimated as follows:

$$\mathrm{DistanceRT}=\left[\begin{array}{ccccc}{\mathrm{d}}_{11}& {\mathrm{d}}_{12}& {\mathrm{d}}_{13}& {\mathrm{d}}_{14}& {\mathrm{d}}_{15}\\ {\mathrm{d}}_{21}& {\mathrm{d}}_{22}& {\mathrm{d}}_{23}& {\mathrm{d}}_{24}& {\mathrm{d}}_{25}\\ {\mathrm{d}}_{31}& {\mathrm{d}}_{32}& {\mathrm{d}}_{33}& {\mathrm{d}}_{34}& {\mathrm{d}}_{35}\end{array}\right]$$

(9)

which is numerically given by:

$$\mathrm{DistanceRT}=\left[\begin{array}{ccccc}2.8284& 6.0000& 2.8284& 4.4721& 5.0000\\ 7.2111& 4.0000& 4.4721& 4.0000& 6.0828\\ 6.3246& 7.2111& 2.8284& 2.0000& 1.0000\end{array}\right]$$

(10)

As explained before, in this subsection we assume that these distances are estimated using RSSI.

Then the MVPA solves the optimization problem to calculate $\left(x_1,y_1\right)$,$\left(x_2,y_2\right),$ $\left(x_3,y_3\right)$, $\left(x_4,y_4\right)$, and $\left(x_5,y_5\right)$ while minimizing the objective function given by Equation (7). The results (i.e., the coordinates ($x_i,y_i)$) along with the mean squared errors (MSE) obtained using MVPA and the other five algorithms are tabulated in

Table 1. Comparison of actual locations with those obtained using different algorithms for case 1.

Actual Values		MVPA		BBO		DE		PSO		GA		SQP
xi	yi	xi	yi	xi	yi	xi	yi	xi	yi	xi	yi	xi	yi
4.000	2.000	4.000	2.000	4.037	2.017	3.940	1.975	4.003	2.003	3.157	1.439	4	2
8.000	4.000	8.000	4.000	8.011	4.018	7.999	3.994	8.000	3.999	8.154	3.560	7.999	4
4.000	6.000	4.000	6.000	4.045	5.926	4.036	6.018	4.005	5.999	3.919	6.289	4	6
4.000	8.000	4.000	8.000	4.024	7.948	4.015	8.134	4.013	7.994	3.973	8.058	4	8
2.000	9.000	2.000	9.000	1.986	9.005	1.997	9.003	2.003	9.000	1.971	8.975	2	8.999
MSE		0	0	8.57 × 10−4	1.76 × 10−3	1.03 × 10−3	3.79 × 10−3	4.24 × 10−5	9.40 × 10−6	1.48 × 10−1	1.19 × 10−1	2.00 × 10−7	2.00 × 10−7

. It can be seen from this table that the MVPA along with the SQP were able to calculate the actual coordinates of all target nodes with an accuracy of less than 5 cm (tolerance on estimation error). However, all the remaining algorithms have found some difficulties and made some mistakes to calculate the coordinates of the target nodes as highlighted in soft red in Table 1. 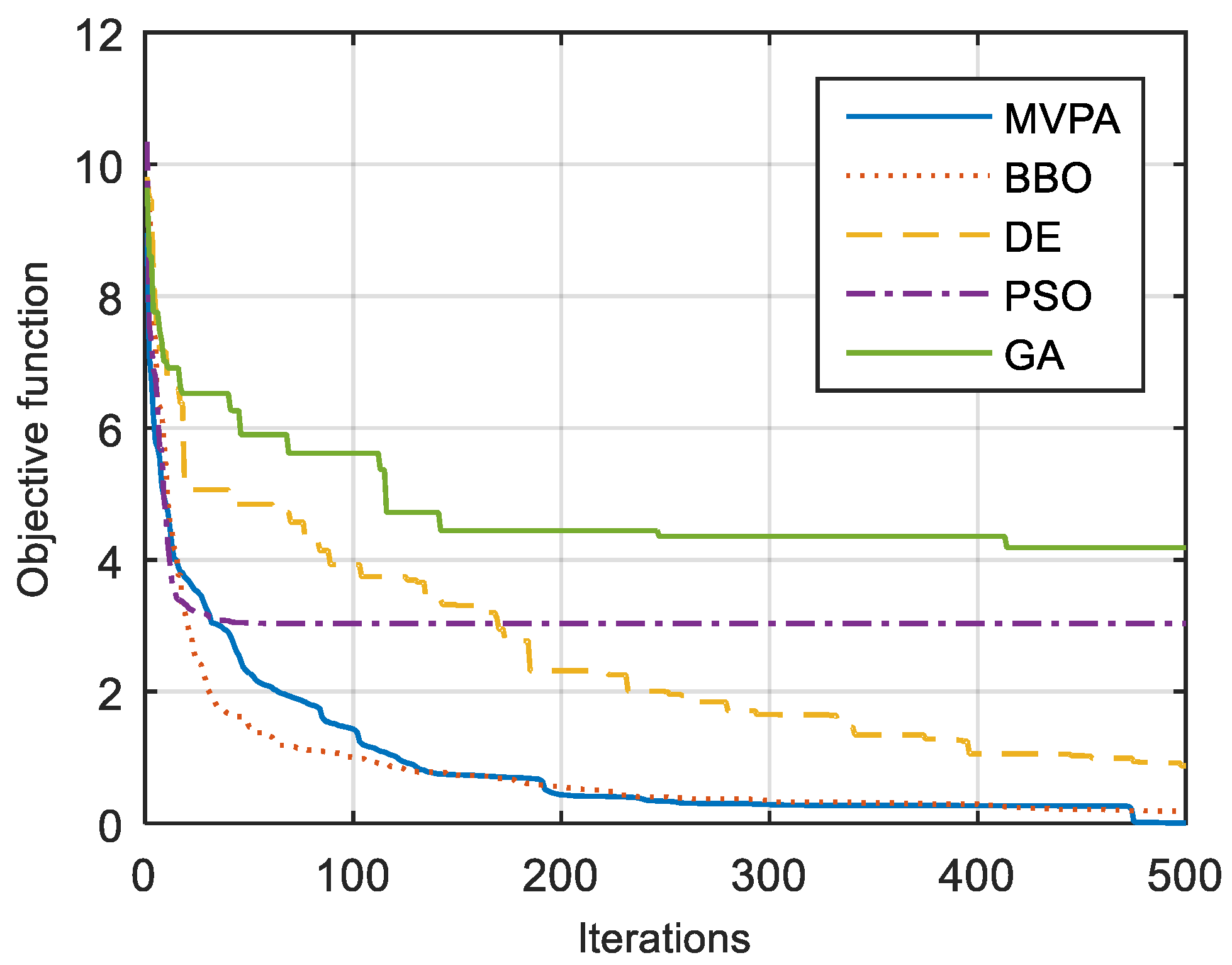The evolution of the objective function is sketched in Figure 3. It can be seen from this figure that the MVPA has the best convergence among all other algorithms.

3.1.2. Case 2

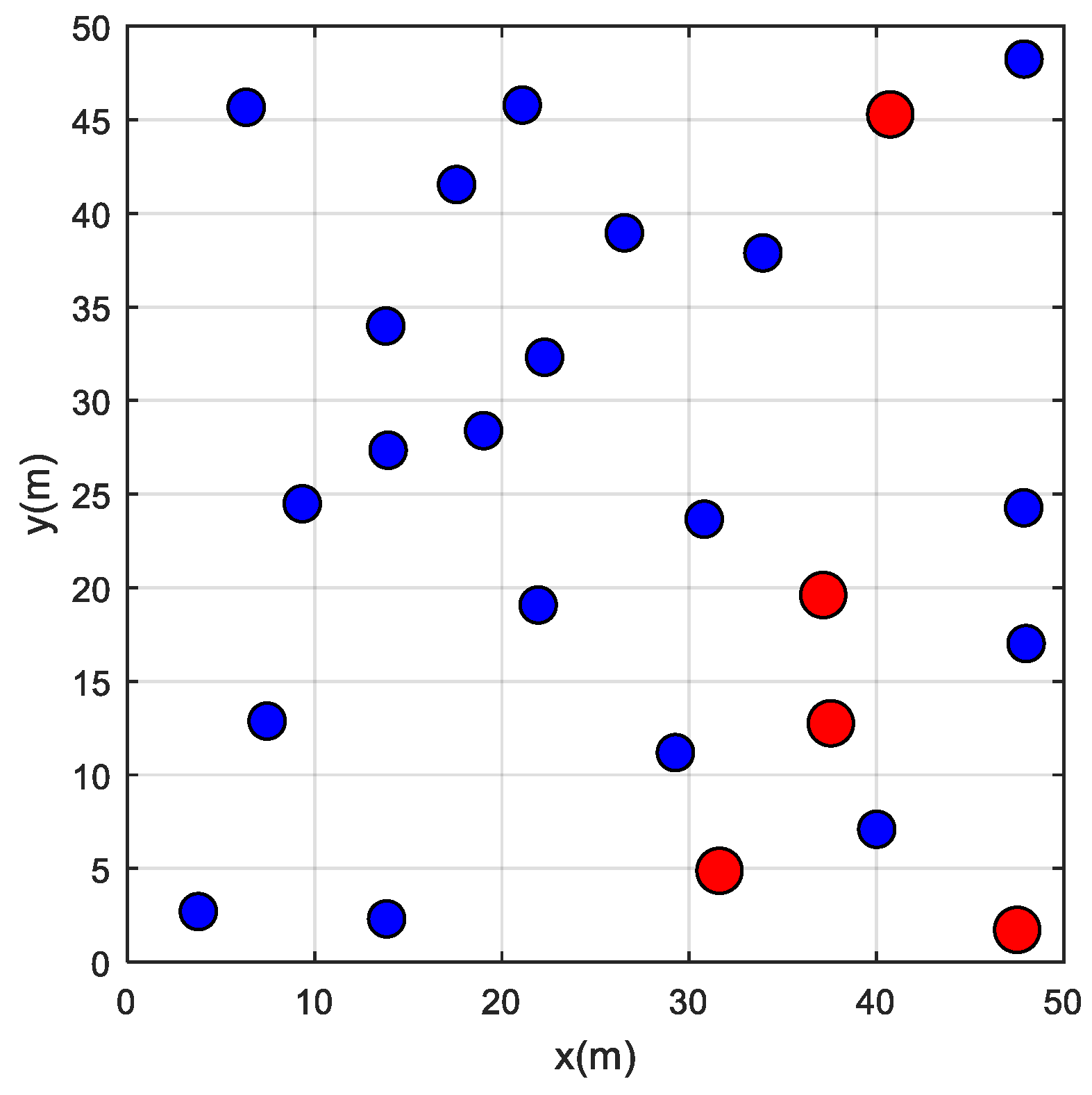
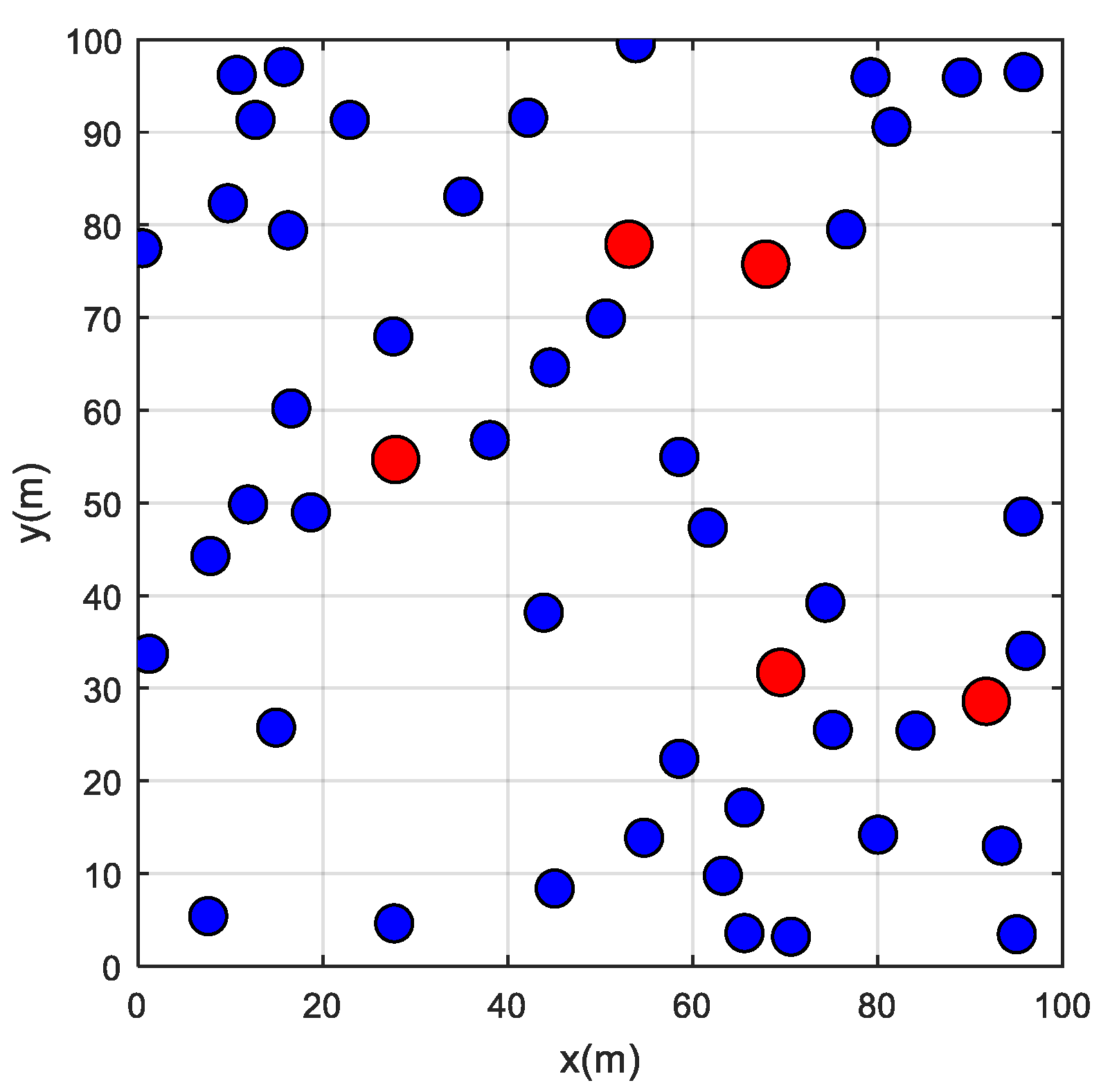
In this case, 25 nodes are generated randomly in a given space of 50 m × 50 m among these 25 nodes, 5 nodes are considered as reference nodes (i.e., their location is known and the distances from these nodes to the remaining target nodes are also known). This case is represented in Figure 4, where red and blue circles represent reference and target nodes, respectively.

The obtained results along with the MSE for this case are tabulated in

Table 2. Comparison of actual locations with those obtained using different algorithms for case 2.

Actual Values		MVPA		BBO		DE		PSO		GA		SQP
xi	yi	xi	yi	xi	yi	xi	yi	xi	yi	xi	yi	xi	yi
6.349	45.669	6.349	45.671	7.091	46.351	5.523	44.833	6.945	50.000	6.359	47.694	6.350	45.669
13.925	27.344	13.930	27.344	14.530	28.207	14.689	27.709	14.645	28.685	12.270	26.938	13.924	27.343
47.875	48.244	47.876	48.245	47.836	48.301	49.990	47.275	30.627	50.000	34.784	39.832	36.593	50.000
47.858	24.269	47.860	24.264	47.775	24.335	47.653	25.338	46.676	25.226	33.002	24.645	29.685	26.043
40.014	7.094	40.011	7.094	39.966	7.073	40.676	5.753	40.194	7.827	32.976	5.548	40.015	7.094
21.088	45.787	21.080	45.782	22.821	46.609	22.213	46.330	27.876	50.000	5.235	30.944	21.089	45.787
33.937	37.887	33.937	37.887	33.922	38.045	41.188	36.005	31.260	37.614	44.707	39.158	33.936	37.887
13.846	2.309	13.849	2.305	14.072	1.926	14.285	0.111	14.243	2.064	7.998	6.728	13.846	2.309
21.937	19.078	21.938	19.079	22.229	19.443	21.113	16.793	20.833	13.989	26.605	14.343	21.937	19.078
9.344	24.488	9.344	24.488	9.028	23.726	9.549	24.523	10.648	33.104	10.288	30.101	9.344	24.489
22.279	32.316	22.305	32.338	22.536	32.517	24.403	33.211	30.403	31.898	41.616	40.008	22.279	32.316
13.801	33.985	13.800	33.984	12.461	32.203	14.294	34.225	25.049	42.029	46.173	37.877	13.802	33.985
47.987	17.019	47.989	17.017	48.039	17.023	48.146	15.529	47.940	16.864	40.028	25.441	28.160	18.953
29.263	11.191	29.263	11.189	28.948	11.192	27.180	10.610	27.120	10.438	30.830	17.431	29.263	11.191
7.465	12.875	7.465	12.868	7.498	12.822	6.891	12.254	3.255	0.000	9.356	18.183	7.464	12.874
30.802	23.664	30.803	23.665	30.539	23.325	29.288	25.269	29.287	2.963	31.765	23.716	30.801	23.664
17.583	41.541	17.585	41.544	17.549	41.478	17.302	40.801	18.890	42.364	20.673	45.154	17.584	41.543
19.022	28.391	19.018	28.386	18.742	28.140	19.117	28.745	49.260	34.181	23.388	9.763	19.023	28.392
3.793	2.698	3.793	2.698	3.782	2.749	4.879	0.507	13.096	38.414	4.875	13.265	3.793	2.697
26.540	38.958	26.538	38.958	27.670	39.572	49.634	38.548	25.875	38.815	19.978	40.503	26.540	38.958
MSE		4.09 × 10−5	3.24 × 10−5	3.78 × 10−1	3.28 × 10−1	3.04 × 101	1.53 × 100	7.88 × 101	1.06 × 102	1.22 × 102	5.30 × 101	4.25 × 101	4.99 × 10−1

. From this table, the proposed approach using the MVPA was able to find all the locations of target nodes within a small range compared with the actual coordinates. However, the remaining algorithms have struggled to find the desired locations as highlighted in the table. From the curves plotted in Figure 5, it can be noticed that the MVPA converges to the lowest value of the objective function.

3.1.3. Case 3

In this case, the number of nodes is increased to 50. Among these nodes, 10 nodes are considered reference nodes. This case is represented in Figure 6.

The obtained results along with the MSE for this case are tabulated in

Table 3. Comparison of actual locations with those obtained using different algorithms for case 3.

Actual Values		MVPA		BBO		DE		PSO		GA		SQP
xi	yi	xi	yi	xi	yi	xi	yi	xi	yi	xi	yi	xi	yi
12.699	91.338	12.699	91.337	12.246	91.452	23.450	99.898	67.819	43.367	57.194	80.899	16.675	92.279
95.751	96.489	95.752	96.486	95.664	96.742	93.672	97.088	100.000	100.000	85.411	95.000	95.792	96.220
95.717	48.538	95.715	48.540	94.633	48.943	97.965	52.156	51.644	52.110	89.651	65.937	95.737	48.586
80.028	14.189	80.028	14.189	80.069	13.723	79.099	15.970	100.000	47.662	89.123	6.799	80.202	14.176
42.176	91.574	42.175	91.574	41.939	92.433	41.442	92.775	100.000	41.654	31.685	68.365	42.150	91.550
65.574	3.571	65.575	3.572	65.438	3.082	63.702	2.177	61.999	0.000	66.842	0.415	62.978	2.757
67.874	75.774	67.873	75.775	67.915	75.966	71.358	74.339	60.897	76.547	70.118	72.706	68.094	75.754
74.313	39.223	74.313	39.223	75.280	39.208	74.540	40.229	65.807	22.725	58.647	44.445	74.252	39.262
65.548	17.119	65.550	17.121	65.001	16.975	65.120	15.413	65.515	17.193	48.742	71.543	65.512	17.145
27.692	4.617	27.692	4.617	27.534	4.629	28.339	1.928	59.921	0.000	3.998	43.964	28.082	4.633
9.713	82.346	9.711	82.344	10.726	83.293	12.359	82.819	29.189	91.251	12.537	88.115	17.071	86.644
69.483	31.710	69.483	31.710	69.292	31.674	70.394	33.256	68.524	35.604	69.694	31.371	69.440	31.672
95.022	3.445	95.034	3.483	94.655	2.866	99.987	7.607	92.216	0.000	92.905	7.713	94.821	3.388
43.874	38.156	43.874	38.155	44.793	38.660	42.800	38.000	57.791	38.897	19.503	77.192	43.867	38.253
76.552	79.520	76.554	79.516	76.308	79.666	76.066	78.949	79.428	78.965	9.717	61.033	76.495	79.615
18.687	48.976	18.672	49.012	19.153	48.743	16.738	53.314	47.193	58.484	43.772	37.002	18.950	49.336
44.559	64.631	44.560	64.632	44.655	64.690	44.222	63.587	58.420	61.330	32.093	58.520	44.571	64.656
11.900	49.836	11.900	49.836	11.633	50.090	15.387	49.337	0.000	57.195	11.234	64.018	12.049	49.839
95.974	34.039	95.974	34.038	95.959	34.118	95.988	34.809	100.000	37.356	97.447	24.454	96.163	34.481
58.527	22.381	58.534	22.389	58.454	22.415	58.041	23.659	54.764	22.780	22.065	5.481	58.346	22.385
75.127	25.510	75.127	25.510	75.420	25.545	74.007	26.876	43.232	0.000	33.387	29.323	75.160	25.526
50.596	69.908	50.599	69.903	50.503	69.806	51.752	69.659	79.471	65.574	71.484	65.652	50.570	69.776
89.090	95.929	88.148	97.000	89.143	95.624	89.726	94.805	35.527	94.501	92.343	90.431	89.391	95.651
54.722	13.862	54.754	13.868	54.162	12.975	55.111	16.911	39.090	37.988	64.894	22.507	54.555	13.689
14.929	25.751	14.929	25.751	14.960	25.747	13.934	24.061	0.000	39.281	49.906	19.330	12.047	25.429
61.604	47.329	61.605	47.330	61.717	47.458	60.619	45.897	35.657	31.427	35.196	15.720	62.129	47.431
35.166	83.083	35.167	83.083	35.136	83.105	36.565	82.958	0.000	72.830	32.123	87.218	35.145	83.190
58.526	54.972	58.526	54.972	58.373	54.848	57.535	54.157	62.384	53.592	47.001	61.169	58.584	54.990
91.719	28.584	91.720	28.585	91.956	28.850	91.227	28.124	73.554	7.758	93.684	4.164	91.753	28.489
53.080	77.917	53.080	77.917	52.835	77.846	51.846	76.636	100.000	76.681	53.339	82.263	53.086	77.841
93.401	12.991	93.407	12.999	92.878	12.247	92.444	13.878	36.041	0.000	79.693	50.300	93.362	12.859
1.190	33.712	1.190	33.716	1.046	34.120	1.849	32.622	1.995	31.367	35.917	15.566	11.965	21.770
16.218	79.428	16.208	79.419	16.173	79.437	16.016	80.130	17.977	80.552	12.996	45.995	15.081	78.974
16.565	60.198	16.565	60.198	16.658	60.213	17.541	65.071	22.569	53.924	25.304	42.153	16.484	60.225
45.054	8.382	45.055	8.382	45.186	8.461	44.530	8.662	45.771	11.927	82.188	24.607	45.000	8.379
22.898	91.334	22.906	91.338	22.289	91.143	28.249	92.909	28.479	100.000	42.461	93.581	20.232	90.099
53.834	99.613	53.834	99.614	54.354	99.318	53.784	99.947	80.081	61.974	38.189	84.211	53.782	99.364
7.818	44.268	7.817	44.268	8.039	44.116	7.569	44.696	26.861	36.811	18.129	32.177	7.787	44.177
10.665	96.190	10.445	95.959	10.946	96.487	9.954	96.057	10.633	100.000	21.210	90.468	46.631	96.050
0.463	77.491	0.463	77.491	1.447	78.725	0.045	77.860	38.547	94.239	5.972	95.552	40.015	84.358
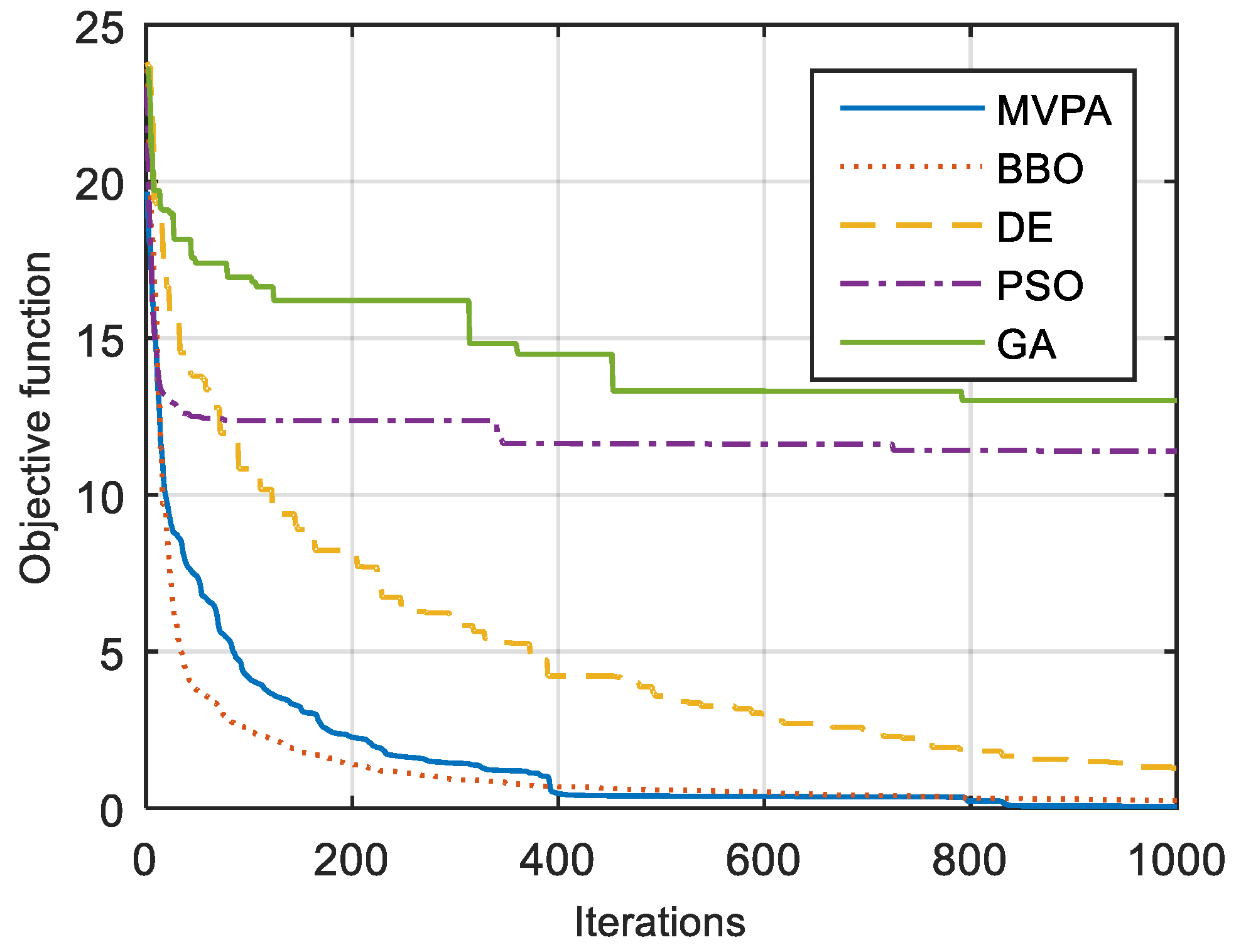
MSE		2.34 × 10−2	3.01 × 10−2	1.94 × 10−1	1.65 × 10−1	5.87 × 100	4.96 × 100	6.80 × 102	2.71 × 102	4.67 × 102	3.57 × 102	7.67 × 101	5.31 × 100

. It can be seen from this table that the MVPA was able to find the coordinates of all target points with good accuracy (less than 5 cm) except for two locations; at the same time, the remaining algorithms have struggled to do so. Moreover, the objective function minimized over the iterations is sketched in Figure 7.

3.1.4. Case 4

In this case, the number of nodes is 50 nodes in a space of 100 m × 100 m. Among these nodes, 5 nodes only are considered as reference nodes. This case is represented in Figure 8. Compared to the previous case a smaller number of reference nodes and a wider space are considered here. This will test the efficiency and robustness of the MVPA.

This case, which is the hardest case to solve because of the low number of reference points and the high number of target points, is solved using MVPA and the results are tabulated in

Table 4. Comparison of actual locations with those obtained using different algorithms for case 4.

Actual Values		MVPA		BBO		DE		PSO		GA		SQP
xi	yi	xi	yi	xi	yi	xi	yi	xi	yi	xi	yi	xi	yi
81.472	90.579	81.472	90.579	81.622	90.435	78.378	90.224	81.689	100.000	84.558	83.656	47.894	83.877
12.699	91.338	12.619	91.293	12.992	91.439	10.423	88.999	12.857	93.491	22.661	84.089	0.000	36.845
63.236	9.754	63.233	9.754	62.775	9.721	63.374	10.437	83.680	12.557	90.613	10.385	62.599	10.597
95.751	96.489	96.351	95.718	95.603	96.009	93.465	98.841	100.000	92.989	4.755	32.923	24.279	41.997
15.761	97.059	15.731	97.031	17.060	98.208	16.154	96.484	15.718	97.986	12.683	23.494	0.000	36.888
95.717	48.538	95.718	48.538	95.946	48.800	96.293	46.623	69.863	21.991	67.347	16.979	78.486	29.237
80.028	14.189	80.067	14.205	79.648	14.265	100.000	22.887	87.651	21.467	57.249	18.007	80.712	14.171
42.176	91.574	41.102	90.642	43.037	92.096	39.906	89.198	40.129	88.434	30.518	87.646	41.981	91.744
79.221	95.949	79.196	95.982	79.144	95.937	83.066	92.968	85.625	96.827	97.578	96.873	43.699	89.282
65.574	3.571	65.550	3.572	65.765	3.327	61.235	3.108	100.000	0.249	68.704	16.588	69.084	3.359
74.313	39.223	74.328	39.253	74.788	39.849	71.359	34.319	72.187	47.572	75.755	53.111	74.502	39.160
65.548	17.119	65.542	17.118	65.826	16.989	66.736	16.309	65.516	12.782	45.037	27.523	65.979	17.160
70.605	3.183	70.613	3.183	71.102	3.320	68.269	0.000	76.485	0.000	75.203	20.143	76.192	5.046
27.692	4.617	27.692	4.617	27.990	4.384	29.523	1.298	27.587	4.127	29.085	33.031	27.135	5.203
9.713	82.346	9.713	82.345	9.681	82.375	1.322	76.777	15.949	100.000	26.714	30.503	0.000	36.932
95.022	3.445	95.019	3.443	93.308	2.268	90.011	0.275	90.994	0.813	59.760	4.881	78.949	0.000
43.874	38.156	43.871	38.156	43.399	38.402	44.013	37.637	35.497	35.558	37.923	37.127	44.795	38.240
76.552	79.520	76.551	79.520	76.358	80.122	73.576	81.110	34.532	100.000	63.853	81.347	76.777	79.106
18.687	48.976	18.701	48.954	18.392	48.935	23.816	63.073	23.753	89.436	56.002	63.902	16.985	52.233
44.559	64.631	44.554	64.632	44.444	64.926	42.640	62.851	48.073	68.041	50.117	67.701	44.626	64.077
27.603	67.970	27.600	67.970	27.487	67.904	28.052	69.193	14.130	55.495	33.654	76.068	27.983	67.478
11.900	49.836	11.896	49.849	12.185	49.240	12.379	51.198	13.827	57.349	26.958	39.969	11.843	49.967
95.974	34.039	95.976	34.040	95.484	33.502	99.985	38.517	0.000	35.958	80.464	23.020	95.943	33.456
58.527	22.381	58.527	22.380	57.882	21.986	63.999	22.290	89.097	44.735	71.527	8.229	58.354	22.686
75.127	25.510	75.161	25.524	76.136	26.478	72.353	24.298	100.000	43.713	94.905	30.350	74.812	25.280
50.596	69.908	50.596	69.908	50.926	69.321	49.197	72.392	49.713	76.378	73.980	67.512	50.594	70.075
89.090	95.929	89.084	95.931	88.200	97.095	83.616	98.416	100.000	69.950	90.881	92.395	36.544	80.275
54.722	13.862	54.718	13.870	54.762	13.855	54.356	13.657	100.000	26.890	69.775	30.512	54.276	13.648
14.929	25.751	14.929	25.751	17.493	23.741	12.519	29.020	80.373	0.000	27.675	51.527	15.467	25.731
84.072	25.428	84.072	25.429	85.009	26.074	86.790	27.913	89.767	9.534	43.845	47.376	84.934	26.552
61.604	47.329	61.572	47.276	61.698	47.265	63.376	48.688	89.398	92.890	71.801	59.939	58.607	43.789
35.166	83.083	35.166	83.082	35.468	82.778	34.334	84.193	13.744	43.546	34.856	85.713	35.202	83.401
58.526	54.972	58.527	54.972	57.839	55.065	56.642	53.500	86.713	77.649	49.642	23.494	57.932	54.584
38.045	56.782	38.048	56.783	37.312	57.219	37.614	57.238	44.186	61.747	43.857	56.733	37.841	58.355
7.585	5.395	7.588	5.389	6.852	5.803	1.023	11.594	4.367	0.000	32.946	94.879	9.141	3.298
93.401	12.991	93.385	12.981	95.156	13.445	91.985	14.383	100.000	22.190	99.174	5.443	79.441	4.864
1.190	33.712	1.181	33.724	1.233	34.075	0.383	34.815	25.763	0.001	9.035	94.611	1.420	35.517
16.218	79.428	16.219	79.433	15.712	79.061	13.911	77.422	15.108	100.000	51.585	63.772	6.811	54.286
16.565	60.198	16.561	60.190	16.346	60.400	14.969	57.770	18.732	75.761	79.249	90.307	16.245	60.869
45.054	8.382	45.035	8.384	45.744	8.029	48.384	9.465	5.489	28.395	45.197	14.296	45.410	8.065
22.898	91.334	22.898	91.334	22.537	91.202	31.659	100.000	16.565	74.060	46.148	4.891	11.287	58.981
53.834	99.613	53.719	99.547	51.648	98.465	52.622	99.230	24.007	70.406	43.745	84.854	48.629	96.527
7.818	44.268	7.823	44.256	7.641	44.777	0.000	57.017	17.193	35.972	13.080	31.052	6.095	46.505
10.665	96.190	10.665	96.190	8.035	93.554	15.125	99.743	13.075	100.000	11.818	50.961	0.002	36.758
0.463	77.491	0.465	77.496	2.017	80.343	17.213	99.932	0.000	0.000	25.185	59.080	0.463	34.980
MSE		3.42 × 10−2	3.28 × 10−2	8.19 × 10−1	6.68 × 10−1	2.72 × 101	2.81 × 101	6.02 × 102	4.44 × 102	5.69 × 102	9.20 × 102	2.65 × 102	4.33 × 102

. It can be seen that the MVPA is by far the best algorithm in estimating the coordinates of target nodes compared to the remaining algorithms. It has estimated five nodes with less accuracy than 5 cm whereas other algorithms have shown low accuracy for most of the cases, or rather have wrongly estimated the location of a few nodes. The curves of the evolution of the objective function are sketched in Figure 9.

Looking at Figure 5, Figure 7 and Figure 9, it can be noticed that although the BBO has a quick speed of convergence, the MVPA converges to a better final solution. This statement is confirmed by the results tabulated in Table 1, Table 2 and Table 3 where the MSEs obtained using MVPA are lower than the ones obtained using all the comparing algorithms including the BBO in all cases.

3.2. B. Real-Time Experimental Study

In [23] a real wireless network with three reference nodes and one target node (that can be moved to have multiple measurements) were studied. The target node and reference nodes are created using Zigbee series two modules, that were chosen for being less expensive and power-efficient [37,38]. As aforesaid, the reference nodes are acting as three routers whereas the target node acts as a device that receives signals from three transmitting devices (reference nodes) at any instant. A local coordinate system was established such that both x and y coordinates increase by half feet i.e., each integer in the coordinate system is representative of two feet (0.6096 m). The coordinates of the three reference nodes on a local coordinate system are (0,0), (6,0), and (3,8) for both indoor and outdoor settings as shown in [23].

The target node was relocated to ten independent positions as shown by the blue dots in Figure 10. The coordinates of these nodes along with the distances measured between reference nodes and target nodes, in meters, are tabulated in

Table 5. Coordinates and distances of target nodes.

Coordinates of Target Nodes in the Local Coordinate System	Coordinates of Target Nodes (m)	Distance from Ref Node # 1 (m)	Distance from Ref Node # 2 (m)	Distance from Ref Node # 3 (m)	Average Distance (m)
(2,4)	(1.219, 2.438)	2.73	3.45	2.51	2.90
(3,3)	(1.829, 1.829)	2.59	2.59	3.05	2.74
(6,4)	(3.658, 2.438)	4.40	2.44	3.05	3.29
(1,2)	(0.610, 1.219)	1.36	3.28	3.86	2.83
(1,3)	(0.610, 1.829)	1.93	3.55	3.28	2.92
(5,4)	(3.048, 2.438)	3.90	2.51	2.73	3.05
(2,5)	(1.219, 3.048)	3.28	3.90	1.93	3.04
(3,6)	(1.829, 3.658)	4.09	4.09	1.22	3.13
(5,7)	(3.048, 4.267)	5.24	4.31	1.36	3.64
(6,8)	(3.658, 4.877)	6.10	4.88	1.83	4.27

. The last column gives the average of the distances of the target node from all three nodes.

3.2.1. Distance Estimation Based on Measured RSSI

As aforesaid, to determine the coordinates of a real system, first, the distances are estimated from the measured RSSI using a nonlinear regression model and approximating that model on LNSM of Equation (3). Then the proposed MVPA is run to localize the coordinates of the local grid. RSSI is measured for each of the ten locations of the target node using range testing of the XCTU software (XCTU offers a convenient graphical interface where developers can deal with multiple Digi RF modules simultaneously. It is available in several platforms as an open-source application) [39]. The coordinates of the ten locations where the target node is kept are given in the first column of Table 5. At each location, ten values of RSSI are noted and their average RSSI is computed. 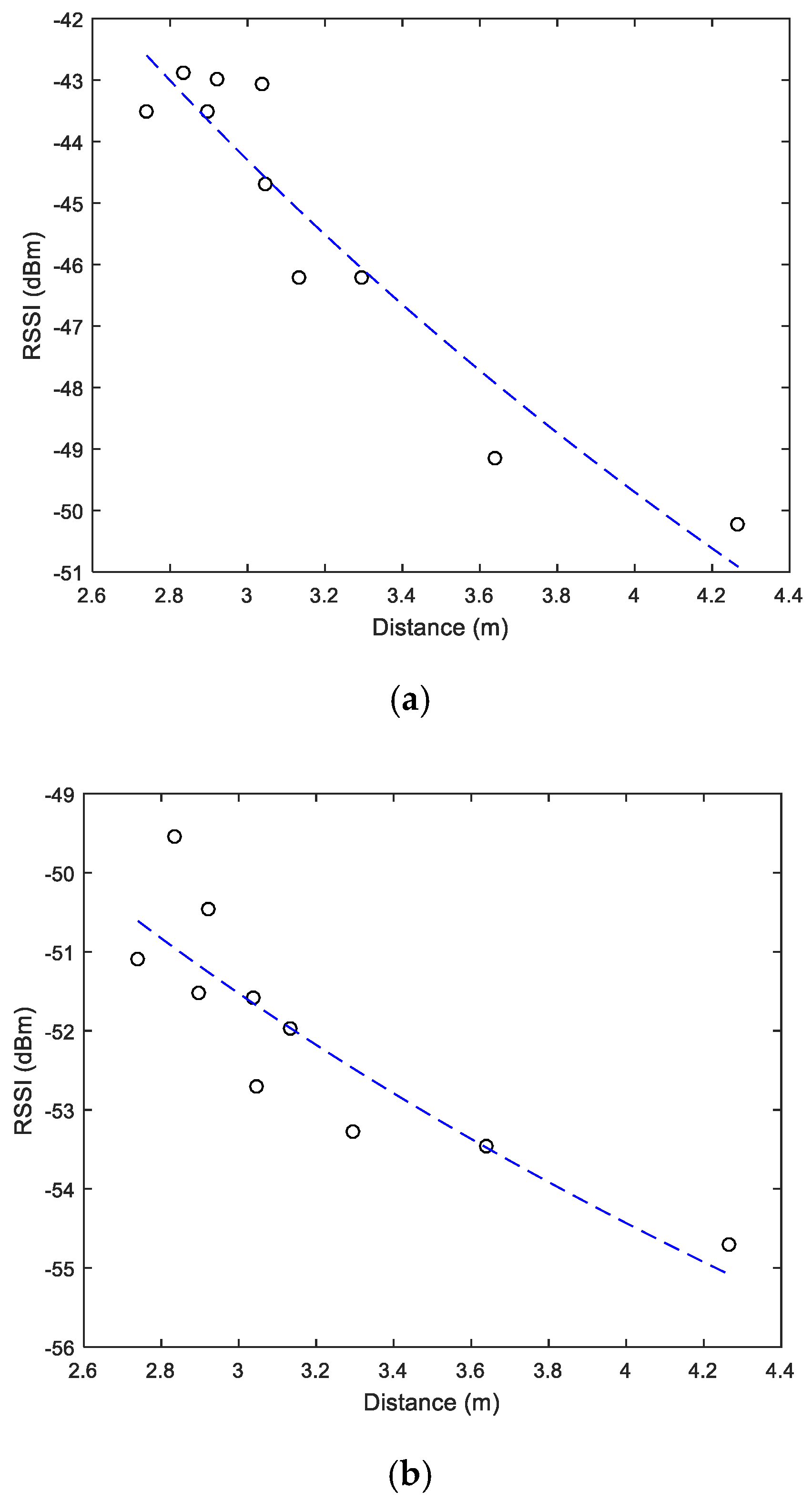The average RSSI of each location for both indoor and outdoor settings is shown in Figure 11. It can be noted that as the target node is moved far away from a specific reference node, the received RSSI is decreased. Moreover, the signal strength observed in the outdoor environment is less than that observed in the indoors. Based on these measurements, a nonlinear regression model is developed to estimate the distances from measured RSSI.

The relationship between RSSI and distance obtained using our nonlinear regression model for indoor experiments is expressed as follows:

$$RSSI=-23.671-18.78\times log\left(d\right)$$

(11)

and therefore:

$$d={10}^{-\frac{RSSI+23.671}{18.78}}$$

(12)

The relationship between RSSI and distance obtained using our model for outdoor experiments is expressed as follows:

$$RSSI=-40.425-10.10\times log\left(d\right)$$

(13)

and therefore:

$$d={10}^{-\frac{RSSI+40.425}{10.10}}$$

(14)

Comparing (10) and (12) with (3) reveals that the terms $P_t-P_L\left(d_0\right)+X_{\sigma }$ is equal to −23.671 (dBm) for the indoor case and −40.425 (dBm) for the outdoor case. However, the value of $10 n\log 10$ can be approximated to −18.78 (dBm) and −10.10 (dBm) for indoor and outdoor scenarios, respectively. Equations (10) and (12) are plotted in Figure 12a,b, respectively. It can be seen that the nonlinear curves approximate the best function such that the error function between the measured values and the approximated curve is minimized.

3.2.2. Coordinate Estimation Using MVPA

The distances estimated in the previous section for outdoor application are given to the MVPA algorithm to determine the coordinates of the target nodes. The results are displayed in

Table 6. Comparison of actual locations with those obtained using MVPA for outdoor application.

Actual Values		MVPA
xi	yi	xi	yi
2	4	2.05	4.01
3	3	3.1	3.02
6	4	6.04	4.03
1	2	1.02	2.02
1	3	1.00	3.03
5	4	4.92	3.98
2	5	2.02	5.08
3	6	3.02	5.95
5	7	4.96	7.04
6	8	5.94	8.02

. It can be seen from this table that the locations are well estimated, and the error is mainly due to the estimation of the distances from RSSI using the nonlinear regression model.

4. Conclusions

Localization of sensor nodes has always intrigued wireless network engineers as it enables them to deploy efficient network protocols and minimize the traffic and hence the latency on a given channel. To realize the effective and accurate localization, this paper has effectively demonstrated the two-fold technique toward localization; first, a nonlinear regression model is used to establish an approximate relationship between RSSI and distance between the sensors, later, those distances are fed to MVPA to figure out the geometrical coordinates in the local 2d space. The model is first implemented on four simulation-based test cases, where the results obtained from MVPA are compared with the contemporary techniques for benchmarking. Finally, the applicability of the proposed method is demonstrated on actual WSN in both indoor and outdoor environments. It is found that the proposed MVPA estimation method preceded by nonlinear regression has given good results for distance estimation and node localization. The approach is tested under rigorous simulation scenarios spanning a large area and equipped with a very low number of reference nodes. Even in the most constrained problem (case 4), the MSE in the x-coordinate of the proposed approach is 24 times less than the second-best approach (BBO). Similarly, for the y-coordinate, the MSE obtained with the proposed MVPA is 20 times less than that of the BBO approach, the second-best performer. Future directions can focus more on how to improve the estimation of distances based on RSSI using regression models or even Artificial Neural Networks (ANNs). Another future work can also be to test the developed approach for a network with obstacles like walls for example.