Abstract
The development of micromechanical models to predict the effective properties of multiphase composites is important for the design and optimization of new materials, as well as to improve our understanding about the structure–properties relationship. In this work, the two-scale asymptotic homogenization method (AHM) is implemented to calculate the out-of-plane effective complex-value properties of periodic three-phase elastic fiber-reinforced composites (FRCs) with parallelogram unit cells. Matrix and inclusions materials have complex-valued properties. Closed analytical expressions for the local problems and the out-of-plane shear effective coefficients are given. The solution of the homogenized local problems is found using potential theory. Numerical results are reported and comparisons with data reported in the literature are shown. Good agreements are obtained. In addition, the effects of fiber volume fractions and spatial fiber distribution on the complex effective elastic properties are analyzed. An analysis of the shear effective properties enhancement is also studied for three-phase FRCs.
1. Introduction
Multiphase elastic fiber-reinforced composites (FRCs) are still important in applications because their yields exceed those of their constituents and they offer very interesting properties compared to more conventional materials. Improved levels of functionality can be achieved through the manipulation of physical properties by means of structure optimization [1,2,3]. Therefore, the effective properties prediction for FRCs by means of micromechanical models and numerical approaches is a useful tool for technological innovation [4,5,6,7,8,9,10].
Periodic multiphase elastic FRCs have found applications related to transport problems (conductivity, shear elasticity, dielectric constant, thermal expansion, and others). In this sense, different micromechanical and experimental models have been developed to analyze elastic FRCs. For example, the elastic effective properties of two-phase elastic FRCs with periodic square [11] and hexagonal [12] cells were found by applying the asymptotic homogenization method (AHM). Jiang et al. [13] calculated the effective elastic moduli of FRCs with cylindrical inclusions under longitudinal shear by means of the Eshelby equivalent inclusion concept [14], combining the results of a doubly quasiperiodic Riemann boundary value problem [15]. Artioli et al. [16] applied the AHM to determine the effective longitudinal shear properties of elastic FRCs with radially graded fibers, assuming imperfect interface conditions. Shu and Stanciulescu [17] proposed an analytical approach using multiscale homogenization to characterize FRCs with imperfect interphase through the shear-lag model. Dhimole et al. [18] implemented a multiscale modeling based on homogenization method to predict the accurate mechanical behavior of 3D four-directional braided composites.
In addition, Bisegna and Caselli [19] investigated the effective complex conductivity for a periodic FRC with interfacial impedance and hexagonal symmetry by AHM. Godin computed the complex effective dielectric properties for two-phase FRCs with circular inclusions [20] and for periodic tubular structures [21]. These tubular structures were modeled as a three-phase FRC. Analytic bounds on the complex dielectric constant were reported by the authors of [22]. A correspondence between orthotropic complex-value dielectric media and non-orthotropic elastic media was developed by the authors of [23] through an affine transformation. Mackay and Lakhatia [24] reported the gain and loss enhancement for particulate homogenized composite materials whose active constituents have complex values. Guild et al. [25] analyzed the enhancement of homogenized dielectric effective properties for acoustic waves using multiscale sonic crystals. Luong et al. [26] estimated the complex shear modulus using the least mean square/algebraic helmholtz inversion (LMS/AHI) algorithm for 1D heterogeneous tissue. On the other hand, fiber-matrix interaction region has also been studied for multiphase FRCs. In this case, a thin mesophase is added between the fiber and the matrix in a three-phase FRC. This contact zone is commonly defined as imperfect contact region, see, for instance, [17,27,28,29,30].
The AHM has proved to be advantageous in the description of the multiscale mechanics of composite materials. Many studies have dealt with the theoretical bases of the AHM [31,32,33,34,35]. In general, the AHM makes it possible to obtain an effective characterization of the heterogeneous system or phenomenon under study by encoding the information available at the microscale into the so-called effective coefficients. In particular, multiscale AHM take advantage of the information available at the smaller scales of a given heterogeneous medium to predict the effective properties at its larger scales, see, for instance, [36,37,38,39]. This, in turn, dramatically reduces the computational complexity of the resulting boundary problems. However, the main disadvantage of AHM is that the analytical solution of the local problems has been derived for only a few composite structures [40,41].
The main aim of this work is the estimation by AHM of the effective elastic complex-values properties for periodic three-phase elastic FRC with complex-valued constituent properties and a parallelogram cell. The out-of-plane case for three-phase composite is considered. Both matrix and fibers have isotropic or transversely isotropic properties, and they are in welded contact. The mathematical statement is presented, and the associated local problems are derived. Simple closed formulas are provided for the shear effective coefficients of three-phase FRCs. Validations of the present model with results reported in literature are shown. The AHM accuracy and convergence is analyzed based on the truncations of the infinite system from the local problems solutions. Also, the effect of volume fraction and spatial fiber distribution on the complex effective elastic properties is analyzed. An example of longitudinal shear enhancement is considered as a function of reinforcement volume fractions for three-phase FRCs with complex-value constituents. Good agreements are obtained.
The novelty of this work is to calculate by AHM the out-of-plane effective properties of periodic three-phase elastic FRC with parallelogram unit cell whose constituents have complex-valued properties. It generalizes earlier works in which the same method has been applied to two- and three-phase FRCs with real-values constituents and square, hexagonal, and parallelogram unit cells, see, for instance, [11,12,40,42]. This generalization allows the study of the shear effective properties enhancement for three-phase FRCs.
2. Statement of the Problem and Method of Solution
2.1. Mathematical Formulation for the Elastic Heterogeneous Media
A heterogeneous periodic three-phase elastic FRC (fiber/mesophase/matrix) with a doubly periodic microstructure is studied, which consisted of a parallelepiped array of two concentric and unidirectional cylinders within a homogeneous matrix (Figure 1a). The fibers are infinitely long in the direction and periodically distributed. At the microstructural level, the composite cross-section (periodic unit cell ) is defined by a matrix with two concentric circles of different radii located at the parallelogram center, see Figure 1c. The constituent elastic properties, belonging to a crystal symmetry class of 6mm, are assumed to be complex numbers. In addition, as a unidirectional FRC, the composite microstructure is considered to remain constant along the reinforcement’s direction (i.e., perpendicular to plane of cross-section).
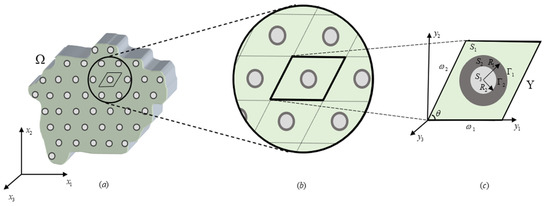
Figure 1.
(a) Heterogeneous three-phase fiber-reinforced composites (FRC); (b) blow-up of periodic structure; (c) the representative parallelogram-like unit cell Y.
The periodic parallelogram-like unit cell is characterized by a principal angle and the periods and in the plane. Also, it is satisfied that and , , where is the region occupied by matrix phase defined by a parallelogram with a central circular hole of radius , contour , and volume . represents the mesophase of volume and is surrounded by two circular interfaces and of radius and , respectively, and is the central fiber with circular boundary of radius and volume . The volume V of the cell satisfies that .
In the out-of-plane mechanical deformation state, the mechanical displacement of a media satisfies that , , and the non-null stresses involved in this problem are and . Thus, the static governing equation for an elastic FRC is defined by the partial differential equations system:
where the absence of body forces is considered. Here, are Y-periodic and rapidly oscillating coefficients which denotes the elastic stiffness modulus, and .
The Equation (1) subject to the prescribed boundary conditions:
represent the out-of-plane classical elliptic boundary value problem associated with the linear elasticity theory for heterogeneous structures. Here, is the traction vector on , is an infinitely differentiable function on the external boundary , and is the component of the outward unit normal vector on . The boundary of the composite is partitioned in such a way that and . In Equations (1)–(3), and are the out-of-plane mechanical stresses and displacements.
In addition to Equations (1)–(3), perfect contact conditions at the circular interfaces are assumed, i.e.,
where means jump of across , see for instance [11].
2.2. Method of Solution: Local Problems and Effective Coefficients
The two-scale AHM [32,33,43] is used to solve the elliptic boundary value problem (Equations (1)–(4)). The solution is found by means of a two-scale asymptotic representation of in powers of the small geometrical parameter by the ansatz:
where the macroscale or fast variable and the microscale or slow variable are related by , and the parameter is the ratio between the periodic unit cell length and the macroscopic dimension of the composite . In Equation (5), the second term is a periodic function of , which represents a correction of the term . Also, it is satisfied that , where is a periodic local function, which is the solution of the local problems. It is possible to obtain an asymptotic solution of the problem (Equations (1)–(4)) when . More details and the rigorous theoretical background of AHM have been described in classical works [31,33,43] and are omitted here.
The out-of-plane local problems on , denoted as for a three-phase elastic FRC (see Figure 1), is stated as follows:
where and are the Kronecker’s delta functions related to the and local problems, respectively. To guarantee the uniqueness of the local problems solutions, the local functions should satisfy the null average condition on , where and is the area of .
Once the out-of-plane local problems (Equations (6)–(8)) are solved, the corresponding effective elastic coefficients can be calculated by the formulas:
Notice that the out-of-plane effective elastic coefficients (Equations (9) and (10)) depend on the local functions and relative to the and local problems, respectively. Then, and need to be found. Therefore, an analytical solution of Equations (6)–(8) is determined.
On the other hand, the homogenized elastic problem equivalent to the boundary value problem (Equations (1)–(3)) is defined by the equation system
subject to the homogenized boundary conditions
where is the solution of the homogenized problem, and are the out-of-plane effective elastic coefficients defined in Equations (9) and (10).
2.3. Analytical Solution of the Local Problems
By means the potential methods of a complex variable theory, the solution of the local problem (Equations (6)–(8)) is calculated. Here, the doubly periodic Weierstrass’ elliptic functions are used to obtain an analytical solution, i.e., the double periodic solution is found in terms of Laurent and powers expansions as a function of , see, for instance, [44,45], as follows
where with , , and . By
and
In Equations (13)–(15), the coefficients , , , , and are complex and undetermined numbers. They need to be determined in order to find the local problems solution and the out-of-plane effective elastic coefficients (Equations (9) and (10)). Here, it can be highlighted that the summation symbol with superscript means that the sum only runs over odd integers, and the symbols Re and Im represent the real and imaginary parts of complex numbers, respectively. Details of Laurent and powers expansions and its relationship with the double periodic elliptic Weierstrass function of periods and , and related expressions can be found in [45,46].
From the double periodicity condition of , it is satisfied that:
see, for instance, [45]. Then, it can be proved that is linked with by the equation:
where , and is the complex conjugate of . In addition, is the quasiperiodic condition and is the Weierstrass quasiperiodic Zeta function defined by where means that the summation does not include the point , see [45].
Finally, replacing Equations (13)–(15) into the interface conditions (Equations (7) and (8)) and after some mathematical manipulations, we obtain the normal infinity system of linear equations [47] with unknown complex constants , in compact form:
where , , and . In Equation (18), , and are the volume fractions of the mesophase and the central fiber, and the symbol is the Kronecker’s delta function. Also, the system solution of each local problem depends on the elastic constituent properties, the phase volume fractions and the fibers spatial distribution within the matrix. Details of the system construction can be found in [40] and are omitted here. Once the unknown constants are calculated, the local problem solution and the effective coefficients can be determined. Details on the system solution is given in Appendix A.
The non-null out-of-plane effective properties for three-phase elastic FRC are listed as follows:
where is the Voigt’s average, , and the constant is defined by
Simple closed-form formulas for the effective properties equivalent to Equations (19) and (20) are given in Appendix B.
3. Numerical Results
The accuracy of the AHM model is determined through comparisons with other results reported in the literature for three-phase elastic FRC (fiber/mesophase/matrix) with complex-values constituent properties. In addition, the effect of the volume fraction of inclusions and the spatial fiber distribution on the complex effective elastic properties is investigated. Also, an example of shear enhancement is reported as a function of reinforcement volume fractions.
Limit cases for the present model can be determined when Equations (19) and (20) and system (18) are reduced to those that represent a two- and three-phase FRC with parallelogram-like unit cell. In these cases, isotropic or transversely isotropic constituents are considered with real-values elastic properties, as reported by the authors of [11,40,42].
The real and imaginary parts of the complex effective elastic properties are given for some biological applications, for example, the behaviors of biological tissues, skeletal muscle, sclera, and other ones in which material properties depends on time [48,49,50,51]. This behavior can be analyzed in viscoelastic materials in which the shear wave speed is connected to the enhancement and lessening of the shear modulus. Besides, in the context of transport properties, the mathematical statement for shear linear responses is identical to conductivity, dielectric permittivity, and so on in equivalent media [52].
In the literature, to the authors’ knowledge, the longitudinal shear homogenization problem has not been reported with complex-values coefficients. A comparison with Godin [21] is possible because the governing equation for both models has the same mathematical formula, although they model different physical magnitudes. Both models find an infinity equation system to solve the problem. However, there are differences between the model implementations. The Godin model goes directly to a representative element of analysis and the governing equation is directly solved. The effective properties are proposed as a linear relation between averaged physical magnitudes. The AHM described herein in previous sections is based on a procedure that ends up in the solutions of local problems, the boundary conditions, and the effective properties.
In Table 1, the real (Re) and imaginary (Im) parts of complex effective property are illustrated for two different three-phase FRCs as a function of normalized radius with a square and hexagonal unit cell, respectively. Here, , is the outer interface radius, and represents the minimum distance between the centers of the fibers. In addition, an analysis of the relative error is shown: [21]. Hence, the numerical values of the effective property is compared with the complex effective dielectric constant provided by the authors of [21]. The numerical calculations are carried out considering that the matrix, the mesophase, and the fiber have the complex-values properties , , and for the FRC with the square array and , , and for the FRC with the hexagonal array. In both three-phase FRCs, the concentric fibers radius relation is . As can be seen, good agreements are achieved by AHM for only a system truncation (Equation (18)) to a finite order . Only a very slight discrepancy is observed near the close-packing condition, although the relative error is below 0.27% in every case.

Table 1.
Real and imaginary parts of the complex effective property as a function of normalized radius for two three-phase FRCs with a square and hexagonal unit cell, respectively.
In Table 2, the variations of the real and imaginary parts of the complex effective shears , , and in terms of system truncate orders are presented for a three-phase elastic FRC with a parallelogram unit cell of . In addition, two different normalized radii and (close to percolation value) are also considered. For the analysis, the material properties of matrix, mesophase, and fiber have isotropic complex properties, such as , , and . The relation between the concentric fiber’s radius is . Notice that the AHM convergence is achieved quickly when low values of are assumed, i.e., only smaller values of are needed. Therefore, truncations of higher order must be considered for high values of , as well as for higher contrast among the matrix mesophase and fiber properties, in order to obtain a better accuracy. For example, is required to obtain the effective properties values with at least five accuracy digits when . Similar conclusions are achieved when the same analysis is developed for a three-phase elastic FRC with a parallelogram unit cell of and complex-values constituent properties , , and .

Table 2.
Real and imaginary parts of the complex effective shears , , and obtained by AHM in term of order system for a three-phase FRC with a parallelogram unit cell of and for two different normalized radii and .
Table 3 shows the real and imaginary parts of the overall out-of-plane shear properties , , and for two three-phase FRCs with different parallelogram-like unit cells. The numerical values are computed considering four different parallelogram-like unit cells (i.e., parallelogram cells characterized by a principal angle equal to and ), a system order truncation , and (value of the normalized radius near to the percolation point volume 0.38268, for ). In addition, the composite structure-property relationship is also analyzed. From Table 3, it is noticed that, when the periodic unit cells are characterized by parallelograms with different to and , the composites belong to monoclinic symmetric class, i.e., 13 non-null effective elastic constants are attained. However, in the out-of-plane case, only and are remained. In the case of the periodic hexagonal and square unit cells, the composite behavior is transversely isotropic, i.e., and . These results have also been satisfied in elastic FRCs with real effective properties, see, for instance, [40]. In addition, it can be concluded that a decrease (increase) in the real (imaginary) part of the complex effective shears and resulted as the angle of the periodic unit cell increased. Higher values for the real and imaginary parts of and are obtained when and the normalized radius is the same. Besides, for the composite with complex-value constituents , , and , the real and imaginary parts of are negative for and positive for In a composite with complex-value constituents , , and , the real (imaginary) part of run from negative (positive) to positive (negative) when . It should be noted that there are three different effective behaviors.

Table 3.
Real and imaginary parts of the complex effective shears , , and for two three-phase FRCs with different parallelogram-like unit cells and a normalized radius .
In Figure 2, an analysis of enhancement of the real part of the shear effective property is illustrated for a three-phase FRC with periodic hexagonal unit cell. Notice that, for this type of unit cell, and . Here, the enhancement is studied as function of reduced mesophase filling fraction , i.e., the enhancement of i obtained for four configurations of the annular inclusion (mesophase and fiber inclusions) with fixed volume fraction . For this analysis, two different three-phase FRCs are considered with complex-values constituents , , and (Figure 2a) or (Figure 2b). These properties are considered assuming that the mesophase properties attain an interval of realistic physical properties as a combination of the matrix and fiber phases. From Figure 2, it is important to note that the real part of increase as increase when , and that higher values of are always obtained in comparison when (two-phase FRC—solid black line). In the figures, the red dashed dot and the blue dashed lines represent the real part values of the matrix and mesophase properties, respectively. In addition, it can be concluded that the imaginary part values of both three-phase FRCs vary monotonically between the values of the matrix and mesophase phases. This picture, in which the three-phase FRCs are considered with distinct constituents, is different than Figure 2 reported by the authors of [7]. In this reference, the enhancement was analyzed for a three-phase FRC with the same values of matrix and fiber and different mesophase, as an annular inclusion. Besides, it should be noted that the volume fraction interval where enhancement appeared is much larger. In one case, it is the whole interval.
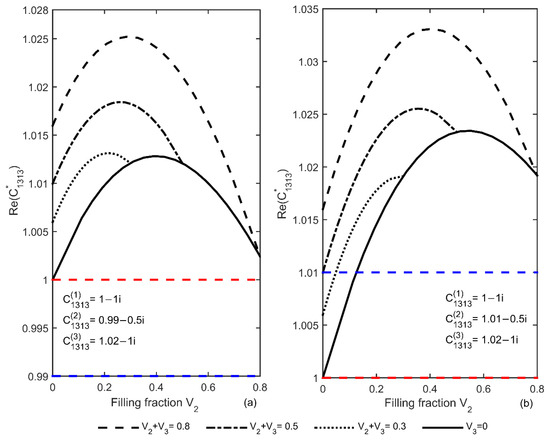
Figure 2.
Enhancement of the real part of effective shear property as a function of reduced mesophase filling fraction for two three-phase FRCS with hexagonal unit cell and mesophase complex-values property (a) and (b) .
4. Conclusions
In this work, the effective shear properties of periodic three-phase fiber-reinforced composites with complex-values constituent properties and parallelogram unit cells are calculated by AHM. Easy-to-handle formulas and fast numerical implementation are derived for all shear effective properties. We conclude that:
- (i)
- The fiber spatial distribution, represented as parallelogram-like unit cell, is capable of describing three class of symmetry point group: tetragonal 4 mm (square unit cell), hexagonal 6 mm (hexagonal unit cell), and monoclinic 2 (other parallelogram unit cells) structures.
- (ii)
- The enhancement in the shear effective property is more remarkable for three-phase FRC than two-phase FRC.
- (iii)
- The volume fraction interval where enhancement appeared is larger for a three-phase FRC than the interval for the two-phase FRC.
- (iv)
- The presence of negative values for the real and imaginary parts of appears for some parallelogram unit cells.
- (v)
- The manipulation of the mesophase can be used as a way to enhance the real and imaginary parts of the shear elastic properties.
- (vi)
- The numerical results prove that the AHM is an accurate and efficient approach for the study of FRC with a mesophase and for different spatial fiber distributions in a matrix.
Author Contributions
Conceptualization, F.J.S., R.R.-R.; methodology, Y.E.-A., H.C.-M.; software and validation, R.G.-D., Y.E.-A.; formal analysis and investigation, F.J.S., R.R.-R.; writing—original draft preparation, Y.E.-A., R.R.-R.; writing—review and editing, H.C.-M., Y.E.-A.; supervision, F.J.S., R.R.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
Y.E.-A. gratefully acknowledges the Program of Postdoctoral Scholarships of DGAPA from UNAM, Mexico. F.J.S. thanks the funding of PAPIIT-DGAPA-UNAM IA100919. R.R.-R. would like to thank the Department of Mathematics and Mechanics at IIMAS, UNAM. H.C.-M. and Y.E.-A. are grateful for the support of the CONACYT Basic science grant A1-S-9232.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The infinite system (Equation (18)) is solved by truncation to a finite order through blocks for different values of k and p (odd natural numbers) with the unknown complex coefficients . The sub-matrix systems ( blocks) are solved by the Gauss’s method. A fast convergence of successive truncations is assured due to the system regularity, hence, the method of successive approximations can be applied, see for instance [47].
The above infinite system (Equation (18)) can be rewritten in matrixial form as follows:
where is the unit matrix, , is made up of different blocks of order 2 and the infinite vectors and are defined by and , respectively.
In order to find the solution of system (A1), it is reduced by means of two separate systems of real and imaginary magnitudes, considering that , and where , , , , and are real numbers and , see for instance [40].
Consequently, following the same procedure applied in examples of alike systems [7,40,53], the solution of Equation (18) can be computed in the matrixial form by
where and are infinite matrices of blocks of by rows and by columns, respectively. Here, , , and the usual index sum is applied by .
Therefore, the system solution associated to the local problem is explicitly determined as follows:
where the matrix and is the inverse matrix of .
Appendix B
An equivalent representation of the effective coefficients Equations (19) and (20) can be obtained replacing Equations (21), (A3) and (A4) into Equations (19) and (20), such as:
where and .
References
- Bonfoh, N.; Coulibaly, M.; Sabar, H. Effective properties of elastic composite materials with multi-coated reinforcements: A new micromechanical modelling and applications. Compos. Struct. 2014, 115, 111–119. [Google Scholar] [CrossRef]
- Prashanth, S.; Subbaya, K.M.; Nithin, K.; Sachhidananda, S. Fiber Reinforced Composites—A Review. J. Mater. Sci. Eng. 2017, 6, 1000341. [Google Scholar]
- Egbo, M.K. A fundamental review on composite materials and some of their applications in biomedical engineering. J. King Saud. Univ. Eng. Sci. 2020, in press. [Google Scholar] [CrossRef]
- Wang, M.; Pan, N. Predictions of effective physical properties of complex multiphase materials. Mater. Sci. Eng. R Reports 2008, 63, 1–30. [Google Scholar] [CrossRef]
- Beicha, D.; Kanit, T.; Brunet, Y.; Imad, A.; El Moumen, A.; Khelfaoui, Y. Effective transverse elastic properties of unidirectional fiber reinforced composites. Mech. Mater. 2016, 102, 47–53. [Google Scholar] [CrossRef]
- Dinzart, F.; Sabar, H.; Berbenni, S. Homogenization of multi-phase composites based on a revisited formulation of the multi-coated inclusion problem. Int. J. Eng. Sci. 2016, 100, 136–151. [Google Scholar] [CrossRef]
- Sabina, F.J.; Guinovart-Díaz, R.; Espinosa-Almeyda, Y.; Rodríguez-Ramos, R.; Bravo-Castillero, J.; López-Realpozo, J.C.C.; Guinovart-Sanjuán, D.; Böhlke, T.; Sánchez-Dehesa, J. Effective transport properties for periodic multiphase fiber-reinforced composites with complex constituents and parallelogram unit cells. Int. J. Solids Struct. 2020, 204–205, 96–113. [Google Scholar] [CrossRef]
- Nasirov, A.; Fidan, I. Prediction of mechanical properties of fused filament fabricated structures via asymptotic homogenization. Mech. Mater. 2020, 145, 103372. [Google Scholar] [CrossRef]
- Nasirov, A.; Gupta, A.; Hasanov, S.; Fidan, I. Three-scale asymptotic homogenization of short fiber reinforced additively manufactured polymer composites. Compos. Part B Eng. 2020, 202, 108269. [Google Scholar] [CrossRef]
- Jin, J.-W.; Jeon, B.-W.; Choi, C.-W.; Kang, K.-W. Multi-Scale Probabilistic Analysis for the Mechanical Properties of Plain Weave Carbon/Epoxy Composites Using the Homogenization Technique. Appl. Sci. 2020, 10, 6542. [Google Scholar] [CrossRef]
- Rodríguez-Ramos, R.; Sabina, F.J.; Guinovart-Díaz, R.; Bravo-Castillero, J. Closed-form expressions for the effective coefficients of a fiber-reinforced composite with transversely isotropic constituents–I. Elastic and square symmetry. Mech. Mater. 2001, 33, 223–235. [Google Scholar] [CrossRef]
- Guinovart-Díaz, R.; Bravo-Castillero, J.; Rodríguez-Ramos, R.; Sabina, F.J.; Rodríguez-Ramos, R.; Bravo-Castillero, J.; Guinovart-Díaz, R. Closed-form expressions for the effective coefficients of a fibre-reinforced composite with transversely isotropic constituents. II: Piezoelectric and hexagonal symmetry. J. Mech. Phys. Solids 2001, 49, 1463–1479. [Google Scholar] [CrossRef]
- Jiang, C.P.; Xu, Y.L.; Cheung, Y.K.; Lo, S.H. A rigorous analytical method for doubly periodic cylindrical inclusions under longitudinal shear and its application. Mech. Mater. 2004, 36, 225–237. [Google Scholar] [CrossRef][Green Version]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A 1957, 241, 376–396. [Google Scholar]
- Lu, J.-K. Boundary Value Problems for Analytic Functions; Series in Pure Mathematics; World Scientific: London, UK, 1994; Volume 16. [Google Scholar]
- Artioli, E.; Bisegna, P.; Maceri, F. Effective longitudinal shear moduli of periodic fibre-reinforced composites with radially-graded fibres. Int. J. Solids Struct. 2010, 47, 383–397. [Google Scholar] [CrossRef]
- Shu, W.; Stanciulescu, I. Multiscale homogenization method for the prediction of elastic properties of fiber-reinforced composites. Int. J. Solids Struct. 2020, 203, 249–263. [Google Scholar] [CrossRef]
- Dhimole, V.K.; Chen, Y.; Cho, C. Modeling and Two-Step Homogenization of Aperiodic Heterogenous 3D Four-Directional Braided Composites. J. Compos. Sci. 2020, 4, 179. [Google Scholar] [CrossRef]
- Bisegna, P.; Caselli, F. A simple formula for the effective complex conductivity of periodic fibrous composites with interfacial impedance and applications to biological tissues. J. Phys. D. Appl. Phys. 2008, 41, 115506. [Google Scholar] [CrossRef]
- Godin, Y.A. Effective complex permittivity tensor of a periodic array of cylinders. J. Math. Phys. 2013, 54, 53505. [Google Scholar] [CrossRef]
- Godin, Y.A. Effective properties of periodic tubular structures. Q. J. Mech. Appl. Math. 2016, 69, 181–193. [Google Scholar] [CrossRef][Green Version]
- Milton, G.W. Bounds on the complex dielectric constant of a composite material. Appl. Phys. Lett. 1980, 37, 300–302. [Google Scholar] [CrossRef]
- Milton, G.W.; Movchan, A.B. A correspondence between plane elasticity and the two-dimensional real and complex dielectric equations in anisotropic media. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1995, 450, 293–317. [Google Scholar]
- Mackay, T.G.; Lakhtakia, A. Gain and loss enhancement in active and passive particulate composite materials. Waves Random Complex Media 2016, 26, 553–563. [Google Scholar] [CrossRef]
- Guild, M.D.; Garcia-Chocano, V.M.; Kan, W.; Sánchez-Dehesa, J. Enhanced inertia from lossy effective fluids using multi-scale sonic crystals. AIP Adv. 2014, 4, 124302. [Google Scholar] [CrossRef]
- Luong, Q.; Nguyen, M.; TonThat–Long; Tran, D. Complex Shear Modulus Estimation using Integration of LMS/AHI Algorithm. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 584–589. [Google Scholar] [CrossRef]
- Hashin, Z. Thin interphase/imperfect interface in elasticity with application to coated fiber composites. J. Mech. Phys. Solids 2002, 50, 2509–2537. [Google Scholar] [CrossRef]
- Sevostianov, I.; Rodríguez-Ramos, R.; Guinovart-Díaz, R.; Bravo-Castillero, J.; Sabina, F.J. Connections between different models describing imperfect interfaces in periodic fiber-reinforced composites. Int. J. Solids Struct. 2012, 49, 1518–1525. [Google Scholar] [CrossRef]
- Guinovart-Díaz, R.; Rodríguez-Ramos, R.; López-Realpozo, J.C.; Bravo-Castillero, J.; Otero, J.A.; Sabina, F.J.; Lebon, F.; Dumont, S. Analysis of fibrous elastic composites with nonuniform imperfect adhesion. Acta Mech. 2016, 227, 57–73. [Google Scholar] [CrossRef]
- Le, T.-T. Multiscale Analysis of Elastic Properties of Nano-Reinforced Materials Exhibiting Surface Effects. Application for Determination of Effective Shear Modulus. J. Compos. Sci. 2020, 4, 172. [Google Scholar] [CrossRef]
- Bensoussan, A.; Lions, J.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; North-Holland Publishing Company: Amsterdam, The Netherlands, 1978; ISBN 0444851720. [Google Scholar]
- Sánchez-Palencia, E. Non Homogeneous Media and Vibration Theory; Lecture Notes in Physiscs; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Bakhvalov, N.S.; Panasenko, G.P. Homogenization Averaging Processes in Periodic Media; Kluwer Academic: Dordrecht, The Netherlands, 1989. [Google Scholar]
- Allaire, G.; Briane, M. Multiscale convergence and reiterated homogenisation. Proc. R. Soc. Edinb. Sect. A Math. 1996, 126, 297–342. [Google Scholar] [CrossRef]
- Auriault, J.L.; Boutin, C.; Geindreau, C. Homogenization of Coupled Phenomena in Heterogenous Media; Wiley-ISTE: Hoboken, NJ, USA, 2009. [Google Scholar]
- Penta, R.; Gerisch, A. Investigation of the potential of asymptotic homogenization for elastic composites via a three-dimensional computational study. Comput. Vis. Sci. 2015, 17, 185–201. [Google Scholar] [CrossRef]
- Ramírez-Torres, A.; Penta, R.; Rodríguez-Ramos, R.; Merodio, J.; Sabina, F.J.; Bravo-Castillero, J.; Guinovart-Díaz, R.; Preziosi, L.; Grillo, A. Three scales asymptotic homogenization and its application to layered hierarchical hard tissues. Int. J. Solids Struct. 2018, 130–131, 190–198. [Google Scholar] [CrossRef]
- Ramírez-Torres, A.; Penta, R.; Rodríguez-Ramos, R.; Grillo, A.; Preziosi, L.; Merodio, J.; Guinovart-Díaz, R.; Bravo-Castillero, J. Homogenized out-of-plane shear response of three-scale fiber-reinforced composites. Comput. Vis. Sci. 2019, 20, 85–93. [Google Scholar] [CrossRef]
- Dong, H.; Zheng, X.; Cui, J.; Nie, Y.; Yang, Z.; Yang, Z. High-order three-scale computational method for dynamic thermo-mechanical problems of composite structures with multiple spatial scales. Int. J. Solids Struct. 2019, 169, 95–121. [Google Scholar] [CrossRef]
- Guinovart-Díaz, R.; López-Realpozo, J.C.; Rodríguez-Ramos, R.; Bravo-Castillero, J.; Ramírez, M.; Camacho-Montes, H.; Sabina, F.J. Influence of parallelogram cells in the axial behaviour of fibrous composite. Int. J. Eng. Sci. 2011, 49, 75–84. [Google Scholar] [CrossRef]
- Kalamkarov, A.L.; Andrianov, I.V.; Pacheco, P.M.C.L.; Savi, M.A.; Starushenko, G.A. Asymptotic Analysis of Fiber-Reinforced Composites of Hexagonal Structure. J. Multiscale Model. 2016, 7, 1650006–1650270. [Google Scholar] [CrossRef]
- Rodríguez-Ramos, R.; Yan, P.; López-Realpozo, J.C.; Guinovart-Díaz, R.; Bravo-Castillero, J.; Sabina, F.J.; Jiang, C.P. Two analytical models for the study of periodic fibrous elastic composite with different unit cells. Compos. Struct. 2011, 93, 709–714. [Google Scholar] [CrossRef]
- Cioranescu, D.; Donato, P. An Introduction to Homogenization; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity; Noordhoff: Groningen, Holland, 1953. [Google Scholar]
- Grigolyuk, E.I.; Fil’shtinskii, L.A. Perforated plates and shells; Nauka: Moscow, Russia, 1970; Volume 1, pp. 6–31. [Google Scholar]
- Markushevich, A.I. Theory of Functions of a Complex Variable; Silverman, R.A., Ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1967. [Google Scholar]
- Kantorovich, L.V.; Krylov, V.I. Approximate Methods of Higher Analysis, 3rd ed.; Interscience: INC, Groningen, The Netherlands, 1964. [Google Scholar]
- Van Loocke, M.; Lyons, C.G.; Simms, C.K. Viscoelastic properties of passive skeletal muscle in compression: Stress-relaxation behaviour and constitutive modelling. J. Biomech. 2008, 41, 1555–1566. [Google Scholar] [CrossRef]
- Sharafi, B.; Blemker, S.S. A micromechanical model of skeletal muscle to explore the effects of fiber and fascicle geometry. J. Biomech. 2010, 43, 3207–3213. [Google Scholar] [CrossRef]
- Frolova, K.P.; Vilchevskaya, E.N.; Bauer, S.M.; Müller, W.H. Determination of the shear viscosity of the sclera. ZAMM J. Appl. Math. Mech. Z. Angew. Math. Mech. 2019, 99, e201800156. [Google Scholar] [CrossRef]
- Marcucci, L.; Bondì, M.; Randazzo, G.; Reggiani, C.; Natali, A.N.; Pavan, P.G. Fibre and extracellular matrix contributions to passive forces in human skeletal muscles: An experimental based constitutive law for numerical modelling of the passive element in the classical Hill-type three element model. PLoS ONE 2019, 14, e0224232. [Google Scholar] [CrossRef] [PubMed]
- Kolpakov, A.; Kolpakov, A. Capacity and Transport. In Contrast Composite Structures: Asymptotic Analysis and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- López-Realpozo, J.C.; Rodríguez-Ramos, R.; Guinovart-Díaz, R.; Bravo-Castillero, J.; Otero, J.A.; Sabina, F.J.; Lebon, F.; Dumont, S.; Sevostianov, I. Effective elastic shear stiffness of a periodic fibrous composite with non-uniform imperfect contact between the matrix and the fibers. Int. J. Solids Struct. 2014, 51, 1253–1262. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).