Abstract
A mathematical model employing the concept of energy-equivalent inhomogeneity is applied to analyze short cylindrical fiber composites with interfaces described by the Steigmann–Ogden material surface model. Real inhomogeneity consists of a cylindrical fiber of finite length, and its surface possessing different properties is replaced by a homogeneous, energy-equivalent cylinder. The properties of the energy-equivalent fiber, incorporating properties of the original fiber and its interface, are determined on the basis of Hill’s energy equivalence principle. Closed-form expressions for components of the stiffness tensor of equivalent fiber have been developed and, in the limit, shown to compare well with the results available in the literature for infinite fibers with the Steigmann–Ogden interface model. Dependence of those components on the radius, length of the cylindrical fiber, and surface parameters is included in these expressions. The effective stiffness tensor of the short-fiber composites with so-defined equivalent cylindrical fibers can be determined by any homogenization method developed without accounting for interface.
1. Introduction
Interphases between inhomogeneities and the matrix may have a very pronounced influence on the effective behavior of entire composites. The interphases are typically three-dimensional continua, but treating them as such is feasible only for simple geometry of the inhomogeneities and for simple loading conditions.
To cover more complex situations, some effort has been invested into developing various simplified models of interphases [1,2,3,4,5,6,7,8,9,10,11], among others. The most practical and popular of them are the Gurtin–Murdoch [12,13] model and the spring layer model [1,4,5,14,15,16,17,18,19]. The former is a membrane-type model in which the bending stiffness of the interphase is assumed to be negligible and which preserves kinematic continuity. The latter allows for displacement discontinuity and relates forces transmitted across the interphase to the tangential and normal components of that discontinuity. The Gurtin–Murdoch and related models of surface elasticity have been used to study beams, plates, and shells [20,21].
Generalization of the Gurtin–Murdoch model was proposed by Steigmann and Ogden [22,23], who introduced the resistance of the surface to both stretching and bending. Their development is based on the Kirchhoff–Love shell kinematics and, as such, implies that the surface energy in the Steigmann–Ogden model includes both the surface membrane strain tensor and the surface curvature tensor. The Steigmann–Ogden model was used in [24,25] to study bending of nano-sized cantilever beams. In these investigations, the Steigmann–Ogden constants were determined by using a combination of atomistic simulations and a simple continuum model. A similar analysis within the Steigmann–Ogden model but for laminates was provided in [26], where the formula for the effective bending stiffness and its dependence on the surface elastic moduli were derived.
In [27,28,29,30], it was demonstrated that higher-gradient theories could entail surface tensors of stresses and couple stresses as well as other stress resultants.
Within Toupin–Mindlin formulation [31,32,33] of the strain gradient elasticity, the mathematical study of static and dynamic boundary value problems with surface stresses described by Steigmann-Ogden model was presented in [34,35].
The boundary conditions for the Steigmann–Ogden [22,23] model for a two-dimensional surface using general expression for surface energy were re-derived in [36]. The effect of curvature-dependent interfacial energy was also studied in [37] for finite deformation. The effective moduli of nanocomposites were analyzed in [38]. The effective properties of the isotropic particulate composites with Steigmann–Ogden interface were derived in [39,40].
In this work, the energy-equivalent inhomogeneity (EEI) approach, recently presented in [19,41,42,43], is applied to short fibers modeled as cylindrical inhomogeneity of finite length with a Steigmann–Ogden model of interface. The presented approach can be used for determination of the properties of equivalent homogeneous cylindrical fiber for which the properties incorporate properties of the interface and then, in combination with any homogenization method developed for composites without interfaces, for determination of effective properties of short-fiber composites with an interface.
This paper is organized as follows. The next section briefly introduces the notion of energy equivalence and its subsequent specification for cylinders of finite length and the Steigmann–Ogden model of interface; it also defines the properties of the energy-equivalent cylinder. In Section 3, this is followed by a comparison with the results available in the literature for infinite cylindrical fibers with Gurtin–Murdoch and Steigmann–Ogden interface models. The paper final section contains some overall comments about the approach pursued herein and the results obtained. Several technical details are presented in Appendix A and Appendix B.
2. Energy-Equivalent Short Cylindrical Fiber with Steigmann–Ogden Surface Model
2.1. General Considerations
To find properties of the equivalent inhomogeneity of any shape meant to incorporate properties of the original inhomogeneity and those of its interphase, the system is subjected to boundary displacements consistent with constant straining, represented by an arbitrary constant tensor . The elastic energy of this system is
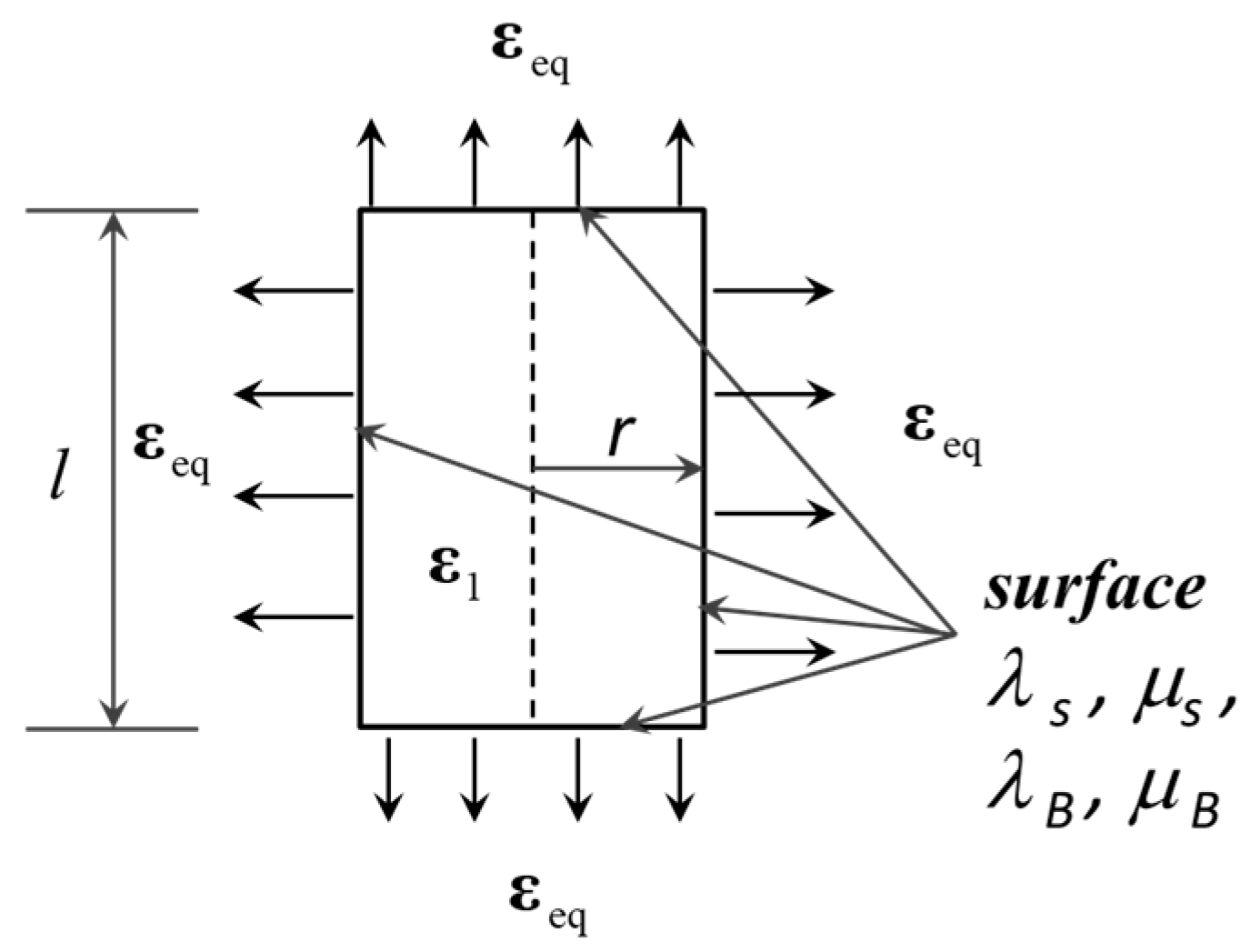
where is the strain energy of the interphase appropriate for the Steigmann–Ogden model, is the strain within the original inhomogeneity caused by , and is the rank four tensor of the elastic moduli of the original cylindrical inhomogeneity (Figure 1).
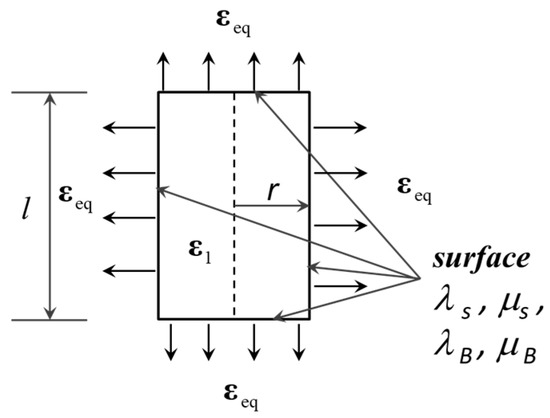
Figure 1.
Schematic illustration of cylindrical inhomogeneity.
The mathematical description of energy equivalence is expressed by the following equation:
where is the unknown constitutive tensors of the equivalent inhomogeneity and depends on the specific model of the interphase employed and on the data characterizing the system. Under the assumption of linearly elastic interphase, at equilibrium, both terms on the far right-hand side are quadratic functions of and Equation (2) can be used to determine . As shown in [19,41], that simple idea may be technically quite demanding, particularly for complex shapes of inhomogeneity, but it is executable and, in the cases considered so far, leads to remarkably accurate, closed-form results.
2.2. Steigmann–Ogden Surface Model and Associated Elastic Energy
The original development of the Steigmann–Ogden model, including equilibrium equations and related boundary conditions, are presented in [22,23]. These relations are derived within the Toupin–Mindlin formulation of the strain gradient elasticity in [35] and have following forms:
Displacements continuity on
Stress discontinuity on
The unit vector in the above equation is normal to , and it is assumed to point away from the inhomogeneity. The square brackets indicate the jump of the field quantities across the interface, defined as their value on the side towards which vector points minus their value on the side from which it points; is the surface gradient operator; is the main curvature; is the curvature tensor; and the surface membrane stress tensor [12,13] is defined as
where is the interface/surface membrane strain tensor, represents the second-rank identity tensor in the plane tangent to the surface, is the magnitude of the deformation-independent (residual) surface/interfacial tension (assumed “hydrostatic” and constant in Gurtin–Murdoch model), and are surface Lamé parameters, while denotes the surface gradient of the interface displacement field.
The surface couple stress tensor (moments), which described surface bending [35,36,40], has the following form:
The symbols and are the material parameters describing the bending stiffness of the (isotropic) material surface. The surface strain tensor and the bending strain measure (tensor representing changes of curvature due to bending) are as follows:
in which represents rotation of the surface (more specifically, it is displacement of the tip of vector due to rotation of the surface)
In the case of Steigmann–Ogden interface Equations (3)–(9), the surface energy can be represented as
where and are the energies related to surface tension and surface bending:
In [42], it is shown that, for cylindrical approximation of short fibers described by Gurtin–Murdoch surface expressed in Equations (3)–(9), if , the stiffness tensors have transversely isotropic symmetry, characterized by 5 independent constants, and have the following form:
where is the stiffness tensor of the original inhomogeneity while represents an additional contribution of surface elasticity to the properties of an equivalent cylindrical fiber (see details in [42]). This specific form of Equation (13) results from the fact that the Gurtin–Murdoch model assumes vanishingly thin interphase and preserves kinematic continuity, so in Equation (2), —a property that is also preserved in the Steigmann–Ogden interface model and is exploited subsequently. The transversely isotropic symmetry of equivalent elasticity stiffness tensor will be subsequently written in Voigt’s notation assuming the following identification scheme:
with index 3 denoting the longitudinal axis of the fiber. As shown in [42], the expressions for the six non-vanishing components of matrix , five of which are independent, have the following forms:
where and are the modified Lamé parameters of isotropic tensor of surface elasticity, appearing as a result of the surface tension contribution in Equations (5) and (11); is the radius of the cylinder; and is its length (see Figure 1). In the adopted Steigmann–Ogden interface model, the tenor should be also transversely isotropic and can be defined as
where is a contribution of surface bending.
The development neglecting the term of Equations (4) and (6) was presented in [42]. Here, the focus of evaluation of the properties of EEI is on the contribution of surface bending. The use of the complete Equation (4) in analysis may turn out to be important in some practical applications, where bending of the surface should be accounted for.
Inclusion of the complete Equation (4) within the framework of the EEI is outlined in the next subsection, with some supporting derivations presented in the related Appendix A and Appendix B.
2.3. Contribution of the Surface Bending to the Energy of Equivalent Cylinder
2.3.1. Evaluation of the Surface Energy Related to the Bending
In order to determine the surface contribution described by Equation (12), the tensor of curvature changes will be evaluated first.
It is assumed that the strains, , that an inhomogeneity is subjected to are constant. Under those conditions, displacements in the surface of that inhomogeneity can be expressed as
where is the position vector of a point on that surface which is locally parameterized by , . Consequently, cf. [44]
where are the vectors of the natural basis associated with the parametrization (tangent to the surface) and is the vectors of the dual, or reciprocal, basis also tangent to the surface) satisfying the condition , with being the “Kronecker delta”.
The tensor of curvature changes is determined as
with
where
Considering Equation (18), can be defined as
which gives
The above formula indicates that contracted with the first 2 vectors of and operate on the third vector of dyadic product in . This means that multiplication by eliminates () and the remaining two parts are unchanged. Therefore,
Evaluation of the components of the tensors and is illustrated in Appendix A, where curvature tensors for spherical inhomogeneity of radius are given in Table A1. Considering values and from Table A1, the tensor of curvature changes can be defined as
Then, the surface strain energy in the case of the Steigmann–Ogden model of interface is defined as (see, for details, [35,36,40])
The first three terms of the above integrand are identical to the surface strain energy given by the Gurtin–Murdoch model, and properties of equivalent inhomogeneities related to these terms are determined in [42]. The last two terms of Equation (27) represent the surface strain energy related to surface bending. In the next section, the working formula for the properties of the equivalent inhomogeneity is presented.
2.3.2. Constitutive Tensor of the Energy-Equivalent Cylinder
Considering Equation (26), the last two terms of Equation (27) are given as
The surface energy of Equation (27) is a sum of the surface tension and the surface bending Equations (11) and (12), and we focus only on the latter:
where is defined as
and is
These last formulas in Equations (30)–(32) can be put in Equation (10), and the following form of the surface energy yields
where
The last result for and the energy equivalence expressed by Equation (2) leads to the following formula for the effective moduli of equivalent inhomogeneity:
Then, the problem of properties of equivalent inhomogeneities is reduced to evaluation of the components of the above tensors and , which is illustrated in Appendix B Equations (A35)–(A37). Contribution of surface bending to the stiffness tensor Equation (35) in this case is
where and are additional material parameters describing the bending stiffness of the material surface in Equation (6). In the presence of in Equation (4), the tenor is also transversely isotropic and its constants are defined in Equation (35), where is defined in Equation (15).
Remark 1.
It should be noted that the properties of equivalent cylindrical fibers can be used in combination with any homogenization method developed without accounting for interfaces.
3. Comparison with the Existing Results for the Cylinder of Infinite Length with Gurtin–Murdoch and Steigmann–Ogden Interfaces
To validate the proposed approach, the equivalent properties of cylinder of infinite length are obtained as a limiting case and compared with two-dimensional solutions of the problem, which are the only currently available results for cylindrical inhomogeneities with Gurtin–Murdoch and Steigmann–Ogden surfaces.
In the limit and , one obtains the results for an equivalent infinite cylindrical fiber with Gurtin–Murdoch interface. The independent constants of matrix in this case are
Four out of the above five constants, , , , , can be presented in the form of Hill’s phase moduli [45], and in that form, they are exactly the same as those presented in [15,16]. In those publications, the properties of an equivalent infinite cylindrical fiber with Gurtin–Murdoch interface have been determined first using the concept of neutral inhomogeneity [46]. The authors subsequently observed that the same equivalent properties are obtained if the constitutive tensor of the fibers is augmented by the terms shown in Equations (37). Such an agreement with the values obtained “a posteriori” and by a different approach furnishes an additional support for the concept of equivalent inhomogeneity presented herein.
The fifth constant, the transverse shear modulus, constitutes an exception in the sense that, in [15], it could not be determined by the same approach as the other four, i.e., by a neutral composite cylinder approach or composite cylinder assembly [5,16]. Thus, the generalized self-consistent method [47] has been employed in [16] instead, which turned out not to allow for identification of the contribution of surface elasticity to the fifth constant of the equivalent cylinder.
The properties of an equivalent infinite cylindrical fiber with a Steigmann–Ogden interface can be also compared with the two-dimensional solutions presented in [36]. Two of the constants listed in Equations (36) and (37), and , and for surface bending and surface tension, were presented in the form of the plane bulk modulus and transverse shear modulus (Hill’s notation) and compared with those obtained in [36] for two-dimensional solutions of the problem (limit if ). Properties of equivalent circular inhomogeneity [36] are obtained based on well-known elasticity solutions for two complementary problems: one of the circular discs subjected to the unknown tractions at any boundary point and another one from an infinite matrix subjected to the uniform far-field load and containing a circular hole under the action of unknown boundary tractions. The solutions for both problems can be obtained by the complex variables approach. It is shown in [36] that surface bending does not affect the plane bulk modulus , and at the same time, the contribution of the surface tension to the plane bulk modulus of equivalent cylinder presented herein is identical to the results in [36], really, Equation (54) in [46] (in notations adopted in the present article):
Comparing Equations (35)–(38), it is evident that
The above Equations (39) are identical to Equations (36) and (37).
Given that and are considerably smaller then Lamé parameters of bulk material (see, e.g., [24,25,36,40]), it is possible to check that first-order approximation of the results for transverse shear moduli and presented in [36] (in Equation (59)) coincides with the ones presented here. Thus, Equation (59) in [36] (in notations adopted in the present article) is
where and . It should be noted that the properties of an equivalent infinite cylinder are obtained on the basis of a solution for an infinite matrix subjected to the uniform far-field load and containing a circular hole under the action of unknown boundary tractions, and as a result, they depend on the properties of the infinite matrix . The first-order approximation of Equation (40) is as follows:
and it is identical to Equations (35)–(37).
4. Conclusions
A mathematical model employing the concept of the EEI [19,41,42,43] has been generalized to introduce the surface effects described by the Steigmann–Ogden model [22,23] derived within the strain gradient elasticity [35]. A particular focus was centered on accounting for surface bending contribution in the definition of the EEI.
The properties of an equivalent cylinder of finite length with the Steigmann–Ogden model of interface is determined based on the corresponding definition of surface energy, which includes both surface tension and surface bending. As typically done in Hill’s equivalence principle, a uniform state of strains within the cylinder is assumed. The stiffness tensor of the equivalent cylinder has transversely isotropic symmetry, and five independent constants of this tensor are presented in a closed form.
Unfortunately, due to a lack of solutions for problems involving finite-length cylindrical fibers, the main results presented herein could not be verified by direct comparisons. This could be accomplished only by the asymptotic transformation of those results to obtain equivalent stiffness tensors for infinite cylindrical inhomogeneity. As shown in Section 3, in the asymptotic limit, the results obtained in this work are in a good agreement with those of [15,16] obtained for infinite cylindrical inhomogeneities with Gurtin–Murdoch interface (by solving a number of two-dimensional problems). They are also in good agreement with results obtained for the plane bulk and transverse shear moduli derived for the two-dimensional problem of circular inhomogeneities with the Steigmann–Ogden model of interface.
To conclude, it is worth mentioning that the definition of the EEI is general and can be used in the case of inhomogeneities of shapes other than cylindrical, e.g., ellipsoidal. It can be very naturally combined with any homogenization method developed for composite materials without accounting for interface and appears to be potentially amenable for inclusion of models other than the Gurtin–Murdoch or Steigmann–Ogden interface models. The important characteristic of the proposed approach is its ability to provide closed-form expressions for the properties of equivalent inhomogeneities. Closed-form results are important, especially if the influence of different problem parameters needs to be analyzed.
Author Contributions
The conception of the idea as well as drafting and revising various versions of the manuscript was a truly collaborative effort. The idea was born during discussion of previous jointly coauthored articles. The preparation of the manuscript involved several iterations in which all authors took consecutive turns in reading the manuscript and inserting their comments. The individual authors have been largely responsible for the following technical aspects of the paper: H.S., governing equations of the problem and evaluation of the formula for energy of the system (original inhomogeneity and interphase); L.N., development of equations for determination of the properties of equivalent inhomogeneity and their implementation, and the equivalent properties of cylinders with the Steigmann–Ogden model of interface; H.A., addition of some important references, analysis and interpretation of obtained results, and final approval of the version to be published. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the German Research Foundation (DFG), grant number AL 341/51-1.
Acknowledgments
L.N. and H.A. gratefully acknowledge the financial support by the German Research Foundation (DFG) via project AL 341/51-1.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Components of Curvature Tensors for Cylinder
Let us assume that the surface of interest is locally parameterized by , , and that the position vector of a point on that surface is expressed as . Then, one can define a couple of vectors :
which forms the vector basis in the linear space tangent to the surface S, called the natural basis. Another basis in the same tangent space, denoted by and called dual or reciprocal, is defined as follows:
where represents the “dot” (or “inner”) product of vectors and is the Kronecker “delta”. The bases and are functions of , and their derivatives can be expressed by the well-known Gauss–Weingarten formulas (see [44], for example). For the natural basis, these formulas are (cf. Equation (A1) for notations)
with a unit vector n normal to the surface. Here (as shown in the above equation), an index repeated in the subscript and superscript position implies summation, are the so-called Christoffel symbols (of the second kind), and the components of the local curvature tensor are
Equation (A3) together with Equation (A1) imply that , whereas definition of the Christoffel symbols and Equation (A1) imply the following symmetry property: . The analogical formulas for the derivatives of vectors of the dual basis are
where is the so-called mixed components of the local curvature tensor. The curvature tensor B can be represented as
In the above equation, double summation is implied and the (indexed) coefficients multiplying the dyadic are various components of tensor . They all can be different, but they are related to each other by transformation formulas involving the so-called gram matrices related to the natural or dual bases. Those matrices are defined as follows:
Using the relationship between various components of the curvature tensor B, one can present the following:
In the case of cylindrical inhomogeneity of radius , the position vector of a point on the surface of the inhomogeneity and the corresponding unit vector n, normal to that surface may be expressed in cylindrical coordinates as follows:
Consequently, the local vectors of the natural basis are
and
The dual basis is defined as
Then, the curvature tensors for cylindrical inhomogeneity of radius are given:

Table A1.
Curvature tensors for a cylinder of radius .
Table A1.
Curvature tensors for a cylinder of radius .
| 1 | 1 | ||
| 1 | 2 | 0 | 0 |
| 2 | 2 | 0 | 0 |
| 2 | 1 | 0 | 0 |
The local vectors of the natural basis on the circular part of the cylinder’s surface (i.e., on its two ends) are
and
Substituting (A14) in (A4), it is seen that the curvature tensor of the circular part of the cylinder’s surface (two ends of cylinder) is as follows:
As a result, we have that the contribution of the circular part of the cylinder’s surface to surface bending of cylindrical inhomogeneity is equal to zero.
Appendix B. Properties of the Energy-Equivalent Cylinder of Finite Length Accounting for Surface Bending
For illustration of some technical details, and of Equations (31)–(34) are evaluated in this Appendix. In addition to and , the contribution of surface tension to properties of equivalent inhomogeneity includes another term present in Equation (34); however, evaluation of this term is presented in [42].
Assuming that inhomogeneities are cylinders of radius and length (Figure 1) and using the cylindrical coordinate system in Equation (A9), of Equations (31) and (33) is described by the following:
It is seen that tensor has transversely isotropic symmetry. of Equations (32) and (34) is described by the following:
As expected, tensor is transversely isotropic.
The contribution of surface bending to the stiffness tensor of the equivalent inhomogeneity Equation (35) is
In addition to , the contribution of surface tension to properties of equivalent inhomogeneity includes another term present in Equation (15); however, evaluation of this term is presented in [42].
References
- Benveniste, Y.; Miloh, T. Imperfect soft and stiff interfaces in two-dimensional elasticity. Mech. Mater. 2001, 33, 309–323. [Google Scholar] [CrossRef]
- Dong, C.Y.; Zhang, G.L. Boundary element analysis of three dimensional nanoscale inhomogeneities. Int. J. Solids Struct. 2013, 50, 201–208. [Google Scholar] [CrossRef]
- Dong, H.; Wang, J.; Rubin, M. Cosserat interphase models for elasticity with application to the interphase bonding a spherical inclusion to an infinite matrix. Int. J. Solid. Struct. 2014, 51, 462–477. [Google Scholar] [CrossRef][Green Version]
- Hashin, Z. Thermoelastic properties of fiber composites with imperfect interface. Mech. Mater. 1990, 8, 333–348. [Google Scholar] [CrossRef]
- Hashin, Z. Thermoelastic properties of particulate composites with imperfect interface. J. Mech. Phys. Solids 1991, 39, 745–762. [Google Scholar] [CrossRef]
- He, L.H.; Li, Z.R. Impact of surface stress on stress concentration. Int. J. Solids Struct. 2006, 43, 6208–6219. [Google Scholar] [CrossRef]
- Huang, Z.P.; Wang, J. A theory of hyperelasticity of multi-phase media with surface/interface effect. Acta Mech. 2006, 182, 195–210. [Google Scholar] [CrossRef]
- Jasiuk, I.; Kouider, M.W. The effect of an inhomogeneous interphase on the elastic constants of transversely isotropic composites. Mech. Mat. 1993, 15, 53–63. [Google Scholar] [CrossRef]
- Serpilli, M.; Rizzoni, R.; Lebon, F.; Dumont, S. An asymptotic derivation of a general imperfect interface law for linear multiphysics composites. Int. J. Solids Struct. 2019, 180–181, 97–107. [Google Scholar] [CrossRef]
- Zhang, W.X.; Wang, T. Effect of surface energy on the yield strength of nanoporous materials. Appl. Phys. Lett. 2007, 90, 063104. [Google Scholar] [CrossRef]
- Rubin, M.; Benveniste, Y.A. Cosserat shell model for interphases in elastic media. J. Mech. Phys. Solids 2014, 52, 1023–1052. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Murdoch, A.I. A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 1975, 57, 291–323. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Murdoch, A.I. Surface stress in solids. Int. J. Solids Struct. 1978, 14, 431–440. [Google Scholar] [CrossRef]
- Brisard, S.; Dormieux, L.; Kondo, D. Hashin–Shtrikman bounds on the bulk modulus of a nanocomposite with spherical inhomogeneities and interface effects. Comput. Mater. Sci. 2010, 48, 589–596. [Google Scholar] [CrossRef]
- Chen, T.; Dvorak, G.J. Fibrous nano-composites with interface stresses: Hill’s and Levin’s connection for effective moduli. Appl. Phys. Lett. 2006, 88, 211912. [Google Scholar] [CrossRef]
- Chen, T.; Dvorak, G.J.; Yu, C.C. Size-dependent elastic properties of unidirectional nano-composites with interface stresses. Acta Mech. 2007, 188, 39–54. [Google Scholar] [CrossRef]
- Duan, H.L.; Wang, J.; Huang, Z.P.; Karihaloo, B.L. Size-dependent effective elastic constants of solids containing nanoinhomogeneities with interface stress. J. Mech. Phys. Solids 2005, 53, 1574–1596. [Google Scholar] [CrossRef]
- Lim, C.W.; Li, Z.R.; He, L.H. Size-dependent, non-uniform elastic field inside a nano-scale spherical inclusion due to interface stress. Int. J. Solids Struct. 2006, 43, 5055–5065. [Google Scholar] [CrossRef]
- Nazarenko, L.; Stolarski, H. Energy-based definition of equivalent inhomogeneity for various interphase models and analysis of effective properties of particulate composites. Comp. Part B. 2016, 94, 82–94. [Google Scholar] [CrossRef]
- Altenbach, H.; Eremeyev, V.A. On the shell theory on the nanoscale with surface stresses. Int. J. Eng. Sci. 2011, 49, 1294–1301. [Google Scholar] [CrossRef]
- Miller, R.E.; Shenoy, V.B. Size-dependent elastic properties of nanosized structural elements. Nanotechnology 2000, 11, 139–147. [Google Scholar] [CrossRef]
- Steigmann, D.J.; Ogden, R.W. Plane deformations of elastic solids with intrinsic boundary elasticity. Proc. R. Soc. Lond. A 1997, 453, 853–877. [Google Scholar] [CrossRef]
- Steigmann, D.J.; Ogden, R.W. Elastic surface-substrate interactions. Proc. R. Soc. Lond. A 1999, 455, 437–474. [Google Scholar] [CrossRef]
- Chhapadia, P.; Mohammadi, P.; Sharma, P. Curvature-dependent surface energy and implications for nanostructures. J. Mech. Phys. Solids 2011, 59, 2103–2115. [Google Scholar] [CrossRef]
- Mohammadi, P.; Sharma, P. Atomistic elucidation of surface roughness on curvature-dependent surface energy, surface stress, and elasticity. Appl. Phys. Latter 2012, 100, 133110. [Google Scholar] [CrossRef]
- Eremeyev, V.A.; Wiczenbach, T. On Effective Bending Stiffness of a Laminate Nanoplate Considering Steigmann–Ogden Surface Elasticity. Appl. Sci. 2020, 10, 7402. [Google Scholar] [CrossRef]
- Dell’Isola, F.; Seppecher, P. Edge contact forces and quasi-balanced power. Meccanica 1997, 32, 33–52. [Google Scholar] [CrossRef]
- Dell’Isola, F.; Seppecher, P.; Madeo, A. How contact interactions may depend on the shape of Cauchy cuts in Nth gradient continua: Approach “à la d’Alembert”. Z. Angew. Math. Phys. 2012, 63, 1119–1141. [Google Scholar] [CrossRef]
- Javili, A.; Dell’Isola, F.; Steinmann, P. Geometrically nonlinear higher-gradient elasticity with energetic boundaries. J. Mech. Phys. Solids 2013, 61, 2381–2401. [Google Scholar] [CrossRef]
- Javili, A.; Ottosen, N.S.; Ristinmaa, M.; Mosler, J. Aspects of interface elasticity theory. Math. Mech. Solids 2018, 23, 1004–1024. [Google Scholar] [CrossRef]
- Mindlin, R.D. Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 1964, 16, 51–78. [Google Scholar] [CrossRef]
- Mindlin, R.D. Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1965, 1, 417–438. [Google Scholar] [CrossRef]
- Toupin, R.A. Elastic materials with couple-stresses. Arch. Ration. Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Eremeyev, V.A.; Lebedev, L.P. Mathematical study of boundary-value problems within the framework of Steigmann–Ogden model of surface elasticity. Contin. Mech. Therm. 2016, 28, 407–422. [Google Scholar] [CrossRef]
- Eremeev, V. On dynamic boundary conditions within the linear Steigmann-Ogden model of surface elasticity and strain gradient elasticity. In Dynamical Processes in Generalized Continua and Structures. Advanced Structured Materials; Altenbach, H., Belyaev, A., Eremeyev, V., Krivtsov, A., Porubov, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 103. [Google Scholar]
- Zemlyanova, A.Y.; Mogilevskaya, S.G. Circular inhomogeneity with Steigmann–Ogden interface: Local fields, neutrality, and Maxwell’s type approximation formula. Int. J. Solids Struct. 2018, 135, 85–98. [Google Scholar] [CrossRef]
- Gao, X.; Huang, Z.; Qu, J.; Fang, D. A curvature-dependent interfacial energy-based interface stress theory and its applications to nanostructured materials: (I) general theory. J. Mech. Phys. Solids 2014, 66, 59–77. [Google Scholar] [CrossRef]
- Gao, X.; Huang, Z.; Fang, D. Curvature-dependent interfacial energy and its effects on the elastic properties of nanomaterials. Int. J. Solid. Struct. 2017, 113, 100–107. [Google Scholar] [CrossRef]
- Nazarenko, L.; Stolarski, H.; Altenbach, H. Effective properties of random nano-materials including Steigmann–Ogden interface model of surface. Comput. Mech. under review.
- Zemlyanova, A.Y.; Mogilevskaya, S.G. On spherical inhomogeneity with Steigmann–Ogden interface. J. Appl. Mech. 2018, 85, 121009. [Google Scholar] [CrossRef]
- Nazarenko, L.; Bargmann, S.; Stolarski, H. Energy-equivalent inhomogeneity approach to analysis of effective properties of nano-materials with stochastic structure. Int. J. Solids Struct. 2015, 59, 183–197. [Google Scholar] [CrossRef]
- Nazarenko, L.; Stolarski, H.; Altenbach, H. Effective properties of short-fiber composites with Gurtin-Murdoch model of interphase. Int. J. Solids Struct. 2016, 97–98, 75–88. [Google Scholar] [CrossRef]
- Nazarenko, L.; Bargmann, S.; Stolarski, H. Closed-form formulas for the effective properties of random particulate nanocomposites with complete Gurtin–Murdoch model of material surfaces. Contin. Mech. Thermodyn. 2017, 29, 77–96. [Google Scholar] [CrossRef]
- Itskov, M. Tensor Algebra and Tensor Analysis for Engineers; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Milton, G.W. The Theory of Composites; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Christensen, R.M.; Lo, K.M. Solution for effective shear properties in three phase sphere and cylinder models. J. Mech. Phys. Solids 1979, 27, 315–330. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).