Review of Computational Methods on Brain Symmetric and Asymmetric Analysis from Neuroimaging Techniques
Abstract
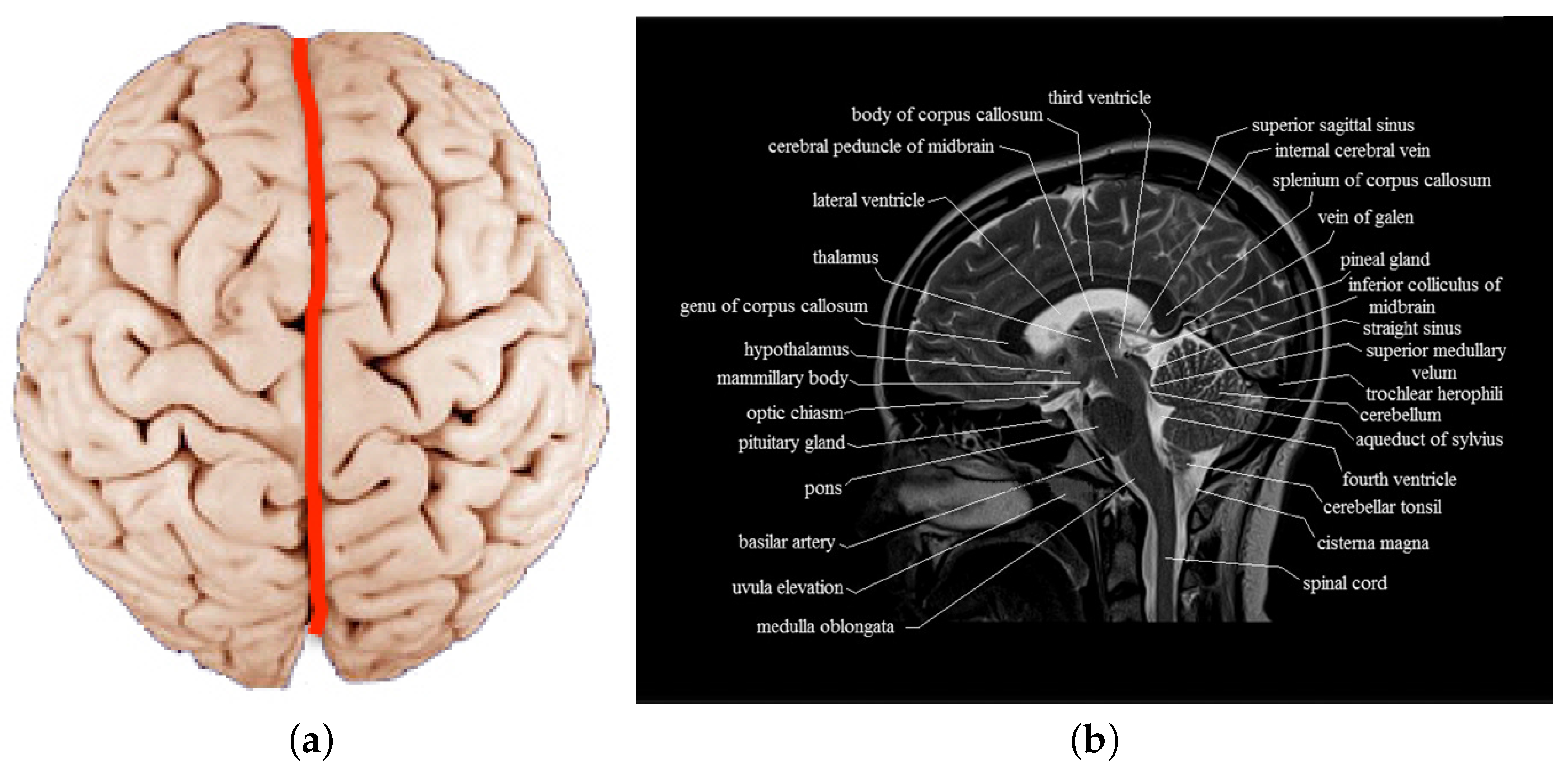
:1. Introduction
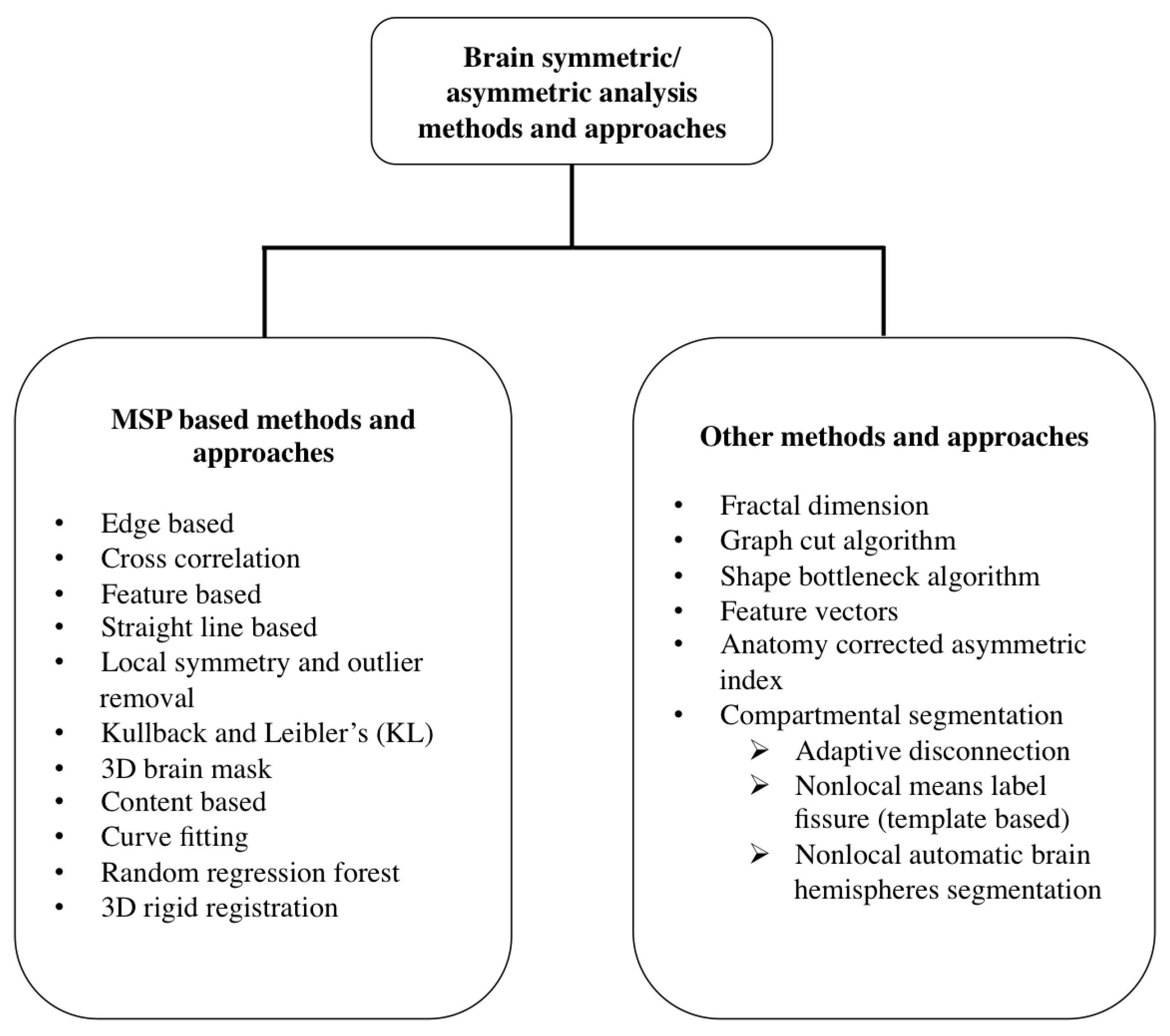
2. Review of Brain Symmetric/Asymmetric Analysis Methods
2.1. MSP Based Methods and Approaches
2.2. Other Methods and Approaches
3. Conclusions
Author Contributions
Conflicts of Interest
References
- Sonka, M.; Tadikonda, S.K.; Collins, S.M. Knowledge-based interpretation of MR brain images. IEEE Trans. Med. Imaging 1996, 15, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Damasio, H. Human Brain Anatomy in Computerized Images, 2nd ed.; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Wang, S.; Zhang, Y.; Yang, X.; Sun, P.; Dong, Z.; Liu, A.; Yuan, T.F. Pathological brain detection by a novel image feature—fractional Fourier entropy. Entropy 2015, 17, 8278–8296. [Google Scholar] [CrossRef]
- Wang, S.; Lu, S.; Dong, Z.; Yang, J.; Yang, M.; Zhang, Y. Dual-tree complex wavelet transform and twin support vector machine for pathological brain detection. Appl. Sci. 2016, 6, 169. [Google Scholar] [CrossRef]
- MRIMASTER.COM. Available online: https://mrimaster.com/anatomybrainsagittal.html (accessed on 18 April 2017).
- Kalavathi, P.; Prasath, V.B.S. Methods on skull stripping of MRI head scan images—A review. J. Digit. Imaging 2016, 29, 365–379. [Google Scholar] [CrossRef] [PubMed]
- Toga, A.W.; Thompson, P.M. Mapping brain asymmetry. Nat. Rev. Neurosci. 2003, 4, 37–48. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, J.A.; Zielinski, B.A.; Ferguson, M.A.; Lainhart, J.E.; Anderson, J.S. An evaluation of the left-brain vs. right-brain hypothesis with resting state functional connectivity magnetic resonance imaging. PLoS ONE 2013, 8, e71275. [Google Scholar]
- Harisson, P. The neuropathology of schizophrenia: A critical review of the data and their interpretation. Brain 1999, 122, 593–624. [Google Scholar] [CrossRef]
- Thompson, P.; Moussai, J.; Zohoori, S.; Goldkorn, A.; Khan, A.; Mega, M.; Small, G.; Cummings, J.; Toga, A. Cortical variability and asymmetry in normal aging and Alzheimer’s disease. Cereb. Cortex 1998, 8, 492–509. [Google Scholar] [CrossRef] [PubMed]
- Herbert, M.R.; Ziegler, D.; Deutsch, C.; O’Brien, L.; Kennedy, D.; Filipek, P.; Bakardjiev, A.; Hodgson, J.; Takeoka, M.; Makris, N.; et al. Brain asymmetries in autism and developmental language disorder: A nested whole-brain analysis. Brain 2005, 128, 213–226. [Google Scholar] [CrossRef] [PubMed]
- Bilder, R.M.; Wu, H.; Bogerts, B.; Degreef, G.; Ashtari, M.; Alvir, J.M.; Snyder, P.J.; Lieberman, J.A. Absence of regional hemispheric volume asymmetries in first-episode schizophrenia. Am. J. Psychiatry 1994, 151, 1437–1447. [Google Scholar] [PubMed]
- Pepe, A.; Zhao, L.; Koikkalainen, J.; Hietala, J.; Ruotsalainen, U.; Tohka, J. Automatic statistical shape analysis of cerebral asymmetry in 3D T1-weighted magnetic resonance images at vertex-level: Application to neuroleptic-naïve schizophrenia. Magn. Reson. Imaging 2013, 31, 676–687. [Google Scholar] [CrossRef] [PubMed]
- Sarmiento, C.I.; Prasath, V.B.S. Design of a Novel Servo-motorized Laser Device for Visual Pathways Diseases Therapy. BRAIN. Broad Res. Artif. Intell. Neurosci. 2015, 6, 84–90. [Google Scholar]
- Wang, S.; Yang, M.; Zhang, Y.; Li, J.; Zou, L.; Lu, S.; Liu, B.; Yang, J.; Zhang, Y. Detection of left-sided and right-sided hearing loss via fractional Fourier transform. Entropy 2016, 18, 194. [Google Scholar] [CrossRef]
- Jayasuriya, S.A.; Liew, A.W.C. Fractal dimension as a symmetry measure in 3D brain MRI analysis. In Proceedings of the IEEE International Conference on Machine Learning and Cybernetics, Xi’an, China, 15–17 July 2012; pp. 1118–1123. [Google Scholar]
- Boykov, Y.; Veksler, O.; Zabih, R. Fast approximate energy minimization via graph cuts. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1222–1239. [Google Scholar] [CrossRef]
- Zhao, L.; Tohka, J.; Ruotsalainen, U. Accurate 3D left-right brain hemisphere segmentation in MR images based on shape bottlenecks and partial volume estimation. In Proceedings of the 15th Scandinavian Conference on Image Analysis, SCIA’07, Aalborg, Denmark, 10–14 June 2007; pp. 581–590. [Google Scholar]
- Brummer, M.E. Hough transform detection of the longitudinal fissure in tomographic head images. IEEE Trans. Med. Imaging 1991, 10, 74–81. [Google Scholar] [CrossRef] [PubMed]
- Ruppert, G.; Teverovskiy, L.; Yu, C.P.; Falcao, A.X.; Liu, Y. A new symmetry-based method for mid-sagittal plane extraction in neuroimages. In Proceedings of the IEEE International Symposium on Biomedical Imaging, Chicago, IL, USA, 30 March–2 April 2011; pp. 285–288. [Google Scholar]
- Ardekani, B.A.; Kershaw, J.; Braun, M.; Kanuo, I. Automatic detection of the mid-sagittal plane in 3-D brain images. IEEE Trans. Med. Imaging 1997, 16, 947–952. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Collins, R.T.; Rothfus, W.E. Robust midsagittal plane extraction from normal and pathological 3-D neuroradiology images. IEEE Trans. Med. Imaging 2001, 20, 175–192. [Google Scholar] [PubMed]
- Prima, S.; Ourselin, S.; Ayache, N. Computation of the mid-sagittal plane in 3-D brain images. IEEE Trans. Med. Imaging 2002, 21, 122–138. [Google Scholar] [CrossRef] [PubMed]
- Brett, M.; Johnsrude, I.S.; Owen, A.M. The problem of functional localization in the human brain. Nat. Rev. Neurosci. 2002, 3, 243–249. [Google Scholar] [CrossRef] [PubMed]
- Tuzikov, A.V.; Colliot, O.; Bloch, I. Brain symmetry plane computation in MR images using inertia axes and optimization. In Proceedings of the International Conference on Pattern Recognition, Québec City, QC, Canada, 11–15 August 2002; Volume 1, pp. 516–519. [Google Scholar]
- Tuzikov, A.V.; Colliot, O.; Bloch, I. Evaluation of the symmetry plane in 3D MR brain images. Pattern Recognit. Lett. 2003, 24, 2219–2233. [Google Scholar] [CrossRef]
- Hu, Q.; Nowinski, W.L. A rapid algorithm for robust and automatic extraction of the midsagittal plane of the human cerebrum from neuroimages based on local symmetry and outlier removal. NeuroImage 2003, 20, 2153–2165. [Google Scholar] [CrossRef] [PubMed]
- Ekin, A. Feature-based brain mid-sagittal plane detection by RANSAC. In Proceedings of the European Signal Processing Conference, Florence, Italy, 4–8 September 2006; pp. 1–4. [Google Scholar]
- Volkau, I.; Prakash, B.; Ananthasubramaniam, A.; Gupta, V.; Aziz, A.; Nowinski, W.L. Quantitative analysis of brain asymmetry by using the divergence measure: normal-pathological brain discrimination. Acad. Radiol. 2006, 13, 752–758. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Rehm, K.; Woods, R.P.; Rottenberg, D.A. Automatic segmentation of left and right cerebral hemispheres from MRI brain volumes using the graph cuts algorithm. NeuroImage 2007, 34, 1160–1170. [Google Scholar] [CrossRef] [PubMed]
- Song, E.; Wang, Q.; Ma, G.; Liu, H. Symmetry analysis to detect pathological brain in MRI. In Proceedings of the International Symposium on Multispectral Image Processing and Pattern Recognition, Wuhan, China, 15–17 November 2007; p. 67891F. [Google Scholar]
- Liu, S.X.; Imielinska, C.; Laine, A.; Millar, W.S.; Connolly, E.S.; D’Ambrosio, A.L. Asymmetry analysis in rodent cerebral ischemia models. Acad. Radiol. 2008, 15, 1181–1197. [Google Scholar] [CrossRef] [PubMed]
- Bergo, F.P.; Falcão, A.X.; Yasuda, C.L.; Ruppert, G.C. Fast, accurate and precise mid-sagittal plane location in 3D MR images of the brain. In Proceedings of the Biomedical Engineering Systems and Technologies, Funchal, Madeira, Portugal, 28–31 January 2008; pp. 278–290. [Google Scholar]
- Zhou, L.; Dupont, P.; Baete, K.; Van Paesschen, W.; Van Laere, K.; Nuyts, J. Detection of inter-hemispheric metabolic asymmetries in FDG-PET images using prior anatomical information. NeuroImage 2009, 44, 35–42. [Google Scholar] [CrossRef] [PubMed]
- Teverovskiy, L.; Li, Y. Truly 3D midsagittal plane extraction for robust neuroimage registration. In Proceedings of the IEEE International Symposium on Biomedical Imaging, Arlington, VA, USA, 6–9 April 2006; pp. 860–863. [Google Scholar]
- Qi, X.; Belle, A.; Shandilya, S.; Chen, W.; Cockrell, C.; Tang, Y.; Ward, K.R.; Hargraves, R.H.; Najarian, K. Ideal midline detection using automated processing of brain CT image. Open J. Med. Imaging 2013, 3, 51–53. [Google Scholar] [CrossRef]
- Favretto, F.O.; Bergo, F.P.; Falcao, A.X. A fast and automatic method for 3D rigid registration of MR images of the human brain. In Proceedings of the Brazilian Symposium on Computer Graphics and Image Processing (SIBGRAPI), Campo Grande, Brazil, 12–15 October 2008; pp. 121–128. [Google Scholar]
- Kuijf, H.J.; van Veluw, S.J.; Geerlings, M.I.; Viergever, M.A.; Biessels, G.J.; Vincken, K.L. Automatic Extraction of the Midsagittal Surface from Brain MR Images using the Kullback–Leibler Measure. Neuroinformatics 2014, 12, 395–403. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Wang, D.; Shi, L.; Wen, Z.; Ming, Z. Midsagittal plane extraction from brain images based on 3D SIFT. Phys. Med. Biol. 2014, 59, 1367. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Wang, D.; Shi, L.; Wen, Z.; Ming, Z. Fast and robust symmetry detection for brain images based on parallel scale-invariant feature transform matching and voting. Int. J. Imaging Syst. Technol. 2013, 23, 314–326. [Google Scholar] [CrossRef]
- Liu, Y.; Dawant, B.M. Automatic Localization of the Anterior Commissure, Posterior Commissure, and Midsagittal Plane in MRI Scans using Regression Forests. IEEE J. Biomed. Health Inform. 2015, 19, 1362–1374. [Google Scholar] [CrossRef] [PubMed]
- Kalavathi, P.; Prasath, V.B.S. Automatic segmentation of cerebral hemispheres in MR human head scans. Int. J. Imaging Syst. Technol. 2016, 26, 15–23. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, Z.; Wang, S.; Ji, G.; Yang, J. Preclinical diagnosis of magnetic resonance (MR) brain images via discrete wavelet packet transform with Tsallis entropy and generalized eigenvalue proximal support vector machine (GEPSVM). Entropy 2015, 17, 1795–1813. [Google Scholar] [CrossRef]
- Minoshima, S.; Frey, K.A.; Koeppe, R.A.; Foster, N.L.; Kuhl, D.E. A diagnostic approach in Alzheimer’s disease using three-dimensional stereotactic surface projections of fluorine-18-FDG PET. J. Nuclear Med. 1995, 36, 1238–1248. [Google Scholar]
- Marias, P.; Guillernaud, R.; Sakuma, M.; Zisserman, A.; Brady, M. Visualising cerebral asymmetry. In Visualization in Biomedical Computing; Springer: Berlin/Heidelberg, Germany, 1996; pp. 411–416. [Google Scholar]
- Blatter, D.D.; Bigler, E.D.; Johnson, C.S.; Anderson, C.; Gale, S.D. A normative database from magnetic resonance imaging. In Neuroimaging I; Springer: Berlin/Heidelberg, Germany, 1996; pp. 79–95. [Google Scholar]
- Mangin, J.F.; Régis, J.; Frouin, V. Shape bottlenecks and conservative flow systems. In Proceedings of the Workshop on Mathematical Methods in Biomedical Image Analysis, San Francisco, CA, USA, 21–22 June 1996; pp. 319–328. [Google Scholar]
- Maes, F.; Van Leemput, K.; DeLisi, L.E.; Vandermeulen, D.; Suetens, P. Quantification of cerebral grey and white matter asymmetry from MRI. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention (MICCAI), Cambridge, UK, 19–22 September 1999; pp. 348–357. [Google Scholar]
- Amunts, K.; Jäncke, L.; Mohlberg, H.; Steinmetz, H.; Zilles, K. Interhemispheric asymmetry of the human motor cortex related to handedness and gender. Neuropsychologia 2000, 38, 304–312. [Google Scholar] [CrossRef]
- Lee, J.M.; Yoon, U.; Kim, J.J.; Kim, I.Y.; Lee, D.S.; Kwon, J.S.; Kim, I.Y. Analysis of the hemispheric asymmetry using fractal dimension of a skeletonized cerebral surface. IEEE Trans. Biomed. Eng. 2004, 51, 1494–1498. [Google Scholar] [PubMed]
- Grigaitis, D.; Meilunas, M. Automatic extraction of symmetry plane from falx cerebri areas in CT slices. In Bildverarbeitung für die Medizin; Springer: Berlin/Heidelberg, Germany, 2007; pp. 267–271. [Google Scholar]
- Zhao, L.; Ruotsalainen, U.; Hirvonen, J.; Hietala, J.; Tohka, J. Automatic cerebral and cerebellar hemisphere segmentation in 3D MRI: adaptive disconnection algorithm. Med. Image Anal. 2010, 14, 360–372. [Google Scholar] [CrossRef] [PubMed]
- Coupé, P.; Manjón, J.V.; Fonov, V.; Pruessner, J.; Robles, M.; Collins, D.L. Patch-based segmentation using expert priors: Application to hippocampus and ventricle segmentation. NeuroImage 2011, 54, 940–954. [Google Scholar] [CrossRef] [PubMed]
- Romero, J.E.; Manjón, J.V.; Tohka, J.; Coupé, P.; Robles, M. NABS: non-local automatic brain hemisphere segmentation. Magn. Reson. Imaging 2015, 33, 474–484. [Google Scholar] [CrossRef] [PubMed]
- Prasath, V.B.S.; Kalavathi, P. Adaptive nonlocal filtering for brain MRI restoration. In Proceedings of the Second International Symposium on Signal Processing and Intelligent Recognition Systems (SIRS), Trivandrum, Kerala, India, 16–19 December 2015; Thampi, S.M., Bandyopadhyay, S., Krishnan, S., Li, K.-C., Mosin, S., Ma, M., Eds.; Springer AISC: Chennai, India; pp. 571–580. [Google Scholar]
| Methods | Techniques Used | Image Modality |
|---|---|---|
| [19] | Hough transformation | MRI |
| [21] | Line fitting algorithm | MRI |
| [22] | Edge and cross correlation methods | MRI, PET, SPECT |
| [23] | Block matching procedure | MRI, CT, PET, SPECT |
| [24] | Linear stereotaxic registration and template matching | MRI |
| [25] | Based on similarity measures | MRI |
| [27] | Local symmetry histogram based outlier removal | MRI, CT |
| [28] | Feature based approach | 2D and 3D MRI |
| [29] | Kullback–Leibler measure | MRI, CT |
| [30] | Graph cuts algorithm | T1-weighted MRI |
| [31] | Parallel line fitting and correlation | MRI |
| [32] | Similarity measure and optimization technique | MRI |
| [33] | Heuristic maximization method | 3D MRI |
| [34] | Anatomy corrected asymmetry index (ACAI) | FDG-PET |
| [20] | Edge based technique and multi scale correlation | 3D MRI, CT |
| [35] | Intensity based cross correlation approach | 3D MRI |
| [16] | Intensity based reflection approach | MRI, CT, PET, SPECT |
| [36] | Edge based and Hough Transformation method | CT |
| [37] | 3D rigid registration method, greedy search algorithm | MRI |
| [38] | Kullback–Leibler measure, surface deformation | MRI |
| [39] | GPU-K Dimensional tree algorithm, 3D edge registration | MRI |
| [41] | Random regression forest method | T1 weighted MRI |
| [42] | Curve fitting method | T1, T2 and PD Weighted MRI |
| Methods | Techniques Used | Image Modality |
|---|---|---|
| [44] | Surface projection | PET |
| [45] | Linear Snake Modal, Orthogonal regression | MRI, CT |
| [46] | Intensity gradient based method | MRI |
| [47] | Shape bottleneck algorithm | MRI |
| [48] | Non rigid registration and template matching | MRI |
| [49] | Central sulcus measuring | 3D MRI |
| [50] | Fractal dimension | MRI |
| [18] | Extended shape bottleneck algorithm and partial volume estimate | 3D MRI |
| [51] | Content based cellular neural networks method and image registration | 3D, 2D MRI |
| [52] | Adaptive disconnection method | 3D MRI |
| [53] | Non localized label fusion and template | MRI |
| [54] | NABS method and patch based multi template segmentation | T1 Weighted MRI |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalavathi, P.; Senthamilselvi, M.; Prasath, V.B.S. Review of Computational Methods on Brain Symmetric and Asymmetric Analysis from Neuroimaging Techniques. Technologies 2017, 5, 16. https://doi.org/10.3390/technologies5020016
Kalavathi P, Senthamilselvi M, Prasath VBS. Review of Computational Methods on Brain Symmetric and Asymmetric Analysis from Neuroimaging Techniques. Technologies. 2017; 5(2):16. https://doi.org/10.3390/technologies5020016
Chicago/Turabian StyleKalavathi, P., M. Senthamilselvi, and V. B. Surya Prasath. 2017. "Review of Computational Methods on Brain Symmetric and Asymmetric Analysis from Neuroimaging Techniques" Technologies 5, no. 2: 16. https://doi.org/10.3390/technologies5020016
APA StyleKalavathi, P., Senthamilselvi, M., & Prasath, V. B. S. (2017). Review of Computational Methods on Brain Symmetric and Asymmetric Analysis from Neuroimaging Techniques. Technologies, 5(2), 16. https://doi.org/10.3390/technologies5020016





