The Electromechanical Modeling and Parametric Analysis of a Piezoelectric Vibration Energy Harvester for Induction Motors
Abstract
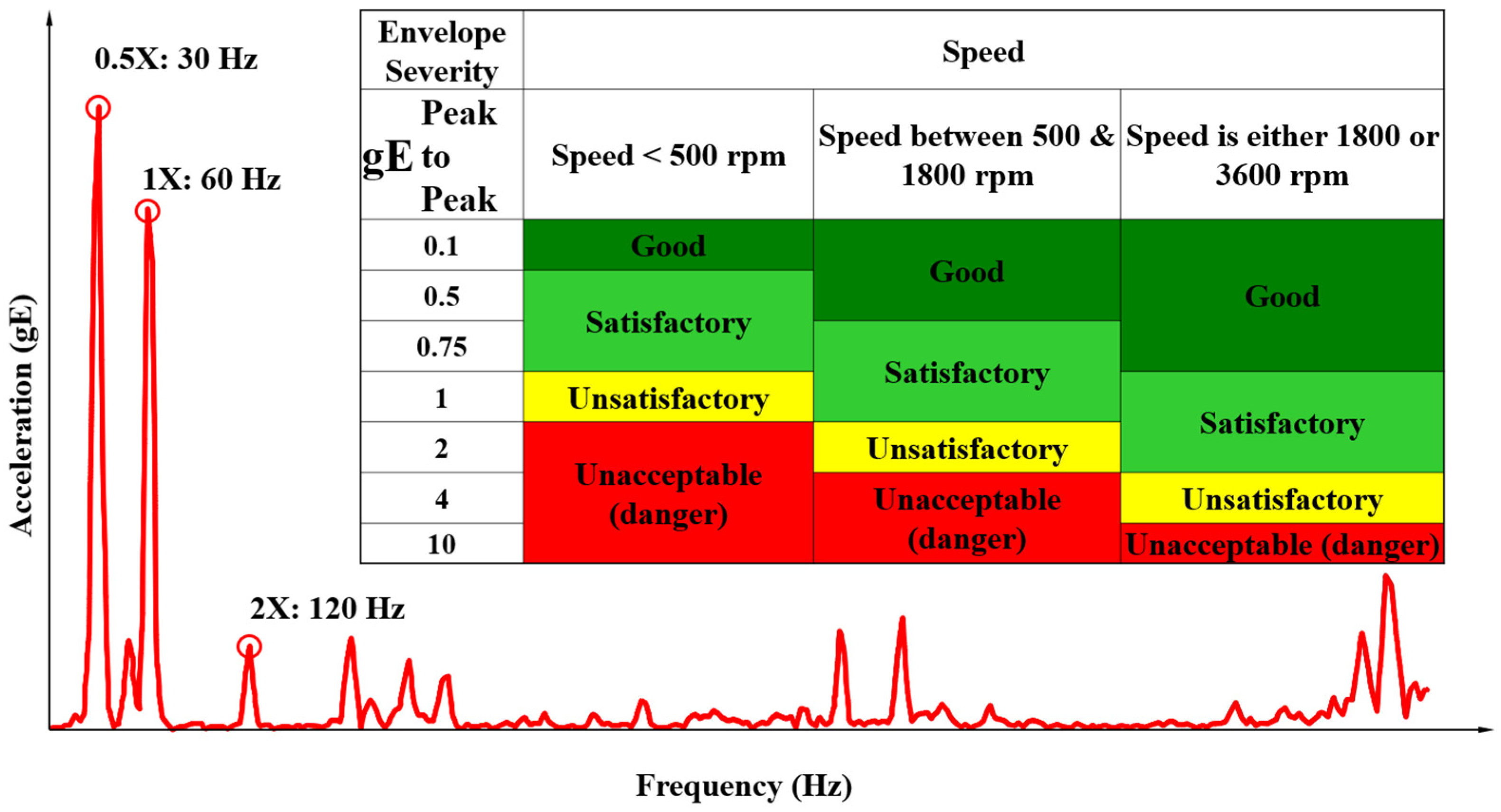
1. Introduction
2. Electromechanical Modeling
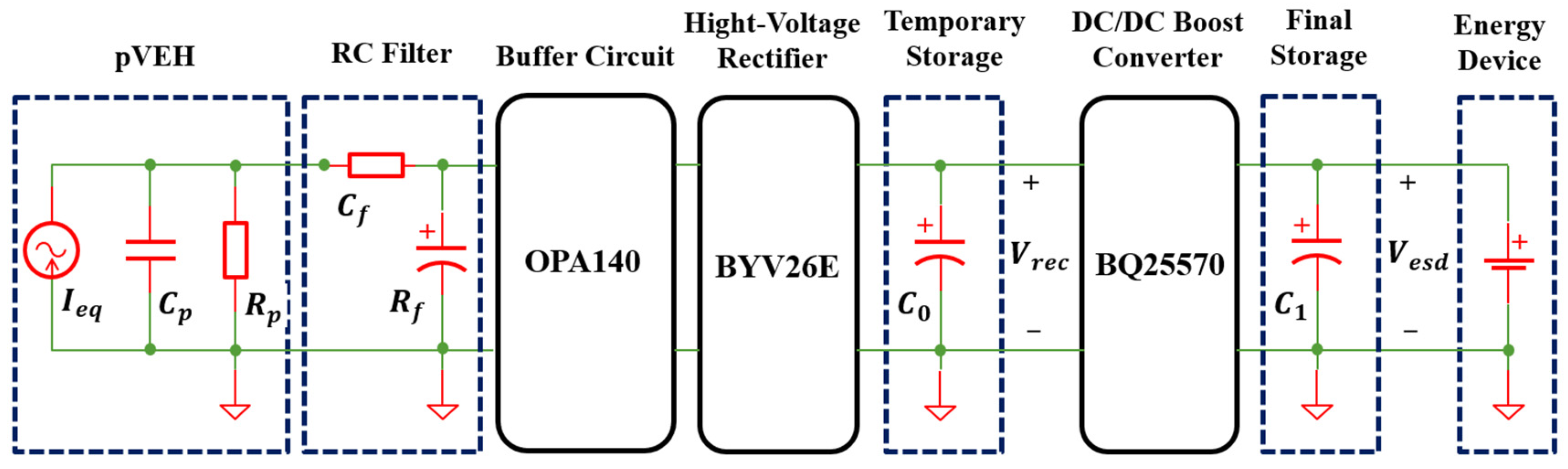
2.1. Operating Principle

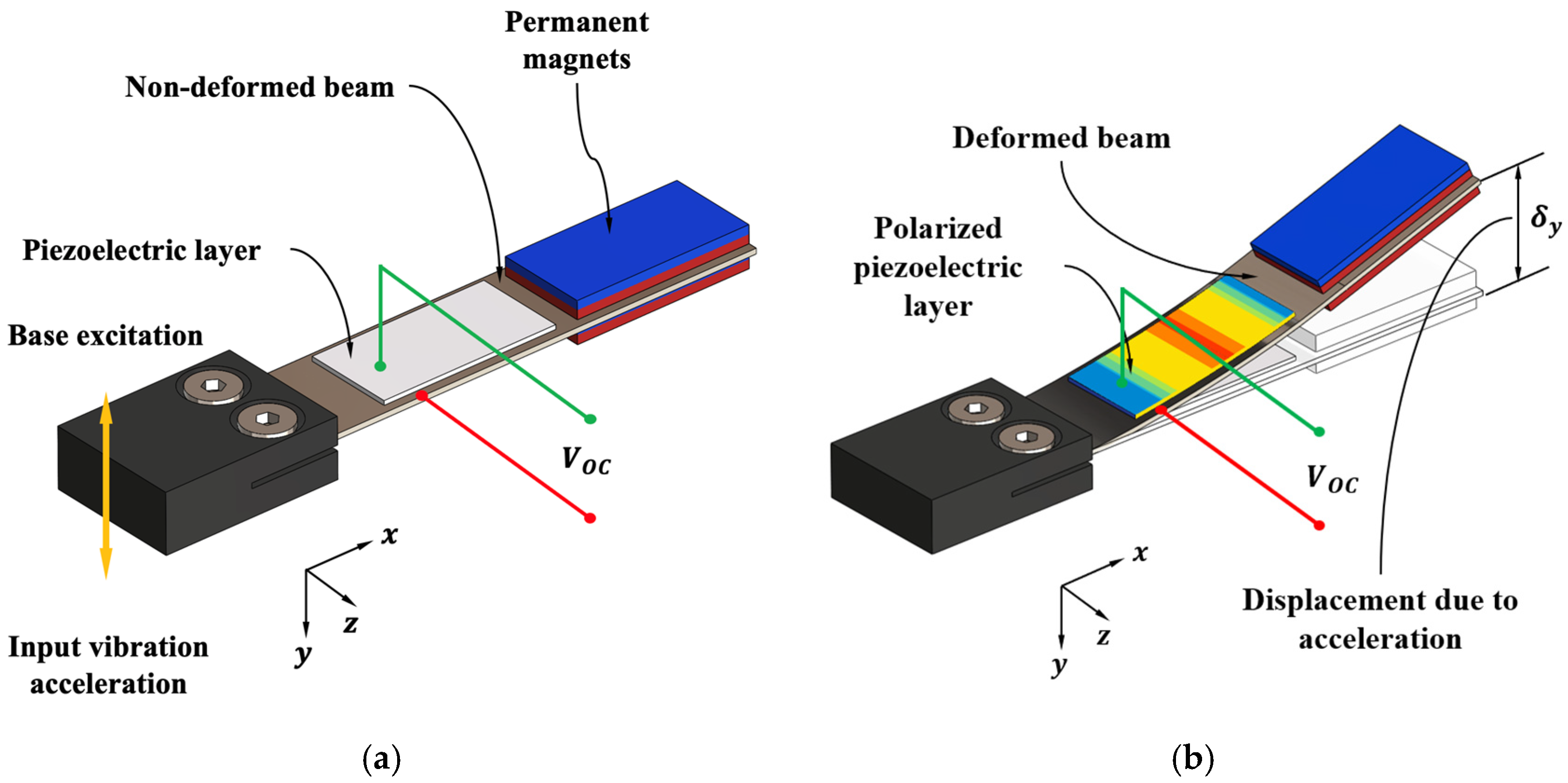
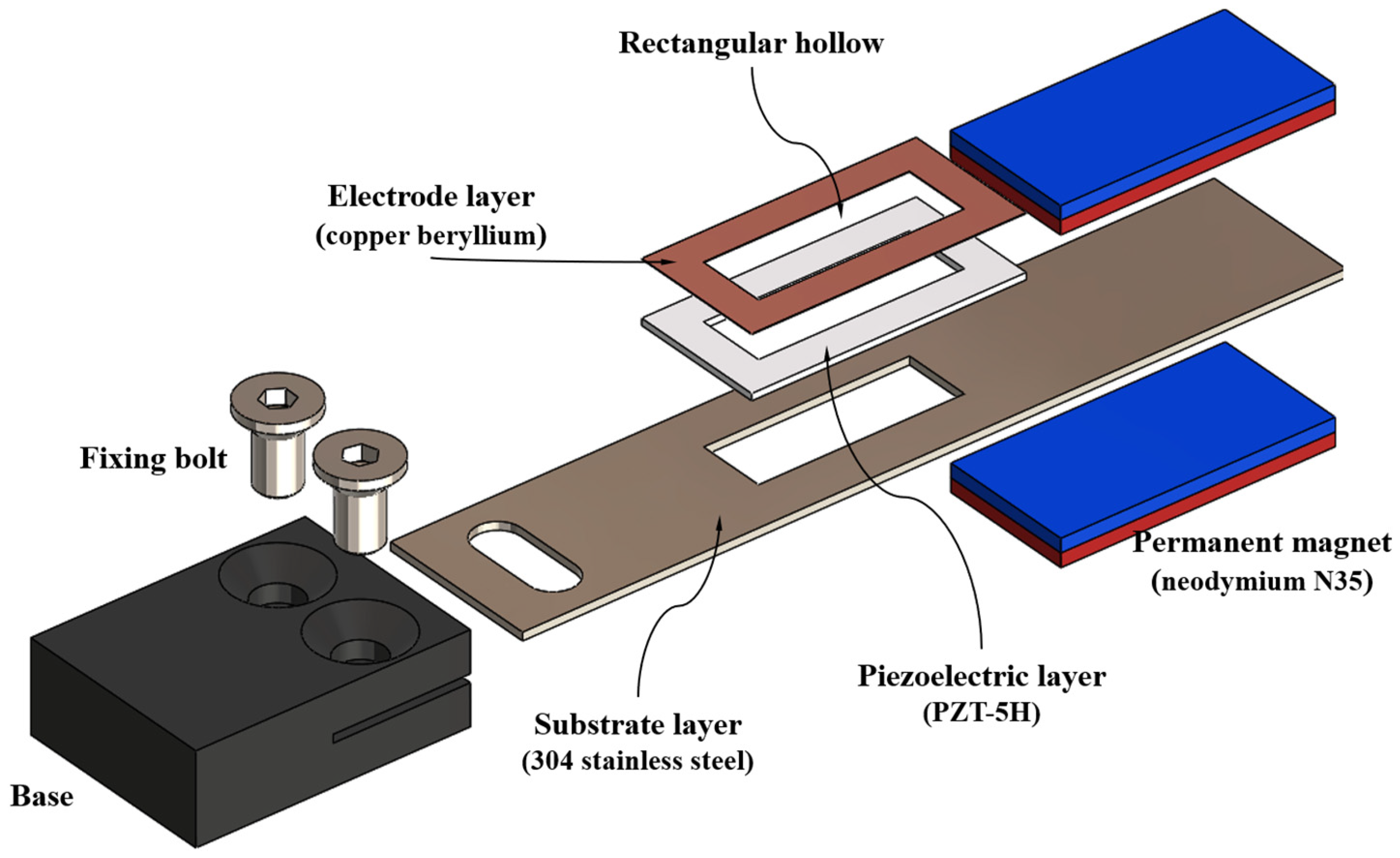
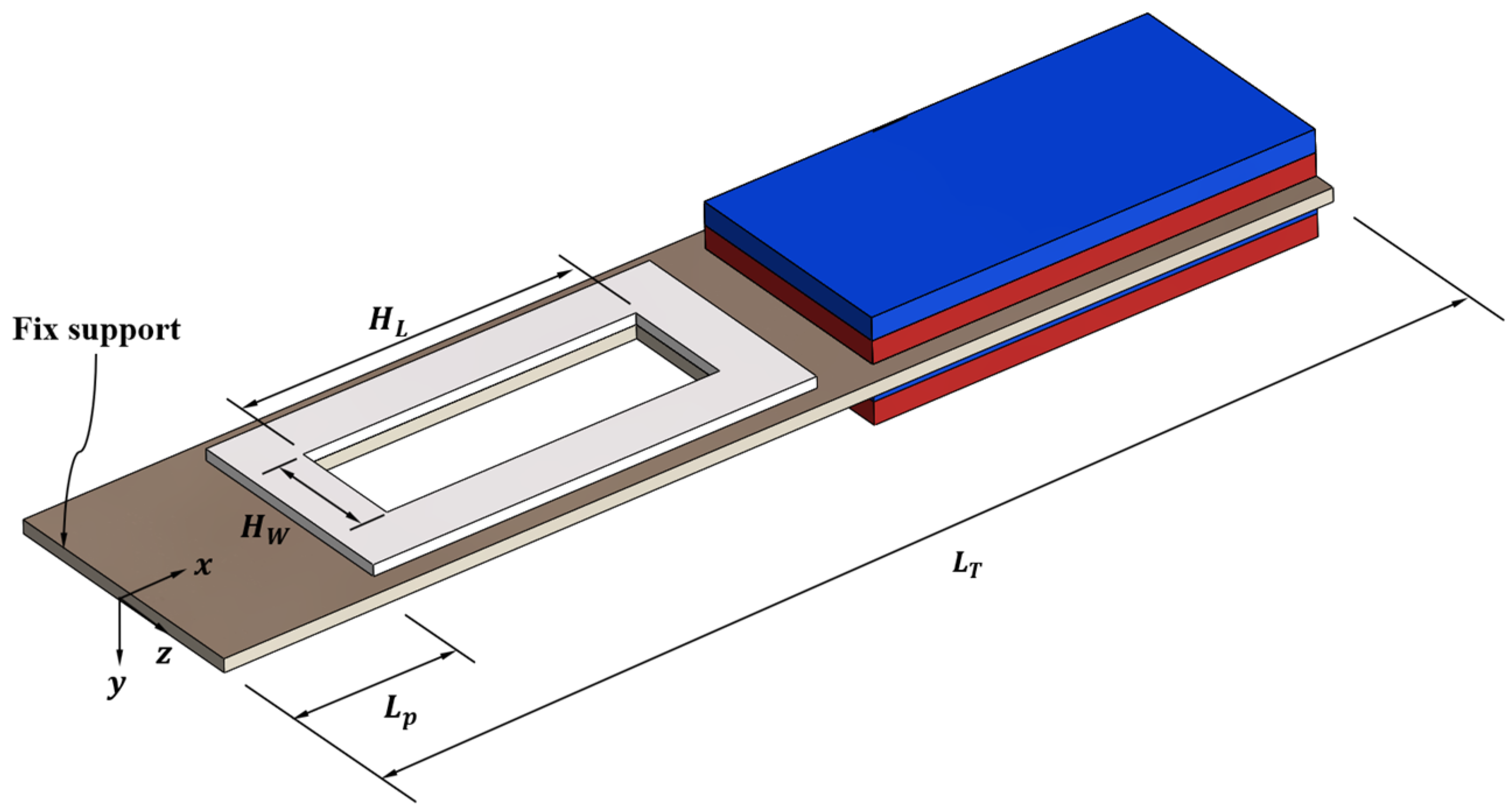
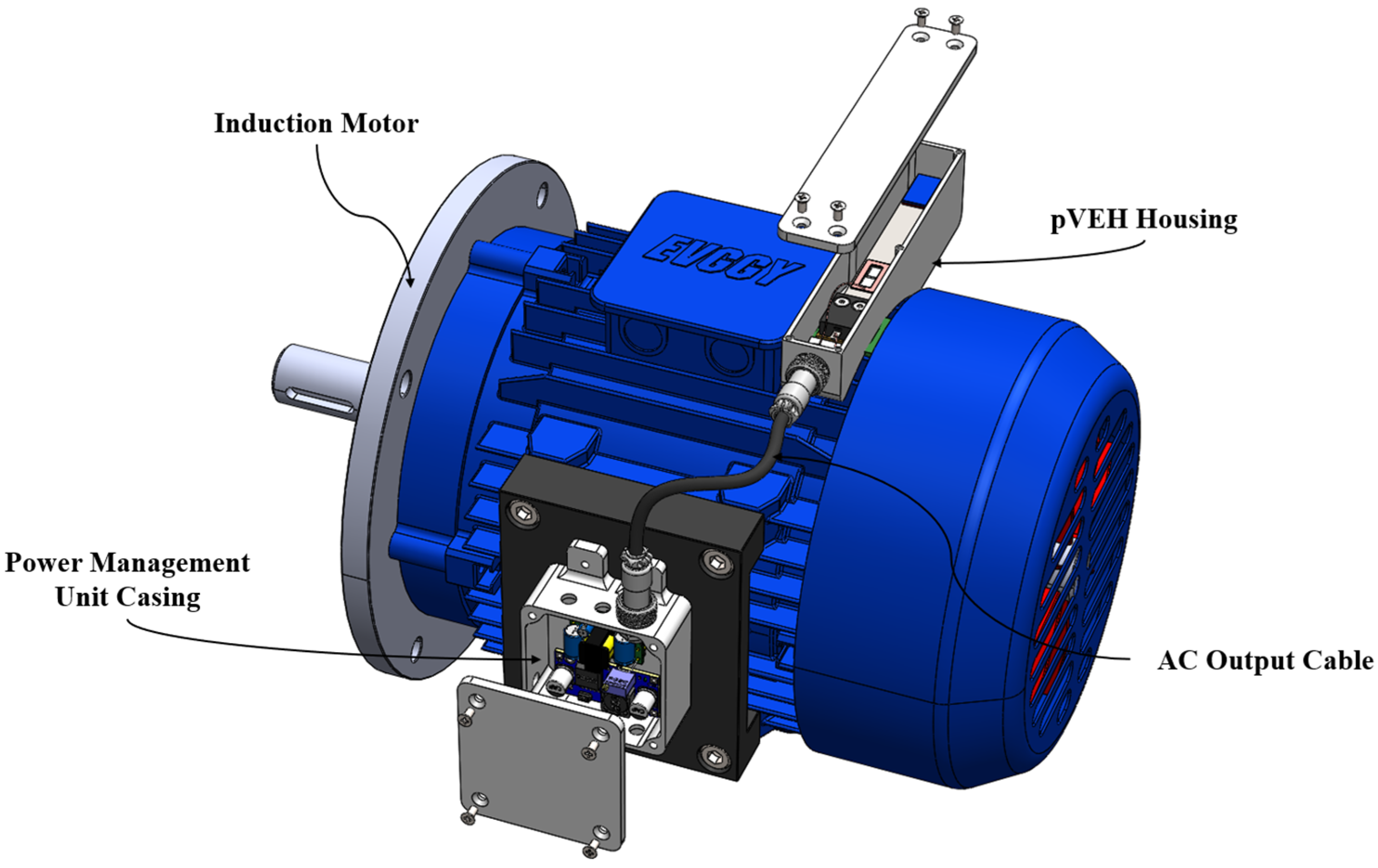
2.2. Design
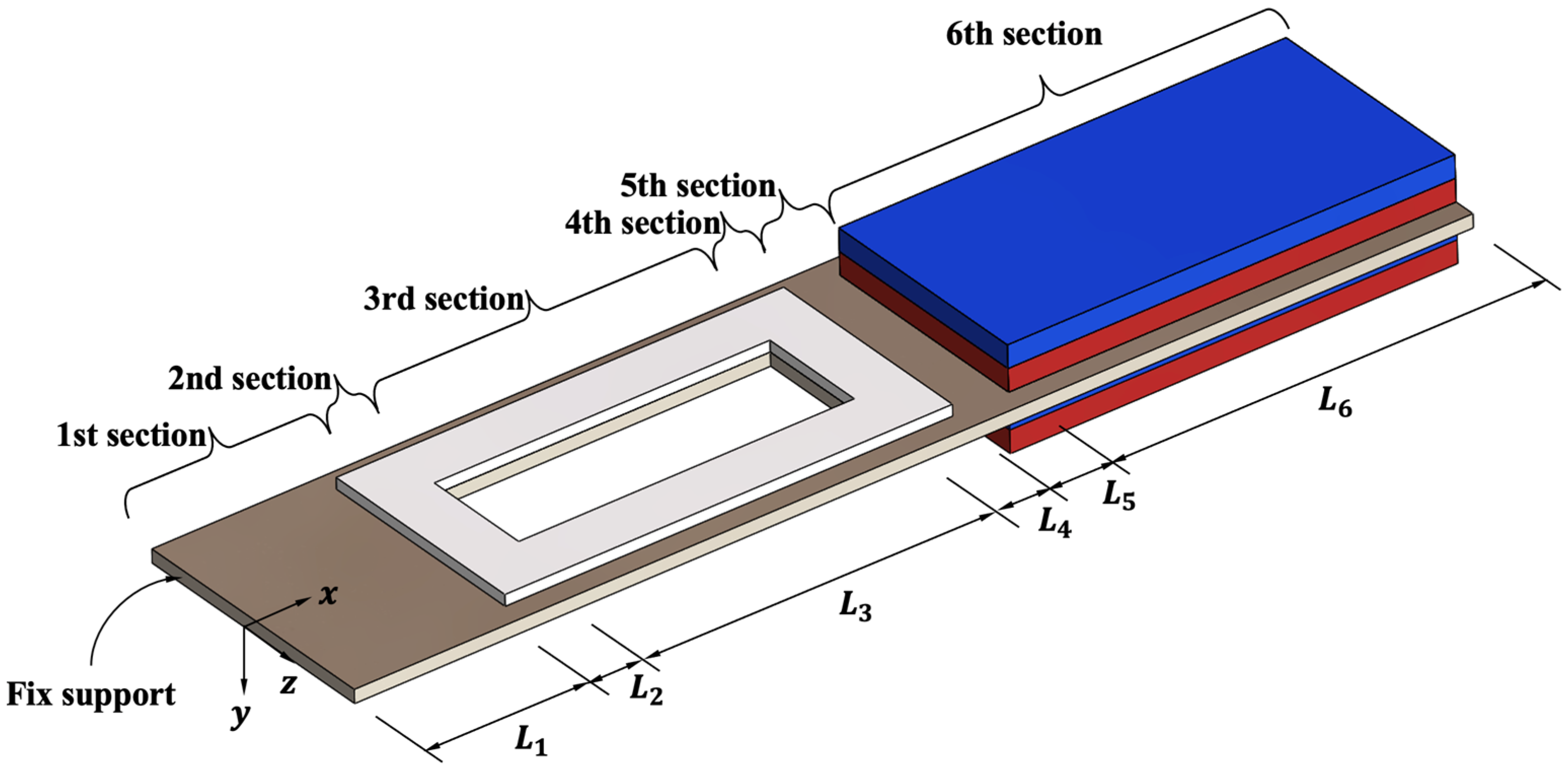
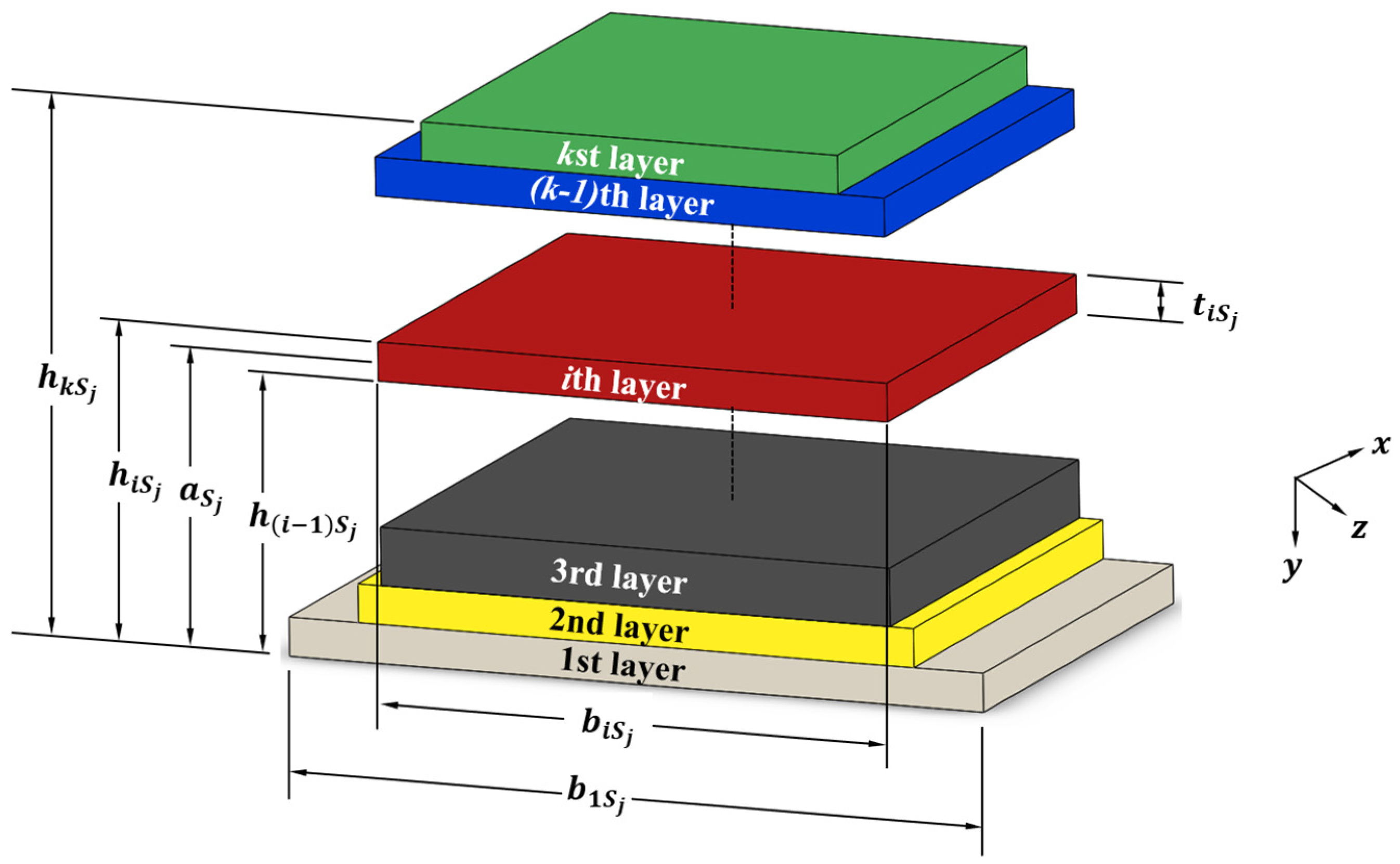
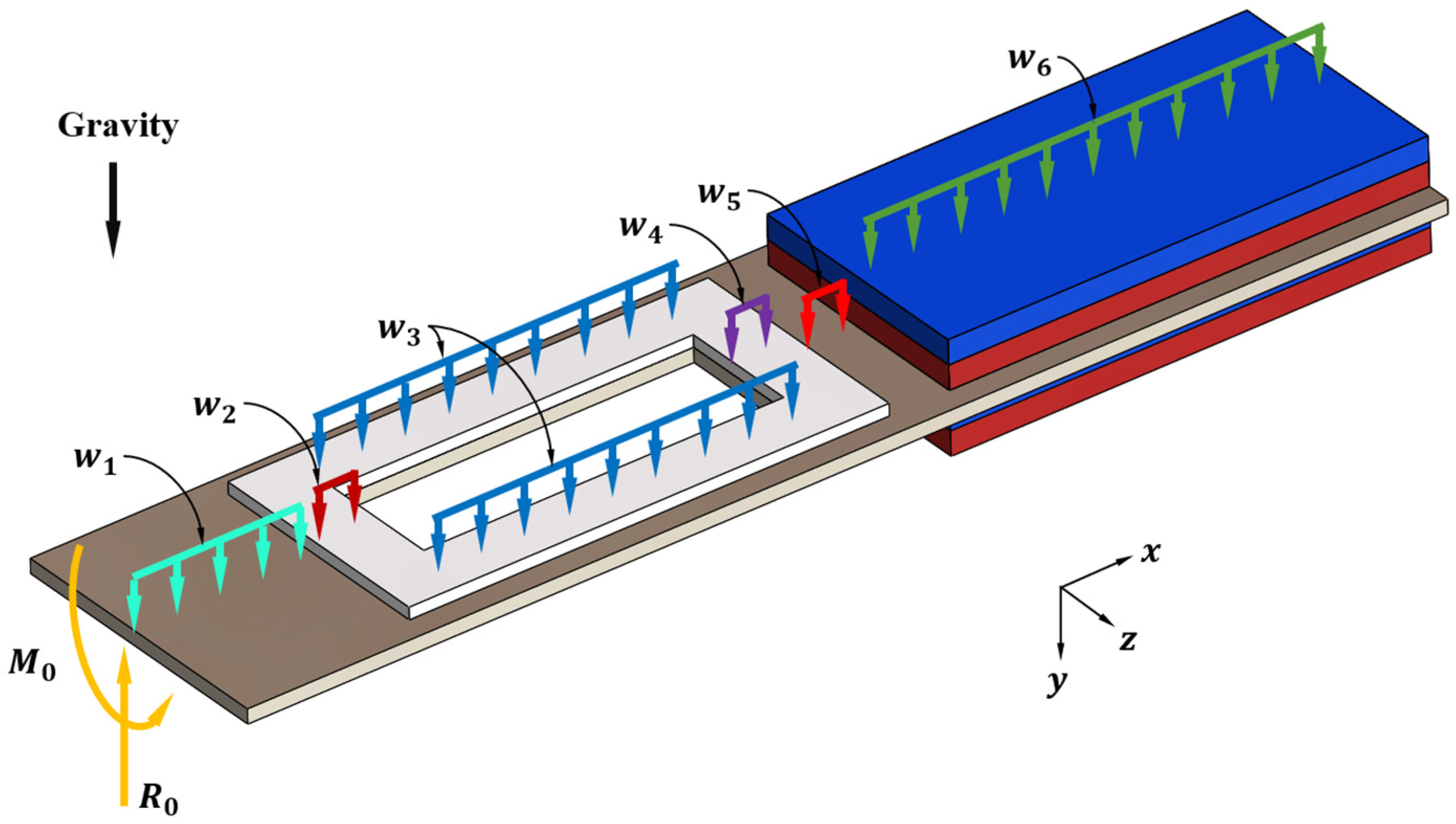
2.3. The Mathematical Modeling of a Multilayered Resonant Cantilever
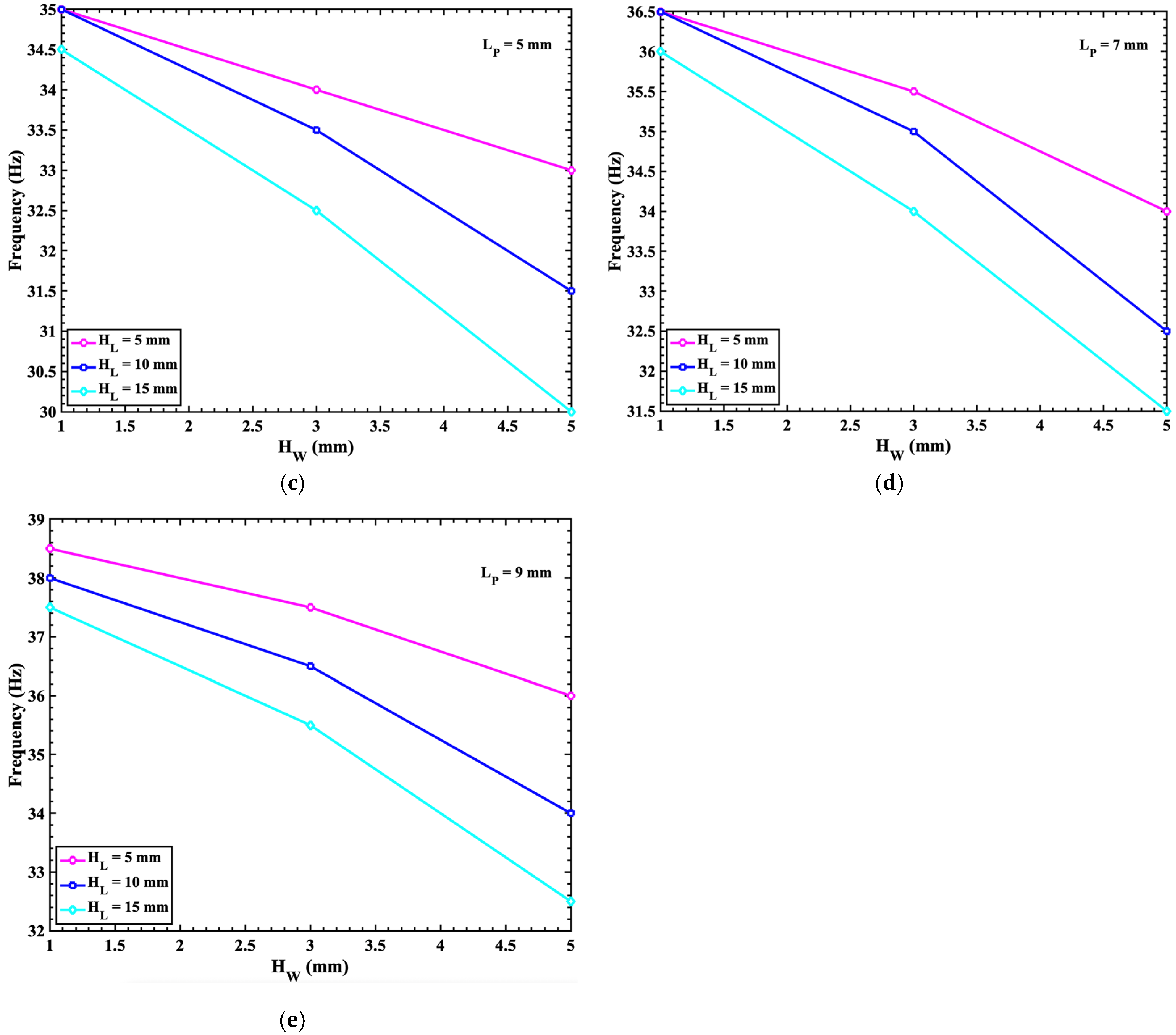
3. Parametric Design
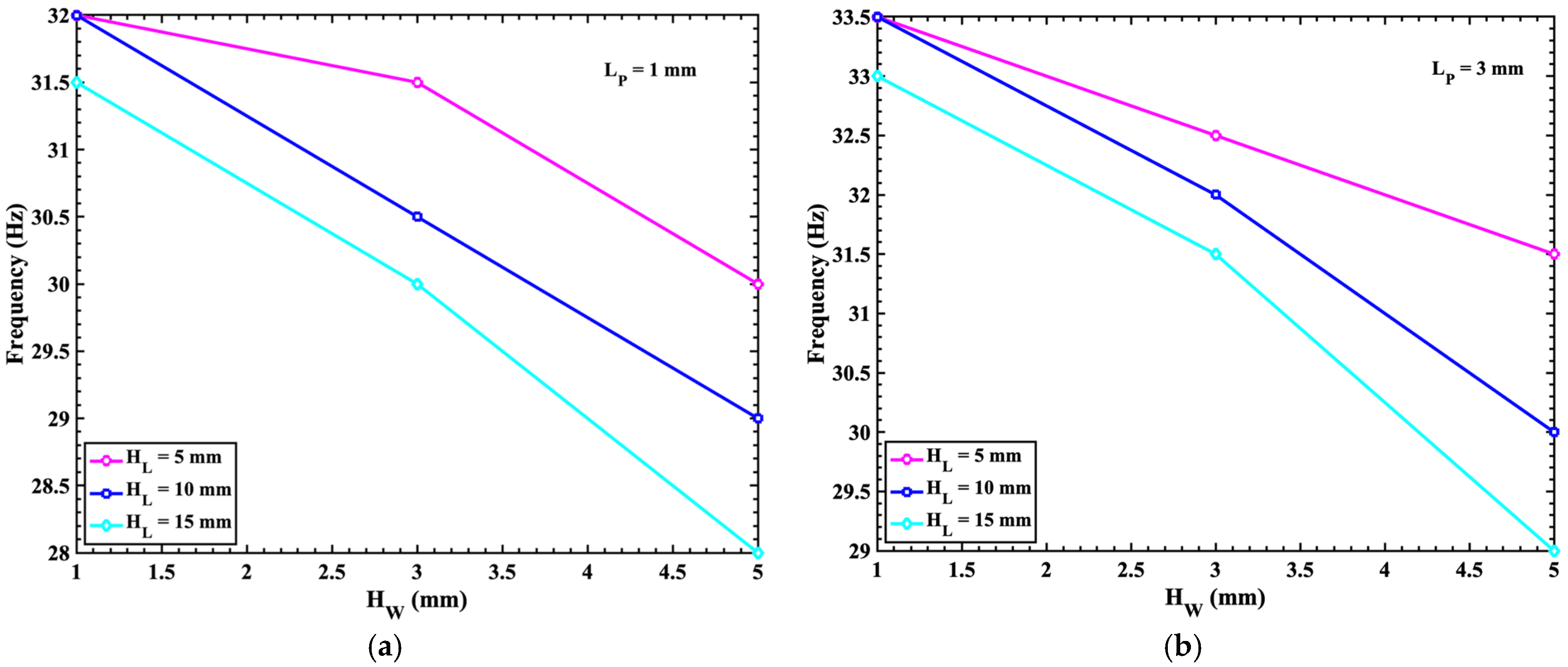
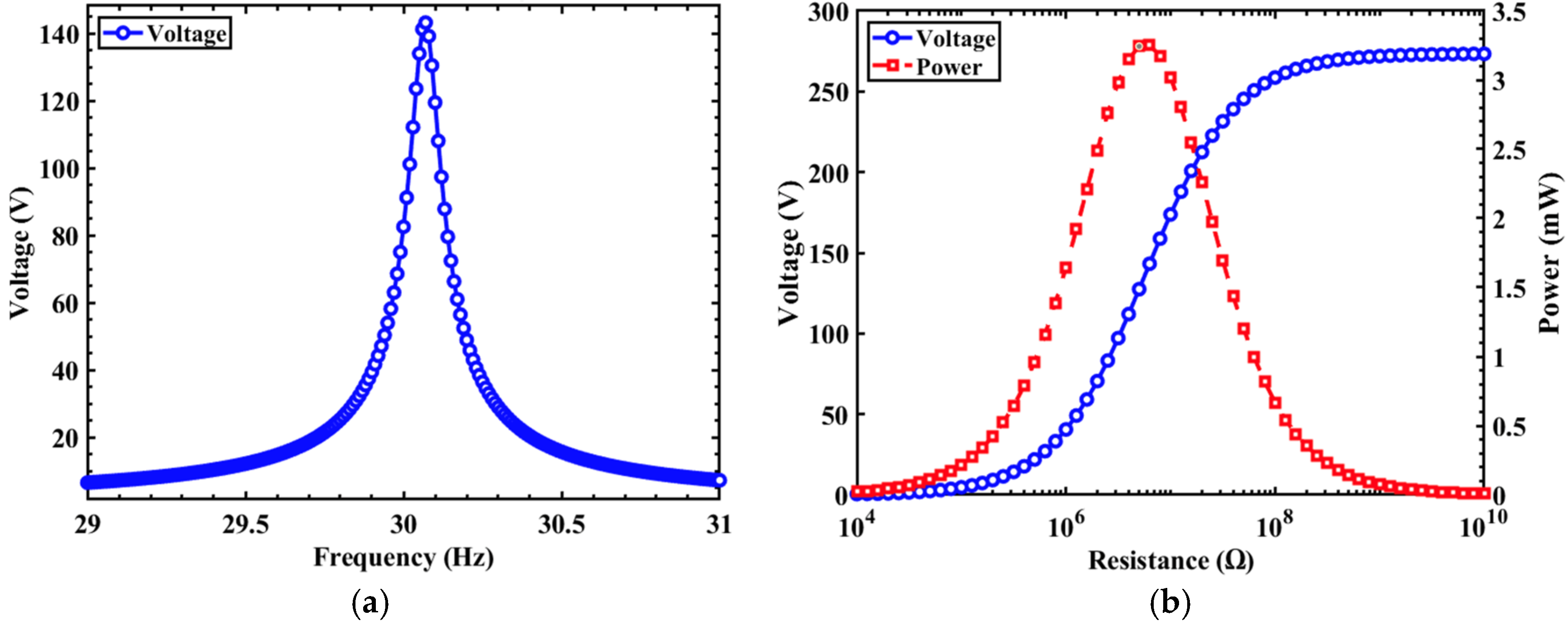
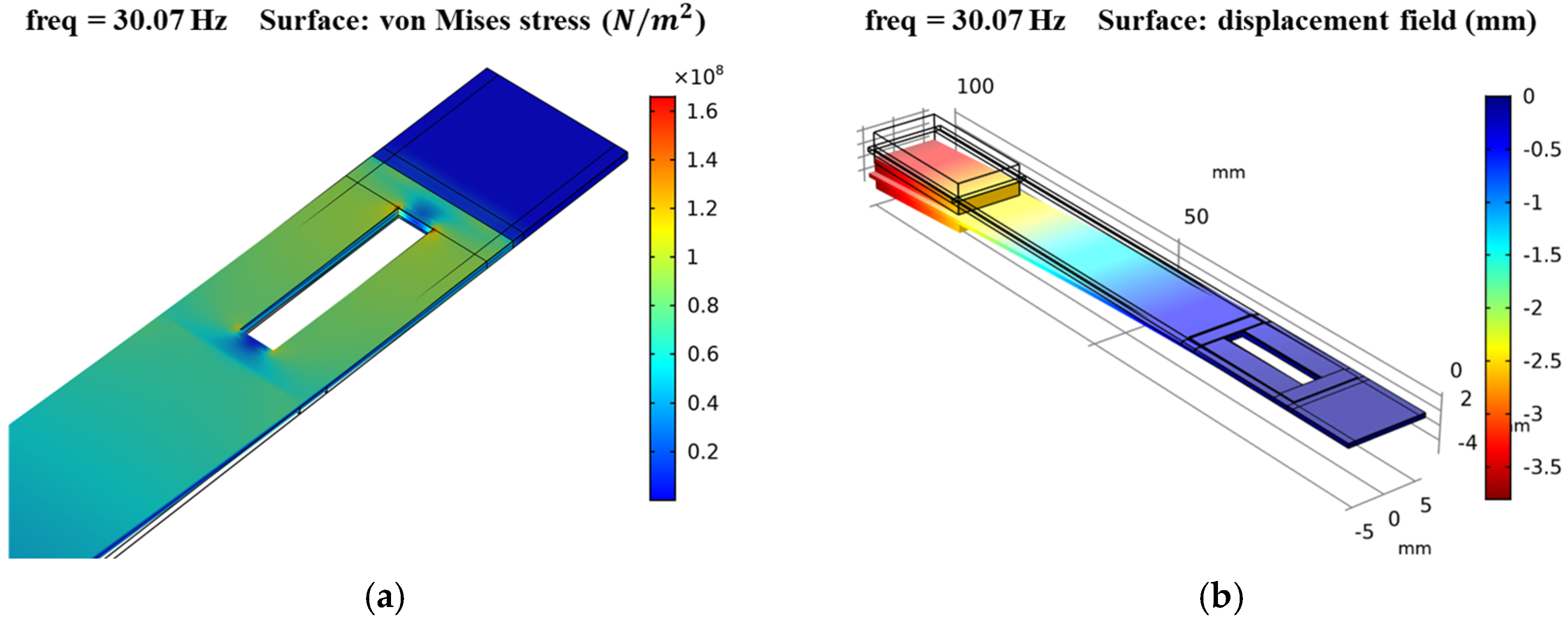
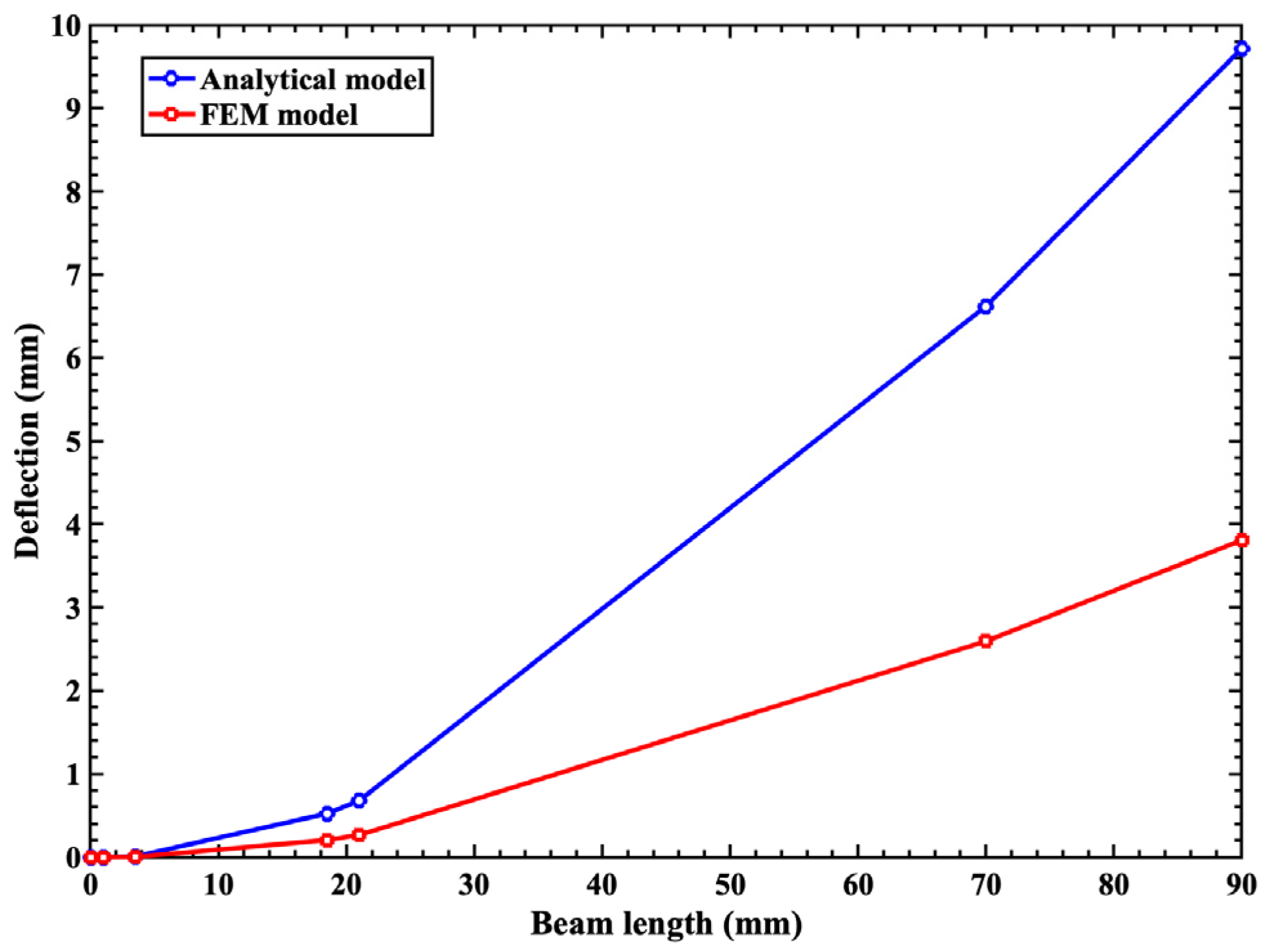
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdelaziz, E.A.; Saidur, R.; Mekhilef, S. A Review on Energy Saving Strategies in Industrial Sector. Renew. Sustain. Energy Rev. 2011, 15, 150–168. [Google Scholar] [CrossRef]
- Dyer, C.H.; Hammond, G.P.; Jones, C.I.; McKenna, R.C. Enabling Technologies for Industrial Energy Demand Management. Energy Policy 2008, 36, 4434–4443. [Google Scholar] [CrossRef]
- Gmyrek, Z. Optimal Electric Motor Designs of Light Electric Vehicles: A Review. Energies 2024, 17, 3462. [Google Scholar] [CrossRef]
- Krishnamoorthy, S.; Panikkar, P.P.K. A Comprehensive Review of Different Electric Motors for Electric Vehicles Application. Int. J. Power Electron. Drive Syst. 2024, 15, 74–90. [Google Scholar] [CrossRef]
- Bairagi, S.; Shahid-ul-Islam; Shahadat, M.; Mulvihill, D.M.; Ali, W. Mechanical Energy Harvesting and Self-Powered Electronic Applications of Textile-Based Piezoelectric Nanogenerators: A Systematic Review. Nano Energy 2023, 111, 108414. [Google Scholar] [CrossRef]
- Goundar, S.S.; Pillai, M.R.; Mamun, K.A.; Islam, F.R.; Deo, R. Real Time Condition Monitoring System for Industrial Motors. In Proceedings of the 2015 2nd Asia-Pacific World Congress on Computer Science and Engineering (APWC on CSE), Nadi, Fiji, 2–4 December 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Bhandari, M.; Silwal, B. Development of Machine Learning Model Applied to Industrial Motors for Predictive Maintenance. In Proceedings of the 2022 International Interdisciplinary Humanitarian Conference for Sustainability (IIHC), Kathmandu, Nepal, 21–23 December 2022; pp. 1632–1635. [Google Scholar] [CrossRef]
- Murtaza, A.A.; Saher, A.; Zafar, M.H.; Moosavi, S.K.R.; Aftab, M.F.; Sanfilippo, F. Paradigm Shift for Predictive Maintenance and Condition Monitoring from Industry 4.0 to Industry 5.0: A Systematic Review, Challenges and Case Study. Results Eng. 2024, 24, 102935. [Google Scholar] [CrossRef]
- Rumbak, S.; Mudronja, V.; Šakić, N.; Cajner, H.; Bogut, M. Analysis of Ignition Risk to Ball Bearings in Rotating Equipment in Explosive Atmospheres. In Proceedings of the PCIC Europe 2010, Oslo, Norway, 8–10 June 2010; pp. 1–8. [Google Scholar]
- Grantham, C. Electrical Machines and Drives for Potentially Explosive Atmospheres. J. Int. Conf. Electr. Mach. Syst. 2012, 1, 128–134. [Google Scholar] [CrossRef]
- Leon, P.; Rosca, S.D. Measurement and Analysis of Vibrations of Electric Motors on Board Container Ships. Sci. Bull. Nav. Acad. 2021, 24, 145–156. [Google Scholar] [CrossRef]
- Njema, G.G.; Ouma, R.B.O.; Kibet, J.K. A Review on the Recent Advances in Battery Development and Energy Storage Technologies. J. Renew. Energy 2024, 2024, 2329261. [Google Scholar] [CrossRef]
- Lee, L.T.; Mohamed, M.A.; Yahya, I.; Kulothungan, J.; Muruganathan, M.; Mizuta, H. Comparison of Piezoelectric Energy Harvesting Performance Using Silicon and Graphene Cantilever Beam. Microsyst. Technol. 2018, 24, 3783–3789. [Google Scholar] [CrossRef]
- Siddique, A.R.M.; Mahmud, S.; Van Heyst, B. A Comprehensive Review on Vibration Based Micro Power Generators Using Electromagnetic and Piezoelectric Transducer Mechanisms. Energy Convers. Manag. 2015, 106, 728–747. [Google Scholar] [CrossRef]
- Polonelli, T.; Bentivogli, A.; Comai, G.; Magno, M. Self-Sustainable IoT Wireless Sensor Node for Predictive Maintenance on Electric Motors. In Proceedings of the 2022 IEEE Sensors Applications Symposium (SAS), Sundsvall, Sweden, 1–3 August 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Oliveira, L.; Chaves, P.; Mozena, A.; Branquinho, O.; Morais, F.; Manera, L. Development of an Electromagnetic Energy Harvesting System Based on a Current Transformer for Use in Industrial Electric Motors. IEEE Lat. Am. Trans. 2023, 21, 976–983. [Google Scholar] [CrossRef]
- Oliveira, L.; Oliveira, F.J.; Manera, L.T. Development of a Hybrid Energy Harvesting System Based on Thermoelectric and Electromagnetic Generators for Use in Industrial Electric Motors. Sustain. Energy Technol. Assess. 2024, 66, 103802. [Google Scholar] [CrossRef]
- Karady, G.G.; Berisha, S.H.; Muralidhar, M.; Demcko, J.A.; Samotyj, M. Variable Speed Motor Drive Generated Magnetic Fields. IEEE Trans. Power Deliv. 1994, 9, 1639–1646. [Google Scholar] [CrossRef]
- Le Coat, G.; Foggia, A.; Bongiraud, J.; Le Thiec, P. Electromagnetic Signature of Induction Machines. IEEE Trans. Energy Conversat. 1999, 14, 628–632. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, P.; Mariscotti, A.; Motta, A.; Pozzobon, P. Electromagnetic Emissions from Electrical Rotating Machinery. IEEE Trans. Energy Conversat. 2001, 16, 68–73. [Google Scholar] [CrossRef]
- Koroglu, S.; Adam, A.A.; Umurkan, N.; Gulez, K. Leakage Magnetic Flux Density in the Vicinity of Induction Motor during Operation. Electr. Eng. 2009, 91, 15–21. [Google Scholar] [CrossRef]
- Lecointe, J.-P.; Morganti, F.; Brundy, J.-F.; Jacq, T.; Streiff, F. Energy Harvesting from the External Magnetic Flux Generated by AC Electrical Rotating Machines. Przegląd Elektrotech. 2012, 88, 94–97. [Google Scholar]
- Wakshume, D.G.; Płaczek, M.Ł. Optimizing Piezoelectric Energy Harvesting from Mechanical Vibration for Electrical Efficiency: A Comprehensive Review. Electronics 2024, 13, 987. [Google Scholar] [CrossRef]
- Sarker, M.R.; Julai, S.; Sabri, M.F.M.; Said, S.M.; Islam, M.M.; Tahir, M. Review of Piezoelectric Energy Harvesting System and Application of Optimization Techniques to Enhance the Performance of the Harvesting System. Sens. Actuators A Phys. 2019, 300, 111634. [Google Scholar] [CrossRef]
- Chen, N.; Jung, H.J.; Jabbar, H.; Sung, T.H.; Wei, T. A Piezoelectric Impact-Induced Vibration Cantilever Energy Harvester from Speed Bump with a Low-Power Power Management Circuit. Sens. Actuators A Phys. 2017, 254, 134–144. [Google Scholar] [CrossRef]
- Li, H.; Tian, C.; Deng, Z.D. Energy Harvesting from Low Frequency Applications Using Piezoelectric Materials. Appl. Phys. Rev. 2014, 1, 041301. [Google Scholar] [CrossRef]
- Yadav, N.; Kumar, R. Harvesting Electric Energy from Waste Vibrations of an Electric Motor Using the Piezoelectric Principle. In Recent Advances in Manufacturing, Automation, Design and Energy Technologies; Natarajan, S.K., Prakash, R., Sankaranarayanasamy, K., Eds.; Springer: Singapore, 2022; pp. 955–964. [Google Scholar]
- Prušáková, L.; Majzlíková, P.; Václavík, J.; Beneš, L.; Vrláková, J.; Jakubec, I.; Kašlík, J. Modeling and Fabrication of Single Cantilever Piezoelectric Microgenerator with Optimized ZnO Active Layer. Thin Solid Films 2015, 591, 305–310. [Google Scholar] [CrossRef]
- Wang, P.; Du, H. ZnO Thin Film Piezoelectric MEMS Vibration Energy Harvesters with Two Piezoelectric Elements for Higher Output Performance. Rev. Sci. Instrum. 2015, 86, 075001. [Google Scholar] [CrossRef]
- Elvira-Hernández, E.A.; Uscanga-González, L.A.; de León, A.; López-Huerta, F.; Herrera-May, A.L. Electromechanical Modeling of a Piezoelectric Vibration Energy Harvesting Microdevice Based on Multilayer Resonator for Air Conditioning Vents at Office Buildings. Micromachines 2019, 10, 211. [Google Scholar] [CrossRef]
- Qin, L.; Ma, Z.; Tang, Y.; He, J.; Wang, W.; Liu, S.; Shi, Y. A Hybrid Triboelectric-Piezoelectric Smart Squirrel Cage with Self-Sensing and Self-Powering Capabilities. Nano Energy 2024, 124, 109506. [Google Scholar] [CrossRef]
- Xiao, Y.; Song, D.; Wu, N. Development of Compact Smart Bearing and Novel Hybrid Feature Assessment for Weak Defect Identification. Nondestruct. Test. Eval. 2024, 1–27. [Google Scholar] [CrossRef]
- Safian, A.; Wu, N.; Liang, X. Development of an Embedded Piezoelectric Transducer for Bearing Fault Detection. Mech. Syst. Signal Process. 2023, 188, 109987. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, F.; Qin, Z.; Han, Q.; Wang, T.; Chu, F. Piezoelectric Energy Harvester for Rolling Bearings with Capability of Self-Powered Condition Monitoring. Energy 2022, 238, 121770. [Google Scholar] [CrossRef]
- Kucuker, A.; Bayrak, M. Detection of Mechanical Imbalances of Induction Motors with Instantaneous Power Signature Analysis. J. Electr. Eng. Technol. 2013, 8, 1116–1121. [Google Scholar] [CrossRef]
- Carbajal-Hernández, J.J.; Sánchez-Fernández, L.P.; Suárez-Guerra, S.; Hernández-Bautista, I. Rotor Unbalance Detection in Electrical Induction Motors Using Orbital Analysis. In Pattern Recognition; Martínez-Trinidad, J.F., Carrasco-Ochoa, J.A., Olvera-Lopez, J.A., Salas-Rodríguez, J., Suen, C.Y., Eds.; Springer: Cham, Switzerland, 2014; pp. 371–379. [Google Scholar]
- Lin, J.-L.; Liu, J.Y.-C.; Li, C.-W.; Tsai, L.-F.; Chung, H.-Y. Motor Shaft Misalignment Detection Using Multiscale Entropy with Wavelet Denoising. Expert Syst. Appl. 2010, 37, 7200–7204. [Google Scholar] [CrossRef]
- Dutta, S.; Basu, B.; Talukdar, F.A. Classification of Induction Motor Fault and Imbalance Based on Vibration Signal Using Single Antenna’s Reactive Near Field. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Lee, Y.-S.; Lee, C.-W. Modelling and Vibration Analysis of Misaligned Rotor-Ball Bearing Systems. J. Sound Vib. 1999, 224, 17–32. [Google Scholar] [CrossRef]
- Jang, I.-S.; Lee, Y.-J.; Kim, J.-H.; Lee, C.-J.; Lee, S.-B. Method for Analyzing Vibrations Due to Electromagnetic Force in Electric Motors. IEEE Trans. Mag. 2014, 50, 297–300. [Google Scholar] [CrossRef]
- Seghiour, A.; Seghier, T.; Zegnini, B. Diagnostic of the Simultaneous of Dynamic Eccentricity and Broken Rotor Bars Using the Magnetic Field Spectrum of the Air-Gap for an Induction Machine. In Proceedings of the 2015 3rd International Conference on Control, Engineering & Information Technology (CEIT), Tlemcen, Algeria, 25–27 May 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Yu-Ling, G.-J.T.; He, F.-L.; Wang, M.-Q.; Ke, M.-Q. Analysis on Steady-State Electromagnetic Characteristics and Online Monitoring Method of Stator Inter-Turn Short Circuit of Turbo-Generator. Electr. Power Compon. Syst. 2017, 45, 198–210. [Google Scholar] [CrossRef]
- Saito, A.; Suzuki, T. Forced Response Vibration Analysis of Induction Motor Stators Induced by Electromagnetic Forces. IFAC-Pap. Online 2022, 55, 155–159. [Google Scholar] [CrossRef]
- Liu, H.; Zhong, J.; Lee, C.; Lee, S.-W.; Lin, L. A Comprehensive Review on Piezoelectric Energy Harvesting Technology: Materials, Mechanisms, and Applications. Appl. Phys. Rev. 2018, 5, 041306. [Google Scholar] [CrossRef]
- Sezer, N.; Koç, M. A Comprehensive Review on the State-of-the-Art of Piezoelectric Energy Harvesting. Nano Energy 2021, 80, 105567. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Yang, Y.; Zhao, W.; Chen, C.; Liu, L.; Wang, Z.L. High-Performance Piezoelectric Nanogenerators Based on Hierarchical ZnO@CF/PVDF Composite Film for Self-Powered Meteorological Sensor. J. Mater. Chem. A 2023, 11, 13708–13719. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO 10816-1: Mechanical Vibration—Evaluation of Machine Vibration by Measurements on Non-Rotating Parts—Part 1: General Guidelines; ISO: Geneva, Switzerland, 1995. [Google Scholar]
- Larsson, S.; Holmström, S.T.; Ilic, B.; Håkanson, M.; Parameswaran, L.; Johansson, S. Simple Method for Quality Factor Estimation in Resonating MEMS Structures. J. Phys. Conf. Ser. 2018, 1052, 012100. [Google Scholar] [CrossRef]
- Chakhchaoui, N.; Ennamiri, H.; Hajjaji, A.; Eddiai, A.; Meddad, M.; Boughaleb, Y. Theoretical Modeling of Piezoelectric Energy Harvesting in the System Using Technical Textile as a Support. Polym. Adv. Technol. 2017, 28, 1170–1178. [Google Scholar] [CrossRef]
- Blom, F.R.; Bouwstra, S.; Elwenspoek, M.; Fluitman, J.H.J. Dependence of the Quality Factor of Micromachined Silicon Beam Resonators on Pressure and Geometry. J. Vac. Sci. Technol. B 1992, 10, 19–26. [Google Scholar] [CrossRef]
- Anton, S.R.; Erturk, A.; Inman, D.J. Bending Strength of Piezoelectric Ceramics and Single Crystals for Multifunctional Load-Bearing Applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 1085–1092. [Google Scholar] [CrossRef]
- MatWeb. MatWeb: Online Materials Information Resource. Available online: https://www.matweb.com/ (accessed on 2 May 2025).
- COMSOL. Material Library User’s Guide. Available online: https://doc.comsol.com/6.0/doc/com.comsol.help.matlib/MaterialLibraryUsersGuide.pdf (accessed on 2 May 2025).
- Weaver, W., Jr.; Timoshenko, S.P.; Young, D.H. Vibration Problems in Engineering, 5th ed.; John Wiley & Sons Inc.: New York, NY, USA, 1990. [Google Scholar]
- Herrera-May, A.L.; Aguilera-Cortés, L.A.; Plascencia-Mora, H.; Rodríguez-Morales, Á.L.; Lu, J. Analytical Modeling for the Bending Resonant Frequency of Multilayered Microresonators with Variable Cross-Section. Sensors 2011, 11, 8203–8226. [Google Scholar] [CrossRef] [PubMed]
- Bao, M. Analysis and Design Principles of MEMS Devices, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]



| Properties | Substrate Layer | Piezoelectric Layer | Electrode Layer | Mass |
|---|---|---|---|---|
| Material | 304 stainless steel | PZT-5H | Copper beryllium | Neodymium N35 |
| Young’s modulus (GPa) | 193 | 63 | 125 | 150 |
| Density (kg/m3) | 8000 | 7500 | 8250 | 7400 |
| Poisson’s ratio | 0.9 | 0.31 | 0.3 | 0.25 |
| Yield strength (MPa) | 215 | 123.2 | 172 | - |
| Tensile strength (MPa) | 505 | 469 | - |
| Geometric Parameters | Dimensions (mm) | Geometric Parameters | Dimensions (mm) |
|---|---|---|---|
| L1 | 1 | b2S2= b2S4= b1S6= b3S6 | 10 |
| L2= L4 | 2.5 | b2S3 | 7 |
| L3 | 15 | h1S1= h1S2= h1S3= h1S4= h1S5 | 0.6 |
| L5 | 49 | h1S6 | 2 |
| L6 | 20 | h2S2= h2S3= h3S4 | 0.8 |
| b1S1= b1S2= b1S4= b1S5= b2S3 | 12 | h2S6 | 2.6 |
| b1S3 | 11 | h3S6 | 4.6 |
| Parameters | Magnitude | Parameters | Magnitude |
|---|---|---|---|
| (EI)S1= (EI)S5 | 0.063 Nm2 | w3 | 35.119 Nm−1 |
| (EI)S2= (EI)S4 | 0.091 Nm2 | w4 | 284.882 Nm−1 |
| (EI)S3 | 0.067 Nm2 | w5 | 11.531 Nm−1 |
| (EI)S6 | 18.273 Nm2 | w6 | 173.441 Nm−1 |
| w1 | 565.056 Nm−1 | R0 | 6.4265 N |
| w2 | 284.882 Nm−1 | M0 | 0.325 Nm |
| Layer Position (mm) | Hole Length (mm) | Hollow Width (mm) | Voltage (V) | Stress (MPa) | Efficiency Factor (V/MPa) |
|---|---|---|---|---|---|
| 1 | 5 | 5 | 48.3 | 153.7 | 0.31 |
| 1 | 15 | 3 | 132.6 | 296.3 | 0.45 |
| 3 | 10 | 5 | 77.4 | 223.7 | 0.35 |
| 5 | 15 | 5 | 87.8 | 230.3 | 0.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vázquez-Toledo, M.; León, A.d.; López-Huerta, F.; García-Ramírez, P.J.; Elvira-Hernández, E.A.; Herrera-May, A.L. The Electromechanical Modeling and Parametric Analysis of a Piezoelectric Vibration Energy Harvester for Induction Motors. Technologies 2025, 13, 194. https://doi.org/10.3390/technologies13050194
Vázquez-Toledo M, León Ad, López-Huerta F, García-Ramírez PJ, Elvira-Hernández EA, Herrera-May AL. The Electromechanical Modeling and Parametric Analysis of a Piezoelectric Vibration Energy Harvester for Induction Motors. Technologies. 2025; 13(5):194. https://doi.org/10.3390/technologies13050194
Chicago/Turabian StyleVázquez-Toledo, Moisés, Arxel de León, Francisco López-Huerta, Pedro J. García-Ramírez, Ernesto A. Elvira-Hernández, and Agustín L. Herrera-May. 2025. "The Electromechanical Modeling and Parametric Analysis of a Piezoelectric Vibration Energy Harvester for Induction Motors" Technologies 13, no. 5: 194. https://doi.org/10.3390/technologies13050194
APA StyleVázquez-Toledo, M., León, A. d., López-Huerta, F., García-Ramírez, P. J., Elvira-Hernández, E. A., & Herrera-May, A. L. (2025). The Electromechanical Modeling and Parametric Analysis of a Piezoelectric Vibration Energy Harvester for Induction Motors. Technologies, 13(5), 194. https://doi.org/10.3390/technologies13050194













