Development of 6D Electromagnetic Actuation for Micro/Nanorobots in High Viscosity Fluids for Drug Delivery

Abstract

This research focuses on the development, design, implementation, and testing (with complete hardware and software integration) of a 6D Electromagnetic Actuation (EMA) system for the precise control and navigation of micro/nanorobots (MNRs) in high-viscosity fluids, addressing critical challenges in targeted drug delivery within complex biological environments, such as blood vessels. The primary objective is to overcome limitations in the actuation efficiency, trajectory stability, and accurate path-tracking of MNRs. The EMA system utilizes three controllable orthogonal pairs of Helmholtz coils to generate uniform magnetic fields, which magnetize and steer MNRs in 3D for orientation. Another three controllable orthogonal pairs of Helmholtz coils generate uniform magnetic fields for the precise 3D orientation and steering of MNRs. Additionally, three orthogonal pairs of Maxwell coils generate uniform magnetic field gradients, enabling efficient propulsion in dynamic 3D fluidic environments in real time. This hardware configuration is complemented by three high-resolution digital microscopes that provide real-time visual feedback, enable the dynamic tracking of MNRs, and facilitate an effective closed-loop control mechanism. The implemented closed-loop control technique aimed to enhance trajectory accuracy, minimize deviations, and ensure the stable movement of MNRs along predefined paths. The system’s functionality, operation, and performance were tested and verified through various experiments, focusing on hardware, software integration, and the control algorithm. The experimental results show the developed system’s ability to activate MNRs of different sizes (1 mm and 0.5 mm) along selected desired trajectories. Additionally, the EMA system can stably position the MNR at any point within the 3D fluidic environment, effectively counteracting gravitational forces while adhering to established safety standards for electromagnetic exposure to ensure biocompatibility and regulatory compliance.

1. Introduction

Micro/nanorobots (MNRs) are widely recognized in various research fields due to their miniature size and versatile structures, offering advantages of flexibility, controllability, adaptability, and effective navigational capabilities [1]. These miniature agents are becoming increasingly crucial for precision medical applications, enabling advanced treatments, drug delivery, diagnostics, disease detection, and streamlined surgical procedures [2,3]. Consequently, research focusing on technologies that empower MNRs to navigate within blood vessels has become a significant focus [4,5,6].

However, the effective actuation and accurate path tracking of MNRs in three-dimensional (3D) and six-dimensional (6D) space remain key challenges, particularly in the context of targeted drug delivery within blood vessels [7,8,9]. Reliable power sources are crucial for maintaining sustained operation and executing tasks efficiently.

MNRs require a power source to operate within their designated environment and complete assigned tasks. A promising approach is internal power generation, such as utilizing bloodstream flow, body temperature, microbial fuel cells, electrogenic bacteria, chemical fuel, or bioreactors [10,11,12]. However, a critical question remains: how much power is required for MNRs to perform actuation and computation tasks effectively? Furthermore, ensuring that internal power generation can sustain prolonged operation and travel within the human body remains an unresolved challenge [13].

MNRs can be powered by either exogenous sources (e.g., light energy, magnetic fields, electric fields, or acoustic fields) or endogenous sources (e.g., chemical interaction energy) [7,13,14,15,16]. Various driving techniques have been explored, including piezoelectric sources [17], thermal actuation [18], electro-osmotic forces [19], biological bacteria-based driving [20], and chemically powered micro-motors [21]. Despite their potential, many of these methods face significant limitations, such as cytotoxicity, limited adaptability to biological environments, and inefficient energy transfer [7].

Among external power sources, electromagnetic actuation (EMA) has gained recognition due to its ability to penetrate deep biological tissues safely while minimizing interactions with living cells [22,23]. The EMA surpasses other actuation techniques in terms of controllability, speed, adaptability, and safety profile [24,25]. However, achieving precise control, real-time tracking, and stable actuation in high-viscosity, dynamic fluidic environments remains an ongoing challenge [14,26,27]. While studies support the safety of EMA under certain conditions, further assessments are needed to understand the long-term effects of exposure. The Electromagnetic Power and Safety Considerations section discusses these aspects in detail.

Several electromagnetic actuation (EMA) systems have been developed to control MNRs in biomedical applications. Notably, OctoMag and MiniMag represent state-of-the-art EMA platforms yet present key limitations [28]. OctoMag provides five degrees of freedom (DoF) control, restricting full 6D maneuverability and limiting precise trajectory stabilization in complex, high-viscosity environments. MiniMag, while enabling motion control in 3D, lacks real-time closed-loop feedback and adaptive control, making it less effective for applications that require high-precision targeting, such as drug delivery [29].

The proposed 6D EMA system overcomes these limitations by integrating three Helmholtz and three Maxwell coil pairs, enabling independent control over six degrees of freedom (three translational and three rotational). The inclusion of real-time tracking and adaptive closed-loop control enhances trajectory accuracy and stability, allowing precise actuation in high-viscosity biological environments. This advancement ensures reliable MNR manipulation across different sizes and configurations, making it more adaptable for biomedical applications, mainly targeted drug delivery.

Recent advancements in electromagnetic actuation (EMA) have significantly improved MNR control precision, adaptability, and real-time feedback capabilities. Hybrid coil configurations and AI-based magnetic field adjustments have been introduced to optimize control for biomedical applications [8,30]. However, achieving robust actuation in high-viscosity environments and developing real-time closed-loop tracking solutions remain critical challenges [9,31].

Additionally, advancements in untethered MNR propulsion have introduced new methods for precise trajectory control, leveraging adaptive AI-based magnetic fields [32]. These innovations align with the objectives of this study, which aims to develop a 6D EMA system that integrates real-time tracking, optimized power efficiency, and high-precision actuation in complex fluidic environments.

This study addresses these challenges by proposing a 6D electromagnetic-based actuation (EMA) system to enable the seamless and accurate navigation of MNRs in complex biomedical environments. The following section provides an in-depth review of related actuation technologies, highlighting key contributions from previous research.

The remainder of this paper is organized as follows: Section 2 explores Electromagnetic Power and Safety Considerations, addressing critical aspects of energy efficiency, power transfer, and safety protocols for MNR systems. Section 3 reviews the Current State, Challenges, and Advances in Micro/Nanorobot Actuation Systems, identifying key limitations and emerging solutions. Section 4 focuses on State-of-the-Art Electromagnetic Actuator Systems, including analysis and novel contributions, evaluation of existing technologies, and presentation of the proposed 6D EMA system. Section 5 elaborates on the Proposed EMA Structure and Architecture, detailing kinematics, motion control, and control algorithms. Section 6 presents the Physical Experimental EMA System and Testing, showcasing practical examples and validating results. Finally, Section 7 concludes the paper and highlights potential directions for future research.

2. Electromagnetic Power and Safety Considerations

Electromagnetic actuation (EMA) has become a leading technique for powering and controlling micro/nanorobots (MNRs) due to its ability to safely penetrate biological tissues while minimizing adverse interactions with living organisms. Research shows that low-frequency magnetic fields interact minimally with biological tissues, even at intensities as high as 8 Tesla (T), with no significant changes observed in participants’ vital signs under controlled exposure conditions [28]. Furthermore, MRI-based technologies have been routinely used in clinical applications without adverse effects, operating at field strengths of 1.5–2 T [29].

Different driving techniques face limitations when used in biomedical contexts [7,31]. However, external magnetic fields are a reliable and feasible power source for MNRs. Magnetic fields can penetrate deep tissue while remaining biologically inert under standard operating conditions [22,23,33,34]. Studies involving human participants exposed to magnetic fields up to 8 T reported no significant physiological alterations [35]. Additionally, MRI systems, which rely on static magnetic fields up to 2 T, have been universally recognized as safe for human use [36]. These findings align with established safety guidelines from WHO and ICNIRP, reinforcing the suitability of magnetic fields for powering nanorobots in complex biomedical environments [37,38,39].

Despite these positive findings, long-term exposure risks associated with electromagnetic fields remain partially understood. Research gaps persist in evaluating the effects of prolonged and repeated exposure, particularly in dynamic environments involving real-time electromagnetic actuation [8,30]. Variables such as exposure frequency, duration, and biological tissue variability require further investigation [31,32].

Compliance with international guidelines from organizations such as the WHO and ICNIRP is essential to ensure patient safety and system reliability [40]. These regulatory frameworks provide standardized thresholds for field intensity, duration, and frequency of exposure, ensuring optimal safety margins in clinical and experimental applications [41]. Future advancements must focus on real-time exposure monitoring systems, shielding technologies, and improved safety assessment protocols to address current limitations [32,41].

In conclusion, electromagnetic actuation (EMA) is a safe and effective power source for MNRs, provided that health and safety guidelines are strictly adhered to and ongoing evaluations continue to refine our understanding of the long-term exposure impacts.

3. Current State, Challenges, and Advances in Micro/Nanorobot Actuation Systems

The previous sections established the significance of electromagnetic actuation (EMA) in addressing power and safety challenges for micro/nanorobots (MNRs). Despite the demonstrated potential of EMA systems, achieving precise actuation, trajectory control, and stability in dynamic, high-viscosity biological environments remain a persistent technical challenge. This section reviews state-of-the-art advancements in EMA technologies, analyzes key technical configurations, and evaluates experimental contributions from existing research. Additionally, it identifies ongoing challenges and discusses the novel 6D EMA system proposed in this study as a step forward in overcoming these limitations.

As shown in

Table 1. Comparison of the various actuation techniques and driving force developments for MNRs.

Actuation Method	Controllability	Speed	Potential Harmfulness	Working Medium	Penetration Depth	Energy Efficiency	Positioning Accuracy (µm-Scale)	Operating Frequency
Biological (Bacterial)	Limited	Fast	Cytotoxicity (immune response, infection risk)	Requires nutrient-rich medium	<1 mm	Low (nutrient-dependent)	~10 µm	Not applicable
Chemical Fuel Driven	Limited	Fast	Potential byproducts, toxicity	Requires chemical reactants (e.g., H2O2)	<1 mm	Low (reactant consumption)	~10–50 µm	Not applicable
Electrostatic	Moderate (surface-restricted)	Fast	Requires specific surface conditions	Conductive/micro-patterned surfaces	<1 mm	Medium	~1 µm	Not applicable
Optical Tweezers	High	Slow	Localized heating risk	Transparent fluidic medium	1–3 mm	High power demand	~0.1–1 µm	Typically > THz
Electromagnetic (EMA) (Including our Study)	Excellent (Closed-loop real-time control)	Fast	Minimal (Biocompatible Fields <100 Hz)	Flexible, adaptable to various fluids	Deep (~several cm, MRI-level fields)	High (non-invasive, continuous operation)	Sub-micrometer (~0.1–1 µm)	<100 Hz

, electromagnetic actuation (EMA) exhibits superior performance compared to other actuation techniques, particularly in terms of control precision, adaptability, and operational safety [24,25,42]. Unlike bacterial or chemically driven propulsion, which exhibits limited controllability and relies on environmental factors, EMA enables real-time closed-loop control via external field manipulation [32]. Optical and electrostatic methods, while offering high precision, often face challenges related to surface constraints, localized heating, or energy inefficiencies [6].

A key advantage of EMA is its deep tissue penetration (~several cm), non-invasive nature, and sub-micrometer positioning accuracy [24,25,42]. This is particularly critical for biomedical applications, where penetration depth and precise movement control dictate the feasibility of real-world implementation [43]. Compared to other techniques, which are often restricted to millimeter-range or surface-level operations, EMA provides the most viable approach for in vivo applications [8,44].

Safety considerations are also essential. Biological and chemical actuation mechanisms may induce cytotoxicity or require reactive chemical inputs [28], whereas optical methods carry risks of localized tissue heating due to high-intensity lasers [29]. In contrast, EMA operates within low-frequency ranges (<100 Hz), significantly reducing risks of thermal buildup, bioelectric interference, and tissue damage [2,24,30]. Electromagnetic fields at clinically accepted intensities are routinely used in MRI applications, thereby reinforcing the suitability of EMA for long-term biomedical use [8,31].

These characteristics establish EMA as one of the most effective, scalable, and biocompatible actuation strategies for micro/nanorobot (MNR) systems, as detailed in Table 1.

Table 2. Comparison of the different electromagnetic actuation systems.

Configuration	Magnetic Field	Application	DoF	Magnetic Field Strength (mT)	Stability	Scalability	Real-Time Tracking (Closed-Loop Control)
3D Helmholtz Coils [28]	Uniform Magnetic Field	2D/3D Free Motion	3T	10–50	High	Low	No
Uniform Saddle Coils [45]	Magnetic Gradient	1D Motion Control	1T	5–30	Medium	Low	No
OctoMag [46]	Magnetic Gradient	3D Motion with Limited DoF	5 (2R + 3T)	20–100	Medium	Medium	Partial (Position-Based, No Feedback)
Minimag [47]	Magnetic Gradient	3D Motion, No Closed-Loop Control	5 (2R + 3T)	30–100	Medium	Medium	No
Helmholtz Pair + 1 Saddle Pair + Motor [48]	Combined Magnetic Field	2D Constrained Motion	3 (2R + 1T)	5–20	Medium	Low	No
Helmholtz Pair + 2 Maxwell Pairs [2,49]	Combined Magnetic Field	2D Motion with Improved Stability	4 (2R + 2T)	10–50	Medium	Medium	No
Our 6D EMA System (This Study)	Hybrid Helmholtz + Maxwell	6-DoF Precision Control for High-Viscosity Navigation and Drug Delivery	6 (3R + 3T)	50–200	High	High	Yes

further expands on different EMA configurations, providing a comparative analysis of system scalability, field strength, and tracking capabilities.

Table 2 presents a comparative evaluation of various electromagnetic actuation (EMA) systems, providing insights into their degrees of freedom (DoF), control mechanisms, and biomedical applicability. The proposed 6D EMA system offers key advantages over previous 5-DoF configurations, such as OctoMag and Minimag, by providing fully independent six-axis control (three rotational and three translational degrees of freedom). In contrast, 5-DoF systems often rely on constrained motion models that limit precise trajectory correction in complex, high-viscosity environments.

One major limitation of prior 5-DoF EMA systems is the exclusive reliance on magnetic gradient-based field generation. While this approach is practical for coarse positioning, it introduces spatial field distortions, reducing precision in fine trajectory stabilization. Our system integrates a hybrid Helmholtz-Maxwell configuration, ensuring a uniform and stable field across multiple spatial orientations, reducing unwanted drift, and enabling high-precision motion control.

Additionally, real-time closed-loop tracking, a feature absent in traditional 5-DoF configurations, enables our system to adjust actuation parameters based on MNR feedback dynamically. This is particularly important for biomedical applications such as targeted drug delivery and microsurgical navigation, where minor deviations can impact procedural success. The modular scalability of our system further enhances adaptability, making it suitable for different MNR sizes and clinical applications. These comparative aspects are outlined in Table 2.

3D Helmholtz coils generate a uniform magnetic field, enabling precise control over motion in both 2D and 3D spaces. These systems offer high stability but exhibit moderate scalability constraints due to their structural design [45]. In contrast, uniform saddle coils utilize a magnetic gradient, making them practical for 1D motion control, although they face limitations in both stability and scalability within dynamic biological environments [46].

Advanced systems, such as OctoMag and MiniMag, employ gradient-based control mechanisms, achieving higher degrees of freedom (five DoF and four DoF, respectively) and enabling fine-tuned motion control in 3D spaces. Both systems demonstrate high field strength and stability, but their scalability remains moderately challenging [47,48].

Hybrid configurations, such as the one Helmholtz pair + one Saddle pair + motor, integrate static and motorized control mechanisms, facilitating 2D motion control with moderate scalability and field strength [35]. On the other hand, setups involving two Helmholtz pairs and two Maxwell pairs incorporate hybrid gradient control, supporting complex 2D motion control with exceptional field strength, stability, and scalability [2,49].

These comparisons highlight the evolution of electromagnetic actuation systems, emphasizing the shift towards multi-coil gradient-based architectures for enhanced precision, stability, and adaptability. Advanced configurations, particularly OctoMag and two Helmholtz + two Maxwell systems, showcase clear advantages in addressing the technical challenges of MNR actuation in dynamic and high-viscosity biological environments.

The following discussion will build upon these insights by examining key contributions from the existing literature. This section discusses the significant experimental achievements, advancements in control algorithms, and the integration of novel system architectures that have influenced the development of electromagnetic actuation technologies for MNRs.

Previous research has established foundational EMA systems for microrobot actuation, notably those by Martel, Nelson, and Choi. However, these systems exhibit key limitations that have driven the development of our proposed 6D EMA system.

Martel et al. pioneered MRI-based microrobot navigation, leveraging strong magnetic gradients for in vivo control [50,51]. However, this approach is constrained by the fixed workspace of the MRI scanner, low temporal resolution, and limited torque control, which reduces actuation precision in dynamic environments. Our 6D EMA system overcomes these constraints with independent coil configurations, providing scalable workspace coverage and real-time adaptive control.

Nelson et al. introduced Helmholtz-Maxwell actuation for microrobot manipulation [52]. While achieving 3D motion, their system is limited to five DoF (2R + 3T), lacking full six-axis maneuverability for precise trajectory correction. The absence of real-time closed-loop tracking also restricts its adaptability to unpredictable biomedical conditions. Our system integrates fully independent 6-DoF actuation with real-time closed-loop feedback, enhancing motion accuracy and stability.

Choi et al. developed a Maxwell-Helmholtz hybrid actuation platform for microrobot locomotion [2,53]. However, it relies on rotational field control, limiting the precise translational movement required for drug delivery applications. Furthermore, the lack of modular scalability constrains its applicability to diverse microrobot sizes. Our 6D EMA system addresses these issues by employing hybrid field control mechanisms, allowing precise positioning and scalability across various MNR configurations.

These evaluations highlight the significant limitations of prior EMA systems, including workspace constraints, DoF limitations, lack of real-time feedback, and reduced adaptability to high-viscosity environments. By integrating six DoF motion control, real-time closed-loop tracking, and scalable Helmholtz-Maxwell configurations, our system provides a robust solution to the current challenges in microrobot navigation for biomedical applications. In a related study, Choi et al. developed an EMA system utilizing two Helmholtz and Maxwell coils to control a cylindrical microrobot [2,53]. Further refining this approach, Choi et al. presented a 2D locomotion platform featuring a Maxwell coil along the z-axis and two Helmholtz coils, which enables motion through a radial magnetic gradient [54].

Building on these advancements, Yu et al. engineered an EMA system comprising three Helmholtz coil pairs, one stationary Maxwell coil pair, and one rotating Maxwell coil pair, designed for a 3 mm spherical robot [46]. This configuration demonstrated enhanced spatial precision and multi-axis control.

Palagi et al. implemented a two-degrees-of-freedom (DoF) magnetic actuation system tailored for gel-based microrobots [1]. Subsequently, Lucarini et al. refined this setup to achieve closed-loop control, minimizing the positioning error to 260 µm [49].

Expanding into 3D locomotion, Song et al. introduced a 3D EMA system designed for cylindrical microrobots [55]. Zhang et al. extended this work to integrate a closed-loop feedback mechanism, improving trajectory accuracy [56].

Xu et al. and Temel et al. focused on 3D spiral microrobot actuation, employing three Helmholtz coils to achieve multidimensional control with improved efficiency [57,58].

Meanwhile, Ramos et al. designed a 3D EMA system utilizing three Helmholtz and three Maxwell coils, providing spherical microrobots with highly flexible 3D motion capabilities [59].

These studies highlight the evolution of electromagnetic actuation technologies, showcasing a progressive trend towards multi-axis control, spatial precision, and adaptability in biological environments. Integrating Helmholtz and Maxwell coil systems has proven effective in achieving consistent and precise control across diverse operational scenarios.

The comparative analysis presented in

Table 3. Examples of the evolution of electromagnetic actuation (EMA) systems.

	[51]	[52]	[53]	[54]	[1,49]	[55,56]	[57,58]	[59]
EMA	MRI	Rotating 1 H and 1 M	2 H and 2 M	2 H and 1M	2 H and 2 M	3 H and 3 M	3 H	3 H and 3 M
Dimensionality	1D	2D	2D	2D	2D	3D	3D	3D
MNR structure	-	Spherical	Cylindrical	Cylindrical	Spherical	Cylindrical	Spherical	Spherical
MNR Diameter (mm)	-	0.5	2	2	0.6	2	1.5	5
MNR length (mm)	-	-	2	2	-	3	14	-

illustrates the evolution of electromagnetic actuation (EMA) systems from early 1D MRI-based designs to advanced 3D multi-axis architectures. The table reveals key differences in dimensionality, microrobot structure, and size, highlighting trends in design choices and control mechanisms. Advanced configurations, particularly those incorporating Helmholtz and Maxwell coil pairs, demonstrate enhanced spatial precision, stability, and adaptability in dynamic environments. However, scalability, energy efficiency, and consistent performance under fluidic conditions remain persistent challenges across most systems. These insights underscore the need for further innovation in EMA technologies, setting the stage for a subsequent discussion on a novel 6D EMA system designed to effectively address these limitations.

4. Paper Contributions

This section outlines the key contributions of this paper, emphasizing the innovative aspects of the developed 6D electromagnetic-based actuation (EMA) system and its capabilities.

4.1. Cost-Effective 6D Electromagnetic-Based Actuation System

This study introduces a 6D EMA system that balances the precision of micro/nanorobots, affordability, and maintaining cost efficiency. The system has been designed, implemented, tested, and optimized for cost efficiency without compromising performance. This ensures a scalable and economically viable platform for microrobot control in fluidic environments.

4.2. Integrated Helmholtz and Maxwell Coil Architecture

Unlike traditional Helmholtz-only systems, the developed EMA system integrates three Helmholtz and three Maxwell coils, enabling dynamic and accurate microrobot actuation in six spatial dimensions (6D). The system’s architecture combines simulation precision, robust hardware integration, and adaptive software control, achieving high accuracy and real-time responsiveness.

4.3. Six-Dimensional Navigation with Real-Time Tracking

The developed system enables real-time six-dimensional (6D) navigation, enhancing precise microrobot control across three positional axes (x, y, z) and three rotational axes (yaw, pitch, roll). This functionality facilitates complex maneuvers, adaptive control, and seamless navigation in dynamic fluidic environments.

4.4. Large Navigation Region of Interest (ROI)

The developed EMA-based system enables micro/nanorobot navigation within a large Region of Interest (ROI) spanning 40 × 40 × 40 mm³, ensuring a uniform magnetic field is generated across 1D, 2D, and 3D configurations that provide consistent spatial coverage, allowing microrobots to execute tasks across extended workspaces with high stability.

4.5. Adaptability Across Multiple Microrobot Sizes

The developed system supports microrobot actuation across various sizes (0.5 mm to several mm), validating its scalability and adaptability across different microrobot geometries and dimensions and confirming its consistent performance in diverse experimental conditions.

4.6. Experimental Validation and Precision Analysis

Extensive experimental validation demonstrated high precision with minimal positioning errors across various trajectories and environmental setups, including different robot sizes.

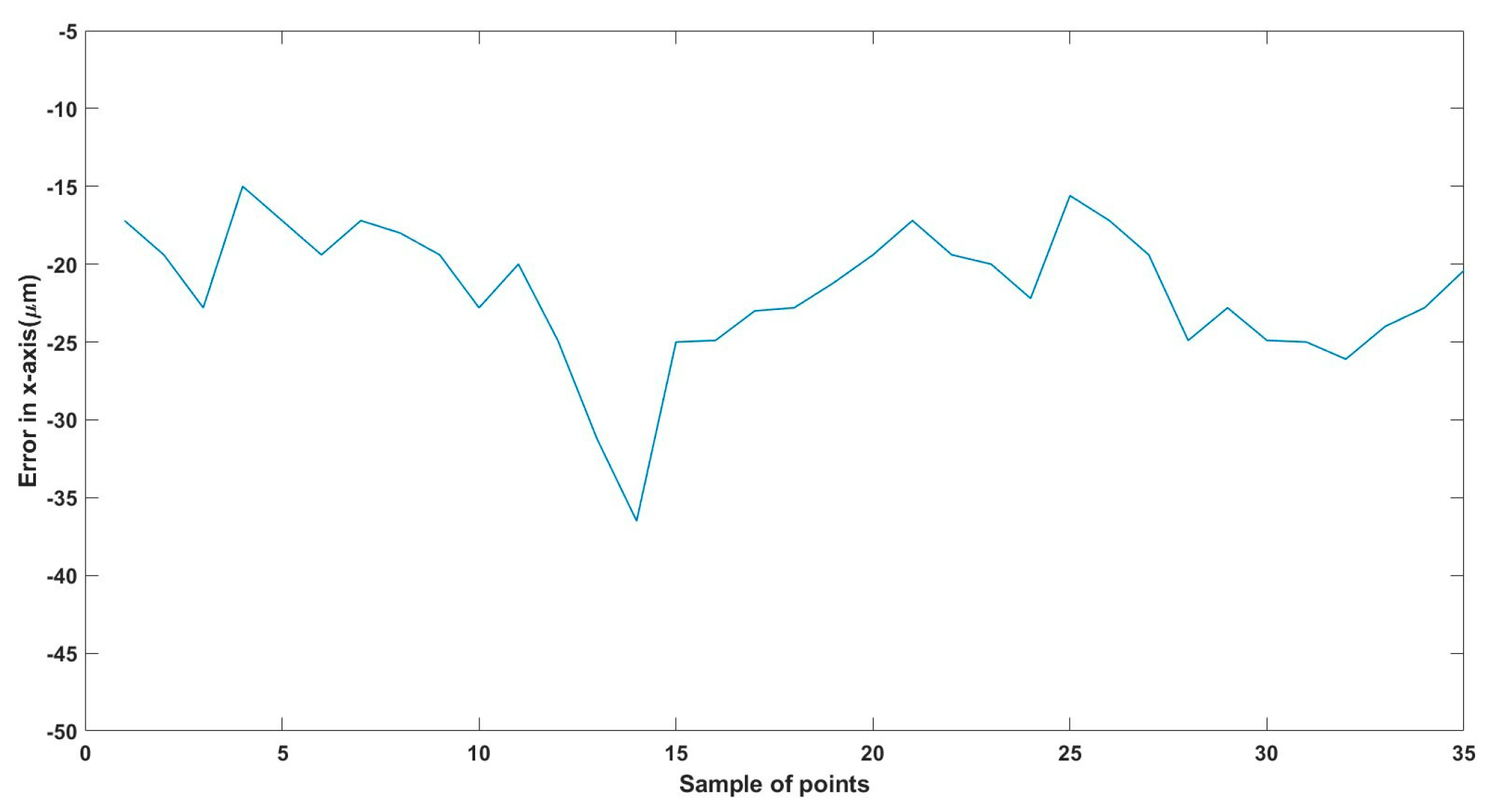
• Smaller Microrobots (0.5 mm length, 0.3 mm diameter): Positioning errors were recorded at 36 µm (x-axis), 32 µm (y-axis), and 33 µm (z-axis).
• Larger Microrobots (1.5 mm length, 1 mm diameter): Positioning errors were measured at 35 µm (x-axis), 24 µm (y-axis), and 28 µm (z-axis).

These results demonstrate the system’s reliability, precision, and adaptability in managing complex microrobot trajectories under varying fluidic conditions.

4.7. Insights into Challenges and System Optimization

This study provides in-depth insights into addressing the challenges of microrobot actuation, including magnetic field uniformity, trajectory stability, scalability, and control precision. The iterative refinement of the EMA system, combined with detailed experimental analysis, contributes to a robust and adaptable platform for future biomedical and industrial microrobot applications.

5. Design of the Driving EMA

5.1. Mathematical Modelling

For any electromagnetically actuated MNR, the robot object is subjected to torque and force in the generated magnetic field. The magnetic torque is directly correlated with the magnetic field intensity and acts to align the MNR’s internal magnetization with the field. In contrast, the magnetic propulsion force is proportional to the gradient of the magnetic field and serves to move the robot toward regions of increasing field strength, as described by the following equations [1,60,61]:

τ = V(M × B)

(1)

F = V(M · ∇)B

(2)

where V represents the volume of the MNR, M represents its magnetization saturation, and B represents magnetic flux density.

A compact device for generating uniform and sustained magnetic fields and gradients consisting of a 3D configuration of Helmholtz and 3D Maxwell coils was designed and built to steer and navigate the MNRs by utilizing controlled magnetic torque and force. The developed EMA is shown in Figure 1, and its configuration provides the following functionalities:

• Three orthogonal pairs of Helmholtz coils generate a uniform magnetic field, which serves to magnetize and steer the MNR;
• Three orthogonal pairs of Maxwell coils generate a uniform field gradient, providing propulsion.

The following equations describe the magnetic field and its gradient due to a controlled current flowing through the coils. These equations allow the calculation of the magnetic field produced by each Helmholtz coil pair and the magnetic field gradient generated by each Maxwell coil pair at the system’s central region, which encompasses the entire arena [60,61]:

$$B_{Hx}={\displaystyle \frac{8}{5\sqrt{5}}}{\displaystyle \frac{{\mu }_{0N_{Hx}{I}_{Hx}}}{r_{Hx}}}=k_x{I}_{Hx}$$

(3)

$$\nabla B_{Mx}={\displaystyle \frac{48}{49}}\sqrt{{\displaystyle \frac{3}{7}}}{\displaystyle \frac{{\mu }_0{N_{Mx}I}_{Mx}}{r_{Mx}^2}}=g_x{I}_{Mx}$$

(4)

where µ_o is the permeability of the space, k_x and g_x are constants determined by the coil’s geometric properties, N_H and N_M are the numbers of turns, and r_H and r_M are the radii of the Helmholtz and Maxwell coils, respectively. Thus, the total magnetic field generated by the three Helmholtz coil pairs and the field gradients by the three pairs of Maxwell coils in the 3D (x-y-z) coordinate space can be expressed as [61]:

$$B_H=\left[\begin{array}{c}{B}_{Hx}\\ B_{Hy}\\ B_{Hz}\end{array}\right]=\left[\begin{array}{c}{k}_x{I}_{Hx}\\ k_y{I}_{Hy}\\ k_z{I}_{Hz}\end{array}\right]$$

$$\nabla B_M=\left[\begin{array}{c}{\nabla B}_{Mx}\\ \nabla B_{My}\\ \nabla B_{Mz}\end{array}\right]=\left[\begin{array}{c}{\displaystyle \frac{{\partial B}_{Mx}}{\partial x}}\\ {\displaystyle \frac{{\partial B}_{My}}{\partial y}}\\ {\displaystyle \frac{{\partial B}_{Mz}}{\partial z}}\end{array}\right]=\left[\begin{array}{c}{g}_x{I}_{Mx}\\ g_y{I}_{My}\\ g_z{I}_{Mz}\end{array}\right]$$

(5)

The parameters k_x, k_y, and k_z represent the magnetic field generation coefficients for the Helmholtz coils in the x, y, and z directions, respectively. These parameters define how Helmholtz coils are used to generate a uniform magnetic field in a controlled manner when a current I_H is applied. Additionally, these parameters are either empirical or calculated coefficients that describe the efficiency with which the Helmholtz coils generate a uniform magnetic field. The values depend on the coil radius, number of turns, and geometry.

The primary role of the Helmholtz coil-generated field is to:

• Control the orientation of the MNR by applying a torque that aligns its magnetic moment with the applied field.
• Stabilize the magnetic environment to ensure consistent MNR orientation without unintended drift.
• Enable rotational control, allowing the MNR to change its heading direction in response to time-varying field inputs.

Thus, the Helmholtz coils do not directly produce propulsion forces but instead ensure the correct control alignment of the MNR, allowing the propulsion forces generated by the Maxwell coils to act in the desired direction.

The parameters g_x, g_y, and g_z describe how efficiently Maxwell coils generate magnetic field gradients. These parameters depend on the coil design, separation distance, and number of turns, which define how the magnetic field strength changes spatially. Unlike Helmholtz coils, which create a uniform field, Maxwell coils generate a controlled spatial variation in field strength, which induces a magnetic force that moves the MNR. This occurs because a magnetic moment in a field gradient experiences a force, given by Equation (2).

Since the propulsion force is directly proportional to the field gradient ∇B, Maxwell coils are responsible for generating propulsion forces. Their function is to:

• Create controlled magnetic field gradients, which exert a net force on the MNR.
• Enable propulsion and actuation, allowing movement in the x, y, or z directions.
• Be dynamically adjusted, enabling the MNR to change speed and direction by modifying the applied coil currents.

Since motion requires a gradient rather than a uniform field, Maxwell coils are the primary contributors to propulsion, ensuring precise control of the MNR’s movement.

In addition to the axial magnetic field gradient, Maxwell coils also generate a radial gradient component, where the radial gradient is half the value of the axial uniform gradient [2]. This effect arises due to the symmetry of the Maxwell coil design, where the coil pairs are arranged to evenly distribute the magnetic field gradient.

As a result of this symmetry, the gradient components in the x and y directions are equal, i.e., g_x = g_y. This assumption simplifies the force model, ensuring that the microrobot experiences a uniform gradient effect in both horizontal directions. However, g_z is independent and is not affected by this radial constraint, as it represents the dominant axial gradient in the system.

While the gradient along each axis is primarily dictated by its corresponding Maxwell coil pair, the total gradient field also includes radial contributions from the other two axes. This is reflected in the off-diagonal terms (−0.5 coefficients) in Equation (6), which represent how each axis is influenced by the gradients from the other two directions.

Although g_z is independent, it still contributes to the field gradients in x and y through a weaker interaction (−0.5 g_z), due to electromagnetic symmetry in the coil setup. Likewise, the field gradients along x and y also contribute weakly to z, leading to the −0.5 g_x, −0.5 g_y terms in the z-gradient equation.

The full 3D magnetic field gradient, considering these axial and radial components, is given by:

$$\left[\begin{array}{c}{V}_{g_x}\\ V_{g_y}\\ V_{g_z}\end{array}\right]=\left[\begin{array}{c}{\nabla B}_x\\ \nabla B_y\\ {\nabla B}_z\end{array}\right]=I_M.\left[\begin{array}{ccc}{g}_x& -0.5g_y& -0.5g_z\\ -0.5g_x& g_y& -0.5g_z\\ -0.5g_x& -0.5g_y& g_z\end{array}\right].\left[\begin{array}{c}x\\ y\\ z\end{array}\right]$$

(6)

Equation (6) describes the spatial variation of the magnetic field gradient generated by three Maxwell coil pairs. The matrix formulation highlights how axial and radial components interact to influence the microrobot’s motion.

In Equation (6), the terms g_x, g_y, and g_z represent the magnetic field gradient components along the x, y, and z axes, respectively. These coefficients define how the applied current influences the net magnetic field gradients generated by the Maxwell coils in each direction.

On the other hand, the variables x, y, and z in the equation correspond to spatial coordinates within the region of interest (ROI). These represent the position of the microrobot in Cartesian space and are not to be confused with the field gradient coefficients. The interaction between the field gradients g_x, gy, and gz and the spatial coordinates x, y, and z determines the net magnetic force applied to the microrobot, ensuring precise control over its movement.

• The diagonal terms (g_x, g_y, g_z) represent direct contributions to the field gradient along each axis.
• The off-diagonal terms (−0.5 coefficients) represent radial interactions, showing how the other two directions influence each axis’ field gradient.
• Since Maxwell coils are engineered to generate symmetric gradients in the horizontal plane, the assumption g_x = g_y simplifies the force modeling. However, g_z remains independent, as it corresponds to the axial propulsion field.

This formulation is crucial for understanding how precise coil current control influences MNR propulsion, enabling real-time actuation in a controlled direction.

5.2. Analysis of Uniformity of Magnetic Field

To control the actuation of an MNR under the effect of a magnetic field, a 3D EMA coil system must offer a controllable magnetic field in 3D space. Adjusting the currents that flow through the coils can control the magnetic field produced by the coils and, consequently, the motion of the magnetic MNR. The main concept of the proposed EMA, a 3D EMA system, is constructed by arranging three sets of Helmholtz coils and three sets of Maxwell coils along three orthogonal axes. A uniform magnetic field is produced by Helmholtz coils, whereas Maxwell coils generate a uniform and sustained magnetic field gradient. Therefore, Helmholtz coils control the MNR’s orientation, and Maxwell coils control its motion and activation. Finite element analysis was conducted to verify the uniformity of the magnetic field generated from both Helmholtz and Maxwell coils and along each of their axes, as we reported in our previous work [24,25].

5.3. Simulation and Coils Parameters

The sizes and configuration of the coil systems were considered when designing the entire system to situate the ROI, which is 40 × 40 × 40 mm³, inside the Helmholtz and Maxwell coils. The Helmholtz coil’s diameter is also intended to be different from the Maxwell coil’s to reduce space restrictions. Because of this, each coil pair meets the requirements for a coil pair despite having a different diameter from the others. Finally, the placement and the number of coil turns are selected so that each pair of Maxwell coils (M_x, M_y, and M_z) and each pair of Helmholtz coils (Hx, Hy, and Hz) has the same gradient of magnetic flux with the same current.

Table 4. Main parameters of the proposed EMA coils [61].

Coil	Radius (mm)	No. of Turn N	Weight (gm)
X Helmholtz coil (Hx)	50	100	245
X Maxwell coil (Mx)	45	130	250
Y Helmholtz coil (Hy)	80	145	515
Y Maxwell coil (My)	700	400	1130
Z Helmholtz coil (Hz)	125	600	3200
Z Maxwell coil (Mz)	112	1250	5950

summarizes the coil system’s specifications [62,63].

The coil dimensions presented in Table 4 were chosen to optimize magnetic field generation, uniformity, and actuation efficiency while balancing power consumption and workspace coverage. The Helmholtz (Hx) and Helmholtz (Hy) coils have a radius of 50 mm, which ensures a homogeneous field in the XY plane while maintaining a compact footprint for precision-based control. In contrast, the Helmholtz (H_Z) coil has a larger 125 mm radius, which is necessary to generate a sufficiently strong and uniform field in the vertical (Z) axis, compensating for the natural attenuation of magnetic field strength in this direction due to workspace depth.

Maxwell coil dimensions were similarly selected based on gradient field generation requirements. The coil spacing and winding density were optimized to ensure smooth transitions in force application without field distortions, ensuring robust six-degree-of-freedom (6-DoF) control across the entire operational volume. These design considerations collectively enhance system stability, precision, and adaptability for microrobot actuation in dynamic biological environments.

The spatial field distribution and gradient uniformity of the electromagnetic actuation (EMA) system were validated through numerical analysis, as detailed in [62,63]. These studies confirmed that the Maxwell coil configuration generates a uniform gradient field, ensuring precise control over microrobot movement while maintaining minimal spatial field distortions. The uniformity of the generated field plays a crucial role in maintaining stable and repeatable microrobot actuation, particularly in dynamic fluidic environments.

Additionally, the trajectory tracking performance of the system was validated through simulation studies in [61], demonstrating the effectiveness of the closed-loop control approach. The study confirmed that a 3D electromagnetic actuation system comprising three pairs of Helmholtz and Maxwell coils could navigate microrobots with high precision, achieving trajectory tracking errors as low as 13 µm.

These results were obtained using a closed-loop control strategy, where real-time adjustments to coil currents ensured accurate trajectory following and minimal deviation from the desired path. The PID-based control system in the simulation dynamically regulated the field gradients to compensate for external disturbances, improving overall stability and positioning accuracy.

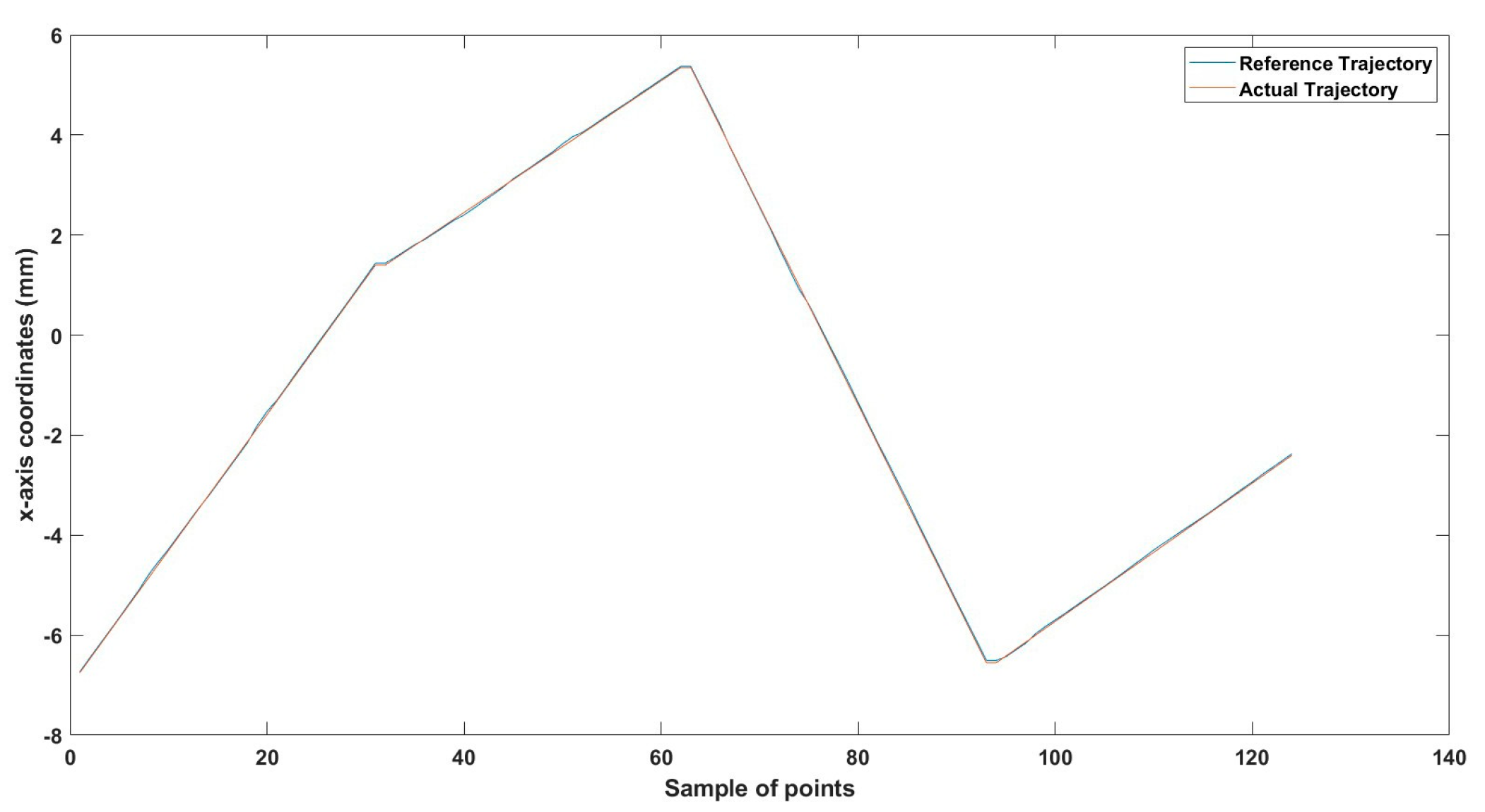
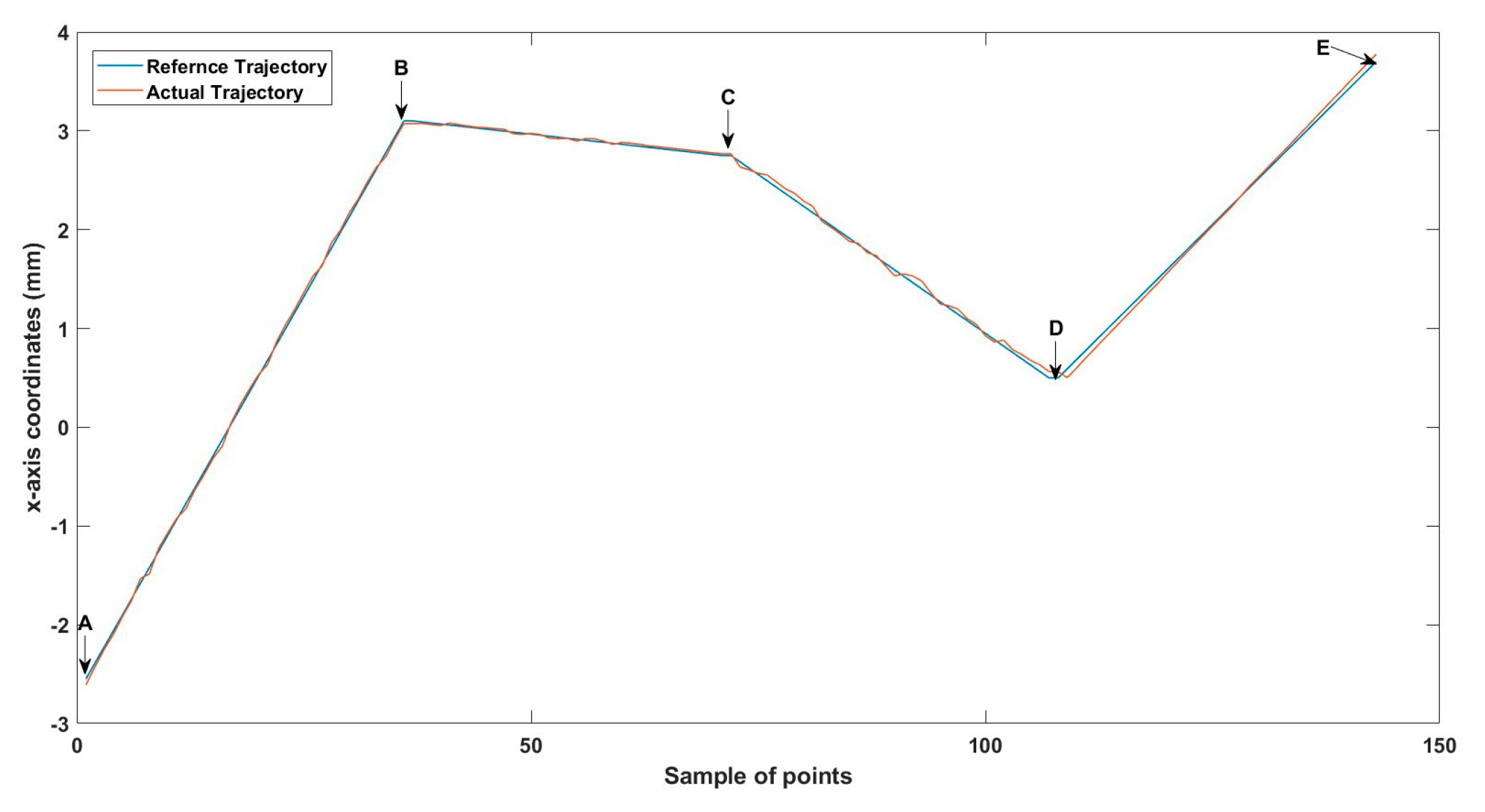
Figures 8–15 illustrate the simulated trajectory tracking results, demonstrating that the closed-loop system effectively maintains microrobot stability and minimizes trajectory errors in real-time. These simulations confirm that the proposed system can provide robust six-degree-of-freedom (6-DoF) control, ensuring reliable microrobot actuation in complex biomedical environments.

While the present study focuses on experimental validation, these prior simulations substantiate the system’s accuracy, real-time adaptability, and closed-loop control efficiency, reinforcing its suitability for biomedical applications, such as targeted drug delivery and minimally invasive micromanipulation.

Figure 2 shows the coils after manufacturing and implementation.

5.4. Closed-Loop Control of EMA

The MNR is aligned to the desired direction in the x-y plane by applying a uniform magnetic field generated by the two orthogonal Helmholtz coil pairs. Taking θ as the desired orientation angle, the following relationship holds:

$$\mathit{tan}\theta ={\displaystyle \frac{B_{Hy}}{B_{Hx}}}={\displaystyle \frac{K_y{I}_{Hy}}{K_x{I}_{Hx}}}$$

(7)

Therefore, if both k_y and k_x have the same value, the coil currents can be adjusted to align the MNR with the desired orientation in the X-Y plane. However, for full 3-D navigation, two additional angles must be considered.

$$\mathit{tan}\beta ={\displaystyle \frac{B_{Hx}}{B_{Hz}}}$$

(8)

$$\mathit{tan}\alpha ={\displaystyle \frac{B_{Hz}}{\sqrt{B_{Hx}^2+B_{Hy}^2}}}$$

(9)

The MNR achieves propulsion through the magnetic field gradient generated by three orthogonal pairs of Maxwell coils. These coils create a spatially varying magnetic field, activating the MNR’s magnetic moment and enabling movement. The three force components driving the MNR along the x, y, and z directions are derived as follows:

$$F=MT{V}_g$$

where

$$F=\left[\begin{array}{c}{F}_x\\ F_y\\ F_z\end{array}\right]=\left[\begin{array}{ccc}{M}_x& 0& 0\\ 0& M_y& 0\\ 0& 0& M_z\end{array}\right]\left[\begin{array}{ccc}cos\beta \mathit{cos}\theta & -\cos \beta \sin \theta & \sin \beta \\ cos\alpha \sin \theta +\mathit{sin}\alpha sin\beta \cos \theta & cos\alpha \cos \theta -\sin \alpha sin\beta \sin \theta & -\sin \alpha \cos \beta \\ \mathit{sin}\alpha \mathit{sin}\theta +\mathit{cos}\alpha sin\beta \mathit{cos}\theta & \sin \alpha \mathit{cos}\theta +\cos \alpha sin\beta \mathit{sin}\theta & cos\alpha \cos \beta \end{array}\right]\left[\begin{array}{c}{V}_{gx}\\ V_{gy}\\ V_{gz}\end{array}\right]$$

(10)

Equation (10) defines the relationship between the propulsion force F, the magnetic moment M, the transformation matrix T (which accounts for the angular orientation angles θ, β, α following Euler angles transformation, T = Rx(α)Ry(β)Rz(θ)), and the magnetic field gradient Vg.

To determine θ, β, α, from the known properties of the generated transformation matrix T.

$$\tan \theta =-{\displaystyle \frac{T_{12}}{T_{11}}}$$

$$\tan \beta ={\displaystyle \frac{T_{13}}{\sqrt{T_{11}^2+T_{12}^2}}}$$

$$\tan \alpha ={\displaystyle \frac{T_{32}}{T_{33}}}$$

Since the magnetic field gradient, V_g , is produced by the Maxwell coil, it is directly related to the coil-generated gradient ∇ B_M:

$$V_g=\nabla B_M=\left[\begin{array}{c}{V}_{gx}\\ V_{gy}\\ V_{gz}\end{array}\right]=\left[\begin{array}{c}{g}_x{I}_{Mx}\\ g_y{I}_{My}\\ g_z{I}_{Mz}\end{array}\right]$$

(11)

For the MNR to be effectively controlled and propelled in the desired direction, the ratio of propulsion forces in the x and y directions must satisfy:

$${\displaystyle \frac{F_x}{F_y}}=\mathit{tan}\theta ={\displaystyle \frac{M_x{V}_{gx}\mathit{sin}\theta \mathit{cos}\beta }{M_y{V}_{gy}\mathit{cos}\theta \mathit{sin}\beta \mathit{cos}\alpha }}$$

(12)

Since Maxwell coils in the x and y directions generate equal magnetic field gradients, it follows that g_x = g_x is deduced, and g_m leads to a generalized magnetic gradient constant g_m = g_x = g_y.

Since the gravitational and buoyant forces acting in the z-direction are both constant, the net force in the z-direction, F_zg, consists of F_zg, a force component that balances the gravitational and buoyant forces, and F_zd, a force component that serves as the magnetic driving force along the z-axis. Thus, the total driving force in the z-direction is F_z = F_zg + F_zd.

Similarly, the magnetic field gradient g_z in the z-direction comprises g_zg, the field gradient required to counteract gravity and buoyancy forces, and g_zd, the field gradient required for MNR propulsion along z. This means that g_z = g_zg + g_zd.

F_z is subdivided into F_zg and F_zd, with F_zg balancing the gravitational and buoyant forces and F_zd serving as the z-axis’ magnetic driving force. The magnetic flux gradient, g_z, is further subdivided into g_zg, which opposes the gravitational force, and g_zd, the magnetic gradient used to actuate the MNR. These relationships lead to the following governing equations: [55].

$${\displaystyle \frac{F_{zd}}{\sqrt{F_x^2+F_y^2}}}=\cot \beta ={\displaystyle \frac{{MV}_{gzd}\cos \beta }{{MV}_{gm}\sin \beta }}={\displaystyle \frac{g_{zd}\cos \beta }{g_m\sin \beta }}$$

(13)

Since g_zd and g_m are both magnetic field gradient components but represent different spatial effects, this equation serves as a normalization constraint, ensuring that the vertical propulsion gradient g_zd is balanced correctly with the total field gradient g_m. The equation enforces a geometric proportionality, ensuring that the propulsion forces maintain a correct force-to-field ratio in the z-direction while aligning with the overall field gradient structure.

The force F_zg is responsible for counteracting the gravitational and buoyant forces acting on the MNR, ensuring that it remains stable at a given height before propulsion is applied. This is expressed as:

F_zg = MVg_zgcosβ = V(ρ − ρ f)g = F_g − F_b

(14)

F_b is the buoyancy force, ρ f is the fluid density, and ρ is the MNR’s density. The alignment of an MNR to the required orientation (β) requires that g_zd = g_m, which may be inferred from Equation (13). The current I_mz is split into two components, one of which generates F_zg to hold and lock the MNR at any point along the z-axis and the other of which generates (g_zd) F_zd to activate the MNR in a vertical position. This calculation and keeping of F_zg as a constant value are carried out using Equation (14) [61].

6. EMA System Implementation Setup and Experimental Results

6.1. EMA Setup

The overall experimental setup for the locomotion experiments is depicted in Figure 3 and includes:

• Coil configuration and holding base.
• Cytron driver for each pair of coils.
• Power supply.
• Output interface.
• Digital microscope
• MNR (neodymium magnet)
• System software

The developed EMA includes a three-axis Maxwell coil set with a three-axis Helmholtz coil set, which was manufactured in-house. The desired position is first specified through the computer’s control algorithm, after which the control action is delivered to the drivers, each of which regulates the current flow in each pair of coils. To actuate an MNR, the coil pairs in the system will provide the necessary magnetic field. Three digital microscopes were used as visual feedback to track the MNR and determine its location.

Two channels of bi-directional Cytron drivers are used to control the current to the coils. In addition, this can deliver a bi-directional signal to switch the current’s direction.

Since the Cytron MDD10A (Penang, Malaysia) driver provides 10 Amp 5 V–30 V, it is used for x-Helmholtz coils (Hx), X-Maxwell coils (MX), Y-Helmholtz coils (HY), and Y-Maxwell coils (MY). While the Cytron MDDS60 driver supports input voltages between 7 and 45 V, it is used for Z-Helmholtz coils (MZ). Since the resistance of the z-axis Maxwell coils is relatively high (20 Ω), a high power source is required (80 V). A customized driver is manufactured in-house to adjust the current provided to the Z Maxwell coils.

Three digital microscopes with a resolution of 640 × 480 are used to visualize the ROI, determine the MNR’s coordinates, and track the MNR. The utilized digital is the Hiview magnification microscope, which has an eight-LED endoscope. Its magnification is 50–1000×. The three microscopes are used in three different planes: (x,y), (x,z), and (y,z). Figure 4 shows the three microscopes integrated with the EMA system.

Two different sizes of MNRs are used. They are cylindrical NdFeB (N42) magnets, one with a 0.3 mm diameter and 0.5 mm height. In contrast, the other is 1.5 mm in diameter and 2 mm in height. Figure 5 shows the MNRs. The MNR is placed in a transparent container filled with viscous fluid, silicon oil with kinematic viscosity (350 cs), as shown in Figure 6.

Silicone oil (350 cSt) was chosen as the testing medium to simulate a high-viscosity environment that challenges microrobot actuation, enabling stress testing of the system’s adaptability and robustness. While blood has a viscosity of approximately 3–4 cP, in vivo conditions are far more complex due to variable shear rates, pulsatile flow dynamics, and interaction with vessel walls, which cannot be fully replicated in a static fluid model. Using a higher viscosity medium allows us to assess the performance of the electromagnetic actuation system under more demanding fluidic conditions, ensuring that control mechanisms remain effective even in restrictive environments. The results serve as an upper-bound validation, demonstrating that if the system performs well in high-viscosity conditions, it will likely function efficiently in lower-viscosity physiological conditions such as blood plasma.

Future work will focus on experimental validation in biologically relevant fluids, including synthetic blood analogs or microfluidic flow systems, to refine control parameters for in vivo applications.

6.2. Experimental Results

Different experiments were conducted to validate the ability of the proposed EMA system to actuate the MNR in 3D space, holding the MNR in a vertical position and moving horizontally in 3D space.

To ensure precise regulation of the Maxwell coil currents for effective propulsion and orientation, a PID (Proportional-Integral-Derivative) controller is implemented. The PID controller dynamically adjusts the input current to achieve the desired field gradients while compensating for disturbances. The controller parameters were optimized using a genetic algorithm optimization technique to enhance system stability and performance. The optimized PID parameters are: proportional gain (Kp) = 6, integral gain (Ki) = 0.01, and derivative gain (Kd) = 6 [61].

This closed-loop control mechanism ensures stable trajectory tracking and minimizes deviations from the desired path, enhancing the system’s accuracy and responsiveness in real-time applications. Unlike open-loop control systems, which rely solely on pre-calculated force values, this approach continuously monitors position feedback and dynamically adjusts actuation currents to maintain precise microrobot positioning.

The list of experiments conducted is:

• 3D space using small-sized MNR.
• Horizontal experiment using small MNR.
• Horizontal experiment using large MNR.
• 3D space using large-sized MNR.

6.2.1. 3D Space Using Small MNR

A 3D space trajectory experiment was conducted using the small MNR. Figure 7, Figure 8 and Figure 9 show the result of this trajectory in the (X-Z), (X-Y), and (Y-Z) planes, respectively. The results demonstrate high tracking accuracy, with the microrobot following predefined paths with minimal deviation. The system successfully maintains positional control within an average error margin of ≤36 µm, validating the effectiveness of the real-time closed-loop feedback mechanism in compensating for disturbances.

Specifically, Figure 7 shows linear trajectory tracking, where the microrobot follows a straight-line path with consistent velocity and minimal drift. Figure 8 illustrates circular trajectory control, demonstrating the system’s ability to execute continuous curved motion without compromising stability. Figure 9 presents a complex trajectory, demonstrating that the system can precisely adjust to intricate movement patterns, which is crucial for targeted drug delivery and microsurgical applications.

Table 5. Error in small MNR 3D experiment.

			x-Axis				y-Axis				z-Axis
	Start	Final Desired	Final Actual	Error (µm)	Start	Final Desired	Final Actual	Error (µm)	Start	Final Desired	Final Actual	Error (µm)
AB	−2.55	3.1	3.072	36	2.2	−0.4	−0.376	39	2.15	1	1.042	45
BC	3.1	2.75	2.768	17	−0.4	2.3	2.3602	41	1	0.6	0.63	24
CD	2.75	0.5	0.563	43	2.3	0.1	0.081	33	0.6	0	0.0208	31
DE	0.5	3.7	37	46	0.1	0	−0.017	17	0	−0.85	−0.8709	30

then compares the desired and actual trajectory segments, alongside their calculated errors.

Beyond trajectory validation, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28, Figure 29, Figure 30 and Figure 31 illustrate performance across different actuation parameters, including variations in magnetic field strength, response time, and microrobot scaling effects. These results collectively highlight the system’s robustness across multiple operational scenarios.

The x, y, and z trajectories are shown in Figure 10, Figure 11 and Figure 12, respectively. The error in the three axes is illustrated in Figure 13, Figure 14, and Figure 15.

6.2.2. Horizontal Experiment Using Small MNR9

The second experiment tests the ability of the MNR to be actuated in a horizontal line in 3D space. Figure 16 and Figure 17 show the ability to move the MNR horizontally while being held. In the z-axis, the highest RMS inaccuracy is 19 µm, as seen in

Table 6. Small-sized MNR Horizontal Experiment Error.

Axis	Error (µm)
x error	24 µm
y error	23 µm
z error	19 µm

. Figure 18, Figure 19 and Figure 20 show the trajectory in the x-axis, y-axis, and z-axis, respectively. Figure 21, Figure 22 and Figure 23 show the error in each axis.

The observed positioning error of 36 µm remains within acceptable biomedical tolerances, particularly for targeted drug delivery and microsurgical applications. Studies suggest that 50–100 µm accuracy is sufficient for localized drug deposition in microvascular networks [40], whereas high-precision applications such as neuronal micromanipulation may require tolerances below 10–20 µm [35]. Given that our system achieves an error margin below 50 µm, it meets accuracy standards for microfluidic drug targeting and controlled-release applications.

Furthermore, the resolution of the digital microscope used to track the MNR’s motion is a key factor influencing positioning accuracy. The digital scopes were calibrated following the specifications provided by the manufacturer of the digital microscopes; the acquired images were transformed into coordinates using standard image processing techniques, including contrast-based tracking. The current system employs a 640 × 480 resolution microscope, each pixel corresponding to 15 µm, which inherently affects tracking precision and contributes to baseline positioning errors observed in our results. Higher-resolution imaging and advanced real-time processing techniques could refine localization accuracy and minimize trajectory errors. Future iterations of this system will incorporate higher-resolution sensors and enhanced real-time closed-loop correction mechanisms to actively mitigate actuation deviations and improve performance in dynamic biological environments.

Figure 16. X-Y view Motion of the small-sized MNR in a horizontal line in 3D space.

Figure 16. X-Y view Motion of the small-sized MNR in a horizontal line in 3D space.

Figure 17. X-Z view Motion of the small-sized MNR in a horizontal line in 3D space.

Figure 17. X-Z view Motion of the small-sized MNR in a horizontal line in 3D space.

Figure 18. Small-sized MNR horizontal Experiment: x-axis of the desired and actual trajectory.

Figure 18. Small-sized MNR horizontal Experiment: x-axis of the desired and actual trajectory.

Figure 19. Small-sized MNR horizontal Experiment: y-axis of the desired and actual trajectory.

Figure 19. Small-sized MNR horizontal Experiment: y-axis of the desired and actual trajectory.

Figure 20. Small-sized MNR horizontal Experiment: z-axis of the desired and actual trajectory.

Figure 20. Small-sized MNR horizontal Experiment: z-axis of the desired and actual trajectory.

Figure 21. Small--sized MNR horizontal Experiment: Total error in x-axis.

Figure 21. Small--sized MNR horizontal Experiment: Total error in x-axis.

Figure 22. Small--sized MNR horizontal Experiment: Total error in y-axis.

Figure 22. Small--sized MNR horizontal Experiment: Total error in y-axis.

Figure 23. Small-sized MNR horizontal Experiment: Total error in z-axis.

Figure 23. Small-sized MNR horizontal Experiment: Total error in z-axis.

6.2.3. Horizontal Experiment Using Large MNR

Another two experiments were carried out to verify the ability of the proposed EMA to actuate larger MNRs. The first experiment was to check the ability of the EMA to move the big MNR along a horizontal line in 3D space. The ability to move the MNR horizontally while being held is seen in Figure 24. In the z-axis, the highest RMS inaccuracy is 32 µm, as seen in

Table 7. Large-sized MNR Horizontal Experiment Error.

Axis	Error (µm)
x error	25 µm
y error	30 µm
z error	32 µm

.

Figure 24. Large-sized MNR horizontal move in 3D experiment.

Figure 24. Large-sized MNR horizontal move in 3D experiment.

6.2.4. 3D Trajectory Experiment Using Large MNR

The other experiment was carried out in a 3D trajectory. The result is shown in Figure 25. Figure 26, Figure 27 and Figure 28 show the trajectory in the three axes. While the error in each axis is shown in Figure 29, Figure 30 and Figure 31.

Figure 25. Large-sized MNR 3D experiment.

Figure 25. Large-sized MNR 3D experiment.

Figure 26. Large--sized MNR XYZ Experiment: x-axis of the desired and actual trajectory.

Figure 26. Large--sized MNR XYZ Experiment: x-axis of the desired and actual trajectory.

Figure 27. Large--sized MNR XYZ Experiment: y-axis of the desired and actual trajectory.

Figure 27. Large--sized MNR XYZ Experiment: y-axis of the desired and actual trajectory.

Figure 28. Large--sized MNR XYZ Experiment: z-axis of the desired and actual trajectory.

Figure 28. Large--sized MNR XYZ Experiment: z-axis of the desired and actual trajectory.

Figure 29. Large--sized MNR XYZ Experiment: Total error in x-axis.

Figure 29. Large--sized MNR XYZ Experiment: Total error in x-axis.

Figure 30. Large--sized MNR XYZ Experiment: Total error in y-axis.

Figure 30. Large--sized MNR XYZ Experiment: Total error in y-axis.

Figure 31. Large--sized MNR XYZ Experiment: Total error in z-axis.

Figure 31. Large--sized MNR XYZ Experiment: Total error in z-axis.

6.2.5. Results Summary

The error results in the trajectories in the different experiments mainly resulted from two main issues:

• The resolution of the microscopes (640 × 480), where just one pixel resembles 15 µm, so at least 15 µm error is found in all the experiments, so replacing the used microscopes with better resolution will enhance the performance of the developed EMA system.
• The radial effect of the Maxwell coils has a negative impact on the trajectory of the MNR, especially the z-Maxwell coils with a large radius and the number of turns relative to the two other Maxwell coils.

Table 8. Results Comparison.

	Our Paper	[46]	[59]	[7]	[64]
EMA	3 Helmholtz and 3 Maxwell	3 Helmholtz and 3 Maxwell	3 Helmholtz	3 Helmholtz and 3 Maxwell	2 Helmholtz and 2 Maxwell
Dimensionality	3D	3D	3D	2D	2D
ROI (mm)	40 × 40 × 40	25 × 25 × 25	56 × 56 × 56	60	-
MNR structure	Cylinderical	Cyliderical	Spherical	Cylinderical	Cylinderical
MNR Diameter (mm)	0.3	2	5	1	2
MNR length (mm)	0.5	3	-	1	2
Error (µm)	46	-	398	200	60

compares the achieved results with the available results in the most relevant literature, 285. From this table, it can be deduced that the results achieved are significant regarding the error and the size of the MNR.

The EMA system actuates all six degrees of freedom, including rotational movement, based on the calculated Euler angles and applied magnetics torque as defined in Equations (7)–(10). However, we acknowledge that orientation control was not quantifiably demonstrated in the figures, as no visual markers or angular tracking methods were used to measure or display rotational changes. While orientation actuation was implemented during the experiments, the current results focus on translational accuracy. Future work will incorporate dedicated visualization and tracking tools to quantify orientation control across all three rotational axes explicitly.

7. Conclusions

This paper investigated developing and implementing a low-cost six-dimensional Electromagnetic Actuation (EMA) system to precisely manipulate micro/nanorobots (MNRs) within complex fluidic environments. This innovative approach addresses a significant gap in existing MNR actuation technologies, particularly in high-viscosity environments like those found in biomedical applications.

The heart of this system is the integration of three pairs of Helmholtz coils and three pairs of Maxwell coils, which together create a highly controllable and adaptable magnetic field essential for precise MNR manipulation.

By incorporating a closed-loop Proportional-Integral-Derivative (PID) control technique and real-time visual feedback from three digital microscopes across distinct planes, our EMA system demonstrates its potential to navigate and manipulate MNRs effectively. The effectiveness of the PID control in enhancing the system’s accuracy and responsiveness highlights its suitability for delicate and precise operations required in biomedical applications.

Notably, the system’s region of interest (ROI) spanning a volume of 40 × 40 × 40 mm³ provides significant experimental space for testing and validation. This substantial ROI enables the simulation of various navigational challenges and scenarios MNRs may encounter in real-world applications. However, it is essential to recognize that this scale does not apply to the dimensions of the entire human body. Future work will involve scaling up the system to accommodate larger areas aligned with magnetic resonance imaging (MRI) dimensions to more accurately simulate conditions within the human body. This research marks a good advancement in micro/nanorobotics, setting a foundation for future developments and applications in targeted drug delivery and precision medical diagnostics.

To replicate the dense nature of human blood, we utilized silicone oil within the ROI, enabling us to closely mimic the challenges posed by fluid dynamics in a biological environment. We conducted a series of meticulously designed experiments using two different sizes of MNRs, effectively showcasing the system’s ability to actuate these agents within desired trajectories. The experimental outcomes confirm the system’s proficiency in achieving this goal, with a maximum error of 46 µm observed across the trials.

However, we also identified two main factors that impact the precision of the EMA system: the resolution of the utilized digital microscopes and the radial effect of the Maxwell coils. We recommend enhancing system performance by replacing the existing microscopes with higher-resolution alternatives. Moreover, addressing the radial effect of the Maxwell coils is essential to further reducing errors and improving overall accuracy.

Additionally, given the potential challenges associated with the presence of neodymium-based microrobots in the human body, retrieval strategies must be carefully considered. One proposed solution is to reverse the trajectory of the microrobot, guiding it back to the insertion point for safe extraction. An alternative approach is to develop microrobots from biodegradable materials, allowing them to safely degrade after completing their intended function. While this study focuses on laboratory testing, future work will explore biocompatible materials and ensure compliance with biomedical safety regulations.

It is important to note that the current EMA system dimensions are designed for experimental and laboratory testing purposes rather than full-body biomedical applications. To achieve real-world clinical implementation, a significantly larger system—similar to the scale of Magnetic Resonance Imaging (MRI) devices—would be required. Future research will focus on scaling up the system while ensuring precision and control remain effective for microrobot actuation in the human body.

In conclusion, our work has introduced a novel and cost-effective solution for the precise control and navigation of MNRs in three-dimensional space. By addressing the challenges of fluid dynamics and gravitational forces, we have established the foundation for advancing biomedical applications by manipulating MNRs. This research opens the way for future developments, facilitating more complex and effective interventions within targeted drug delivery, diagnostics, and other precision biomedical procedures.