The Compact Model Synthesis for the RADFET Device
Abstract
1. Introduction
- Using SPICE subcircuits (.SUBCKT directive) or macromodels [27]. The compact model is assembled as a set of primitive devices (resistor, capacitor, inductor) and behavioral (B-type) sources representing current on voltage or voltage on current dependencies. This method is supported by every SPICE simulation kernel, but complex models may have a poor performance, because the model parsing is required every time when netlist is loaded.
- Using Verilog-A hardware description language [28]. The Verilog-A is an extension of Verilog for analog circuits. The Verilog-A models are compiled into binary shared objects that could be attached to the simulator at the execution time. Therefore Verilog-A provides a better performance than subcircuits.
- Using XSPICE extensions [29,30]. XSPICE modules are written in C programming language with macros and also compiled as shared objects. XSPICE extension are much more difficult to design, but allows to provide a more deep integration of the model and simulation kernel. XSPICE brings no benefit for RADFET model because of design difficulties and no possibility of direct export from schematic. The deep integration with SPICE simulation kernel provided by XSPICE is not required for RADFET device compact model.
2. Materials and Methods
2.1. Used RADFET Device
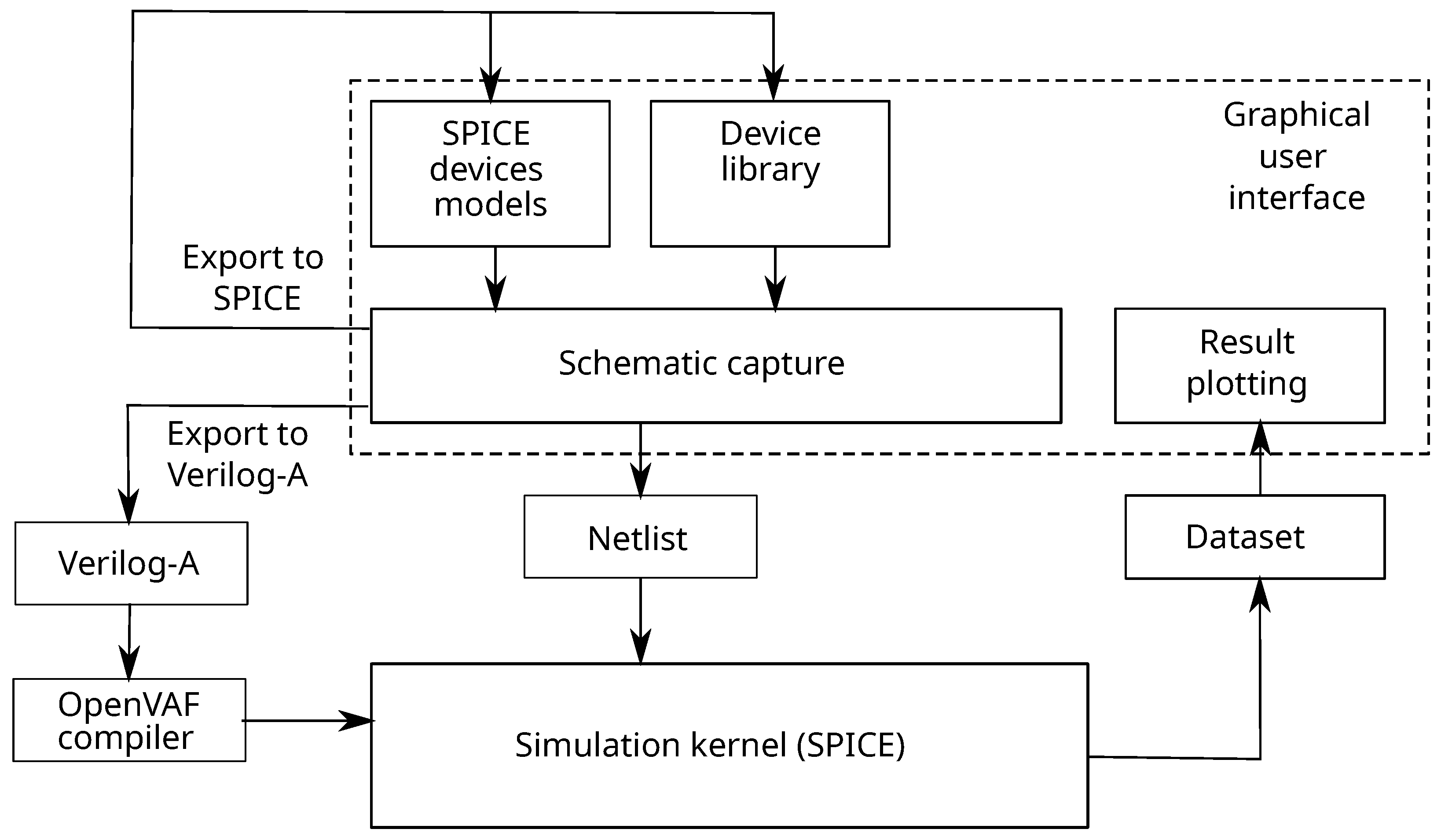
2.2. Circuit Simulation Software
2.3. Basic RADFET Model Equations
2.4. Radiation Dependency of the Threshold Voltage
2.5. Gate Current Model
3. Results
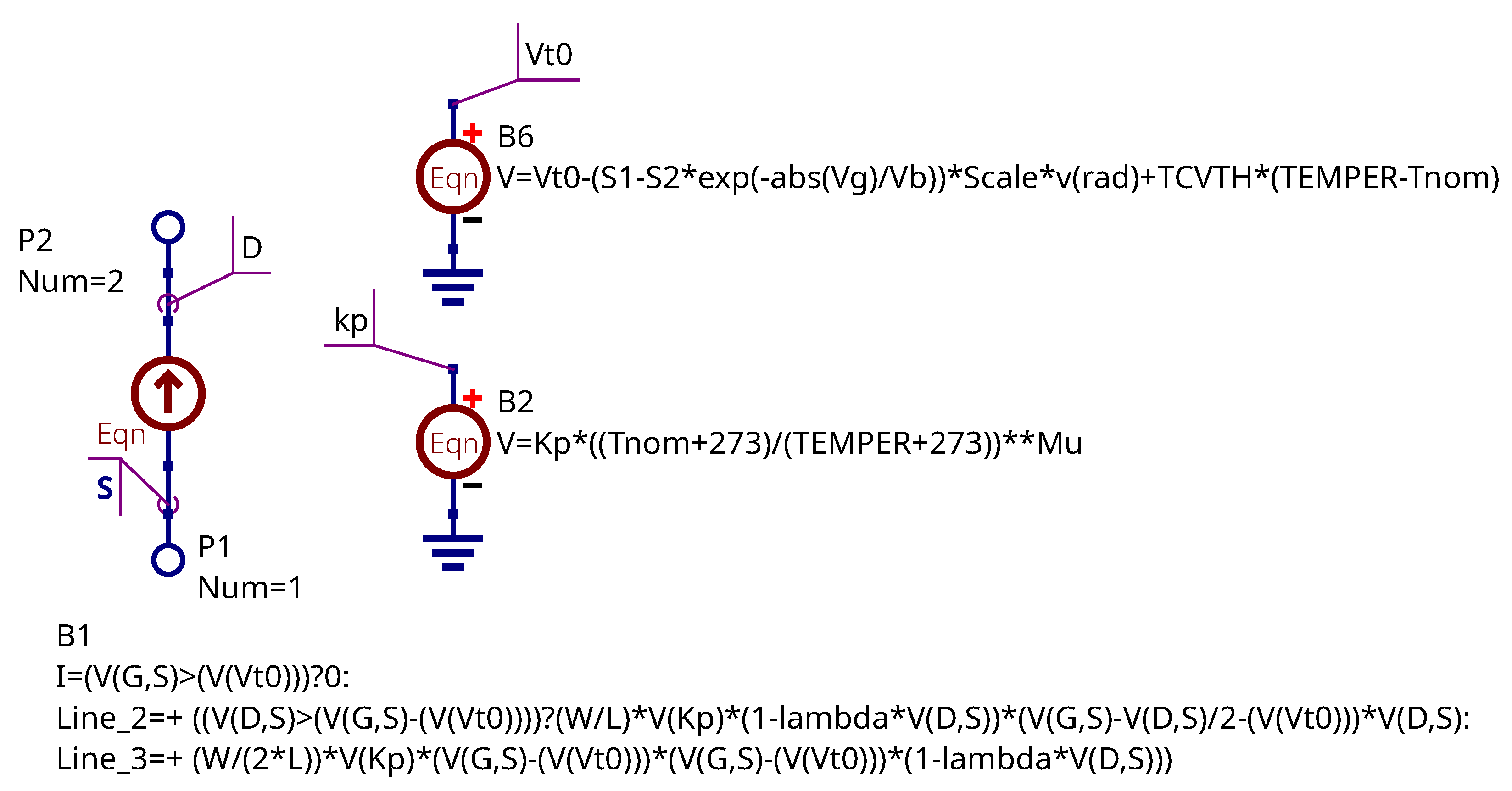
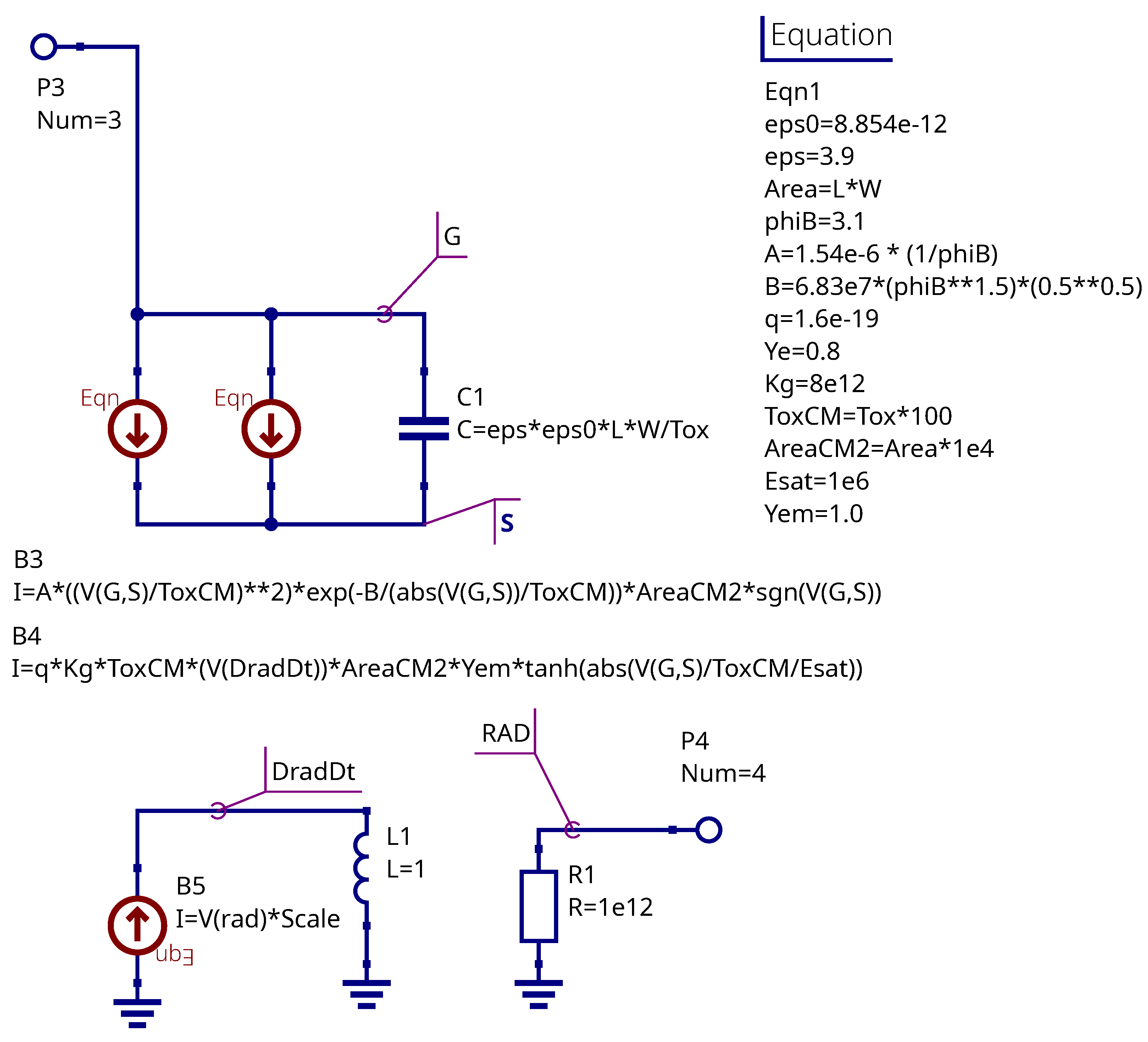
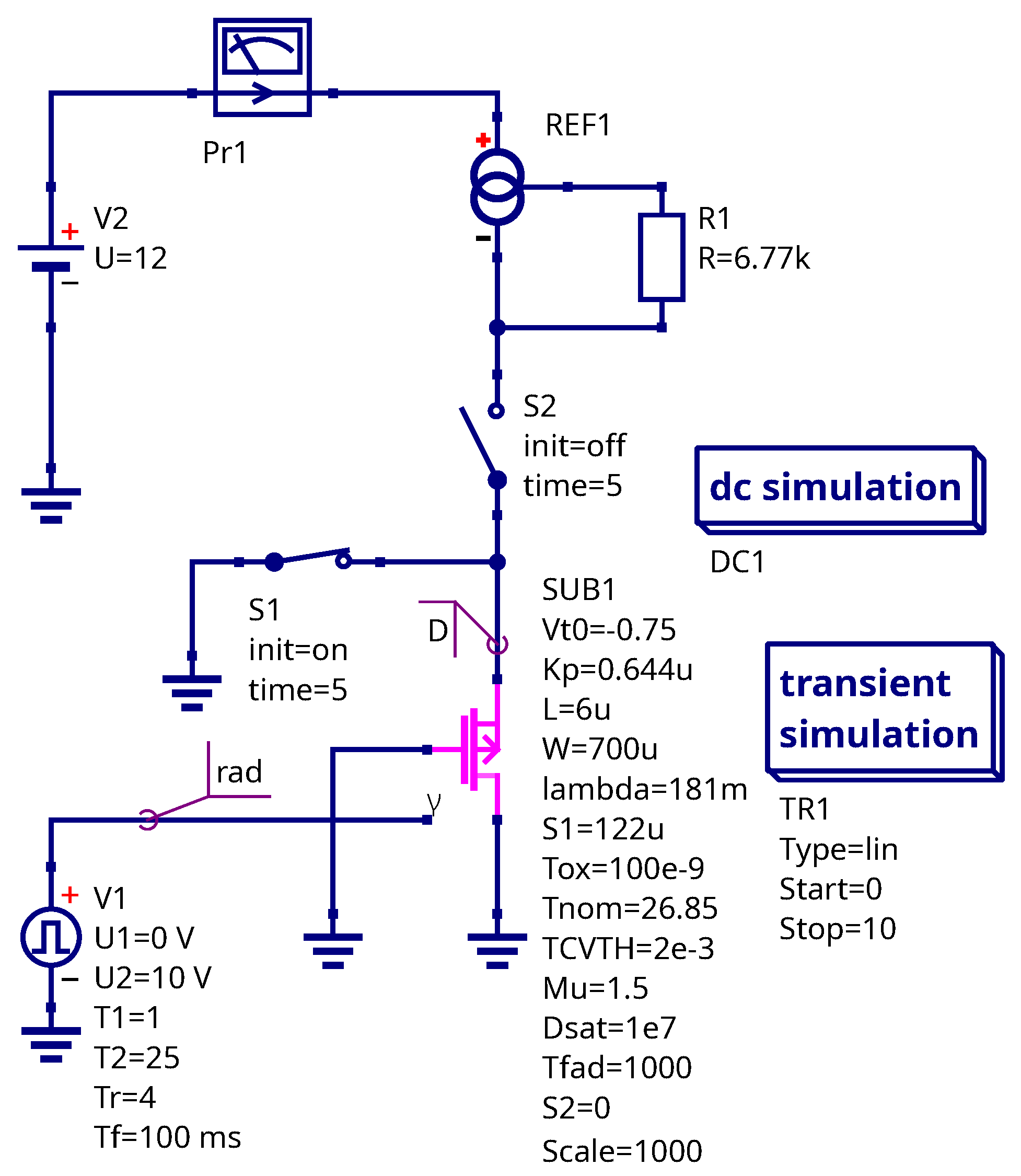
3.1. The Equivalent Circuit of the RADFET Device
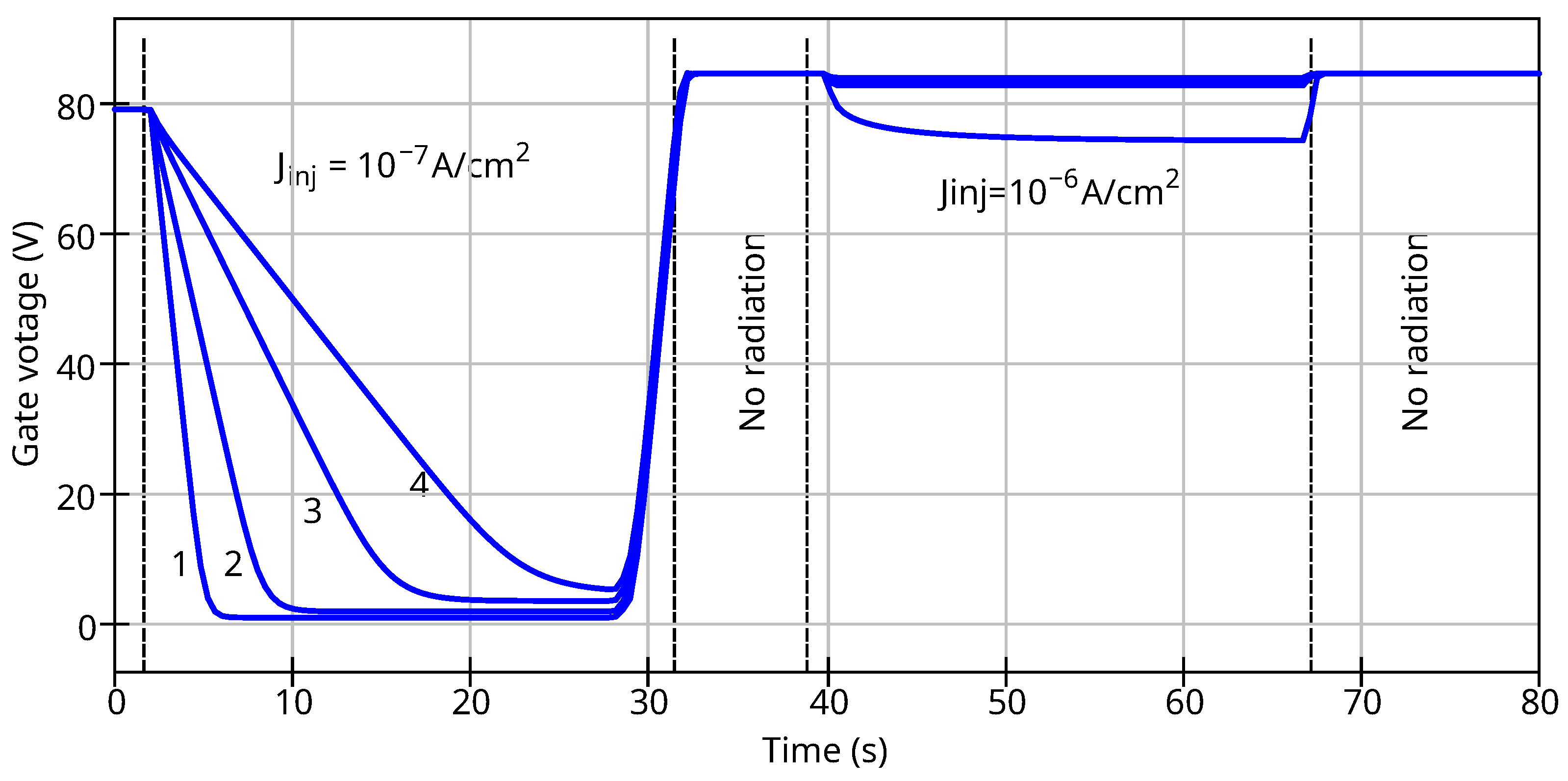
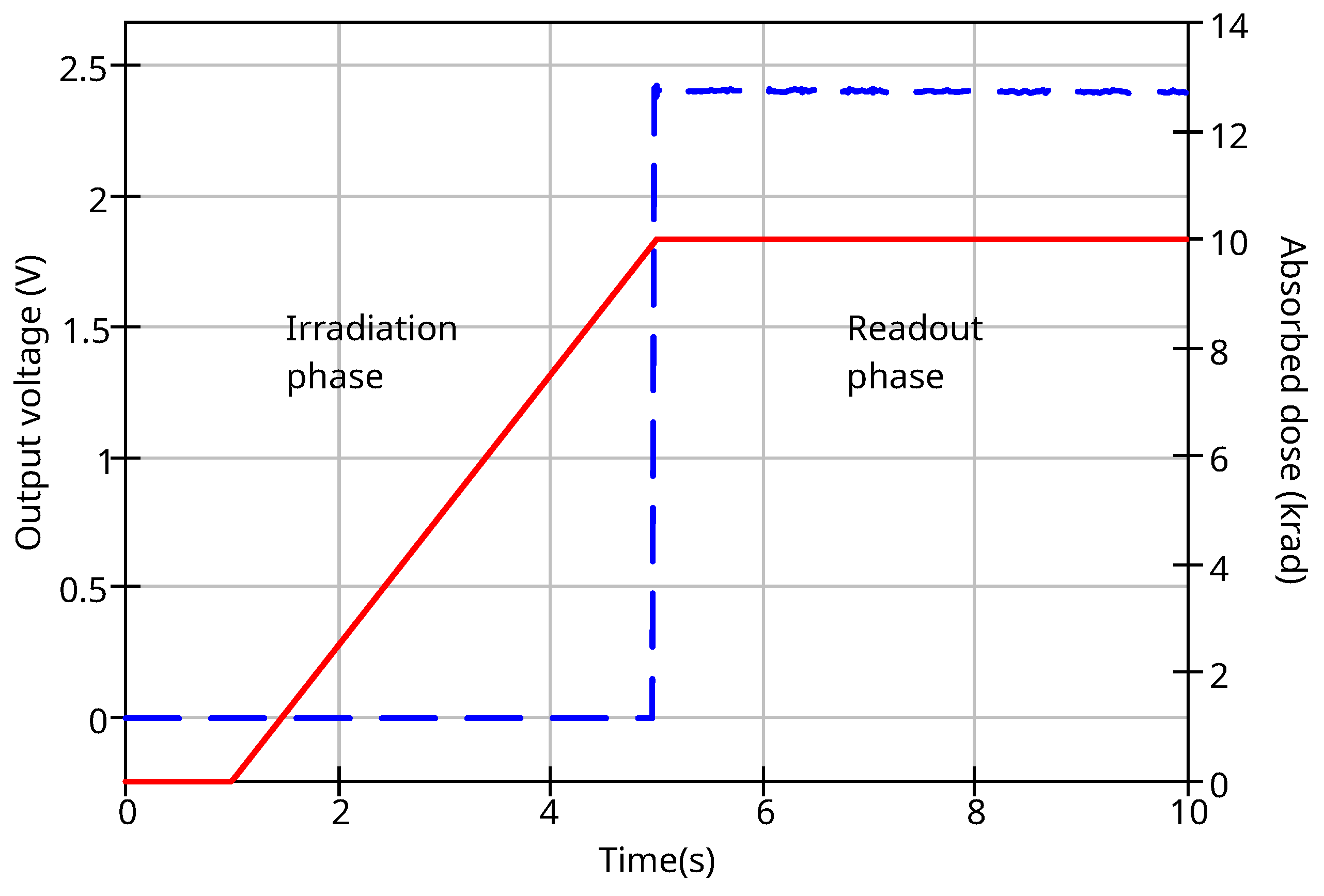
3.2. Equivalent Circuit Representing Dose Accumulation and Fading
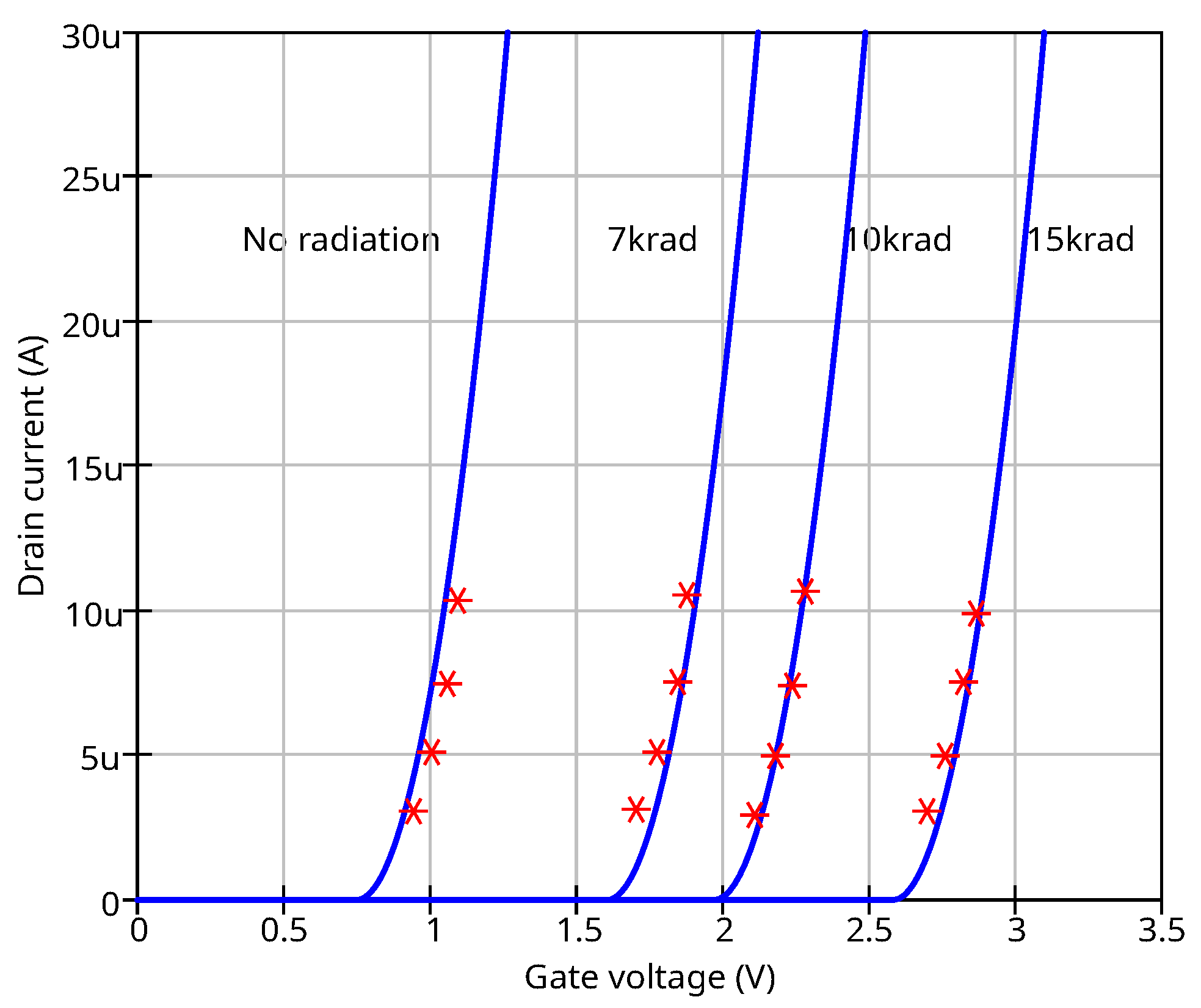
3.3. IV-Curves Simulation
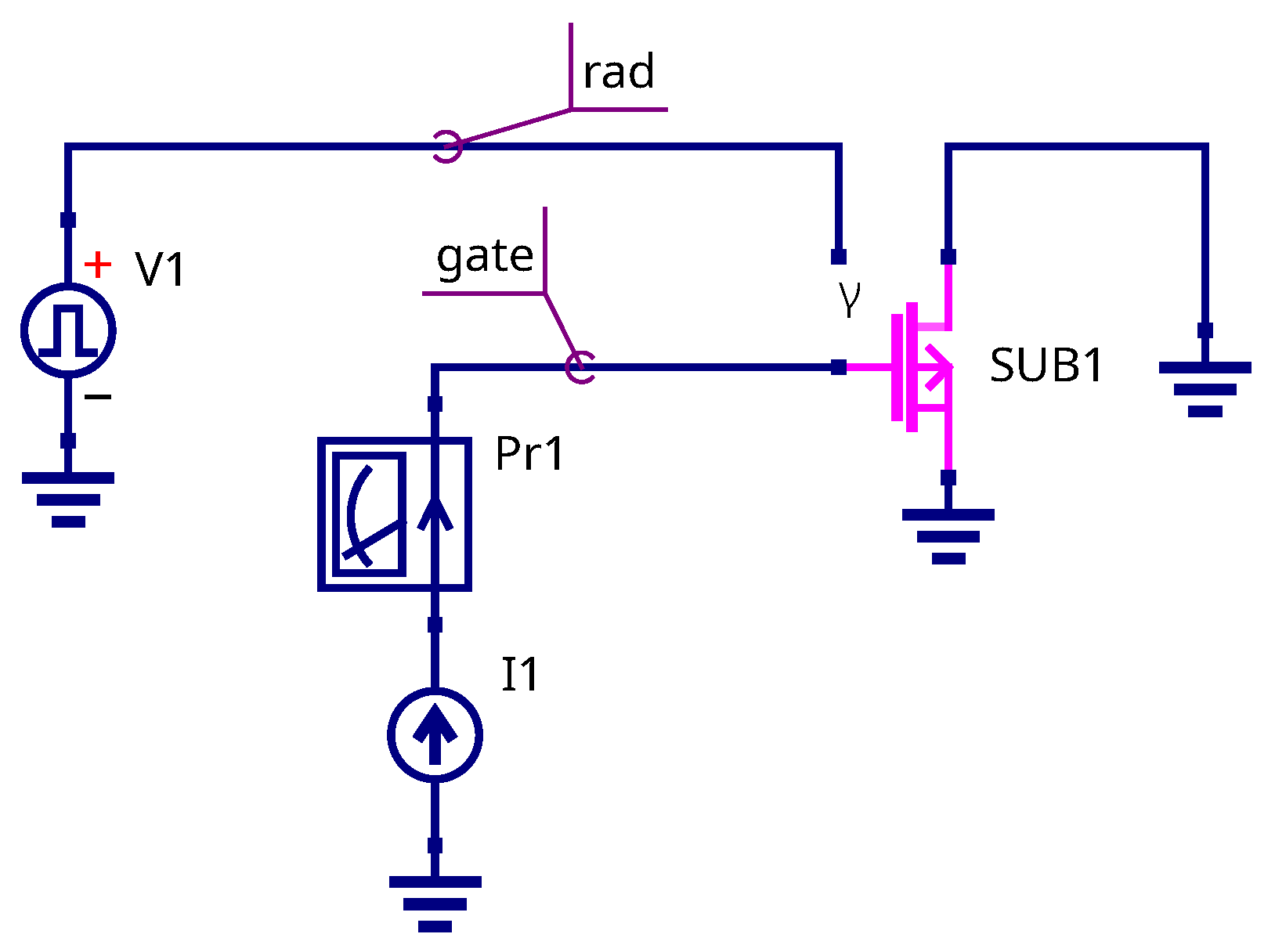
3.4. Sensitivity Simulation
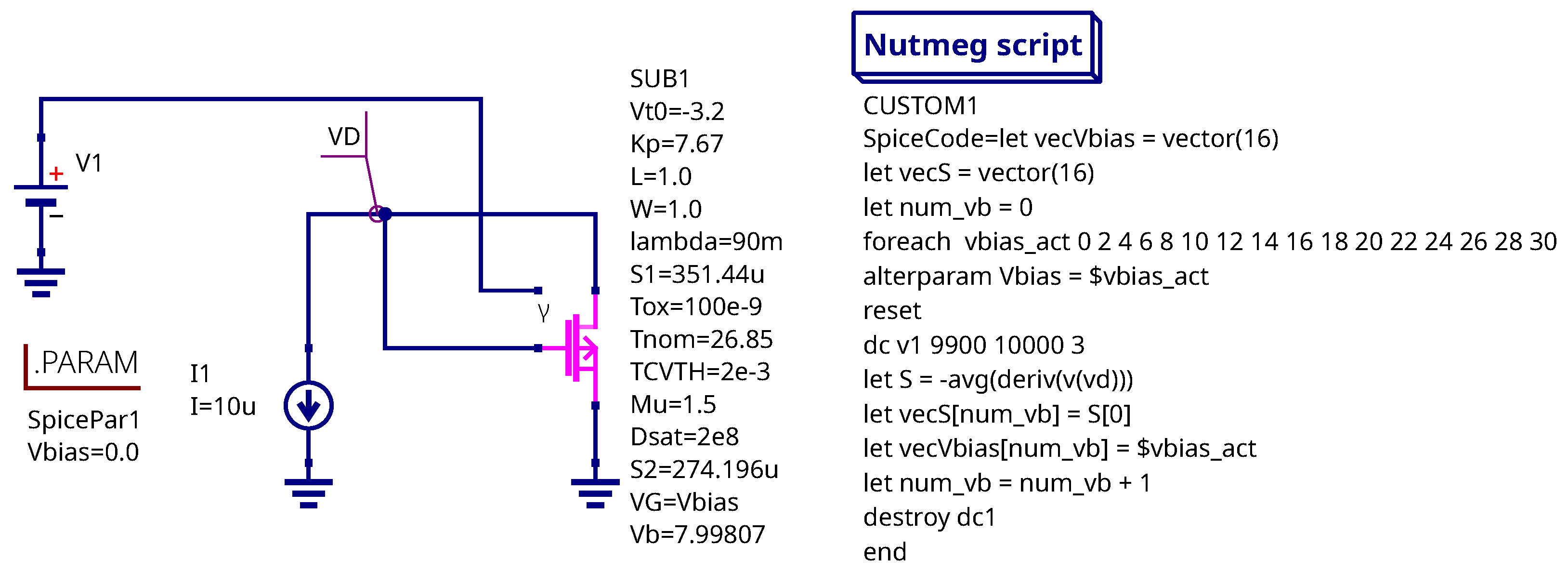
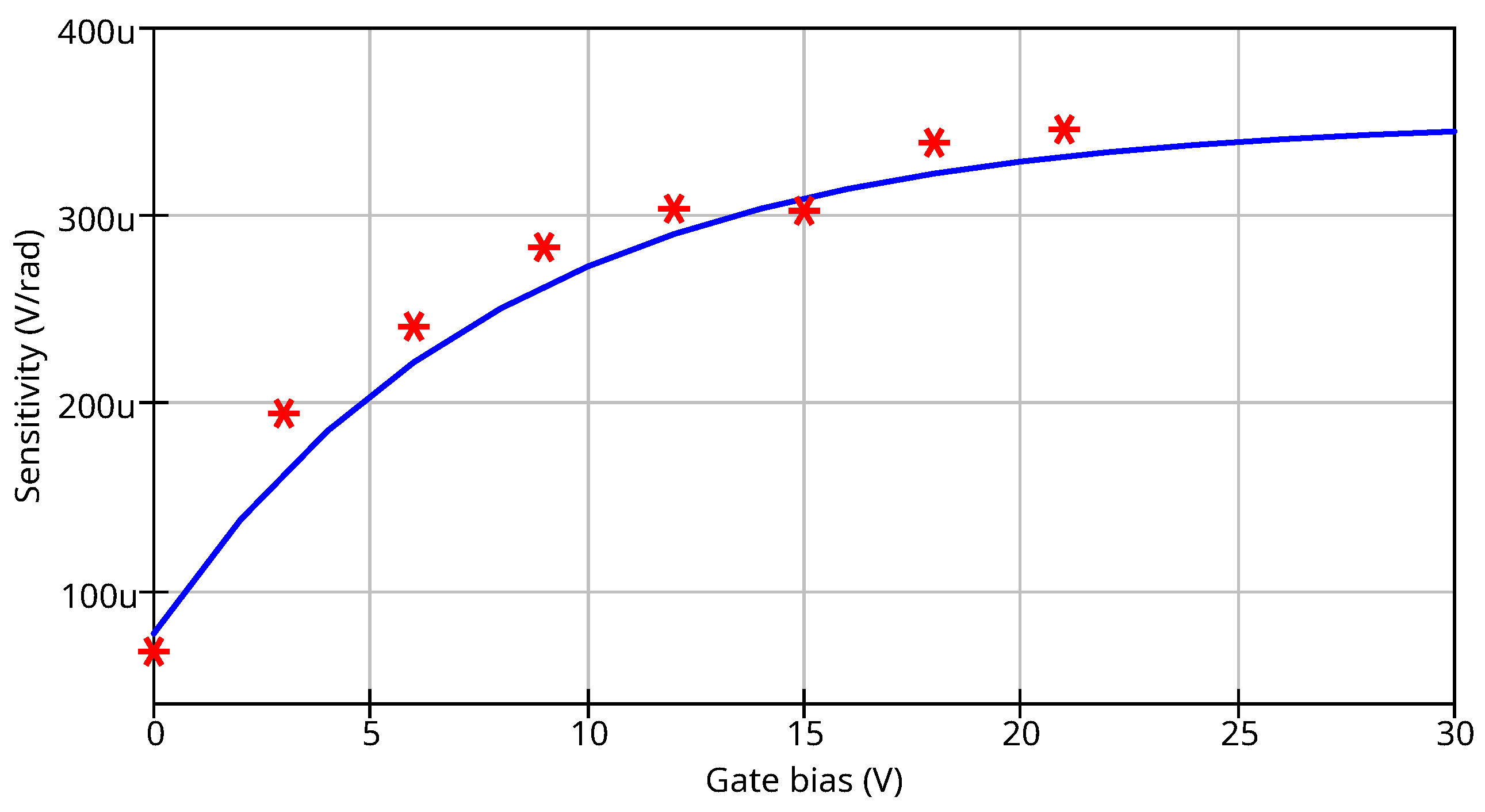
3.5. Gate Bias Dependency of Sensitivity
3.6. Gate Current Simulation
4. Discussion
5. Conclusions
- Basic MOSFET IV-curve dependency;
- Threshold voltage shift dependency on the adsorbed does and gate bias at the irradiation phase;
- Saturation at high absorbed dose;
- Gate dielectric properties;
- Tunneling gate current and irradiation gate current;
- Threshold voltage fading after the irradiation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Holmes -Siedle, A.; Adams, L. RADFET: A review of the use of metal-oxide-silicon devices as integrating dosimeters. Int. J. Radiat. Appl. Instrum. Part C Radiat. Phys. Chem. 1986, 28, 235–244. [Google Scholar] [CrossRef]
- Kulhar, M.; Dhoot, K.; Pandya, A. Gamma Dose Rate Measurement Using RadFET. IEEE Trans. Nucl. Sci. 2019, 66, 2220–2228. [Google Scholar] [CrossRef]
- Camanzi, B.; Holmes-Siedle, A.G. The race for new radiation monitors. Nat. Mater. 2008, 7, 343–345. [Google Scholar] [CrossRef]
- Ristić, G.S.; Ilić, S.D.; Veljković, S.; Jevtić, A.S.; Dimitrijević, S.; Palma, A.J.; Stanković, S.; Andjelković, M.S. Commercial P-Channel Power VDMOSFET as X-ray Dosimeter. Electronics 2022, 11, 918. [Google Scholar] [CrossRef]
- Assaf, J. Characterization of Commercial P-MOSFETs for Using as a Gamma-Rays Dosimeter. Silicon 2022, 14, 1767–1774. [Google Scholar] [CrossRef]
- Pejovic, M.M. Application of p-Channel Power VDMOSFET as a High Radiation Doses Sensor. IEEE Trans. Nucl. Sci. 2015, 62, 1905–1910. [Google Scholar] [CrossRef]
- Andjelković, M.S.; Ristić, G.S.; Jakšić, A.B. Using RADFET for the real-time measurement of gamma radiation dose rate. Meas. Sci. Technol. 2015, 26, 025004. [Google Scholar] [CrossRef]
- Veljković, S.; Mitrović, N.; Davidović, V.; Golubović, S.; Djorić-Veljković, S.; Paskaleva, A.; Spassov, D.; Stanković, S.; Andjelković, M.; Prijić, Z.; et al. Response of Commercial P-Channel Power VDMOS Transistors to Ionizing Irradiation and Bias Temperature Stress. J. Circuits Syst. Comput. 2022, 31, 2240003. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, T.; Liu, Z.; Xu, J. Investigation of irradiation effects and model parameter extraction for VDMOS field effect transistor exposed to gamma rays. Radiat. Phys. Chem. 2021, 185, 109478. [Google Scholar] [CrossRef]
- Ravotti, F. Dosimetry Techniques and Radiation Test Facilities for Total Ionizing Dose Testing. IEEE Trans. Nucl. Sci. 2018, 65, 1440–1464. [Google Scholar] [CrossRef]
- Siebel, O.; Pereira, J.; Souza, R.; Ramirez-Fernandez, F.; Schneider, M.; Galup-Montoro, C. A very-low-cost dosimeter based on the off-the-shelf CD4007 MOSFET array for in vivo radiotherapy applications. Radiat. Meas. 2015, 75, 53–63. [Google Scholar] [CrossRef]
- Ristić, G.S.; Vasović, N.D.; Kovačević, M.; Jakšić, A.B. The sensitivity of 100nm RADFETs with zero gate bias up to dose of 230Gy(Si). Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2011, 269, 2703–2708. [Google Scholar] [CrossRef]
- Pejović, M.M.; Pejović, S.M. VDMOSFET as a prospective dosimeter for radiotherapy. Appl. Radiat. Isot. 2018, 132, 1–5. [Google Scholar] [CrossRef]
- Ristic, G.S.; Ilic, S.D.; Andjelkovic, M.S.; Duane, R.; Palma, A.J.; Lalena, A.M.; Krstic, M.D.; Jaksic, A.B. Sensitivity and fading of irradiated RADFETs with different gate voltages. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2022, 1029, 166473. [Google Scholar] [CrossRef]
- Schwank, J.R.; Shaneyfelt, M.R.; Fleetwood, D.M.; Felix, J.A.; Dodd, P.E.; Paillet, P.; Ferlet-Cavrois, V. Radiation Effects in MOS Oxides. IEEE Trans. Nucl. Sci. 2008, 55, 1833–1853. [Google Scholar] [CrossRef]
- Oldham, T.; McLean, F. Total ionizing dose effects in MOS oxides and devices. IEEE Trans. Nucl. Sci. 2003, 50, 483–499. [Google Scholar] [CrossRef]
- Lipovetzky, J.; Holmes Siedle, A.; Garcia Inza, M.; Carbonetto, S.; Redin, E.; Faigon, A. New Fowler-Nordheim Injection, Charge Neutralization, and Gamma Tests on the REM RFT300 RADFET Dosimeter. IEEE Trans. Nucl. Sci. 2012, 59, 3133–3140. [Google Scholar] [CrossRef]
- Andreev, D.V.; Andreev, V.V.; Konuhova, M.; Popov, A.I. Technique of High-Field Electron Injection for Wafer-Level Testing of Gate Dielectrics of MIS Devices. Technologies 2024, 12, 102. [Google Scholar] [CrossRef]
- Peng, L.; Hu, D.; Jia, Y.; Wu, Y.; An, P.; Jia, G. Analysis on the Rapid Recovery of Irradiated VDMOSFETs by the Positive High Electric Field Stress. IEEE Trans. Nucl. Sci. 2017, 64, 2633–2638. [Google Scholar] [CrossRef]
- Andreev, D.V.; Bondarenko, G.G.; Andreev, V.V. Change in the Charge State of MOS Structures with a Radiation-Induced Charge under High-Field Injection of Electrons. J. Surf. Investig. X-Ray Synchrotron Neutron Tech. 2023, 17, 48–53. [Google Scholar] [CrossRef]
- Andreev, D.V.; Bondarenko, G.G.; Andreev, V.V.; Stolyarov, A.A. Use of High-Field Electron Injection into Dielectrics to Enhance Functional Capabilities of Radiation MOS Sensors. Sensors 2020, 20, 2382. [Google Scholar] [CrossRef] [PubMed]
- Andreev, V.V.; Bondarenko, G.G.; Andreev, D.V.; Stolyarov, A.A. Use of MIS Sensors of Radiation in High-Field Electron Injection Modes. J. Contemp. Phys. (Armenian Acad. Sci.) 2020, 55, 144–150. [Google Scholar] [CrossRef]
- Andreev, V.V.; Maslovsky, V.M.; Andreev, D.V.; Stolyarov, A.A. Charge effects in dielectric films of MIS structures being under high-field injection of electrons at ionizing radiation. In Proceedings of the International Conference on Micro- and Nano-Electronics 2018, Zvenigorod, Russia, 1–5 October 2018; Lukichev, V.F., Rudenko, K.V., Eds.; International Society for Optics and Photonics (SPIE): Bellingham, WA, USA, 2019; Volume 11022, p. 1102207. [Google Scholar] [CrossRef]
- Mitrović, N.; Guirado, D.; Danković, D.; Palma, A.J.; Ristić, G.; Carvajal, M.A. Thermal Annealing-Induced Recovery of the VT of Irradiated Commercial MOS Transistors. J. Circuits Syst. Comput. 2025, 34, 2541002. [Google Scholar] [CrossRef]
- Vladirmirescu, A. Shaping the History of SPICE. IEEE Solid-State Circuits Mag. 2011, 3, 36–39. [Google Scholar] [CrossRef]
- De Graaff, H.C.; Kloosterman, W.J.; Versleyen, M. Compact Modelling for Analoge Circuit Design. In Proceedings of the ESPRIT ’90, Brussels, Belgium, 12–15 November 1990; pp. 65–76. [Google Scholar]
- Oh, J.H.; Yu, Y.S. Macro-Modeling for N-Type Feedback Field-Effect Transistor for Circuit Simulation. Micromachines 2021, 12, 1174. [Google Scholar] [CrossRef]
- Ji, S.; Mappes, J.; Koudelka, P.; Scardelletti, M.C.; Zorman, C.; Lavasani, H.M. An Enhanced Verilog-A Model for Graphene Field-Effect Transistors Using Variable Fermi Velocity. Electronics 2024, 13, 5051. [Google Scholar] [CrossRef]
- Kasprowicz, D. Table-Based Model of a Dual-Gate Transistor for Statistical Circuit Simulation. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2019, 38, 1493–1500. [Google Scholar] [CrossRef]
- Kuznetsov, V. Microstrip Line Modeling Taking into Account Dispersion Using a General-Purpose SPICE Simulator. J. Low Power Electron. Appl. 2025, 15, 42. [Google Scholar] [CrossRef]
- Marjanović, M.; Ilić, S.D.; Veljković, S.; Mitrović, N.; Gurer, U.; Yilmaz, O.; Kahraman, A.; Aktag, A.; Karacali, H.; Budak, E.; et al. The SPICE Modeling of a Radiation Sensor Based on a MOSFET with a Dielectric HfO2/SiO2 Double-Layer. Sensors 2025, 25, 546. [Google Scholar] [CrossRef]
- Mrozovskaya, E.; Zimin, P.; Chubunov, P.; Zebrev, G. Compact modeling of electrical characteristics of p-MNOS based RADFETs. In Proceedings of the International Conference on Micro- and Nano-Electronics 2018, Zvenigorod, Russia, 1–5 October 2018; Lukichev, V.F., Rudenko, K.V., Eds.; International Society for Optics and Photonics (SPIE): Bellingham, WA, USA, 2019; Volume 11022, p. 110220I. [Google Scholar] [CrossRef]
- Meguellati, M.; Djeffal, F. New Dual-Dielectric Gate All Around (DDGAA) RADFET dosimeter design to improve the radiation sensitivity. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2012, 683, 24–28. [Google Scholar] [CrossRef]
- Andreev, D.V.; Maslovsky, V.M.; Andreev, V.V.; Stolyarov, A.A. Modified Ramped Current Stress Technique for Monitoring Thin Dielectrics Reliability and Charge Degradation. Phys. Status Solidi A 2022, 219, 2100400. [Google Scholar] [CrossRef]
- Fleetwood, D.M. Perspective on radiation effects in nanoscale metal–oxide–semiconductor devices. Appl. Phys. Lett. 2022, 121, 070503. [Google Scholar] [CrossRef]
- Brinson, M.; Kuznetsov, V. Qucs-0.0.19S: A new open-source circuit simulator and its application for hardware design. In Proceedings of the 2016 International Siberian Conference on Control and Communications (SIBCON), Moscow, Russia, 12–14 May 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Grabinski, W.; Scholz, R.; Verley, J.; Keiter, E.R.; Vogt, H.; Warning, D.; Nenzi, P.; Lannutti, F.; Salfelder, F.; Davis, A.; et al. FOSS CAD for the Compact Verilog-A Model Standardization in Open Access PDKs. In Proceedings of the 2024 8th IEEE Electron Devices Technology & Manufacturing Conference (EDTM), Bangalore, India, 3–6 March 2024; pp. 1–3. [Google Scholar] [CrossRef]
- Lannutti, F.; Nenzi, P.; Olivieri, M. KLU sparse direct linear solver implementation into NGSPICE. In Proceedings of the 19th International Conference Mixed Design of Integrated Circuits and Systems—MIXDES 2012, Warsaw, Poland, 24–26 May 2012; pp. 69–73. [Google Scholar]
- Kuthe, P.; Müller, M.; Schröter, M. VerilogAE: An Open Source Verilog-A Compiler for Compact Model Parameter Extraction. IEEE J. Electron Devices Soc. 2020, 8, 1416–1423. [Google Scholar] [CrossRef]
- Chauhan, Y.S.; Venugopalan, S.; Paydavosi, N.; Kushwaha, P.; Jandhyala, S.; Duarte, J.P.; Agnihotri, S.; Yadav, C.; Agarwal, H.; Niknejad, A.; et al. BSIM compact MOSFET models for SPICE simulation. In Proceedings of the 20th International Conference Mixed Design of Integrated Circuits and Systems—MIXDES 2013, Gdynia, Poland, 20–22 June 2013; pp. 23–28. [Google Scholar]
- Ristic, G.S.; Ilic, S.D.; Duane, R.; Andjelkovic, M.S.; Palma, A.J.; Lallena, A.M.; Krstic, M.D.; Stankovic, S.J.; Jaksic, A.B. Radiation sensitive MOSFETs irradiated with various positive gate biases. J. Radiat. Res. Appl. Sci. 2021, 14, 353–357. [Google Scholar] [CrossRef]
- Pejović, M.M. Dose response, radiation sensitivity and signal fading of p-channel MOSFETs (RADFETs) irradiated up to 50Gy with 60Co. Appl. Radiat. Isot. 2015, 104, 100–105. [Google Scholar] [CrossRef]
- Vasović, N.D.; Ristić, G.S. A new microcontroller-based RADFET dosimeter reader. Radiat. Meas. 2012, 47, 272–276. [Google Scholar] [CrossRef]






| Radiation Source | (MV/cm) | |
|---|---|---|
| Co60 -ray | 0.6 | 1.5 |
| 10 keV X-ray | 0.8 | 3.0 |
| 700 keV protons | 0.4 | 4.0 |
| 2 MeV particles | 0.16 | 3.0 |
| Model Parameter | Default Value | Unit | Description |
|---|---|---|---|
| −1.0 | V | Threshold voltage at no radiation | |
| A/V2 | Transconductance coefficient | ||
| 1/V | Channel modulation | ||
| L | 1.0 | m | Device length |
| W | 1.0 | m | Device width |
| m | Gate dielectric thickness | ||
| 3.9 | – | Gate dielectric relative permittivity | |
| 1 | V/K | Threshold voltage temperature coefficient | |
| 1.5 | – | Transconductance temperature coefficient | |
| 0.0015 | V/rad | Linear sensitivity component | |
| 0.0 | V | Exponential sensitivity | |
| 3.0 | V | Exponential sensitivity fitting coefficient | |
| 0.0 | V | Gate bias at the irradiation time | |
| rad | Saturation dose | ||
| 26.85 | °C | temperature at which device parameters were measured | |
| 1 | V/rad | Unit scale for the radiation input |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuznetsov, V.; Andreev, D.; Andreev, V.; Piskunov, S.; Popov, A.I. The Compact Model Synthesis for the RADFET Device. Technologies 2025, 13, 492. https://doi.org/10.3390/technologies13110492
Kuznetsov V, Andreev D, Andreev V, Piskunov S, Popov AI. The Compact Model Synthesis for the RADFET Device. Technologies. 2025; 13(11):492. https://doi.org/10.3390/technologies13110492
Chicago/Turabian StyleKuznetsov, Vadim, Dmitrii Andreev, Vladimir Andreev, Sergei Piskunov, and Anatoli I. Popov. 2025. "The Compact Model Synthesis for the RADFET Device" Technologies 13, no. 11: 492. https://doi.org/10.3390/technologies13110492
APA StyleKuznetsov, V., Andreev, D., Andreev, V., Piskunov, S., & Popov, A. I. (2025). The Compact Model Synthesis for the RADFET Device. Technologies, 13(11), 492. https://doi.org/10.3390/technologies13110492








