Prediction of Battery Electric Vehicle Energy Consumption via Pre-Trained Model Under Inconsistent Feature Spaces
Abstract
1. Introduction
- A universal model for BEV trip energy consumption prediction, the IFS-Former, was developed and trained, achieving higher accuracy than vehicle-specific models.
- Feature missing was introduced in large-scale datasets during pre-training to enable the IFS-Former to adapt to inconsistent vehicle feature spaces.
- The robust strength of the IFS-Former under extremely inconsistent feature spaces was demonstrated through feature ablation experiments.
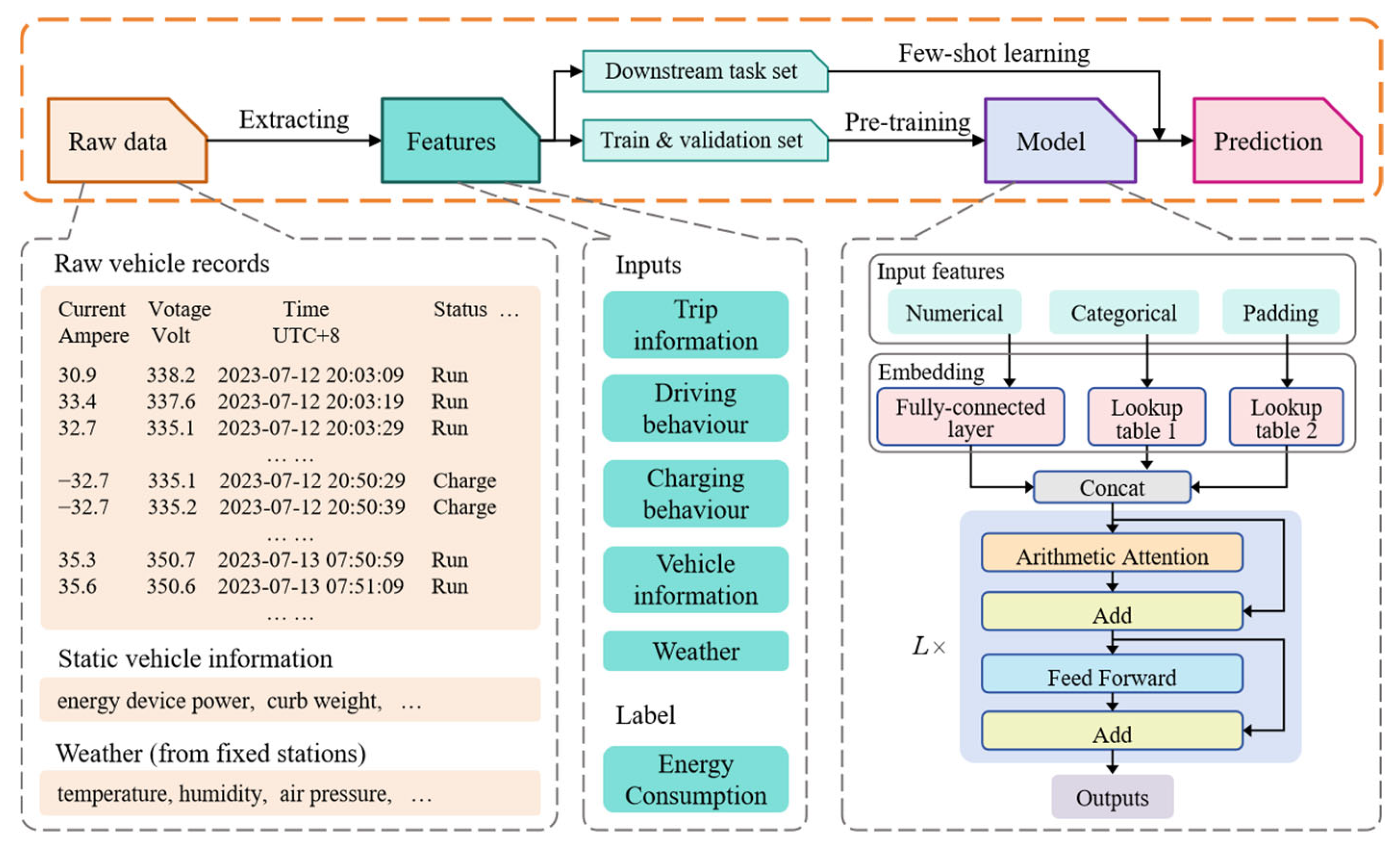
2. Scenarios and Data
2.1. Data Description and Pre-Processing
2.2. Trip Extraction
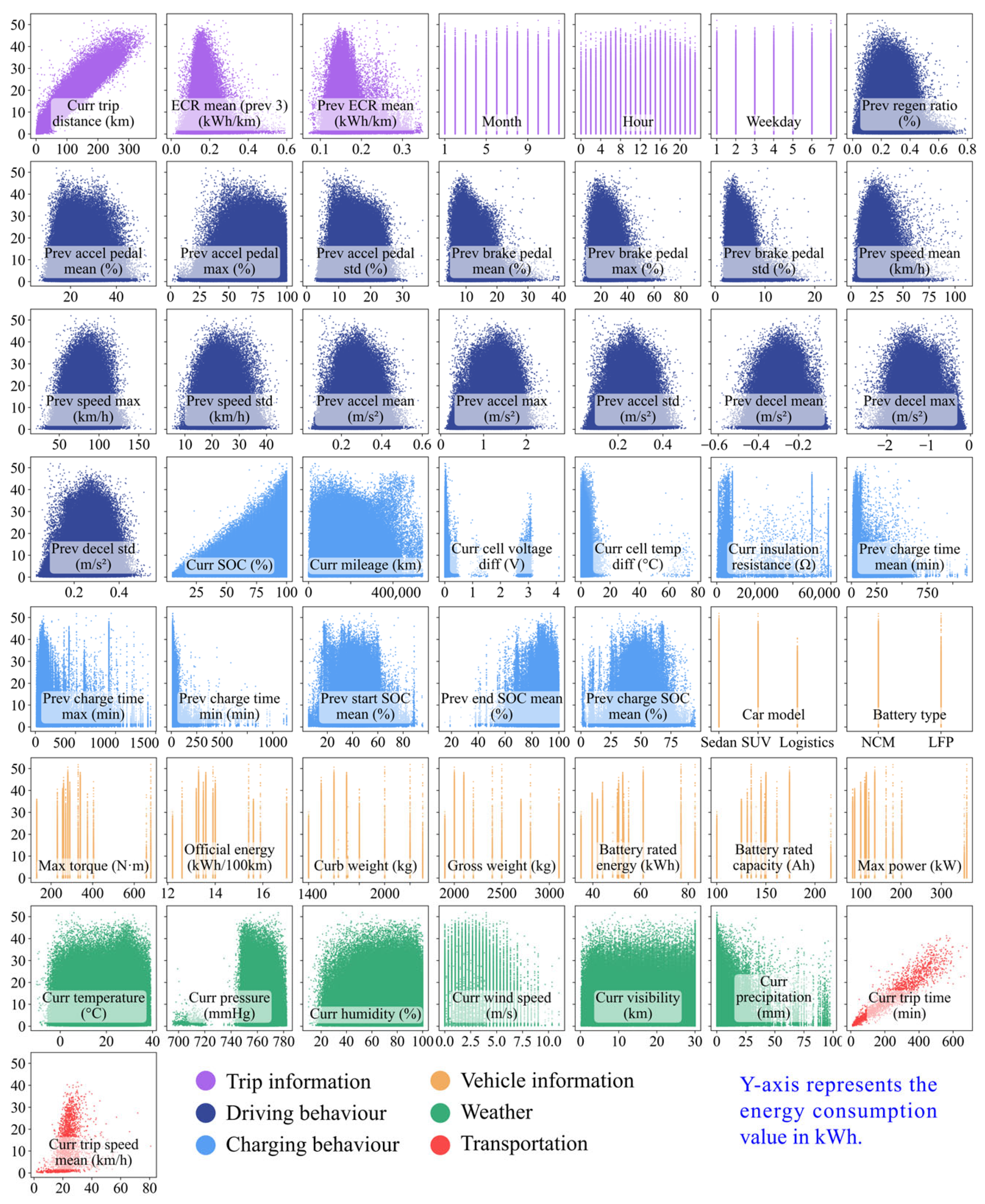
2.3. Feature Construction
3. Methodologies
3.1. The Transformer Architecture for Inconsistent Feature Spaces
3.2. The Loss Function
3.3. Settings for Numerical Experiments
3.3.1. Pre-Training and Transfer Learning
3.3.2. Baseline Models
3.3.3. Evaluation Metrics
4. Results and Discussion
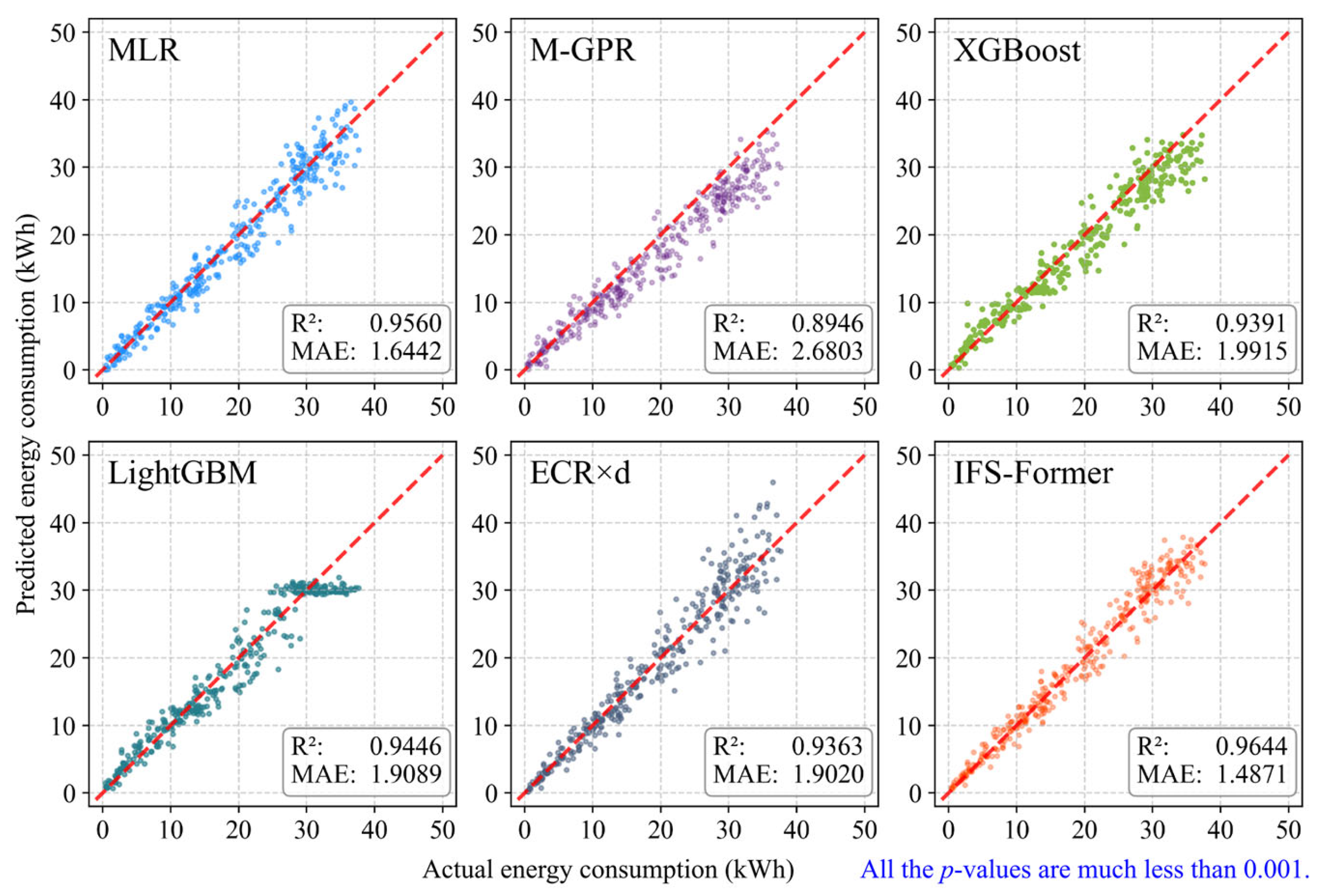
4.1. Accuracy of Downstream Tasks
4.2. Ablation Analysis of Features
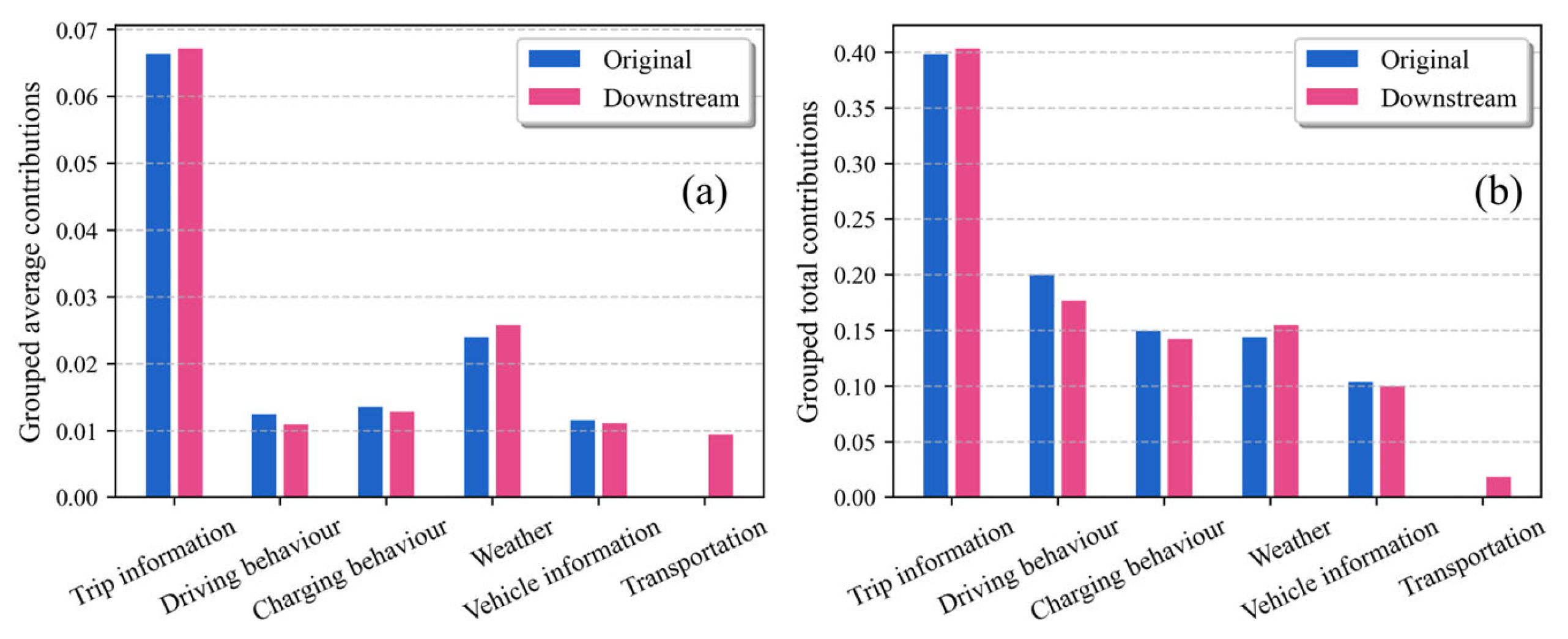
4.3. Efficiency and Interpretability of the Model
5. Conclusions
- The proposed pre-trained IFS-Former model demonstrates superior performance over baseline models in BEV energy consumption prediction. After extensive pre-training, the IFS-Former achieves high accuracy on downstream tasks even without few-short learning (zero-shot, R2 = 0.97, Bias = −0.07, MAE = 1.19), and its performance further improves with few-shot learning (384-shot, Bias decreasing by 15.42%), and the MAE of the baseline models increases by 18.62% to 157.47% compared to the IFS-Former under the same setting.
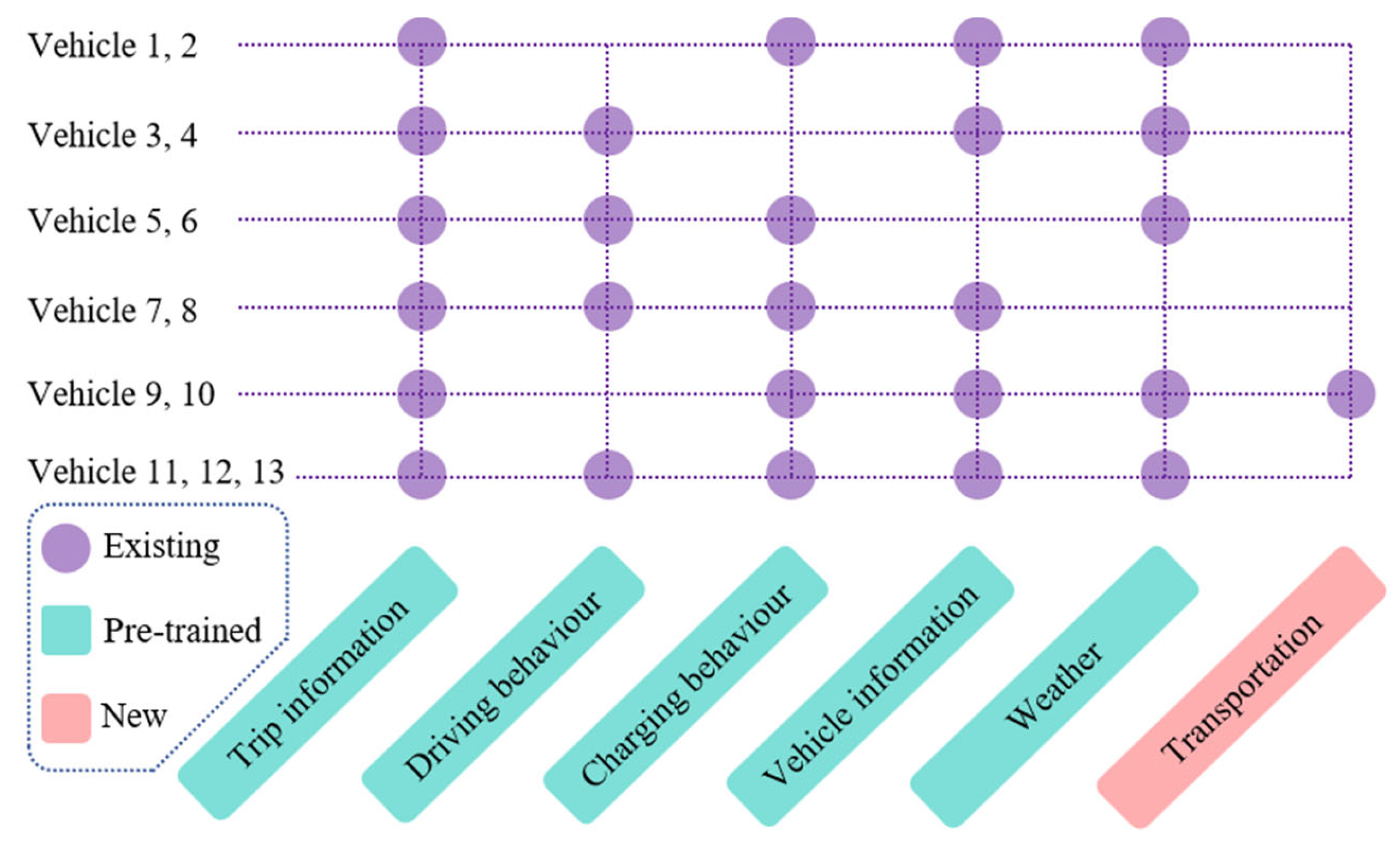
- Large-scale pre-training is leveraged to address inconsistent feature spaces in downstream tasks. Trainable missing-feature embeddings are introduced to enable the IFS-Former to handle feature missing scenarios. Moreover, artificially induced feature missing is incorporated into the pre-training data to help the IFS-Former learn effective strategies for dealing with missing features. Results of downstream tasks indicate that the IFS-Former retains strong performance under feature-missing scenarios (in the case of Figure 5, baseline models experience an increase in MAE ranging from 10.56% to 80.23%).
- The IFS-Former exhibits robustness under highly inconsistent downstream feature spaces. Feature ablation experiments reveal that, although the IFS-Former performance gradually declines as features are reduced (the MAE increases of 9.91%), it consistently surpasses baseline models with the same feature spaces (in the 384-shot setting, baseline models experience an increase in MAE ranging from 7.94% to 95.05%). This demonstrates the pre-training process successfully enables the IFS-Former to learn strategies for handling missing features.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, H.; He, H.; Peng, Z. Urban-Scale Estimation Model of Carbon Emissions for Ride-Hailing Electric Vehicles during Operational Phase. Energy 2024, 293, 130665. [Google Scholar] [CrossRef]
- Koroma, M.S.; Costa, D.; Philippot, M.; Cardellini, G.; Hosen, M.S.; Coosemans, T.; Messagie, M. Life Cycle Assessment of Battery Electric Vehicles: Implications of Future Electricity Mix and Different Battery End-of-Life Management. Sci. Total Environ. 2022, 831, 154859. [Google Scholar] [CrossRef]
- Ntombela, M.; Musasa, K.; Moloi, K. A Comprehensive Review for Battery Electric Vehicles (BEV) Drive Circuits Technology, Operations, and Challenges. WEVJ 2023, 14, 195. [Google Scholar] [CrossRef]
- Bin Ahmad, M.S.; Pesyridis, A.; Sphicas, P.; Mahmoudzadeh Andwari, A.; Gharehghani, A.; Vaglieco, B.M. Electric Vehicle Modelling for Future Technology and Market Penetration Analysis. Front. Mech. Eng. 2022, 8, 896547. [Google Scholar] [CrossRef]
- International Energy Agency. Global EV Outlook 2024; International Energy Agency (IEA): Paris, France, 2024. [Google Scholar]
- Huang, H.; Li, B.; Wang, Y.; Zhang, Z.; He, H. Analysis of Factors Influencing Energy Consumption of Electric Vehicles: Statistical, Predictive, and Causal Perspectives. Appl. Energy 2024, 375, 124110. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, R. Studying Battery Range and Range Anxiety for Electric Vehicles Based on Real Travel Demands. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting, Online, 25–28 October 2021; Volume 65, pp. 332–336. [Google Scholar]
- Petersen, P.; Sax, E. A Fully Automated Methodology for the Selection and Extraction of Energy-Relevant Features for the Energy Consumption of Battery Electric Vehicles. SN Comput. Sci. 2022, 3, 342. [Google Scholar] [CrossRef]
- Enthaler, A.; Gauterin, F. Method for Reducing Uncertainties of Predictive Range Estimation Algorithms in Electric Vehicles. In Proceedings of the 2015 IEEE 82nd Vehicular Technology Conference (VTC2015-Fall), Boston, MA, USA, 6–9 September 2015; IEEE: Boston, MA, USA, 2015; pp. 1–5. [Google Scholar]
- Miri, I.; Fotouhi, A.; Ewin, N. Electric Vehicle Energy Consumption Modelling and Estimation—A Case Study. Int. J. Energy Res. 2021, 45, 501–520. [Google Scholar] [CrossRef]
- Hussain, I.; Ching, K.B.; Uttraphan, C.; Tay, K.G.; Noor, A.; Memon, S.A. Optimizing Electric Vehicle Energy Consumption Prediction through Machine Learning and Ensemble Approaches. Sci. Rep. 2025, 15, 29065. [Google Scholar] [CrossRef]
- Zhu, Q.; Huang, Y.; Feng Lee, C.; Liu, P.; Zhang, J.; Wik, T. Predicting Electric Vehicle Energy Consumption From Field Data Using Machine Learning. IEEE Trans. Transp. Electrific. 2025, 11, 2120–2132. [Google Scholar] [CrossRef]
- Qi, X.; Wu, G.; Boriboonsomsin, K.; Barth, M.J. Data-Driven Decomposition Analysis and Estimation of Link-Level Electric Vehicle Energy Consumption under Real-World Traffic Conditions. Transp. Res. Part D Transp. Environ. 2018, 64, 36–52. [Google Scholar] [CrossRef]
- Yılmaz, H.; Yagmahan, B. Electric Vehicle Energy Consumption Prediction for Unknown Route Types Using Deep Neural Networks by Combining Static and Dynamic Data. Appl. Soft Comput. 2024, 167, 112336. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: San Francisco, CA, USA, 2016; pp. 785–794. [Google Scholar]
- Vapnik, V.; Golowich, S.E.; Smola, A. Support Vector Method for Function Approximation, Regression Estimation and Signal Processing. In Proceedings of the 10th International Conference on Neural Information Processing Systems, Denver, CO, USA, 3–5 December 1996; MIT Press: Cambridge, MA, USA, 1996; pp. 281–287. [Google Scholar]
- Pokharel, S.; Sah, P.; Ganta, D. Improved Prediction of Total Energy Consumption and Feature Analysis in Electric Vehicles Using Machine Learning and Shapley Additive Explanations Method. WEVJ 2021, 12, 94. [Google Scholar] [CrossRef]
- Liu, R.; Cai, J.; Hu, L.; Lou, B.; Tang, J. Electric Bus Battery Energy Consumption Estimation and Influencing Features Analysis Using a Two-Layer Stacking Framework with SHAP-Based Interpretation. Sustainability 2025, 17, 7105. [Google Scholar] [CrossRef]
- Huang, H.; Gao, K.; Wang, Y.; Najafi, A.; Zhang, Z.; He, H. Sequence-Aware Energy Consumption Prediction for Electric Vehicles Using Pre-Trip Realistically Accessible Data. Appl. Energy 2025, 401, 126673. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 6000–6010. [Google Scholar]
- CV, M.S.; Amal, M.K.; Satheesh, R.; Alhelou, H.H. Enhanced Electric Vehicle Energy Consumption Prediction With TabTransformer, TabNet, and Bidirectional Encoder Representations From Transformers Embeddings. IEEE Trans. Ind. Inf. 2025, 21, 7445–7454. [Google Scholar] [CrossRef]
- Feng, Z.; Zhang, J.; Jiang, H.; Yao, X.; Qian, Y.; Zhang, H. Energy Consumption Prediction Strategy for Electric Vehicle Based on LSTM-Transformer Framework. Energy 2024, 302, 131780. [Google Scholar] [CrossRef]
- Huang, H.; He, H.; Wang, Y.; Zhang, Z.; Wang, T. Energy Consumption Prediction of Electric Vehicles for Data-Scarce Scenarios Using Pre-Trained Model. Transp. Res. Part D Transp. Environ. 2025, 146, 104830. [Google Scholar] [CrossRef]
- Ma, Y.; Sun, W.; Zhao, Z.; Gu, L.; Zhang, H.; Jin, Y.; Yuan, X. Physically Rational Data Augmentation for Energy Consumption Estimation of Electric Vehicles. Appl. Energy 2024, 373, 123871. [Google Scholar] [CrossRef]
- Adnane, M.; Khoumsi, A.; Trovão, J.P.F. Efficient Management of Energy Consumption of Electric Vehicles Using Machine Learning—A Systematic and Comprehensive Survey. Energies 2023, 16, 4897. [Google Scholar] [CrossRef]
- Thorgeirsson, A.T.; Scheubner, S.; Funfgeld, S.; Gauterin, F. Probabilistic Prediction of Energy Demand and Driving Range for Electric Vehicles With Federated Learning. IEEE Open J. Veh. Technol. 2021, 2, 151–161. [Google Scholar] [CrossRef]
- Tseng, C.-M.; Chau, C.-K. Personalized Prediction of Vehicle Energy Consumption Based on Participatory Sensing. IEEE Trans. Intell. Transport. Syst. 2017, 18, 3103–3113. [Google Scholar] [CrossRef]
- Zhao, Y.; Geng, L.; Shan, S.; Du, Z.; Hu, X.; Wei, X. Review of Sensor Fault Diagnosis and Fault-Tolerant Control Techniques of Lithium-Ion Batteries for Electric Vehicles. J. Traffic Transp. Eng. (Engl. Ed.) 2024, 11, 1447–1466. [Google Scholar] [CrossRef]
- Amirkhani, A.; Haghanifar, A.; Mosavi, M.R. Electric Vehicles Driving Range and Energy Consumption Investigation: A Comparative Study of Machine Learning Techniques. In Proceedings of the 2019 5th Iranian Conference on Signal Processing and Intelligent Systems (ICSPIS), Shahrood, Iran, 18–19 December 2019; IEEE: Shahrood, Iran, 2019; pp. 1–6. [Google Scholar]
- Solano, J.; Sanni, M.; Camburu, O.-M.; Minervini, P. SparseFit: Few-Shot Prompting with Sparse Fine-Tuning for Jointly Generating Predictions and Natural Language Explanations. In Proceedings of the 62nd Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Bangkok, Thailand, 11–16 August 2024; Association for Computational Linguistics: Bangkok, Thailand, 2024; pp. 2053–2077. [Google Scholar]
- Park, K.-H.; Song, K.; Park, G.-M. Pre-Trained Vision and Language Transformers Are Few-Shot Incremental Learners. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16 June 2024; IEEE: Seattle, WA, USA, 2024; pp. 23881–23890. [Google Scholar]
- Fukushima, A.; Yano, T.; Imahara, S.; Aisu, H.; Shimokawa, Y.; Shibata, Y. Prediction of Energy Consumption for New Electric Vehicle Models by Machine Learning. IET Intell. Trans. Sys. 2018, 12, 1174–1180. [Google Scholar] [CrossRef]
- Čivilis, A.; Petkevičius, L.; Šaltenis, S.; Torp, K.; Markucevičiūtė-Vinckė, I. Few-Shot Learning for Triplet-Based EV Energy Consumption Estimation. Appl. Artif. Intell. 2025, 39, 2474785. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16x16 Words: Transformers for Image Recognition at Scale. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 3–7 May 2021. [Google Scholar]
- Aroca-Ouellette, S.; Mackraz, N.; Theobald, B.-J.; Metcalf, K. Aligning LLMs by Predicting Preferences from User Writing Samples. In Proceedings of the Forty-second International Conference on Machine Learning, Vancouver, BC, Canada, 13–19 July 2025. [Google Scholar]
- Zheng, S.; Lu, J.; Zhao, H.; Zhu, X.; Luo, Z.; Wang, Y.; Fu, Y.; Feng, J.; Xiang, T.; Torr, P.H.S.; et al. Rethinking Semantic Segmentation from a Sequence-to-Sequence Perspective with Transformers. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, 19–25 June 2021; IEEE: Nashville, TN, USA, 2021; pp. 6877–6886. [Google Scholar]
- Hollmann, N.; Müller, S.; Purucker, L.; Krishnakumar, A.; Körfer, M.; Hoo, S.B.; Schirrmeister, R.T.; Hutter, F. Accurate Predictions on Small Data with a Tabular Foundation Model. Nature 2025, 637, 319–326. [Google Scholar] [CrossRef]
- Gorishniy, Y.; Rubachev, I.; Khrulkov, V.; Babenko, A. Revisiting Deep Learning Models for Tabular Data. In Proceedings of the 35th International Conference on Neural Information Processing Systems, Virtual, 6–14 December 2021; Curran Associates Inc.: Red Hook, NY, USA, 2021; pp. 18932–18943. [Google Scholar]
- Cheng, Y.; Hu, R.; Ying, H.; Shi, X.; Wu, J.; Lin, W. Arithmetic Feature Interaction Is Necessary for Deep Tabular Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Stanford, CA, USA, 25–27 March 2024; Volume 38, pp. 11516–11524. [Google Scholar]
- Na, K.; Lee, J.-H.; Kim, E. LF-Transformer: Latent Factorizer Transformer for Tabular Learning. IEEE Access 2024, 12, 10690–10698. [Google Scholar] [CrossRef]
- GB/T 32960-2016; Technical Specifications for Remote Service and Management System for Electric Vehicles. Standards Press of China: Beijing, China, 2016.
- Zhao, Y.; Wang, Z.; Shen, Z.-J.M.; Sun, F. Assessment of Battery Utilization and Energy Consumption in the Large-Scale Development of Urban Electric Vehicles. Proc. Natl. Acad. Sci. USA 2021, 118, e2017318118. [Google Scholar] [CrossRef]
- Al-Wreikat, Y.; Serrano, C.; Sodré, J.R. Driving Behaviour and Trip Condition Effects on the Energy Consumption of an Electric Vehicle under Real-World Driving. Appl. Energy 2021, 297, 117096. [Google Scholar] [CrossRef]
- Janpoom, K.; Suttakul, P.; Achariyaviriya, W.; Fongsamootr, T.; Katongtung, T.; Tippayawong, N. Investigating the Influential Factors in Real-World Energy Consumption of Battery Electric Vehicles. Energy Rep. 2023, 9, 316–320. [Google Scholar] [CrossRef]
- He, Z.; Ni, X.; Pan, C.; Hu, S.; Han, S. Full-Process Electric Vehicles Battery State of Health Estimation Based on Informer Novel Model. J. Energy Storage 2023, 72, 108626. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, L.; Ou, Y.; Wang, Y.; Wang, S.; Yu, J.; Feng, R. A Comparative Study on the Energy Flow of Electric Vehicle Batteries among Different Environmental Temperatures. Energies 2023, 16, 5253. [Google Scholar] [CrossRef]
- Parker, N.C.; Kuby, M.; Liu, J.; Stechel, E.B. Extreme Heat Effects on Electric Vehicle Energy Consumption and Driving Range. Appl. Energy 2025, 380, 125051. [Google Scholar] [CrossRef]
- Hebala, A.; Abdelkader, M.I.; Ibrahim, R.A. Comparative Analysis of Energy Consumption and Performance Metrics in Fuel Cell, Battery, and Hybrid Electric Vehicles Under Varying Wind and Road Conditions. Technologies 2025, 13, 150. [Google Scholar] [CrossRef]
- Dongmin, K.; HuiZhi, N.; Kitae, J. The Analysis of Traffic Variables for EV’s Driving Efficiency in Urban Traffic Condition. In Proceedings of the 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; IEEE: Macau, China, 2022; pp. 1994–2000. [Google Scholar]
- Wang, L.; Yang, Y.; Zhang, K.; Liu, Y.; Zhu, J.; Dang, D. Enhancing Electric Vehicle Energy Consumption Prediction: Integrating Elevation into Machine Learning Model. In Proceedings of the 2024 IEEE Intelligent Vehicles Symposium (IV), Jeju Island, Republic of Korea, 2 June 2024; IEEE: Jeju Island, Republic of Korea, 2024; pp. 2936–2941. [Google Scholar]
- Zhang, J.; Wang, Z.; Liu, P.; Zhang, Z. Energy Consumption Analysis and Prediction of Electric Vehicles Based on Real-World Driving Data. Appl. Energy 2020, 275, 115408. [Google Scholar] [CrossRef]
- Cui, Y.; Jia, M.; Lin, T.-Y.; Song, Y.; Belongie, S. Class-Balanced Loss Based on Effective Number of Samples. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9260–9269. [Google Scholar]
- Eisenmann, C.; Plötz, P. Two Methods of Estimating Long-Distance Driving to Understand Range Restrictions on EV Use. Transp. Res. Part D Transp. Environ. 2019, 74, 294–305. [Google Scholar] [CrossRef]
- Jiang, J.; Yu, Y.; Min, H.; Cao, Q.; Sun, W.; Zhang, Z.; Luo, C. Trip-Level Energy Consumption Prediction Model for Electric Bus Combining Markov-Based Speed Profile Generation and Gaussian Processing Regression. Energy 2023, 263, 125866. [Google Scholar] [CrossRef]
- Wang, Y.-Z.; He, H.-D.; Huang, H.-C.; Yang, J.-M.; Peng, Z.-R. High-Resolution Spatiotemporal Prediction of PM2.5 Concentration Based on Mobile Monitoring and Deep Learning. Environ. Pollut. 2025, 364, 125342. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Wallace, B.C. Attention Is Not Explanation. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, MN, USA, 2–7 June 2019; Burstein, J., Doran, C., Solorio, T., Eds.; Association for Computational Linguistics: Minneapolis, MN, USA, 2019; pp. 3543–3556. [Google Scholar]
- Chefer, H.; Gur, S.; Wolf, L. Transformer Interpretability Beyond Attention Visualization. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, 19–25 June 2021; pp. 782–791. [Google Scholar]


| Categories | Details | |||
|---|---|---|---|---|
| Real-time vehicle records | Collection time | City | Status (Run, Charge, Park) | |
| 13 July 2023 07:03:09 | Shanghai | Run | ||
| Sum mileage (km) | Sum votage (V) | Max battery single Temp (°C) | ||
| 92,735 | 338.2 | 26 | ||
| State of charge (%) | Sum current (A) | Min battery single Temp (°C) | ||
| 73 | 30.9 | 17 | ||
| Speed (km/h) | Accelerator pedal (%) | Max battery single voltage (V) | ||
| 53 | 36 | 4.1 | ||
| Insulation resistance (Ω) | Brake padel (%) | Min battery single voltage (V) | ||
| 6668 | 0 | 3.1 | ||
| Vehicle information | Max power (kW) | Max torque (N∙m) | Model (SUV, Sedan, Logistics) | |
| 220 | 465 | Sedan | ||
| Curb weight (kg) | Battery rated capacity (Ah) | Battery type (NCM, LFP) | ||
| 1850 | 150 | NCM | ||
| Gross weight (kg) | Battery rated energy (kWh) | Official energy (kWh/100 km) | ||
| 2350 | 75 | 13.5 | ||
| Weather | Time | Temperature (°C) | Pressure (mmHg) | Visibility (km) |
| 12 July 2023 23:00:00 | 27 | 760 | 15 | |
| Precipitation (mm) | Humidity (%) | Wind speed (m/s) | City | |
| 0 | 56 | 3 | Shanghai | |
| Category | Trip Distance (km) | Total Number | |
|---|---|---|---|
| Short trips | 0 ≤ d < 16 | 173,083 | 0.949 |
| Ordinary trips | 16 ≤ d < 100 | 237,252 | 0.692 |
| Long trips | d ≥ 100 | 82,499 | 1.991 |
| Method | Few-Shot | R2 | Bias | MAE | RMSE | MAPE |
|---|---|---|---|---|---|---|
| MLR | 384 | 0.8231 ± 0.2477 | 0.2438 ± 2.7070 | 2.9754 ± 1.5980 | 3.9616 ± 2.0100 | 0.6529 ± 0.6577 |
| M-GPR | 256 | 0.6454 ± 0.2451 | −1.1394 ± 3.6872 | 4.5983 ± 1.2714 | 5.9443 ± 1.9802 | 1.2655 ± 1.0998 |
| 384 | 0.8194 ± 0.2108 | −1.2605 ± 2.3911 | 3.0778 ± 1.4423 | 4.1931 ± 2.2244 | 0.6014 ± 0.3241 | |
| XG Boost | 32 | 0.8073 ± 0.1576 | −1.4693 ± 1.7727 | 3.0696 ± 1.5183 | 4.5203 ± 2.2154 | 0.3677 ± 0.2344 |
| 64 | 0.8426 ± 0.1882 | −1.2654 ± 1.6969 | 2.7848 ± 1.5559 | 4.0377 ± 2.3077 | 0.3541 ± 0.2569 | |
| 128 | 0.9009 ± 0.0617 | −0.5644 ± 1.1222 | 2.2085 ± 0.7212 | 3.3040 ± 1.1022 | 0.3009 ± 0.1239 | |
| 256 | 0.9033 ± 0.0646 | −0.4790 ± 1.0827 | 2.1605 ± 0.5501 | 3.2389 ± 0.9576 | 0.2936 ± 0.1112 | |
| 384 | 0.9315 ± 0.0250 | −0.7053 ± 0.7745 | 1.8895 ± 0.5167 | 2.8442 ± 0.7486 | 0.2168 ± 0.0492 | |
| Light GBM | 128 | 0.8506 ± 0.1224 | −0.4134 ± 1.7330 | 2.8047 ± 1.1791 | 3.9648 ± 1.5878 | 0.4680 ± 0.3204 |
| 256 | 0.9195 ± 0.0430 | −0.2591 ± 1.0165 | 2.0809 ± 0.6086 | 3.0246 ± 0.8921 | 0.2917 ± 0.1002 | |
| 384 | 0.9331 ± 0.0482 | −0.6522 ± 0.7154 | 1.8180 ± 0.5746 | 2.7466 ± 1.0033 | 0.2274 ± 0.0629 | |
| ECR × d | All | 0.9590 ± 0.0114 | 0.0330 ± 0.0612 | 1.4181 ± 0.3502 | 2.2050 ± 0.4954 | 0.1420 ± 0.0246 |
| IFS- Former | 0 | 0.9741 ± 0.0087 | −0.0791 ± 0.3815 | 1.1989 ± 0.3513 | 1.7674 ± 0.5065 | 0.1363 ± 0.0343 |
| 32 | 0.9741 ± 0.0086 | −0.0698 ± 0.3799 | 1.1987 ± 0.3491 | 1.7665 ± 0.5038 | 0.1369 ± 0.0346 | |
| 64 | 0.9741 ± 0.0088 | −0.0629 ± 0.3874 | 1.1985 ± 0.3493 | 1.7668 ± 0.5060 | 0.1366 ± 0.0339 | |
| 128 | 0.9739 ± 0.0092 | −0.0509 ± 0.4143 | 1.2012 ± 0.3540 | 1.7722 ± 0.5163 | 0.1363 ± 0.0324 | |
| 256 | 0.9740 ± 0.0083 | −0.0543 ± 0.4116 | 1.2004 ± 0.3493 | 1.7723 ± 0.5044 | 0.1379 ± 0.0353 | |
| 384 | 0.9743 ± 0.0083 | −0.0669 ± 0.4046 | 1.1954 ± 0.3495 | 1.7638 ± 0.5044 | 0.1361 ± 0.0325 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Huang, H.; Hao, R.; Luo, L.; He, H.-D. Prediction of Battery Electric Vehicle Energy Consumption via Pre-Trained Model Under Inconsistent Feature Spaces. Technologies 2025, 13, 493. https://doi.org/10.3390/technologies13110493
Wang Y, Huang H, Hao R, Luo L, He H-D. Prediction of Battery Electric Vehicle Energy Consumption via Pre-Trained Model Under Inconsistent Feature Spaces. Technologies. 2025; 13(11):493. https://doi.org/10.3390/technologies13110493
Chicago/Turabian StyleWang, Yizhou, Haichao Huang, Ruimin Hao, Liangying Luo, and Hong-Di He. 2025. "Prediction of Battery Electric Vehicle Energy Consumption via Pre-Trained Model Under Inconsistent Feature Spaces" Technologies 13, no. 11: 493. https://doi.org/10.3390/technologies13110493
APA StyleWang, Y., Huang, H., Hao, R., Luo, L., & He, H.-D. (2025). Prediction of Battery Electric Vehicle Energy Consumption via Pre-Trained Model Under Inconsistent Feature Spaces. Technologies, 13(11), 493. https://doi.org/10.3390/technologies13110493






