Modelling the Trust Value for Human Agents Based on Real-Time Human States in Human-Autonomous Teaming Systems
Abstract
1. Introduction
- This paper proposes a trust model to estimate human trust value in real-time. The proposed trust model was applied to a ball collection task with robot agents, which presents uses of the proposed trust model in the human-autonomous teaming framework.
- The proposed trust model considers multiple pieces of information from a human agent, e.g., attention level, stress index and situational awareness, by leveraging a fuzzy fusion model. In this research, the attention level and the stress index are evaluated based on pupil response and heart rate variability, respectively; situational awareness is measured from the environment through visual perception.
- We further use a Q-learning algorithm with a fuzzy reward to adaptively learn the fusion weight of the fusion model. The fuzzy reward is generated by a TSK-type fuzzy inference system, which facilitates the defending reward for complex scenarios and is able to handle the uncertainty of human information.
2. Related Works
3. Multi-Human-Evidence-Based Trust Evaluation Model
3.1. Trust Evaluation Metrics
3.1.1. Attention Level
3.1.2. Stress Index
3.1.3. Human Perception
3.2. Trust Metric Fusion Model
3.2.1. Reinforcement Learning
3.2.2. Fuzzy Reward
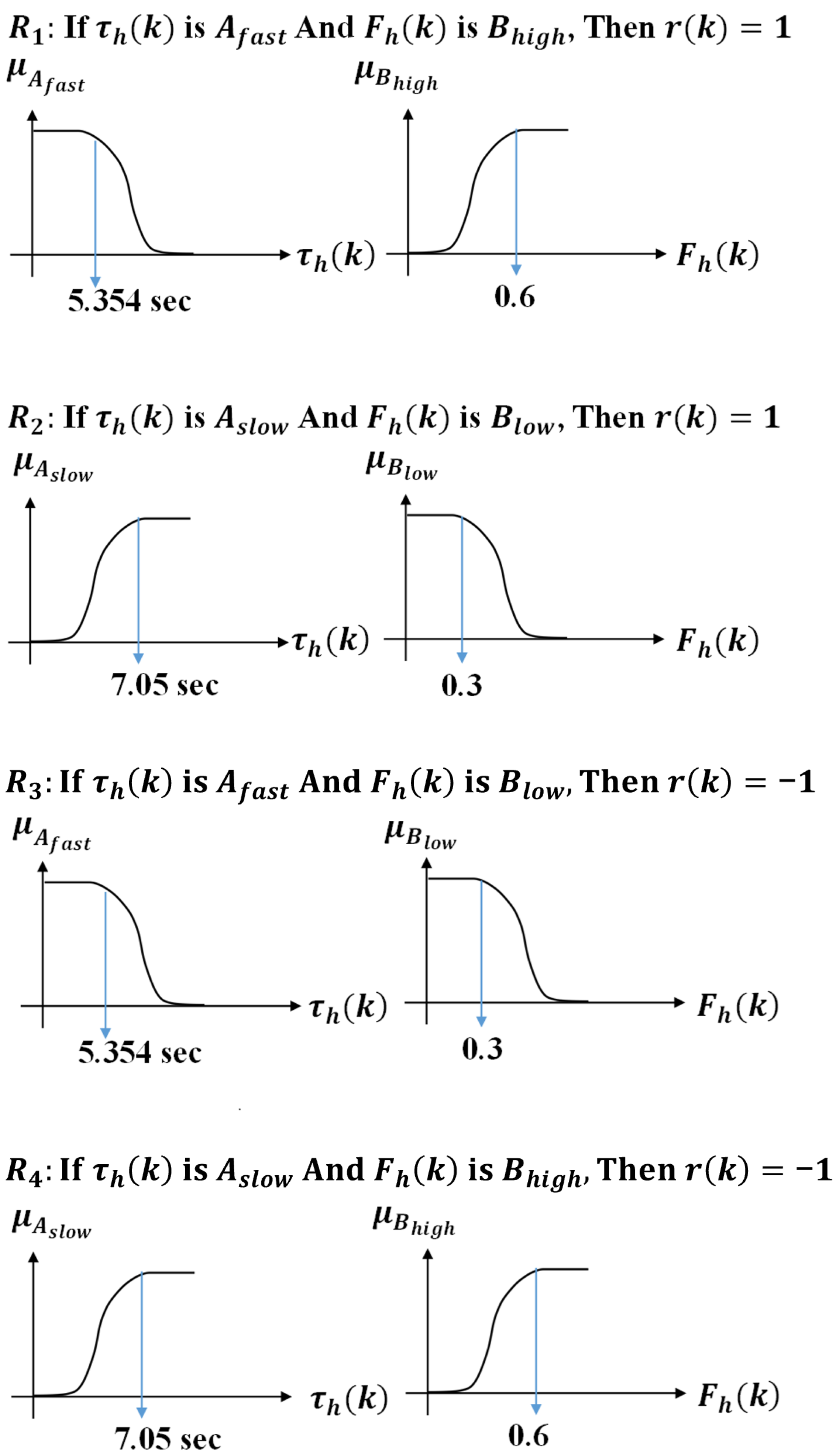
- R1:
- If is and is , then .
- R2:
- If is and is , then .
- R3:
- If is and is , then .
- R4:
- If is and is , then .
4. Methods
4.1. Participants
4.2. Scenario Design
4.3. Human-Agent Setup and Recording
4.4. Experimental Procedures
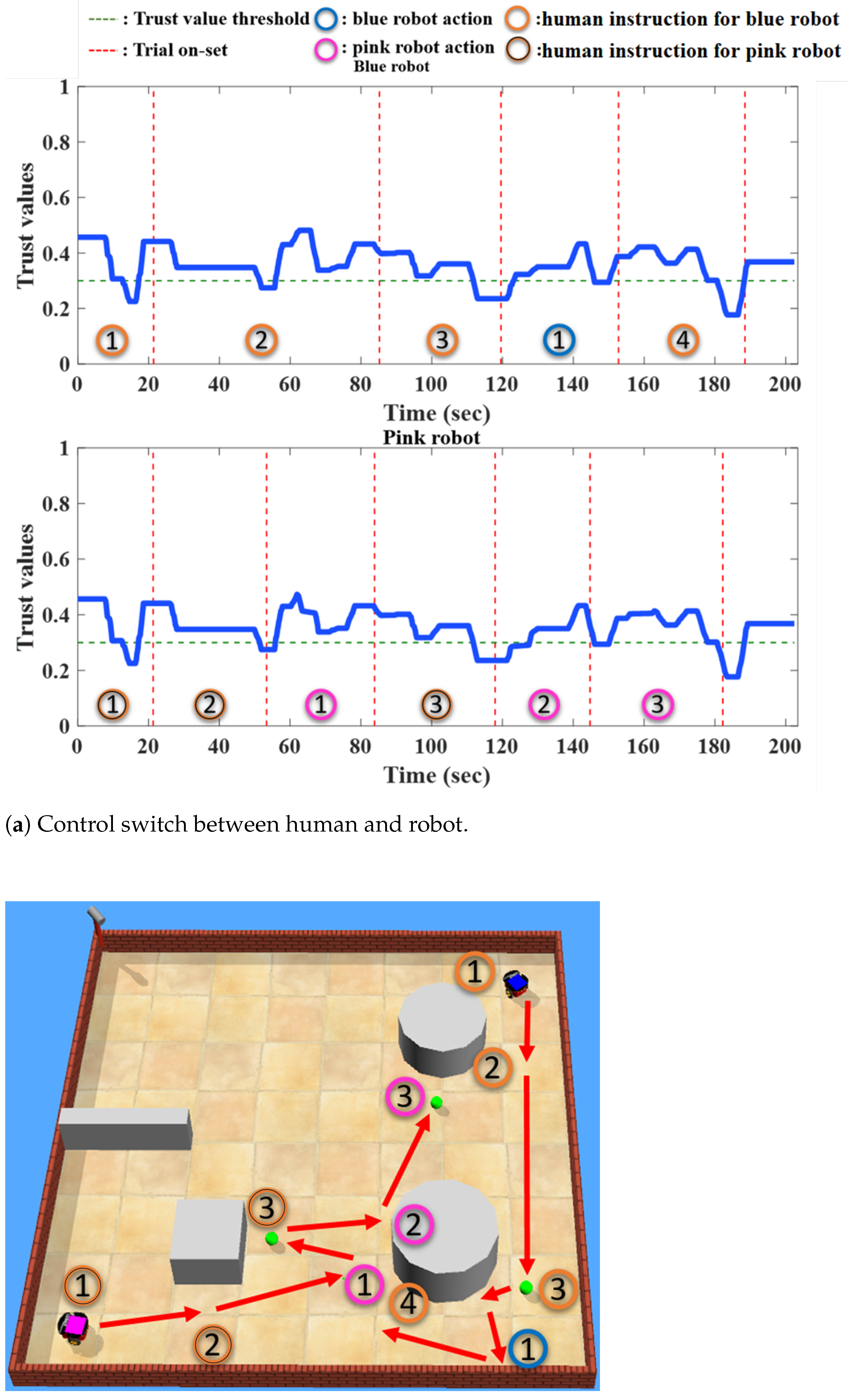
5. Results
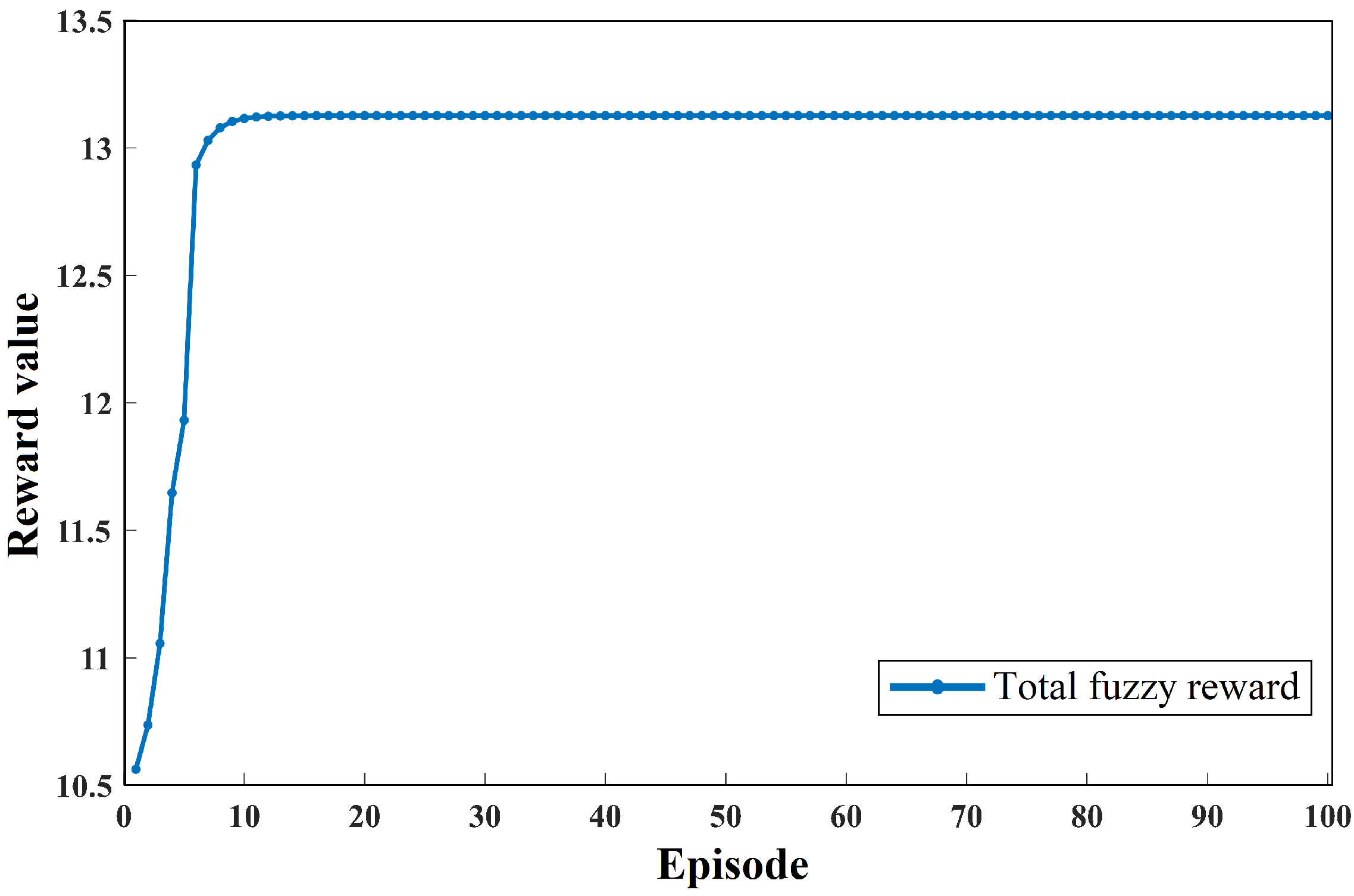
5.1. Training Results
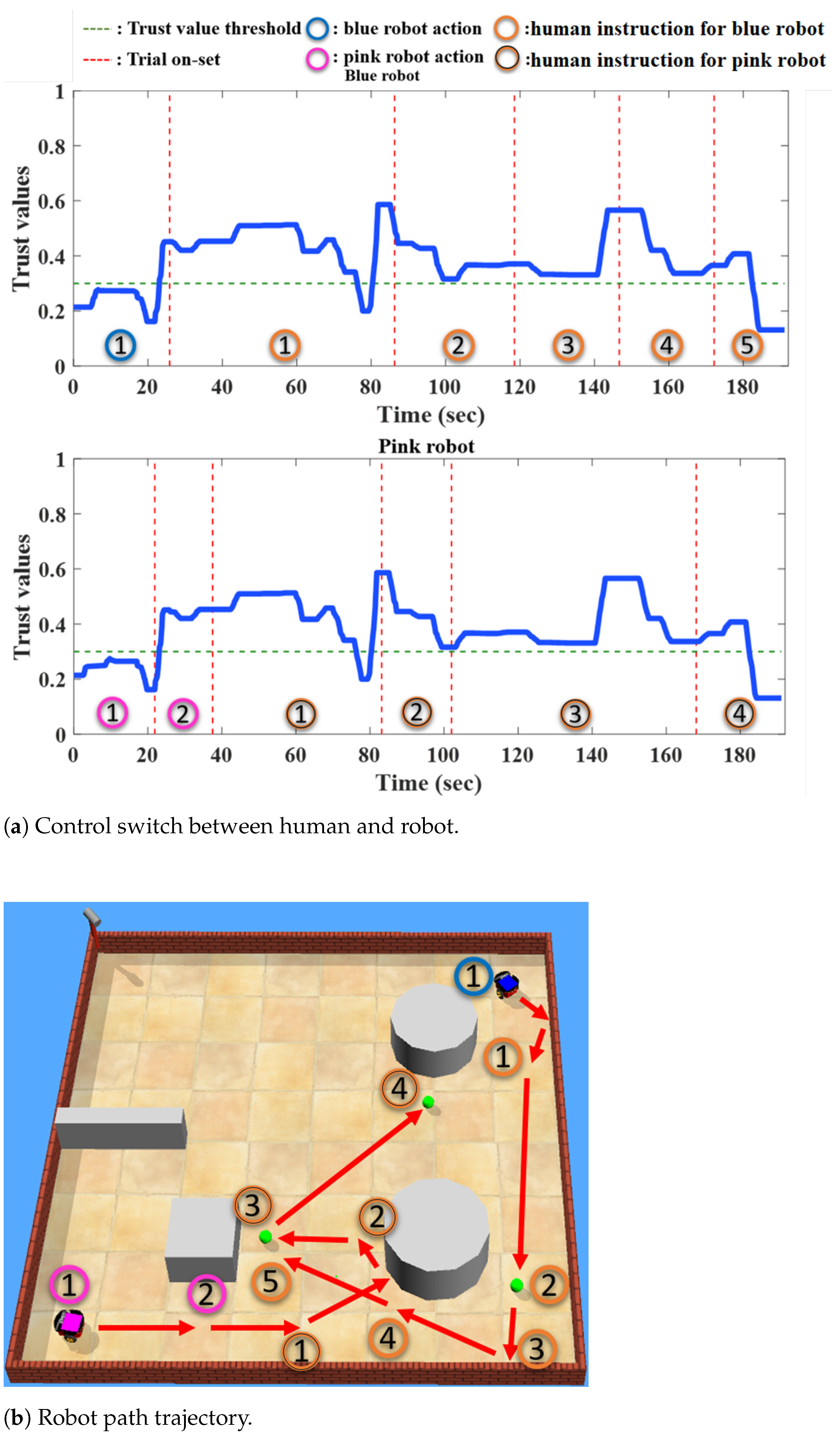
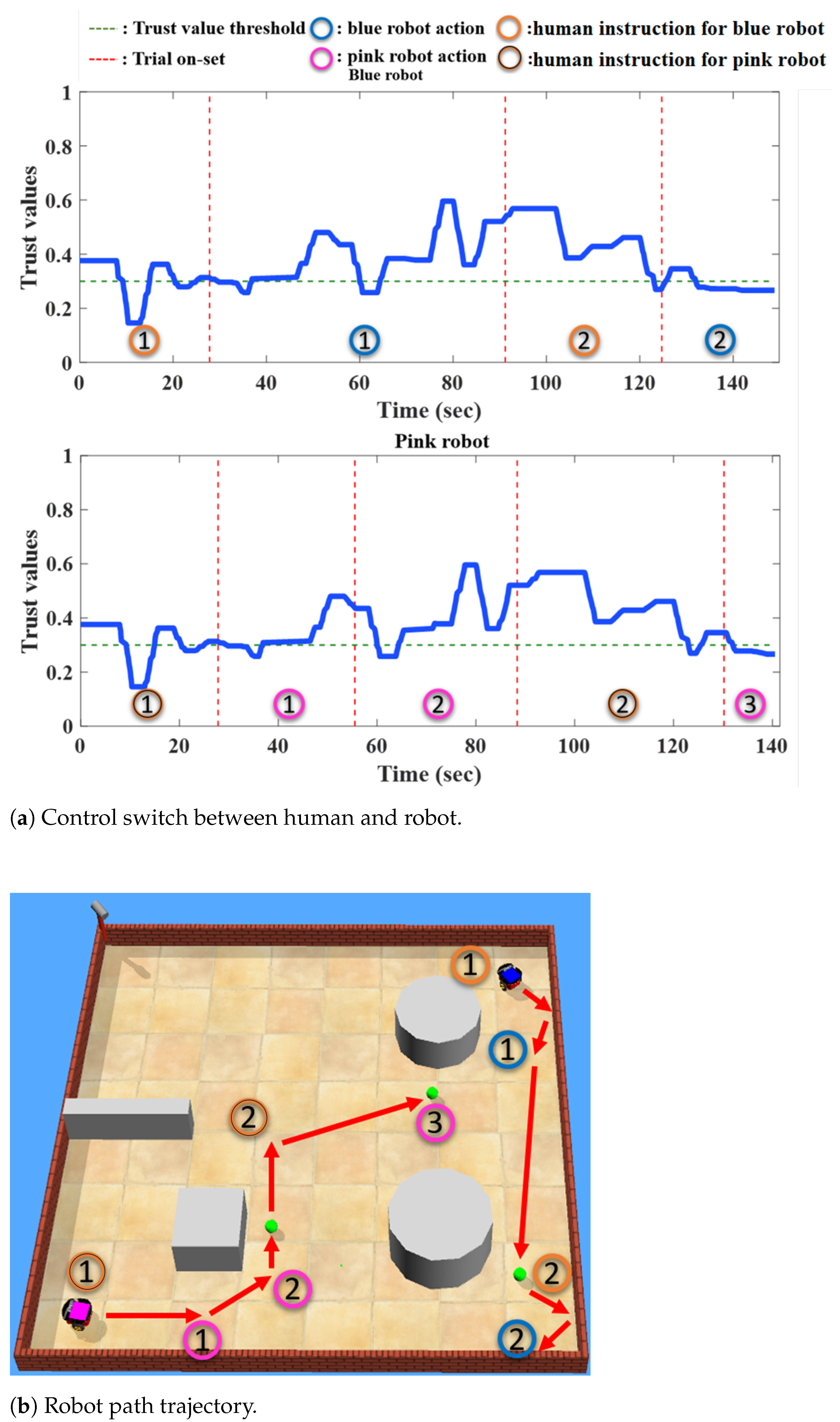
5.2. Testing Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shneiderman, B. Human-centered artificial intelligence: Reliable, safe & trustworthy. Int. J. Hum. Comput. Interact. 2020, 36, 495–504. [Google Scholar]
- Doroodgar, B.; Ficocelli, M.; Mobedi, B.; Nejat, G. The search for survivors: Cooperative human-robot interaction in search and rescue environments using semi-autonomous robots. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 2858–2863. [Google Scholar]
- Söffker, D. From human–machine-interaction modeling to new concepts constructing autonomous systems: A phenomenological engineering-oriented approach. J. Intell. Robot. Syst. 2001, 32, 191–205. [Google Scholar] [CrossRef]
- Benderius, O.; Berger, C.; Lundgren, V.M. The best rated human–machine interface design for autonomous vehicles in the 2016 grand cooperative driving challenge. IEEE Trans. Intell. Transp. Syst. 2017, 19, 1302–1307. [Google Scholar] [CrossRef]
- Demir, M.; McNeese, N.J.; Gorman, J.C.; Cooke, N.J.; Myers, C.W.; Grimm, D.A. Exploration of teammate trust and interaction dynamics in human-autonomy teaming. IEEE Trans. Hum. Mach. Syst. 2021, 51, 696–705. [Google Scholar] [CrossRef]
- Dorronzoro Zubiete, E.; Nakahata, K.; Imamoglu, N.; Sekine, M.; Sun, G.; Gomez, I.; Yu, W. Evaluation of a home biomonitoring autonomous Mobile Robot. Comput. Intell. Neurosci. 2016, 2016, 9845816. [Google Scholar] [CrossRef]
- Robinette, P.; Howard, A.M.; Wagner, A.R. Effect of robot performance on human–robot trust in time-critical situations. IEEE Trans. Hum. Mach. Syst. 2017, 47, 425–436. [Google Scholar] [CrossRef]
- Pippin, C.; Christensen, H. Trust modeling in multi-robot patrolling. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 59–66. [Google Scholar]
- Holbrook, J.; Prinzel, L.J.; Chancey, E.T.; Shively, R.J.; Feary, M.; Dao, Q.; Ballin, M.G.; Teubert, C. Enabling urban air mobility: Human-autonomy teaming research challenges and recommendations. In Proceedings of the AIAA AVIATION 2020 FORUM, Virtual, 15–19 June 2020; p. 3250. [Google Scholar]
- Huang, L.; Cooke, N.J.; Gutzwiller, R.S.; Berman, S.; Chiou, E.K.; Demir, M.; Zhang, W. Distributed dynamic team trust in human, artificial intelligence, and robot teaming. In Trust in Human-Robot Interaction; Elsevier: Amsterdam, The Netherlands, 2021; pp. 301–319. [Google Scholar]
- Tjøstheim, T.A.; Johansson, B.; Balkenius, C. A computational model of trust-, pupil-, and motivation dynamics. In Proceedings of the 7th International Conference on Human-Agent Interaction, Kyoto, Japan, 6–10 October 2019; pp. 179–185. [Google Scholar]
- Pavlidis, M.; Mouratidis, H.; Islam, S.; Kearney, P. Dealing with trust and control: A meta-model for trustworthy information systems development. In Proceedings of the 2012 Sixth International Conference on Research Challenges in Information Science (RCIS), Valencia, Spain, 16–18 May 2012; pp. 1–9. [Google Scholar]
- Kaniarasu, P.; Steinfeld, A.M. Effects of blame on trust in human robot interaction. In Proceedings of the The 23rd IEEE International Symposium on Robot and Human Interactive Communication, Edinburgh, UK, 25–29 August 2014; pp. 850–855. [Google Scholar]
- Sadrfaridpour, B.; Saeidi, H.; Burke, J.; Madathil, K.; Wang, Y. Modeling and control of trust in human-robot collaborative manufacturing. In Robust Intelligence and Trust in Autonomous Systems; Springer: Berlin/Heidelberg, Germany, 2016; pp. 115–141. [Google Scholar]
- Hu, W.L.; Akash, K.; Jain, N.; Reid, T. Real-time sensing of trust in human-machine interactions. IFAC-PapersOnLine 2016, 49, 48–53. [Google Scholar] [CrossRef]
- Mahani, M.F.; Jiang, L.; Wang, Y. A Bayesian Trust Inference Model for Human-Multi-Robot Teams. Int. J. Soc. Robot. 2020, 13, 1951–1965. [Google Scholar]
- Lu, Y.; Sarter, N. Modeling and inferring human trust in automation based on real-time eye tracking data. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting; SAGE Publications Sage CA: Los Angeles, CA, USA, 2020; Volume 64, pp. 344–348. [Google Scholar]
- Alves, C.; Cardoso, A.; Colim, A.; Bicho, E.; Braga, A.C.; Cunha, J.; Faria, C.; Rocha, L.A. Human–Robot Interaction in Industrial Settings: Perception of Multiple Participants at a Crossroad Intersection Scenario with Different Courtesy Cues. Robotics 2022, 11, 59. [Google Scholar] [CrossRef]
- Jacovi, A.; Marasović, A.; Miller, T.; Goldberg, Y. Formalizing trust in artificial intelligence: Prerequisites, causes and goals of human trust in AI. In Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency, Virtual, 3–10 March 2021; pp. 624–635. [Google Scholar]
- Wang, Q.; Liu, D.; Carmichael, M.G.; Aldini, S.; Lin, C.T. Computational Model of Robot Trust in Human Co-Worker for Physical Human-Robot Collaboration. IEEE Robot. Autom. Lett. 2022, 7, 3146–3153. [Google Scholar] [CrossRef]
- Xing, Y.; Lv, C.; Cao, D.; Hang, P. Toward human-vehicle collaboration: Review and perspectives on human-centered collaborative automated driving. Transp. Res. Part C Emerg. Technol. 2021, 128, 103199. [Google Scholar] [CrossRef]
- Liu, Y.; Habibnezhad, M.; Jebelli, H. Brainwave-driven human-robot collaboration in construction. Autom. Constr. 2021, 124, 103556. [Google Scholar] [CrossRef]
- Chang, Y.C.; Wang, Y.K.; Pal, N.R.; Lin, C.T. Exploring Covert States of Brain Dynamics via Fuzzy Inference Encoding. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 2464–2473. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Yang, X.J. Modeling and Predicting Trust Dynamics in Human–Robot Teaming: A Bayesian Inference Approach. Int. J. Soc. Robot. 2021, 13, 1899–1909. [Google Scholar] [CrossRef]
- Azevedo-Sa, H.; Jayaraman, S.K.; Esterwood, C.T.; Yang, X.J.; Robert, L.P.; Tilbury, D.M. Real-time estimation of drivers’ trust in automated driving systems. Int. J. Soc. Robot. 2021, 13, 1911–1927. [Google Scholar] [CrossRef]
- Nian, R.; Liu, J.; Huang, B. A review on reinforcement learning: Introduction and applications in industrial process control. Comput. Chem. Eng. 2020, 139, 106886. [Google Scholar] [CrossRef]
- Joo, T.; Jun, H.; Shin, D. Task Allocation in Human–Machine Manufacturing Systems Using Deep Reinforcement Learning. Sustainability 2022, 14, 2245. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Z.; He, L.; Zhao, R. A systematic study of reward for reinforcement learning based continuous integration testing. J. Syst. Softw. 2020, 170, 110787. [Google Scholar] [CrossRef]
- Chen, M.; Lam, H.K.; Shi, Q.; Xiao, B. Reinforcement learning-based control of nonlinear systems using Lyapunov stability concept and fuzzy reward scheme. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 2059–2063. [Google Scholar] [CrossRef]
- Kofinas, P.; Vouros, G.; Dounis, A.I. Energy management in solar microgrid via reinforcement learning using fuzzy reward. Adv. Build. Energy Res. 2018, 12, 97–115. [Google Scholar] [CrossRef]
- Jafarifarmand, A.; Badamchizadeh, M.A.; Khanmohammadi, S.; Nazari, M.A.; Tazehkand, B.M. A new self-regulated neuro-fuzzy framework for classification of EEG signals in motor imagery BCI. IEEE Trans. Fuzzy Syst. 2017, 26, 1485–1497. [Google Scholar] [CrossRef]
- Lin, F.C.; Ko, L.W.; Chuang, C.H.; Su, T.P.; Lin, C.T. Generalized EEG-based drowsiness prediction system by using a self-organizing neural fuzzy system. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 2044–2055. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, Y.; Chang, Y.C.; Lin, C.T. Hierarchical Fuzzy Neural Networks With Privacy Preservation for Heterogeneous Big Data. IEEE Trans. Fuzzy Syst. 2020, 29, 46–58. [Google Scholar] [CrossRef]
- Shayesteh, S.; Ojha, A.; Jebelli, H. Workers’ Trust in Collaborative Construction Robots: EEG-Based Trust Recognition in an Immersive Environment. In Automation and Robotics in the Architecture, Engineering, and Construction Industry; Springer: Berlin/Heidelberg, Germany, 2022; pp. 201–215. [Google Scholar]
- Hoeks, B.; Ellenbroek, B.A. A neural basis for a quantitative pupillary model. J. Psychophysiol. 1993, 7, 315. [Google Scholar]
- Baevsky, R.M.; Chernikova, A.G. Heart rate variability analysis: Physiological foundations and main methods. Cardiometry 2017, 66–76. [Google Scholar] [CrossRef]
- Silambarasan, I.; Sriram, S. Hamacher sum and Hamacher product of fuzzy matrices. Intern. J. Fuzzy Math. Arch. 2017, 13, 191–198. [Google Scholar]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Clifton, J.; Laber, E. Q-learning: Theory and applications. Annu. Rev. Stat. Its Appl. 2020, 7, 279–301. [Google Scholar] [CrossRef]
- Lin, J.L.; Hwang, K.S.; Wang, Y.L. A simple scheme for formation control based on weighted behavior learning. IEEE Trans. Neural Netw. Learn. Syst. 2013, 25, 1033–1044. [Google Scholar]
- Qin, B.; Chung, F.L.; Wang, S. KAT: A Knowledge Adversarial Training Method for Zero-Order Takagi-Sugeno-Kang Fuzzy Classifiers. IEEE Trans. Cybern. 2020, 52, 6857–6871. [Google Scholar] [CrossRef]
- Tkachenko, R.; Izonin, I.; Tkachenko, P. Neuro-Fuzzy Diagnostics Systems Based on SGTM Neural-Like Structure and T-Controller. In Proceedings of the International Scientific Conference “Intellectual Systems of Decision Making and Problem of Computational Intelligence”; Springer: Berlin/Heidelberg, Germany, 2021; pp. 685–695. [Google Scholar]
- Lin, C.J.; Lin, C.T. Reinforcement learning for an ART-based fuzzy adaptive learning control network. IEEE Trans. Neural Netw. 1996, 7, 709–731. [Google Scholar] [PubMed]
- Xie, J.; Xu, X.; Wang, F.; Liu, Z.; Chen, L. Coordination Control Strategy for Human-Machine Cooperative Steering of Intelligent Vehicles: A Reinforcement Learning Approach. IEEE Trans. Intell. Transp. Syst. 2022, 1–15. [Google Scholar] [CrossRef]
- Lin, C.T.; Kan, M.C. Adaptive fuzzy command acquisition with reinforcement learning. IEEE Trans. Fuzzy Syst. 1998, 6, 102–121. [Google Scholar]





| Human Perception | |
|---|---|
| First situation | Agent + Target |
| Second situation | No Agent + Target |
| Third situation | Agent + No Target |
| Fourth situation | No Agent + No Target |
| Evaluation of | Participant | ||||||
|---|---|---|---|---|---|---|---|
| Completion Time | 1 | 2 | 3 | 4 | 5 | 6 | |
| Scenario | Setting | Time (s) | |||||
| human instruction | 223 | 175 | 194 | 196 | 177 | 216 | |
| Scenario_1 | HAT | 194 | 138 | 171 | 140 | 131 | 143 |
| random search | 287 | ||||||
| human instruction | 165 | 181 | 168 | 121 | 132 | 129 | |
| Scenario_2 | HAT | 117 | 119 | 123 | 98 | 100 | 90 |
| random search | 185 | ||||||
| human instruction | 408 | 428 | 407 | 469 | 427 | 450 | |
| Scenario_3 | HAT | 372 | 343 | 371 | 403 | 380 | 359 |
| random search | 573 | ||||||
| human instruction | 209 | 237 | 248 | 229 | 222 | 242 | |
| Scenario_4 | HAT | 178 | 208 | 195 | 201 | 197 | 213 |
| random search | 330 | ||||||
| Evaluation of Number | Participant | ||||||
|---|---|---|---|---|---|---|---|
| of Decisions Made | 1 | 2 | 3 | 4 | 5 | 6 | |
| Scenario | Setting | Number of Decisions | |||||
| Scenario_1 | human instruction | 6 | 6 | 6 | 6 | 6 | 6 |
| human/robot | 4 / 2 | 4 / 2 | 4 / 2 | 4 / 2 | 5 / 1 | 4 / 2 | |
| human instruction | 6 / 6 | 5 / 6 | 6 / 6 | 4 / 5 | 4 / 6 | 4 / 5 | |
| Scenario_2 | human/blue | 4 / 2 | 4 / 1 | 5 / 1 | 3 / 1 | 3 / 1 | 2 / 2 |
| human/pink | 2 / 4 | 3 / 3 | 4 / 2 | 3 / 2 | 5 / 1 | 2 / 3 | |
| Scenario_3 | human instruction | 12 | 12 | 13 | 12 | 12 | 11 |
| human/robot | 9 / 3 | 9 / 3 | 7 / 6 | 7 / 5 | 8 / 4 | 6 / 5 | |
| human instruction | 5 / 7 | 6 / 7 | 6 / 8 | 6 / 7 | 6 / 7 | 8 / 7 | |
| Scenario_4 | human/blue | 3 / 2 | 3 / 3 | 2 / 4 | 2 / 4 | 4 / 2 | 4 / 2 |
| human/pink | 7 / 0 | 7 / 0 | 5 / 3 | 5 / 2 | 4 / 3 | 4 / 3 | |
| Scenario | Setting | Participant | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | Avg | ||
| Improvement Rates | ||||||||
| H vs. RS | 22.29 | 39.02 | 32.4 | 31.71 | 38.33 | 24.74 | 31.42 | |
| Scenario_1 | HAT vs. RS | 32.4 | 51.92 | 40.42 | 51.22 | 54.36 | 50.17 | 46.75 |
| HAT vs. H | 13.01 | 21.14 | 11.86 | 28.57 | 25.99 | 33.79 | 22.39 | |
| H vs. RS | 10.81 | 2.16 | 9.19 | 34.59 | 28.65 | 30.27 | 19.28 | |
| Scenario_2 | HAT vs. RS | 36.76 | 35.68 | 33.51 | 47.02 | 45.95 | 51.35 | 41.71 |
| HAT vs. H | 29.09 | 34.25 | 26.79 | 19.01 | 24.24 | 30.23 | 27.27 | |
| H vs. RS | 28.8 | 25.31 | 28.97 | 18.15 | 25.48 | 21.47 | 24.69 | |
| Scenario_3 | HAT vs. RS | 35.08 | 40.14 | 35.25 | 29.67 | 33.68 | 37.35 | 35.19 |
| HAT vs. H | 8.82 | 19.86 | 8.85 | 14.07 | 11.01 | 20.22 | 13.81 | |
| H vs. RS | 36.67 | 28.18 | 24.85 | 30.61 | 32.73 | 26.67 | 29.95 | |
| Scenario_4 | HAT vs. RS | 46.06 | 36.97 | 40.91 | 39.09 | 40.3 | 35.45 | 39.79 |
| HAT vs. H | 14.83 | 12.24 | 21.37 | 12.22 | 11.26 | 11.98 | 13.98 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-T.; Fan, H.-Y.; Chang, Y.-C.; Ou, L.; Liu, J.; Wang, Y.-K.; Jung, T.-P. Modelling the Trust Value for Human Agents Based on Real-Time Human States in Human-Autonomous Teaming Systems. Technologies 2022, 10, 115. https://doi.org/10.3390/technologies10060115
Lin C-T, Fan H-Y, Chang Y-C, Ou L, Liu J, Wang Y-K, Jung T-P. Modelling the Trust Value for Human Agents Based on Real-Time Human States in Human-Autonomous Teaming Systems. Technologies. 2022; 10(6):115. https://doi.org/10.3390/technologies10060115
Chicago/Turabian StyleLin, Chin-Teng, Hsiu-Yu Fan, Yu-Cheng Chang, Liang Ou, Jia Liu, Yu-Kai Wang, and Tzyy-Ping Jung. 2022. "Modelling the Trust Value for Human Agents Based on Real-Time Human States in Human-Autonomous Teaming Systems" Technologies 10, no. 6: 115. https://doi.org/10.3390/technologies10060115
APA StyleLin, C.-T., Fan, H.-Y., Chang, Y.-C., Ou, L., Liu, J., Wang, Y.-K., & Jung, T.-P. (2022). Modelling the Trust Value for Human Agents Based on Real-Time Human States in Human-Autonomous Teaming Systems. Technologies, 10(6), 115. https://doi.org/10.3390/technologies10060115






