Abstract
Efforts to develop high-energy laser (HEL) weapons that are capable of being integrated and operated aboard naval platforms have gained an increased interest, partially due to the proliferation of various kinds of unmanned systems that pose a critical asymmetric threat to them, both operationally and financially. HEL weapons allow for an unconstrained depth of magazine and cost exchange ratio, both of which are essential characteristics to effectively oppose small unmanned systems, compared to their kinetic weapons counterparts. However, HEL performance is heavily affected by atmospheric conditions between the weapon and the target; therefore, the more precise and accurate the atmospheric characterization, the more accurate the performance estimation of the HEL weapon. To that end, the Directed Energy Group of the Naval Postgraduate School (NPS) is conducting experimental, theoretical and computational research on the effects of atmospheric conditions on HEL weapon efficacy. This paper proposes a new approach to the NPS laser performance code scheme, which leverages artificial neural networks (ANNs) for the prediction of optical turbulence strength. This improvement could allow for near real-time and location-independent HEL weapon performance estimation. Two experimental datasets, which were obtained from the NPS facilities, were utilized to perform regression modeling using an ANN, which achieved a decent fit (R2 = 0.75 for the first dataset and R2 = 0.78 for the second dataset).
1. Introduction
Since the 1960s, directed energy weapons and, in particular, high-energy laser weapons have promised to add their unique capabilities to modern warfare; however, they have consistently failed to fulfil these promises [1]. After many decades of research and development efforts, and despite having spent billions of dollars, many laser weapon systems have failed to mature enough to be used in the field. However, during the last decade, the focus has switched from the strategic (i.e., airborne lasers, space-based lasers, etc.) to the tactical level, resulting in several operational laser weapons (e.g., LaWS) [1]. The prospects of HEL weapon deployment in the field include, but are not limited to, (a) the offer of a precise and scalable non-kinetic weapon primarily for defensive applications, although perhaps also for offensive applications in the future, (b) the offer of an excellent cost exchange ratio compared to kinetic weapon counterparts and, while employed alongside them, an extension to the depth of the magazine and an increase in platform survivability and (c) the provision of operational flexibility in terms of the platforms into which they can be integrated and the missions that they can execute, depending on their design parameters [1].
The scope of this paper concerned HEL weapon systems that are integrated into maritime platforms and, therefore, operate in maritime environments. The US Navy has been developing solid-state lasers for quite a few years and, in 2014, achieved the integration of the first HEL weapon (LaWS) aboard the USS Ponce. LaWS, which has a reported output power of 30 kW, was initially tested on land against UAVs in different scenarios and has subsequently been operationally evaluated during a deployment of the USS Ponce in the Persian Gulf [2]. Another prototype, called the Maritime Laser Demonstrator (MLD), has also been tested and has produced very encouraging results. Currently, the US Navy is working on four separate programs and has already installed several systems into different types of ships: (a) the Solid-State Laser Technology Maturation (SSL-TM) effort, which is a 150-kW weapon system that offers new capabilities against asymmetric threats; (b) the Optical Dazzling Interdictor, Navy (ODIN), which is a low-power system that provides C-ISR capabilities to dazzle UASs and other platforms; (c) the Surface Navy Laser Weapon System (SNLWS) Increment 1, also called HELIOS, which is a 60-kW system with the potential to reach 150 kW and provide an integrated weapon and dazzler system against small and soft targets; and (d) the High-Energy Laser Counter-ASCM program, which is a high-power system that provides defense against anti-ship cruise missiles [2].
The Directed Energy Group (DEG) of the Naval Postgraduate School conducts systematic research activities on the design, development, integration and operation of high-energy laser weapons in maritime environments. To support this experimental work, a MATLAB-based code (i.e., ANCHOR) has been developed to simulate engagement scenarios at the tactical level and produce estimates of the weapon performance. This code has been upgraded ever since in order to account for different aspects of HEL research. In [3], different energy storage solutions to power a HEL weapon aboard a naval ship were investigated at three different output power levels. The proposed solution included lead acid and lithium-ion batteries. The latter were found to provide a more effective, albeit more dangerous, solution. The feasibility in terms of size, weight and power (SWaP) requirements, as well as the resulting performance of a HEL weapon deployed from a UAV, was studied in [4,5]. Alternative HEL designs were identified to achieve equivalent results under certain conditions and their corresponding weights were estimated. In [5], an advanced experimental design analysis was applied to identify the most significant parameters of a laser, as well as their interactions. A systems engineering approach was followed in [6] in order to identify the integration trade space of a HEL weapon within an LPD 17 class ship. Priority was given to the location of the weapon to account for certain SWaP limitations and requirements. This study designated eight potential locations for a HEL weapon. In [7], the effects of rain and haze on the performance of a HEL weapon in maritime environments were studied to investigate changes in the extinction coefficient that are caused when such conditions occur.
The characterization of the atmosphere and its corresponding effects on laser beam propagation have been thoroughly examined for years [8], yet new and more efficient ways to model and predict various atmospheric phenomena are required in order to achieve more accurate laser performance estimations. The primary focus of this paper was to present a new approach to laser weapon performance modeling through optical turbulence modeling utilizing machine learning (ML) algorithms and, specifically, ANNs. A comprehensive integrated model flow was proposed, which elaborated a previous “traditional” approach.
2. Materials and Methods
2.1. Atmospheric Effects on Laser Beam Propagation in Maritime Environments
A number of atmospheric phenomena exist that seriously affect laser propagation through random media, including the following [9]: (a) diffraction; (b) atmospheric attenuation; (c) atmospheric turbulence; (d) thermal blooming. The first two phenomena can be assumed to be system-dependent, whereas the latter mostly affects laser beams of very high power (>150 kW); therefore, the laser applications community has paid special attention to optical turbulence.
Quite a few software packages have been used to model the beam attenuation of certain wavelengths (e.g., MODTRAN, HITRAN, PCLNWIN, etc.), whereas diffraction can be modeled using the known relationship of a beam’s divergence angle [9]:
Optical turbulence effects are caused by random fluctuations in the refractive index, which are caused by temperature differences at the microscopic level and are mathematically produced by the structure function of the refractive index, as follows [10]:
where is the refractive index structure constant, which physically represents the strength of the refractive index fluctuations. Extended research efforts have been conducted to model in different locations around the world and over various terrains. Although microscopic meteorology is required for this task, many models exist that are based on local macroscopic parameters, such as wind, temperature, humidity, air pressure, etc. Some of these are simple regression models that capture the overall trends of turbulence strength; however, they cannot explicitly model the highly non-linear variations and are constrained to upper and lower parameter values [10]. Maritime environments exhibit different characteristics compared to terrestrial environments; therefore, special attention needs to be paid [11]. Conducting direct measurements of atmospheric parameters in maritime environments is not an easy task due to the sensitivity of sensors, flow distortion and thermal contamination on ships. This difficulty calls for a model that utilizes easily obtained macroscopic atmospheric parameters.
The meteorological department of NPS developed the Navy Atmospheric Vertical Surface Layer Model (NAVSLaM), based on the Monin–Obukhov similarity theory (MOST), to compute vertical profiles over the ocean up to 50–100 m above the surface. The NAVSLaM model is valid for wavelengths in the range of 0.3–14 μm and requires the wind speed, air and sea temperature, humidity and pressure as inputs. The expression of the NAVSLaM model is given by [12]:
where A and B are the partial derivatives of the refractive index with respect to temperature and specific humidity, respectively, f(ξ) is an empirically determined dimensionless function, z is the height above the surface, k is the von Kármán constant (≈0.4), g is the gravitational acceleration, Ψ is the integrated form of the respective dimensionless profile function, zoT is the height at which the log-z profile T reaches its surface value and rTq is the temperature-specific humidity correlation coefficient. A detailed derivation of the NAVSLaM model was not within the scope of this paper and can be found in [12].
2.2. NPS Experimental Sites
Of particular interest for the NPS DEG is atmospheric characterization and its effects on the performance of HEL weapons in maritime environments. For that reason, two experimental sites have been set up: one at the NPS campus and the other within the broader Monterey Bay area. At these sites, various atmospheric parameters are measured, focusing on the modeling of optical turbulence effects on laser beam propagation in coastal environments [13].
The NPS campus site includes a tripod, which is located on the roof of Spanagel Hall (Figure 1), with four devices: an IRGASON (Integrated CO2/H2O Open-Path Gas Analyzer and 3D Sonic Anemometer); an infrared radiometer; a net radiometer; and a GPS receiver. The data collection period spanned almost a year (the end of January to the end of November 2021) and included measurements of air temperature, ground temperature, solar flux, wind speed and water vapor concentration (almost 550,000 data points).

Figure 1.
The NPS experimental site with the exact location of the sensors.
The estimations of optical turbulence strength () were extracted from the wind velocity and sonic temperatures by utilizing the Kolmogorov theory. Thus, the power spectral density (PSD) of the sonic temperatures was used over ~40-s intervals (acquired at 50 Hz) to calculate , whereas average values for all other measurements were calculated over the same time interval.
The Monterey Bay site includes an MZA DELTA (Figure 2), located in the south-west part of the bay (Coast Guard Pier), and observes a target board that is 1563 m away and located in the south-east part of the bay, close to the sea on a coastal bluff. The DELTA produces path-resolved estimates of by tracking the turbulence-induced jitter of image points within frames from a video of the target board. A major part of the optical path (~95%) is over water (Figure 3). Additional measurement instruments include a portable weather station (WS-2000), which measures macroscopic environmental parameters, such as wind speed, pressure, relative humidity, solar flux, air temperature, dew point and rainfall rate. A National Oceanic Atmospheric Administration (NOAA) weather station that is located few meters south (Municipal Pier) provides additional real-time data. During our MZA DELTA measurements, two CSAT3 sonic anemometers and a fine wire thermocouple were also deployed as a different method to measure turbulence strength.

Figure 2.
The laser propagation path over Monterey Bay, CA. The MZA DELTA transmitter is located on the Coast Guard Pier (upper left) and the target board is on a coastal bluff.
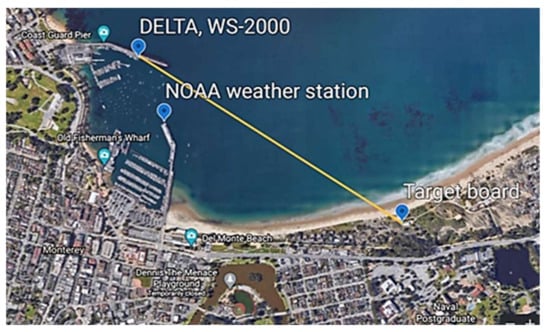
Figure 3.
The laser propagation path over Monterey Bay, CA. The MZA DELTA transmitter is located on the Coast Guard Pier (upper left) and the target board is on a coastal bluff.
3. Results
The accurate prediction of atmospheric turbulence strength is of great importance for many laser applications, such as directed energy weapons (DEWs), because it could allow for better performance estimation. The performance of a DEW is highly affected by several atmospheric phenomena and the resulting effects on certain targets could vary for different atmospheric conditions. One way to measure optical turbulence strength is to use special instruments (i.e., scintillometers); however, it is not practical to deploy these on moving platforms. Therefore, being able to predict optical turbulence strength based on meteorological parameters would offer significant flexibility, since these parameters can be easily measured from any platform or location. For that reason, several empirical models have been constructed to predict the parameter using macroscopic meteorological parameters [14]. The most popular methods are MOST-based methods and a representative example is the NAVSLaM model. However, the constraints that these models face in order to be valid require a new class of models that are unconstrained by their input parameter values.
3.1. Research on Artificial Neural Networks
This paper adopted machine learning-based algorithms (i.e., ANNs) to model and predict optical turbulence and proposed the integration of such methods into the NPS laser performance code for accurate and near real-time prediction. A growing number of research papers have already demonstrated the prediction capabilities of ML algorithms and their superiority compared to traditional empirical models [15,16,17,18,19,20].
The NPS DEW group developed a laser performance code (ANCHOR) to assess atmospheric effects on the performance of HEL weapons at the tactical level. It uses well-known and experimentally validated atmospheric propagation scaling laws and it is many orders of magnitude faster than full-scale wave equation propagation codes. As shown in Figure 4, ANCHOR is fed by three main sets of input parameters: the Laser Environmental Effects Definition and Reference (LEEDR) and NAVSLaM models are used for the atmospheric and weather data inputs and the design scenario parameters, such as output power, platform jitter, beam director, beam quality, geometry of engagement, etc.; the LEEDR model is an Air Force Institute of Technology (AFIT) line-by-line (or 1 cm–1 band model) atmospheric characterization code that captures the effects of wavelengths from 200 nm to 8.6 m. The capabilities of LEEDR include the creation of physically realizable horizontal and vertical profiles of meteorological and weather event data and the associated radiative effects (i.e., optical extinction, path radiance, etc.), aerosol and surface observation climatology, numerical weather forecasts and profiles of optical turbulence [21]. The Coupled Ocean Atmosphere Mesoscale Prediction System (COAMPS) is also utilized for actual weather data predictions for a given location and date. The output of the performance code is the figures of merit of the HEL weapon, including irradiance on target, power in bucket and dwell time [22].
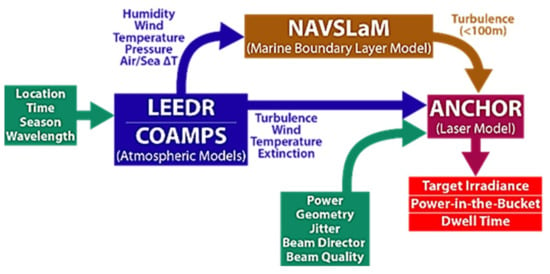
Figure 4.
The NPS laser performance code scheme.
To improve the prediction accuracy, as well as transform this code into a near real-time system, we proposed the integration of an ML algorithm-based model to predict and a weather sensor to provide macroscopic atmospheric parameters as inputs, as shown in Figure 5. Therefore, a weather sensor located in a certain place (i.e., a naval platform) could feed the ML algorithm with parameters, on which it has already been trained, to output the refraction index structure parameter. The proper conversion of estimates into heights (other than those measured) could involve the Tatarski and LeClerc approaches [23]:
where is the reference height-measured and n = −4/3 (Tatarski) or n = −2/3 (LeClerc). Both approaches have been validated but the −2/3 approach has been found to yield estimations that are closer to the measured values.
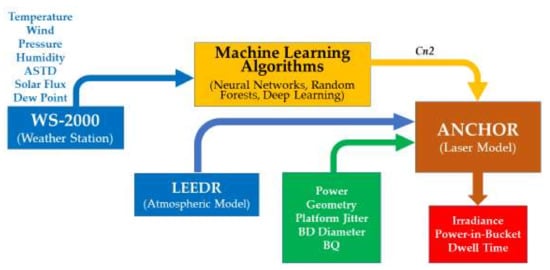
Figure 5.
The improved ML-based NPS laser performance code scheme.
Another model that produces the vertical dependence of the refractive index structure parameter and is widely used is the Hufnagel–Valley model [24]:
where h is the height above the ground in kilometers, is the squared average of the wind speed at a height of 5–20 km and A is a constant with a typical value of 1.7 × 10−4. A modified version of this model was introduced by Hufnagel, Andrew and Phillips (HAP) [24]:
The ML-based estimates directly feed the ANCHOR code, along with the LEEDR model that provides the laser extinction coefficients.
A representative ML-based algorithm that can be utilized for estimation is the artificial neural network (ANN), which is a model that imitates the main functions of a human brain [15] using either single-layer or deep neural networks. The principal component of an ANN is the perceptron, which receives a weighted input signal with a certain bias that is added through a summation junction and passed through an activation function f to provide the final output [15]. This complex structure allows for the modeling of highly non-linear relationships, such as those between macroscopic atmospheric parameters and the corresponding refractive index structure parameter, for example. To validate the modeling performance of the ANN algorithm, we developed a single-layer perceptron model (Figure 6) that used the values of seven macroscopic atmospheric parameters as inputs, which were measured by the WS-2000 weather station, with a targeted output the corresponding value for the same instance. During training, an early stopping technique was applied to avoid overfitting, i.e., when the error on the validation dataset typically begins to rise. When that error increased for a specified number of iterations, the training stopped and the weights and biases at the minimum of the validation error were returned. The software utilized to execute this neural network model was the built-in neural network application on MATLAB.
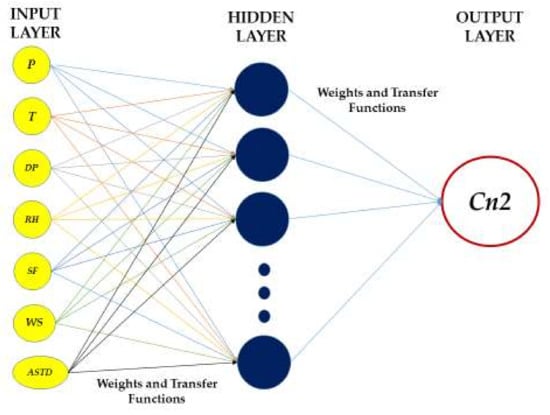
Figure 6.
The single-layer perceptron network architecture for the prediction of the refractive index parameter.
3.2. Regression Analysis
A preliminary dataset, which was obtained from the Monterey Bay site during September to October 2020, included 6042 data points and was split accordingly in order to train (70%), validate (10%) and test (20%) the model using a standard Levenberg–Marquardt backpropagation algorithm. The optimum number of nodes in the hidden layer was found to be thirty, as higher numbers of nodes did not result in a better fit, as measured by the coefficient of determination R2. The higher the value of R2, the better the performance (i.e., accuracy) of the regression model. The R2 metric has the form:
where is defined as and is , where represents the mean value of the observations.
The results after 178 epochs, which took approximately five minutes, showed that the model achieved a very good estimation of the extremely non-linear refractive index structure parameter values (R2 = 0.75), as shown in Figure 7. All ANN regression analyses were executed in MATLAB.
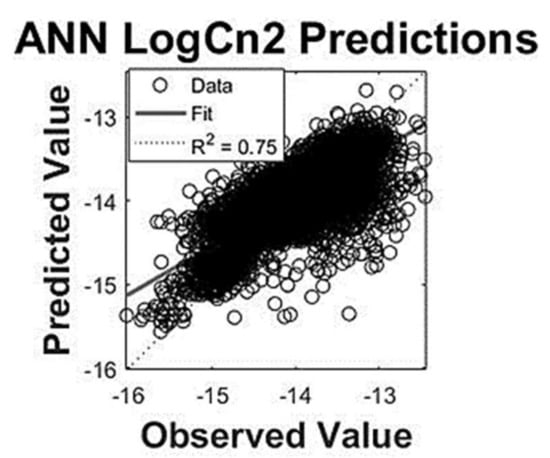
Figure 7.
The ANN regression plot for the observed values against the predicted values for the Monterey Bay dataset.
Another dataset, which was much larger than the previous dataset, was obtained from the NPS campus site during January to November 2021. This dataset included almost 550,000 data points and was split in the same way (70% for training, 10% for validation and 20% for testing) using a standard Levenberg–Marquardt backpropagation algorithm. The optimum number of nodes in the hidden layer this time was found to be fifty. Once more, after 213 epochs, which took approximately seven minutes, the model achieved an even better fit to the measured data (R2 = 0.78), as shown in Figure 8.
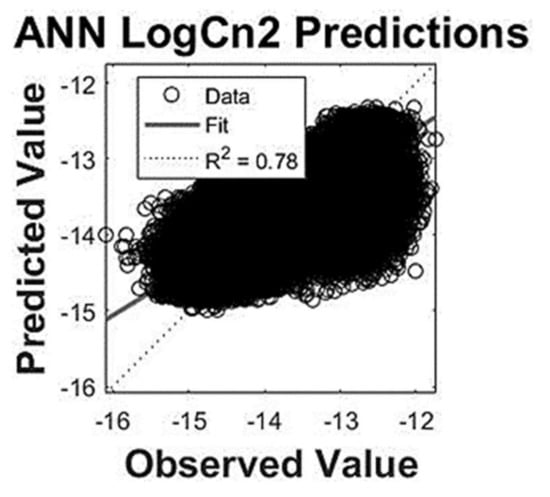
Figure 8.
The ANN regression plot for the observed values against the predicted values for the NPS site dataset.
4. Discussion
In the previous section, we demonstrated the capabilities of machine learning algorithms and, specifically, artificial neural networks for the prediction of complex parameters. The existing mathematical models are unable to predict to an acceptable degree of accuracy [25,26]. In comparison to existing research works on this topic, we can state that the accuracy achieved in this work was significant [18,24]. At the same time, the integration of this model into an integrated model for laser weapon performance prediction could result in a very impressive prediction tool within a near real-time framework.
Over the past decade, the Hellenic Naval Academy (HNA), Piraeus, Greece, has been conducting focused applied research on optical turbulence characterization and modeling, along with analyses of laser communication systems [10,27]. A variety of measurement sensors are located on the roof of the Hellenic Naval Academy (HNA) and the lighthouse of Psitalia island, which are 2958 m apart and 35 m above sea level. The collected data include the bit rate and received signal strength (RSSI) of laser communication systems, various atmospheric parameters (such as air pressure, temperature, wind speed and direction, rainfall rate, dew point, solar flux and relative humidity) and, finally, the refractive index structure parameter (), the structure parameter of the temperature fluctuations (), the sensible heat flux, the scintillation index, the intensity and the Fried parameter. All these data could feed efficient and novel machine learning and deep learning algorithms to provide more accurate predictions. These predictions could then be evaluated against real values that are measured by the scintillometer (BLS-450) that is co-located in the FSO terminal.
5. Conclusions
The paper presented a new approach to modeling and estimating the performance of a laser weapon. This approach leverages the capabilities of artificial neural networks to model optical turbulence in the atmosphere based on macroscopic meteorological parameters and estimate the refractive index structure parameter. Therefore, a near real-time predictive tool for HEL weapon performance could be achieved. Two experimental datasets were obtained from NPS facilities and utilized to perform regression modeling using an ANN, which achieved a decent fit (R2 = 0.75 for the first dataset and R2 = 0.78 for the second dataset). This accuracy was pretty decent for the highly complex parameter of , which indicates the improved capabilities of ANNs.
Author Contributions
Conceptualization, A.L. and K.C.; methodology, A.L. and K.C.; software, A.L.; validation, A.L.; formal analysis, A.L. and K.C.; investigation, A.L. and A.T.; resources, K.C. and A.T.; data curation, A.L.; writing—original draft preparation, A.L.; writing—review and editing, A.T. and K.C.; visualization, A.L.; supervision, K.C. and A.T.; project administration, A.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ellis, J.D. Directed Energy Weapons: Promise and Prospects; Centre for a New American Security: Washington, DC, USA, 2015. [Google Scholar]
- O’Rourke, R. Navy Lasers, Railgun and Gun-Launched Guided Projectile: Background and Issues for Congress; CRS Report No RL44175; Congressional Research Service: Washington, DC, USA, 2021; Available online: https://fas.org/sgp/crs/weapons/R44175.pdf (accessed on 1 March 2022).
- Valiani, J.H. Power and Energy Storage Requirements for Ship Integration of Solid-State Lasers on Naval Platforms. Master’s Thesis, Physics Department, Naval Postgraduate School, Monterey, CA, USA, 2016. [Google Scholar]
- Romero, C.A. Feasibility of High Energy Lasers for Interdiction Activities. Master’s Thesis, Physics Department, Naval Postgraduate School, Monterey, CA, USA, 2017. [Google Scholar]
- Lionis, A.; Cohn, K.; Pogue, C. Experimental Design of a UCAV-based High Energy Laser Weapon. Nausivios Chora J. 2016, 6, 3–17. [Google Scholar]
- Gildemeyer, S.J.; Hager, D.B.; Malone, A.C.; Mugerditchian, K.A.; Liensdorf, D. Analysis of Shipboard Effects and Coverage for the Integration of a High-Energy Laser on a LPD 17; Systems Engineering Capstone Project, Systems Engineering Department, Naval Postgraduate School: Monterey, CA, USA, 2018. [Google Scholar]
- Kui, J.R. Effectiveness of Laser Weapons in the Environment of South Asia. Master’s Thesis, Physics Department, Naval Postgraduate School, Monterey, CA, USA, 2019. [Google Scholar]
- Sprangle, P.; Hafizi, B.; Ting, A.; Fischer, R. High-power laser for directed energy applications. Appl. Opt. 2015, 54, F201–F209. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L.; Hopen, C.Y. Laser Beam Scintillation with Applications, 2nd ed.; SPIE Optical Engineering Press: Bellingham, WA, USA, 2001. [Google Scholar]
- Lionis, A.; Peppas, K.; Nistazakis, H.E.; Tsigopoulos, A.D.; Cohn, K. Statistical Modeling of Received Signal Strength for an FSO Channel over Maritime Environment. Opt. Commun. 2020, 489, 126858. [Google Scholar] [CrossRef]
- Kaushal, H.; Jain, V.K.; Kar, S. Free Space Optical Communication; Springer: New Delhi, India, 2017. [Google Scholar] [CrossRef]
- Frederickson, P.; Hammel, S.; Tsintikidis, D. Measurements and Modeling of Optical Turbulence in a Maritime Environment; International Society for Optics and Photonics: San Diego, CA, USA, 2006. [Google Scholar] [CrossRef]
- Lionis, A.; Chaskakis, G.; Cohn, K.; Blau, J.; Peppas, K.; Nistazakis, H.E.; Tsigopoulos, A. Optical Turbulence Measurements and Modeling Over Monterey Bay. Opt. Commun. J. 2022, 520, 128508. [Google Scholar] [CrossRef]
- Wang, Y.; Basou, S. Estimation of Optical Turbulence in the Atmospheric Surface Layer from Routine Meteorological Observations. In Laser Communication and Propagation through the Atmosphere and Oceans III; SPIE: Bellingham, WA, USA, 2014; Volume 9224. [Google Scholar] [CrossRef]
- Lionis, A.; Peppas, K.; Nistazakis, H.E.; Tsigopoulos, A.; Cohn, K.; Zagouras, A. Using Machine Learning Algorithms for Accurate Received Optical Power Prediction of an FSO Link over a Maritime Environment. Photonics 2021, 8, 212. [Google Scholar] [CrossRef]
- Jellen, C.; Burkhardt, J.; Brownell, C.; Nelson, C. Machine learning informed predictor importance measures of environmental parameters in maritime optical turbulence. Appl. Opt. 2020, 59, 6379–6389. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Basu, S. Using an artificial network approach to estimate surface-layer optical turbulence at Mauna Loa, Hawaii. Opt. Lett. 2016, 41, 2334–2337. [Google Scholar] [CrossRef] [PubMed]
- Jellen, C.; Oakley, M.; Burkhardt, J.; Brownell, C.; Nelson, C. Machine-learning informed macro-meteorological models for the near maritime environment. Appl. Opt. 2021, 60, 2938–2951. [Google Scholar] [CrossRef] [PubMed]
- Vorontsov, A.; Vorontsov, M.; Filimonov, G.; Polnau, E. Atmospheric Turbulence Study with Deep Machine Learning of Intensity Scintillation Patterns. Appl. Sci. 2020, 10, 8136. [Google Scholar] [CrossRef]
- Lohani, S.; Glasser, R.T. Turbulence correction with artificial neural networks. Opt. Lett. 2018, 43, 2611–2614. [Google Scholar] [CrossRef] [PubMed]
- Fiorino, S. An Overview of Weather Effects on HEL Propagation. Lecture Notes. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2019. [Google Scholar]
- Frederickson, P. Modeling Optical Turbulence and its Impacts on HEL Performance in a Maritime Environment. Lecture Notes. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2019. [Google Scholar]
- Oermann, R.J. Novel Methods for the Quantification of Atmospheric Turbulence Strength in the Atmospheric Surface Layer. Ph.D. Thesis, School of Chemistry and Physics, University of Adelaide, Adelaide, Australia, 2014. [Google Scholar]
- Xu, M.; Shao, S.; Liu, Q.; Sun, G.; Han, Y.; Weng, N. Optical Turbulence Profile Forecasting and Verification in the Offshore Atmospheric Boundary Layer. Appl. Sci. 2021, 11, 8523. [Google Scholar] [CrossRef]
- Lamprecht, C.; Bekhrad, P.; Ivanov, H.; Leitgeb, E. Modelling the Refractive Index Structure Parameter: A ResNet Approach. In Proceedings of the 2020 International Conference on Broadband Communications for Next Generation Networks and Multimedia Applications (CoBCom), Graz, Austria, 7–9 July 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Xu, R.; Lv, P.; Xu, F.; Shi, Y. A survey of approaches for implementing optical neural networks. Opt. Laser Technol. 2021, 136, 106787. [Google Scholar] [CrossRef]
- Lionis, A.; Peppas, K.; Nistazakis, H.E.; Tsigopoulos, A.D.; Cohn, K. Experimental Performance Analysis of an Optical Communication Channel over Maritime Environment. Electronics 2020, 9, 1109. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).