Two-Step Validation of a New Wireless Inertial Sensor System: Application in the Squat Motion
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
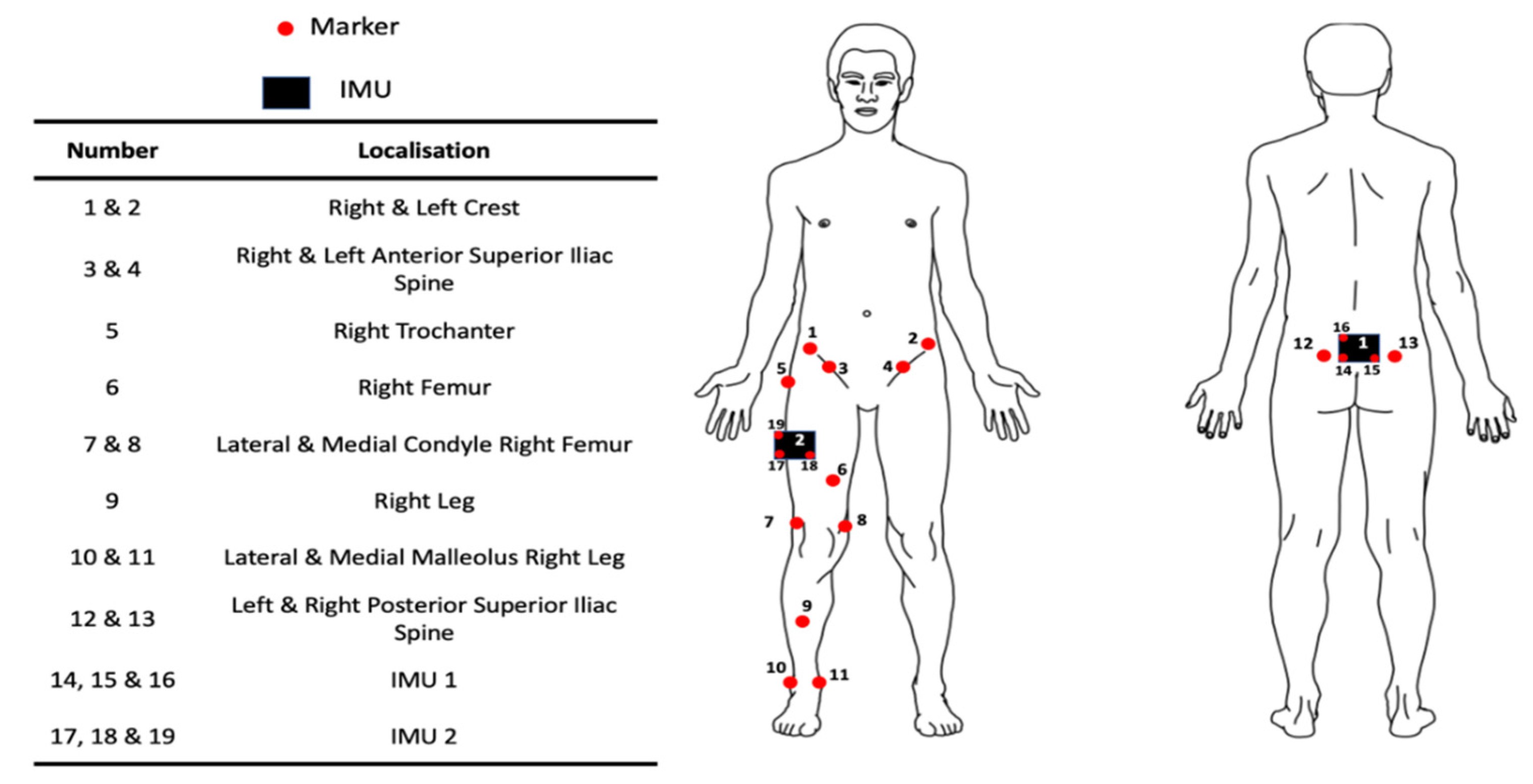
2.2. Sensor Validation
2.3. Functional Validation
2.4. Data Processing
2.4.1. Filtering and Interpolation
2.4.2. Linear Acceleration Computation
2.4.3. Thigh and IMU Sensor Orientation
2.5. Data Analysis
3. Results
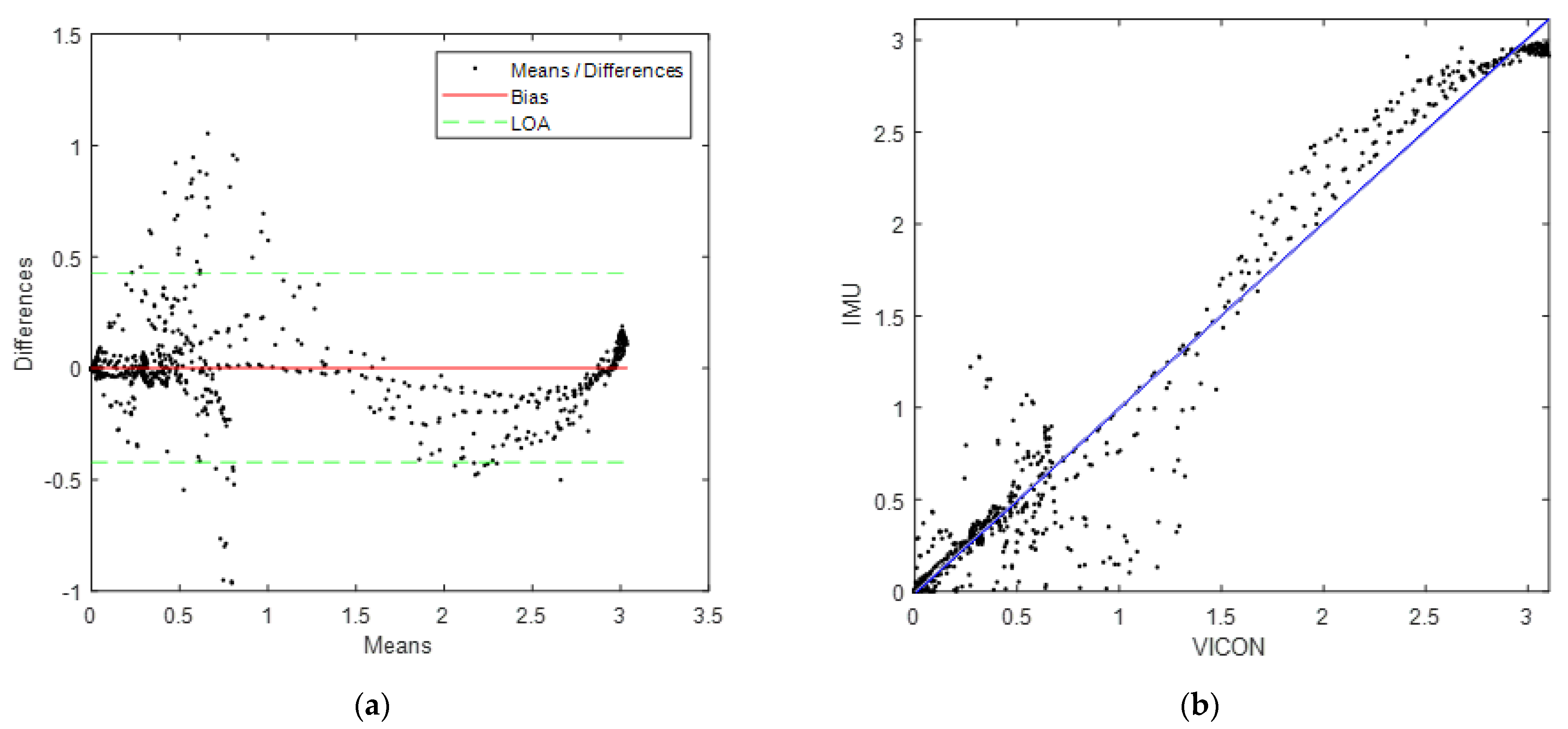
3.1. Sensor Validation
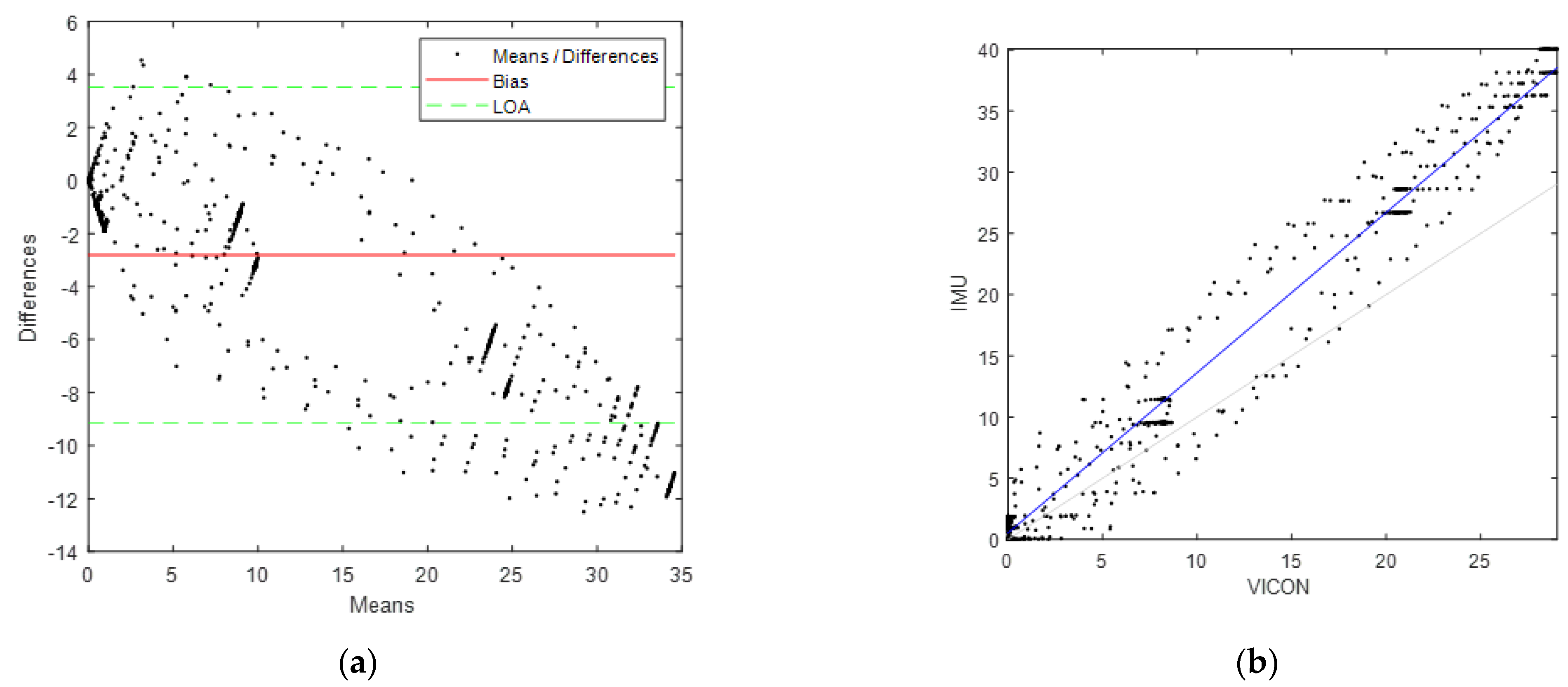
3.2. Segmental Functional Validation
4. Discussion
4.1. Limitations
4.2. Validation Methodological Tools
4.3. Sensor Validation
4.4. Functional Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Cross-Correlation Algorithm
- Computing the average point of the pelvis cluster in VICON.
- Double derivation of the trajectory to obtain linear acceleration (accel_vic).
- Cross-correlation (xcorr MATLAB build-in function) of the accel_vic with accel_imu, i.e., the computed linear acceleration of the pelvis IMU (see Figure A1).
- Identification of the cross-correlation maximum value r_max.
- Synchronization of the IMU and VICON signals at r_max time.
- Cropping of the IMU and VICON data to obtain similar length for both signals.


References
- Cieza, A.; Causey, K.; Kamenov, K.; Hanson, S.W.; Chatterji, S.; Vos, T. Global Estimates of the Need for Rehabilitation Based on the Global Burden of Disease Study 2019: A Systematic Analysis for the Global Burden of Disease Study 2019. Lancet 2020, 396, 2006–2017. [Google Scholar] [CrossRef]
- Hartvigsen, J.; Hancock, M.J.; Kongsted, A.; Louw, Q.; Ferreira, M.L.; Genevay, S.; Hoy, D.; Karppinen, J.; Pransky, G.; Sieper, J.; et al. What Low Back Pain Is and Why We Need to Pay Attention. Lancet 2018, 391, 2356–2367. [Google Scholar] [CrossRef] [Green Version]
- Dionne, C.E.; Dunn, K.M.; Croft, P.R.; Nachemson, A.L.; Buchbinder, R.; Walker, B.F.; Wyatt, M.; Cassidy, J.D.; Rossignol, M.; Leboeuf-Yde, C.; et al. A Consensus Approach Toward the Standardization of Back Pain Definitions for Use in Prevalence Studies. Spine 2008, 33, 95–103. [Google Scholar] [CrossRef] [Green Version]
- Bourigua, I.; Simoneau, E.; Leteneur, S.; Gillet, C.; Barbier, F. Revue de la littérature La lombalgie chronique: Définitions, Evaluation et Traitement. Sci. Technol. Handicap. 2010, 4, 9–38. [Google Scholar] [CrossRef]
- Mounce, K. Back Pain. Rheumatol. Oxf. Engl. 2002, 41, 1–5. [Google Scholar] [CrossRef]
- Andersson, G.B. Epidemiological Features of Chronic Low-Back Pain. Lancet 1999, 354, 581–585. [Google Scholar] [CrossRef]
- Poiraudeau, S.; Lefevre Colau, M.-M.; Fayad, F.; Rannou, F.; Revel, M. Lombalgies. EMC Rhumatol. Orthop. 2004, 1, 295–319. [Google Scholar] [CrossRef]
- Poiraudeau, S.; Palazzo, C. Avancées thérapeutiques de la lombalgie chronique: Revue systématique de la littérature des 5 dernières années. Ann. Phys. Rehabil. Med. 2012, 55, e282. [Google Scholar] [CrossRef] [Green Version]
- Dagenais, S.; Caro, J.; Haldeman, S. A Systematic Review of Low Back Pain Cost of Illness Studies in the United States and Internationally. Spine J. 2008, 8, 8–20. [Google Scholar] [CrossRef]
- Christie, H.J.; Kumar, S.; Warren, S.A. Postural Aberrations in Low Back Pain. Arch. Phys. Med. Rehabil. 1995, 76, 218–224. [Google Scholar] [CrossRef]
- Mientjes, M.I.V.; Frank, J.S. Balance in Chronic Low Back Pain Patients Compared to Healthy People under Various Conditions in Upright Standing. Clin. Biomech. 1999, 14, 710–716. [Google Scholar] [CrossRef]
- Della Volpe, R.; Popa, T.; Ginanneschi, F.; Spidalieri, R.; Mazzocchio, R.; Rossi, A. Changes in Coordination of Postural Control during Dynamic Stance in Chronic Low Back Pain Patients. Gait Posture 2006, 24, 349–355. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.A.; Stabbert, H.; Bagwell, J.J.; Teng, H.-L.; Wade, V.; Lee, S.-P. Do People with Low Back Pain Walk Differently? A Systematic Review and Meta-Analysis. J. Sport Health Sci. 2022. [Google Scholar] [CrossRef] [PubMed]
- Lee, R.Y.W.; Laprade, J.; Fung, E.H.K. A Real-Time Gyroscopic System for Three-Dimensional Measurement of Lumbar Spine Motion. Med. Eng. Phys. 2003, 25, 817–824. [Google Scholar] [CrossRef]
- Stolwijk, C.; Ramiro, S.; Vosse, D.; Landewé, R.; van der Heijde, D.; van Tubergen, A. Comparison of Tests for Lumbar Flexion and Hip Function in Patients with and without Axial Spondyloarthritis: Mobility Tests in Patients with and without Axial SpA. Arthritis Care Res. 2015, 67, 538–545. [Google Scholar] [CrossRef] [PubMed]
- Royer, A.; Cecconello, R. Bilans articulaires cliniques et goniométriques. Généralités. EMC Podol. Kinésithér. 2004, 1, 82–91. [Google Scholar] [CrossRef]
- Newton, M.; Waddell, G. Reliability and Validity of Clinical Measurement of the Lumbar Spine in Patients with Chronic Low Back Pain. Physiotherapy 1991, 77, 796–800. [Google Scholar] [CrossRef]
- Shirley, F.R.; O’Connor, P.; Robinson, M.E.; MacMillan, M. Comparison of Lumbar Range of Motion Using Three Measurement Devices in Patients with Chronic Low Back Pain. Spine 1994, 19, 779–783. [Google Scholar] [CrossRef]
- Hughes, G.T.G.; Camomilla, V.; Vanwanseele, B.; Harrison, A.J.; Fong, D.T.P.; Bradshaw, E.J. Novel Technology in Sports Biomechanics: Some Words of Caution. Sports Biomech. 2021, 1–9. [Google Scholar] [CrossRef]
- Mulders, J.V.; Goossens, S.; Monteyne, L.; Strycker, L.D.; Perre, L.V.D. Contactless Multi-Sensor Solution for E-Treatment of Musculoskeletal Disorders. IEEE Access 2021, 9, 20368–20375. [Google Scholar] [CrossRef]
- Cappelle, J.; Monteyne, L.; Van Mulders, J.; Goossens, S.; Vergauwen, M.; Van der Perre, L. Low-Complexity Design and Validation of Wireless Motion Sensor Node to Support Physiotherapy. Sensors 2020, 20, 6362. [Google Scholar] [CrossRef] [PubMed]
- Kobsar, D.; Charlton, J.M.; Tse, C.T.F.; Esculier, J.-F.; Graffos, A.; Krowchuk, N.M.; Thatcher, D.; Hunt, M.A. Validity and Reliability of Wearable Inertial Sensors in Healthy Adult Walking: A Systematic Review and Meta-Analysis. J. Neuroeng. Rehabil. 2020, 17, 62. [Google Scholar] [CrossRef] [PubMed]
- Robert-Lachaine, X.; Mecheri, H.; Muller, A.; Larue, C.; Plamondon, A. Validation of a Low-Cost Inertial Motion Capture System for Whole-Body Motion Analysis. J. Biomech. 2020, 99, 109520. [Google Scholar] [CrossRef] [PubMed]
- Robert-Lachaine, X.; Mecheri, H.; Larue, C.; Plamondon, A. Validation of Inertial Measurement Units with an Optoelectronic System for Whole-Body Motion Analysis. Med. Biol. Eng. Comput. 2017, 55, 609–619. [Google Scholar] [CrossRef] [PubMed]
- Bland, M.J.; Altman, D.G. Statistical Methods for Assessing Agreement between Two Methods of Clinical Measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Poitras, I.; Dupuis, F.; Bielmann, M.; Campeau-Lecours, A.; Mercier, C.; Bouyer, L.J.; Roy, J.-S. Validity and Reliability of Wearable Sensors for Joint Angle Estimation: A Systematic Review. Sensors 2019, 19, 1555. [Google Scholar] [CrossRef] [Green Version]
- Della Croce, U.; Leardini, A.; Chiari, L.; Cappozzo, A. Human Movement Analysis Using Stereophotogrammetry: Part 4: Assessment of Anatomical Landmark Misplacement and Its Effects on Joint Kinematics. Gait Posture 2005, 21, 226–237. [Google Scholar] [CrossRef]
- Lebel, K.; Boissy, P.; Hamel, M.; Duval, C. Inertial Measures of Motion for Clinical Biomechanics: Comparative Assessment of Accuracy under Controlled Conditions-Effect of Velocity. PLoS ONE 2013, 8, e79945. [Google Scholar] [CrossRef]
- Taylor, L.; Miller, E.; Kaufman, K.R. Static and Dynamic Validation of Inertial Measurement Units. Gait Posture 2017, 57, 80–84. [Google Scholar] [CrossRef]
- Lepetit, K.; Ben Mansour, K.; Boudaoud, S.; Kinugawa-Bourron, K.; Marin, F. Evaluation of the Kinetic Energy of the Torso by Magneto-Inertial Measurement Unit during the Sit-to-Stand Movement. J. Biomech. 2018, 67, 172–176. [Google Scholar] [CrossRef]
- Miller, E.J.; Kaufman, K.R. Cross-Sectional Validation of Inertial Measurement Units for Estimating Trunk Flexion Kinematics during Treadmill Disturbances. Med. Eng. Phys. 2019, 70, 51–54. [Google Scholar] [CrossRef] [PubMed]
- Burns, S.A.; Cleland, J.A.; Rivett, D.A.; Snodgrass, S.J. Examination Procedures and Interventions for the Hip in the Management of Low Back Pain: A Survey of Physical Therapists. Braz. J. Phys. Ther. 2019, 23, 419–427. [Google Scholar] [CrossRef] [PubMed]
- Thiry, P.; Nocent, O.; Buisseret, F.; Bertucci, W.; Thevenon, A.; Simoneau-Buessinger, E. Sample Entropy as a Tool to Assess Lumbo-Pelvic Movements in a Clinical Test for Low-Back-Pain Patients. Entropy 2022, 24, 437. [Google Scholar] [CrossRef] [PubMed]
- Horenstein, R.E.; Lewis, C.L.; Yan, S.; Halverstadt, A.; Shefelbine, S.J. Validation of Magneto-Inertial Measuring Units for Measuring Hip Joint Angles. J. Biomech. 2019, 91, 170–174. [Google Scholar] [CrossRef]
- Hubaut, R.; Guichard, R.; Greenfield, J.; Blandeau, M. Validation of an Embedded Motion-Capture and EMG Setup for the Analysis of Musculoskeletal Disorder Risks during Manhole Cover Handling. Sensors 2022, 22, 436. [Google Scholar] [CrossRef]
- Storm, F.A.; Cesareo, A.; Reni, G.; Biffi, E. Wearable Inertial Sensors to Assess Gait during the 6-Minute Walk Test: A Systematic Review. Sensors 2020, 20, 2660. [Google Scholar] [CrossRef]
- Dumas, R.; Aissaoui, R.; de Guise, J.A. A 3D Generic Inverse Dynamic Method Using Wrench Notation and Quaternion Algebra. Comput. Methods Biomech. Biomed. Eng. 2004, 7, 159–166. [Google Scholar] [CrossRef]
- Dumas, R.; Chèze, L.; Verriest, J.-P. Adjustments to McConville et al. and Young et al. Body Segment Inertial Parameters. J. Biomech. 2007, 40, 543–553. [Google Scholar] [CrossRef]
- Dumas, R.; Robert, T.; Pomero, V.; Cheze, L. Joint and Segment Coordinate Systems Revisited. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 183–185. [Google Scholar] [CrossRef]
- Montenij, L.J.; Buhre, W.F.; Jansen, J.R.; Kruitwagen, C.L.; de Waal, E.E. Methodology of Method Comparison Studies Evaluating the Validity of Cardiac Output Monitors: A Stepwise Approach and Checklist. Br. J. Anaesth. 2016, 116, 750–758. [Google Scholar] [CrossRef] [Green Version]
- Ranstam, J. Methodological Note: Accuracy, Precision, and Validity. Acta Radiol. 2008, 49, 105–106. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.I.-K. A Concordance Correlation Coefficient to Evaluate Reproducibility. Biometrics 1989, 45, 255. [Google Scholar] [CrossRef] [PubMed]
- Desquilbet, L. Guide pratique de validation statistique de méthodes de mesure: Répétabilité, reproductibilité, et concordance. 2020; 48, preprint. [Google Scholar]
- Guichard, R.; Blandeau, M.; Leteneur, S. Localization of IMU Sensors Affects the Estimation of Soft Tissue Wobbling: A Preliminary Study. Comput. Methods Biomech. Biomed. Eng. 2021, 24, 3. [Google Scholar]
- Koska, D.; Gaudel, J.; Hein, T.; Maiwald, C. Validation of an Inertial Measurement Unit for the Quantification of Rearfoot Kinematics during Running. Gait Posture 2018, 64, 135–140. [Google Scholar] [CrossRef]
- Kottner, J.; Streiner, D.L. The Difference between Reliability and Agreement. J. Clin. Epidemiol. 2011, 64, 701–702. [Google Scholar] [CrossRef]
- ISO 5725-2:2019; Accuracy (Trueness and Precision) of Measurement Methods and Results—Part 2: Basic Method for the Determination of Repeatability and Reproducibility of a Standard Measurement Method. ISO: Geneva, Switzerland, 2019. Available online: https://www.iso.org/cms/render/live/en/sites/isoorg/contents/data/standard/06/94/69419.html (accessed on 2 September 2021).
- Lepetit, K. Évaluation Biomécanique des Capacités Musculo-Squelettiques Lors de la Transition Assis/Debout au Moyen D’une Centrale Inertielle en Situation Ecologique. Ph.D. Thesis, Université de Technologie de Compiègne, Compiègne, France, 2019. [Google Scholar]
- Cappozzo, A.; Catani, F.; Della Croce, U.; Leardini, A. Position and Orientation in Space of Bones during Movement: Anatomical Frame Definition and Determination. Clin. Biomech. 1995, 10, 171–178. [Google Scholar] [CrossRef]


| Age (Years) | Weight (kg) | Height (cm) | |
|---|---|---|---|
| All subjects | 30.7 ± 10.2 | 72.6 ± 15.6 | 173.1 ± 7.7 |
| Female | 34.7 ± 9.3 | 60.3 ± 13.7 | 165.0 ± 3.5 |
| Male | 30.9 ± 11.1 | 76.9 ± 15.1 | 176.4 ±6.9 |
| Sensor | Parameter Name | IMU Back | IMU Thigh |
|---|---|---|---|
| Accelerometer (m/s2) | bias | 0.001 (0.004) | 0.000 (0.022) |
| lower LOA | −0.252 (0.111) | −0.293 (0.152) | |
| upper LOA | 0.254 (0.119) | 0.294 (0.180) | |
| precision | 0.067 (0.039) | 0.078 (0.052) | |
| r2 | 0.962 (0.005) | 0.951 (0.031) | |
| Lin’s CCC | 0.978 (0.003) | 0.971 (0.017) | |
| Gyroscope (°/s) | bias | −4.265 (2.119) | −4.328 (2.068) |
| lower LOA | −11.597 (3.491) | −11.555 (3.428) | |
| upper LOA | 3.067 (0.863) | 2.899 (0.902) | |
| precision | 4.405 (2.134) | 4.470 (2.078) | |
| r2 | 0.983 (0.007) | 0.982 (0.007) | |
| Lin’s CCC | 0.886 (0.045) | 0.885 (0.045) |
| Sensor | Parameter Name | IMU Thigh |
|---|---|---|
| Yaw orientation angle (°) | bias | 1.742 (3.178) |
| lower LOA | −7.883 (3.387) | |
| upper LOA (°) | 11.367 (6.252) | |
| precision (°) | 4.756 (2.402) | |
| r2 | 0.965 (0.041) | |
| Lin’s CCC | 0.971 (0.039) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blandeau, M.; Guichard, R.; Hubaut, R.; Leteneur, S. Two-Step Validation of a New Wireless Inertial Sensor System: Application in the Squat Motion. Technologies 2022, 10, 72. https://doi.org/10.3390/technologies10030072
Blandeau M, Guichard R, Hubaut R, Leteneur S. Two-Step Validation of a New Wireless Inertial Sensor System: Application in the Squat Motion. Technologies. 2022; 10(3):72. https://doi.org/10.3390/technologies10030072
Chicago/Turabian StyleBlandeau, Mathias, Romain Guichard, Rémy Hubaut, and Sébastien Leteneur. 2022. "Two-Step Validation of a New Wireless Inertial Sensor System: Application in the Squat Motion" Technologies 10, no. 3: 72. https://doi.org/10.3390/technologies10030072
APA StyleBlandeau, M., Guichard, R., Hubaut, R., & Leteneur, S. (2022). Two-Step Validation of a New Wireless Inertial Sensor System: Application in the Squat Motion. Technologies, 10(3), 72. https://doi.org/10.3390/technologies10030072






