Two-Level Hierarchical-Interaction-Based Group Formation Control for MAV/UAVs
Abstract
:1. Introduction
2. Preliminaries and Problem Formulation
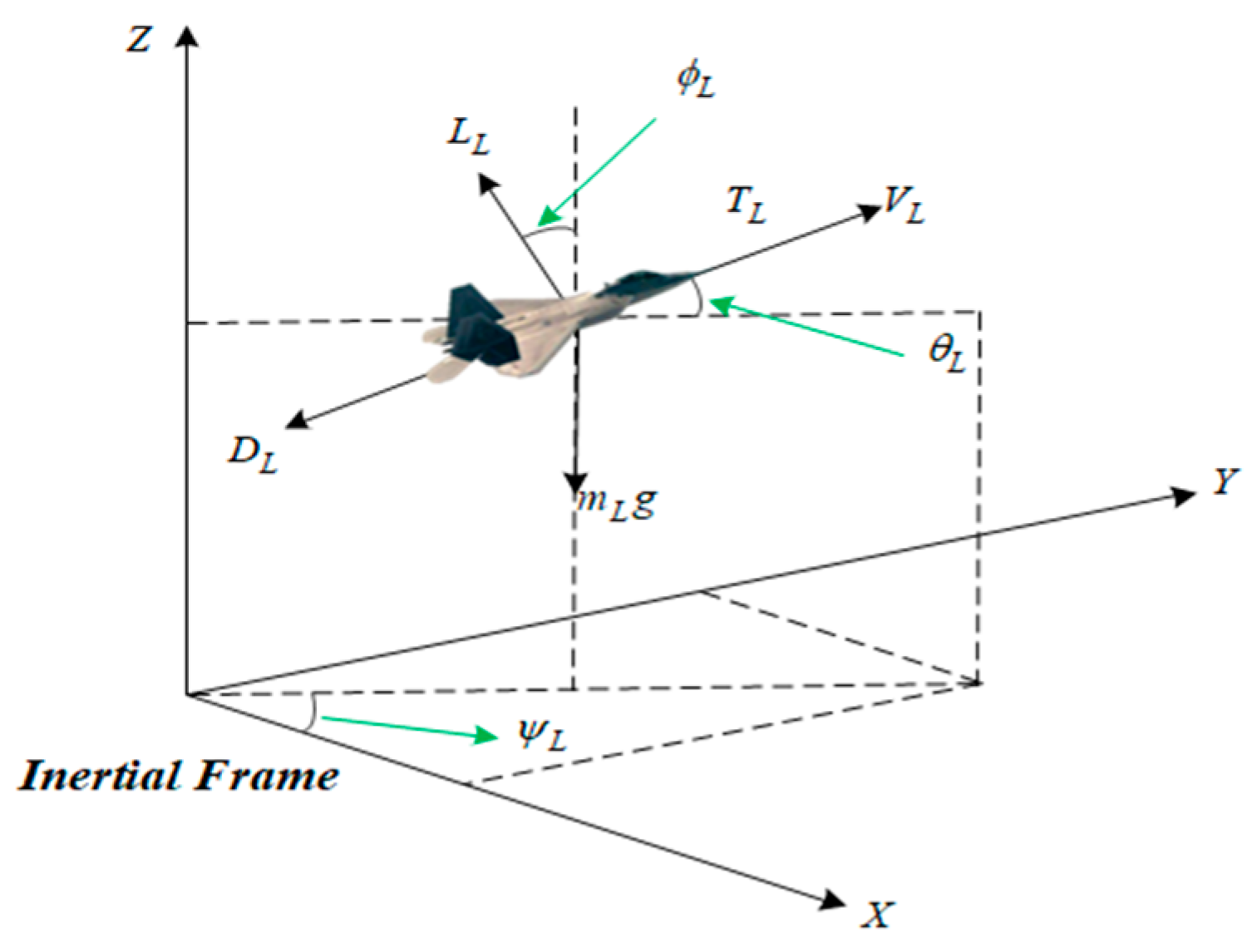
2.1. Mathematical Model of MAV
2.2. Mathematical Model of UAVs
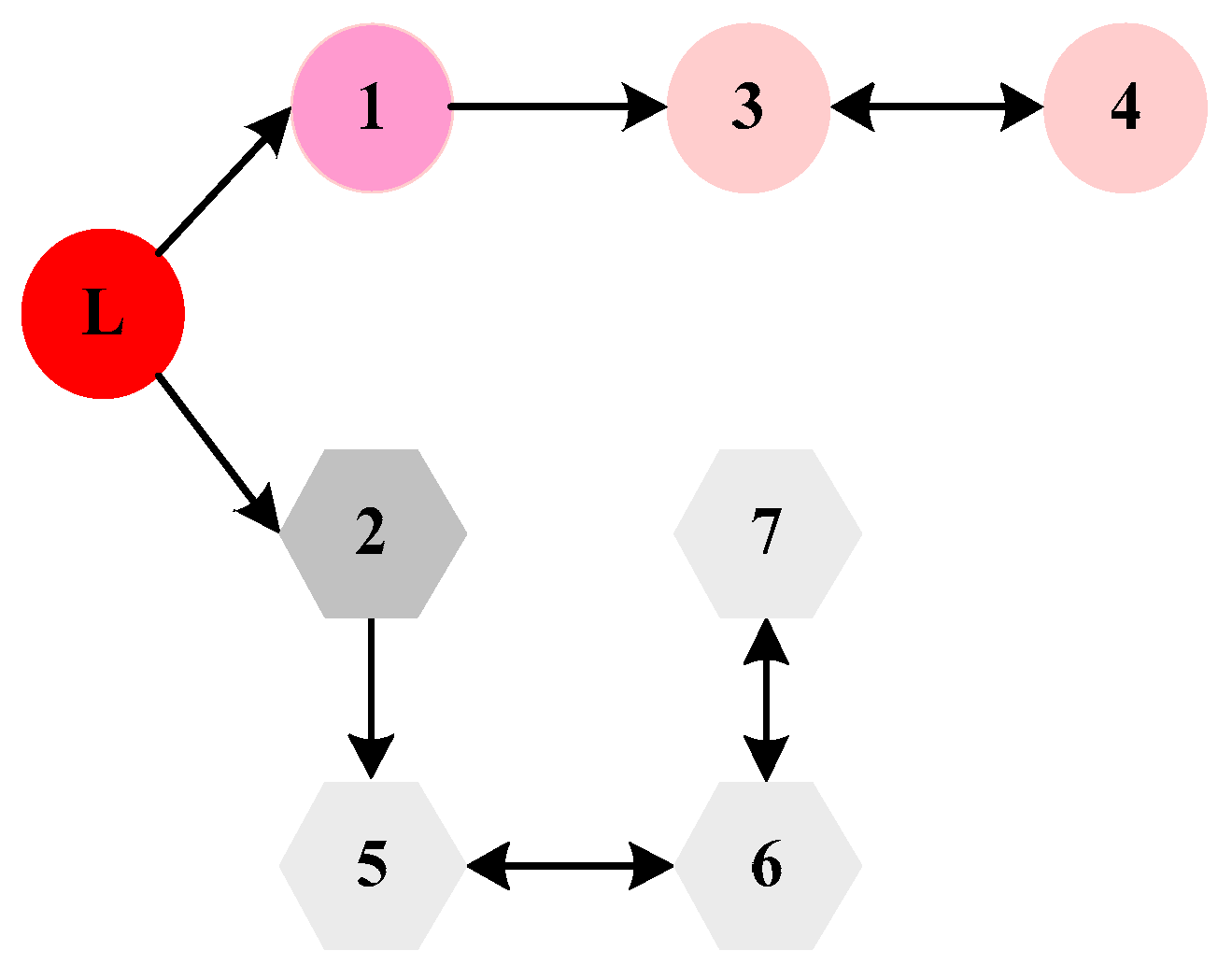
2.3. Group Formation Interaction Topology
2.4. Group-Based Hierarchical Structure of MAV/UAVs
2.5. Group Formation Control Objective
3. MAV/UAV Group Formation Controllers Design
3.1. MAV Trajectory Tracking Controller Design
3.2. UAVs Formation Controller Design
3.3. Stability Analysis
3.3.1. Stability Analysis of Theorem 1
3.3.2. Stability Analysis of Theorem 2
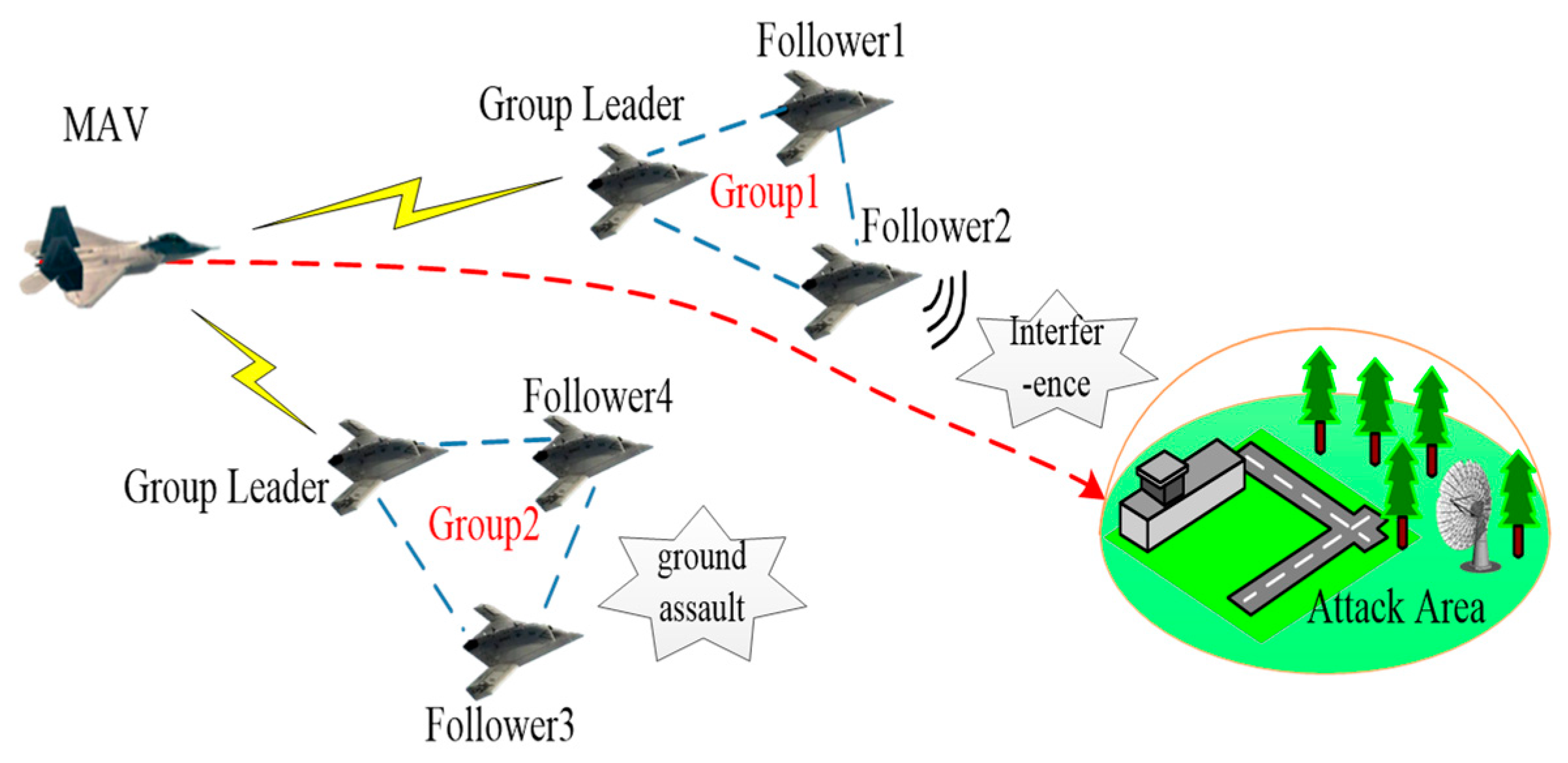
4. Applications: Penetration and Assault Missions of MAV/UAVs
4.1. Simulation Scenario
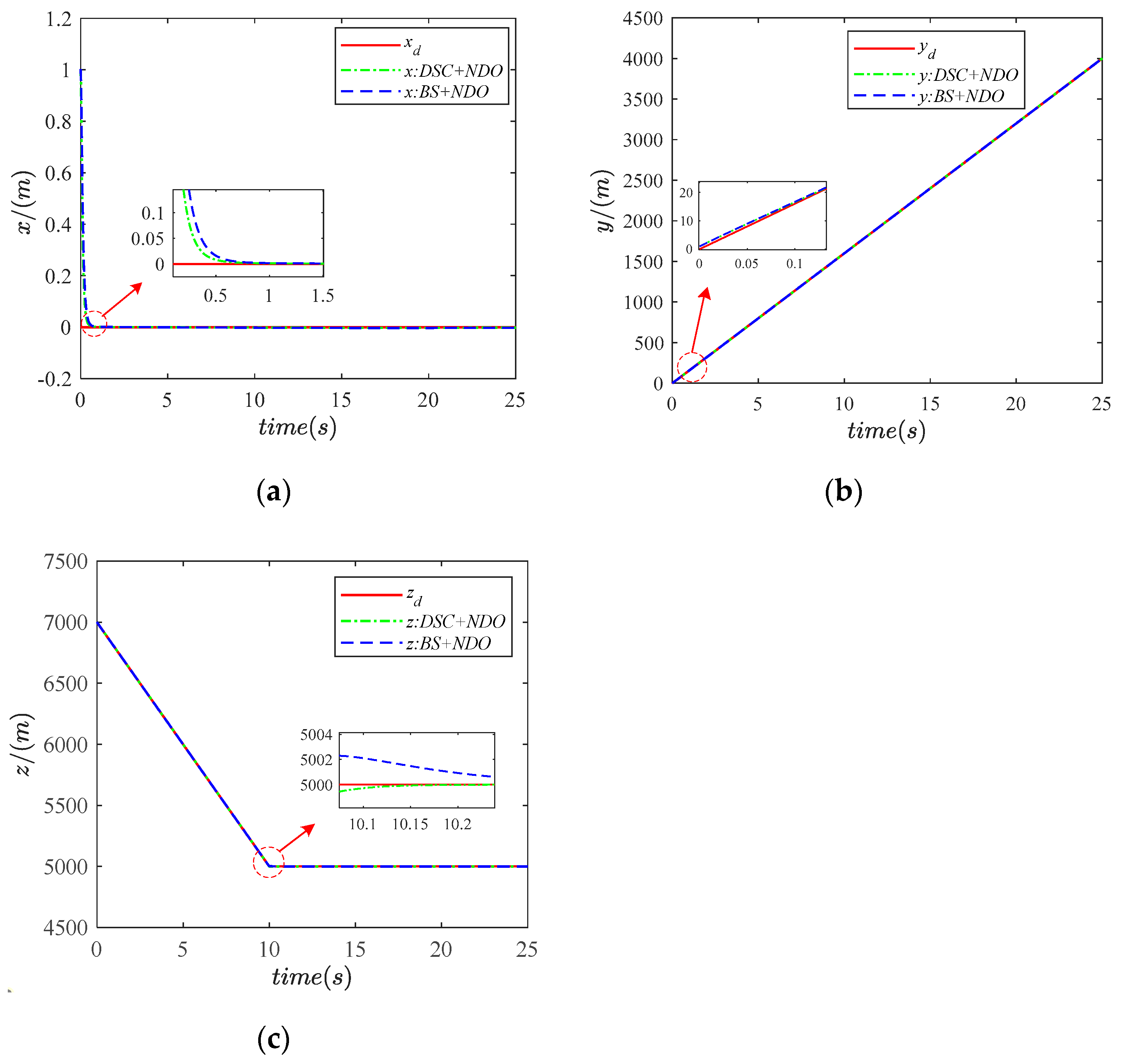
4.2. Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fan, J.R.; Li, D.G.; Li, R.P.; Wang, Y. Analysis on MAV/UAV cooperative combat based on complex network. Def. Technol. 2020, 16, 150–157. [Google Scholar] [CrossRef]
- Zhong, Y.; Yao, P.Y.; Zhang, J.Y.; Wan, L. Formation and adjustment of manned/unmanned combat aerial vehicle cooperative engagement system. J. Syst. Eng. Electron. 2018, 29, 756–767. [Google Scholar]
- Yin, S.; He, R.J.; Li, J.J.; Chen, L.; Zhang, S. Research on the operational mode of manned/unmanned collaboratively detecting drone swarm. In Proceedings of the IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 15–17 October 2021. [Google Scholar]
- Gong, Z.; Zhou, Z.; Wang, Z.; Lv, Q.; Xu, J.; Jiang, Y. Coordinated formation guidance law for fixed-wing UAVs based on missile parallel approach method. Aerospace 2022, 9, 272. [Google Scholar] [CrossRef]
- Rosa, M.R. Leader-Follower synchronization of uncertain Euler-Lagrange dynamics with input constraints. Aerospace 2020, 7, 127. [Google Scholar] [CrossRef]
- Liu, S.G.; Huang, F.P.; Yan, B.B.; Zhang, T.; Liu, R.; Liu, W. Optimal design of multimissile formation based on an adaptive SA-PSO algorithm. Aerospace 2021, 9, 21. [Google Scholar] [CrossRef]
- Zhou, D.J.; Wang, Z.J.; Schwager, M. Agile coordination and assistive collision avoidance for quadrotor swarms using virtual structures. IEEE Trans. Robot. 2018, 34, 916–923. [Google Scholar] [CrossRef]
- He, L.L.; Peng, B.; Liang, X.L.; Zhang, J.Q.; Wang, W.J. Feedback formation control of UAV swarm with multiple implicit leaders. Aerosp. Sci. Technol. 2018, 72, 327–334. [Google Scholar] [CrossRef]
- Alfeo, A.L.; Cimino, M.; Vaglini, G. Enhancing biologically inspired swarm behavior: Metaheuristics to foster the optimization of UAVs coordination in target search. Comput. Oper. Res. 2019, 110, 34–47. [Google Scholar] [CrossRef]
- Qiu, H.X.; Duan, H.B.; Fan, Y.M. Multiple unmanned aerial vehicle autonomous formation based on the behavior mechanism in pigeon flocks. Control Theory Appl. 2015, 32, 1298–1304. [Google Scholar]
- Dong, X.W.; Hu, G.Q. Time-varying formation control for general linear multi-agent systems with switching directed topologies. Automatica. 2016, 73, 47–55. [Google Scholar] [CrossRef]
- Sun, J.; Geng, Z.; Lv, Y.; Li, Z.; Ding, Z. Distributed adaptive consensus disturbance rejection for multi-agent systems on directed graphs. IEEE Trans. Control Netw. Syst. 2018, 5, 629–639. [Google Scholar] [CrossRef]
- Yan, D.H.; Zheng, W.G.; Chen, H. Design a multi-constraint formation controller based on improved MPC and consensus for quadrotors. Aerospace 2022, 9, 94. [Google Scholar] [CrossRef]
- Wu, L.Y.; Han, W. Design of cooperative control system for a carrier-based aircraft/unmanned aerial vehicles formation. In Proceedings of the 5th International Conference on Control Science and Systems Engineering (ICCSSE), Shanghai, China, 14–16 August 2019. [Google Scholar]
- Guezy, H.M. Hybrid consensus-based formation control of fixed-wing MUAVs. Cybern. Syst. 2017, 48, 71–83. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, Y.; Xu, S.D. Multiple UAVs cooperative formation forming control based on back-stepping-like approach. J. Syst. Eng. Electron. 2018, 29, 816–822. [Google Scholar]
- Chen, H.; Wang, X.; Shen, L.; Cong, Y. Formation flight of fixed-wing UAV swarms: A group-based hierarchical approach. Chin. J. Aeronaut. 2021, 34, 504–515. [Google Scholar] [CrossRef]
- Dong, Z.N.; Zhang, M.Y.; Liu, Y. Control method of manned/unmanned aerial vehicle cooperative formation based on mission effectiveness. In Proceedings of the IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016. [Google Scholar]
- Waydo, S.; Hauser, J.; Bailey, R.; Klavins, E.; Murray, R. UAV as a reliable wingman: A flight demonstration. IEEE Trans. Control Syst. Technol. 2007, 15, 680–688. [Google Scholar] [CrossRef]
- Ma, Q.; Wang, Z.; Miao, G.Y. Second-order group consensus for multi-agent systems via pinning leader-following approach. J. Frankl. Inst. 2014, 351, 1288–1300. [Google Scholar] [CrossRef]
- Dong, X.W.; Li, Q.D.; Zhao, Q.L.; Ren, Z. Time-varying group formation analysis and design for second-order multi-agent systems with directed topologies. Neurocomputing 2016, 205, 367–374. [Google Scholar] [CrossRef]
- Li, Y.F.; Dong, X.W.; Li, Q.D.; Ren, Z. Time-varying group formation control for second-order multi-agent systems with switching directed topologies. In Proceedings of the 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017. [Google Scholar]
- Li, Y.F.; Dong, X.W.; Li, Q.D.; Ren, Z. Time-varying group formation tracking for second-order multi-agent systems with switching directed topologies. In Proceedings of the Name of the IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018. [Google Scholar]
- Yang, D.; Feng, Z.; Sha, R.; Ren, X. Robust control of a class of under-actuated mechanical systems with model uncertainty. Int. J. Control 2019, 92, 1567–1579. [Google Scholar] [CrossRef]
- Xu, J.L.; Hao, Y.P.; Wang, J.J.; Li, L. The control algorithm experimentation of coaxial rotor aircraft trajectory tracking based on backstepping sliding mode. Aerospace 2021, 8, 337. [Google Scholar] [CrossRef]
- Korayem, A.H.; Nekoo, S.R.; Korayem, M.H. Sliding mode control design based on the state-dependent Riccati equation: Theoretical and experimental implementation. Int. J. Control 2019, 92, 2136–2149. [Google Scholar] [CrossRef]
- Muslimov, T.Z.; Munasypov, R.A. Adaptive decentralized flocking control of multi-UAV circular formations based on vector fields and backstepping. ISA Trans. 2020, 107, 143–159. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wu, Z. Nonlinear attitude control scheme with disturbance observer for flexible spacecrafts. Nonlinear Dyn. 2015, 81, 257–264. [Google Scholar] [CrossRef]
- Fang, X.; Wu, A.; Shang, Y.; Dong, N. A novel sliding mode controller for small-scale unmanned helicopters with mismatched disturbance. Nonlinear Dyn. 2016, 83, 1053–1068. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Finite time fault tolerant control for robot manipulators using time delay estimation and continuous nonsingular fast terminal sliding mode control. IEEE Trans. Cybern. 2016, 47, 1681–1693. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, F.; Guo, Y.; Hua, C. Multivariable sliding mode backstepping controller design for quadrotor UAV based on disturbance observer. Sci. China Inf. Sci. 2018, 61, 112207. [Google Scholar] [CrossRef]
- Wu, L.Y.; Han, W.; Zhang, Y. Formation keeping control for a manned/unmanned aerial vehicle formation based on leader-follower strategy. Control Decis. 2021, 36, 2435–2441. [Google Scholar]
- Wang, D.D.; Zong, Q.; Tian, B. Neural network disturbance observer-based distributed finite-time formation tracking control for multiple unmanned helicopters. ISA Trans. 2018, 73, 208–226. [Google Scholar] [CrossRef]
- Yu, Z.Q.; Zhang, Y.M.; Qu, Y.H. Prescribed performance-based distributed fault-tolerant cooperative control for multi-UAVs. Trans. Inst. Meas. Control 2019, 41, 975–989. [Google Scholar] [CrossRef]
- Spooner, J.T.; Maggiore, M.; Ordonez, R. Stable Adaptive Control and Estimation for Nonlinear Systems: Neural and Fuzzy Approximator Techniques, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2004; pp. 31–36. [Google Scholar]
- Chen, L.; Duan, H. Collision-free formation-containment control for a group of UAVs with unknown disturbances. Aerosp. Sci. Technol. 2022, 126, 107618. [Google Scholar] [CrossRef]
- Qin, J.; Yu, C. Cluster consensus control of generic linear multi-agent systems under directed topology with acyclic partition. Automatica 2013, 49, 2898–2905. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Wang, S. Three-dimensional formation-containment control of underactuated AUVs with heterogeneous uncertain dynamics and system constraints. Ocean Eng. 2021, 238, 109661. [Google Scholar] [CrossRef]
- Li, D.Y.; Zhang, W.; He, W.; Li, C.; Ge, S.S. Two-layer distributed formation-containment control of multiple Euler–Lagrange systems by output feedback. IEEE Trans. Cybern. 2018, 49, 675–687. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Bhowmick, P.; Lanzon, A. Distributed adaptive time-varying group formation tracking for multiagent systems with multiple leaders on directed graphs. IEEE Trans. Control Netw. Syst. 2019, 7, 140–150. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Van, M. An enhanced robust fault tolerant control based on an adaptive fuzzy PID-nonsingular fast terminal sliding mode control for uncertain nonlinear systems. IEEE/ASME Trans. Mechatron. 2018, 23, 1362–1371. [Google Scholar] [CrossRef] [Green Version]




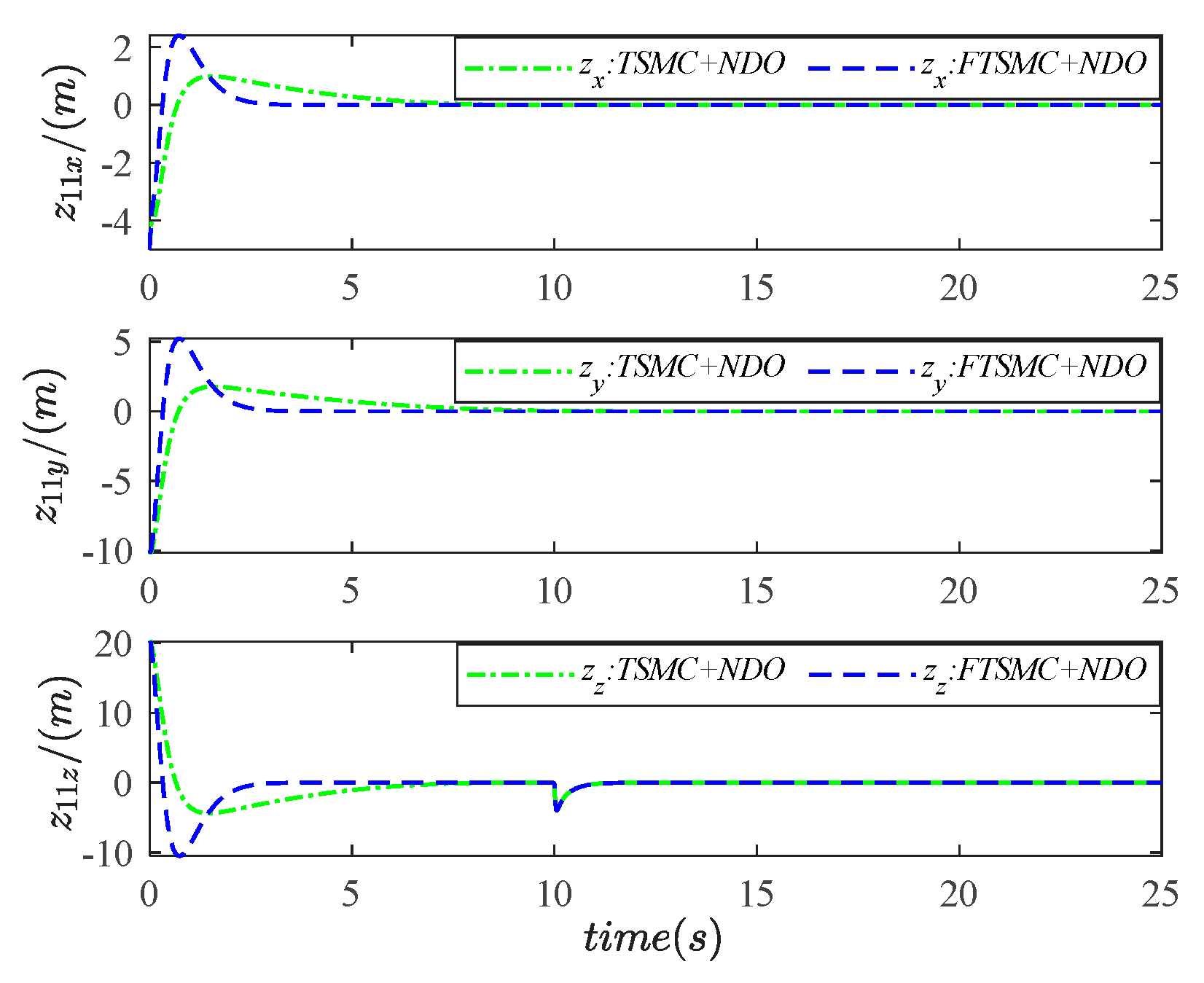
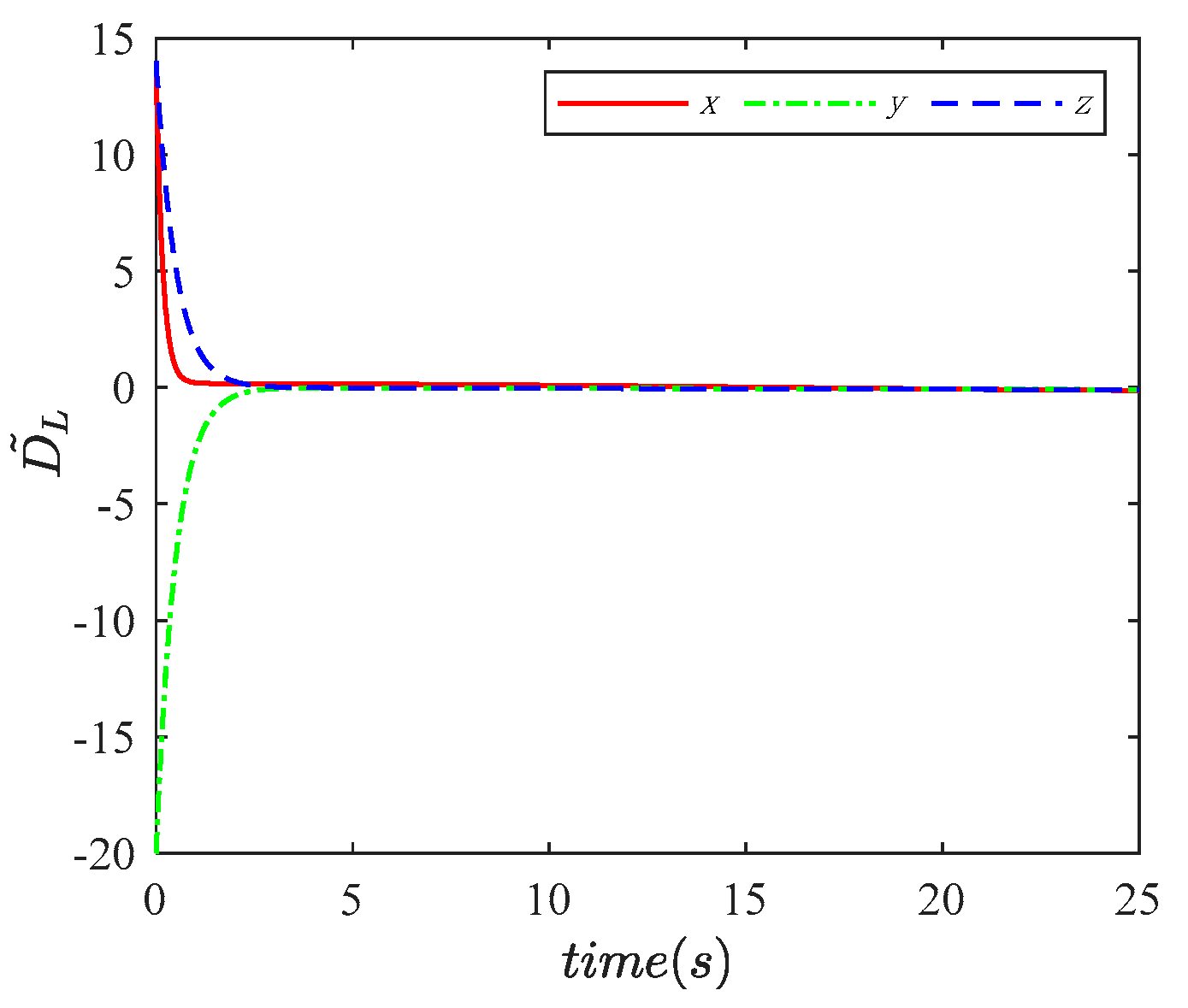

| Initial Position/(m) | Initial Velocity/(m/s) |
|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Liu, S.; Lv, M.; Zhang, B. Two-Level Hierarchical-Interaction-Based Group Formation Control for MAV/UAVs. Aerospace 2022, 9, 510. https://doi.org/10.3390/aerospace9090510
Wang H, Liu S, Lv M, Zhang B. Two-Level Hierarchical-Interaction-Based Group Formation Control for MAV/UAVs. Aerospace. 2022; 9(9):510. https://doi.org/10.3390/aerospace9090510
Chicago/Turabian StyleWang, Huan, Shuguang Liu, Maolong Lv, and Boyang Zhang. 2022. "Two-Level Hierarchical-Interaction-Based Group Formation Control for MAV/UAVs" Aerospace 9, no. 9: 510. https://doi.org/10.3390/aerospace9090510





