Multi-UAV Unbalanced Targets Coordinated Dynamic Task Allocation in Phases

Abstract

Unmanned aerial vehicles (UAVs) can be used in swarms to achieve multiple tasks cooperatively. Multi-UAV and multi-target cooperative task assignments are difficult. To solve the problem of unbalanced, phased, cooperative assignment between UAVs and tasks, we establish an unbalanced, phased task assignment model that considers the constraints of task execution, time, and target task execution demand. Based on an improved consensus-based bundle algorithm (CBBA), we propose a two-tier task bidding mechanism. According to dynamic changes in new tasks, we study a dynamic assignment strategy and propose a mechanism based on task continuity adjustment and time windows. Finally, a simulation experiment is used to verify the feasibility and effectiveness of the proposed allocation method in multi-UAV target assignment scenarios. The results show that the dynamic task assignment strategy can efficiently assign random new tasks as they arise.

1. Introduction

Under the current military context, unmanned aerial vehicles (UAVs) are widely used in reconnaissance, searching, firefighting, effectiveness evaluation, and other operational tasks [1]. However, in the future air combat environment, UAVs will be faced with complex and changeable environments. The cooperative environment and requirements of UAVs will also become complex [2], which will require efficient cooperation among UAVs to complete various objectives and tasks [3].

The UAV multi-objective assignment problem is a typical NP-hard problem. Reasonable consideration of the influences of practical factors and the constraint relationships between UAVs and targets are very important in establishing cooperative task assignment models and improving design and solution algorithms. The problem of multi-task cooperative assignment has been studied from the two aspects of random speed and time windows. When considering the constraints of kinematics, time, and resources, an improved genetic algorithm was proposed to solve the problem of random task assignment [4]. In [5], a discrete adaptive whale search optimization algorithm was proposed to study the task assignment problem. It comprehensively considers various constraints, such as limited resources, task priority, and obstacle avoidance. It features a search-intensity adaptive mechanism that balances exploration and development intensity and effectively improves the exploration ability. In [6], a two-stage hybrid auction algorithm was proposed. In its first level, urgent tasks are selected by using a selection function and task attribute values. In its second level, a new objective function is proposed that generates a reasonable task auction sequence, which improves the efficiency and robustness of the task allocation model.

In recent years, many scholars at home and abroad have carried out research on the UAV task assignment problem and proposed a variety of different types of task assignment problem models and solving methods. The problem model establishment is mainly divided into single-task assignment models and multi-task assignment models. The single task assignment model mainly includes the Multiple Travelling Salesman Problem [7] model and the Vehicle Routing Problem [8] model. The main feature of the model is that the UAV needs to traverse all the task targets. The model is simple but needs to be standardized in the actual problem processing process and is suitable for fewer task targets. In the multi-task assignment model, the Mixed-Integer Linear Programming [9] model is beneficial for describing the global constraints of numerical problems, better optimizing the UAV task execution sequence, and improving task assignment efficiency. However, the method is difficult to apply to situations where there is an imbalance between the number of UAVs and the number of tasks. The distribution idea of the Network Flow Optimization [10] model is to use the eigenvectors of network traffic for hierarchical division, which has good optimization characteristics, but the problem of low distribution efficiency often occurs when the number of tasks surges. Therefore, this paper aims at the problem of multi-UAV cooperative task assignment in stages, considers a variety of practical constraints, and combines the different execution requirements of various tasks in different time periods to establish a hierarchical multi-stage multi-UAV cooperative task allocation model so as to achieve reasonable planning of UAV formation collaborative execution tasks in different phases of task execution time windows.

In combat environments, the various battlefield situations are constantly changing. The emergence of new situations can make the original task allocation strategy unable to meet the new task execution requirements. Hence, there is an urgent need to carry out research on dynamic task allocation for multiple UAVs. In [11], aiming to solve the problem of the calculation times and flight distance involved in task allocation are too long, and so a dynamic task allocation mechanism based on a bionic algorithm was proposed. It dynamically allocates UAVs according to the number of task points and optimizes the allocation via a comparison mechanism. In [12], an improved task–assignment algorithm was proposed, which was applied to combat scenes with sudden threats and UAV losses. The algorithm is market-based and simulates the four stages of market bidding. Simulations prove that the algorithm has good robustness and can be well applied to the dynamic assignment of UAV cooperative timing tasks. In [13], a dynamic task allocation algorithm based on a task sequence mechanism was proposed. The available time period and task resources of each UAV are defined, and a conflict-free task allocation scheme is allocated to each UAV in real-time through an auction mechanism and consistency coordination. At present, research on the dynamic task allocation of multiple UAVs has mostly focused on execution costs and path planning. However, in actual situations, the task execution of multiple UAVs has strong time constraints [14], and the relationships between task completion time constraints and task benefits need to be considered [15].

At the current stage, the methods for solving the multi-UAV cooperative task assignment problem mainly include heuristic methods, mathematical programming methods, and intelligent optimization algorithms. Among them, the heuristic methods mainly include clustering methods [16]. The principle is to treat each task as a cluster for clustering and complete the task assignment when the task cluster and the number of system members reach an agreement. The advantage is that the time and space complexity of the algorithm is low, but its robustness and accuracy are poor. Mathematical programming methods mainly include exhaustive methods, integer programming methods, etc. Among them, integer programming methods [17] take small-scale problems as the research object and establish objective functions and constraints around the problem objectives to solve. The algorithm is flexible and easy to solve, but the computational load is large, and the solution efficiency is low, and it is difficult to adapt to the solution of large-scale problems. The principle of the intelligent optimization algorithm [18] is to adjust the solution time and quality to obtain a satisfactory solution within an acceptable time range. Its advantage is that the solution is stable and simple and can be combined with other methods, mainly including evolutionary algorithms and swarm intelligence algorithms. The above-solving algorithms are all applicable to the centralized task assignment mechanism. The centralized solution method has a simple solution mechanism and can theoretically obtain the optimal task assignment result. However, the algorithm solution is easily limited by the centralized structure and is not suitable for application in dynamic, uncertain task allocation scenarios, the real-time assignment performance is low, and the robustness is poor, which reduces the overall task assignment efficiency to a certain extent.

In the actual multi-UAV cooperative task assignment process, each UAV needs to assign tasks coordinately through information communication interaction. The distributed control system structure [19] has better structural flexibility and autonomy, and the current more widely used task allocation methods are the contract network algorithm and the auction algorithm in the market-like mechanism, and its core idea is to use the market auction mechanism to achieve task allocation [20]. Therefore, this paper adopts an improved algorithm of auction algorithm-consensus-based bundle algorithm to solve the distributed task assignment problem of multiple UAVs. Compared with the previous traditional distributed assignment algorithm, this algorithm adopts a task bidding concurrency mechanism and UAV neighborhood communication. The negotiation mechanism has better task allocation flexibility and efficiency and uses the consistency strategy to effectively avoid the occurrence of task conflicts.

Aiming at the above problems, this paper first establishes a multi-UAV, multi-objective, unbalanced, cooperative task assignment model that comprehensively considers various constraints [21]. An improved consensus-based bundle algorithm (CBBA) is used to solve the model [22,23]. Secondly, according to the dynamics of new task occurrence, a dynamic assignment mechanism based on task continuity adjustment and time-window matching is proposed [24,25] to achieve multi-UAV cooperative dynamic task assignment. Finally, a simulation experiment verifies the feasibility and effectiveness of the proposed method.

2. Materials and Methods

2.1. Task Assignment in Multi-UAV Cooperative Combat

2.1.1. Description of the Multi-UAV Cooperative Task Assignment Decision Problem

The multi-UAV cooperative task assignment problem refers to a cooperative task assignment scheme for multiple UAVs that considers their performance and task characteristics. It can meet specific constraints and maximize the benefit of task assignments. In the process of establishing a collaborative task allocation model, it is necessary to analyze the model’s constraints and optimization objectives [26]. The task execution constraints are related to timing, time, quantity, and demand.

(1)

For the ith UAV, the number of tasks it can perform should not exceed the maximum it can perform, namely:

$${\displaystyle \sum _{j=1}^{NT}}{x}_{ij}\le L_t$$

(1)

where $I$ and $J$ represent the UAV set and task set, respectively, where $I\triangleq \left\{1,\dots ,N_n\right\}$ and $J\triangleq \left\{1,\dots ,N_t\right\}$. $x_{ij}$ represents the assignment of UAV $i$ to task $j$. If the value is 1, it means that UAV $i$ is assigned to the task; otherwise, it is 0 (not assigned). $L_t$ represents the maximum number of tasks that each UAV can perform. $NT$ represents the number of tasks.

(2)

The number of UAVs that execute the jth goal should not exceed the upper limit of the number of UAVs, namely:

$${\displaystyle \sum _{i=1}^{NU}}{x}_{ij}\le L_i$$

(2)

where $L_i$ represents the maximum number of UAVs. $NU$ represents the number of UAVs.

(3)

When a UAV performs its mission, it needs to abide by certain task execution timing constraints; that is, it should first perform a reconnaissance mission before performing a strike mission, namely:

$$t_r^{T_j}\le t_c^{T_j}\begin{array}{cc}& \left(j=1,2,\cdots ,NT\right)\end{array}$$

(3)

where $t_r^{T_j}$ and $t_c^{T_j}$ indicate the starting times of the reconnaissance and strike missions, respectively.

(4)

A UAV’s mission needs to be executed within the executable time range of the mission, namely:

$$E{t}_i\le t_i\le L{t}_i$$

(4)

where $E{t}_i$ and $L{t}_i$ represent the start and end execution times, respectively. $t_i$ represents the time when the UAV $i$ performed the mission.

(5)

Different stages of task execution require different numbers of UAVs to perform cooperatively, namely:

$$TarU\left(t_{e{t}_i^k,l{t}_i^k}^{{}_j}\right)\in UAV\left(t_{e{t}_i^{*k},l{t}_i^{*k}}^{{}_j}\right)$$

(5)

where $TarU\left(t_{e{t}_i^k,l{t}_i^k}^{{}_j}\right)$ represents the required number of UAVs in the kth execution period $[e{t}_i^k,l{t}_i^k]$. of the jth target. $UAV\left(t_{e{t}_i^{*k},l{t}_i^{*k}}^{{}_j}\right)$ indicates the number of UAVs that can reach the task during period $\left[e{t}_i^{*k},l{t}_i^{*k}\right]$, and $\left[e{t}_i^k,l{t}_i^k\right]\in \left[e{t}_i^{*k},l{t}_i^{*k}\right]$.

In model optimization, the main considerations are to maximize the number of tasks performed by the UAVs and minimize the time spent on task execution. The cooperative tasks of the UAVs are defined as:

$$f_1={\displaystyle \sum _{i=1}^{NU}}\left({\displaystyle \sum _{j=1}^{NT}}{c}_{ij}\left(x_i,p_i\right)x_{ij}\right)$$

(6)

where $c_{ij}$ represents the revenue from task execution.

We define the time cost as:

$$f_2=\sum t_{ij}\cdot x_{ij}$$

(7)

In summary, the mathematical model of UAV cooperative target assignment is as follows:

$$\min \left(f_1^{-1},f_2\right)$$

$$s.t.\{\begin{array}{c}{\displaystyle \sum _{j=1}^{N_t}}{x}_{ij}\le L_t\\ {\displaystyle \sum _{j=1}^{N_n}}{x}_{ij}\le L_i\\ t_r^{T_j}\le t_c^{T_j}\\ E{t}_i\le t_i\le L{t}_i\\ TarU\left(t_{e{t}_i^k,l{t}_i^k}^j\right)\in UAV\left(t_{e{t}_i^{*k},l{t}_i^{*k}}^j\right)\\ x_{ij}\in \left\{0,1\right\}\end{array}$$

(8)

where the set revenue function satisfies $c_{ij}\left(x_i,p_i\right)\ge 0$ under any distribution scheme $x_i$ and task execution sequence $p_i$.

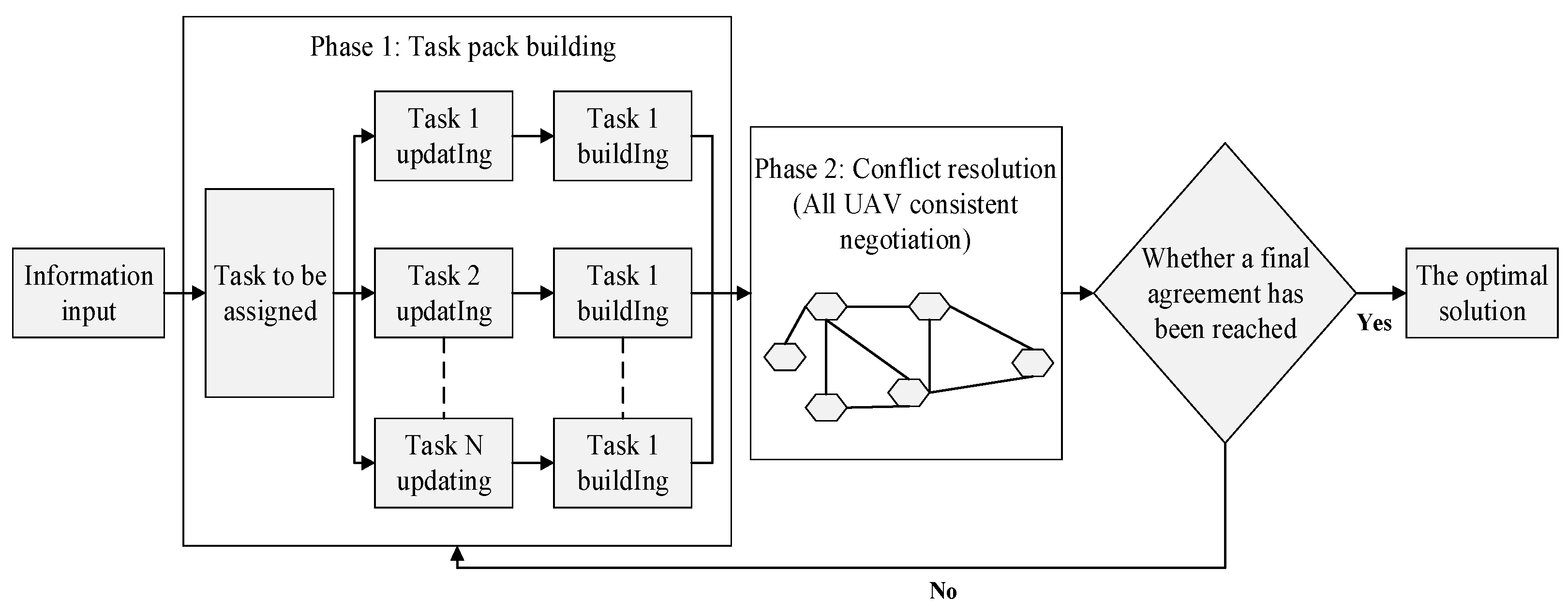
2.1.2. Consensus-Based Bundle Algorithm

In this paper, the consensus-based bundle algorithm is used to solve the dynamic task assignment problem of multi-UAV cooperation [27]. The assignment process mainly consists of task selection and conflict resolution. First, based on the construction of their own task package and execution path, each agent calculates the income from adding new tasks and compares it with the winning bid price of the current task. When the income is higher than the winning bid, it is added to the task package to achieve task selection. Secondly, to achieve consistent mission selection, the agent needs to know all kinds of bidding information with all agents, which mainly contains the winning bid, the winner of the sets, and a timestamp. According to these information interactions, all agents update their task packages and task execution paths in real time. Through continuous task selection and conflict resolution, conflict-free task assignment results are finally obtained. The specific execution mechanism is shown in Figure 1.

2.1.3. Algorithmic Information Structure

Assume that all UAVs in the UAV formation are set as $L\triangleq \left\{1,2,\dots ,N_n\right\}$, and the task execution target is represented by $J\triangleq \left\{1,2,\dots ,N_t\right\}$. The various elements that need to be stored and updated by each UAV in the process of task allocation mainly include:

(1)

Task package $b_i$: Vector $b_i=\left\{b_{i1},b_{i2}\dots ,b_{in}\right\}$ represents the task set assigned to UAV $i$, which is arranged in the order of insertion.

(2)

Task path $p_i$: $p_i=\left\{p_{i1},p_{i2},\dots ,p_{in}\right\}$ represents the execution list of the task set assigned to UAV $i$, and each task element starts its specific execution according to the task path.

(3)

Winner set $z_i$: $N_n\times N_t$-dimensional matrix $z_i$ represents the task bidding information currently acquired by UAV $i$; $z_{ij}^k=1$ represents that UAV $i$ confirms that UAV $k$ is the bidding winner of task $j$; otherwise, it is 0.

(4)

Winning bid price set $y_i$: Matrix $y_i$ represents the UAV bidding information confirmed by UAV $i$, which corresponds to the matrix of the winner set.

(5)

Timestamp $s_i$: $s_i$ represents the latest moment of information exchange between UAV $i$ and its neighbouring UAVs. This plays an important role in the conflict resolution stage and represents the update degree of information obtained by the current interaction between UAV and other UAVs.

2.1.4. Task Selection Mechanism Improvement

In the process of task selection, in order to maximize the benefits of task execution, task $j$ is added to task set $b_i$ in each UAV iteration until the end of the iteration cycle. The total revenue of UAV i’s task allocation is:

$$S_i^{p_i}={\displaystyle \sum _j}\left(c_{ij}-{\zeta }_{ij}\right)$$

(9)

where $c_{ij}$ is the revenue from task execution, which is expressed as follows:

$$\grave{{\mathrm{c}}_{ij}}=\{\begin{array}{cc}{K}_{ij}\times e^{-\lambda \left(t_{ijs}-t_{js}\right)}& t_{ijs}\in \left[t_{js},t_{je}\right]\\ 0& \mathrm{otherwise}\end{array}$$

(10)

where $t_{ijs}$ is the start time of UAV $i$ performing task $j$, $\left[t_{js},t_{je}\right]$ is the executable time range of task $j$, and $\exp \left(-\lambda \left(t_{ijs}-t_{js}\right)\right)$ is a time penalty term for UAV $i$ performing task $j$.

Where ${\zeta }_{ij}$ is the mission distance cost of the UAV, which has the specific form:

$${\zeta }_{ij}=d_{ij}\gamma$$

(11)

where $d_{ij}$ is the straight-line distance between UAV $i$ and task $j$, and $\gamma$ is the distance cost coefficient.

Using the change in revenue of UAV $i$ after adding new task $j$, the marginal gain of task $j$ can be expressed as:

$$c_{ij}^{}\left[b_i\right]=\{\begin{array}{c}0,j\in b_i,\\ \underset{n\le \left|p_i\right|+1}{\max }{S}_i^{p_i{\oplus }_n\left\{j\right\}}-S_i^{p_i},\mathrm{otherwise}.\end{array}$$

(12)

where $n$ represents all possible positions where the new task is added to the task path; $a{\oplus }_n\left\{b\right\}$ means that $b$ is inserted into the nth bit of $a$, and the nth bit of $a$ and the elements that follow it are moved back. We try to insert each UAV at all possible positions in the execution path to determine the position with the maximum marginal gain of the task, add all tasks to the task package and finally, maximize the UAV execution benefit. For multiple-UAV task co-allocation, we construct a winning information matrix $B$ of size $N_n\times N_t$ from the set winner $z_i$ and set winning bid $y_i$ information, with rows and columns representing tasks and UAVs, respectively. $B_{ij}$ is UAV $i$’s bid for mission $j$. When $z\left(i,j\right)=k$, there is $B_{kj}^i=y\left(k,j\right)$, indicating that UAV $i$ thinks that UAV $k$ bids for task $j$.

To solve assignment problems where the target tasks are at different execution stages, the bidding mechanism of the original algorithm is improved and two-level task bidding selection is implemented [6,28]. The specific process is as follows.

Firstly, for tasks at different execution stages in the target, the tasks with different execution time stages in the target are ranked according to the starting execution time; that is, $T_j=\left[T_1,T_2,\dots ,T_e\right]$. The first-level task bidding expression of the improved algorithm task selection mechanism is:

$$\grave{c_{ij}}=\{\begin{array}{cc}{K}_{ij}\times e^{-\lambda \left(t_{ijs}-t_{js}^1\right)}& t_{ijs}\in \left[t_{js}^1,t_{je}^e\right]\\ 0& \mathrm{otherwise}\end{array}$$

(13)

where $t_{ijs}$ is the execution start time of UAV $i$’s task $j$, and $t_{js}^k$ and $t_{je}^e$ are the start time of task $T_1$ and the end time of task $T_e$ in $T_j$, respectively. $K_{ij}$ is the coefficient. The bidding function is mainly used to screen out the UAV sets that meet the target $T_j$ execution time period $\left[t_{js}^1,t_{je}^e\right]$, and prepare for the next specific task bidding event.

After screening out the UAV sets that meet the task execution time period, the second task bidding expression is:

$$c_{ij}^{*}=\{\begin{array}{cc}{K}_{ij}\times e^{-\lambda \left(t_{ijs}-t_{js}^n-t^{*}\right)}& t_{ijs}\in \left[t_{js}^n,t_{je}^n\right]\\ 0& \mathrm{otherwise}\end{array}$$

(14)

where $\left[t_{js}^n,t_{je}^n\right]$ is the start and end times of task n in $\left[t_{js}^1,t_{je}^e\right]$, $t^{*}$ is the difference in the start execution times of adjacent tasks, that is, $t^{*}=t_{js}^{n+1}-t_{js}^n$. The bidding function is mainly used to assign the task sets of different execution time periods in target $j$ to a specific UAV for execution.

After the task package is built, it needs to be populated with information such as the winner set, winning price set and time stamp. Each UAV needs to judge whether its own task package built on the basis of the other UAVs’ task bidding information is true or not, so it also needs to resolve any task conflict to obtain the final consistent task allocation scheme.

2.1.5. Conflict Resolution

Conflict resolution is based on task construction and solves the problem of task assignment conflict through information exchange between UAVs [29]. The information exchanged between UAVs mainly includes the winner set, winning price set, and time stamp. When a task only needs to be performed by a single UAV, its conflict resolution mechanism is consistent with the CBBA. The main processes are to judge whether the task can be obtained by comparing its own bidding information after all UAVs complete an information exchange and to obtain the winner set and winning price set information of other UAVs. When UAV $i$ bids the highest for task $j$, it will obtain it and release all tasks $j$ and subsequent tasks in the task set of all other UAVs containing the task $j$. When the timestamp is updated after complete information exchange occurs, the update form is as follows:

$$s_{ik}=\{\begin{array}{cc}{\tau }_r,\hfill & g_{ik}=1\hfill \\ \underset{m:g_{im}=1}{\max }{\mathrm{s}}_{mk},\hfill & \mathrm{otherwise}\hfill \end{array}$$

(15)

where $g_{ik}=1$ represents information interaction between UAV $i$ and UAV $k$; otherwise, it is 0; and ${\tau }_r$ indicates the time of message receipt.

In the process of conflict resolution, via information interaction between all UAVs, the information receiver of the UAV will update the corresponding information according to the winner set, winning bid set, and timestamp of the current moment. When UAV $i$ receives information from neighbouring UAV $k$, it will react according to the time stamp and UAV winning information. The UAV reaction mechanism mainly includes an:

$$\begin{array}{c}• \mathrm{Update} \mathrm{mechanism}: y_{ij}=y_{kj}, z_{ij}=z_{kj};\hfill \\ • \mathrm{Reset} \mathrm{mechanism}: y_{ij}=0, Z_{ij}=\varnothing ;\hfill \\ • \mathrm{Leaving} \mathrm{mechanism}: y_{ij}=y_{ij}, z_{ij}=z_{ij}.\hfill \end{array}$$

(16)

According to the above processing mechanism, when a UAV changes the information in the winner set and winning bidding set, it is necessary to check whether there is any task update or reset in the task set. When there is, it is necessary to release the task and all subsequent tasks to achieve consistent task allocation. When the information of the sender UAV $k$ and receiver UAV $i$ are updated, we check the information of UAV $n$ that UAV $k$ thinks is assigned to task $j$. When $B_{mj}^i=0$ exists and the number of UAVs executed by task $j$ does not meet the requirement, the allocation matrix is updated by $B_{mj}^i=B_{mj}^k$ and UAV $i$ is assigned to task $j$. When the number of UAVs executing task $j$ meets the requirement, if their existing bidding value is less than that considered by UAV $k$, that is, $\min \left(y_{nj}^i\forall n\right)<y_{mj}^k$, the task is updated by $B_{nj}^i=0,B_{mj}^i=B_{mj}^k$. To avoid deadlock when the bidding value is the same, the UAV with the higher identification is selected. Throughout the process, task selection and conflict resolution are carried out in a continuous cycle. When the winner set of all UAVs and the information of the winner bidding set no longer change, it indicates that the task assignment results of all UAVs have reached consistency, and task assignment ends.

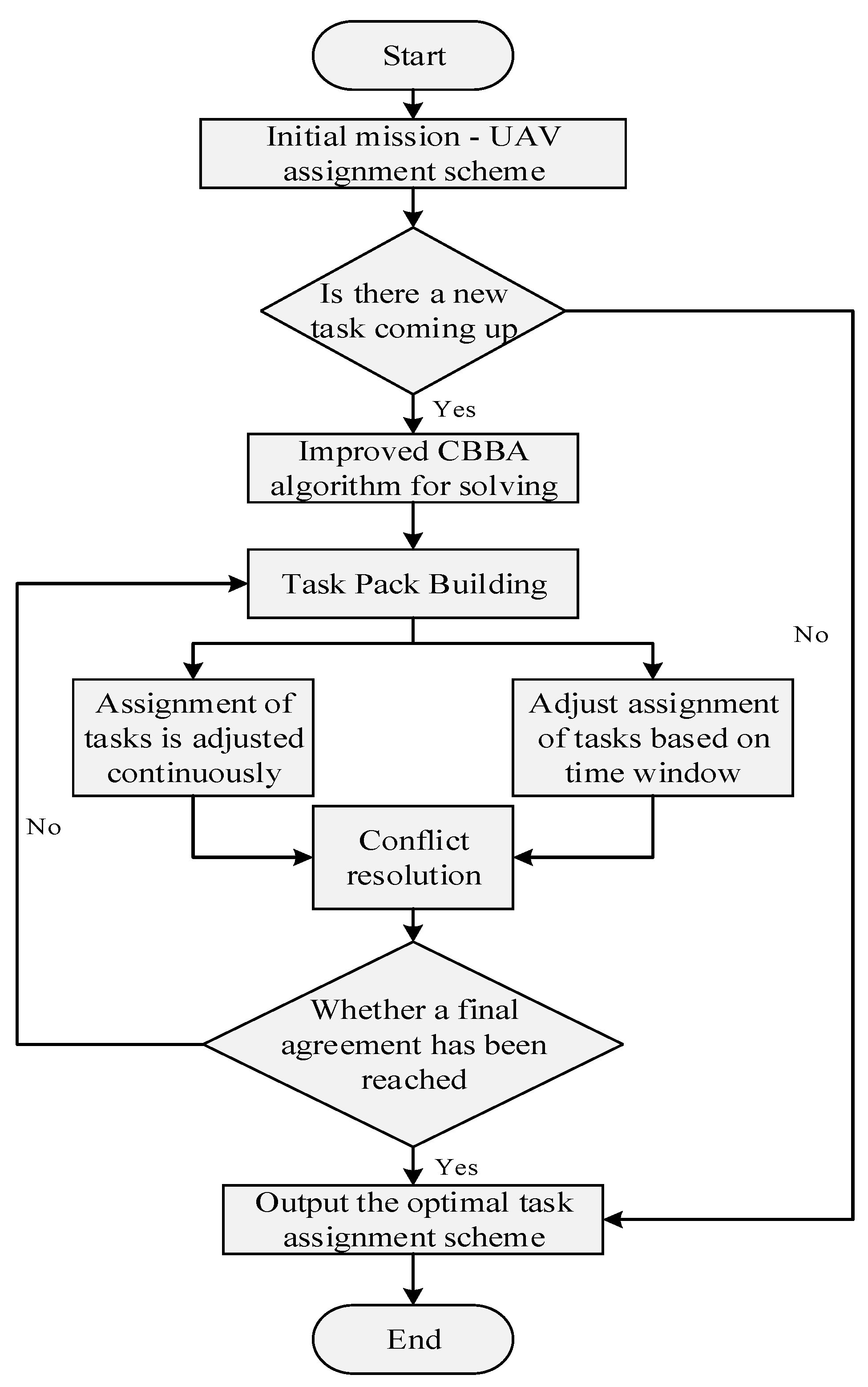
2.2. Dynamic Task Assignment Based on Improved CBBA

2.2.1. Overall Flow of the Algorithm

In the process of task allocation, all UAVs perform tasks according to the previously established task allocation, and new tasks appear at time $T$, which influences the original task allocation scheme. The task allocation sequence needs to be adjusted to regain the optimal consistent allocation result [30,31]. In the process of solving the problem by using the improved CBBA, task continuity adjustment and task allocation adjustment through the time window are used in the task package construction stage to optimize the efficiency of the task allocation results and improve the dynamic effect of the final task allocation scheme [32]. The specific algorithm flow is shown in Figure 2:

Step 1: On the basis of the initial UAV task allocation scheme, we judge whether there is an event occurring in a new task at time $T$. If so, we go to Step 2; if not, go to Step 5 directly to output the optimal task allocation scheme.

Step 2: If there are any new tasks, the improved CBBA approach is used to solve them. Firstly, we reconstruct the task package and task execution path of the UAVs that meet the task execution conditions. On the basis of the task package construction and task execution path, we optimize and adjust the task allocation scheme through task continuity adjustment and task adjustment based on the time window.

Step 3: On the basis of task package construction and task assignment scheme adjustment, conflict resolution is carried out to obtain consistent task assignment results for all UAVs.

Step 4: Judge whether the final task allocation is consistent. If so, go to Step 5 to output the optimal task allocation scheme; if not, go to Step 2 to re-allocate tasks.

Step 5: Select the optimal task assignment scheme as the adjusted optimal scheme for output.

In the process of task assignment, for UAVs before and after continuous task execution revenue and cost considerations, we comprehensively consider the combination of the currently executed task and related tasks to adjust the task allocation sequence. At the same time, for each task allocation relationship within the execution time window, reasonably plan the time sequence of the execution window of each task, the task allocation efficiency can be better optimized. The detailed processes of these two parts are introduced below.

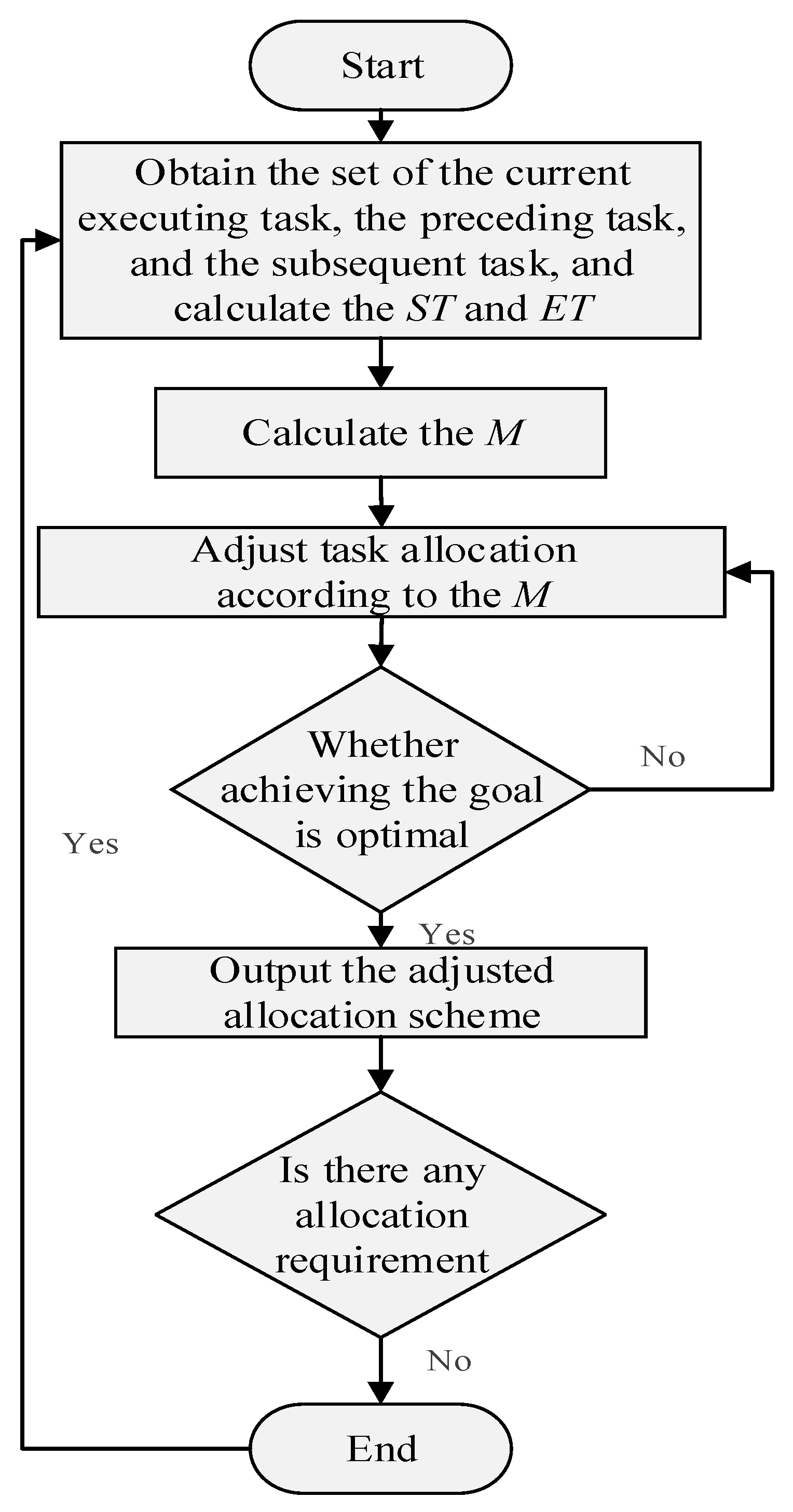
2.2.2. Task Continuity Adjustment Distribution

If at moment $T$ a new task appears that needs to be performed, the UAV that meets the task execution conditions deletes its original task allocation and rebuilds the work and task execution path. On this basis, combined with all UAVs and task execution path information, we optimize the arrangement of pre- and post-tasks of all tasks in UAV i’s task execution sequence [33,34].

The set of all UAVs is $I$, and the task execution sequence of UAV $i$ is $T_i=\left\{t_{i1},t_{i2},\cdot \cdot \cdot ,t_{ih}\right\}$, where $h$ represents the order of the task in the execution sequence. The conflict-free task set at any execution time after $t$ is $T_t=\left\{t_{g1},t_{g2},\cdot \cdot \cdot ,t_{gw}\right\}$, where $g$ is the individual UAV in the task execution sequence to which the task belongs, and $w$ is the total number of tasks. Let $AS$ as the algorithm iteration counter, and make its initial value as 0. The algorithm flow is as follows:

Step 1: Firstly, UAV $i$ is selected from UAV set $I$;

Step 2: Select task $t_{ih}$ from the task execution sequence $T_i$ of UAV $i$;

Step 3: Select the task $t_{gw}$ and $t_{ih}$ indices from the conflict-free task set $T_t$ that was executed at any time after time $t$ and exchange them. Record the trip costs ${\zeta }_i$ and ${\zeta }_j$ and the original trip costs $\grave{{\varsigma }_i}$ and $\grave{{\varsigma }_j}$ executed by UAV $i$ and UAV $j$, respectively.

Step 4: Calculate $d_i=\frac{{\varsigma }_i}{\grave{{\varsigma }_i}}$ and $d_j=\frac{{\varsigma }_j}{\grave{{\varsigma }_j}}$, and if $d_i$ and $d_j$ are both within the threshold range $\left[d^{-},d^{+}\right]$, go to Step 5; otherwise, go to Step 3;

Step 5: Adjust the assignment of tasks;

Step 6: Judge whether the adjustment is completed; if so, go to Step 7, otherwise, go to Step 2;

Step 7: Let $AS=AS+1$, and determine whether $AS\le NU$; if so, then go to Step 8, otherwise, go to Step 1;

Step 8: Output the final allocation result.

2.2.3. Task Allocation Adjustment Based on Time Windows

A task window refers to the period between the earliest and latest times a task may be started. Within a task window, the different execution times of each task will influence the probability of each task being executed [35]. Within the task window, different task execution schedules will cause the interval between execution times of adjacent tasks to be too long or too short, thus making the overall task execution sequence too close or too sparse, which can also affect the overall task execution benefits.

We define $u_{ij}$ to represent the execution relationship between UAV $i$ and task $j$. When $u_{ij}=1$, it means that UAV $i$ performs task $j$; otherwise, when the value is 0, it means that there is no execution relationship; $du$ indicates the execution time of a task. The earliest start time of a task is $st$ and the latest is $et$, the start time of the current task is $t$, $dt$ is the time that the UAV takes to reach the task location, and the earliest task end time in the time window is represented as $st+du-dt$. The latest end time of the tasks in the time window is expressed as $et-du+dt$. $M$ is used to represent the proportion of the task time window of the UAV to start the task at time $t$ in the overall time window. When there is a time set $P$ of all tasks that can be started within the time window, and the time set of tasks that can be started to be executed at time $t$ is $P_t$, then $M\left(t\right)=\left|P_t\right|/\left|P\right|$, $t\in \left[st,et\right]$. The allocation adjustment objective is expressed as ${\displaystyle \sum _{j\in N}}{M}_j\left(t\right)u_{ij}$, and its result is minimized to optimize the overall task allocation adjustment. If a task is executed at $t$, the earliest execution time cannot be earlier than $st$, and the earliest execution time can start from $t-du+dt$. Therefore, the earliest execution time of a task executed at $t$ is $\max \left\{t-du+dt,st\right\}$. Similarly, the latest start time of a task executed at time $t$ is $\max \left\{t-du+dt,st\right\}$. To sum up, for a time window $\left[st,et\right]$, $P=\left[st,et-du+dt\right]$, $\left|P\right|=et-st-du+dt+1$, and the time window matching degree of the task executed at $t$ time is $M\left(t\right)=\left(\min \left\{t,et-du+dt\right\}-\max \left\{t-du+dt,st\right\}+1\right)/\left(et-st-du+dt+1\right)$.

When the earliest task end time in the time window is earlier than the latest end time, that is, when $st+du-dt<et-du+dt$, and when $t\in \left[st,st+du-dt\right]$, there are $\min \left\{t,et-du+dt\right\}=t$ and $\max \left\{t-du+dt,st\right\}=st$; then, $M\left(t\right)=\frac{\left(t-st+1\right)}{\left(et-st-du+dt+1\right)}$. Similarly, when $t\in \left(st+du-dt,et-du+dt\right]$, $M\left(t\right)=\frac{du-dt+1}{et-st-du+dt+1}$; and when $t\in \left(et-du+dt,et\right]$, $M\left(t\right)=\frac{et-t+1}{et-st-du+dt+1}$. That is:

$$M\left(t\right)=\{\begin{array}{l}\frac{t-st+1}{et-st-du+dt+1}, st\le t\le st+du-dt\\ \frac{du-dt+1}{et-st-du+dt+1},st+du-dt<t\le et-du+dt\\ \frac{et-t+1}{et-st-du+dt+1},et-du+dt<t\le et\\ \hspace{1em}\hspace{1em}0,\hspace{1em}\hspace{1em}t<st,t>et\end{array}$$

(17)

The pre-task set is defined as $tP$, and the follow-up task set is defined as $tN$. When $tP=\varnothing$, $d{t}_1$ is defined as the distance between UAV $i$ and the currently executed task, $ad$ is the expected task execution time, and $st=\max \left\{t,ad+d{t}_1\right\}$. On the contrary, when $tP\ne \varnothing$, $t_p$ is defined as the start time of the prior task, $t_{pd}$ is the execution time of the prior task, $d{t}_2$ is the distance between the locations of prior and current tasks, and $s_t=\max \left\{t,t_p+t_{pd}+d{t}_2\right\}$. $t_{ce}$ is defined as the end time of the current task, $d{t}_3$ represents the distance between the follow-up and current task locations, $t_n$ is defined as the start time of the follow-up task, $t_{du}$ is defined as the execution time of the current task. When $tN=\varnothing$, $r=t_{ce}$. When $tN\ne \varnothing$, $r=\min \left\{t_{ce},t_n-t_{du}-d{t}_3\right\}$. The algorithm flow is as follows.

Step 1: Firstly, obtain the current task, its predecessor and the subsequent task set. Calculate the earliest execution time range $st$ and the latest execution time range $et$;

Step 2: Calculate the of $M$ every task at time $t$;

Step 3: Adjust the assignment of tasks according to the size of $M$;

Step 4: Judge whether the allocation target ${\displaystyle \sum _{j\in N}}{M}_j\left(t\right)u_{ij}$ reaches the minimum. If so, go to Step 5; otherwise, go to Step 3;

Step 5: Output the adjusted allocation scheme;

Step 6: Judge whether there is still a need for allocation adjustment; if so, go to Step 1; otherwise, go to Step 7;

Step 7: The adjustment and distribution are finished.

Combining the above steps, the implementation process for dynamic adjustment of tasks based on a time window is as shown in Figure 3:

3. Results

3.1. Simulation Experiment Settings

Aiming at the problem of multi-target, unbalanced, phased, collaborative task assignment of heterogeneous multi-UAVs, when the numbers of UAVs and targets are inconsistent, the number of UAVs is allocated according to the requirements at different stages of the target task. To solve this problem, simulation verification of the proposed method was carried out. In order to facilitate the simulation experiment for the problem, the unit of task allocation time in the simulation scenario of the following case is seconds, and the unit of flight distance in kilometers and in (4) and (5) in the performance testing section of the algorithm in Section 3.3.2, the time unit is 100 s. The UAV object studied in the simulation experiment is considered a mass point, and there are research indicators about the UAV, which mainly include position coordinates, flight speed, and mission execution time. The UAV object studied in the simulation and the relevant research indicators in this paper are consistent with the references [15,26]. The hardware configuration used for the algorithm simulation experiments in this chapter is Intel(R) Core(TM) i7-9750HF CPU @ 2.60GHz Processor, memory is 32 GB, and the graphics card is NVIDIA GeForce GTX 1060 Ti. The software environment is MATLAB 2020a. The simulation settings are as follows.

Scenario 1: A formation of UAVs performs combat missions. There are five UAVs of two types: two type-I UAVs and three type-II UAVs. The two types of UAVs can execute tasks in cooperation for different mission types. Combat missions are mainly divided into two categories: reconnaissance and strike. There are four of each in this scenario. The initial situation is given in the following

Table 1. Task target information.

Task Identity	Task Coordinates	Task Type
		Reconnaissance Class	Strike Class
1	(−1.3,2.6)	√
2	(0.3,2.7)		√
3	(−1.1,2.5)		√
4	(1.1,4.4)		√
5	(0.3,4.5)	√
6	(0.7,5.5)	√
7	(1.7,5.2)	√
8	(0.7,2.0)		√

and

Table 2. UAV information.

UAV Identity	Initial Position	Ability Type	Maximum Number of Tasks That Can Be Executed	Speed (m/s)
1	(0.05,3.3)	I	5	30
2	(1.4,5.3)	I	5	35
3	(1.9,−0.9)	II	5	50
4	(−0.9,5.4)	II	5	40
5	(2.0,2.3)	II	5	30

:

For the operational replanning of cooperative task execution by multiple UAVs, we must conduct cooperative task redistribution as unexpected new tasks arise. For this problem, simulation verification of the proposed method was carried out. The simulation scenario was set as follows.

Scenario 2: UAVs perform combat missions in formation. There are five UAVs of two types: two Type-I and three Type-II. At first, the operational tasks carried out in the course of operations are mainly divided into two types: reconnaissance and strike, of which there are six and nine, respectively. Type-I UAVs perform reconnaissance missions, while Type-II UAVs perform strike missions. One new task is suddenly generated, and its corresponding execution relationship can be executed by the two types of UAVs. The specific initial situation is listed in the following

Table 3. Task objective information.

Task Identity	Task Coordinates	Task Type
		Reconnaissance Class	Strike Class
1	(−1.3,2.1)		√
2	(−0.6,3.0)		√
3	(1.0,3.3)		√
4	(2.4,4.2)		√
5	(−1.1,2.5)		√
6	(−0.5,2.0)		√
7	(1.7,2.8)		√
8	(−0.3,0.8)		√
9	(0.6,−1.1)		√
10	(1.2,4.4)	√
11	(1.7,0.8)	√
12	(−1.8,−1.0)	√
13	(−1.5,0.5)	√
14	(−1.3,2.8)	√
15	(−1.9,3.1)	√

and

Table 4. UAV information.

UAV Identity	Initial Position	Ability Type	Maximum Number of Tasks That Can Be Executed	Speed (m/s)
1	(0.1,3.3)	I	5	30
2	(1.4,5.2)	I	5	35
3	(2.0,−1.0)	II	5	50
4	(−0.9,5.4)	II	5	40
5	(2.1,2.3)	II	5	30

.

3.2. Simulation Results and Analysis

Simulation Scenario 1: According to the initial state of each target in Scenario 1, we use the improved CBBA collaborative target allocation algorithm to allocate targets as follows:

As shown in Figure 4, the overall execution time for the UAV formation to complete the collaborative tasks is 362.634 s, with the UAV formation taking 254.634 s to make a task decision and complete all task assignment processes when faced with the current task environment. UAVs A1 and A5 arrived at the position of reconnaissance mission one in 31 s and 37 s, respectively, when they performed the mission in coordination, and the mission execution time was 15 s. UAVs A1 and A5 cooperated to perform the task in phases during execution periods {31,46} and {37,52} of Reconnaissance Task 1. After reconnaissance, they flew from the current mission point to the position of strike mission two, and they started their mission in 69 s and 69.7 s, respectively, and they cooperated to perform the task during execution periods {69,74} and {69.7,74.7} of Strike Task 2, respectively. The initial coordinated mission of the UAVs A3 and A4 was reconnaissance mission six, and they arrived at the mission point at 35 s and 32 s, respectively, both with a mission execution time of 5 s. UAVs 3 and 4 cooperated to perform the task in phases during execution periods {35,40} and {32,37} of Reconnaissance Task 6. After reconnaissance, UAV A4 flew from the current mission point to the position of strike mission four and carried out this mission in conjunction with UAV A2, which arrived at the position of strike mission four at 39 s. UAVs 2 and 4 cooperated to perform the task in phases during the execution periods {32,47} and {39,54} of Strike Task 4, respectively. After that, UAV A2 and UAV A4 cooperated to perform reconnaissance mission five, and their respective time to reach the mission position were 67 s and 72 s, respectively. UAVs 2 and 4 cooperated with each other in phases during execution periods {67,82} and {72,87} of reconnaissance mission five, respectively. After reconnaissance, UAV A1 took 23 s to fly from the position of strike mission two to the position of strike mission three. UAVs 1 and 4 cooperated with each other in execution periods {97,102} and {98,103} of strike mission three, respectively. UAV A3 took 27 s to fly from the position of reconnaissance mission six to the position of reconnaissance mission seven. UAV 3 carried out reconnaissance mission seven in {67,82}. After the reconnaissance, UAV A5 flew from the position of strike mission two to the position of strike mission eight at 84 s. UAVs 3 and 5 cooperated with each other to carry out the mission in stages during execution time periods {93,108} and {84,99} of strike mission eight, respectively. To sum up, it can be seen that the proposed algorithm can well solve the problem of multi-UAV, multi-task, unbalanced, cooperative, and phased task assignment.

Simulation Scenario 2: The proposed task dynamic adjustment mechanism is simulated and tested. In the case of no new tasks, the original task allocation route and assignment timing result are shown in Figure 5.

As shown in

Table 5. Original task assignment results of UAV.

UAV Identity	Task Execution Path	Flight Distance	Task Execution Time
1	(15,I)→(11,I)→(14,I)→(12,I)	16	{10,15},{64,69},{76,81},{86,91}
2	(13,I)→(10,I)	9	{15,20},{45,50}
3	(9,II)→(6,II)	5	{18,33},{67,82}
4	(5,II)→(2,II)→(1,II)	14	{10,25},{47,62},{69,84}
5	(7,II)→(8,II)→(4,II)→(3,II)	20	{21,37},{49,64},{83,98},{99,114}

, the overall execution time for the UAV formation to complete the coordinated tasks is 345.884 s, with the UAV formation taking 230.884 s to make a task decision and complete the process of assigning all tasks in the face of the current task environment. In the absence of new tasks, the execution by the UAVs is as follows: UAV 1 performs the type-I task sequence as 15→11→14→12, the execution time of various tasks is 5 s, and the time when UAV A1 arrives at the initial task point and starts to perform the task is 10 s. For its subsequent task set, the time when the UAV starts to execute the task is 64 s, 76 s, and 86 s, respectively. The time to complete the overall task is 91 s. UAV 2 performs the type-I task sequence as 13→10, the execution time for each type of task is 5 s, where the moment when UAV A2 arrives at the initial task point and starts the task is 15 s, after which it takes 25 s to fly from that task point to the location of task 10, the moment when the UAV starts that task is 45 s, and the overall task execution is completed in 50 s. UAV 3 performs the type-II task sequence as 9→6, the execution time for each type of task is 15 s, where the moment when UAV A3 arrives at the initial task point and starts its task is 18 s, after which it takes 34 s to fly from that task point to the location of task 6, the moment when the UAV starts that task is 67 s and the overall task execution is completed in 82 s. UAV 4 performs the type-II task sequence as 5→2→1, the execution time for each type of task is 15 s, where the moment when UAV A4 arrives at the initial task point and starts its task is 10 s, and for its subsequent set of tasks, the UAV starts its execution at 47 s and 69 s, respectively, and the overall task completion time is 84 s, and UAV 5 performs the type-II task sequence as 7→8→4→3, the execution time for each type of task is 15 s, where the moment when UAV A5 arrives at the initial task point and starts its task is 21 s, and for its subsequent set of tasks, the UAV starts its execution at 49 s, 83 s, and 99 s, respectively, and the overall task completion time is 114 s. The total revenue of task allocation is 1456.

When a new task appears, its task allocation route and assignment timing result change as follows:

(1)

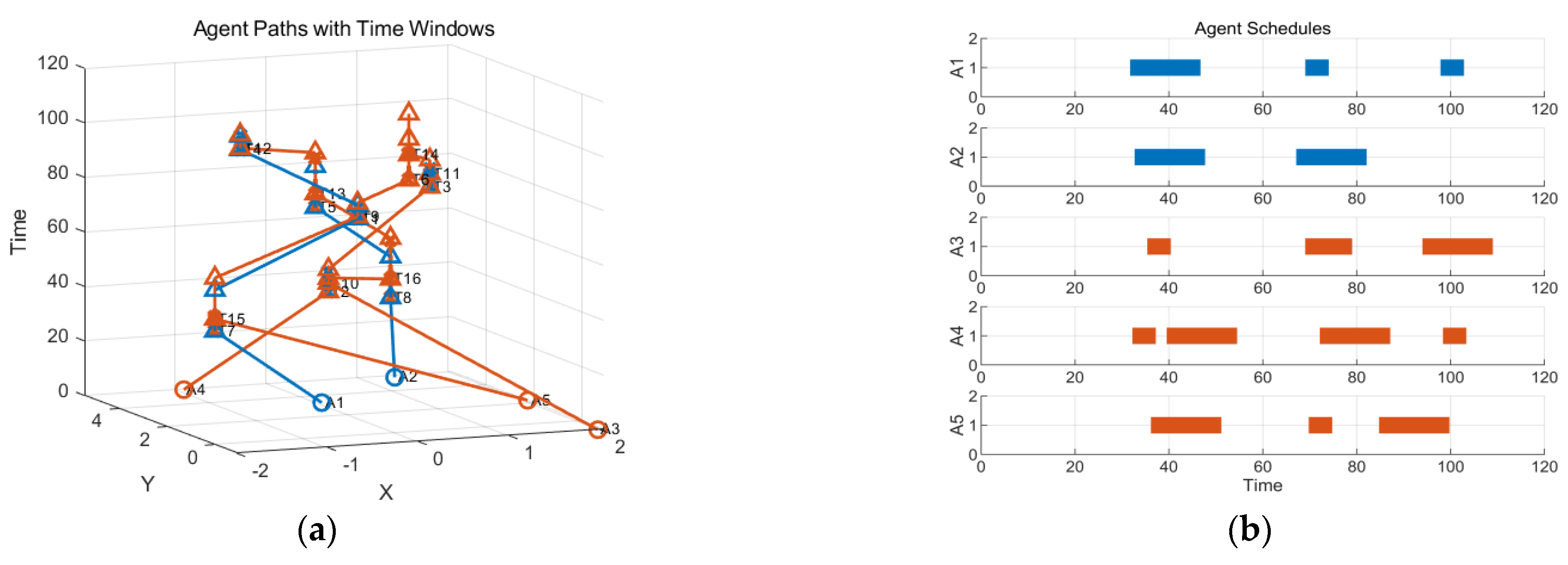
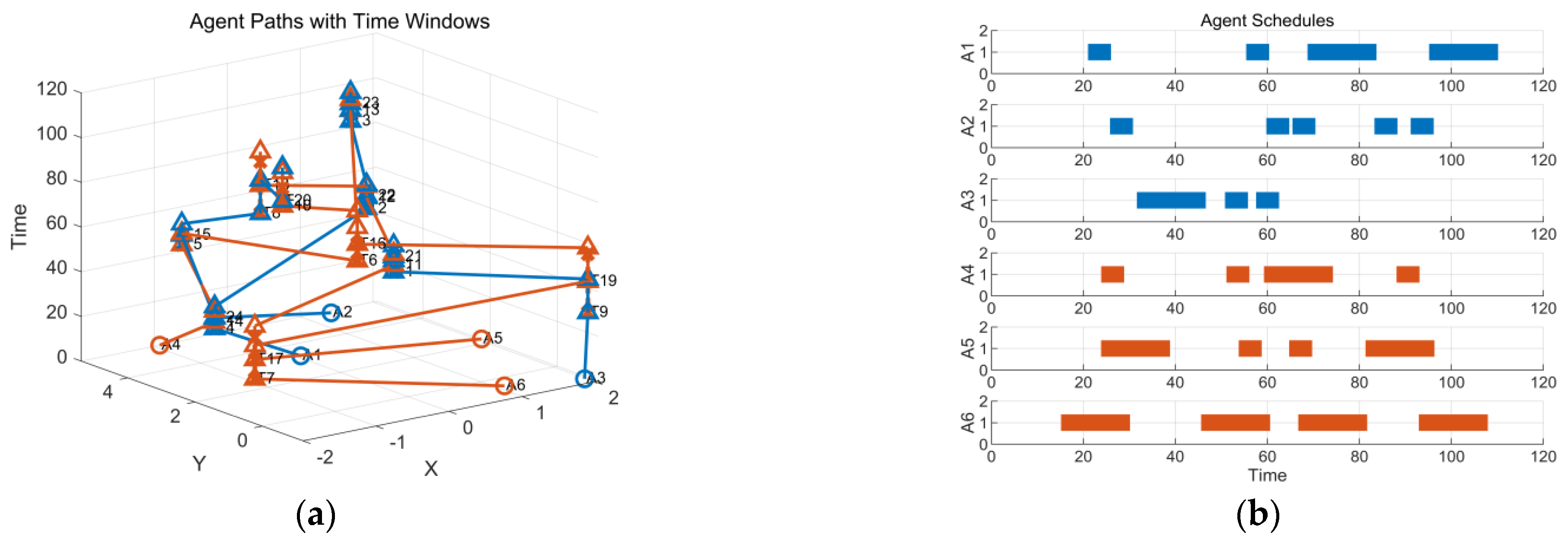
New tasks occur when multiple UAVs perform tasks in the early stage, as shown in the following simulation (Figure 6):

As shown in

Table 6. UAV dynamic task assignment results.

UAV Identity	Task Execution Path	Flight Distance	Task Execution Time
1	(15,I)→(14,I)→(16,I)	10	{10,15},{76,81},{82,87}
2	(13,I)→(10,III)→(11,I)→(12,I)	15	{15,20},{45,55},{64,69},{86,91}
3	(9,II)→(8,II)→(6,II)→(4,II)	21	{18,33},{49,64},{67,82},{83,98}
4	(5,II)→(2,II)→(1,II)	14	{10,25},{47,62},{69,84}
5	(7,II)→(3,II)	15	{21,37},{99,114}

, the overall execution time for the UAV formation to complete the coordinated tasks is 157.003 s, with the UAV formation taking 43.003 s to make a task decision and complete the process of assigning all tasks in the face of the current task environment. The time of the emergence of a new task is {45,55}. After the emergence of a new task, the improved CBBA is used to change the execution of all UAVs based on the initial task allocation scheme: UAV 1 carries out type-I task sequence as 15→14→16, the execution time for each type of task is 5 s, where the moment when UAV A1 arrives at the initial task point and starts its task is 10 s, and for its subsequent set of tasks, the UAV starts its execution at 76 s and 82 s, respectively, and the overall task completion time is 87 s; UAV 2 carries out type-I task sequence as 13→10→11→12, the execution time of the new task 10 is 10 s, the execution time of the remaining types of tasks is 5 s, the moment when UAV A2 arrives at the initial task point and starts executing the task is 15 s, and for its subsequent set of tasks, the UAV starts executing at 45 s, 64 s and 86 s, respectively, and the overall task execution completion time is 91 s; UAV 3 carries out type-II task sequence as 9→8→6→4, the execution time for each type of task is 15 s, with UAV A3 arriving at the initial task point and starting its task at 18 s, and for its subsequent set of tasks, the UAVs start execution at 49 s, 67 s and 83 s, respectively, and the overall task completion time is 98 s; UAV 4 carries out type-II task sequence as 5→2→1, the execution time for each type of task is 15 s, where the moment when UAV A4 arrives at the initial task point and starts its task is 10 s, and for its subsequent set of tasks, the UAV starts its execution at 47 s and 69 s, respectively, and the overall task completion time is 84 s; And UAV 5 carries out type-II task sequence as 7→3, the moment when UAV A5 arrives at the initial task point and starts the task is 21 s and the task execution time is 16 s, after which it takes 62 s to fly from this task point to the location of task 3, the moment when the UAV starts this task is 99 s and the task execution time is 15 s, and the overall task execution completion time is 114 s. The total revenue of the UAV mission allocation is 5215.3.

(2)

New tasks occur in the late stage of multi-UAV missions, as shown in the simulation below (Figure 7):

As shown in

Table 7. UAV dynamic task assignment results.

UAV Identity	Task Execution Path	Flight Distance	Task Execution Time
1	(15,I)→(10,I)→(14,I)→(16,I)	16	{10,15},{45,50},{76,81},{82,92}
2	(13,I)→(11,I)→(12,I)	11	{15,20},{64,69},{86,91}
3	(9,II)→(8,II)→(6,II)→(4,II)	21	{18,33},{49,64},{67,82},{83,98}
4	(5,II)→(2,II)→(1,II)	14	{10,25},{47,62},{69,84}
5	(7,II)→(3,II)	15	{21,37},{99,114}

, the overall execution time for the UAV formation to complete the coordinated tasks is 216.206 s, with the UAV formation taking 102.206 s to make a mission decision and complete the process of assigning all tasks in the face of the current mission environment. The time of the emergence of a new task is {82,92}. The improved CBBA is used to change the execution of all UAVs based on the initial task allocation scheme: UAV 1 carries out type-I task sequence as 15→10→14→16, the execution time of the sudden new task 16 is 10 s, the execution time of the remaining types of tasks is 5 s, the moment when UAV A1 arrives at the initial task point and starts executing the task is 10 s, for its subsequent set of tasks, the moments when the UAV starts executing are 45 s, 76 s and 82 s respectively, and the overall task execution is completed in 92 s; UAV 2 carries out type-I task sequence as 13→11→12, the execution time for each type of task is 5 s, where the moment when UAV A2 arrives at the initial task point and starts its task is 15 s, and for its subsequent set of tasks the UAV starts its execution at 64 s and 86 s, respectively, and the overall task completion time is 91 s; UAV 3 carries out type-II task sequence as 9→8→6→4, the execution time for each type of task is 15 s, with UAV A3 arriving at the initial task point and starting its task at 18 s, and for its subsequent set of tasks, the UAVs start execution at 49 s, 67 s and 83 s, respectively, and the overall task completion time is 98 s; UAV 4 carries out type-II task sequence as 5→2→1, the execution time for each type of task is 15 s, where the moment when UAV A4 arrives at the initial task point and starts its task is 10 s, and for its subsequent set of tasks, the UAV starts its execution at 47 s and 69 s, respectively, and the overall task completion time is 84 s; And UAV 5 carries out type-II task sequence as 7→3, the moment when UAV A5 arrives at the initial task point and starts the task is 21 s and the task execution time is 16 s, after which it takes 62 s to fly from this task point to the location of task 3, the moment when the UAV starts this task is 99 s and the task execution time is 15 s, and the overall task execution completion time is 114 s. The total revenue of the UAV mission allocation is 5283.3.

3.3. Algorithm Performance Evaluation

3.3.1. Performance Evaluation of Multi-UAV and Multi-Target Collaborative Task Assignment in Stages

In order to test the influence of different combinations of UAVs performing tasks collaboratively at different times on the task allocation algorithm, six UAVs are set up to assign tasks to 24 targets, with equal numbers of UAV types and task types. Among them, there are two types of tasks, one is to assign UAVs to cooperate in three phases at different times, and the other is to assign UAVs to cooperate in two phases at different times. The specific simulation results are as follows.

As shown in Figure 8, UAVs 1, 2 and 4 cooperate with each other in execution time periods {20.9,25.9}, {26,31}, and {23.8,28.8} of Reconnaissance Task 1. After completing the reconnaissance task, UAVs 1 and 4 are in the execution time periods {55.3,60.3} and {51.8, 56.8} of Strike Task 2, respectively. In the same way, it can be seen that different UAVs cooperated to complete other target tasks. It can be seen that target tasks with different cooperative execution stages can be achieved at different times. Different UAVs cooperate in executing the target tasks in combination, and the allocation result of the algorithm is not affected by the combination of target tasks with different requirements of execution stages, which well the problem of the numbers of UAVs and target tasks being unbalanced and the target tasks needing to be executed cooperatively in stages.

3.3.2. Dynamic Allocation Algorithm Performance Evaluation

(1)

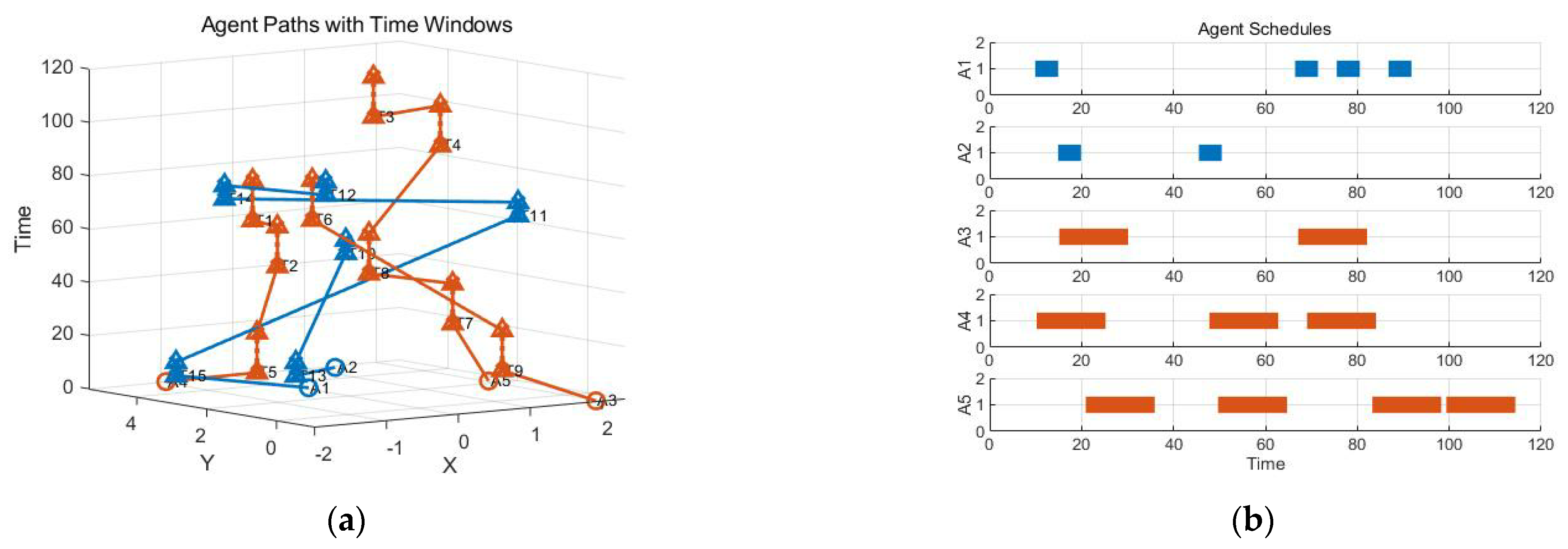
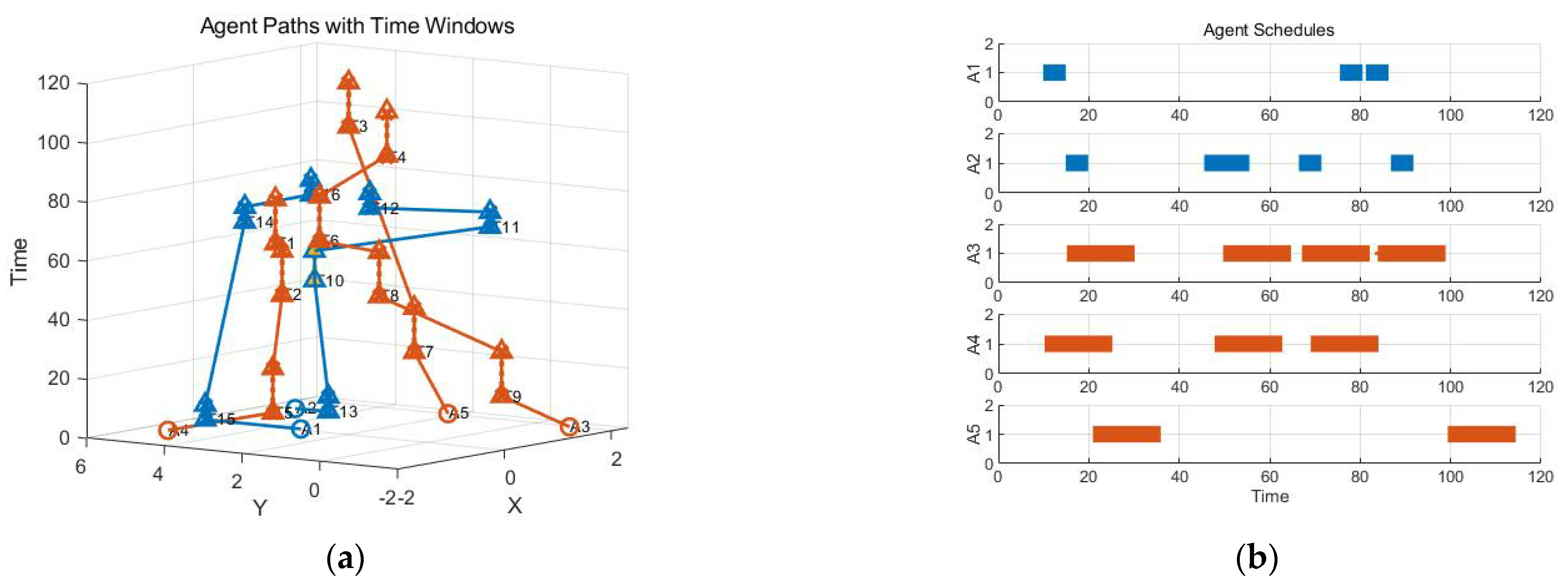
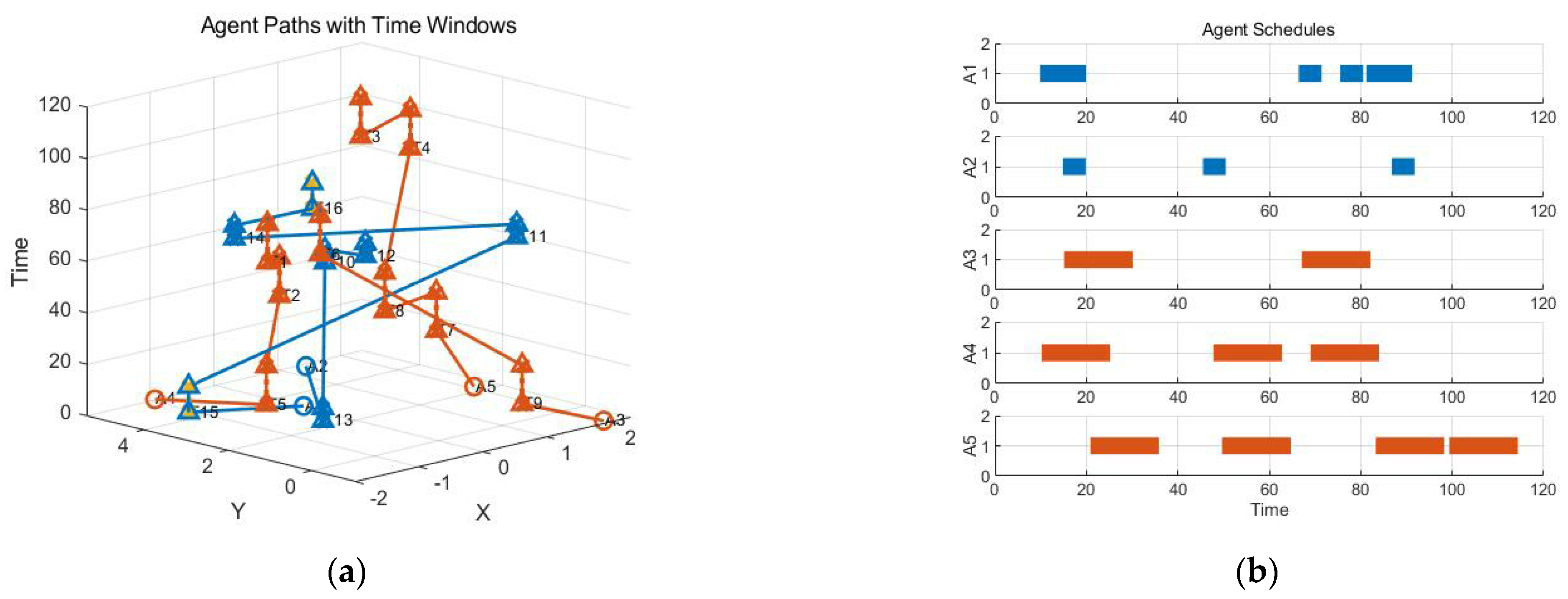
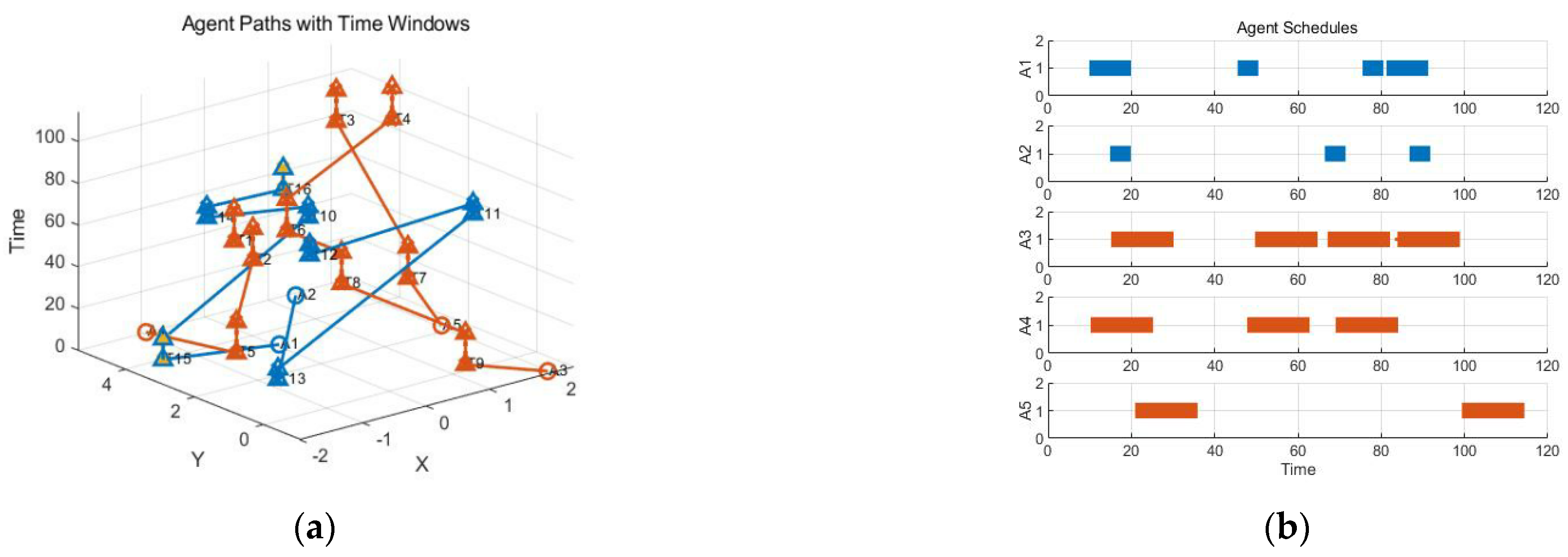
In order to further compare the performance of dynamic task allocation by the CBBA, two new tasks were added on the basis of Scenario 1 for comparative simulation, and the results were compared with the CBBA’s complete reallocation strategy. In the CBBA used for the complete reallocation strategy, the UAV meets the task execution requirements, clears its original task assignment, and reconstructs its task package and task execution path for the new task, finally achieving the dynamic assignment of the new task. The reassignment result of the CBBA’s complete reallocation strategy is shown in Figure 9.

As shown in

Table 8. UAV mission execution relationship.

UAV Identity	Task Execution Path	Flight Distance	Task Execution Time
1	(15,III)→(11,I)→(14,I)→(16,III)	18	{10,20},{64,69},{76,81},{82,92}
2	(13,I)→(10,I)→(12,I)	10	{15,20},{45,50},{86,91}
3	(9,II)→(6,II)	13	{18,33},{67,82}
4	(5,II)→(2,II)→(1,II)	14	{10,25},{47,62},{69,84}
5	(7,II)→(8,II)→(4,II)→(3,II)	22	{21,37},{49,64},{83,98},{99,114}

, the overall execution time for the UAV formation to complete the collaborative tasks is 362.093 s, with the UAV formation taking 248.093 s to make a task decision and complete all task assignment processes when faced with the current task environment. The times of the emergence of new tasks are {10,20} and {82,92}. After the emergence of new tasks, the implementation of UAVs using CBBA for complete redistribution based on the initial task allocation scheme changes as follows: UAV 1 carries out type I task sequence as 15→11→14→16, the execution time of the sudden new tasks 15 and 16 is 10 s, the execution time of the remaining types of tasks is 5 s, the moment when UAV A1 arrives at the initial task point and starts executing the task is 10 s, for its subsequent set of tasks, the UAV starts executing at 64 s, 76 s and 82 s respectively, and the overall task execution completion time is 92 s; UAV 2 carries out type I task sequence as 13→10→12, the execution time for each type of task is 5 s, the moment when UAV A2 arrives at the initial task point and starts its task is 15 s, for its subsequent set of tasks, the moment when the UAV starts its execution is 45 s and 86 s respectively, and the time when the overall task is completed is 91 s; UAV 3 carries out type II task sequence as 9→6, the moment when UAV A3 arrives at the initial task point and starts its task is 18 s, after which it takes 34 s to fly from this task point to the position of task 6, the moment when the UAV starts this task is 67 s, the execution time for each type of task is 15 s and the overall task execution is completed in 82 s; UAV 4 carries out type II task sequence as 5→2→1, the execution time for each type of task is 15 s, the moment when UAV A4 arrives at the initial task point and starts executing the task is 10 s, for its subsequent set of tasks, the UAV starts executing at 47 s and 69 s respectively, and the overall task execution is completed in 84 s; And UAV 5 carries out type II task sequence as 7→8→4→3, the moment when UAV A5 arrives at the initial task point and starts its task is 21 s, with a task execution time of 16 s. For its subsequent set of tasks, the UAVs start execution at 49 s, 83 s, and 99 s, with an execution time of 15 s for each type of task, and the overall task execution is completed in 114 s. The total revenue of the UAV mission allocation is 1552.4.

(2)

For the same scenario, the specific situation of task continuity adjustment allocation in the improved CBBA is as shown in Figure 10.

As shown in

Table 9. UAV mission execution relationship.

UAV Identity	Task Execution Path	Flight Distance	Task Execution Time
1	(15,III)→(16,III)	9	{10,20},{82,92}
2	(13,I)→(10,I)→(11,I)→(14,I)→(12,I)	19	{15,20},{45,50},{64,69},{76,81},{86,91}
3	(9,II)→(8,II)→(6,II)→(4,II)	16	{18,33},{49,64},{67,82},{83,98}
4	(5,II)→(2,II)→(1,II)	14	{10,25},{47,62},{69,84}
5	(7,II)→(3,II)	10	{21,37},{99,114}

, the overall execution time for the UAV formation to complete the collaborative tasks is 362.093 s, with the UAV formation taking 248.093 s to make a task decision and complete all task assignment processes when faced with the current task environment. The times of the emergence of new tasks are {10,20} and {82,92}. After the emergence of new tasks, compared with the CBBA’s complete reallocation strategy, the changes in the task execution sequence after using the improved CBBA with the task continuity adjustment allocation strategy are as follows: UAV 1 carries out type I task sequence as 15→16, the moment when UAV A1 arrives at the initial task point and starts its task is 10 s, after which it takes 62 s to fly from that mission point to the location of task 16, the moment when the UAV starts that task is 82 s, the execution time for each type of task is 10 s, and the overall task execution completion time is 92 s; UAV 2 carries out Type I task sequence as 13→10→11→14→12, the execution time for each type of task is 5 s, the moment when UAV A2 arrives at the initial task point and starts executing the task is 15 s, for its subsequent set of tasks, the UAV starts executing at 45 s, 64 s, 76 s and 86 s respectively, and the overall task completion time is 91 s; UAV 3 carries out Type II task sequence as 9→8→6→4, the execution time for each type of task is 15 s, the moment when UAV A3 arrives at the initial task point and starts its task is 18 s, for its subsequent set of tasks the UAV starts its execution at 49 s, 67 s and 83 s respectively, and the overall task completion time is 98 s; UAV 4 carries out Type II task sequence as 5→2→1, the execution time for each type of task is 15 s, the moment when UAV A4 arrives at the initial task point and starts executing the task is 10 s, for its subsequent set of tasks, the UAV starts executing at 47 s and 69 s respectively, and the overall task execution is completed in 84 s; And UAV 5 carries out Type II task sequence as 7→3, the moment when UAV A5 arrives at the initial task point and starts the task is 21 s and the task execution time is 16 s, after which it takes 62 s to fly from this task point to the location of task 3, the moment when the UAV starts this task is 99 s and the task execution time is 15 s, and the overall task execution completion time is 114 s. The total revenue of the UAV mission allocation is 5251.5.

(3)

For the same scenario test, the CBBA was used to add the adjustment allocation based on the task time window on the basis of the former test, as shown in Figure 11.

As shown in

Table 10. UAV mission execution relationship.

UAV Identity	Task Execution Path	Flight Distance	Task Execution Time
1	(15,III)→(10,I)→(14,I)→(16,III)	11	{10,20},{45,50},{76,81},{82,92}
2	(13,I)→(11,I)→(12,I)	12	{15,20},{64,69},{86,91}
3	(9,II)→(8,II)→(6,II)→(4,II)	16	{18,33},{49,64},{67,82},{83,98}
4	(5,II)→(2,II)→(1,II)	14	{10,25},{47,62},{69,84}
5	(7,II)→(3,II)	10	{21,37},{99,114}

, the overall execution time for the UAV formation to complete the collaborative tasks is 224.013 s, with the UAV formation taking 100.013 s to make a task decision and complete the process of assigning all tasks in the face of the current task environment. The times of the emergence of new tasks are {10,20} and {82,92}. After the emergence of new tasks, the implementation of UAVs using the task continuity adjustment allocation in the improved CBBA and the adjustment allocation based on the time window change based on the task allocation scheme of the complete redistribution strategy CBBA: UAV 1 carries out type I task sequence as 15→10→14→16, the execution time of the new tasks 15 and 16 is 10 s, the execution time of the remaining types of tasks is 5 s, the moment when UAV A1 arrives at the initial task point and starts executing the task is 10 s, for its subsequent set of tasks, the moments when the UAV starts executing are 45 s, 76 s and 82 s respectively, and the overall task execution is completed in 92 s; UAV 2 carries out type I task sequence as 13→11→12, the execution time for each type of task is 5 s, the moment when UAV A2 arrives at the initial task point and starts executing the task is 15 s, for its subsequent set of tasks the UAV starts executing at 64 s and 86 s respectively, and the overall task completion time is 91 s; UAV 3 carries out type II task sequence as 9→8→6→4, the execution time for each type of task is 15 s, the moment when UAV A3 arrives at the initial task point and starts its task is 18 s, for its subsequent set of tasks the UAV starts its execution at 49 s, 67 s and 83 s respectively, and the overall task completion time is 98 s; UAV 4 carries out type II task sequence as 5→2→1, the execution time for each type of task is 15 s, the moment when UAV A4 arrives at the initial task point and starts executing the task is 10 s, for its subsequent set of tasks, the UAV starts executing at 47 s and 69 s respectively, and the overall task execution is completed in 84 s; And UAV 5 carries out type II task sequence as 7→3, the moment when UAV A5 arrives at the initial task point and starts the task is 21 s and the task execution time is 16 s, after which it takes 62 s to fly from this task point to the location of task 3, the moment when the UAV starts this task is 99 s and the task execution time is 15 s, and the overall task execution completion time is 114 s. The total revenue of the UAV mission allocation is 5419.2.

(4)

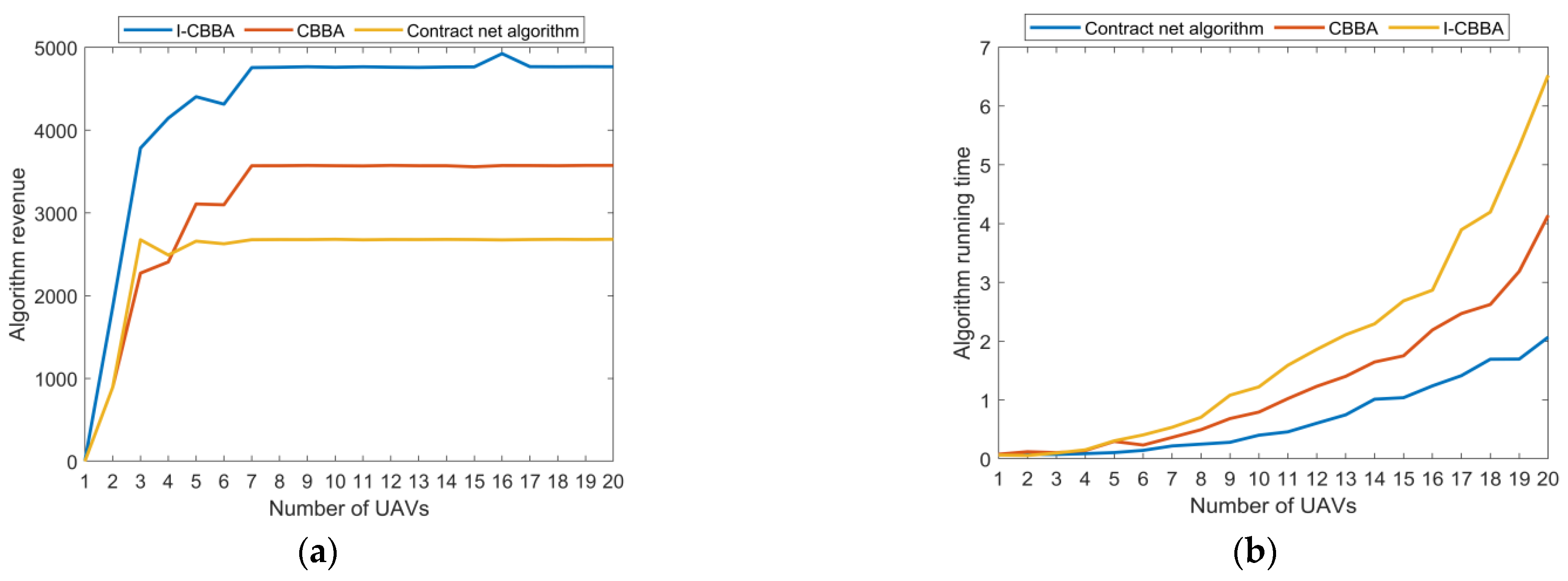
To further test the performance of the improved CBBA in unbalanced staged collaborative task assignments for multiple UAVs and targets, 1-20 UAVs were set up for collaborative execution of 15 tasks. The task assignment performance was compared with those of the original CBBA and contract network algorithms. The results are shown in Figure 12.

As shown in Figure 12, compared with the original CBBA and contract network algorithms, the improved CBBA has a higher profit value when the task allocation reaches the final saturation state. This is because the original CBBA and contract network algorithms do not consider the imbalance between the numbers of UAVs and target tasks. At the same time, the assignment of target tasks with different execution stages is not satisfied well. The running time of the CBBA is higher than that of the original CBBA and contract net algorithms. This is because the improved CBBA is much more considerate of the matching relationship between UAVs and tasks and reasonably allocates UAVs to perform tasks in different task execution stages. In summary, it can be seen that the improved CBBA has better allocation performance in solving the problem of multi-UAV and multi-target unbalanced coordinated task allocation in stages.

(5)

To further test the applicability and effectiveness of the algorithm in UAV dynamic task assignment scenarios, 1 to 18 UAVs were assigned to 16 target tasks, including nine type I tasks, five type II tasks, and two dynamic tasks. The UAV type ratio was 1:1. The simulation test is shown in Figure 13.

As shown in Figure 13, in the process of UAVs performing multiple tasks, the benefit of the improved algorithm is higher than that of the algorithm of the complete reprogramming strategy. In the early stage, due to there being a small number of UAVs and too many tasks, the benefits of the TCW-CBBA, TW-CBBA, and TC-CBBA algorithms are roughly the same. When the number of UAVs is approximately 3–7, the profit values of the algorithms are ranked from high to low as TCW-CBBA, TW-CBBA, and TC-CBBA. In the later period, due to the excessive number of UAVs and the relatively small number of tasks, the total profit values of multiple UAVs tend to be the same. In terms of running time, the TCW-CBBA, TW-CBBA, and TC-CBBA algorithms have large running times, with TCW-CBBA and TW-CBBA algorithms taking longer than TC-CBBA because the TCW-CBBA and TW-CBBA algorithms consider the effect of the task window when assigning tasks.

4. Discussion

To solve the problem of multi-UAV and multi-target cooperative task assignment while considering the constraints of multi-type task assignment and mismatched numbers of UAVs and target tasks, the CBBA was improved to achieve task assignment by stages. The improved CBBA was used to improve the dynamic task allocation process of multi-UAVs from two aspects: continuous task planning and dynamic adjustment of task execution time windows. The simulation results show that the proposed multi-UAV cooperative multi-objective phased assignment algorithm and multi-UAV dynamic task assignment mechanism can effectively solve the multi-UAV multi-objective cooperative task assignment problem and enable timely response to unexpected new tasks. The next step will focus on the joint planning of task execution time windows among different UAVs.

5. Conclusions

For the multi-UAV phased cooperative task allocation problem, the multi-UAV multi-task cooperative phased allocation model was established by considering the constraints of task execution timing constraint, task execution time constraint, task execution quantity constraint, and task execution demand constraint. An improved consensus-based bundle algorithm was proposed to improve the algorithm task packet and task execution path construction mechanism, to realize the cooperative execution of multiple tasks by multiple UAVs, and to increase the design of a two-tier task bidding mechanism to better meet the execution needs of various tasks in different time periods. Aiming at the problem of task reassignment of sudden new tasks in the process of task execution, on the basis of the original complete replanning strategy, a task continuity adjustment mechanism and a task time window-based adjustment mechanism were added. The task continuity adjustment mechanism is used to comprehensively weigh the execution relationship between pre-order tasks and subsequent tasks in the task execution path and better take into account the relationship between the overall task execution benefits and execution costs. Use the adjustment mechanism based on the task time window to reasonably plan the task execution time arrangement of various tasks in the task execution path of various UAVs, optimize the overall task execution list, and improve the task execution efficiency. Through specific simulation cases, it is verified that the proposed cooperative phased task assignment algorithm can well realize the coordinated execution of different tasks by multiple UAVs in different time periods and meet the execution requirements of various time periods of the tasks. At the same time, the improved dynamic task allocation mechanism proposed in this paper can well deal with the allocation conflict between the original task sequence and the sudden new task and better take into account the task execution benefits and execution costs in the task execution path after replanning. This makes the overall task execution time window planning and arrangement more reasonable and effectively improves the overall task dynamic allocation efficiency and effectiveness.