Potential Estimation of Load Alleviation and Future Technologies in Reducing Aircraft Structural Mass
Abstract
1. Introduction
2. Reference Aircraft and Its Aeroservoelastic Modeling
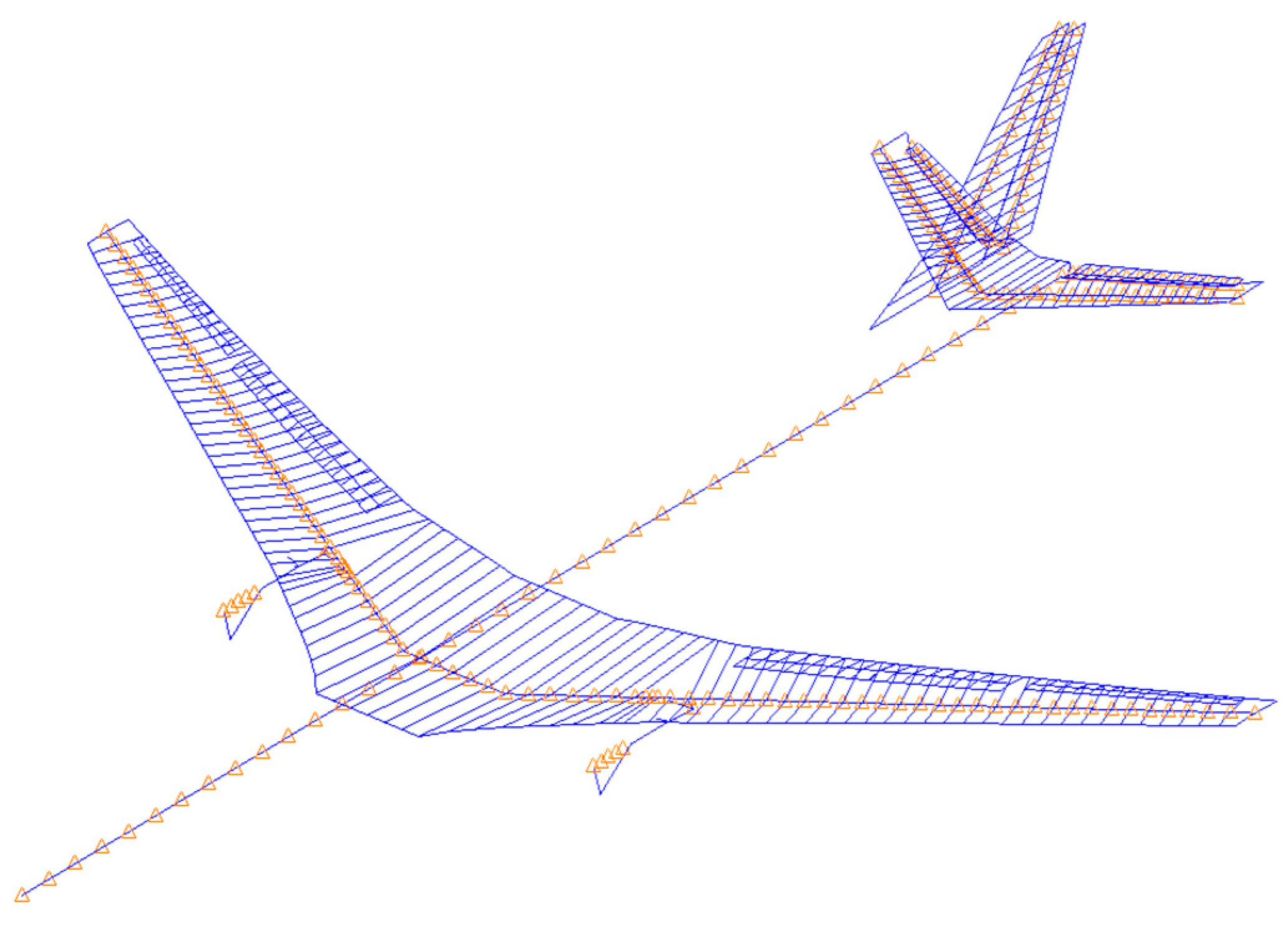
2.1. Reference Aircraft
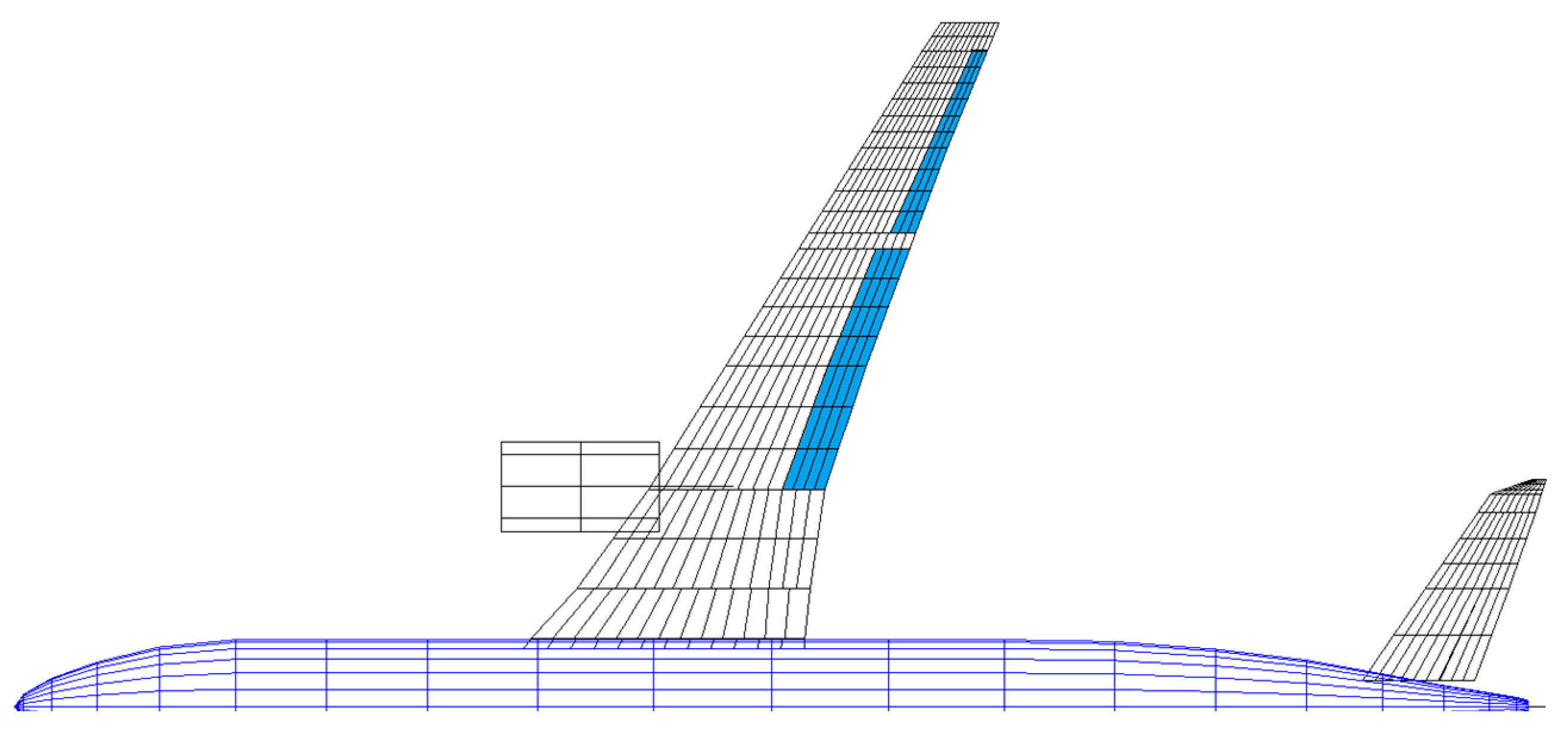
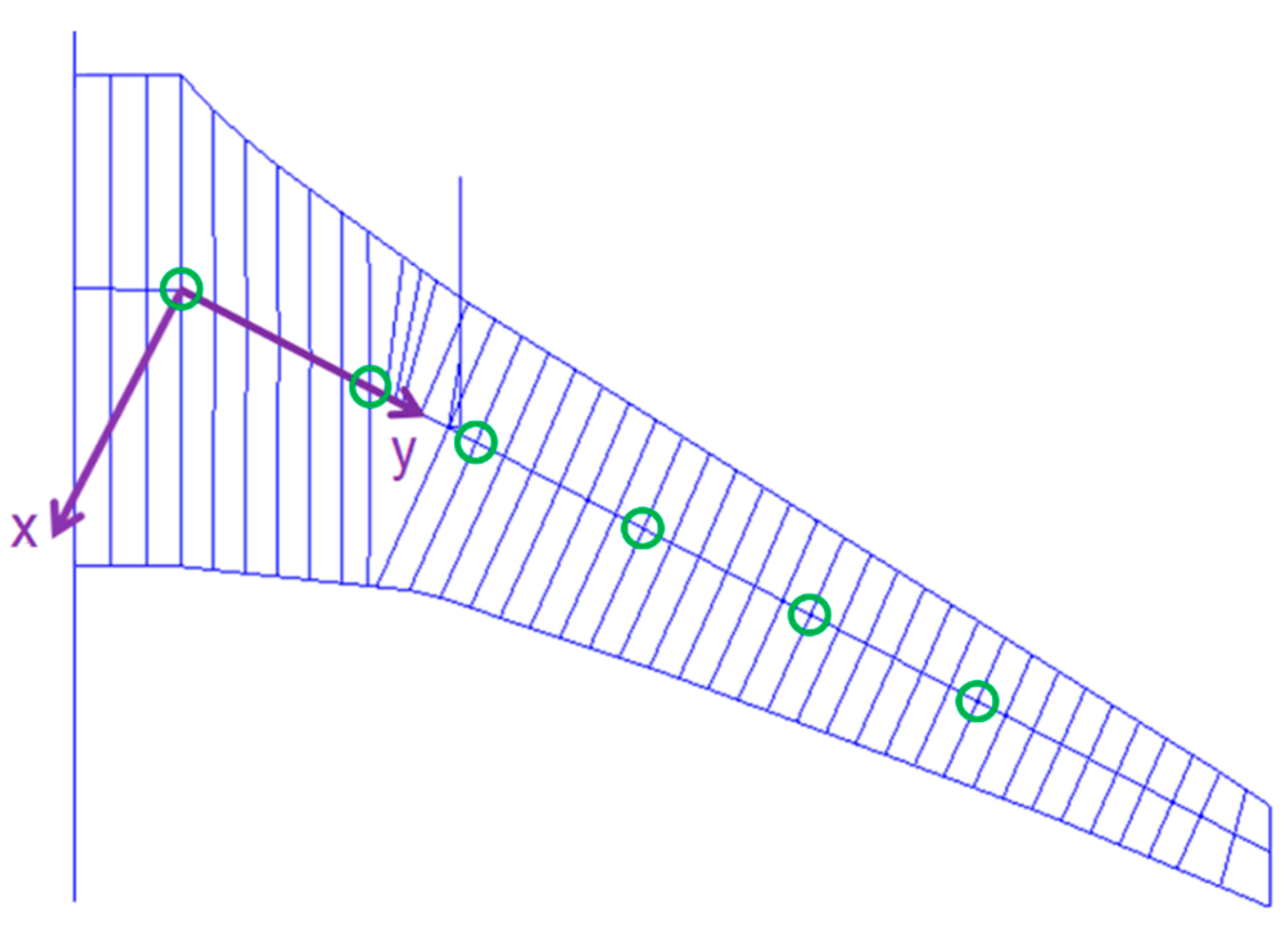
2.2. Aeroservoelastic Modeling
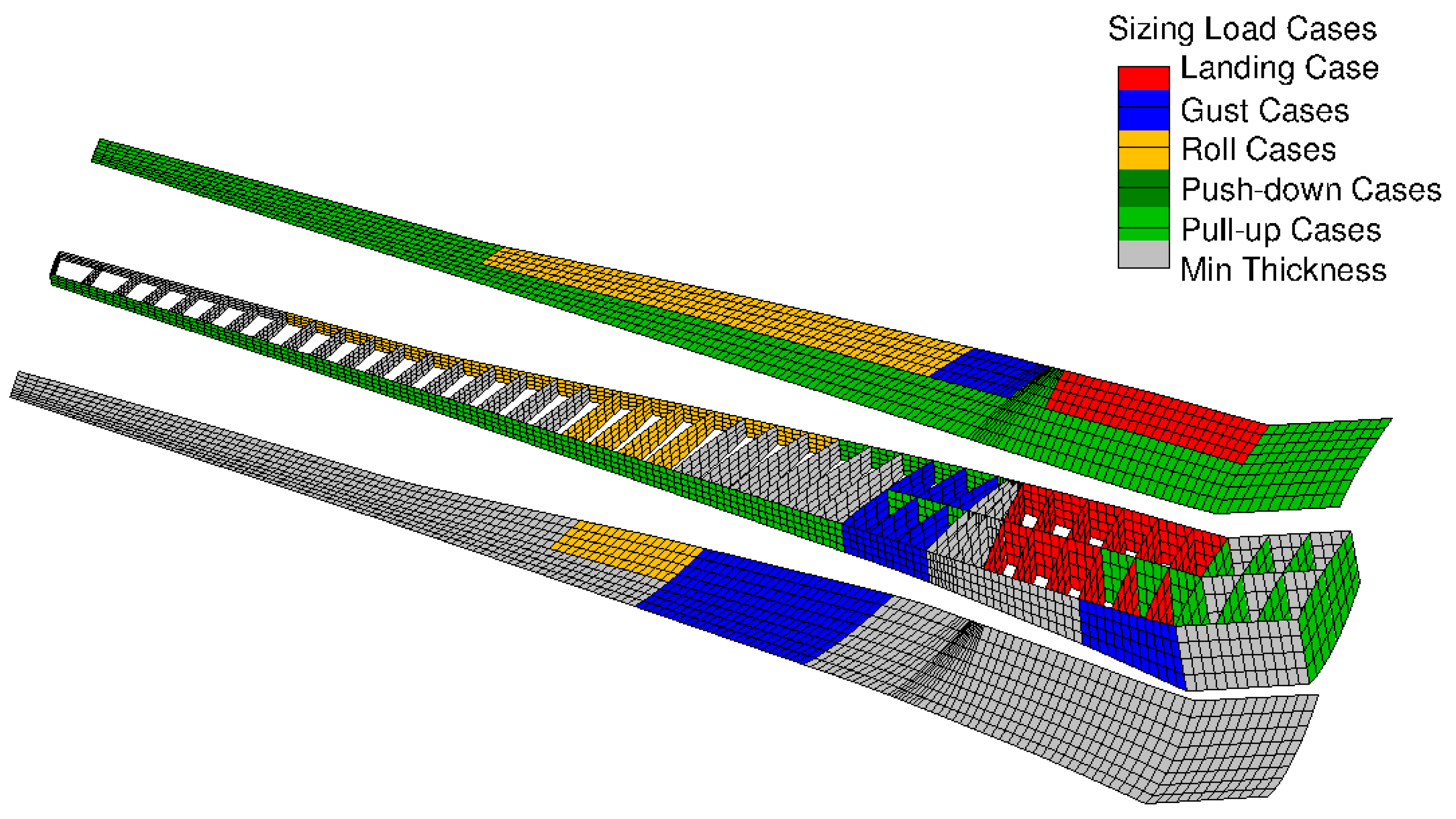
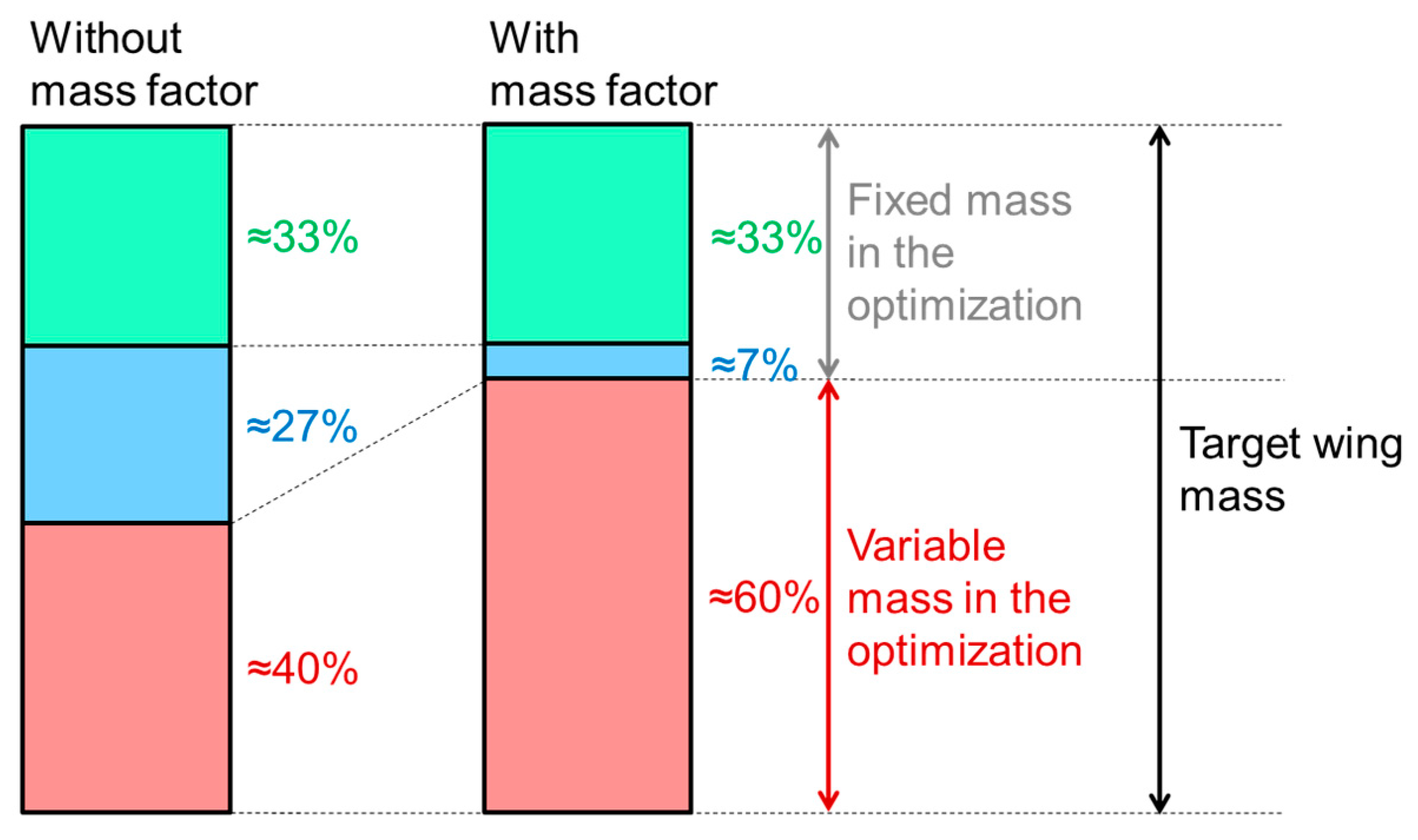
- In the primary structure, the FE model provided an integral structure without holes, fasteners, joints, etc. All those parts require structure reinforcements which would increase the total mass of the manufactured structure. For this aspect, Chiozzotto [18] introduced the term “mass factor” in his dissertation and this aspect is addressed in Section 6.
- The mass estimation of the secondary structure is, in general, difficult since every aircraft can have, for example, unique set of systems which have unique masses. Torenbeek [19] indeed proposed mass estimation methods, among others, for leading and trailing edge devices; however, those methods do not cover all the secondary masses which are contained, for example, in the wing. Chiozzotto [18] proposed the total secondary mass estimation as a constant fraction of the maximum take-off mass which is a rough empirical approximation; however, the distribution of the secondary masses in the different aircraft components was not considered. Furthermore, the OEM also contains, among others, hydraulic fluid, lubricant and unusable fuel masses which are unique for every aircraft. At this point, it is concluded that the uncertainty in the estimation of the secondary masses is significant, and that it could cause uncertainties with respect to the target component masses.
3. Design Process with Loads Analysis and Structural Optimization
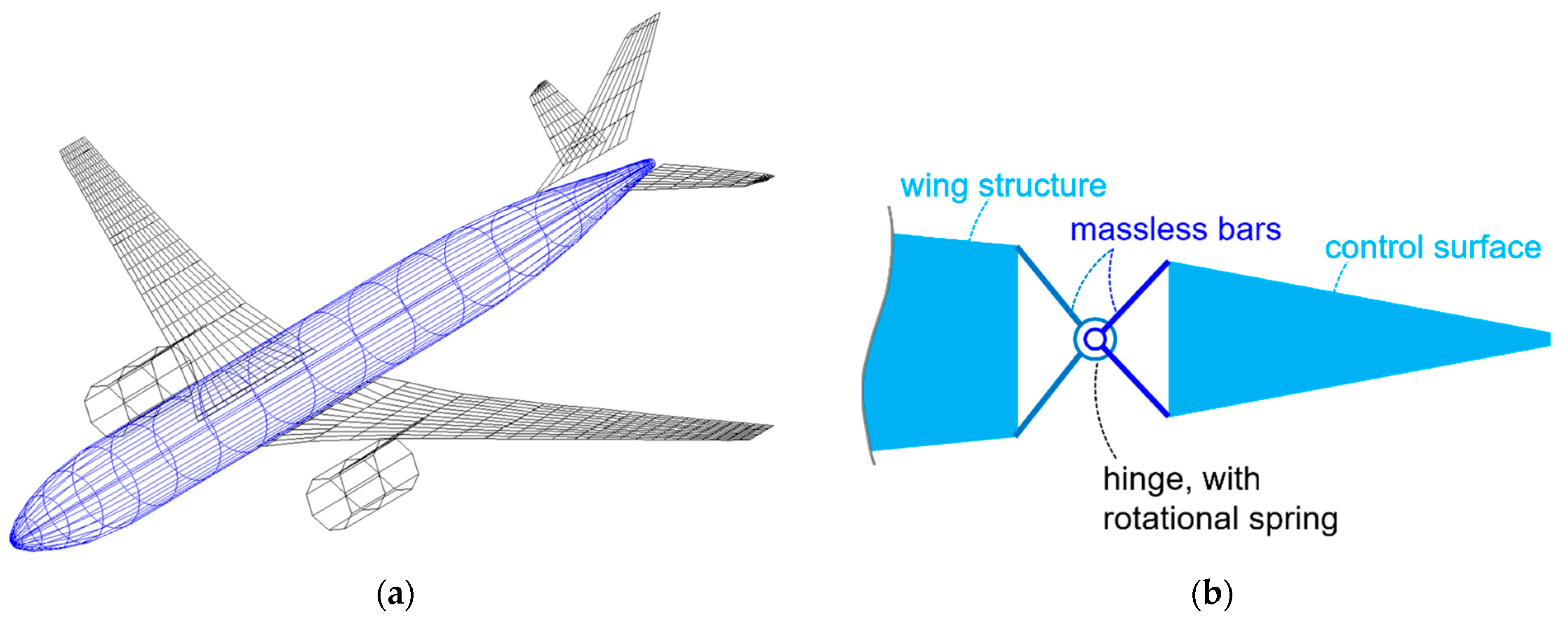
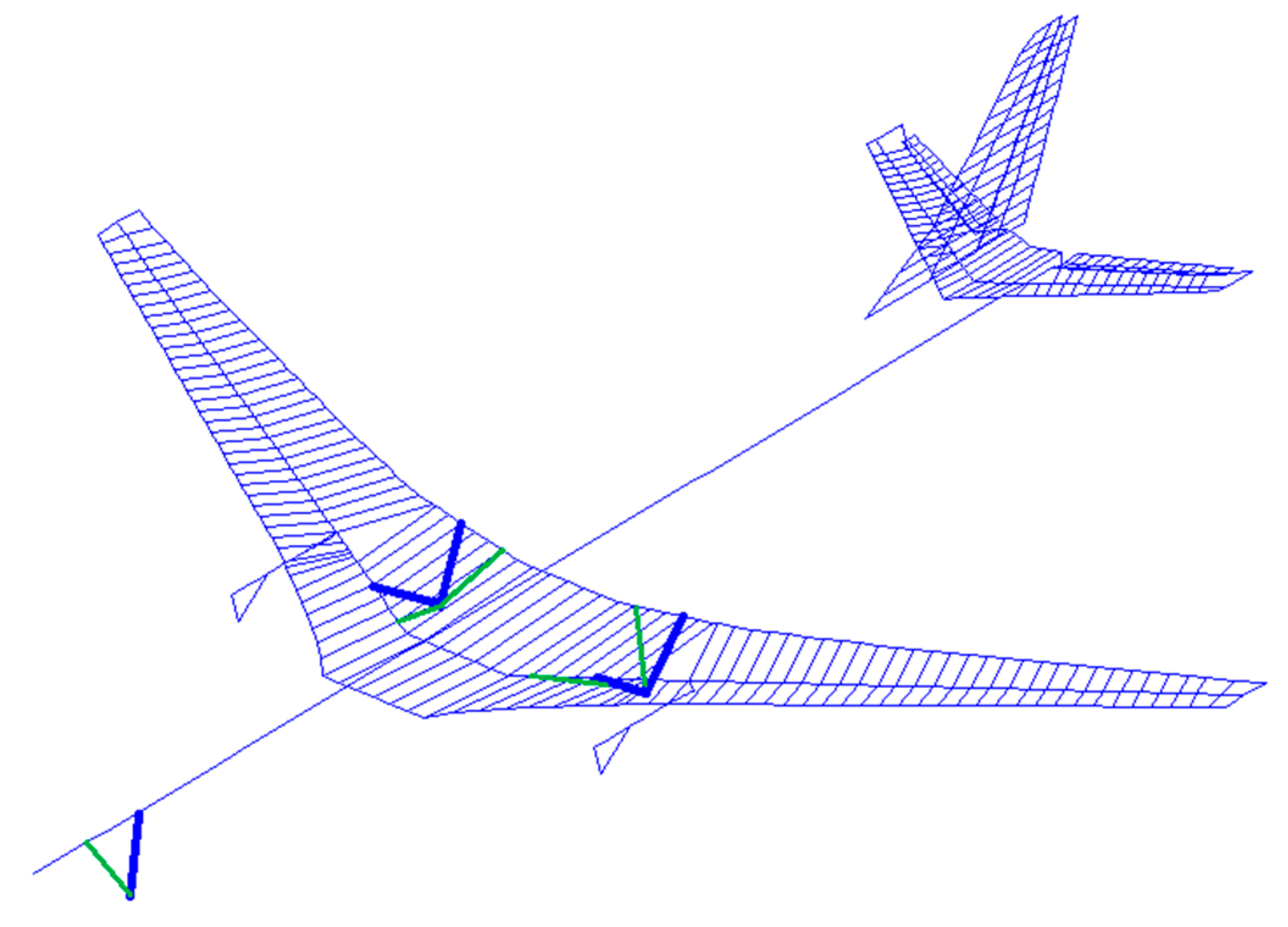
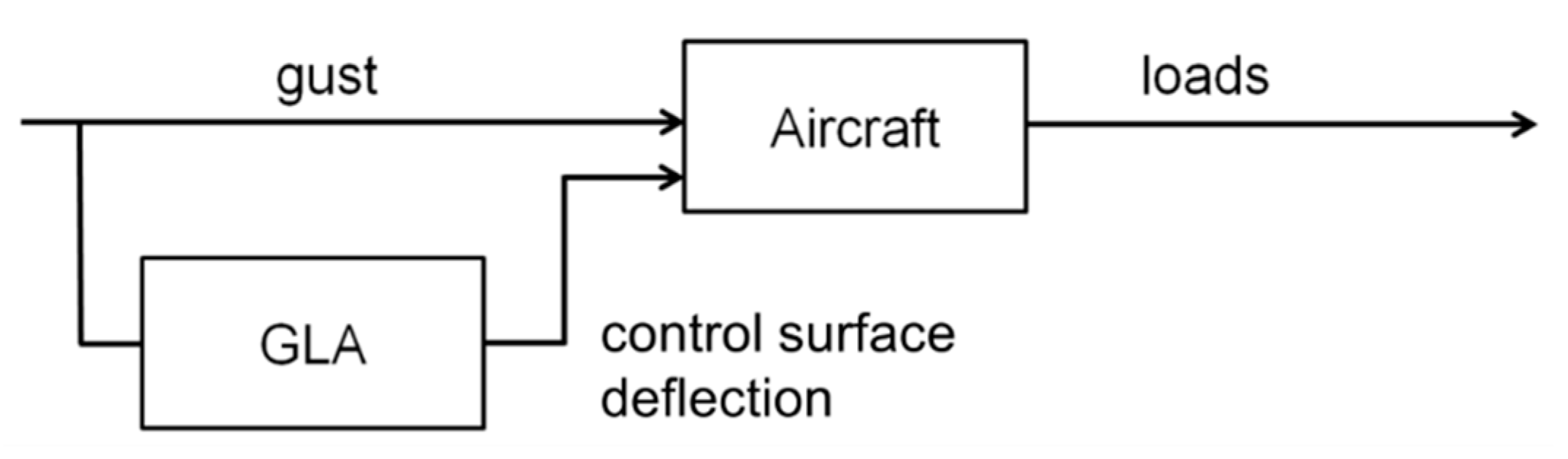
4. Modeling of Load Alleviation Systems
5. Loads and Mass Results of Test Cases
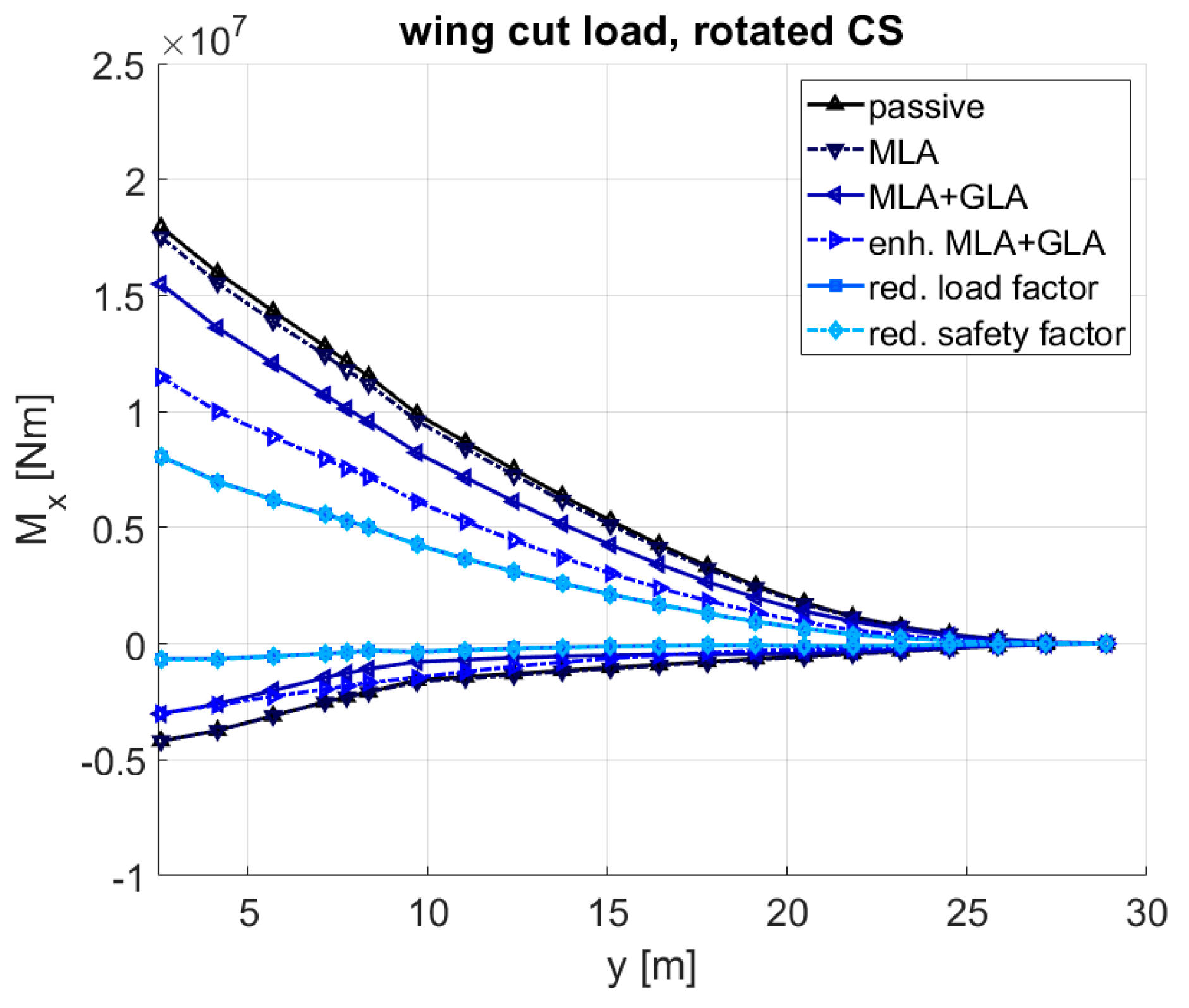
- The reference variant which incorporates the maneuver load alleviation (MLA).
- Passive variant. The term passive means that MLA is inactive. This test case was intended to provide an insight into how much mass reduction is already achieved by MLA.
- Maneuver and gust load alleviation (MLA + GLA). This corresponds to the reference with an additional GLA function.
- MLA + GLA, enhanced control surface layout and MLA/GLA algorithms (enh. MLA + GLA). While the previous test case used the available control surfaces only, this case featured load alleviation with additional control surfaces.
- MLA + GLA, enhanced control surface layout, MLA/GLA algorithms and reduced design load factor (red. load factor). According to the statistical loads data of the Boeing 777-200ER [25], load factors above 1.5 were hardly reached during the surveyed 10,000 flights; therefore, while assuming that the technologies will improve, the maximum design load factor was reduced from 2.5 to 1.5 and the design gust speeds were halved.
- MLA + GLA, enhanced control surface layout, MLA/GLA algorithms, reduced design load factor and reduced safety factor (red. safety factor). With an assumption of a more accurate tolerance in the materials, the safety factor was reduced from 1.5 to 1.3.
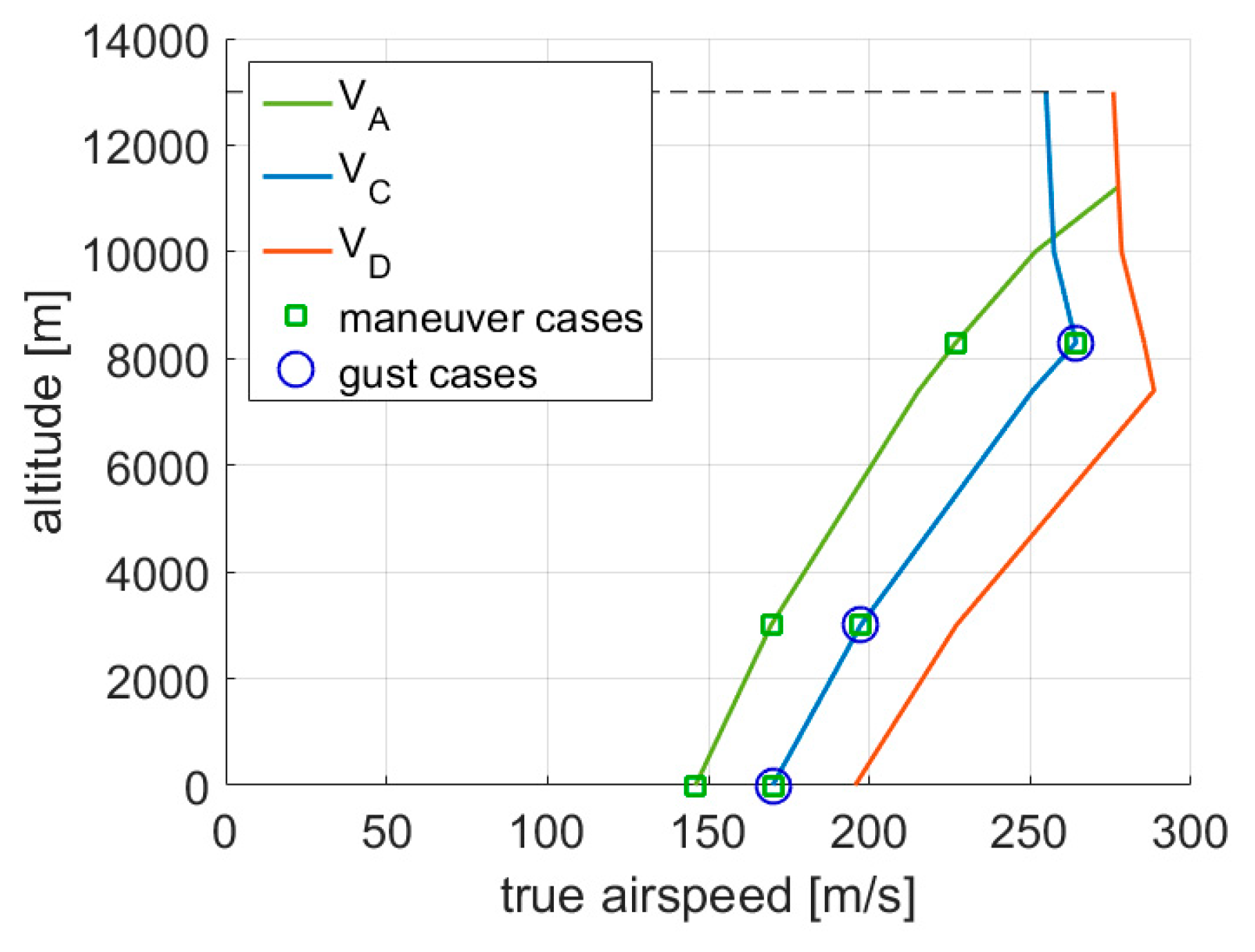
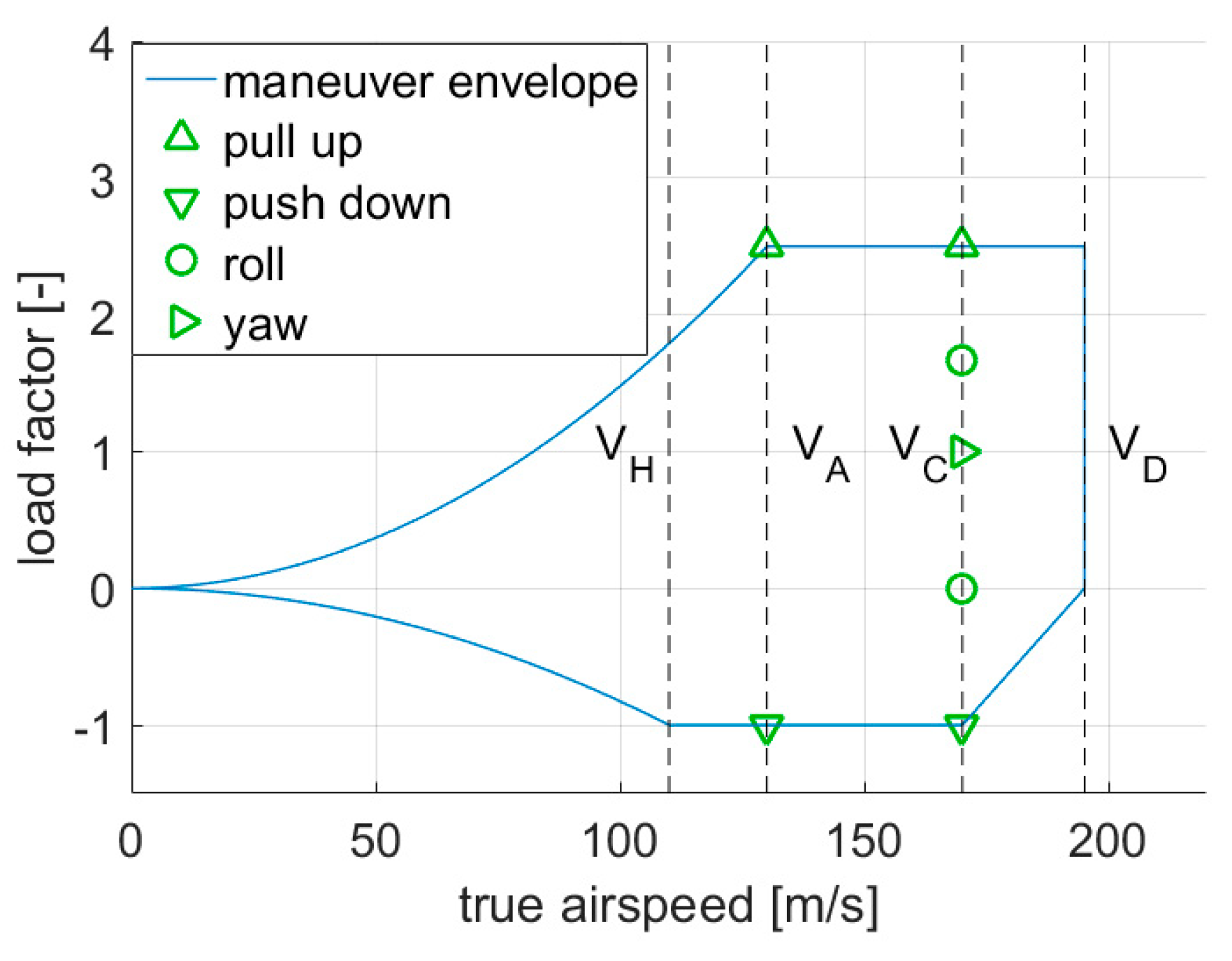
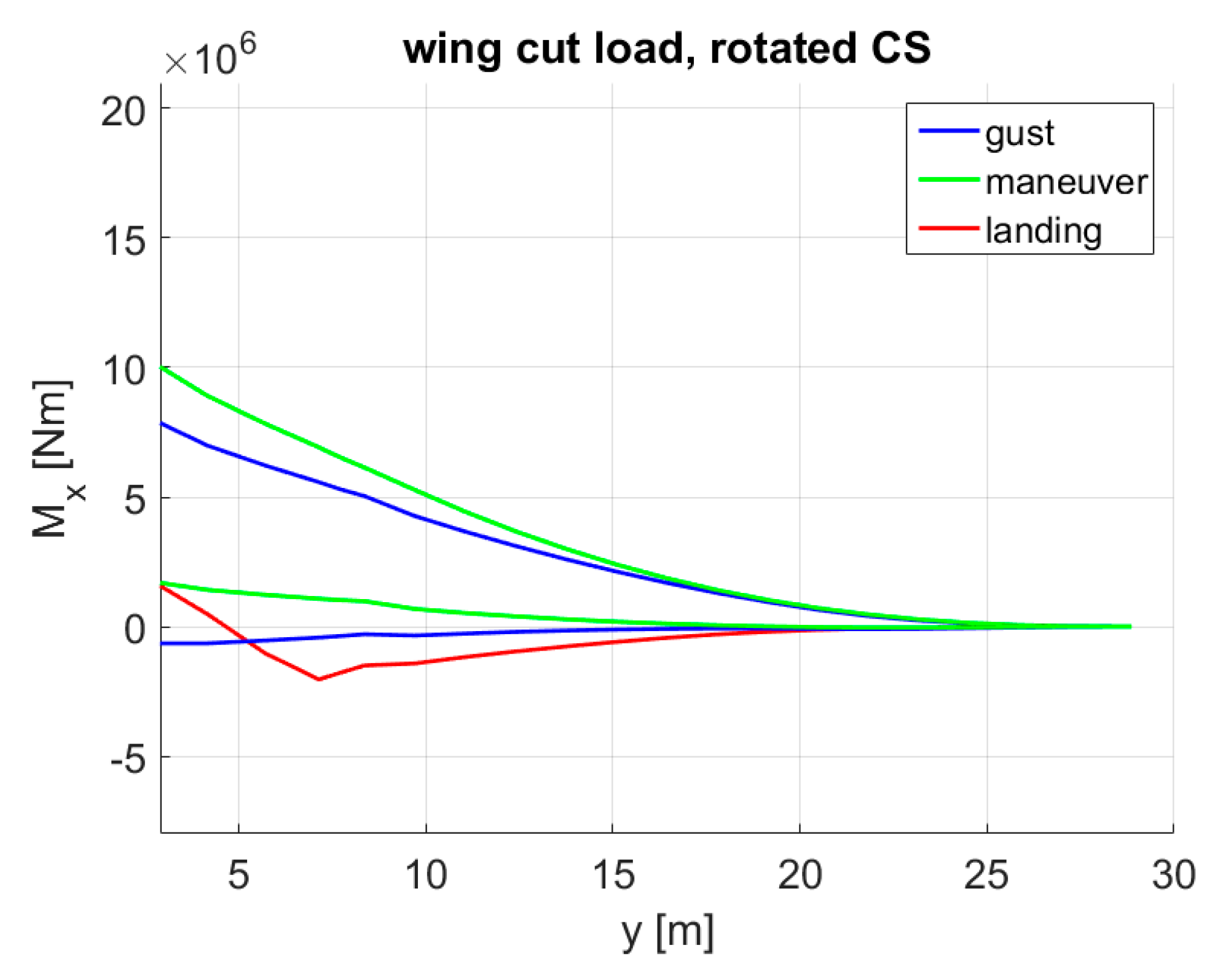
5.1. Parameter Space
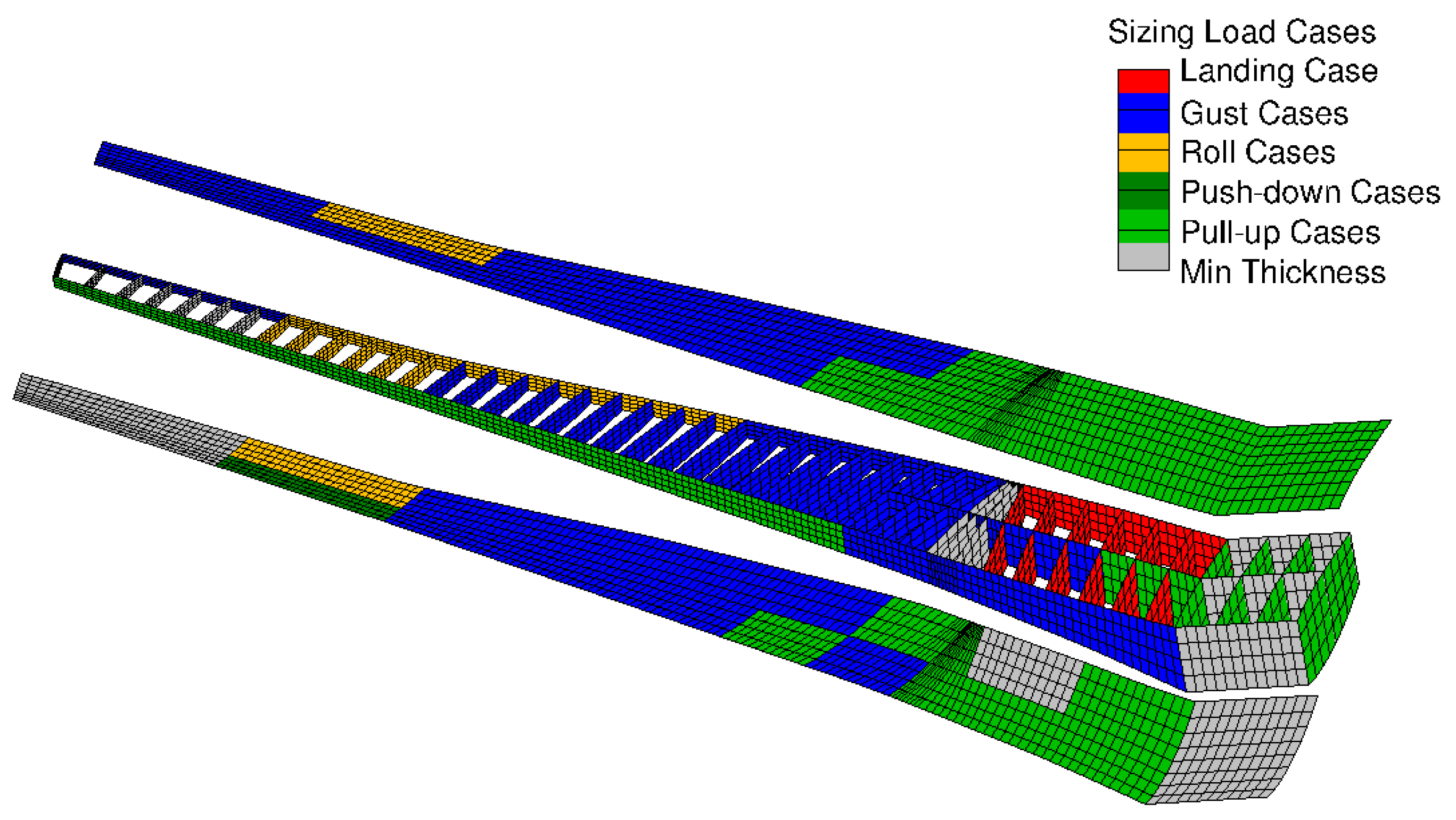
- 2.5 g pull-up at and ,
- −1.0 g push-down at and ,
- Steady roll at 0 g and 1.67 with a roll velocity of 15°/s, at ,
- Accelerated yaw maneuver with a 5° rudder angle at .
- Vertical upward and downward gusts on the clean configuration at ,
- Vertical upward and downward gusts with airbrakes out (flight spoilers were deflected by 30°) at .
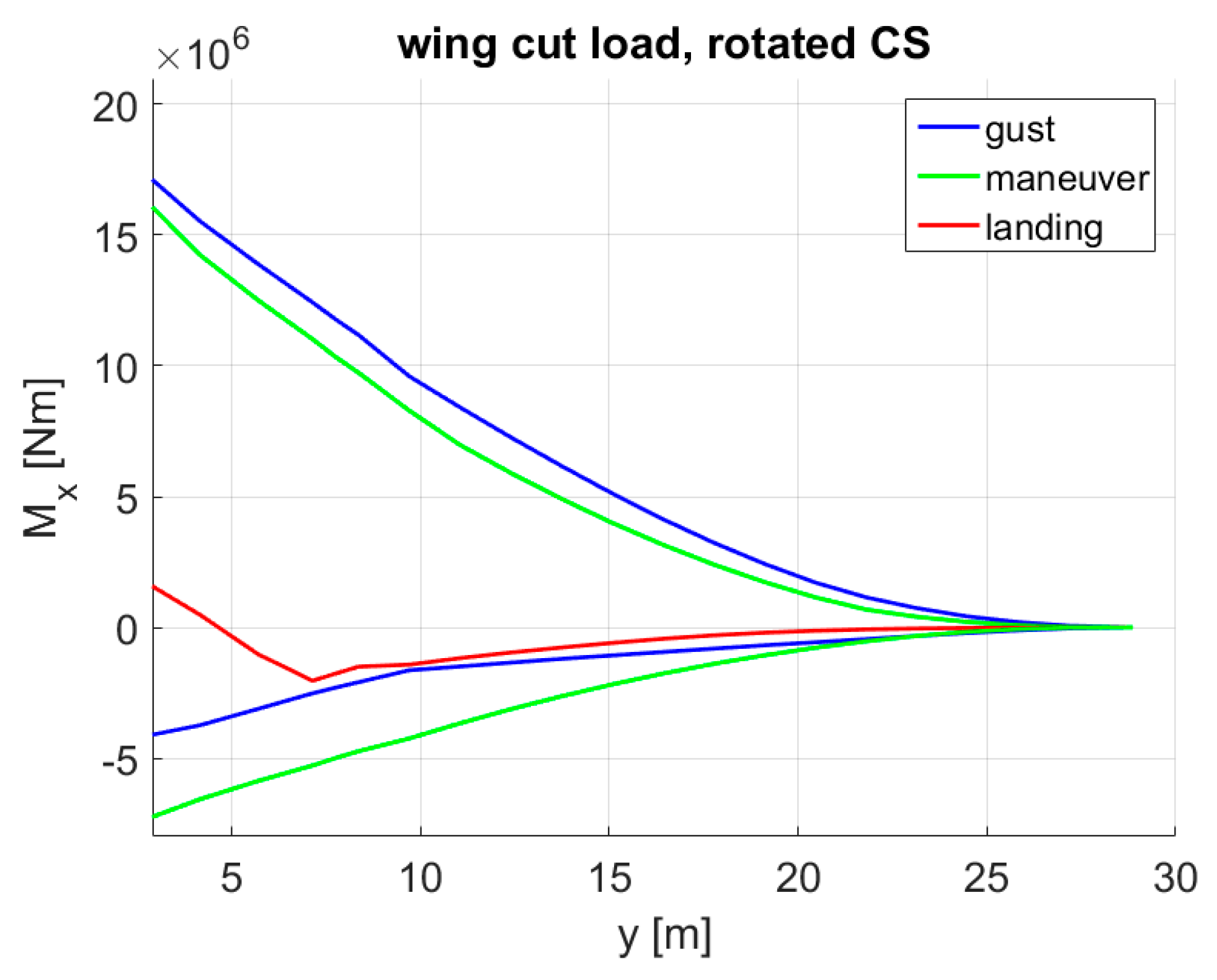
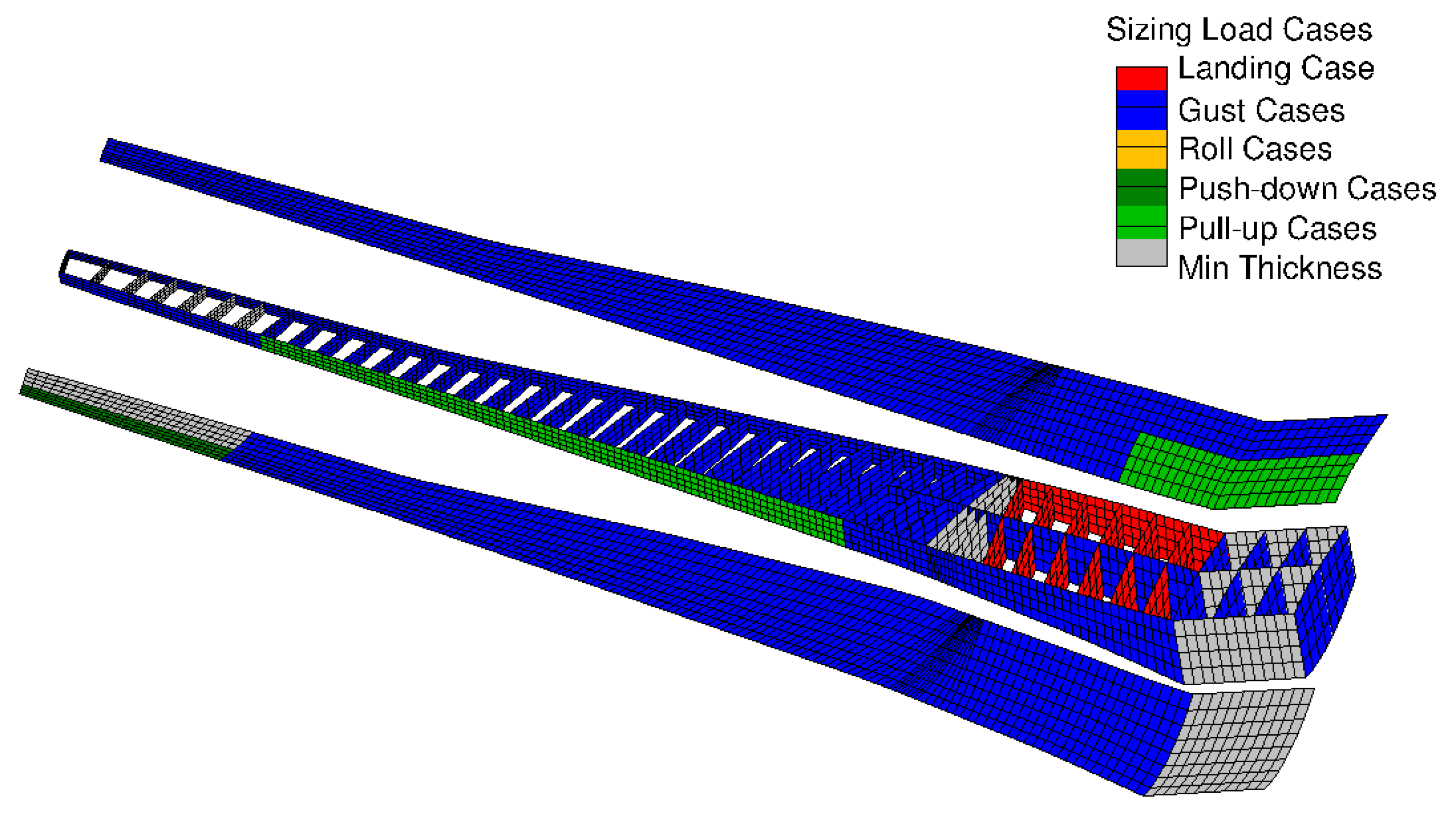
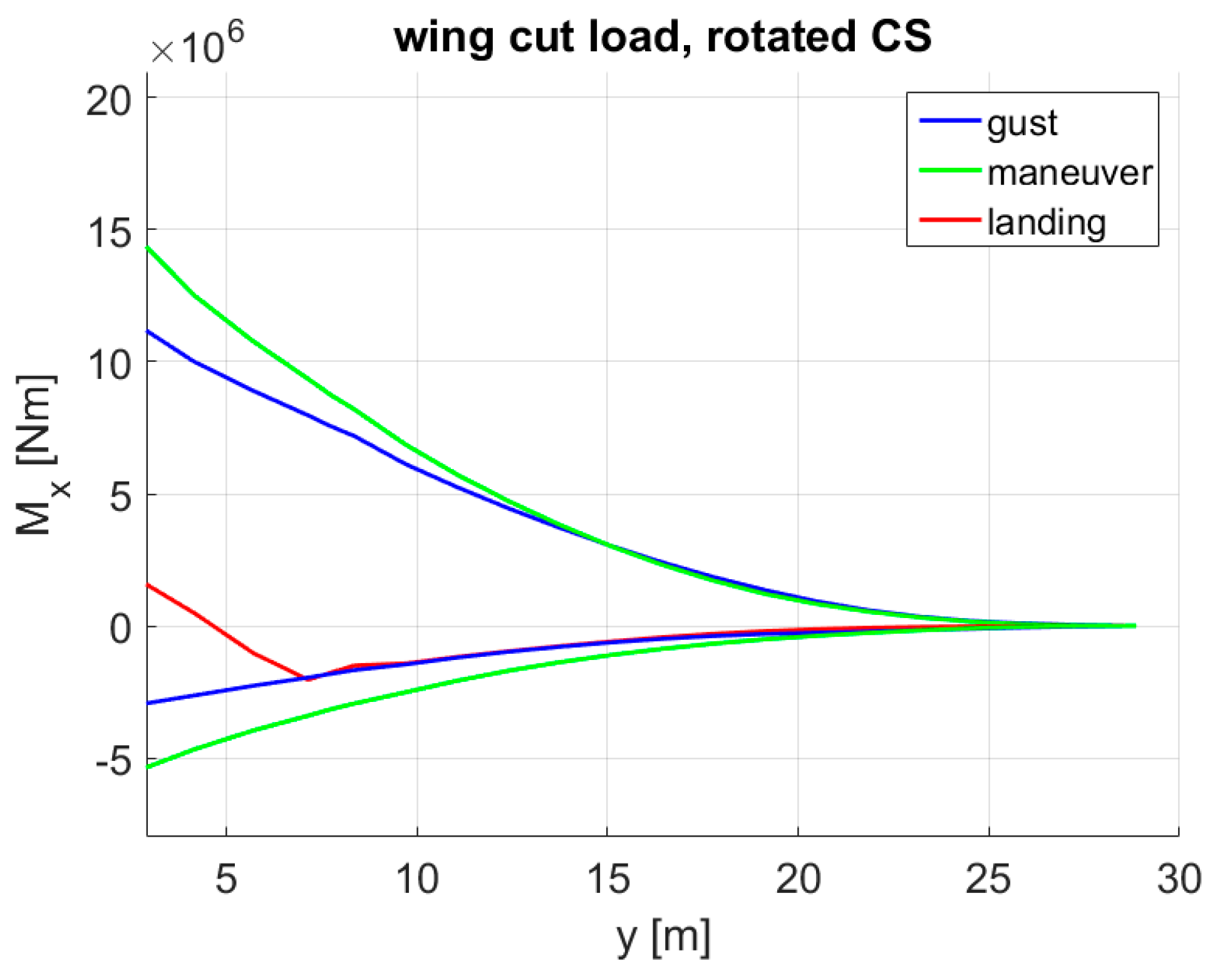
5.2. Reference with MLA
- During 2.5 g pull-up maneuvers, the inner, outer ailerons and the outer three spoilers were deflected by −20° (trailing edge up).
- During −1 g push-down maneuvers, the control surfaces were not deflected.
5.3. Passive Variant
5.4. MLA + GLA
5.5. MLA + GLA + Enhanced CS Layout (Enh. MLA + GLA)
- At the wing span positions where the high lift flaps were mounted, trailing edge control surfaces were assumed instead. This assumption was based on the multifunctional wing movable concept as elaborated by Reckzeh [28].
- MLA algorithm and control surface assignation. Instead of setting a fixed control surface deflection for every 2.5 g pull-up maneuver, the deflection was then a function of the equivalent airspeed:
- ○
- −20° (trailing edge up) for the ailerons,
- ○
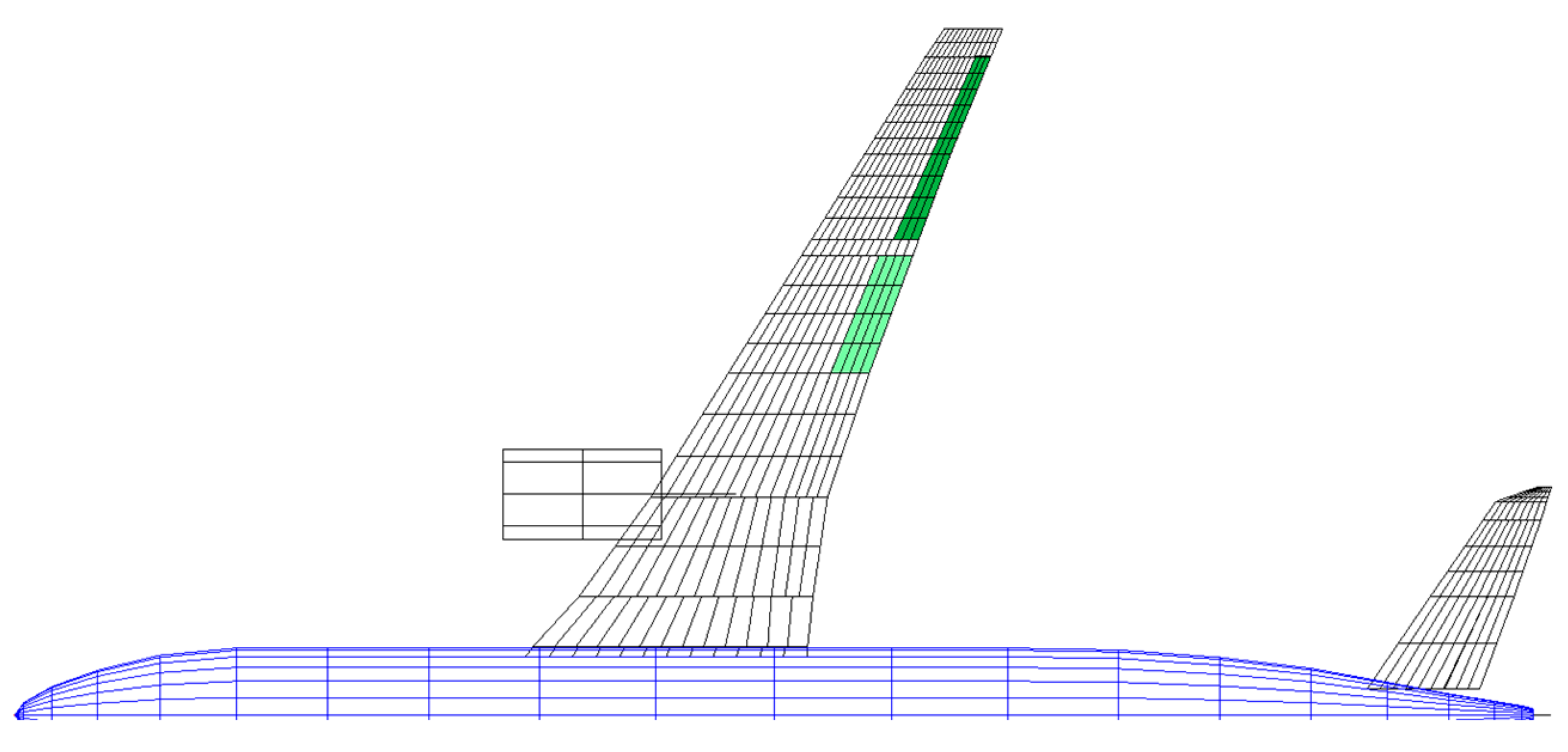
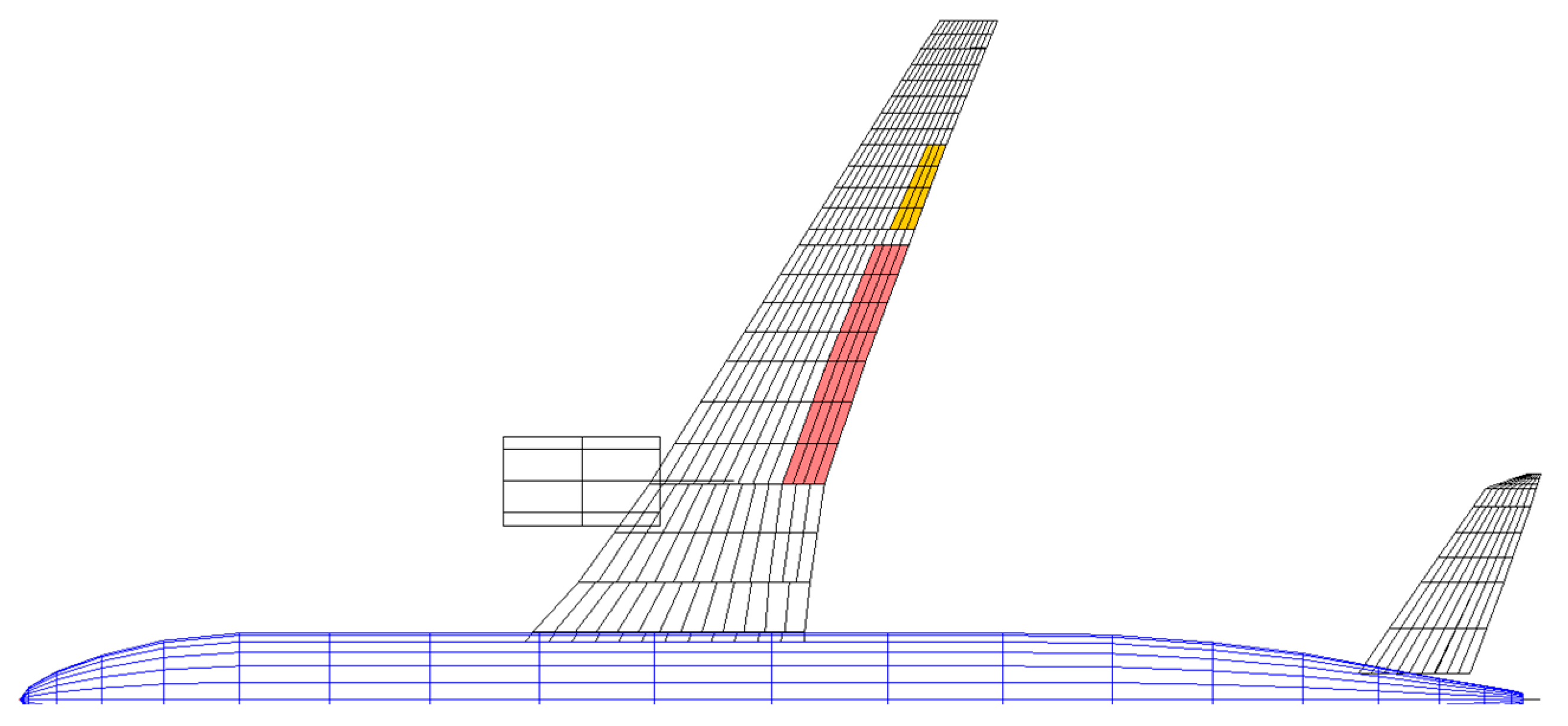
- −10° (trailing edge up) for the outer half of the outer flaps (bright green area in Figure 29),
- ○
- +10° (trailing edge down) for the inner flaps (light green are near the root).
- ○
- +20° (trailing edge down) for the ailerons,
- ○
- +10° (trailing edge down) for the outer half of the outer flaps,
- ○
- −10° (trailing edge up) for the inner flap.
- GLA gain and control surface assignment. The implemented GLA was designed to reduce the incremental gust loads. In doing so, the more control surfaces that were deflected by GLA, the higher were the achievable gust load reductions; hence, the outer flaps were also deflected beside the ailerons in the enhanced GLA algorithm, see Figure 30.Theoretically, the inner flaps could be deflected as well; however, those are seen to be ineffective in reducing the wing root bending moment since the lever is relatively short. Moreover, due to the large wing chord around the root, an inner flap deflection is expected to evoke large torsion moments which are undesirable. With the aileron and outer flap deflection, the GLA gain was reduced to −2.0 to avoid having an excessive increase in the torsion moments due to the larger total area of the deflected control surfaces. Furthermore, gust cases with airbrakes were not considered, since the airbrakes with the enhanced layout were assumed not to change the lift distribution.
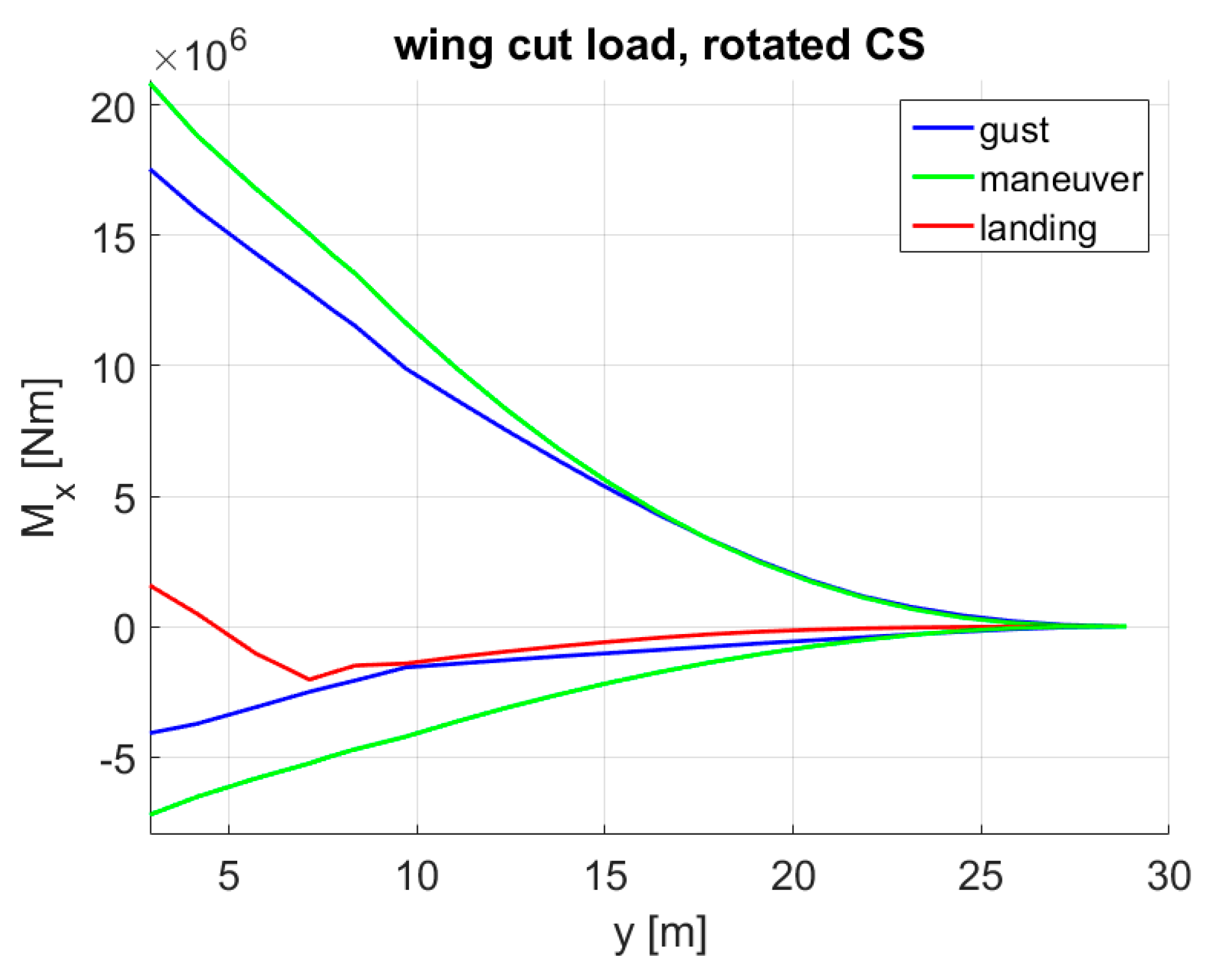
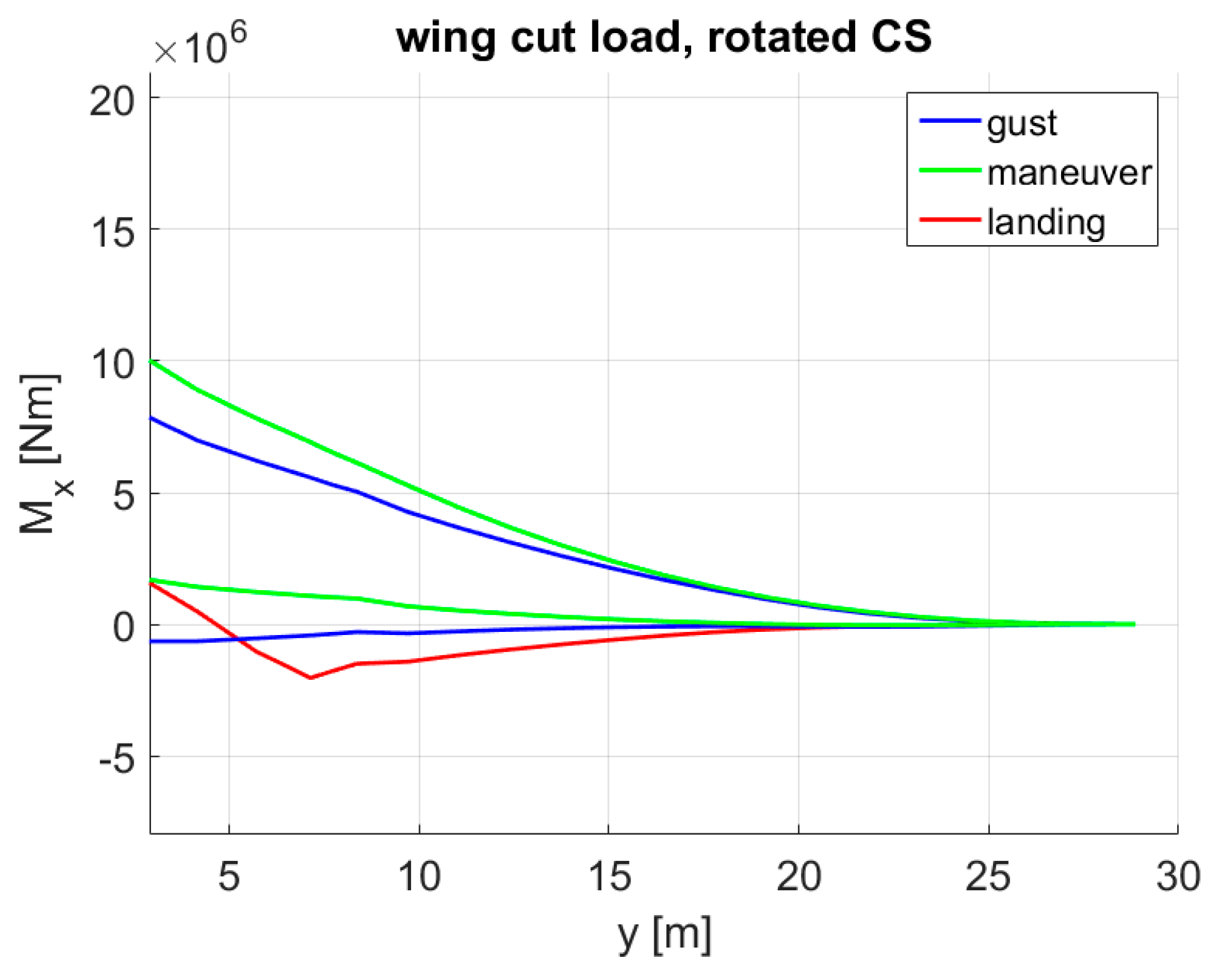
5.6. MLA + GLA + Enhanced CS Layout + Reduced Design Load Factor (Red. Load Factor)
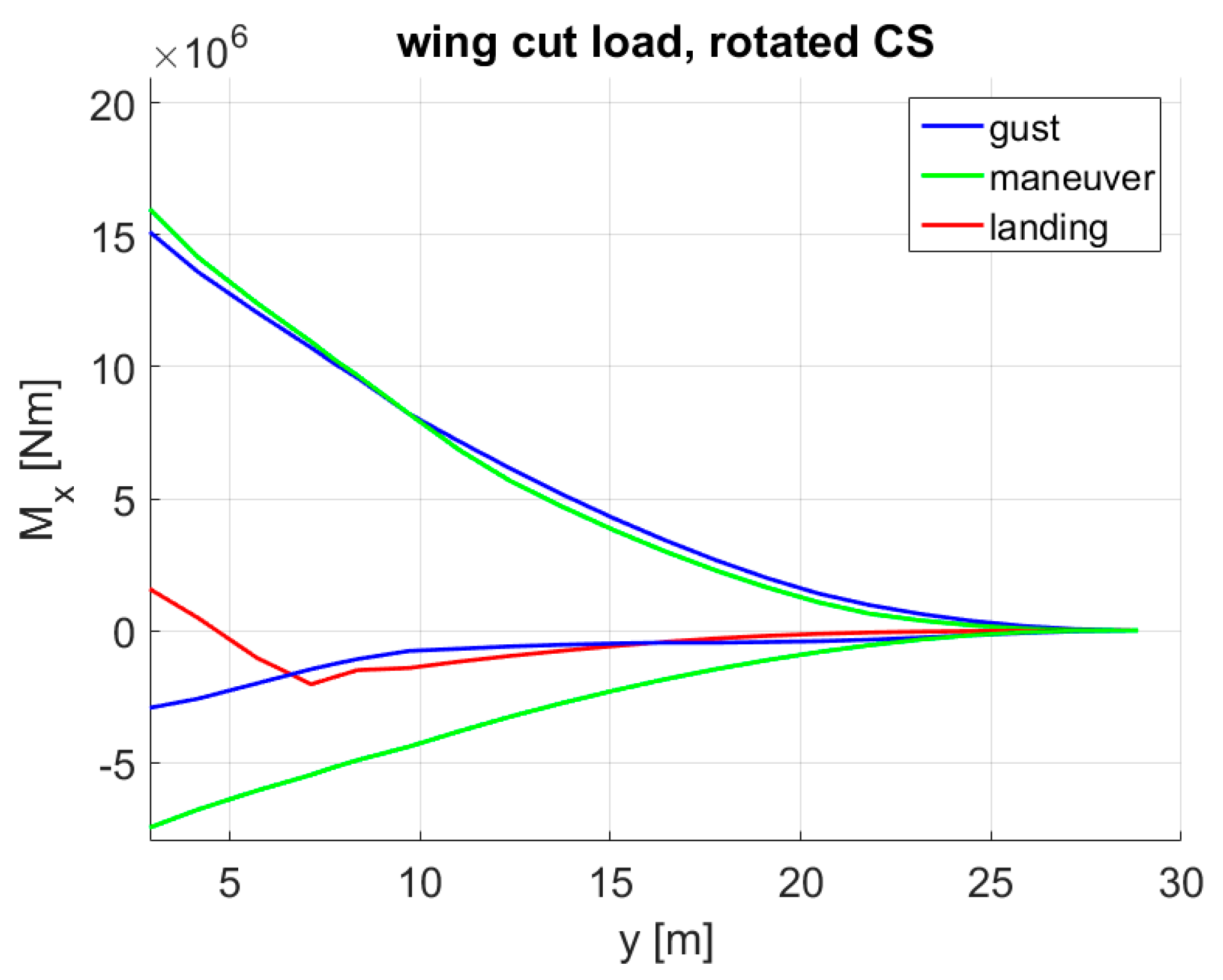
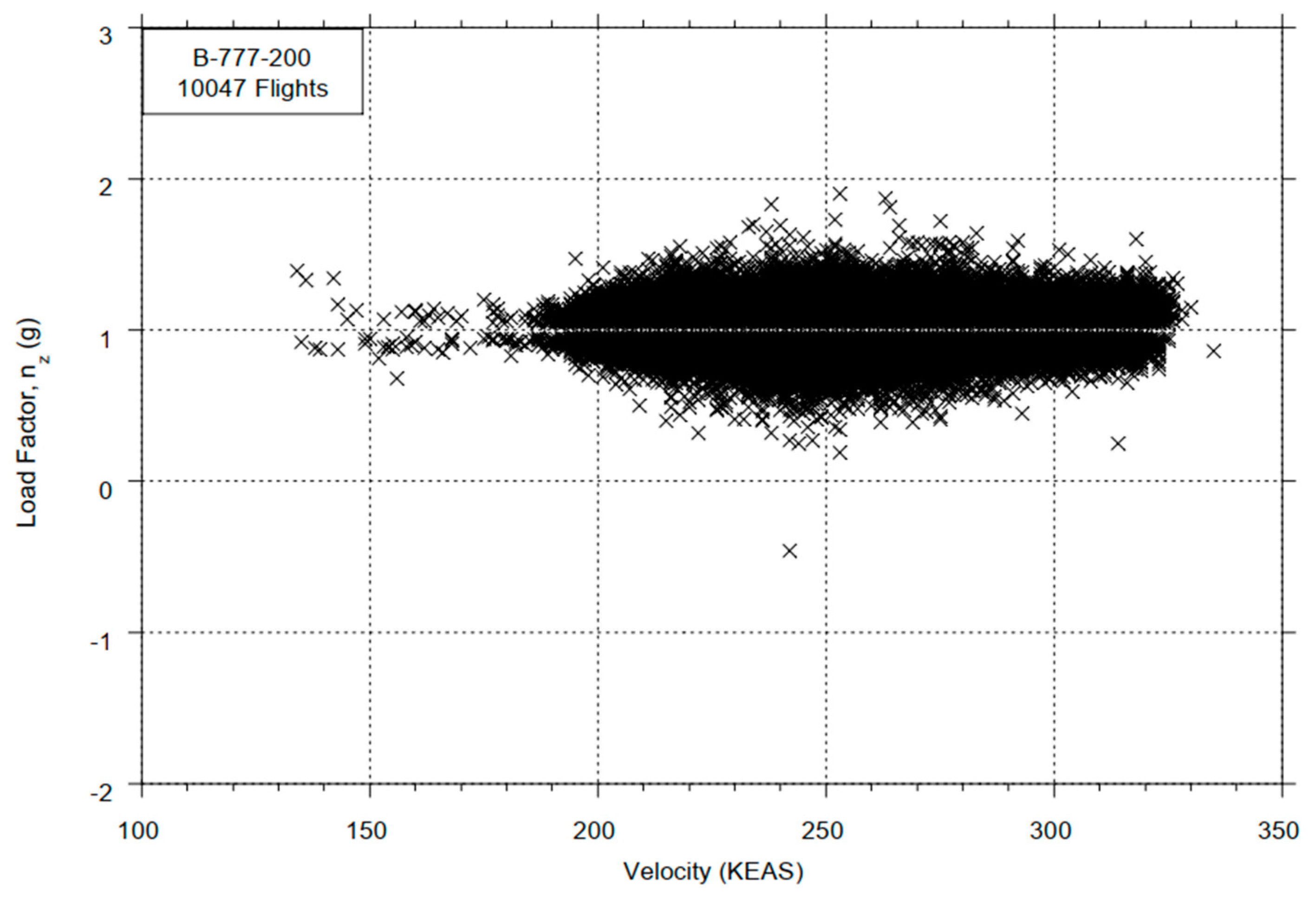
- The range of the design load factor was reduced to +0.5 g – +1.5 g. This assumption was based on the statistical loads data of a Boeing 777-200ER provided by the FAA [25]. According to the data extracted from 10,047 flights, accelerations below +0.5 g and above +1.5 g were exceeded in less than 1% of the samples, see Figure 34. Furthermore, it has to be remarked that the highest accelerations were more likely to be reached with lighter mass configurations where the wing loads were relatively low. Hence, a design load factor up to 1.5 g at masses up to MTOM is seen as more conservative.
- For the 1.5 g pull-up maneuvers at , the MLA deflection was set to:
- ○
- −10° (trailing edge up) for the ailerons,
- ○
- −5° (trailing edge up) for the outer half of the outer flaps (bright green area in Figure 29),
- ○
- +5° (trailing edge down) for the inner flaps (light green are near the root).
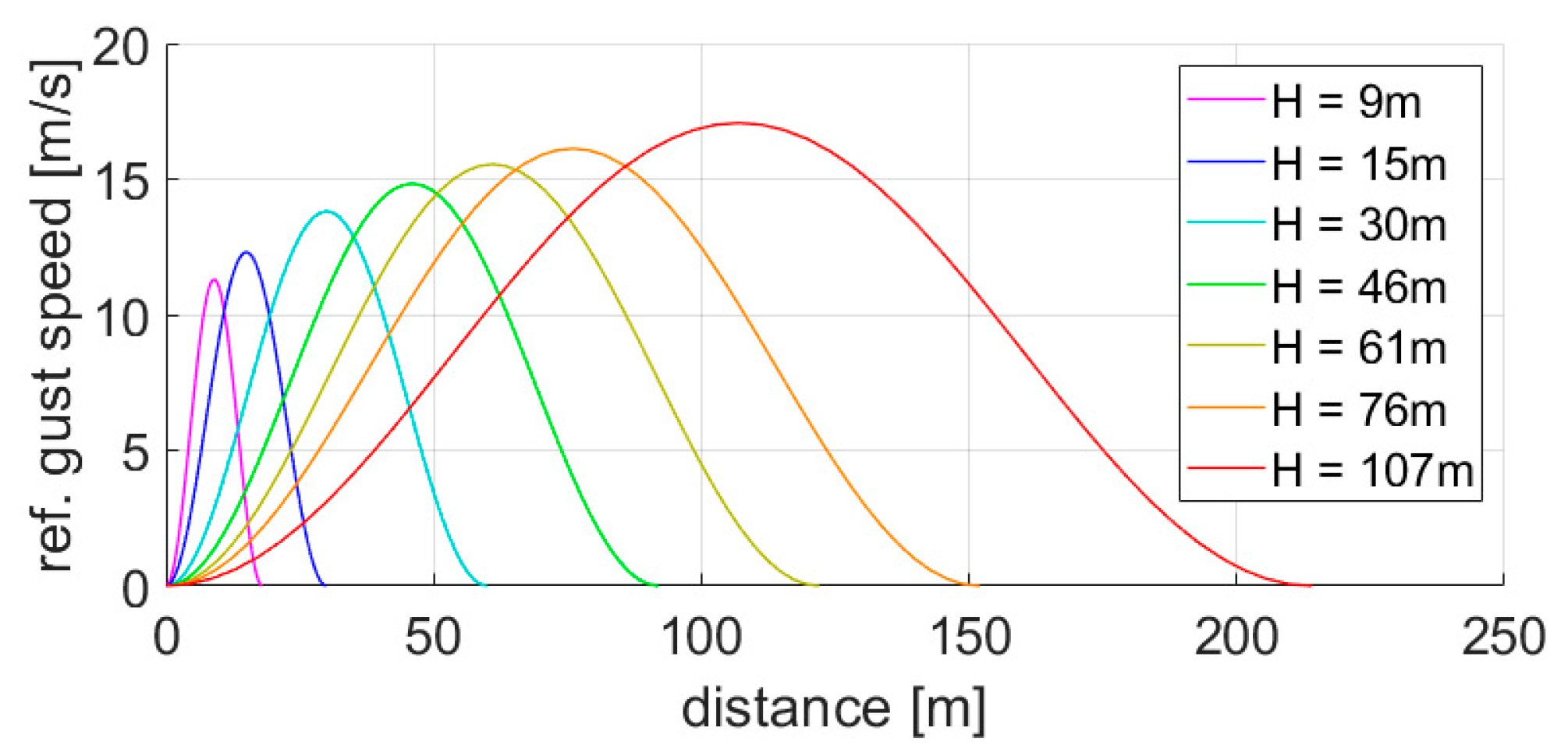
- The design gust speeds prescribed in CS25 [27] were reduced to half of the initial values. This is based on the data on turbulence intensities according to MIL-STD-1797A [29] as shown in Figure 35. At this point, the gust speeds given in CS25 were assumed to be equivalent to a probability of 1 × 10−5/h. If future technologies can predict turbulences and gusts with a higher reliability, the design gust speeds can be reduced so that they are equivalent to a probability of exceedance of 1 × 10−3/h. In Figure 35, if the altitude of 10,000 ft is taken as a reference, the turbulence intensity with a probability of 1 × 10−3/h is approx. half of that with a 1 × 10−5/h probability. In this case, the GLA gain was kept constant. With the lower gust speeds, the control surface deflection was accordingly smaller.

5.7. MLA + GLA + Enhanced CS Layout + Reduced Design Load Factor + Reduced Safety Factor (Red. Safety Factor)
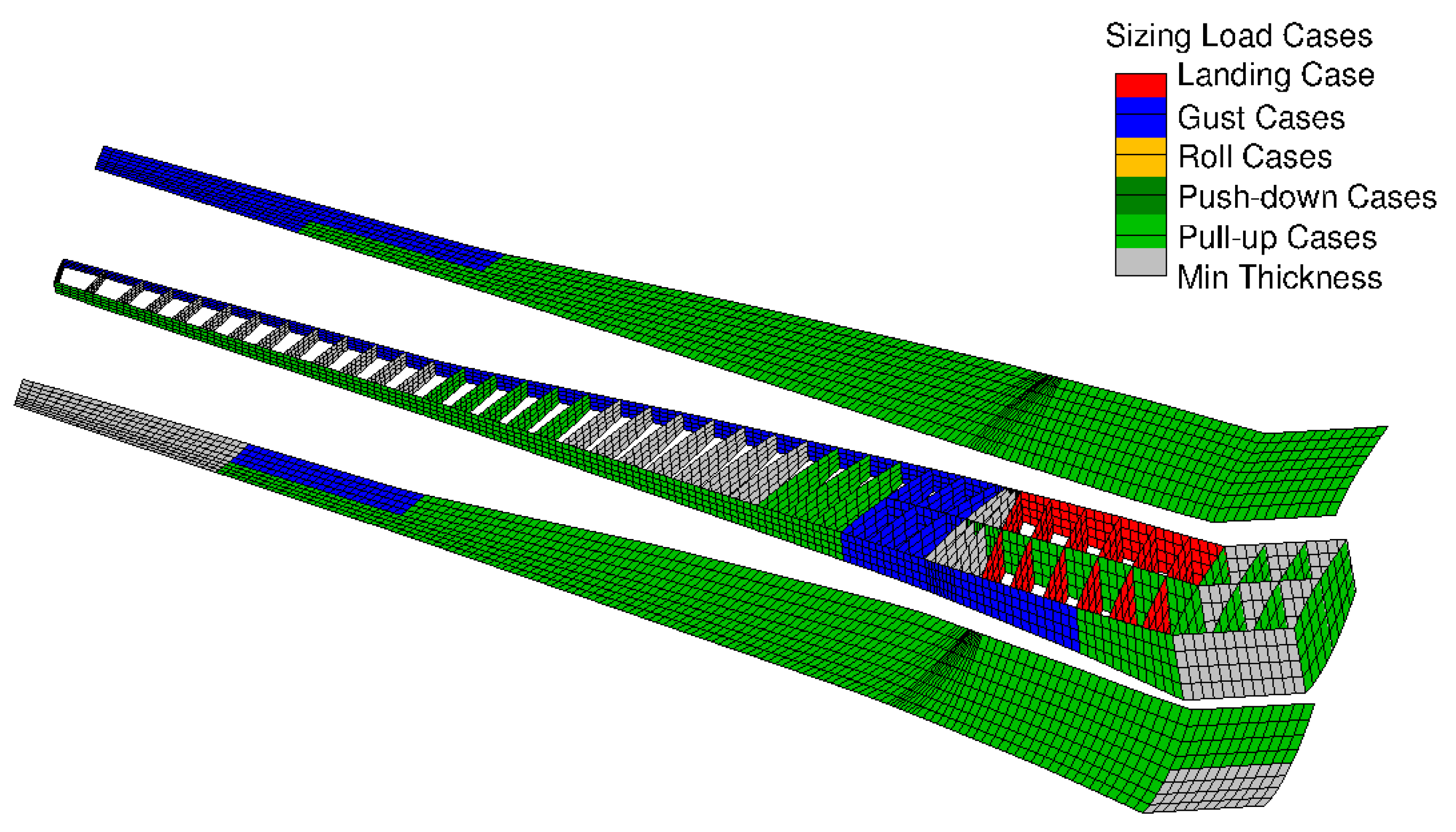
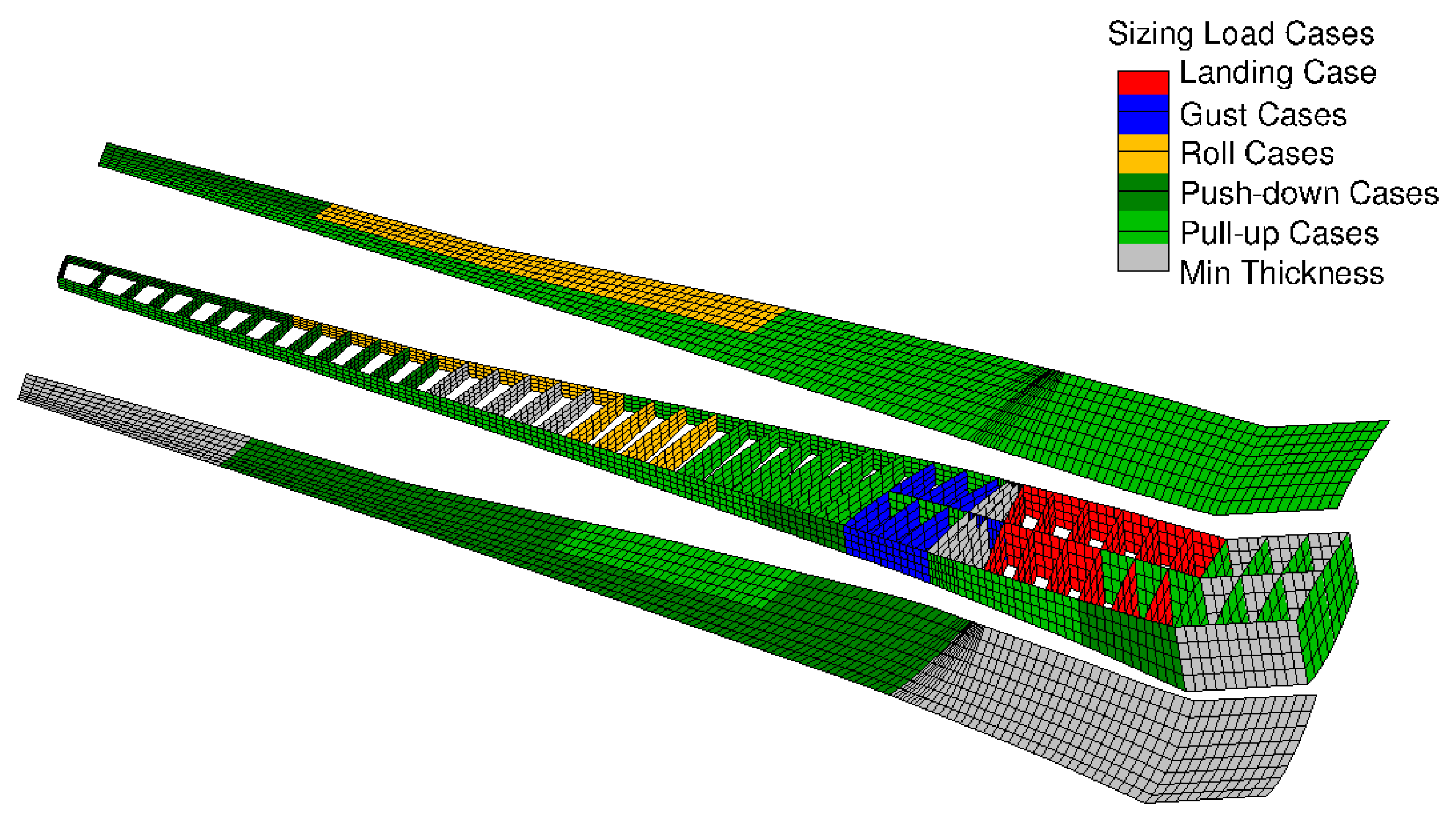
5.8. Minimum Thickness
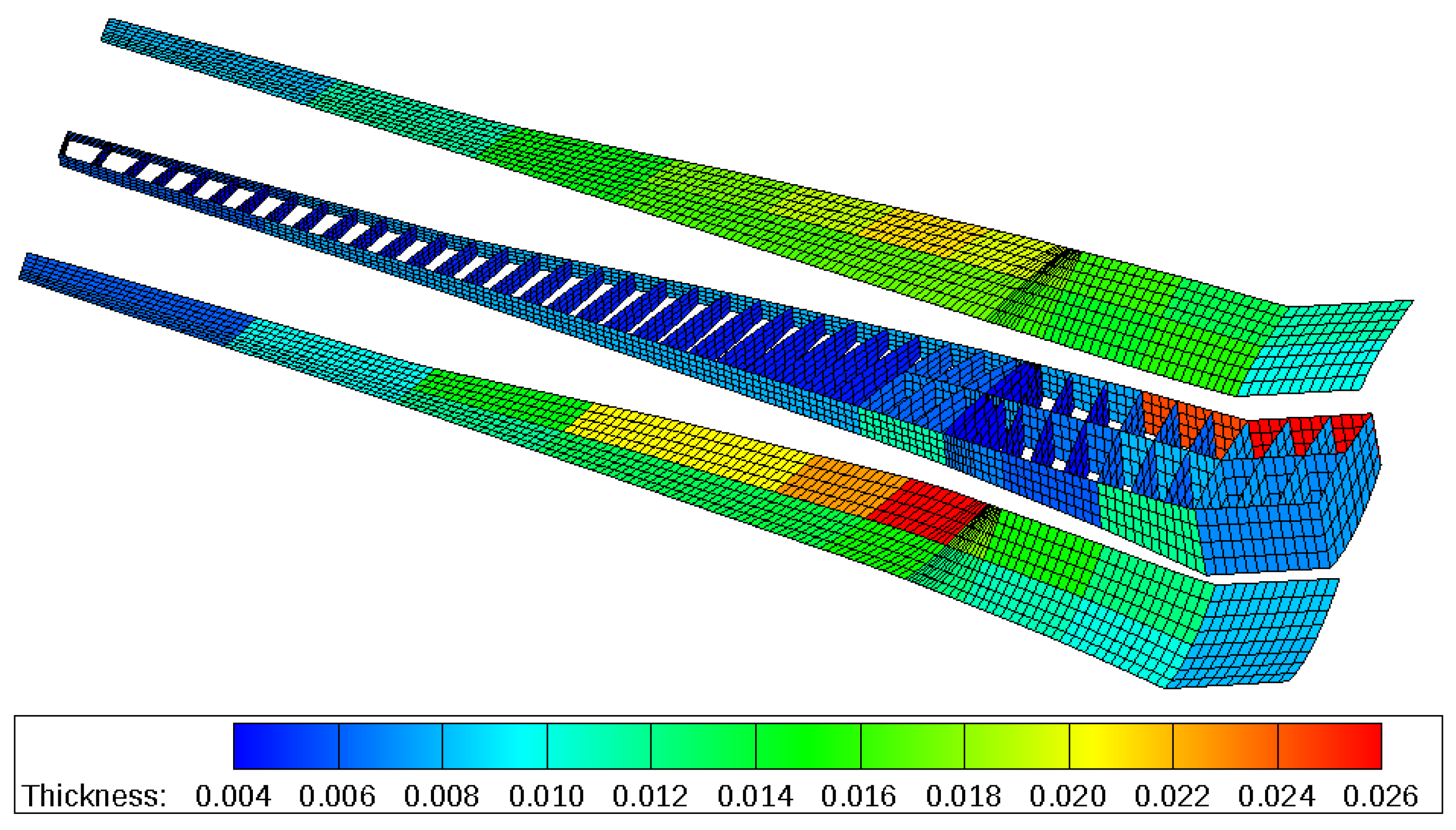
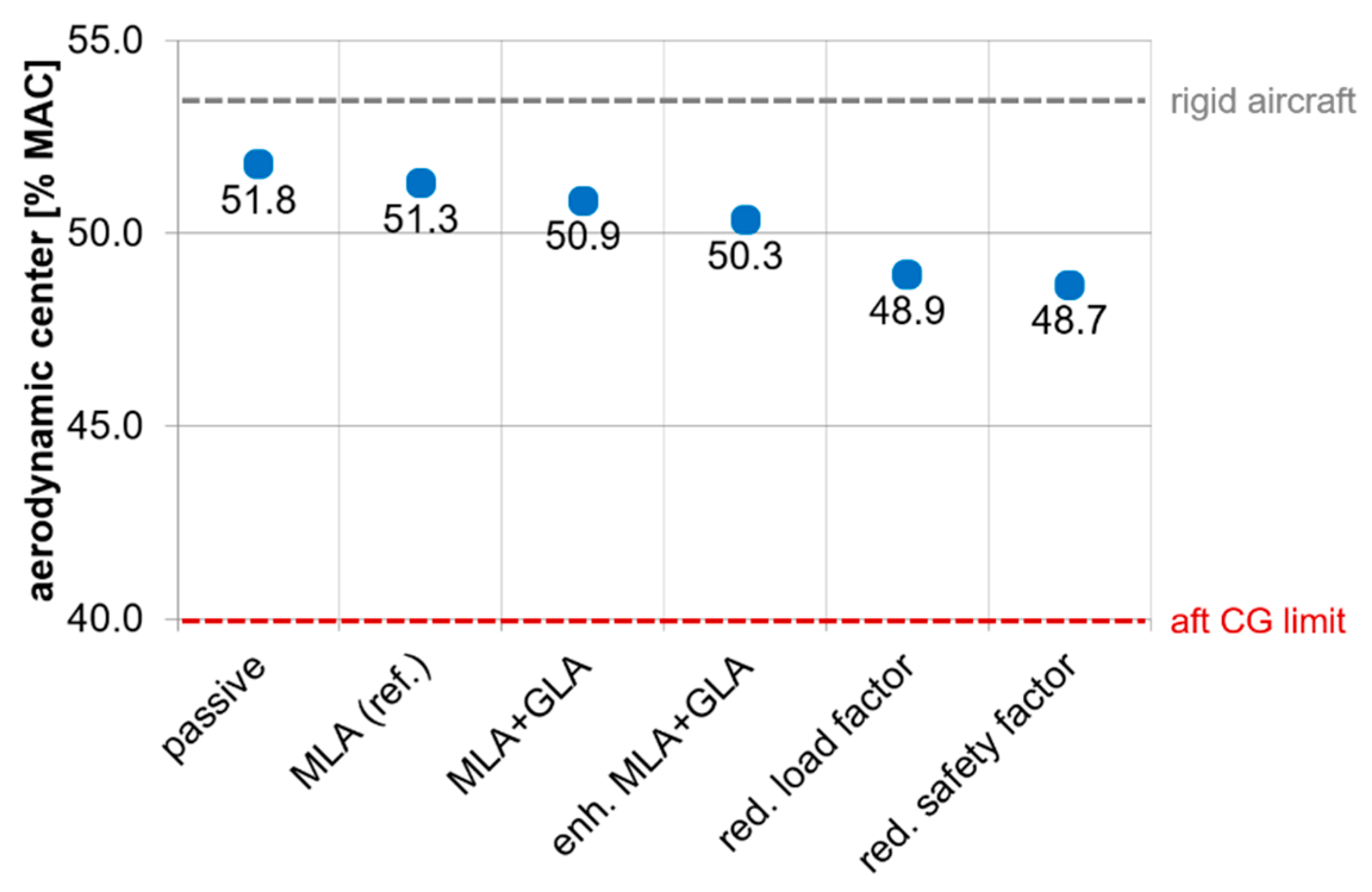
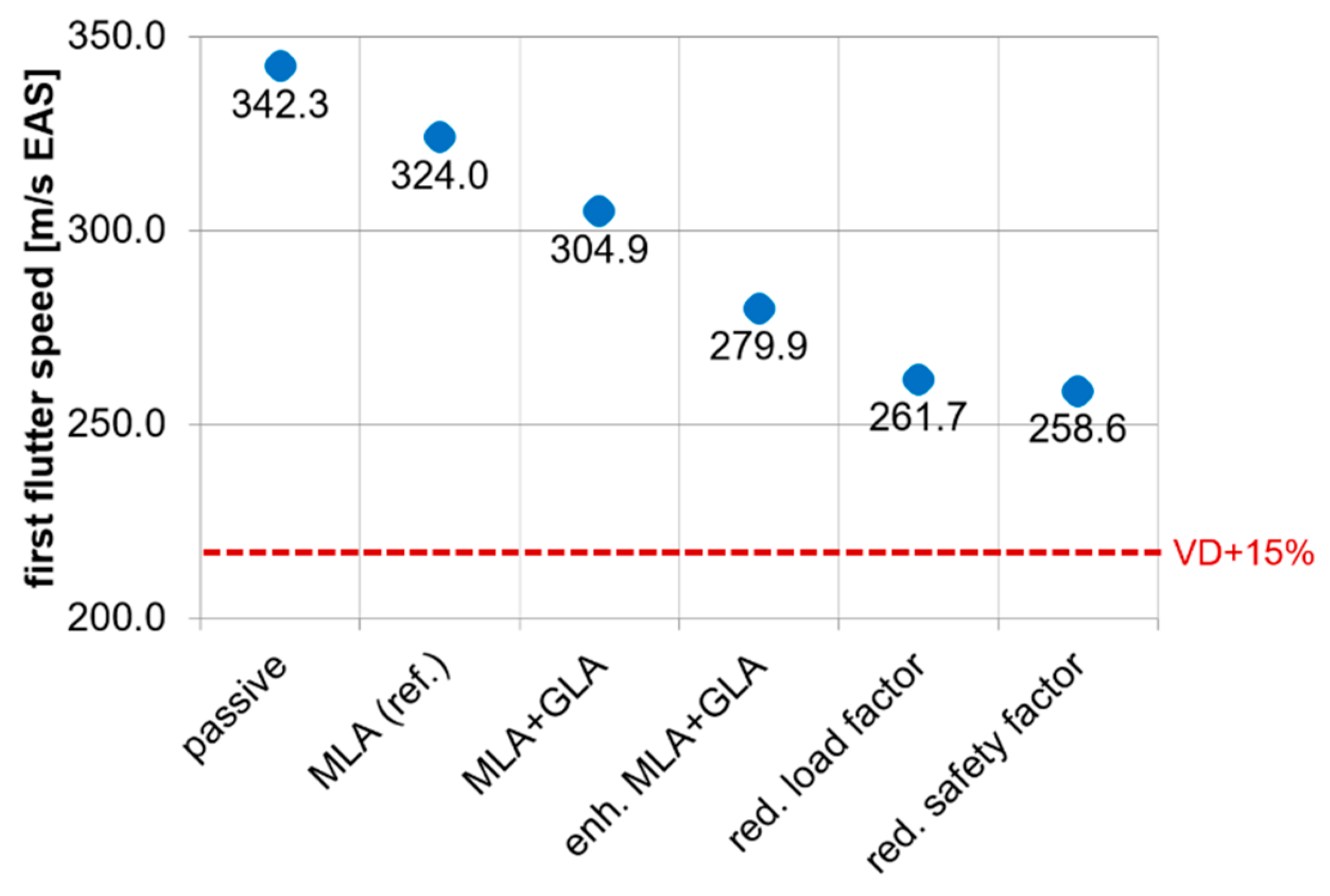
5.9. Summary of Load Results and Aeroelastic Parameters
6. Evaluation, Conclusions and Outlook
6.1. Evaluation
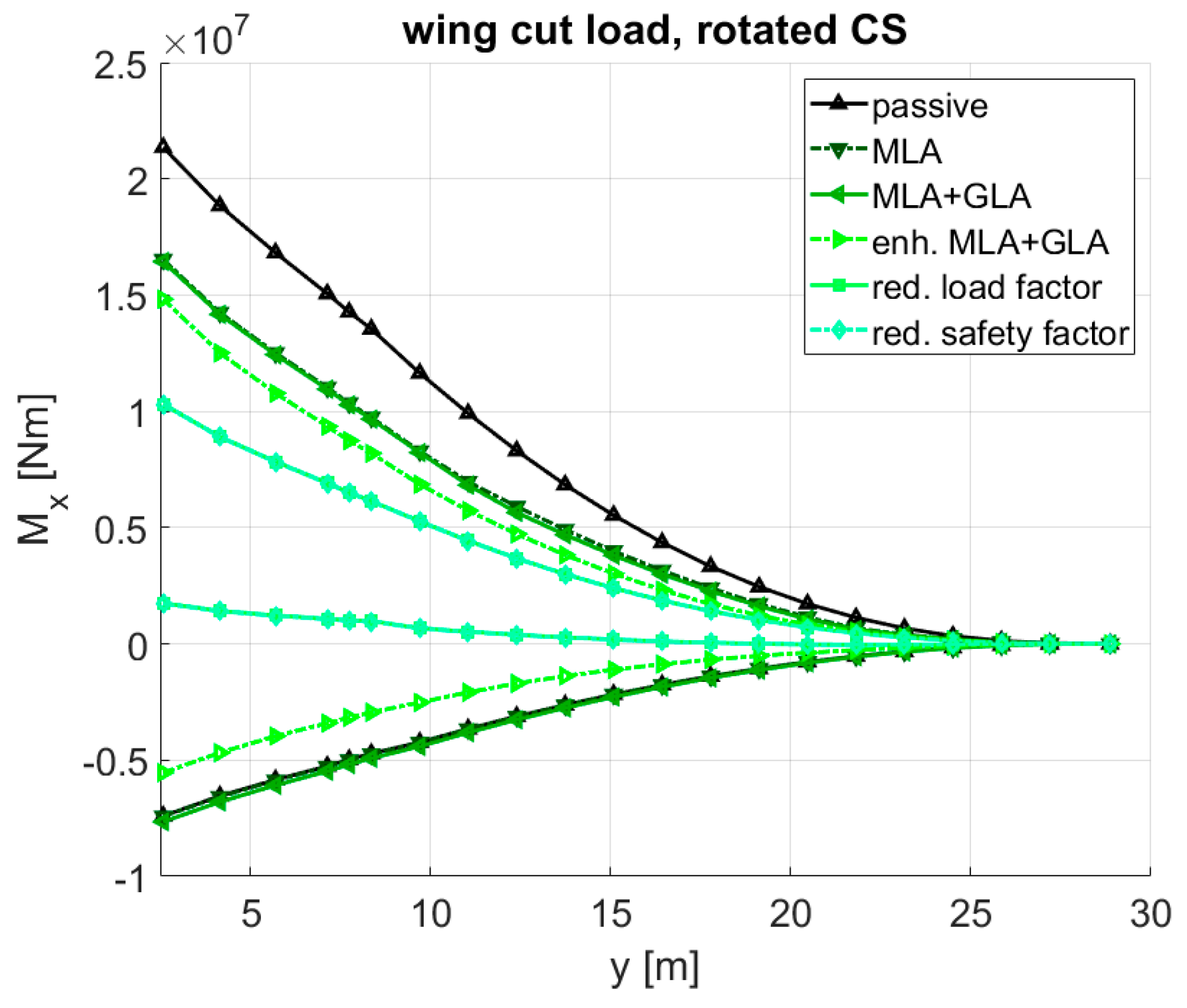
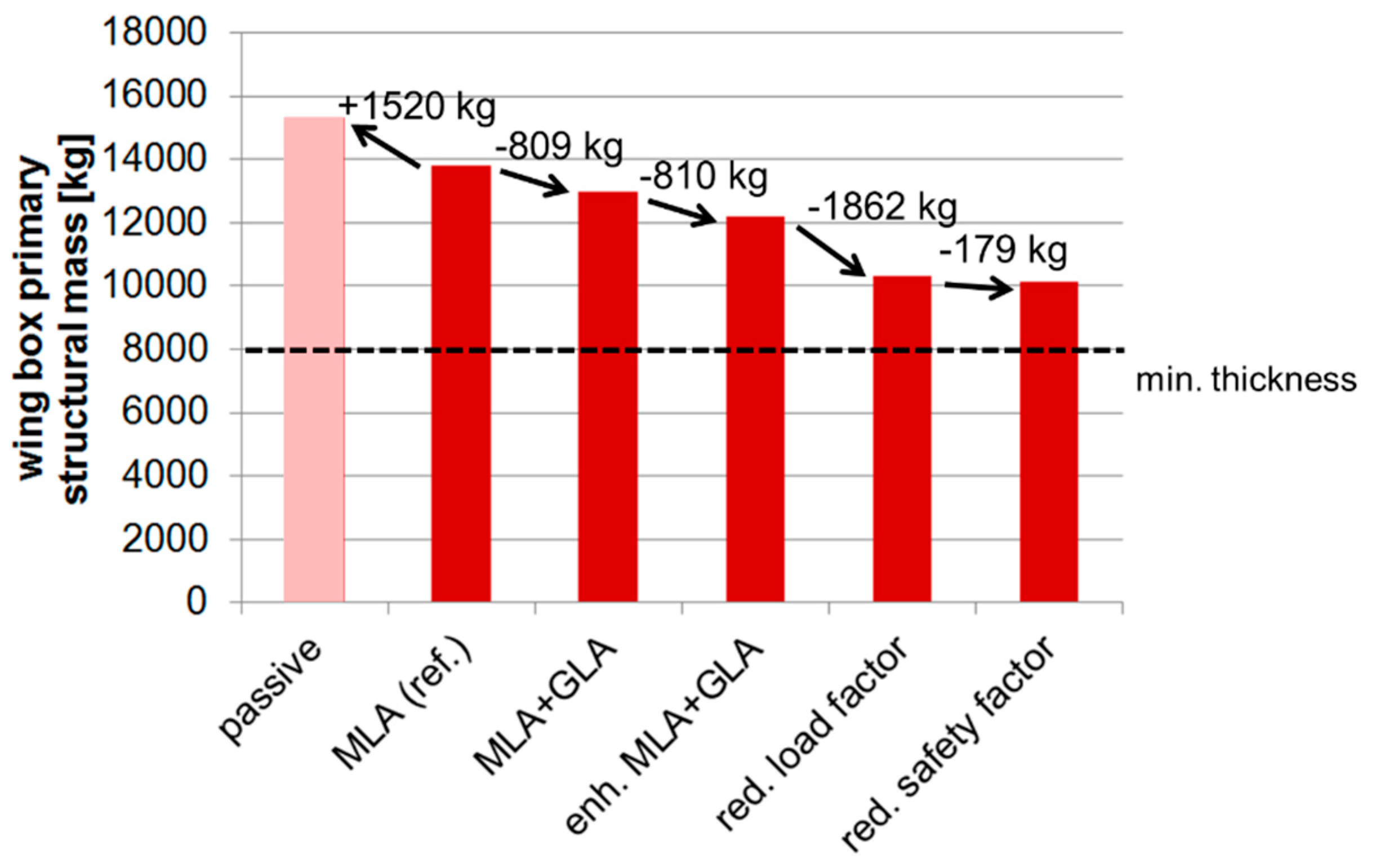
- The MLA on the reference variant already yielded a significant mass reduction of 1520 kg compared to its passive counterpart.
- If the reference were combined with a simple GLA, an 809 kg of mass saving would be obtained.
- An enhanced control surface layout and enhanced MLA/GLA algorithms yielded another 810 kg of mass reduction (the difference between MLA + GLA and enh. MLA + GLA).
- The largest step in the mass reduction by 1862 kg was achieved by reducing the design load factor to 1.5 (between the enh. MLA + GLA and red. load factor).
- A reduction of the safety factor from 1.5 to 1.3 (from the red. load factor to the red. safety factor) did not yield any significant mass reduction since a large portion of the wing box was already at the minimum thickness and could not be made thinner.
- With the inclusion of all future technologies and scenarios, the wing box mass can be reduced by up to 3660 kg (the difference between the reference and the red. safety factor).
- The wing box mass with the minimum thickness (7992 kg) already made up 57.9% of the reference wing box mass (13,803 kg).
6.2. Conclusions
- Among the implemented technologies, the largest mass benefit was obtained through a reduction in the design load factors and the design gust speeds.
- If the structure was already close to the minimum thickness, a further load reduction had no significant effect on the mass.
6.3. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| frequency [Hz] | |
| second order high pass filter | |
| GLA gain [-] | |
| second order low pass filter | |
| design cruise Mach number [-] | |
| design dive Mach number [-] | |
| time delay | |
| transfer function in general | |
| design maneuvering airspeed [m/s EAS] | |
| design cruise airspeed [m/s EAS] | |
| design dive airspeed [m/s EAS] | |
| gust angle of attack [deg] | |
| GLA deflection [deg] | |
| MLA deflection [deg] | |
| equivalent airspeed [m/s] | |
| CG | center of gravity |
| GLA | gust load alleviation |
| HTP | horizontal tailplane |
| LRA | load reference axis |
| MLA | maneuver load alleviation |
| VTP | vertical tailplane |
Appendix A
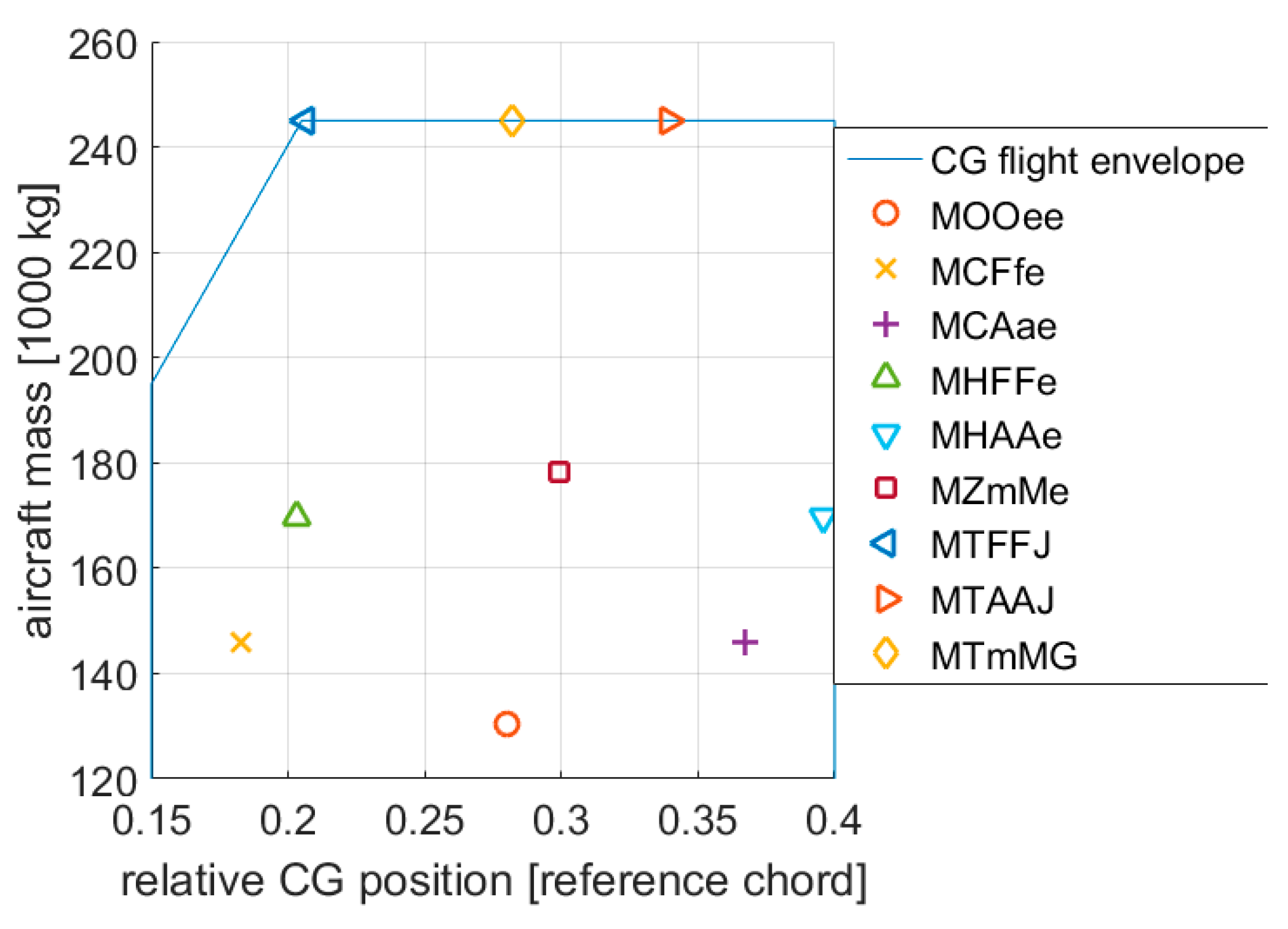
| Label | Mass [t] | CG [Ref. Chord] | Remark |
|---|---|---|---|
| MOOee | 130.3 | 0.28 | Operating empty mass |
| MCFfe | 145.7 | 0.18 | Forward CG, lightly loaded |
| MCAae | 145.7 | 0.37 | Rear CG, lightly loaded |
| MHFFe | 169.7 | 0.20 | Forward CG, heavily loaded |
| MHAAe | 169.7 | 0.40 | Rear CG, heavily loaded |
| MZmMe | 178.1 | 0.30 | Central CG, full payload |
| MTFFJ | 245.0 | 0.21 | MHFFe with 75.2 t fuel |
| MTAAJ | 245.0 | 0.34 | MHAAe with 75.2 t fuel |
| MTmMG | 244.8 | 0.28 | MZmMe with 66.6 t fuel |
| Passive | MLA (Ref.) | MLA + GLA | Enh. MLA + GLA | Red. Load Factor | Red. Safety Factor | min. Thickness | |
|---|---|---|---|---|---|---|---|
| Upper cover | 5921 | 5179 | 4871 | 4495 | 3453 | 3411 | 1995 |
| Lower cover | 5342 | 4704 | 4235 | 3929 | 3275 | 3240 | 3139 |
| Ribs | 2251 | 2179 | 2193 | 2133 | 2040 | 1986 | 1676 |
| Forward spar | 669 | 646 | 571 | 539 | 492 | 492 | 419 |
| Middle spar | 351 | 348 | 344 | 331 | 313 | 309 | 259 |
| Rear spar | 789 | 747 | 779 | 757 | 749 | 705 | 504 |
| Total | 15,323 | 13,803 | 12,994 | 12,184 | 10,322 | 10,143 | 7992 |
| Rel. diff. | +11.0% | 0.0% | −5.9% | −11.7% | −25.2% | −26.5% | −42.1% |
| Passive | MLA (Ref.) | MLA + GLA | Enh. MLA + GLA | Red. Load Factor | Red. Safety Factor | min. Thickness | |
|---|---|---|---|---|---|---|---|
| Wing box | 15,323 | 13,803 | 12,993 | 12,184 | 10,322 | 10,143 | 7992 |
| HTP box | 962 | 970 | 1004 | 911 | 835 | 812 | 722 |
| VTP box | 624 | 624 | 622 | 622 | 622 | 614 | 590 |
| Total OEM | 131,842 | 130,330 | 129,552 | 128,650 | 126,712 | 126,502 | 124,237 |
| Rel. diff. | 1.16% | 0.00% | −0.60% | −1.29% | −2.78% | −2.94% | −4.68% |
| Rel. diff. with mass factor | 1.74% | 0.00% | −0.90% | −1.93% | −4.16% | −4.41% | −7.02% |
References
- Hönlinger, H.; Zimmermann, H. Structural Aspects of Active Control Technology. In Flight Mechanics Panel Symposium; AGARD: Turin, Italy, 1994. [Google Scholar]
- Regan, C.; Jutte, C. Survey of Applications of Active Control Technology for Gust Alleviation and New Challenges for Lighter-Weight Aircraft; Dryden Flight Research Center: Edwards, CA, USA, 2012. [Google Scholar]
- Himisch, J. Winglet Shape and Load Optimization with a numerically supported Lifting Line Method. In Proceedings of the 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Victoria, BC, Canada, 10–12 September 2008. [Google Scholar]
- Handojo, V.; Lancelot, P.; de Breuker, R. Implementation of Active and Passive Loads Alleviation Methods on a Generic Mid-Range Aircraft Configuration. In Proceedings of the AIAA Aviation Forum, Multidisciplinary Analysis and Optimization Conference, Atlanta, GA, USA, 25−29 June 2018. [Google Scholar] [CrossRef][Green Version]
- Kenway, G.K.W.; Martins, J.R.R.A. Multipoint high-fidelity aerostructural optimization of a transport aircraft configuration. J. Aircr. 2014, 51, 144–160. [Google Scholar] [CrossRef]
- Kennedy, G.J.; Martins, J.R.R.A. A comparison of metallic and composite aircraft wings using aerostructural design optimization. In Proceedings of the AIAA Aviation Technology, Integration, and Operations (ATIO) Conference and 14th AIAA/ISSM, Indianapolis, IN, USA, 17–19 September 2012. [Google Scholar] [CrossRef]
- Dillinger, J.K.S.; Abdalla, M.M.; Klimmek, T.; Gürdal, Z. Static aeroelastic stiffness optimization and investigation of forward swept composite wings. In Proceedings of the World Congress on Structural and Multidisciplinary Optimization, Orlando, FL, USA, 19–24 May 2013. [Google Scholar]
- Binder, S. Simultaneous Optimisation of Composite Wing Structures and Control Systems for Active and Passive Load Alleviation. Ph.D. Thesis, Technical University of Delft, Delft, The Netherlands, 2021. [Google Scholar]
- Wildschek, A.; Hanis, T.; Stroscher, F. L∞-optimal Feedforward Gust Load Alleviation Design for a Large Blended Wing Body Airliner. Prog. Flight Dyn. GNC Avion. 2013, 6, 707–728. [Google Scholar]
- Bramsiepe, K.; Handojo, V.; Meddaikar, Y.; Schulze, M.; Klimmek, T. Loads and Structural Optimisation Process for Composite Long Range Transport Aircraft Configuration. In Proceedings of the AIAA Aviation Forum, Multidisciplinary Analysis and Optimization Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Kroll, N.; Abu-Zurayk, M.; Dimitrov, D.; Franz, T.; Führer, T.; Gerhold, T.; Görtz, S.; Heinrich, R.; Ilic, C.; Jepsen, J.; et al. DLR project Digital-X: Towards virtual aircraft design and flight testing based on high-fidelity methods. CEAS Aeronaut. J. 2015, 7, 3–27. [Google Scholar] [CrossRef]
- Görtz, S.; Abu-Zurayk, M.; Ilic, C.; Wunderlich, T.; Keye, S.; Schulze, M.; Klimmek, T.; Kaiser, C.; Süelözgen, Ö.; Kier, T.; et al. Overview of Collaborative Multi-Fidelity Multidisciplinary Design Optimization Activities in the DLR Project VicToria. In Proceedings of the AIAA Aviation Forum 2020, Virtual Event. 15–19 June 2020. [Google Scholar] [CrossRef]
- Bertram, O. Nekon—Neue Entwurfsmethoden Zukünftiger Steuerflächenkonzepte (im LuFo V.2 Con.Move-Verbundprojekt); Project Report DLR-IB-FT-BS-2020-232; Deutsches Zentrum für Luft- und Raumfahrt: Braunschweig, Germany, 2020. [Google Scholar]
- Klimmek, T.; Schulze, M.; Abu-Zurayk, M.; Ilic, C.; Merle, A. cpacs-MONA—An Independent and in High-Fidelity Based MDO Tasks Integrated Process for the Structural and Aeroelastic Design of Aircraft Configurations. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics, Savannah, GA, USA, 9–13 June 2019. [Google Scholar]
- Klimmek, T. Parametric Set-Up of a Structural Model for FERMAT Configuration for Aeroelastic and Loads Analysis. ASD J. 2014, 2, 31–49. [Google Scholar]
- JJsselmuiden, S.I. Optimal Design of Variable Stiffness Composite Structures Using Lamination Parameters. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 2011. [Google Scholar]
- Klimmek, T. Statische Aeroelastische Anforderungen beim Multidisziplinären Strukturentwurf von Transportflugzeugflügeln. Ph.D. Thesis, Deutsches Zentrum für Luft- und Raumfahrt, Göttingen, Germany, 2016. [Google Scholar]
- Chiozzotto, G. Improving Aircraft Conceptual Design with Methods for Wing Loads, Aeroelasticity and Mass Estimation. Ph.D. Thesis, TU Berlin, Berlin, Germany, 2019. [Google Scholar]
- Torenbeek, E. Development and Application of a Comprehensive, Design-Sensitive Weight Prediction Method for Wing Structures of Transport Category Aircraft; Report LR-693; TU Delft: Delft, The Netherlands, 1992. [Google Scholar]
- Albano, E.; Rodden, W. A Doublet Lattice Method for Calculating Lift Distributions on Oscillating Surfaces in Subsonic Flows. In Proceedings of the AIAA 6th Aerospace Sciences Meeting, New York, NY, USA, 22–24 January 1968. [Google Scholar]
- MSC.Software Corporation, MSC.Nastran Version 68—Aeroelastic Analysis User’s Guide, MSC.Software. Available online: https://simcompanion.hexagon.com/customers/s/article/aeroelastic-analysis-user-s-guide-doc9182 (accessed on 29 April 2022).
- Handojo, V. Contribution to Load Alleviation in Aircraft Pre-Design and Its Influence on Structural Mass and Fatigue. DLR-FB-2020-47. Ph.D. Thesis, DLR Institut für Aeroelastik, Göttingen, Germany, 2020. [Google Scholar]
- Tetlow, R. Design Charts for Carbon Fibre Composites; Technical Report; Cranfield Institute of Technology: Cranfield, UK, 1970. [Google Scholar]
- Schlichting, H.; Truckenbrodt, E. Aerodynamik des Flugzeuges, Zweiter Band; Springer: Berlin/Heidelberg, Germany, 1969. [Google Scholar]
- Federal Aviation Administration. Statistical Loads Data for the Boeing 777-200ER Aircraft in Commercial Operations, Report DOT/FAA/AR-06/11. Available online: http://www.tc.faa.gov/its/worldpac/techrpt/ar06-11.pdf (accessed on 29 April 2022).
- Handojo, V.; Klimmek, T. ALLEGRA Meilensteinbericht M3.3.2: Böensimulation des Elastischen Flugzeugs mit Basisverfahren; DLR Institut für Aeroelastik: Göttingen, Germany, 2015. [Google Scholar]
- European Aviation Safety Agency, CS25—Certification Specifications and Acceptable Means of Compliance for Large Aeroplanes-Amendment 23. 2019. Available online: https://www.easa.europa.eu/sites/default/files/dfu/CS-25_Amdt%203_19.09.07_Consolidated%20version.pdf (accessed on 29 April 2022).
- Reckzeh, D. Multifunctional Wing Moveables: Design of the A350 XWB and the Way to Future Concepts. In Proceedings of the 29th Congress of the International Council of the Aeronautical Sciences, St. Petersburg, Russia, 7–12 September 2014. [Google Scholar]
- US Department of Defense. MIL-STD-1797A—Flying Qualities of Piloted Aircraft. Report MIL-STD-1797A. 2004. Available online: https://engineering.purdue.edu/~andrisan/Courses/AAE490F_S2008/Buffer/mst1797.pdf (accessed on 29 April 2022).
- Hesse, H.; Palacios, R. Dynamic load alleviation in wake vortex encounters. J. Guid. Control Dyn. 2016, 39, 801–813. [Google Scholar] [CrossRef]
- Hansen, J.H.; Duan, M.; Kolmanovsky, I.V.; Cesnik, C.E.S. Load Alleviation of Flexible Aircraft by Dynamic Control Allocation. J. Guid. Control Dyn. 2022; article in advance. [Google Scholar] [CrossRef]
















| Parameter | Value |
|---|---|
| Wing area | 363 m2 |
| Wing span | 58 m |
| Mean aerodynamic chord | 7.28 m |
| Operating Empty Mass (OEM) | 130,000 kg |
| Maximum Take-Off Mass (MTOM) | 245,000 kg |
| ) | 170 m/s CAS, Mach 0.86 |
| Service ceiling | 13,106 m (43,000 ft) |
| Component Part | Value |
|---|---|
| Bending material | 1.45 |
| Spar webs | 1.47 |
| Ribs | 3.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Handojo, V.; Himisch, J.; Bramsiepe, K.; Krüger, W.R.; Tichy, L. Potential Estimation of Load Alleviation and Future Technologies in Reducing Aircraft Structural Mass. Aerospace 2022, 9, 412. https://doi.org/10.3390/aerospace9080412
Handojo V, Himisch J, Bramsiepe K, Krüger WR, Tichy L. Potential Estimation of Load Alleviation and Future Technologies in Reducing Aircraft Structural Mass. Aerospace. 2022; 9(8):412. https://doi.org/10.3390/aerospace9080412
Chicago/Turabian StyleHandojo, Vega, Jan Himisch, Kjell Bramsiepe, Wolf Reiner Krüger, and Lorenz Tichy. 2022. "Potential Estimation of Load Alleviation and Future Technologies in Reducing Aircraft Structural Mass" Aerospace 9, no. 8: 412. https://doi.org/10.3390/aerospace9080412
APA StyleHandojo, V., Himisch, J., Bramsiepe, K., Krüger, W. R., & Tichy, L. (2022). Potential Estimation of Load Alleviation and Future Technologies in Reducing Aircraft Structural Mass. Aerospace, 9(8), 412. https://doi.org/10.3390/aerospace9080412







