Abstract
Current predictions for future operations with drones estimate traffic densities orders of magnitude higher than any observed in manned aviation. Such densities call for further research and innovation, in particular, into conflict detection and resolution without the need for human intervention. The layered airspace concept, where aircraft are separated per vertical layer according to their heading, has been widely researched and proven to increase traffic capacity. However, aircraft traversing between layers do not benefit from this separation and alignment effect. As a result, interactions between climbing/descending and cruising aircraft can lead to a large increase in conflicts and intrusions. This paper looks into ways of reducing the impact of vertical transitions within the environment. We test two reinforcement learning methods: a decision-making module and a control execution module. The former issues a lane change command based on the planned route. The latter performs operational control to coordinate the longitude and vertical movement of the aircraft for a safe merging manoeuvre. The results show that reinforcement learning is capable of optimising an efficient driving policy for layer change manoeuvres, decreasing the number of conflicts and losses of minimum separation compared to manually defined navigation rules.
1. Introduction
The European Drones Outlook Study [1] estimates that as many as 400 k drones will be operating in the airspace by 2050. Moreover, this study underlines the need to further develop and validate current conflict detection and resolution (CD&R) for high-density operating environments without the need for human intervention. The use of machine learning in tactical CD&R is highlighted as a potential tool to support advanced and scalable U-space services. The present work aids this research by developing reinforcement learning modules that decrease conflict rate and severity for an unmanned aviation operation in an urban environment.
In the current study, we employ a layered airspace, a concept developed by the Metropolis project [2], which separates traffic vertically based on their heading. The separation of the existent traffic density into smaller groups of aircraft travelling in similar directions helps reduce occurrences of conflicts and losses of minimum separation (LoSs) during the cruising phase. However, in an environment where aircraft cannot fly a straight line from the origin to destination, changes in heading force the vertical deviations to a different layer where the new direction is allowed. These vertically manoeuvring aircraft may have to cross through multiple layers of cruising aircraft, potentially running into multiple conflicts and intrusions.
Using reinforcement learning (RL) to improve lane change decision-making has been widely used with road vehicles [3,4]. Optimal lane selection and longitudinal/lateral merging control can lead to better separation of agents, preventing traffic flow disruptions and collisions. Urban air traffic has several similarities with road traffic that justify exploring machine learning techniques that have been successfully applied in the latter. First, unmanned aviation is set to follow road infrastructure. Thus, the effects of the environment topology on traffic agglomeration are similar in both cases. Highway lane merging is comparable to layer merging in a layered airspace: (1) aircraft must also keep a minimum separation distance from each other; (2) both types of agents prefer to remain close to their desired cruising speed so as not to increase travel time. Thus, we apply these same methods to a layered airspace environment. First, a decision-making module determines the layer that the aircraft should move into based on the cruising traffic and the distance to the next turning point. Second, a control execution module decides on the best longitudinal/vertical control for a safe merging manoeuvre. However, there are remarkable differences between drones and road vehicles; the latter can become stationary, contrary to (most) drones. Additionally, in aviation, minimum separation distances are typically larger. These challenges will be further examined in this work.
Experiments are conducted with the open-source, multi-agent ATC simulation tool BlueSky [5]. During flight, aircraft follow a pre-planned route avoiding collision with the static surrounding infrastructure. To avoid LoSs between operating aircraft, all employ the conflict resolution method Modified Voltage Potential (MVP) [6]. Finally, the RL modules for the lane change procedure make use of the Deep Deterministic Policy Gradient (DDPG) model, as created by Lillicrap [7]. The operational efficiency of these modules, both individually and when working together, is directly compared with previous analytical rules for lane change behaviour.
Section 3 describes the characteristics of a layered airspace in more detail and how it is used in the simulation environment. This information is necessary to better understand how lane change behaviour is set with reinforcement learning, as specified in Section 4. Section 6 further details the experiment herein performed, and Section 5, the hypotheses considered. Section 7 shows the results of the experiments, comparing usage of the decision making and control execution RL modules to the baseline navigation rules. Finally, Section 8 and Section 9 present the discussion and conclusion, respectively.
2. Related Work
Given the interdisciplinary nature of this work, this section analyses the state-of-the-art in two different areas. First, we go over how the RL methods employed in this work have been used in previous research related to road vehicles. Second, we describe the main methods used to improve safety in a layered airspace operational environment, especially regarding layer change decisions.
RL has been widely applied to road vehicles. The research includes, but is not limited to, controlling traffic flow to prevent agglomeration of traffic [8,9], implementing velocity speed limits resulting in a more homogeneous traffic situation [10,11], and maintaining minimum distance gaps between vehicles during lane change decisions [3,4,12,13]. We focus on the latter. Wang [3] showed that an RL-based vehicle agent was capable of successfully learning a lane change policy and ensuring a minimum safety distance under current speeds. Hoel [4] developed a deep Q-Network agent that matched or surpassed the performance of hand-crafted rules and emphasised that, rather than depending on rules laboriously created by domain experts, RL can create a much larger set of rules adapted to a multitude of different traffic situations. Alizadeh [12] showed that RL can adapt to the performance limits of each individual vehicle, achieving better performance within uncertain and stochastic environments than hand-crafted methods. Finally, Shi [13] shows that an RL method can smoothly move a vehicle towards the target lane.
The layered airspace concept was first introduced by the Metropolis project [2]. In previous work, the authors point out that the safety benefits of this concept apply only to the cruising phase. Transitions between vertical layers can trigger a substantial number of merging conflicts, thus cancelling out a large part of the benefits gained from airspace structuring. Recently, a hand-crafted method for improving safety during merging manoeuvres was developed by Doole [14]. Results show that, with a limited number of rules, it is difficult to create solutions that can defend against the different topology of every street, as well as the relative relationship between the merging and cruising aircraft in different conflict geometries. These are comparable to the limitations previously seen with hand-crafted rules in lane change manoeuvres with road vehicles. Thus, we attempt to apply the same solutions that researchers found in that field. To the best of the author’s knowledge, this is the first time that RL methods previously successfully applied to lane change decision are applied to layer merging in an aviation environment. Nevertheless, several questions remain on whether it is possible to translate the success of RL methods for road vehicles to aviation. The present work adds to this discussion.
3. Layered Airspace Design
Operating in an urban environment raises several challenges. First, aircraft must avoid collision with the surrounding urban infrastructure. Although detection of edges of static obstacles is possible through instrumentation, the only way to make sure that aircraft follow the shortest path towards the destination, or even that they do not end up in a closed space when following the edge of an obstacle, is by setting a pre-defined route based on the known characteristics of the environment. Second, conflict avoidance manoeuvres must be adapted toward respecting the borders of the static obstacles. To guarantee that knock-on effects of successive manoeuvres do not lead to collisions, especially near non-uniform static obstacles, conflict resolution is limited to speed and altitude variation.
Limiting the freedom of conflict avoidance manoeuvres naturally limits the number of conflict geometries that aircraft are capable of successfully resolving. The focus must then be put on additional elements that decrease conflict rate and severity. One of these elements is the structure of the airspace, which directly influences the likelihood of aircraft meeting in conflict. The Metropolis project has shown that a layered airspace structure considerably reduces the rate of conflicts [2]. Two effects contribute to this reduction: (1) segmentation: the total traffic density is divided into groups of aircraft allocated in different altitude layers; (2) alignment: the groups are divided per aircraft’s heading, enforcing a degree of alignment between aircraft, which decreases the likelihood of conflicts in each layer.
3.1. Simulated Environment
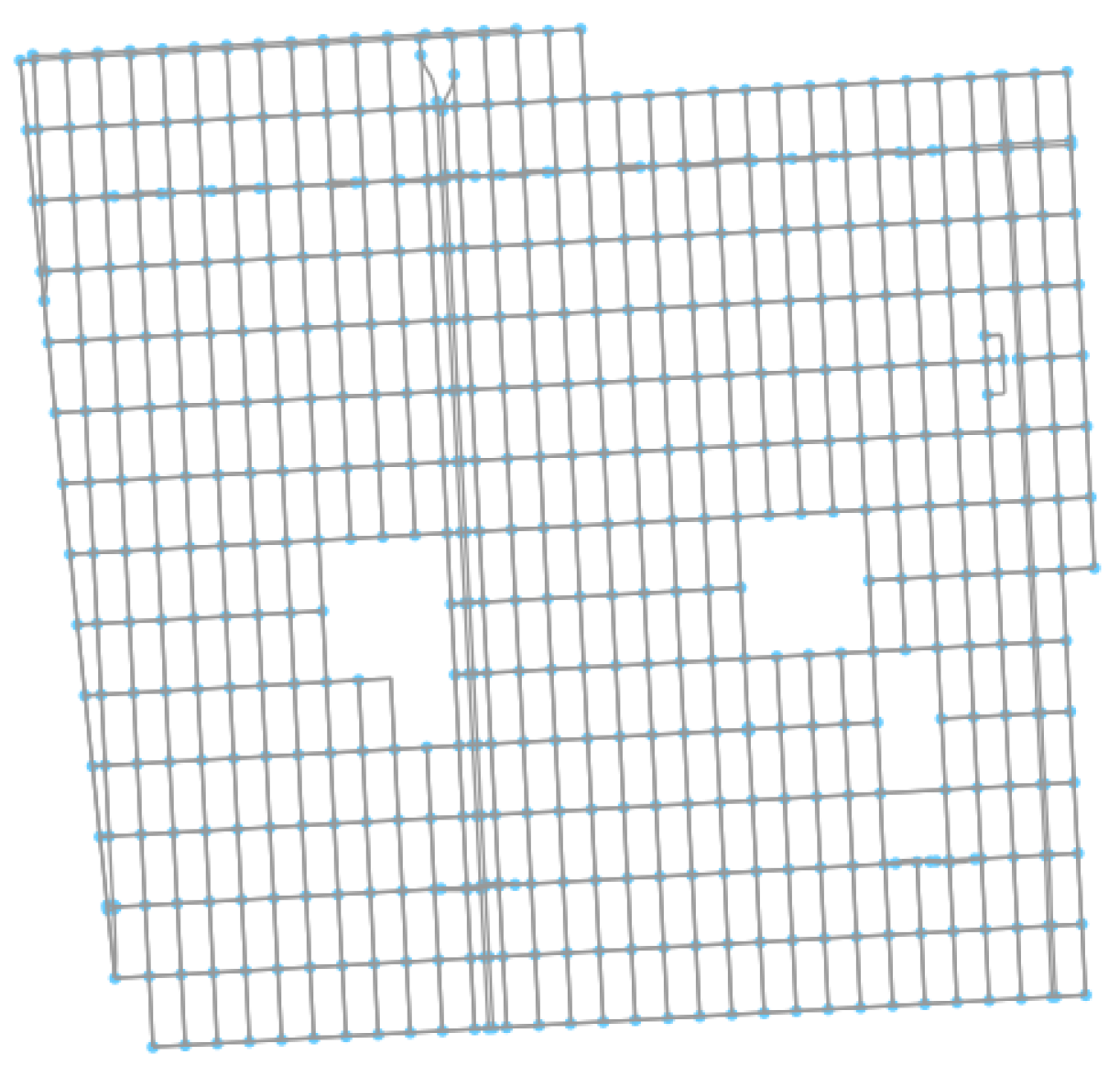
The urban operational area is built using the Open Street Map networks (OSMnx) python library [15], an open-source tool for street network analysis. We use an excerpt from the San Francisco Area, representing an orthogonal street layout with a total area of NM2, as shown in Figure 1. Note that the RL method herein developed could, in theory, be used in any environment. We make use of an orthogonal layout for simplification, as non-orthogonal layouts typically have a high number of conflicts associated with merging streets and non-regular street shapes. This simplification allows us to focus on the conflicts resulting from vertical deviations. The OSMnx library returns a set of nodes, with two adjacent nodes defining the edges of a road. A flight route is formed by connecting adjacent nodes that form a road. To reduce complexity, an intersection is considered to have at most four connecting roads. Each road is unidirectional per altitude level.
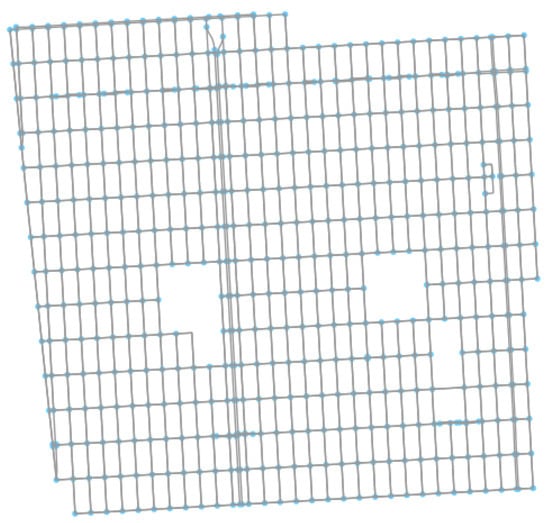
Figure 1.
Map of the urban environment used in this work. Data obtained from the OSMnx python library [15].
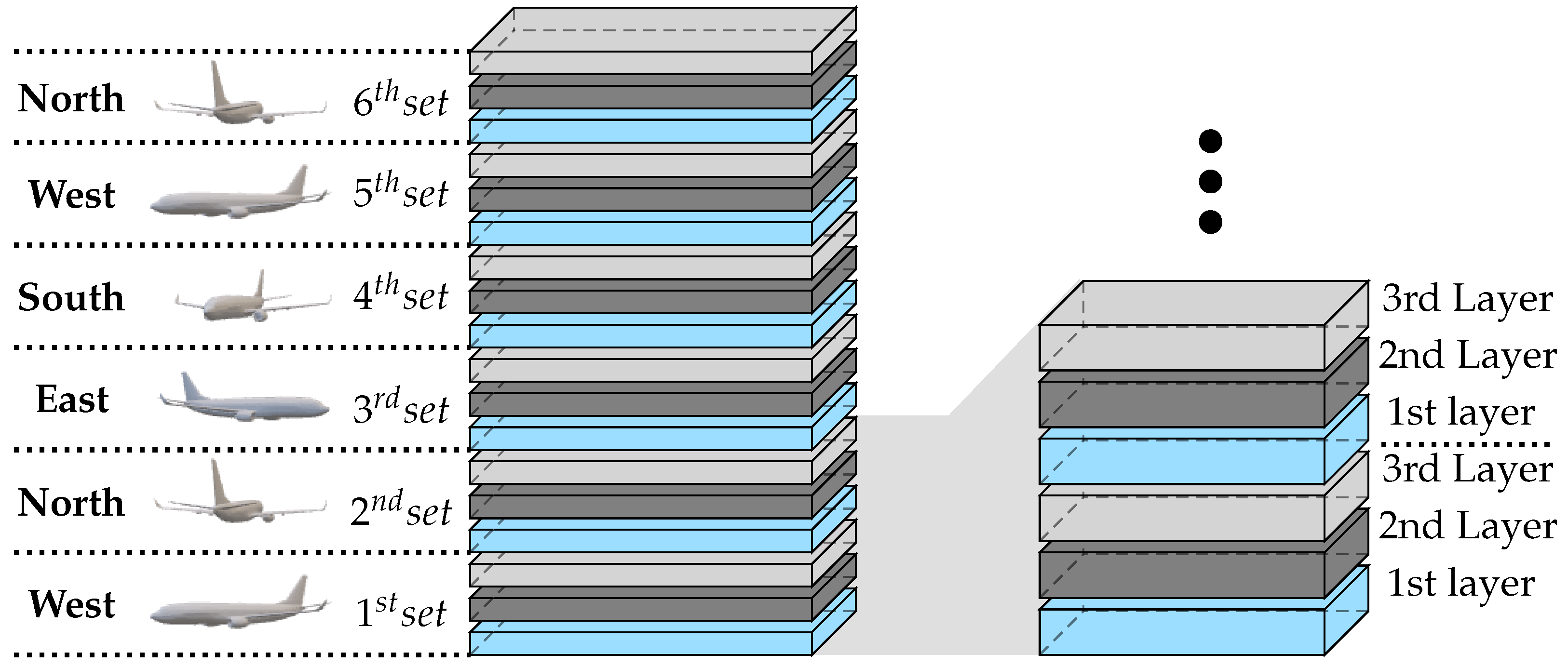
We allow directions per altitude, as defined in Figure 2. In conventional aviation, temporary altitude layers are often used as a level-off at an intermediate flight level along a climb or descent to avoid conflicts [16]. In our urban airspace, we apply the same concept: for each direction, three vertical layers exist, with increasing altitude. These are comparable to lanes on a highway. Each layer may adopt different uses for optimising cruising and turning. For example, following the rules of a highway, the middle layer may be used for longer cruising while the 1st and 3rd are used by aircraft about to turn in the directions below and above, respectively.
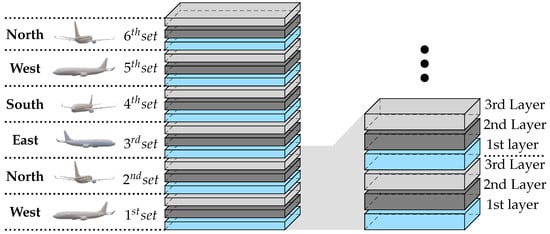
Figure 2.
Altitude sets employed in this study. All layers have a height of 15 ft. A margin of 5 ft between the layers is used to prevent false conflicts.
4. Layer Change Behaviour with Reinforcement Learning
Research into automated lane-changing manoeuvres with road vehicles can broadly be divided into two functional categories. First, a decision-making module determines which layer the agent should move into and emits a lane change command. Second, a control execution receives this command and coordinates the longitudinal and lateral movement of the vehicle for an efficient lane merging manoeuvre [3]. Figure 3 depicts the decisions taken by each module, translated to an aviation environment.
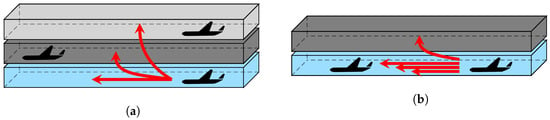
Figure 3.
Visual depiction of the range of the responsibilities of each reinforcement learning module. (a) Decision-making module: issues layer change commands based on the planned route and the current traffic scenario. (b) Control execution module: longitudinal and vertical coordinates control for a safe vertical manoeuvre based on the traffic scenario surrounding the ownship.
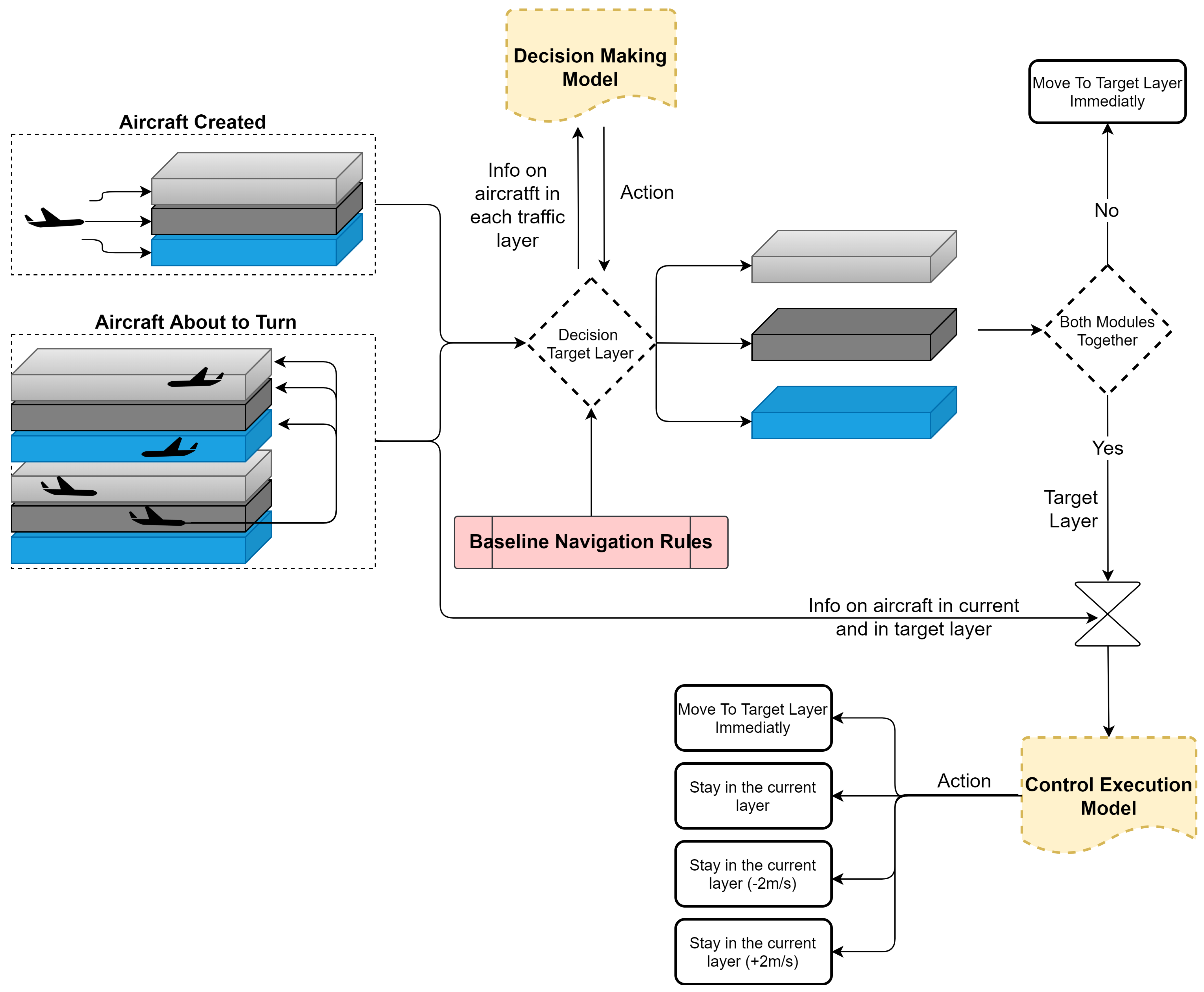
Figure 4 depicts a high-level functioning of the decision making and the control execution modules. The decision-making module is called upon whenever a new aircraft is created (and thus requires a starting layer) or whenever an aircraft is about to perform a turn, which results in a vertical deviation to a new set of layers where its new heading is allowed. When this module is used independently, the layer change action is immediately performed. In turn, when the control execution module is used independently, the target layer is dictated by the baseline rules (see Section 6.4.2 for more detail). When the two modules are used together, the decision-making module decides upon the target layer, and the control execution modules can decide whether to merge immediately towards the target layer or to delay the action.
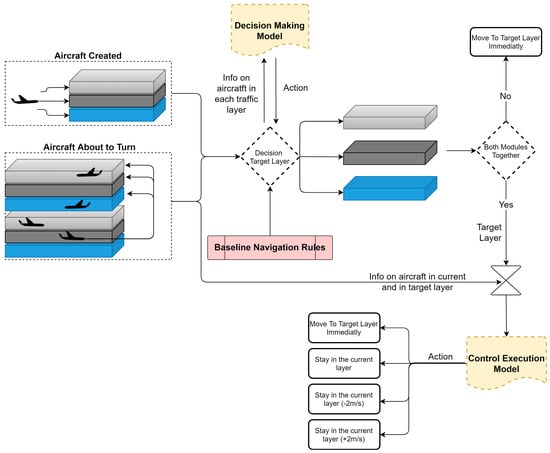
Figure 4.
High level diagram of the functioning of the decision making and the control execution modules, both independently and together.
Both RL modules have centralised learning with decentralised policies. In a setting with an extremely high number of agents, as is the case with the expected traffic densities for unmanned aviation, representing the full state of the environment is too complex to train an RL method within an acceptable amount of time. Moreover, we assume that, in a real-world implementation, each aircraft would only (have to) be aware of its immediate surroundings. However, during training in a simulated environment, we have access to additional information. Thus, although the policies of the modules are based only on the surrounding information and executed in a decentralised manner, during training, the reward is based on a larger amount of information, specifically conflict/LoSs in each layer. Furthermore, each module should be able to learn an optimal policy independently of the other module. In theory, when used together, their improvements in the airspace should accumulate. In practice, it may be that actions of one module modify the environment in a way that reduces the efficiency of the actions of the other module. Past research has often focused on one of the modules; their conjugation is normally not tested. It is, thus, of interest to examine how these two modules work together.
4.1. Reinforcement Learning Algorithm
An RL method consists of an agent that interacts with an environment E in discrete timesteps. At each timestep, the agent receives the current state s of the environment and performs an action a in accordance, for which it receives a reward . An agent’s behaviour is defined by a policy, , which maps states to a probability distribution over the available actions. The goal is to learn a policy which maximises the reward. Many RL algorithms have been researched in terms of defining the expected reward following the action a. In this work, we used the deep deterministic policy gradient (DDPG), defined in Lillicrap [7].
Policy gradient algorithms first evaluate the policy and then follow the policy gradient to maximise performance. DDPG is a deterministic actor–critic policy gradient algorithm designed to handle continuous and high-dimensional state and action spaces. It has been proven to outperform other RL algorithms in environments with stable dynamics [17]. However, it can become unstable, being particularly sensitive to reward scale settings [18,19]. The pseudo-code for DDPG is displayed in Algorithm 1.
DDPG uses an actor–critic architecture. The actor produces an action given the current state of the environment. The critic estimates the value of any given state, which is used to update the preference for the executed action. DDPG uses two neural networks, one for the actor and one for the critic. The actor function (also called policy) specifies the output action a as a function of the input (i.e., the current state s of the environment) in the direction suggested by the critic. The critic evaluates the actor’s policy by estimating the state–action value of the current policy. It evaluates the new state to determine whether it is better or worse than expected. The critic network is updated from the gradients obtained from a temporal-difference error signal from each time step. The output of the critic drives learning in both the actor and the critic. and represent the weights of each network. Updating the actor and critic neural network weights with the values calculated by the networks may lead to divergence. As a result, target networks are used to generate the targets. The target networks are time-delayed copies of their original networks, and target critic that slowly track the learned networks. All hidden neural networks use the non-sigmoidal rectified linear unit (ReLU) activation function, as this has been shown to outperform other functions in statistical performance and computational cost [20].
| Algorithm 1 Deep Deterministic Policy Gradient |
|
The neural network parameters used in our experimental results are based on Lillicrap [7]. Other hyperparameters may be used; nevertheless, the parameters defined by Lillicrap [7] has shown promising results. Experience replay is used in order to improve the independence of samples in the input batch. Past experiences are stored in a replay buffer, a finite-sized cache R. At each timestamp, the actor and critic are updated by sampling data from this buffer. However, if the replay buffer becomes full, the oldest samples are discarded. Finally, exploration noise is used in order to promote the exploration of the environment; an Ornstein–Uhlenbeck process [21] is used in parallel to the authors of the DDPG model.
4.2. Decision-Making Module
The decision-making module chooses the layer the ownership should move into based on the current traffic scenario and planned route. This decision is made when an aircraft enters the airspace at the beginning of its flight and when a heading turn requires a deviation to a different layer where the new direction is allowed. It should be noted that this module could potentially be used for aircraft to move to adjacent intermediate layers during cruising in order to overtake a slower leading aircraft, for example. However, this would heavily increase the complexity of the learning environment. When evaluating the results of a lane change action, the module can only learn if most of the alteration to the environment was caused by that one action. With multiple simultaneous deviations, the change to the environment is a result of the impact of all actions combined. It would, thus, be near impossible to connect an action to a direct alteration of the environment.
4.2.1. State
The state input must contain the necessary data for the module to be able to successfully determine an optimal solution. Ideally, the complete environment would be represented. However, a large state formation leads to a large number of possible states and state-action combinations. In practice, such results in the RL method have an exponential number of solutions to test, which may increase training time to an impracticable amount. Thus, we focus on the information we find essential: the current state of the ownship, the number of aircraft currently in each layer, the time to loss of separation to the leader and follower aircraft (if the ownship would move to the layer in this longitudinal/lateral position), and the number of waypoints until the next turn as per the planned route (see Table 1).

Table 1.
State formulation for the decision-making module.
We consider the relation between the leader and follower aircraft to be the most important information. The distance to the surrounding aircraft will, at least, account for the LoSs directly suffered by the ownship. The module must decide whether the gap available for merging is adequate to ensure a minimum safety distance at the current speed. Moreover, the module should also give preference to layers with fewer cruising aircraft. A merging manoeuvre can cause the follower aircraft to reduce its speed to prevent getting too close to the ownship, for example. When there is not enough distance between aircraft in the layer, this deceleration can cause a propagation of conflicts as aircraft slow down in succession to prevent becoming too close to the leader aircraft.
4.2.2. Action
The module determines the action to be performed for the current state. We use a softmax activation function that turns an input vector into an output vector with values between zero and one, which sum to one. These values represent a probability distribution and are used to define which layer the ownship should move into, as per Table 2. Staying in the same layer is also possible.

Table 2.
Action formulation for the decision-making module. The layers increase in altitude from the 1st to the 3rd layer. For a visual representation, see Figure 2.
As described in Section 3.1, there are three layers for each direction set. These decrease conflict likelihood and speed heterogeneity during turns. However, they can be used with a different rationale. As per Figure 2, the first layer has the closest access to the direction just below, and the third layer is the closest to the direction above. An aircraft in the first layer, which needs to turn into the direction just above the current direction, will need to cross the second and third layers; an aircraft in the third layer would only have to climb towards the top layer.
4.2.3. Reward
The objective is for the module to favour lane change decisions that reduce the likelihood of LoSs. However, often the number of LoSs, especially in environments where CD&R is applied, is too scarce to provide enough information for the module to train within an optimal amount of time. Thus, we consider conflicts as well: the module receives a reward of −1 for each conflict, and of −10 for each LoS. As conflicts represent future detected LoSs, reducing the total number of conflicts is expected to also reduce the total number of LoSs. Although not an ideal reward formulation, as this should be as simple as possible, it was found necessary for the module to converge towards optimal decisions. Note that it is the relative relation between the values, −1 and −10, not the absolute values, that influence the behaviour of the RL method. The method follows the highest rewards. Nevertheless, a different weight relation could have been applied. These weights were found to be the best empirical values for the particular operational environment/traffic scenarios herein employed. Nevertheless, it was taken into consideration that LoSs are the paramount values and should (heavily) outweigh the value of each conflict to make sure that the RL method does not opt for having one LoS in favour of preventing a small number of conflicts.
Moreover, the conflicts and LoSs included in the reward are not only the ones that the ownship (which performed the action) is involved in. The reward will also consider the effect on the layer that the ownship moves into. Such was found to be an important factor in guaranteeing that the module converged to optimal solutions, which have a positive effect on the global environment. It may be that the ownship does not suffer a conflict/LoS situation due to the follower aircraft decreasing its speed, or the leader aircraft increasing its speed, in order to keep a minimum distance from the ownship. However, these changes in speed disrupt the traffic flow; successive acceleration/deceleration over the following aircraft may result in an LoS further down the layer.
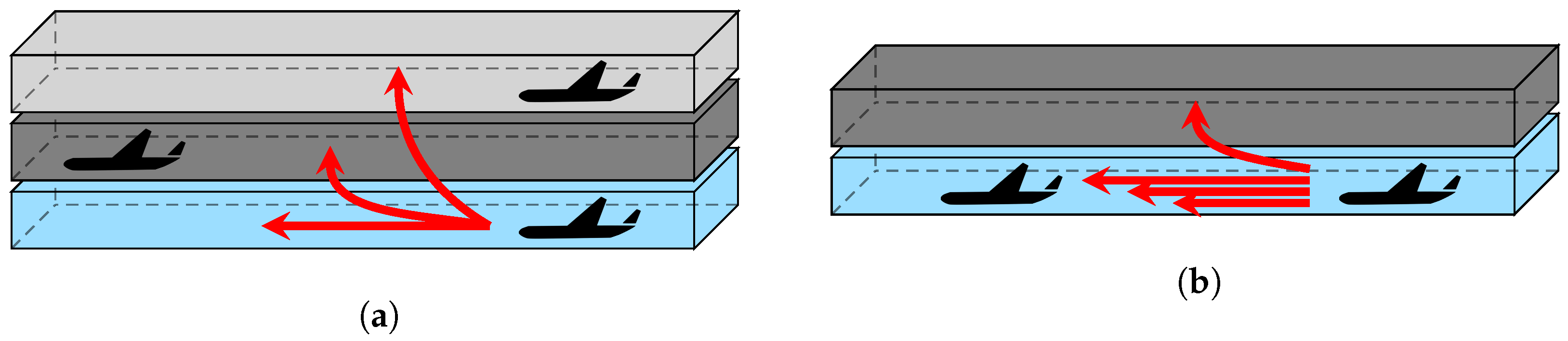
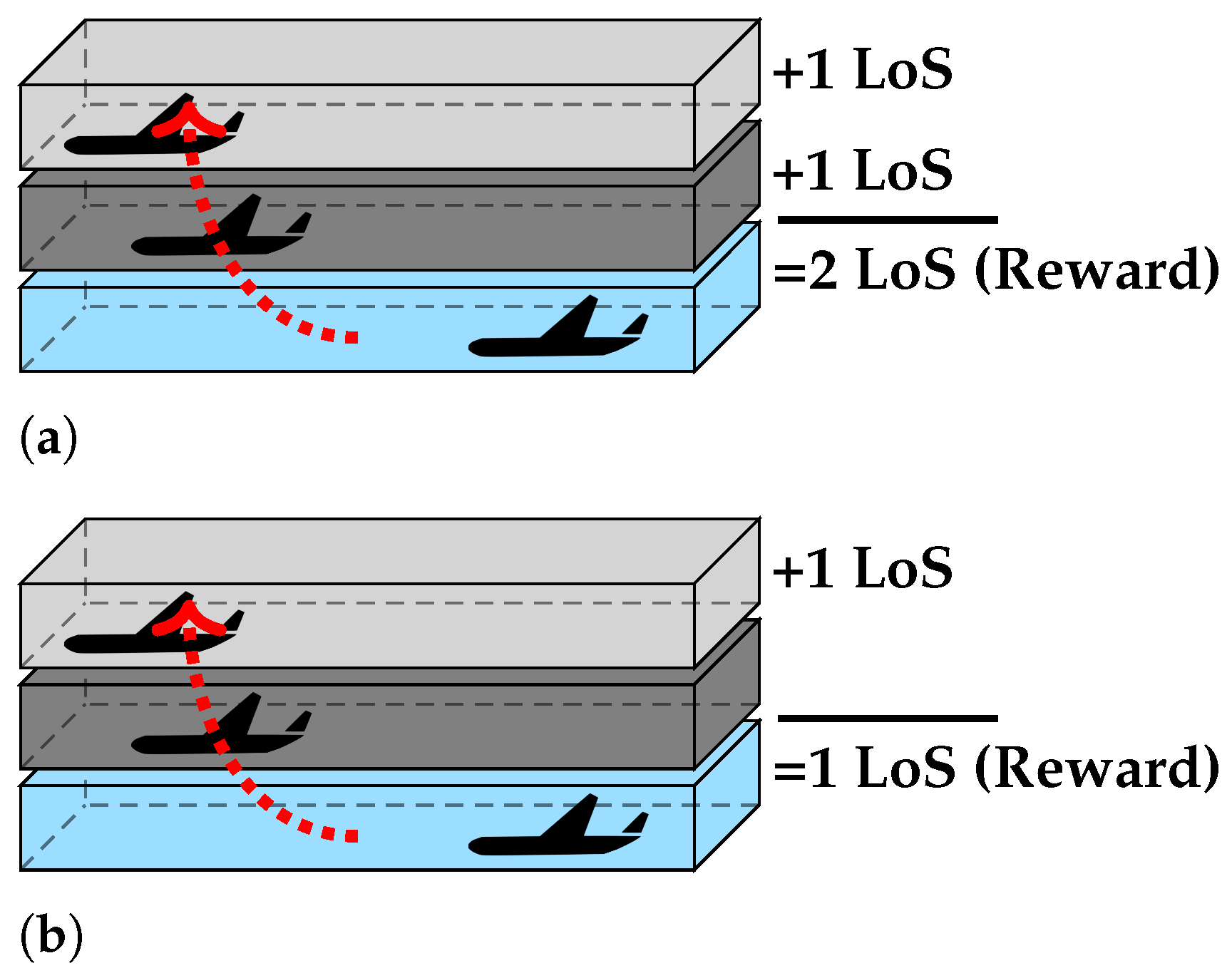
Finally, an important question related to the decision-making module is whether it should consider conflicts/LoSs occurring in the intermediate layers between the initial and target layer, as depicted in Figure 5. On the one hand, considering intermediate conflict/LoSs may decrease the total number of conflicts/LoSs during lane change actions. On the other hand, it may be considered that the decision-making module should focus only on finding the best target layer for cruising and not having this decision hindered over favouring nearer layers (i.e., that do not require crossing a great vertical distance). Within the total duration of their flight, aircraft will spend more time cruising than vertically manoeuvring between layers (which the module is unaware of). Thus, selecting the optimal cruising layer may be better for the global number of conflicts/LoSs. In this case, the control execution module is then solely responsible for decreasing conflicts/LoSs encountered during transition between the initial and target layers. The effects of considering intermediate conflicts/LoSs will be analysed with the experimental simulations.
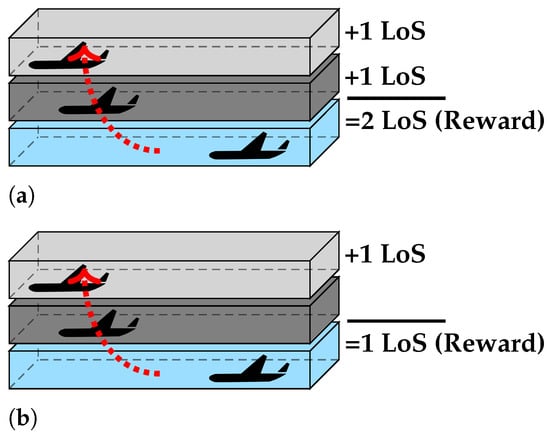
Figure 5.
Difference in the final reward received by the decision-making module when: (a) intermediate conflicts/LoSs are considered; (b) intermediate conflicts/LoSs are not considered.
4.3. Control Execution Module
Once a lane change decision is produced, the control execution module takes over to guide the ownship towards the best action to prevent conflicts/LoSs with aircraft both at the current layer and target layer. The existing gap on both layers is evaluated, and the RL module may choose to move the ownship vertically towards the target layer or to modify its current state in order to improve the gap in the future. When the module decides on an action that keeps the ownship in the current layer, this action is considered to have a duration of five seconds. After these five seconds, the execution module is called again to decide which longitudinal/vertical movement the ownship should follow now. This process is repeated until the ownship reaches its target layer.
4.3.1. State
The state formulation, as shown in Table 3, focuses on giving enough information to the module to decide whether the gaps in the current and target layers are sufficient to guarantee minimum separation between the leader and follower aircraft. Moreover, the number of layers until the target may influence how long the ownship delays the move to the next layer, as it may affect the following merging actions that the ownship must perform until reaching the target layer.

Table 3.
State formulation for the control execution module.
4.3.2. Action
This module also uses a softmax activation function for classification. As displayed in Table 4, the control execution module controls the ownship’s longitudinal and vertical movements. When merging into the target layer is not yet safe, the module may opt instead for: (1) accelerating the ownship, (2) decelerating the ownship, or (3) keeping the same speed, while remaining in its current layer. Naturally, this decision must also consider the time to LoS with the neighbouring aircraft in the current layer.

Table 4.
Action formulation for the control execution module.
Note that different speed change values could have been employed. Nevertheless, these should always take into account the performance limits of the operational vehicles. The main reason for this (low) speed change value was the acceleration performance of the simulated aircraft. At each timestep, there is a maximum state variation that an aircraft may achieve. With great state variations, the reward received by the RL method may not be based on the results with the state output by the method but, instead, on the maximum variation that the aircraft was able to achieve within the available time. This may make it harder for the RL method to correctly relate actions to expected rewards.
4.3.3. Reward
The reward received by the module is based not only on the conflicts/LoSs suffered by the module but also on the immediate effect on the layer occupied by the ownship (this is the target layer when the module moves the ownship vertically, or the current layer otherwise). Similarly to the decision-making module, the control execution module receives a reward of −1 for each conflict, and of −10 for each LoS. Additionally, +1 is given for a completed merging manoeuvre, guaranteeing that in a safe situation, the module will favour moving to the target layer.
5. Experiment: Hypotheses
5.1. Efficiency of the Decision-Making Module
It is hypothesised that the decision making RL module decreases the number of conflicts/LoSs by segmenting aircraft optimally per the available layers, with special emphasis on scenarios where all aircraft are placed in the same layers (i.e., the scenarios where the majority of aircraft start from the same direction). Regarding the decision of whether to include conflicts/LoSs resulting from the ownship crossing the intermediate layers between the initial and target layer, it is hypothesised that not including them will lead to the module picking a more optimal cruising segmentation. Since aircraft spend more time cruising than manoeuvering vertically, it is expected that this will lead to a reduction in the global number of conflicts/LoSs.
5.2. Efficiency of the Control Execution Module
The control execution RL module is hypothesised to decrease the number of conflicts/LoSs compared to a situation where aircraft simply move to the target layer when a layer change command is received. However, the effect of this module will only be noticeable in an environment where a high number of turns is expected.
5.3. When the Two Modules Work Together
In theory, the best case scenario is when both modules are used together. The decision-making module will output a lane-changing command towards the best cruising layer, and the control execution module will control the longitudinal and vertical moment of the ownship, making sure that the merging action is as safe as possible. In practice, it may be that one of these modules alters the environment in such a way that decreases the efficiency of the other module. Nevertheless, the control execution module is hypothesised to reduce the extreme LoSs cases resulting from lane change commands that cross multiple intermediate layers.
5.4. Effect of Traffic Densities
The RL modules will be tested with: the same traffic density they were tested in and lower and higher densities in comparison. Different traffic densities help analyse the capability of the module to generalise to unseen and more complex multi-actor conflict geometries. It is hypothesised that the agent will perform better in the exact conditions it was trained in and that, within different conditions, the agent may be the least effective in higher traffic densities.
6. Experiment: Safety Optimised Lane Change Decision
The following subsections describe the properties of the performed experiment. Note that the experiment is divided between training and testing phases. First, the two RL modules are trained continuously with a fixed training scenario. Second, they are tested with a set of previously unknown traffic scenarios; the performance of these modules is directly compared to baseline navigation rules.
6.1. Scenario Design
Aircraft spawn on the edge of the simulation area in a layer that allows for the initial direction. Origin points are separated by at least a minimum separation distance to avoid conflicts between just spawned aircraft. Each route is formed by connecting adjacent nodes of the map. Aircraft are removed from the experiment when they move away from an edge node, once they finish their route. Different trajectories will be tested, with the objective of evaluating the performance of the RL modules in multiple situations. The following settings are defined per traffic scenario:
- Heading distribution: the heading adopted by the simulated aircraft. Having the majority of the aircraft following the same direction leads to an agglomeration of a high number of aircraft in one layer, which likely decreases the average distance between aircraft and, in turn, increases the number of conflicts. A more uniform heading distribution increases the distribution of aircraft per the airspace, reducing the likelihood of conflicts. Using different heading range distributions tests the capacity of the RL modules to successfully segment different traffic scenarios over the available airspace. The heading distribution (per percentage) is defined in Table 5. In traffic scenario #1, for example, 100% of the aircraft travel East. In practice, if 100 aircraft are simulated, all 100 will be travelling East. In comparison, traffic scenario #15 has a uniform distribution: with 100 aircraft, 25 aircraft would travel east, 25 travel south, 25 travel west, and 25 travel north. Note that all aircraft start at a side of the map, which allows for a straight route towards their initial direction (e.g., an aircraft with initial direction east will start at the west end of the map).
 Table 5. A total of 15 different heading distributions are used.
Table 5. A total of 15 different heading distributions are used. - Different number of turns: a turn in a layered airspace signifies a necessary change in the evertical layer. Thus, a different number of turns are used to elicit sufficient layer changes to analyse the (1) effect of a different number of vertical deviations in the environment, and (2) the ability of the modules to protect against successive changes in heading distribution. Five different turning settings are employed, as per Table 6. If there are no turns, aircraft will travel toward their initial direction throughout the complete route. For example, running traffic scenario #1 with turning option #A means that all aircraft travel East throughout the complete duration of the traffic scenario. In comparison, running traffic scenario #1 with turning option #E signifies that each aircraft will perform five turns throughout their flight route. Thus, they all start their flights heading east but then change direction a total of five times. Note that a turn to the right from an aircraft with an initial direction east indicates that the aircraft will turn towards the direction south during its route. A turn to the left would result in this aircraft turning toward the north.
 Table 6. A total of 5 different turning options aree used.
Table 6. A total of 5 different turning options aree used.
Each heading distribution is performed five times with a different turning option, i.e., heading distributions #1 to #15 are each run with turning options #A to #E. In total, 75 traffic scenarios (15 heading distributions × 5 turning options) are run for each traffic density. A total of three different traffic densities are tested: low, medium, and high traffic densities. More detail on these is given in Section 6.4.3.
6.2. Vehicle/Agent Characteristics
We employ open Air Traffic Simulator Bluesky [5] to test the efficacy of the lane change RL modules. Aircraft are defined per the performance characteristics of the DJI Mavic Pro drone model. Speed and mass were obtained from the manufacturer’s data, and common conservative values were assumed for turn rate (max: ) and acceleration/braking (). Aircraft have a preferred cruising speed of 30 kts. However, in line with their performance limits, aircraft must decrease their speed prior to a turn to guarantee that the turning radius does not lead to a collision with any surrounding static obstacle. Once the aircraft has completed a turn, the aircraft will again accelerate towards its desired cruising speed. It is assumed that the aircraft have constant altitude and speed during a turn.
6.3. Conflict Detection and Resolution
This work employs a horizontal separation of 50 m, which is commonly used in works with unmanned aviation [22]. A vertical separation of 15 ft is assumed based on the dimension of the vertical layers. Conflicts are detected by linearly propagating the current state of all aircraft involved and determining if two aircraft will be closer than the minimum separation distance within a look-ahead time of 30 s. For conflict resolution, we employ the Modified Voltage Potential (MVP) method, as defined by Hoekstra [6,23]. Once a conflict is found, MVP displaces the predicted future positions of both ownship and intruder at the closest point of approach (CPA) in the shortest way out of the protected zone of the intruder. More details on state-based detection and the avoidance manoeuvres calculated by MVP can be gathered from previous work [24].
6.4. Independent Variables
During training, the only independent variable is the reward formulation for the decision-making module. During testing, different traffic densities are introduced to analyse how both RL modules perform at traffic densities they were not trained in. Additionally, we compare employing the decision making and control execution modules with baseline analytical rules.
6.4.1. Reward Formulation for the Decision-Making Module
In Section 4.2.3, it was mentioned that it is not clear if considering intermediate conflicts will limit the ability of the module to select the best layer for the cruising phase. This module will be trained with and without considering intermediate conflicts. The results will be directly compared.
6.4.2. Using Reinforcement Learning vs. Baseline Analytical Rules
The effect of employing either the decision making or control execution module will be compared with resorting to baseline analytical rules. With the latter, aircraft initially always move into the first layer, which is the main cruising layer. The second layer is used for vertical conflict resolution. The third layer is used for deceleration and turning prior to moving to a different traffic layer with a different direction. This prevents conflicts resulting from heterogeneous speed situations caused by aircraft reducing speed in preparation for a turn. In this baseline situation, the aircraft immediately perform the lane change command.
Both the decision making and the control execution modules are first trained and tested individually in order for their effect to be directly analysed. When the decision-making module is tested alone, the aircraft follows its lane change commands and immediately performs them. Regarding the control execution module, when tested individually, aircraft follow the lane change commands as defined by the baseline rules and perform/delay this manoeuvre as instructed by the command execution module.
6.4.3. Traffic Density
Three traffic densities, in an increasing number of operating aircraft, are used. The exact values are shown in Table 7. At high densities, aircraft spend more than 10% of their flight time in conflict avoidance mode [25]. Both RL modules are trained first in a medium traffic density and are then tested with low, medium, and high traffic densities as to assess their efficiency in lower/higher traffic densities.

Table 7.
Traffic volume used in the experimental simulations (in 1 h of simulation time). The range of results from different flight paths as the necessary time to traverse the environment is dependent on the initial direction(s) and number of turns.
6.5. Dependent Variables
The effect of the RL modules on the environment is measured on multiple metrics: safety, stability, and efficiency. The first includes occurrences and duration of conflicts and LoSs. The inclusion of the RL modules in the operational environment should reduce these elements. Additionally, LoSs are evaluated on their severity according to how close aircraft get to one another:
Stability evaluates the secondary conflicts created by tactical conflict avoidance manoeuvres. When the free airspace is scarce, having aircraft move laterally and occupying a bigger portion of the airspace often results in conflict chain reactions [2]. This effect has been measured using the Domino Effect Parameter (DEP) [26]:
where is the number of conflicts with CD&R ON, and the number with CD&R OFF. Higher DEP values signify destabilising behaviours.
Finally, efficiency is evaluated in terms of the total distance travelled by the aircraft and the duration of flight. Methods that do not result in a considerable increase in the path and/or the duration of the flight are considered more efficient.
7. Experiment: Results
7.1. Training of the Reinforcement Learning Modules
Both RL modules, decision making and control execution, are first trained in a medium traffic density. Each module is trained repetitively on one traffic scenario; an episode corresponds to a repetition of this traffic scenario, which runs for 1 h. Within one episode, each module is called thousands of times. Here, we focus on analysing the choices made by the modules. Only speed conflict resolution was added to the environment during training.
Safety Analysis
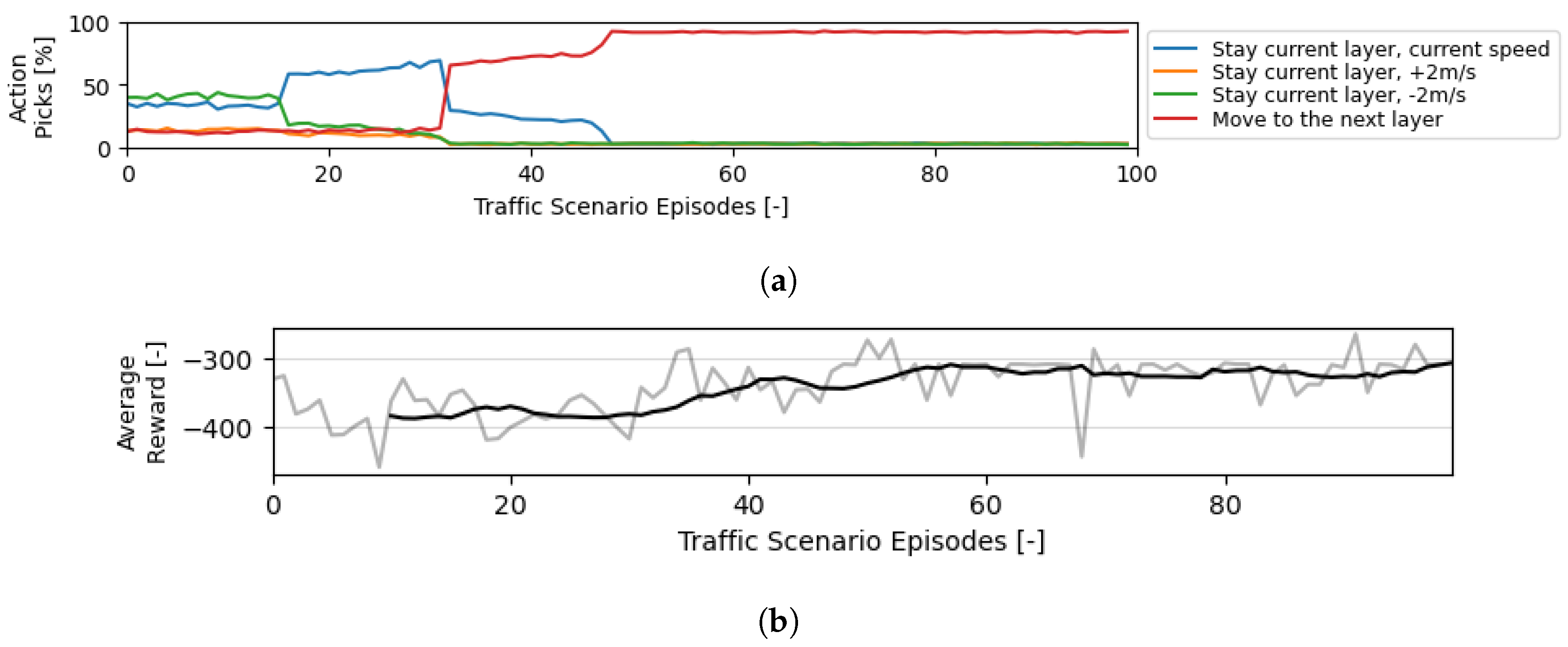
Figure 6 and Figure 7 display the evolution of the actions picked by the decision-making module throughout training. In each episode, the module is called upon when an aircraft is introduced into the environment to decide the layer that the aircraft is to be introduced in, and this occurs before a turn as the aircraft will have to change to a different layer set where the new direction is allowed.
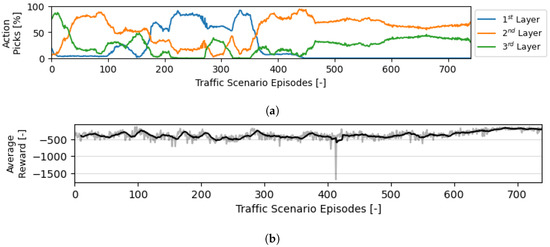
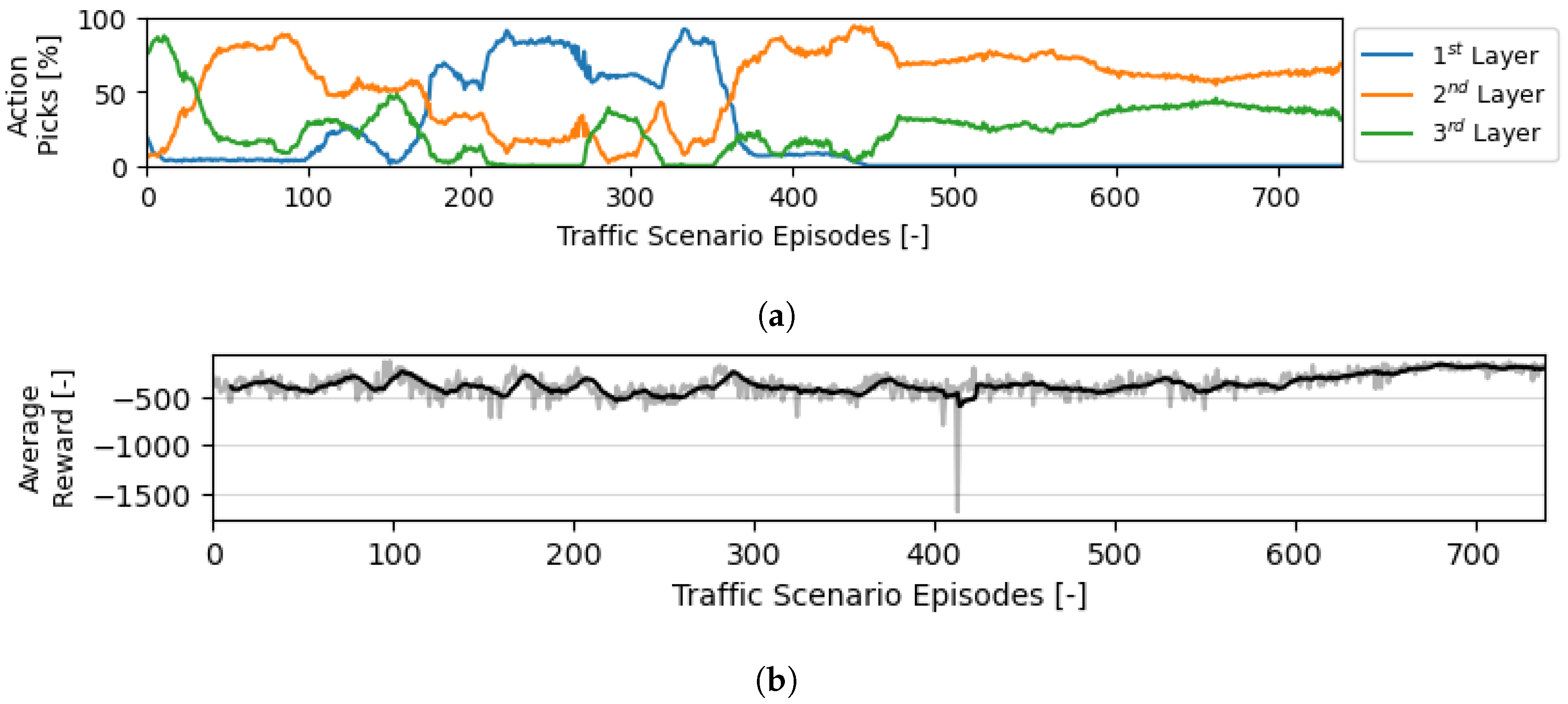
Figure 6.
Evolution of the actions and rewards during the training of the decision-making module when intermediate conflicts/LoSs are considered. Roughly M actions were performed. (a) Evolution of the balance between possible actions throughout episodes during training. (b) Evolution of the average reward per action throughout episodes during training.
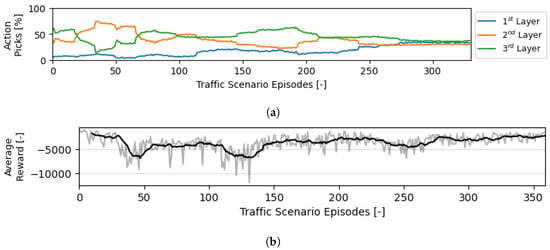
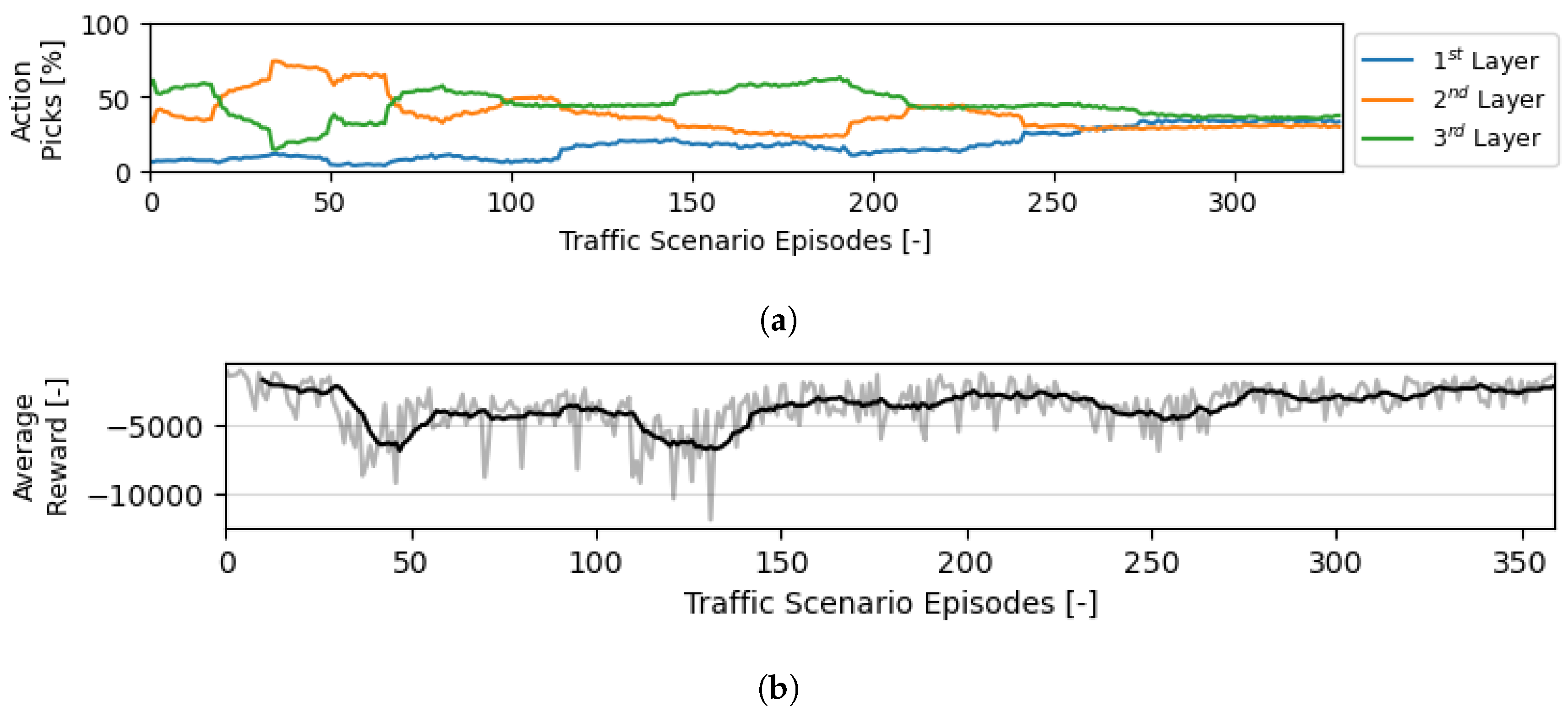
Figure 7.
Evolution of the actions and rewards during the training of the decision-making module when intermediate conflicts/LoSs are not considered. Roughly M actions were performed. (a) Evolution of the balance between possible actions throughout episodes during training. (b) Evolution of the balance between possible actions throughout episodes during training.
In Figure 6, intermediate conflicts/LoSs are considered. As mentioned above, the graphs show the evolution of the decisions of the RL method during training. At the end of its training, in practice, the RL module ‘discards’ a layer, allocating aircraft mainly in the second and third layers. This division is optimal in decreasing intermediate conflicts/LoSs when aircraft are divided per the second and third layers according to their next turn. Aircraft in the third layer only climb one layer towards the next direction. Aircraft in the second layer can move to the direction below by descending two layers; however, the first layer does not contain cruising traffic, and thus, the ownship is not likely to run into conflicts/LoSs here. Finally, Figure 6b show that this behaviour adopted by the module leads to a reduction in conflicts/LoSs per action.
Figure 7 shows the evolution of the decision-making module when intermediate conflicts are not added to the reward. In comparison with Figure 6a, this version of the module heavily prioritises proper segmentation of the aircraft per the available vertical space. Keeping the traffic density to a minimum in each layer helps reduce conflicts/LoSs during the cruising phase.
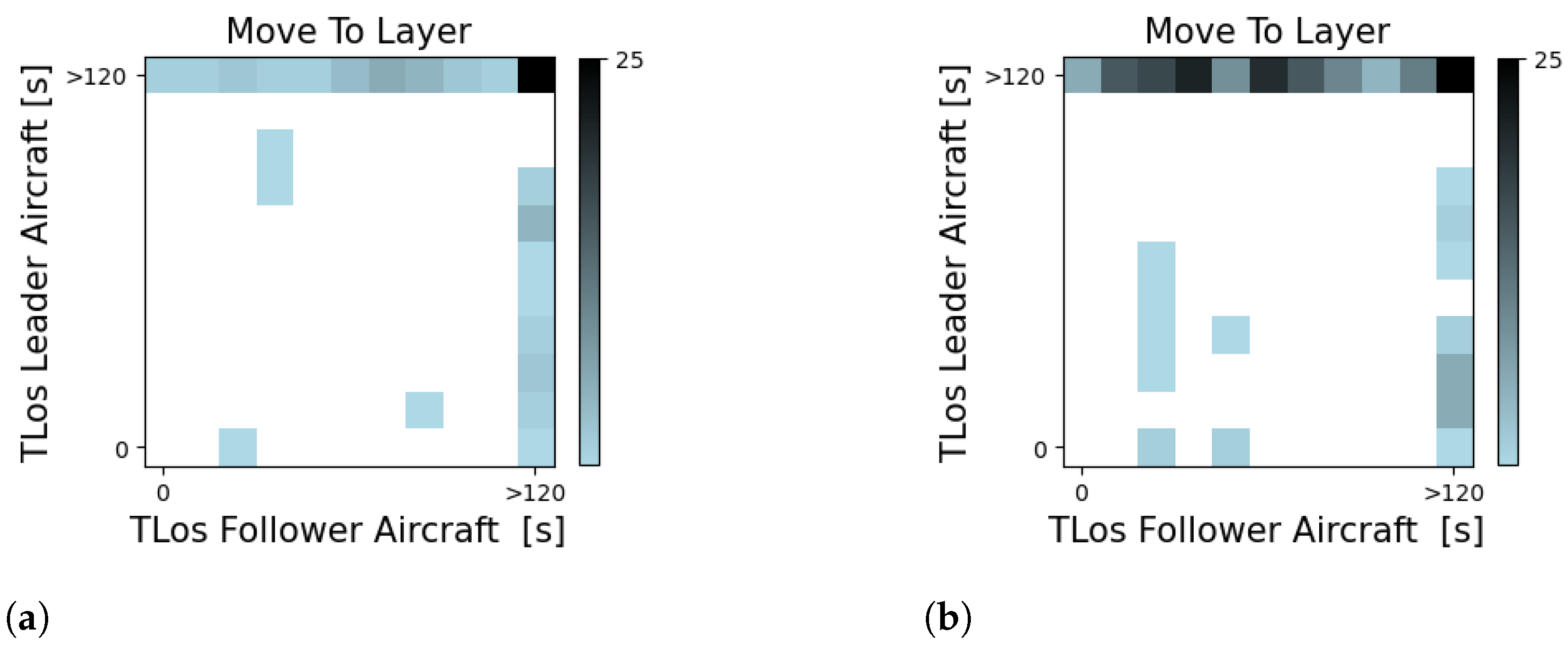
Figure 8 displays the time to LoS to the leader and follower aircraft in the target layer. In Figure 8a, aircraft move to layers with higher traffic densities (as seen in Figure 6, the module mainly makes use of two layers per set only). In this case, the module prefers to move aircraft to layers where the time to loss of separation between the ownship and the surrounding aircraft is greater than 120 s. In Figure 8b, the traffic density is expected to be lower as the module prioritised segmentation per the three layers per set (see Figure 7a). In this case, the module will still occasionally move to a layer even if the time to LoS with the follower aircraft is below 60 s. This is likely due to the fact that, with fewer aircraft per layer, the follower aircraft has ‘more space’ to decelerate to avoid an LoS with the ownship, analogously to what occurs in a highway. This shows the relevance of looking into the effect of a merging action in the complete layer—aircraft consecutively breaking down to avoid conflicts may result in back-end conflicts.
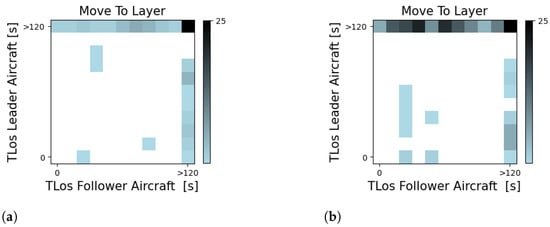
Figure 8.
Time to loss of separation between the ownship and the leader and follower aircraft for the actions performed by the decision-making module. (a) Module trained considering all conflicts/LoSs. (b) Module trained not considering intermediate conflicts/LoSs.
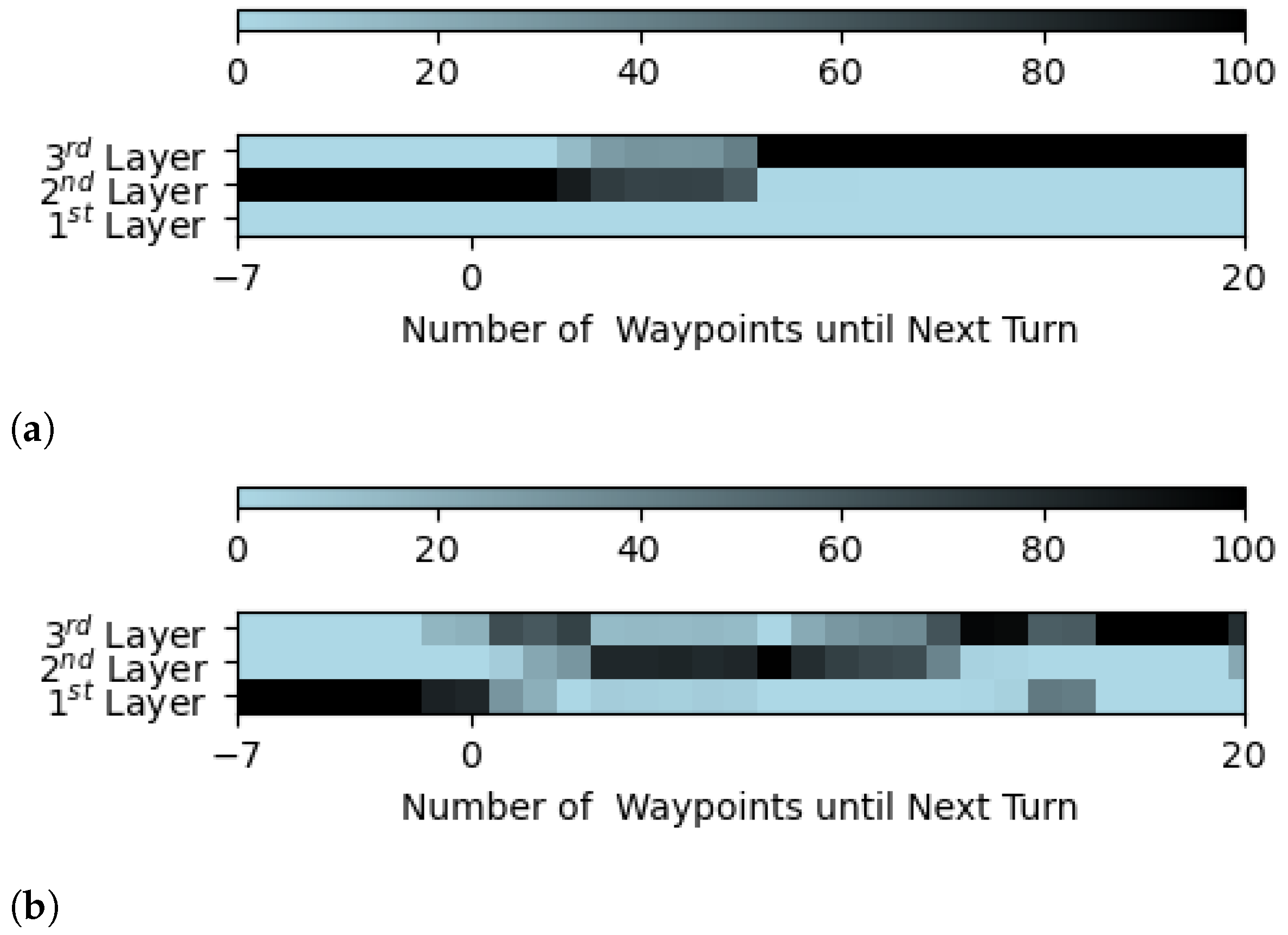
Figure 9 shows the likelihood of aircraft being set on each layer according to the number of waypoints until their next turn. Negative waypoint values mean that the aircraft will descend to a different layer set, and positive values indicate a climb. The modules place aircraft that will climb in the third layer and aircraft that will descend in the lowest cruising layer (i.e., the 2nd layer in Figure 9a and the 1st layer in Figure 9b). This is an optimal choice, as these aircraft are already closer to their next layer set in altitude.
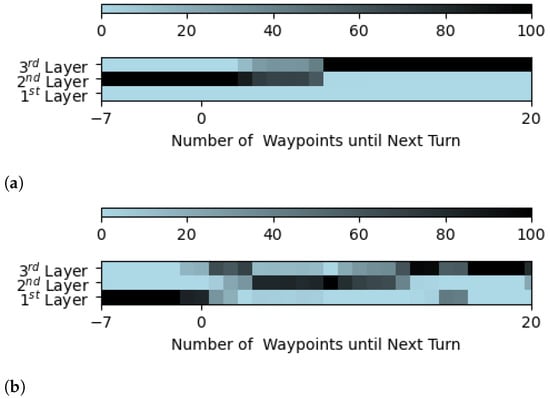
Figure 9.
Likelihood (in percentage) of aircraft being set on each layer according to the number of waypoints until their next turn. (a) Module trained considering all conflicts/LoSs. (b) Module trained not considering intermediate conflicts/LoSs.
Figure 10 displays the actions chosen by the control execution module. During training, this module is called upon when a lane change decision command is output based on the baseline navigation rules (see Section 6.4.2). The module opts for a move to the next layer about 95% of the time. Note that when the module decides to delay merging towards the target layer by selecting to stay in the current layer instead, the module will again be called after 5 s to check upon the viability of a merging manoeuvre. This process is repeated until the ownship moves into the target layer. Performing a ‘move to the next layer’ action 100% of the time would be the same as not having a control execution module; the lane-changing command is always performed immediately. Thus, the main focus is when this module decides to ‘delay’ the merge, which hopefully decreases conflict/LoSs during vertical transitions. Figure 10b shows that the actions adopted by the module lead to a reduction in conflicts/LoSs.
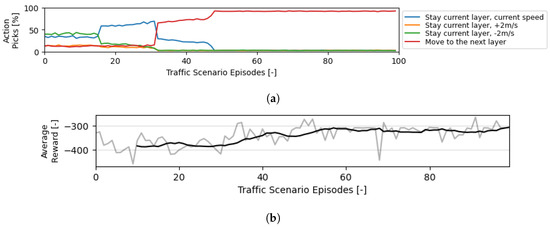
Figure 10.
Evolution of the actions and rewards during the training of the control execution module. Roughly M actions were performed. (a) Evolution of the balance between possible actions throughout episodes during training. (b) Evolution of the balance between possible actions throughout episodes during training.
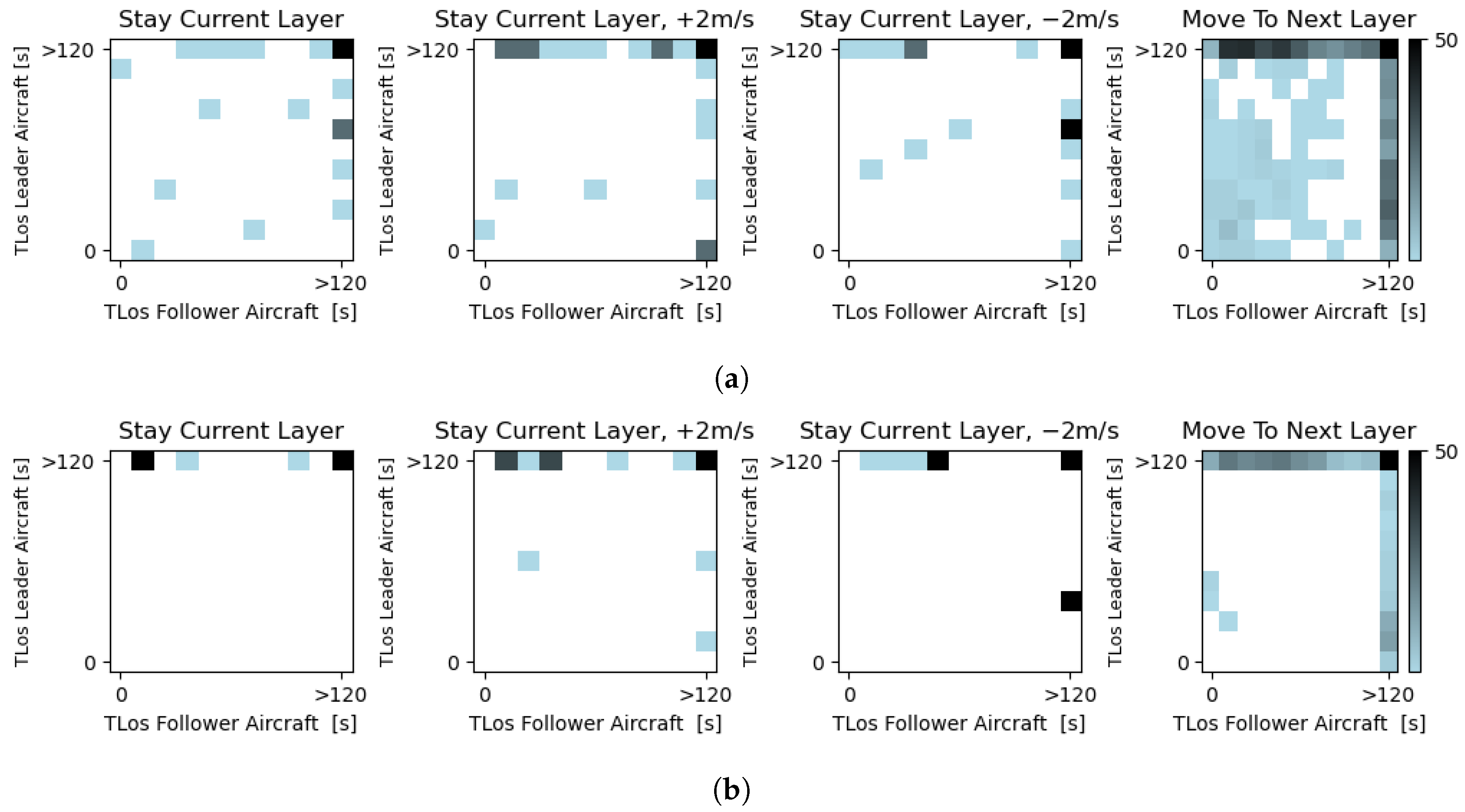
Figure 11 displays the environment status during each action of the control execution module. Figure 11a shows the time to LoS to the leader and follower aircraft on the ownship’s current layer. Figure 11b maps the time to LoS to the leader and follower aircraft on the target layer. First, the main motivator of whether to move to the next layer seems to be the distance between the leader and follower aircraft in the next layer. Nevertheless, on some occasions, the module will still move aircraft to the next layer when the follower aircraft is in close proximity (see darker points on the top left of the ‘Move to Next Layer’ action in Figure 11b). Other variables (such as TLoS to the neighbouring aircraft in the current layer, the ownship’s speed, and the number of waypoints to the final target layer) also affect this decision. However, how these values combine for this decision is not clear when looking at them individually. Second, although small, there is a preference for accelerating when the follower aircraft is closer (see darker points on the top left of the ‘Stay Current Layer, +2 m/s’ actions in Figure 11a) and for decelerating when the leader is near (see darker points on the right side of the ‘Stay Current Layer, −2 m/s’ actions in Figure 11a). Finally, similarly to the decision-making module, the control execution module seems to prioritise a larger distance to the leader than to the follower aircraft.
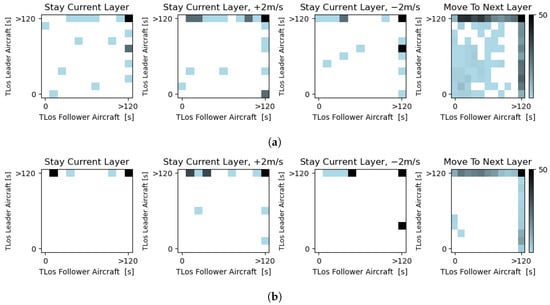
Figure 11.
Time to loss of separation between the ownship and the leader and follower aircraft. (a) Time to loss of separation between the ownship and the leader and follower aircraft in the current layer for each possible action. (b) Time to loss of separation between the ownship and the leader and follower aircraft in the target layer for each possible action.
7.2. Testing of the Reinforcement Learning Modules
The RL modules were tested with a total of 225 traffic scenarios; 75 scenarios in each one of the traffic densities (i.e., low, medium, and high). These vary in the number of turns and initial direction(s), as previously described in Section 6.1. The RL modules were previously trained within a medium traffic density; it is of interest to see how they behave at lower and higher traffic densities. All testing episodes are different from the one the modules were trained in. For each traffic scenario (i.e., combination of specific traffic density, initial direction(s), and number of turns), three repetitions with different flight trajectories are performed. Each traffic scenario ran for an hour. In all graphics, the ‘baseline’ comparison data correspond to the traffic scenarios run with the analytical rules previously described in Section 6.4.2. Speed and vertical conflict resolution are performed during testing. When traffic scenarios have different trends, line graphs are used to show the results for all scenarios. When the trend is similar to all scenarios, boxplot graphs display the results for all traffic scenarios in each traffic density in favour of simplicity.
7.2.1. Safety Analysis
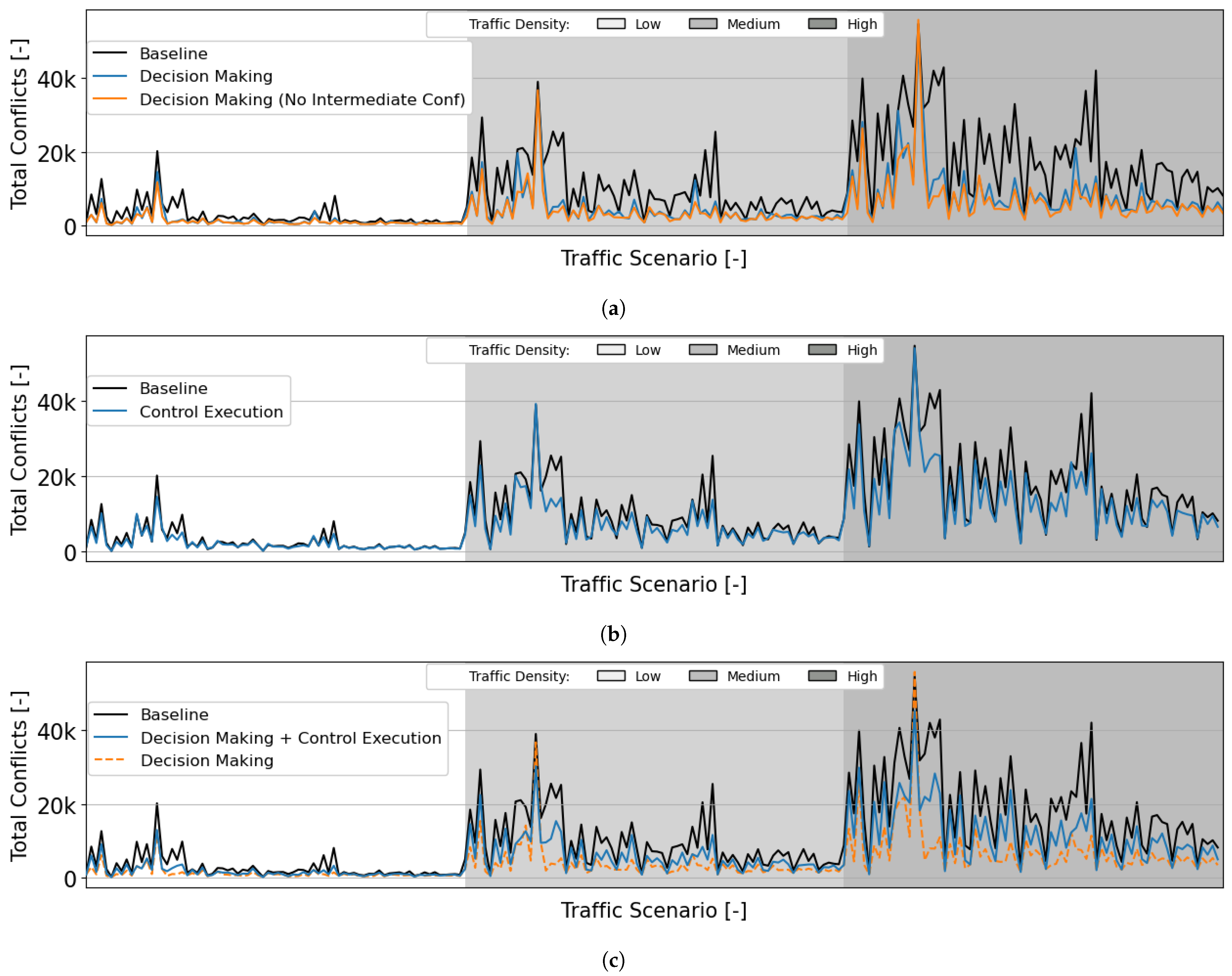
Figure 12 shows the mean total number of pairwise conflicts. Both RL modules are tested independently and together; all decreased the total number of conflicts when compared to the baseline navigation rules. Figure 12a displays the difference between training the decision-making module with and without considering intermediate conflicts/LoSs. Although a small difference, the module trained without considering intermediate movements achieved a higher reduction in conflicts. Not considering intermediate conflicts has a negative impact locally, as merging actions will suffer more conflicts/LoSs. However, globally, the fact that the module focuses on efficient segmentation throughout the complete airspace becomes the most beneficial factor. This segmentation is especially relevant at higher traffic densities. Thus, at these densities, better traffic segmentation may outweigh reserving free space for vertical deconflicting manoeuvres.
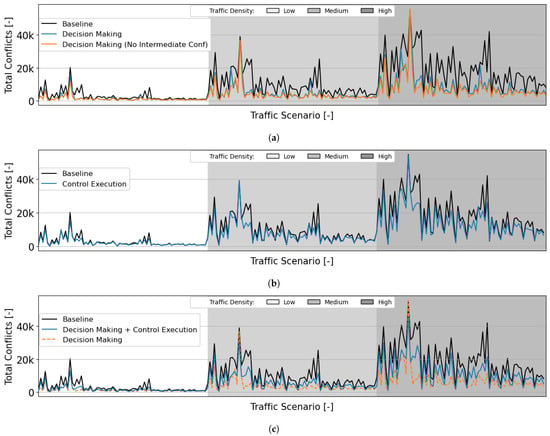
Figure 12.
Mean total number of pairwise conflicts during the testing of the RL modules. All traffic densities have 75 traffic scenarios, with initial direction(s) and number of turns as defined in Section 6.1. (a) Mean total number of pairwise conflicts during testing of the decision-making module. A comparison is made between the RL module when trained considering all conflicts/LoSs (in blue), and when no intermediate conflicts are considered (in orange). (b) Mean total number of pairwise conflicts during testing of the control execution module. (c) Mean total number of pairwise conflicts during testing of the two RL modules together.
The test results for the control execution module are shown in Figure 12b. When used independently, this module receives lane change commands from the baseline rules. Its ‘delay’ actions (i.e., when it chooses to stay in the current layer instead of merging into the target layer) are able to reduce the total number of conflicts for all traffic scenarios and densities. Naturally, the module is only called when there are heading turns, so there is no impact in traffic scenarios with only straight flight routes. The impact is greater in traffic scenarios with a high number of turns. Initial hypotheses considered that the module would lose efficiency at high traffic densities due to more intruders and smaller distance gaps between aircraft. However, its influence is especially noticeable in these densities, where it can prevent a large number of conflicts/LoSs occurring due to merging manoeuvres within these small gaps.
Finally, Figure 12c displays the testing of both modules together. In this case, the decision-making module outputs a layer change command, which is received by the control execution module. We employ the decision-making module trained without considering intermediate conflicts due to the best testing results. The combination of both modules has fewer conflicts than the baseline navigation rules. However, the combination of both modules increases the total number of conflicts for some traffic scenarios when compared to using the decision-making module alone with immediate merging upon the lane change command. The following safety graphs will show the results of decision-making next to the combination of both modules to analyse the reason for the worsening of the total number of conflicts.
Figure 13 shows the mean total number of LoSs. The two modules were able to reduce the number of LoSs for all traffic scenarios and densities when compared to the baseline navigation rules. The total number of LoSs is not a direct result of the total number of conflicts (see Figure 12). However, reducing the number of conflicts has a positive influence on the number of LoSs.
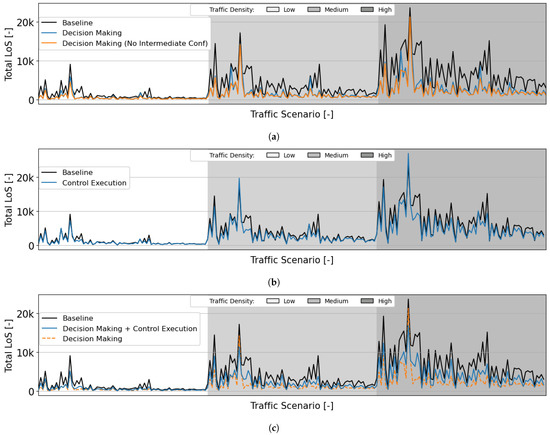
Figure 13.
Mean total number of losses of separation (LoSs) during the testing of the RL modules. All traffic densities have 75 traffic scenarios, with initial direction(s) and number of turns as defined in Section 6.1. (a) Mean total number of losses of separation during testing of the decision-making module. (b) Mean total number of losses of separation during testing of the control execution module. (c) Mean total number of losses of separation during testing of the two RL modules together.
Similarly to the total number of conflicts in Figure 12c, for some traffic scenarios, adding the control execution module results in an increase in the total number of LoSs compared to employing the decision-making module alone and having immediate merging manoeuvres. The ‘delays’ caused by the control execution module increase the total number of conflicts/LoSs, especially for traffic scenarios with a single origin (i.e., all aircraft start their route in the same direction) and multiple turns. Per Figure 12c and Figure 13c, this effect worsens as the traffic density increases. The fact that aircraft all have the same origin means that delaying the vertical manoeuvres also delays the dispersion of this localised high traffic density per the rest of the available airspace. Reducing this concentration of traffic as fast as possible has a greater effect globally in reducing the total number of conflicts and LoSs. Although the control execution module reduces the conflicts/LoSs resulting from merging manoeuvres, in these specific traffic scenarios, these are negligible compared with the instability effect resulting from having such a high number of aircraft travelling in the same layers for a long period of time.
However, there is one traffic scenario where adding the control execution reduced the total number of conflicts/LoSs when compared to using the decision-making module alone, and it does it at medium and high traffic densities. Here, all aircraft start their flight heading north and will perform four turns to the left during their flight. This traffic scenario has the highest number of conflicts/LoSs of all 75 scenarios, meaning that this particular direction with a high amount of turns tends to be unsafe in this operational environment. This shows that a control execution module, as hypothesised, is essential when the merging conflicts/LoSs are the main source of risk. Such is the case for flight routes with multiple turns at higher traffic densities, where likely distance gaps between aircraft are smaller. The module reduces merging conflicts while, unfortunately, delaying dispersion of aircraft clusters in the process, increasing cruising conflicts. Its value is thus highly connected to the traffic scenario.
Figure 14 displays the amount of time each aircraft spends in conflict with other aircraft. While in conflict, aircraft will follow the new state computed by the CR method. Aircraft return to their pre-defined route state once detected that they are no longer in a conflict situation with intruders. The final solution, using both RL modules, was able to reduce the time in conflict for all traffic scenarios and densities when compared to the baseline rules. Note that the total number of conflicts (see Figure 12) and the total time in conflict do not have a direct correlation. Fewer pairwise conflicts do not necessarily mean less time in conflict per aircraft and vice versa.
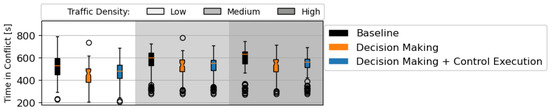
Figure 14.
Total time in conflict per aircraft. All traffic densities have 75 traffic scenarios, with initial direction(s) and the number of turns following the order defined in Section 6.1.
Figure 15 displays the intrusion severity. For most traffic scenarios, there is no relevant discrepancy between the efficiency of the combination of the two RL modules and the baseline rules. However, there is a difference between these and the average intrusion severity when employing the decision-making module solely. This is expected: the decision-making module does not take intermediate conflicts/LoSs into account; thus, it does not try to reduce proximity with other aircraft in intermediate layers, leading to severe intrusions. As a result, adding the control execution module could be a trade-off between the total number of LoSs (see Figure 13c) and their severity.
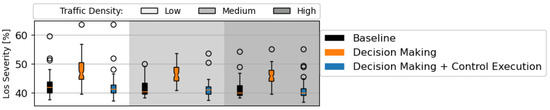
Figure 15.
Mean intrusion severity rate. All traffic densities have 75 traffic scenarios, with initial direction(s) and number of turns following the order defined in Section 6.1.
Figure 16 depicts the relative speed between two aircraft in an LoS situation. Higher relative speeds indicate speed heterogeneity, which increases complexity in the airspace. With the baseline rules, transition layers are in place to minimise the effect of high relative speeds from aircraft exiting and entering a cruising layer; aircraft only decelerate/turn/accelerate within the third layer. These layers are considered safer for this state change, as they are expected to be (almost) devoid of aircraft. Although the RL solution does not leave a layer ‘free’, such does not result in a considerable increase in relative speed between aircraft. In some traffic scenarios, it even achieved a slight improvement. Optimal segmentation is also beneficial in reducing relative speeds. With fewer conflicts and less time in conflict (see Figure 12c and Figure 14, respectively), aircraft can spend a higher amount of time at the ideal cruising speed. Frequent speed variations for conflict resolution may increase speed heterogeneity. Finally, employing the decision making RL module alone shows some peaks of low relative speeds. These also correspond to traffic scenarios where all aircraft are initially flying in the same direction. Once again, these differences in performance result from a delay in the dispersion of these clusters of aircraft.
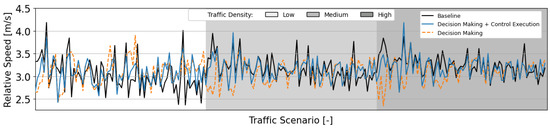
Figure 16.
Mean relative speed between pairs of aircraft in loss of separation. All traffic densities have 75 traffic scenarios, with initial direction(s) and number of turns following the order defined in Section 6.1.
7.2.2. Stability Analysis
Figure 17 shows the mean DEP value. The RL solution shows considerably better stability than the baseline navigation rules. This is likely due to the better segmentation of aircraft; the greater distance between aircraft reduces the chance of secondary conflicts when aircraft alter their state.

Figure 17.
Domino effect parameter values. All traffic densities have 75 traffic scenarios, with initial direction(s) and number of turns following the order defined in Section 6.1.
7.2.3. Efficiency Analysis
Figure 18 shows the average length of the 3D flight path per aircraft. The differences in length of the flown trajectory originate mainly from: (1) the different vertical distances between traffic layers that the aircraft occupy throughout their path, and (2) the different number of vertical manoeuvres to avoid conflicts. Employing both RL modules shows a slight reduction in flight path length for some of the traffic scenarios when compared to the baseline navigation rules. A bigger flight path reduction can potentially be achieved when efficiency is also added to the reward formulation. However, this may have the same effect as considering intermediate conflicts in the decision-making module: an optimal cruising layer may be disregarded in favour of a smaller vertical deviation.
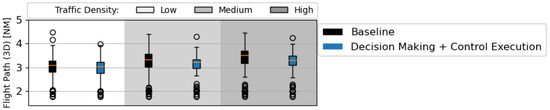
Figure 18.
Flight path length per aircraft. All traffic densities have 75 traffic scenarios, with initial direction(s) and number of turns following the order defined in Section 6.1.
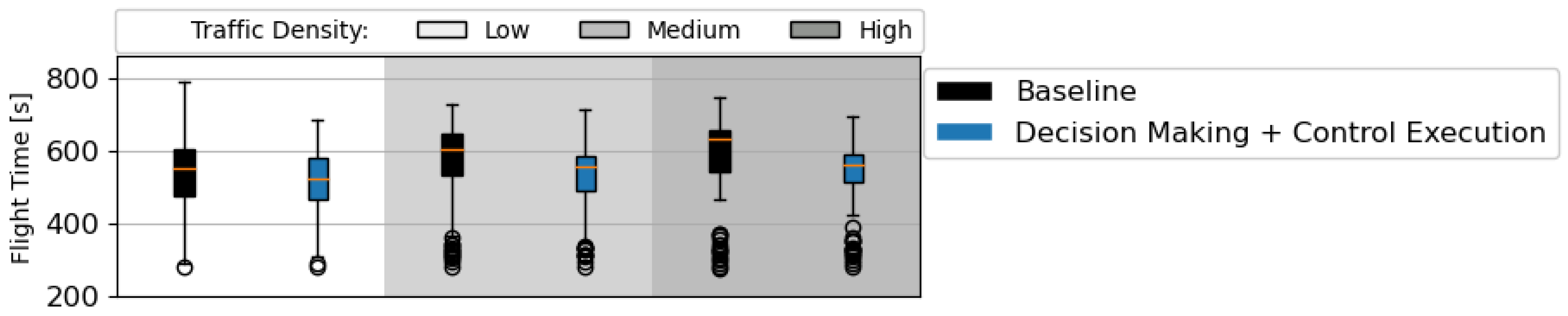
Figure 19 displays the average flight time per aircraft. For most of the traffic scenarios, employing the RL solution achieved a faster flight than with the baseline navigation rules. The difference in flight time increases alongside the traffic density. This results not only from shorter flight paths (see Figure 18) but also from aircraft spending less time in conflict (see Figure 14). Often conflict avoidance manoeuvres lead to aircraft adopting lower deconflicting speeds, which increase flight time.
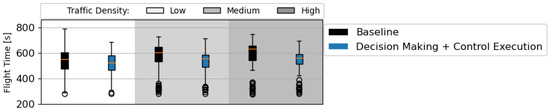
Figure 19.
Flight time per aircraft. All traffic densities have 75 traffic scenarios, with initial direction(s) and number of turns following the order defined in Section 6.1.
8. Discussion
Using reinforcement learning to improve the lane change decision proved more successful, safety- and efficiency-wise, than using manually defined baseline rules, both for different traffic scenarios and different traffic densities. First, a decision-making module was used to output lane change commands based on the planned route of the ownship and the position of neighbouring aircraft. The decision-making module proved better at reducing the global number of conflicts and LoSs when conflicts/LoSs resulting from crossing intermediates layers between the initial and the target layer are not taken into consideration. This way, the module is able to focus on optimising the cruising phase, which is beneficial to the global traffic scenario, as aircraft try to maximise the cruising phase on their planned route. Second, a control execution module improves safety during merging manoeuvres by controlling the longitudinal and vertical movement of the merging aircraft. It reduces the negative local impact of the lane change decisions when the ownship crosses multiple layers. By delaying the merging manoeuvre until an adequate distance gap exists between the ownship and the leader and follower aircraft, the intrusion severity during vertical manoeuvres is reduced.
The optimal actions found by an RL method can be used to improve the rules of current navigation analytical methods. Looking at the choices made by the two modules previously described, the following guidelines can be defined:
- At high traffic densities, a high degree of segmentation during the cruising phase is the most beneficial element towards decreasing conflict and losses of minimum separation.
- With multiple layers, the separation of aircraft per layer should be performed in relation to how close aircraft are to the next turn. Aircraft closer to a turn should be positioned at the outward layers, as they will move out sooner.
- Delaying a merging manoeuvre may result in a trade-off between reducing the number of LoSs or keeping LoS severity to a minimum. At high traffic densities, when gaps between neighbouring aircraft are minimal, most aircraft will likely delay their vertical movement. However, these decisions together result in the local traffic density staying the same, with no improvement in the local situation. Whereas in a method without delays, although the first dispersed aircraft are expected to encounter several conflicts/LoSs, their movement reduces local traffic density. Consequently, distance gaps between aircraft increase, facilitating the next vertical manoeuvres.
The unexpected finding that adding the control executing module to the decision-making module increased the total number of conflicts/LoSs raises questions regarding the observability and reward formulation of the trained RL modules. The control execution module still has a positive effect locally by reducing the intrusion severity during vertical manoeuvres. However, it also has a negative global effect, delaying the dispersion of aircraft per the available airspace. These elements are further discussed in the next sections.
8.1. Centralised Learning with Decentralised Policies
Both modules presented in this work have partial observability: the agent has information only on its surroundings, making the observations correlated with its geographical position. However, the results obtained show that the information available is not sufficient for the agent to fully understand the repercussions of its actions. First, given that most of the flight routes favour spending most of their flight cruising, for global safety, it is more beneficial to optimise the cruising phase than to decrease the number of conflicts/LoSs resulting from crossing multiple vertical layers. The latter may result in the module preferring to move to a nearer vertical layer instead of one further away that is potentially safer to cruise in. However, this is not clear to the module as its observability/reward is restricted to the lane change action. Second, delaying the merging manoeuvre until there is a safe distance gap in the target layer prevents the high severity LoSs that the ownship would otherwise suffer, but it also delays the reduction in the local traffic density. Depending on the number of aircraft involved, this may be a source of instability.
A possible solution would be to increase the amount of information that each agent has access to. For example, the decision-making module can be extended to have more information on the ownship’s flight route, hopefully resulting in a more informed decision between prioritization of cruising and/or turning phases. The reward must also then reflect the safety during the following cruising phase so that the total impact of the layer change manoeuvre plus the cruising phase on the selected layer can be evaluated. However, safety in the cruising phase is also dictated by the other aircraft that join the layer after the ownship. Therefore, it is not clear whether it is possible for the module to correctly evaluate the impact of cruising in a layer. In turn, the control execution module can be improved to take into account the instability of the surroundings in the form of the local traffic density and relative distance between all aircraft. Increasing the information that each agent has access to requires the exploration of more powerful states, which also heavily increases the training time and complexity of the state-actions formulations. These are balanced considerations that should be present in future research.
8.2. Reward Formulation
The efficacy of a reinforcement learning method is highly dependent on the reward values. The reward formulation herein used was based on the number of conflicts and LoSs, as these are considered the main elements of safety. However, the reduction in the absolute value of these elements may have a negative impact on LoS severity (see Figure 15). This can be a simple action as, for example, the ownship moving away from one intruder and becoming closer to a second intruder in the process. This may result in two not so severe LoSs, versus one severe LoS. This raises the question of whether to prioritise: (1) a low number of LoSs, or (2) low LoS severity even when at the cost of a higher number of LoSs.
Future implementations may benefit from including intrusion severity in the training of RL methods. Nevertheless, a trade-off must be established between these two aspects. For example, in this work, one LoS was valued as 10 conflicts. The same would need to be established with LoS severity: (1) what are low and high severity intrusions? (2) how many low severity intrusions count for one high severity intrusion? These seem arbitrary decisions, but they heavily influence the decisions made by the RL module and are also dependent on the traffic scenario and simulation environments.
9. Conclusions
This paper focused on mitigating the impact of vertical deviations in a layered airspace. Previous hand-crafted rules have limited impact. Notwithstanding the arduous work of experts on the development of these rules, these do not cover the great multitude of different relative geometries between merging, follower, and leader aircraft during a merging manoeuvre. This work took inspiration from the extensive research with road vehicles in the area of lane change decisions, where reinforcement learning (RL) techniques have surpassed the performance of hand-crafted rules. We translated these methods into an aviation environment, where they are used for vertical layer change decisions.
We compared the behaviour of a reinforcement learning-based solution for layer-changing decisions versus employing manually defined navigation rules. Two RL modules were used: a decision-making module, which outputs lane change commands, and a control execution module, which controls the aircraft longitudinally and vertically to ensure a safe merging manoeuvre. Both modules, working independently and combined, reduced the total number of conflicts/LoSs when compared to manually defined baseline rules. The benefit of this approach was especially noticeable at high traffic densities and with routes with a high number of turns. However, it was also shown that delaying a merging manoeuvre, while the gap between the aircraft is yet not sufficient for a safe manoeuvre, also delays the dispersion of aircraft clusters in the process, negatively affecting global safety. Future work should look into the local and global effects, as an action that protects the ownship may increase the risk of conflicts for other neighbouring aircraft.
There is still a long way ahead before these RL methods can be implemented within a real-world scenario. Nevertheless, the behaviour of the methods can already provide guidelines for the implementation of navigation rules. Optimal segmentation during the cruising phase, setting aircraft closer to turns in outward layers, and delaying merging actions so as to limit intrusion severity can be used to improve current analytical layer navigation rules. For future improvement of the performance of the RL methods, the reward formulation can be extended to include other safety factors such as intrusion severity. Finally, this work can also be extended to more heterogeneous operational environments in terms of differences in performance limits, as well as preference for efficiency over safety.
Author Contributions
Conceptualization, M.R., J.E. and J.H.; methodology, M.R., J.E. and J.H.; software, M.R., J.E. and J.H.; writing—original draft preparation, M.R.; writing—review and editing, J.E. and J.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sesar Joint Undertaking. U–Space, Supporting Safe and Secure Drone Operations in Europe; Technical Report; Sesar Joint Undertaking: Brussels, Belgium, 2020. [Google Scholar]
- Tra, M.; Sunil, E.; Ellerbroek, J.; Hoekstra, J. Modeling the Intrinsic Safety of Unstructured and Layered Airspace Designs. In Proceedings of the Twelfth USA/Europe Air Traffic Management Research and Development Seminar, Seattle, WA, USA, 27–30 June 2017. [Google Scholar]
- Wang, P.; Chan, C.Y.; de La Fortelle, A. A Reinforcement Learning Based Approach for Automated Lane Change Maneuvers. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium, Changshu, China, 26–30 June 2018. [Google Scholar]
- Hoel, C.J.; Wolff, K.; Laine, L. Automated Speed and Lane Change Decision Making using Deep Reinforcement Learning. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018. [Google Scholar] [CrossRef]
- Hoekstra, J.; Ellerbroek, J. BlueSky ATC Simulator Project: An Open Data and Open Source Approach. In Proceedings of the Conference: International Conference for Research on Air Transportation, Vienna, Austria, 10–11 November 2016. [Google Scholar]
- Hoekstra, J.; van Gent, R.; Ruigrok, R. Designing for safety: The ‘free flight’ air traffic management concept. Reliab. Eng. Syst. Saf. 2002, 75, 215–232. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016—Conference Track Proceedings, International Conference on Learning Representations, ICLR, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Mushtaq, A.; Haq, I.U.; Imtiaz, M.U.; Khan, A.; Shafiq, O. Traffic Flow Management of Autonomous Vehicles Using Deep Reinforcement Learning and Smart Rerouting. IEEE Access 2021, 9, 51005–51019. [Google Scholar] [CrossRef]
- Garg, D.; Chli, M.; Vogiatzis, G. Deep Reinforcement Learning for Autonomous Traffic Light Control. In Proceedings of the 2018 3rd IEEE International Conference on Intelligent Transportation Engineering (ICITE), Singapore, 3–5 September 2018; pp. 214–218. [Google Scholar] [CrossRef]
- Walraven, E.; Spaan, M.T.; Bakker, B. Traffic flow optimization: A reinforcement learning approach. Eng. Appl. Artif. Intell. 2016, 52, 203–212. [Google Scholar] [CrossRef]
- Li, Z.; Liu, P.; Xu, C.; Duan, H.; Wang, W. Reinforcement Learning-Based Variable Speed Limit Control Strategy to Reduce Traffic Congestion at Freeway Recurrent Bottlenecks. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3204–3217. [Google Scholar] [CrossRef]
- Alizadeh, A.; Moghadam, M.; Bicer, Y.; Ure, N.K.; Yavas, U.; Kurtulus, C. Automated Lane Change Decision Making using Deep Reinforcement Learning in Dynamic and Uncertain Highway Environment. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 1399–1404. [Google Scholar] [CrossRef]
- Shi, T.; Wang, P.; Cheng, X.; Chan, C.Y.; Huang, D. Driving Decision and Control for Automated Lane Change Behavior based on Deep Reinforcement Learning. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 2895–2900. [Google Scholar] [CrossRef]
- Doole, M.; Ellerbroek, J.; Hoekstra, J. Investigation of Merge Assist Policies to Improve Safety of Drone Traffic in a Constrained Urban Airspace. Aerospace 2022, 9, 120. [Google Scholar] [CrossRef]
- Boeing, G. OSMnx: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Comput. Environ. Urban Syst. 2017, 65, 126–139. [Google Scholar] [CrossRef]
- Paielli, R.A. Tactical conflict resolution using vertical maneuvers in en route airspace. J. Aircr. 2008, 45, 2111–2119. [Google Scholar] [CrossRef]
- Henderson, P.; Islam, R.; Bachman, P.; Pineau, J.; Precup, D.; Meger, D. Deep Reinforcement Learning that Matters. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Duan, Y.; Chen, X.; Edu, C.X.B.; Schulman, J.; Abbeel, P.; Edu, P.B. Benchmarking Deep Reinforcement Learning for Continuous Control. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016. [Google Scholar]
- Islam, R.; Henderson, P.; Gomrokchi, M.; Precup, D. Reproducibility of Benchmarked Deep Reinforcement Learning Tasks for Continuous Control. arXiv 2017, arXiv:1708.04133. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, AISTATS, Ft. Lauderdale, FL, USA, 11–13 April 2011. [Google Scholar]
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of the Brownian motion. Phys. Rev. 1930, 36, 823–841. [Google Scholar] [CrossRef]
- Alejo, D.; Conde, R.; Cobano, J.; Ollero, A. Multi-UAV collision avoidance with separation assurance under uncertainties. In Proceedings of the 2009 IEEE International Conference on Mechatronics, Changchun, China, 9–12 August 2009. [Google Scholar] [CrossRef]
- Hoekstra, J.M. Free Flight in a Crowded Airspace? 2000. Available online: https://www.semanticscholar.org/paper/Free-Flight-in-a-Crowded-Airspace-Hoekstra/9b85d3bd167044d479a11a98aa510e92b66af87b (accessed on 1 November 2021).
- Ribeiro, M.; Ellerbroek, J.; Hoekstra, J. Velocity Obstacle Based Conflict Avoidance in Urban Environment with Variable Speed Limit. Aerospace 2021, 8, 93. [Google Scholar] [CrossRef]
- Golding, R. Metrics to Characterize Dense Airspace Traffic; Technical Report 004; Altiscope: Beijing, China, 2018. [Google Scholar]
- Bilimoria, K.; Sheth, K.; Lee, H.; Grabbe, S. Performance evaluation of airborne separation assurance for free flight. In Proceedings of the 18th Applied Aerodynamics Conference, Denver, CO, USA, 14–17 August 2000; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2000. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).