Aerodynamic Analysis of a Supersonic Transport Aircraft at Low and High Speed Flow Conditions
Abstract
:1. Introduction
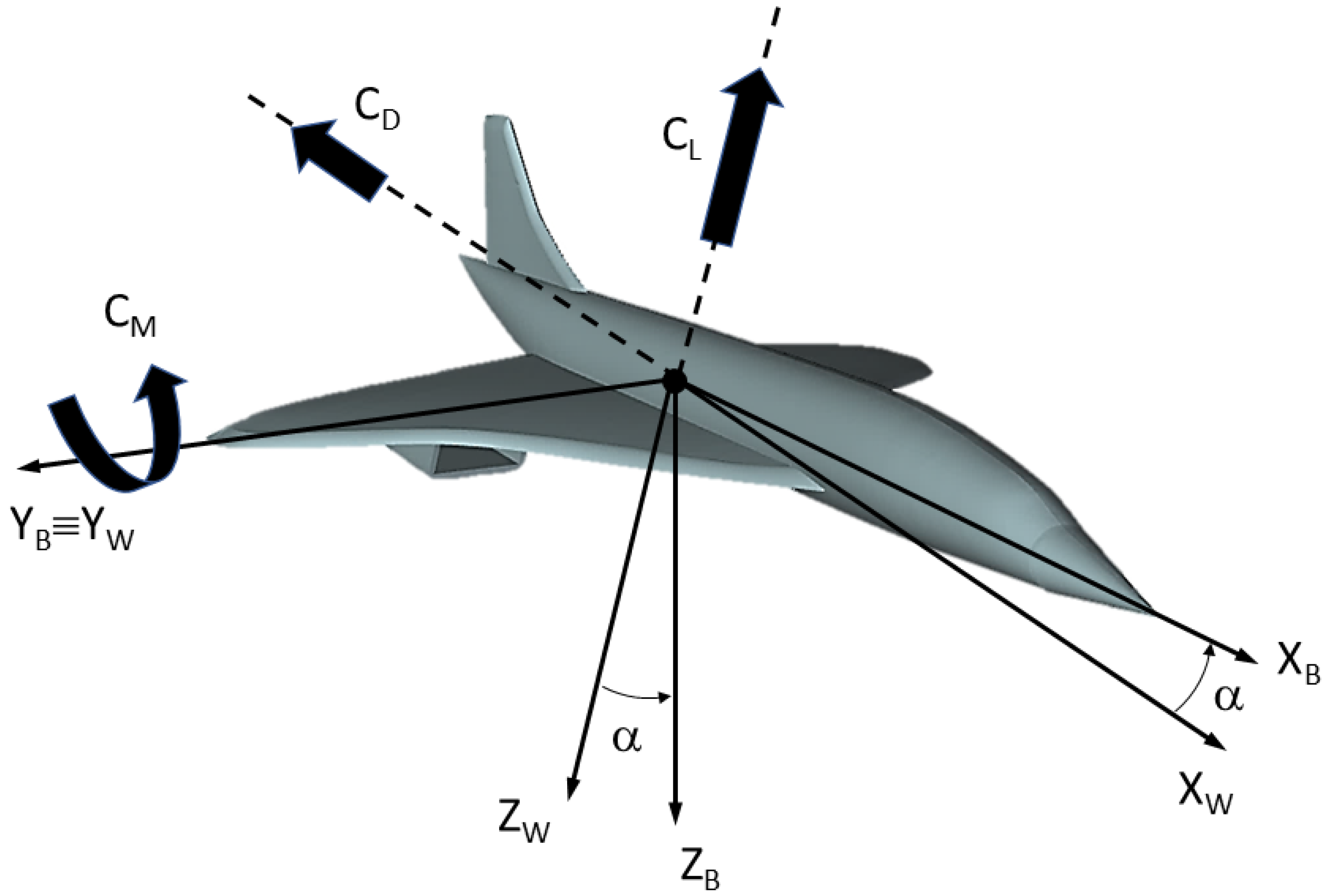
2. Aircraft Static Stability
3. Aerodynamic Analysis
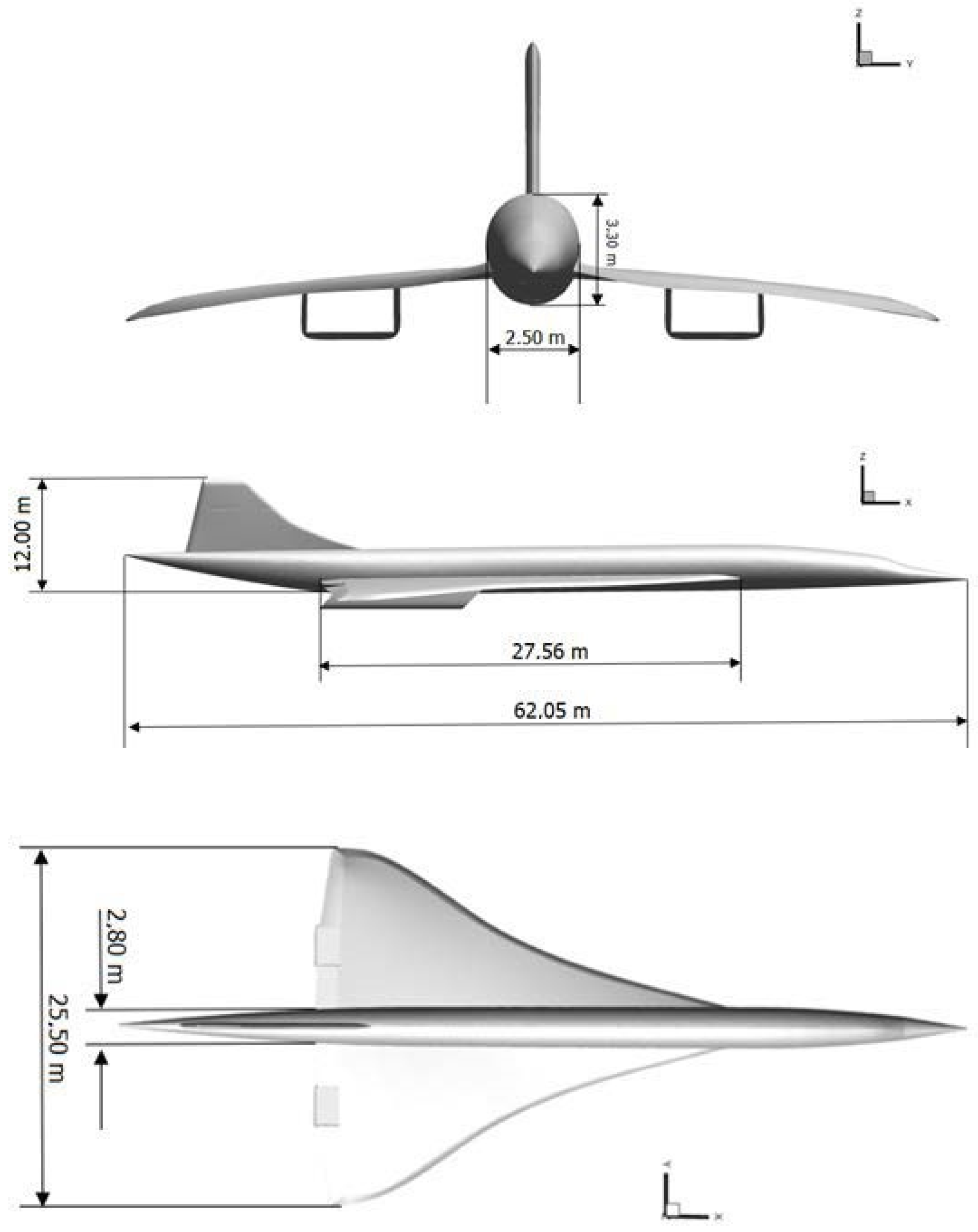
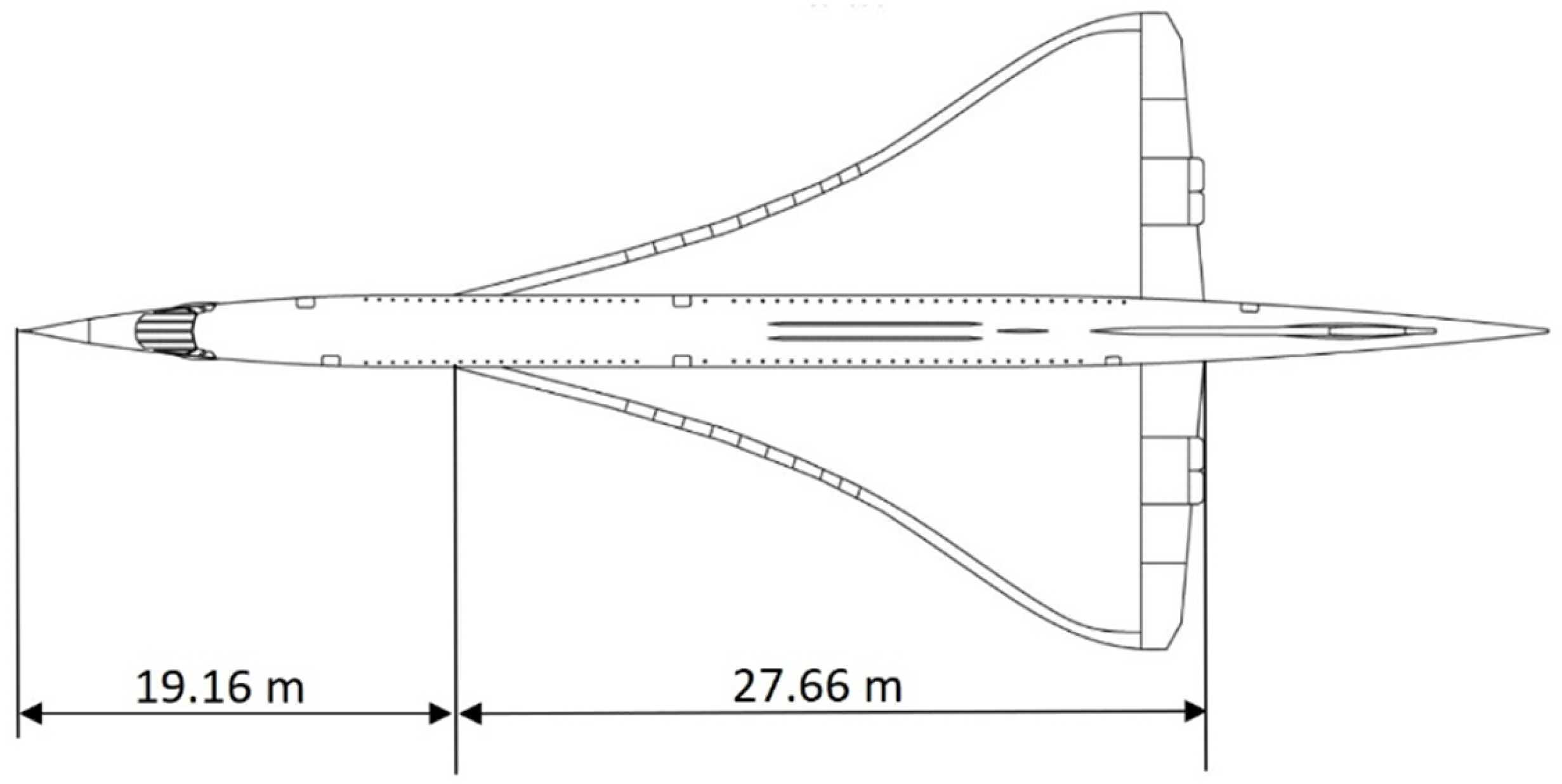
3.1. Aircraft Configuration
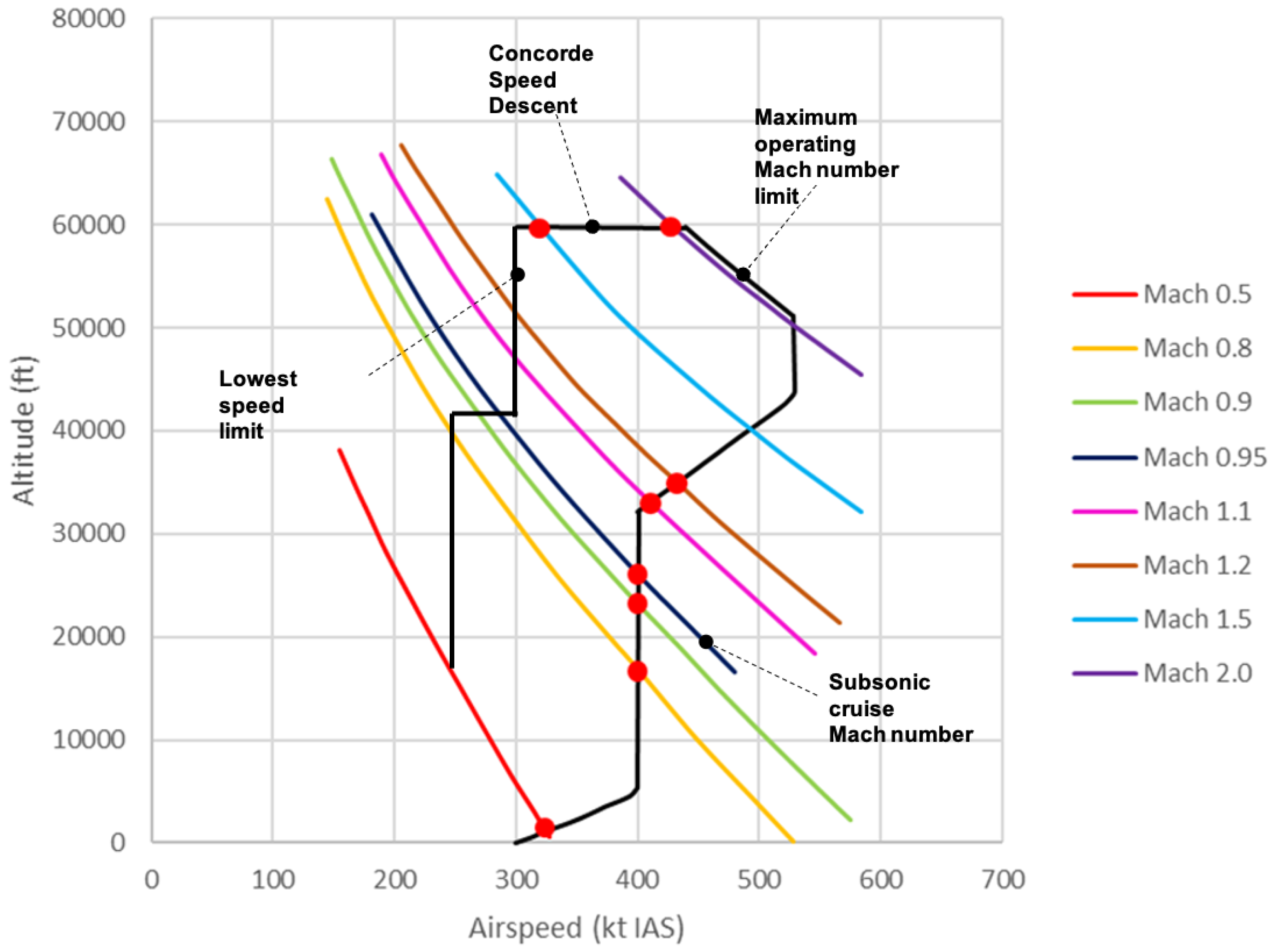
3.2. Flight Envelope
3.3. CFD Test Matrix
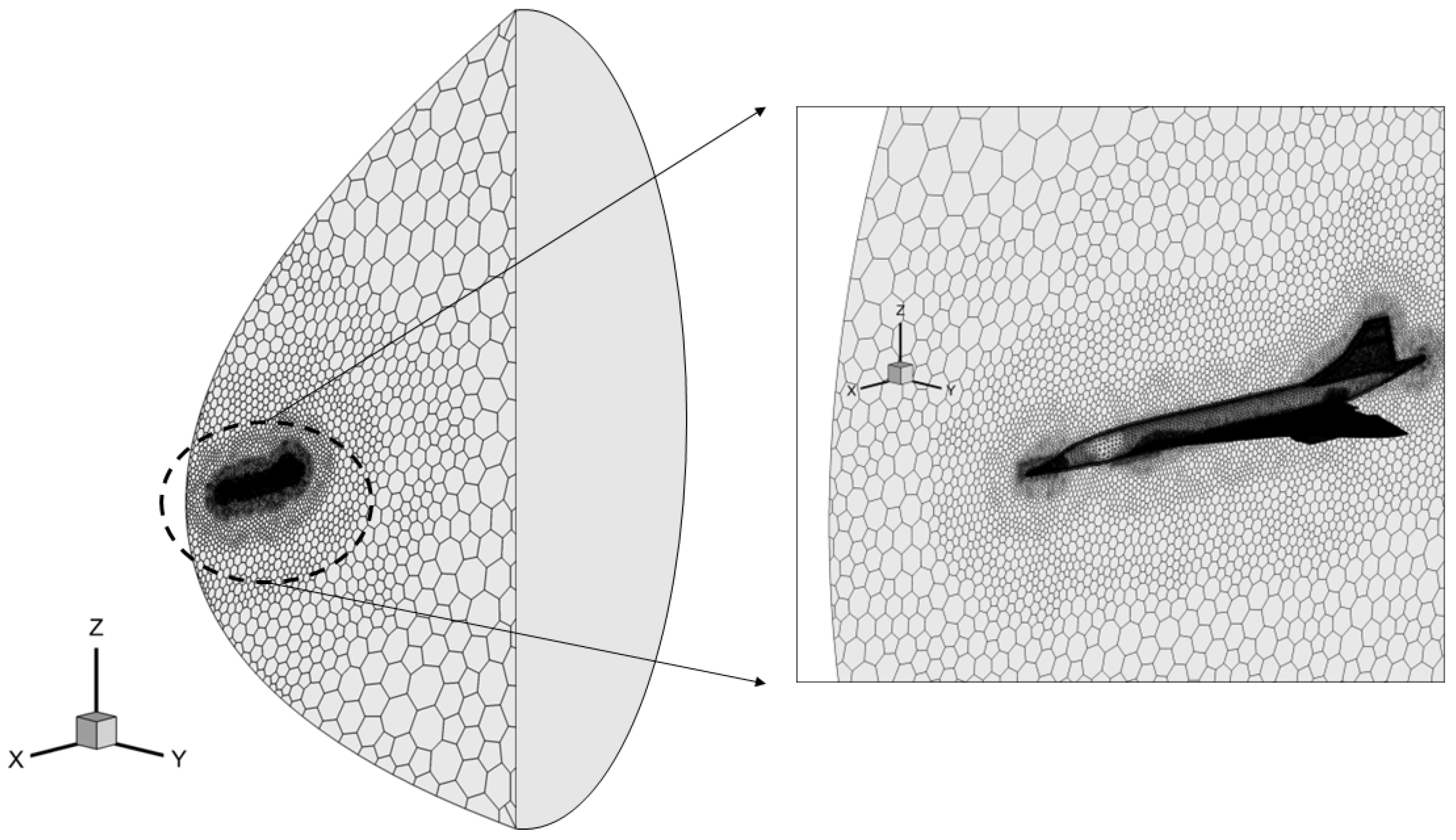
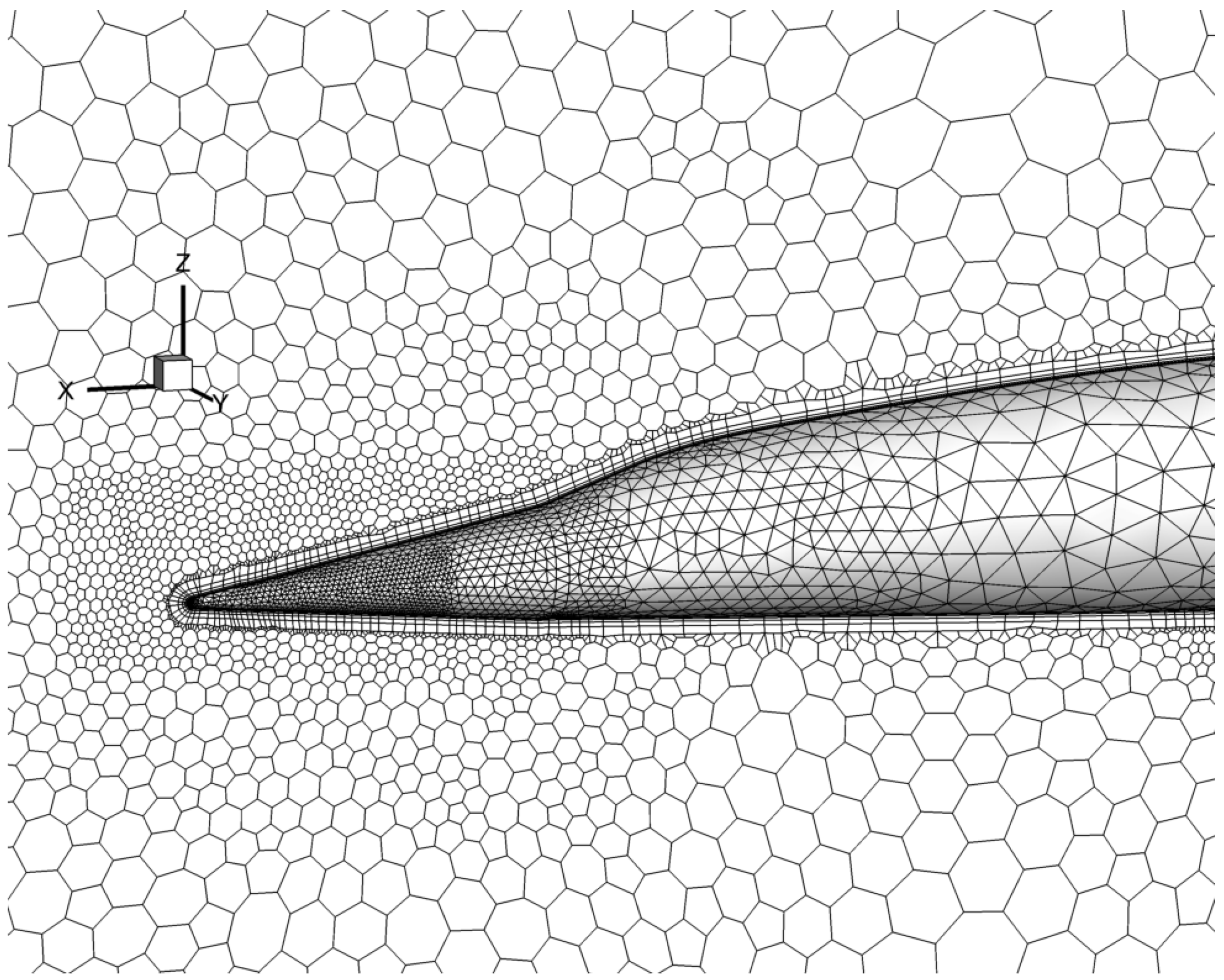
3.4. Grid Generation
3.5. CFD Modeling and Numerical Discretization
3.5.1. The FLUENT Solver
3.5.2. The SU2 Solver
3.5.3. Remarks on JST Scheme
3.5.4. Effect of Dissipation Operator
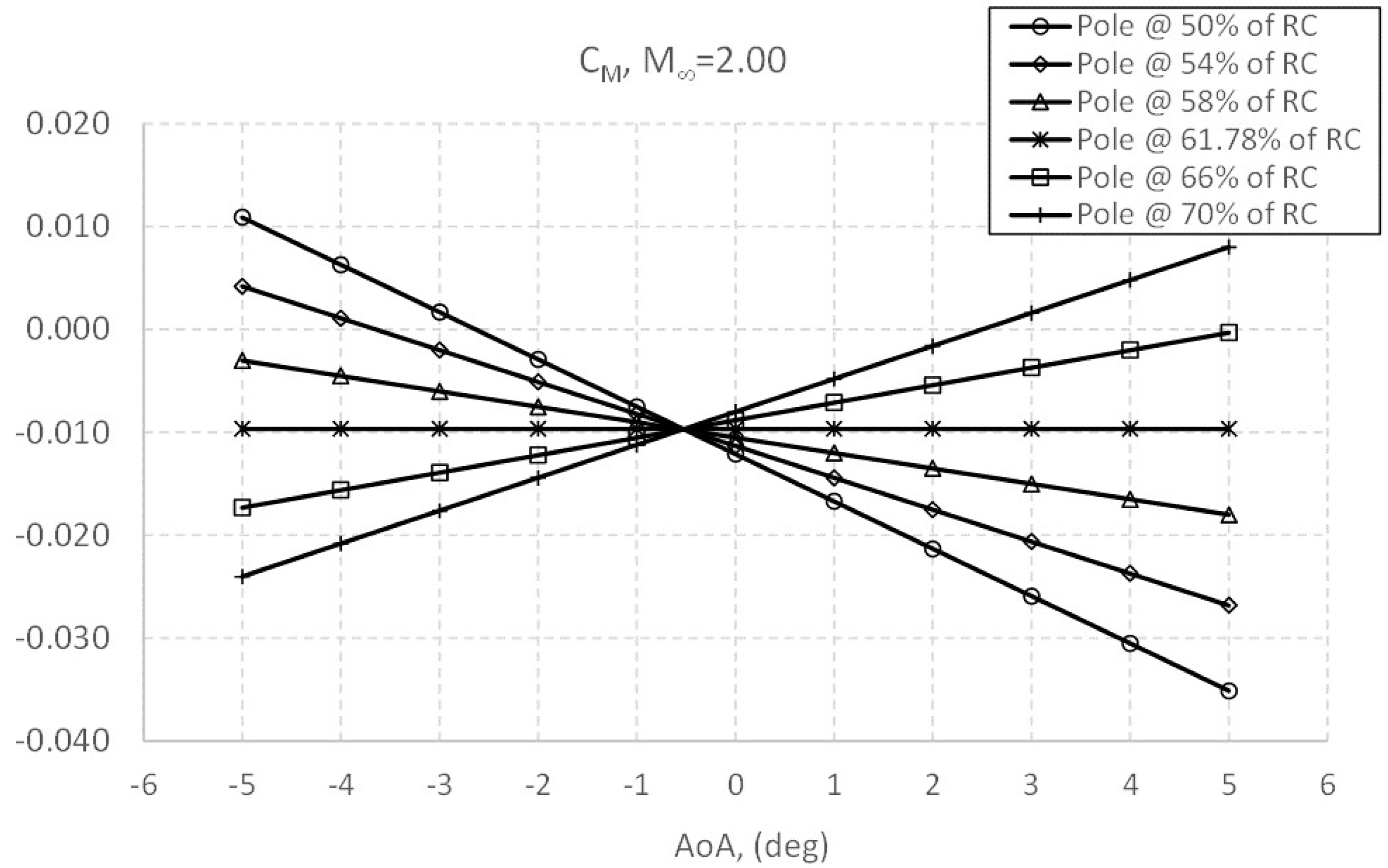
4. Computation of the Aircraft Aerodynamic Coefficients and Aerodynamic Center
5. Aerodynamic Results
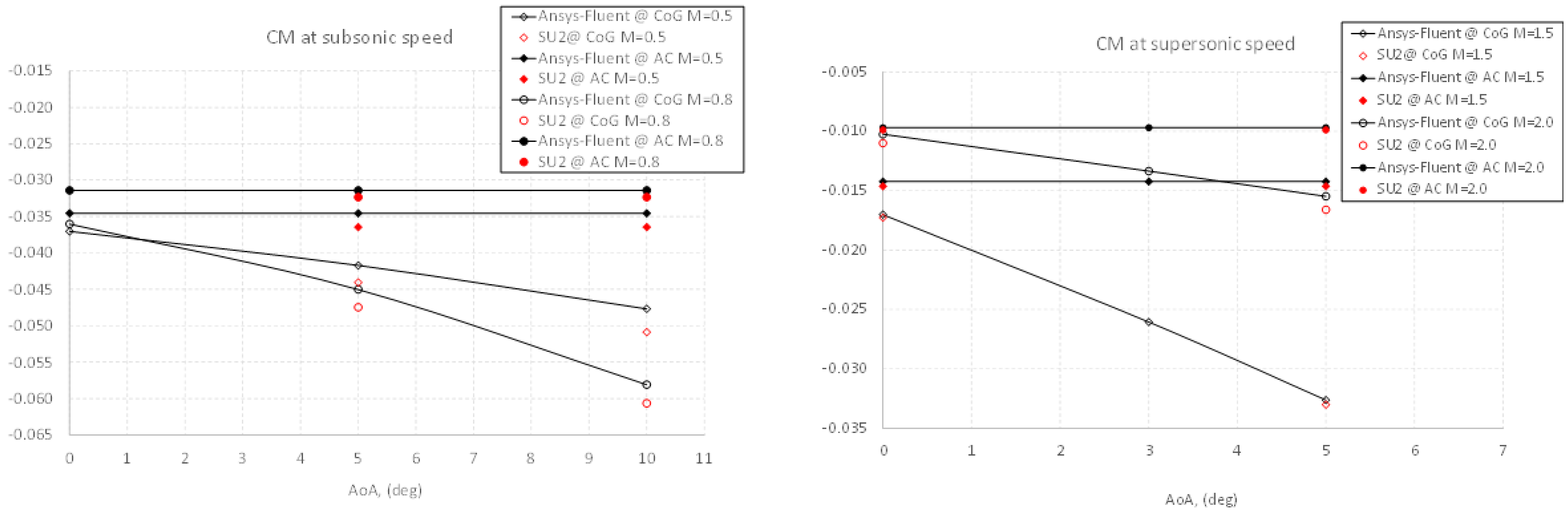
5.1. Force and Moment Coefficients Versus Attitude
5.2. Force and Moment Coefficients Versus Mach
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1
| 0.24 | 0 | 0.02278 | 0.12510 | −0.18960 | −0.03481 | 0.02280 | 0.12510 | 5.48684 |
| 0.24 | 5 | 0.01042 | 0.35050 | −0.47730 | −0.03481 | 0.04080 | 0.34730 | 8.51225 |
| 0.24 | 10 | 0.00438 | 0.65710 | −0.86720 | −0.03481 | 0.11840 | 0.64640 | 5.45946 |
| 0.50 | 0 | 0.02238 | 0.12677 | −0.19272 | −0.03456 | 0.02238 | 0.12677 | 5.66494 |
| 0.50 | 5 | 0.01101 | 0.35684 | −0.47995 | −0.03456 | 0.04207 | 0.35452 | 8.42631 |
| 0.50 | 10 | 0.00543 | 0.66480 | −0.86412 | −0.03456 | 0.12079 | 0.65376 | 5.41237 |
| 0.80 | 0 | 0.02510 | 0.11926 | −0.18349 | −0.03142 | 0.02510 | 0.11926 | 4.75083 |
| 0.80 | 5 | 0.01394 | 0.38045 | −0.51544 | −0.03142 | 0.04704 | 0.37779 | 8.03108 |
| 0.80 | 10 | 0.00813 | 0.71955 | −0.94782 | −0.03142 | 0.13296 | 0.70721 | 5.31897 |
| 0.90 | 0 | 0.02943 | 0.11126 | −0.17347 | −0.03008 | 0.02943 | 0.11126 | 3.78045 |
| 0.90 | 5 | 0.01877 | 0.39781 | −0.54273 | −0.03008 | 0.05337 | 0.39466 | 7.39439 |
| 0.95 | 0 | 0.03397 | 0.10616 | −0.16827 | −0.02913 | 0.03397 | 0.10616 | 3.12474 |
| 0.95 | 5 | 0.02498 | 0.40919 | −0.56493 | −0.02913 | 0.06055 | 0.40546 | 6.69619 |
| 1.02 | 0 | 0.04132 | 0.08010 | −0.13016 | −0.02305 | 0.04132 | 0.08010 | 1.9384 |
| 1.02 | 5 | 0.03270 | 0.41104 | −0.57253 | −0.02305 | 0.06840 | 0.40633 | 5.94493 |
| 1.10 | 0 | 0.04004 | 0.07630 | −0.12145 | −0.01929 | 0.04004 | 0.07630 | 1.9554 |
| 1.10 | 5 | 0.03136 | 0.38857 | −0.53941 | −0.01929 | 0.06511 | 0.38436 | 5.90311 |
| 1.20 | 0 | 0.03931 | 0.07512 | −0.12012 | −0.02048 | 0.03931 | 0.07512 | 1.91121 |
| 1.20 | 5 | 0.03168 | 0.36445 | −0.50491 | −0.02048 | 0.06332 | 0.36030 | 5.68984 |
| 1.50 | 0 | 0.03567 | 0.04353 | −0.07230 | −0.01423 | 0.03587 | 0.04086 | 1.13923 |
| 1.50 | 3 | 0.03397 | 0.19165 | −0.26948 | −0.01423 | 0.04396 | 0.18961 | 4.31344 |
| 1.50 | 5 | 0.03189 | 0.29632 | −0.40898 | −0.01423 | 0.05753 | 0.28946 | 5.03137 |
| 1.80 | 0 | 0.03223 | 0.02413 | −0.04252 | −0.01066 | 0.03223 | 0.02047 | 0.74872 |
| 1.80 | 5 | 0.03004 | 0.24066 | −0.32823 | −0.01066 | 0.05090 | 0.23713 | 4.65908 |
| 2.00 | 0 | 0.03038 | 0.02047 | −0.03653 | −0.00970 | 0.03038 | 0.02047 | 0.67398 |
| 2.00 | 3 | 0.02950 | 0.13798 | −0.19051 | −0.00979 | 0.03668 | 0.13625 | 3.71415 |
| 2.00 | 5 | 0.02887 | 0.21709 | −0.29420 | −0.00970 | 0.04768 | 0.21375 | 4.48329 |
| 0.5 | 5 | 0.00981 | 0.37316 | −0.51314 | −0.03645 | 0.04230 | 0.37088 | 8.76763 |
| 0.5 | 10 | 0.00502 | 0.69145 | −0.92005 | −0.03645 | 0.12502 | 0.68007 | 5.43959 |
| 0.8 | 5 | 0.01230 | 0.40531 | −0.56036 | −0.03234 | 0.04758 | 0.40270 | 8.46338 |
| 0.8 | 10 | 0.00703 | 0.75923 | −1.0214 | −0.03234 | 0.13877 | 0.74648 | 5.37923 |
| 1.5 | 0 | 0.03568 | 0.04559 | −0.0765 | −0.01463 | 0.03568 | 0.04559 | 1.27776 |
| 1.5 | 5 | 0.03197 | 0.30584 | −0.4292 | −0.01463 | 0.05850 | 0.30189 | 5.15974 |
| 2.0 | 0 | 0.03150 | 0.02188 | −0.0388 | −0.00990 | 0.03150 | 0.02188 | 0.69462 |
| 2.0 | 5 | 0.02970 | 0.22400 | −0.30400 | −0.00990 | 0.04911 | 0.22056 | 4.49114 |
References
- Carioscia, S.A.; Locke, J.W.; Boyd, L.D.; Lewis, M.J.; HalionSun, R.P.; Smith, H. Commercial Decelopment of Civilian Supersonic Aircraft; Coument D-10845; IDA: Alexandria, VA, USA, 2019. [Google Scholar]
- Sun, Y.; Smith, H. Review and prospect of supersonic business jet design. Prog. Aerosp. Sci. 2017, 90, 12–38. [Google Scholar] [CrossRef]
- Liebhardt, B.K. An Analysis of the Market Environment for Supersonic Business Jets. Prog. Aerosp. Sci. 2011, 39, 185–248. [Google Scholar]
- Davies, R.E.G. Supersonic (Airliner) Non-Sense—A Case Study in Applied Market Research; Coument D-10845; IDA: Alexandria, VA, USA, 1998. [Google Scholar]
- Smith, H. A review of supersonic business jet design issues. Aeronaut. J. 2007, 111, 761–764. [Google Scholar] [CrossRef]
- Smith, H. Supersonic Experimental Airplane (NEXST) for Next Generation SST Technology-Development and flight test plan for the Unmanned Scaled Supersonic Glider. In Proceedings of the AIAA-2002-0527. 39th Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 8–11 January 2001; pp. 761–764. [Google Scholar]
- Henne, P.A. Case for Small Supersonic Civil Aircraft. J. Aircr. 2005, 39, 765–774. [Google Scholar] [CrossRef]
- Sun, Y.; Smith, H.; Chen, H. Conceptual design of Low-Boom Low-Drag Supersonic Transports. In Proceedings of the AIAA Aviation Forum, 15–19 June 2020; Virtual Event. [Google Scholar]
- Aerion Supersonic. 2017. Available online: https://www.aerionsupersonic.com (accessed on 16 July 2022).
- Spike Aerospace. 2021. Available online: https://www.spikeaerospace.com/spike-images/ (accessed on 16 July 2022).
- Boom Airliner. Available online: https://boomsupersonic.com/airliner (accessed on 16 July 2022).
- Hardeman, A.B.; Maurice, L.Q. Sustainability:key to enable next generation supersonic passenger flight. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Sanya, China, 12–14 November 2021. [Google Scholar]
- Lee, D.S.; Fahey, D.W.; Forster, P.M.; Newton, P.J.; Wit, R.C.; Owen, B.; Sausen, R. Aviation and global climate change in the 21st century. Atmos. Environ. 2009, 43, 3520–3537. [Google Scholar] [CrossRef]
- Feng, X.; Li, Z.; Song, B. Research of low boom and low drag supersonic aircraft design. Chin. J. Aeronaut. 2014, 27, 531–541. [Google Scholar]
- Choi, S.; Alonso, J.J.; Kroo, I.; Wintzer, M. Multi-fidelity design optimization of low boom supersonic jets. J. Aircr. 2008, 45, 106–118. [Google Scholar] [CrossRef]
- Takeshi, F.; Yoshikazu, M. Conceptual design and aerodynamic optimization of silent supersonic aircraft at JAXA. In Proceedings of the 25th AIAA Applied Aerodynamics Conference, Miami, FL, USA, 25–28 June 2007. [Google Scholar]
- Sun, Y.; Smith, H. Low-boom low-drag optimization in a multidisciplinary design analysis optimization environment. Aerosp. Sci. Technol. 2019, 94, 105387. [Google Scholar] [CrossRef]
- Sun, Y.; Smith, H. Design and operational assessment of a low-boom low-drag supersonic business jet. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2022, 236, 82–95. [Google Scholar] [CrossRef]
- Yoshida, K. Supersonic drag reduction technology in the scaled supersonic experimental airplane project by JAXA. Prog. Aerosp. Sci. 2009, 45, 124–146. [Google Scholar] [CrossRef]
- Mangano, M.; Martins, J.R. Multipoint aerodynamic optimization for subsonic and supersonic regimes. J. Aircr. 2021, 58, 650–662. [Google Scholar] [CrossRef]
- Seraj, S.; Martins, J.R.R.A. Aerodynamic shape optimization of a supersonic transport considering low-speed stability. In Proceedings of the AIAA Scitech 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Gursul, Z.W.I.; Vardaki, E. Review of flow control mechanisms of leading-edge vortices. Prog. Aerosp. Sci. 2007, 43, 246–270. [Google Scholar] [CrossRef]
- Gursul, I. Review of unsteady vortex flow over delta wings. J. Aircr. 2005, 42, 299–319. [Google Scholar] [CrossRef]
- Aprovitola, A.; Di Nuzzo, P.E.; Pezzella, G.; Viviani, A. Aerodynamic Analysis of a Supersonic Transport Aircraft at Landing Speed Conditions. Energies 2021, 14, 6615. [Google Scholar] [CrossRef]
- Luckring, J. The discovery and prediction of vortex flow aerodynamics. Aeronaut. J. 2019, 123, 729–804. [Google Scholar] [CrossRef]
- Rech, J.; Leyman, C. A Case Study by Aerospatiale and British Aerospace on the Concorde. AIAA Prof. Study Ser. 1980. [Google Scholar] [CrossRef]
- Eames, J.D. Concorde Operations. SAE Trans. J. Aerosp. 1991, 100 Pt 2, 2603–2619. [Google Scholar]
- Krus, P.; Abdallah, A. Modelling of Transonic and Supersonic Aerodynamics for Conceptual Design and Flight Simulation. In Proceedings of the Aerospace Technology Congress, Stockholm, Sweden, 8–9 October 2019; Swedish Society of Aeronautics and Astronautics (FTF): Stockholm, Sweden, 2019. [Google Scholar]
- British Airways Overseas Division. Concorde Flying Manual II a; British Airways: London, UK, 1977. [Google Scholar]
- Aprovitola, A.; Aurisicchio, F.; Di Nuzzo, P.E.; Pezzella, G.; Viviani, A. Low Speed Aerodynamic Analysis of the N2A Hybrid Wing—Body. Aerospace 2022, 9, 89. [Google Scholar] [CrossRef]
- Bykerk, T.; Pezzella, G.; Verstraete, D.; Viviani, A. Longitudinal And Lateral-Directional Aerodynamics of a Re-Usable High-Speed Vehicle. In Proceedings of the 32nd Congress of the International Council of the Aeronautical Sciences, Shanghai, China, 6–10 September 2021. [Google Scholar]
- Schettino, A.; Pezzella, G.; Marini, M.; Di Benedetto, S.; Villace, V.F.; Steelant, J.; Choudhury, R.; Gubanov, A.; Voevodenko, N. Aerodynamic database of the HEXAFLY-INT hypersonic glider. CEAS Space J. 2020, 12, 295–311. [Google Scholar] [CrossRef]
- ANSYS-FLUENT. Ansys Fluent User’s Guide; ANSYS-FLUENT: Canonsburg, PA, USA, 2019. [Google Scholar]
- Economon, T.; Palacios, F.; Copeland, S.; Lukaczyck, T.; Alonso, J. SU2: An Open-SOurce suite for multiphysics simulation and design. AIAA J. 2016, 54, 828–846. [Google Scholar] [CrossRef]
- van Leer, B.; Powell, K. Introduction to Computational Fluid Dynamics. In Encyclopedia of Aerospace Engineering; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Jameson, A. Origins and further development of the Jameson-Smith-Turkel scheme. AIAA J. 2017, 55. [Google Scholar] [CrossRef]
- Hirsh, C. Numerical Computation of Internal and External Flow; Butterworth-Heinemann: Oxford, UK, 2007. [Google Scholar]
- Ekaterinaris, J.A.; Schiff, L.B. Numerical simulation of incidence and sweeep effects on delta wing vortex breakdown. J. Aircr. 1994, 31, 1043–1049. [Google Scholar] [CrossRef]



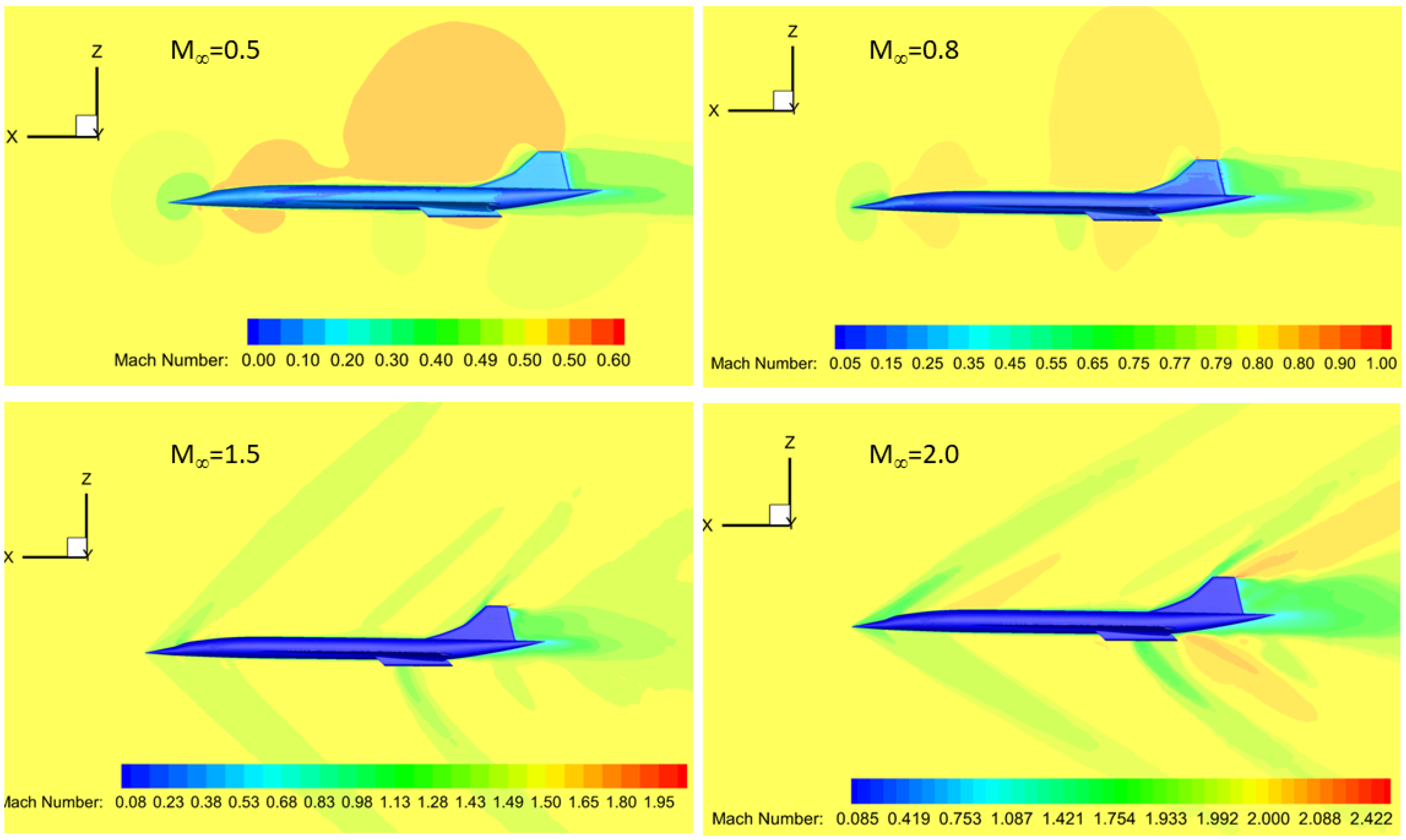
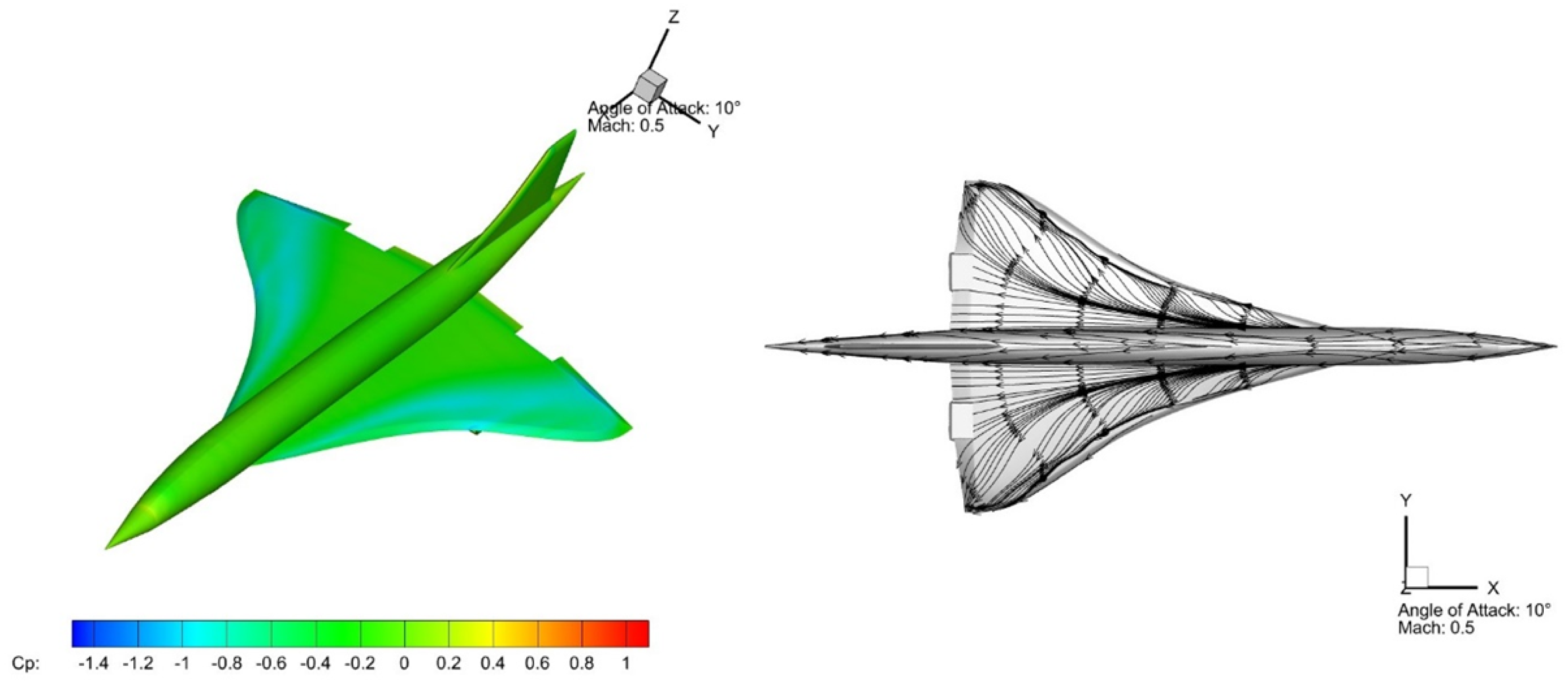
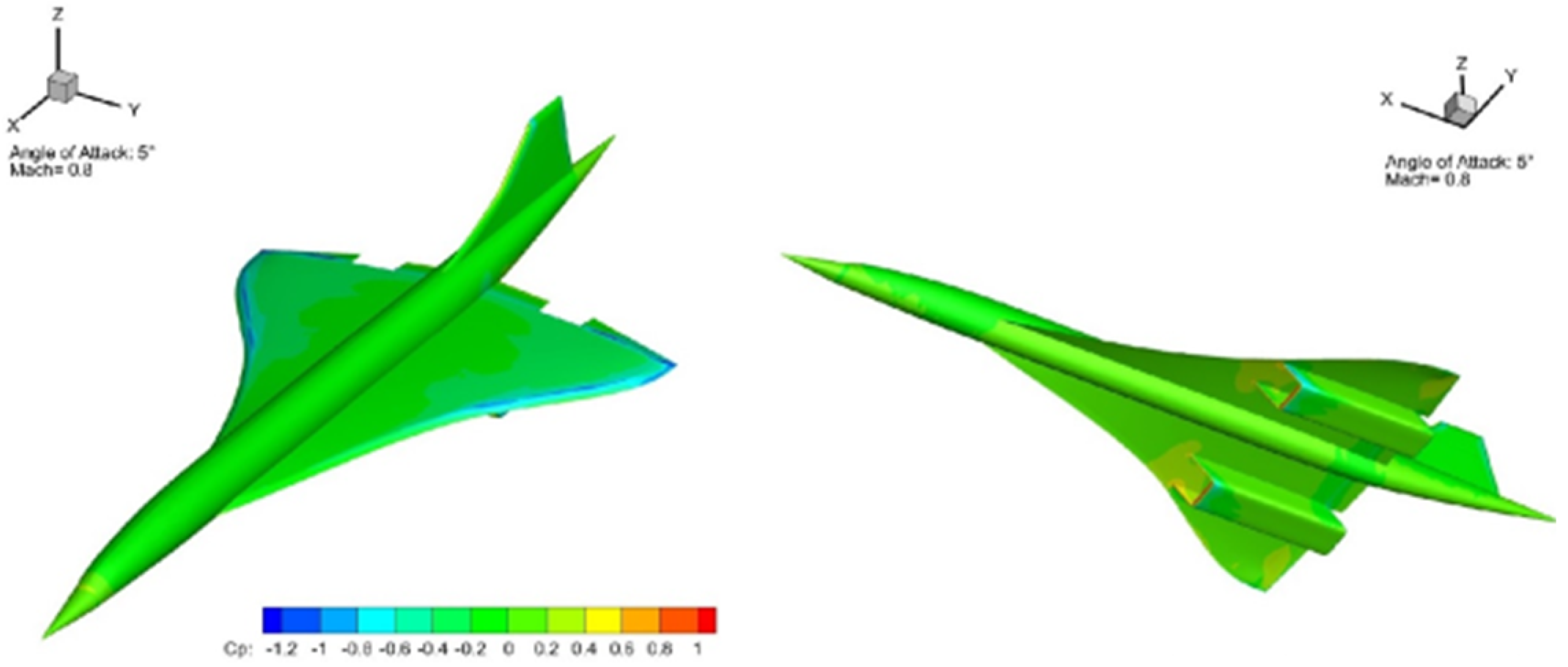

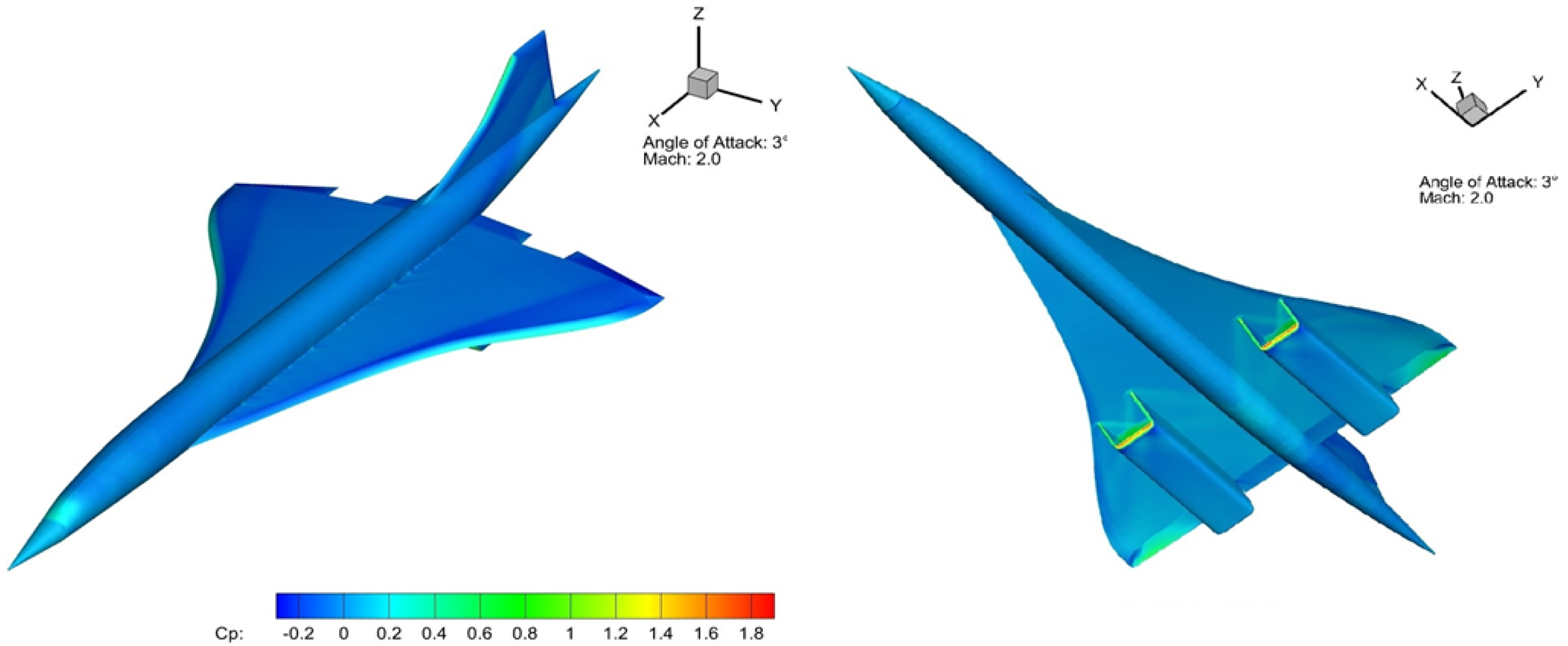
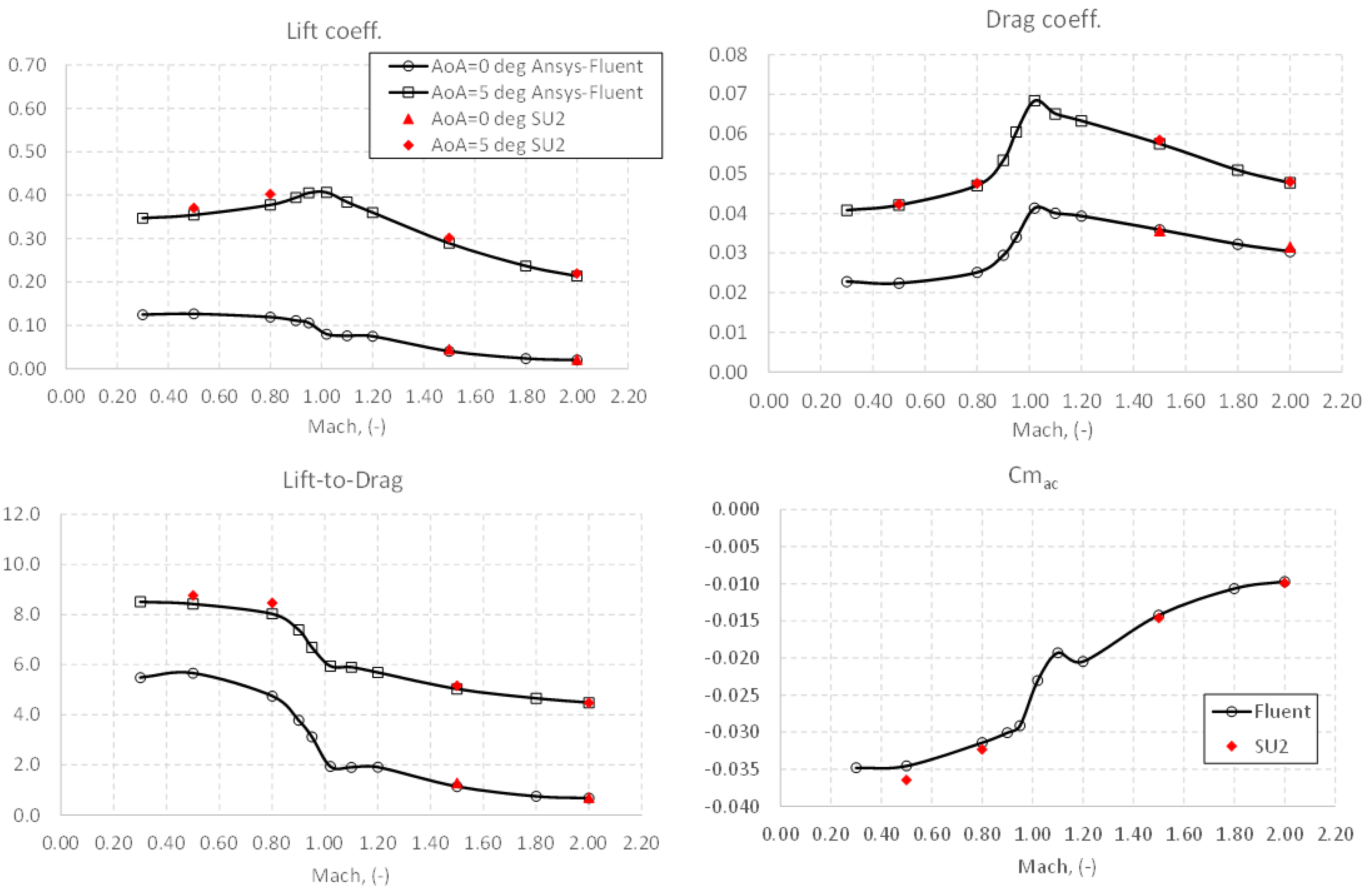
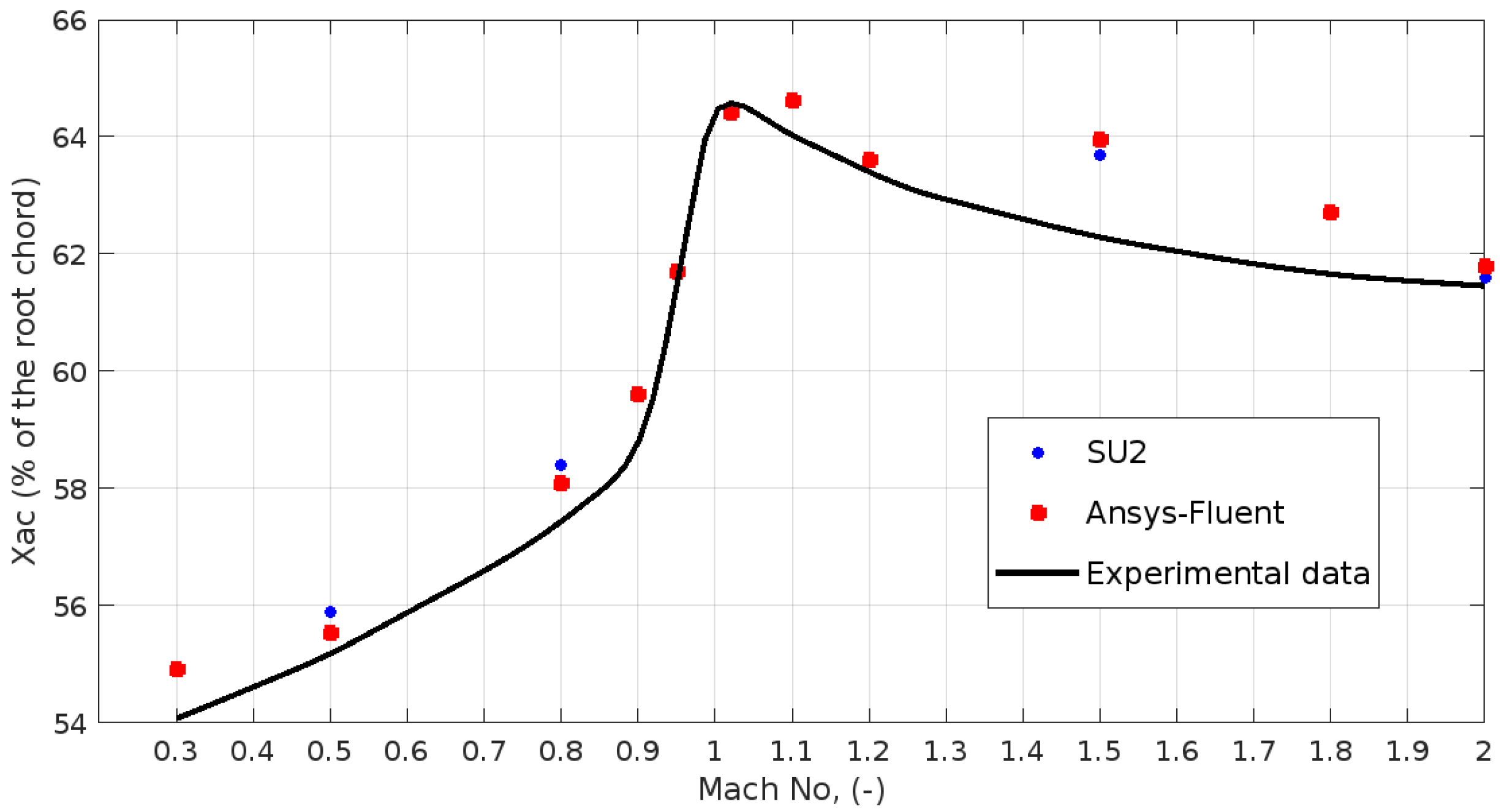
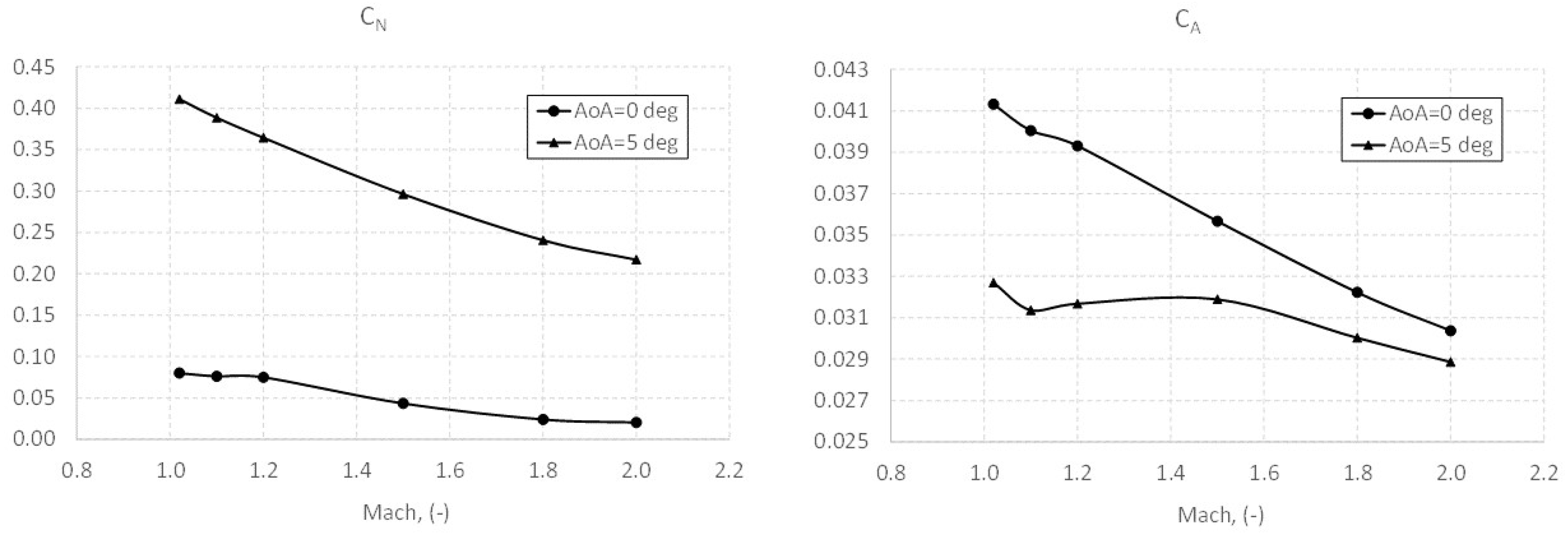
| Altitude | Pressure | Temperature | |||
|---|---|---|---|---|---|
| 0.24 | 1.60 | 0 | 0.030 | 100,965.40 | 287.95 |
| 0.24 | 1.60 | 5 | 0.030 | 100,965.40 | 287.95 |
| 0.24 | 1.60 | 10 | 0.030 | 100,965.40 | 287.95 |
| 0.50 | 3.12 | 0 | 0.349 | 97,202.10 | 285.88 |
| 0.50 | 3.12 | 5 | 0.349 | 97,202.10 | 285.88 |
| 0.50 | 3.12 | 10 | 0.349 | 97,202.10 | 285.88 |
| 0.80 | 3.18 | 0 | 5.090 | 53,402.00 | 255.09 |
| 0.80 | 3.18 | 5 | 5.090 | 53,402.00 | 255.09 |
| 0.80 | 3.18 | 10 | 5.090 | 53,402.00 | 255.09 |
| 0.90 | 2.91 | 0 | 7.080 | 40,645.40 | 242.13 |
| 0.90 | 2.91 | 5 | 7.080 | 40.645.40 | 242.13 |
| 0.95 | 2.81 | 0 | 7.940 | 35,961.00 | 236.60 |
| 0.95 | 2.81 | 5 | 7.940 | 35,961.00 | 236.60 |
| 1.02 | 2.81 | 0 | 7.940 | 35,961.00 | 236.60 |
| 1.02 | 2.81 | 5 | 7.940 | 35,961.00 | 236.60 |
| 1.10 | 2.56 | 0 | 10.070 | 26,154.20 | 222.70 |
| 1.10 | 2.56 | 5 | 10.070 | 26,154.20 | 222.70 |
| 1.20 | 2.61 | 0 | 10.660 | 23,872.10 | 218.86 |
| 1.20 | 2.61 | 5 | 10.660 | 23,872.10 | 218.86 |
| 1.50 | 1.01 | 0 | 18.288 | 7231.20 | 216.65 |
| 1.50 | 1.01 | 3 | 18.288 | 7231.20 | 216.65 |
| 1.50 | 1.01 | 5 | 18.288 | 7231.20 | 216.65 |
| 1.80 | 1.01 | 0 | 18.288 | 7231.20 | 216.65 |
| 1.80 | 1.01 | 5 | 18.288 | 7231.20 | 216.65 |
| 2.00 | 1.01 | 0 | 18.288 | 7231.20 | 216.65 |
| 2.00 | 1.01 | 3 | 18.288 | 7231.20 | 216.65 |
| 2.00 | 1.01 | 5 | 18.288 | 7231.20 | 216.65 |
| ANSYS-FLUENT | SU2 | |
|---|---|---|
| 0.24 | 0.5490 | - |
| 0.50 | 0.5552 | 0.539 |
| 0.80 | 0.5808 | 0.584 |
| 0.90 | 0.5960 | - |
| 0.95 | 0.6170 | - |
| 1.02 | 0.6440 | - |
| 1.10 | 0.6460 | - |
| 1.20 | 0.6360 | - |
| 1.50 | 0.6395 | 0.637 |
| 1.80 | 0.6270 | - |
| 2.00 | 0.6178 | 0.616 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aprovitola, A.; Dyblenko, O.; Pezzella, G.; Viviani, A. Aerodynamic Analysis of a Supersonic Transport Aircraft at Low and High Speed Flow Conditions. Aerospace 2022, 9, 411. https://doi.org/10.3390/aerospace9080411
Aprovitola A, Dyblenko O, Pezzella G, Viviani A. Aerodynamic Analysis of a Supersonic Transport Aircraft at Low and High Speed Flow Conditions. Aerospace. 2022; 9(8):411. https://doi.org/10.3390/aerospace9080411
Chicago/Turabian StyleAprovitola, Andrea, Oleksandr Dyblenko, Giuseppe Pezzella, and Antonio Viviani. 2022. "Aerodynamic Analysis of a Supersonic Transport Aircraft at Low and High Speed Flow Conditions" Aerospace 9, no. 8: 411. https://doi.org/10.3390/aerospace9080411
APA StyleAprovitola, A., Dyblenko, O., Pezzella, G., & Viviani, A. (2022). Aerodynamic Analysis of a Supersonic Transport Aircraft at Low and High Speed Flow Conditions. Aerospace, 9(8), 411. https://doi.org/10.3390/aerospace9080411