1. Introduction
With the advancement of space exploration leaving a substantial amount of large disused objects in orbit as well as the recently growing interest in extending the life of existing satellites by in-orbit servicing, the relevance of satellite robots capable of mechanically manipulating those orbiting objects is growing. The mitigation of space debris is an important priority of space exploration agencies [
1]. A collision of two objects in space above the size of approximately 10 cm is going to produce objects capable of causing further destruction of in-orbit equipment, producing again objects of a size sufficient to continue this perpetual destruction and littering. The highest risk is posed by large defunct satellites occupying important and populated orbits such as the geostationary or low Earth orbits [
2]. The successful interception of large objects in orbit opens possibilities to stop them from becoming dangerous space debris either by deorbiting them safely or extending their useful life by providing refueling or maneuverability. In either case, the success of the capture operation depends on the ability of the robotic arm to bring its end effector in contact with the object being captured and establish a mechanical connection between them.
The mechanical connection between the chaser satellite equipped with a robotic grappler arm and the intercepted object can be achieved by closing the grappler around a geometric feature of the target, e.g., a rim of separation ring [
3], or interlocking an expandable mechanical penetrator tip inside a sufficiently stiff opening, e.g., inside a thruster combustion chamber like in [
4]. The chaser and target velocities and angular rates will very likely vary since in many cases the target will be in an uncontrolled motion. This difference needs to be accounted for when coming into contact with the target, since it may cause abrupt forces to act on the gripping robot. A common method to manage such interaction as contact in robotic applications is the mechanical impedance control of the end effector with the use of a full robot dynamical model [
5], although other methods exist, most of which achieve the commanded impedance at the end effector by suitably controlling all the robot joints [
4,
5,
6,
7,
8]. The impedance matching to the target satellite was proposed as a means to shape the dynamic properties of the capturing robotic arm of the intercepting satellite [
4], and in a more recent study a frequency-independent method was proposed to match the velocity of the end effector and the target satellite, hence guaranteeing capture [
9]. The control of free-floating space manipulators using the Generalized Jacobian Matrix (GJM) has established history [
10,
11] and numerous applications, including optimization [
12] and control under nonlinear predictive control [
13], as well as evolution to multiple manipulators on a single satellite [
14]. The work on the application of impedance control to a satellite-based robot [
15] employs the GJM in the formulation of control, and while it approaches formulation of model-based impedance control, it focuses on the topics of computational complexity and uncertainty of the intercepted object. The approach to compliance control of the satellite manipulator using a force controller is proposed in [
16], but the concept of a compliant manipulator wrist is introduced in the work [
17]. The work does not focus on the manipulator architecture, but on the coefficient of restitution and its relationship with the impedance parameters as well as a method to establish desired impedance control parameters for attaining a controlled coefficient of restitution between the target and a robotic arm. Importantly, the verification work is carried out using a ground-based robot and a fixed wall as a target. The work [
18] discusses a combined method involving resolved motion rate control and admittance control for providing compliant contact control and shows simulation results for a 3-DoF (degree of freedom) robot capturing a rotating target body.
In the presented work, we perform a simulation study of the robot with an impedance-controlled prismatic joint at the end effector in a three-dimensional simulation of a 7-DoF free-floating robot and a free-floating target. The robot configuration used in this study is based on the 7-DoF configuration common in the European Space Agency’s projects [
19], although the method is applicable to any robot with six or more degrees of freedom. In our previous research we investigated free-floating robot manipulators where the impedance control law was incorporating the dynamic model of the manipulator [
20] involving all robot joints in the realization of the impedance control. This kind of control law allows the independent shaping of the mechanical impedance along each direction xyz in Cartesian space as well as the corresponding three torsional components. Observing that in the intercept missions the final approach and contact establishment between the end effector and the target usually happens along a single dominant direction of action, we analyze how a controlled impedance can be achieved along a single translational degree of freedom, while keeping the rest of the joints under classical position and velocity control, rather than torque control. In the case of space applications, where reliability and low complexity are highly valued design features, a simplification of the system while maintaining its key functionality is a useful gain. In order to account for the attitude change of the target, the work [
21] proposed a 2D contact model and dual manipulator setup. The presented work addresses the attitude tracking by separating the function of impedance control and orientation-position control into two separate control tasks. As a consequence, the complexity of the method is lowered in terms of computational requirements and by allowing the limitation of the necessity for high-bandwidth hardware needed for the impedance control to one prismatic joint. We simulate a free-floating robotic manipulator with a single impedance-controlled joint at the end effector coming into contact with a target body in a final approach maneuver scenario. We compare the resulting loads on the joints and the overall satellite disturbance with a full model-based impedance-controlled free-floating space robot in the same scenario. We then discuss the limitations and possibilities of such architecture in a practical setting. A similar architecture, i.e., using a prismatic stage at the end effector, was also proposed for a space manipulator, though one with a controlled base (non-free-floating) [
22], and not with a focus on simplification, but rather on introducing an additional layer of interaction between the robot pose control and impedance control. Our earlier work considered a two-dimensional simulation case of a robot with a prismatic compliant stage at the end effector focusing on disturbance to the base of the satellite [
23], whereas this work expands it to a three-dimensional case. In the work [
24], the authors considered stabilization of contact using position-based impedance control, which relies only on kinematic information about the space robot. The authors stressed the aspects of low computational complexity of the method.
The contributions of this work are the following: The distinction of the dominant direction of contact is made as a prerequisite for single-axis prismatic impedance control for providing control of an end effector in contact with the target body. The GJM is modified to include the prismatic stage at the end effector in the mathematical model of the free-floating robot and the simulation of the space robot with a prismatic impedance-controlled stage at the end effector is carried out in three dimensions, where both the robot and the target are free-floating.
The text is organized as follows: In
Section 2, the mathematical model of the system is elaborated.
Section 2.2 derives the equations of motion of the space robot and the model-based Cartesian impedance control law for a free-floating robot. The simplified architecture of a 7-DoF space robot with only one compliant joint is presented and described in
Section 2.8. In
Section 3, the simulation environment for the space robotics platforms is used to simulate two free-floating impedance-controlled robot architectures: the full model-based Cartesian impedance control from [
11] and the one based on a single-axis prismatic joint with impedance control. Both share the same GJM.
Section 4 discusses the results obtained with both approaches to impedance control and compares their performance and implementational complexity.
2. Mathematical Model of the Space Robot
In this section we derive the dynamics model of the free-floating robot manipulator. The logical steps we take are the following: First, in
Section 2.1 we start with a brief introduction to the nonholonomic nature of the robot system. Then, in
Section 2.2 we define the reference frames of the satellite with a robot manipulator.
Section 2.3 focuses on the description of the kinematics of such robot. In the
Section 2.4, the dynamics of the free-floating robot are derived by taking the following steps: in
Section 2.4, the dynamical model of a full, free-flying satellite-based robot is presented. The Free-flying robot is one which is mounted on a base equipped with actuators, e.g., thrusters [
25]. In
Section 2.4., we discuss the constraints of the robot having zero initial momentum and angular momentum which are then needed to reformulate the dynamical model of the satellite as a free-floating robot in
Section 2.4.2. This way, we obtain the free-floating robot dynamics equations where the state vector contains only the joint variables and is independent of the base coordinates. The gravity gradient effects, as well as orbital mechanics, solar wind pressure, residual atmospheric drag, etc., are ignored in the following analysis.
2.1. The Nonholonomic Nature of the Free-Floating Space Robot
The free-floating satellite equipped with manipulator arm exhibits nonholonomic properties as the angular momentum of the system consisting of the satellite and manipulator chain is not integrable [
25]. The presented control method does not address the nonholonomic aspects of the trajectory planning and tracking, unlike, e.g., [
26], but the simulation cases are selected such that the simulated trajectories are unlikely to evolve into singular ones.
2.2. Reference Frames in a Space Robot
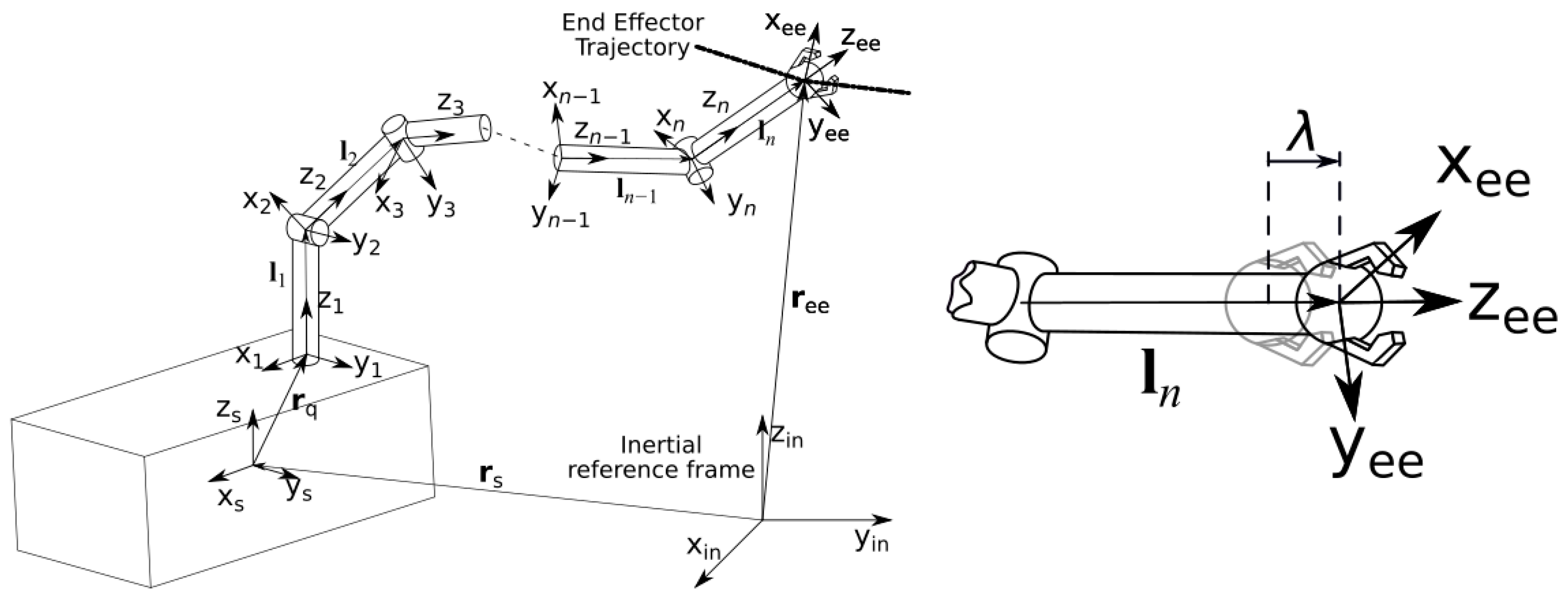
The satellite equipped with robotic arm is modelled as a multibody system. It is described using the coordinate systems depicted in
Figure 1.
2.3. Kinematics of the Free-Floating Space Robot
In this subsection, the standard description of the manipulator kinematic equations is recalled after [
10,
24].
In the inertial reference system, the satellite’s center of gravity position
is:
Its orientation
is expressed using Euler angles as follows:
The series-type manipulator with n rotational joints and a prismatic joint before the end effector is described by a vector of configuration variables corresponding to the angles of each joint
and the translational position of the slider in the prismatic joint
:
The vector of generalized coordinates
, describing the system of satellite base and manipulator, is assembled from definitions (1)–(3)
The differentiation of the state vector yields the following expression, where
transforms the angular velocities into the time derivatives of the Euler angles:
The symbol
vs is the satellite base velocity,
is its angular velocity,
is the vector of angular rates of the joint angles. The position vector of the end effector in the inertial frame is determined by the sum of positions of the links of the robot manipulator and the satellite position:
As depicted in
Figure 1. The
is the unit vector of the translation axis of the prismatic joint. By taking the time derivative of the expression for position vector, we arrive at the end effector velocity in the Cartesian inertial frame:
For an
i-th joint,
represents the unit vector of the rotation axis and
is its angular rate, while
represents the position of the ith kinematic pair. The angular velocity of the end effector is simply:
Having arrived at the kinematic expressions for the velocities, the model of dynamics of the satellite manipulator system can be formulated.
2.4. Dynamics of the Space Robot
This section introduces the dynamics of a full (non-free-floating) space robot without nonholonomic constraints. The reaction forces and torques acting on the system are the following:
where
and
are the forces and torques acting on the satellite base center of mass, e.g., from the thrusters. Vector
is the torques in the joints of the robotic arm. The generalized equations of motion for the satellite equipped with a robotic manipulator, using the Lagrangian equations of the second kind, take the following form [
11]:
The mass matrix
M [
10,
24] for the general case is:
The velocity-dependent effects are modelled by the Coriolis matrix which has entries with the following form [
27]:
where the
and
and the sub-matrices are defined below, with the tilde symbol ~ denoting a skew symmetric matrix of a vector and
Ii denoting the inertia matrices of each link.
I is an identity matrix of suitable size.
with
, where the
is the position of the center of mass of the
i-th link, while the
are the translational and rotational components of a standard Jacobian of the manipulator [
28,
29]:
In the architecture proposed in this work, the last joint before the end effector is prismatic; thus, including its effect in the Jacobian requires the use of the nonzero
term for this last joint, while in our previous work [
20] we considered impedance control of a free-floating manipulator with all rotational joints only.
2.4.1. Free-Floating Space Manipulator
In case of a free-floating manipulator system, being the scope of this research, the above formulations of the kinematics and dynamics equations change.
The manipulator’s angular momentum is described as follows:
with
L0 being the initial angular momentum and
P being the linear momentum for which the following relationship holds:
with
We consider a drift-less case; hence, the initial momentum and angular momentum above is zero. A different case is discussed in [
30]. The system is free floating; hence, the Equation (21) is equated to zero. The relationship between the angular velocities of the joints of the space robot and the linear and angular velocity of the end effector
are given by:
where finally the Generalized Jacobian Matrix GJM emerges as
JDThe Jacobian
JM is a standard manipulator Jacobian mentioned earlier and the satellite Jacobian
JS is defined as below, with
being the end effector position with respect to the satellite:
2.4.2. Dynamics of the Free-Floating Manipulator
The center of mass of the satellite-arm system remains constant under the assumption of no momentum exchange with the environment and by neglecting the orbital motion, but the base is free to change its orientation and position in the inertial reference frame. In such a case, the state vector
in (4) contains only the joint positions.
The vector of generalized forces becomes:
By using the approach used in the paper [
17] and using constrained Lagrangian formulation, the mass matrix becomes:
2.5. The Impedance Control
Impedance control [
4,
5,
6,
7,
8,
11,
22,
31] is a paradigm which aims to achieve desired characteristics of the interaction between the robot and its environment. It draws from the long-recognized analogies between electrical and mechanical building blocks of dynamic systems and became an important toolbox for modeling robotics interacting with environments and humans, cooperative robotics, exoskeletons, etcetera. Impedance describes the dynamic behavior of the system at its interaction port with the environment which is the end effector in the case of most robotic manipulators.
The impedance is fundamentally a relationship between the input “flow variables”
such as velocity or electric current and output “effort variables”
—force or voltage. In the Laplace domain this can be written as the following ratio:
Since most robotic tasks involving interaction with an environment are naturally defined in coordinates relative to the environment, it is useful to replace the
with relative displacement
. Specifically, the relative displacement is understood as the difference between the current actual position of the interaction port
X relative to the intended one, often referred to as the “virtual” trajectory
X0 [
5].
The virtual trajectory is useful in its generality since it can be defined in terms of position space, as well as velocity or acceleration spaces and need not be within the reachable space of the manipulator [
5]. In a basic form, the mechanical impedance is typically described to be composed of elements which exhibit an inertia-like or mass-like behavior, represented below as matrix
Md, with damping-like behavior described by
D and elastic-like behavior described by matrix
E.
Substituting (31) and (32) into (30), rearranging terms and taking the inverse Laplace transform gives the time-domain differential equation describing the interaction point forces
F as a function of the difference between current and virtual trajectory, parametrized by the desired inertia parameters:
The above basic formulation of a generic impedance control law can be described from the point of view of the environment as “hiding” the natural dynamics of the manipulator and exposing only the desired dynamics at the interaction port. At the implementation level, there are numerous ways by which the dynamic behavior of the robot’s interaction port can be shaped. There exist purely mechanical methods such as springs and dampers or exploiting the redundancies of the manipulator to achieve different inertial properties by the virtue of their dependence of the manipulator’s configuration [
5,
31]. The software-based methods rely on using control strategies which reproduce the dynamic behavior with robot’s actuators based on the loop closed via sensors. Three important types of software approaches to impedance implementation are [
6]:
- -
Position-based approach, where typically the controller’s outer loop gives the desired position based on the desired impedance parameters and feedback information about interaction force, and the inner loop tracks the position simply as a position servo,
- -
Torque/force-based approach, where instead of the position, the outer loop commands the torque or force and the inner loop is the torque/force servo.
- -
Model-based approach, which fundamentally differs from the previous two, because it uses the known manipulator dynamics and substitutes into it the desired dynamics described by the impedance parameters.
An exhaustive discussion and comparison of the above methods is presented in [
6]. In this work, we propose the use of a Cartesian, model-based impedance controller to a space robot on a free-floating satellite platform.
2.6. Cartesian Impedance Control
In this section we briefly recall the Cartesian impedance control after [
5,
31] and show how the dynamics model of the free-floating satellite robot is incorporated into the control law. We, with a slight abuse of the notation, reuse the symbol
in this section to symbolize a vector of rotational configuration coordinates of a robot with purely rotational joints, whereas outside of the description of model-based Cartesian impedance control, this symbol retains its meaning set in
Section 2.3.
General robotic manipulator dynamics are modeled by the configuration-dependent inertia
, configuration- and velocity-dependent inertial coupling between the links, e.g., Coriolis and centrifugal effects
, and
the velocity-dependent terms, e.g., the viscous friction. There, static forces
such as gravitational loads are assumed to be zero, since the application we are discussing is set in the microgravity context of an on-orbit operation. The manipulator control torques are denoted as
Tact and
Tint, and
Fint are the torques and force due to interaction at the interface.
The desired behavior in Cartesian space can be expressed as follows:
Note, however, that in this case, the impedance control is achieved with rotational joints only, and the Jacobian does not include any terms other than rotational. With use of the standard manipulator Jacobian, the transformation between the Cartesian and joint space is as follows:
The Cartesian impedance control law takes the form:
2.7. Free-Floating Platform-Based Space Robot under Cartesian Impedance Control
In the case of the free-floating satellite platform equipped with a robotic manipulator, the Jacobian in (34)–(39) is replaced with its dynamic counterpart given by (25). The mass matrix (29) encodes the configuration-dependent inertial properties of the manipulator and base. Combining the above, we arrive at the following expression:
The equation relates the driving torques Tact of the joints to the end effector’s deviation from the virtual trajectory, parametrized by desired impedance terms, in essence expressing the Cartesian impedance control law for the robot on a free-floating satellite base.
2.8. The Simplified Robot Architecture with Controlled Impedance on a Single Axis
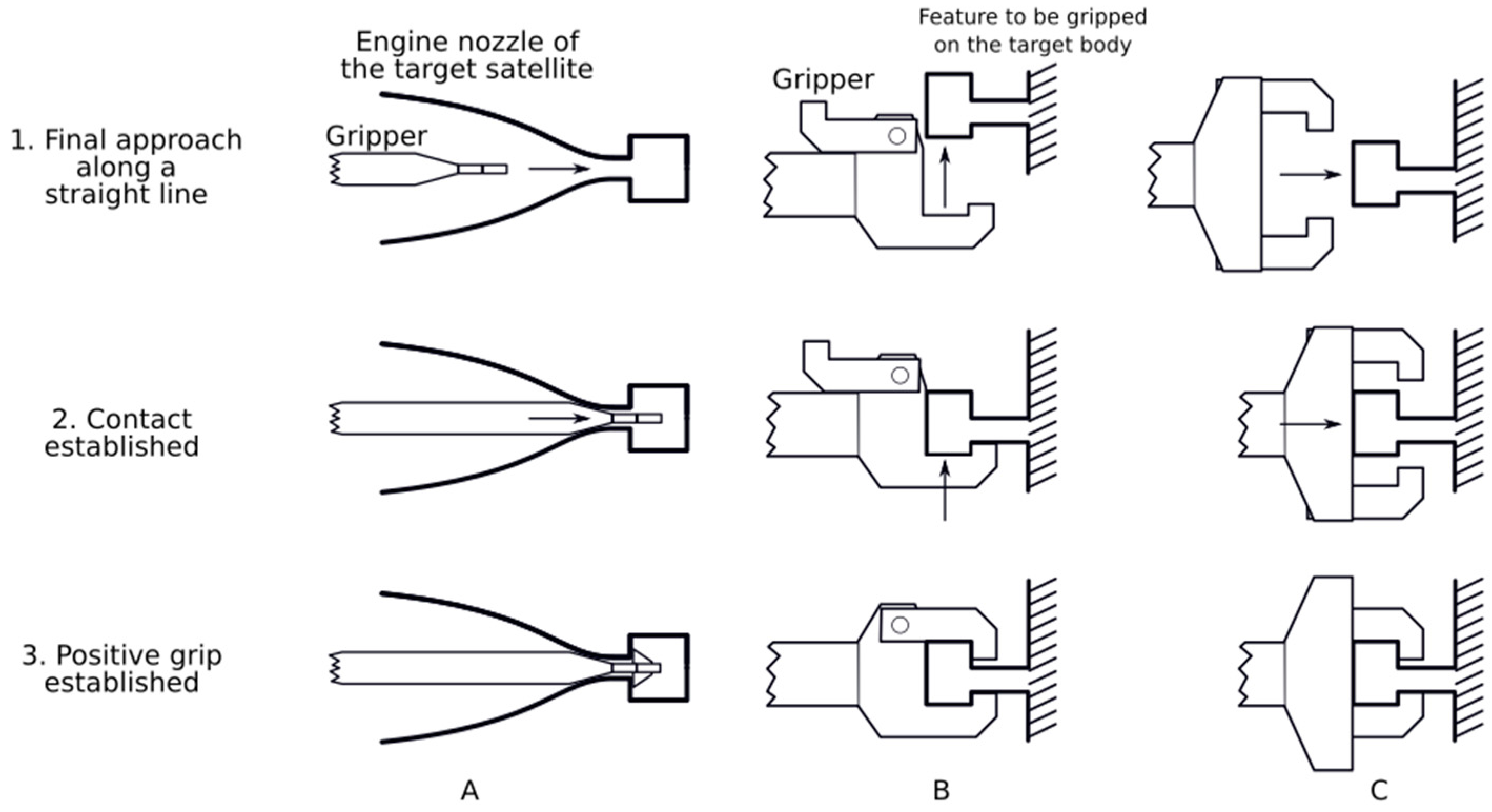
During the last part of the intercept maneuver when the gripper is closing, the controlled impedance of the end effector shall maintain stable contact with the target feature. Typically, the chaser and target satellite will be moving with respect to each other, and as a consequence there will be a dominating direction along which the displacement of the contact point will take place throughout the time required for closing the gripper. Simplified illustrations of various gripping scenarios of in-orbit intercept are shown in
Figure 2. Scenario A is applicable to many defunct satellites equipped with maneuvering and orbit-correction engines [
5], which is typical for large geostationary communication and meteorological and observational missions. Scenario B is a simplified illustration of a clamping gripper locking on a feature from a side, like the docking gripper for locking on a satellite’s separation ring [
3]. The scenario C depicts a symmetrically acting gripper, similar to the one from e.Deorbit project [
19]. In case of a tumbling target satellite, the dominant direction will be collinear with the vector of a momentary linear velocity of the feature to be gripped. Assuming that this dominating direction can be tracked with the end effector orientation control, so that the gripper center point stays on the line and the gripper orientation with respect to the feature to be gripped is kept constant throughout the final approach and gripping phase, it is sufficient that the compliance due to impedance control is present only in the axis of the dominant direction.
The mechanical impedance control presented in previous sections allows the shaping of the end effector’s impedance properties along Cartesian axes independently. The control law involves interface forces as seen Equation (40). In a practical setting, those forces and torques need to be measured by a hardware sensor and appropriately conditioned. This adds complexity to the spaceborne hardware of the robot. The whole control loop, including calculation of the torques and generation of the appropriate currents in the motors in each joint, needs to be fast to cope with the dynamics of the contact. Calculation of the torques with the control law (40) requires numerous multiplications of 6 × 6 and 6 × 7 matrices by the control computer, which needs to provide adequate processing power to meet the timing requirements.
By using a single prismatic impedance-controlled joint, like the one discussed in [
32], as the last joint before the end effector, a controlled mechanical impedance along the dominant direction of the contact can be achieved and the hardware and control laws of the whole free-floating space manipulator can be substantially simplified. Although this joint provides an additional degree of freedom and can be incorporated into the GJM by translational term in a construction of the Jacobian, its primary objective is to provide space for the compliant behavior of the mechanical impedance, not to play any major role in the planning or realization of a trajectory.
The single-degree-of-freedom impedance control of the prismatic joint can be expressed as a scalar version of Equation (33), where the displacement
x and virtual trajectory
x0 are expressed as positions in the direction collinear with
in terms of
in such a way that the point
lies in
x0 and
is in line with the dominant direction of the final approach and contact:
This way, the impedance control law does not involve the whole state vector of the robot, only the prismatic stage. Defining the impedance control law in the above way is useful for practical applications, e.g., involving an electromagnetic linear actuator, where the force
after scaling by a motor force constant becomes the immediate input for the actuator’s quadrature current controller [
32].
The realization of the virtual trajectory and keeping the kprism oriented along the dominant direction of the approach can be conducted using known strategies for the joint control of a free-floating space robot, which require less calculation effort than the model-based impedance control. One example of such control methods is the Cartesian joint control based on the GJM presented in the following subsection.
2.9. Basic Cartesian Controller for Free-Floating Robot
A simple control strategy for a trajectory-following task in Cartesian coordinates can be realized for a space robot using the GJM. This strategy can be used to bring the end effector to follow the virtual trajectory required by the impedance control.
The dynamic Jacobian relates the velocity space to joint space, so a simple controller computing the joint velocities as given by the Equation (24). It can be used to find joint velocities
, minimizing the deviation
ev between the intended and actual velocity as follows:
Since the planned virtual trajectory of the end effector,
, is typically not defined in the velocity space but rather in the position space, we use the approximation of the velocity error
ev by the position error
, where
xc is the current EE position, multiplied by some gain matrix
Gee. The joint control torques defined by the simple Cartesian trajectory-following controller are given by:
where
is the gain matrix converting the difference between
and current joint angular velocities
to the control torque.
Variable Impedance
The impedance parameters,
, do not need to be constants. Their values may be varied over the course of the maneuver to the required values. A useful case for varying the impedance is the following: during the initial approach phase when the chaser satellite is closing in on the target and moving the manipulator arm into the position of readiness to start the final approach, the end effector’s inertia experienced by the rest of the manipulator and base should be minimized. This would be achieved by fully retracting the prismatic stage, e.g., by keeping
x0 at a value corresponding to a fully retracted state, and setting the
to very high impedance. The prismatic stage should then be extended by setting new
and thus
, to prepare it for being compressed after coming into contact with the target. Shortly before the end effector comes into contact with the target, the impedance parameters,
, should be set to values suitable for the given target, e.g., using the virtual mass impedance matching (VIM) method for mechanical impedance matching [
17] or other methods, e.g., [
9]. Finally, once the positive gripping is confirmed, the impedance can be further changed to meet the requirements of post-capture activities, e.g., rigidizing it to bring the target and chaser relative velocity to zero [
19], detumbling or docking.
4. Discussion
The parameters which were used for the comparison of the performance of the two schemes were the following:
The torque magnitudes are plotted in
Figure 4. In the model-based impedance control they were on the same order of magnitude as in the case with a single prismatic impedance-controlled joint, i.e., 10
0…10
−1 Nm for joint 1 and 10
−1…10
−2 Nm for the subsequent joints although on average the loads on the joints were on average 38% higher for the proposed architecture. The peak torques in the joints are summarized in
Table 2. Importantly, the torque about joint 2 was 67 × 10
−3 Nm for the proposed architecture with the prismatic impedance-controlled joint instead of 4 × 10
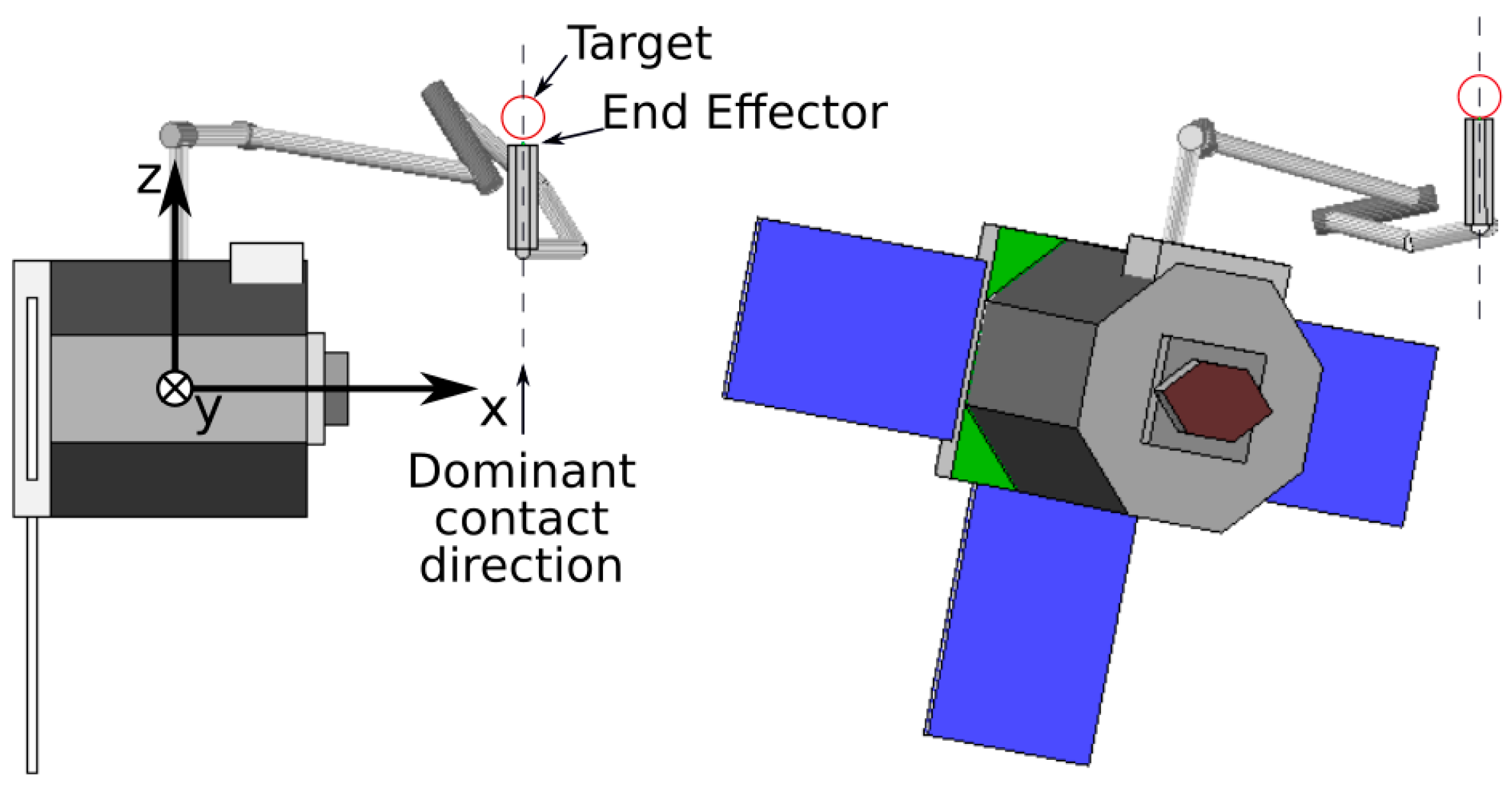
−2 Nm in the case of the baseline model-based impedance control. In the pose which the robot had during the contact (
Figure 3), the torque on this joint acted about axis close to the y-axis of the base, and was significantly contributed to by the contact force via the long “lever arm” of the whole manipulator. The 40% lower torque on joint 2 in the case of the proposed impedance controller translated to a much lower disturbance of the base about the y-axis: 24 × 10
−3 °/s with the proposed control instead of the −6 × 10
−2 °/s with the baseline impedance control. The reason for this behavior is the following: in the case of the baseline controller, where all the joints took part in realizing the impedance control behavior at the end effector, the masses and inertias of all the links preceding the end effector needed to be suitably accelerated, while in the case of the proposed architecture, in principle, just the mass of the end effector needed to be accelerated to realize the impedance behavior of the end effector.
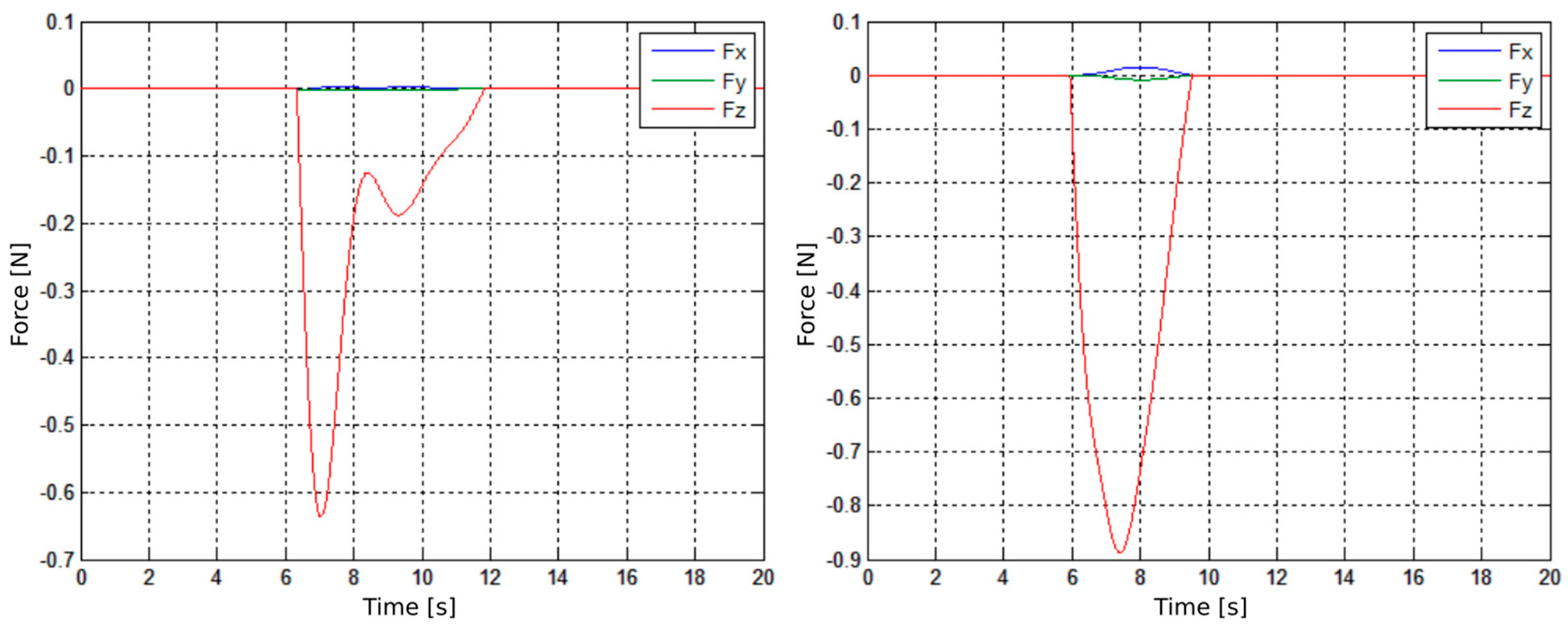
The contact force magnitude was higher in the case of a prismatic joint case (−0.89 N rather than −0.63 N in baseline case), but also the contact was shorter: 1.8 s for the prismatic impedance-controlled joint architecture vs. 2.8 s for the baseline, as depicted in
Figure 5. The disturbances of the base of the free-floating robot in both cases are compared in
Table 3. The disturbance was higher under the Cartesian control with a prismatic impedance-controlled joint, in the sense that its center of mass came out of the maneuver moving and rotating faster.
The impedance parameters selection and optimization could likely lead to closing the gap between the sets of results eventually. Rather than elaborating on the impedance parameters selection method, the purpose and scope of this work was to verify the possibility of replacing the full robot model-based impedance control with the simplified scheme for the free-floating robot. The initial expectation was to arrive with the prismatic joint approach at the same order of magnitude of the joint torques, contact force and base disturbance as in the full model-based impedance control of the robot. Even without more accurate impedance parameters selection, the results met that criteria.
The potential technical benefit of the approach based on a single prismatic impedance-controlled joint to provide tunable compliance at the end effector in contact with a target body is twofold: Firstly, the overall computational effort is lower. Both methods require computation of inverse of the generalized Jacobian matrix and keeping it updated throughout the maneuver since it is present in both the model-based control law (40) and in the simple Cartesian joint controller (43) used to follow the virtual trajectory with the prismatic impedance-controlled joint. Nonetheless the control law (40) also requires the computing and inverting of the instantaneous mass matrix, and four more matrix multiplications. Secondly, the full model-based impedance control also requires a current, measured value of the forces and torques at the interface between the end effector and the target , a rather significant complication for the gripper to be designed for reliable operation in space. The impedance control of the single axis actuator, however, requires a positional feedback. This type of a sensor is not free of its own drawbacks, in particular the noise increased by taking the derivatives of its signal, but still some type of position feedback is required for all the joints of the robot in any case.