Numerical Solution for the Single-Impulse Flyby Co-Orbital Spacecraft Problem
Abstract
:1. Introduction
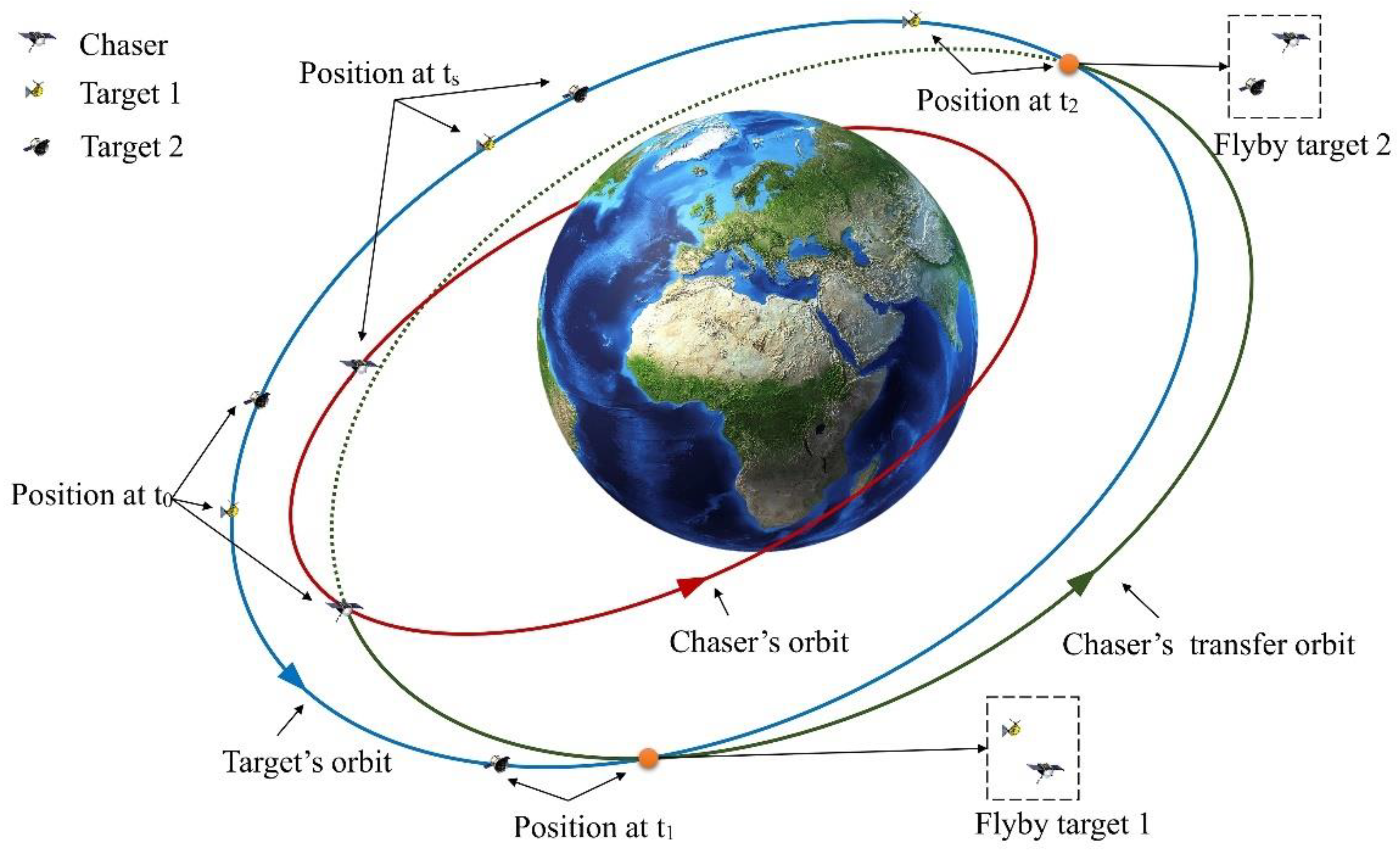
2. Description of the Problem
3. Mathematical Formulation of the Problem
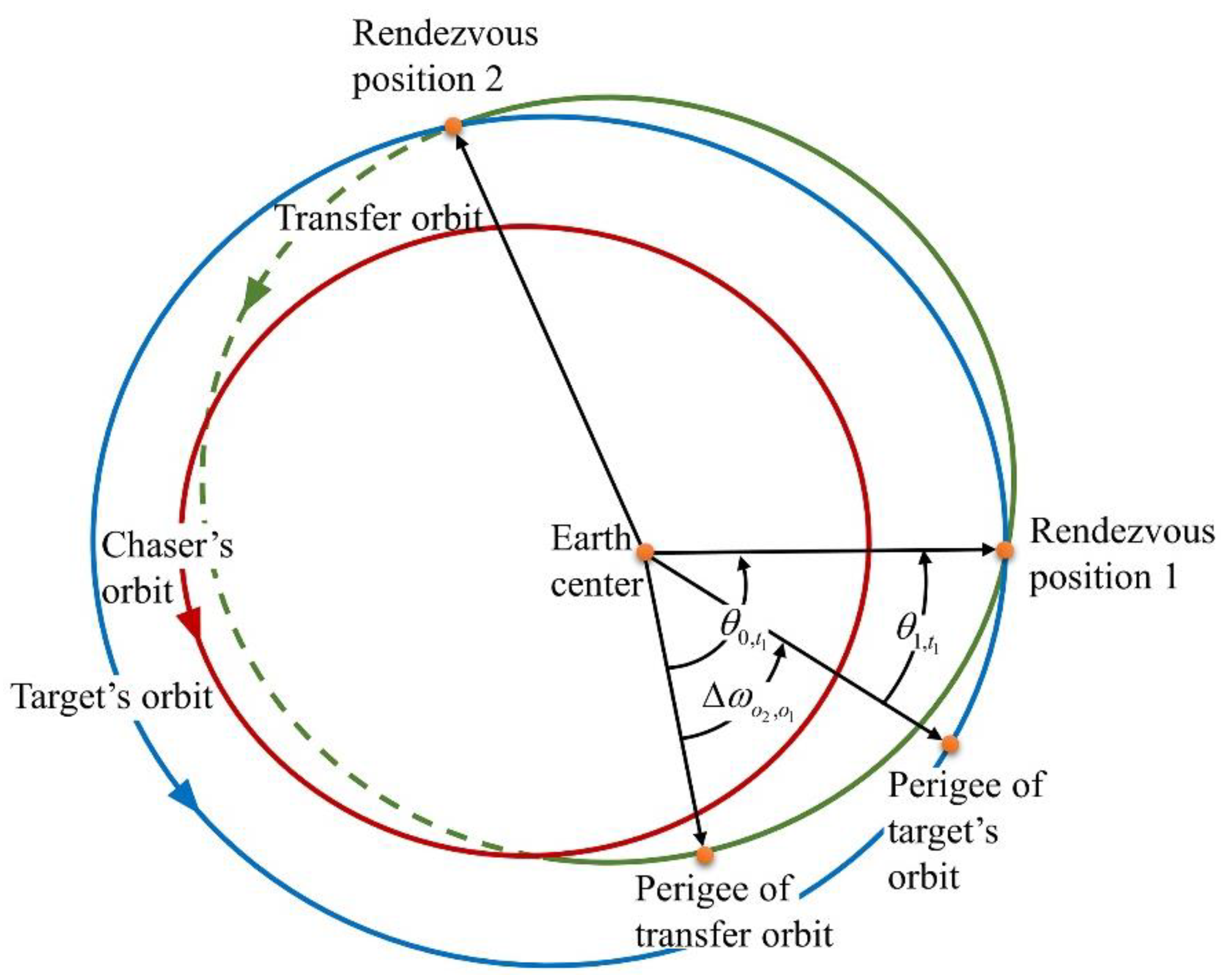
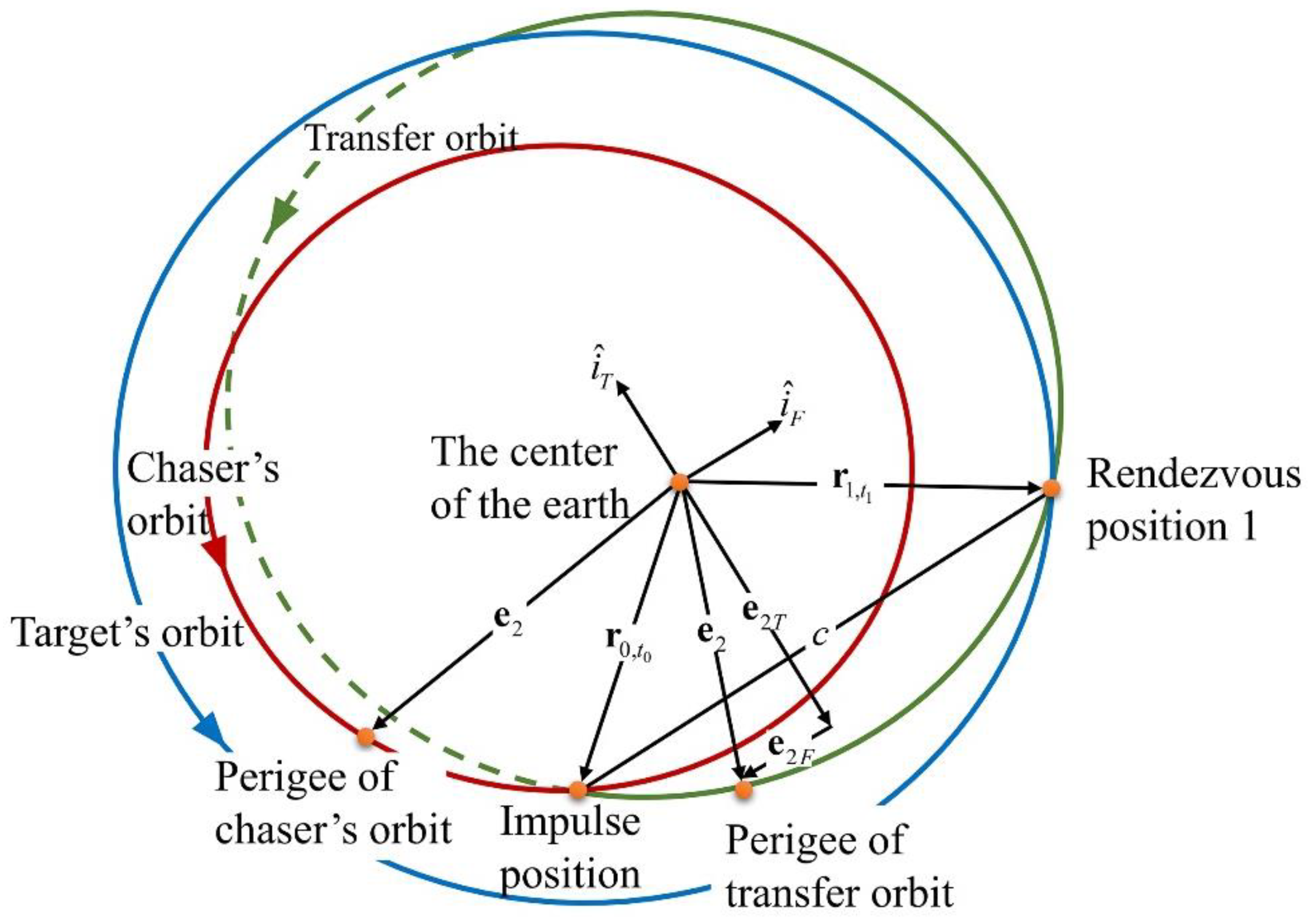
3.1. Nonlinear Equations for Terminal Constraints
3.2. Nonlinear Equations for Coplanar Lambert Problem
4. Numerical Method without Derivation for the Two Equations
4.1. Solution of Lambert Problem without Derivation
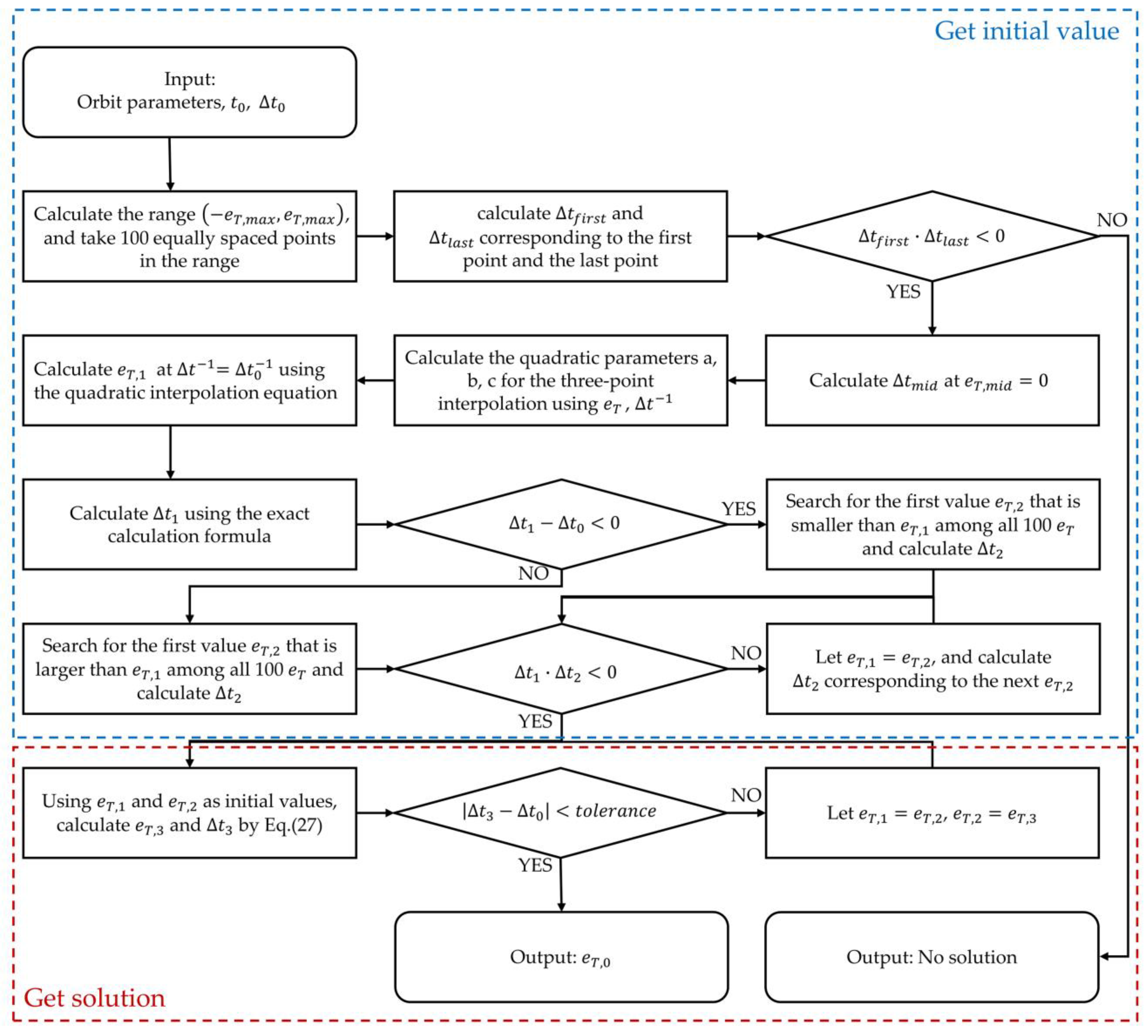
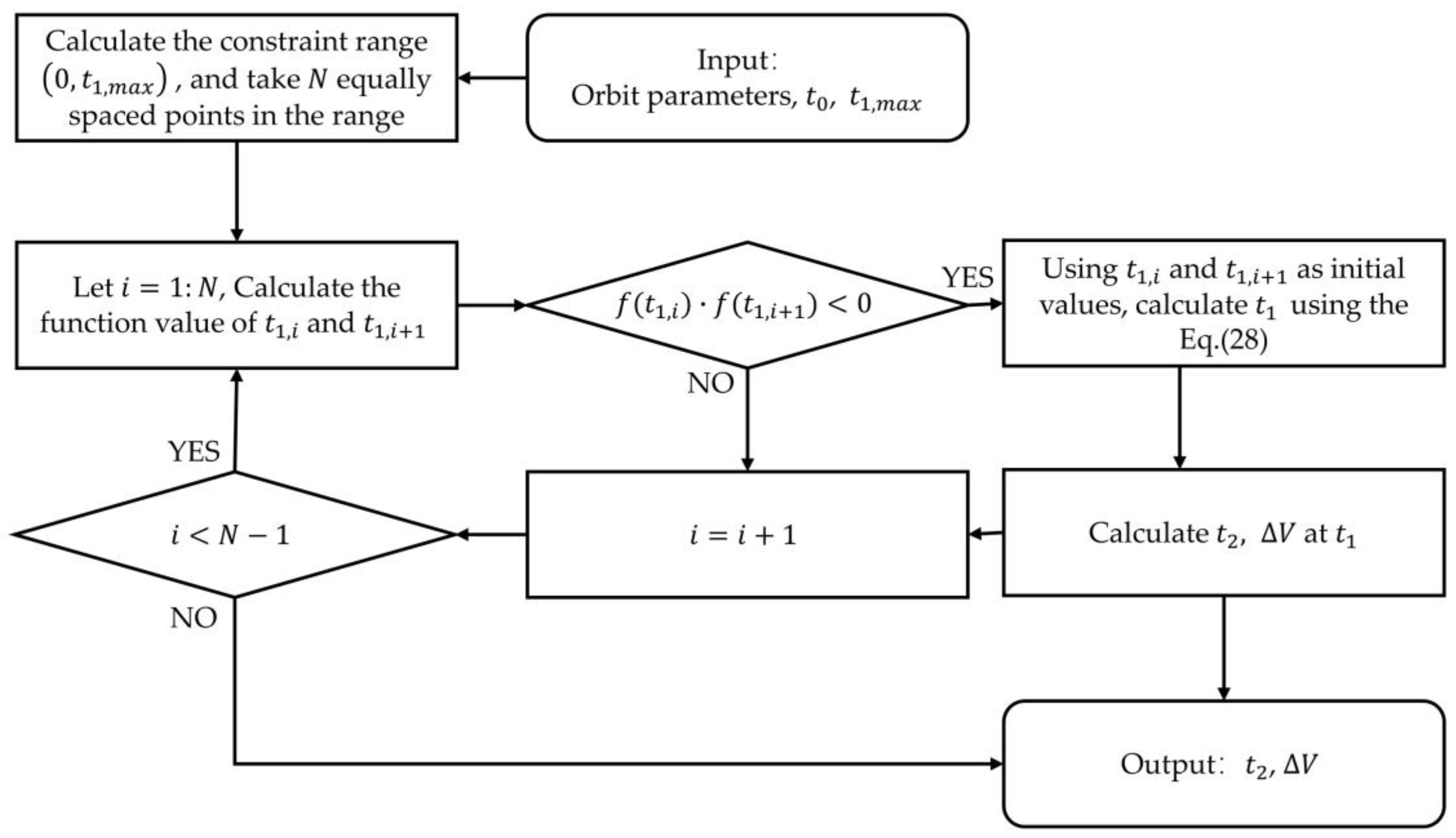
4.2. Solution of Single-Impulse Flyby Two Co-Orbital Spacecraft Problem without Derivation
5. Numerical Examples
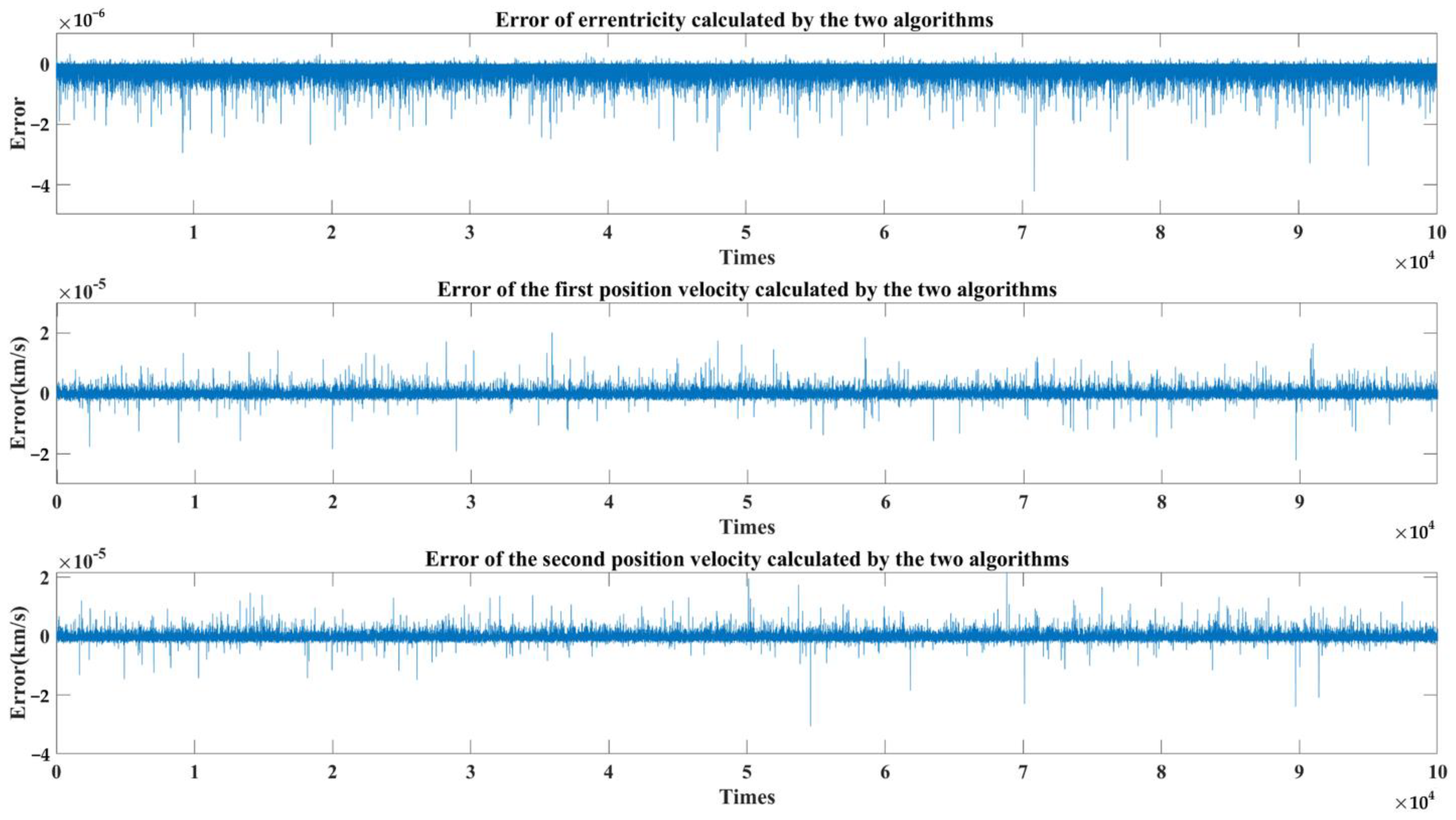
5.1. The Lambert Problem
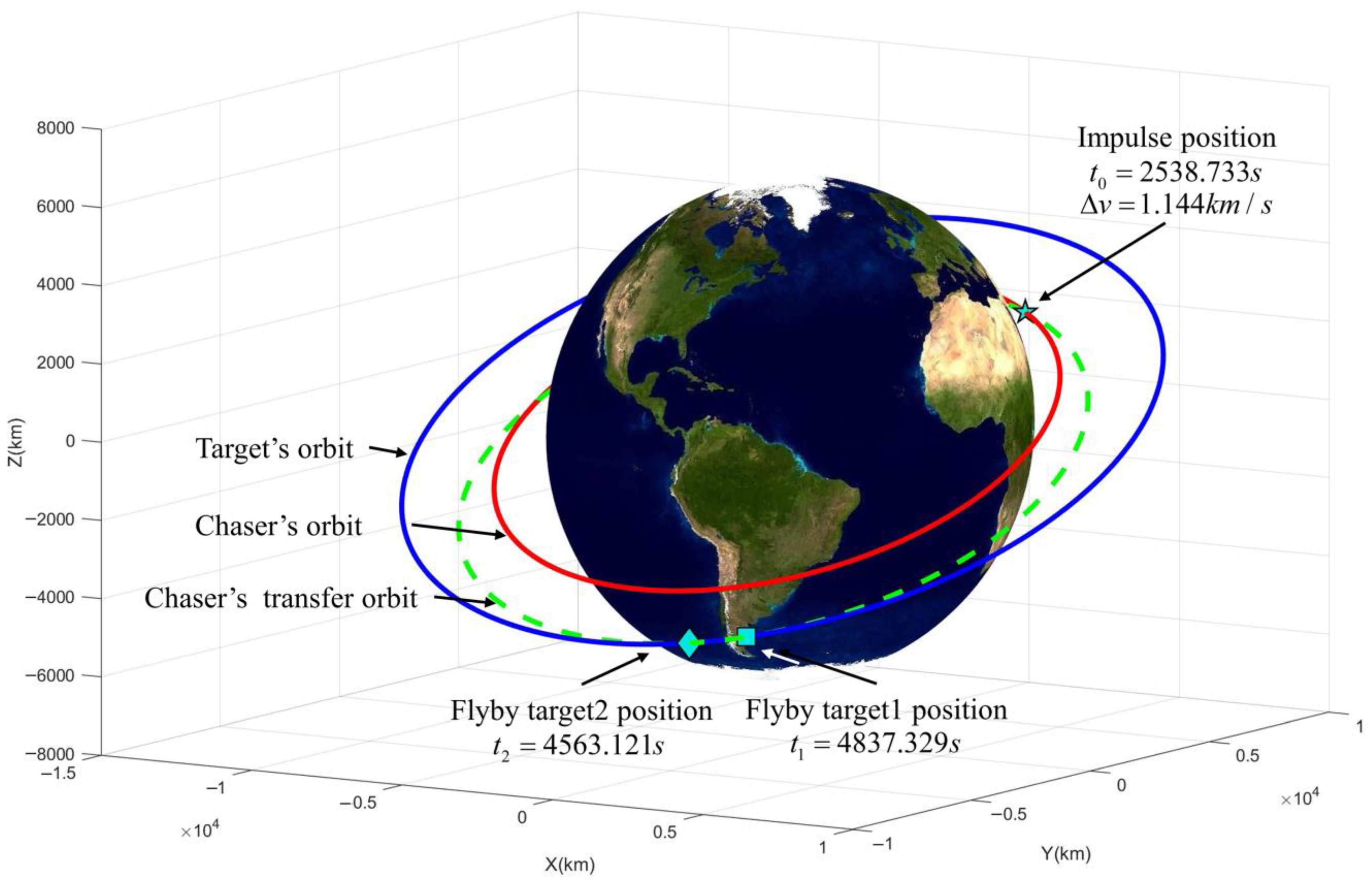
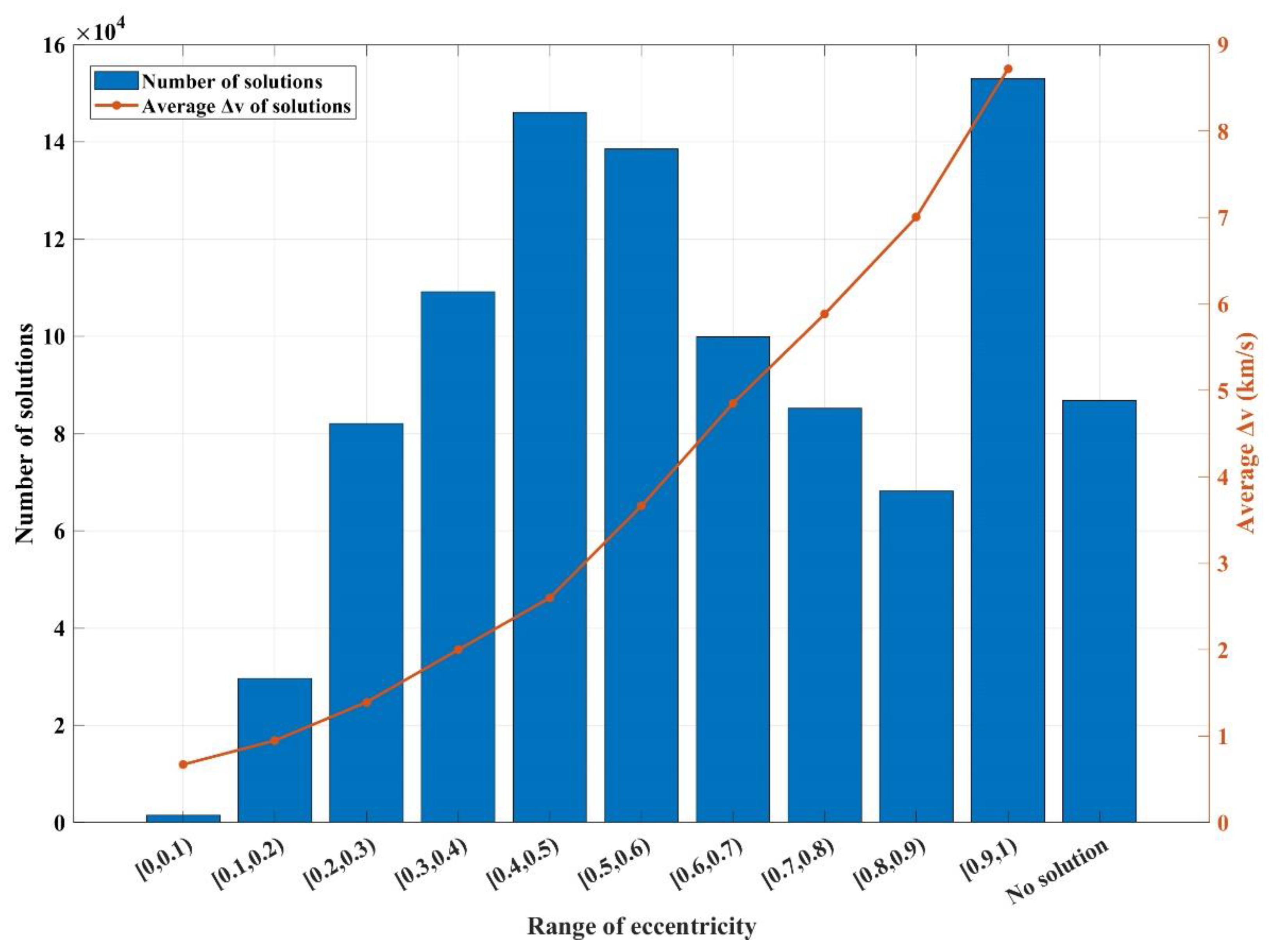
5.2. The Single-Impulse Flyby Co-Orbital Spacecraft Problem
Random Initial Orbital Elements
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Glossary
| Length of the transfer chord | |
| Eccentricity vector of orbit | |
| Eccentricity of orbit | |
| Perpendicular component of the transfer chord | |
| Parallel component of the transfer chord | |
| Mean anomaly of spacecraft at time | |
| Mean motion of orbit | |
| Semi-latus rectum of orbit | |
| Position of spacecraft at time | |
| Distance between spacecraft and earth center at time | |
| Anomaly of spacecraft at time | |
| Perigee of orbit | |
| Angle between perigees of two orbits (from to ) |
References
- Osoro, O.B.; Oughton, E.J. A Techno-Economic Framework for Satellite Networks Applied to Low Earth Orbit Constellations: Assessing Starlink, OneWeb and Kuiper. IEEE Access 2021, 9, 141611–141625. [Google Scholar] [CrossRef]
- Shank, K.S.H. Fidelity and utility of GPS loggers as a tool for understanding community participation of older adults. Scand. J. Occup. Ther. 2022, 29, 282–292. [Google Scholar] [CrossRef] [PubMed]
- Toh, J.-J. A Consider on Trend of GPS-based Investigation in Some Countries. Ajou Law Rev. 2021, 15, 267–289. [Google Scholar] [CrossRef]
- Wu, M.K.; Luo, S.; Wang, W.; Liu, W.K. Performance Assessment of BDS-2/BDS-3/GPS/Galileo Attitude Determination Based on the Single-Differenced Model with Common-Clock Receivers. Remote Sens. 2021, 13, 4845. [Google Scholar] [CrossRef]
- Zhang, J.J.; Li, J. Development and Application of Big Data in the Field of Satellite Navigation. Wirel. Commun. Mob. Comput. 2021, 2021, 12. [Google Scholar] [CrossRef]
- Farhangian, F.; Landry, R. Multi-Constellation Software-Defined Receiver for Doppler Positioning with LEO Satellites. Sensors 2020, 20, 5866. [Google Scholar] [CrossRef]
- Peng, C.Y.; Zhang, J.; Yan, B.; Luo, Y.Z. Multisatellite Flyby Inspection Trajectory Optimization Based on Constraint Repairing. Aerospace 2021, 8, 274. [Google Scholar] [CrossRef]
- Englander, J.A.; Vavrina, M.A.; Hinckley, D. Multi-Objective Hybrid Optimal Control for Multiple-Flyby Interplanetary Mission Design using Chemical Propulsion. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Vail, CO, USA, 11–13 August 2015; pp. 2333–2352. [Google Scholar]
- Bull, R.; Mitch, R.; Atchison, J.; McMahon, J.; Rivkin, A.; Mazarico, E. Optical Gravimetry mass measurement performance for small body flyby missions. Planet. Space Sci. 2021, 205, 20. [Google Scholar] [CrossRef]
- Celik, O.; Dei Tos, D.A.; Yamamoto, T.; Ozaki, N.; Kawakatsu, Y.; Yam, C.H. Multiple-Target Low-Thrust Interplanetary Trajectory of DESTINY+. J. Spacecr. Rocket. 2021, 58, 830–847. [Google Scholar] [CrossRef]
- Tang, X.; Ye, D.; Huang, L.; Sun, Z.W.; Sun, J.Y. Pursuit-evasion game switching strategies for spacecraft with incomplete-information. Aerosp. Sci. Technol. 2021, 119, 20. [Google Scholar] [CrossRef]
- Wen, C.X.; Zhao, Y.S.; Shi, P. Derivative Analysis and Algorithm Modification of Transverse-Eccentricity-Based Lambert Problem. J. Guid. Control Dyn. 2014, 37, 1195–1201. [Google Scholar] [CrossRef]
- Pan, B.F.; Ma, Y.Y. Lambert’s problem and solution by non-rational Bezier functions. Proc. Inst. Mech. Eng. Part G-J. Aerosp. Eng. 2018, 232, 227–245. [Google Scholar] [CrossRef]
- Zhang, G. Terminal-Velocity-Based Lambert Algorithm. J. Guid. Control Dyn. 2020, 43, 1529–1539. [Google Scholar] [CrossRef]
- Thompson, B.F.; Rostowfske, L.J. Practical Constraints for the Applied Lambert Problem. J. Guid. Control Dyn. 2020, 43, 967–974. [Google Scholar] [CrossRef]
- Chen, H.; Han, C.; Rao, Y.R.; Yin, J.F.; Sun, X.C. Algorithm of Relative Lambert Transfer Based on Relative Orbital Elements. J. Guid. Control Dyn. 2019, 42, 1413–1422. [Google Scholar] [CrossRef]
- Yang, H.W.; Li, S. Fuel-Optimal Asteroid Descent Trajectory Planning Using a Lambert Solution-Based Costate Initialization. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4338–4352. [Google Scholar] [CrossRef]
- Kim, M.; Park, S. Optimal Control Approach to Lambert’s Problem and Gibbs’ Method. Appl. Sci.-Basel 2020, 10, 2419. [Google Scholar] [CrossRef] [Green Version]
- Leeghim, H.; Jaroux, B.A. Energy-Optimal Solution to the Lambert Problem. J. Guid. Control Dyn. 2010, 33, 1008–1010. [Google Scholar] [CrossRef]
- Wei, Q.; Cai, Y.L. A Modified Algorithm for The Time-fixed Orbital Interception. In Proceedings of the IEEE International Conference on Information and Automation 2015, Lijiang, China, 8–10 August 2015; pp. 3057–3061. [Google Scholar]
- Liu, Y.F.; Li, R.F.; Wang, S.Q. Particle Swarm Optimization applied to Orbital Three-Player Conflict. In Proceedings of the 8th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 11–12 September 2016; pp. 513–517. [Google Scholar]
- Wang, Z.W.; Dong, Y.M.; Feng, W.M.; Zhao, J.F. Optimization for far-distance and fuel-limited cooperative rendezvous between two coplanar spacecraft based on Lambert method. Proc. Inst. Mech. Eng. Part G-J. Aerosp. Eng. 2020, 234, 1301–1310. [Google Scholar] [CrossRef]
- Soyinka, O.K.; Duan, H.B. Optimal Impulsive Thrust Trajectories for Satellite Formation via Improved Brainstorm Optimization. In Proceedings of the 7th International Conference on Swarm Intelligence (ICSI), Bali, Indonesia, 25–30 June 2016; pp. 491–499. [Google Scholar]
- Song, X.M.; Chen, Y.; Lin, Q. Orbit Plan Method for General Rendezvous Problems. Appl. Mech. Mater. 2014, 543–547, 1385–1388. [Google Scholar] [CrossRef]
- Yang, B.; Li, S.; Feng, J.L.; Vasile, M. Fast Solver for J2-Perturbed Lambert Problem Using Deep Neural Network. J. Guid. Control Dyn. 2022, 45, 875–884. [Google Scholar] [CrossRef]
- Osler, S.; Sands, T. Controlling Remotely Operated Vehicles with Deterministic Artificial Intelligence. Appl. Sci. 2022, 12, 2810. [Google Scholar] [CrossRef]
- Sandberg, A.; Sands, T. Autonomous Trajectory Generation Algorithms for Spacecraft Slew Maneuvers. Aerospace 2022, 9, 135. [Google Scholar] [CrossRef]
- Battin, R.H. An Introduction to the Mathematics and Methods of Astrodynamics; Aiaa: Reston, VA, USA, 1999. [Google Scholar]
- Wu, G.Q.; Tan, L.G.; Li, X.; Song, S.M. Multi-objective Optimization for Time-Open Lambert Rendezvous Between Non-coplanar Orbits. Int. J. Aeronaut. Space Sci. 2020, 21, 560–575. [Google Scholar] [CrossRef]
- Li, Y.F.; Zhang, Y.S. A Method of Determining Multiple-Targets Interception Based on Traversing Points. Appl. Mech. Mater. 2013, 437, 1081–1084. [Google Scholar] [CrossRef]
- Dutta, A. Grasp algorithm for multi-rendezvous mission planning with optimized trip times. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Vail, CO, USA, 11–13 August 2015; pp. 1121–1133. [Google Scholar]
- Xia, C.; Zhang, G.; Geng, Y. Two-target interception problem with a single impulse. Aerosp. Sci. Technol. 2021, 119, 107110. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, G.; Geng, Y. Coplanar multi-target interception with a single impulse. Acta Aeronaut. Et Astronaut. Sin. 2022, 43, 325093. [Google Scholar] [CrossRef]
- Avanzini, G. A Simple Lambert Algorithm. J. Guid. Control Dyn. 2008, 31, 1587–1594. [Google Scholar] [CrossRef]
- Curtis, H. Orbital Mechanics for Engineering Students; Butterworth-Heinemann: Waltham, MA, USA, 2013. [Google Scholar]
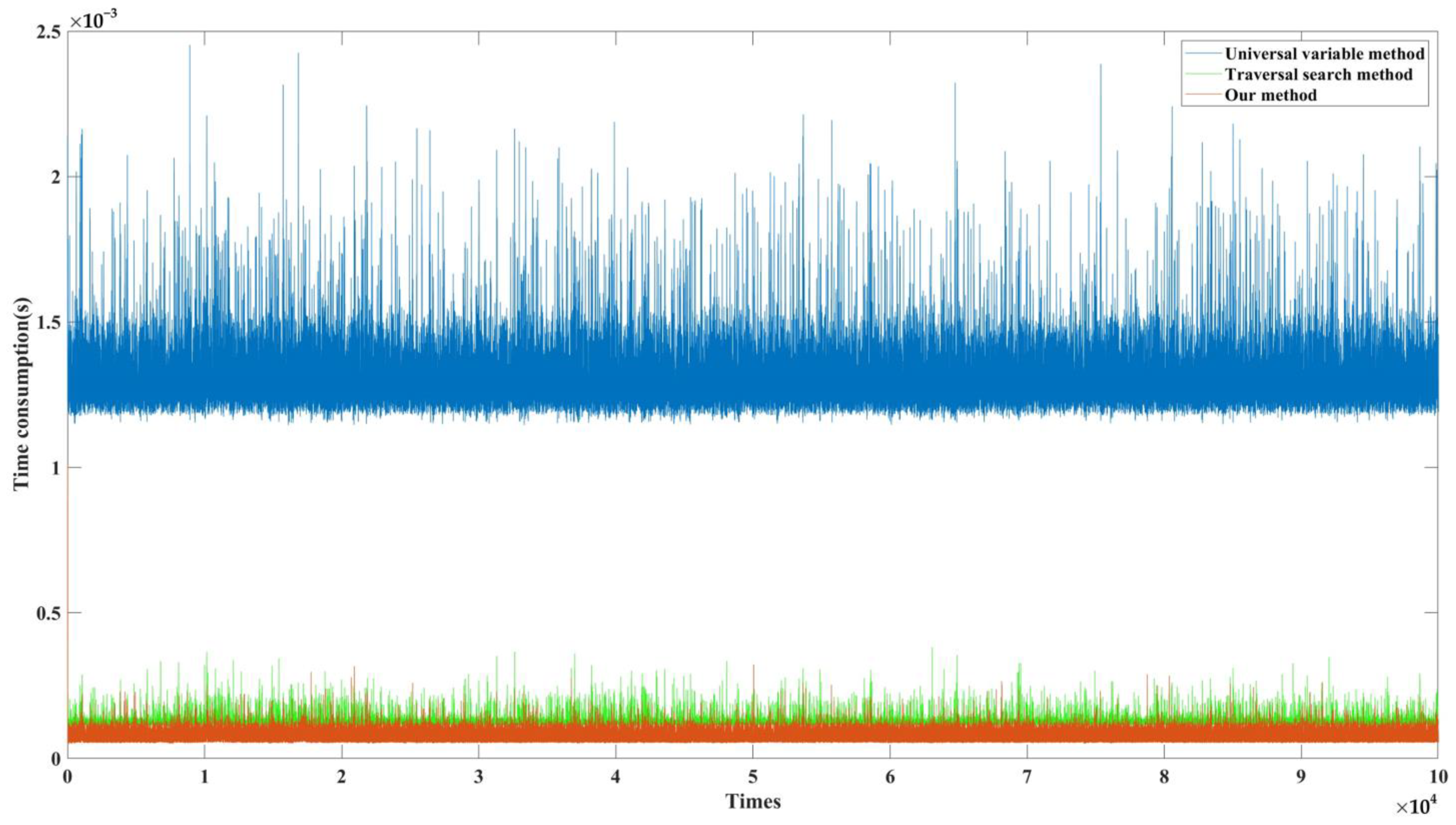

| Average Computation Time (ms) | 1000 Times | 10,000 Times | 50,000 Times | 100,000 Times | Efficiency Improvement |
|---|---|---|---|---|---|
| Universal variable method [35] | 1.3581 | 1.3593 | 1.3547 | 1.3543 | 92.09% |
| Traversal search method | 0.2120 | 0.2039 | 0.1977 | 0.1972 | 45.69% |
| Our method | 0.1118 | 0.1114 | 0.1075 | 0.1071 |
| Spacecraft | (°) | (°) | (°) | (°) | ||
|---|---|---|---|---|---|---|
| 7134 | 7861 | 23 | 11 | 38 | 17 | |
| 9871 | 10,306 | 40 | 81 | |||
| 82 |
| Spacecraft | (°) | (°) | (°) | (°) | ||
|---|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, H.; Dong, Z.; Liu, L.; Xia, L. Numerical Solution for the Single-Impulse Flyby Co-Orbital Spacecraft Problem. Aerospace 2022, 9, 374. https://doi.org/10.3390/aerospace9070374
Su H, Dong Z, Liu L, Xia L. Numerical Solution for the Single-Impulse Flyby Co-Orbital Spacecraft Problem. Aerospace. 2022; 9(7):374. https://doi.org/10.3390/aerospace9070374
Chicago/Turabian StyleSu, Haoxiang, Zhenghong Dong, Lihao Liu, and Lurui Xia. 2022. "Numerical Solution for the Single-Impulse Flyby Co-Orbital Spacecraft Problem" Aerospace 9, no. 7: 374. https://doi.org/10.3390/aerospace9070374
APA StyleSu, H., Dong, Z., Liu, L., & Xia, L. (2022). Numerical Solution for the Single-Impulse Flyby Co-Orbital Spacecraft Problem. Aerospace, 9(7), 374. https://doi.org/10.3390/aerospace9070374





