Layout Design of Strapdown Array Seeker and Extraction Method of Guidance Information
Abstract
:1. Introduction
- (1)
- The layout of the multi-sensor was explored;
- (2)
- An MIEKF was constructed to estimate guidance information;
- (3)
- Based on the 6-DOF trajectory simulation model, the performance of the monocular seeker and the multi-eye seeker were compared and analyzed, and the performance of the EKF, Iterated EKF (IEKF), and MIEKF were also compared.
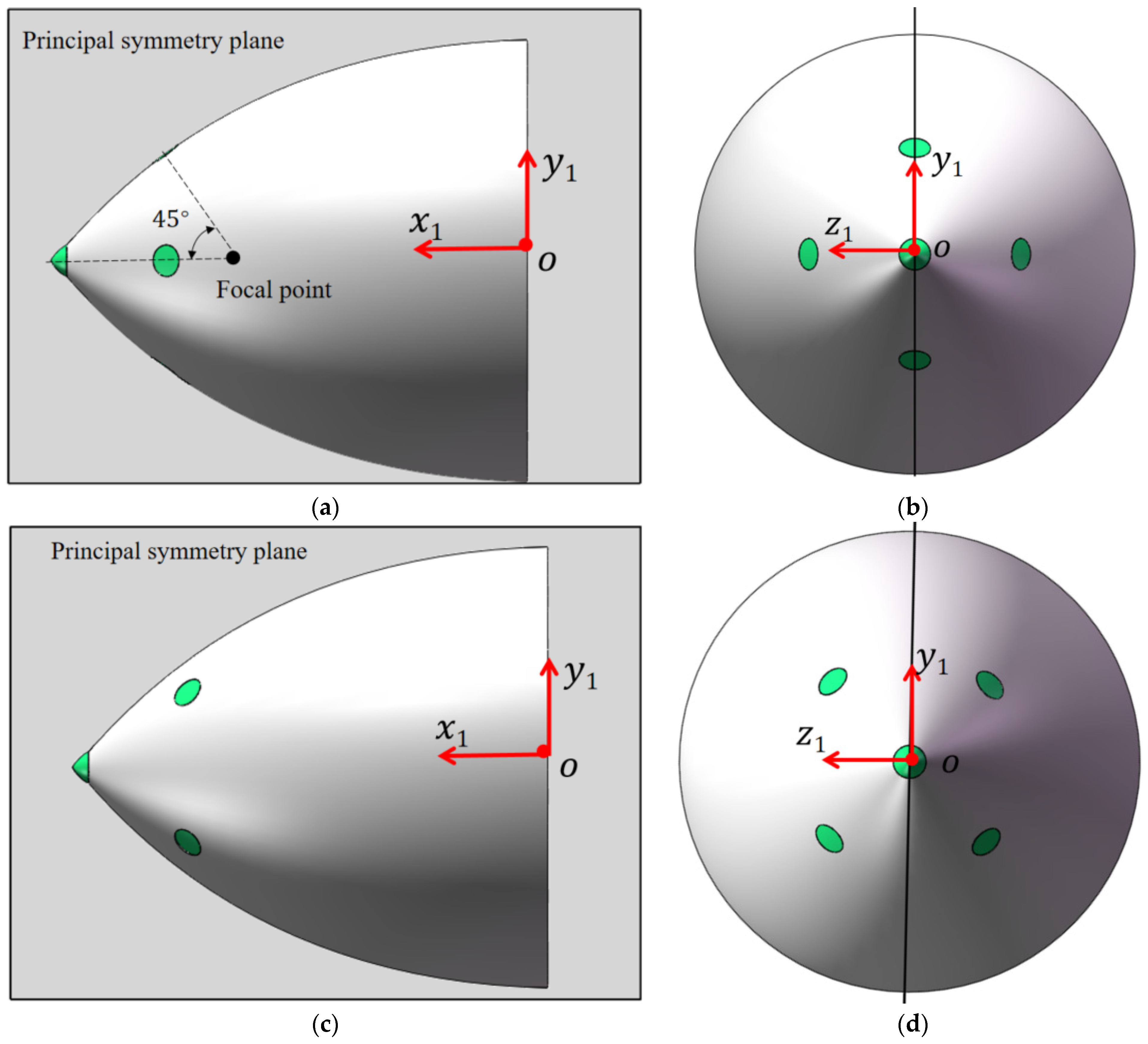
2. Layout Design of the Sensors
- The head of the missile is ellipsoidal, and the sensor mounting plane is tangent to the shell;
- Each sensor is qualified, and thus, the measurement error distribution is known;
- Each sensor has its own independent signal processor and can output LOS angle information;
- Through installation and adjustment, the focuses of each sensor are at the same point as the body axes of the missile.
2.1. Circular FOV Sensors
2.2. Rectangular FOV Sensor
3. Strapdown Array Seeker Guidance Information Extraction Model
3.1. Normalization Processing
3.2. System State Equation
3.3. System Observation Equation
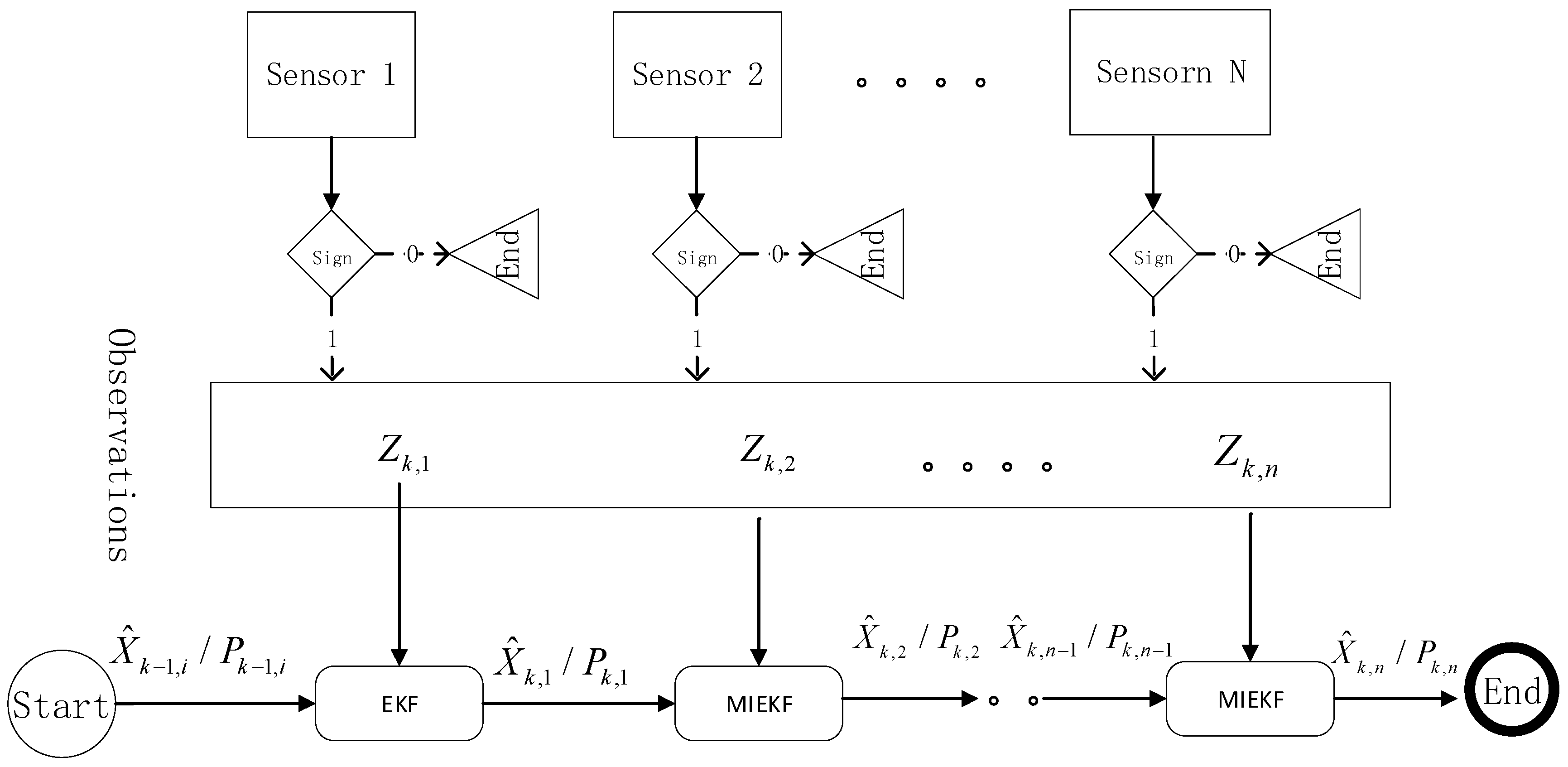
4. Filter Design
4.1. Extended Kalman Filters
- State forecast
- 2.
- Filter correction
- 3.
- Measurement update
4.2. Iterated Extended Kalman Filter
4.3. Multivariate Iterated Extended Kalman Filter
5. Numerical Simulations
5.1. Generation of Measurement Data
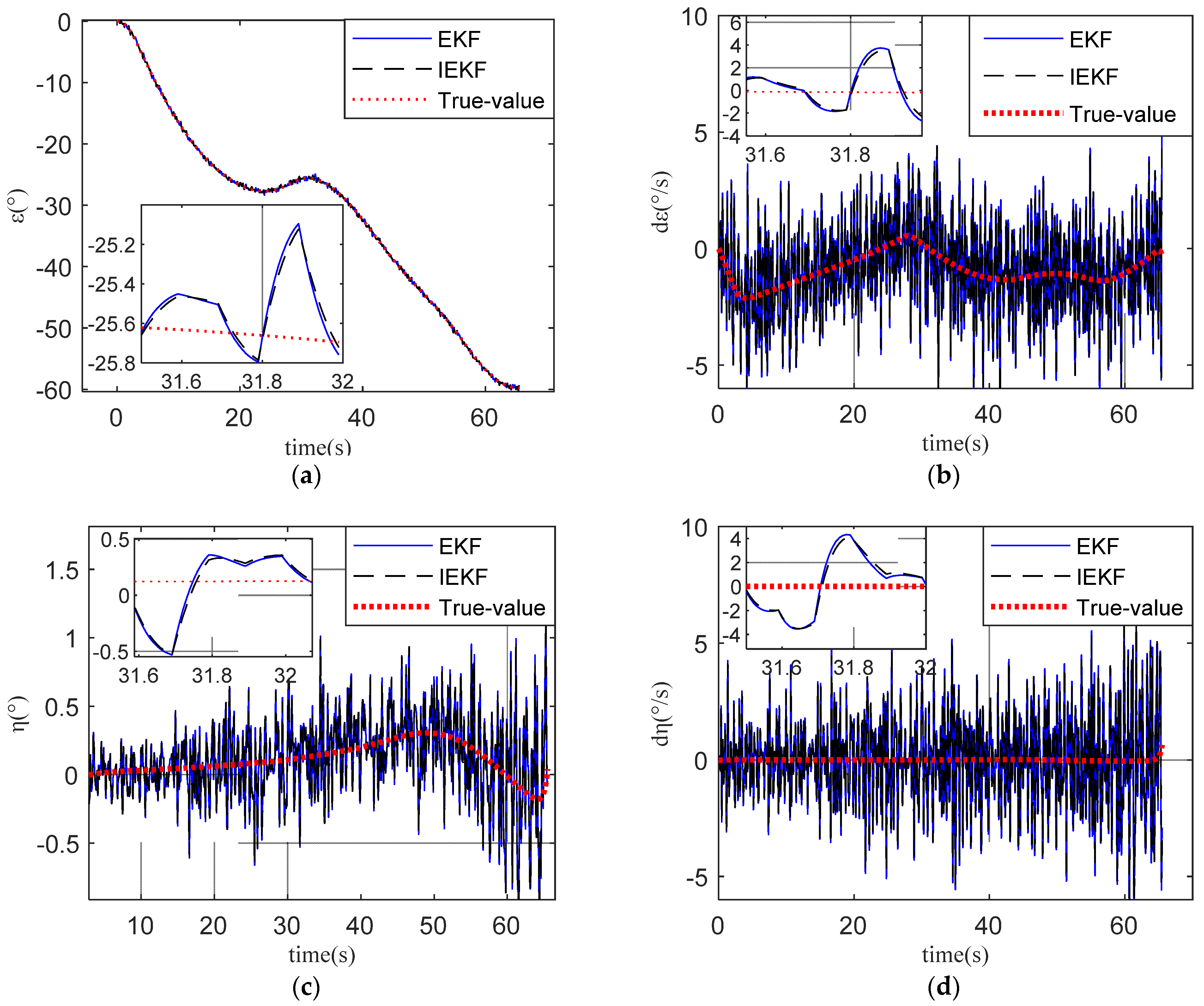
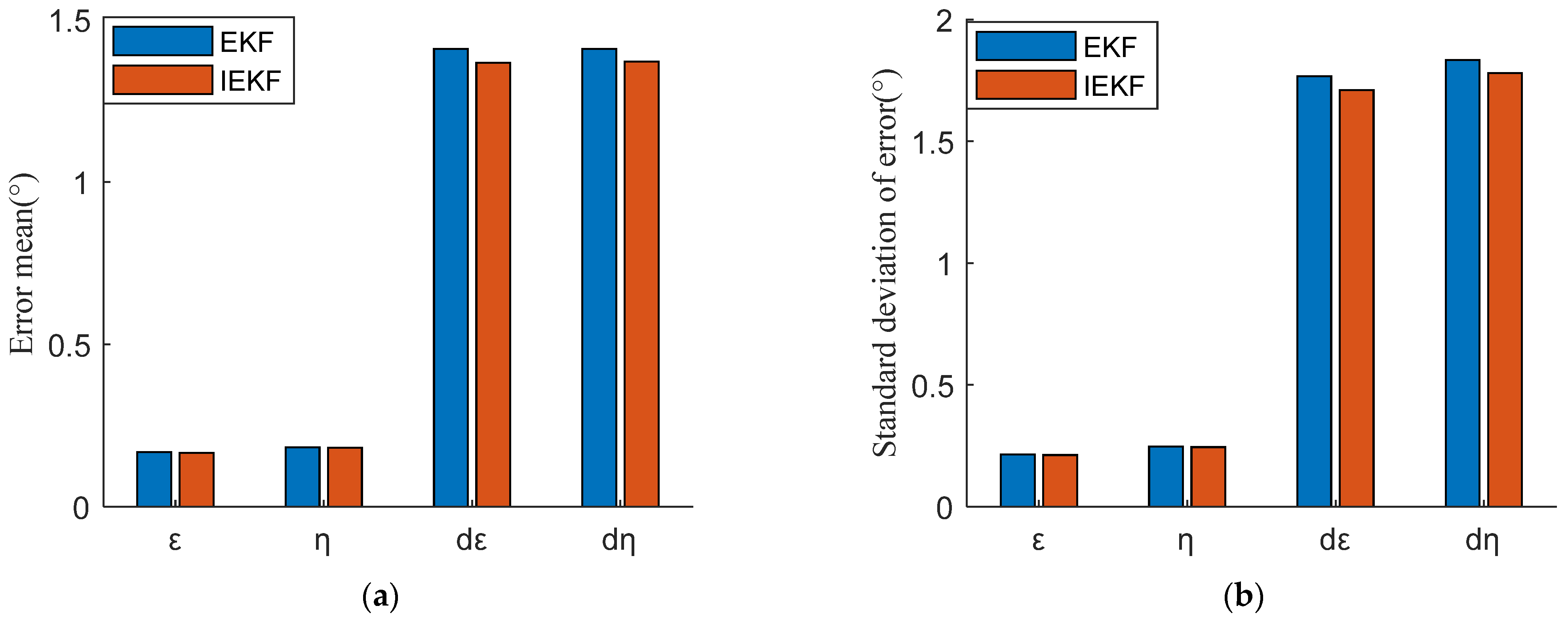
5.2. Results of IKEF and EKF
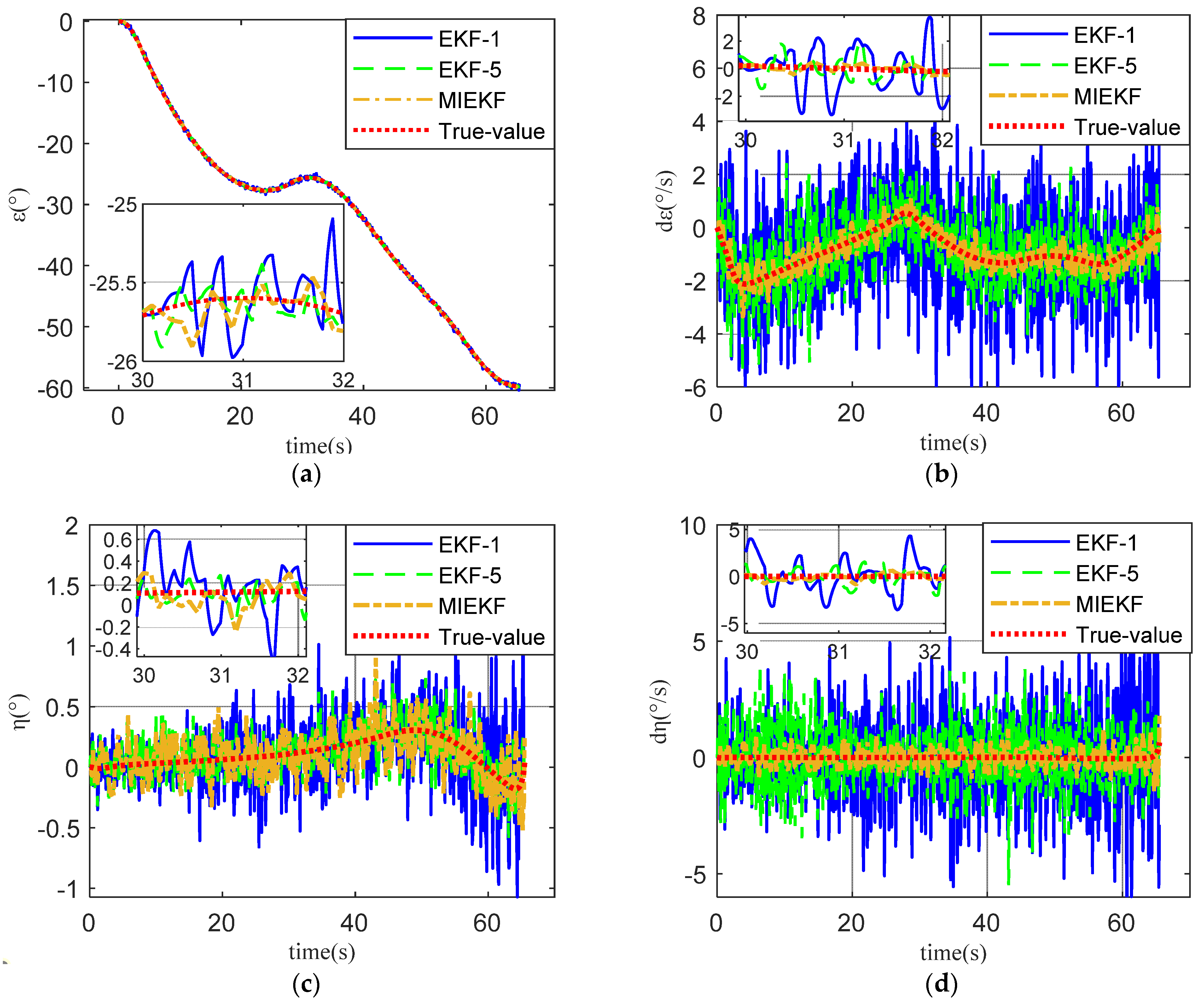
5.3. Results of MIKEF and EKF
6. Conclusions
- (1)
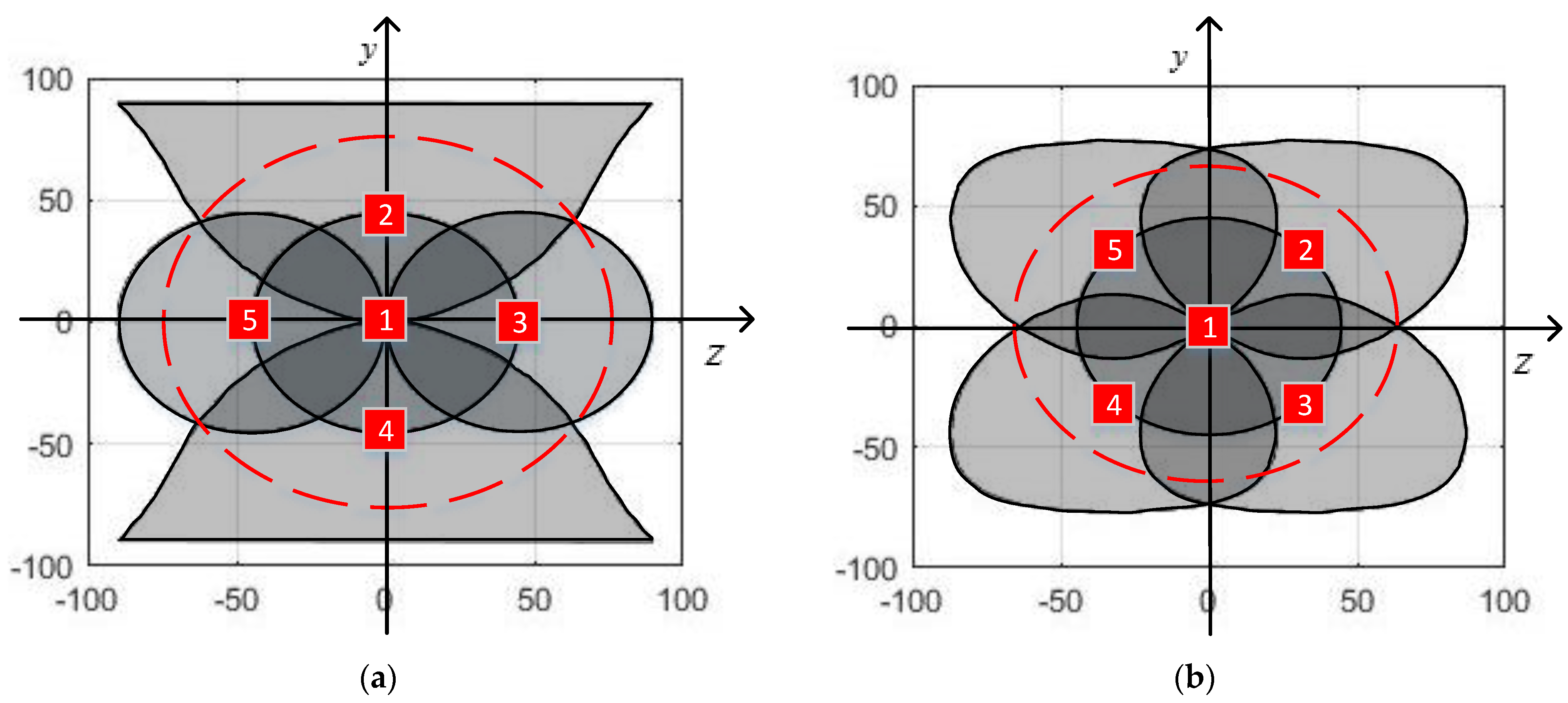
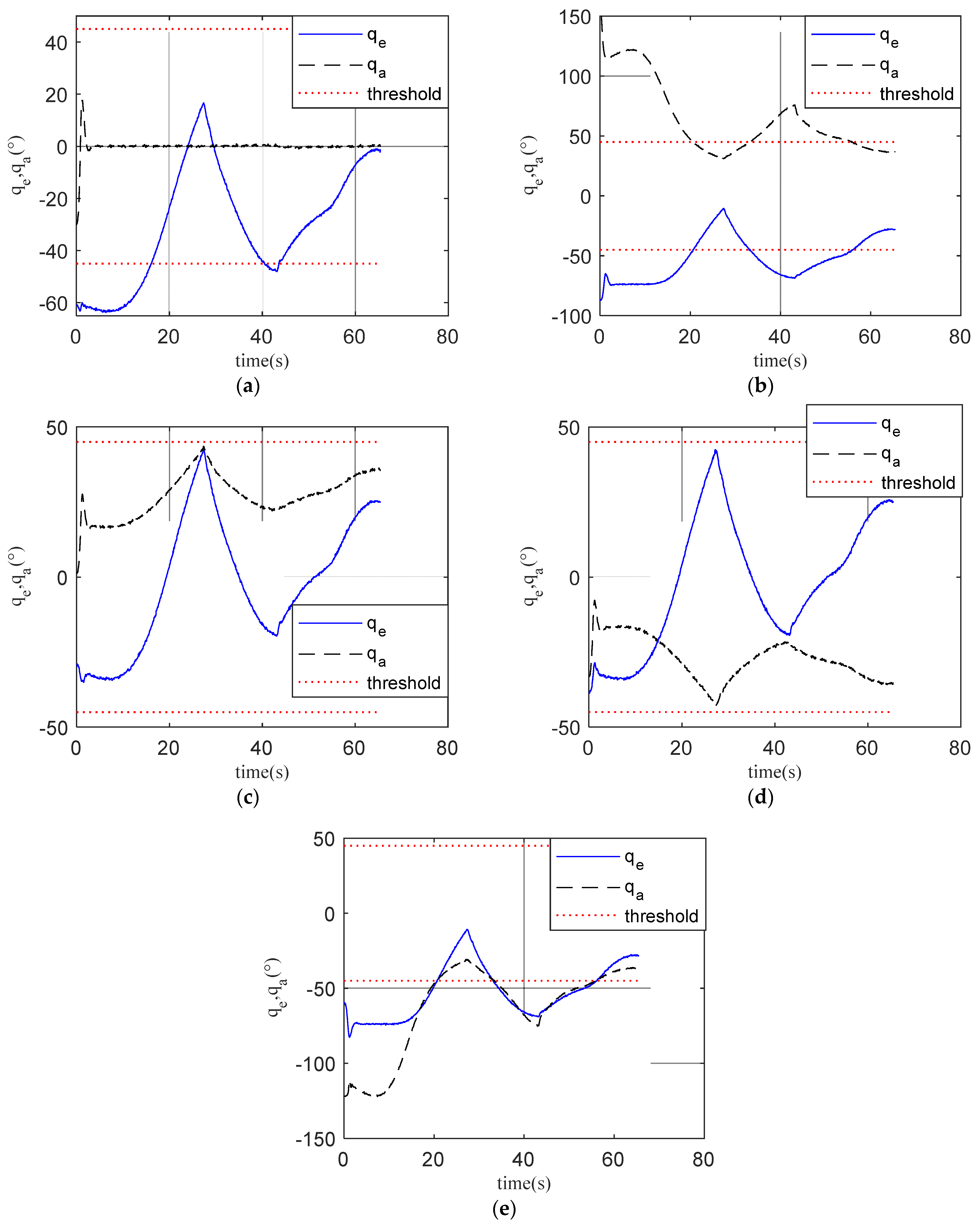
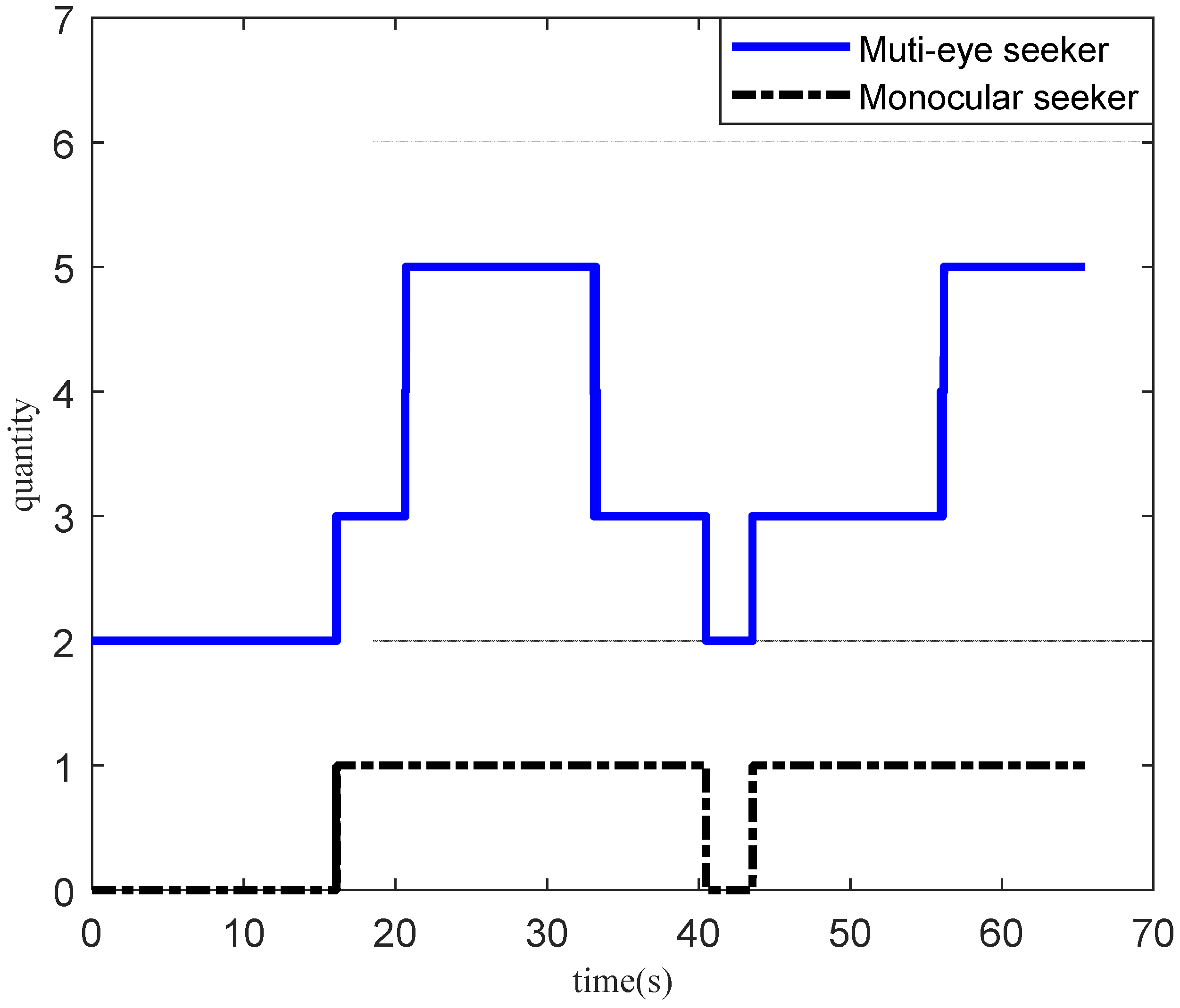
- The field distribution of the circular FOV sensor and the rectangular FOV sensor in the +-shaped layout and the X-shaped layout were explored. The FOV after the array superposition was characterized by the FOV of the central sensor, and the equivalent FOV of the monocular seeker was obtained. The results show that the FOV angle is enlarged to 75.1° and 63.8° in +-shape and X-shape layout when five circular FOV sensors with 45° × 45° FOV angle are used. The FOV angle is enlarged to 70.5° × 90° and 72° × 75° in +-shape and X-shape layout when five rectangular FOV sensors with 45°FOV angle are used. Although the +-shape layout has a larger FOV angle, the X-shape layout has better FOV coverage. In an X-shape layout, there are at least two sensors around the y-axis to provide coverage. In the central area, coverage can be up to five sensors, which is an ideal sensor layout.
- (2)
- In order to solve the problem that the number of observations changes during the observation process, the measurement results , and noise errors , of surface array sensors were normalized and characterized in the FOV of the central sensor. The equivalent observations , and the corresponding error distributions , were obtained. A model of guidance information extraction (28) and (34) was established based on the observations and error distributions.
- (3)
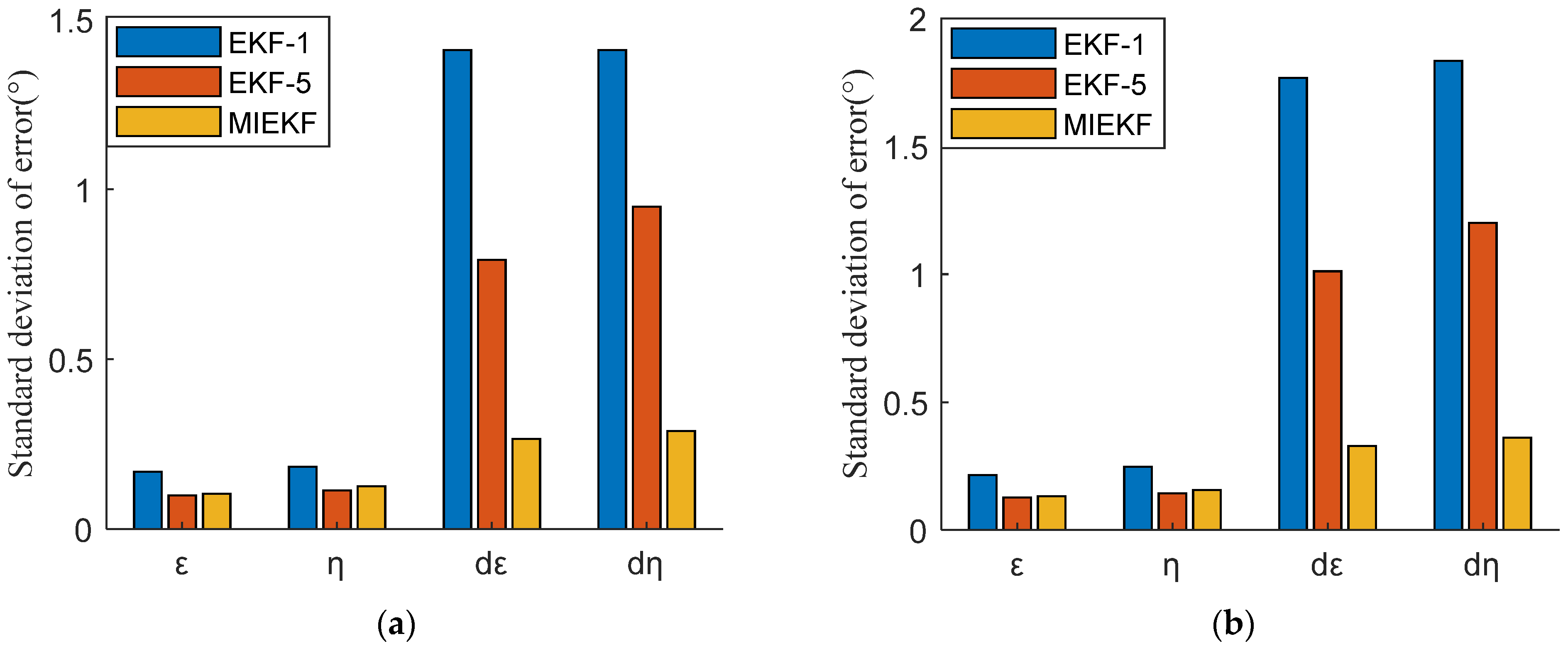
- For the established continuous nonlinear model, the EKF was used for processing. The IEKF was adopted for comparative analysis to overcome the nonlinear error in the filtering process. However, the simulation results show that, compared with EKF, IEKF improves the accuracy of the LOS angle and LOS angle rate by less than 5%. This means that the nonlinear error was not the main error source. In order to make full use of the observed values of the array sensors, improve the filtering quality, and reduce the noise error, the MIEKF was proposed. The simulation results show that the MIEKF can improve the estimation accuracy of LOS angle ε and η by at least 30% and the estimation accuracy of LOS angle rate dε and dη by nearly 80% compared with EKF. So, the MIEKF proposed in this paper is helpful for improving the accuracy of guidance information.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| FOV | Field-of-view |
| LOS | Line-of-sight |
| UKF | Unscented Kalman filter |
| EKF | Extended Kalman filter |
| IEKF | Iterated extended Kalman filter |
| MIEKF | Multivariate iterated extended Kalman filter |
| SCS I | Sensor coordinate system |
| BCS B | Body fixed coordinate system |
| BLCS L | Body LOS coordinate system |
| LCS S | LOS coordinate system |
| LaunchCS A | Launch coordinate system |
| Attitude Angle pitch/yaw/roll | |
| i | Sensor number |
| IB | Transformation matrix from B to I |
| / | Install azimuth/altitude angle |
| Body-LOS-azimuth/altitude angle (in BCS B) | |
| Body-LOS-azimuth/altitude angle (in SCS I) | |
| LOS-transfer angle | |
| Sensor’s FOV boundary (azimuth, altitude) | |
| The coordinates of the target in coordinate frame I | |
| r | The distance between missile and target |
| LOS-azimuth/altitude angle | |
| Xk | State variable at the moment k |
| Zk | Observations at the moment k |
| State transition matrix at the moment k | |
| Rk | Observed noise matrix at the moment k |
| Pk | Variance matrix at the moment k |
| Kk | Kalman gain matrix at the moment k |
| Hk | Measurement matrix at the moment k |
| Qk | System noise matrix at the moment k |
References
- Zuo, W.; Zhou, B.; Li, W. Analysis of Development of Multi-mode and compound Precision Guidance Technology. Air Space Def. 2019, 2, 44–52. [Google Scholar]
- Lee, J.Y. Generalized Guidance Formulation for Impact Angle Interception with Physical Constraints. Aerospace 2021, 8, 307. [Google Scholar]
- Park, B.G.; Kwon, H.H.; Kim, Y.H. Composite Guidance Scheme for Impact Angle Control Against a Nonmaneuvering Moving Target. J. Guid. Control. Dyn. 2016, 39, 1129–1136. [Google Scholar] [CrossRef]
- Tekin, R.; Erer, K.S. Switched-Gain Guidance for Impact Angle Control Under Physical Constraints. J. Guid. Control Dyn. 2015, 38, 205–216. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Tang, S.J.; Guo, J. A Two-Phased Guidance Law for Impact Angle Control with Seeker’s Field-of-View Limit. Int. J. Aerosp. Eng. 2018, 2018, 740363. [Google Scholar] [CrossRef]
- Park, B.G.; Kim, T.H.; Tahk, M.J. Biased PNG With Terminal-Angle Constraint for Intercepting Nonmaneuvering Targets Under Physical Constraints. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1562–1572. [Google Scholar] [CrossRef]
- Wang, Z. Field-of-View Constrained Impact Time Control Guidance via Time-Varying Sliding Mode Control. Aerospace 2021, 8, 251. [Google Scholar]
- Singh, N.K.; Hota, S. Moving Target Interception Guidance Law for Any Impact Angle with Field-of-View Constraint. AIAA Scitech 2021 Forum 2021, 1462. [Google Scholar] [CrossRef]
- Qian, S.K.; Yang, Q.H.; Geng, L.N. SDRE Based Impact Angle Control Guidance Law Considering Seeker’s Field-of-View Limit. In Proceedings of the Chinese Guidance, Navigation and Control Conference, Nanjing, China, 12–14 August 2016. [Google Scholar]
- Lee, S.; Ann, S.; Cho, N.; Kim, Y. Capturability of Impact-Angle Control Composite Guidance Law Considering Field-of-View Limit. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1077–1093. [Google Scholar] [CrossRef]
- Ma, S.; Wang, Z.Y.; Wang, X.G. Three-Dimensional Impact Time Control Guidance Considering Field-of-View Constraint and Velocity Variation. Aerospace 2022, 9, 202. [Google Scholar] [CrossRef]
- Zhao, B.; Xu, S.Y.; Guo, J.G. Integrated Strapdown Missile Guidance and Control Based on Neural Network Disturbance Observer. Aerosp. Sci. Technol. 2019, 84, 170–181. [Google Scholar] [CrossRef]
- Sun, T.T. Research on the Key Technology of Strapdown; University of Chinese Academy of Sciences: Beijing, China, 2016. [Google Scholar]
- Sun, X.T.; Luo, X.B.; Liu, Q.S. Application and Key Technologies of Guided Munition Based on Strapdown Seeker. J. Ordnance Equip. Eng. 2019, 40, 58–61. [Google Scholar]
- Song, Y.F.; Hao, Q.; Cao, J. Research and development of foreign Wide-Field-of-View seeker based on artificial compound eye. Infrared Laser Eng. 2021, 51, 20210593. [Google Scholar]
- Zhang, X.; Xu, Y.; Fu, K. Field of View Selection and Search Strategy Design for Infrared Imaging Seeker. Infrared Laser Eng. 2014, 43, 3866–3871. [Google Scholar]
- Hu, J.T.; Huang, F.; Zhang, C. Research status of super resolution reconstruction based on compound-eye imaging technology. Laser Technol. 2015, 39, 492–496. [Google Scholar]
- Cao, J.; Hao, Q.; Zhang, F.H. Research progress of bio-inspired retina-like imaging. Infrared Laser Eng. 2020, 49, 9–16. [Google Scholar]
- Duparré, J.; Wippermann, F.; Dannberg, P. Artificial compound eye zoom camera. Bioinspirat. Biomim. 2008, 3, 046008. [Google Scholar] [CrossRef]
- Duparré, J.; Wippermann, F.; Dannberg, P. Chirped arrays of refractive ellipsoidal microlenses for aberration correction under oblique incidence. Opt. Express 2005, 13, 10539–10551. [Google Scholar] [CrossRef]
- Nakamura, T.; Horisaki, R.; Tanida, J. Computational superposition compound eye imaging for extended depth-of-field and field-of-view. Opt. Express 2012, 20, 27482–27495. [Google Scholar] [CrossRef]
- Horisaki, R.; Tanida, J. Preconditioning for multidimensional TOMBO imaging. Opt. Lett. 2011, 36, 2071–2073. [Google Scholar] [CrossRef]
- Zhai, Y.; Niu, J.; Liu, J. Bionic Artificial Compound Eyes Imaging System Based on Precision Engraving. In Proceedings of the 2021 IEEE 34th International Conference on Micro Electro Mechanical Systems, Gainesville, FL, USA, 25–29 January 2021. [Google Scholar]
- Fan, Y. Design and Simulation of the Artificial Compound Eyes with Large Field of View; Tianjin University: Tianjin, China, 2013. [Google Scholar]
- Song, L.P. Design of Distributed Full Strapdown Guidance Bomb Guidance Information Extraction and Guidance System; Harbin Institute of Technology: Harbin, China, 2019. [Google Scholar]
- Jang, S.A.; Ryoo, C.K.; Choi, K. Guidance Algorithms for Tactical Missiles with Strapdown Seeker. In Proceedings of the 2008 SICE Annual Conference, Chofu, Japan, 20–22 August 2008. [Google Scholar]
- Raj, K.D.; Ganesh, I.S. Estimation of Line-of-Sight Rate in a Homing Missile Guidance Loop Using Optimal Filters. In Proceedings of the International Conference on Communications, Melmaruvathur, India, 2–4 April 2015. [Google Scholar]
- Hong, J.H.; Ryoo, C.K. Compensation of Parasitic Effect in Homing Loop with Strapdown Seeker via PID Control. In Proceedings of the International Conference on Informatics in Control, Vienna, Austria, 1–3 September 2014; Volume 1, pp. 711–717. [Google Scholar]
- Liu, Y.; Tian, W.F.; Zhao, J.K. Line-of-Sight Angle Rate Reconstruction for Phased Array Strapdown Seeker. Adv. Mater. Res. 2013, 645, 196–201. [Google Scholar] [CrossRef]
- Mi, W.; Shan, J.; Liu, Y. Adaptive Unscented Kalman Filter Based Line of Sight Rate for Strapdown Seeker. In Proceedings of the Chinese Automation Congress (CAC), Xian, China, 30 November–2 December 2018. [Google Scholar]
- Vergez, P.L.; Mcclendon, J.R. Optimal control and estimation for strapdown seeker guidance of tactical missiles. J. Guid. Control Dyn. 2012, 5, 225–226. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Li, J.J.; Li, H.Y. Line of sight rate estimation of strapdown imaging seeker based on particle filter. In Proceedings of the 2010 3rd International Symposium on Systems and Control in Aeronautics and Astronautics, Harbin, China, 8–10 June 2010. [Google Scholar]
- Lan, J.; Li, X.R. Nonlinear Estimation by Linear Estimation with Augmentation of Uncorrelated Conversion. In Proceedings of the 17th International Conference on Information Fusion, Salamanca, Spain, 7–10 July 2014. [Google Scholar]
- Lan, J.; Li, X.R. Nonlinear Estimation by LMMSE-Based Estimation with Optimized Uncorrelated Augmentation. IEEE Trans. Signal Processing 2015, 63, 4270–4283. [Google Scholar] [CrossRef]
- Lan, J.; Li, X.R. Multiple Conversions of Measurements for Nonlinear Estimation. IEEE Trans. Signal Processing 2017, 65, 4956–4970. [Google Scholar] [CrossRef]
- Chen, K.J.; Liu, L.H.; Meng, Y.H. Launch Vehicle Flight Dynamics and Guidance; National Defense Industry Press: Beijing, China, 2014. [Google Scholar]
- Bucy, R.; Joseph, P. Filtering for Stochastic Processes with Applications to Guidance; John Wiley & Sons: New York, NY, USA, 1968. [Google Scholar]
- Bellantoni, J.F.; Dodge, K.W. A square root formulation of the Kalman- Schmidt filter. AIAA J. 1967, 5, 1309–1314. [Google Scholar] [CrossRef]
- Simon, D.J. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; Wiley-Interscience: New York, NY, USA, 2006. [Google Scholar]
- Yuan, Y.F. Research on Guidance and Control Technology for Strapdown Guided Munition; Beijing Institute of Technology: Beijing, China, 2014. [Google Scholar]





| Sensor No. | +-Shaped Layout | X-Shaped Layout | ||
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 |
| 2 | 45 | 0 | 45/ | −45/ |
| 3 | 0 | −45 | −45/ | −45/ |
| 4 | −45 | 0 | 45/ | −45/ |
| 5 | 0 | 45 | 45/ | 45/ |
| Filter | Error Mean | Standard Deviation of Error | ||||||
|---|---|---|---|---|---|---|---|---|
| ε [°] | η [°] | dε [°/s] | dη [°/s] | ε [°] | η [°] | dε [°/s] | dη [°/s] | |
| EKF | 0.1685 | 0.1833 | 1.4103 | 1.4102 | 0.2148 | 0.2471 | 1.7671 | 1.8347 |
| IEKF | 0.1662 | 0.1818 | 1.3667 | 1.3704 | 0.2121 | 0.2446 | 1.7103 | 1.7808 |
| Filter | Error Mean | Standard Deviation of Error | ||||||
|---|---|---|---|---|---|---|---|---|
| ε [°] | η [°] | dε [°/s] | dη [°/s] | ε [°] | η [°] | dε [°/s] | dη [°/s] | |
| EKF-1 | 0.1685 | 0.1833 | 1.4103 | 1.4102 | 0.2148 | 0.2471 | 1.7671 | 1.8347 |
| EKF-5 | 0.0990 | 0.1132 | 0.7928 | 0.9491 | 0.1276 | 0.1439 | 1.0115 | 1.2013 |
| MIEKF | 0.1039 | 0.1256 | 0.2652 | 0.2883 | 0.1325 | 0.1572 | 0.3295 | 0.3612 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Bai, X.; Zhang, S. Layout Design of Strapdown Array Seeker and Extraction Method of Guidance Information. Aerospace 2022, 9, 373. https://doi.org/10.3390/aerospace9070373
Yang H, Bai X, Zhang S. Layout Design of Strapdown Array Seeker and Extraction Method of Guidance Information. Aerospace. 2022; 9(7):373. https://doi.org/10.3390/aerospace9070373
Chicago/Turabian StyleYang, Hao, Xibin Bai, and Shifeng Zhang. 2022. "Layout Design of Strapdown Array Seeker and Extraction Method of Guidance Information" Aerospace 9, no. 7: 373. https://doi.org/10.3390/aerospace9070373
APA StyleYang, H., Bai, X., & Zhang, S. (2022). Layout Design of Strapdown Array Seeker and Extraction Method of Guidance Information. Aerospace, 9(7), 373. https://doi.org/10.3390/aerospace9070373





