A Passivity-Based Velocity Control Method of Hardware-in-the-Loop Simulation for Space Robotic Operations
Abstract
1. Introduction
2. Modelling of the HIL Simulation System
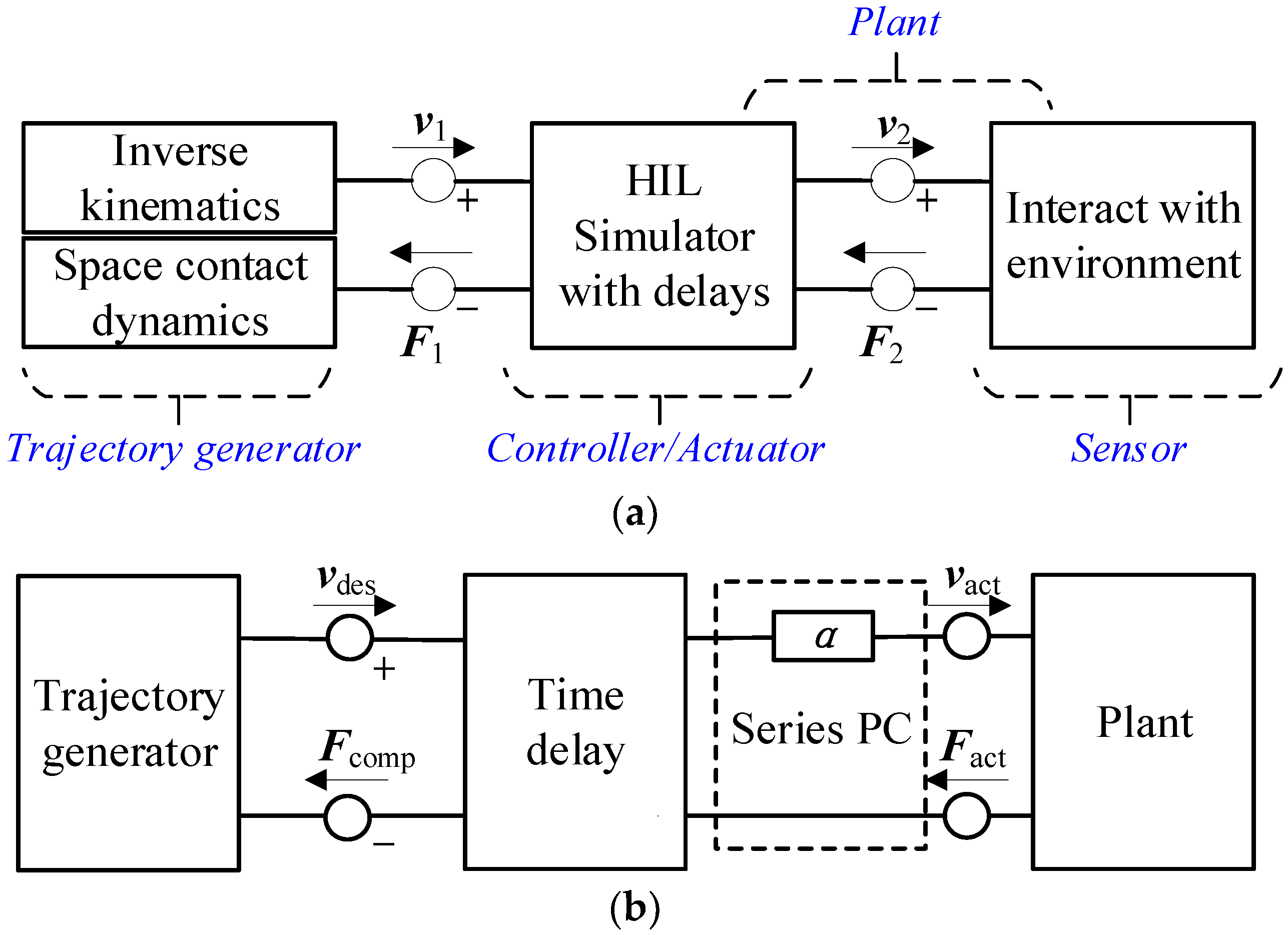
2.1. The HIL Simulation System
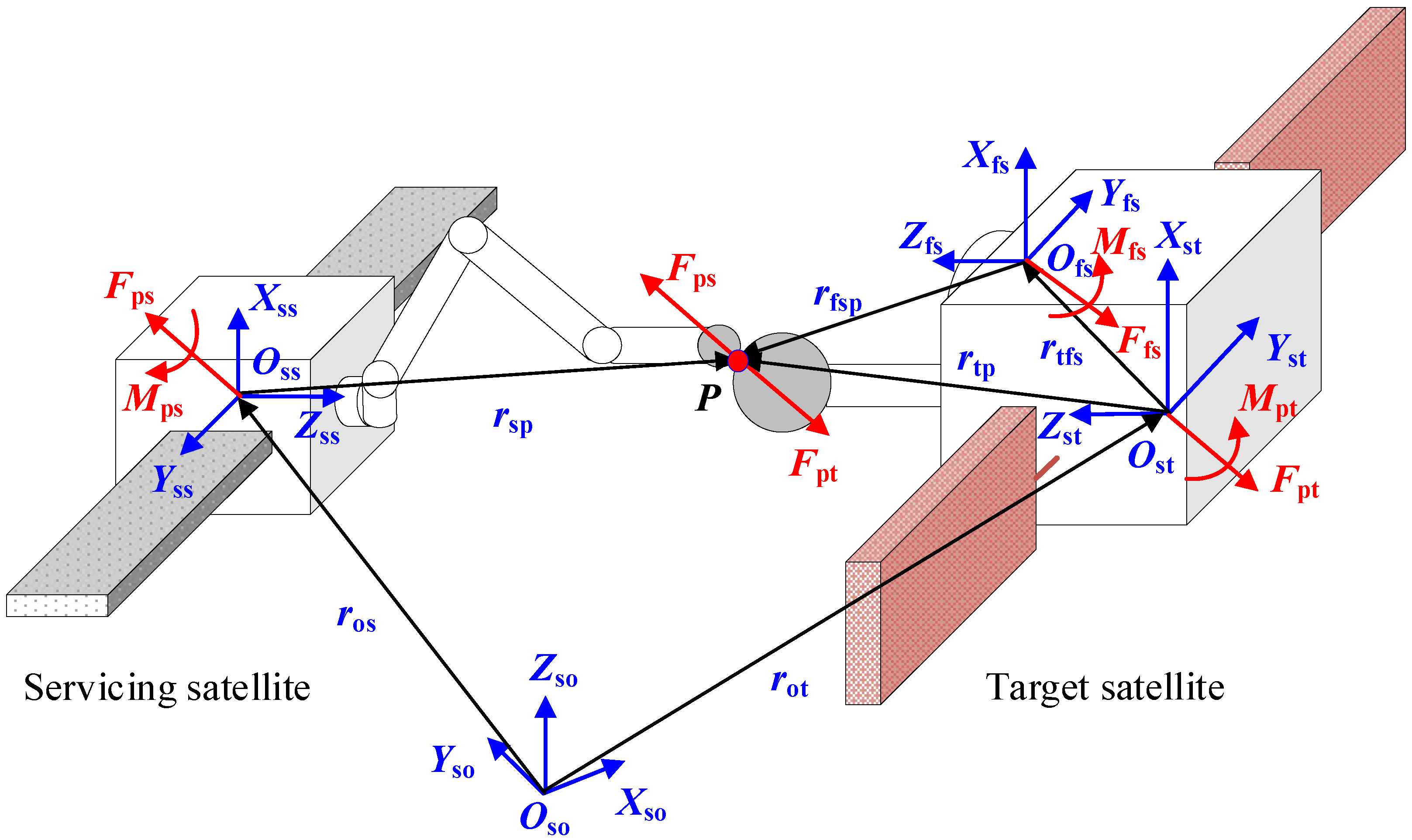
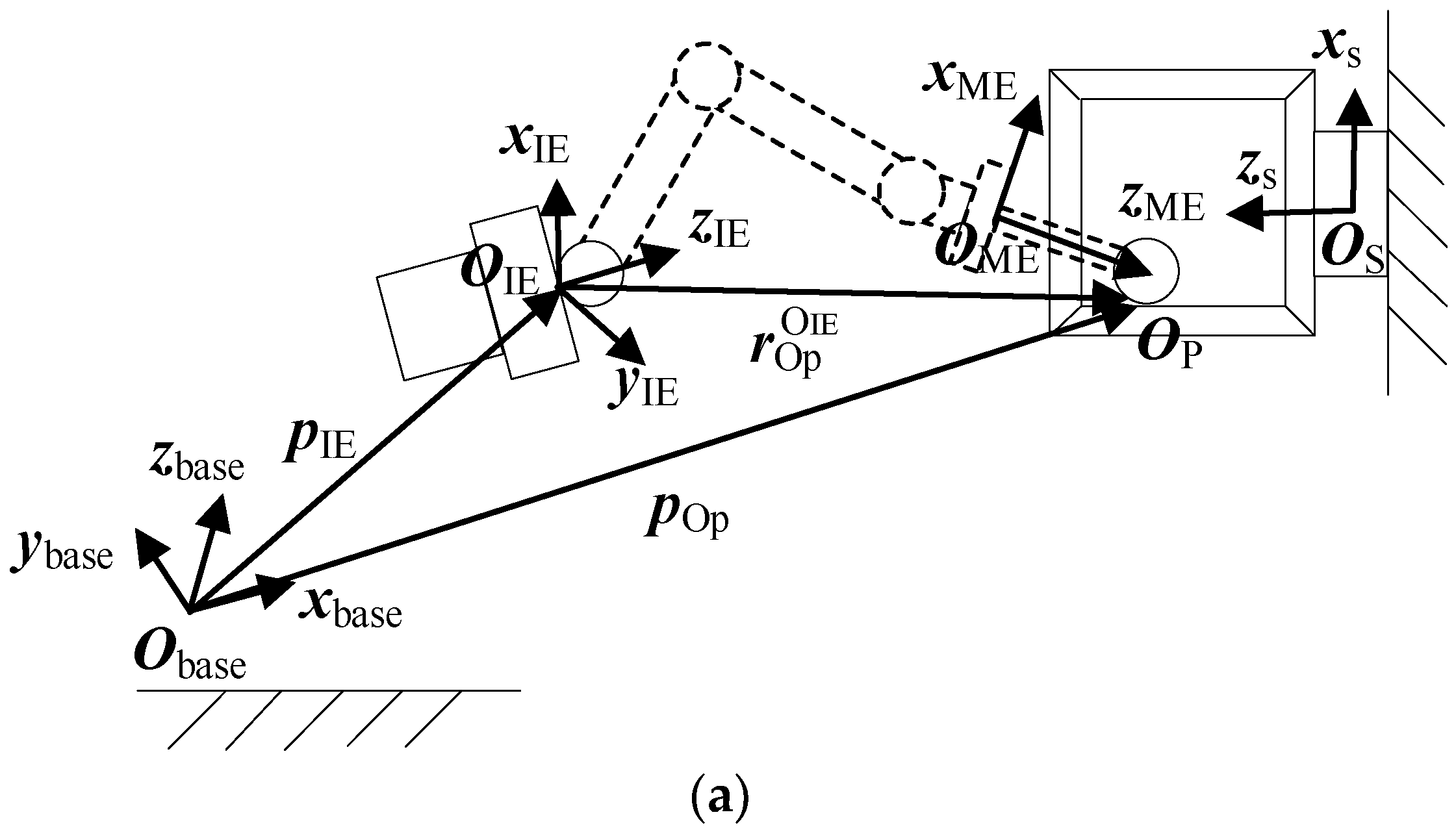
2.2. Kinematics of the Simulator
2.3. Free-Floating Dynamics
3. Methodology
3.1. Passive Network
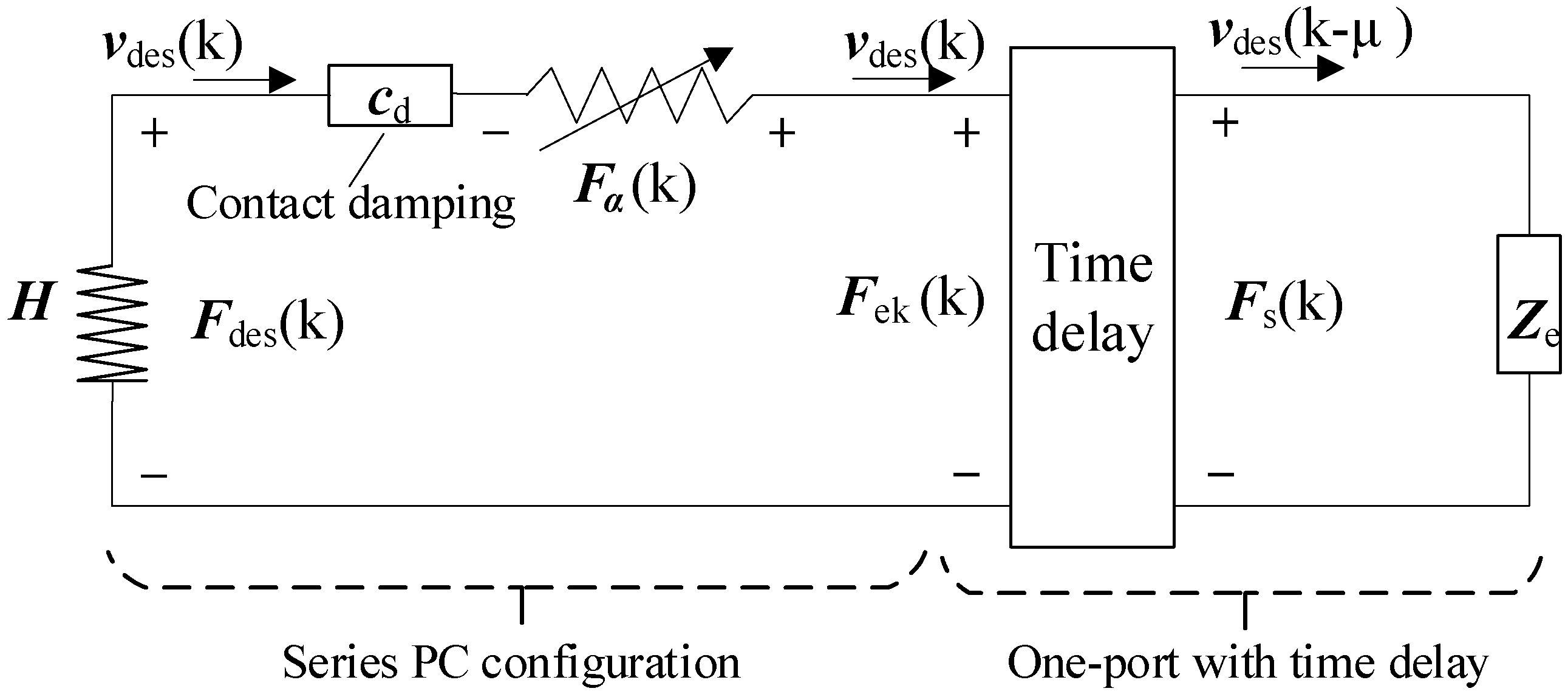
3.2. PO and PC
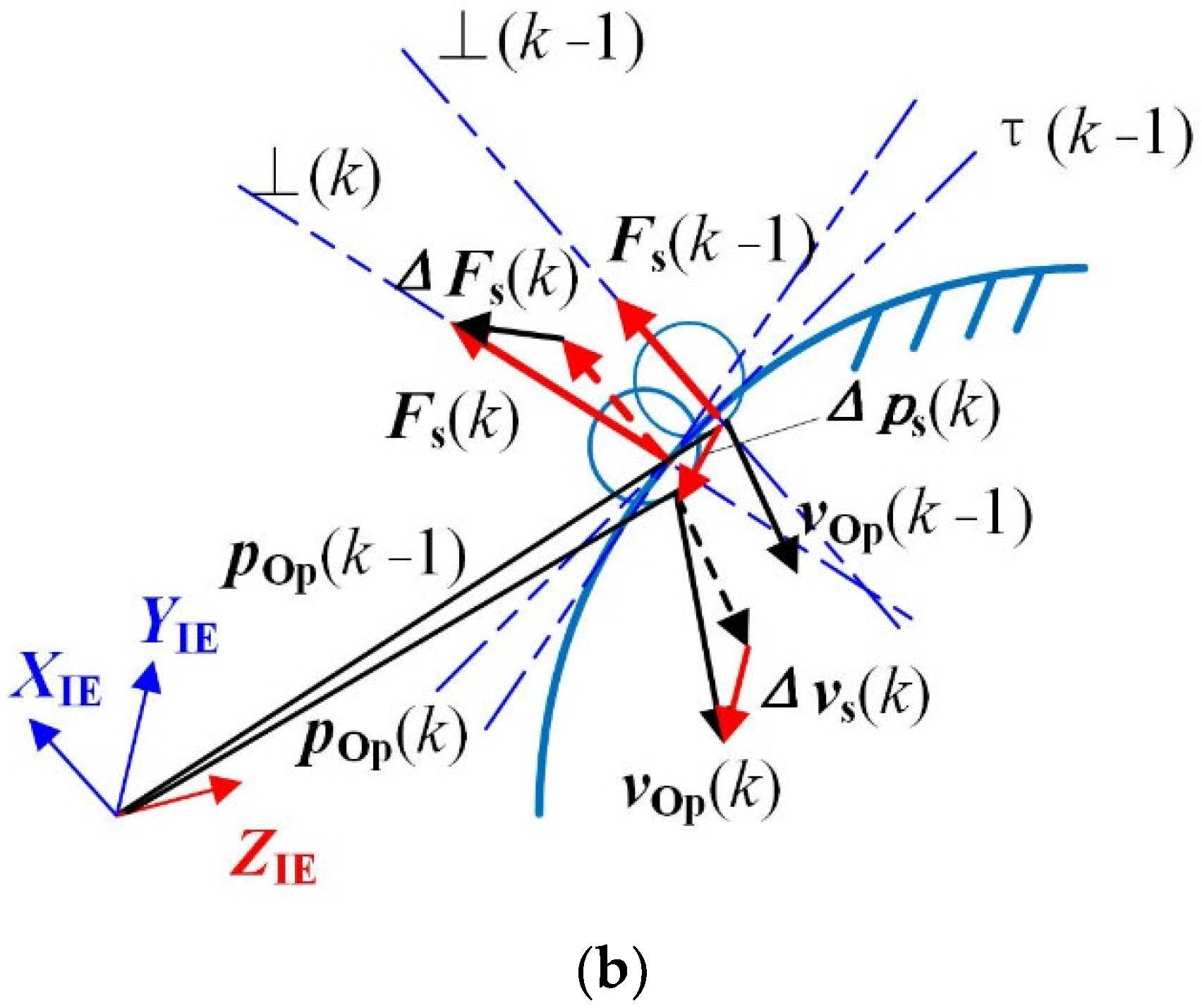
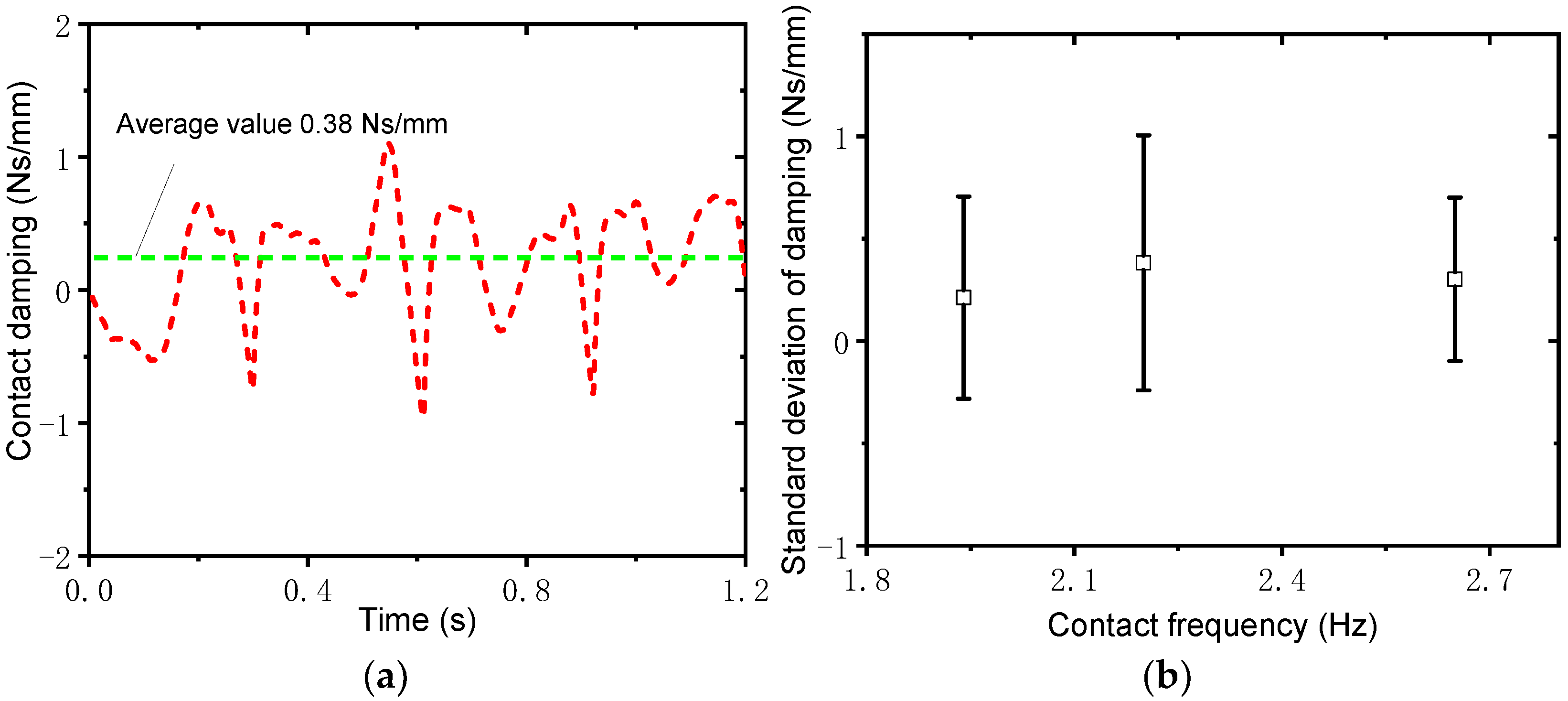
3.3. Damping Estimation
3.4. Control Strategy
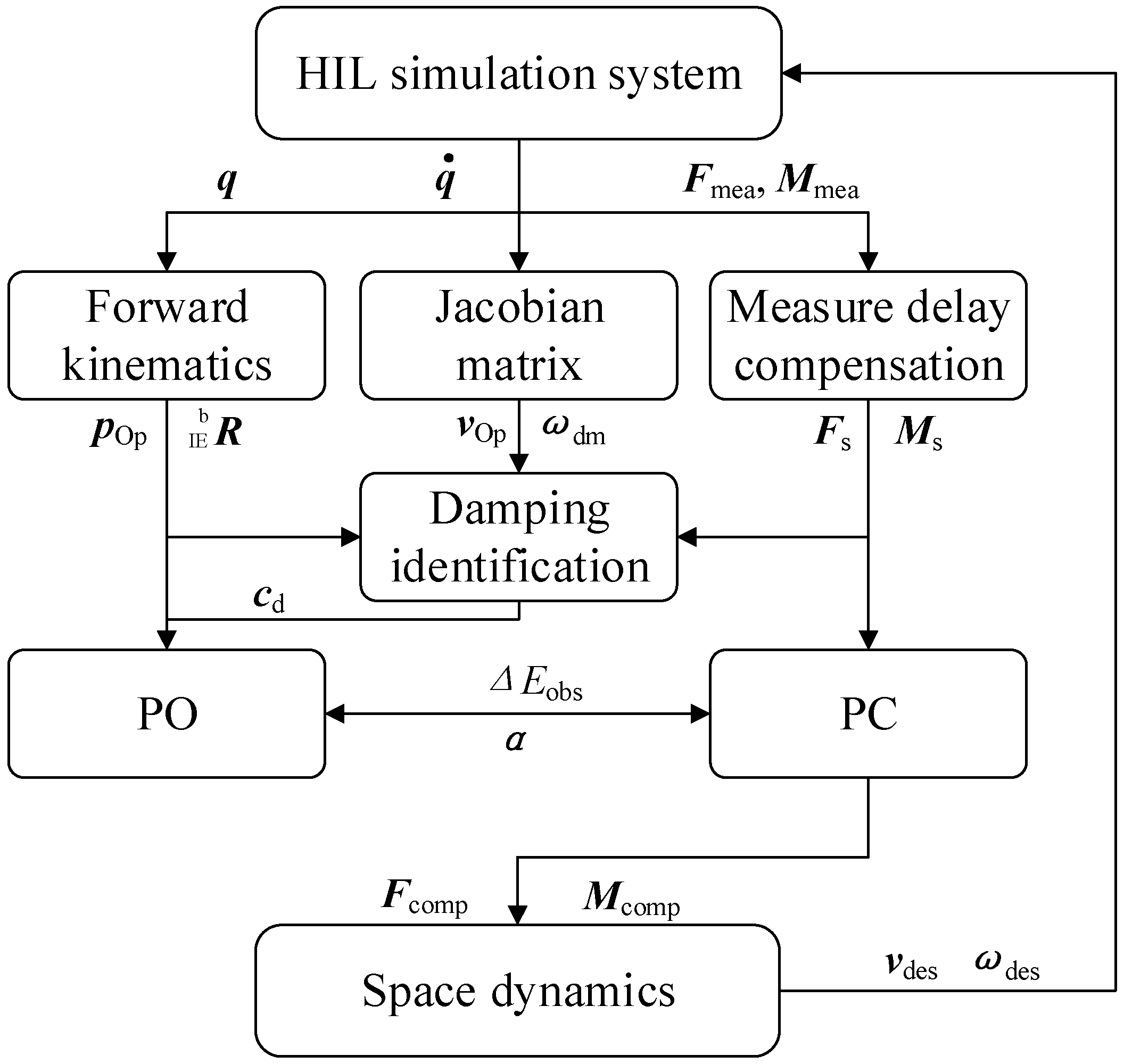
- (1)
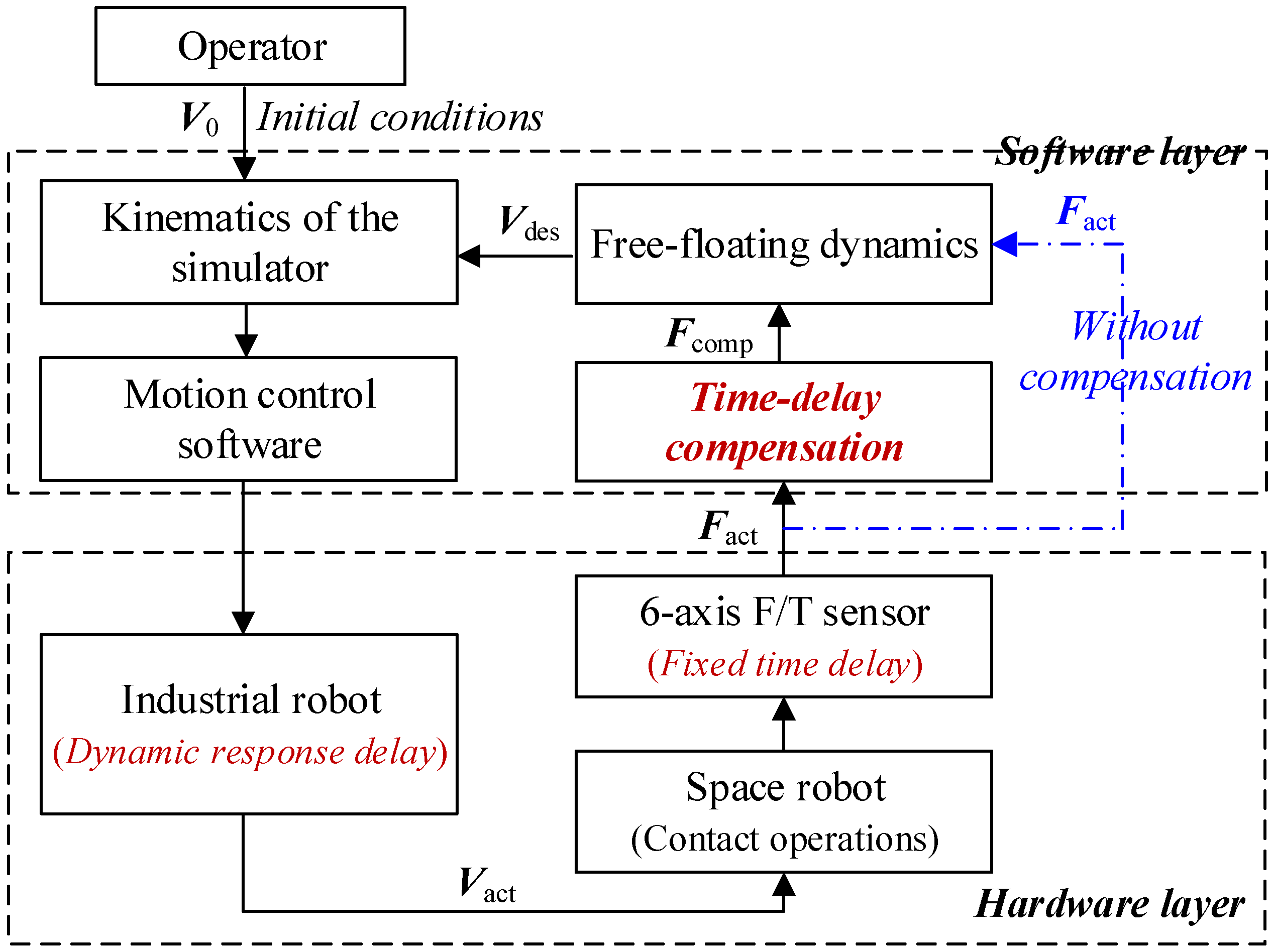
- Given the initial displacements, velocities, and accelerations of two satellites, s0, v0, and a0, respectively, the robotic simulator follows the motion trajectory to realize the first collision between the docking imitation mechanisms.
- (2)
- The six-axis F/T sensor measures the contact force and moment, Fmea and Mmea. Then, the pure time delay τm caused by the measurement system is compensated by a low-pass filter, and the actual measuring force and moment Fs and Ms are obtained.
- (3)
- By substituting Fs, Ms, pOp, and vOp into Equations (16)–(22), the contact damping, cd, is identified using the AKF method.
- (4)
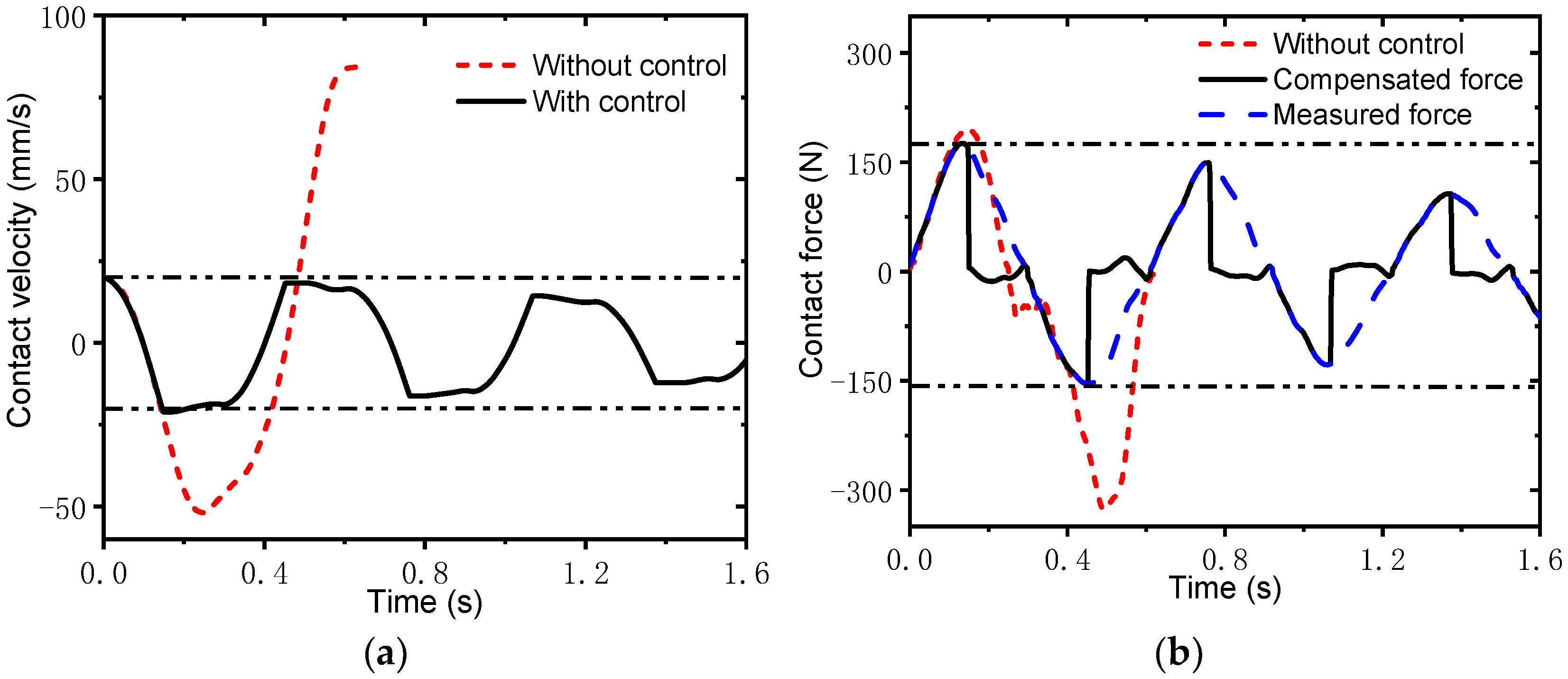
- According to the identified contact damping, the elastic contact force, Fek, is calculated. Then, by substituting Fek, Ms, , and into the PO yields the time-varying damping matrix, and thus the PC compensation force and moment, Fα and Mα, are calculated through Equations (12) and (14). Accordingly, the compensated force and moment, Fcomp and Mcomp, are obtained using Equation (15).
- (5)
- Fcomp and Mcomp are substituted into the space dynamic equations, Equations (3) and (4), to calculate the new motion trajectory of the robotic simulator, including s, v, and a. By repeating steps (1)–(5), the HIL simulation can be continued until the conclusion of the experiment.
4. Experiment and Discussion
4.1. Collisions against a Virtual Wall
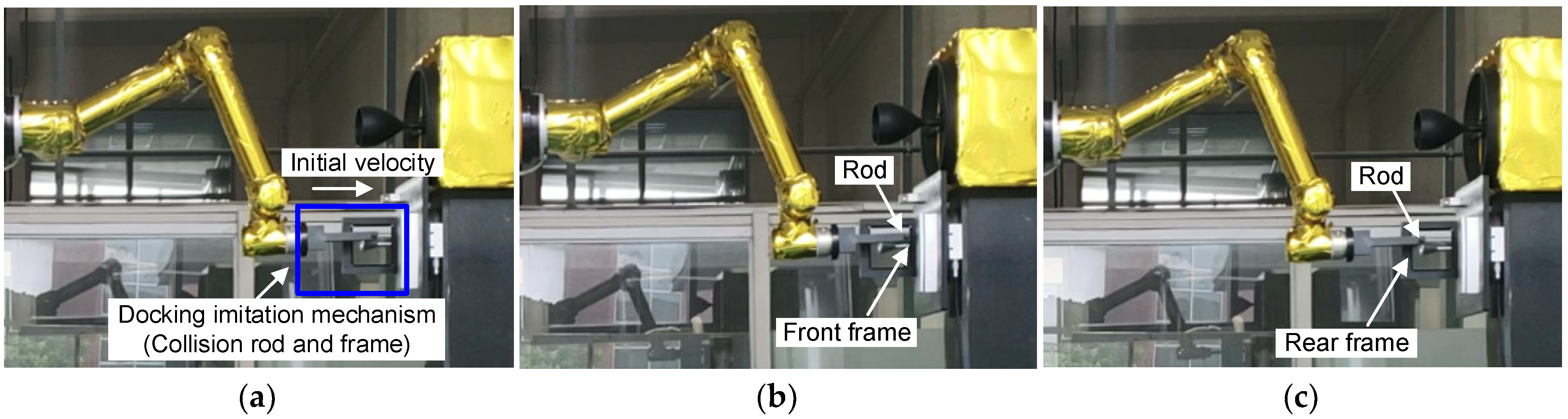
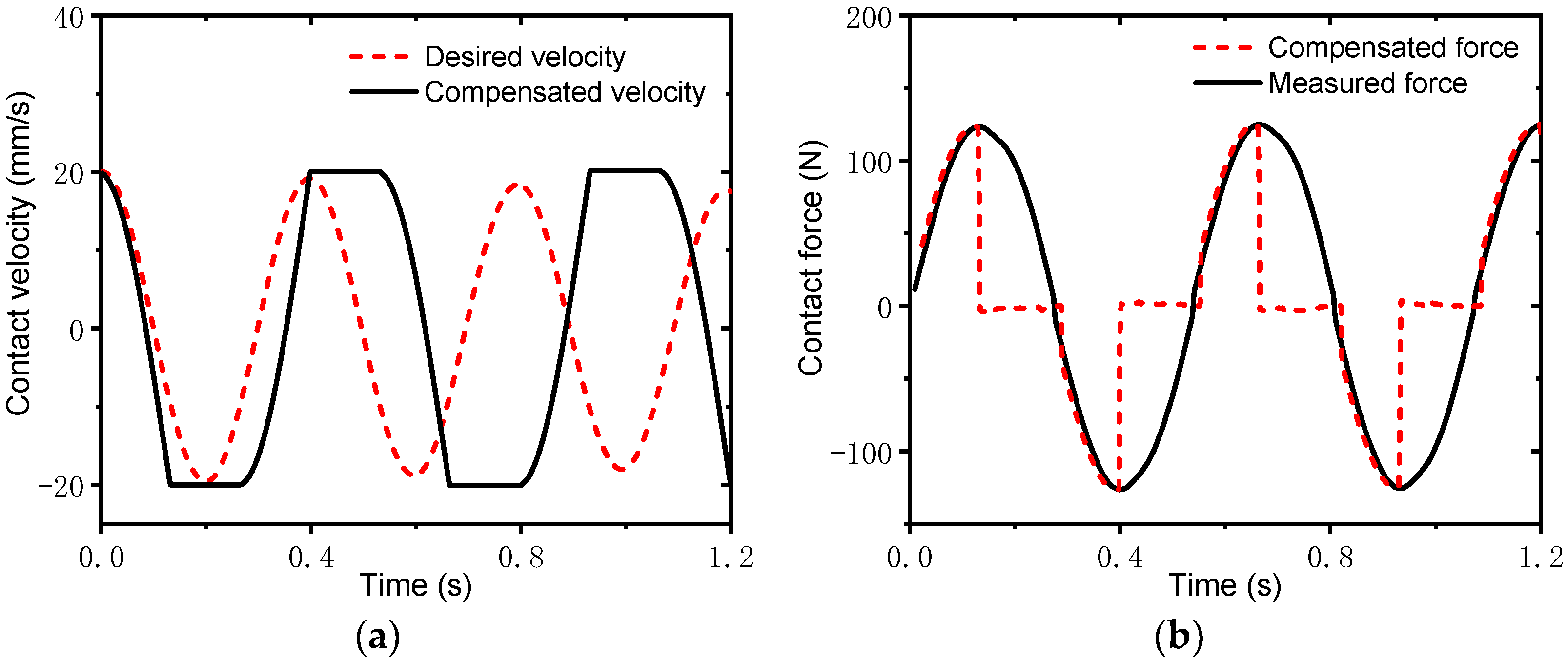
4.2. Collisions between Docking Imitation Mechanisms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Flores-Abad, A.; Ma, O.; Pham, K.; Ulrich, S. A review of space robotics technologies for on-orbit servicing. Prog. Aerosp. Sci. 2014, 68, 1–26. [Google Scholar] [CrossRef]
- Ma, B.; Xie, Z.; Jiang, Z.; Liu, H. Precise semi-analytical inverse kinematic solution for 7-DOF offset manipulator with arm angle optimization. Front. Mech. Eng. 2021, 16, 435–450. [Google Scholar] [CrossRef]
- Qi, C.; Ren, A.; Gao, F.; Zhao, X.; Wang, Q.; Sun, Q. Compensation of Velocity Divergence Caused by Dynamic Response for Hardware-in-the-Loop Docking Simulator. IEEE/ASME Trans. Mechatron. 2016, 22, 422–432. [Google Scholar] [CrossRef]
- Ma, O.; Wang, J. Model order reduction for impact-contact dynamics simulations of flexible manipulators. Robotica 2007, 25, 397–407. [Google Scholar] [CrossRef]
- Virgili-Llop, J.; Drew, J.V.; Zappulla, R.; Romano, M. Laboratory experiments of resident space object capture by a spacecraft–manipulator system. Aerosp. Sci. Technol. 2017, 71, 530–545. [Google Scholar] [CrossRef]
- He, J.; Zheng, H.; Gao, F.; Zhang, H. Dynamics and control of a 7-DOF hybrid manipulator for capturing a non-cooperative target in space. Mech. Mach. Theory 2019, 140, 83–103. [Google Scholar] [CrossRef]
- Carignan, C.; Akin, D. The reaction stabilization of on-orbit robots. IEEE Control Syst. 2000, 20, 19–33. [Google Scholar] [CrossRef]
- Watanabe, Y.; Nakamura, Y. Experiments of a space robot in the free-fall environment. In Proceedings of the 5th International Symposium on Artificial Intelligence, Robotics and Automation in Space, Noordwijk, The Netherlands, 1–3 June 1999. [Google Scholar]
- Shimoji, H.; Inoue, M.; Tsuchiya, K.; Niomiya, K.; Nakatani, I.; Kawaguchi, J. Simulation system for a space robot using six-axis servos. Adv. Robot. 1991, 6, 179–196. [Google Scholar] [CrossRef][Green Version]
- Mitchell, J.D.; Cryan, S.P.; Baker, K.; Martin, T.; Goode, R.; Key, K.W.; Manning, T.; Chien, C. Integrated docking simulation and testing with the Johnson Space Center six-degree-of-freedom dynamic test system. In Proceedings of the Space Technology and Applications International Forum—STAIF 2008, Albuquerque, NM, USA, 10–14 February 2008. [Google Scholar]
- Takahashi, R.; Ise, H.; Konno, A.; Uchiyama, M.; Sato, D. Hybrid simulation of a dual-arm space robot colliding with a floating object. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, LA, USA, 19–23 May 2008. [Google Scholar]
- Matunaga, S.; Yoshihara, K.; Takahashi, T.; Tsurumi, S.; Ui, K. Ground experiment system for dual-manipulator-based capture of damaged satellites. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Takamatsu, Japan, 30 October–5 November 2000; pp. 1847–1852. [Google Scholar]
- Rekleitis, I.; Martin, E.; Rouleau, G.; L’Archevêque, R.; Parsa, K.; Dupuis, E. Autonomous capture of a tumbling satellite. J. Field Robot. 2007, 24, 275–296. [Google Scholar] [CrossRef]
- Ma, O.; Flores-Abad, A.; Boge, T. Use of industrial robots for hardware-in-the-loop simulation of satellite rendezvous and docking. Acta Astronaut. 2012, 81, 335–347. [Google Scholar] [CrossRef]
- Sellmaier, F.; Boge, T.; Spurmann, J.; Gully, S.; Rupp, T.; Huber, F. On-orbit servicing missions: Challenges and solutions for spacecraft operations. In Proceedings of the 11th International Conference on Space Operations, Huntsville, AL, USA, 25–30 April 2010. [Google Scholar]
- Gao, F.; Qi, C.; Ren, A.; Zhao, X.; Cao, R.; Sun, Q.; Wang, Q.; Hu, Y.; He, J.; Jin, Z.; et al. Hardware-in-the-loop simulation for the contact dynamic process of flying objects in space. Sci. China Technol. Sci. 2016, 59, 1167–1175. [Google Scholar] [CrossRef]
- Osaki, K.; Konno, A.; Uchiyama, M. Delay Time Compensation for a Hybrid Simulator. Adv. Robot. 2010, 24, 1081–1098. [Google Scholar] [CrossRef]
- Diolaiti, N.; Niemeyer, G.; Barbagli, F.; Salisbury, J. Stability of Haptic Rendering: Discretization, Quantization, Time Delay, and Coulomb Effects. IEEE Trans. Robot. 2006, 22, 256–268. [Google Scholar] [CrossRef]
- Meng, Q.; Xie, F.; Liu, X.-J. Conceptual design and kinematic analysis of a novel parallel robot for high-speed pick-and-place operations. Front. Mech. Eng. 2017, 13, 211–224. [Google Scholar] [CrossRef]
- Abiko, S.; Satake, Y.; Jiang, X.; Tsujita, T.; Uchiyama, M. Delay time compensation based on coefficient of restitution for collision hybrid motion simulator. Adv. Robot. 2014, 28, 1177–1188. [Google Scholar] [CrossRef]
- Arnold, V.I. Mathematical Methods of Classical Mechanics, 2nd ed.; Springer: New York, NY, USA, 1989; pp. 59–60. [Google Scholar]
- Colgate, J.E.; Hogan, N. Robust control of dynamically interacting systems. Int. J. Control 1988, 48, 65–88. [Google Scholar] [CrossRef]
- Berghuis, H.; Nijmeijer, H. A passivity approach to controller-observer design for robots. IEEE Trans. Robot. Autom. 1993, 9, 740–754. [Google Scholar] [CrossRef]
- Ajwad, S.A.; Iqbal, J.; Ullah, M.I.; Mehmood, A. A systematic review of current and emergent manipulator control approaches. Front. Mech. Eng. 2015, 10, 198–210. [Google Scholar] [CrossRef]
- Ryu, J.-H.; Kwon, D.-S.; Hannaford, B. Stability Guaranteed Control: Time Domain Passivity Approach. IEEE Trans. Control Syst. Technol. 2004, 12, 860–868. [Google Scholar] [CrossRef]
- Ryu, J.-H.; Kwon, D.-S.; Hannaford, B. Stable Teleoperation with Time-Domain Passivity Control. IEEE Trans. Robot. Autom. 2004, 20, 365–373. [Google Scholar] [CrossRef]
- Hannaford, B.; Ryu, J.H. Time domain passivity control of haptic interfaces. In Proceedings of the IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001. [Google Scholar]
- Marco, D.S.; Ribin, B.; Cristian, S. A passivity-based approach for simulating satellite dynamics with robots: Discrete-time integration and time-delay compensation. IEEE Trans. Rob. 2020, 36, 189–203. [Google Scholar]
- Craig, J.J. Introduction to Robotics, 3rd ed.; Pearson Education: Upper Saddle River, NJ, USA, 2005; pp. 11–117. [Google Scholar]
- Lu, P.; Zhao, L.; Chen, Z. Improved Sage-Husa adaptive filtering and its application. J. Syst. Simul. 2007, 19, 3503–3505. [Google Scholar]
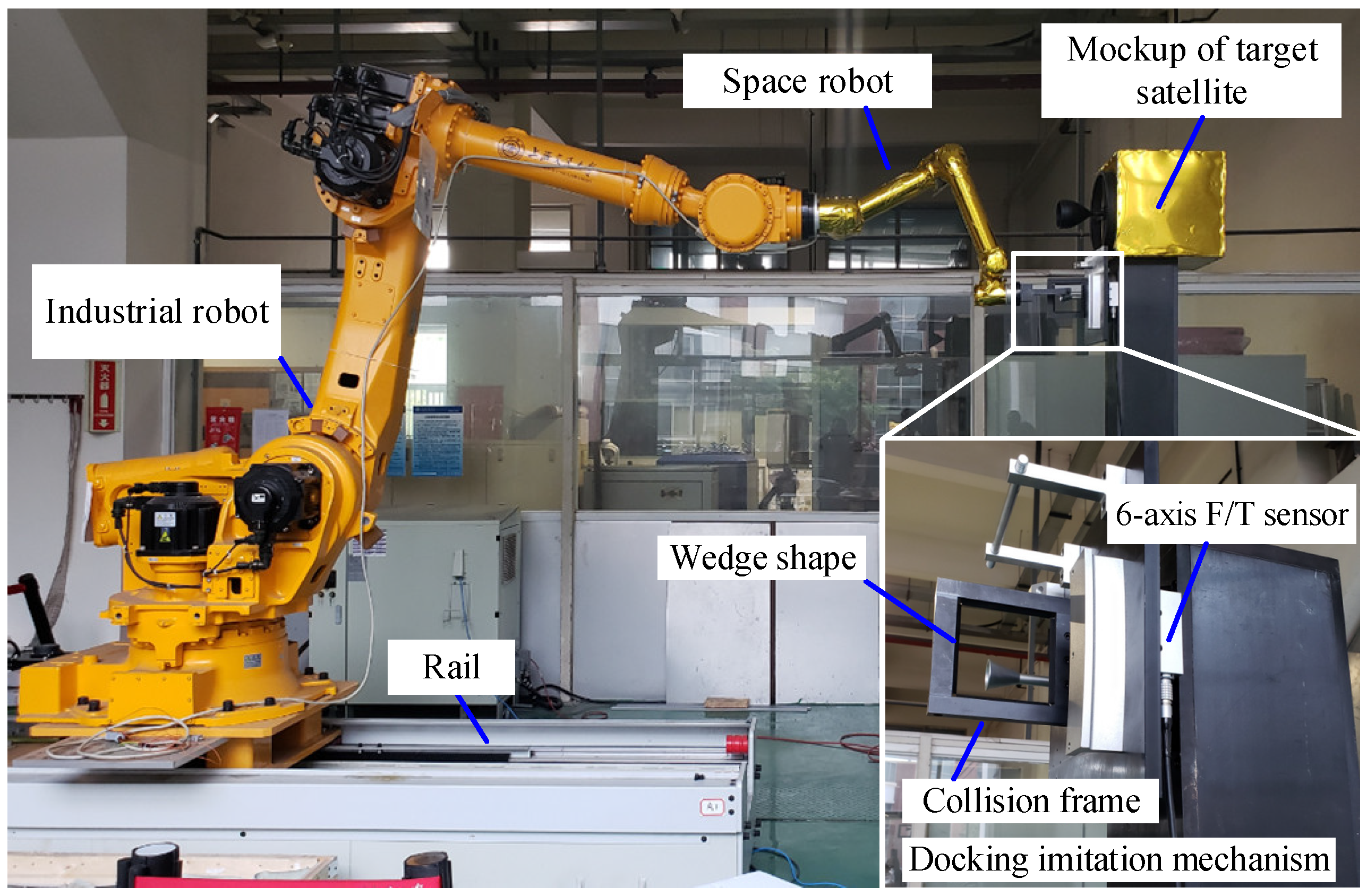
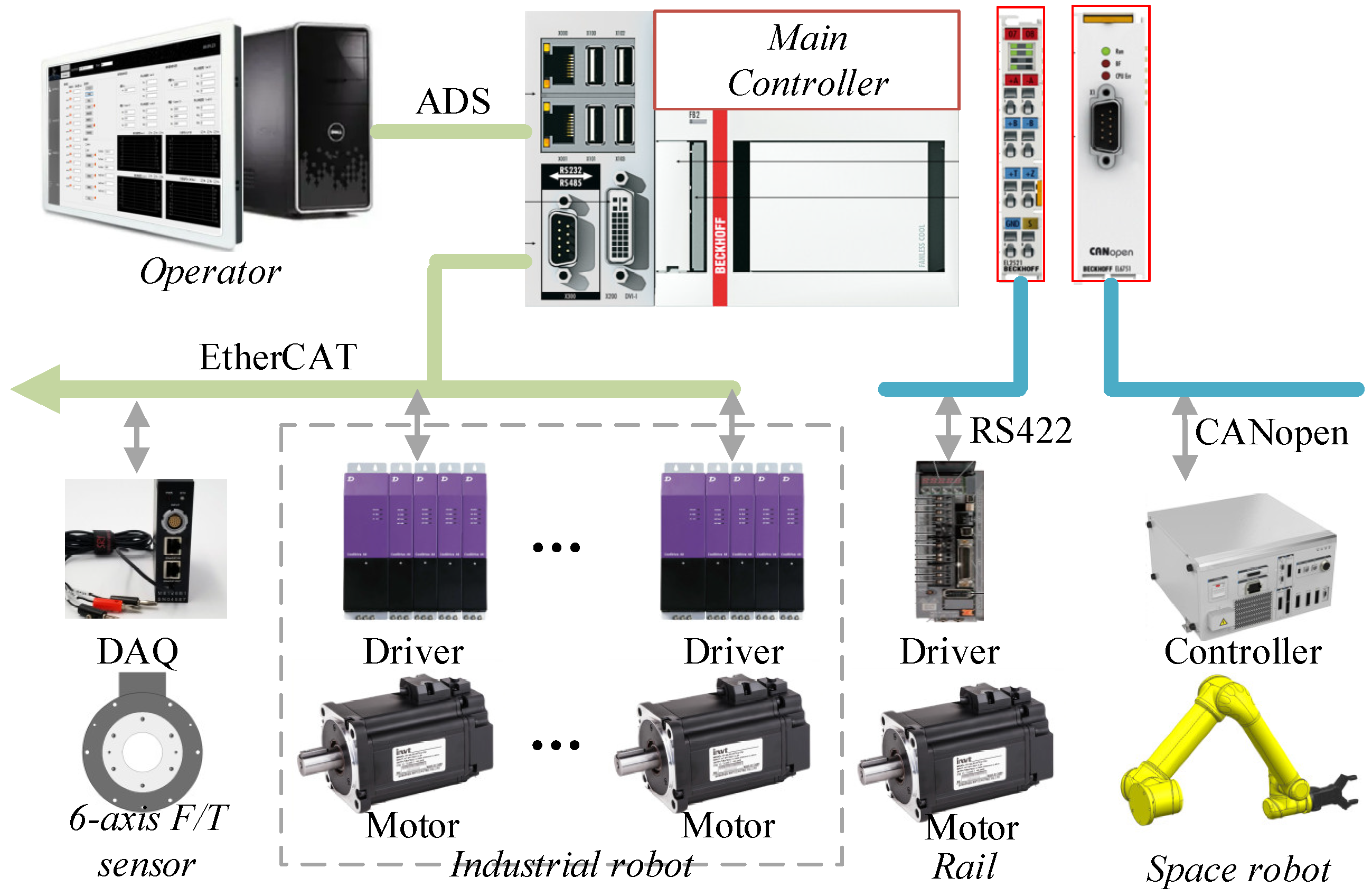
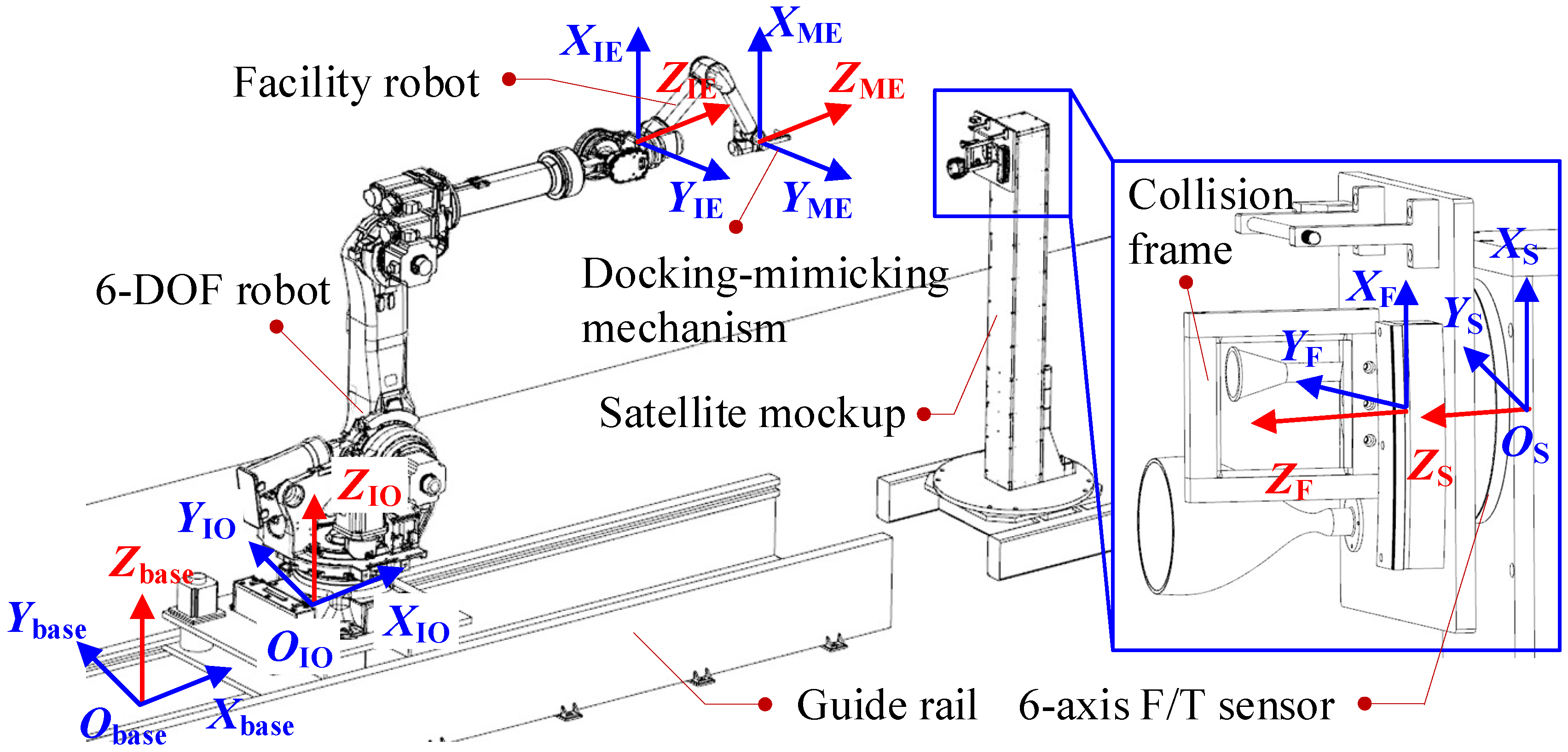




| Module | Specifications | Unit | Value |
|---|---|---|---|
| Industrial robot | DoF | - | 6 |
| Payload | kg | 210 | |
| Maximum reach | mm | 2674 | |
| Repeatability | mm | ±0.3 | |
| Rail | DoF | - | 1 |
| Payload | kg | 3000 | |
| Length | mm | 12,000 | |
| Speed | mm/s | 1600 | |
| Repeatability | mm | ±0.05 | |
| Space robot | DoF | - | 6 |
| Payload | kg | 5 | |
| Maximum reach | mm | 800 | |
| Repeatability | mm | ±0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Shen, M.; Gao, F. A Passivity-Based Velocity Control Method of Hardware-in-the-Loop Simulation for Space Robotic Operations. Aerospace 2022, 9, 368. https://doi.org/10.3390/aerospace9070368
He J, Shen M, Gao F. A Passivity-Based Velocity Control Method of Hardware-in-the-Loop Simulation for Space Robotic Operations. Aerospace. 2022; 9(7):368. https://doi.org/10.3390/aerospace9070368
Chicago/Turabian StyleHe, Jun, Mingjin Shen, and Feng Gao. 2022. "A Passivity-Based Velocity Control Method of Hardware-in-the-Loop Simulation for Space Robotic Operations" Aerospace 9, no. 7: 368. https://doi.org/10.3390/aerospace9070368
APA StyleHe, J., Shen, M., & Gao, F. (2022). A Passivity-Based Velocity Control Method of Hardware-in-the-Loop Simulation for Space Robotic Operations. Aerospace, 9(7), 368. https://doi.org/10.3390/aerospace9070368





