A New ϵ-Adaptive Algorithm for Improving Weighted Compact Nonlinear Scheme with Applications
Abstract
:1. Introduction
2. Numerical Methods
2.1. Difference Scheme
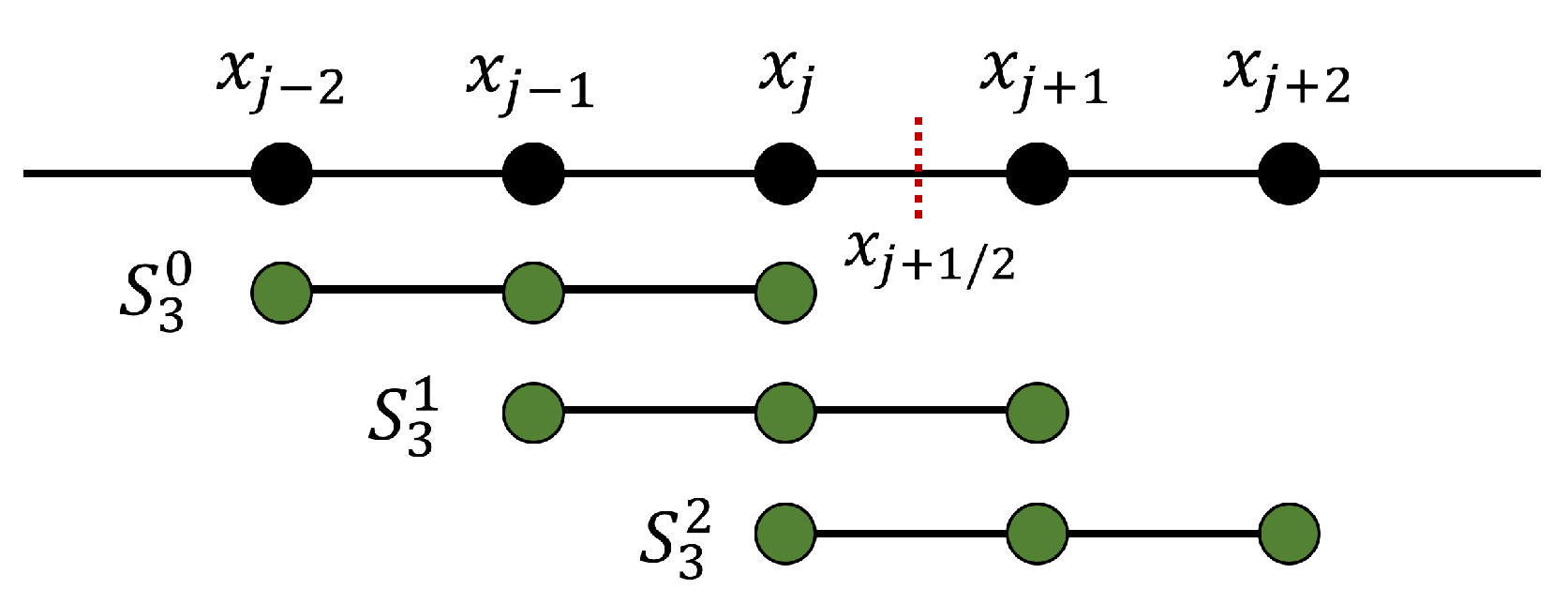
2.2. Interpolation Scheme
2.3. Adaptive Algorithms of
2.3.1. Discussion on
2.3.2. New -Adaptive Algorithms
- (1)
- In smooth regions, the smoothness indicator of each sub-stencil is uniformly small. To make the nonlinear weights approach the optimal weights, should take a much larger value than to cover up the difference of , thereby reducing the nonlinear error and improving accuracy.
- (2)
- In discontinuous regions, of the sub-stencil with discontinuity is very large. To avoid interpolation across discontinuities, should take a much smaller value than to preserve the difference of , thereby reducing the weight of the discontinuous sub-stencil to suppress numerical oscillations.
2.4. Analysis of
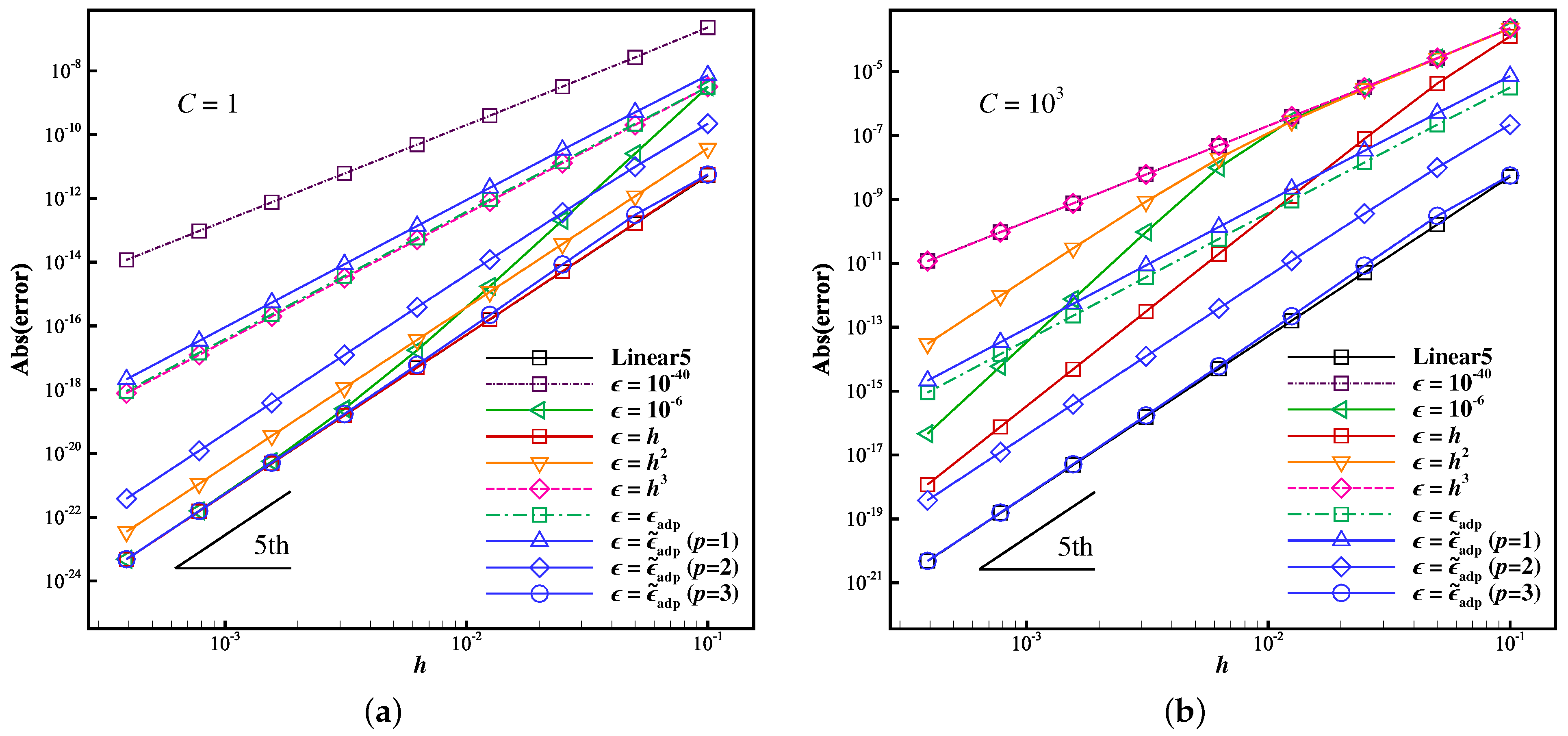
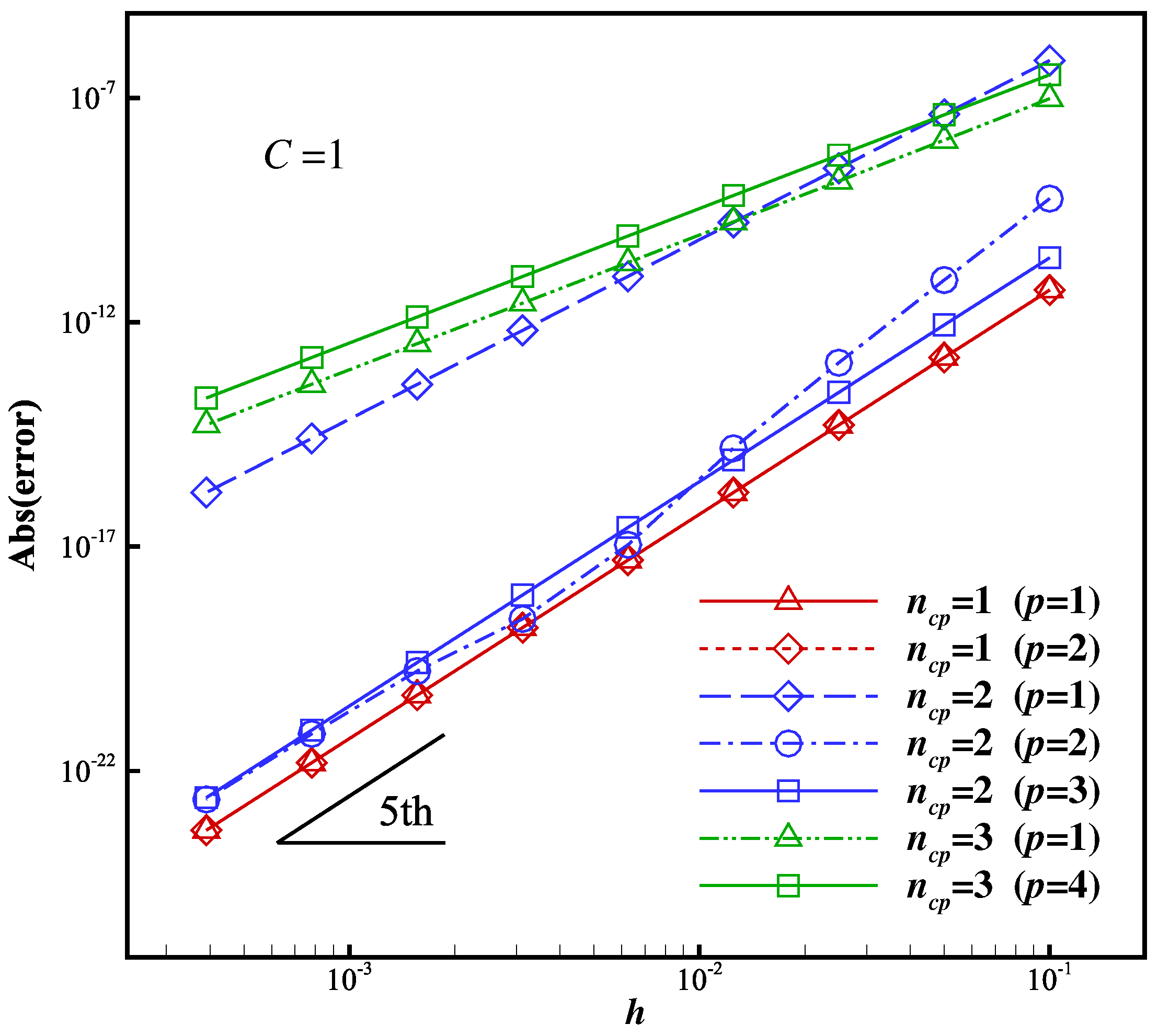
2.4.1. Convergence Accuracy
2.4.2. Convergence at Critical Points
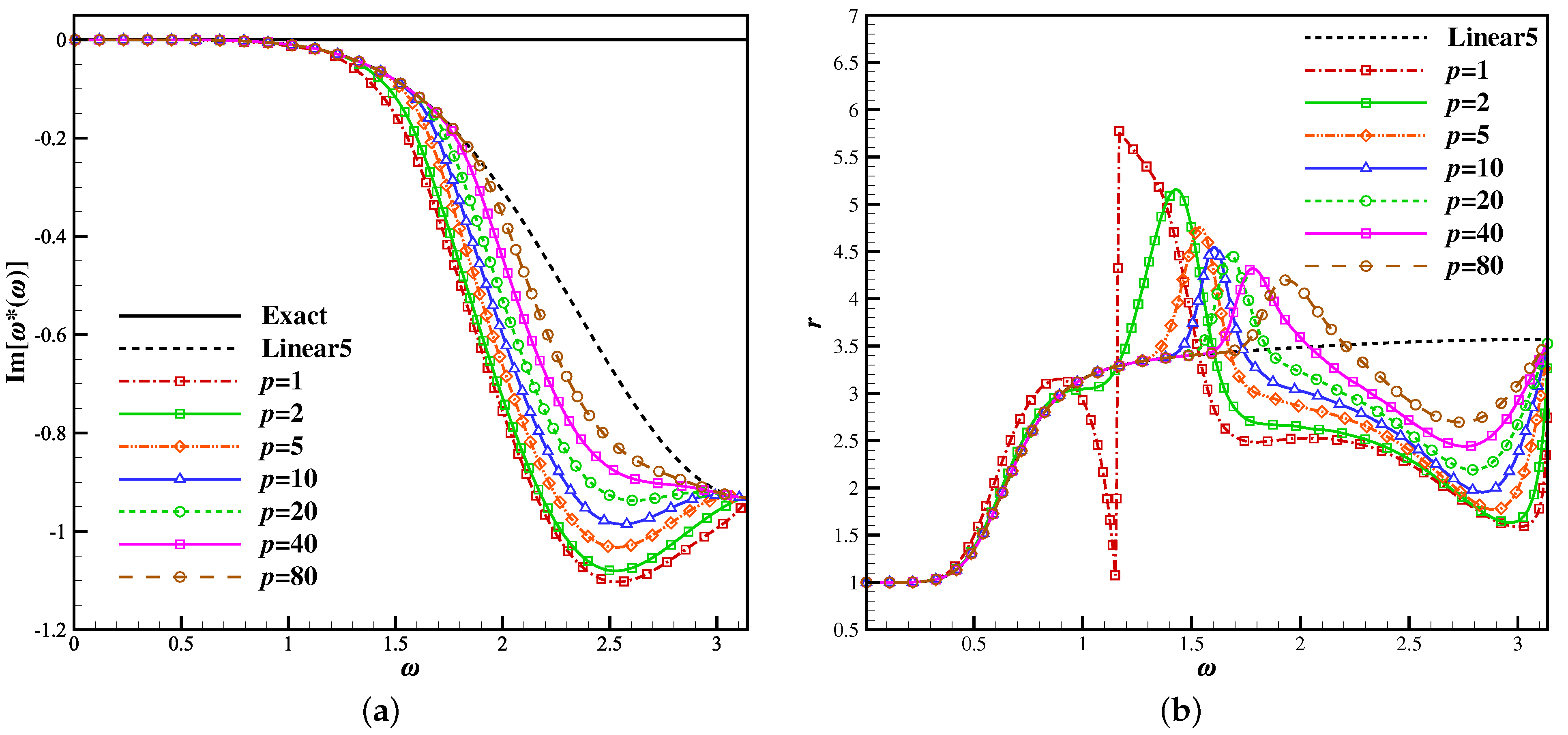
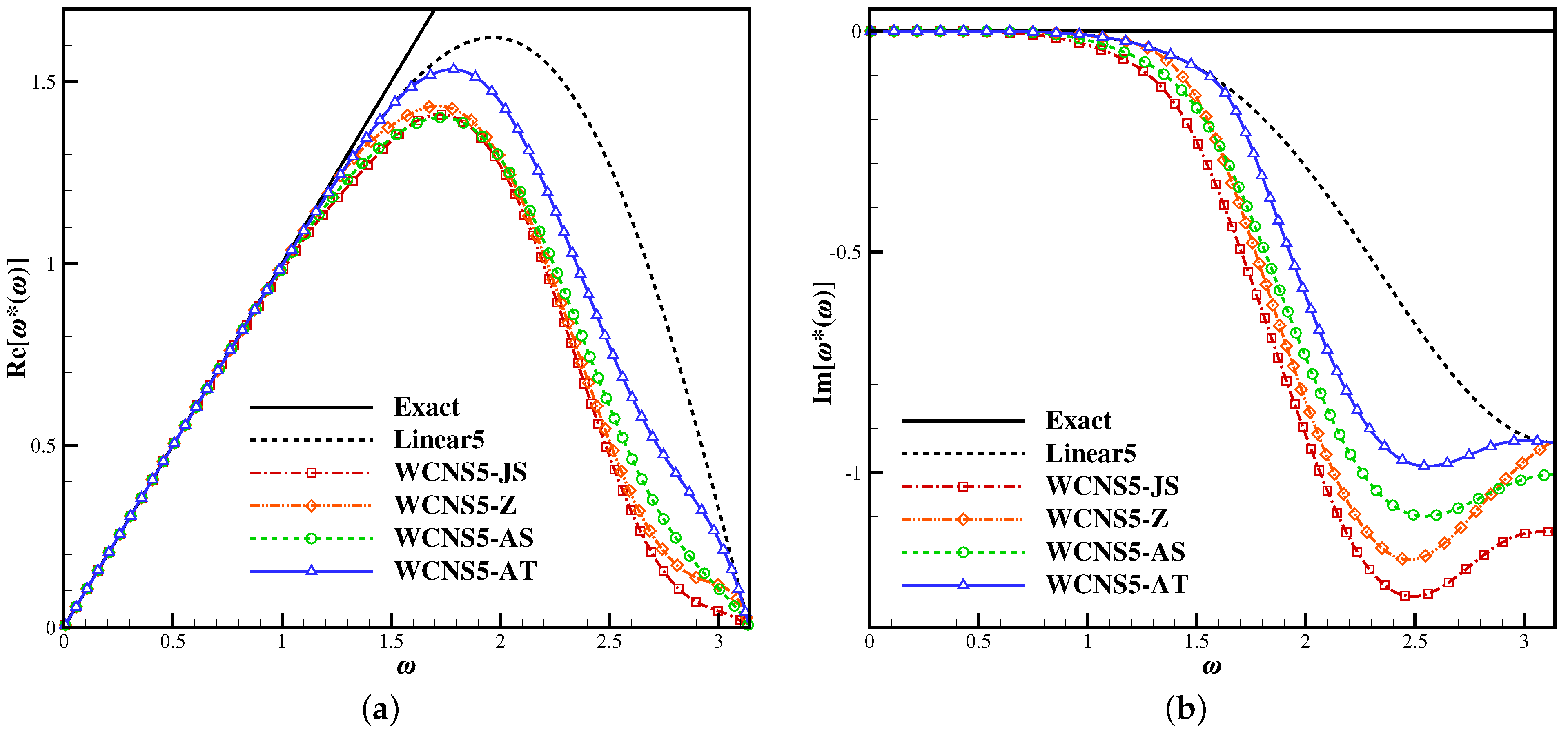
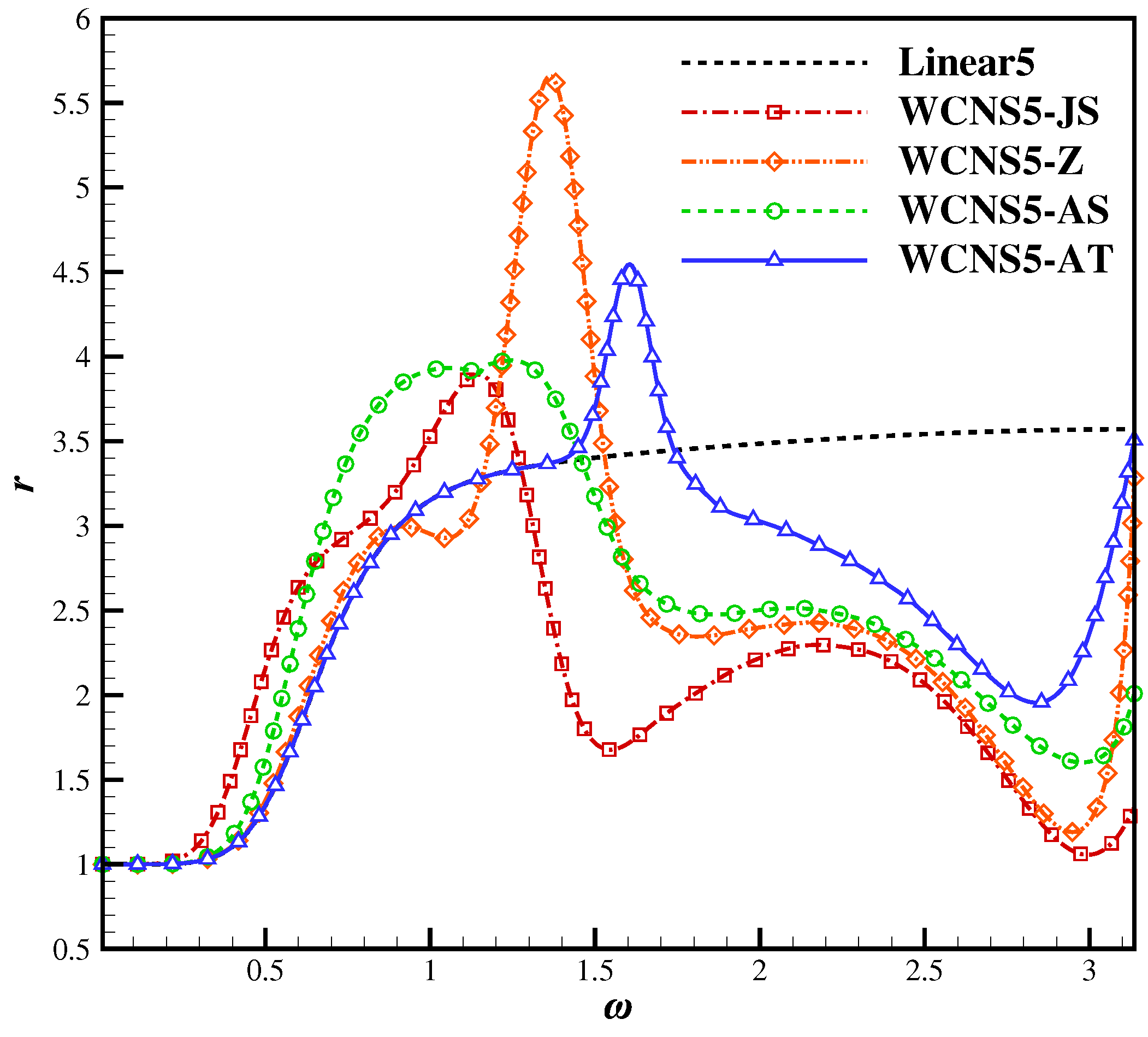
2.4.3. Spectral Properties
3. Numerical Tests
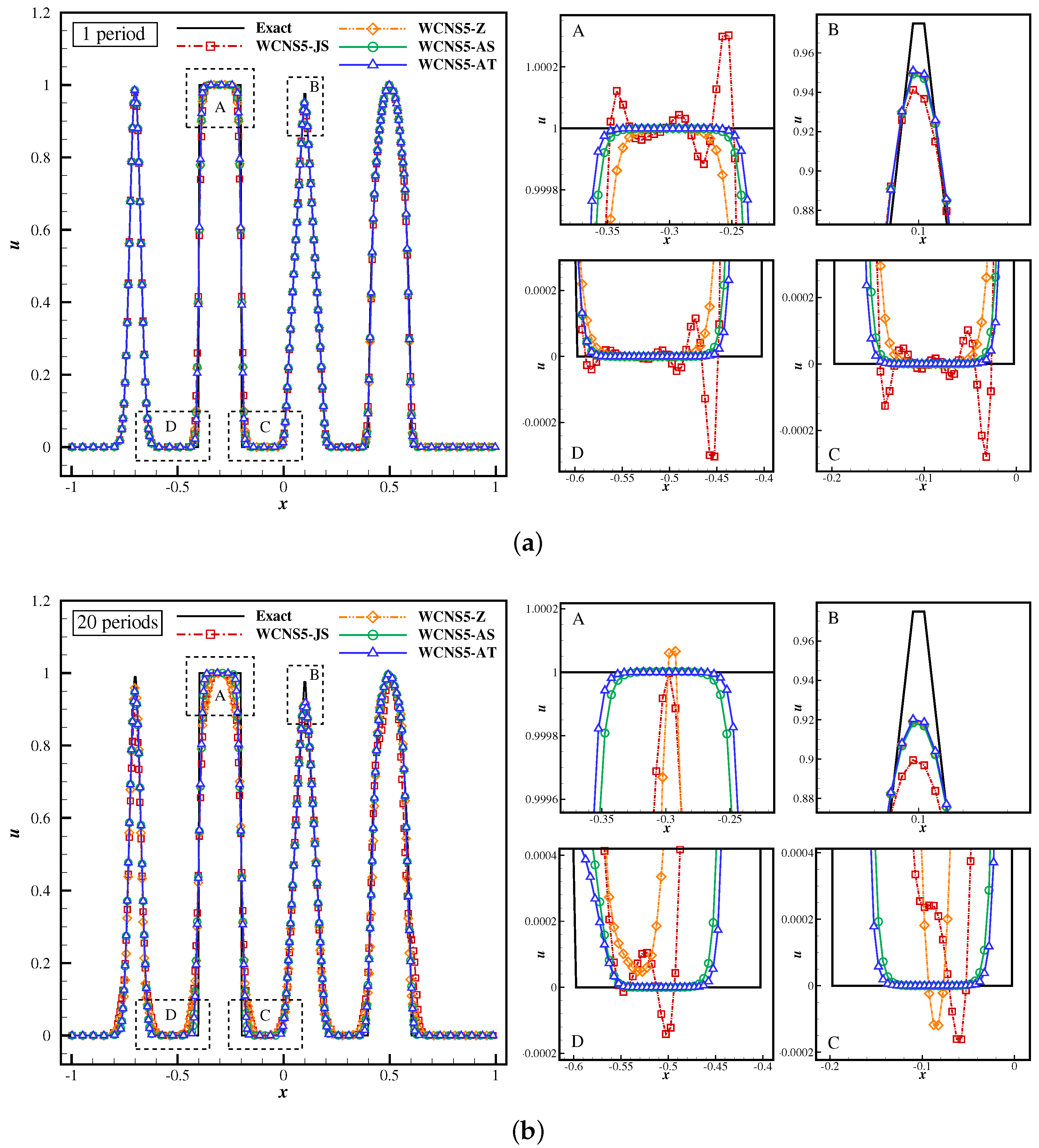
3.1. One-Dimensional Linear Advection Equation
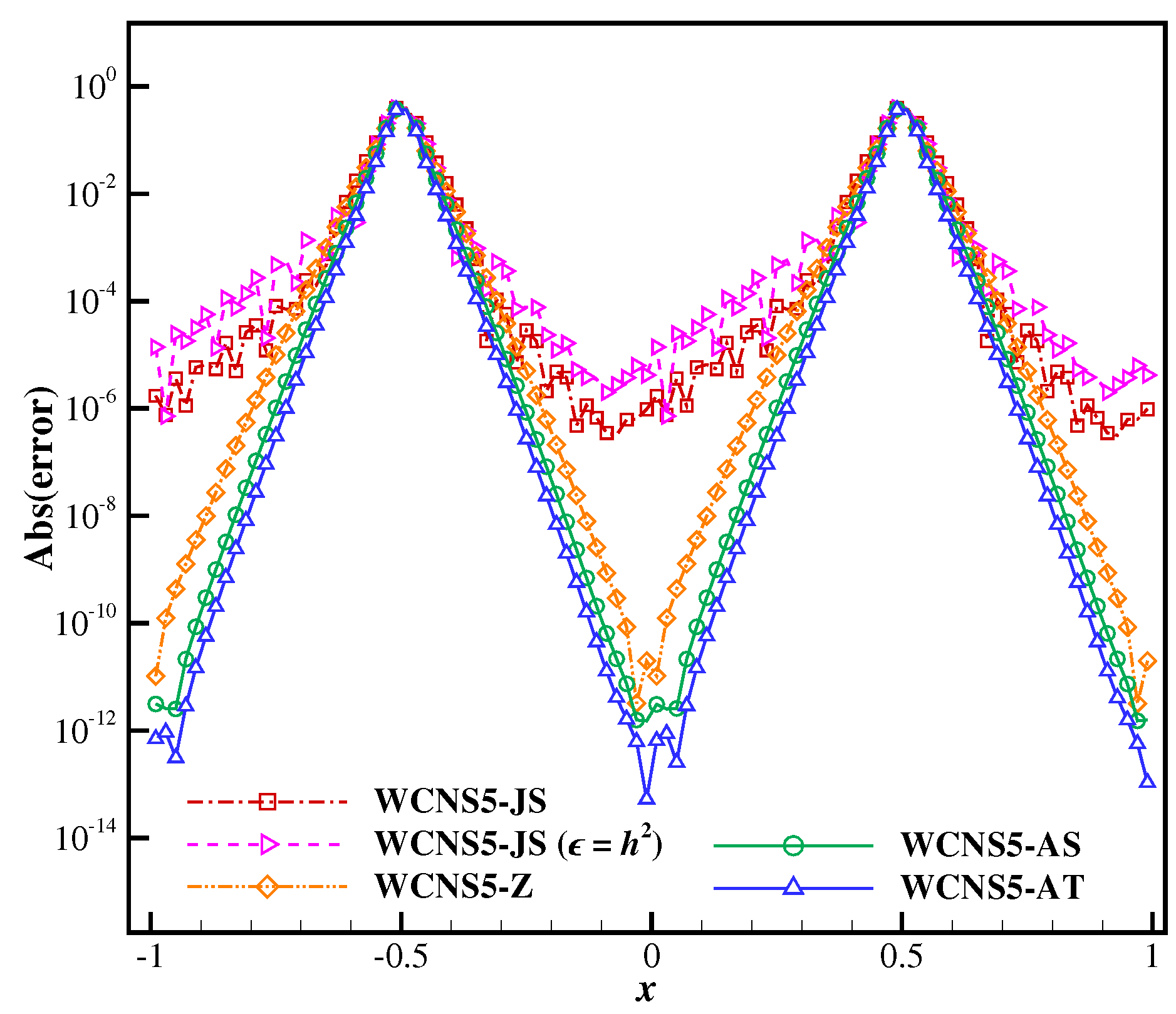
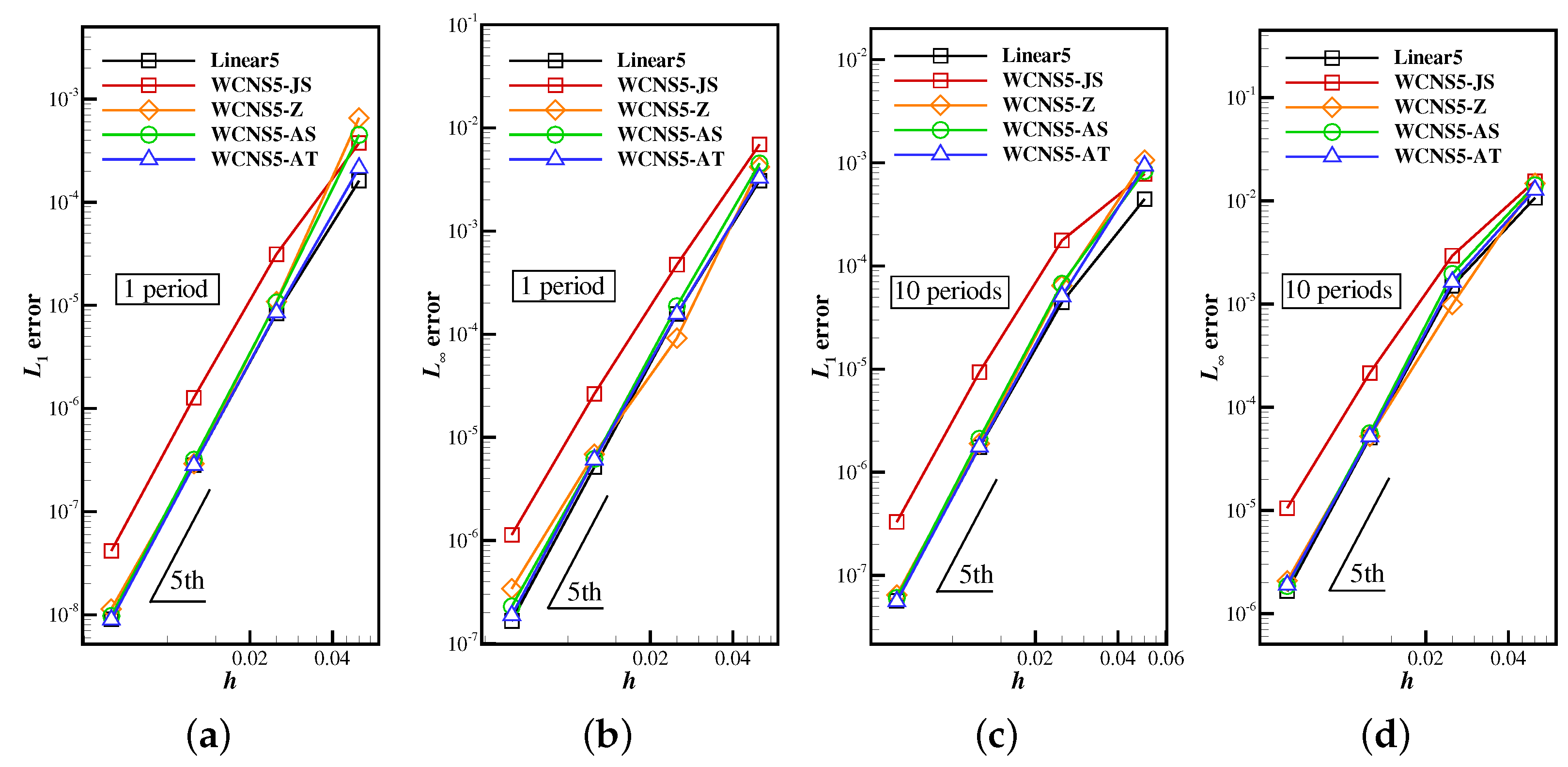
3.1.1. Wave Packet
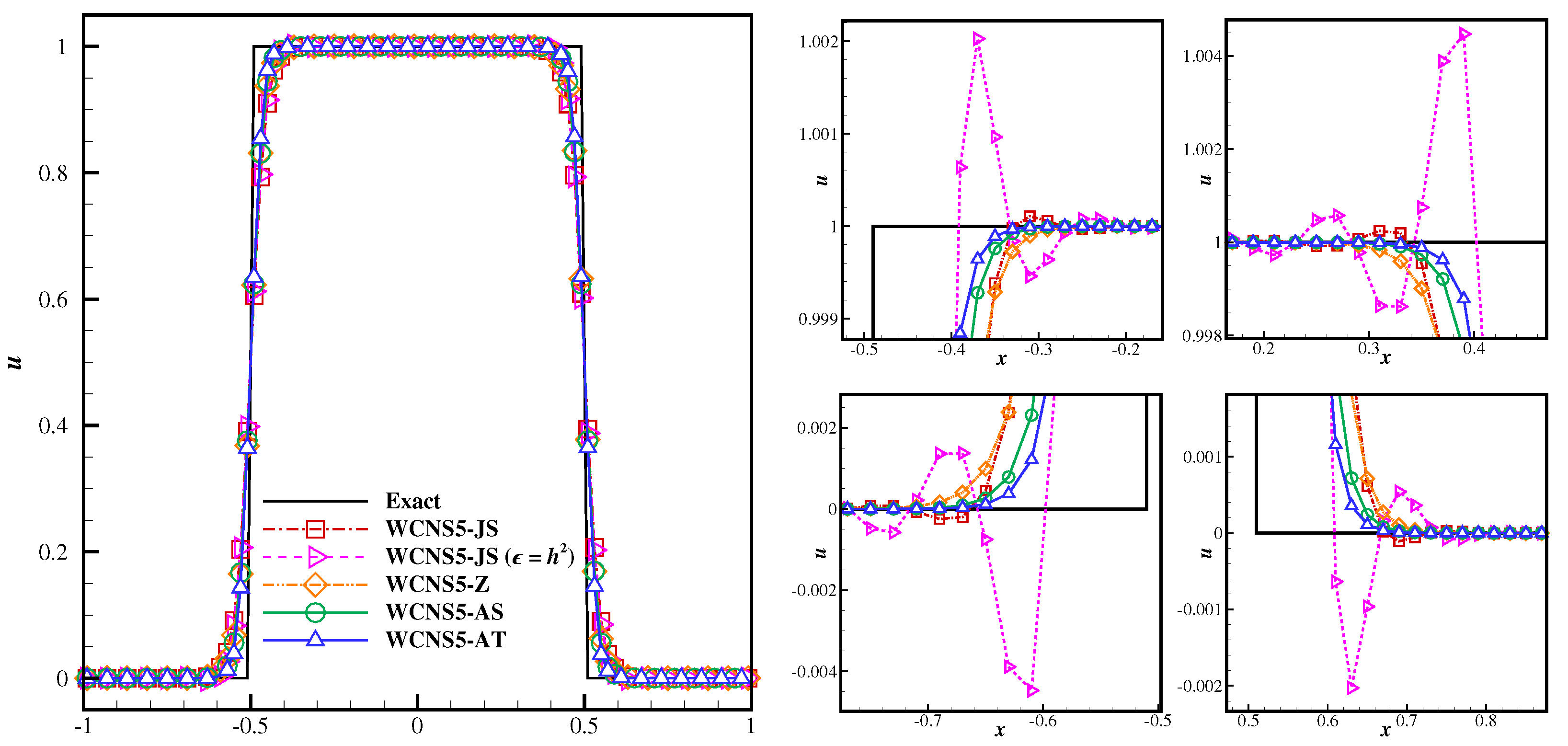
3.1.2. Square Wave
3.1.3. Composite Wave
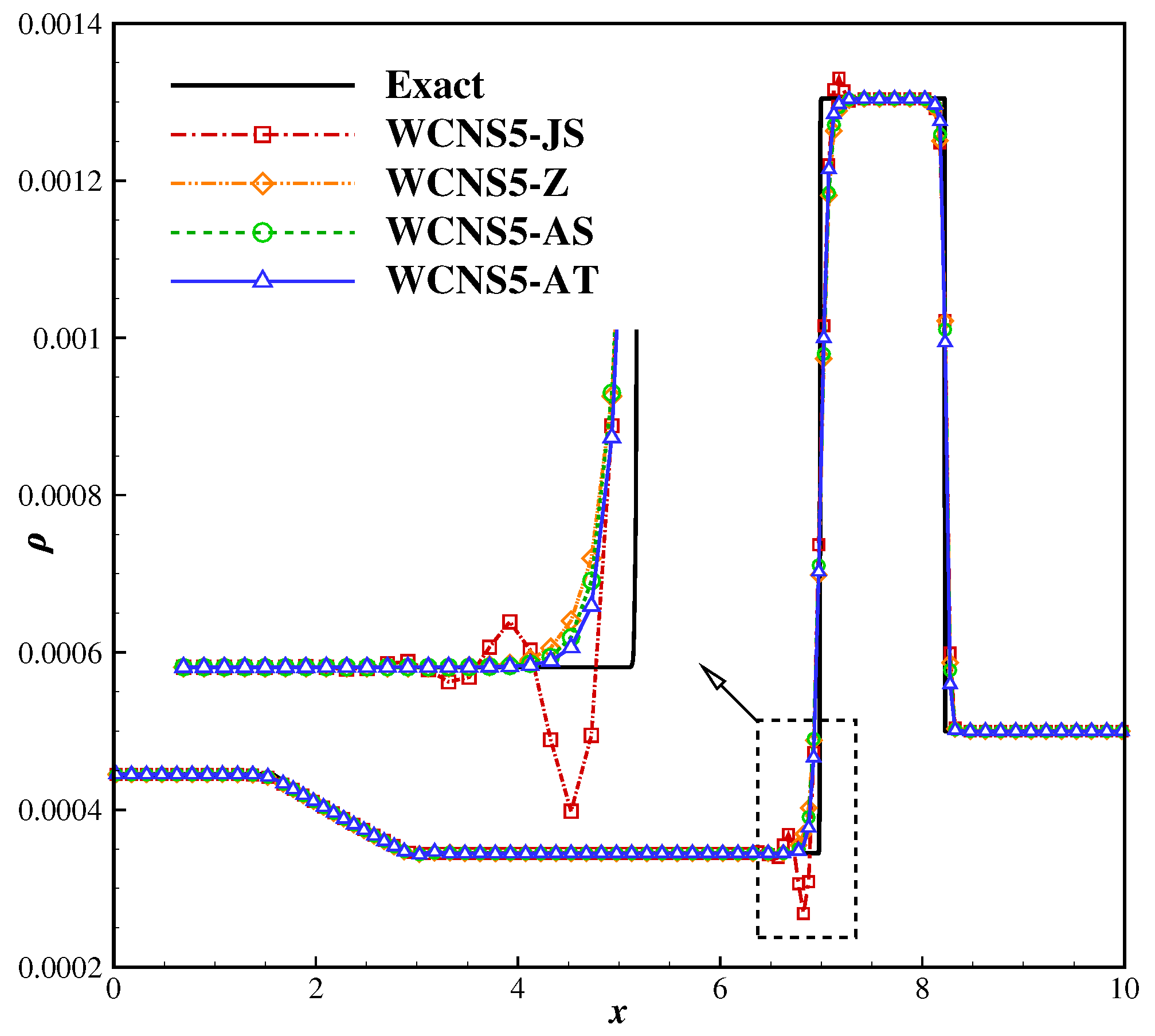
3.2. One-Dimensional Euler Equations
3.2.1. Shock Tube Problem
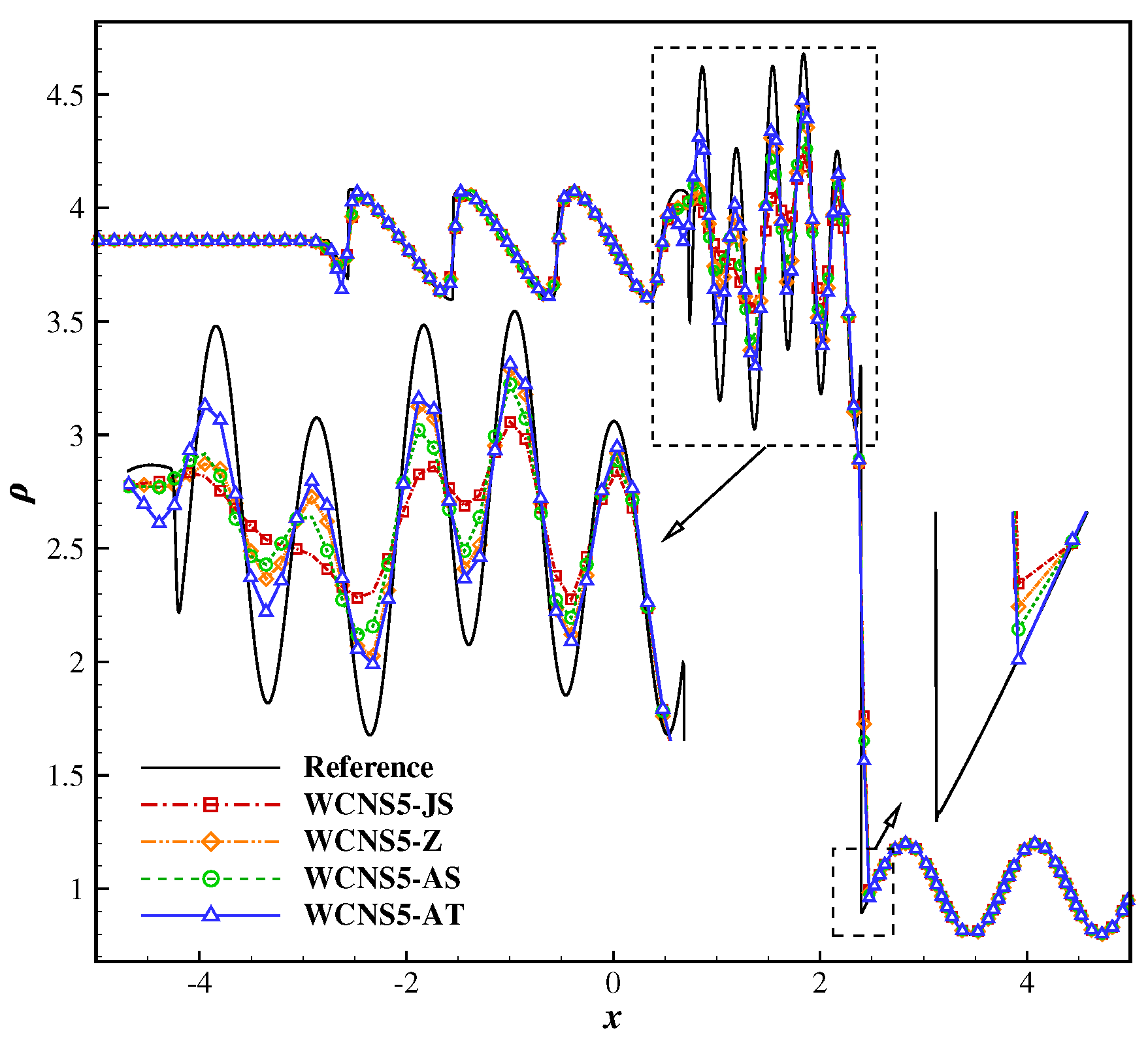
3.2.2. Shu-Osher Problem
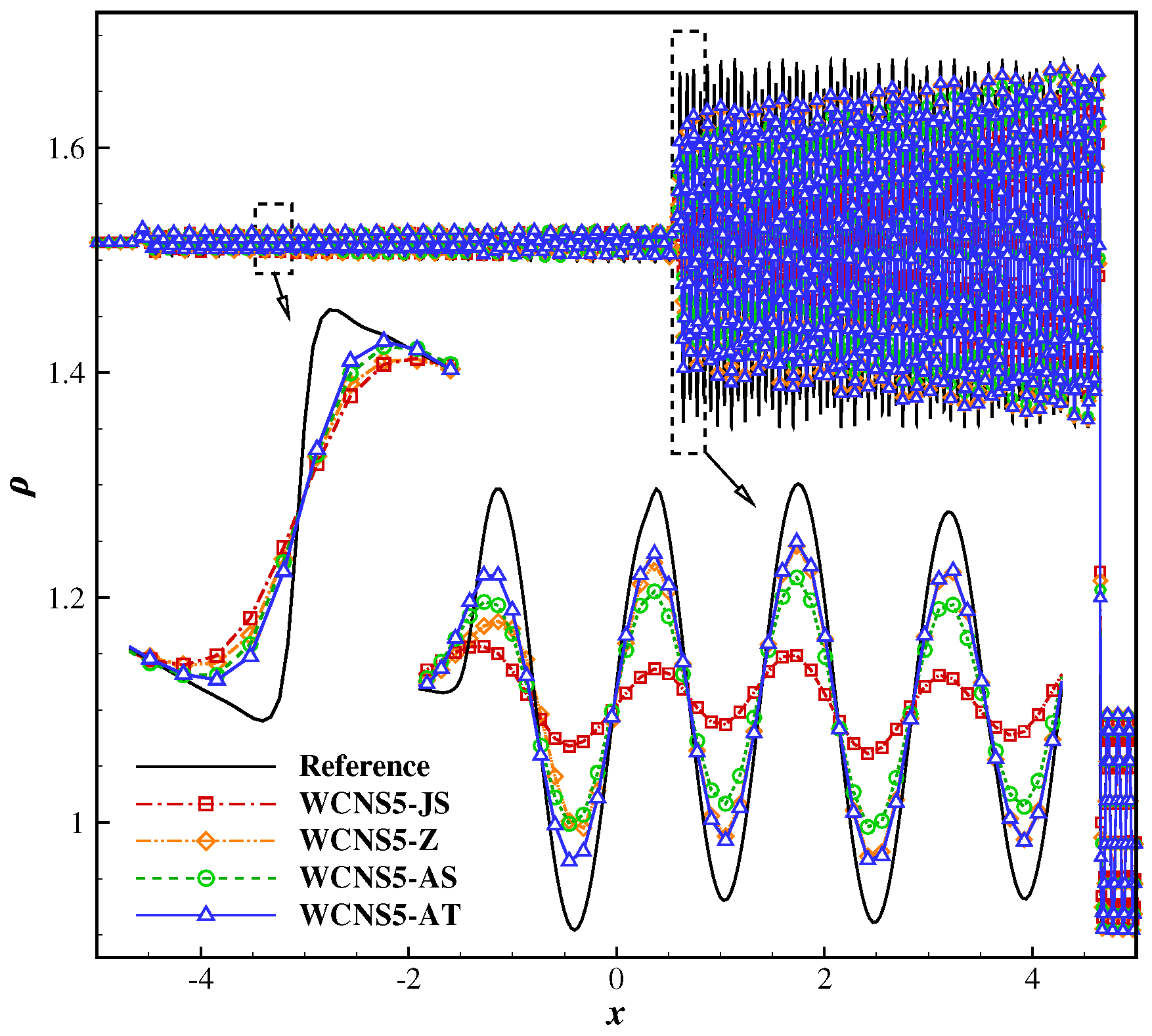
3.2.3. Titarev-Toro Problem
3.3. Two-Dimensional Euler Equations
3.3.1. Isentropic Vortex Transport
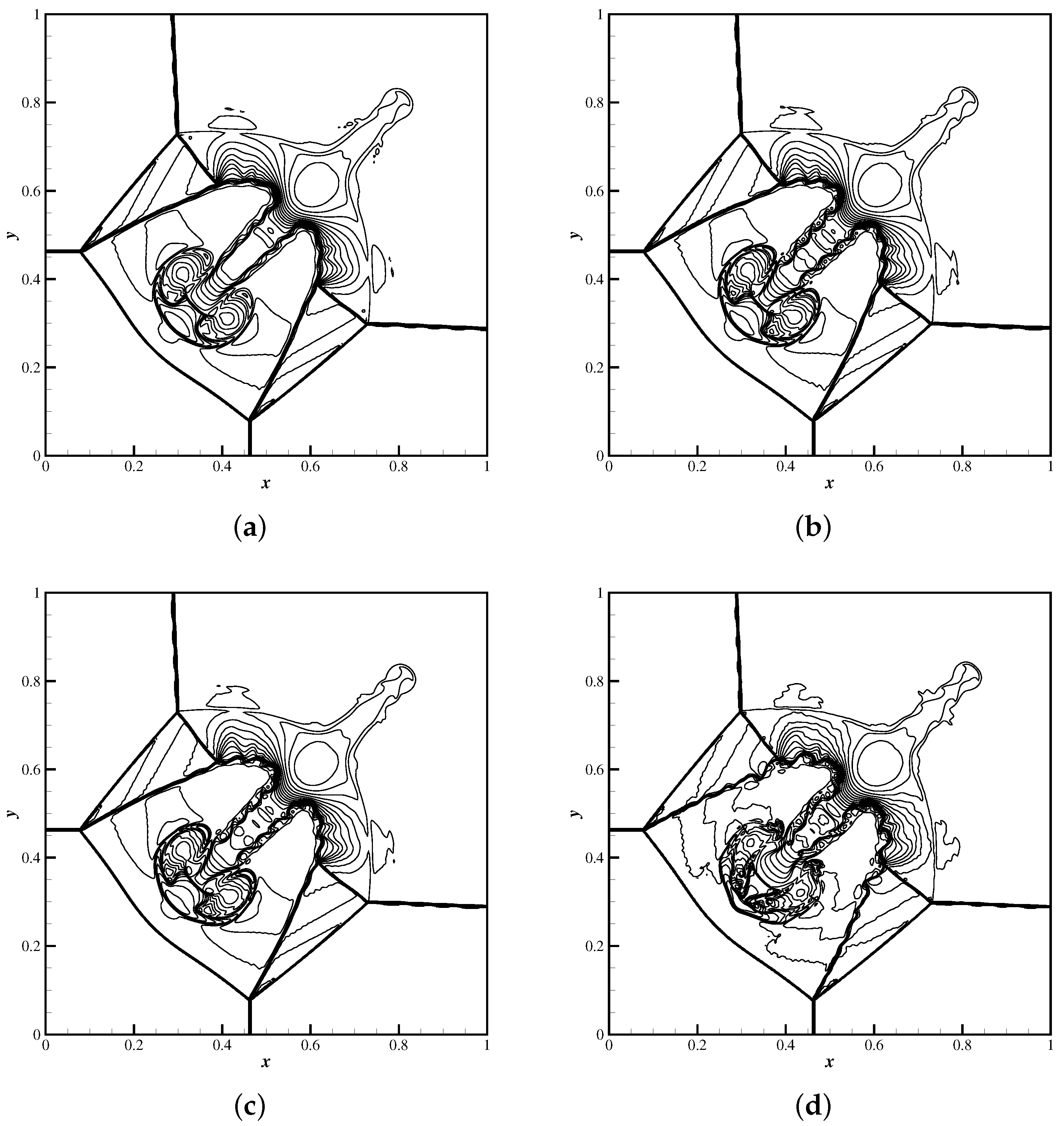
3.3.2. Two-Dimensional Riemann Problem
3.3.3. Rayleigh-Taylor Instability
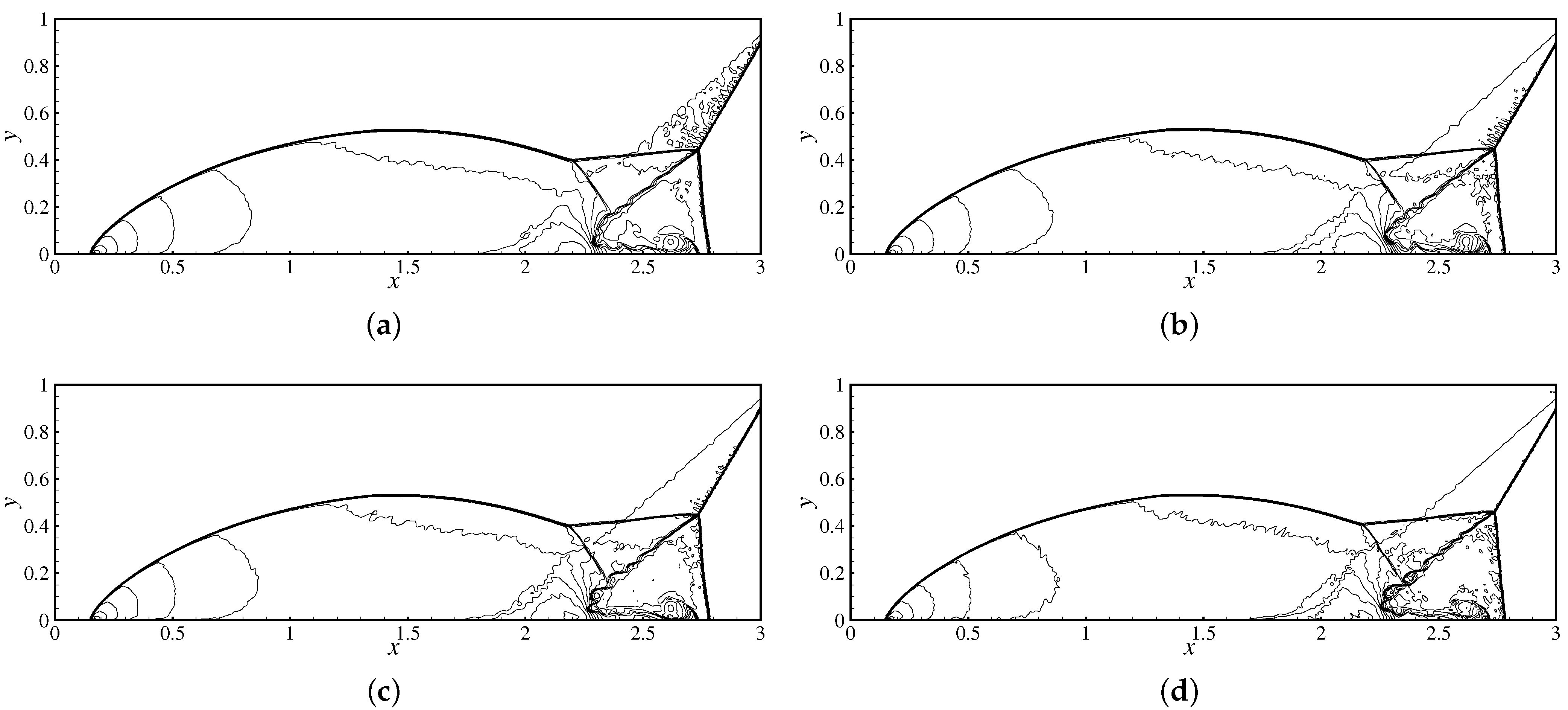
3.3.4. Double Mach Reflection
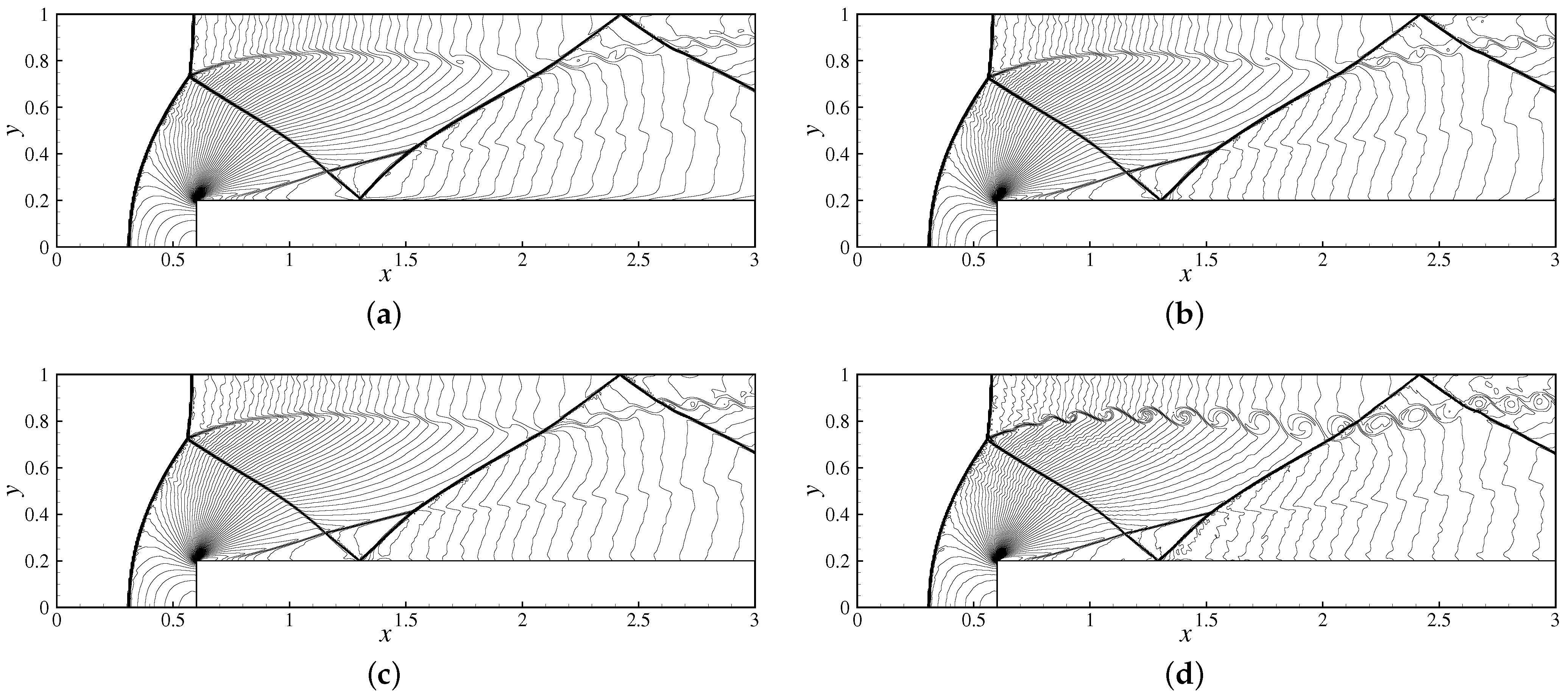
3.3.5. Forward Facing Step
3.4. Three-Dimensional Navier–Stokes Equations
3.5. Computational Efficiency
4. Conclusions
- (1)
- helps the WCNS5-JS scheme recover spectral characteristics of the background linear scheme in the medium and low wavenumber range, and maintain design order at critical points by concealing the relative disparity in smoothness indicators.
- (2)
- makes nonlinear schemes scale-invariant of flow variables, which yields consistent suppression for strong numerical oscillations near discontinuities caused by scaling down, thus improving the applicability and robustness of the WCNS scheme.
- (3)
- significantly reduces nonlinear error in smooth regions, improves resolution for both complex small-scale flow structures and discontinuities, and further suppresses numerical oscillations, with a minor increment in computational cost.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Harten, A. High Resolution Schemes for Hyperbolic Conservation Laws. J. Comput. Phys. 1997, 135, 260–278. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.D.; Osher, S.; Chan, T. Weighted Essentially Non-oscillatory Schemes. J. Comput. Phys. 1994, 115, 200–212. [Google Scholar] [CrossRef] [Green Version]
- Jiang, G.S.; Shu, C.W. Efficient Implementation of Weighted ENO Schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef] [Green Version]
- Henrick, A.K.; Aslam, T.D.; Powers, J.M. Mapped Weighted Essentially Non-Oscillatory Schemes: Achieving Optimal Order near Critical Points. J. Comput. Phys. 2005, 207, 542–567. [Google Scholar] [CrossRef]
- Borges, R.; Carmona, M.; Costa, B.; Don, W.S. An Improved Weighted Essentially Non-Oscillatory Scheme for Hyperbolic Conservation Laws. J. Comput. Phys. 2008, 227, 3191–3211. [Google Scholar] [CrossRef]
- Don, W.S.; Borges, R. Accuracy of the Weighted Essentially Non-Oscillatory Conservative Finite Difference Schemes. J. Comput. Phys. 2013, 250, 347–372. [Google Scholar] [CrossRef]
- Wang, R.; Feng, H.; Huang, C. A New Mapped Weighted Essentially Non-oscillatory Method Using Rational Mapping Function. J. Sci. Comput. 2016, 67, 540–580. [Google Scholar] [CrossRef]
- Acker, F.; Borges, R.D.; Costa, B. An Improved WENO-Z Scheme. J. Comput. Phys. 2016, 313, 726–753. [Google Scholar] [CrossRef]
- Luo, X.; Wu, S.P. An Improved WENO-Z+ Scheme for Solving Hyperbolic Conservation Laws. J. Comput. Phys. 2021, 445, 110608. [Google Scholar] [CrossRef]
- Castro, M.; Costa, B.; Don, W.S. High Order Weighted Essentially Non-Oscillatory WENO-Z Schemes for Hyperbolic Conservation Laws. J. Comput. Phys. 2011, 230, 1766–1792. [Google Scholar] [CrossRef]
- Musa, O.; Huang, G.; Wang, M. A New Smoothness Indicator of Adaptive Order Weighted Essentially Non-Oscillatory Scheme for Hyperbolic Conservation Laws. Mathematics 2021, 9, 69. [Google Scholar] [CrossRef]
- Shen, Y.; Zha, G.; Wang, B. Improvement of Stability and Accuracy for Weighted Essentially Nonoscillatory Scheme. AIAA J. 2009, 47, 331–344. [Google Scholar] [CrossRef]
- Yamaleev, N.K.; Carpenter, M.H. A Systematic Methodology for Constructing High-Order Energy Stable WENO Schemes. J. Comput. Phys. 2009, 228, 4248–4272. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Adams, N. Scale Separation for Implicit Large Eddy Simulation. J. Comput. Phys. 2011, 230, 7240–7249. [Google Scholar] [CrossRef]
- Aràndiga, F.; Martí, M.C.; Mulet, P. Weights Design For Maximal Order WENO Schemes. J. Sci. Comput. 2014, 60, 641–659. [Google Scholar] [CrossRef]
- Peer, A.; Dauhoo, M.; Bhuruth, M. A Method for Improving the Performance of the WENO5 Scheme near Discontinuities. Appl. Math. Lett. 2009, 22, 1730–1733. [Google Scholar] [CrossRef] [Green Version]
- Jia, F.; Gao, Z.; Don, W.S. A Spectral Study on the Dissipation and Dispersion of the WENO Schemes. J. Sci. Comput. 2015, 63, 49–77. [Google Scholar] [CrossRef]
- Zheng, S.; Deng, X.; Wang, D.; Xie, C. A Parameter-free ε-adaptive Algorithm for Improving Weighted Compact Nonlinear Schemes. Int. J. Numer. Methods Fluids 2019, 90, 247–266. [Google Scholar] [CrossRef]
- Deng, X.; Maekawa, H. Compact High-Order Accurate Nonlinear Schemes. J. Comput. Phys. 1997, 130, 77–91. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, H. Developing High-Order Weighted Compact Nonlinear Schemes. J. Comput. Phys. 2000, 165, 22–44. [Google Scholar] [CrossRef]
- Wang, D.; Deng, X.; Wang, G.; Dong, Y. Developing a Hybrid Flux Function Suitable for Hypersonic Flow Simulation with High-Order Methods. Int. J. Numer. Methods Fluids 2016, 81, 309–327. [Google Scholar] [CrossRef]
- Deng, X.; Mao, M.; Tu, G.; Liu, H.; Zhang, H. Geometric Conservation Law and Applications to High-Order Finite Difference Schemes with Stationary Grids. J. Comput. Phys. 2011, 230, 1100–1115. [Google Scholar] [CrossRef]
- Deng, X.; Min, Y.; Mao, M.; Liu, H.; Tu, G.; Zhang, H. Further Studies on Geometric Conservation Law and Applications to High-Order Finite Difference Schemes with Stationary Grids. J. Comput. Phys. 2013, 239, 90–111. [Google Scholar] [CrossRef]
- Deng, X.; Liu, X.; Mao, M.; Zhang, H. Investigation on Weighted Compact Fifth-Order Nonlinear Scheme and Applications to Complex Flow. In Proceedings of the 17th AIAA Computational Fluid Dynamics Conference, Toronto, ON, Canada, 6–9 June 2005; American Institute of Aeronautics and Astronautics: Toronto, ON, Canada, 2005. [Google Scholar] [CrossRef]
- Sun, X.W.; Yang, X.L.; Liu, W. Aero-Optical and Aero-Heating Effects of Supersonic Turbulent Boundary Layer with a Tangential Wall-Injection Film. Phys. Fluids 2021, 33, 035118. [Google Scholar] [CrossRef]
- Nonomura, T.; Fujii, K. Effects of Difference Scheme Type in High-Order Weighted Compact Nonlinear Schemes. J. Comput. Phys. 2009, 228, 3533–3539. [Google Scholar] [CrossRef]
- Yan, Z.; Liu, H.; Mao, M.; Zhu, H.; Deng, X. New Nonlinear Weights for Improving Accuracy and Resolution of Weighted Compact Nonlinear Scheme. Comput. Fluids 2016, 127, 226–240. [Google Scholar] [CrossRef]
- Pirozzoli, S. On the Spectral Properties of Shock-Capturing Schemes. J. Comput. Phys. 2006, 219, 489–497. [Google Scholar] [CrossRef]
- Hu, X.Y.; Tritschler, V.K.; Pirozzoli, S.; Adams, N.A. Dispersion-Dissipation Condition for Finite Difference Schemes. arXiv 2014, arXiv:1204.5088. [Google Scholar]
- Steger, J.L.; Warming, R.F. Flux Vector Splitting of the Inviscid Gasdynamic Equations with Application to Finite-Difference Methods. J. Comput. Phys. 1981, 40, 263–293. [Google Scholar] [CrossRef]
- Gottlieb, S.; Shu, C.W.; Tadmor, E. Strong Stability-Preserving High-Order Time Discretization Methods. SIAM Rev. 2001, 43, 89–112. [Google Scholar] [CrossRef]
- Lax, P.D. Weak Solutions of Nonlinear Hyperbolic Equations and Their Numerical Computation. Commun. Pure Appl. Math. 1954, 7, 159–193. [Google Scholar] [CrossRef]
- Sod, G.A. A Survey of Several Finite Difference Methods for Systems of Nonlinear Hyperbolic Conservation Laws. J. Comput. Phys. 1978, 27, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Shu, C.W.; Osher, S. Efficient Implementation of Essentially Non-Oscillatory Shock-Capturing Schemes, II. J. Comput. Phys. 1989, 83, 32–78. [Google Scholar] [CrossRef]
- Titarev, V.A.; Toro, E.F. Finite-Volume WENO Schemes for Three-Dimensional Conservation Laws. J. Comput. Phys. 2004, 201, 238–260. [Google Scholar] [CrossRef]
- Balsara, D.S.; Shu, C.W. Monotonicity Preserving Weighted Essentially Non-oscillatory Schemes with Increasingly High Order of Accuracy. J. Comput. Phys. 2000, 160, 405–452. [Google Scholar] [CrossRef] [Green Version]
- Lax, P.D.; Liu, X.D. Solution of Two-Dimensional Riemann Problems of Gas Dynamics by Positive Schemes. SIAM J. Sci. Comput. 1998, 19, 319–340. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Zhang, Y.T.; Shu, C.W. Resolution of High Order WENO Schemes for Complicated Flow Structures. J. Comput. Phys. 2003, 186, 690–696. [Google Scholar] [CrossRef] [Green Version]
- Woodward, P.; Colella, P. The Numerical Simulation of Two-Dimensional Fluid Flow with Strong Shocks. J. Comput. Phys. 1984, 54, 115–173. [Google Scholar] [CrossRef]
- Brachet, M.E.; Meiron, D.I.; Orszag, S.A.; Nickel, B.G.; Morf, R.H.; Frisch, U. Small-Scale Structure of the Taylor–Green Vortex. J. Fluid Mech. 1983, 130, 411. [Google Scholar] [CrossRef] [Green Version]
- Zheng, S.; Deng, X.; Wang, D. New Optimized Flux Difference Schemes for Improving High-Order Weighted Compact Nonlinear Scheme with Applications. Appl. Math. Mech. 2021, 42, 405–424. [Google Scholar] [CrossRef]
- van Rees, W.M.; Leonard, A.; Pullin, D.I.; Koumoutsakos, P. A Comparison of Vortex and Pseudo-Spectral Methods for the Simulation of Periodic Vortical Flows at High Reynolds Numbers. J. Comput. Phys. 2011, 230, 2794–2805. [Google Scholar] [CrossRef]





| 0 | ||||
| 1 | ||||
| 2 | ||||
| 3 |
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| Schemes | Composite Wave | Titarev-Toro | Double Mach | Viscous Taylor-Green Vortex | ||||
|---|---|---|---|---|---|---|---|---|
| WCNS5-JS | 4.896 | - | 13.259 | - | 272.297 | - | 298.975 | - |
| WCNS5-Z | 5.021 | 2.55% | 14.078 | 6.17% | 277.783 | 2.02% | 299.995 | 0.34% |
| WCNS5- | 14.479 | 195.73% | 25.744 | 94.16% | 473.617 | 73.93% | 364.610 | 21.95% |
| WCNS5- | 5.473 | 11.2% | 14.343 | 8.17% | 291.249 | 6.96% | 303.341 | 1.46% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Zheng, S.; Wang, D.; Deng, X. A New ϵ-Adaptive Algorithm for Improving Weighted Compact Nonlinear Scheme with Applications. Aerospace 2022, 9, 369. https://doi.org/10.3390/aerospace9070369
Huang Z, Zheng S, Wang D, Deng X. A New ϵ-Adaptive Algorithm for Improving Weighted Compact Nonlinear Scheme with Applications. Aerospace. 2022; 9(7):369. https://doi.org/10.3390/aerospace9070369
Chicago/Turabian StyleHuang, Ziquan, Shichao Zheng, Dongfang Wang, and Xiaogang Deng. 2022. "A New ϵ-Adaptive Algorithm for Improving Weighted Compact Nonlinear Scheme with Applications" Aerospace 9, no. 7: 369. https://doi.org/10.3390/aerospace9070369
APA StyleHuang, Z., Zheng, S., Wang, D., & Deng, X. (2022). A New ϵ-Adaptive Algorithm for Improving Weighted Compact Nonlinear Scheme with Applications. Aerospace, 9(7), 369. https://doi.org/10.3390/aerospace9070369






