A Numerical Study on the Water Entry of Cylindrical Trans-Media Vehicles
Abstract
1. Introduction
2. Problem Definition
3. Numerical Methods
3.1. Governing Equations
3.2. VOF Method
3.3. 6DOF Motion Solver
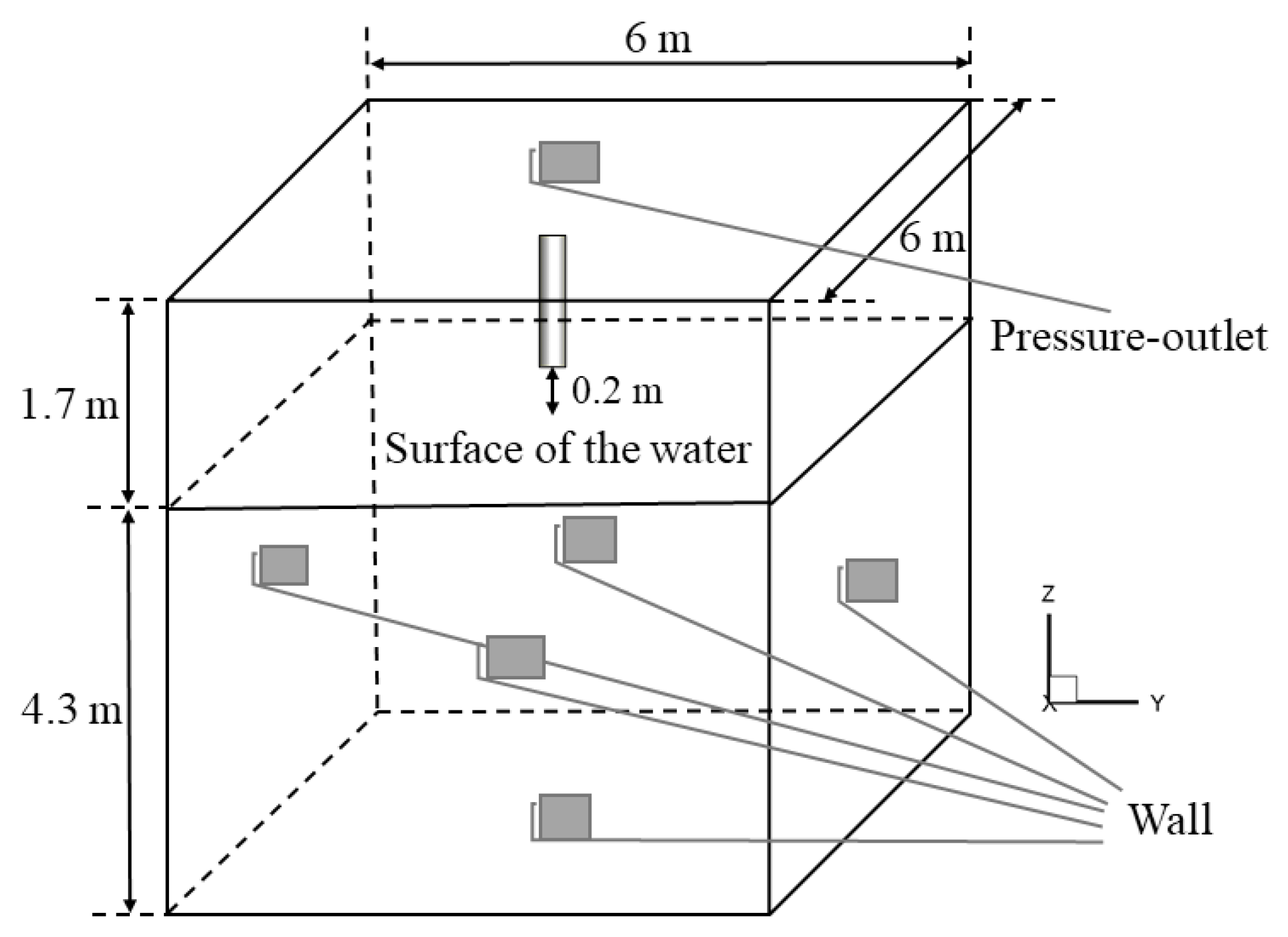
3.4. Grid, Boundary and Initial Conditions
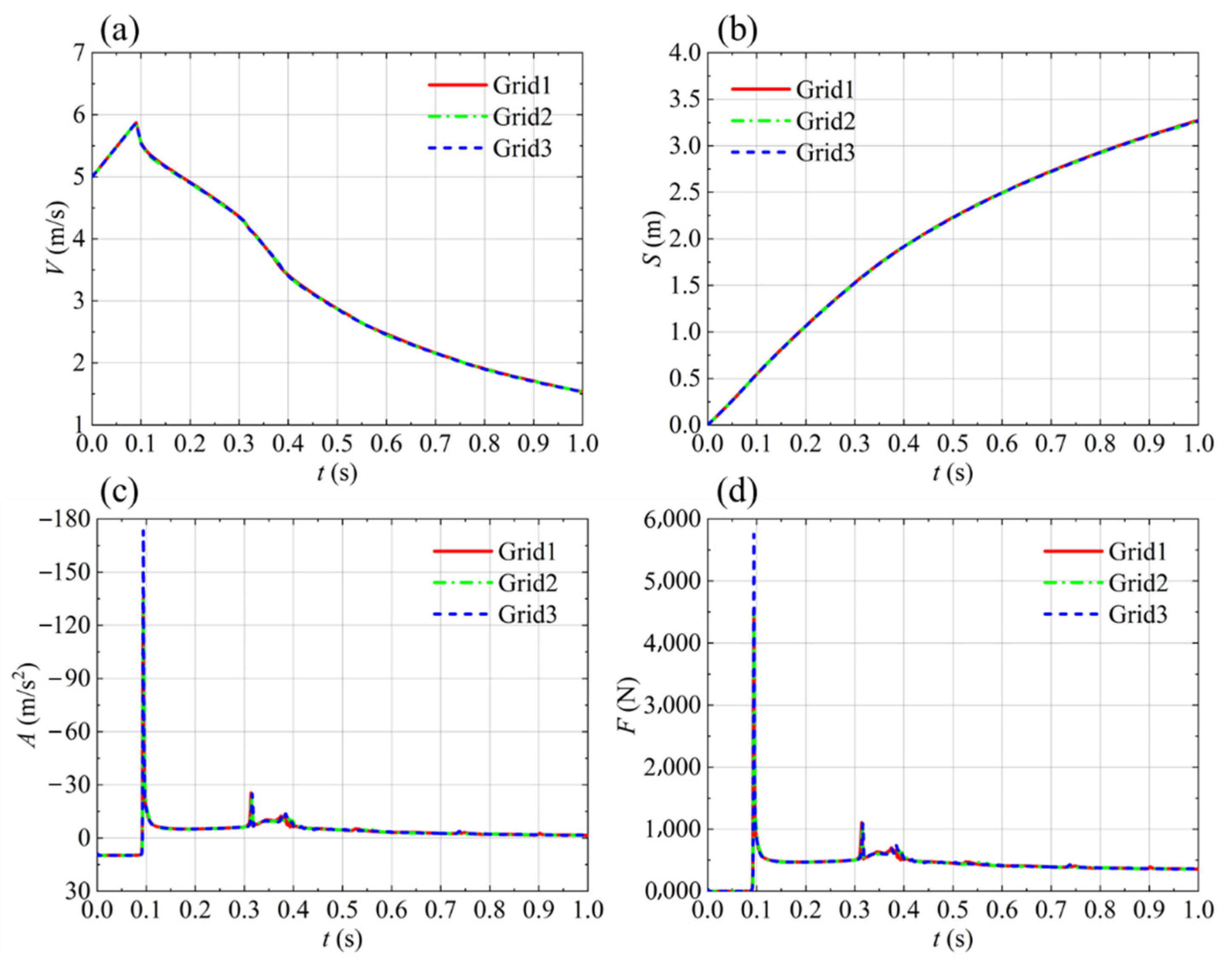
3.5. Grid Convergence Study
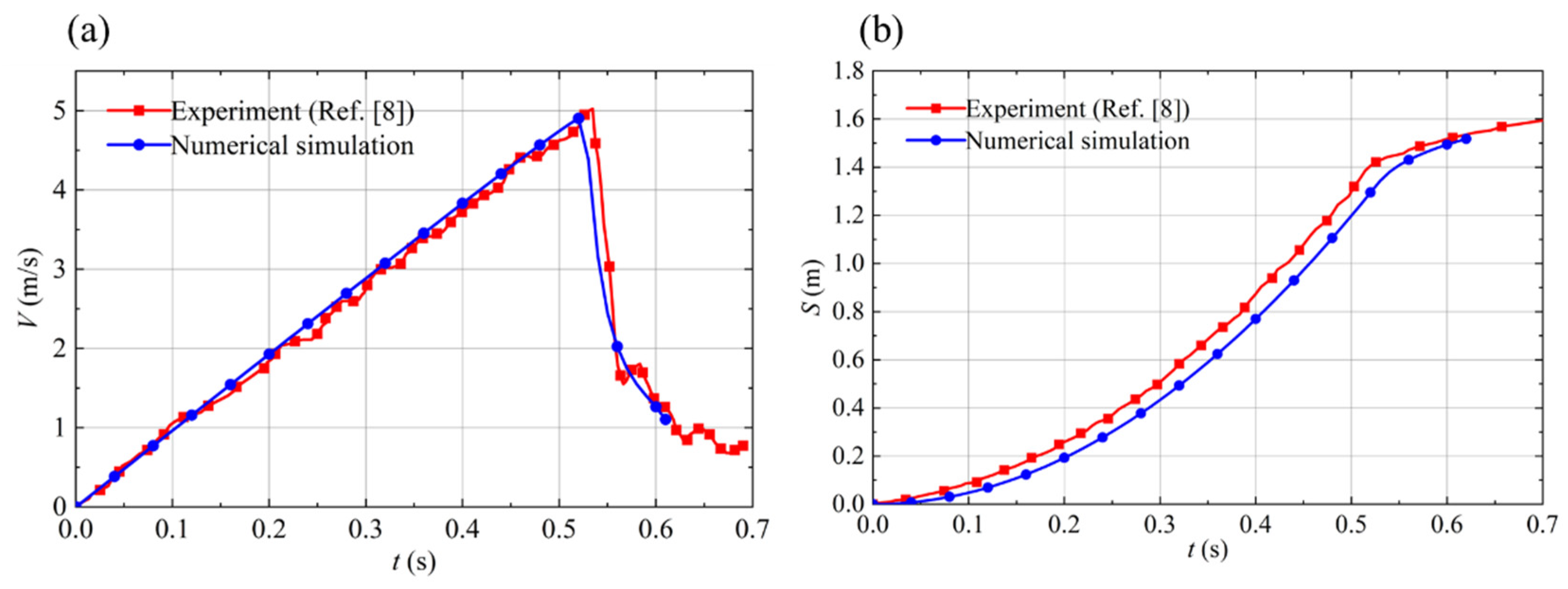
3.6. Validation of Numerical Methods
4. Results and Discussion
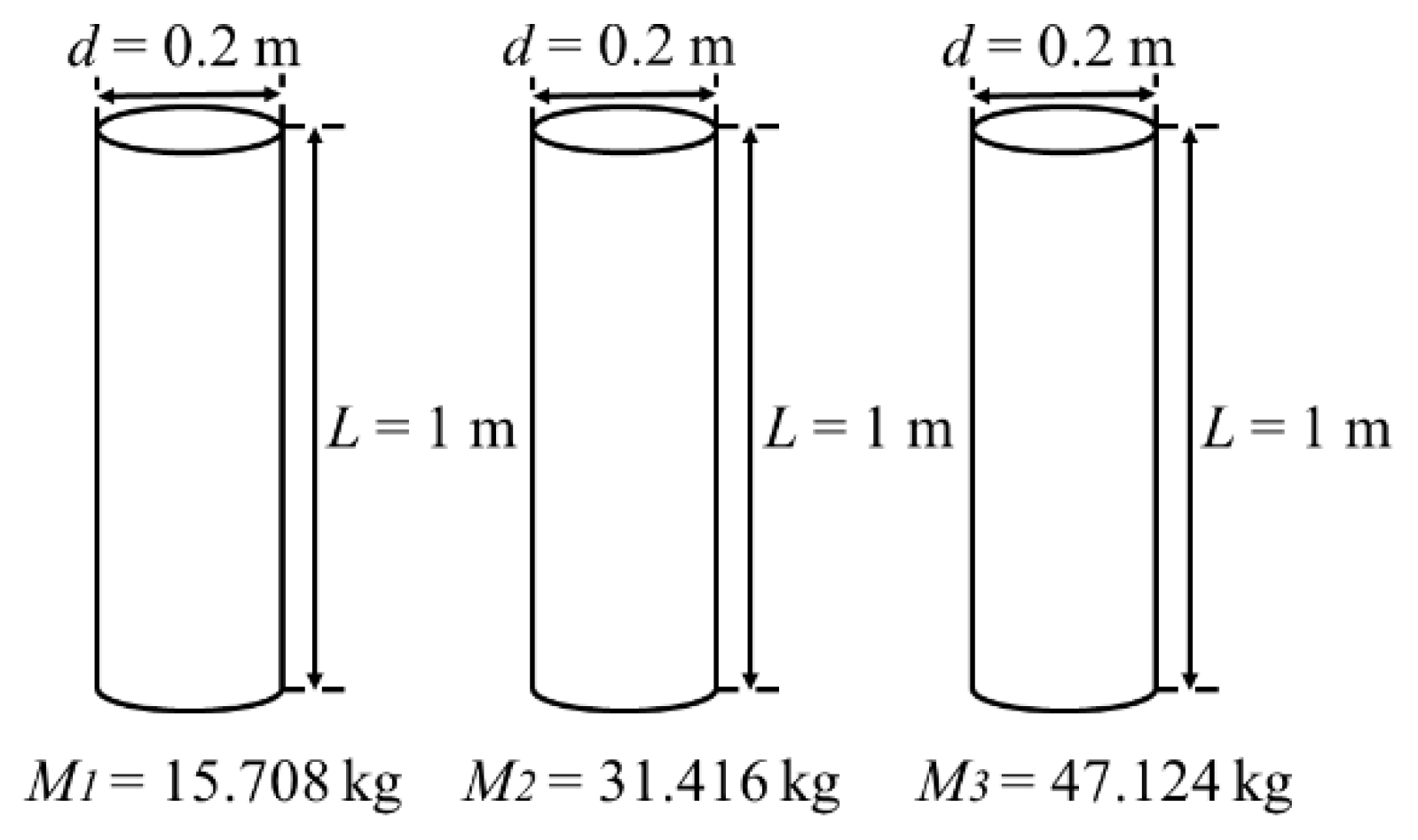
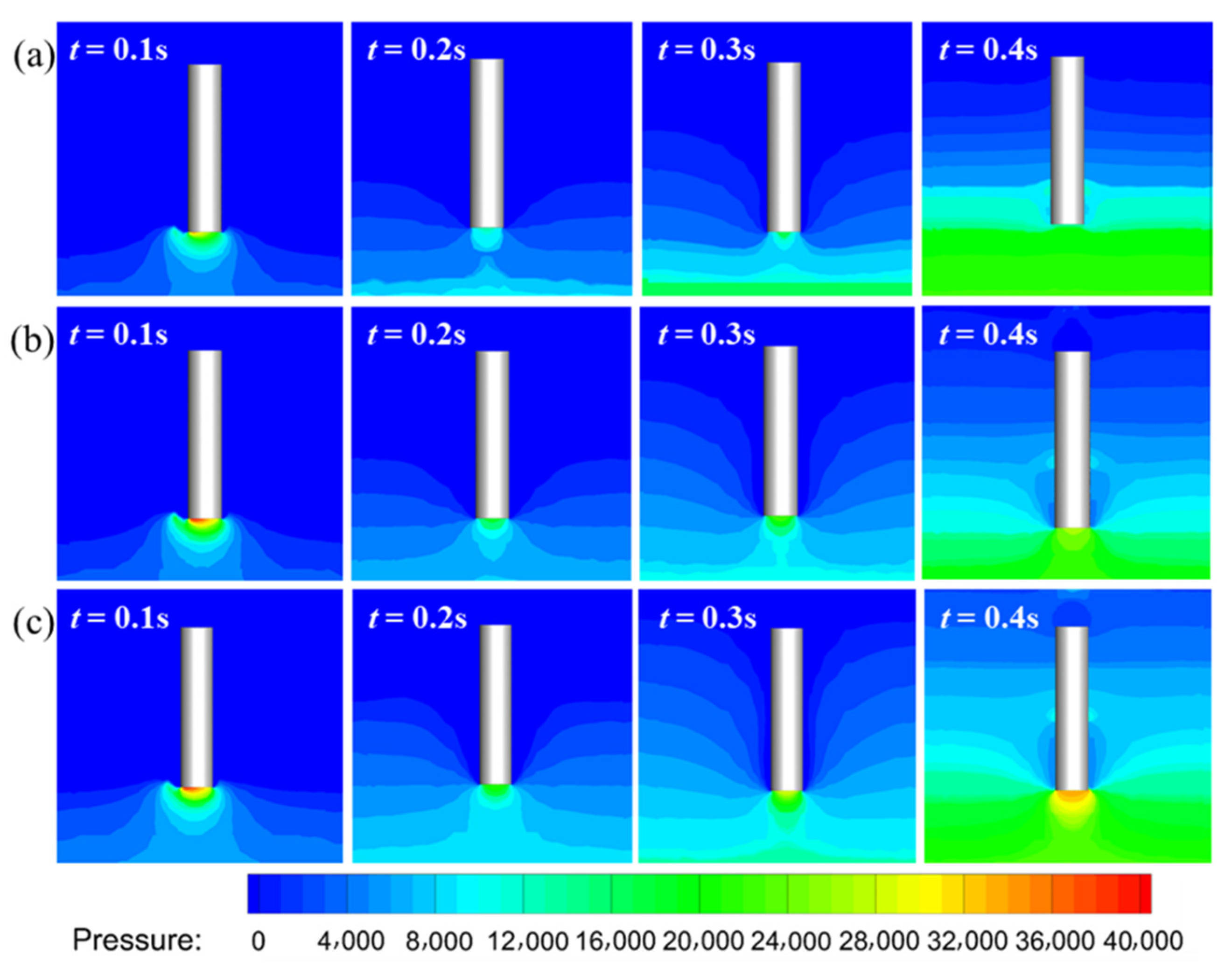
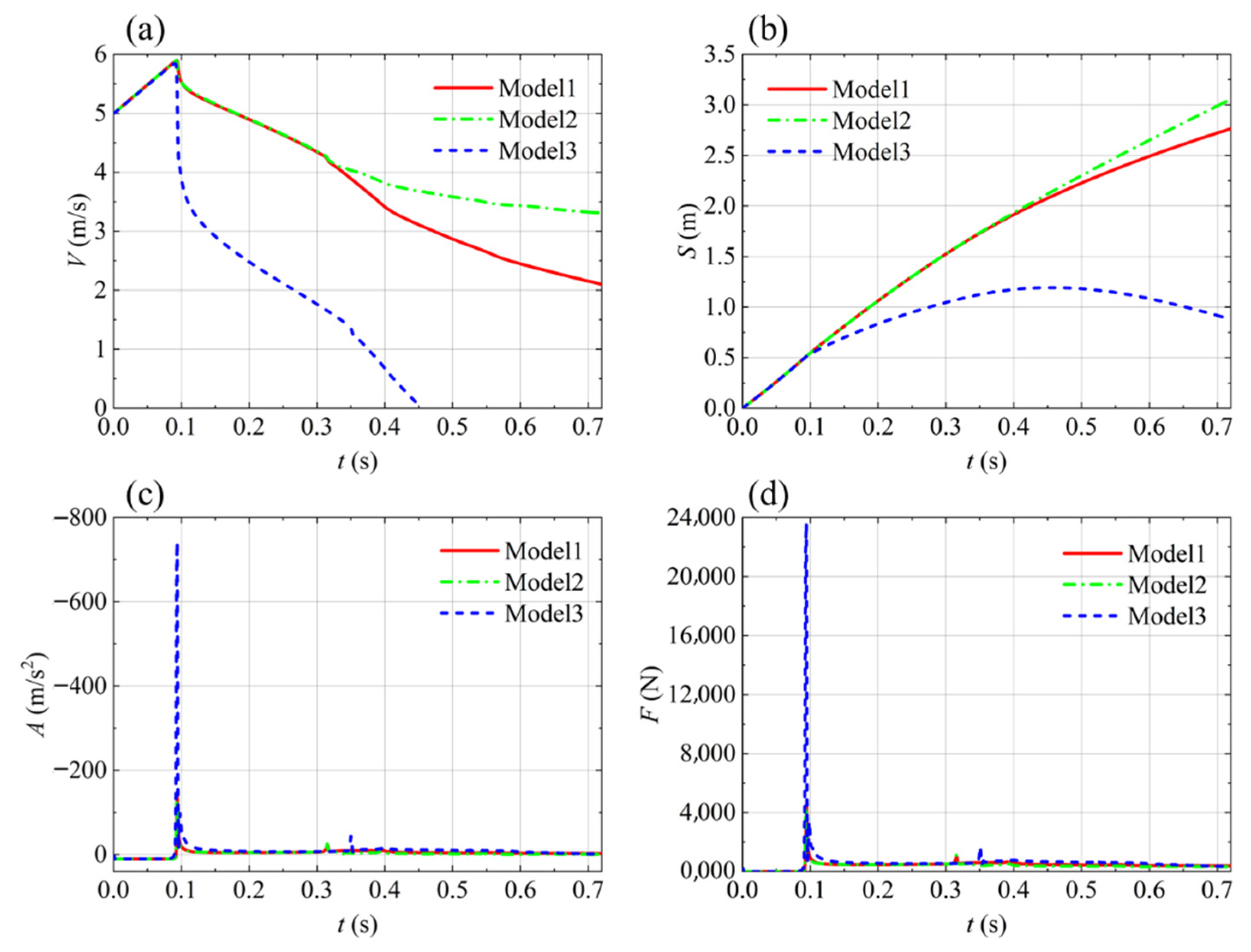
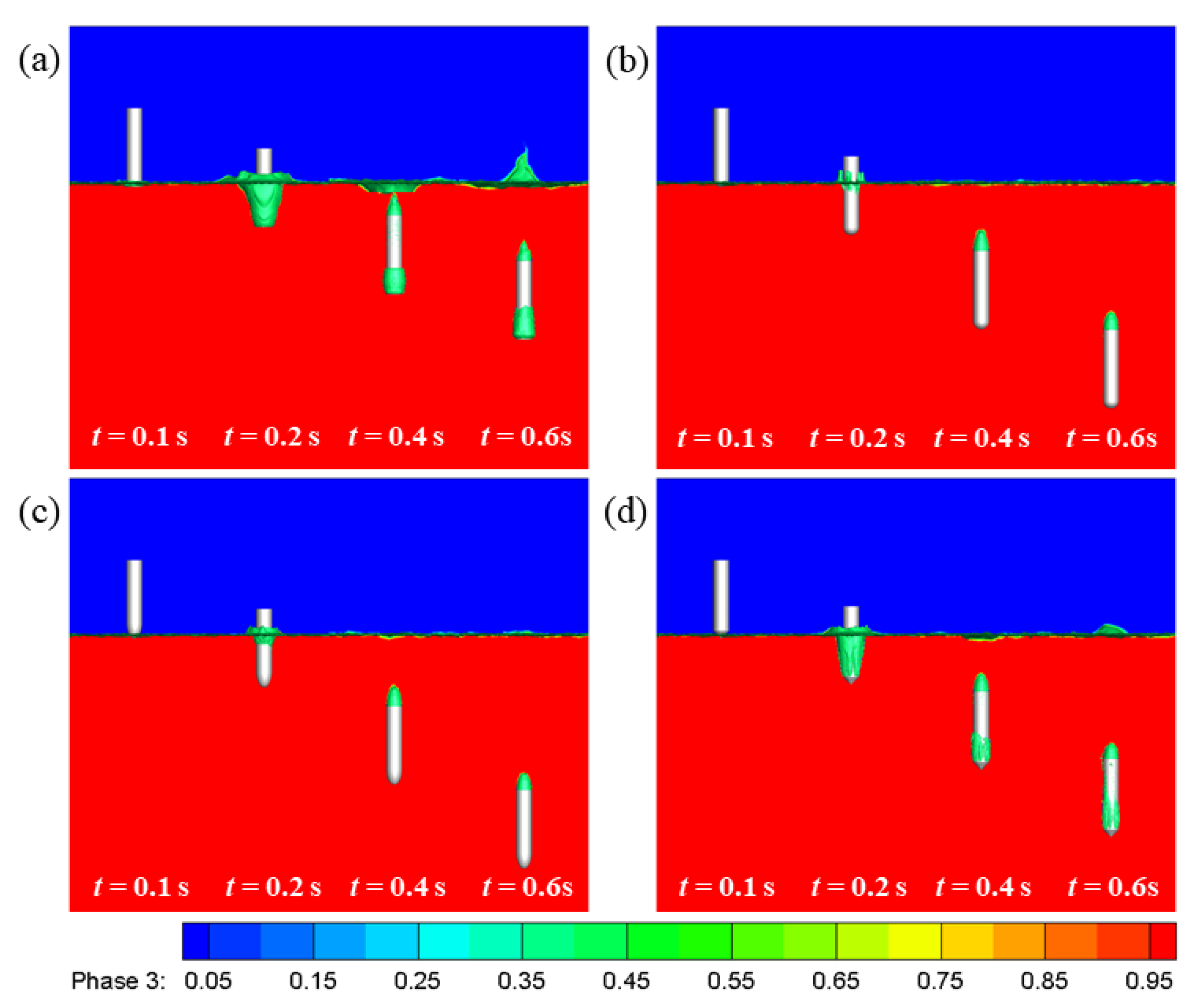
4.1. The Effect of Body Mass
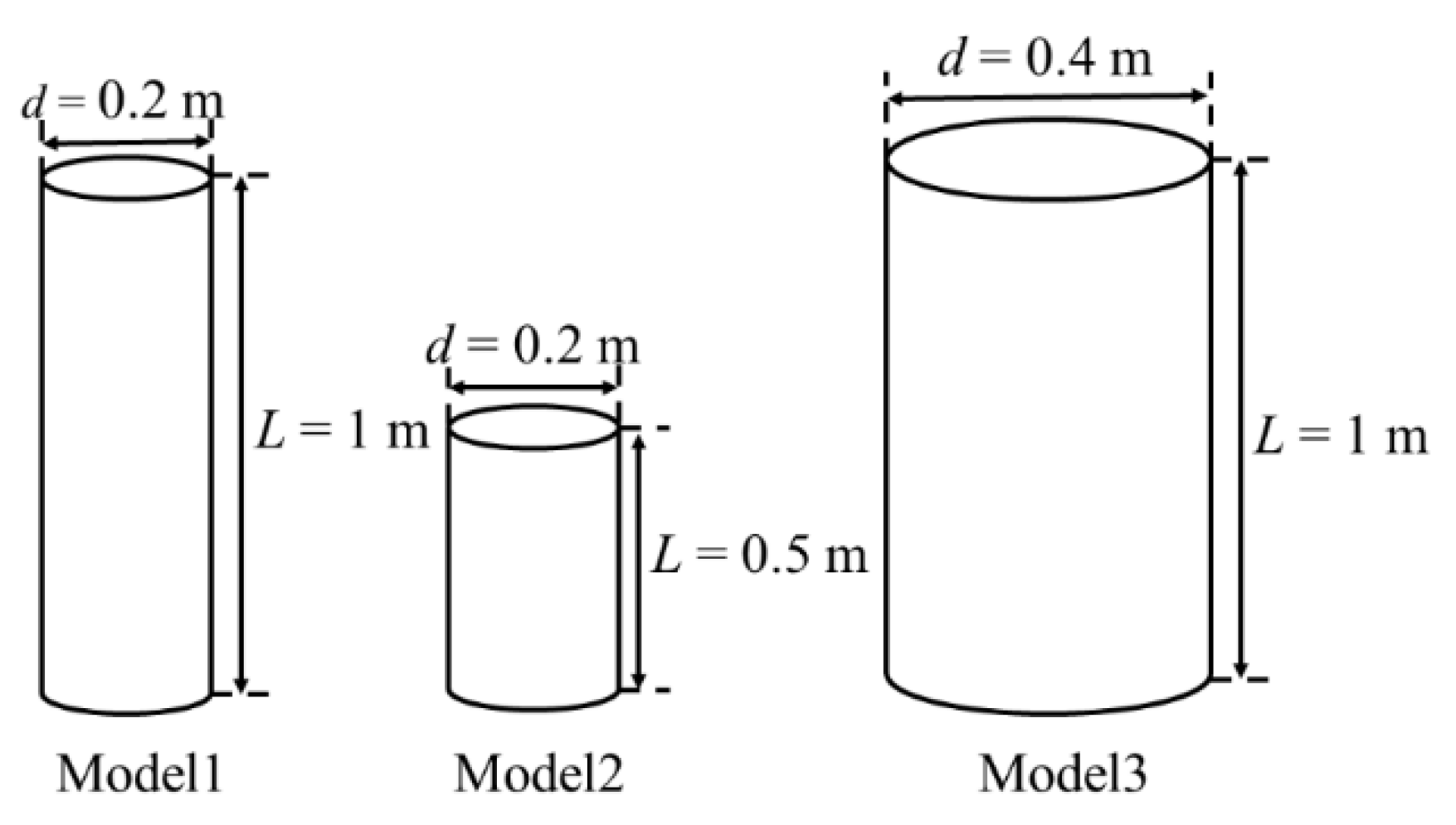
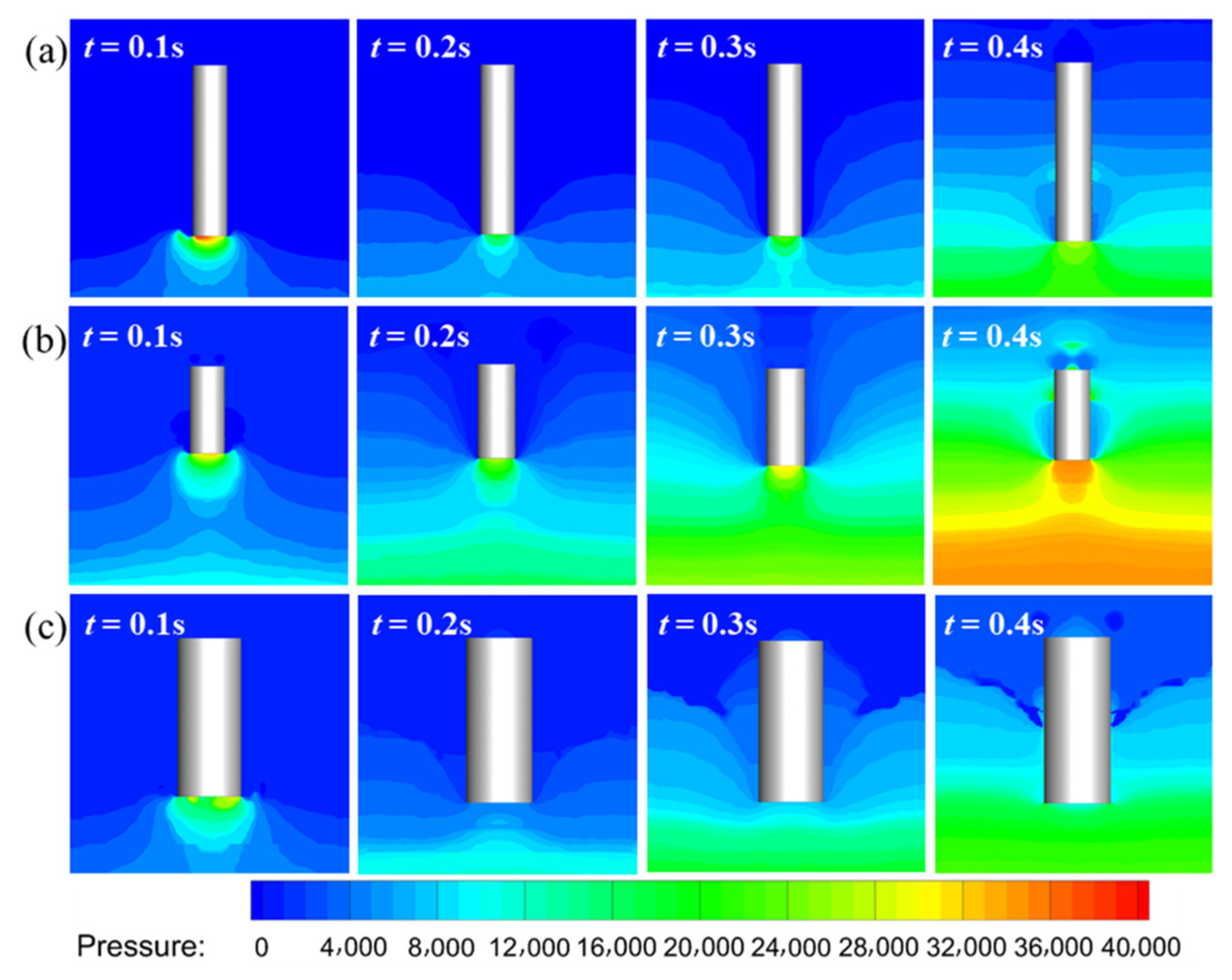
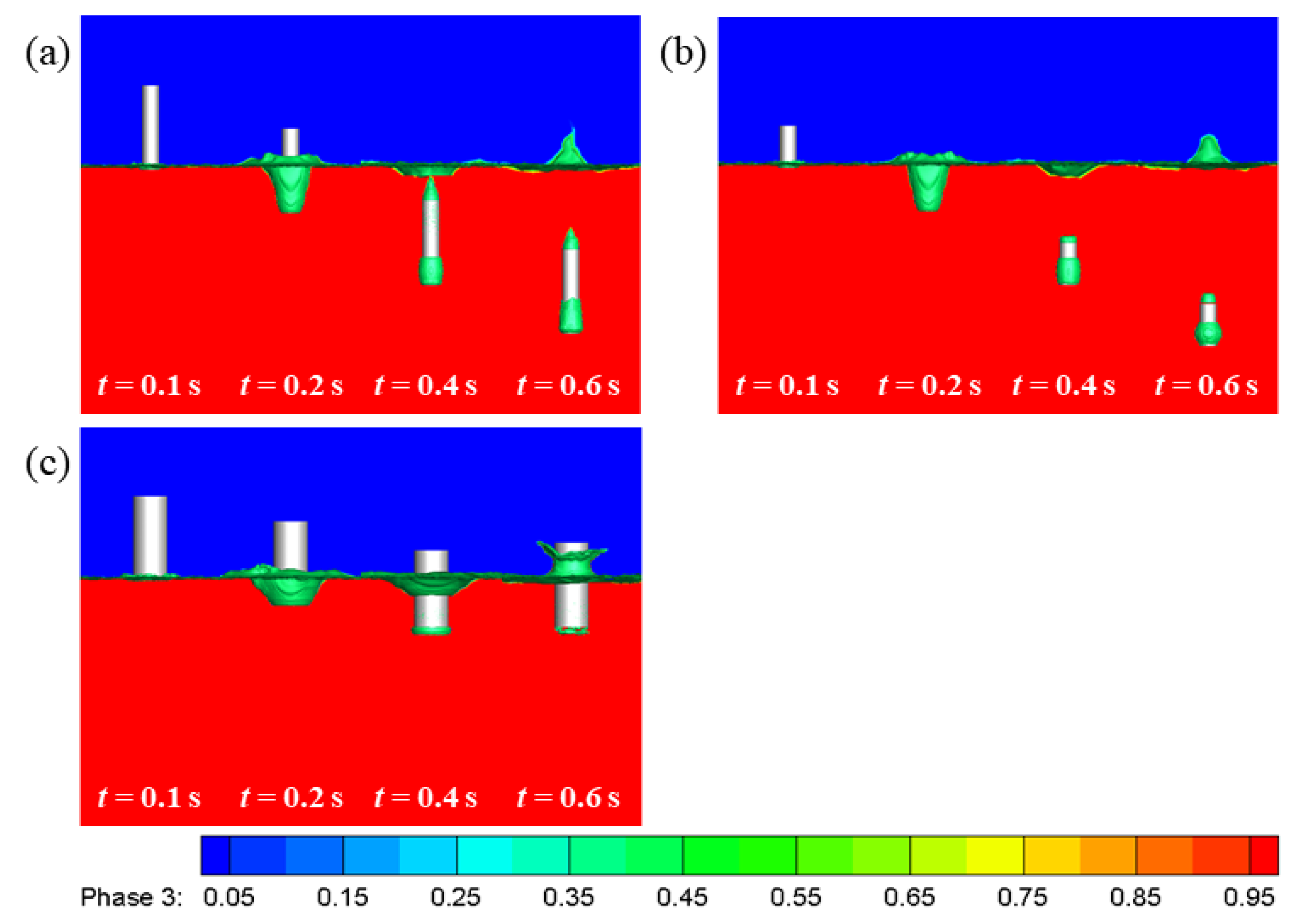
4.2. The Effect of Diameter-to-Length Ratio
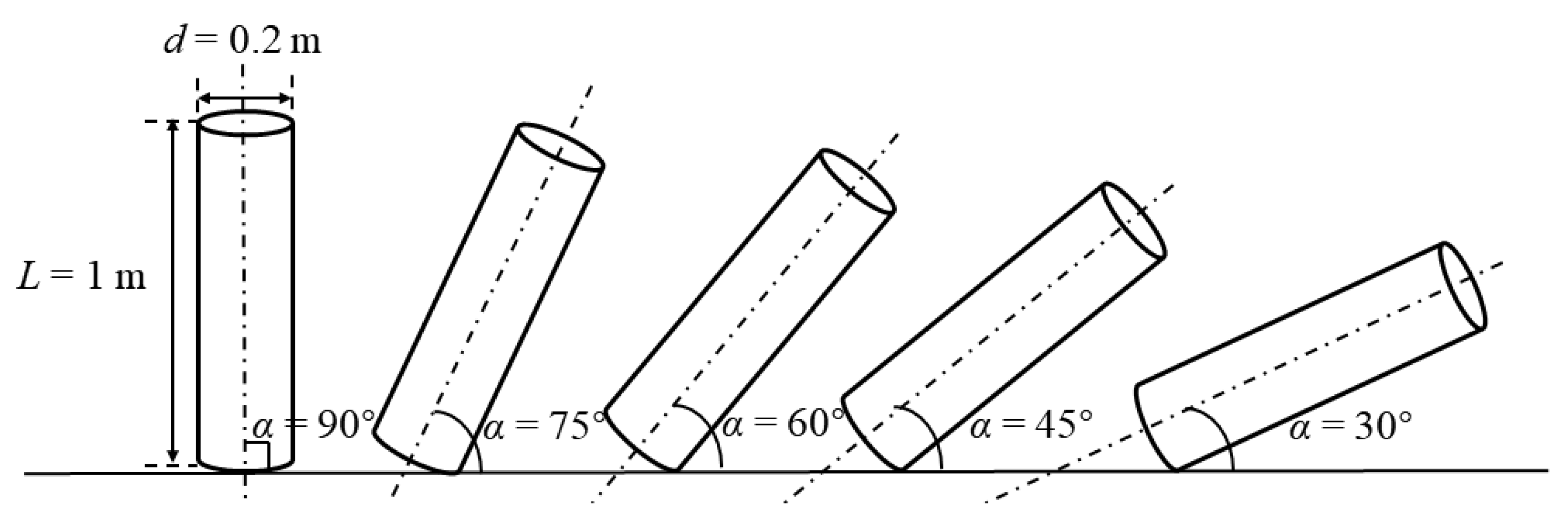
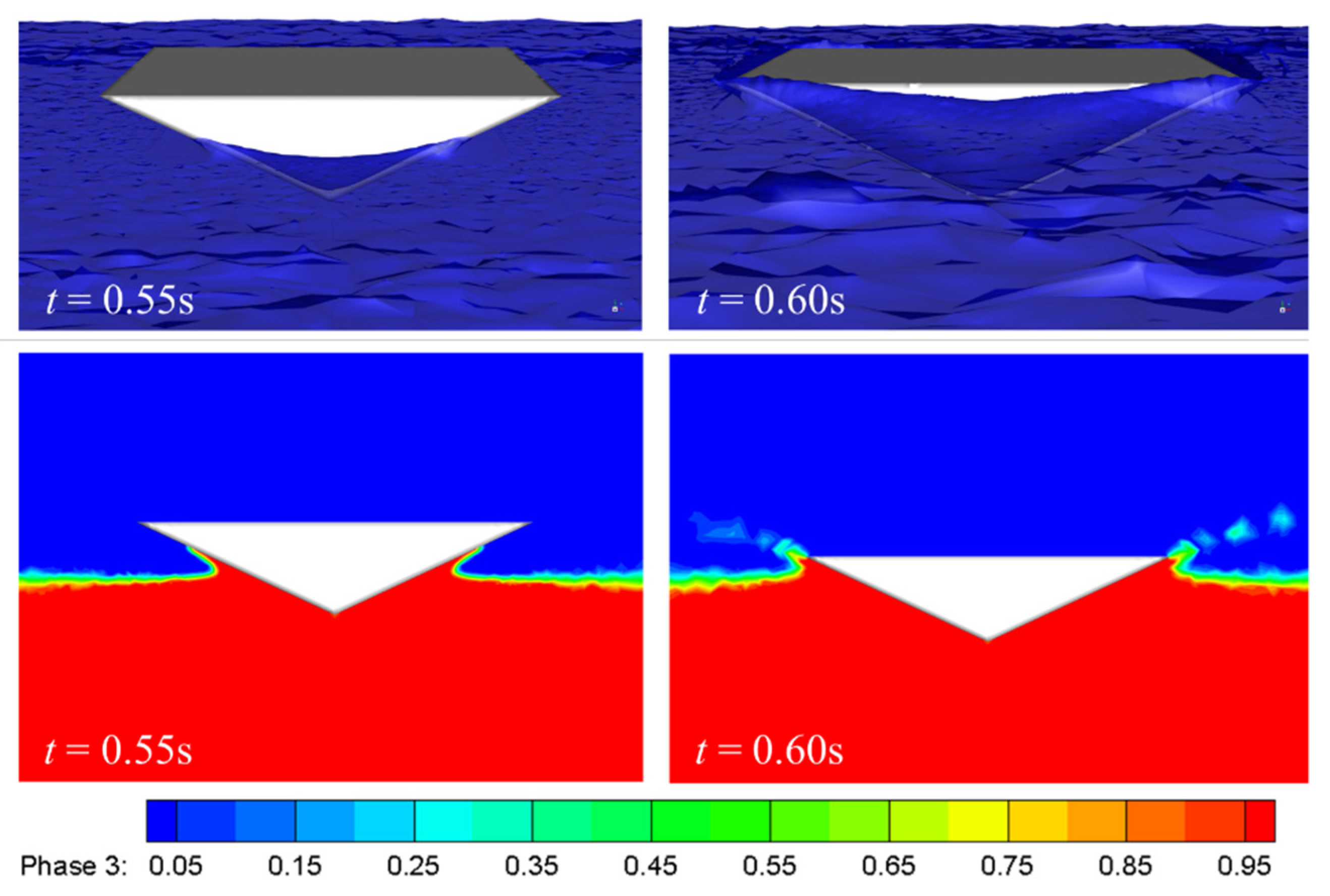
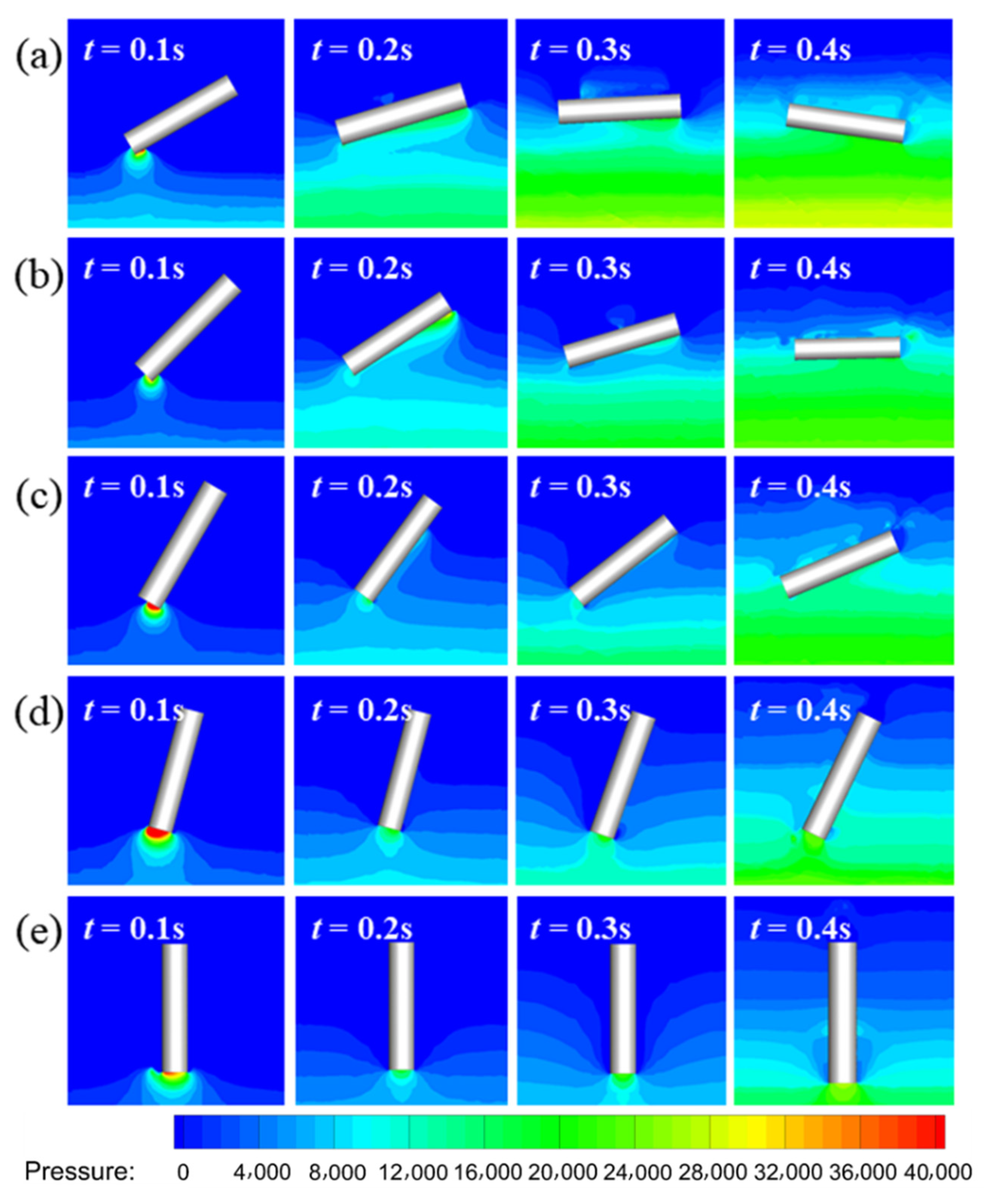
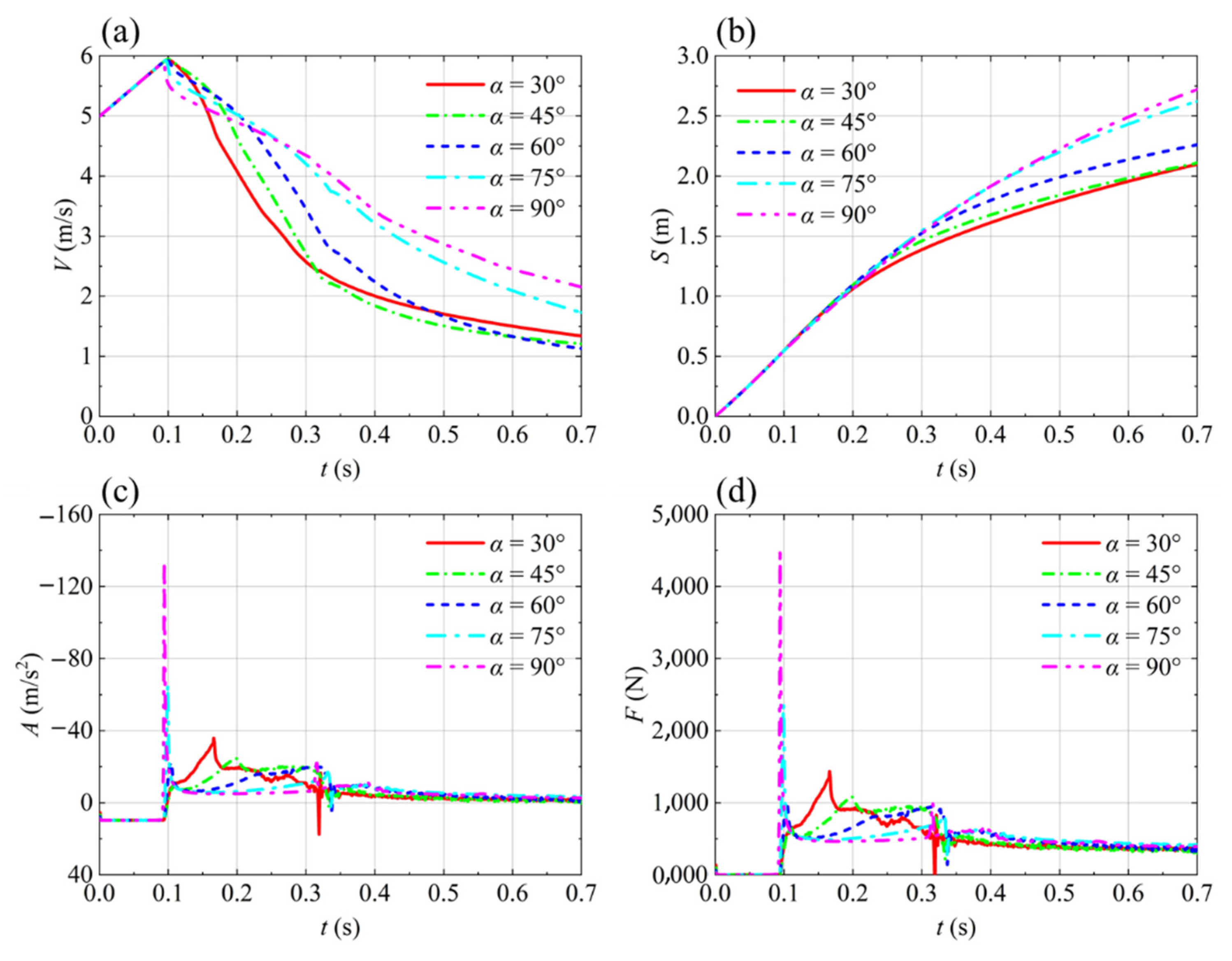
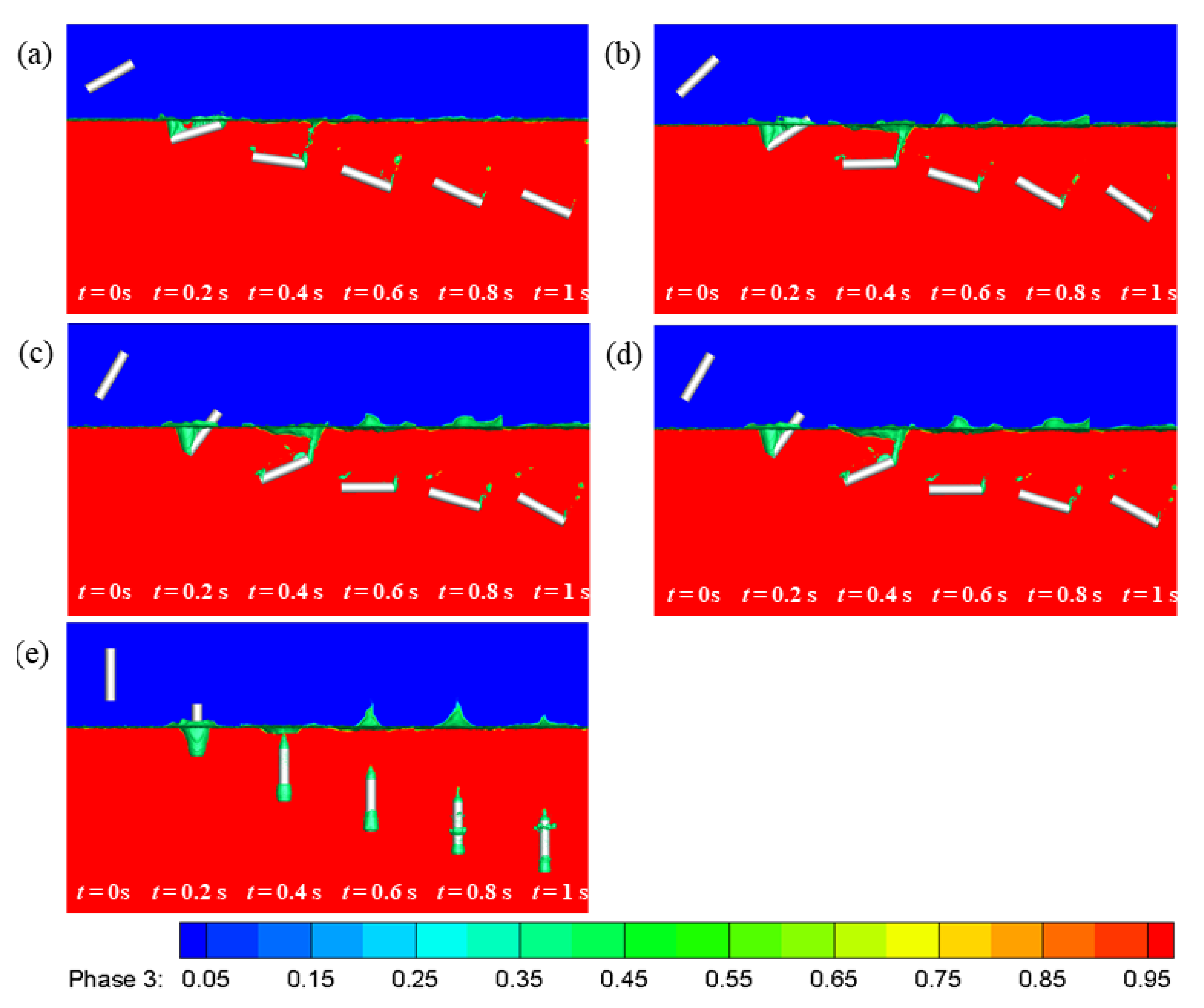
4.3. The Effect of Water-Entry Angle
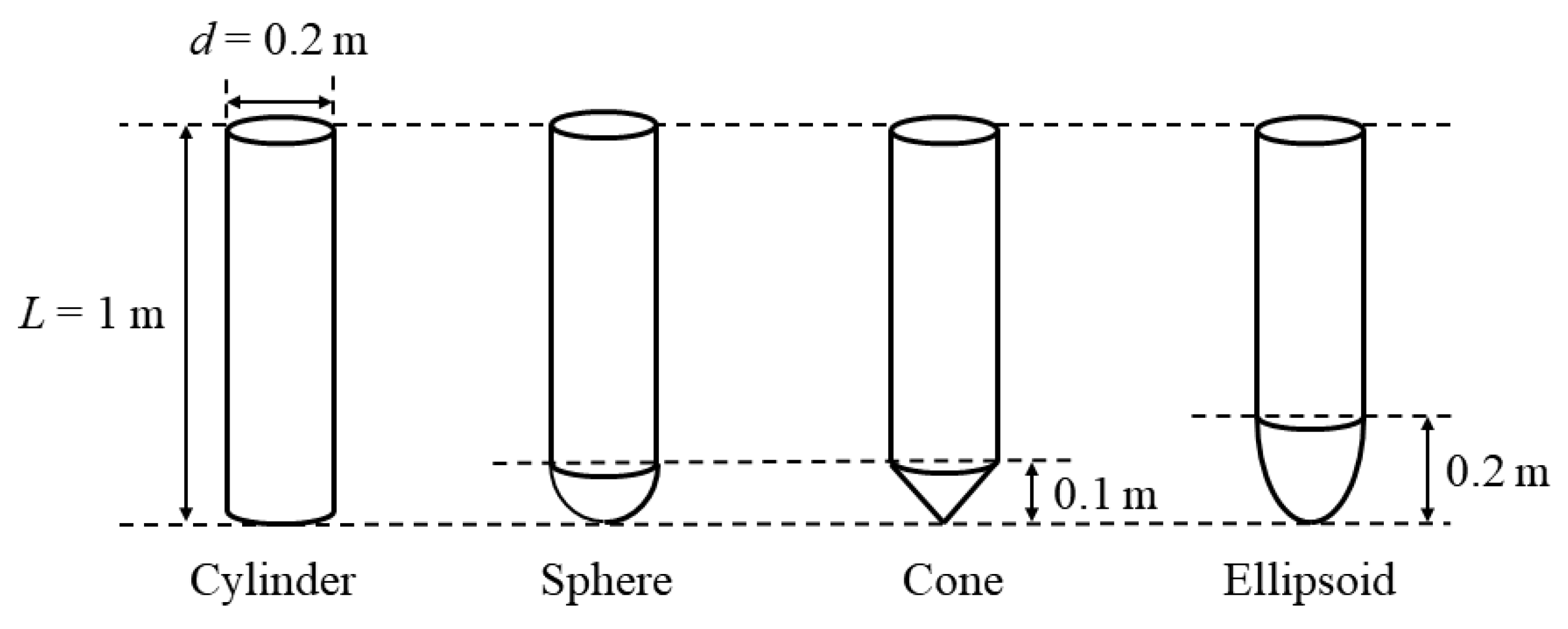
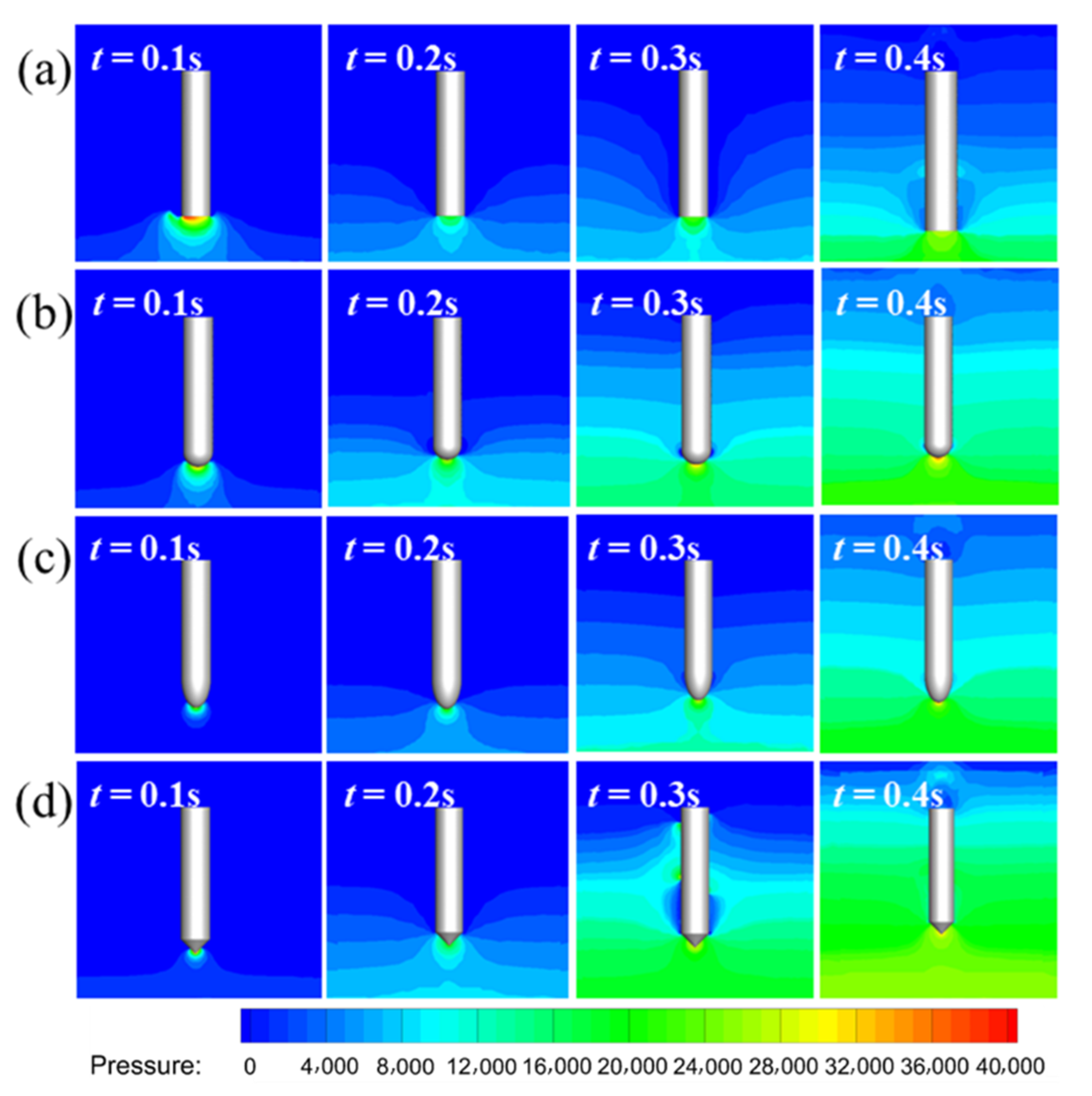
4.4. The Effect of Head Shape
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Von Kármán, T. The Impact on Seaplane Floats during Landing; NACA Technical Note No. 321; National Advisory Committee on Aeronautics: Washington, DC, USA, 1929. [Google Scholar]
- Wagner, H. Über Stoß-und Gleitvorgänge an der Oberfläche von Flüssigkeiten. ZAMM-J. Appl. Math. Mech. Angew. Math. Mech. 1932, 12, 193–215. [Google Scholar] [CrossRef]
- Zhao, R.; Faltinsen, O.; Aarsnes, J. Water Entry of Arbitrary Two-Dimensional Sections with and without Flow Separation. In Proceedings of the 21st Symposium on Naval Hydrodynamics, Trondheim, Norway, 24 June 1996; pp. 408–423. [Google Scholar]
- Verhagen, J.H.G. The Impact of a Flat Plate on a Water Surface. J. Ship Res. 1967, 11, 211–223. [Google Scholar] [CrossRef]
- Peseux, B.; Gornet, L.; Donguy, B. Hydrodynamic Impact: Numerical and Experimental Investigations. J. Fluids Struct. 2005, 21, 277–303. [Google Scholar] [CrossRef]
- May, A.; Woodhull, J.C. The Virtual Mass of a Sphere Entering Water Vertically. J. Appl. Phys. 1950, 21, 1285–1289. [Google Scholar] [CrossRef]
- Chu, P.C.; Gilles, A.; Fan, C. Experiment of Falling Cylinder through the Water Column. Exp. Therm. Fluid Sci. 2005, 29, 555–568. [Google Scholar] [CrossRef]
- Yettou, E.-M.; Desrochers, A.; Champoux, Y. Experimental Study on the Water Impact of a Symmetrical Wedge. Fluid Dyn. Res. 2006, 38, 47. [Google Scholar] [CrossRef]
- Alaoui, A.E.M.; Nême, A.; Tassin, A.; Jacques, N. Experimental Study of Coefficients during Vertical Water Entry of Axisymmetric Rigid Shapes at Constant Speeds. Appl. Ocean Res. 2012, 37, 183–197. [Google Scholar] [CrossRef]
- Truscott, T.T.; Epps, B.P.; Belden, J. Water Entry of Projectiles. Ann. Rev. Fluid Mech. 2014, 46, 355–378. [Google Scholar] [CrossRef]
- Van Nuffel, D.; Vepa, K.S.; De Baere, I.; Lava, P.; Kersemans, M.; Degrieck, J.; De Rouck, J.; Van Paepegem, W. A Comparison between the Experimental and Theoretical Impact Pressures Acting on a Horizontal Quasi-Rigid Cylinder during Vertical Water Entry. Ocean Eng. 2014, 77, 42–54. [Google Scholar] [CrossRef]
- Takagi, K. Numerical Evaluation of Three-Dimensional Water Impact by the Displacement Potential Formulation. J. Eng. Math. 2004, 48, 339–352. [Google Scholar] [CrossRef]
- Aquelet, N.; Souli, M.; Olovsson, L. Euler–Lagrange Coupling with Damping Effects: Application to Slamming Problems. Comput. Methods Appl. Mech. Eng. 2006, 195, 110–132. [Google Scholar] [CrossRef]
- Stenius, I.; Rosén, A.; Kuttenkeuler, J. Explicit FE-Modelling of Fluid–Structure Interaction in Hull–Water Impacts. Int. Shipbuild. Prog. 2006, 53, 103–121. [Google Scholar]
- Stenius, I.; Rosén, A.; Kuttenkeuler, J. Explicit FE-Modelling of Hydroelasticity in Panel-Water Impacts. Int. Shipbuild. Prog. 2007, 54, 111–127. [Google Scholar]
- Wick, A.T.; Zink, G.A.; Ruszkowski, R.A.; Shih, T.I.P. Computational Simulation of an Unmanned Air Vehicle Impacting Water. In Proceedings of the 45th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 8 January 2007. [Google Scholar]
- Yang, Q.; Qiu, W. Numerical Simulation of Water Impact for 2D and 3D Bodies. Ocean Eng. 2012, 43, 82–89. [Google Scholar] [CrossRef]
- Abraham, J.; Gorman, J.; Reseghetti, F.; Sparrow, E.; Stark, J.; Shepard, T. Modeling and Numerical Simulation of the Forces Acting on a Sphere during Early-Water Entry. Ocean Eng. 2014, 76, 1–9. [Google Scholar] [CrossRef]
- Qu, Q.; Hu, M.; Guo, H.; Liu, P.; Agarwal, R.K. Study of Ditching Characteristics of Transport Aircraft by Global Moving Mesh Method. J. Aircr. 2015, 52, 1550–1558. [Google Scholar] [CrossRef]
- Facci, A.L.; Porfiri, M.; Ubertini, S. Three-Dimensional Water Entry of a Solid Body: A Computational Study. J. Fluids Struct. 2016, 66, 36–53. [Google Scholar] [CrossRef]
- Xiao, T.; Qin, N.; Lu, Z.; Sun, X.; Tong, M.; Wang, Z. Development of a Smoothed Particle Hydrodynamics Method and Its Application to Aircraft Ditching Simulations. Aerosp. Sci. Technol. 2017, 66, 28–43. [Google Scholar] [CrossRef]
- Xiang, G.; Wang, S.; Soares, C.G. Study on the Motion of a Freely Falling Horizontal Cylinder into Water Using OpenFOAM. Ocean Eng. 2020, 196, 106811. [Google Scholar] [CrossRef]
- Shi, Y.; Pan, G.; Yan, G.-X.; Yim, S.C.; Jiang, J. Numerical Study on the Cavity Characteristics and Impact Loads of AUV Water Entry. Appl. Ocean Res. 2019, 89, 44–58. [Google Scholar] [CrossRef]
- Wang, X.; Shi, Y.; Pan, G.; Chen, X.; Zhao, H. Numerical Research on the High-Speed Water Entry Trajectories of AUVs with Asymmetric Nose Shapes. Ocean Eng. 2021, 234, 109274. [Google Scholar] [CrossRef]
- Wu, X.; Chang, X.; Liu, S.; Yu, P.; Zhou, L.; Tian, W. Numerical Study on the Water Entry Impact Forces of an Air-Launched Underwater Glider under Wave Conditions. Shock Vib. 2022, 2022, 4330043. [Google Scholar] [CrossRef]
- Deng, F.; Sun, X. Trans-Media Unmanned Aerial Vehicle Device And Control Method Thereof. PCT/CN2021/098354, 4 June 2021. Chinese Patent Application No. 202110441374.7, 23 April 2021. [Google Scholar]
- Anderson, J.D. Governing Equations of Fluid Dynamics. In Computational fluid dynamics; Springer: Berlin, Germany, 2009; pp. 15–51. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]








| Year | Authors | Research Objects | Numerical Methods |
|---|---|---|---|
| 2004 | Takagi [12] | 3D elliptic paraboloids | Potential method |
| 2006 | Aquelet et al. [13] | 2D wedges | Explicit FEM |
| 2006 | Stenius et al. [14] | 2D wedges | Explicit FEM |
| 2007 | Stenius et al. [15] | 2D elastomers | Explicit FEM |
| 2007 | Wick et al. [16] | A UAV | VOF method |
| 2012 | Yang and Qiu [17] | 2D and 3D wedges | CIP method |
| 2014 | Abraham et al. [18] | 3D balls | VOF method |
| 2014 | Van Nuffel et al. [11] | Horizontal cylinders | VOF method |
| 2015 | Qu et al. [19] | An airplane | VOF method |
| 2016 | Facci et al. [20] | Multi-curvature structures | VOF method |
| 2017 | Xiao et al. [21] | A helicopter | SPH method |
| 2019 | Shi et al. [23] | AUVs | Explicit FEM |
| 2020 | Xiang et al. [22] | Horizontal cylinders | VOF method |
| 2021 | Wang et al. [24] | AUVs | VOF method |
| 2022 | Wu et al. [25] | An air-launched underwater glider | VOF method |
| Grid Name | Minimum Size of Moving Grid Region (mm) | Minimum Size of Overall Grid Region (mm) | |
|---|---|---|---|
| Grid 1 | 1.210 | 37.372 | 2.754 |
| Grid 2 | 0.903 | 37.372 | 3.878 |
| Grid 3 | 0.903 | 29.066 | 4.565 |
| Mass (kg) | Ixx (kg·m2) | Iyy (kg·m2) | Izz (kg·m2) | Ixy (kg·m2) | Ixz (kg·m2) | Iyz (kg·m2) |
|---|---|---|---|---|---|---|
| 15.708 | 1.388 | 1.388 | 0.157 | 0.000 | 0.000 | 0.000 |
| 31.416 | 2.775 | 2.775 | 0.314 | 0.000 | 0.000 | 0.000 |
| 47.124 | 4.163 | 4.163 | 0.417 | 0.000 | 0.000 | 0.000 |
| Model | Ixx (kg·m2) | Iyy (kg·m2) | Izz (kg·m2) | Ixy (kg·m2) | Ixz (kg·m2) | Iyz (kg·m2) |
|---|---|---|---|---|---|---|
| Model 1 | 0.812 | 0.812 | 0.314 | 0.000 | 0.000 | 0.000 |
| Model 2 | 2.775 | 2.775 | 0.314 | 0.000 | 0.000 | 0.000 |
| Model 3 | 3.246 | 3.246 | 1.257 | 0.000 | 0.000 | 0.000 |
| Water-Entry Angle | Ixx (kg·m2) | Iyy (kg·m2) | Izz (kg·m2) | Ixy (kg·m2) | Ixz (kg·m2) | Iyz (kg·m2) |
|---|---|---|---|---|---|---|
| 30° | 2.775 | 0.929 | 2.160 | 0.000 | 0.000 | −1.066 |
| 45° | 2.775 | 1.545 | 1.545 | 0.000 | 0.000 | −1.230 |
| 60° | 2.775 | 2.160 | 0.929 | 0.000 | 0.000 | −1.066 |
| 75° | 2.775 | 2.610 | 0.479 | 0.000 | 0.000 | −0.615 |
| 90° | 2.775 | 2.775 | 0.314 | 0.000 | 0.000 | 0.000 |
| Head Shape | Ixx (kg·m2) | Iyy (kg·m2) | Izz (kg·m2) | Ixy (kg·m2) | Ixz (kg·m2) | Iyz (kg·m2) |
|---|---|---|---|---|---|---|
| Cylinder | 2.775 | 2.775 | 0.314 | 0.000 | 0.000 | 0.000 |
| Sphere | 2.278 | 2.278 | 0.314 | 0.000 | 0.000 | 0.000 |
| Ellipsoid | 1.833 | 1.833 | 0.314 | 0.000 | 0.000 | 0.000 |
| Cone | 2.278 | 2.278 | 0.314 | 0.000 | 0.000 | 0.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, F.; Sun, X.; Chi, F.; Ji, R. A Numerical Study on the Water Entry of Cylindrical Trans-Media Vehicles. Aerospace 2022, 9, 805. https://doi.org/10.3390/aerospace9120805
Deng F, Sun X, Chi F, Ji R. A Numerical Study on the Water Entry of Cylindrical Trans-Media Vehicles. Aerospace. 2022; 9(12):805. https://doi.org/10.3390/aerospace9120805
Chicago/Turabian StyleDeng, Feng, Xiaoyuan Sun, Fenghua Chi, and Ruixue Ji. 2022. "A Numerical Study on the Water Entry of Cylindrical Trans-Media Vehicles" Aerospace 9, no. 12: 805. https://doi.org/10.3390/aerospace9120805
APA StyleDeng, F., Sun, X., Chi, F., & Ji, R. (2022). A Numerical Study on the Water Entry of Cylindrical Trans-Media Vehicles. Aerospace, 9(12), 805. https://doi.org/10.3390/aerospace9120805







