Abstract
The plasma brake is a propellantless device conceived for de-orbiting purposes. It consists of an electrically charged thin tether that generates a Coulomb drag by interacting with the ionosphere. In essence, a plasma brake may be used to decelerate an out-of-service satellite and to ensure its atmospheric re-entry within the time limits established by the Inter-Agency Space Debris Coordination Committee. Moreover, since it only needs a small amount of electric power to work properly, the plasma brake is one of the most cost-effective systems for space debris mitigation. This paper exploits a recent plasma brake acceleration model to construct an iterative algorithm for the rapid evaluation of the decay time of a plasma-braked CubeSat, which initially traced a circular low Earth orbit. The altitude loss at the end of each iterative step was calculated using the linearized Hill–Clohessy–Wiltshire equations. It showed that the proposed algorithm, which was validated by comparing the approximate solution with the results from numerically integrating the nonlinear equations of motion, reduced computational time by up to four orders of magnitude with negligible errors in CubeSat position.
1. Introduction
In recent decades, space activities have given rise to an alarming over-crowding of many geocentric orbits used for scientific, communication, and meteorological purposes [,]. Due to atmospheric drag, satellites experience a rapid orbital decay when they orbit below about 400 km []. However, the orbital radius loss associated with atmospheric friction becomes gradually smaller as the altitude increases and becomes negligible for medium-high Earth orbits []. The importance of keeping the geocentric regions in an acceptable condition for safe mission operation [] has driven the scientific community to study deorbiting strategies [,,] to meet the operational constraint according to which the residual orbital life of an out-of-service satellite should be fewer than 25 years [,,].
Among the proposed methods to reduce the decay time of low Earth orbits (LEO) satellites, the electrostatic plasma brake [,,,] represents one of the most promising and fascinating options, as it does not require any propellant consumption, but only a tether-unreeling mechanism and a small amount of electrical power to charge that (conducting) tether. In fact, the plasma brake (PB) generates a Coulomb drag by means of a negatively charged thin tether, which electrostatically interacts with the ionized particles in the upper layers of the Earth’s atmosphere []. The PB tether is usually so thin that a fragment taken from it should rapidly descend into the lower layers of the atmosphere without posing a threat to other spacecraft in those regions. From a conceptual point of view, the PB uses the same physical principle as the Electric Solar Wind Sail (E-sail) [] although it is significantly smaller and less heavy because, instead of requiring an electron emitter, it uses natural charging from highly mobile electrons to maintain a negative voltage. The potential of E-sails has already been investigated in the context of a number of heliocentric mission scenarios, such as a planetary rendezvous [,,], the more challenging in situ study of the outer region of the solar system [,,], or the futuristic exploration of nearby interstellar space [,]. On the other hand, the PB could represent a very promising option for passively deorbiting a spacecraft from a LEO. In fact, passive deorbiting systems may operate without any propellant stored onboard and after deployment are much easier to control than the other (more involved) active deorbiting strategies [,]. Among the passive methods, another interesting option comes from drag sails or similar drag augmentation devices that increase the area-to-mass ratio of the satellite [,]. Another possibility is the unreeling of an electrodynamic tether to exploit current flux and generate a magnetic field that interacts with the Earth’s magnetosphere [,]. In this context, according to preliminary estimates [], a PB could enable shorter deorbiting times than typical drag augmentation devices while requiring a power supply significantly smaller than that of an electrodynamic tether.
In recent years, significant efforts have been devoted to the technical development of both E-sail and PB propulsion concepts, including tether construction, overall mechanical design options, guidance and navigation strategies, and orbital simulations [,]. For example, Seppänen et al. [] demonstrated the feasibility of producing a long conducting tether, while further research has been directed towards practical methods for the automatic manufacture [,] of such tethers. In addition, some space missions have been approved to demonstrate the feasibility of this advanced concept in a geocentric mission scenario. In particular, the Estonian 1U CubeSat ESTCube-1 [,,,], designed by the University of Tartu with the support of ESA and launched on 7 May 2013 aboard a Vega rocket, was the first ever satellite to attempt on-orbit deployment of an E-sail-charged tether. In fact ESTCube-1, with a mass of about 1 kg, was designed to deploy by centrifugal force a 10 m Heytether [], positively charged to 500 volts with its bias maintained by two electron emitters [].
Other mission requirements included using a PB to control spacecraft spin rate and de-orbiting. Unfortunately, the tether deployment failed, possibly due to a stuck reel, and the mission ended on 17 February 2015. Subsequent ground tests showed that the piezoelectric motor was damaged by launch phase vibrations [], which meant that the failure was not due to an intrinsic flaw in the charged tether-related technology, and that the problem could have been solved with suitable spacecraft design improvements [].
The ESTCube project is planning to launch ESTCube-2, an advanced 3U CubeSat to provide in-orbit measurements of the PB-induced Coulomb drag [,]. The launch is scheduled for 2023 when it is hoped that ESTCube-2 will deploy a kV negatively charged 300 m tether to brake CubeSat. The latter is expected to reduce its altitude from 700 to 500 km in half a year []. According to conservative estimates, the conducting tether mass will be about 30 g and the mass of the whole PB system should be less than 500 g; thus, the proposed PB can be thought of as an effective, low-mass de-orbiting system.
The lesson learned from the failure of ESTCube-1 has also led to the design of Aalto-1 [], a Finnish 3U CubeSat designed by Aalto University and launched on 23 June 2017. The Aalto-1 spacecraft has a mass of 3.9 kg and incorporates a PB device designed to perform attitude maneuvers and eventually de-orbit the CubeSat at the end of its operational lifespan []. The PB device consisted of a 100 m conducting tether, a reel mechanism for tether storage, a high voltage source, and electron emitters to maintain the charge []. After one year of technical issues (mainly concerning the communication subsystem) Aalto-1 started its planned remote sensing operations. Unfortunately, after some encouraging preliminary tests, the PB tether did not deploy, probably due to a failure in the boost converter that was supposed to maintain the nominal working voltage of the unreeling mechanism motor [].
Recent interest in PB and Coulomb drag-based devices was also demonstrated by the private satellite AuroraSat-1, which was launched to a LEO on 2 May 2022; see Figure 1. AuroraSat-1 is a 1.5U CubeSat equipped with two payloads: a water resistojet module [] for attitude changes and orbital adjustments and a PB module for spacecraft de-orbiting at the end of the scientific mission.

Figure 1.
AuroraSat-1 includes a PB device for de-orbiting purposes at the end of its life. Image from Aurora Propulsion Technologies.
An even more recent mission that could serve as a technological demonstrator of PB technology is FORESAIL-1, the first satellite designed by the Finnish centre Of excellence in REsearch of SustAInabLe space (FORESAIL) []. The 3U CubeSat FORESAIL-1 was launched into a polar orbit at an altitude of 700 km on 25 May 2022. The CubeSat, which is equipped with a particle detector to provide in situ measurements required for understanding radiation belt physics, has an electrostatic PB device developed by the Finnish Meteorological Institute. It consists of a 40 m conducting tether, which will be employed for de-orbiting purposes at the end of the satellite operative life [].
The aforementioned projects highlight the growing interest of the space community in PB technology. The trajectory analysis of a deorbiting satellite under Coulomb drag is therefore a subject of relevant interest. To deal with this problem, one possibility is numeric integration of Gaussian perturbation equations with a suitable model of the PB-induced Coulomb drag []. A viable alternative is represented by the determination of closed-form approximate models capable of estimating the decay time of a PB-equipped spacecraft (See Ref. []). In this context, this paper proposes a simplified mathematical model capable of estimating the decay time of a PB-based CubeSat simply and efficiently. Under the assumption that the CubeSat initially traced a circular (Keplerian) LEO, the proposed approach analyzes CubeSat motion relative to a virtual point that moves along the initial orbit at a constant speed. In other words, the virtual point represents the position of the small satellite on the circular LEO before the deployment of the PB-conducting tether. The linearized Hill–Clohessy–Wiltshire (HCW) equations [] are used to describe the relative spacecraft motion, in which the magnitude of the PB-induced drag is a constant, while its direction is assumed to be purely circumferential; see Figure 2. The latter assumption is reasonable as long as the eccentricity of the PB-based CubeSat osculating orbit is sufficiently small, a condition that is satisfied by the very low magnitude of the Coulomb drag when compared to the Earth’s gravitational attraction. To simplify the numerical simulations to obtain conservative results, other perturbation sources such as atmospheric drag were neglected.
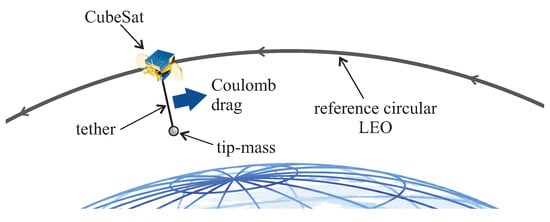
Figure 2.
Plasma brake concept.
We showed that an analytical approximation of the spacecraft relative motion is possible, which allows the orbital decay achieved in N revolutions to be estimated with closed-form expressions. By adopting the analytical PB thrust model proposed by Orsini et al. [], the number of revolutions within which the HCW-based approximations were valid was a function of the spacecraft’s orbital radius and the characteristics of the PB device. An iterative process was proposed to estimate the PB-based CubeSat decay time with a computational cost significantly smaller than that required by numerically integrating nonlinear equations of motion. In particular, each cycle was characterized by constant values of PB-induced acceleration and orbital angular velocity so that the decay time was inversely proportional to the drag acceleration magnitude at the spacecraft’s initial altitude. The resulting decay time was a conservative estimate, since atmospheric drag was not included in our mathematical model.
The paper is organized as follows. Section 2 deals with the approximate plasma brake trajectory and evaluates the maximum number of revolutions within which that solution is valid as a function of the spacecraft altitude, the Coulomb drag acceleration magnitude at the initial altitude, and the maximum allowable position error. Section 2 also shows a comparison of the approximate PB trajectory with reference results obtained by numerically integrating nonlinear equations of motion. Section 3 describes in detail the proposed iterative process and evaluates the decay time of three different CubeSat configurations that initially traced a circular LEO at an altitude of 1000 km above sea level. The last section contains our concluding remarks.
2. Mathematical Model
Consider a PB-based CubeSat that initially traced a circular LEO of radius r and introduced an orbital reference frame at origin O; see Figure 3. The point O coincided with the CubeSat center of mass when the PB device was not deployed. Orbital perturbations were ignored, The y-axis was oriented radially from the Earth’s center of mass to O, while the x-axis was tangent to the reference LEO in the opposite direction of the orbital motion.
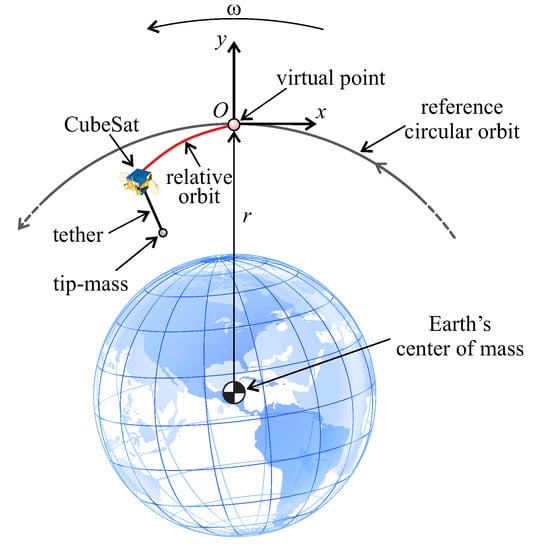
Figure 3.
Rotating reference system and relative trajectory (solid line) of a PB-based CubeSat.
The two-dimensional relative motion of the braked CubeSat after PB deployment with respect to O can be described through linearized HCW equations [], which well approximate the actual spacecraft dynamics as long as the distance between O and the CubeSat is small compared to the orbital radius r. In the same way as in Ref. [], the PB-induced drag acceleration is assumed to be purely circumferential, i.e., perpendicular to the local radial direction. Even though the Coulomb drag on the spacecraft depends on altitude [], the drag acceleration magnitude may be considered as roughly constant during a revolution around the Earth. This assumption is reasonable because the CubeSat orbital radius r has small variation with time due to the fact that the magnitude of the PB-induced drag is much smaller than the weight of the spacecraft. Accordingly, using the model discussed by Chobotov [], the linearized two-dimensional HCW equations are
where is the constant angular velocity along the reference circular LEO, and is the Earth’s gravitational parameter. The linear HCW Equations (1) and (2) are analytically integrated with zero initial conditions, that is, with and . The solutions to Equations (1) and (2) are []
Note that the conditions indicate that the virtual point O coincides with the CubeSat center of mass at initial time .
Starting from Equations (3) and (4), it is now possible to calculate the number N of revolutions around the Earth within which the HCW solutions can be considered valid. To this end, consider the time instant corresponding to orbital periods of the virtual point O, viz.
The corresponding coordinates of the PB-based CubeSat in the rotating reference frame were obtained through Equations (3) and (4) as
so that the distance between the CubeSat and the virtual point O is
the value of which, at , is given by
The maximum value of N (denoted by ) is related to , the maximum admissible value of . The latter can be written as a fraction of the reference circular LEO radius r as
where is a dimensionless parameter depending on the maximum admissible error in position from the linearization process (the greater the , the greater the error). Substituting Equation (10) into Equation (9), in which , we obtained
where is the Earth’s mean radius; h is the spacecraft altitude above sea level; and is the floor function. (Recall that, by definition, N is a natural number.)
As far as the PB-induced drag acceleration is concerned, according to Orsini et al. [] it is described by the equation
where is the initial orbital radius; is the mean molecular mass of the incoming flow (since the dominant atomic species is oxygen); is standard gravity; is the Boltzmann constant; is the (constant) ionosphere temperature (assuming mean solar activity); and is the plasma brake acceleration at the initial radius of the reference LEO. Accordingly, since is a function of r, the maximum number of revolutions within which the solution to the HCW equations is sound is a function of and r, that is, .
Figure 4 shows the dependence of on h and when the PB-induced drag magnitude is and the initial altitude . The selected value of is consistent, for example: total spacecraft mass of and a 300 m tether at an electric voltage of (see Table 1). In this case, the solutions to the HCW equations may be used at an altitude between 300 and 1000 km for at least two revolutions if .
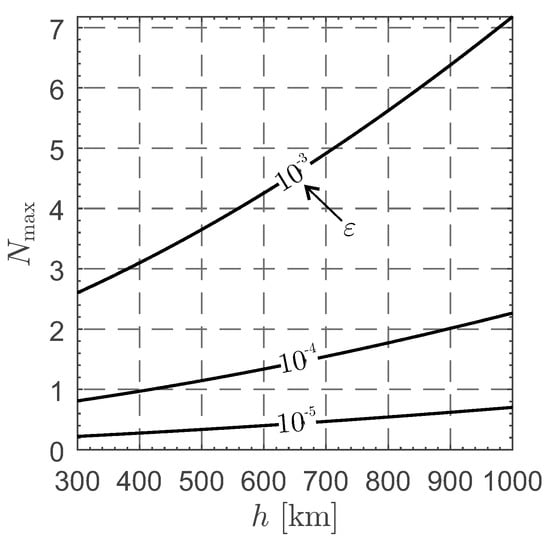
Figure 4.
Variation of with h and when and .

Table 1.
Characteristics of the satellites in the PB-enabled deorbiting simulations when .
Note that the value of increases either when the spacecraft total mass increases or when the Coulomb drag magnitude decreases, that is, when the value of the drag acceleration magnitude falls. This aspect can be analyzed by comparing the approximate results from the analytical Equations (1) and (2) and the outputs of the numerical integration of the nonlinear equations of motion. For example, Figure 5 shows that the approximate solution differs greatly from the numerical one if , while from Figure 6, the approximate solution closely follows the solution from the orbital propagator when . In Figure 5 and Figure 6, the initial value of the PB-induced drag magnitude is and the CubeSat initially covered a circular LEO of altitude .
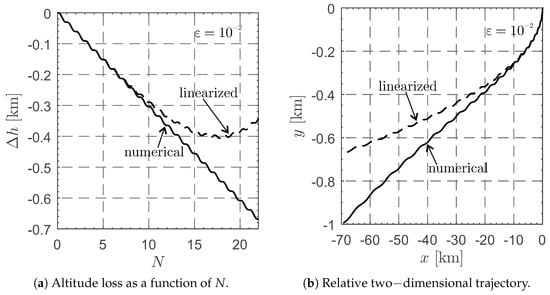
Figure 5.
Comparison between the numerical (solid line) and linearized (dashed line) solutions when , , and .
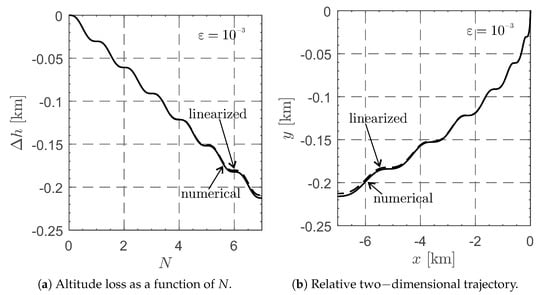
Figure 6.
Comparison between the numerical (solid line) and linearized (dashed line) solutions when , , and .
3. Numerical Simulations and Mission Application
In this section we evaluate the orbital decay time of a CubeSat by using the analytical solutions to the HCW equations from the preceding section. Three different CubeSat configurations were considered for simulation purposes. They were are all consistent with a current or near-term readiness level for nanosatellites. Their main characteristics are summarized in Table 1. Note that spacecraft ③ is characterized by the greatest value of PB-induced drag acceleration; accordingly, it was used as a test case to check the soundness of the approximate (analytical) equations.
In all cases, the approximate results were compared with the solutions from the numerical integration of the (nonlinear) two-body equations of motion. The simulations were on a Intel Core i7-10510U processor using the MATLAB ode113 solver with absolute and relative errors equal to and maximum step size equal to 0.01 terrestrial Canonical Time Units (about 8 s). Starting from altitude , the total decay time required for the spacecraft to reach the final altitude of , corresponding to the value of the minimum orbital radius , was evaluated through an iterative process, in which was assumed to be constant during each cycle. The number of revolutions of the rotating reference system in each cycle came from Equation (11), with , where N coincided with the minimum value of with respect to r:
From the simulation results of the previous section, assuming a PB-induced drag acceleration of at , the HCW equations gave a good approximation of the numerical results when . The values of N are shown in Table 2 for each case study.

Table 2.
Number N of revolutions of the rotating reference system corresponding to each iterative cycle, see Equation (13) with .
The orbital decay in the i-th cycle is given by
where
The i-th cycle was therefore characterized by a constant value of PB-induced acceleration , that is, was approximated by a step function during the whole decay, while the satellite relative position was set equal to zero at the beginning of each cycle. This amounted to modifying the position of the virtual point with respect to which the orbital decay was evaluated at each step, by updating the value of r as
The whole iterative process, which stopped when , is described in Figure 7. Note that the evaluation of N takes place on the right side of the flow chart (i.e., outside the recursive cycle), which means that the value of N is calculated globally.
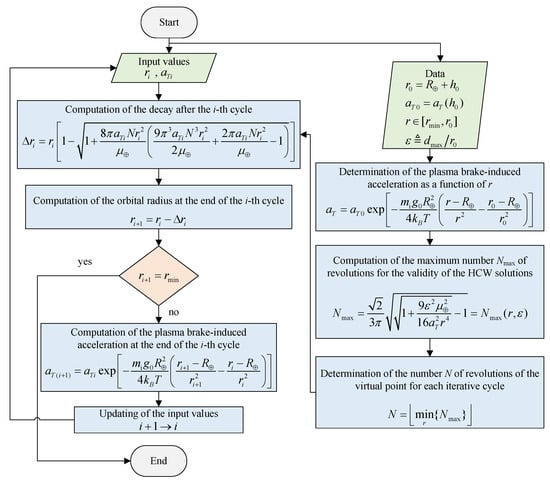
Figure 7.
Flow chart of the algorithm for calculating the orbital decay.
The total decay time is simply the sum of the orbital periods of each cycle multiplied by the corresponding number of revolutions of the rotating reference system, which yields
where
The approximate solutions are shown in Table 3 along with the numerical results given by the orbital propagator. Notice that the final error is indeed very small, while in all of the three cases the computational time was reduced by four orders of magnitude when compared to the simulation time required to integrate the nonlinear equations of motion numerically.

Table 3.
Decay time and computation time for the three cases studied obtained through numerical integration (actual value) and the proposed algorithm (approximate value).
4. Conclusions
A plasma brake device may be used to de-orbit a small satellite from an LEO within a few years when the deceleration induced by the Coulomb drag is about . The problem has been addressed using an iterative procedure in which the altitude loss of the satellite was obtained from the solutions of the two-dimensional linearized Hill–Clohessy–Wiltshire equations. Notably, the required computational time was reduced by four orders of magnitude when compared to a numerical integration of the whole equations of motion. The results turned out to be very accurate, with positional errors of only about . When compared to more conventional approaches based on the numerical integration of the nonlinear equations of motion, the alternative method discussed in this paper for the analysis of the deorbiting trajectory demonstrated that the HCW solutions can be used effectively, under suitable assumptions, to solve the problem even if the deorbiting device interacted with the surrounding space in a complex manner, and a mathematical description of the device-induced drag force represented a difficult problem. Of course, other methods, such as those based on perturbation theories, could be equivalently and successfully used to calculate orbital decay time. However, the HCW solutions were more effective than perturbation theory because, at each iterative cycle, it allowed the spacecraft trajectory to be directly known. As a matter of fact, the knowledge of the actual spacecraft trajectory, not simply the altitude loss, was essential for predicting and preventing possible impacts with other orbiting satellites in LEOs. Future work should concentrate on a refinement of the approximate analytical model by including typical perturbation sources in a LEO.
Author Contributions
Conceptualization, M.B. and A.A.Q.; methodology, M.B. and A.A.Q.; software, M.B.; writing—original draft preparation, M.B., A.A.Q. and G.M.; writing—review and editing, L.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partly supported by the University of Pisa, Progetti di Ricerca di Ateneo (Grant no. PRA_2022_1).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| transverse plasma brake-induced acceleration [] | |
| d | relative distance [m] |
| standard gravity [] | |
| h | altitude [m] |
| i | iteration index |
| Boltzmann constant [] | |
| tether length [m] | |
| m | spacecraft mass [kg] |
| mean molecular mass of the incoming flow [kg] | |
| N | number of revolutions of the virtual point |
| O | origin of |
| r | orbital radius [km] |
| mean Earth’s radius [km] | |
| t | time [s] |
| T | ionosphere temperature [K] |
| tether voltage [V] | |
| x | transverse relative coordinate [km] |
| y | radial relative coordinate [km] |
| dimensionless parameter () | |
| Earth’s gravitational parameter [] | |
| rotating reference system | |
| orbital angular velocity [] | |
| Subscripts | |
| c | numerical |
| d | decay |
| max | maximum |
| min | minimum |
| N | relative to N revolutions of the virtual point |
| 0 | initial conditions |
References
- Li, Q.B.; Wu, K.J.; Niu, C.Y. Determination of the Number of Space Debris’ Materials Based on Spectral Information. Guang Pu Xue Yu Guang Pu Fen Xi/Spectrosc. Spectr. Anal. 2017, 37, 2679–2684. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Wang, W.; Zhang, Y.; Wang, H. Geostationary Orbital Debris Collision Hazard after a Collision. Aerospace 2022, 9, 258. [Google Scholar] [CrossRef]
- Rossi, A.; Colombo, C.; Tsiganis, K.; Beck, J.; Rodriguez, J.B.; Walker, S.; Letterio, F.; Dalla Vedova, F.; Schaus, V.; Popova, R.; et al. ReDSHIFT: A Global Approach to Space Debris Mitigation. Aerospace 2018, 5, 64. [Google Scholar] [CrossRef]
- Hu, M.; Ruan, Y.; Zhou, H.; Xu, J.; Xue, W. Long-Term Orbit Prediction and Deorbit Disposal Investigation of MEO Navigation Satellites. Aerospace 2022, 9, 266. [Google Scholar] [CrossRef]
- Zhang, Y.; An, F.; Liao, S.; Wu, C.; Liu, J.; Li, Y. Study on Numerical Simulation Methods for Hypervelocity Impact on Large-Scale Complex Spacecraft Structures. Aerospace 2022, 9, 12. [Google Scholar] [CrossRef]
- Kvell, U.; Di Cara, D.; Janhunen, P.; Noorma, M.; Gonzalez del Amo, J.A. Deorbiting strategies: Comparison between electrostatic plasma brake and conventional propulsion. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, 31 July–3 August 2011. Paper AIAA 2011-5920. [Google Scholar] [CrossRef]
- Ham, C.; Ngo, D. Deorbiting of LEO small satellites without a conventional propulsion system. In Proceedings of the IEEE SOUTHEASTCON, Charlotte, NC, USA, 30 March–2 April 2017. [Google Scholar] [CrossRef]
- Lv, S.; Zhang, H.; Zhang, Y.; Ning, B.; Qi, R. Design of an Integrated Platform for Active Debris Removal. Aerospace 2022, 9, 339. [Google Scholar] [CrossRef]
- Yakovlev, M. The IADC space debris mitigation guidelines and support document. In Proceedings of the Fourth European Conference on Space Debris, European Space Agency (ESA), Darmstadt, Germany, 18–20 April 2005. [Google Scholar]
- Lambert, F.; Christiansen, E. The Inter-Agency Space Debris Coordination Committee (IADC) protection manual. In Proceedings of the Fourth European Conference on Space Debris, European Space Agency (ESA), Darmstadt, Germany, 18–20 April 2005. [Google Scholar]
- Popova, R.; Schaus, V. The Legal Framework for Space Debris Remediation as a Tool for Sustainability in Outer Space. Aerospace 2018, 5, 55. [Google Scholar] [CrossRef]
- Janhunen, P. Electrostatic plasma brake for deorbiting a satellite. J. Propuls. Power 2010, 26, 370–372. [Google Scholar] [CrossRef]
- Zhong, R.; Zhu, Z.H. Dynamics of nanosatellite deorbit by bare electrodynamic tether in low earth orbit. J. Spacecr. Rocket. 2013, 50, 691–700. [Google Scholar] [CrossRef]
- Janhunen, P. Simulation study of the plasma-brake effect. Ann. Geophys. 2014, 32, 1207–1216. [Google Scholar] [CrossRef]
- Janhunen, P.; Toivanen, P.K.; Envall, J.; Slavinskis, A. Using charged tether Coulomb drag: E-sail and plasma brake. In Proceedings of the 5th International Conference on Tethers in Space, Ann Arbor, Michigan, 24–26 May 2016. [Google Scholar]
- Janhunen, P. On the feasibility of a negative polarity electric sail. Ann. Geophys. 2009, 27, 1439–1447. [Google Scholar] [CrossRef]
- Janhunen, P. Electric sail for spacecraft propulsion. J. Propuls. Power 2004, 20, 763–764. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A.; Janhunen, P. Electric sail performance analysis. J. Spacecr. Rocket. 2008, 45, 122–129. [Google Scholar] [CrossRef]
- Huo, M.; Mengali, G.; Quarta, A.A. Optimal planetary rendezvous with an electric sail. Aircr. Eng. Aerosp. Technol. 2016, 88, 515–522. [Google Scholar] [CrossRef]
- Bassetto, M.; Quarta, A.A.; Mengali, G. Locally-optimal electric sail transfer. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 166–179. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A.; Janhunen, P. Considerations of electric sailcraft trajectory design. JBIS-J. Br. Interplanet. Soc. 2008, 61, 326–329. [Google Scholar]
- Quarta, A.A.; Mengali, G. Electric sail mission analysis for outer solar system exploration. J. Guid. Control. Dyn. 2010, 33, 740–755. [Google Scholar] [CrossRef]
- Janhunen, P.; Lebreton, J.P.; Merikallio, S.; Paton, M.; Mengali, G.; Quarta, A.A. Fast E-sail Uranus Entry Probe Mission. Planet. Space Sci. 2014, 104, 141–146. [Google Scholar] [CrossRef]
- Huo, M.; Mengali, G.; Quarta, A.A. Mission Design for an Interstellar Probe with E-Sail Propulsion System. JBIS-J. Br. Interplanet. Soc. 2015, 68, 128–134. [Google Scholar]
- Matloff, G.L. The Solar-Electric Sail: Application to Interstellar Migration and Consequences for SETI. Universe 2022, 8, 252. [Google Scholar] [CrossRef]
- Bonnal, C.; Ruault, J.M.; Desjean, M.C. Active debris removal: Recent progress and current trends. Acta Astronaut. 2015, 85, 51–60. [Google Scholar] [CrossRef]
- Mark, C.P.; Kamath, S. Review of active space debris removal methods. Space Policy 2019, 47, 194–206. [Google Scholar] [CrossRef]
- Roberts, P.C.E.; Harkness, P.G. Drag sail for end-of-life disposal from low Earth orbit. J. Spacecr. Rocket. 2007, 44, 1196–1203. [Google Scholar] [CrossRef]
- Underwood, C.; Viquerat, A.; Schenk, M.; Taylor, B.; Massimiani, C.; Duke, R.; Stewart, B.; Fellowes, S.; Bridges, C.; Aglietti, G.; et al. InflateSail de-orbit flight demonstration results and follow-on drag-sail applications. Acta Astronaut. 2019, 162, 344–358. [Google Scholar] [CrossRef]
- Hoyt, R.P.; Barnes, I.M.; Voronka, N.R.; Slostad, J.T. The Terminator Tape™: A cost-effective de-orbit module for end-of-life disposal of LEO satellites. In Proceedings of the AIAA Space 2009 Conference and Exposition, Pasadena, CA, USA, 14–17 September 2009. [Google Scholar]
- Valmorbida, A.V.; Olivieri, L.; Brunello, A.; Sarego, G.; Sánchez-Arriaga, G.; Lorenzini, E.C. Validation of enabling technologies for deorbiting devices based on electrodynamic tethers. Acta Astronaut. 2022, 198, 707–719. [Google Scholar] [CrossRef]
- Iakubivskyi, I.; Janhunen, P.; Praks, J.; Allik, V.; Bussov, K.; Clayhills, B.; Dalbins, J.; Eenmäe, T.; Ehrpais, H.; Envall, J.; et al. Coulomb drag propulsion experiments of ESTCube-2 and FORESAIL-1. Acta Astronaut. 2020, 177, 771–783. [Google Scholar] [CrossRef]
- Janhunen, P.; Toivanen, P.K.; Polkko, J.; Merikallio, S.; Salminen, P.; Haeggström, E.; Seppänen, H.; Kurppa, R.; Ukkonen, J.; Kiprich, S.; et al. Electric solar wind sail: Toward test missions. Rev. Sci. Instrum. 2010, 81, 111301. [Google Scholar] [CrossRef]
- Bassetto, M.; Niccolai, L.; Quarta, A.A.; Mengali, G. A comprehensive review of Electric Solar Wind Sail concept and its applications. Prog. Aerosp. Sci. 2022, 128, 1–27. [Google Scholar] [CrossRef]
- Seppänen, H.; Rauhala, T.; Kiprich, S.; Ukkonen, J.; Simonsson, M.; Kurppa, R.; Janhunen, P.; Hæggström, E. One kilometer (1 km) electric solar wind sail tether produced automatically. Rev. Sci. Instrum. 2013, 84, 095102. [Google Scholar] [CrossRef]
- Seppänen, H.; Kiprich, S.; Kurppa, R.; Janhunen, P.; Hæggström, E. Wire-to-wire bonding of μm-diameter aluminum wires for the electric solar wind sail. Microelectron. Eng. 2011, 88, 3267–3269. [Google Scholar] [CrossRef]
- Rauhala, T.; Seppänen, H.; Ukkonen, J.; Kiprich, S.; Maconi, G.; Janhunen, P.; Hæggström, E. Automatic 4-wire Heytether production for the electric solar wind sail. In Proceedings of the International Microelectronics Assembly and Packing Society Topical Workshop and Tabletop Exhibition on Wire Bonding, San Jose, CA, USA; 2013. [Google Scholar]
- Lätt, S.; Slavinskis, A.; Ilbis, E.; Kvell, U.; Voormansik, K.; Kulu, E.; Pajusalu, M.; Kuuste, H.; Sünter, I.; Eenmäe, T.; et al. ESTCube-1 nanosatellite for electric solar wind sail in-orbit technology demonstration. Proc. Est. Acad. Sci. 2014, 63, 200–209. [Google Scholar] [CrossRef]
- Slavinskis, A.; Pajusalu, M.; Kuuste, H.; Ilbis, E.; Eenmäe, T.; Sünter, I.; Laizans, K.; Ehrpais, H.; Liias, P.; Kulu, E.; et al. ESTCube-1 in-orbit experience and lessons learned. IEEE Aerosp. Electron. Syst. Mag. 2015, 30, 12–22. [Google Scholar] [CrossRef]
- Olesk, A. Mediatization of a Research Group: The Estonian Student Satellite ESTCube-1. Sci. Commun. 2019, 41, 196–221. [Google Scholar] [CrossRef]
- Olesk, A.; Noorma, M. Chapter 9 - The Engagement Activities of ESTCube-1: How Estonia Built and Fell in Love With a Tiny Satellite. In Space Science and Public Engagement; Kaminski, A.P., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 169–183. [Google Scholar] [CrossRef]
- Envall, J.; Janhunen, P.; Toivanen, P.K.; Pajusalu, M.; Ilbis, E.; Kalde, J.; Averin, M.; Kuuste, H.; Laizans, K.; Allik, V.; et al. E-sail test payload of the ESTCube-1 nanosatellite. Proc. Est. Acad. Sci. 2014, 63, 210–221. [Google Scholar] [CrossRef]
- Iakubivskyi, I.; Ehrpais, H.; Dalbins, J.; Oro, E.; Kulu, E.; Kütt, J.; Janhunen, P.; Slavinskis, A.; Ilbis, E.; Ploom, I.; et al. ESTCube-2 mission analysis: Plasma brake experiment for deorbiting. In Proceedings of the 67th International Astronautical Congress (IAC), Guadalajara, Mexico, 26–30 September 2016. Paper IAC-16,E2,4,4,x33190. [Google Scholar]
- Dalbins, J.; Allaje, K.; Iakubivskyi, I.; Kivastik, J.; Komarovskis, R.O.; Plans, M.; Sünter, I.; Teras, H.; Ehrpais, H.; Ilbis, E.; et al. ESTCube-2: The Experience of Developing a Highly Integrated CubeSat Platform. In Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022; pp. 1–16. [Google Scholar] [CrossRef]
- Kestilä, A.; Tikka, T.; Peitso, P.; Rantanen, J.; Näsilä, A.; Nordling, K.; Saari, H.; Vainio, R.; Janhunen, P.; Praks, J.; et al. Aalto-1 nanosatellite—Technical description and mission objectives. Geosci. Instrum. Methods Data Syst. 2013, 2, 121–130. [Google Scholar] [CrossRef]
- Khurshid, O.; Selkäinaho, J.; Soken, H.E.; Kallio, E.; Visala, A. Small satellite attitude determination during plasma brake deorbiting experiment. Acta Astronaut. 2016, 129, 52–58. [Google Scholar] [CrossRef]
- Khurshid, O.; Tikka, T.; Praks, J.; Hallikainen, M. Accomodating the plasma brake experiment on-board the Aalto-1 satellite. Proc. Est. Acad. Sci. 2014, 63, 258–266. [Google Scholar] [CrossRef]
- Mughal, M.R.; Praks, J.; Vainio, R.; Janhunen, P.; Envall, J.; Näsilä, A.; Oleynik, P.; Niemelä, P.; Nyman, S.; Slavinskis, A.; et al. Aalto-1, multi-payload CubeSat: In-orbit results and lessons learned. Acta Astronaut. 2021, 187, 557–568. [Google Scholar] [CrossRef]
- O’Reilly, D.; Herdrich, G.; Kavanagh, D.F. Electric Propulsion Methods for Small Satellites: A Review. Aerospace 2021, 8, 22. [Google Scholar] [CrossRef]
- Palmroth, M.; Praks, J.; Vainio, R.; Janhunen, P.; Kilpua, E.K.J.; Afanasiev, A.; Ala-Lahti, M.; Alho, A.; Asikainen, T.; Asvestari, E.; et al. FORESAIL-1 CubeSat mission to measure radiation belt losses and demonstrate deorbiting. J. Geophys. Res. Space Phys. 2019, 124, 5783–5799. [Google Scholar] [CrossRef]
- Niccolai, L.; Bassetto, M.; Quarta, A.A.; Mengali, G. Trajectory approximation of a Coulomb drag-based deorbiting. Aerospace, 2022; Submitted. [Google Scholar]
- Clohessy, W.H.; Wiltshire, R.S. Terminal Guidance System for Satellite Rendezvous. J. Aerosp. Sci. 1960, 27, 653–658. [Google Scholar] [CrossRef]
- Orsini, L.; Niccolai, L.; Mengali, G.; Quarta, A.A. Plasma Brake Model for Preliminary Mission Analysis. Acta Astronaut. 2018, 144, 297–304. [Google Scholar] [CrossRef]
- Chobotov, V.A. (Ed.) Orbital Mechanics; AIAA Education Series; American Institute of Aeronautics and Astronautics, Inc.: Reston, Virginia, 2002; Chapter 7; pp. 155–159. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).