Numerical and Experimental Study on Jet Trajectory and Fuel Concentration Distribution Characteristics of Kerosene Jet in Air Crossflow
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Model
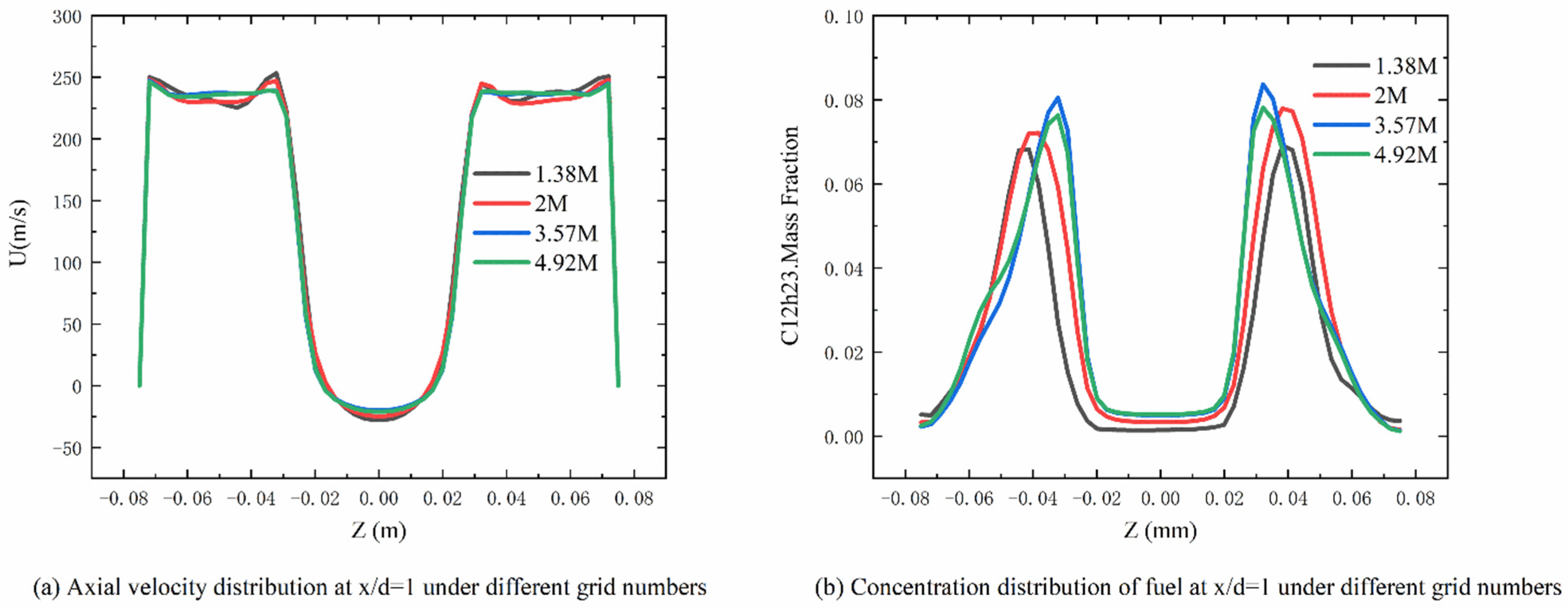
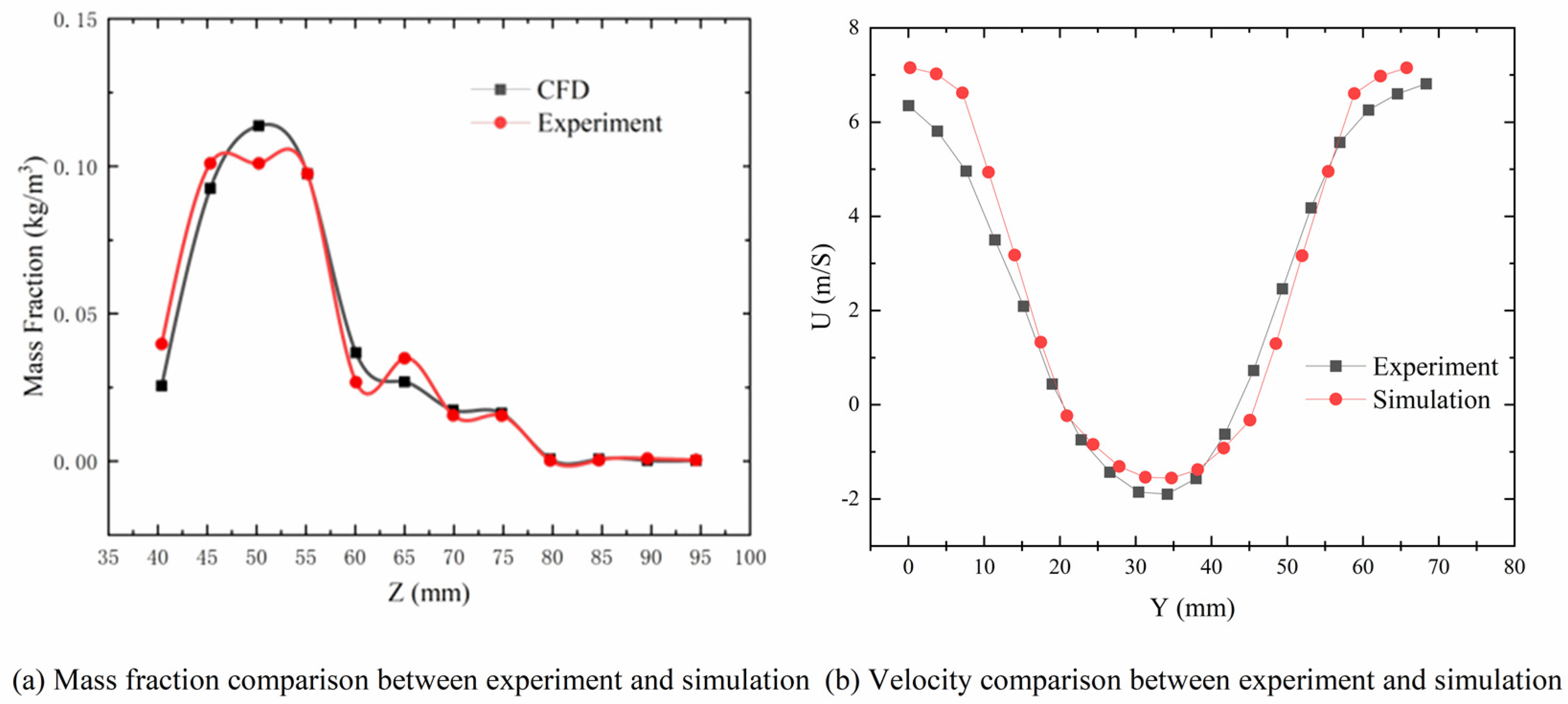
2.2. Numerical Set and Validation
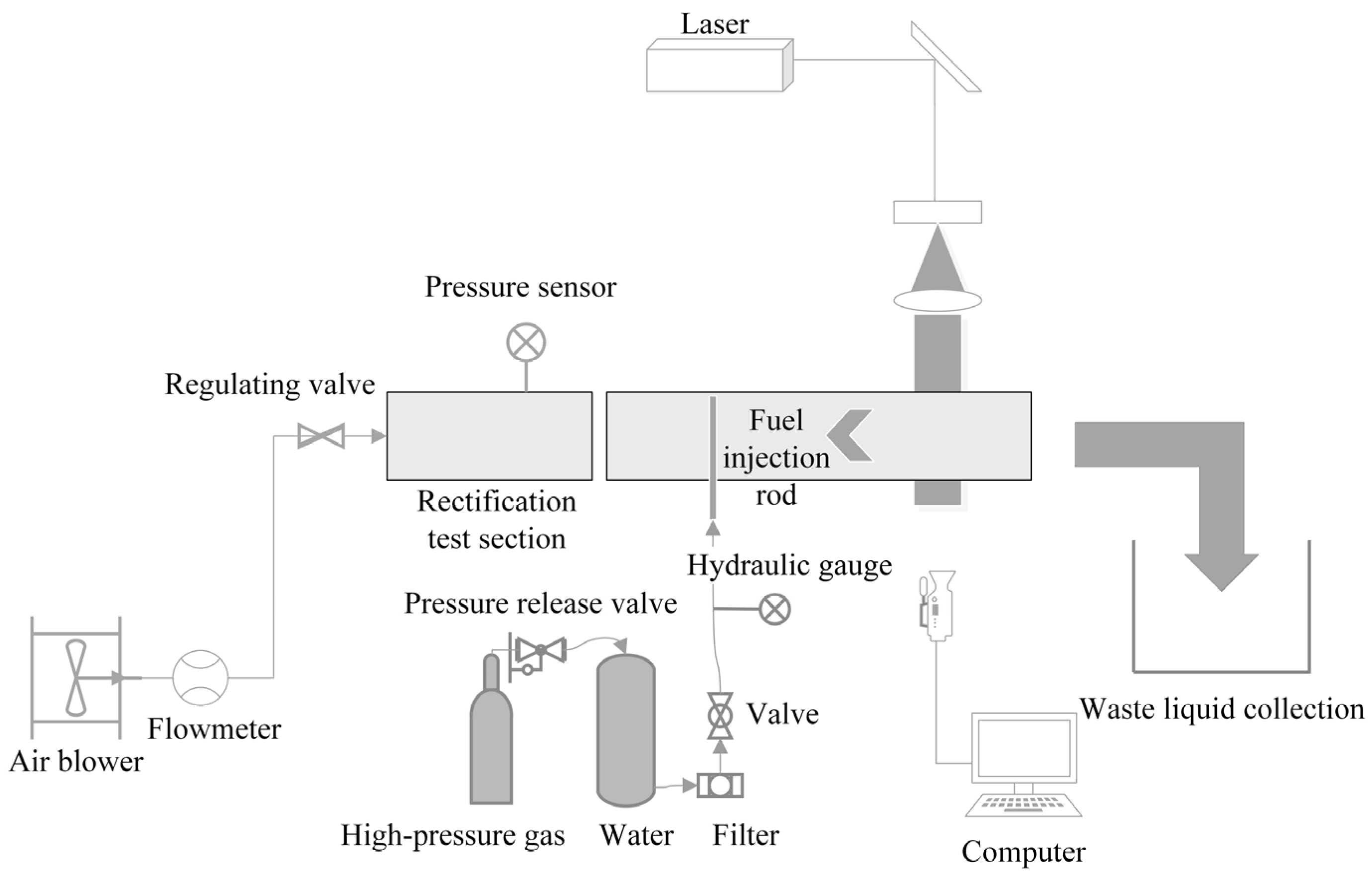
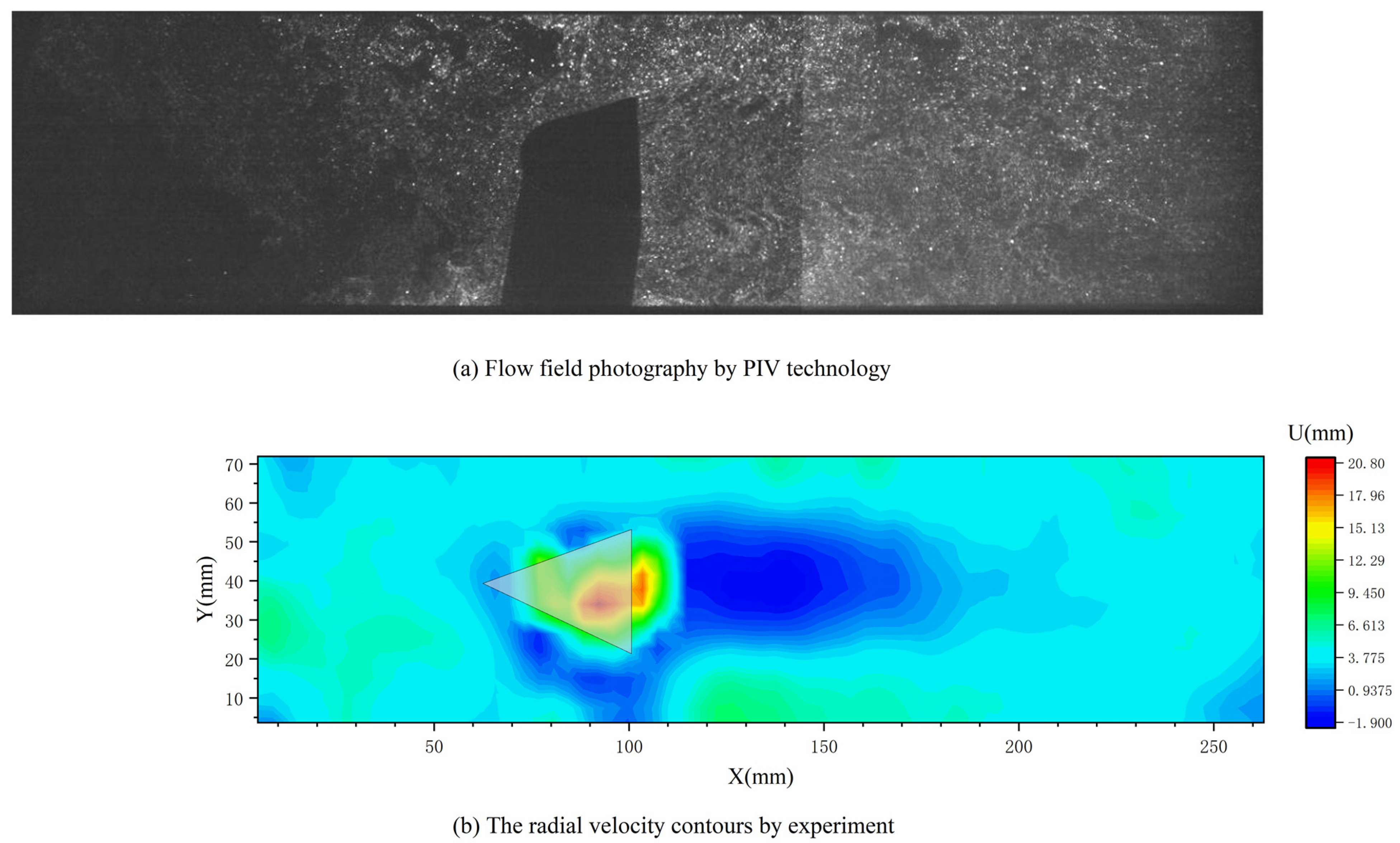
2.3. Experimental Method
3. Results and Discussion
3.1. Jet Trajectory
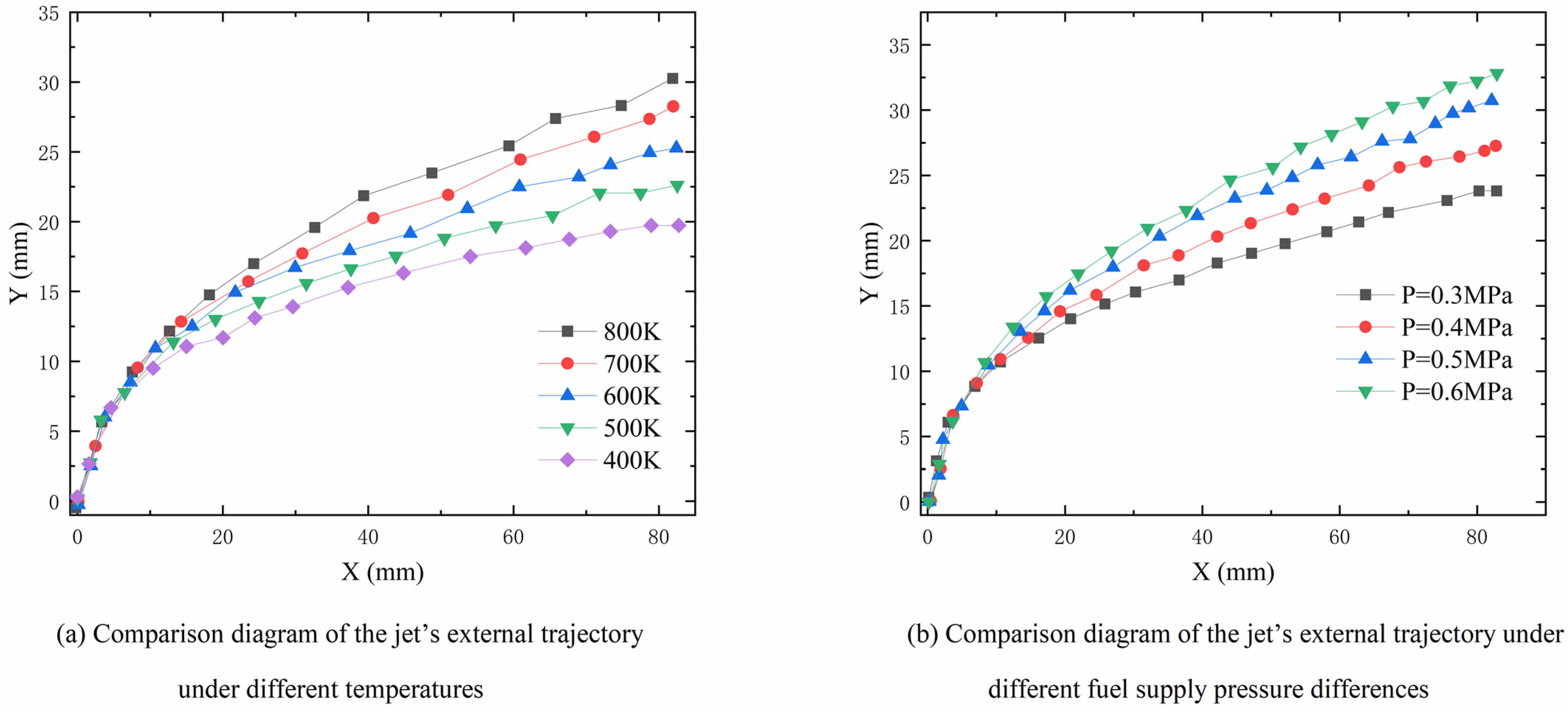
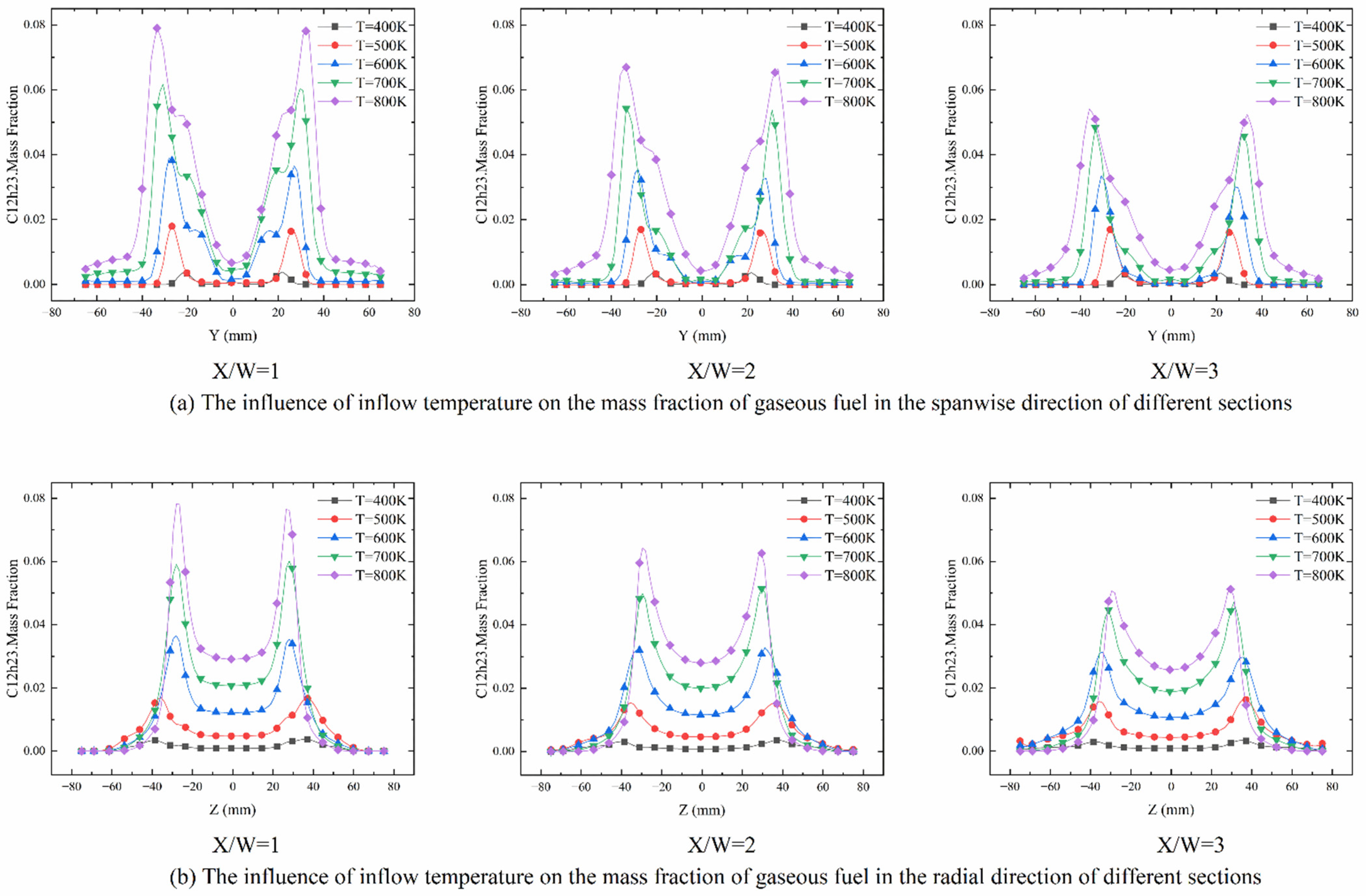
3.1.1. Influence of Inflow Temperature and Fuel Supply Pressure Difference
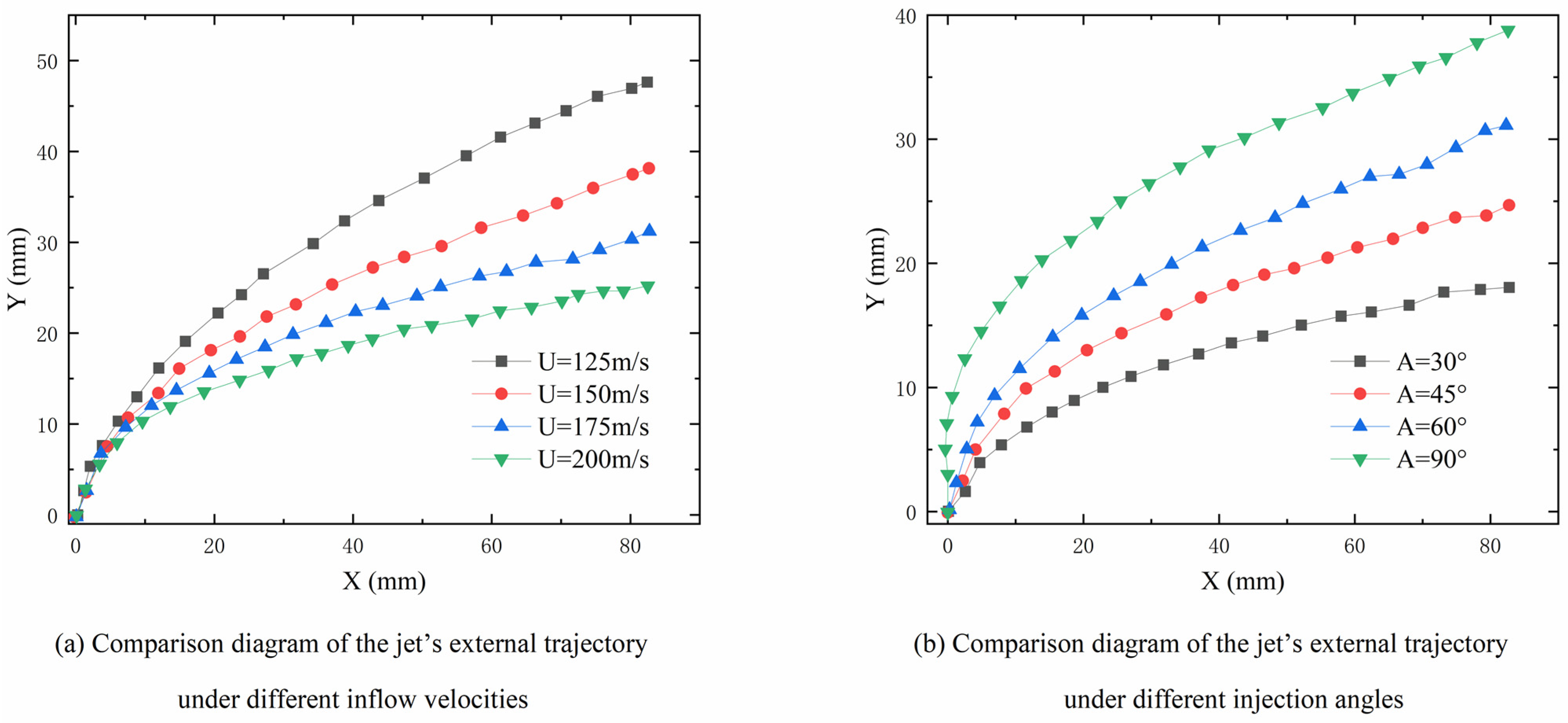
3.1.2. Influence of Inflow Velocities and Injection Angles
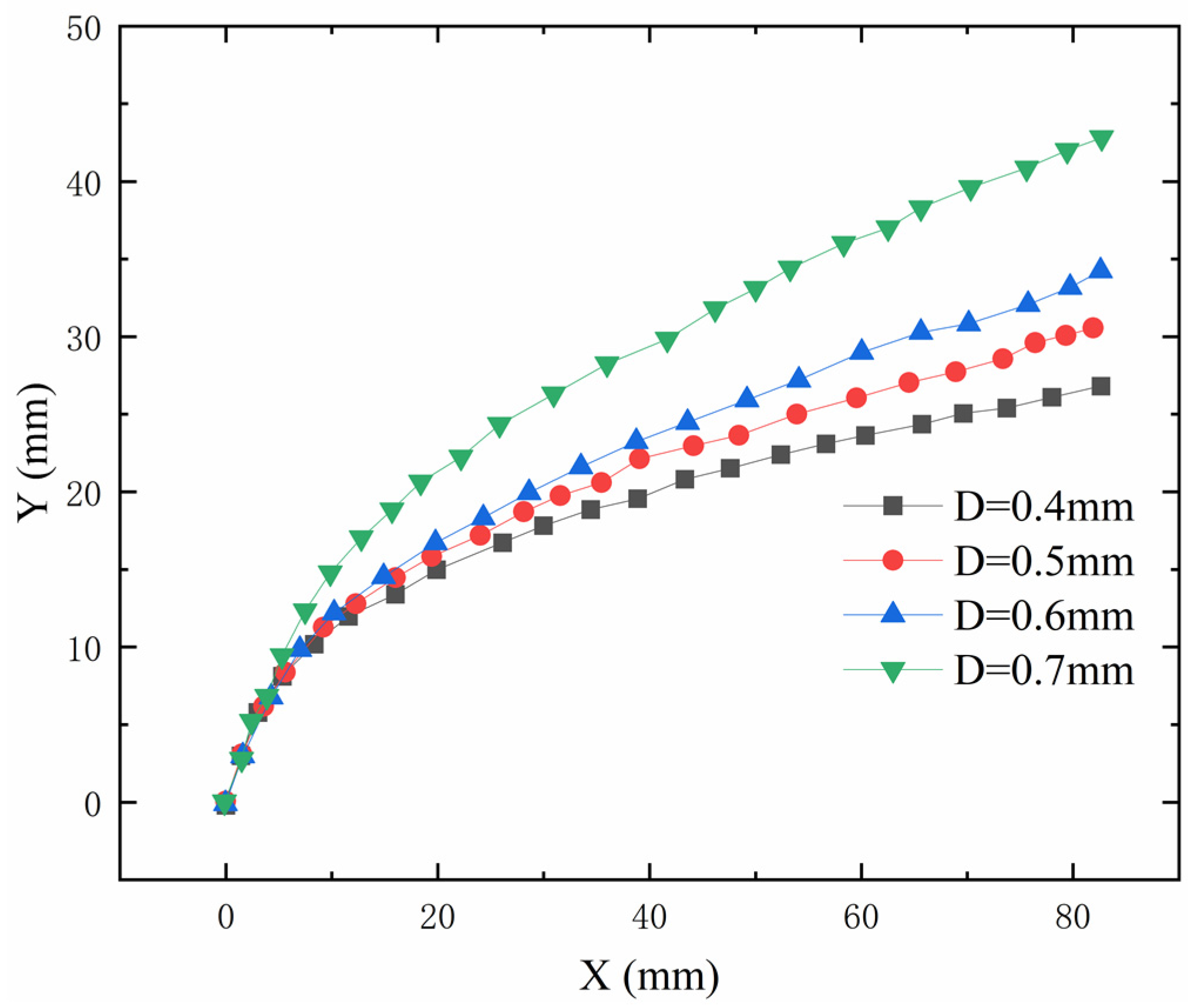
3.1.3. Influence of Nozzle Diameters
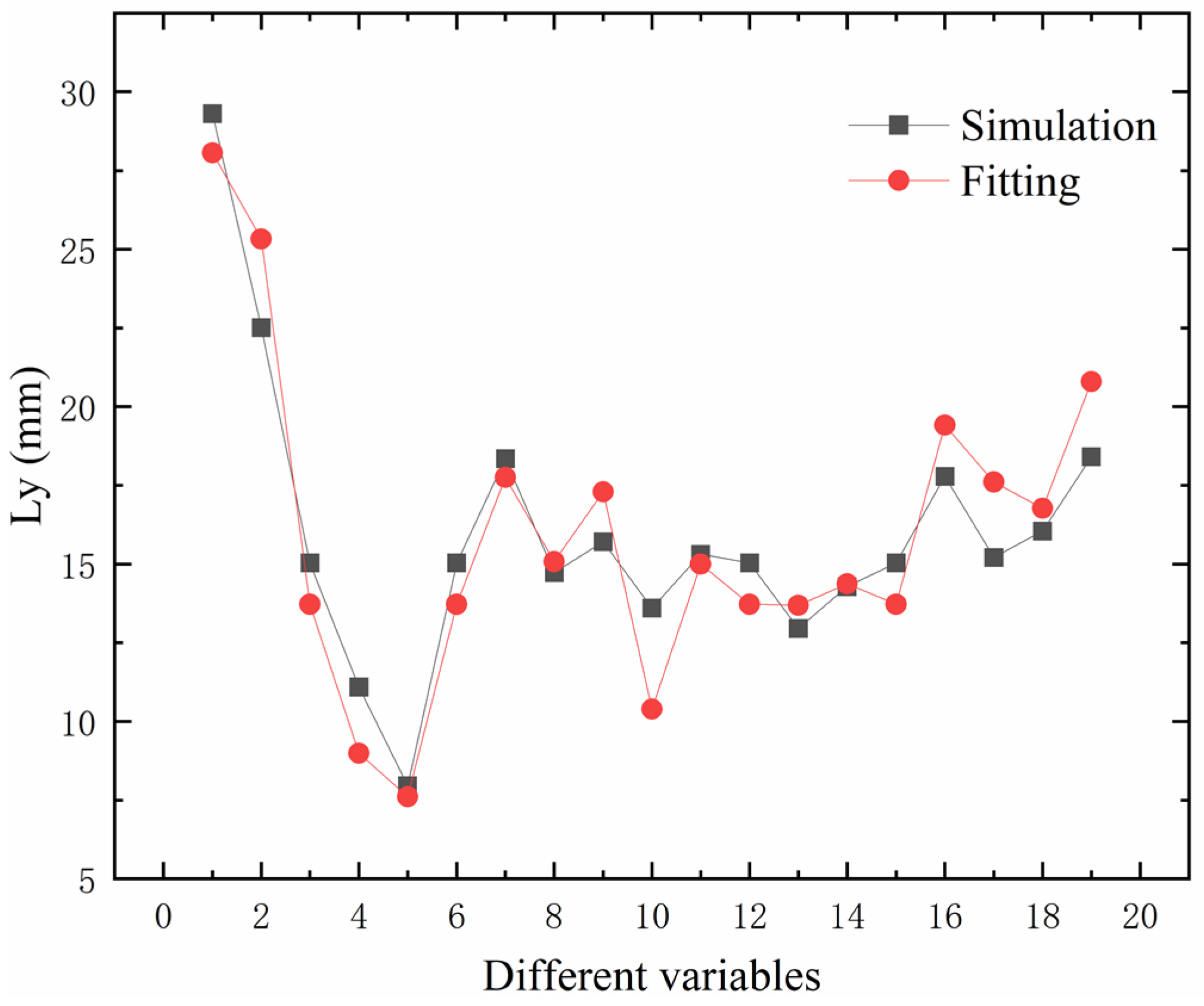
3.1.4. Spanwise Distribution Fitting of Fuel
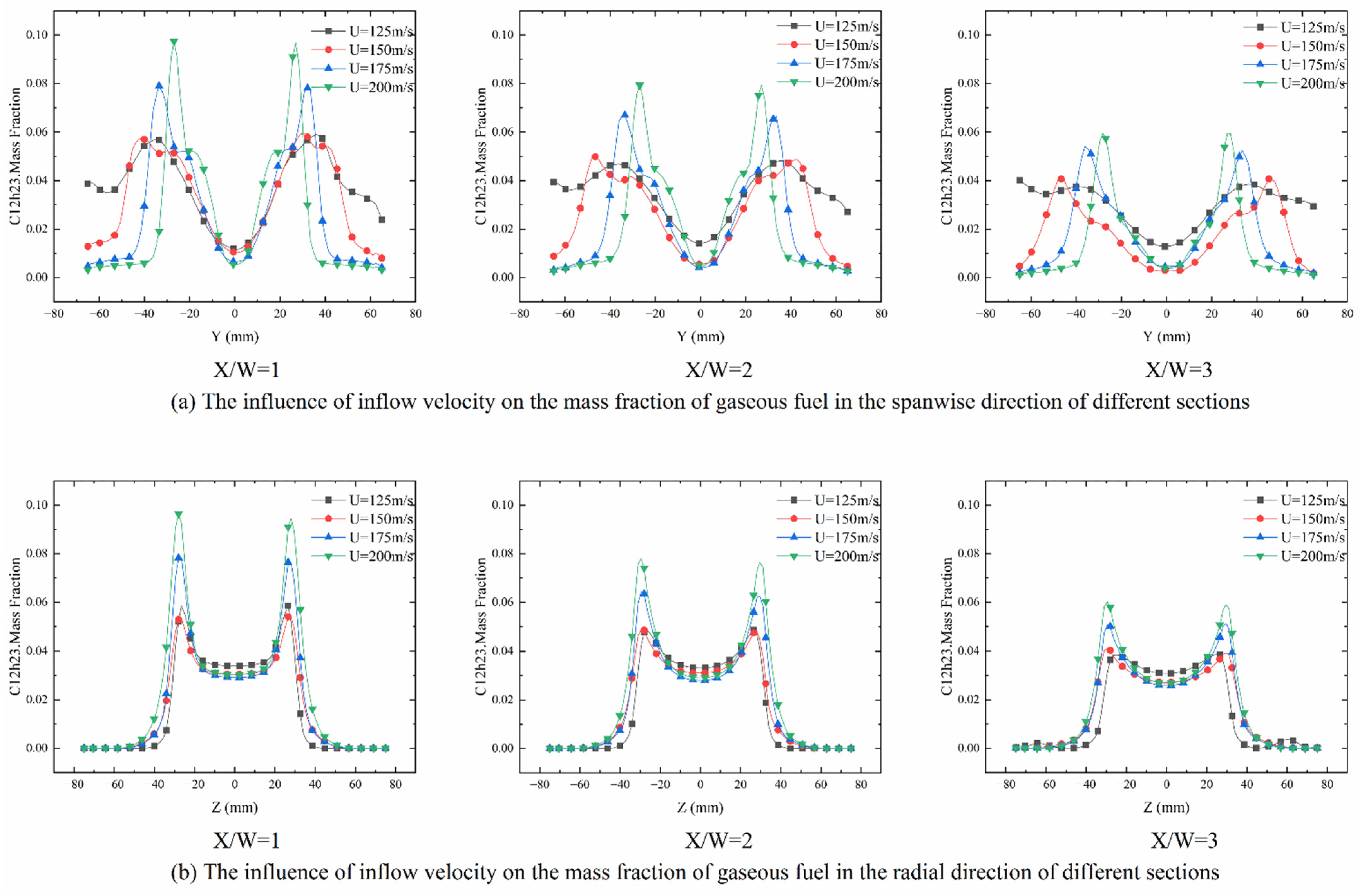
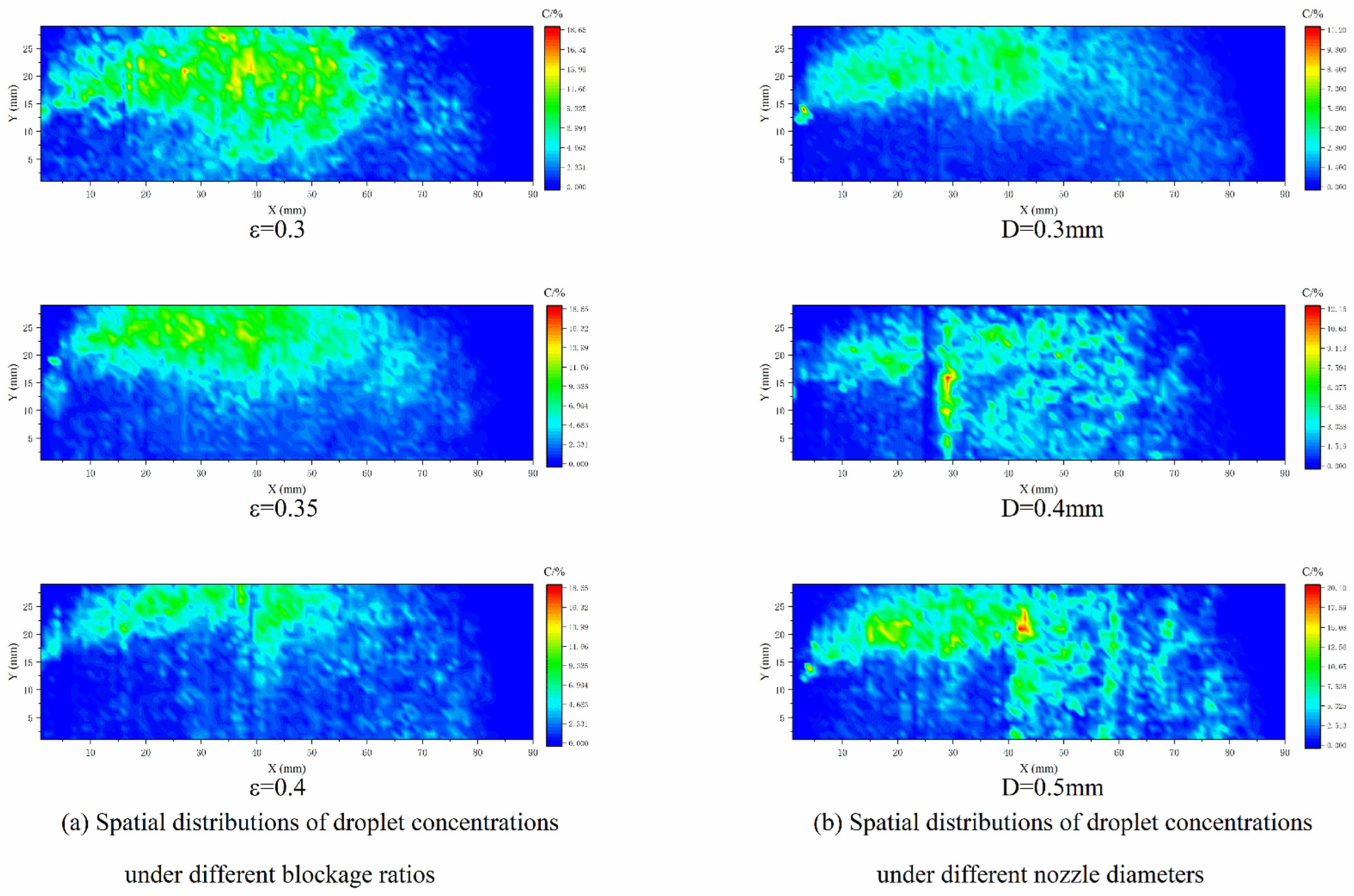
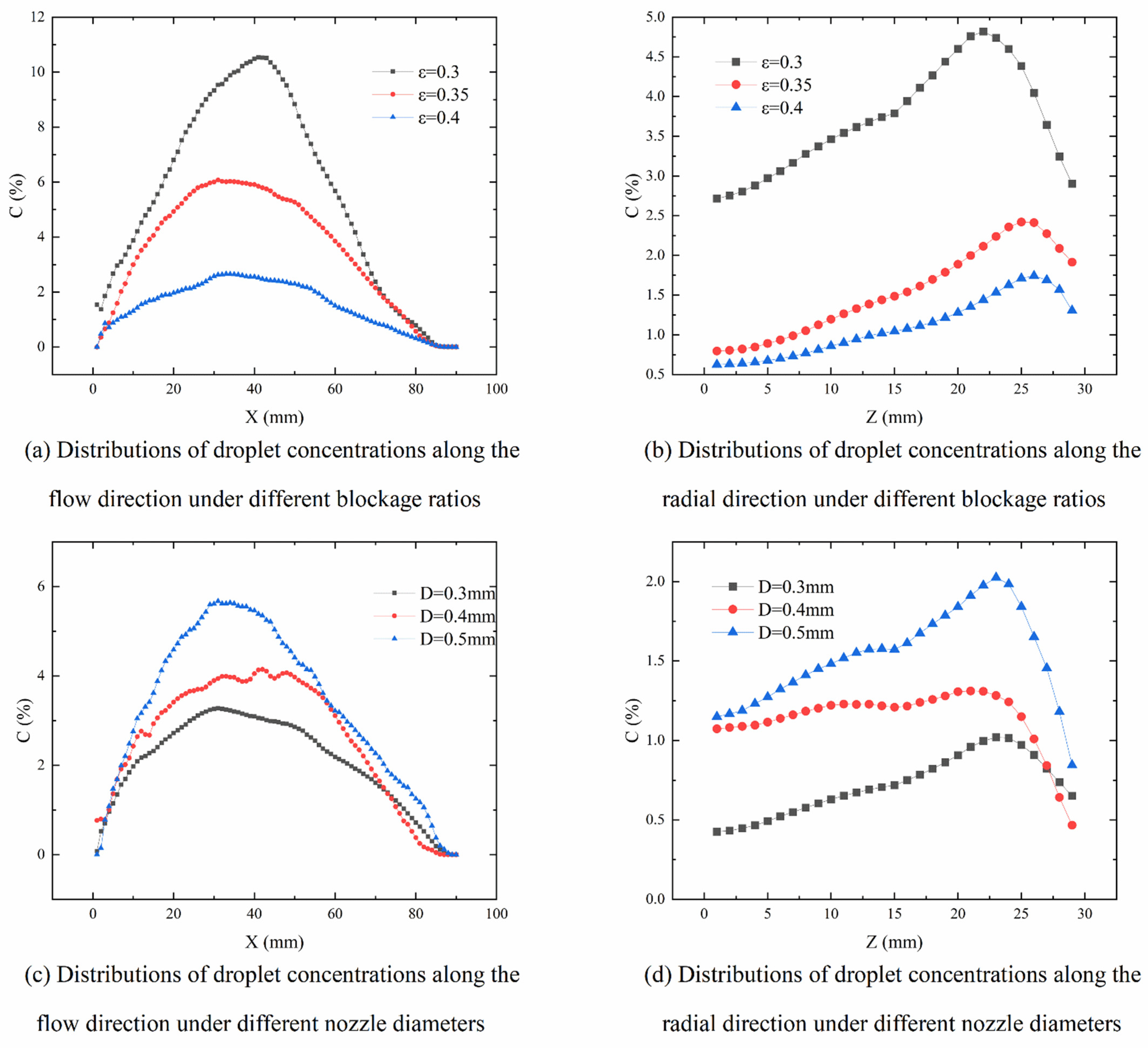
3.2. Fuel Concentration Distribution
3.2.1. Numerical Simulations
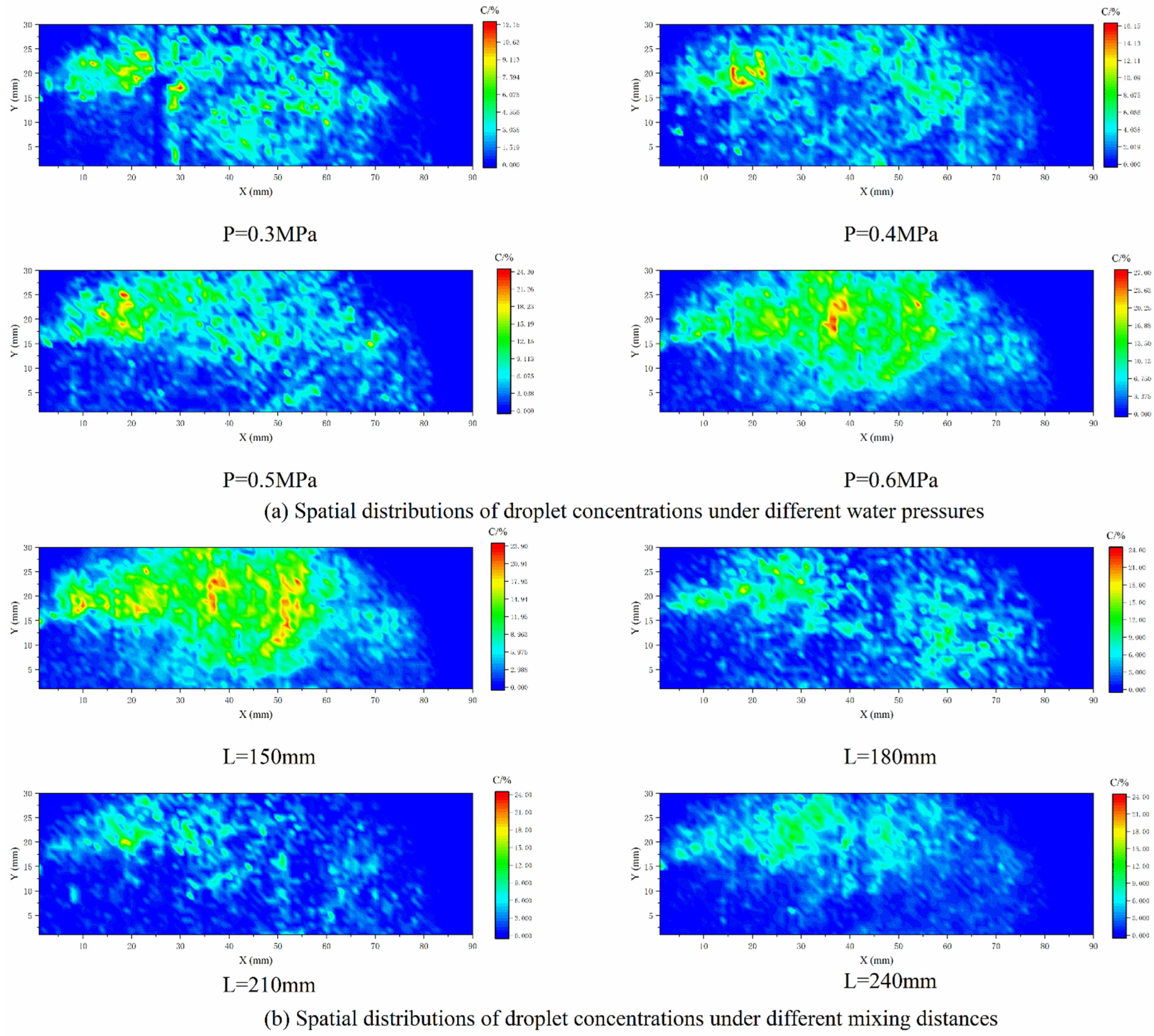
3.2.2. Experimental Research
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Clenci, A.; Berquez, J.; Stoica, R.; Niculescu, R.; Cioc, B.; Zaharia, C.; Iorga-Simăn, V. Experimental Investigation of the Effect of an Afterburner on the Light-off Performance of an Exhaust after-Treatment System. Energy Rep. 2022, 8, 406–418. [Google Scholar] [CrossRef]
- Luo, S.; Feng, Y.; Song, J.; Xu, D.; Xia, K. Progress and Challenges in Exploration of Powder Fueled Ramjets. Appl. Therm. Eng. 2022, 213, 118776. [Google Scholar] [CrossRef]
- Wang, K.; Li, F.; Zhao, K.; Zhou, T. Numerical Study on the Lobed Nozzles for Enhancing the Mixing and Combustion Performance of Rocket-Based Combined Cycle Engine. Energy Rep. 2022, 8, 6645–6658. [Google Scholar] [CrossRef]
- Han, Y.; Shen, C.; Du, Z.; Tang, H. Numerical Study of the Induced Shock on the Mixing Augmentation of Hydrogen Counter-Flow Jet in the Supersonic Flow. Aerospace 2022, 9, 506. [Google Scholar] [CrossRef]
- Chang, M.; Park, S. Spray Characteristics of Direct Injection Injectors with Different Nozzle Configurations under Flash-Boiling Conditions. Int. J. Heat Mass Transf. 2020, 159, 120104. [Google Scholar] [CrossRef]
- Yang, X.; Fan, W.; Zhang, R. Experimental Investigations on Aviation Kerosene Multi-Jets in High Temperature and Low Pressure Air Crossflow. Fuel 2022, 324, 124828. [Google Scholar] [CrossRef]
- Guo, J.P.; Wang, Y.B.; Bai, F.Q.; Du, Q. Unstable Breakup of a Power-Law Liquid Fuel Jet in the Presence of a Gas Crossflow. Fuel 2020, 263, 116606. [Google Scholar] [CrossRef]
- Kazemi Seresht, S.; Mohammadi, A. Liquid Fuel Distribution in the Combustion Chamber by Jet Impingement on Small Cylindrical Obstacles. Fuel 2021, 304, 121387. [Google Scholar] [CrossRef]
- Chang, J.; He, L.; Chen, L.; Shen, Z.; Chuah, L.F.; Bokhari, A.; Klemeš, J.J.; Han, N. Numerical Simulation of Liquid Jet Atomization in Subsonic Crossflow. Energy 2022, 257, 124676. [Google Scholar] [CrossRef]
- Yong, S.H.; Yu, I.J. The Penetration Characteristics of Normally Injected Kerosene Liquid Jet in High Weber Number Flow. In Proceedings of the AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Denver, CO, USA, 2–5 August 2009. [Google Scholar]
- Ragucci, R.; Bellofiore, A.; Cavaliere, A. Breakup and Breakdown of Bent Kerosene Jets in Gas Turbine Conditions. Proc. Combust. Inst. 2007, 31, 2231–2238. [Google Scholar] [CrossRef]
- Birouk, M.; Iyogun, C.O.; Popplewell, N. Role of Viscosity on Trajectory of Liquid Jets in a Cross-Airflow. At. Sprays 2007, 17, 267–287. [Google Scholar] [CrossRef]
- Sallam, K.A.; Ng, C.L.; Sankarakrishnan, R.; Aalburg, C.; Lee, K. Breakup of Turbulent and Non-Turbulent Liquid Jets in Gaseous Crossflows. Collect. Tech. Pap. 44th AIAA Aerosp. Sci. Meet. 2006, 24, 18081–18093. [Google Scholar] [CrossRef]
- Wang, Q.; Mondragon, U.M.; Brown, C.T.; McDonell, V.G. Characterization of Trajectory, Break Point, and Break Point Dynamics of a Plain Liquid Jet in a Crossflow. At. Sprays 2011, 21, 203–219. [Google Scholar] [CrossRef]
- Lubarsky, E.; Shcherbik, D.; Bibik, O.; Gopala, Y.; Zinn, B.T. Fuel Jet in Cross Flow—Experimental Study of Spray Characteristics. Adv. Fluid Dyn 2012, 59, 60–80. [Google Scholar] [CrossRef]
- Chen, T.H.; Smith, C.R.; Schommer, D.G.; Nejad, A. Multi-zone behavior of transverse liquid jet in high-speed flow. In Proceedings of the 31st AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1992. [Google Scholar]
- Inoue, C.; Watanabe, T.; Himeno, T.; Uzawa, S. Numerical and Experimental Study on Liquid Jet Atomization at Near-Field of Coaxial Type Injector. In Proceedings of the AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, 31 July–3 August 2013. [Google Scholar]
- Lin, K.C.; Kennedy, P.; Jackson, T. Penetration heights of liquid jets in high-speed crossflows. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar]
- Stenzler, J.N.; Lee, J.G.; Santavicca, D.A.; Lee, W. Penetration of Liquid Jets in a Crossflow. At. Sprays 2013, 16, 887–906. [Google Scholar] [CrossRef]
- Sasaki, M.; Takahashi, M.; Sakamoto, H.; Kumakawa, A.; Yatsuyanagi, N.; Sei, M.; Yoshimura, K.; Inamura, T. Spray and Combustion Characteristics of a Liquid-fueled Ramjet Combustor. Tech. Rep. Natl. Aerosp. Lab. 1998, 1349, 860–868. [Google Scholar]
- Joshi, P.B.; Schetz, J.A. Effect of Injector Shape on Penetration and Spread of Liquid Jets. Aiaa J. 2015, 13, 1137–1138. [Google Scholar] [CrossRef]
- Horn, K.P.; Kolpin, M.A.; Reichenbach, R.E. A study of penetration of a liquid injectant into a supersonic flow. Aiaa J. 2015, 6, 39. [Google Scholar]
- Tambe, S.B.; Elshamy, O.M.; Jeng, S.M. Liquid Jets Injected Transversely into a Shear Layer. In Proceedings of the Aiaa Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 8–11 January 2013. [Google Scholar]
- Olinger, D.; Sallam, K.; Lin, K.C.; Carter, C. Effects of GLR on the Spray in the Near-Injector Region of Aerated Liquid Jets in Crossflow. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Chin, J.S.; Durrett, R.; Lefebvre, A.H. The study on the interdependence of spray characteristics and evaporation history of fuel spray in high temperature air crossflow-22nd Joint Propulsion Conference (AIAA). J. Eng. Gas Turbines Power 1984, 106, 639–644. [Google Scholar] [CrossRef]
- Cao, M. Semi-Empirical Analysis of Liquid Fuel Distribution Downstream of a Plain Orifice injector Under Cross-Stream Air Flow. J. Eng. Gas Turbines Power 1982, 104, 788–795. [Google Scholar] [CrossRef]
- Lovett, J.A.; Ahmed, K.; Bibik, O.; Smith, A.G.; Lubarsky, E.; Menon, S.; Zinn, B.T. On the Influence of Fuel Distribution on the Flame Structure of Bluff-Body Stabilized Flames. J. Eng. Gas Turbines Power 2014, 136, V01BT04A069. [Google Scholar] [CrossRef]
- Shanjian, G.; Jian, W.; Maolin, Y.; Yong, H. Calculation of two—phase fuel distribution in afterburner flameholder plane. J. Aerosp. Power 1993, 8, 134–137. [Google Scholar]



| Parameter | Variation Range |
|---|---|
| Inflow velocity (m/s) | 125, 150, 175, 200 |
| Inflow temperature (K) | 400, 500, 600, 700, 800 |
| Mixing distance (mm) | 120, 150, 170, 210, 240 |
| Nozzle diameter (mm) | 0.4, 0.45, 0.5, 0.55, 0.6 |
| Injection angle (°) | 30, 60, 90, 120, 150 |
| Fuel supply pressure difference (MPa) | 0.3, 0.4, 0.5, 0.6 |
| Blockage ratio (ε) | 0.25, 0.3, 0.35, 0.4 |
| Inflow Temperature (K) | Inflow Velocity (m/s) | Fuel Supply Pressure Difference (MPa) | Nozzle Diameter (mm) | Injection Angle (°) | Fuel Velocity (m/s) | Fuel–Air Momentum Ratio | Weber Number |
|---|---|---|---|---|---|---|---|
| 400 | 175 | 0.5 | 0.5 | 60 | 25.658 | 19 | 587.52 |
| 500 | 175 | 0.5 | 0.5 | 60 | 25.658 | 23.75 | 470.01 |
| 600 | 175 | 0.5 | 0.5 | 60 | 25.658 | 28.5 | 391.68 |
| 700 | 175 | 0.5 | 0.5 | 60 | 25.658 | 33.25 | 335.72 |
| 800 | 175 | 0.5 | 0.5 | 60 | 25.658 | 38 | 293.76 |
| 800 | 125 | 0.5 | 0.5 | 60 | 25.658 | 74.48 | 149.88 |
| 800 | 150 | 0.5 | 0.5 | 60 | 25.658 | 51.72 | 215.82 |
| 800 | 200 | 0.5 | 0.5 | 60 | 25.658 | 29.09 | 383.68 |
| 800 | 175 | 0.3 | 0.5 | 60 | 19.805 | 22.64 | 293.76 |
| 800 | 175 | 0.4 | 0.5 | 60 | 22.869 | 30.19 | 293.76 |
| 800 | 175 | 0.6 | 0.5 | 60 | 28.009 | 45.28 | 293.76 |
| 800 | 175 | 0.5 | 0.5 | 30 | 25.658 | 38 | 293.76 |
| 800 | 175 | 0.5 | 0.5 | 45 | 25.658 | 38 | 293.76 |
| 800 | 175 | 0.5 | 0.5 | 90 | 25.658 | 38 | 293.76 |
| 800 | 175 | 0.5 | 0.5 | 120 | 25.658 | 38 | 293.76 |
| 800 | 175 | 0.5 | 0.5 | 135 | 25.658 | 38 | 293.76 |
| 800 | 175 | 0.5 | 0.5 | 150 | 25.658 | 38 | 293.76 |
| 800 | 175 | 0.5 | 0.4 | 60 | 25.658 | 38 | 293.76 |
| 800 | 175 | 0.5 | 0.6 | 60 | 25.658 | 38 | 293.76 |
| 800 | 175 | 0.5 | 0.7 | 60 | 25.658 | 38 | 293.76 |
| Parameter | Variation Range |
|---|---|
| Fuel supply pressure difference (MPa) | 0.3, 0.4, 0.5, 0.6, 0.7 |
| Mixing distance L (mm) | 150, 180, 210, 240 |
| Blockage ratio (ε) | 0.3, 0.35, 0.4 |
| Nozzle diameter (mm) | 0.3, 0.4, 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Pei, F.; Li, F. Numerical and Experimental Study on Jet Trajectory and Fuel Concentration Distribution Characteristics of Kerosene Jet in Air Crossflow. Aerospace 2022, 9, 637. https://doi.org/10.3390/aerospace9110637
Wang K, Pei F, Li F. Numerical and Experimental Study on Jet Trajectory and Fuel Concentration Distribution Characteristics of Kerosene Jet in Air Crossflow. Aerospace. 2022; 9(11):637. https://doi.org/10.3390/aerospace9110637
Chicago/Turabian StyleWang, Kefu, Fanqi Pei, and Feng Li. 2022. "Numerical and Experimental Study on Jet Trajectory and Fuel Concentration Distribution Characteristics of Kerosene Jet in Air Crossflow" Aerospace 9, no. 11: 637. https://doi.org/10.3390/aerospace9110637
APA StyleWang, K., Pei, F., & Li, F. (2022). Numerical and Experimental Study on Jet Trajectory and Fuel Concentration Distribution Characteristics of Kerosene Jet in Air Crossflow. Aerospace, 9(11), 637. https://doi.org/10.3390/aerospace9110637





