Prediction of Crack Growth Life at Elevated Temperatures with Neural Network-Based Learning Schemes
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental CG Data of FGH97 at Elevated Temperatures
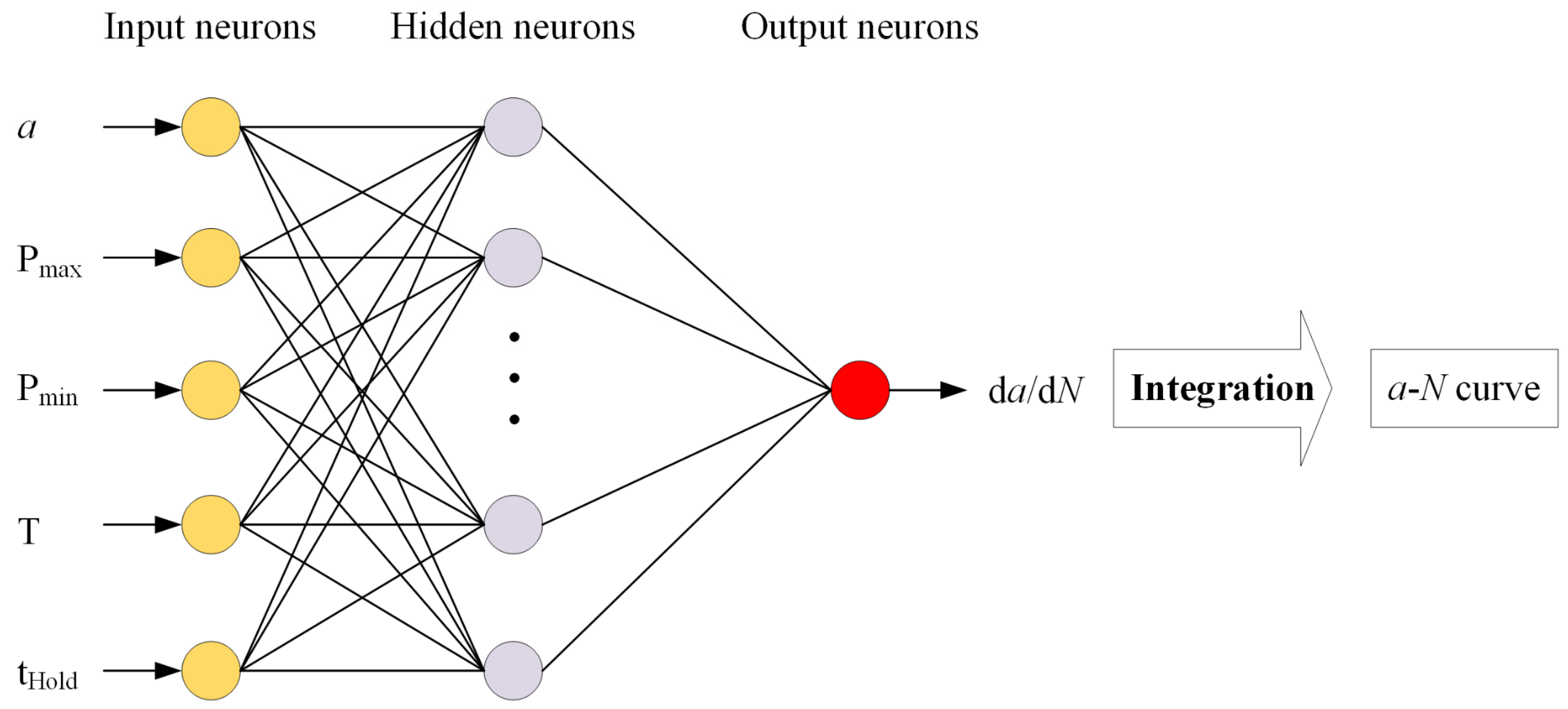
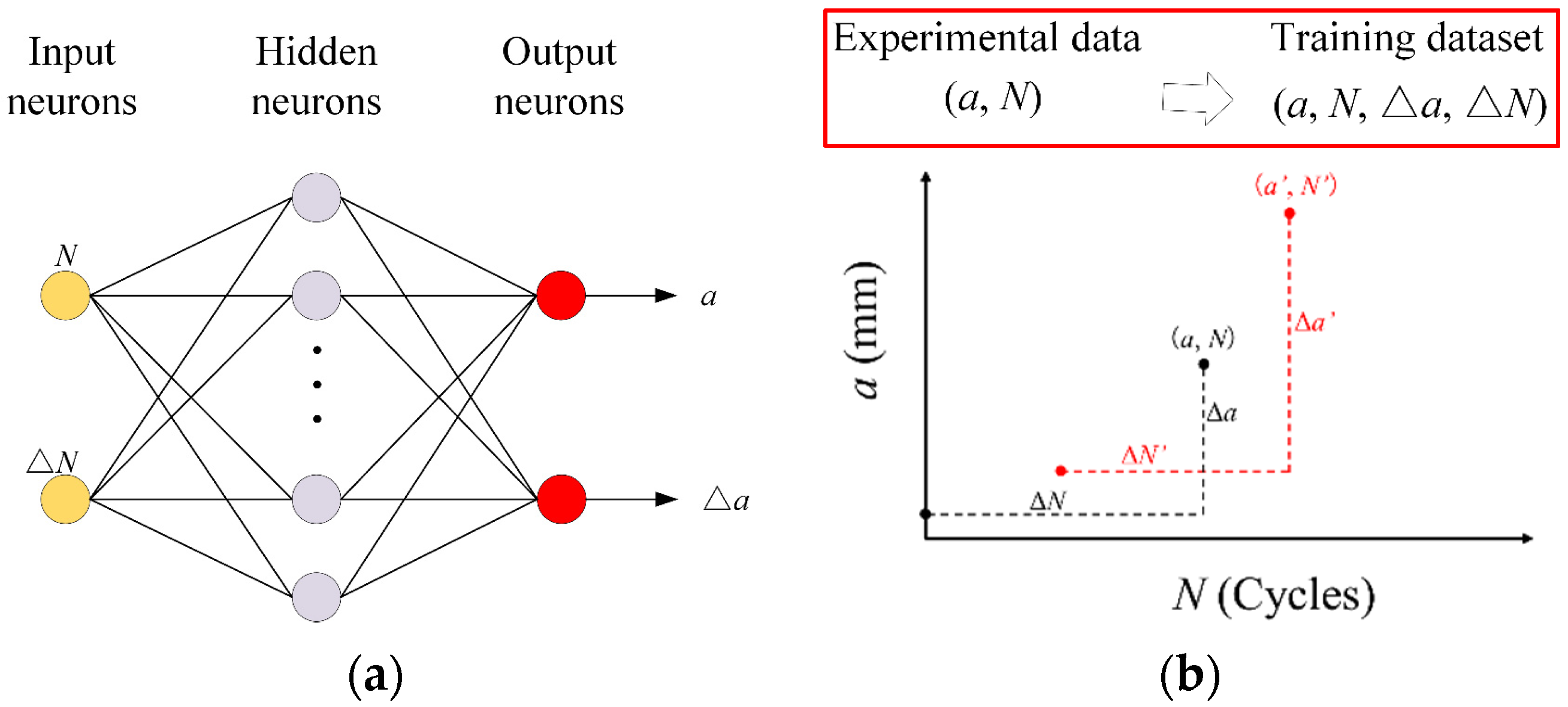
2.2. NN-Based Methods for CG Prediction
3. Results and Discussion
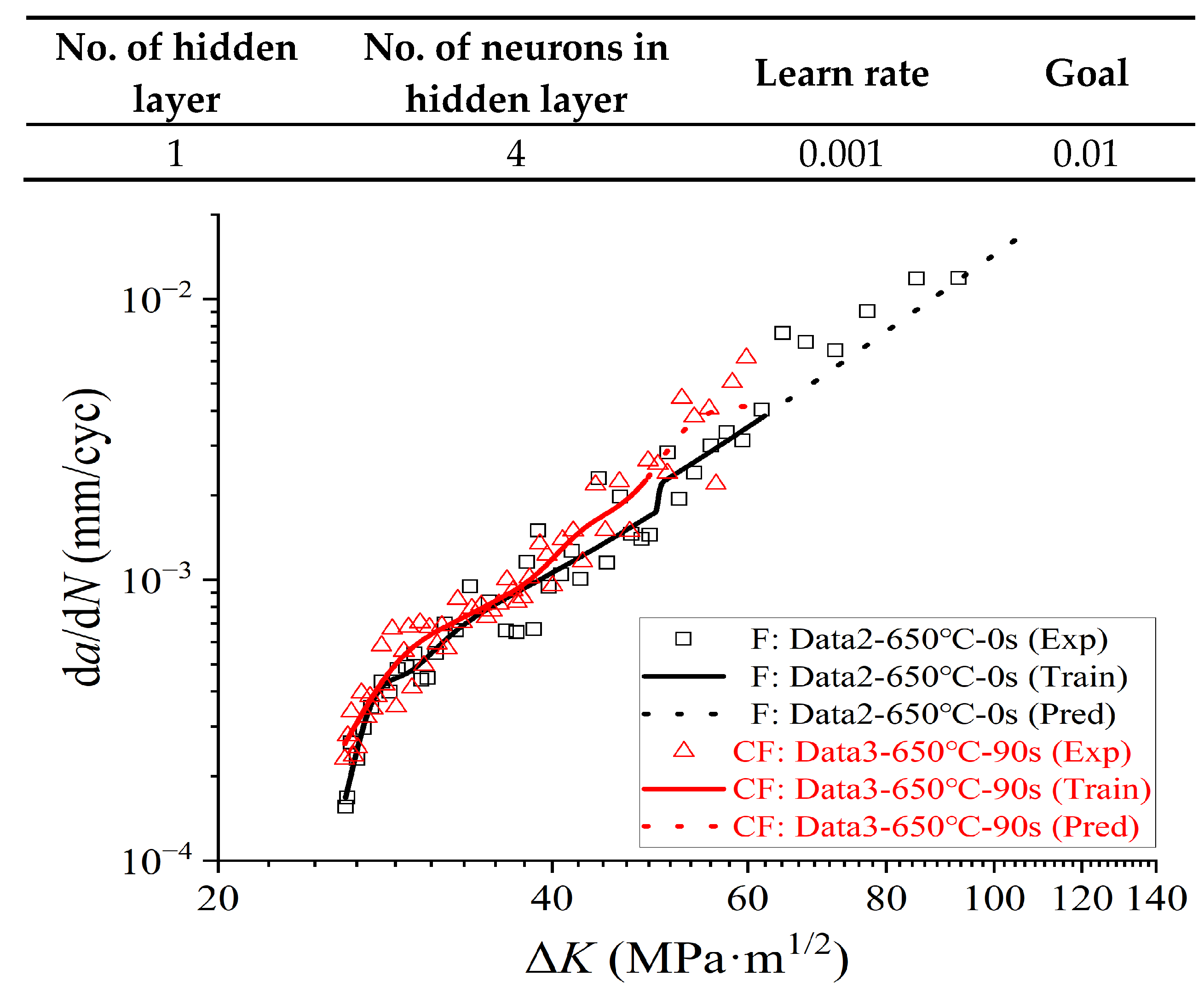
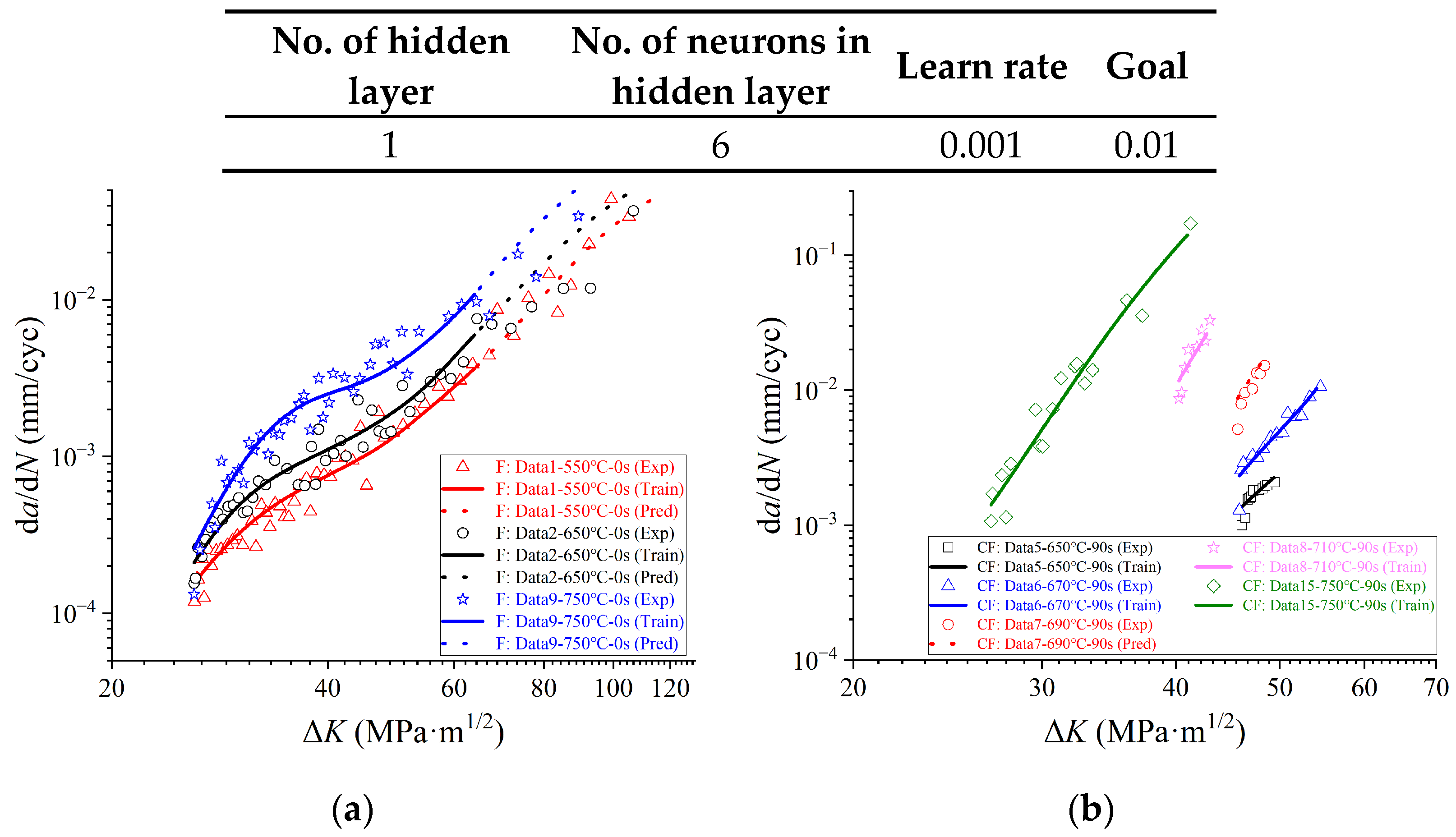
3.1. CG Prediction at Elevated Temperatures Based on CGR
3.2. CG Prediction at Elevated Temperatures Using NN-Based Method Established at Room Temperature
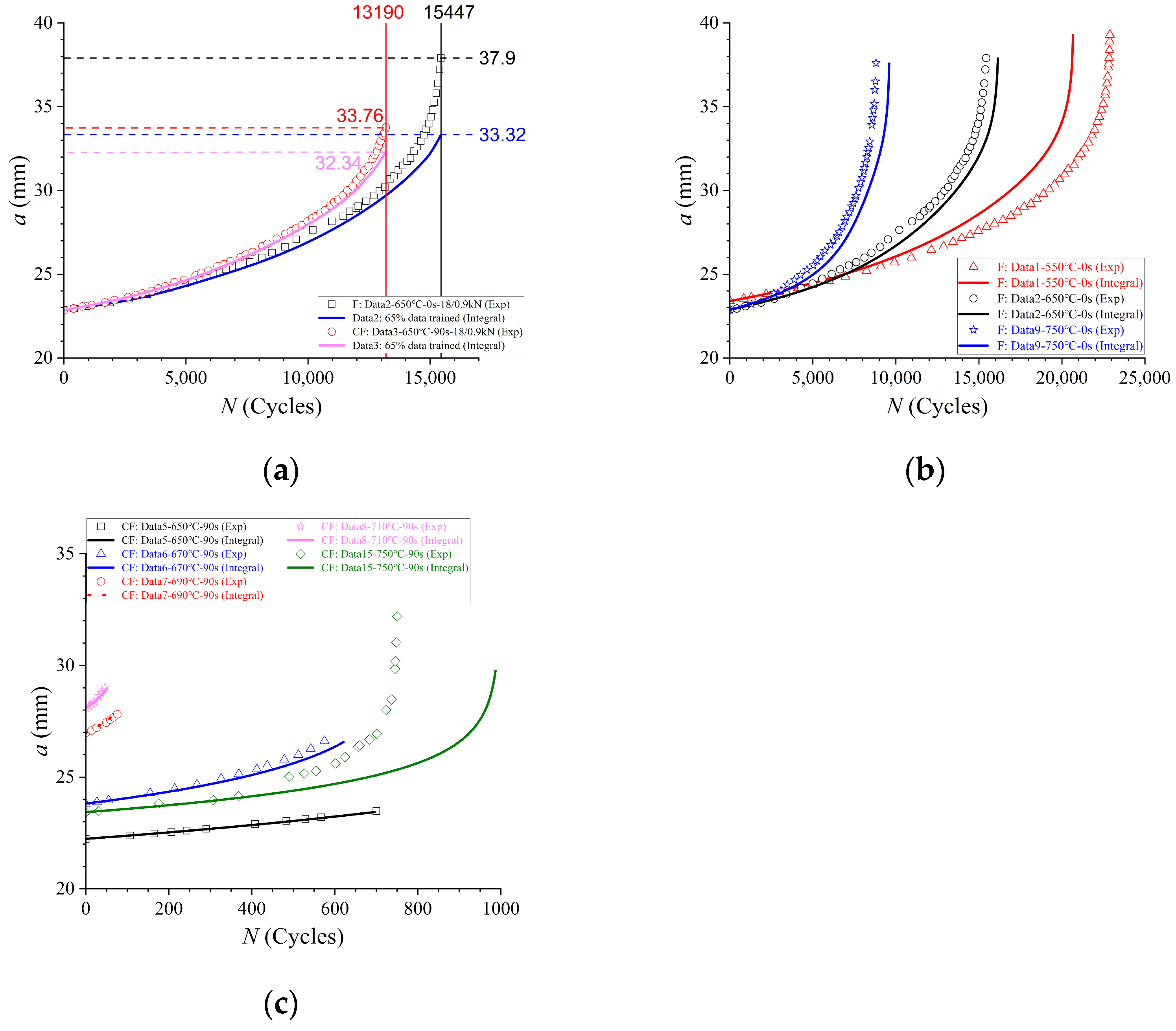
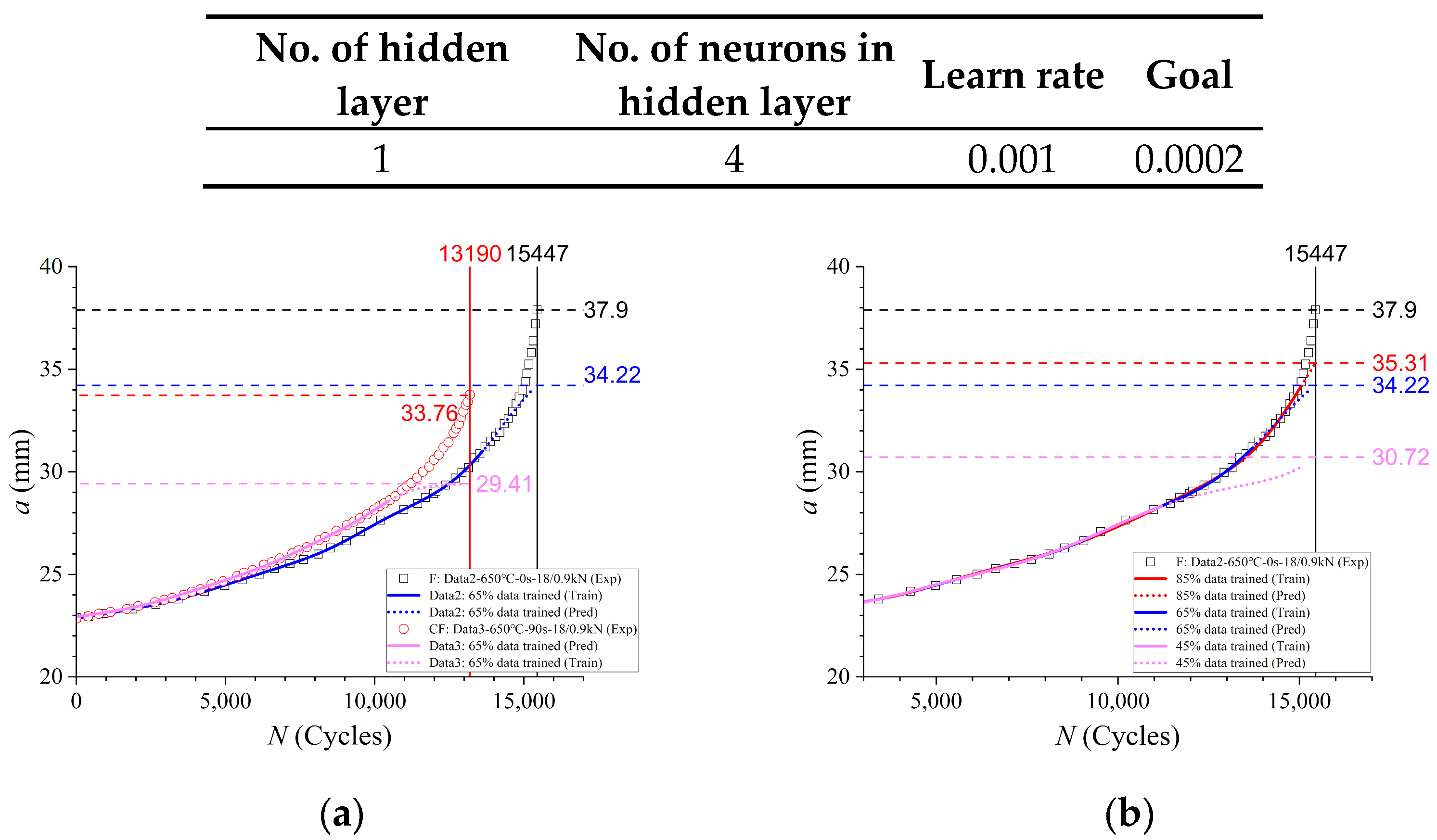
3.2.1. Prediction Using the Basic NN Method
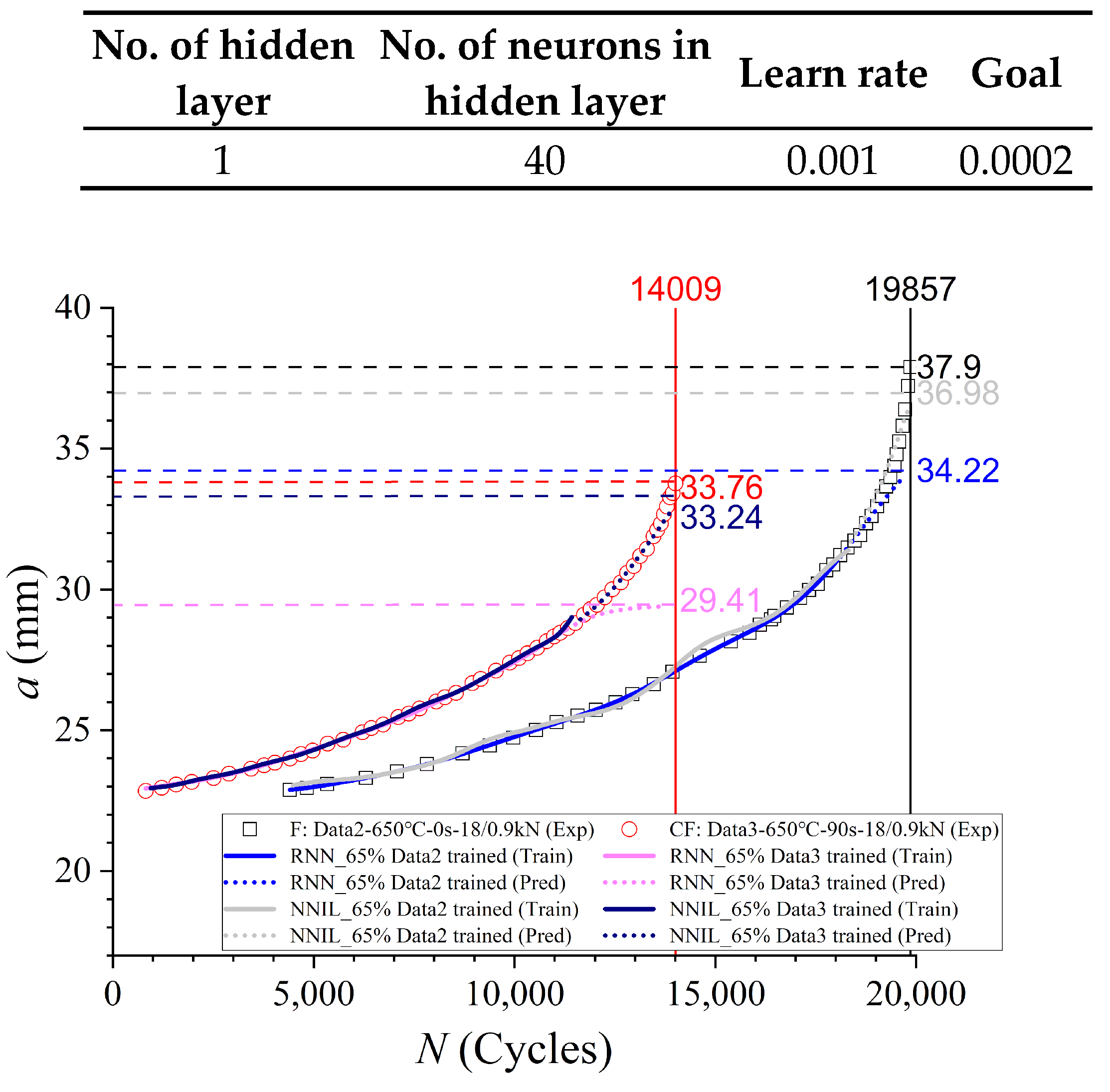
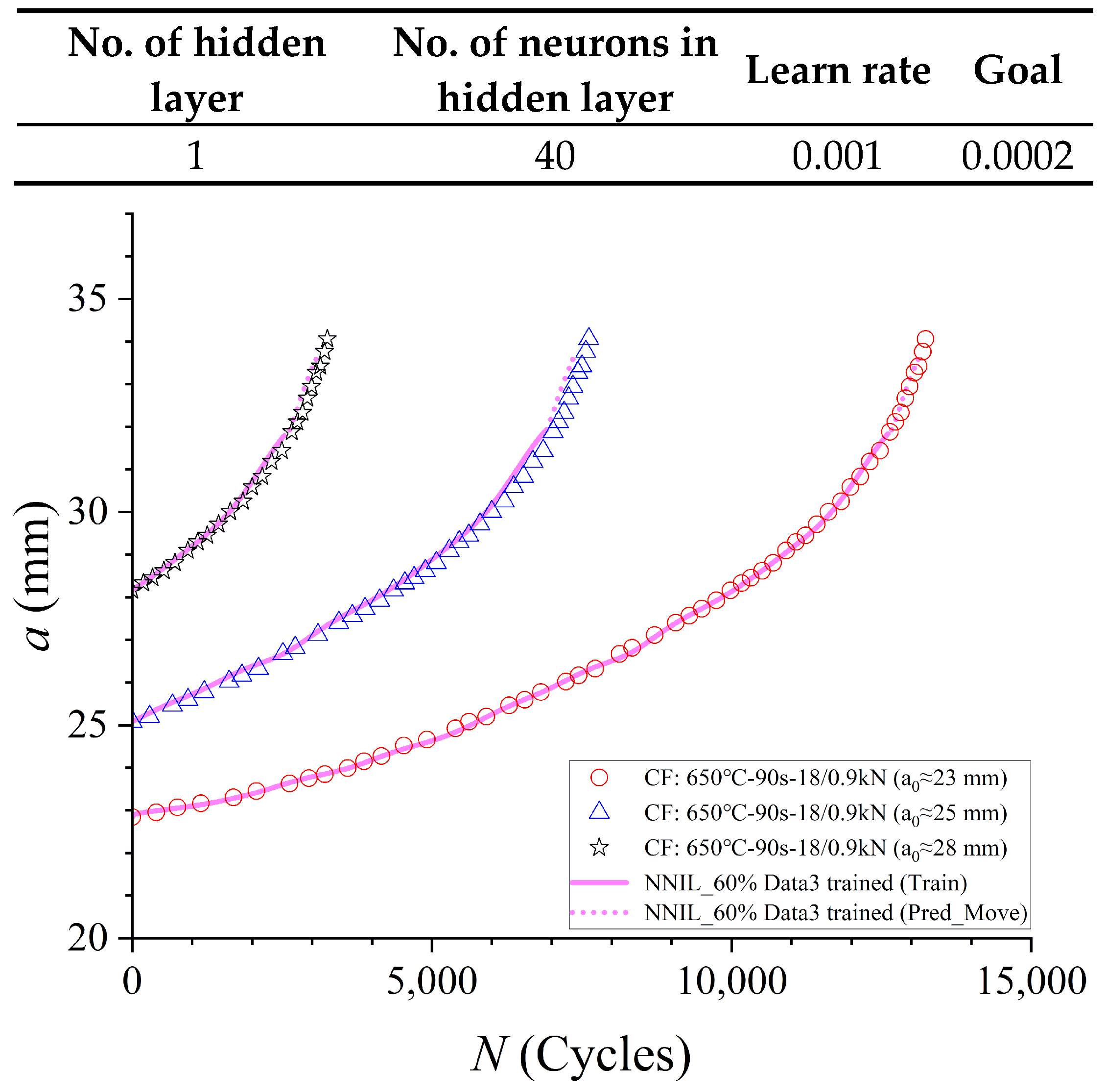
3.2.2. Prediction Using NN-Based Increment Learning Scheme
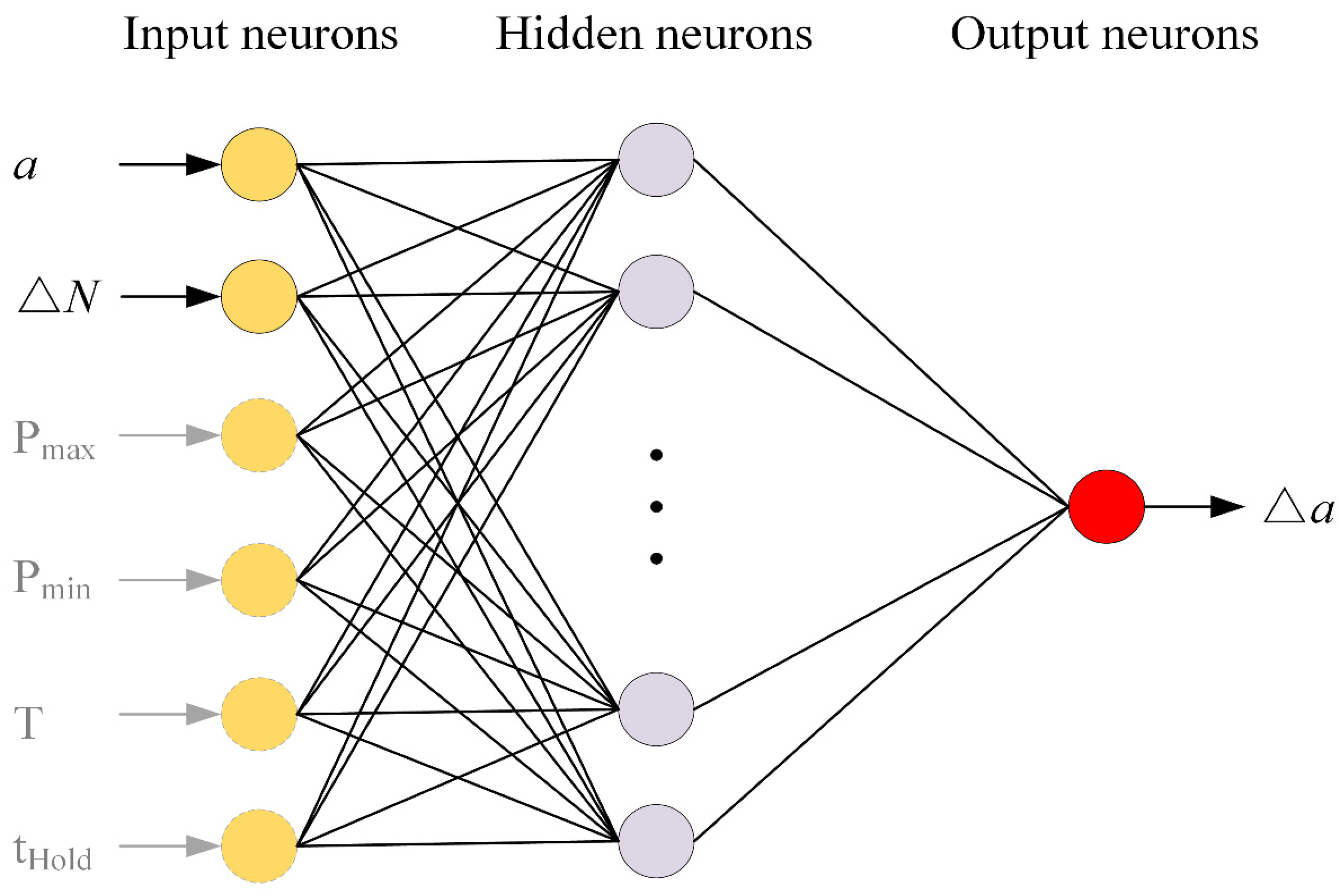
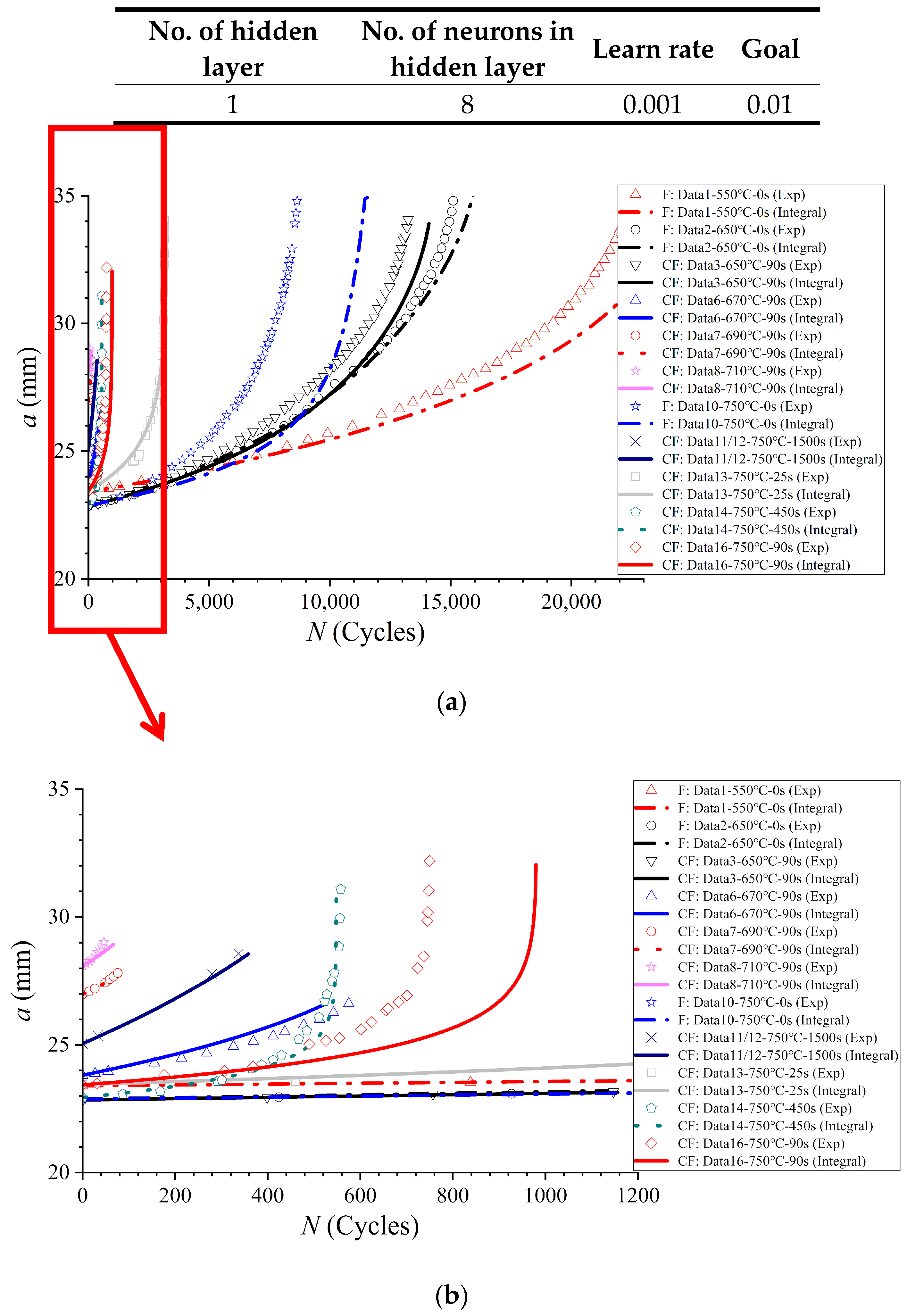
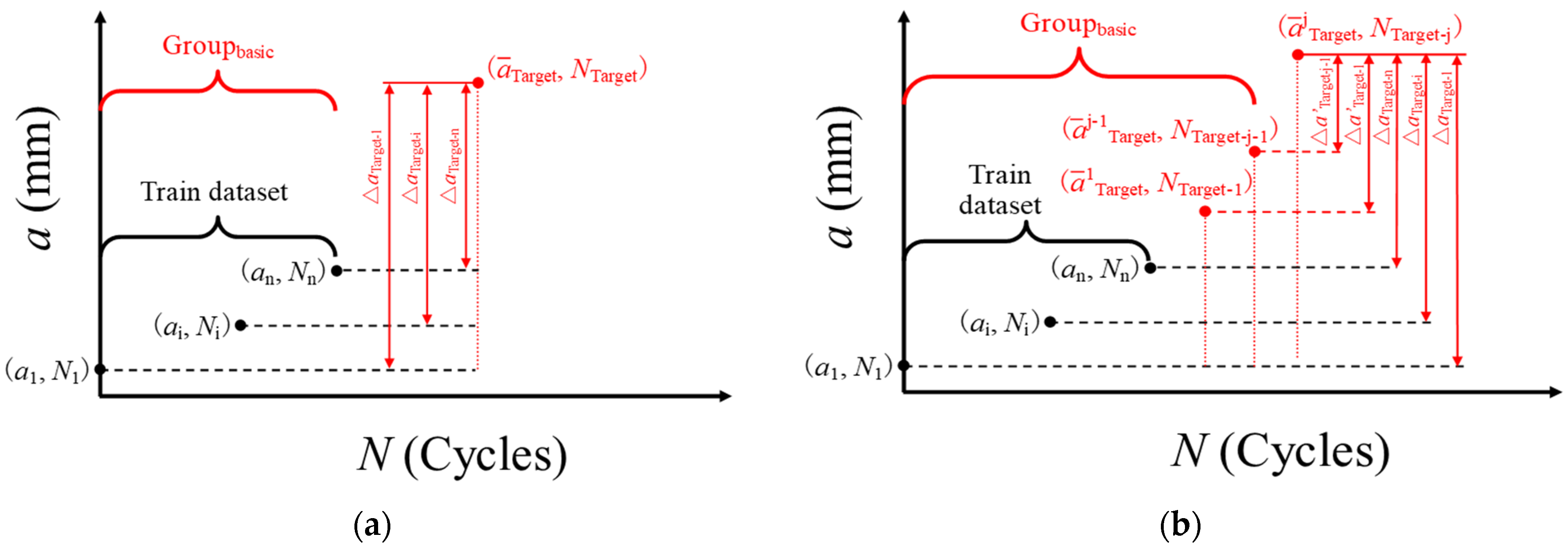
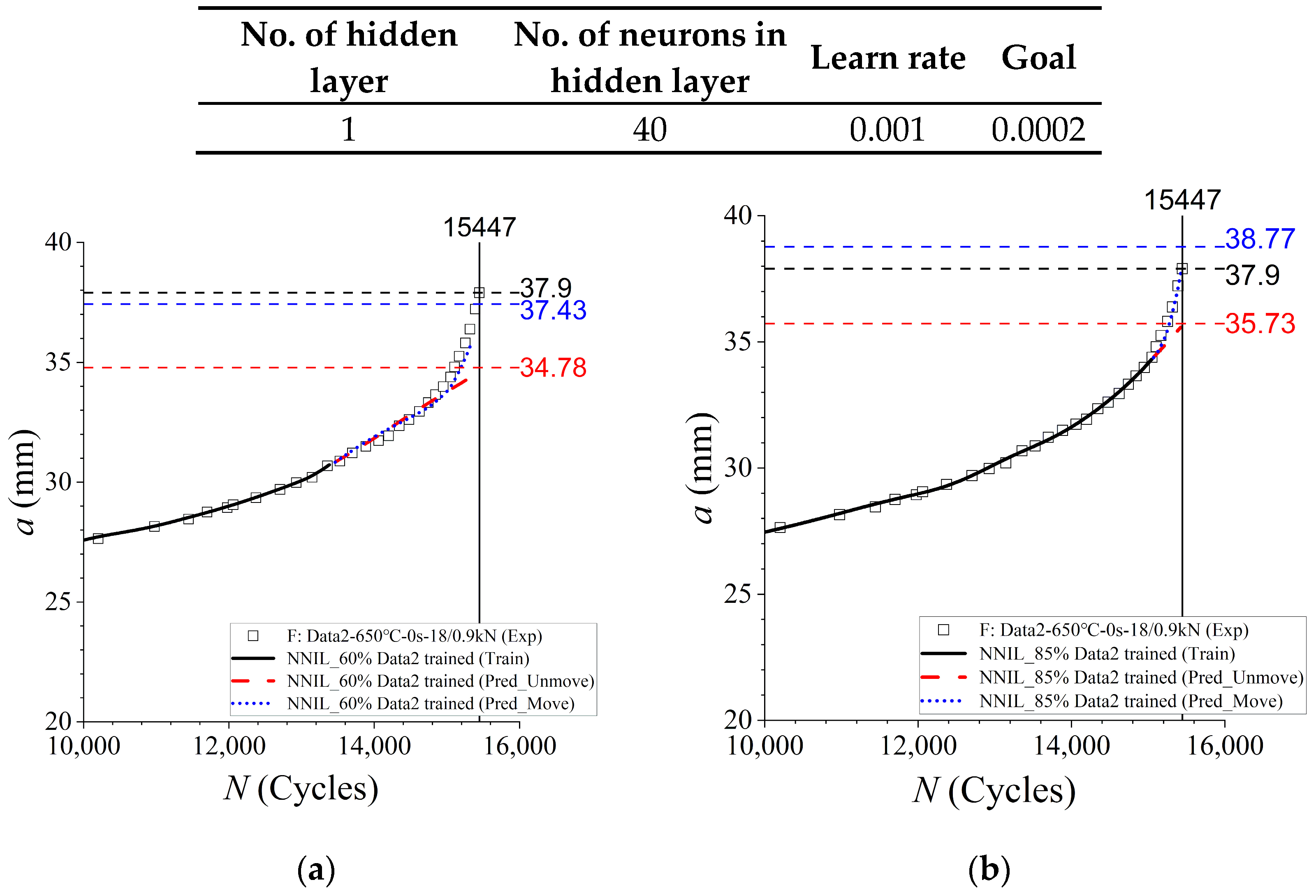
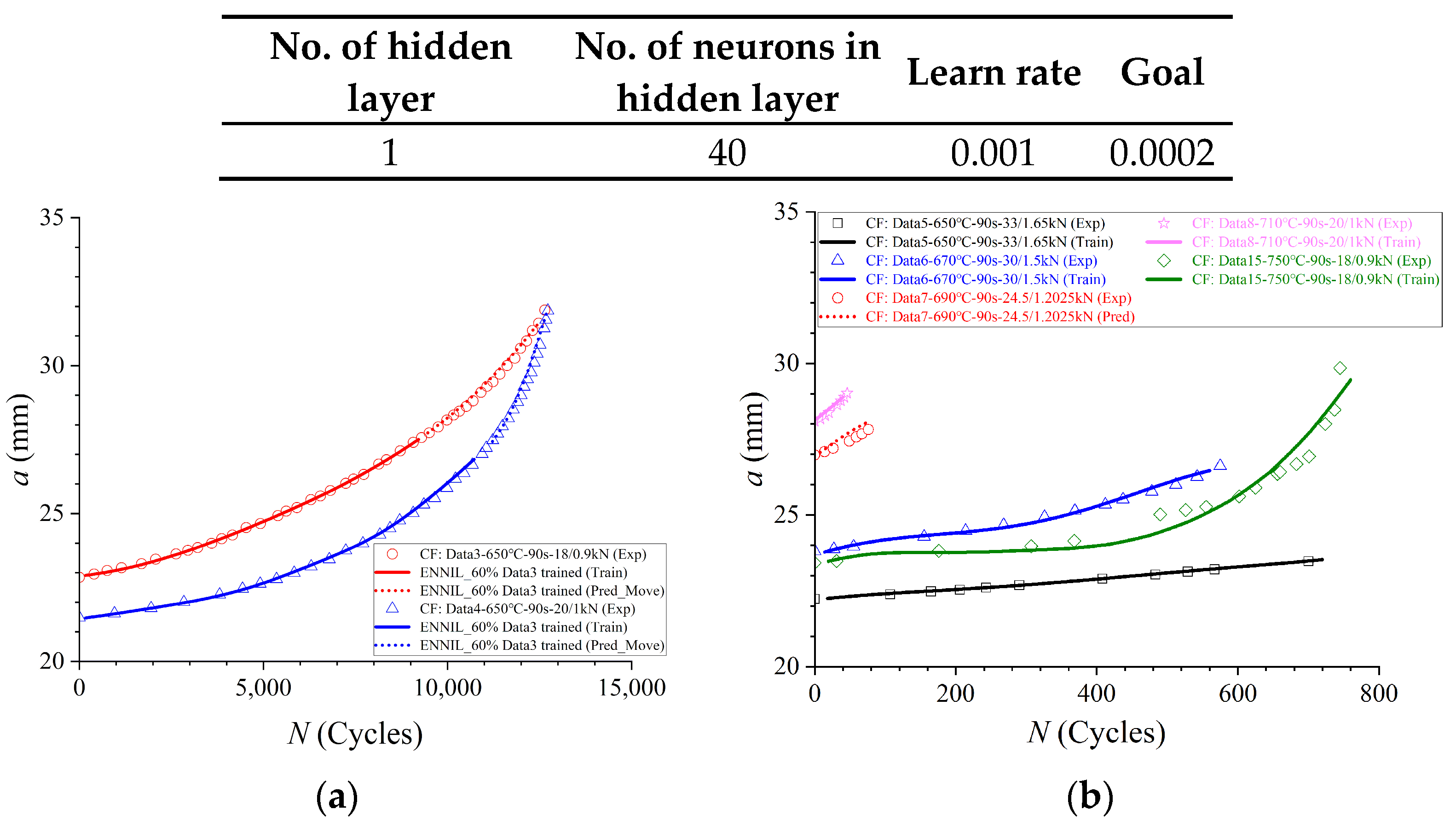
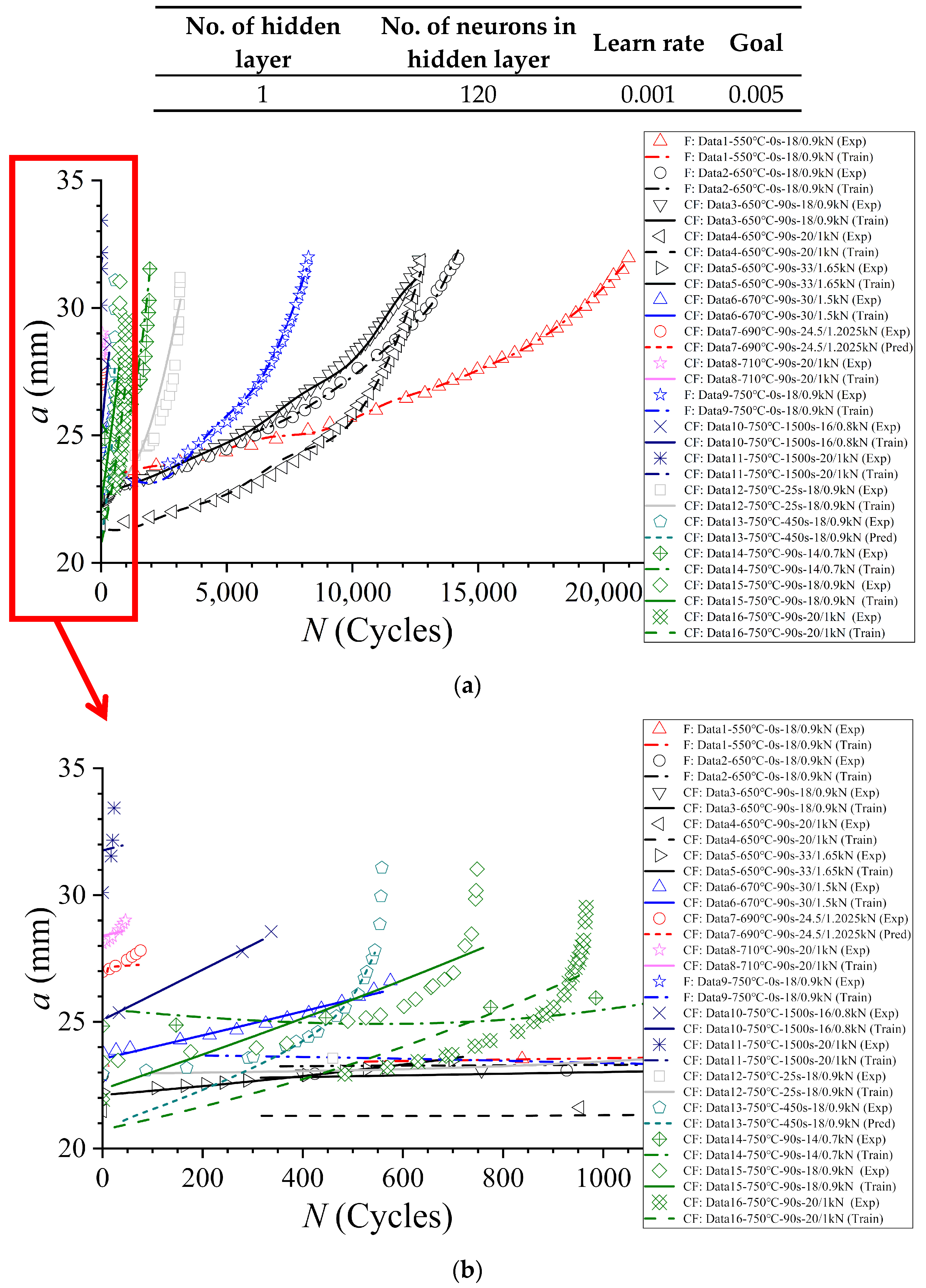
3.3. CG prediction at Elevated Temperature with Amended NNIL Method (ENNIL Method)
- (a)
- The crack lengths at the NTarget of the target testing point were predicted by using each data point in Groupbasic, respectively. The predicted crack length using the ith point of Groupbasic was stated as aTarget−i, whose value was calculated by Equation (3):
- (b)
- The mean value of all predicted crack lengths were calculated by Equation (4):
- (a)
- For the first predicted data point, the “Unmove” way was used to predict the corresponding to based on the train dataset (Group1).
- (b)
- For other predicted data points, the crack length is also calculated using the “Unmove” way, but the Groupbasic used in the calculation of Equation (1) and (2) is composed by Group1 and previously predicted data points. For example, the Groupbasic in the predition of jth data point is composed by Group1 and (A1, A2, …, Aj-1). The equation for the is
4. Conclusions
- (a)
- NN with the input of CDF and other parameters describing service condition can be applied in CGR prediction at elevated temperatures. The CGR at the higher ΔK area are predicted well by this NN but CGR at the lower ΔK area are usually overestimated.
- (b)
- The RNN and NNIL cannot be directly used in CG prediction at elevated temperatures. An important reason for this is that N cannot determine the CG at elevated temperatures together with other affecting factors.
- (c)
- The ENNIL method was developed in this research, where a, ΔN′ replace N, ΔN′ in the NNIL method to serve as the basic input parameters and the Δa becomes the only one output parameter. This method makes the increment schedule can be applied in the CG prediction under general conditions, thus getting over the shortage of using BPNN to model the CG (not good at training on small dataset).
- (d)
- The ENNIL method gives perfectly predicted results for cases with relatively long CG life, while the predicted accuracy of this method for CG with relatively short CG life need to be further improved. However, the NNK method shows high accuracy in CG prediction with relatively short CG life, but low accuracy in CG prediction with relative long CG life. The combination of these two methods may be an effective way to achieve high accuracy in CG prediction at elevated temperatures.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shlyannikov, V.; Iltchenko, B.; Stepanov, N. Fracture analysis of turbine disks and computational–experimental background of the operational decisions. Eng. Fail. Anal. 2001, 8, 461–475. [Google Scholar] [CrossRef]
- Payten, W.M.; Wei, T.; Snowden, K.U.; Bendeich, P.; Law, M.; Charman, D. Crack initiation and crack growth assessment of a high pressure steam chest. Int. J. Press. Vessel. Pip. 2011, 88, 34–44. [Google Scholar] [CrossRef]
- Narasimhachary, S.; Saxena, A. Crack growth behavior of 9Cr−1Mo (P91) steel under creep–fatigue conditions. Int. J. Fatigue 2013, 56, 106–113. [Google Scholar] [CrossRef]
- Shlyannikov, V. Creep–fatigue crack growth rate prediction based on fracture damage zone models. Eng. Fract. Mech. 2019, 214, 449–463. [Google Scholar] [CrossRef]
- Tong, J.; Dalby, S.; Byrne, J.; Henderson, M.B.; Hardy, M.C. Creep, fatigue and oxidation in crack growth in advanced nickel base superalloys. Int. J. Fatigue 2001, 23, 897–902. [Google Scholar] [CrossRef]
- Onofrio, G.; Osinkolu, G.A.; Marchionni, M. Fatigue crack growth of UDIMET 720 Li superalloy at elevated temperature. Int. J. Fatigue 2001, 23, 887–895. [Google Scholar] [CrossRef]
- Pairs, P.; Erdogan, F. A critical analysis of crack propagation laws. J. Basic Eng. 1963, 85, 528–534. [Google Scholar] [CrossRef]
- Djavanroodi, F. Creep-Fatigue Crack Growth Interaction in Nickel Base Supper Alloy. Am. J. Appl. Sci. 2008, 5, 454–460. [Google Scholar] [CrossRef][Green Version]
- Whittaker, M.; Harrison, W.; Hurley, P.; Williams, S. Modelling the behaviour of titanium alloys at high temperature for gas turbine applications. Mater. Sci. Eng. A 2010, 527, 4365–4372. [Google Scholar] [CrossRef]
- Grover, P.S.; Saxena, A. Modelling the effect of creep–fatigue interaction on crack growth. Fatigue Fract. Eng. Mater. Struct. 1999, 22, 111–122. [Google Scholar] [CrossRef]
- Shlyannikov, V.; Tumanov, A.; Boychenko, N. A creep stress intensity factor approach to creep–fatigue crack growth. Eng. Fract. Mech. 2015, 142, 201–219. [Google Scholar] [CrossRef]
- Yang, H.; Bao, R.; Zhang, J. An interaction crack growth model for creep-brittle superalloys with high temperature dwell time. Eng. Fract. Mech. 2014, 124–125, 112–120. [Google Scholar] [CrossRef]
- Lepore, M.A.; Maligno, A.R.; Berto, F. A unified approach to simulate the creep-fatigue crack growth in P91 steel at elevated temperature under SSY and SSC conditions. Eng. Fail. Anal. 2021, 127, 105569. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, L.; Gao, Z.; Han, Y. A novel creep–fatigue interaction damage model with the stress effect to simulate the creep–fatigue crack growth behavior. Int. J. Mech. 2017, 130, 143–153. [Google Scholar] [CrossRef]
- Piard, A.; Gamby, D.; Carbou, C.; Mendez, J. A numerical simulation of creep–fatigue crack growth in nickel-base superalloys. Eng. Fract. Mech. 2004, 71, 2299–2317. [Google Scholar] [CrossRef]
- Bouvard, J.; Chaboche, J.; Feyel, F.; Gallerneau, F. A cohesive zone model for fatigue and creep–fatigue crack growth in single crystal superalloys. Int. J. Fatigue 2009, 31, 868–879. [Google Scholar] [CrossRef]
- Morse, L.; Khodaei, Z.S.; Aliabadi, M. A multi-fidelity modelling approach to the statistical inference of the equivalent initial flaw size distribution for multiple-site damage. Int. J. Fatigue 2018, 120, 329–341. [Google Scholar] [CrossRef]
- Zio, E.; Di Maio, F. Fatigue crack growth estimation by relevance vector machine. Expert Syst. Appl. 2012, 39, 10681–10692. [Google Scholar] [CrossRef]
- Hu, D.; Su, X.; Liu, X.; Mao, J.; Shan, X.; Wang, R. Bayesian-based probabilistic fatigue crack growth evaluation combined with machine-learning-assisted GPR. Eng. Fract. Mech. 2020, 229, 106933. [Google Scholar] [CrossRef]
- Mortazavi, S.; Ince, A. An artificial neural network modeling approach for short and long fatigue crack propagation. Comput. Mater. Sci. 2020, 185, 109962. [Google Scholar] [CrossRef]
- Mohanty, J.; Verma, B.; Parhi, D.; Ray, P. Application of artificial neural network for predicting fatigue crack propagation life of aluminum alloys. Arch. Comput. Mater. Sci. Surf. Eng. 2009, 1, 133–138. [Google Scholar]
- Zhang, W.; Bao, Z.; Jiang, S.; He, J. An Artificial Neural Network-Based Algorithm for Evaluation of Fatigue Crack Propagation Considering Nonlinear Damage Accumulation. Materials 2016, 9, 483. [Google Scholar] [CrossRef] [PubMed]
- Pidaparti, R.M.V.; Palakal, M.J. Neural network approach to fatigue-crack-growth predictions under aircraft spectrum loadings. J. Aircr. 1995, 32, 825–831. [Google Scholar] [CrossRef]
- Do, D.; Lee, J.; Hung, N. Fast evaluation of crack growth path using time series forecasting. Eng. Fract. Mech. 2019, 218, 106567. [Google Scholar] [CrossRef]
- Ma, X.; He, X.; Tu, Z. Prediction of fatigue–crack growth with neural network-based increment learning scheme. Eng. Fract. Mech. 2020, 241, 107402. [Google Scholar] [CrossRef]
- Yang, H.; Bao, R.; Zhang, J.; Peng, L.; Fei, B. Crack growth behaviour of a nickel-based powder metallurgy superalloy under elevated temperature. Int. J. Fatigue 2011, 33, 632–641. [Google Scholar] [CrossRef]
- Bao, R.; Yang, H.; Zhang, J.; Peng, L.; Fei, B. Fatigue crack growth measurement in a superalloy at elevated temperature. Int. J. Fatigue 2013, 47, 189–195. [Google Scholar] [CrossRef]
- Yang, H. Sub-Critical Fatigue Crack Growth Behaviour Analysis for a P/M Superalloy under Elevated Temperature. Ph.D. Thesis, Beihang University, Beijing, China, 2010. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Zhang, N.; Jia, J. Heat treatment processes and microstructure and properties research on P/M superalloy FGH97. Chin. J. Aero. Mater. 2008, 28, 5–9. [Google Scholar]
- ASTM E647-08; Standard Test Method for Measurement of Fatigue Crack Growth Rates. ASTM Committee: Seattle, WA, USA, 2008.
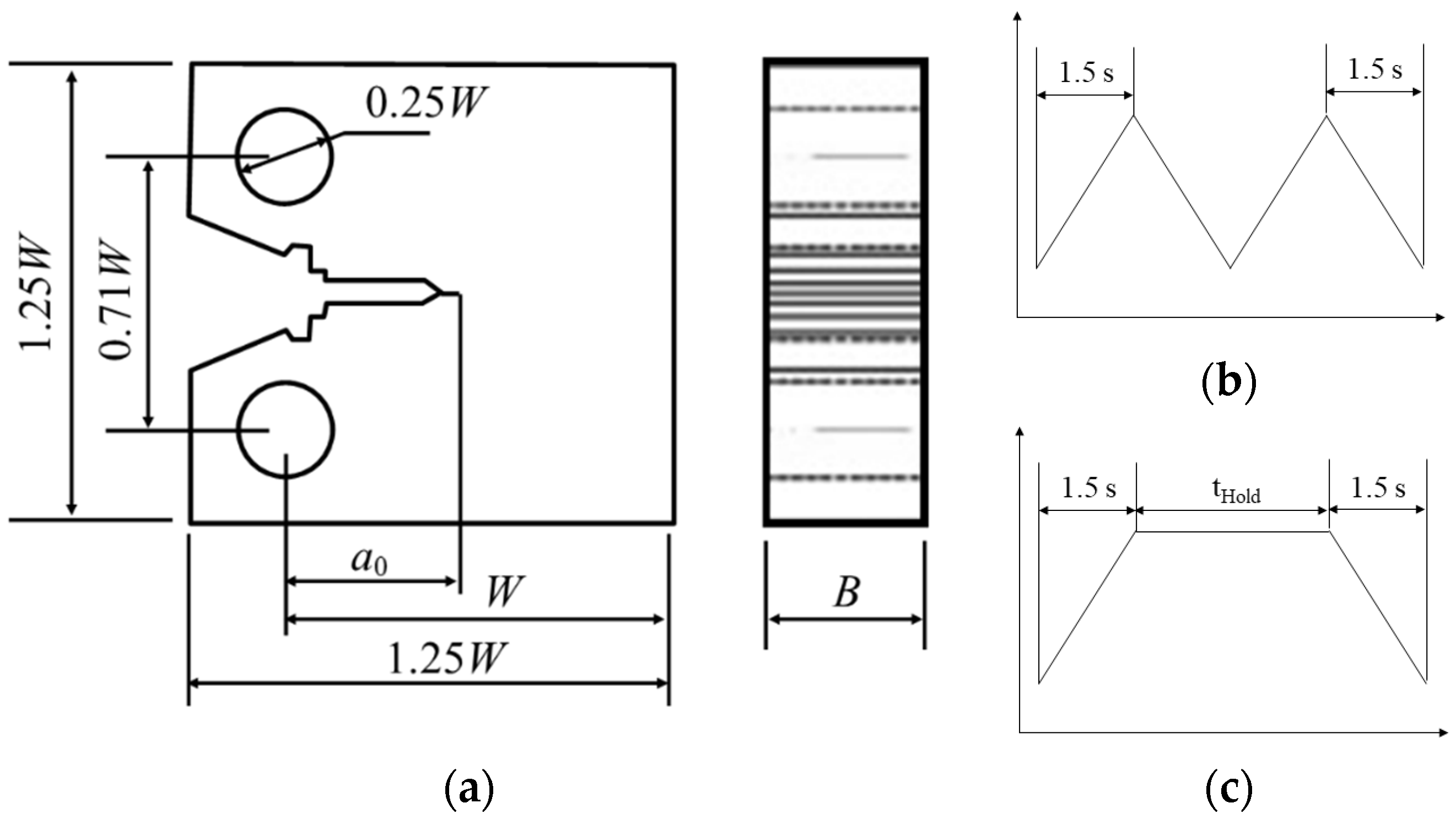

| C | Cr | Mo | W | Al | Ti | Co | Nb | Hf | Mg | Zr | B | Ce | Ni |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.02–0.06 | 8.0–10 | 3.5–4.2 | 5.2–5.9 | 4.8–5.3 | 1.6–2.0 | 15.0–16.5 | 2.4–2.8 | 0.1–0.4 | ≤0.02 | ≤0.02 | ≤0.02 | ≤0.01 | Remains |
| Dataset Name | Condition Name | T (°C) | tHold (s) | PMax (kN) | PMin (kN) | Type |
|---|---|---|---|---|---|---|
| Data 1 | C1 | 550 | 0 | 18 | 0.9 | F |
| Data 2 | C2 | 650 | 0 | 18 | 0.9 | F |
| Data 3 | C3 | 650 | 90 | 18 | 0.9 | CF |
| Data 4 | C4 | 650 | 90 | 20 | 1 | CF |
| Data 5 | C5 | 650 | 90 | 33 | 1.65 | CF |
| Data 6 | C6 | 670 | 90 | 30 | 1.5 | CF |
| Data 7 | C7 | 690 | 90 | 24.5 | 1.2025 | CF |
| Data 8 | C8 | 710 | 90 | 20 | 1 | CF |
| Data 9 | C9 | 750 | 0 | 18 | 0.9 | F |
| Data 10 | C10 | 750 | 1500 | 16 | 0.8 | CF |
| Data 11 | C11 | 750 | 1500 | 20 | 1 | CF |
| Data 12 | C12 | 750 | 25 | 18 | 0.9 | CF |
| Data 13 | C13 | 750 | 450 | 18 | 0.9 | CF |
| Data 14 | C14 | 750 | 90 | 14 | 0.7 | CF |
| Data 15 | C15 | 750 | 90 | 18 | 0.9 | CF |
| Data 16 | C16 | 750 | 90 | 20 | 1 | CF |
| Method | NN Name | NN Input | NN Output |
|---|---|---|---|
| NNK | NNK-K | Kmax, ΔK | da/dN |
| NNK-KT | Kmax, ΔK, T | ||
| NNK-KTt | Kmax, ΔK, T, tHold | ||
| RNN | RNN-N | N | a |
| NNIL | NNIL-N | N, ΔN′ | a, Δa′ |
| ENNIL | ENNIL-a | a, ΔN | Δa |
| ENNIL-aP | a, ΔN, PMax, PMin | ||
| ENNIL-aPT | a, ΔN, PMax, PMin, T | ||
| ENNIL-aPTt | a, ΔN, PMax, PMin, T, tHold |
| Method | NN Name | NN Input | NN Output | Dataset (Type of Testing Conditions: Train Data + Test Data) |
|---|---|---|---|---|
| NNK | NNK-K | Kmax, ΔK | da/dN | FCG: 80% Data 2 + 20% Data 2 CFCG: 80 % Data 3 + 20% Data 3 |
| NNK-KT | Kmax, ΔK, T | FCG with different T: 80% Data 1, 2, 9 + 20% Data 1, 2, 9 CFCG with same thold: Data 5, 6, 8, 15 + Data 7 | ||
| NNK-KTt | Kmax, ΔK, T, tHold | FCG + CFCG: Data 1–3, 6, 8–11, 13, 15 + Data 7, 12 |
| Method | NN Name | NN Input | NN Output | Dataset (Type of Testing Conditions: Train Data + Test Data) |
|---|---|---|---|---|
| RNN | RNN-N | N | a | FCG: 45% Data 2 + 55% Data 2 FCG: 65% Data 2 + 35% Data 2 FCG: 85% Data 2 + 15% Data 2 CFCG: 65% Data 3 + 35% Data 3 |
| NNIL | NNIL-N | N, ΔN′ | a, Δa′ | FCG: 80% Data 2 + 20% Data 2 CFCG: 80% Data 3 + 20% Data 3 |
| Method | NN Name | NN Input | NN Output | Dataset (Type of Testing Conditions: Train Data + Test Data) |
|---|---|---|---|---|
| ENNIL | ENNIL-a | a, ΔN′ | Δa | F: 80% Data 2 + 20%Data 2 CF: 80% Data 3 + 20%Data 3 |
| ENNIL-aP | a, ΔN′, PMax, PMin | CF with effects of loads: 80% Data 3, 4 + 20%Data 3, 4 | ||
| ENNIL-aPT | a, ΔN′, PMax, PMin, T | CF with effect of loads and temperature: Data 5, 6, 8, 15 +Data7 | ||
| ENNIL-aPTt | a, ΔN′, PMax, PMin, T, tHold | F + CF: Data 1–6, 8–12, 14–16 +Data 7, 13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, S.; Liu, B.; Yang, R.; Wang, Q.; Bao, R. Prediction of Crack Growth Life at Elevated Temperatures with Neural Network-Based Learning Schemes. Aerospace 2022, 9, 600. https://doi.org/10.3390/aerospace9100600
Lu S, Liu B, Yang R, Wang Q, Bao R. Prediction of Crack Growth Life at Elevated Temperatures with Neural Network-Based Learning Schemes. Aerospace. 2022; 9(10):600. https://doi.org/10.3390/aerospace9100600
Chicago/Turabian StyleLu, Songsong, Binchao Liu, Rong Yang, Qiuyi Wang, and Rui Bao. 2022. "Prediction of Crack Growth Life at Elevated Temperatures with Neural Network-Based Learning Schemes" Aerospace 9, no. 10: 600. https://doi.org/10.3390/aerospace9100600
APA StyleLu, S., Liu, B., Yang, R., Wang, Q., & Bao, R. (2022). Prediction of Crack Growth Life at Elevated Temperatures with Neural Network-Based Learning Schemes. Aerospace, 9(10), 600. https://doi.org/10.3390/aerospace9100600






