In this paper, it is assumed that the spacecraft orbits in a circular sun-synchronous orbit at an altitude of 1000 km and a descent node time of 18:00 (i.e., a dawn–dusk orbit). The solar light is approximately perpendicular to the plane of the spacecraft orbit and the spacecraft is continuously supplied with available solar radiation pressure. It is worth noting that there is no geosynchronous shadow zone in the sun-synchronous orbit. Disturbances from the upper atmosphere of the planet are neglected, because the atmospheric drag perturbation is of the magnitude of 10
−7–10
−6 N at the altitude orbital studied in the paper, while the tension and the solar radiation pressure are of the magnitude of 10
−3 N. In addition, according to [
15], a tether length of 1000 m was chosen for close formation and imaging missions.
2.1. Definition of Coordinate Systems
The coordinate systems mainly used in this paper are defined as follows:
Inertial coordinate system : The origin coincides with the center of the Earth. The x-axis points from the Earth to the point of ascending intersection with the orbit, the z-axis is perpendicular to the orbital plane, the y-axis is in the orbital plane, and the right-hand rule is observed.
Orbital coordinate system : The origin is coincident with the center of the main satellite, the x-axis is oriented along the Earth towards the host star, and the y-axis is along the orbital velocity vector. The z-axis follows the right-hand rule.
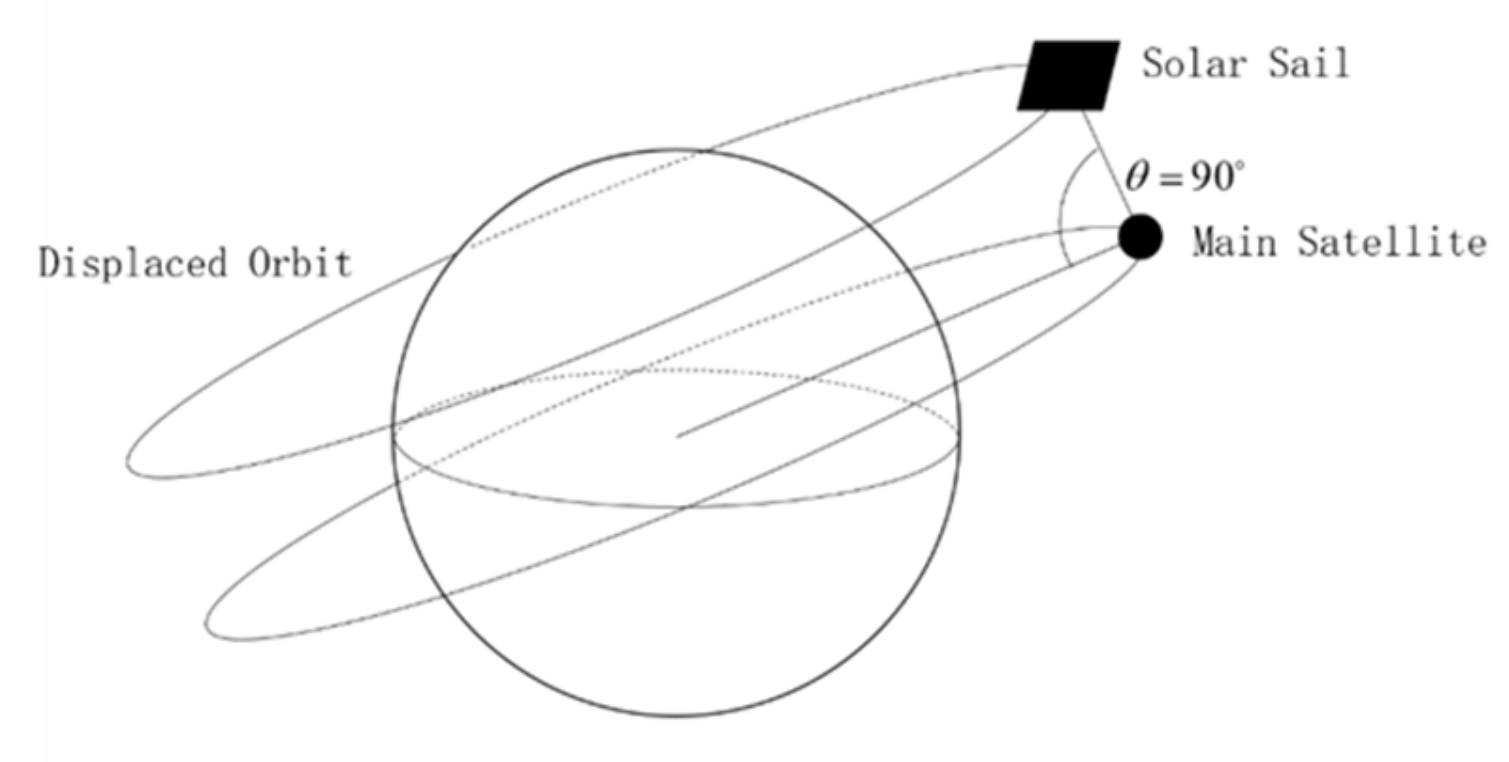
In general, the state of a space tethered system is described by the three generalized coordinates of the in-plane angle, the out-plane angle, and the length of the tether. This is a clear physical definition with the simplest dynamic equations and is widely used in research on space tethered systems. However, according to the requirements of the traverse formation, as shown in
Figure 1, when the traverse formation configuration reaches a steady state, the tether is perpendicular to the orbit and the in-plane angle is not defined, i.e., singular.
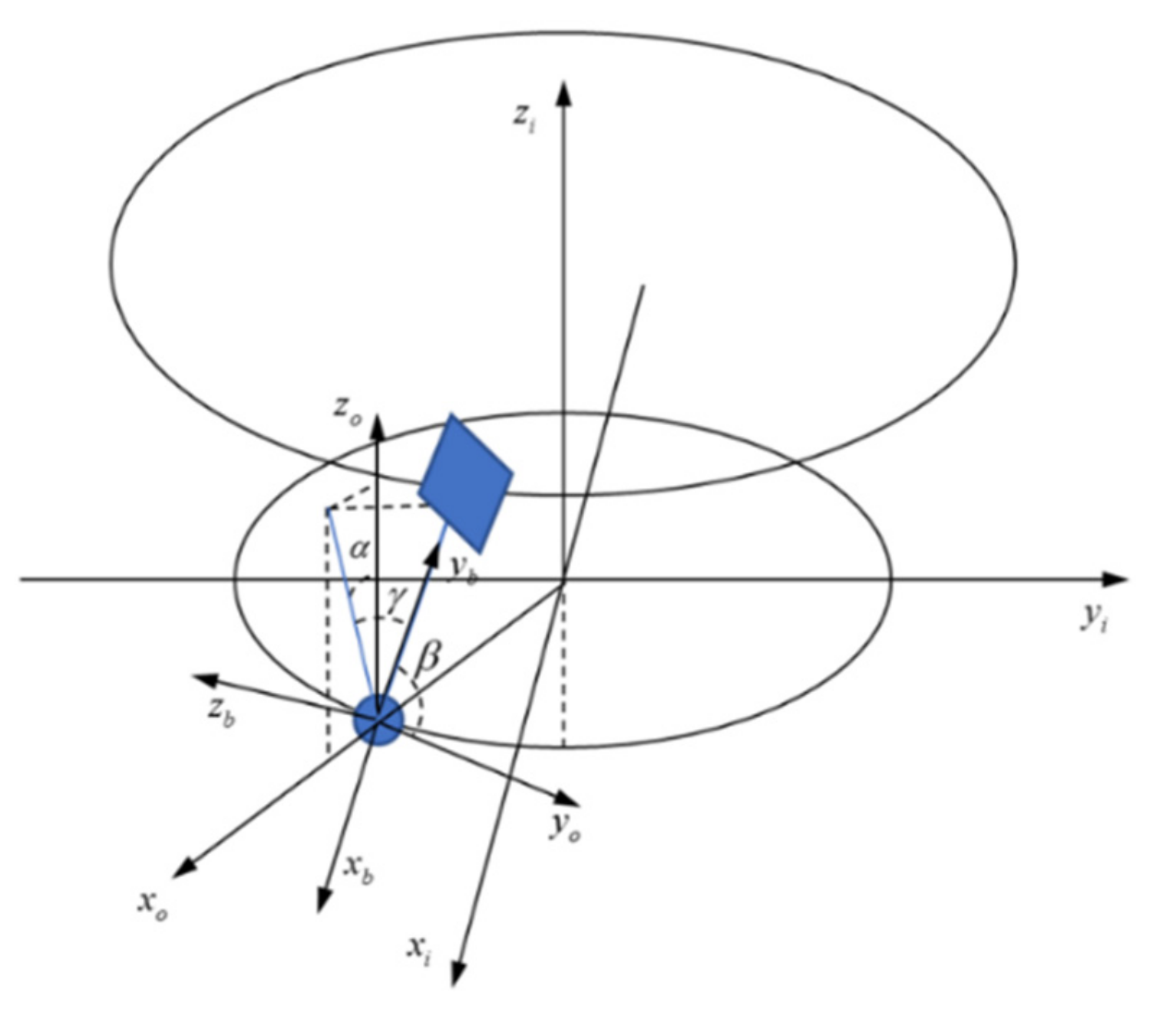
To overcome the singularities, two attitude angles,
and
, are defined in this study of a satellite-sail system, as shown in
Figure 2. Based on the new attitude angles, a spacecraft body coordinate system is defined.
Spacecraft body coordinate system
: The origin is coincident with the main satellite and the directions of the axes are shown in
Figure 2. The coordinate transformation relationship between
and
is defined as follows:
Finally, to describe the solar sail attitude, the solar sail body coordinate system is defined.
Solar sail body coordinate system
: As shown in
Figure 3, the origin coincides with the center of the solar sail and the
z-axis is opposite to the direction of sunlight irradiation, which can be regarded as parallel to the orbital plane since the satellite orbits in a sun-synchronous orbit and the solar–terrestrial distance is much greater than the orbital radius. The
x- and
y-axes are parallel to the
x- and
y-axes of
, respectively.
2.2. Dynamic Model
It is assumed that during a stable deployment, the solar sail is completely unfolded and the tether is tight. In this case, the control forces of the system consist of the solar radiation pressure and the tension on the tether. As the main satellite and the solar sail are both sufficiently small, they could be considered masses in the dynamic model. The following assumptions are considered. The elastic deformation of the tether is insignificant and the tether is extremely light in comparison to the main satellite and the solar sail. The solar sail system in a transverse formation is modeled with reference to the dumbbell model of an ordinary tethered satellite.
The Lagrange equation in generalized coordinates is used for modeling. According to Equation (1), the coordinate transformation matrix between
and
could be described as follows:
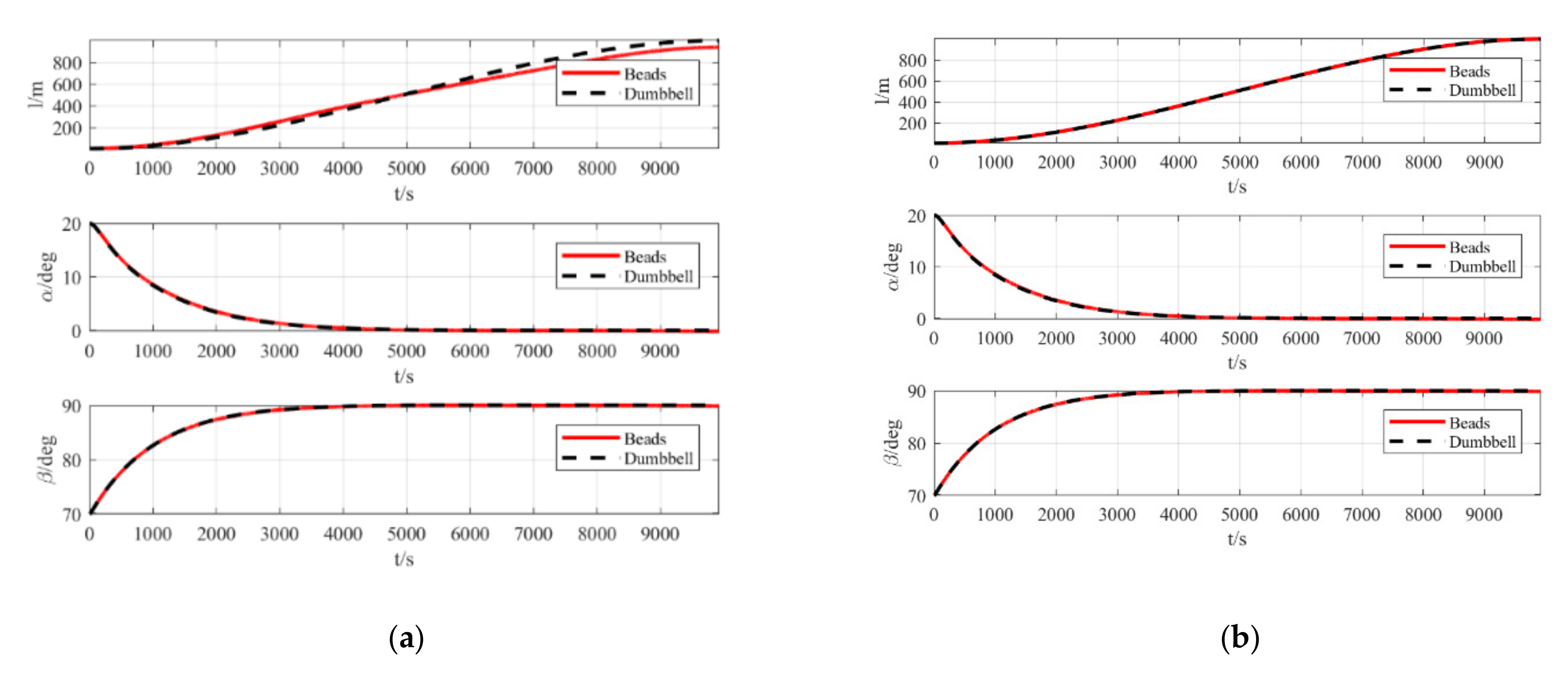
In research on space tethered systems, the control laws of deployment, retrieval, and maintenance are generally designed based on the dumbbell model and a more accurate beads model used for simulation verification. For a space tether system where the mass of the spacecraft at both ends is significantly larger than the mass of the tether, the dumbbell model and simplified model ignore the mass of the tether and are sufficient for simulation and control law design. However, solar sail spacecraft are large enough and light enough. In the simulation of the above study, the mass of the solar sail used is assumed to be 1 kg. The tether material commonly applied in the space tethered system trials is Dyneema. The linear density of a Dyneema tether of 1.5 mm diameter is approximately 1.2 g/m for a 1000 m tether, and thus the mass of the tether is approximately 1.2 kg, which is in the same order of magnitude as the solar sail. Therefore, the mass of the tether is an important factor contributing to model uncertainty during the deployment and retrieval of a satellite-sail system.
In the following, the dumbbell model for a satellite-sail system considering the mass of the tether will be derived based on the Lagrange equation. At this time, in addition to the kinetic and potential energy of the satellites at the ends of the tether, this is in addition to considering the kinetic and potential energy of the tether. The tether is a continuum. Assuming that the mass of the tether is uniformly distributed, the tether could be considered a continuous elementary mass and the kinetic and potential energy of the complete tether could be obtained by integration, as follows:
where
is the linear density of the tether and
is the distance from the sail to the elementary mass. It is important to note that the mass of the main satellite
is the variable in this case.
where
is the initial mass of the main satellite.
Firstly, the kinetic energy of the system is calculated. The kinetic energy of the main satellite is calculated as follows:
The result of deriving Equation (3) is as follows:
Projecting Equation (7) onto the spacecraft body coordinate system, the result is as follows:
where
,
,
, and
are projections of
,
,
, and
in the coordinate system
separately. The results of the calculations are as follows:
Similarly, the kinetic energy of the solar sail is calculated as follows:
The kinetic energy of the tether can be derived from the following integral equation:
The final result is shown directly as follows:
where the expression of the parameters of mass is:
Further, the potential energy of the system is calculated. As an example, the gravitational potential energy of the main satellite is as follows:
Similarly, the gravitational potential energy of the sail and tether are as follows:
The total potential energy of the system is as follows:
Projecting the above equation onto
and converting to a scalar, the result is as follows:
Thus, the Lagrange function expression for the system is as follows:
For circular or near-circular orbits,
. The final kinetic equations are as follows:
In Equations (22)–(24),
,
, and
are the generalized forces corresponding to the respective variables. In general, the mass of the main satellite is much greater than the solar sail, where it could be considered
. The control force of the system consists of the solar radiation pressure and the tether tension. The generalized forces are related to the control forces as follows:
where
,
, and
are the projected components of the solar radiation pressure on the three axes of
and
is the tension of the tether.
2.3. Simplified Dynamic Model for Controller Design
Since the rope length is generally of a much larger magnitude than the angular magnitude in practice, causing considerable difficulty in calculation and analysis, the kinetic equations are normalized. The dimensionless time and dimensionless length are defined and expressed as follows:
The physical definition of dimensionless time is in fact the true anomaly. is the nominal length of the tether, which could be either the initial or the target length of the tether. In this paper, is chosen as the target length.
The dynamic equations are analyzed with dimensionless time and dimensionless length of tether. Alternatively, for the design of the controller, the residual angle
is substituted for
. Equations (22)–(24) can be expressed as follows:
where
.
Under the assumption of small angles (i.e., less than 20°), the higher-order terms of the angles are ignored. Equations (28)–(30) can be expressed as follows:
Then, Equations (31)–(33) can be expressed in state-space equations. Assuming that
is the target length of the tether, the state-space variables are defined as follows:
The state-space equations are as follows:
To facilitate the design of the controller, the nonlinear dynamic Equation (35) is linearized. Considering
and
as small quantities, the linearized first-order approximation model is obtained by expanding at point
, as follows:
where
According to the stability in the first approximation, it is known that the stability analysis of the nonlinear system (35) can be transformed into the stability analysis of the linear system (36).
Theorem 1. If all eigenvalues of the matrix contain negative real parts and holds consistently in the interval , then for the differential equation , any solution satisfying sufficiently small always exists and the solution is asymptotically stable.
According to the simplified linear Equation (36), it can be seen that the length of the tether is decoupled from the angles in the small-angle case of the transverse formation.
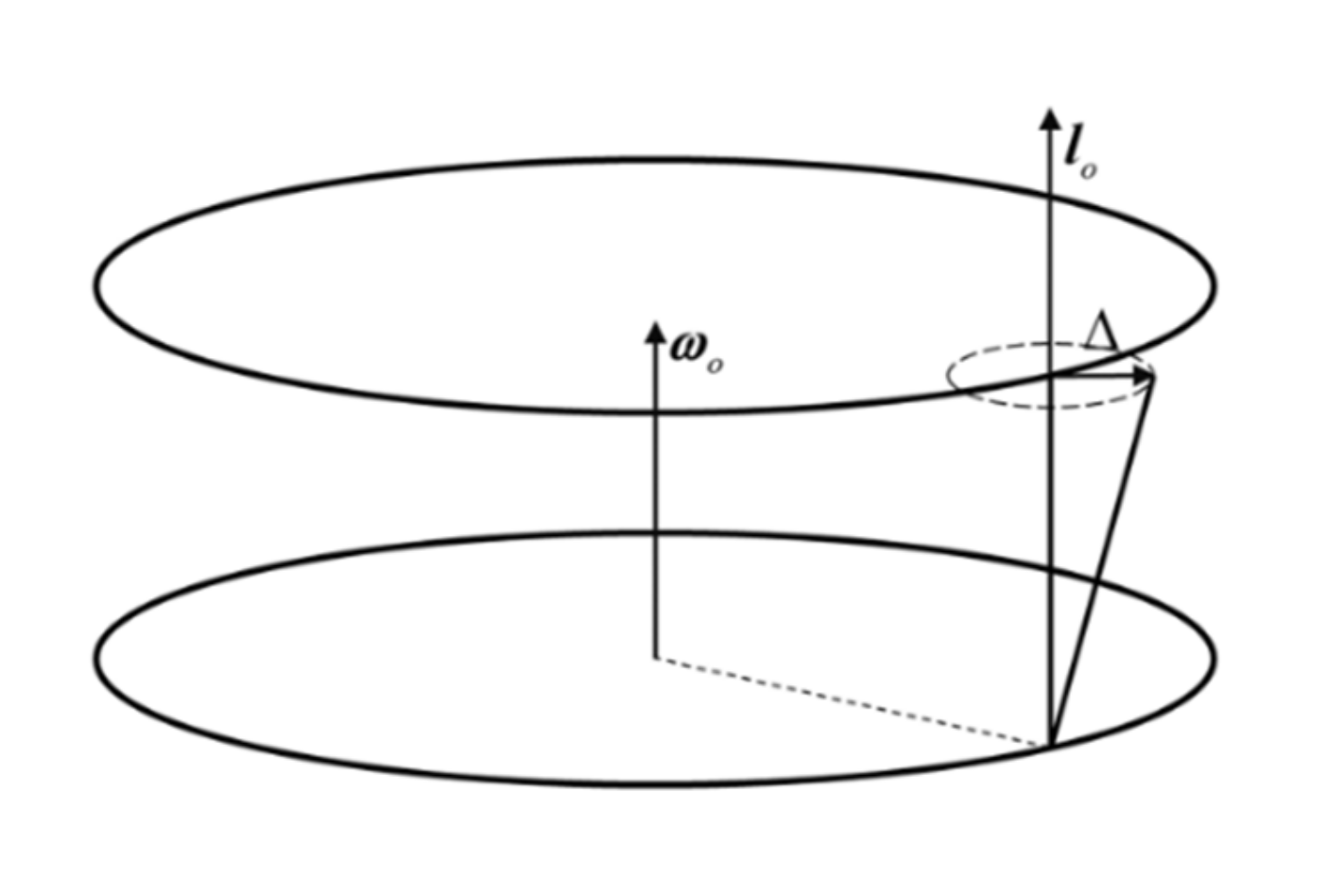
The physics of this conclusion can be explained. As shown in
Figure 4, the effect of tether velocity on the angular velocity is reflected in the Coriolis force; however, the Coriolis force is remarkably insignificant due to the fact that the tether velocity is in the same direction as the angular velocity and the cross product is equal to zero. Hence, the effect of tether velocity on the angular velocity can also be neglected. According to the above conclusion, only for the traverse formation, the controller of angle and the controller of tether length could be designed separately under the assumption of small angles.
2.4. Beads Model for Satellite-Sail System
The space tether system is a complex nonlinear system, and it is further complicated by features with the coupled solar sail attitude and orbit, which results in a more complex satellite-sail system model. Model uncertainty is one of the factors that have a large impact in the control of satellite-sail systems. In this chapter, the influence of the mass of the tether on the state of the satellite-sail system is investigated. A model with high accuracy based on the beads model for a tethered system is developed to investigate the result of the controller under the high-accuracy model. The effect of model uncertainty on the rope-system solar sail system is discussed.
The dumbbell model cannot describe the flexibility of the tether, and in several cases the dumbbell model cannot describe the characteristics of the tethered system accurately, especially in the simulation; therefore, the dumbbell model is not accurate enough and a more accurate model is required.
The beads model describes the motion of the tether and simulates the configuration change of the tether more explicitly and accurately. An accurate model, the beads model has extensive application in the accurate dynamic simulation of tethered systems, although it has several disadvantages. The accuracy of the model depends hugely on the number of beads, and as the number of beads increases, the computational effort increases rapidly and computational speed becomes slower. Therefore, the beads model is generally applied as an accurate model for simulation and not for the design of control laws.
The basic structure of the beads model is shown in
Figure 5. The space tethered system is discretized into N beads connected by springs without mass, and the mass of each section of the tether is concentrated at the point. The dispersion of the tether can be asymmetrical and the density also. The system is transformed into a multibody system consisting of N + 2 rigid bodies. The distributed and concentrated forces are transformed into the forces and moments on the main satellite, the subsail, and the beads according to the principle of force equivalence.
The dynamics of the main satellite and beads are similar to the beads model for a general space tethered system, except that the solar radiation pressure on the solar sail instead of a general subsatellite is considered. The dynamic equations could be as follows:
where
is the tension of the segments of the tether,
is the perturbative force,
is the control force of the main satellite,
is the solar radiation pressure, and
is the number of a bead (
).