ASRS-CMFS vs. RoBERTa: Comparing Two Pre-Trained Language Models to Predict Anomalies in Aviation Occurrence Reports with a Low Volume of In-Domain Data Available

Abstract

We consider the problem of solving Natural Language Understanding (NLU) tasks characterized by domain-specific data. An effective approach consists of pre-training Transformer-based language models from scratch using domain-specific data before fine-tuning them on the task at hand. A low domain-specific data volume is problematic in this context, given that the performance of language models relies heavily on the abundance of data during pre-training. To study this problem, we create a benchmark replicating realistic field use of language models to classify aviation occurrences extracted from the Aviation Safety Reporting System (ASRS) corpus. We compare two language models on this new benchmark: ASRS-CMFS, a compact model inspired from RoBERTa, pre-trained from scratch using only little domain-specific data, and the regular RoBERTa model, with no domain-specific pre-training. The RoBERTa model benefits from its size advantage, while the ASRS-CMFS benefits from the pre-training from scratch strategy. We find no compelling statistical evidence that RoBERTa outperforms ASRS-CMFS, but we show that ASRS-CMFS is more compute-efficient than RoBERTa. We suggest that pre-training a compact model from scratch is a good strategy for solving domain-specific NLU tasks using Transformer-based language models in the context of domain-specific data scarcity.

1. Introduction

In recent years, pre-trained language models (PLM) based on Transformers [1] such as RoBERTa [2] have advanced the state-of-the-art performances on Natural Language Understanding (NLU) tasks. Because the Transformer architecture is commonly used in the literature, we will not do an exhaustive description of how it works. NLU is a field of Natural Language Processing (NLP) that aims at maximizing the ability of machine learning models to understand language. Document classification, question answering, or story comprehension are all examples of NLU tasks.

By using the pre-training + fine-tuning (PF) approach, one can use PLMs for any NLU task. For instance, if one wants to classify documents, one can fine-tune the off-the-shelf pre-trained RoBERTa language model on the text classification task (the pre-trained version of RoBERTa is freely available [3]). Little adaptation is needed to switch between the initial language modeling task and the downstream document classification task. In our example, a linear layer is added on top of the language model to adapt it to the new task. The linear layer allows the model to produce categories as outputs. During fine-tuning, the language model and the added layer are trained together to categorize input documents. Their internal parameters change through the continuous comparison between the expected outcomes (the true label of a document in this case) and the model’s predictions (the output of the final layer in this case).

However, applications such as classifying medical reports or classifying court cases are more complicated for off-the-shelf PLMs because they use textual data that is vastly different from standard everyday language. The difference between the pre-training data that is not domain-specific and the domain-specific fine-tuning data negatively impacts the performance of fine-tuned PLMs [4].

To mitigate this problem, one can use domain-specific data during the pre-training step. We refer to this kind of data as in-domain data.

A possible implementation of this strategy is pre-training from scratch, which is pre-training a language model using only in-domain data. In the work of [5], the authors obtain very good results on various medical NLU tasks, by using PubMed as a corpus for pre-training. In the work of [6], the authors also find that the pre-training from scratch approach is highly efficient in the context of legal NLU tasks.

However, overcoming domain specificity using the pre-training from scratch strategy requires an abundance of in-domain pre-training data. A low volume of data availability can be a legitimate problem when it causes language models to repeat training on the same examples during pre-training: according to [7], one can estimate the number of repetitions of data during pre-training by calculating the ratio between the number of tokens seen by the model during pre-training and the number of tokens that compose the pre-training data (before it is processed, textual data are decomposed into a sequence of individual units of language called tokens). The former is equivalent to the product of the training batch size, the number of pre-training steps, and the model’s maximum input sequence length. The training batch size is the number of training samples the model uses as input before it updates its internal parameters. A pre-training step corresponds to an update of the model’s parameter. The maximum input sequence length is the maximal number of tokens that can constitute an input for the model.

For instance, for the pre-training of RoBERTa, the batch size and number of pre-training steps correspond to pre-training on approximately 2.2 T tokens. Given a pre-training corpus made of 1.1 T tokens, there will be two repetitions during pre-training: each example in the pre-training data are seen twice during pre-training by the model.

In the work of [7], the authors show that an increase in the number of repetitions negatively impacts the performance of language models on downstream tasks, and suggest that this phenomenon is stronger for larger language models. For their Transformer-based language model of similar size to RoBERTa, they find that 1024 and 4096 repetitions lead to a respective decrease of performance of $4.4\%$ and $8.3\%$ on the “General Language Understanding Evaluation benchmark” (GLUE) [8]. GLUE is composed of multiple datasets used to train and evaluate the models on different NLU tasks, and is commonly used in the literature to compare NLP models.

In some cases, there is low in-domain data availability, relative to the number of tokens required for pre-training the model, and finding or producing more in-domain data on a large scale is not always possible. In particular, for cases where corpus size leads to repetitions ranging from tens of thousands to more than a hundred thousand during pre-training, the pre-training from scratch approach will not be optimal.

To summarize, pre-training from scratch allows for overcoming the negative effect of a mismatch between the pre-training data and the domain-specific data of a fine-tuning task. However, a drawback of the pre-training from scratch approach is that it requires a great amount of data to be performed optimally because of the repetition problem.

Interestingly, the repetition problem induced by low pre-training data availability does not affect as much compact language models (compact language models are language models with a smaller architecture, relative to the baseline PLMs such as RoBERTa). In the work of [7], the authors mention that compact language models are less affected by repetitions during learning. In the work of [9], the authors fine-tune a compact PLM on the question-answering task. They pre-train their language model using different volumes of data. When increasing the pre-training data volume from 10 to 4000 MB (10, 100, 500, 1000, 2000 and 4000 MB), they find that past the smallest dataset of 10 MB, increasing the pre-training data volume does not increase significantly downstream performance. For reference, the volume of RoBERTa’s pre-training data is 160 GB.

In this context, we propose to compare two approaches that use PLMs on the problem of domain-specific NLU tasks, compounded with little in-domain data availability for pre-training. In the first approach, we use a standard PLM, the off-the-shelf pre-trained RoBERTa. In the second approach, we use a compact version of RoBERTa, which we pre-train from scratch on low-volume in-domain data (75 MB). The former benefits from his large size advantage: other things being equal, bigger PLMs perform better than smaller ones [10]. However, the compact model benefits from the pre-training from scratch strategy. Hence, it is not affected by the discrepancy between the pre-training data and the data of the downstream task.

To assess which approach is more advantageous, we use a custom in-domain NLU benchmark. The benchmark is built using the Aviation Safety Reporting System (ASRS) corpus. We present this corpus further in Section 2.1, and the benchmark we built from it in Section 2.2. Details about the pre-training parameters, models architecture, and size of the in-domain available pre-training data are presented further in Section 2.3. In Section 3, we show and compare our results. In Section 4, we discuss our findings and the limits of our work.

2. Materials and Methods

2.1. The ASRS Corpus

The ASRS is a voluntary, confidential, and non-punitive aviation occurrence reporting program. In the context of the ASRS, an occurrence describes any event excluding accidents that, in the eye of the reporter, could have safety significance. An accident is an event that results in either a person being fatally or seriously wounded, the aircraft sustaining important damage, or the aircraft missing [11]. The ASRS was created in 1976 by both the National Aeronautics and Space Administration (NASA) and the Federal Aviation Administration (FAA).

Other industries have since then copied this model of voluntary reporting [12]. This popularity motivates selecting the ASRS for our study. We assume that our results will apply to a certain degree to other cases where the data structure is similar.

An extract of a report is shown in Figure 1.

ASRS is a semi-structured dataset. Part of it consists of textual data, in the form of narratives, and synopses, as in the report extract above. A narrative describes an occurrence from a reporter’s point of view. For each narrative, a synopsis is produced by an ASRS staff member. This short document summarizes the narrative from a safety point of view.

The other part of the ASRS dataset is made of metadata that is either generated by reporters or by an ASRS analyst. The reporter-produced metadata consist of structured information on the occurrence context (for instance, weather-related information, or aircraft-related information as in the example of the report above). The reporter provides the metadata upon completion of the reporting form. There are four different types of forms, based on the job of the reporter: the Air Traffic Control (ATC) reporting form, the cabin reporting form, the maintenance form, and the general form (see https://asrs.arc.nasa.gov/report/electronic.html, accessed on 29 September 2022).

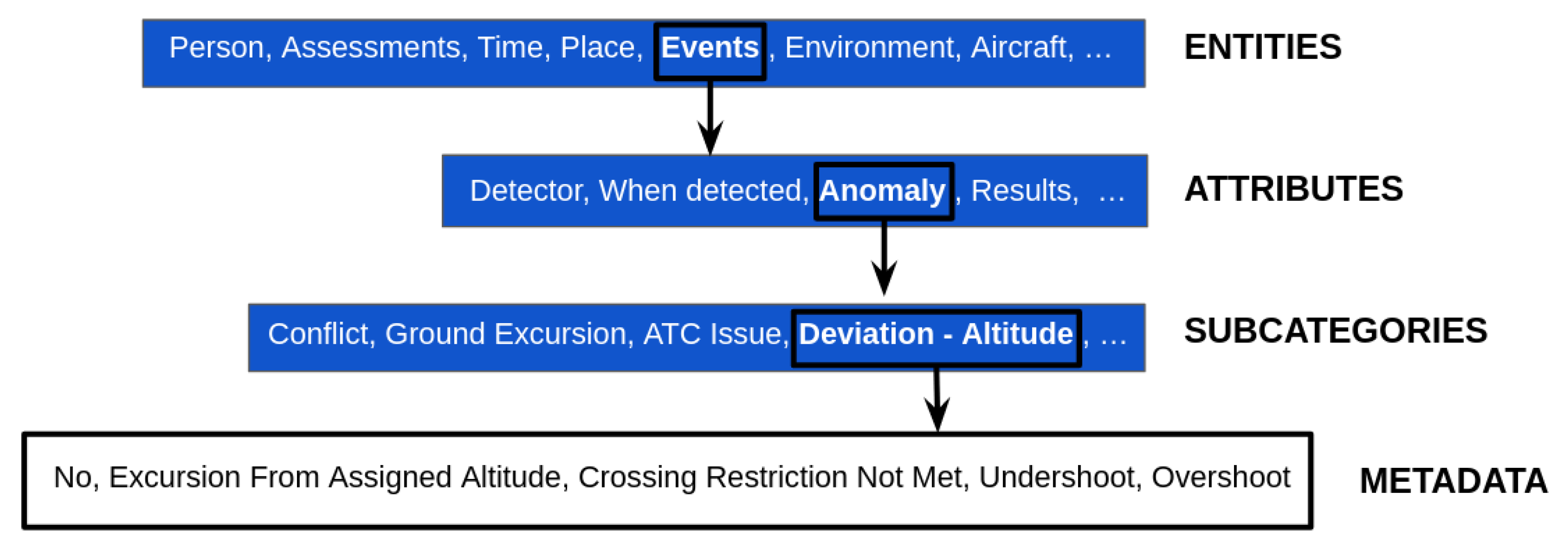
The analyst-generated metadata follow the ASRS taxonomy. In this context, the term taxonomy refers to the categories and sub-categories that are used to classify occurrence reports. The ASRS taxonomy provides a structured description and assessment of occurrences on a safety level. It is built around an entity-based structure [13]. At the top level of the taxonomy are entities (Time, Place, Environment, Aircraft, Component, Person, Events, and Assessments). At the lowest branch of the taxonomy are metadata and their values. In between the two, there are entities’ attributes, and in some cases, attributes’ subcategories. An example of how the ASRS taxonomy architecture works is in Figure 2.

As can be seen in Figure 2, there are five possible values for the metadata that correspond to the subcategory “Deviation—Altitude”: “No anomaly of this kind” (reduced to “No” in Figure 2), “Excursion from assigned Altitude”, “Crossing Restriction Not Met”, “Undershoot” and “Overshoot”. The “Deviation Altitude” is itself a Subcategory of “Anomaly”, which is an attribute of the “Event” entity.

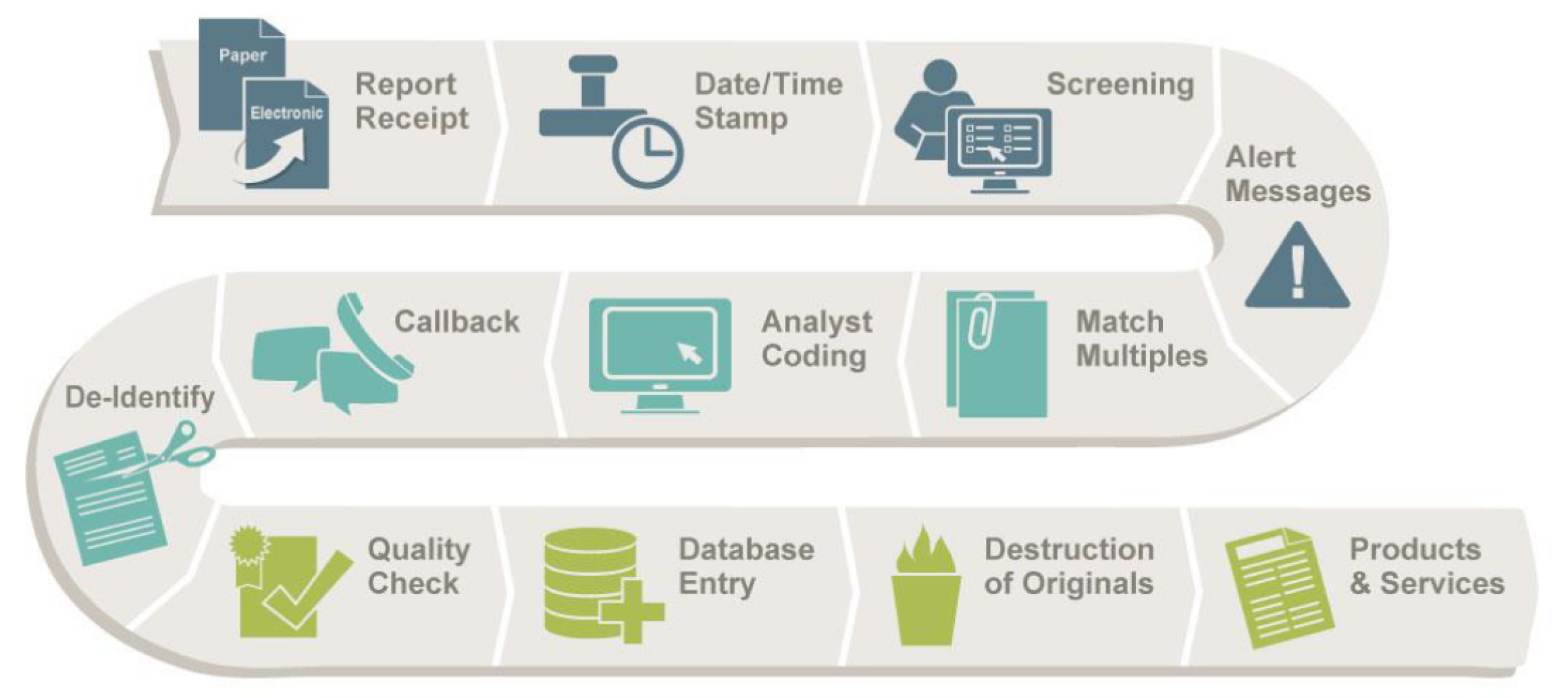
Since its creation, ASRS has received 1,625,738 occurrence reports up to July 2019 (see https://asrs.arc.nasa.gov/docs/ASRS_ProgramBriefing.pdf, accessed on 29 September 2022). In 2019, the average number of reports received per week was 2248. To better understand the ASRS, the full report processing flow is described below for clarity, and is also depicted in Figure 3.

The first step is receiving the reports. The second step consists of time stamping the reports based on the date of reception. During the third step, analysts screen reports to provide high-level initial categorization. The “Alert Messages” step occurs if a hazardous situation is identified, requiring organizations with authority for further evaluations and putting in place potential corrective actions. During the “Match Multiples” step, reports on the same event are brought together to form one database record. The previously mentioned analyst-generated metadata are created during the “Analyst coding” step. The “Callback” step happens if an ASRS analyst contacts a reporter to seek further details on an occurrence. It can result in a third type of textual data: callbacks. These are written with the purpose to report what was learned during conversations between the analysts and the reporters. During the last five steps, the information is de-identified, a quality check is done to ensure coding quality, and the original reports are destroyed. Finally, the ASRS database is used to produce services designed to enhance safety aviation.

We obtained our version of the public dataset through a request on the ASRS website. The dataset size is 287 MB, with a total of 385,492 documents and 50,204,970 space-delimited words. The occurrences range from 1987 to 2019.

The textual data style from 1987 to 2008 included is vastly different from the style used after. Documents from this era are characterized by upper-case letters, fragmented sentences (missing words), and heavy use of abbreviations, as can be seen in the extract of the narrative of an occurrence report in Figure 4.

It stands in contrast with documents after this era, which have both upper and lower-case letters, where sentences are not fragmented, and the use of abbreviations is standardized, as can be seen in the first extract.

2.2. Constituting the Benchmark

In this section, we present how we constructed the benchmark on which we compared our machine learning models. We use the definition of benchmark provided in the work of [14]. In their article, the authors study the current practices of benchmarking in the context of NLU. In the light of this study, they provide the following definition: “A benchmark attempts to evaluate performance on a task by grounding it to a text domain and instantiating it with a concrete dataset and evaluation metric”.

We will present our benchmark in the following order: the task, the dataset, and the evaluation metrics.

2.2.1. The Task

For the task, we chose the coding of the occurrences, as done by the ASRS analyst in the sixth step of report processing. This is an interesting task to choose for mainly two reasons.

First, it constitutes a legitimate application of language models in a real-world context. As a result of the growth of global air traffic and the development of “just culture” which encourages the practice of occurrence reporting within the different aviation institutions, there are more occurrences reports. In the context of aviation safety, this phenomenon spurs the need for some form of support to process the reports. A way to do it is to perform automatic document classification according to a pre-established taxonomy [15,16].

Coding occurrences is a practical choice as well as it constitutes a ready-made set of supervised text classification (TC) problems. A text classification problem involves a textual input and one or multiple elements from a set of classes (or labels) as expected outputs. It is supervised when there is a labeled dataset that can be used to train a model on the task. Supervised text classification is a common NLU task.

2.2.2. Dataset

When instantiating the task above with a concrete dataset, one must make two choices. First, one needs to choose which part of the ASRS taxonomy will be the expected outputs. Secondly, one will have to choose which part of the ASRS corpus will be used to create the textual inputs. When making these choices, we take into account benchmark construction good practices as reported in the work of [14]. We also take into consideration the argument presented in the work of [17], where the authors argue that, in the context of classifying aviation occurrences, the value of TC algorithms lies in their performance under field condition exposure. This is why we try to emulate realistic field use of the PLMs to classify aviation occurrences.

With regard to the first choice (choosing the expected outputs), there is a wide array of analyst-generated metadata that are created during the sixth step of the reporting process that one can choose from. However, in the work of [18], the author shows that the categories of the ASRS taxonomy that cover the assessment of ASRS occurrences from the human factor perspective all present a high inter-annotator disagreement rate (disagreements between different annotators regarding what is the correct prediction for a classification problem). He suggests that this is because “categorizing narratives in accordance with a human factors taxonomy is an inherently subjective process”. Inconsistent annotations have been reported to happen on datasets used across a wide range of NLP tasks [19]. Supervised machine learning techniques do not perform as well in such instances. The inevitable drop in performance can induce a sub-optimal workload reduction for the safety analysts that use the text classification machine learning models to alleviate their work [15]. Finally, according to [14], one of the criteria that indicates a good benchmark is reliable annotation.

As such, we made the choice to select the metadata associated with the 14 subcategories of the “Anomaly” attribute, which belongs to the “Events” entity (following the taxonomy described in Section 2.1 and Figure 2) as our expected outputs, resulting in 14 different text classification (TC) problems.

This choice is based on the assumption that analysts converge more easily on the identification of anomalies (metadata attached to the “Anomaly” attribute) than Human Factors issues. This strong hypothesis is driven by the difference in nature of the two groups of metadata. In the work of [13], the author introduces the distinction between metadata that support the factual description of an occurrence, and metadata that operate an analysis of the accident requiring “expert reasoning and inference to produce”. The former is factual metadata, while the latter is analytical metadata. Human factors’ categories are strongly analytical metadata. In contrast, most anomaly subcategories, such as “Ground excursion” (which can be any of the following: “No”, “Runway”, “Taxiway”, “Ramp”), are factual metadata. The only noticeable exceptions are for the “Equipment Problem” and “Conflict” subcategories. In both of these cases, a class comes in two flavors: critical and less Severe, as seen in

Table 1. Anomaly subcategories that are multi-classification problems.

Name	Composition	Shannon Equitability Index
Aircraft Equipment Problem	No (54.66%), Critical (24.39%), Less Severe (20.95%)	0.912
Conflict	No (85.32%), NMAC (6.2%), Airborne Conflict (4.5%), Ground Conflict, Critical (2.39%), Ground Conflict, Less Severe (1.59%)	0.374
Deviation—Altitude	No (91.2%), Excursion From Assigned Altitude (4.35%), Overshoot (2.37%), Crossing Restriction Not Met (1.62%), Undershoot (0.46%)	0.249
Deviation—Procedural	No (51.16%), Published Material/Policy (27.76%), Clearance (12.09%), FAR (4.01%), Maintenance (1.45%), Other/Unknown (1.29%), MEL (0.79%), Weight In addition, Balance (0.63%), Hazardous Material Violation (0.34%), Landing Without Clearance (0.28%), Security (0.19%)	0.55
Flight Deck/Cabin/Aircraft Event	No (92.32%), Smoke/Fire/Fumes/Odor (3.51%), Other/Unknown (2.63%), Illness (1.25%), Passenger Misconduct (0.24%), Passenger Electronic Device (0.05%)	0.201
Ground Event/Encounter	No (91.03%), Other/Unknown (3.1%), Loss Of Aircraft Control (1.94%), Ground Strike—Aircraft (1.6%), Object (0.98%), Gear Up Landing (0.4%), Vehicle (0.4%), Person/Animal/Bird (0.23%), Aircraft (0.2%), FOD (0.12%)	0.2
Ground Excursion	No (96.89%), Runway (2.58%), Taxiway (0.47%), Ramp (0.06%)	0.112
Ground Incursion	No (96.38%), Runway (2.26%), Taxiway (1.35%)	0.163
Inflight Event/Encounter	No (76.97%), Weather/Turbulence (7.3%), CFTT/CFIT (3.07%), Fuel Issue (2.93%), Loss Of Aircraft Control (2.48%), Wake Vortex Encounter (2.17%), Other/Unknown (1.85%), Unstabilized Approach (1.83%), Bird/Animal (0.49%), Object (0.48%), VFR In IMC (0.43%)	0.417

. We made the assumption that choosing between the two alternatives required less expert inference than predicting Human Factor issues because of a higher chance of convergence in the training of the annotators.

With regard to the second choice, we created a training and a testing dataset for each anomaly subcategory. The narratives are the inputs, and the manually coded metadata values are the expected outputs. To simplify the interpretation of the data (e.g., homogeneity of reporter vocabulary and issues faced), we only used reports produced by reporters that filled the general form, as done in the work of [18]. More importantly, they constitute the majority of the occurrences, with $74.2\%$ of the total number of reports being filed through the general form. We only worked on events that occurred after 2009 to avoid having two different writing styles in our documents.

The training datasets consist of 30,293 reports from 2009 to 2018 included. The testing datasets consist of 1154 reports from 2019. As mentioned in the work of [13], “safety is a lot about responding to such change and dealing with novel and unseen combinations of factors before they start resonating and create an unsafe state [20]”. Part of the complexity faced by practitioners when classifying new reports is the evolving nature of safety. This means that, with time, new safety threats can emerge. This is why, in the spirit of replicating real-world field conditions, we chose to chronologically split the data between the training and testing datasets.

By selecting these 14 different text classification problems, we tried to reflect the different facets of predicting aviation occurrences with data diversity. Some of these TC problems are multi-classification problems, meaning that there are at least three classes (see Table 1); others are binary classification problems (see

Table 2. Anomaly subcategories that are binary classification problems.

Name	Composition	Shannon Equitability Index
ATC Issue	No (86.51%), All Types (13.49%)	0.571
Airspace Violation	No (97.44%), All Types (2.56%)	0.172
Deviation—Speed	No (96.89%), All Types (3.11%)	0.2
Deviation—Track/Heading	No (92.14%), All Types (7.86%)	0.397
No Specific Anomaly Occurred	No (98.77%), All Types (1.23%)	0.096

). For instance, predicting the subcategory “Aircraft Equipment Problem” is a multi-classification problem with three classes: critical, less severe, and no (meaning “No anomaly of this kind”). The number of classes of our TC problems varies from 2 to 11.

As described in Table 1 and Table 2, the proportion of documents per class can be very unevenly distributed depending on the TC problem, which is also a sign of diversity. When the data sparsity is high, the data are said to be imbalanced. This is further characterized in the two tables with the Shanon equitability index [21]:

$$E_H=\frac{H}{log\left(K\right)},$$

(1)

with:

$$H=-\sum _{i=1}^K\frac{c_i}{n}log\left(\frac{c_i}{n}\right),$$

(2)

where K is the number of classes, $c_i$ is the number of elements in class i, and n is the total number of elements. The result is a number between 0 and 1. The higher the score, the more balanced the dataset is. To give an example, the lowest value of $0.096$ is for the “No Specific Anomaly Occurred” anomaly in Table 2. This anomaly is made up of two classes, and the majority class represents 98.77% of the documents. In our case, values range from $0.096$ to $0.912$.

2.2.3. Selection of Metrics to Compare the Models—Performance

In the context of TC performance, many evaluation metrics exist. They all have different pros and cons [22]. After considering the literature on evaluation metrics for classification problems, we chose the Matthews correlation coefficient ($MCC$) score [23] as our performance metric. After a brief presentation of the metric, we justify our choice.

Let $\widehat{C}={\left({\widehat{c}}_{i,j}\right)}_{0\le i,j\le K-1}$ be the empirical confusion square matrix obtained by a classification model on a K classes TC problem, on a testing set of N elements:

$${\widehat{c}}_{i,j}=\sum _{n=0}^{N-1}{X}_n(i,j)$$

(3)

with

$$X_n(i,j)={\mathrm{𝟙}}_{k_{n=\mathrm{i}}}{\mathrm{𝟙}}_{l_{n=j}},$$

(4)

where, for each text n, the true class is $l_n$, and the predicted class is $k_n$.

Then, the empirical Matthews Correlation Coefficient ($\widehat{MCC}$) metric is defined by:

$$\widehat{MCC}=\frac{N\times {\sum }_{k=0}^{K-1}{\widehat{c}}_{k,k}-{\sum }_{k=0}^{K-1}({\sum }_{i=0}^{K-1}{\widehat{c}}_{i,k}\times {\sum }_{j=0}^{K-1}{\widehat{c}}_{k,j})}{\sqrt{N^2-{\sum }_{k=0}^{K-1}{\left({\sum }_{i=0}^{K-1}{\widehat{c}}_{i,k}\right)}^2}\times \sqrt{N^2-{\sum }_{k=0}^{K-1}{\left({\sum }_{j=0}^{K-1}{\widehat{c}}_{k,j}\right)}^2}}.$$

(5)

The $MCC$ computes the correlation coefficient between the actual labels and the predicted ones. When the classifier is perfect, we obtain 1. When its output is random, we obtain 0.

Now that we have defined the $MCC$ metric, let us give the different reasons that prompt us to choose this metric as opposed to the other popular metrics: $precision$, $recall$, F1-score, and $accuracy$. To add clarity, we will be using examples of confusion matrices. A confusion matrix is a convenient way to visualize how many of our predictions are correct for each class. In

Table 3. Confusion matrix of a binary classification problem.

	Classes	Postive	Negative
Predictions
Positive		TP	FP
Negative		FN	TN

, we show an example of a confusion matrix for a binary classification problem, with a negative and positive class. $TP$ corresponds to True positive; it is the number of times the model predicts correctly that a sample belongs to the class positive. Similarly, $FP$ stands for False positive, $FN$ for False negative, and $TN$ for True negative.

In this context, we have that:

$$Precision=\frac{TP}{TP+FP},$$

(6)

$$Recall=\frac{TP}{TP+FN},$$

(7)

$$F1-score=\frac{2\times Precision\times Recall}{Precision+Recall},$$

(8)

$$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}.$$

(9)

The first advantage of the MCC score is that it is symmetric: in a binary setting with a positive and negative class, the MCC score will remain the same when swapping the two classes. That stands in contrast with the precision, the recall, or the F1-score, as can be deduced from their formula.

In addition, its score is not biased towards classes with more samples, as for the accuracy or F1-score metrics. To show this effect, let us consider the two confusion matrices in

Table 4. Confusion matrix A.

	Classes	Postive	Negative
Predictions
Positive		15	20
Negative		40	1

and

Table 5. Confusion matrix B.

	Classes	Postive	Negative
Predictions
Positive		24	32
Negative		400	10

.

The two confusion matrices have the same proportion of correct predictions for each class (respectively 3 to 4 for positive predictions and 1 to 40 for negative predictions). However, in the case of matrix A, there are 55 samples in the positive class, and 21 samples in the negative class, which is roughly two times less than in the positive class. In contrast, for matrix B, there are 424 samples in the positive class and 42 samples in the negative class, which is 10 times less than in the positive class.

When we calculate the MCC score, the F1-score and the accuracy score in each case, we obtain the scores shown in

Table 6. Comparison of the performance metrics for matrices A and B.

	Matrix	A	B
Score
MCC		0.60	0.62
F1		0.33	0.1
accuracy		0.21	0.07

.

As can be seen with this example, the MCC is much less affected by the number difference between the classes. For the other performance metrics, the final performance score is heavily influenced by the majority class. Because the MCC score is not biased towards any class, we chose the MCC score as our metric to indicate performance.

2.2.4. Selection of Metrics to Compare the Models—Efficiency

We define efficiency as the amount of computational work required to generate a result with our machine learning models. In the work of [24], the authors advocate that efficiency should be an evaluation criterion for research in machine learning because of the carbon footprint and financial cost of deep-learning models such as Transformer-based language models. Additionally, there are several works where the authors argue that lack of efficiency constitutes a barrier to the use of algorithms in real-world applications [25,26,27]. This is why we compare the efficiency of the two models.

Different efficiency metrics exist. Following the work of [24], we favour reporting the total number of floating point operations (FLOPs) required to generate our results (both for pre-training and for inference).

FLOPs provide a measure of the amount of work done when executing a specific instance of a model. It is tied to the amount of energy consumed and is strongly correlated with the running time of the model. However, unlike other metrics such as electricity usage or elapsed real time, this metric is not hardware dependent. It allows for a fair comparison between models.

Additionally, to obtain a sense of the amount of memory required to run the models, we provide the number of parameters.

2.3. Pre-Training and Fine-Tuning Procedure

2.3.1. Language Models

We studied two language models. The powerful Transformer-based language model RoBERTa, and a compact version of RoBERTa, called ASRS-CMFS (for Aviation Safety Reporting System—Compact Model pre-trained From Scratch). We chose RoBERTa as our base model because it is a well-studied and sturdy transformer-based model with good performance in the Natural Language Understanding landscape [8].

As mentioned in the Introduction, RoBERTa re-uses the Transformer architecture, a multi-layered neural network. Each layer is characterized by the following parameters, which we will not review in detail: hidden dimension size, FFN inner hidden size, and the number of attention heads.

To create a compact model out of the RoBERTa model, one can either reduce the depth, which corresponds to the number of layers, or the width, which corresponds to the size of a single layer. The latter is proportional to the parameters we have mentioned above.

Following the work of [28], when building the ASRS-CMFS model from the initial RoBERTa architecture, we favored maintaining depth, while reducing the width, to obtain the best performances.

The difference in size between the two models is well-shown through the various architecture parameters in

Table 7. Comparison of the architecture of the two models.

Architecture	ASRS-CMFS	RoBERTa
Layers	12	12
Hidden dimension	256	768
FFN inner hidden size	1024	3072
Attention Head	4	12
# of parameters	18 M	125 M
Maximum input length	512	512

.

2.3.2. Pre-Training Data

As mentioned in the Introduction, our interest with language models in the context of their use for in-domain NLU tasks with little in-domain data availability for pre-training. In our case, we define our available in-domain pre-training data as all the textual data in the ASRS dataset that ranges from 2009, and before 2019.

We avoid using reports from before the 2009 era that are very different, as mentioned in Section 2.1. To modify the data before the 2009 era so that they are up to today’s standards would be a challenge in its own right. We would have to convert the text back to mixed upper/lowercase, add missing words, and “un-abbreviate” the non-standards abbreviated words. However, some of the abbreviations can map to multiple possible words. For instance, depending on the context, the word “RESTR” could mean restriction, restrictions, restrict or restricted [29].

We obtain a very small set of data. As indicated in

Table 8. Comparison of amount of textual data used for pre-training.

Architecture	ASRS-CMFS	RoBERTa
Data	ASRS 2009–2019	Web Crawl
Size	74.5 MB	160 GB
Type	Aviation-related English	Standard English

, our pre-training corpus is roughly 2000 times smaller in size than the one used by RoBERTa.

If we wanted to pre-train from scratch RoBERTa on ASRS 2009–2019 using the same parameters as for the freely accessible fully pre-trained RoBERTa model, it would result in 126,356 repetitions. This high number of repetitions discourages us from applying the pre-training from scratch approach on this model.

With the pre-training parameters of our model shown in the Pre-training procedure section, the ASRS-CMFS has only 3015 repetitions during pre-training. This is why we chose to compare ASRS-CMFS pre-trained from scratch against the already pre-trained on general-domain data RoBERTa language model.

2.3.3. Pre-Training Procedure

For our compact model’s main pre-training hyperparameters (see Appendix B), we have used another transformer-based language model, Electra-small [30], as our reference. Hyperparameters are the particular parameters that characterize the learning process configuration. For example, the training batch size is an instance of a hyperparameter. Our choice of using Electra-small for reference when choosing hyperparameters is guided by the sizes of the two models that are comparable: 18 M for our model and 14 M for Electra-small.

Our model’s pre-training lasted for 14 days on the eight total GPUs available in our lab (see Appendix A for details on hardware).

2.3.4. Fine-Tuning Procedure

We separately fine-tuned the models on 14 different text classification tasks derived from the ASRS corpus. The fine-tuning data selection is described in Section 2.2.2.

As mentioned in the Introduction, a pre-requisite to fine-tuning our language models on the classification tasks is to add a linear layer on top of them. The added layer allows the models to produce categories as outputs. Its internal parameters are generated randomly and converge to their final values during training. Upon initializing the added layer, one can manually choose a seed which will generate a particular set of internal parameters for the layer. Distinct seeds will result in substantial performance discrepancies for the different randomly-initiated models [31]. For this reason, we do the fine-tuning with five different seeds and report the average result for each model–task combination.

For the ASRS-CMFS model, we used the same fine-tuning hyperparameters as the ones used for Electra-Small, when fine-tuned on the GLUE benchmark tasks. This is because the sizes of the two models are comparable and our downstream tasks are NLU tasks, similar to the GLUE benchmark tasks.

In the work of [2], the authors systematically tried six different configurations of hyperparameters to fine-tune RoBERTa on the GLUE benchmark tasks. As ASRS-CMFS used only one configuration, we randomly chose one of the six possible configurations (learning rate of $1\times {10}^{-5}$ and batch size of 16) to ensure fairness. Additionally, as each configuration requires averaging over five runs with different randomization of the final layer, this decision minimizes prohibitively expensive resource consumption. Both sets of fine-tuning hyperparameters are available in

Table 9. Comparison of fine-tuning hyperparameters.

Hyperparameters	ASRS-CMFS	RoBERTa
Learning rate	$3\times {10}^{-4}$	{$1\times {10}^{-5}$, $2\times {10}^{-5}$, $3\times {10}^{-5}$}
Weight Decay	0	0.1
Batch size	32	{16, 32}
Max Train Epoch	3	10
Warmup ratio	0.1	0.06

.

To take into account the imbalanced nature of the classification datasets, we used the “class weight” feature of Simpletransformer [32]. Simpletransformer is a library built on the Hugging Face Transformer library [3] that eases the use of Transformer-based language models. The “class weight” feature allows for assigning weights to each label and is a commonly used tactic to deal with an imbalanced dataset in the context of the text classification task [33]. The weight of each label was calculated as the inverse proportion of the class frequency.

The max input length of RoBERTa and ASRS-CMFS is 512 tokens, but some documents are four times longer. To mitigate this length problem, we used the “sliding window” feature of SimpleTransformers [32]. When training a model with the sliding window feature activated, a document that exceeds the limit of input of the classification model is split into sub-sequences. Each sub-sequence is then assigned the same label as the original sequence, and the model trains on the sub-sequences. During evaluation and prediction, the model predicts a label for each window or sub-sequence of an example. The final prediction for a given long document was originally the mode of the sub-sequences’ predictions. We changed the code so that the final prediction was the means of the predictions of the sub-sequences. We did that to prevent having a default value proposed in the case of a tie.

2.4. Summary

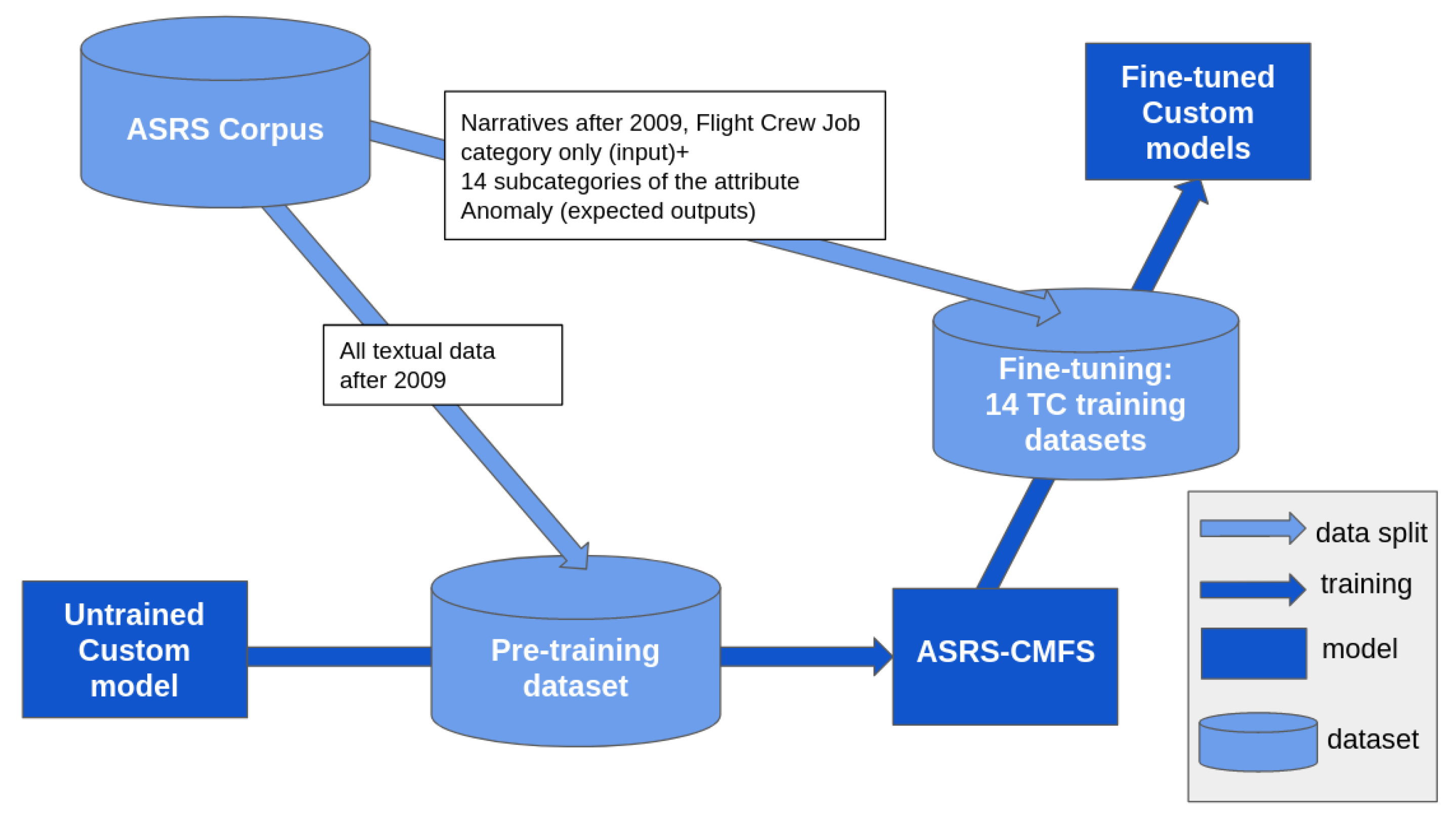
To help summarize the content in this section, we provide a visual description of the NLP pipeline for ASRS-CMFS in Figure 5. The datasets are in light blue, and the dark blue boxes represent the different stages of training of ASRS-CMFS: the first box is the untrained model. The second box is the PLM using the pre-training dataset, which consists of all the textual data extracted from the ASRS corpus after 2009 included. The third box corresponds to the 14 ASRS-CMFS models separately fine-tuned on the 14 text classification training datasets, which are also extracted from the ASRS corpus.

3. Results

3.1. Performance of the Two Models

In

Table 10. The results for the different classification problems, the best results are in bold.

Anomaly	5 Seed MCC Average
	ASRS-CMFS	RoBERTa
ATC Issue	0.627	0.664
Aircraft Equipment Problem	0.579	0.572
Airspace Violation	0.559	0.719
Conflict	0.726	0.736
Deviation—Altitude	0.412	0.43
Deviation—Procedural	0.372	0.411
Deviation—Speed	0.531	0.636
Deviation—Track/Heading	0.64	0.715
Flight Deck/Cabin/Aircraft Event	0.662	0.689
Ground Event/Encounter	0.556	0.594
Ground Excursion	0.725	0.806
Ground Incursion	0.505	0.45
Inflight Event/Encounter	0.494	0.554
No Specific Anomaly Occurred	0.099	0.124
AVERAGE	0.535	0.579

, we provide the five seeds MCC average of our models on each anomaly. When we average all the scores to obtain a sense of the performance difference between the two models on a higher level, we obtain that the ASRS-CMFS model retains 92% of the performance of the RoBERTa model. However, as we will see in the following analysis, there is no strong statistical evidence that RoBERTa and the ASRS-CMFS model perform differently.

As can be seen in Table 10, in most cases, the RoBERTa model has the upper hand, although to a varying degree. Remarkably, for the “Aircraft Equipment Problem” and the “Ground Incursion” anomalies, the ASRS-CMFS model outperforms RoBERTa, which invalidates the potential narrative that RoBERTa is clearly better than the ASRS-CMFS model. This impression is reinforced when we take into consideration the distributions of the two models’ performance scores across the five seeds.

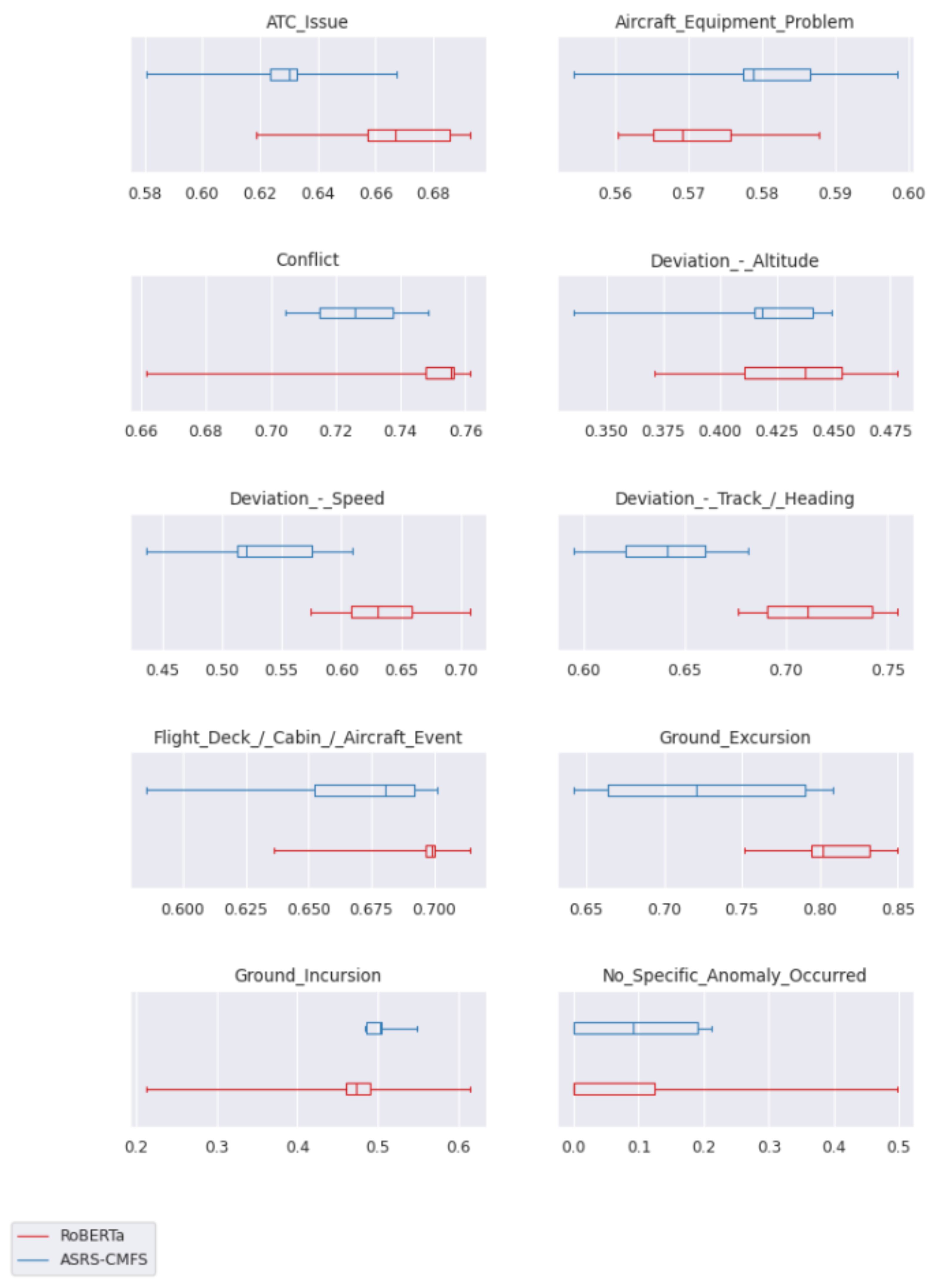
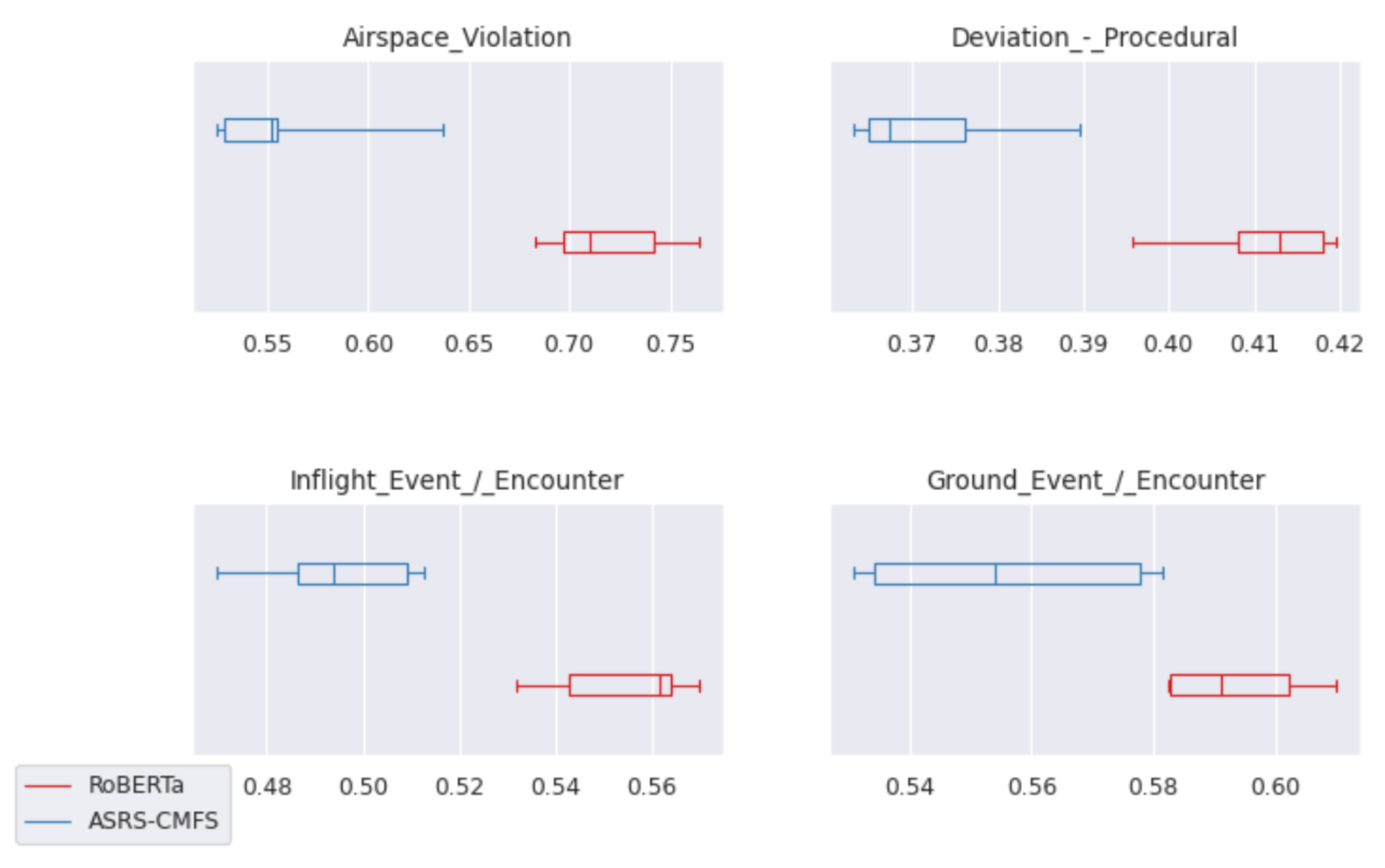
In Figure 6 and Figure 7, we use boxplots to show these distributions. Because there are five samples in each distribution, the extremities of the boxplots are respectively the minimum and the maximum scores. The median value which is the vertical bar in the box represents the third highest score, while the respective extremities of the box represent the second and fourth highest scores. In red, we have the performance scores of RoBERTa and, in blue, the performance scores of ASRS-CMFS.

Figure 6 shows overlapping distributions, while Figure 7 shows the classification problems where the distribution of scores does not overlap between models.

We see that only 4 out of the 14 classification problems have distributions with no overlaps between the two models. It shows that the models are competitive to a degree.

To obtain a deeper understanding of how significant the performance difference is between the two models depending on the anomaly, we use statistical hypothesis testing. The statistical study framework is described in details in the Supplementary Materials.

We test $H_0:MC{C}_{true1}=MC{C}_{true2}$ against $H_1:MC{C}_{true1}\ne MC{C}_{true2}$, where $MC{C}_{true1}$ is the true $MCC$ value for the RoBERTa model, and $MC{C}_{true2}$ is the $MCC$ value for the ASRS-CMFS model.

For each anomaly, we conduct 25 tests with a $0.05$ level of significance. We pair each of the five randomly-initiated RoBERTa models with each of the five randomly-initiated ASRS-CMFS models. We report the values of $\frac{H1}{Total}$ for each anomaly in

Table 11. Statistical hypothesis testing to study the significance of the performance gap between the two models for each anomaly.

Anomaly	H1/Total
Inflight Event/Encounter	0.88
No Specific Anomaly Occurred	0.76
Airspace Violation	0.68
Deviation—Procedural	0.6
Deviation—Track/Heading	0.6
ATC Issue	0.48
Deviation—Speed	0.48
Ground Excursion	0.48
Conflict	0.44
Deviation—Altitude	0.32
Flight Deck/Cabin/Aircraft Event	0.32
Ground Event/Encounter	0.28
Ground Incursion	0.2
Aircraft Equipment Problem	0.04

. $\frac{H1}{Total}$ is the ratio between statistical tests that leads to H1 and the total number of statistical tests. For clarity, we have sorted the rows of Table 11 by values of $\frac{H1}{Total}$, from the highest value to the lowest.

When we consider Table 11, we notice that H1 is the less frequent outcome ($\frac{H1}{Total}<0.5$) for a majority of the anomalies. In nine of the fourteen cases, the most frequent outcome is that we cannot conclude whether the difference in performance between the two models is statistically significant. Additionally, the averaged ratio across the anomalies is $0.47<0.5$. These observations reinforce the impression that the two models do not perform significantly differently.

In Figure 8, we show what happens when we lower the level of significance of our hypothesis testing from $0.05$ to $0.01$ with incremental steps of $0.005$. The x-axis represents the confidence level (which is equivalent to 1—$\mathrm{level}\mathrm{of}\mathrm{significance}$), and the y-axis represents the value of $\frac{H1}{Total}$.

We see that, for a test level of 0.01, $\frac{H1}{Total}$ is 0.316. It means that the two models are statistically different in only one-third of the cases when the test level is 0.01.

To better understand how the change of test level affects the value of $\frac{H1}{Total}$ of the different anomalies, we trace in Figure 9 a bar plot. Its x-axis is divided into four range of values: 0 to 0.25, 0.25 to 0.5, 0.5 to 0.75 and 0.75 to 1. The y-axis represents the number of anomalies for which the associated ratio falls within one of the four ranges. We respectively plot in blue and orange the values for test levels of 0.05 and 0.01. For instance, one can see in the bar plot that, for a test level of 0.05 (in blue), there are seven anomalies for which the value of $\frac{H1}{Total}$ is within the range of 0.25 to 0.5.

We notice that, when the test level diminishes to 0.01, the number of anomalies for which $\frac{H1}{Total}<0.5$ increases from nine to twelve. H1 occurs more frequently for only two anomalies when the test level is 0.01: “Inflight Event/Encounter” and “No specific Anomaly occurred”.

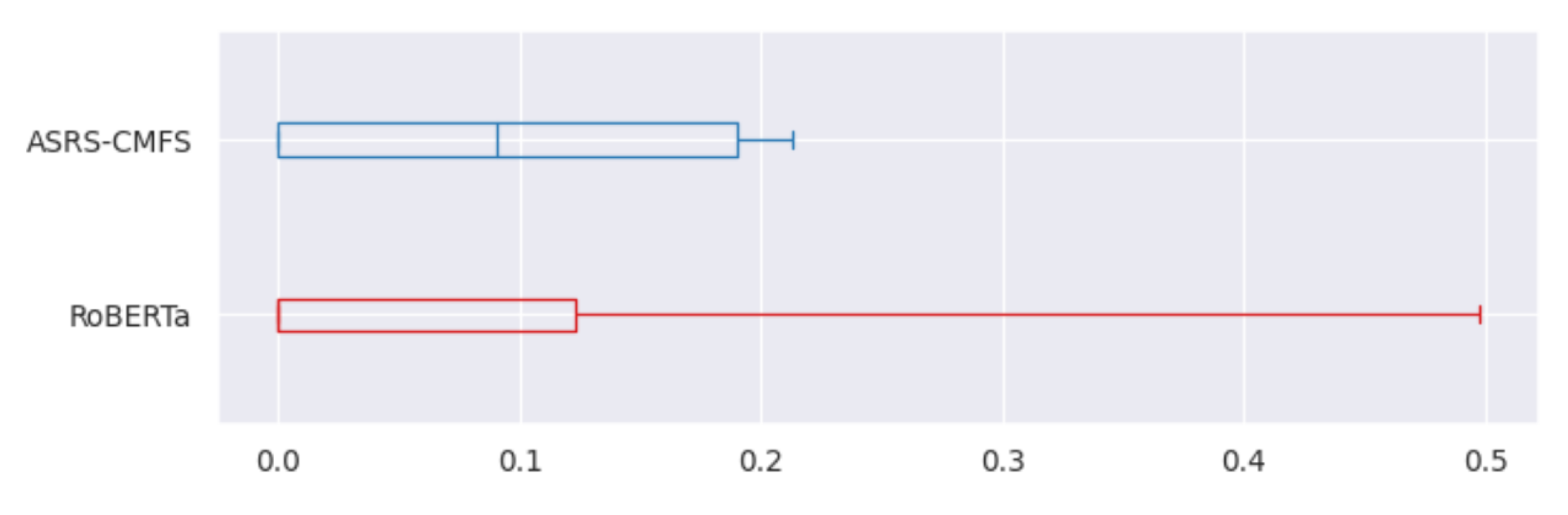
The case of “No specific Anomaly occurred” in particular is interesting. In Figure 10, we plot the boxplots of the score distributions of the two models over the five seeds. We notice that models are extremely unreliable for this anomaly, and there is a strong outlier in the distribution of RoBERTa, where one of the models obtains a performance score of 0.5 while three of the other models obtain a performance score of 0. This high variability might be due to the extreme lack of balance in the class distribution, with the lowest Shannon equitability index of 0.096, as can be seen in Table 2. These observations lead us to believe that we should disregard the anomaly “No specific Anomaly occurred” in our analysis.

In the end, when considering the results on all of the anomalies, there is no conclusive statistical evidence that RoBERTa and ASRS-CMFS perform differently.

3.2. Efficiency of the Two Models

Results are reported in

Table 12. Efficiency of the two models.

Models	# of Parameters	FLOPS		FLOPS Ratio
		Pre-Training	Inference	Pre-Training	Inference
ASRS-CMFS	18 M	$2.35\times {10}^{18}$	$2.17\times {10}^{10}$	1×	1×
RoBERTa	125 M	$1.15\times {10}^{21}$	$1.38\times {10}^{11}$	489×	5.1×

. To count the FLOPs, we have re-used the code produced in the work of [30]. The assumptions we made are the same as those presented in the article and the corresponding code.

ASRS-CMFS is seven times smaller than the regular RoBERTa model. With regard to FLOPs, ASRS-CMFS beats the RoBERTa model by a factor of 489 for pre-training, and 5 for inference.

The gain in efficiency is particularly impressive in the case of pre-training. For practitioners, it is a good indication of the relative cost between pre-training a full-sized model from scratch and pre-training a compact model from scratch.

The speedup in inference is more modest. Still, the ASRS-CMFS model is more compute-efficient and consumes less memory, which can be critical in the context of real-world applications.

4. Discussion

4.1. Efficiency vs. Performance

The data we worked with have two main defining features. Firstly, it is highly domain-specific. Secondly, its volume is vastly below the standard of what is usually required to pre-train a full-sized language model. In this context, we tried to compare two approaches: a pre-trained from scratch compact language model and an off-the-shelf PLM. We made the comparison based on the criteria of performance and efficiency. From a strict performance point of view, the off-the-shelf language model seems to have the upper-hand, although there is no conclusive statistical evidence that it is the case. From an efficiency point of view, the compact model has the upper hand.

The drawback of this approach relative to using an off-the-shelf model is the initial cost of pre-training the model. This cost is mitigated partly by the cheaper subsequent uses in terms of speed and memory requirements.

Another advantage of the compact model is that fine-tuning is also cheaper. During hyperparameter tuning, a compact model can sample the space of hyperparameter combinations using fewer computing resources. This characteristic of compact models seems highly advantageous when considering how much the seed-parameter that we have described before can influence the downstream performance of the PLMs.

These advantages might truly shine in usage scenarios where frequent fine-tuning of a PLM is needed. For instance, in the work of [15], the authors propose the following approach to support the browsing of the ASRS corpus: a safety analyst assigns an arbitrary category to a group of reports that interest him, and uses a TC algorithm to find other similar reports on the fly: “we start with a rough estimation of what the expert considers as the target (positive) reports. We train a classifier based on this data, and then apply it to the entire collection. Due to the nature of classification algorithms (and their need for generalisation), this classifier provides a different set of positive reports. Using the error margin (or probabilistic confidence score) provided by the classifier, we can identify borderline reports, on both sides of the decision: we select these few fairly positive and fairly negative items and submit them to the expert’s judgement. Based on his decisions, we obtain a new approximation of his needs, and can train another classifier, and so on until the expert reaches a satisfactory result.” This approach requires training a TC algorithm iteratively every time one defines a custom category. In this scenario, if one wanted to use a PLM to classify the occurrence reports, efficiency might be a critical factor to obtain good results quickly and in a cost-efficient manner.

4.2. Hypothesis Testing

We have used hypothesis testing to compare our two PLMs. It could also be used to evaluate the impact of any distinctive feature of occurrence reports on the classification performance of a single model. This could be especially useful for documents that have metadata, which is the case of the ASRS occurrence reports. As an example, one could investigate if a model performs significantly differently on occurrences depending on the value of reporter-generated metadata, such as the flight phase. It provides a simple tool to add understanding on what aspect of an occurrence impacts a model’s performance. We leave exploring this option for future work.

4.3. Overlap between the Pre-Training Data and Fine-Tuning Data

Because the domain-specific data volume was small, we included our fine-tuning training data set narratives in our pre-training data. To the best of our knowledge, there are currently no studies on the potential beneficial or adverse effects of such large overlaps between the pre-training data and the fine-tuning data in the context of NLP.

Interestingly, in the work of [34], the authors found that, in the context of image classification in computer vision, “performance on the target data can be improved when similar data are selected from the pre-training data for fine-tuning”.

In the light of our model’s relatively good performance, it might be worth considering investigating if this result holds true in the context of NLP.

5. Conclusions

We constituted a benchmark that reproduced as much as possible field conditions for the task of classifying aviation occurrence reports following a pre-established taxonomy. Through the comparison on the benchmark, we found that the ASRS-CMFS model was competitive with the regular RoBERTa model that is seven times larger, and also more efficient. For performance in particular, we used statistical hypothesis testing to reinforce our assessment. Finally, we proposed that pre-training a compact model from scratch was a good strategy in the particular context of low-resource domains (in-domain data scarcity and/or lack of computing resources).