Autonomous Recovery from Spacecraft Plan Failures by Regulatory Repair While Retaining Operability

Abstract

Pre-designed spacecraft plans suffer from failure due to the uncertain space environment. In this case, instead of spending a long time waiting for ground control to upload a feasible plan in order to achieve the mission goals, the spacecraft could repair the failed plan while executing another part of the plan. This paper proposes a method called Isolation and Repair Plan Failures (IRPF) for a spaceship with durable, concurrent, and resource-dependent actions. To enable the spacecraft to perform some actions when a plan fails, IRPF separates all defective actions from executable actions in the pre-designed plan according to causal analysis between the failure state and the established plan. Then, to address the competition between operation and repair during the partial execution of the plan, IRPF sets up several regulatory factors associated with the search process for a solution, and then repairs the broken plan within the limits of these factors. Experiments were carried out in simulations of a satellite and a multi-rover system. The results demonstrate that, compared with replanning and other plan-repair methods, IRPF creates an execution plan more quickly and searches for a recovery plan with fewer explored state nodes in a shorter period of time.

1. Introduction

A spacecraft plan, which is expected to achieve certain mission goals, is usually pre-programmed before liftoff or uploaded from ground control during a mission. Nevertheless, when applied in practice, this established plan has to deal with environmental uncertainties that can undermine the plan [1], i.e., the plan fails. For example, the Philae could not land at the original intended site because of the failure of its active descent system and anchoring harpoons [2]. In such a case, ground control would not be aware of the problem in a timely manner, nor could they quickly deliberate over a workable solution, taking into account the delay and accessibility between the spacecraft and the ground.

There are two ways to address plan failures: plan from scratch (i.e., replanning) and plan repair based on the existing plan. While replanning reuses the planner as a black box and obtains its output by feeding in a new initial state, plan repair adapts the failed plan to the new situation, e.g., deleting inapplicable activities and adding appropriate steps. Although plan repair is not easier than replanning in theory [3], it can find a solution faster in practice [4,5,6,7]. However, to the best of our knowledge, most current research on plan repair seems to be carried out in systems full of instant operations, and little attention has been paid to resource management. Since spacecraft actions are durable, concurrent, and resource-dependent, the existing repair methods are difficult to be applied directly to the synthesis of a recovery plan in spacecraft systems.

A spacecraft is a complex system composed of multiple subsystems such as attitude control, communication, and data management. When something goes wrong with one of these operational subsystems, some of them will be affected, while others will not. If, for example, the spacecraft cannot turn itself, the communication subsystem will be impacted by pointing restrictions. However, the data management subsystem will not be affected. Therefore, instead of waiting a long time for ground control to come up with a new plan to achieve the unaccomplished mission goal, it is more efficient to allow the spacecraft to amend the failed plan while performing other activities. Moreover, with multiple spacecraft systems, it is often more efficient to use another space vehicle to complete the tasks of a malfunctioning one.

In this paper, we propose a principled approach for spacecraft called Isolate and Repair Plan Failures (IRPF). IRPF extracts defective actions from the failed plan that are not suitable for the current operational environment according to the inherent causal chain, and then repairs an isolated set of actions while executing the remaining executable actions in the plan. The final recovery plan can then be merged with these available executable actions at an appropriate time to form a completely new plan, assisting the whole system in achieving its mission goals. Furthermore, the rationality and effectiveness of the new plan can be validated and verified by existing tools such as VAL [8].

When a failure happens, the pre-designed spacecraft plan can generally be divided into three parts: completed, executable, and defective parts. There are two critical issues for IRPF that must be addressed when connecting the executable and defective parts. In order to ensure normal operations, it is crucial to accurately identify actions that are no longer feasible and separate them from the established plan. The other issue is dealing with the conflict between repair and operations. Since there are limited resources onboard, and spacecraft actions are durable, concurrent, and resource-dependent, the operational process may require the same type of resources as the plan-repair process, destroying the initial conditions and resulting in chaos during the repair process. Besides this, it is time-consuming to decide on a recovery plan. Moreover, the execution of activities constantly changes the spacecraft’s status while it is undergoing repair. Therefore, it is difficult for plan repair to choose an appropriate initial state to start its work.

To overcome the challenges outlined above, we propose a bi-loop recognition method for the accurate identification of all invalid actions according to a causal analysis. As failed actions are stripped from the pre-designed plan, the spacecraft can resume the execution of the remaining executable actions. The broken plan could then be fixed during the partial execution of the failed plan. Furthermore, to deal with the competition between operations and repair, a multi-factor regulatory repair method is proposed for the development of a feasible recovery plan. Test results show that IRPF works well; it enables the spacecraft to quickly identify unavailable planned actions, obtain a feasible plan that can be put into use rapidly, and repair invalid actions during operations.

This paper is organized as follows: Section 2 presents some related work; Section 3 defines the plan-repair problem and outlines the structure of IRPF. Then, the following two sections describe methods for isolation and repair, respectively. Several experiments in the next section evaluate the effectiveness of IRPF, and a corresponding discussion is presented. The last section summarizes and outlines future research lines.

2. Related Work

Modern spacecraft operate on a fault-tolerant system supported by a Fault Detection, Isolation, and Recovery (FDIR) module. When something goes wrong with devices onboard, FDIR can detect the problem and replace the damaged equipment with redundant backup equipment [9]. However, these measures are designed for the health and stability of the spacecraft, not for the mission’s success. A spacecraft plan is responsible for guiding the space vehicle to achieve its mission goals, and is always pre-designed and stored onboard. A plan is a course of action for achieving goals, while FDIR usually studies the damage and repair of hardware. When a plan failure happens in the uncertain space environment, not necessarily caused by damaged hardware, the spacecraft cannot fulfill all its tasks until a proper plan is uploaded from ground control.

Onboard planning can actively pursue possible solutions instead of passively waiting for ground control to meet missing goals [10]. Deep Space 1 (DS-1) is the first fully autonomous spacecraft [11] orbiting the world; it generates its daily operations and responds to anomalies without human interference based on the framework of the Heuristic Scheduling Testbed System (HSTS) [12]. It separates planning and execution and follows the principle of planning before execution. When an exception happens, the spacecraft has to pause its operations and wait for a new plan from the planner, resulting in the possible loss of valuable phenomena such as volcanic eruptions. To overcome this, continuous planning, which interleaves planning and execution [13], is widely used in practical applications [14,15,16,17]. In this way, even if the plan is not generated in its entirety, the actions committed to its execution can be carried out.

Ponzoni Carvalho Chanel et al. [18] proposed a flexible algorithmic framework called AMPLE (Anytime Meta PLannEr) for the support of continuous planning in robot applications. In AMPLE, there are two parallel threads: the planning thread, as a server, responds to planning requests and outputs planning results for a certain amount of time, and the execution thread, as a client, generates planning requests according to the current execution status and the future evolution of the system. A probabilistic model is used to anticipate the next execution state, forming belief states for next-stage planning in order to provide possible initial states. However, AMPLE cannot deal with concurrent actions and is restricted to simple action execution schemes.

When a plan failure happens, Cashmore et al. [19] have considered replanning in the context of plan execution. They used timed initial literals (TILs) to capture the effects and conditions of non-interruptible actions and the ability of the output of the “bailout action generator” to replace failed interruptible actions. After that, the replanning problem was framed as a situated temporal planning problem and could be solved by the already existing situated temporal planning method [20]. Nevertheless, their approach only dealt with a particular execution segment rather than continuous execution, and discarded the remainder of the original plan.

Fickert et al. [21] studied methods for the determination of the initial state of a new plan search during a continual online planning task. They proposed the multiple initial state technique (MIST) for dealing with the replanning of a newly generated goal during the execution of the original plan. MIST samples a set of potential states called “reference states” in uniform intervals from the executing plan to serve as initial state speculations for replanning. If a solution is not found when the next reference state is executed, the previous planning efforts will be abandoned, and the initial state will be replaced with a new reference state for searching. Besides this, MIST designs a time-aware evaluation expression to prioritize nodes in the search process, considering both the time consumption of the planning process and the makespan of the resulting plan. However, because actual actions are durable and resource-dependent, it is not easy to predicate the content of reference states according to a time uniform distribution.

Compared with planning or replanning, plan repair is more prevalent in plan failure handling due to its shorter solution time [22,23]. There is much research work on plan repair in the literature, which can be roughly divided into five categories [24]: the rule matching method [25], the local adjustment method [26], the unrefinement and refinement method [27], the state transition method [28] and the new problem construction method [29,30]. However, most of these seem to assume that the agent keeps static when resuming the failed plan, which is discontinuous. The agent has to stop its execution and wait for the generation of a recovery plan whenever a plan failure happens. Therefore, it is imperative to research the plan-repair problem of spacecraft while executing durable, concurrent, and resource-dependent actions.

3. Preliminaries

3.1. Plan-Repair Problem

Like replanning, plan repair is also a reasoning process about a course of action, i.e., a plan, for achieving a set of goals under assigned constraints. The difference lies in that replanning starts from scratch, while plan repair is based on an existing plan. Moreover, the reasoning process is based on actions abstracted from reality.

Definition 1

(operator).An operator o is an action framework without instantiated parameters, which can be expressed as o = <n(o), p(o), d(o), p_re(o), e_ff(o)>, where n(o) represents its unique name, p(o) includes its parameters, and d(o) shows the duration time of o, while p_re(o) indicates the mandatory requirements for execution, and e_ff(o) describes how o changes the world after completion, including positive effects $e_{ff}^{+}(o)$ and negative effects $e_{ff}^{-}(o)$.

A durable operator can be divided into three parts for capturing information at different times: a beginning part $o_{\to }$, an intermediate part $o_{\leftrightarrow }$, and an end part $o_{\leftarrow }$. $o_{\to }$ is described by the conditions and immediate effects of the starting action part, while $o_{\leftrightarrow }$ usually contains the persistent conditions and $o_{\leftarrow }$ covers the preconditions and final effects of the end of the action.

Definition 2

(plan).A plan$P=\{a_1,a_2,\cdots ,a_n\}$is a time-ordered set of instantiated operators, i.e., actions. For any action a in P, it can be expressed as$a=\{n_a,t_a,p_a,d_a\}$, where$n_a$refers to its unique name,$t_a$shows when it starts the operation,$p_a$gives its parameters, and$d_a$specifies its duration time.

When put into practical use, the derived plan is fragile and cannot adapt to the uncertain space environment and anomalous events, such as an abrupt storm or a failure of the magnetorquer, which indicate a plan failure. In such a case, we can define the plan-repair problem as follows:

Definition 3

(plan-repair problem).A plan-repair problem$\mathsf{\Pi }$is a six-tuple, i.e.,$\mathsf{\Pi }=\{P,F,V,O,I_{\mathsf{\Pi }},G_P\}$, where,

–

P is the failed plan.

–

F is a set of Boolean propositions that qualitatively describe the relationship between objects in the spacecraft system. The value of any element in the set is either true or false. In the proposition (on_board cam sat), for example, it shows whether the camera cam is installed on the spacecraft sat.

–

V is a set of numerical fluents that quantitively describe the relationship between objects in the spacecraft system. As an example, the fluent (=(fuel sat) 500) indicates that there are 500 units of fuel on the spacecraft sat.

–

O contains uninstantiated operations that model the way that the spacecraft changes the world and its effects.

–

$I_{\mathsf{\Pi }}$depicts the spacecraft’s state when P fails. It is represented by a subset from F, which is true in that state, and an assignment of real values to all the numeric fluents in V.

–

$G_P$depicts the mission goal that has not yet been achieved.

Then, plan repair is a method for the synthesis of a series of operators from O and their instantiation under the constraints of F and V so that the space vehicle can reach the goal state $G_P$ from the specified initial state $I_{\mathsf{\Pi }}$. After a recovery plan is given, its executability can be verified and validated by checking the constraint satisfiability of all the planned actions, which is integrated into the tool VAL [8].

3.2. Structure of the Isolate and the Repair Plan Failure Method

To facilitate the recovery of the damaged plan while remaining operational, the executable parts whose conditions are all met should be selected from the failed plan to continue their work. A plan-repair method can then be applied to the inexecutable parts. Our proposed method IRPF has a structure as shown in Figure 1. At first, based on the causal analysis between the spacecraft state and the established plan, IRPF separates executable actions and inexecutable actions from the failed plan. Then, under the consideration that the executable parts may change the initial state of repair, IRPF tries to solve the plan-repair problem while remaining operational. After a recovery plan is given, actions not performed in the executable part are merged with the recovery plan. After that, the failed plan can be updated into a new feasible spacecraft plan. Since the update step is relatively easy, this paper ignores it and focuses on isolation and repair.

4. Isolation of Defective Actions by the Bi-Loop Recognition Method

It is necessary to diagnose whether a plan failure is caused by abnormal spacecraft functions, environmental changes, or a combination of the two if a space vehicle cannot perform its intended actions while remaining operational [31,32]. However, it is not within the scope of this study to diagnose whether the spacecraft’s function is abnormal. Thus, this paper assumes that all plan failures are caused by the environment, which means that when the plan failure occurs, all functions of the spacecraft are normal, and the failure is because the execution conditions of the action are no longer satisfied. Then, defective actions can be analyzed from the spacecraft’s state after a failure by inspecting the causal relationship between actions in the failed plan. In addition to the explicit causality between action execution and spacecraft state, there is also a causal relationship between limited onboard storage and resource consumption caused by alternate operations. Therefore, a bi-loop recognition method was designed which first verifies the execution conditions of a single action and then forms a plan in order to separate all defective actions from the failed plan.

The bi-loop recognition method can be found in Algorithm 1. It takes a failed plan and the system state after failure as the input, and outputs executable actions, defective actions, and the corresponding open conditions caused by environmental changes. Considering that the execution conditions of spacecraft actions include not only logical conditions (e.g., the camera needs to be calibrated before imaging operations) but also numerical conditions (e.g., the power onboard needs to be greater than a certain value for imaging operations); therefore, there are two successive for loops in this algorithm. The first loop is designed from both logical and numerical conditions to validate the availability of a single action in the pre-designed plan under the failure state (lines 2–9). In the second loop, to further identify the resource shortage problem caused by alternate operations, numerical conditions are taken into account to determine defective actions (lines 10–16).

In the first loop, it is straightforward to judge the feasibility of an action according to the satisfaction of its logical and numerical conditions. However, for actions in the failed plan, their logical conditions can be provided not only by the environment but also by the actions scheduled before it. Therefore, actions whose logical conditions cannot be supported by the environmental state or by their previous actions can be considered defective (lines 3–4). On the other hand, those individuals whose conditions are met are considered executable (line 7).

Note that an operator is divided into three parts: the beginning, the intermediate part, and the end. It is essential to check conditions in order to determine whether a part is available in a specified situation. Since the three parts are consecutive and jointly represent an action, if the conditions of any of the three parts are not met, the action cannot be completed. As a result, when evaluating the condition satisfiability of the beginning part, the conditions of all the three parts should be considered together. Similarly, when evaluating the condition satisfiability of the intermediate part, the conditions of the end part should also be considered.

The continuous execution of consumable actions may exhaust the limited resources onboard. Therefore, actions without sufficient resources in the executable action set are filtered out and put into the affected action set in the second loop. To this end, the resources consumed by operational actions (not the real consumption value but the estimated consumption level in the model) are accumulated to the level of resources required in the current state and settled. When resources generated for the next activity are not sufficient, the next activity is deemed defective (line 11). In this process, resources are assumed to be step resources: the resource conditions for the action are required in its beginning and intermediate parts, while the actual consumption of resources occurs during the end part.

It is easy to determine which conditions of an action are not satisfied in the current state during the whole verification process. These unsatisfied conditions are stored and regarded as open conditions (line 5 and line 13) for providing attainable goals for subsequent repair work. After this, with these actions identified as defective and executable, the spacecraft can selectively execute them without affecting the overall continuity.

Algorithm 1 Bi-loop recognition of defective planned actions
Input: a failed plan P and current system state S
Output: affected actions Ai and their reasons R, executable actions Ae
1.	$A_i\leftarrow \varnothing$, $R\leftarrow \varnothing$, $A_e\leftarrow \varnothing$
2.	for action a in P do    $⊳$ Availability of an action
3.	if the logical conditions of a cannot be satisfied by S and previous scheduled actions in P, or the numerical conditions of a cannot be met by S, then
4.	$A_i\leftarrow a$
5.	$R\leftarrow$ gather the unsatisfied conditions of a
6.	else
7.	$A_e\leftarrow a$
8.	end if
9.	end for
10.	for action b in Ae do     $⊳$ Availability of a course of action
11.	if the application of b and its previous actions in Ae under S results in insufficient resources, then
12.	$A_i\leftarrow b$
13.	$R\leftarrow$ gather the unsatisfied conditions of b
14.	$A_e\leftarrow$ remove b from Ae
15.	end if
16.	end for
17.	return Ai, R, and Ae

5. Multi-Factor Regulatory Repair

With the support of a planning algorithm, the spacecraft can autonomously obtain a course of action, i.e., a plan, under a given initial state and goal state. However, when the spacecraft cannot perform all planned actions, it is difficult to determine the optimal initial state and goal state for plan repair in advance. The reason is fourfold:

(1)

Planned actions are concurrent. The executed actions will change the spacecraft’s state and affect the occurrence time of the recovery actions. For example, the data transmission and imaging operations in Figure 2 depend on the effects of the respective previous turning operation. So, before repairing them, it is necessary to determine where the spacecraft is pointed.

(2)

Planned actions are resource-dependent and arranged with limited resources. As a result, the resources change with the execution of actions, limiting the repair action’s selection and use.

(3)

Both executed processes and the plan-repair process take time. Suppose a solution is not found before the selected initial state is reached. In that case, the subsequent recovery plan based on the expired initial state will no longer be applicable, which will require a new round of plan repair.

(4)

In addition to mission goals, open conditions of planned actions could also serve as repair goals. Furthermore, improper goal selection will waste plan-repair efforts and increase the repair workload.

5.1. Factor Estimation

Plan repair is time-consuming. Before a repair takes effect, it is necessary to estimate the solvability of the repair problem. In general, it is enough if the goal is reachable. However, this is not the case for repairs carried out during operations. While actions are executed, the spacecraft’s state changes all the time. Therefore, the plan-repair problem is dynamic. The solvability of the problem cannot be judged simply by the goal reachability. To this end, a time limit factor $\mathsf{\Delta }t$ and a time tolerance factor $t_r$ are designed, along with the goal reachability factor h.

The value is calculated heuristically for h, the distance estimation between the specified goal state and the selected initial state. In this paper, a relaxed heuristic called a Temporal Relaxed Planning Graph (TRPG) [33] was used to address the fact that spacecraft activities are durable, concurrent, and resource-dependent. Then, the length of the relaxed plan given by TRPG was used to acquire the distance estimation.

For $\mathsf{\Delta }t$, which stands for the maximum time limit for plan repair, its value is defined by the time difference between the failure and the selected initial state. If there is no recovery plan in the chosen initial state, a new possible initial state takes over, and the value of $\mathsf{\Delta }t$ is updated accordingly.

For $t_r$, which represents an estimation of the time taken to repair, the following equation can give its value based on a phenomenon called search vacillation [34], where there is a gap between the node generation and node expansion.

$$t_r=h\cdot \overline{t}\cdot d$$

(1)

where $h$ is the goal distance estimation, $\overline{t}$ is the average expansion time of each step, and $d$ is the average number of state nodes between node generations and its corresponding expansion, which is called “expansion delay” in [34].

Considering all of the above factors, only if there is a possible solution and enough time can a repair search be carried out, to reduce unnecessary search time. Otherwise, the repair search process is rendered meaningless due to the fact that a suitable solution cannot be found within a limited time.

5.2. Searching for a Recovery Plan

The spacecraft’s state changes while executing the executable part of a failed plan. Moreover, plan repair is time-consuming. Therefore, the initial state of the plan-repair search should be selected from the future state of the spacecraft. Besides this, multiple inexecutable actions produce different open conditions that can be potentially repaired. Despite this, not all of these actions will be used to restore operations, so reasonable strategies should be developed for determining a repair goal. As soon as an initial state and a goal state have been determined, the forward search mechanism is used to determine a recovery plan between the two states.

A predicated state candidate set from the executable part is extracted chronologically to represent possible plan repair initial states. In particular, it is extracted neither at the end of a failed action (e.g., I₀ in Figure 2) or an incomplete action (e.g., I₁ in Figure 2), nor at the boundary of an unexecuted action (e.g., I₂ and I₃ in Figure 2, respectively). There are logical and numerical elements in the state representation, and resources are expressed in a numerical form and are assumed to be step resources. By aggregating the effects of the actions that end at the same time, the state of the next execution can be determined from the state of the last execution. In this way, a queue of future execution state estimations is obtained, which constitutes the possible initial states for plan repair.

For the goal state of the plan repair, a candidate set of expected states are extracted from defective actions to provide available repair goal references. This either gathers the effects of actions that have started but not finished (such as G₀ in Figure 2) or collects the conditions of actions yet to be executed (such as G₁ and G₂ in Figure 2). As planned actions are executed in succession, if only the conditions of one defective action are taken into consideration during repair, an operational failure may occur again if the conditions for the next action are not met—even if the repair succeeds. Thus, the conditions for all subsequent defective actions need to be considered when developing a repair goal. By preserving the precedence links between each defective action in the failed plan, we construct multiple repair goals in accordance with the execution order in the failed plan—such as G₀–G₂ in Figure 2—so that even if the last goal cannot be reached, other options are still available.

Moreover, a state may contain many elements that have no relation to plan repair. For example, when adjusting the attitude pointing of the spacecraft, the status of the inertial navigation device is irrelevant. Thus, if the whole expected state is regarded as a goal for repair, the repair efficiency will undoubtedly be reduced due to the additional search for meaningless parts of the state. We can increase the efficiency of the plan repair by replacing the defective actions’ conditions with the open conditions from the last section when building repair goals.

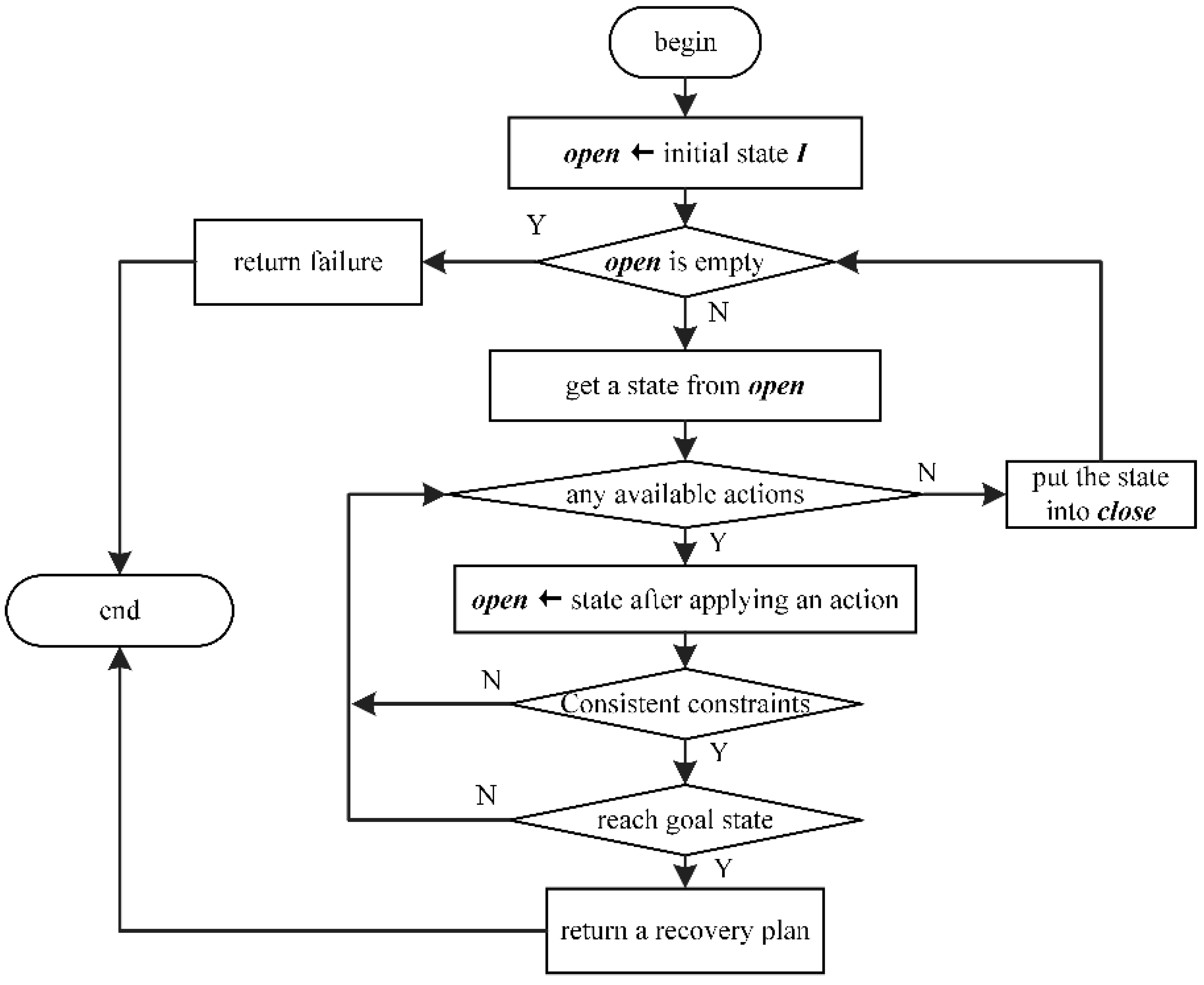
As shown in the planner POPF2 [35], a forward search manner is adopted after the determination of an appropriate initial state and goal state for plan repair. This manner realizes state transition by repeatedly searching for available actions and applying them until all constraints are consistent and the goal state is reached, as shown in Figure 3. States in the search process are collected in two sets: open and close. States to be extended are collected by the set open, while states that have been extended are in the set close. Each search cycle begins with an element from the set open and ends with a state in the set close, after it has been applied. In each cycle, the priority of the elements in the set open is determined by the TRPG heuristic. The state with the minimum evaluation value in the set open, which is the closest to the goal state, has the highest priority.

Recall that repair goals are a chronological set of preconditions or effects that contain the open conditions of all subsequent defective actions. In TRPG, when backtracking, the heuristic values of all subsequent repair goals can be obtained at once when estimating the goal distance for the action with the earliest execution time, thereby reducing the time consumed by frequent heuristic calls. However, time continues to run out while searching for a recovery plan. Within the time limit, if a recovery plan cannot be found to resume the broken plan, the selected initial state will become unsuitable and will no longer be applied. Afterward, a new initial state or a revised goal state should be chosen for a potential repair search.

5.3. The Algorithm for Multi-Factor Regular Repair

When defective actions are not to be executed, the state evolution of the spacecraft depends on the executing component. Moreover, the system state determines a repair plan, including its contents and corresponding start times. In our opinion, it is better to obtain a feasible recovery plan and update the old plan before performing the following executable actions. If such a recovery plan does not exist, a new initial state is established until the repair solution is discovered or the executable part is completed. To find a feasible solution in such a complex situation, a limited search algorithm is developed. The limitations contain three factors, which can be found in Algorithm 2.

Algorithm 2 Multi-factor regulatory repair
Input: defective actions Ai and their reasons R, executable actions Ae
Output: a recovery plan PR
1.	$P_R\leftarrow \varnothing$
2.	calculate the possible initial states set IS from Ae
3.	for a state S in IS, do
4.	$\mathsf{\Delta }t\leftarrow$ the time span between the failure and S   $⊳$$\mathsf{\Delta }t$: time limit
5.	for action {a} that co-occurs in Ai do
6.	G $\leftarrow$ gather the open conditions of all actions no earlier than {a}
7.	$h\leftarrow$ get the distance estimation from S to G $⊳$ goal reachability
8.	if h < 0 then
9.	continue
10.	end if
11.	$t_r\leftarrow$ estimate the time taken to repair
12.	if $t_r$ > $\mathsf{\Delta }t$ then       $⊳$ time tolerance
13.	continue
14.	end if
15.	PR $\leftarrow$ search for a path from S to G
16.	if PR is not empty
17.	return PR
18.	end if
19.	end for
20.	end for
21.	return PR

Algorithm 2 calculates the possible initial states and goal states of the plan repair by taking the result of Algorithm 1 as the input. It then attempts to find a way to link them, and if such a path exists, it outputs a recovery plan. If the goal is judged to be unreachable (lines 8–10) or the repair time exceeds the maximum time limit (lines 12–14), the selected initial state or goal state is not appropriate. Otherwise, the forward search method finds a path from the specified initial state to the chosen target state (line 15). The algorithm outputs a meaningful result only when there is a non-empty recovery plan (lines 16–18).

6. Experimental Evaluation and Discussion

6.1. Setup of the Experiment

To validate the proposed approach for resuming a failed spacecraft plan, we selected two typical mission scenarios, a satellite system and a multi-rover system, as test domains. While rovers are more concerned with ensuring sufficient energy supply for daily activities, satellites are more constrained by time window constraints such as communication and observation windows. Both are modelled in the Planning System Definition Language (PDDL) 2.2 [36] that originated from the International Planning Competition (IPC). The tests were based on a pre-calculated plan given by a planner.

To simulate possible failures, the spacecraft’s state was manually changed at different time instants of the existing plan, including lost facts, altered resource levels, and their combination. Formally, a plan failure can be described as f = <t, e> where t indicates the time at which the failure happens and e signifies the nature of the failure. For example, f₁ = <10.5, (not (camera_calibrated cam))> represents the state at t = 10.5 s in which the camera cam is not calibrated. f₂ = <100, (< (fuel sp) 20)> indicates that less than 20% of the total fuel of the spacecraft sp is available at t = 100 s. When the spacecraft’s state is modified, the operational environment of the planned actions is changed. IRPF then strips inexecutable actions from the infeasible plan and searches for a recovery plan under various constraints, including resource limitations, deadlines, and the precedence order of actions when part of the existing plan is executed.

We implemented our method IRPF based on the POPF2 planner [35] and compared our approach to three other methods:

(1)

Replanning from a static state where all activity executions are stopped immediately after a failure (Replan is used to refer to this method from now on. We reused POPF2 with no modification to implement it).

(2)

Replanning from a dynamic state where all activities in progress are finished and new actions are forbidden after a plan failure (ReplanDynamic is used to refer to this method from now on. It is the same idea as Cashmore [19], but we implemented it on POPF2).

(3)

Repairing without isolation and continued operability (CommonRepair is used to refer to this method from now on. It regards the modified state as the initial state of plan repair and acquires the goal state for recovery by regression of the remaining plan. The same idea as Guzman [28], but we added the processing of durable, concurrent, and resource-dependent actions. We also implemented it on POPF2).

We set up a variety of test problems on which to run the above methods. The problems cover all three types of plan failures: lost facts, altered resource levels, and their combination. Additionally, we established two metrics to evaluate the performance of the different methods: One was the total time taken to perform the process from outage to recovery after a plan failure. For simplicity, we assume it is approximately the period between a plan failure and an updated plan. The other was the search performance achieved when synthesizing a solution, represented by search time and the number of explored state nodes.

We ran all the tests on a laptop (Intel Core i5-4200 CPU @ 1.60 GHz) with a time limit of 600 s and no memory limit (the computer had 8 GB of RAM). The test results of each of the problems were the average values of three trials, taken as the statistical value.

6.2. A Satellite

The satellite can turn itself in order to perform several observational tasks with varying slew times and calibration times, with a limited data capacity and observation time window constraints, and transmit the acquired image data back to the ground station during the data transmission window. The results of the run time (in seconds), the search time for a recovery plan (in milliseconds), and the number of explored nodes are shown in Figure 4.

As we can see in Figure 4a, regardless of the type of input plan failure, i.e., lost facts, altered resource levels, and their combination, both repair methods were effective in resuming the execution of the spacecraft, extending fewer nodes and solving the problem in a shorter time than replanning methods. Especially for the 6th, 8th, 15th, 17th, and 20th scenarios, both replanning methods failed to solve them in the limited solving time, i.e., 600 s. In contrast, both methods of repair produced a recovery plan quickly. Plan repair consists of searching for the missing action sequence in order to connect the failure state to the established plan. However, replanning entails creating a new plan to achieve mission goals. Consequently, plan repair generally has a relatively simple goal with a shorter path length, resulting in a shortened run time for resumed operability and fewer explored nodes than with replanning.

A revised plan is urgently required for spacecraft to continue achieving their mission goals following an operational failure. Instead of waiting for a recovery plan before resuming operations, IRPF quickly identifies the actions not affected by the failure so that the spacecraft will not be interrupted for too long. For clarity, we divided the run time of IRPF into two parts: IRPF (isolation) for identifying executable planned actions and IRPF (repair) for finding a recovery plan during dynamic operability. As shown in Figure 4a, the average operational recovery time of the spacecraft in IRPF (IRPF (isolation)) was much shorter than the other three compared methods.

Under the changing spacecraft state, IRPF is able to devise a recovery plan based on the execution of unaffected actions. As shown in IRPF (repair) in Figure 4a, although IRPF took a slightly longer time than CommonRepair to solve most problems, the difference in time was not overwhelming. This is reasonable because compared with CommonRepair, the initial state of IRPF is not fixed. As a result, IRPF then has to take additional time to predict the future state of the spacecraft based on the executing actions. Nevertheless, the longest-run time of IRPF (repair) is less than 1 s, which is shorter than the duration of all actions in the spacecraft system. Thus, IPPF can output a new feasible plan before executing actions are complete. However, CommonRepair may not be able to provide an effective solution in time. For example, the solution times for problem 6 and problem 15 were 3.984 and 4.982 s, respectively—considerably longer than those of IRPF.

When part of the plan is executed, there are multiple initial and goal states of repair. In order to evaluate the rationality of the design of multiple regulatory factors such as time limits and time tolerance, we depicted the search time actually spent on determining the repair solution in Figure 4b and the number of expansion nodes during searching in Figure 4c. As can be seen from the figures, IRPF has a shorter search time, and fewer expanded nodes than other methods, which shows that unnecessary searching is avoided by using the regulatory search.

To view the performance results in Figure 4 more intuitively, the results are summarized statistically in

Table 1. Summary of statistics for the performance of different methods in the satellite system.

Methods	Run Time (s)		Search Time (s)		Explored Nodes
	${\mathit{\mu }}^1$	${\mathit{\sigma }}^2$	$\mathit{\mu }$	$\mathit{\sigma }$	$\mathit{\mu }$	$\mathit{\sigma }$
IRPF	0.017045	0.00678	0.006141	0.005627	17.25	17.678
CommonRepair	0.472188	1.38177	0.46785	1.374523	899.85	2626.195
Replan	151.8533	265.4573	- 3	-	1519.13	427.035
ReplanDynamic	151.7658	265.512	-	-	1519.13	427.035

¹ The average of all test problem results. ² The standard deviation of all test problem results. ³ Since the run time of replanning is much higher than that of plan repair, we are not interested in its search time, so here it is vacant.

. According to the data, our proposed method, IRPF, performs admirably across a range of dimensions. The data also supports our above analysis. That is, (1) in both metrics, the performance of plan repair was significantly better than replanning; (2) our method, IRPF, output a recovery plan more quickly; (3) IRPF avoided extensive search processes by expanding fewer nodes and conducting searches over a shorter period of time.

6.3. A Multi-Rover System

When a spacecraft resumes operability in a previous system, it either repeats a failed operation, develops a recovery plan in order to reach the subsequent repair goals, or resupplies insufficient energy, which is completed by itself. To evaluate the performance of IRPF in multiple vehicles, we designed some test problems from multi-rover systems in IPC. There are three rovers in the system; each can independently traverse the surface of Mars, take pictures in different modes such as color, high, and low resolution, recharge, collect soil and rock samples, and transmit all the exploration data back to the lander. All these system operators are durable and resource-dependent. Results are shown in Figure 5 and

Table 2. Summary of statistics for the performance of different methods in the multi-rover system.

Methods	Run Time (s)		Search Time (s)		Explored Nodes
	$\mathit{\mu }$	$\mathit{\sigma }$	$\mathit{\mu }$	$\mathit{\sigma }$	$\mathit{\mu }$	$\mathit{\sigma }$
IRPF	0.041915	0.047918	0.035936	0.049353	76.65	95.4354
CommonRepair	0.113925	0.084681	0.087426	0.067032	232.4	164.6513
Replan	95.00949	224.1889	-	-	1952.273	3462.318
ReplanDynamic	70.90196	199.1456	-	-	301	303.6852

.

Recovery plans indicate that other rovers can complete the original mission objectives if a rover is unable to fulfill them. The statistics in Table 2 show that IRPF outperforms the other three comparison methods in terms of both these test metrics. Regarding the run time of the methods when generating a solution, we can see in Figure 5a that IRPF took less time to identify available actions in the failed plan than the run time of CommonRepair. However, its time taken to recover defective actions was slightly higher than CommonRepair in some cases (e.g., problem 1, 2, 3, 5) and lower in other cases (e.g., problem 4, 8). Nevertheless, the average total run time of IPRF was one order of magnitude less than that of CommonRepair, and three orders of magnitude smaller than that of the two replanning methods. As for the search performance, it can be seen from Figure 5b,c that IRPF had a greater advantage in the execution of the plan—especially when the plan was about to be completed (e.g., problems 15–20). This is reasonable because when a failure happens before the execution of the plan, the repair goal of the IRPF is more complicated than that of CommonRepair; the supporting conditions of the defective actions stripped from the plan are no longer met by the environment or by previous executable actions. IRPF then has more open conditions than other methods, which results in more nodes being explored and longer repair search times. However, during the execution process, especially when the plan is about to end, IRPF’s repair goals become almost the same as CommonRepair. At the same time, the initial state of IRPF is closer to the goal because it is extracted from the evolution of executable actions. In this case, IRPF has a shorter search time and fewer exploration nodes.

It is worth noting from Table 2 that in the test problems, ReplanDynamic had fewer explored nodes and lower run times than Replan on average. This confirms the conclusion drawn in [19] that multi-agent replanning is more advantageous if the expected effects of the action that has started but not been completed is taken into consideration. Nevertheless, it is still less efficient than plan repair. Besides this, the two replanning methods cannot output a solution for some problems, e.g., problems 7 and 14, within the limited solving time—but the two plan-repair methods can. This is because in comparison with the long-distance search performed during replanning, the state difference between the initial state and the goal state is minor, and the length of the solution is shorter, so that the recovery plan can be found in a limited time.

6.4. Discussion

The results of the two above test domains demonstrate that plan repair performs better than replanning in dealing with plan failures, regardless of whether replanning is undertaken from a static state or from the effects of unfinished actions. Compared with the non-isolated version of the repair method CommonRepair, our proposed method, IRPF, has a lower run time for resuming the execution of missing goals, and is capable of completing searches in a shorter time, with fewer explored nodes.

Although there are many plan-repair methods in the literature, they do not explain how they can be applied to the real world. In these cases, it appears that the agent will not be able to proceed until the repair plan has been provided. As such, the agent will not operate continuously but intermittently. In light of the fact that spacecraft have a variety of subsystems, this study proposes a method, IRPF, of repairing them in terms of plan failures. Through this method, the spacecraft can continue to operate while undergoing repair work. To take this method one step further, the CubeSat, with its low cost and short development cycle, can serve as a technical demonstration tool. When combined with the reliability design method [37,38], CubeSat can carry out space missions such as Earth science [39] and deep space exploration [40]. As such, we believe that this method can enhance the use of plan repair in practice.

In contrast to the common method of repairing from a fixed initial state, the IRPF method must take into account the impact of executable activities on state evolution in order to extract the initial state from a predictable future, which means that the initial state of IRPF is not fixed. Moreover, as time passes during the repair process, the system state continuously changes, causing a sense of urgency; the repair work must be completed before the predicted initial state. Otherwise, this initial state will become unsuitable, and the newly found plan will no longer be applicable. As a result, the initial state of IRPF is dynamic as well.

However, our approach has some limitations. Firstly, the prediction of the system state is based on the established plan without consideration of the impact of dynamic changes in the surrounding environment. As a result, our method cannot be applied in environments with high dynamic uncertainty, such as the descent and landing on Mars. A possible solution would be to consider the dynamic establishment and prediction of the environmental model in conjunction with the spacecraft model in order to provide a more accurate prediction state for repairs. Secondly, our method only accounts for a single decision center. Even with multi-rovers, this method is also centralized, which limits its application to distributed agents, which require negotiation and cooperation. Decoupling a joint multi-agent, splitting it into independent agents, and then using our method for repairs may be a solution.

7. Conclusions

It is challenging to ensure the success of a pre-designed plan in the uncertain space environment. In this paper, a novel plan-repair method, IRPF, is proposed for plan failures of spacecraft in the process of continuous operability. There are two main contributions to this paper: Firstly, by splitting the failure plan according to causality, IRPF identifies predictable initial states of repair from executable actions in the plan. Secondly, IPRF uses the three regulatory factors of goal reachability, time limits, and time tolerance to estimate repair costs. This reduces the probability of repair failure due to the fact that the predicated initial state is no longer applicable due to the execution of the ongoing actions.

The empirical evaluation of our approach indicates that, compared with other methods including replanning and plan repair, IRPF allows spacecraft to resume operations more quickly and generates a feasible recovery plan while the spacecraft is operating. Besides this, our approach avoids extensive search processes by expanding fewer nodes and conducting searches over a shorter period of time.

It should be pointed out that our method predicts the future state of the spacecraft system according to the executable actions in the established plan. Therefore, the application environment of this method cannot be highly dynamic. In future work, we will investigate how to popularize our method through the modeling and analysis of changes in the environment, as well as the impact of such changes on the system.