Abstract
One of the most critical regulatory issues related to supersonic flight arises from limitations imposed by community noise acceptability. The most efficient way to ensure that future supersonic aircraft will meet low-noise requirements is the verification of noise emissions from the early stages of the design process. Therefore, this paper suggests guidelines for the Landing and Take-Off (LTO) noise assessment of future civil supersonic aircraft in conceptual design. The supersonic aircraft noise model is based on the semi-empirical equations employed in the early versions of the Aircraft NOise Prediction Program (ANOPP) developed by NASA, whereas sound attenuation due to atmospheric absorption has been considered in accordance with SAE ARP 866 B. The simulation of the trajectory leads to the prediction of the aircraft noise level on ground in terms of several acoustic metrics (LAmax, SEL, PNLTM and EPNL). Therefore, a dedicated validation has been performed, selecting the only available supersonic aircraft of the Aircraft Noise and Performance database (ANP), that is, the Concorde, through the matching with Noise Power Distance (NPD) curves for LAmax and SEL, obtaining a maximum prediction error of ±2.19%. At least, an application to departure and approach procedures is reported to verify the first noise estimations with current noise requirements defined by ICAO at the three certification measurement points (sideline, flyover, approach) and to draw preliminary considerations for future low-noise supersonic aircraft design.
1. Introduction: Background and Motivation
The recent rise in environmental concern and renewed interest in supersonic flight has involved intense scientific activity that aims to realize a new generation of sustainable supersonic aircraft [1,2,3,4,5,6,7].
More than two decades ago, the Concorde project brought about a heated debate on the environmental impact of SST [8], which has led to the need for new Standards and Recommended Practices (SARPs) to ensure social acceptability for the next generation of supersonic aircraft [9]. Currently, the International Civil Aviation Organization (ICAO) Committee on Aviation Environmental Protection (CAEP) is cooperating with industries and research institutes to define a specific regulation for SST, allowing the certification of supersonic aircraft in the 2020–2025 time-frame [10].
Specifically, one of the most controversial and least accepted features of Concorde was the high community noise level around the airports, due to the higher thrust, jet speed and lift-off speed required for taking-off [11]. For this reason, one of the indispensable premises for the design of low-noise future supersonic aircraft is the integration of break-through technologies and flight procedures aimed at reducing noise, especially during LTO operations. To ensure that future supersonic aircraft will meet low-noise requirements, it is essential to move LTO noise evaluations up to the early stage of the design process. This will imply a paradigm shift in conceptual design towards a design-to-noise approach, including the integration of noise reduction measures together with preliminary evaluations of their impact on the overall aircraft configuration. Therefore, it will guarantee a significant saving in resources (time and money) and will avoid the generation of new aircraft concepts, which might not be socially acceptable.
To support this approach, this paper focuses on the application of a methodology aiming at predicting noise levels emitted by a supersonic aircraft during LTO operations since pre-conceptual studies (pre-phase A [12]). As a result, this approach will provide guidelines for the LTO noise assessment of future supersonic aircraft in conceptual design.
The supersonic aircraft noise model developed relies on the already existing extensive research about semi-empirical and parametric noise source models to assess aircraft noise, enabling a fast noise prediction within the design process. Since the 1970s, NASA Langley Research Center has started the development of the Aircraft NOise Prediction Program (ANOPP) [13], the first computer program with noise prediction capabilities integrable into the preliminary design process. Nowadays, many comprehensive similar tools have been developed by research institutes, such as the Parametric Aircraft Noise Analysis Module (PANAM) [14] and CARMEN [15]. A brief description for each of the already available tools is given below:
- One of the major applications of ANOPP has been to support the Supersonic Cruise Research (SCR) project at Langley, while the next application has been in conjunction with the Federal Aviation Administration (FAA) study to determine the economic and technological feasibility of noise limits for future supersonic transport [16]. The purpose is a high-fidelity system noise prediction along arbitrary flight paths, ANOPP embeds models for sound propagation, including the effects of the atmosphere and terrain, the installation effect, scattering and shielding. Over the years, the tool has been maintained and updated, including the ongoing development of new methods, essential for a more accurate physics-based prediction. Hence, in 2011, NASA announced the ANOPP2 release, which provides a modern prediction environment with a flexible framework meeting the needs of the future unconventional aircraft noise studies [17].
- PANAM has been developed by the German Aerospace Laboratory (DLR) to integrate noise prediction within the aircraft conceptual design and to support decision-making processes towards low-noise designs. Differently from ANOPP, the current version is only applicable to conventional tube-and-wing aircraft concepts [18]. However, PANAM uses proprietary source models for airframe noise, which are based on real modern aircraft [19]. Major aircraft noise components are modelled stand-alone, neglecting interactions. Sound propagation and convection effects are directly applied to the emitting noise source, to be more representative of the actual flight operating conditions [14].
- CARMEN is a tool developed by French aerospace laboratory ONERA and is connected with IESTA [20], a proprietary modular distributed simulation platform for the evaluation of air transport systems. The model dedicated to aircraft noise can predict the noise footprint around the airport on existing and future aircraft and is composed of three modules: the acoustic source models, the installation effects and the atmospheric propagation [15].
A comparison between these simulation tools has been carried out in [21]. However, all these methods are very similar, with the remaining differences in the individual code implementation. Indeed, Table 1 lists the different semi-empirical models employed within the three tools, considering the following noise contributions:

Table 1.
Summary of simulation models used within PANAM, ANOPP, and CARMEN [21].
- Airframe noise, comprised of: clean/trailing edge noise and flap side edge noise (abbreviation: t.e.), leading edge noise (abbreviation: l.e.), main landing gear noise (abbreviation: m.g.), nose landing gear noise (abbreviation: n.g.);
- Engine tonal and broadband noise, comprised of: fan broadband noise (abbreviation: fan bb), fan tonal noise (abbreviation: fan t), jet noise (abbreviation: jet).
PANAM, ANOPP and CARMEN involve models that represent the state-of-the-art in the field of aircraft noise prediction and are a benchmark for the development of further methods to assess the aircraft system noise.
Unfortunately, none of these tools are open source, thus limiting the exploitation at universities or for research purposes. Although many of the underlying equations used are shown in reports for PANAM [22,23] and ANOPP [24,25], the full and most updated methods are generally not open access. In other cases, the noise models require too many input variables, which might be unknown at the beginning of the design process. In addition, all semi-empirical models developed for conceptual design have been applied to predict the overall aircraft noise of subsonic aircraft only. In some cases, the applicability of these models to supersonic case studies is only theoretically discussed, and no real applications are reported. As far as ANOPP is concerned, the available literature confirms that the model was developed by NASA to support the SCR project, even if real applications are missing as well.
To verify the applicability of already existing models and to guarantee their exploitation at the very beginning of the SST aircraft design process, this paper discloses the application of a methodology that includes a supersonic aircraft noise model in line with the noise models implemented in early versions of ANOPP. This paper confirms the adequacy of this supersonic aircraft noise model to Concorde-like configuration by means of a dedicated validation. In order to overcome the lack of experimental data for modern civil supersonic aircraft required by consolidated validation procedures [26], an alternative approach, more suitable for the conceptual design stage, is addressed in this paper. The methodology is employed to predict NPDs data, thus the accuracy assessment for flyover trajectories is carried out by the comparison with NPD curves provided by the ANP database [27]. ANP is an open-source database provided by Eurocontrol Experimental Centre, which contains noise data for any specific certified aircraft. To support the computation of noise contours around airports, the database is also comprised of NPDs and spectral classes data. NPD curves define received sound event levels directly beneath the aircraft as a function of distance, for steady straight flight at a reference speed and atmospheric conditions in a specified flight configuration.
Notwithstanding the simplified approach, the validation with Concorde data shows that a good accuracy is reached for flyover trajectories. In addition, quantitative estimations for noise increments resulting from the afterburner are derived.
The approach suggested in this paper will also support the ongoing development and update of certification guidelines for the future SST. Considering default flight procedure, the overall noise level produced by traditional supersonic aircraft is assessed at the three certification measurements. Then, the results obtained are compared with the current LTO noise limitations reported in ICAO Annex 16, Volume I, Chapter 12 [28].
Precisely, ICAO recommends taking SARPs defined for subsonic jet aeroplanes as guidelines for new generations of SST aircraft. However, significant differences exist between supersonic and subsonic aircraft, so up-to-date noise standards could not be appropriate for the supersonic case. Therefore, dedicated studies are being undertaken towards the identification of advanced departure and approach flight procedures aimed at reducing noise especially for take-off conditions [29,30,31].
In this context, the EU is supporting ICAO efforts to fund research activities on environmentally sustainable supersonic aviation through the MORE&LESS (MDO and REgulations for Low-boom and Environmentally Sustainable Supersonic aviation) project, a Horizon 2020 initiative which aims to develop a holistic framework that is able to assess the environmental impact of supersonic aviation through a multidisciplinary approach [32].
In conclusion, the current study deals with the application of a simplified LTO noise prediction methodology tailored to civil supersonic aircraft that aims at assessing noise emission from the beginning of the design process. The roadmap followed to achieve this objective is summed up in Figure 1. The present Section specifies the motivations and the background on which the intention of this work lies, also providing an overview of the state-of-the-art in aircraft noise prediction methods. Thereupon, Section 2 describes the overall methodology framework, focusing on the most relevant parts concerning aircraft noise evaluations. Subsequently, Section 3 comprises the validation with ANP experimental data and the application of the proposed methodology to departure and approach procedures, considering the Concorde as a case study. Lastly, conclusions and possible further improvements are drawn in Section 4.
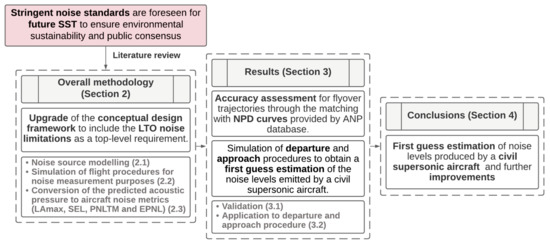
Figure 1.
Roadmap of the performed activities.
2. Overall Methodology
Integrated conceptual design approaches for future advanced aircraft should be drawn on a specific set of top-level requirements, as reported in the literature, for example, by Raymer [33] and Torenbeek [34]. Hence, the first step towards a design-to-noise approach for future SST shall be the upgrade of the conceptual design framework to include LTO noise limitations within this set. Specifically, in order to increase the public consensus towards future SST and to foster their environmental sustainability, the maximum noise levels defined as requirements shall be in line with current standards developed for subsonic civil aviation. Relying on this list of requirements, a first guess of weights and all relevant geometrical, aerodynamics and performance parameters is given and details about the aircraft configuration and engine type are specified, together with the concept of operations. It is essential to incorporate the aircraft noise prediction at this early stage, when all other initial performance analyses are performed [35,36,37,38,39].
The determination of noise levels received on the ground is a complex multidisciplinary problem that must be simplified to be included at a conceptual design level. Figure 2 suggests a possible way to embed aircraft noise prediction into the traditional conceptual design process framework. In detail, in Figure 2, aircraft noise prediction analyses are added to enrich the original activity flow as reported in textbooks [33,34] and are marked in red.
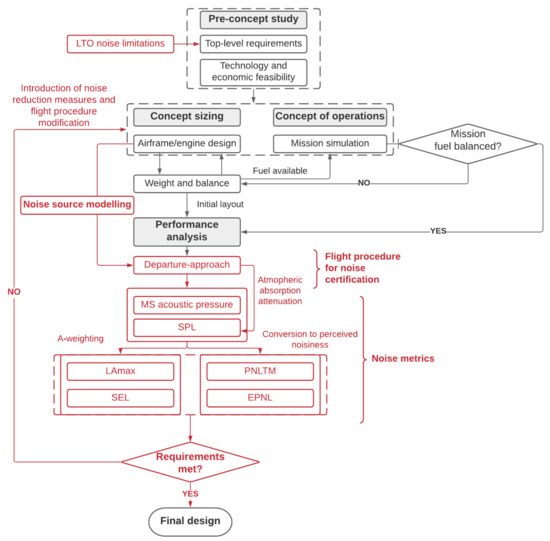
Figure 2.
Overall methodology framework supporting a design-to-noise approach.
A noise source model is needed to provide a mathematical formulation which correlates aircraft noise generation with design and operational parameters. Since there are still some uncertainties about the configuration in this phase of the project, interaction and installation effects are neglected and each noise source is modelled separately. As take-off and approach segments are fully characterized, the aircraft noise analysis can be performed, obtaining a first guess estimation of noise levels at the three certification measurement points defined by ICAO [28]. Thus, noise levels emitted by each source are predicted in terms of mean-square acoustic pressure and are then easily converted to the corresponding Sound Pressure Level (SPL), as a function of frequency expressed in a 1/3 octave centre frequency band. To evaluate the noise received by the observer on the ground, propagation effects shall be considered. In line with SAE ARP 866 B [40], sound losses due to atmospheric absorption are estimated as a function of frequency and temperature. Furthermore, the methodology suggested in this paper includes the possibility to convert the SPL into a set of well-established noise metrics (LAmax, SEL, PNLTM and EPNL). Ultimately, each design loop shall end with requirements verification, including LTO noise related requirements. If the aircraft exceeds the noise requirements, the iterative design-to-noise approach suggests the introduction of noise mitigation technologies or the evaluation of alternative flight procedures.
2.1. Noise Source Modelling
A theoretical and experimental review about noise generation mechanisms for each aircraft component is available in [41]. Complementary noise source modelling techniques are described in [42,43], classified on the basis of their fidelity-levels and suggested for specific applications accordingly. Among these model techniques, the scientific methods have prevailed to estimate the aircraft noise [43].
This paper follows this approach, which starts with the identification of the major noise sources on board the aircraft. Specifically, a clear distinction between non-propulsive noise (airframe) and propulsive noise (engine) is made. Then, both non-propulsive and propulsive noise sources are further broken-down. Figure 3 suggests a break-down specifically tailored on supersonic aircraft.
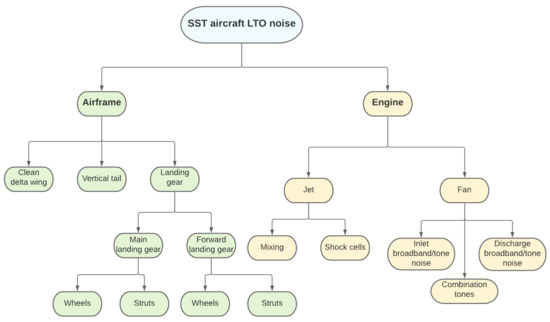
Figure 3.
SST aircraft LTO noise sources break-down.
Differently from the noise sources identified and described in [44] for a subsonic aeroplane, SSTs usually do not have high lift devices and horizontal stabilizer. Furthermore, interaction and installation effects are neglected, as well as turbo-machinery and combustion noise, to keep the approach simple and make it applicable at the conceptual design level. Hence, the airframe noise can be computed by spectrally summing the contributions of clean delta wing, vertical tail and landing gear noise. Similarly, engine noise can be computed by spectrally summing jet and fan noise contributions. Each sub-component identified is modelled using the equations suggested in ANOPP [24].
The ANOPP model correlates noise generation with operational and airframe/engine geometrical parameters, thus leading to the prediction of the mean-square acoustic pressure as a function of directivity angles and frequency. Once the mean-square acoustic pressure is computed for each sub-component, the total noise can be predicted by spectrally summing each acoustic pressure.
The procedure used to predict the overall aircraft noise level is illustrated in Equation (1), where the is the dimensionless mean-square acoustic pressure, referred to as , with as the ambient density and as the ambient speed of sound.
2.1.1. Airframe Noise
Despite the airframe noise not representing the predominant noise source of the aircraft, the introduction of high By-Pass Ratio (BPR) turbofans and the tightening of noise requirements led to a re-evaluation of noise produced by the airframe as a possible noise barrier [45]. A dissertation about the achievements of airframe noise research conducted in the last decades is presented in [46].
Several airframe noise prediction schemes can be employed. Specifically, this work benefits from the formulation suggested by Fink [47] and the mathematical formalism used in ANOPP. Fink’s method is the first semi-empirical prediction method for airframe noise, based on a wide set of experimental data, which is still in use today. It is here applied to predicting the overall airframe noise of a generic supersonic aircraft as a combination of clean delta wing, vertical tail, and landing gear.
Noise radiation from a clean airframe, with all gear and high-lift devices retracted, is assumed to be entirely associated with turbulent boundary layer flow over the trailing edges of the wing and tail surfaces. The contribution of leading edges can be ignored as long as the airfoil chord remains large compared to the acoustic wavelength of the sound produced. Noise contributions from forward landing gear and main landing gear are calculated separately because the differences in architecture and size translate into different peak frequencies. In detail, each landing gear noise contribution is evaluated, considering only the most two dominant sources, which are struts and wheels.
In general, each airframe source can be mathematically modelled following Equation (2). Thereupon, the far-field mean-square acoustic pressure is calculated as:
where:
- : overall acoustic power, re ;
- : directivity function;
- : spectrum function;
- S: Strouhal number;
- : dimensionless distance from source to observer, re ;
- : wingspan of the aerodynamic surface;
- : spherical propagation factor;
- : Doppler factor accounting for the forward velocity effect;
- : aircraft Mach number;
- : polar directivity angle (deg);
- : azimuthal directivity angle (deg).
The acoustic power for the airframe can be expressed as:
where:
- K and a are constants determined from empirical data;
- G is a geometry function different for each airframe component and incorporated all geometrical effects on the acoustic power.
The values of K, a and G reported in Table 2 for each airframe noise source. Specifically, n, d and l are, respectively, the number of wheels per landing gear, the tire diameter and the strut length. The parameter is the dimensionless turbulent boundary-layer thickness, computed from the standard flat-plate turbulent boundary-layer model. Directivity functions and Spectrum function used for each airframe noise source are specified in Table 3.

Table 2.
K, a and G for each airframe noise source [24].

Table 3.
Directivity function D and Spectrum function for each airframe noise source [24].
Each described contribution is then summed over the 1/3 octave frequency band to predict the airframe noise (Equation (4)).
Typically, landing gear noise is the most dominant airframe noise source during the LTO cycle, with the highest contribution during the approach phase [48]. This is true both for subsonic as well as supersonic aircraft. It is worth noting that, despite the differences in wing planform, configuration and landing gear size, the airframe noise of supersonic aircraft is expected to be comparable with the noise coming from a subsonic aircraft. However, a different conclusion could be drawn for unconventional designs. The methodology described in this section can be applied to supersonic aircraft, but it is tailored towards conventional wing-fuselage configuration (Concorde-like). Considering that future SSTs may be characterized by unconventional configurations, the inclusion of additional elements of the airframe noise break-down, such as canard or moving surfaces, or different architectures, such as Blended Wing Body (BWB), is needed to widen the applicability of the methodology.
2.1.2. Engine Noise
Similar to the strategy adopted for airframe noise prediction, the contributions of engine noise can be further decomposed into several noise sources. Noise generated by the engine consists of several contributions, which in the literature are classified into fan noise, jet noise and engine core noise (compressor stages, combustor, turbine stages) [49]. However, considering the limited amount of data available during the early design phases, the engine noise model described in this paper considers only the two most predominant engine noise sources—fan and jet noise. This hypothesis is a well-established practice in conceptual design [19,20] and does not affect the engine noise prediction significantly for SSTs, due to the logarithmic nature of the noise levels and the prevalence of jet noise compared to other sources.
Among the aircraft noise sources, jet noise is the most widely studied and had its foundations in the work of Lighthill [50]. The most relevant finding of that work was the Lighthill’s eighth power law, that states that the power of the sound created by a turbulent motion is proportional to the eighth power of the characteristic turbulent velocity.
In this work, jet noise is predicted using the Stone method [51], which is based on the Lighthill theory. The total far-field jet noise is typically computed as the sum of the jet mixing noise and shock noise, that occurs when is greater than zero, with the primary stream Mach number. The method uses empirical functions to provide the directivity and the spectral content of the field with the computed overall mean-square acoustic pressure at , that is , used to fix the amplitude throughout the field.
The equation used to calculate the jet mixing noise at a distance from the nozzle exit is:
where is the mean-square acoustic pressure for a stationary jet calculated at the reference distance from the nozzle exit at , and is defined as:
where the parameters are:
- : dimensionless distance from the nozzle exit , referred to as ;
- and : fully expanded jet area, density, velocity and total temperature respectively, with all three quantities evaluated for the primary stream, and normalized by , , and ;
- : modified directivity angle, ;
- : directivity function;
- : spectral distribution function;
- : forward flight effects factor;
- and : configuration factors;
- : jet mixing noise Strouhal number;
- : empirical function of .
The 1/3 octave band mean-square acoustic pressure due to shock turbulence interaction noise is calculated through the following equation:
with being the pressure ratio parameter, equal to , which must be greater than zero for shock cell noise to occur. The function provides the dependence of the shock cell noise, for a stationary jet, on the directivity angle and the fully expanded primary stream Mach number . This function is given by:
where is the Mach angle defined by: . The total far-field jet noise is the sum of the shock noise and the jet mixing noise (Equation (7)) and its most influential parameters are the exhaust jet speed and the jet Mach number.
Fan noise dominates most flight conditions and can be higher than jet noise. As far as fan noise is concerned, efforts have been recently made in fan noise reduction and predictive models are available in the literature. These methods allow a first-order estimate of the acoustic pressures arising from any fan identified by a limited number of design parameters, such as diameter, tip chord, number of blades, rotational speed, fan-stator distance, pressure ratio, mass flow ratio, temperature rise across the fan [52]. The method proposed by Heidmann in the mid-1970s has come to dominate the arena of empirical fan and single-stage compressor noise prediction [43]. Heidmann prediction method is applicable to turbojet compressors and to single-and-two-stage turbofans with and without inlet guide vanes [53]. The total noise levels are obtained by spectrally summing the predicted levels of broadband, discrete-tone and combination-tone noise components. Precisely, the predicted free-field radiation patterns (neglecting the reflection of sound) consist of composite of the following separately predicted noise components:
- Noise emitted from the fan or compressor inlet duct (broadband noise, discrete-tone noise, combination-tone noise);
- Noise emitted from the fan discharge duct (broadband noise, discrete-tone noise).
Hence, the total fan noise has been predicted by summing the noise from six separate components: inlet broadband noise, inlet rotor–stator interaction tones, inlet flow distortion tones, combination tone noise, discharge broadband noise and discharge rotor–stator interaction tones. All noise sources are combined into single 1/3 octave band spectrum for each directivity angle.
The general approach is the same for each noise component and is based on the following equation for the computation of far-field mean-square acoustic pressure:
where A is the fan inlet cross sectional area. The frequency parameter is defined as:
where is the blade passing frequency depending on the rotational speed N. The acoustic power for the fan is expressed as:
with:
- : mass flow rate, re ;
- : total temperature rise across fan, re ;
- : relative tip Mach number;
- : defined as , where is the fan rotor relative tip Mach number at design point;
- : rotor-stator spacing, re C (mean rotor blade chord);
- : empirical constants and factors depending on geometry and configuration.
Equation (12) must be specialized for each noise component before computing the overall acoustic power:
- Inlet broadband noise
- Inlet rotor-stator interaction tones
- Inlet flow distortion tones
- Combination tone noisewith for 1/8 fundamental combination tone, for 1/4 fundamental combination tone and for 1/2 fundamental combination tone.
- Discharge broadband noise:
- Discharge rotor-stator interaction tones:
The values of empirical constants and function are reported in [24] for each fan noise component. Afterwards, the total fan noise is computed as the sum of the previously described contributions, obtaining the Equation (19) by appropriately summing broadband and tone noise components:
Usually, the main broadband noise contribution is the discharge noise, whereas combination tone noise causes some peaks in the SPL that depend on the blade passing frequency. The parameters with a higher influence on fan noise generation are the air mass flow, the rotational speed, and the rise of temperature across the fan. Increasing the air mass flow and temperature produces an increment of SPL, whereas variations in rotational speed N can shift peak values along the frequencies band.
It is worth noting that the engine noise model described above perfectly fits the first generation of supersonic aircraft and related propulsive technologies. Indeed, the Olympus 593, which equipped the Concorde, can be described with this model. However, a different conclusion could be drawn for future supersonic propulsive technologies. The under-development of the future generation of SSTs might integrate more turbofan-oriented engines, which might be partially or completely embedded into the airframe. As observed in [54,55], at high power engine operation conditions, especially at take-off conditions, the noise levels observed from such future supersonic engines are very high. A major component of fan noise is expected to be the buzz-saw noise, produced by shocks at the fan blade tips at this high-power engine operation condition.
Ultimately, the total engine noise is computed as:
2.2. Flight Procedure for Noise Certification
LTO noise limitations and flight procedures for subsonic aircraft are specified by regulatory community by ICAO. Therefore, operational requirements can be directly elicited from these certification standards and used as a benchmark during the design process. Conversely, for supersonic aviation standards, flight procedures have not been defined yet. However, in order to guarantee an adequate public consensus towards the future SSTs, the scientific community is anticipating the possibility of extending the current subsonic flight procedures to civil supersonic aircraft [31]. In parallel, the regulatory community is fostering research activities aimed at investigating the technical and technological limitations to the application of already existing flight procedures to SSTs [29,30]. In this context, design methodologies, such as the one disclosed in this paper, are essential for suggesting possible updates of the flight procedures to fill in the gap between subsonic and supersonic aviation.
Therefore, it is necessary to couple traditional flight profile analysis with flight procedure simulations. During the first design loop, the reference ICAO flight procedures are adopted, while in the case of technical evidence of the impossibility of following such procedures, modifications to the main operational parameters are suggested.
Hereafter, the ICAO flight procedures for certification are considered as a reference. Specifically, the noise levels for certification are associated with three different operating conditions, physically represented by a ground reference measurement point (Figure 4):
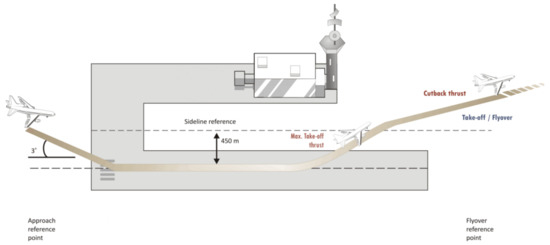
Figure 4.
Aircraft noise certification reference measurement points [56].
- Sideline-maximum power condition: the measurement point is along the line parallel to the axis of the runaway centre line at 450 m, where the noise level is maximum during take-off. This operating condition corresponds to the so-called sideline measurement, which is the maximum sound level reached along the lateral full-power line;
- Flyover-intermediate power condition: the measurement point is along the extended runaway centre line at 6500 m from the start to roll;
- Approach-low power condition: the measurement point is 120 m vertically below the descent path originating from a point 300 m beyond the threshold.
The reference procedures are specified in the Environmental Technical Manual [57], and are specified for different classes of aircraft characterized by different Maximum Take-Off Mass (MTOM) and number of engines. Two take-off flight paths can be modelled: reduced power/thrust (or cutback) and full power/thrust. If a power/thrust reduction is applied, a slight decrease in the climb gradient may occur due to the power/thrust lapse that results from an increased air-craft height. The reference approach flight test configuration for noise certification is constrained by the ILS flight path; therefore the approach angle (steady glide angle) is ± and the target aeroplane height vertically above the noise measurement point is 120 m (394 ft). A detailed description of the flight path is required for noise prediction. Examples of parameters needed include aircraft height, climb angle, airspeed, gross mass, aircraft configuration (flap position, landing gear position), engine thrust (power) setting parameters, and aircraft accessory conditions that may affect the measurement or adjustment of noise data and/or aircraft or engine performance.
For noise modelling purposes, the corresponding trajectory consists of straight flight segments with constant operational and configurational settings. This segmentation modelling is supported by the ANP database, which has been assembled through the years and updated by the aircraft manufacturers together with the noise certifying authorities. The ANP database contains a set of trajectories described by fixed-point data at constant the engine thrust setting, configuration, and acceleration/vertical speed.
In the frame of this work, the take-off and landing trajectories have been simulated as flight paths composed respectively by 5 and 3 flight segments constructed from an ANP set of fixed-point data. In addition, an engine model simulating the on-design and off-design operations is needed, since specific information about geometry, thermodynamic, performance and operational conditions are required to predict noise emitted by the aircraft. To keep the approach as simple as possible, in this paper a one-dimensional model for a two-spool turbojet engine with afterburner has been modelled as an example, taking the Olympus 593 MRK 610 as a reference [58], relying on the data and the results presented in [59]. The afterburner has been modelled by the addition of another component after the low-pressure turbine, which gives, in exit, a flow reaching a total temperature of 1700 K, considering an afterburner efficiency of 0.9. At least, an exhaust system composed by adiabatic, isentropic and variable-geometry convergent-divergent nozzle has been modelled to predict the exhaust jet parameters as a function of thrust.
During the simulation, the evolution of aircraft configuration is considered (e.g., retraction/extraction of landing gear, nozzle area variations) and operating parameters are continuously updated. Information about aircraft distance and noise sources directivity are recorded with a sampling time of 0.5 s over the 10 dB-down period for each aircraft noise certification points.
2.3. Noise Metrics
This sub-section includes the possibility of converting the mean-square acoustic pressure (measured following the method described in the paragraph Section 2.1) into a set of well-established noise metrics (LAmax, SEL, PNLTM and EPNL).
A noise metric is an expression used to assess the loudness or the annoyance of any quantity of noise on human hearing system. A variety of noise metrics are using among different aviation organization, countries, and airports [60]. However, they can be classified into three main groups [61]:
- Single event (or instantaneous) metrics: used to provide a description of noise occurring during one noise event, accounting for sound amplitude only;
- Exposure (or integral) metrics: used to provide a description of the type of noise exposure experienced over a given interval of time;
- Supplementary metrics: measurements often used in conjunction with the above, to provide a more meaningful depiction of the potential impact of noise exposure.
The most internationally accepted aircraft noise metrics in use belong to the first two categories, so they are typically single event or exposure metrics. Furthermore, aircraft noise metrics could be associated with frequency weighted or computed SPL distribution [62]. A-weighting is the most widely used type of weighting by federal, state, and local agencies for environmental noise analyses. In this case, the weighted SPL results from the adjustment of the spectral distribution to de-emphasize the low frequency portion of sounds to gain a better approximation of the human ear’s response to sound. Noise metrics deriving from this correction are LAmax and SEL, which are respectively single event and exposure noise metric; both are expressed in dBA. Otherwise, computed SPL is obtained by the ICAO standardized procedure [63], which involves the conversion of SPL in noisiness levels by means of the correspondence with Noy tables [64] and the correction for spectral irregularities. Noise metrics deriving from this procedure are Maximum Tone Corrected Perceived Noise Level (PNLTM) and Effective Perceived Noise Level (EPNL), which are respectively a single event and exposure noise metric, expressed in PNdB and EPNdB. Based upon these different ways of processing the frequency distribution of energy, LAmax and SEL are considered loudness-based metrics, whereas PNLTM and EPNL are considered annoyance-based [61]. Annoyance-based metrics are more sensitive to the spectral shape and tonal content of the sound, therefore EPNL has been found to be more effective for the assessment of heavy jet-powered aircraft noise [65].
Even though some difference subsists, there is, in practice, a high correlation between the LAmax and PNLTM measures and, consequently, between SEL and EPNL [61]; thus, generally all the mentioned metrics are used for aircraft noise certification, depending on the specific procedure.
Anyway, a few preliminary considerations should be accounted for when predicting the noise levels received by the microphones on the ground. The aircraft noise model described in the previous paragraph gives as its output a dimensionless mean-square acoustic pressure that corresponds to the acoustic pressure of the sound signal at the noise source. Hence, the dimensionless mean-square acoustic pressure must be converted into a 1/3 octave band SPL by means of:
where is the lowest sound pressure possible for the human ear to hear, which is approximately Pa. After that, a number of factors which influence the propagation of noise should be considered to gain a higher fidelity level in prediction. However, the distances between the noise source and the observer on ground are such that sound attenuation in the atmosphere is the most significant phenomenon. Temperature and humidity are the parameters causing a major reduction in sound as distance increases. To determine the entity of these losses, the mathematical procedure suggested in SAE ARP 866 B [40] has been adopted. The SARP considers only the classical and molecular absorption of sound energy by the atmosphere. Precisely, the classical absorption results from energy dissipation through the effects of heat conduction and viscosity and it is a function of frequency and temperature, whereas molecular absorption results principally from rotational and vibrational relaxation process of oxygen and nitrogen molecules and is a function of frequency, temperature, and humidity. The classical absorption is relevant only at higher frequencies and varies slightly with temperature. By contrast, molecular absorption is the main contribution to sound attenuation, varying on a wide range of values, producing a more relevant sound reduction at highest frequencies. The total loss is expressed as the attenuation in dB/100 m and it is a function of frequency, temperature, and relative humidity. As a result, summing algebraically the losses for each centre frequency in 1/3 octave band of the spectrum, the approximated SPL received on ground is obtained. Once these two preliminary steps have been fulfilled, the resulting SPL distribution can be processed to quantify noise emitted by the aircraft. The A-weighting of the frequency spectrum and the ICAO procedure leads respectively to the and , that are function of frequency. Then, the Overall Sound Pressure Level (OASPL) and the Tone Corrected Perceived Noise Level (PNLT) as function of time can be computed with Equations (22) and (23), respectively.
where N (k) is the total perceived noisiness, defined as:
where n (k) is the largest of the 24 values of n (i, k) of the Noy tables, i is the 1/3 frequency band considered between 50 Hz and 10,000 Hz and k the time instant.
Thus, the instantaneous noise metrics can be computed as the maximum sound level reached during the event over the 10 dB-down period, identified by kF and kL, which are the time instants when the sound level decreases up to 10 dB-down with respect to the peak:
Integral noise metrics are duration corrected single event metrics. Hence, SEL is an energy averaged A-weighted sound level over a specified period of time or single event, with a reference duration of 1 second. On the other hand, EPNL is an integration of the PNLT over a certain noise duration, normalized to a reference duration of 10 s. The relative formulas are:
where 13 dB is a constant relating the one-half second values of PNLT(k) to the 10 s reference duration.
To sum up, the flow chart in Figure 5 schematically reports all the mentioned mathematical steps leading to the prediction of aircraft noise levels received on ground in terms of the most common aircraft noise metrics, starting from the normalized mean-square acoustic pressure.
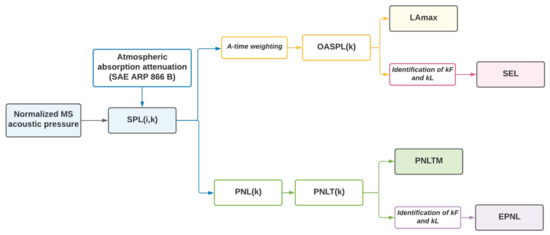
Figure 5.
Procedure employed to assess aircraft noise level received on ground in terms of the most common aircraft noise metric.
3. Results
As outlined in the introduction, the results section is divided into two parts. First, the accuracy of the noise model in predicting overall aircraft noise level is assessed through a dedicated validation with ANP experimental data by the evaluation of the matching with LAmax and SEL NPDs. After that, reference departure and approach procedures reported in the ANP database are simulated and, using the methodology described above, a first guess of aircraft noise levels is evaluated. The only available civil supersonic aircraft of the ANP, that is, the Concorde, has been selected as a case study. Corresponding geometrical parameters affecting noise generation and their values are listed in Table 4. Engine on-design and off-design operations simulation are required, hence a two-spool turbojet with an afterburner is simulated through a one-dimensional model based on the results reported in [59] for the Olympus 593.

Table 4.
Case study geometrical parameters affecting noise generation.
3.1. Validation
By the simulation of different flyover flight paths, ranging the altitude from 630 ft (192 m) to 10,000 ft (3048 m) and the thrust between 10,000 lb (44,482 N) and 32,000 lb (142,342 N), a total of 24 points have been obtained to produce the NPD curves.
The aircraft speed is fixed to 160 knots (82 m/s), in accordance with the reference airspeed used to derive the NPD from experimental measurements, whereas the ambient conditions have been set to the reference conditions suggested in [66] for noise contours modelling around the airports (ambient temperature equal to 15 °C and the relative humidity HR equal to 0.7). The matching with the NPD curves provided by the ANP database for LAmax and SEL are reported in Figure 6 and Figure 7.
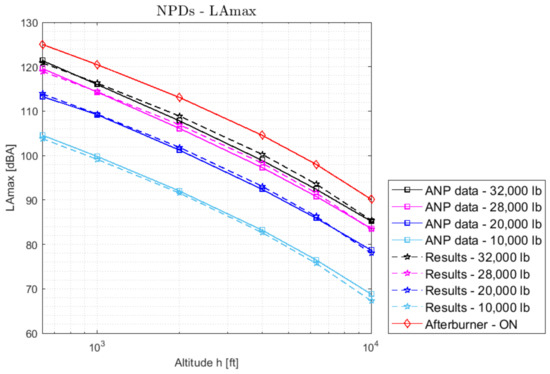
Figure 6.
Matching between predicted and experimental NPDs-LAmax.
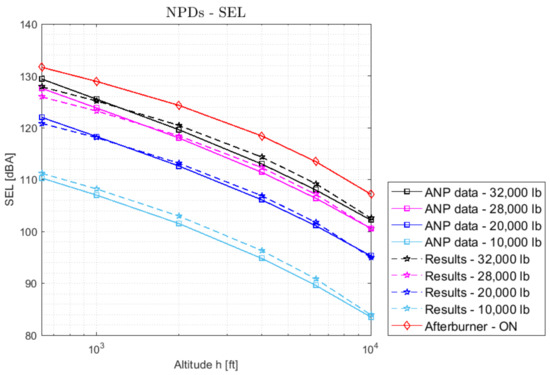
Figure 7.
Matching between predicted and experimental NPDs-SEL.
The degree of matching between predicted and experimental curves has been evaluated in a quantitative way through a numerical indicator for each validation point, respectively for LAmax and SEL:
where and are the predicted values, whereas and are the experimental ones.
The maximum prediction error is ±2.19% around the experimental value, attaining a good accuracy for application at a conceptual design level.
Noise levels reached when the afterburner is turned on are not provided by the ANP database. However, knowing the increment of thrust due to the afterburner, it is possible to obtain a preliminary estimate of the resulting noise impact. The increase in jet exhaust speed and exhaust stream Mach number have been derived by the simulation of the engine model, considering the higher total temperature resulting from reheating and the adaptation of the throat section of the nozzle to avoid the choking of the duct. Hence, the corresponding NPD curve has been obtained setting a thrust level equal to 176,380 N, as it is the maximum thrust value reported in the ANP database for the Concorde take-off procedure (red line in Figure 6 and Figure 7). The increment has been evaluated with respect to the noise level reached with the maximum dry thrust level with the following formulas, respectively for LAmax and SEL:
where and represent the increment in noise levels when the afterburner is turned on. This parameter has been calculated for each point of the NPD curve, and then an arithmetic average has been calculated for both and . The results expressed show that the afterburner causes an increase of 4.24% in instantaneous noise level and 3.52% in integrated noise level.
To assess the correlation between numerical and experimental results in a quantitative way, an adaptation of the Frequency Response Scale Factor (FRSF), usually employed in the field of frequency response analysis ([67]), has been used. Such index evaluates of how much the predicted results overestimate or underestimate the numerical ones, and acceptable values are included in the range 0.95–1.05. Precisely, if FRSF < 1, the predicted curve is on average at a higher level than the experimental one; whereas, if FRSF > 1, the predicted curve is on average at a lower level than the experimental one. The index has been readapted as:
where j indicates the thrust level and d the distance related to the noise data H. The values obtained for and are respectively 0.999 and 1.0033. Hence, this parameter also confirms the good accuracy of the methodology and, in addition, denotes a slight over-prediction for and an underprediction for .
3.2. Application to Departure and Approach Procedures
A set of ANP departure fixed-point data (distance on ground, altitude, thrust, TAS/CAS) has been selected to simulate standard departure and approach procedures Figure 8 and Figure 9.
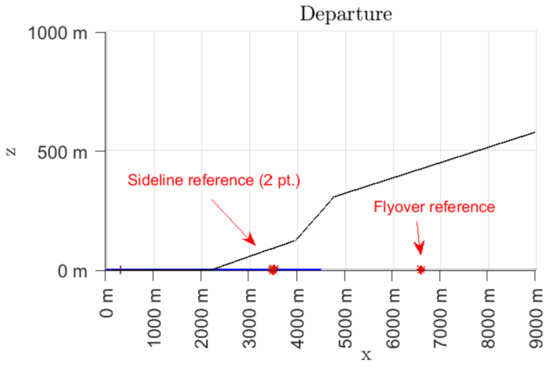
Figure 8.
Simulated departure flight path.
Figure 9.
Simulated approach flight path.
Results are reported in Table 5. As expected, the most critical condition occurs during the departure procedure at the sideline noise measurement point. By contrast, flyover noise is reduced, as a cutback procedure has been simulated, reducing thrust level and, consequently, the climb angle. Ultimately, the approach condition is characterized by the lowest noise levels.

Table 5.
Overall noise level at the three certification measurement point.
In addition, noise contributions and overall noise have been reported for each measurement point in terms of LAmax obtained at the overflight point Figure 10, Figure 11 and Figure 12. It is evident that the high thrust level required for taking-off and the use of the afterburner produces a high jet speed that greatly affect sideline noise. However, the impact of jet noise is significant at all three measuring points, as jet noise suppression measures have not been modelled in the frame of this work. A significant contribution of fan noise appears, especially in the approach condition. This result can be justified as the original method of Heidemann typically overestimates fan noise [68,69].
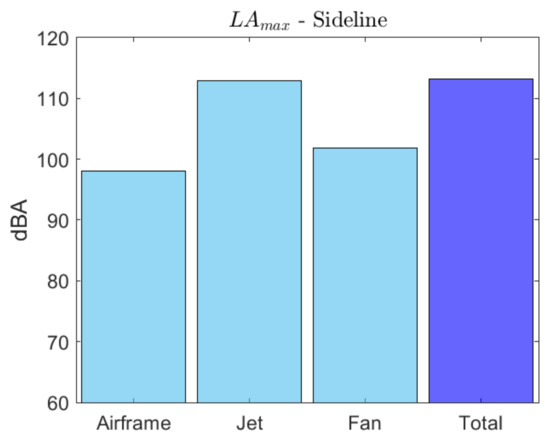
Figure 10.
Noise contributions and overall noise for sideline measurement point.
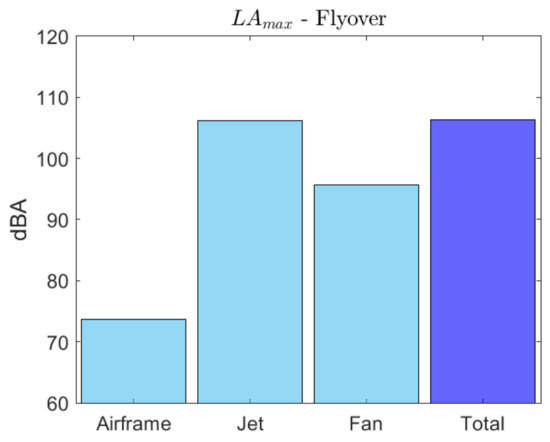
Figure 11.
Noise contributions and overall noise for flyover measurement point.
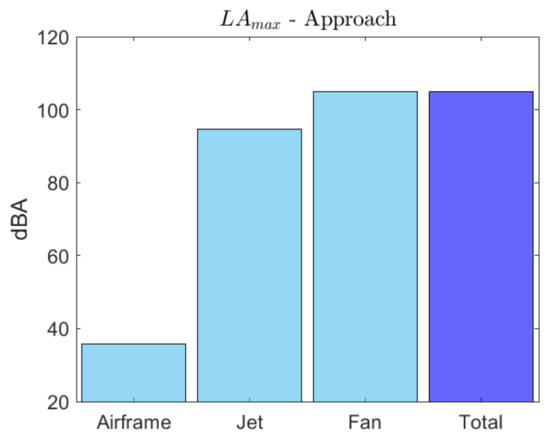
Figure 12.
Noise contributions and overall noise for approach measurement point.
To enable a verification of the first noise estimations, the up-to-date LTO limitations imposed for Concorde-like sized subsonic aircraft equipped with four jet-powered engines have been considered as top-level requirements, as ICAO Annex 16, Volume 1, Chapter 12 [28] refers to subsonic aeroplanes noise standards for the certification of supersonic aeroplanes whose type certificate is issued after 1 January 1975. Therefore, in accordance with [70], the LTO noise requirements derived for = 185,000 Kg are:
- Sideline-full power:
- Flyover-intermediate power:
- Approach-low power condition:
Consider the cumulative noise level, calculated as:
An excess of 36.22 EPNdB has been estimated. Such a large discrepancy can be associated with the inadequacy of current regulation of the traditional civil supersonic aircraft case study. Therefore, it underlines the significance of developing new standards, which are not so penalizing for SST, and the review of traditional supersonic aircraft design with the introduction of innovative noise reduction concepts.
Chevron nozzles are one of the most studied noise reduction technologies, particularly efficient for medium and high by-pass ratio engines of subsonic aircraft [71]. The shaped edges serve to significantly reduce turbulence at the nozzle exit and thus jet noise, leading to over 2–3 EPNdB noise reduction [72]. However, this passive noise control might not be equally efficient for supersonic jets. Chevrons have been shown to be effective at reducing mixing noise for subsonic conditions, but effects on shock-cells associated noise are under investigation, as chevron nozzles reduce the shock cell spacing, causing the peak amplitude of the shock associated noise to shift to higher frequencies [73].
On the contrary, fluidic injection techniques are more efficient active noise reduction methods for supersonic jet, showing potential for over 4 EPNdB noise reduction [74]. By means of fluidic injection it is possible to rearrange the shock diamonds structure arising from the nozzle exit with respect to the throat shock diamonds, thus controlling shock associated noise [75]. However, further improvements in the engine design and performance, together with the adoption of low-noise flight procedures would still be required to ensure the Concorde-like configuration complies with current LTO limitations.
4. Conclusions
To ensure that future supersonic aircraft will meet low-noise requirements, this paper disclosed guidelines aiming at assessing LTO noise emission estimation since the very beginning of the design process. Therefore, a preliminary literature review has been conducted to identify the state-of-the-art methods currently adopted to complement the design process with aircraft noise prediction. Then, in line with the current well-established methods, a semi-empirical noise model has been applied to a civil supersonic aircraft case study. To confirm the adequacy of this noise model for Concorde-like configuration, a dedicated validation has been performed. The results attested a good accuracy for application at a conceptual design level, with a maximum relative prediction error of 2.19%. In addition, a noise level increment arising from the use of the afterburner has been determined, obtaining an increase of 4.24% in LAmax and 3.52% in SEL, which greatly discourage the use of the afterburner during take-off.
Afterwards, the suggested framework has been employed to evaluate LTO aircraft noise levels at the three certification measurement points defined by ICAO along standard departure and approach trajectories. As expected, the predicted LAmax for each contribution confirmed that the dominant noise source during take-off is the jet noise, and that the use of an afterburner greatly affects sideline noise level. By contrast, the approach condition is less critical for noise generation. However, it has been found that jet and fan noise become comparable at this condition. This result could be attributed to the original method of Heidmann, which has been seen in the literature to over-predict the intensity of fan tones. To enable first verification of the estimate, the predicted EPNLs have been compared with current LTO noise limitations for cumulative noise level, highlighting that the predicted values for supersonic aircraft significantly exceed those imposed for similar sized subsonic aircraft.
The outcome of this research activity led to several useful considerations in the field of supersonic aircraft LTO noise prediction. Firstly, the feasibility of introducing an initial noise assessment relying on information available in a conceptual design phase and using semi-empirical models found in the literature has been proven, gaining a good fidelity-level in the prediction of NPD relationships. Therefore, the procedure can theoretically be applied within the conceptual design process to produce NPD curves for different aircraft concepts by changing the design and operational parameters. After that, take-off, and precisely at the sideline noise measurement point, has been confirmed as the most critical noise condition, manly due to the engine contribution. In addition, the comparison with current cumulative noise requirement has remarked the need for both new specific noise standards for supersonic aircraft and a review of a conventional Concorde-like design by the incorporation of noise reduction measures and procedures from the earliest stage of the project.
Adjustments in noise modelling (especially for fan noise prediction) are required to gain a high-fidelity level in departure and approach procedures noise prediction as well as the introduction of simplified models to evaluate newer jet noise reduction concepts. Furthermore, since new supersonic aircraft designs could be very different from the past conventional design, the inclusion of additional elements (e.g., for the airframe noise break-down) is a key improvement to widen the applicability of the methodology employed and enable the exploration of innovative low-noise configurations. Lastly, to obtain a better comprehension of supersonic aircraft noise, further advancements could also concern the evaluation of other annoyance-based or psychoacoustic noise metrics aimed at assessing the subjective response to aircraft noise, as suggested in [76].
Author Contributions
Conceptualization, N.V. and R.F.; methodology, G.P., N.V. and R.F.; software, G.P.; validation, G.P. and L.F.; investigation, G.P.; resources, N.V.; writing—original draft preparation, G.P. and R.F.; writing—review and editing, N.V. and L.F.; visualization, G.P.; supervision, N.V. and L.F.; project administration, N.V.; funding acquisition, N.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by European Union’s HORIZON 2020 research and innovation programme under grant agreement No.101006856—MDO and REgulations for Low boom and Environmentally Sustainable Supersonic aviation (MORE&LESS) Project.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANOPP | Aircraft NOise Prediction Program |
| ANP | Aircraft Noise and Perfomance database |
| CAEP | Committee on Aviation Environmental Protection |
| DLR | German Aerospace Laboratory |
| EPNL | Effective Perceived Noise Level |
| EU | European Union |
| FAA | Federal Aviation Administration |
| FRSF | Frequency Response Scale Factor |
| ICAO | International Civil Aviation Organization |
| LAmax | A-weighted Sound Pressure Level |
| LTO | Landing and Take-Off |
| MORE&LESS | MDO and REgulations for Low-boom and |
| Environmentally Sustainable Supersonic aviation | |
| MTOM | Maximum Take-Off Mass |
| NASA | National Aeronautics and Space Administration |
| NPD | Noise Power Distance |
| OASPL | Overall Sound Pressure Level |
| ONERA | French Aeronautics and Space Research Center |
| PANAM | Parametric Aircraft Noise Analysis Module |
| PNL | Perceived Noise Level |
| PNLTM | Maximum Tone Corrected Perceived Noise Level |
| SAE | Society of Automotive Engineers |
| SARPs | Standard and Recommended Practices |
| SCR | Supersonic Cruise Research |
| SEL | Sound Exposure Level |
| SPL | Sound Pressure Level |
| SST | SuperSonic Transport |
| SAE | Society of Automotive Engineers |
| SARPs | Standard and Recommended Practices |
| SCR | Supersonic Cruise Research |
| SEL | Sound Exposure Level |
| SPL | Sound Pressure Level |
| SST | SuperSonic Transport |
References
- ICAO. Destination Green: The Next Chapter. In Environmental Report; ICAO: Montreal, QC, Canada, 2019. [Google Scholar]
- Hardeman, A.; Maurice, L. Sustainability: Key to enable next generation supersonic passenger flight. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1024, 012053. [Google Scholar] [CrossRef]
- Antoine, N.E.; Kroo, I.M. Aircraft Optimization for Minimal Environmental Impact. J. Aircr. 2004, 41, 790–797. [Google Scholar] [CrossRef]
- X-59 QueSST (Quiet SuperSonic Technology)-Silencing the Sonic Boom. Available online: https://www.lockheedmartin.com/en-us/products/quesst.html (accessed on 25 October 2021).
- Boom Supersonic-Overture. Available online: https://boomsupersonic.com/overture (accessed on 25 October 2021).
- SENECA-LTO noiSe and EmissioNs of supErsoniC Aircraft. Available online: https://seneca-project.eu/ (accessed on 25 October 2021).
- RUMBLE-RegUlation and norM for Low Sonic Boom LEvels. Available online: https://rumble-project.eu/i/project/project-overview (accessed on 25 October 2021).
- Drake, F.; Purvis, M. The effect of supersonic transports on the global environment: A debate revisited. Sci. Technol. Hum. Values 2001, 26, 501–528. Available online: http://www.jstor.org/stable/690166 (accessed on 25 October 2021). [CrossRef]
- Tang, R.Y.; Elias, B.; Luther, L.; Morgan, D. Supersonic Passenger Flights. 2018. Available online: https://sgp.fas.org/crs/misc/R45404.pdf (accessed on 25 October 2021).
- ICAO-Supersonic Aircraft Noise Standards Development. Available online: https://www.icao.int/environmental-protection/pages/Supersonic-Aircraft-Noise-Standards-Development.aspx (accessed on 25 October 2021).
- Hay, J.A. Concorde-Community Noise. Aerospace Engineering and Manufacturing Meeting; Technical Report 0148-7191; SAE International: Warrendale, PA, USA, 1976. [Google Scholar]
- Hirshorn, S.R. NASA Systems Engineering Handbook, 2nd ed.; NASA: Washington, DC, USA, 2016; pp. 17–23. [Google Scholar]
- Raney, J. Development of a new computer system for aircraft noise prediction. In Proceedings of the AIAA 2nd Aeroacoustics Conference, Hampton, VA, USA, 24–26 March 1975. [Google Scholar] [CrossRef]
- Bertsch, L.; Guerin, S.; Looye, G.; Pott-Pollenske, M. The Parametric Aircraft Noise Analysis Module-Status overview and recent applications. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference (32nd AIAA Aeroacoustics Conference), Portland, OR, USA, 5–8 June 2011. [Google Scholar] [CrossRef]
- Sanders, L.; Malbéqui, P.; LeGriffon, I. Capabilities of IESTA-CARMEN to predict aircraft noise. In Proceedings of the 23rd International Congress on Sound & Vibration (ICSV23): “From Ancient to Modern Acoustics”, Athens, Greece, 10–14 July 2016; Available online: https://hal.archives-ouvertes.fr/hal-01385584 (accessed on 25 October 2021).
- Raney, J.P.; Padula, S.L.; Zorumski, W.E. NASA Progress in Aircraft Noise Prediction; NASA Technical Memorandum 81915; National Aeronautics and Space Administration: Washington, DC, USA, 1981. [Google Scholar]
- Lopes, L.V.; Burley, C.L. Design of the Next Generation Aircraft Noise Prediction Program: ANOPP2. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference (32nd AIAA Aeroacoustics Conference), Portland, OR, USA, 5–8 June 2011. [Google Scholar] [CrossRef]
- Bertsch, L.; Heinze, W.; Guerin, S.; Lummer, M.; Delfs, J. 10 years of joint research at DLR and TU Braunschweig toward low-noise aircraft design-what did we achieve? Aeronaut. Aerosp. Open Access J. 2019, 3, 89–104. [Google Scholar] [CrossRef]
- Dobrzynski, W.; Ewert, R.; Pott-Pollenske, M.; Herr, M.; Delfs, J. Research at DLR towards airframe noise prediction and reduction. Aerosp. Sci. Technol. 2008, 12, 80–90. [Google Scholar] [CrossRef]
- Elie, A.; Kervarc, R.; Dubot, T.; Bourrely, J. IESTA: A Modular Distributed Simulation Platform for the Evaluation of Air Transport Systems; MASCOT08-IMACS/ISGG Workshop; IAC-CNR: Roma, Italy, 2008. [Google Scholar]
- Bertsch, L.; Clark, I.A.; Thomas, R.H.; Sanders, L.; Legriffon, I. The Aircraft Noise Simulation Working Group (ANSWr)-Tool Benchmark and Reference Aircraft Results. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019; Available online: https://hal.archives-ouvertes.fr/hal-02196662 (accessed on 30 September 2021).
- Bertsch, L. Noise Prediction Within Conceptual Aircraft Design. Ph.D. Thesis, Technical University of Braunschweig, Braunschweig, Germany, 2012. [Google Scholar]
- Bertsch, L.; Isermann, U. Noise prediction toolbox used by the DLR aircraft noise working group, INTER-NOISE 2013. In Proceedings of the 42nd International Congress and Exposition on Noise Control Engineering, Innsbruck, Austria, 15–18 September 2013. [Google Scholar]
- Zorumski, W.E. Aircraft Noise Prediction Program Theoretical Manual-Part 2; NASA Technical Memorandum 83199; National Aeronautics and Space Administration: Washington, DC, USA, 1982. [Google Scholar]
- ANOPP and ANOPP2. Available online: https://software.nasa.gov/software/LAR-19861-1 (accessed on 30 September 2021).
- Filippone, A.; Bertsch, L.; Pott-Pollenske, M. Validation strategies for comprehensive aircraft noise prediction methods. In Proceedings of the 12th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference and 14th AIAA/ISSM, Indianapolis, IN, USA, 17–19 September 2012. [Google Scholar] [CrossRef]
- ANP-Eurocontrol Experimental Centre. Available online: https://www.aircraftnoisemodel.org/ (accessed on 30 September 2021).
- ICAO. Environmental Protection. In Annex 16 to the Convention on International Civil Aviation, 8th ed.; Vol. I: Aircraft Noise, Chapter 12; ICAO: Montreal, QC, Canada, 2017. [Google Scholar]
- Berton, J.J.; Huff, D.L.; Geiselhart, K.; Seidel, J. Supersonic Technology Concept Aeroplanes for Environmental Studies. In Proceedings of the AIAA SciTech Forum and Exposition, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Nöding, M.; Bertsch, L. Application of Noise Certification Regulations within Conceptual Aircraft Design. Aerospace 2021, 8, 210. [Google Scholar] [CrossRef]
- Berton, J.J.; Jones, S.M.; Seidel, J.A.; Huff, D.L. Noise predictions for a supersonic business jet using advanced take-off procedures. Aeronaut. J. 2018, 122, 556–571. [Google Scholar] [CrossRef]
- Project-MORE&LESS. Available online: https://www.h2020moreandless.eu/project/ (accessed on 25 October 2021).
- Raymer, P.D. Aircraft Design: A Conceptual Approach, 5th ed.; Shetz, J.A., Ed.; AIAA Education Series; Wright-Patterson Air Force Base: Fairborn, OH, USA, 2013. [Google Scholar]
- Torenbeek, E. Advanced Aircraft Design: Conceptual Design, Analysis and Optimization of Subsonic Civil Airplanes; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Ferretto, D.; Fusaro, R.; Viola, N. Innovative Multiple Matching Charts approach to support the conceptual design of hypersonic vehicles. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2020, 234, 1893–1912. [Google Scholar] [CrossRef]
- Ferretto, D.; Fusaro, R.; Viola, N. A conceptual design tool to support high-speed vehicle design. In Proceedings of the AIAA AVIATION 2020 FORUM, Virtual Event, 15–19 June 2020; p. 22. [Google Scholar] [CrossRef]
- Fusaro, R.; Ferretto, D.; Viola, N. MBSE approach to support and formalize mission alternatives generation and selection processes for hypersonic and suborbital transportation systems. In Proceedings of the 2017 IEEE International Systems Engineering Symposium (ISSE), Vienna, Austria, 11–13 October 2017; p. 8088275. [Google Scholar] [CrossRef]
- Fusaro, R.; Viola, N.; Fenoglio, F.; Santoro, F. Conceptual design of a crewed reusable space transportation system aimed at parabolic flights: Stakeholder analysis, mission concept selection, and spacecraft architecture definition. CEAS Space J. 2017, 9, 5–34. [Google Scholar] [CrossRef]
- Nijsse, J. Design and Noise Acceptability of Future Supersonic Transport Aircraft. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2020. [Google Scholar]
- Aerospace Standard ARP86; Standard Values of Atmospheric Absorption as a Function of Temperature and Humidity for Use in Evaluating Aircraft Flyover Noise. SAE International: Warrendale, PA, USA, 1964.
- Hubbard, H.H. Aeroacoustic of Flight Vehicles: Theory and Practice, Volume 1: Noise Sources; NASA Reference Publication 1258, RDC Technical Report 90-3052; NASA Langely Center: Hampton, VA, USA, 1991. [Google Scholar]
- Farassat, F.; Casper, J. Towards an airframe noise prediction methodology: Survey of current approaches. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar] [CrossRef]
- Filippone, A. Aircraft noise prediction. Prog. Aerosp. Sci. 2014, 68, 27–63. [Google Scholar] [CrossRef]
- Bertsch, L.; Simons, D.G.; Snellen, M. Aircraft Noise: The Major Sources, Modelling Capabilities, and Reduction Possibilities; DLR-Interner Berich, DLR-IB 224-2015 A 110, 29 S; 1st Joint DLR & TU Delft Aviation Noise Workshop; Institute of Aerodynamics and Flow Technology: Göttingen, Germany, 2015. [Google Scholar] [CrossRef]
- Morgan, H.G.; Hardin, J.C. Airframe Noise-The Next Aircraft Noise Barrier. J. Aircr. 1975, 12, 622–624. [Google Scholar] [CrossRef]
- Dobrzynski, W. Almost 40 Years of Airframe Noise Research: What Did We Achieve? J. Aircr. 2010, 47, 353–367. [Google Scholar] [CrossRef]
- Fink, M.R. Airframe Noise Prediction Method, FAA Research Report, FAA-RD-77-29; Federal Aviation Administration RD-77-29: Springfield, VA, USA, 1977. [Google Scholar]
- Merino-Martinez, R.; Bertsch, L.; Simons, D.; Snellen, M. Analysis of landing gear noise during approach. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016. [Google Scholar] [CrossRef]
- Ihme, M. Combustion and Engine-Core Noise. Annu. Rev. Fluid Mech. 2017, 49, 277–310. [Google Scholar] [CrossRef]
- Lighthill, M.J. On sound generated aerodynamically I. General theory. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1952, 211, 564–587. [Google Scholar]
- Stone, J.R.; Groesbeck, D.E.; Zola, C.L. Conventional profile coaxial jet noise prediction. AIAA J. 1983, 21, 336–342. [Google Scholar] [CrossRef]
- Feiler, C.E.; Conrad, E.W. Fan Noise from Turbofan Engines. J. Aircr. 1976, 13, 128–134. [Google Scholar] [CrossRef]
- Heidmann, M. Interim Prediction Method for Fan and Compressor Source Noise; Technical Memorandum 19750017876; NASA Lewis Research Center: Cleveland, OH, USA, 1975. [Google Scholar]
- Chima, R.V. Analysis of Buzz in a Supersonic Inlet; NASA, Glenn Research Center: Cleveland, OH, USA, 2012. [Google Scholar]
- Adetifa, O.E. Prediction of Supersonic Fan Noise Generated by Turbofan Aircraft Engines. Ph.D. Thesis, University of Southampton, Faculty of Engineering and the Environment, Southampton, UK, 2015. [Google Scholar]
- ICAO-Reduction of Noise at Source. Available online: https://www.icao.int/environmental-protection/pages/reduction-of-noise-at-source.aspx (accessed on 30 September 2021).
- ICAO. Environmental Technical Manual, Vol. I, Procedures for the Noise Certification of Aircraft; ICAO: Montreal, QC, Canada, 2018. [Google Scholar]
- Talbot, J.E. Concorde Development-Powerplant Installation and Associated Systems, SAE Transactions. J. Aerosp. 1991, 100, 2681–2698. Available online: http://www.jstor.org/stable/44548124 (accessed on 30 September 2021).
- Stiuso, G. Tecnica di Simulazione Numerica delle Prestazioni Stazionarie e Transitorie di Turbomotori. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2019. Available online: http://webthesis.biblio.polito.it/id/eprint/11258 (accessed on 30 September 2021).
- Vasov, L.; Stojiljkovic, B.; Cokorilo, O.; Mirosavljevic, P.; Gvozdenovic, S. Aircraft noise metrics. Saf. Eng. 2014, 4. [Google Scholar] [CrossRef]
- Jones, K.; Cadoux, R. Metrics for Aircraft Noise; R ERCD Report 0904; Environmental Research and Consultancy Department: London, UK, 2009.
- Bennett, R.L.; Pearsons, K.S. Handbook of Aircraft Noise Metrics; NASA Contractor Report; Bolt, Beranek, and Newman, Inc.: Canoga Park, CA, USA, 1981. [Google Scholar]
- ICAO. Environmental Protection. In Annex 16 to the Convention on International Civil Aviation, 8th ed.; Vol. I: Aircraft Noise, Appendix 2; ICAO: Montreal, QC, Canada, 2017. [Google Scholar]
- ICAO. Environmental Protection. In Annex 16 to the Convention on International Civil Aviation, 8th ed.; Vol. I: Aircraft Noise, Appendix 1; ICAO: Montreal, QC, Canada, 2017. [Google Scholar]
- Torija, A.; Woodward, R.; Flindell, I.; McKenzie, A.; Self, R. On the assessment of subjective response to tonal content of contemporary aircraft noise. Appl. Acoust. 2018, 146, 190–203. [Google Scholar] [CrossRef]
- ECAC. CEAC Doc 29, 4th ed. Report on Standard Method of Computing Noise Contours Around Civil Airports. In Proceedings of the European Civil Aviation Conference, European Civil Aviation Conference (ECAC) Document 29, Paris, France, 7 December 2016; Available online: https://www.ecac-ceac.org/ecac-docs (accessed on 30 September 2021).
- Citarella, R.; Federico, L.; Cicatiello, A. Modal acoustic transfer vector approach in a FEM–BEM vibro-acoustic analysis. Eng. Anal. Bound. Elem. 2007, 31, 248–258. [Google Scholar] [CrossRef]
- Kontos, K.B.; Janardan, B.A.; Gliebe, P.R. Improved NASA-ANOPP Noise Prediction Computer Code for Advanced Subsonic Propulsion Systems-Vol. 1 ANOPP Evaluation and Fan Noise Model Imporvements; NASA Contractor Report 195480; NASA: Cincinnati, OH, USA, 2013. [Google Scholar]
- Krejsa, E.A.; Stone, J.R. Enhanced Fan Noise Modeling for Turbofan Engines; NASA Contractor Report 218421; NASA: Cincinnati, OH, USA, 2014. [Google Scholar]
- ICAO. Environmental Protection. In Annex 16 to the Convention on International Civil Aviation, 8th ed.; Vol. I: Aircraft Noise, Chapter 14; ICAO: Montreal, QC, Canada, 2017. [Google Scholar]
- Saiyed, N.; Mikkelsen, K.; Bridges, J. Acoustics and Thrust of Separate-Flow Exhaust Nozzles with Mixing Devices for High Bypass- Ratio Engines. AIAA J. 2003, 41, 372–378. [Google Scholar] [CrossRef]
- Callender, B.; Gutmark, E.; Martens, S. Far-Field Acoustic Investigation into Chevron Nozzle Mechanisms and Trends. AIAA J. 2005, 43, 87–95. [Google Scholar] [CrossRef]
- Rask, O.; Kastner, J.; Gutmark, E. Understanding How Chevrons Modify Noise in Supersonic Jet with Flight Effects. AIAA J. 2011, 49, 1569–1576. [Google Scholar] [CrossRef]
- Cuppoletti, D.R. Supersonic Jet Noise Reduction with Novel Fluidic Injection Techniques. Ph.D. Thesis, University of Cincinnati, Cincinnati, OH, USA, 2013. [Google Scholar]
- Semlitsch, B.; Cuppoletti, D.R.; Gutmark, E.J.; Mihăescu, M. Transforming the Shock Pattern of Supersonic Jets Using Fluidic Injection. AIAA J. 2019, 57, 1851–1861. [Google Scholar] [CrossRef]
- Sahai, A.K. Consideration of Aircraft Noise Annoyance During Conceptual Aircraft Design. Ph.D. Thesis, Rheinisch-Westfälische Technische Hochschule Aachen, Aachen, Germany, 2016. Available online: https://publications.rwth-aachen.de/record/668901 (accessed on 25 October 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).