An Analytical Model for the Uniaxial Tensile Modulus of Plain-Woven Fabric Composites and Its Application and Experimental Validation

Abstract

With advantages in efficiency and convenience, analytical models using experimental inputs to predict the mechanical properties of plain-woven fabric (PWF) composites are reliable in guaranteeing the composites’ engineering applications. Considering the importance of the aspect above, a new analytical model for predicting the uniaxial tensile modulus of PWF is proposed in this article. The composite yarns are first simplified as the lenticular-shaped cross-sections undulate along arc-composed paths. Force analyses of the yarn segments are then carried out with the internal interactions simplified, and the analytical model is subsequently deduced from the principle of minimum potential energy and Castigliano’s second theorem. The PWF of T300/Cycom970 is chosen as the study object to which the proposed analytical model is applied. Microscopic observations and thermal ablation experiments are conducted on the specimens to obtain the necessary inputs. The uniaxial tensile modulus is calculated and tensile experiments on the laminates are performed to validate the analytical prediction. The small deviation between the experimental and analytical results indicates the feasibility of the proposed analytical model, which has good prospects in validating the effectiveness of the experimentally obtained modeling parameters and guaranteeing the accuracy of mesoscale modeling for the PWF.

1. Introduction

With the characteristics of lighter weight in addition to higher stiffness and strength, fiber-reinforced composites have been widely used in the aerospace industry. In order to reduce production costs and simplify the machining processes plain-woven fabric composites are becoming increasingly important in the design and manufacturing of lightweight aerospace structures.

With the aim of improving the level of structural design and analysis, it is necessary to understand the loading response and failure mechanism of plain-woven composites. Research has been widely carried out and various experimental techniques as well as methods have been utilized in the study of plain-woven composites. X-ray tomography and microscale measurement systems are important in measuring the 3D coordinates of plain-woven composites’ mesoscale structures and establishing mesoscale geometric models. Experimental observations based on the above methods [1,2] have contributed to a direct understanding of the composites’ woven morphology and offered enlightenment in the accurate modeling of the interlaced yarns. Wang et al. [3] used micro-CT equipment with a high-resolution lens-coupled detector to reconstruct 3D images of C/epoxy plain-woven composites. Based on the obtained clear 3D image of the T300/epoxy material, the statistical properties of the yarn feature parameters that were then analyzed. Scanning electron microscopes (SEMs) and digital imaging systems are also frequently used in the microscopic observations of composites. With the assistance of microscopic observations, Carvalho et al. [4] investigated the compressive failure of orthogonal 2D woven composites. The regional failure of the load-aligned tows was studied and the damage propagation process was analyzed in detail. Specialized fixtures have also been designed for different test targets. With a picture-frame apparatus Nguyen et al. [5] studied the shearing properties of plain-woven fabrics and prepregs. Experimental investigations on the shear properties of the fabric composites were conducted and the relationships between the shearing angle and the applied load for different weave architectures were analyzed.

Experimental results provide the basis on which plain-woven composites could be modeled. With the numerical models, the finite-element (FE) method has been widely applied in the analysis of plain-woven fabrics due to its advantages in calculation efficiency and low cost. In the FE modeling of plain-woven fabrics the industrial application of advanced meshing methods has attracted a growing interest due to its operational convenience [6]. The applicability of voxel meshes in the numerical modeling of plain-woven composites was studied by Doitrand et al. [7], and the calculation accuracy of the voxel method was evaluated. Grail et al. [8] developed an automated method to generate consistent FE meshes for plain-woven composites. Based on the proposed method, a representative unit cell (RUC) of a compacted and nested multilayer woven composite was generated.

Obtaining the mechanical properties of the plain-woven composites and evaluating the properties’ effects are necessary preconditions for the following structural analysis. With the assistance of RUC models and FE analyses, Goyal et al. [9] investigated the effects of geometric parameters and basic material properties on the effective engineering properties of plain-woven braids. Matveev et al. [10] numerically studied the effects of fiber strength on the macroscale strength of textile composites and found that a wide fiber strength distribution led to a narrow distribution of composite strength. In evaluating the mechanical properties’ effects and predicting the mechanical response of braided composites, Richter et al. [11] proposed a simulation framework with a meshing methodology that considered yarn-to-yarn delamination. The validation of the framework underlined the great potential for further damage modeling of the fabric composites.

The simulation of failure is also an important concern in the FE analysis of fabrics. In order to understand the elementary damage mechanisms and investigate the development of damage in detail, advanced techniques such as improved two-dimensional generalized plane strain FE models [12], the cracking kinetics simulation [13] and shear nonlinearity incorporated failure process modeling [14] have been utilized in investigations. Important damage details have been captured and the relationships between ply damage behaviors and elementary damage mechanisms have been linked.

Macro fabric composite structures could be further studied at the mesoscale of the fiber tows and the microscale of the constituents. In the multiscale failure analyses of the fabric composites micromechanics-based failure theories [15,16,17,18] are becoming increasingly appealing for researchers due to their advantage in explaining the failure of composites at the constituent level [19]. By combining macroscale FE models with RUCs of meso- and microscales the multiscale analysis method takes the advantages of both the efficiency of the macro analysis and the accuracy of the micromechanics-based failure criteria [20]. The effectiveness of the multiscale analysis in predicting the fabric composites’ damage initiation and failure process [21,22,23] indicated the huge potential of the micromechanics-based methods’ further engineering applications.

The mesoscale RUC is an important stress transformation medium of the plain-woven fabric composites’ multiscale analysis, and its accurate establishment is necessary for further failure analysis. Microscopic observations and basic tests could be conducted, making it convenient to obtain the geometric and mechanical parameters of the fabric composites. However, the feasibility of the experimentally obtained parameters in modeling the RUC needs further validation considering the dispersibility and errors in the experiments. In predicting the properties of textile composites, analytical solutions suitable for engineering applications have been proposed [24,25,26,27,28]. Although the theoretical foundations are solid the geometric parameters and internal force analyses have been oversimplified and idealized in previous research [24,28], and the prediction accuracy could be further raised with the improvement of the previous models. Using the fiber tows’ geometric and mechanical parameters as inputs and having an advantage in calculation efficiency, reliable analytical models have broad prospects in engineering applications in validating the effectiveness of the experimentally obtained modeling parameters and guaranteeing the accuracy of the established RUC.

In this article attempts have been made to develop a new reliable analytical model with experimental inputs in calculating the uniaxial tensile modulus of plain-woven fabric composites.

In the Section 2 the cross-section and undulation path of the fiber tows are reasonably simplified and geometrically expressed with parameters and formulations. Within the mesoscale RUC the studied yarn segments are assigned.

In the Section 3 the interactions between the warp and weft yarns are simplified and the internal forces of the studied yarn segments are analyzed in detail.

In the Section 4 the analytical model is developed. The analytical solution for the uniaxial tensile modulus is derived from the elastic deformation energy analysis with the fiber tows’ internal forces more comprehensively considered. The necessary parameters of inputs are referred and the matched experiments to obtain the parameters are designed.

Finally, in the Section 5 the proposed analytical model is applied to predict the uniaxial tensile modulus of T300/Cycom970, and the application process is introduced in detail. Tensile experiments on the T300/Cycom970 laminates are conducted and the effectiveness of the analytical model is validated.

2. Simplification of the Cross-Section and Undulation Path of the Fiber Tows

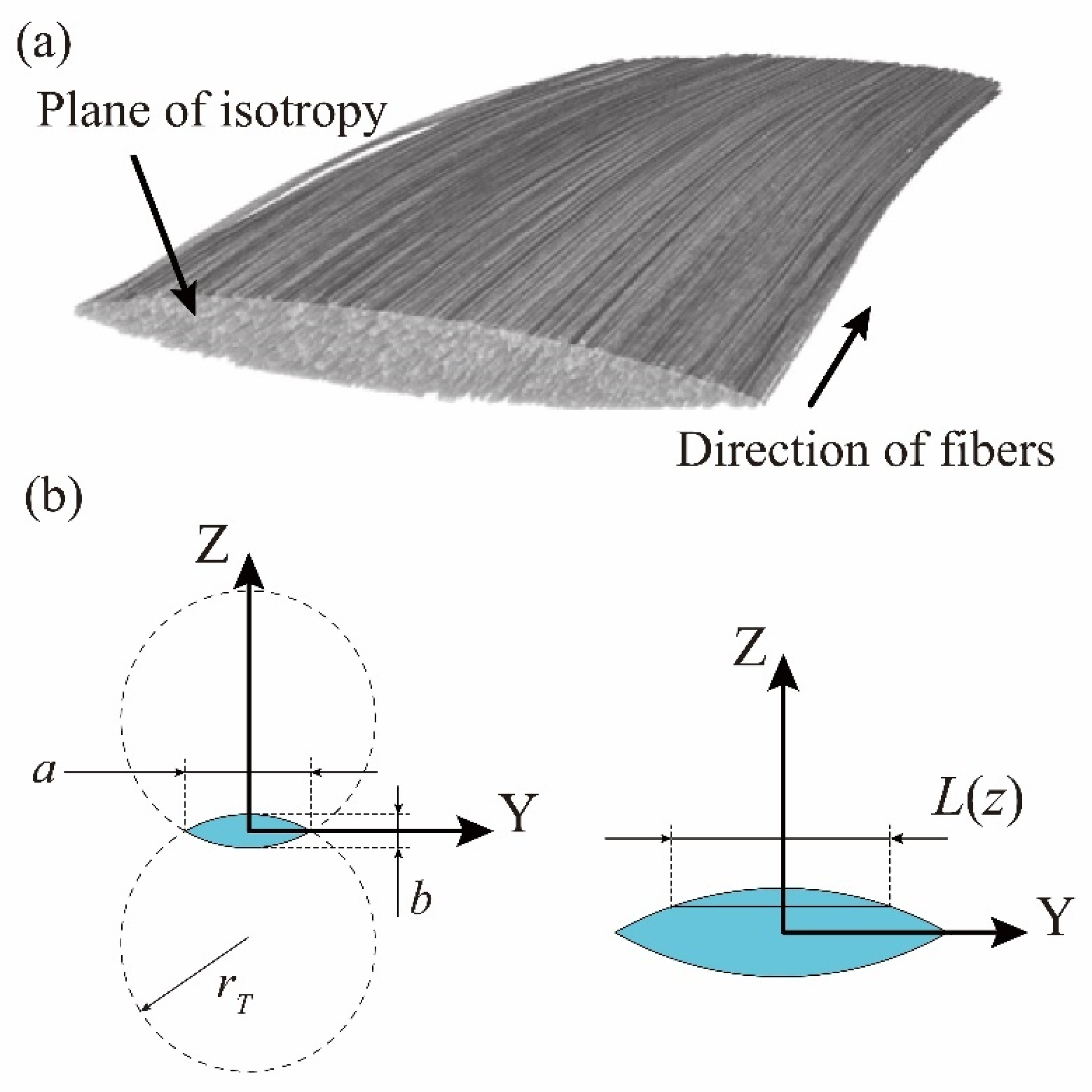
Due to the randomness of the woven prepregs and the influence of the hot-pressing manufacturing process there are difficulties in accurately describing the irregular-shaped cross-section of the fiber tows with certain parameters. Therefore, the simplification of the cross-section is needed as an important basis for the analytical solution of the fabric composites. Compared to the observations from computed tomography (CT), as illustrated in Figure 1a, previous research results [29,30] indicate that the lenticular shape best approaches the cross-section of the plain-woven composites’ fiber tows. Besides, the lenticular-shaped cross-section exceeds the other frequently used sections in ensuring the fiber tows of the warp and weft directions realistically contact without interpenetration. Considering the above advantages, the lenticular shape is chosen to simplify the cross-section of the fiber tows in this article.

The warp yarn is taken as the example and the cross-section is projected onto the Y–Z plane, as presented in Figure 1b. The controlling parameters in defining the lenticular-shaped cross-section are a, b and r_T, which represent the width, thickness and controlling radius of the cross-section, respectively:

$$r_T-\sqrt{r_T{}^2-\frac{1}{4}{a}^2}=\frac{1}{2}b$$

(1)

In Figure 1b, z stands for the ordinate value of the Y–Z plane and L(z) stands for the z-corresponded horizontal intercept of the cross-section. The area, A, and the inertia moment of the cross-section, I, for the fiber tows in the warp and the weft directions are then expressed as follows:

$$A={\displaystyle {\int }_{A}dA}=2{\displaystyle {\int }_0^{b/2}L(z)dz}$$

(2)

$$I=I_x=I_y={\displaystyle {\int }_A{z}^{2}dA}=2{\displaystyle {\int }_0^{b/2}{z}^{2}L(z)dz}$$

(3)

Referring to Equation (1), the area and the inertia moment are further expressed as:

$$A=4{\displaystyle {\int }_0^{b/2}\sqrt{{\left(\frac{a^2+b^2}{4b}\right)}^2-{[\sqrt{{\left(\frac{a^2+b^2}{4b}\right)}^2-{(\frac{1}{2}a)}^2}+z]}^2}dz}$$

(4)

$$I=4{\displaystyle {\int }_0^{b/2}{z}^2\sqrt{{\left(\frac{a^2+b^2}{4b}\right)}^2-{[\sqrt{{\left(\frac{a^2+b^2}{4b}\right)}^2-{(\frac{1}{2}a)}^2}+z]}^2}dz}$$

(5)

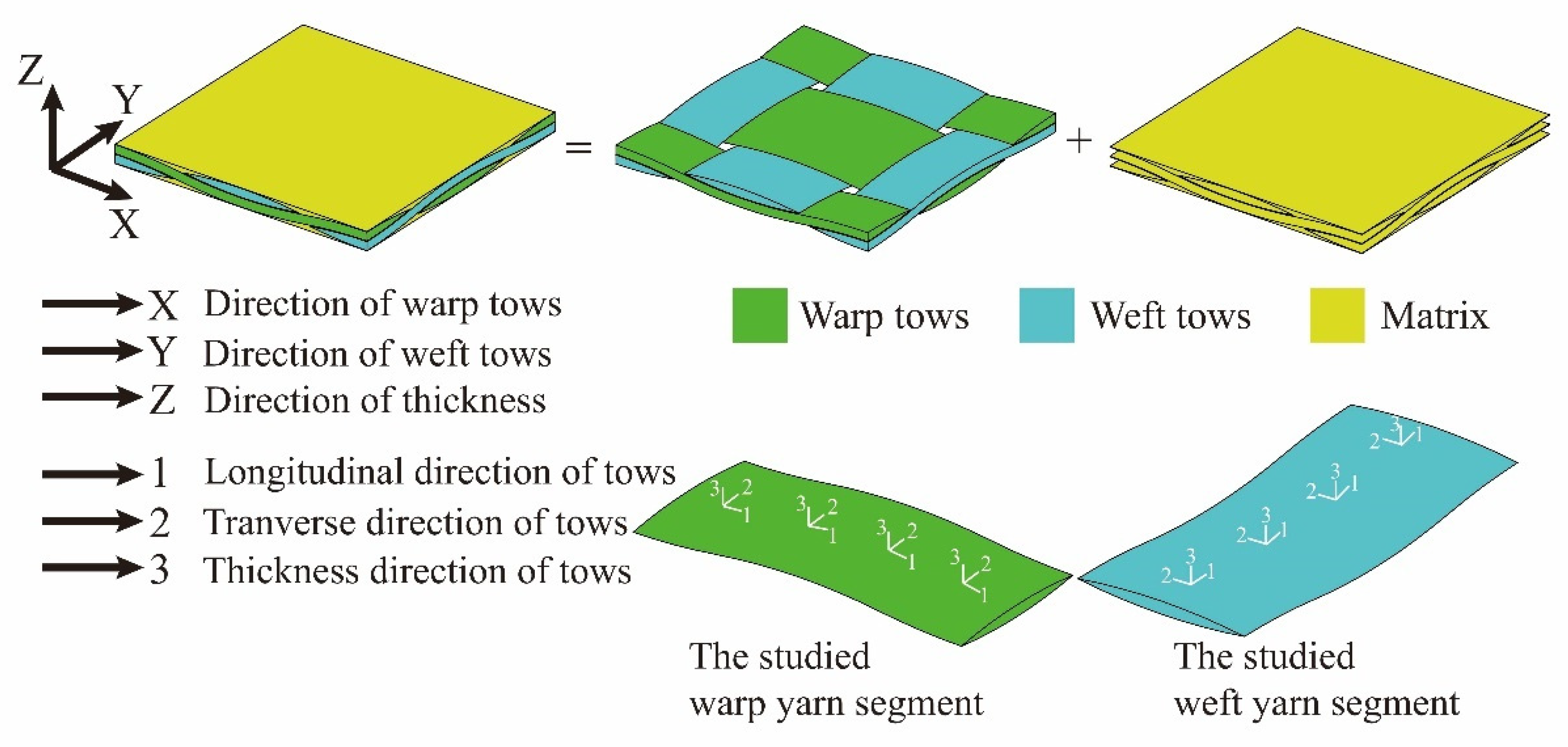
Corresponding to the lenticular-shaped cross-section, the undulation path composed of arcs with the same radius is used in this article. With the periodic characteristics of the plain-woven fabric composites, the analysis is performed on the mesoscale RUC, inside of which the segments of the warp and weft yarns are taken as the study objects, as illustrated in Figure 2.

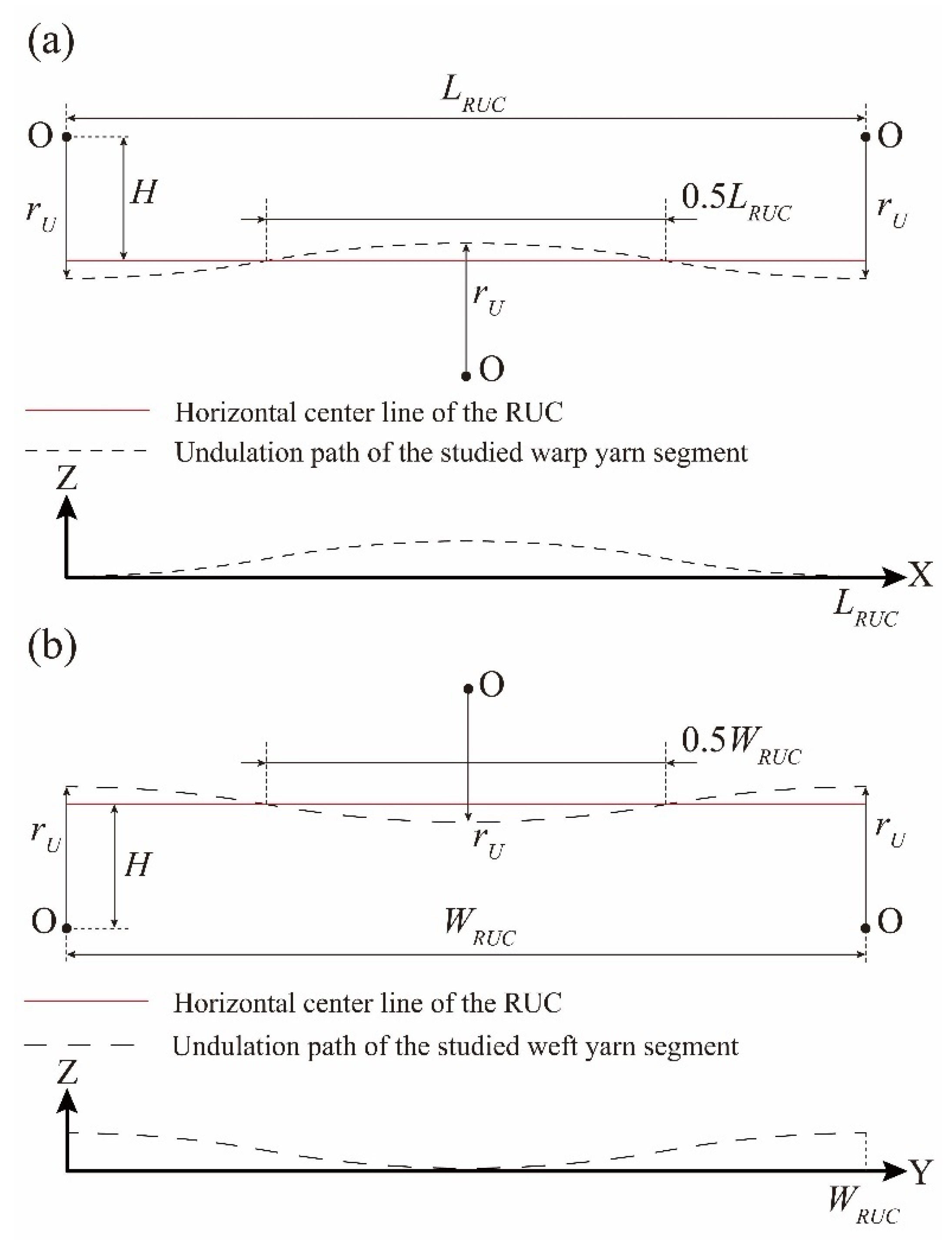
The undulation path of the studied warp yarn segment is presented in Figure 3a. r_U represents the radius of the arcs and L_RUC represents the length of the mesoscale RUC. H stands for the distance between the horizontal center line of the RUC and the center of the arcs in the undulation path:

$$H=\sqrt{r_U{}^2-{(\frac{1}{4}{L}_{RUC})}^2}$$

(6)

For the studied weft yarn segment in Figure 2 the geometric parameters of the undulation path in Figure 3b remain the same, and the width of the mesoscale RUC (W_RUC) is equal to L_RUC, considering the plain-woven structure of the fabric composites.

In the x range of $\left(0,\frac{1}{2}{L}_{RUC}\right)$ the undulation path function z₁(x) of the warp yarn segment corresponding to Figure 3a is expressed as:

$$z_1(x)=\{\begin{array}{c}{r}_U-\sqrt{r_U{}^2-x^2},x=0~\frac{1}{4}{L}_{RUC}\\ r_U-2H+\sqrt{r_U{}^2-{(x-\frac{1}{2}{L}_{RUC})}^2},x=\frac{1}{4}{L}_{RUC}~\frac{1}{2}{L}_{RUC}\end{array}$$

(7)

Similarly, for the weft yarn segment in Figure 3b the undulation path function z₂(y) is expressed as:

$$z_2(y)=\{\begin{array}{c}{r}_U-2H+\sqrt{r_U{}^2-y^2},y=0~\frac{1}{4}{W}_{RUC}\\ r_U-\sqrt{r_U{}^2-{(y-\frac{1}{2}{W}_{RUC})}^2},y=\frac{1}{4}{W}_{RUC}~\frac{1}{2}{W}_{RUC}\end{array}$$

(8)

3. Force Analysis of the Fiber Tows under Uniaxial Tension Load

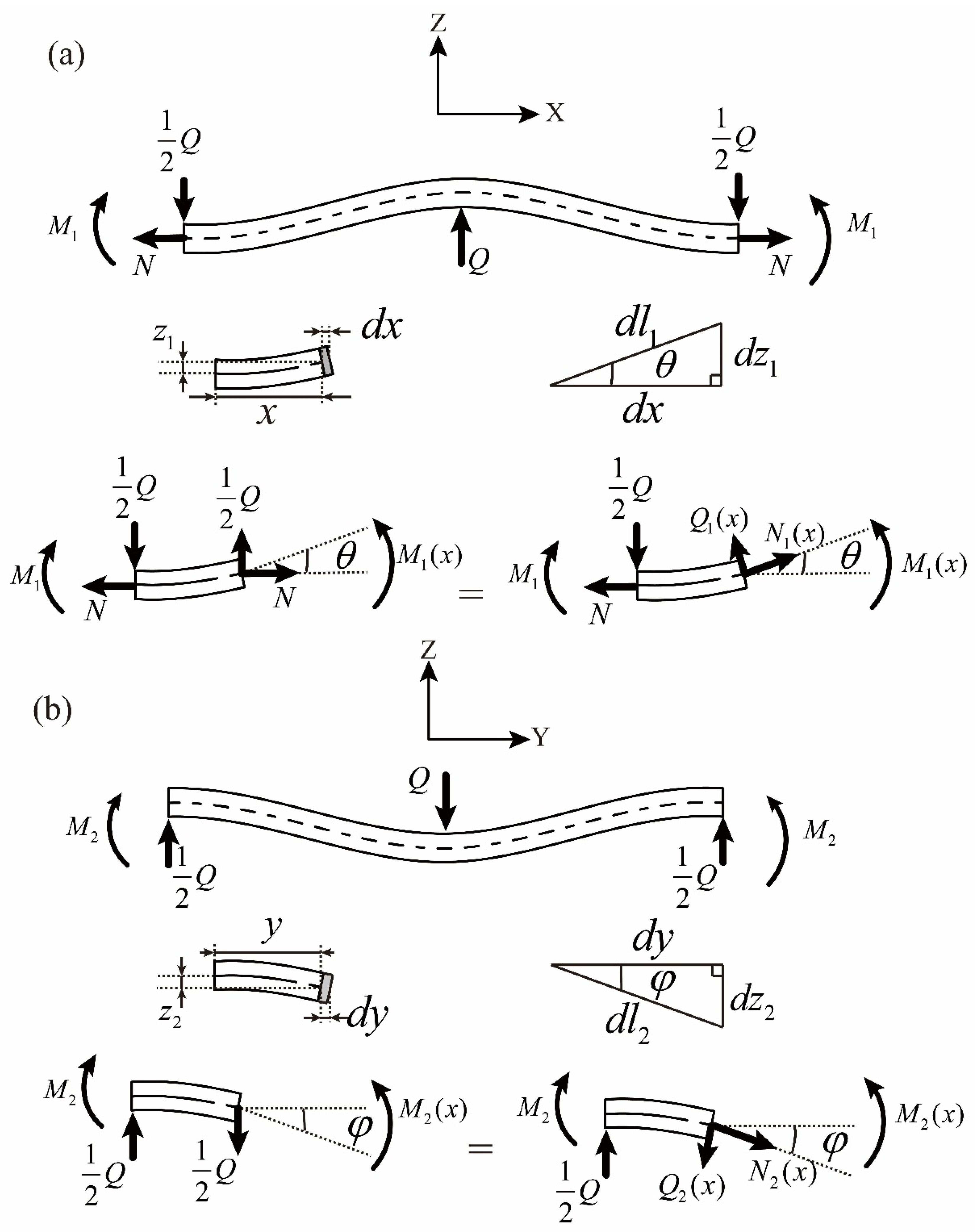
The monolayer of the plain-woven fabric composites under the uniaxial tension load along the warp direction is presented in Figure 4a. As the warp yarns are straightened the distributed interaction force of q between the weft and warp yarns exists in hindering the straightening of the warp yarns and causing the crimping of the weft yarns. For the convenience of the following analyses the distributed interaction force of q is simplified as the concentrate force of Q, as illustrated in Figure 4b.

For the studied mesoscale RUC of the plain-woven fabric composites in Figure 2, the force analyses of the warp and weft yarn segments are illustrated in Figure 5.

In Figure 5a the axial load of N and the constraint moment of M₁ are loaded at the boundary cross-sections of the warp yarn segment. The interaction loads of Q and ½Q from the weft yarns concentrate at the middle location and the left and right endpoints, respectively. dl₁ stands for the differential length of the warp yarn segment and θ stands for the angle between dl₁ and the X-axis. At the x-corresponded cross-section in the warp yarn segment the horizontal internal load of N and the vertical internal load of ½Q, which satisfy the force balance condition, are further converted into the internal tensile load N₁(x) and the internal shearing load Q₁(x), which are perpendicular and parallel to the cross-section, respectively.

For the cross-sections of the studied warp yarn segment, within the range of (0, ½L_RUC) along the X-axis, the internal bending moment M₁(x) is expressed as:

$$M_1(x)=M_1+N{z}_1(x)-\frac{1}{2}Qx$$

(9)

The internal tensile load $N_1\left(x\right)$ is expressed as:

$$N_1(x)=N\cos \theta +\frac{1}{2}Q\sin \theta =\frac{N}{\sqrt{1+{\tan }^2\theta }}+\frac{Q\tan \theta }{2\sqrt{1+{\tan }^2\theta }}$$

(10)

Additionally, the internal shearing load $Q_1\left(x\right)$ is expressed as:

$$Q_1(x)=N\sin \theta -\frac{1}{2}Q\cos \theta =\frac{N\tan \theta }{\sqrt{1+{\tan }^2\theta }}-\frac{Q}{2\sqrt{1+{\tan }^2\theta }}$$

(11)

For the weft yarn segment in Figure 5b the constraint moments of M₂ are loaded at the boundary cross-sections and the interaction loads of Q and ½Q from the warp yarns concentrate at the middle location and the left and right endpoints, respectively. The angle between the differential length of the weft yarn segment dl₂ and the Y-axis is presented as φ. Similar to the warp yarn segment, the vertical internal load of $\frac{1}{2}Q$ at the y-corresponded cross-section in the weft yarn segment is converted into the internal tensile load N₂(y) and the internal shearing load Q₂(y).

For the cross-sections of the studied weft yarn segment, within the range of (0, ½W_RUC) along the Y-axis, the internal bending moment M₂(y) is expressed as:

$$M_2(y)=M_2+\frac{1}{2}Qy$$

(12)

The internal tensile load N₂(y) is expressed as:

$$N_2(y)=\frac{1}{2}Q\sin \phi =\frac{Q\tan \phi }{2\sqrt{1+{\tan }^2\phi }}$$

(13)

Additionally, the internal shearing load Q₂(y) is expressed as:

$$Q_2(y)=\frac{1}{2}Q\cdot \cos \phi =\frac{Q}{2\sqrt{1+{\tan }^2\phi }}$$

(14)

Considering the arc-shaped undulation paths of the warp and weft yarns, the tangents of θ and φ are, respectively, expressed as:

$$\tan \theta =\frac{d{z}_1}{dx}=\{\begin{array}{c}\frac{x}{\sqrt{r_U{}^2-x^2}},x=0~\frac{1}{4}{L}_{RUC}\\ \frac{\frac{1}{2}{L}_{RUC}-x}{\sqrt{r_U{}^2-{(x-\frac{1}{2}{L}_{RUC})}^2}},x=\frac{1}{4}{L}_{RUC}~\frac{1}{2}{L}_{RUC}\end{array}$$

(15)

$$\tan \phi =\frac{d{z}_2}{dy}=\{\begin{array}{c}\frac{-y}{\sqrt{r_U{}^2-y^2}},y=0~\frac{1}{4}{W}_{RUC}\\ \frac{y-\frac{1}{2}{W}_{RUC}}{\sqrt{r_U{}^2-{(y-\frac{1}{2}{W}_{RUC})}^2}},y=\frac{1}{4}{W}_{RUC}~\frac{1}{2}{W}_{RUC}\end{array}$$

(16)

4. Analytical Solution in Predicting the Uniaxial Tensile Modulus of the Plain-Woven Fabric Composites

The parameters of E_11(tow), G_12(tow) and G_13(tow) stand for the longitudinal modulus, the in-plane shear modulus and the out-of-plane shear modulus of the plain-woven fabric composites’ fiber tows, respectively. Under the hypothesis of transverse isotropy G_12(tow) is equal to G_13(tow). L₁ and L₂ stand for the lengths of the warp and weft yarn segments illustrated in Figure 2, respectively. Under the hypothesis that the shearing stress is uniformly distributed on the fiber tow’s cross-section the strain energy of the studied warp yarn segment is presented as U₁:

$$\begin{array}{l}{U}_1=\frac{1}{2E_{11(tow)}I}{\displaystyle {\int }_0^{L_1}{M}_1{(x)}^{2}d{l}_1}+\frac{1}{2E_{11(tow)}A}{\displaystyle {\int }_0^{L_1}{N}_1{(x)}^{2}d{l}_1}+\frac{1}{2G_{13(tow)}A}{\displaystyle {\int }_0^{L_1}{Q}_1{(x)}^{2}d{l}_1}\\ =\frac{1}{2E_{11(tow)}I}{\displaystyle {\int }_0^{L_{RUC}}\frac{M_1{(x)}^2}{\cos \theta }dx}+\frac{1}{2E_{11(tow)}A}{\displaystyle {\int }_0^{L_{RUC}}\frac{N_1{(x)}^2}{\cos \theta }dx}+\frac{1}{2G_{13(tow)}A}{\displaystyle {\int }_0^{L_{RUC}}\frac{Q_1{(x)}^2}{\cos \theta }dx}\end{array}$$

(17)

For the studied weft yarn segment the strain energy U₂ is expressed as:

$$\begin{array}{l}{U}_2=\frac{1}{2E_{11(tow)}I}{\displaystyle {\int }_0^{L_2}{M}_2{(y)}^{2}d{l}_2}+\frac{1}{2E_{11(tow)}A}{\displaystyle {\int }_0^{L_2}{N}_2{(y)}^{2}d{l}_2}+\frac{1}{2G_{13(tow)}A}{\displaystyle {\int }_0^{L_2}{Q}_2{(y)}^{2}d{l}_2}\\ =\frac{1}{2E_{11(tow)}I}{\displaystyle {\int }_0^{W_{RUC}}\frac{M_2{(y)}^2}{\cos \phi }dy}+\frac{1}{2E_{11(tow)}A}{\displaystyle {\int }_0^{W_{RUC}}\frac{N_2{(y)}^2}{\cos \phi }dy}+\frac{1}{2G_{13(tow)}A}{\displaystyle {\int }_0^{W_{RUC}}\frac{Q_2{(y)}^2}{\cos \phi }dy}\end{array}$$

(18)

In the above equations the cosines of θ and φ are, respectively, expressed as:

$$\cos \theta =\frac{1}{\sqrt{1+{\tan }^2\theta }}=\{\begin{array}{c}\frac{\sqrt{r_U{}^2-x^2}}{r_U},x=0~\frac{1}{4}{L}_{RUC}\\ \frac{\sqrt{r_U{}^2-{(x-\frac{1}{2}{L}_{RUC})}^2}}{r_U},x=\frac{1}{4}{L}_{RUC}~\frac{1}{2}{L}_{RUC}\end{array}$$

(19)

$$\cos \phi =\frac{1}{\sqrt{1+{\tan }^2\phi }}=\{\begin{array}{c}\frac{\sqrt{r_U{}^2-y^2}}{r_U},y=0~\frac{1}{4}{W}_{RUC}\\ \frac{\sqrt{r_U{}^2-{(y-\frac{1}{2}{W}_{RUC})}^2}}{r_U},y=\frac{1}{4}{W}_{RUC}~\frac{1}{2}{W}_{RUC}\end{array}$$

(20)

The simplification functions of C₁(x), C₂(y), S₁(x) and S₂(y) are defined as:

$$C_1(x)=\sqrt{r_U{}^2-x^2},C_2(y)=\sqrt{r_U{}^2-y^2}$$

(21)

$$S_1(x)=\sqrt{r_U{}^2-{(x-\frac{1}{2}{L}_{RUC})}^2},S_2(y)=\sqrt{r_U{}^2-{(y-\frac{1}{2}{W}_{RUC})}^2}$$

(22)

Putting the internal loads of Equations (9)–(11) into the strain energy formulation in Equation (17), U₁ could be further expressed with the simplified intermediate coefficients of X₁, X₂, X₃₁, X₅, X₆ and X₇ as follows, considering the symmetrical characteristics of the studied warp yarn segment:

$$\begin{array}{l}{U}_1=\frac{1}{E_{11(tow)}I}\{{\displaystyle {\int }_0^{\frac{L_{RUC}}{4}}\frac{{\{M_1+N[r_U-C_1(x)]-\frac{1}{2}Qx\}}^2{r}_U}{C_1(x)}dx}\\ +{\displaystyle {\int }_{\frac{L_{RUC}}{4}}^{\frac{L_{RUC}}{2}}\frac{{\{M_1+N[r_U-2H+S_1(x)]-\frac{1}{2}Qx\}}^2\cdot r_U}{S_1(x)}dx}\}\\ +\frac{1}{E_{11(tow)}A}\{{\displaystyle {\int }_0^{\frac{L_{RUC}}{4}}\frac{{[2N{C}_1(x)+Q\cdot x]}^2}{4r_U{C}_1(x)}dx}+{\displaystyle {\int }_{\frac{L_{RUC}}{4}}^{\frac{L_{RUC}}{2}}\frac{{[2N{S}_1(x)-Q(x-\frac{L_{RUC}}{2})]}^2}{4r_U{S}_1(x)}dx}\}\\ +\frac{1}{G_{13(tow)}A}\{{\displaystyle {\int }_0^{\frac{L_{RUC}}{4}}\frac{{[2Nx-Q{C}_1(x)]}^2}{4r_U{C}_1(x)}dx}+{\displaystyle {\int }_{\frac{L_{RUC}}{4}}^{\frac{L_{RUC}}{2}}\frac{{[2N(x-\frac{L_{RUC}}{2})+Q{S}_1(x)]}^2}{4r_U{S}_1(x)}dx}\}\\ =M_1{}^2\cdot X_1+N^2\cdot X_2+Q^2\cdot X_{31}+M_{1}N\cdot X_5-M_{1}Q\cdot X_6-NQ\cdot X_7\end{array}$$

(23)

Similarly, for the studied weft yarn segment U₂ could be further expressed with the simplified intermediate coefficients of X₃₂, X₄ and X₈ as:

$$\begin{array}{l}{U}_2=\frac{1}{E_{11(tow)}I}[{\displaystyle {\int }_0^{\frac{W_{RUC}}{4}}\frac{{(M_2+\frac{1}{2}Qy)}^2{r}_U}{C_2(y)}dy}+{\displaystyle {\int }_{\frac{W_{RUC}}{2}}^{\frac{W_{RUC}}{4}}\frac{{(M_2+\frac{1}{2}Qy)}^2{r}_U}{S_2(y)}dy}]\\ +\frac{1}{E_{11(tow)}A}[{\displaystyle {\int }_0^{\frac{W_{RUC}}{4}}\frac{Q^2{y}^2}{4r_U{C}_2(y)}dy}+{\displaystyle {\int }_{\frac{W_{RUC}}{4}}^{\frac{W_{RUC}}{2}}\frac{Q^2{(y-\frac{1}{2}{W}_{RUC})}^2}{4r_U{S}_2(y)}dy}]\\ +\frac{1}{G_{13(tow)}A}[{\displaystyle {\int }_0^{\frac{W_{RUC}}{4}}\frac{Q^2{C}_2(y)}{4r_U}dy}+{\displaystyle {\int }_{\frac{W_{RUC}}{4}}^{\frac{W_{RUC}}{2}}\frac{Q^2{S}_2(y)}{4r_U}dy}]\\ =Q^2\cdot X_{32}+M_2{}^2\cdot X_4+M_{2}Q\cdot X_8\end{array}$$

(24)

The simplified intermediate coefficients in the above equations of (23) and (24) are expressed as follows:

$$X_1={\displaystyle {\int }_0^{\frac{L_{RUC}}{4}}\frac{r_U}{E_{11(tow)}I{C}_1(x)}}dx+{\displaystyle {\int }_{\frac{L_{RUC}}{4}}^{\frac{L_{RUC}}{2}}\frac{r_U}{E_{11(tow)}I{S}_1(x)}dx}$$

(25)

$$\begin{array}{l}{X}_2={\displaystyle {\int }_0^{\frac{L_{RUC}}{4}}\{\frac{r_U{[r_U-C_1(x)]}^2}{E_{11(tow)}I{C}_1(x)}+\frac{C_1(x)}{E_{11(tow)}A{r}_U}+\frac{x^2}{G_{13(tow)}A{r}_U{C}_1(x)}\}}dx\\ +{\displaystyle {\int }_{\frac{L_{RUC}}{4}}^{\frac{L_{RUC}}{2}}\{\frac{r_U{[r_U-2H+S_1(x)]}^2}{E_{11(tow)}I{S}_1(x)}+\frac{S_1(x)}{E_{11(tow)}A{r}_U}+\frac{{(x-\frac{1}{2}{L}_{RUC})}^2}{G_{13(tow)}A{r}_U{S}_1(x)}}\}dx\end{array}$$

(26)

$$\begin{array}{l}{X}_{31}={\displaystyle {\int }_0^{\frac{L_{RUC}}{4}}[\frac{r_U{x}^2}{4E_{11(tow)}I{C}_1(x)}}+\frac{x^2}{4E_{11(tow)}A{r}_U{C}_1(x)}+\frac{C_1(x)}{4G_{13(tow)}A{r}_U}]dx\\ +{\displaystyle {\int }_{\frac{L_{RUC}}{4}}^{\frac{L_{RUC}}{2}}[\frac{r_U{x}^2}{4E_{11(tow)}I{S}_1(x)}+\frac{{(x-\frac{1}{2}{L}_{RUC})}^2}{4E_{11(tow)}A{r}_U{S}_1(x)}+\frac{S_1(x)}{4G_{13(tow)}A{r}_U}]}dx\end{array}$$

(27)

$$\begin{array}{l}{X}_{32}={\displaystyle {\int }_0^{\frac{W_{RUC}}{4}}[\frac{r_U{y}^2}{4E_{11(tow)}I{C}_2(y)}+\frac{y^2}{4E_{11(tow)}A{r}_U{C}_2(y)}+\frac{C_2(y)}{4G_{13(tow)}A{r}_U}]}dy\\ +{\displaystyle {\int }_{\frac{W_{RUC}}{4}}^{\frac{W_{RUC}}{2}}[\frac{r_U{y}^2}{4E_{11(tow)}I{S}_2(y)}}+\frac{{(y-\frac{1}{2}{W}_{RUC})}^2}{4E_{11(tow)}A{r}_U{S}_2(y)}+\frac{S_2(y)}{4G_{13(tow)}A{r}_U}]dy\end{array}$$

(28)

$$X_4={\displaystyle {\int }_0^{\frac{W_{RUC}}{4}}\frac{r_U}{E_{11(tow)}I{C}_2(y)}}dy+{\displaystyle {\int }_{\frac{W_{RUC}}{4}}^{\frac{W_{RUC}}{2}}\frac{r_U}{E_{11(tow)}I{S}_2(y)}}dy$$

(29)

$$X_5={\displaystyle {\int }_0^{\frac{L_{RUC}}{4}}\frac{2r_U[r_U-C_1(x)]}{E_{11(tow)}I{C}_1(x)}}dx+{\displaystyle {\int }_{\frac{L_{RUC}}{4}}^{\frac{L_{RUC}}{2}}\frac{2r_U[r_U-2H+S_1(x)]}{E_{11(tow)}I{S}_1(x)}}dx$$

(30)

$$X_6={\displaystyle {\int }_0^{\frac{L_{RUC}}{4}}\frac{r_{U}x}{E_{11(tow)}I{C}_1(x)}}dx+{\displaystyle {\int }_{\frac{L_{RUC}}{4}}^{\frac{L_{RUC}}{2}}\frac{r_{U}x}{E_{11(tow)}I{S}_1(x)}}dx$$

(31)

$$\begin{array}{l}{X}_7={\displaystyle {\int }_0^{\frac{L_{RUC}}{4}}\{\frac{r_{U}x[r_U-C_1(x)]}{E_{11(tow)}I{C}_1(x)}-\frac{x}{E_{11(tow)}A{r}_U}+\frac{x}{G_{13(tow)}A{r}_U}\}}dx\\ +{\displaystyle {\int }_{\frac{L_{RUC}}{4}}^{\frac{L_{RUC}}{2}}\{\frac{r_{U}x[r_U-2H+S_1(x)]}{E_{11(tow)}I{S}_1(x)}+\frac{x-\frac{1}{2}{L}_{RUC}}{E_{11(tow)}A{r}_U}-\frac{x-\frac{1}{2}{L}_{RUC}}{G_{13(tow)}A{r}_U}\}}dx\end{array}$$

(32)

$$X_8={\displaystyle {\int }_0^{\frac{W_{RUC}}{4}}\frac{r_{U}y}{E_{11(tow)}I{C}_2(y)}}dy+{\displaystyle {\int }_{\frac{W_{RUC}}{4}}^{\frac{W_{RUC}}{2}}\frac{r_{U}y}{E_{11(tow)}I{S}_2(y)}}dy$$

(33)

By defining the intermediate coefficient of X₃ as:

$$X_3=X_{31}+X_{32}$$

(34)

the total strain energy, U, for the part of the fiber tows in the mesoscale RUC of Figure 2 could then be obtained as:

$$\begin{array}{l}U=2(U_1+U_2)\\ =2(M_1{}^2\cdot X_1+N^2\cdot X_2+Q^2\cdot X_3+M_2{}^2\cdot X_4+M_{1}N\cdot X_5-M_{1}Q\cdot X_6-NQ\cdot X_7+M_{2}Q\cdot X_8)\end{array}$$

(35)

Constraint at the left end, the right end’s displacement of the deformed warp yarn segment along the X-axis corresponding to the axial tensile load of N is presented as u₁ in Figure 6.

For the studied warp yarn segment in Figure 2 U₁* stands for its complementary energy. According to Castigliano’s second theorem:

$$u_1=\frac{\partial U_1{}^{*}}{\partial N}$$

(36)

Within the framework of the ideal linear elasticity U₁* is equal to the strain energy U₁, and u₁ in Figure 6 could be expressed as:

$$\begin{array}{l}{u}_1=\frac{\partial U_1}{\partial N}\\ ={\displaystyle {\int }_0^{L_{RUC}}\frac{M_1(x)}{E_{11(tow)}I\cos \theta }\cdot \frac{\partial M_1(x)}{\partial N}dx}+{\displaystyle {\int }_0^{L_{RUC}}\frac{N_1(x)}{E_{11(tow)}A\cos \theta }\cdot \frac{\partial N_1(x)}{\partial N}dx}\\ +{\displaystyle {\int }_0^{L_{RUC}}\frac{Q_1(x)}{G_{13(tow)}A\cos \theta }\cdot \frac{\partial Q_1(x)}{\partial N}dx}\\ =2X_{2}N+X_5{M}_1-X_{7}Q\end{array}$$

(37)

The constraint moments of M₁ and M₂ and the interaction load of $Q$ are all introduced by $N$, which is the only external load applied to warp yarn in the monolayer of the plain-woven fabric composites. Under the linear hypothesis within the small deformation extents the constraint moments and the interaction load are supposed linearly correlated with the external load, N, through the coefficients of k₁, k₂ and k₃:

$$M_1=k_1\cdot N$$

(38)

$$M_2=k_2\cdot N$$

(39)

$$Q=k_3\cdot N$$

(40)

Putting Equations (38)–(40) into Equation (35), the total strain energy of U then turns into:

$$U=2(k_1{}^2{X}_1+X_2+k_3{}^2{X}_3+k_2{}^2{X}_4+k_1{X}_5-k_1{k}_3{X}_6-k_3{X}_7+k_2{k}_3{X}_8)\cdot N^2$$

(41)

For the part of fiber tows in the mesoscale RUC of Figure 2, the total potential energy is defined as Π and the external work is defined as W. Considering the total strain energy of U, Π could be expressed as:

$$\Pi =U-W$$

(42)

According to the principle of minimum potential energy, among all the displacement solutions which satisfy the geometric boundary conditions the real displacement solution minimizes the structural total potential energy. Corresponding to the minimum total potential energy, Π_min, under real structural displacement the reasonable choice of the coefficients k₁, k₂ and k₃ minimizes the total strain energy, U, which leads to:

$$\frac{\partial U}{\partial k_i}=0,i=1~3$$

(43)

The coefficients of k₁, k₂ and k₃ are then determined as:

$$k_1=\frac{\frac{X_7{X}_6}{2X_1}-\frac{X_5{X}_6{}^2}{4X_1{}^2}}{2X_3-\frac{X_6{}^2}{2X_1}-\frac{X_8{}^2}{2X_4}}-\frac{X_5}{2X_1}$$

(44)

$$k_2=\frac{(\frac{X_5{X}_6}{2X_1}-X_7)X_8}{(4X_3-\frac{X_6{}^2}{X_1}-\frac{X_8{}^2}{X_4})X_4}$$

(45)

$$k_3=\frac{X_7-\frac{X_5{X}_6}{2X_1}}{2X_3-\frac{X_6{}^2}{2X_1}-\frac{X_8{}^2}{2X_4}}$$

(46)

The relationships in Equations (38)–(40) with k₁, k₂ and k₃ in Equations (44)–(46) could also be deduced from the principle of the minimum complementary energy as presented in Equations (47)–(49), indicating the rationality of the linear hypothesis:

$$\frac{\partial U_1{}^{*}}{\partial M_1}=0$$

(47)

$$\frac{\partial U_1{}^{*}}{\partial M_2}=0$$

(48)

$$\frac{\partial U_1{}^{*}}{\partial Q}=0$$

(49)

Considering Equations (44)–(46) and putting Equations (38)–(40) into Equation (37), the relationship between u₁ and N in Figure 6 could be further determined with the intermediate coefficient of X₉:

$$u_1=X_{9}N$$

(50)

where:

$$X_9=2X_2-\frac{X_5{}^2}{2X_1}+\frac{2X_5{X}_6{X}_7-2X_1{X}_7{}^2-\frac{X_5{}^2{X}_6{}^2}{2X_1}}{4X_1{X}_3-X_6{}^2-\frac{X_1{X}_8{}^2}{X_4}}$$

(51)

The part composed of fiber tows in the mesoscale RUC is isolated and studied in Figure 7. With the left-end constraint the displacement of the loading end reaches u₁ under the total axial tension of 2N loaded at the cross-sections of the warp yarns with the area of 2A, corresponding to the result of the single warp yarn segment in Figure 6.

For the studied part in Figure 7, define the equivalent modulus along the X-axis as E_tt and u₁ could be expressed as:

$$u_1=\frac{N{L}_{RUC}}{E_{tt}A}$$

(52)

Put Equation (50) into Equation (52) and the modulus of E_tt is determined as:

$$E_{tt}=\frac{L_{RUC}}{X_{9}A}$$

(53)

E_m stands for the elastic modulus of the matrix and V_t stands for the volume fraction of the tows in the plain-woven fabric composites. Based on the rule of mixtures, the uniaxial tensile modulus, E₁₁, of the plain-woven fabric composites could be expressed as:

$$\begin{array}{l}{E}_{11}=E_{tt}{V}_t+E_m(1-V_t)\\ =\frac{L_{RUC}}{X_{9}A}\cdot V_t+E_m(1-V_t)\end{array}$$

(54)

With the above deductions, the proposed analytical model for the uniaxial tensile modulus of the plain-woven fabric composites is illustrated in Figure 8. Based on the experimental observations, the necessary geometric parameters of the fiber tows and the RUC, including a, b, r_U and L_RUC, are first obtained as inputs. The corresponding cross-section area of A and the inertia moment of I are subsequently calculated. Series of experiments including the thermal ablation of the laminates and microscopic observations are needed in order to achieve the fiber volume fraction in tows, V_f, and the volume fraction of tows, V_t. Besides, parameters of the elastic modulus of the matrix, E_m, the shear modulus of the matrix, G_m, the in-plane shear modulus of the fiber, G_f12, and the longitudinal modulus of the fiber, E_f11, need to be obtained, with which the longitudinal modulus of E_11(tow) and the out-of-plane shear modulus of G_13(tow) for the fiber tows could be calculated through the Chamis equations:

$$E_{11(tow)}=V_f{E}_{f11}+(1-V_f)E_m$$

(55)

$$G_{13(tow)}=\frac{G_m}{1-\sqrt{V_f}(1-\frac{G_m}{G_{f12}})}$$

(56)

Subsequently, the intermediate coefficients of $X_1$–$X_9$ could be achieved and the uniaxial tensile modulus of $E_{11}$ is analytically solved. Using the platform of an Intel Core i7-9750H CPU, the single run time of the analytical model in calculating $E_{11}$ is 2 s with the necessary inputs prepared.

5. Application of the Analytical Model and the Experimental Validation

The plain-woven fabric composite of T300/Cycom970 is chosen as the study object in this article and the uniaxial tensile modulus of E₁₁ is predicted with the method proposed above. The mechanical properties of the T300 carbon fiber and the Cycom970 epoxy matrix [31] are presented in

Table 1. Mechanical properties of the fiber and matrix constituents in the T300/Cycom970 composite.

Constituent	Material Property	Value
Fiber (T300)	Longitudinal modulus, Ef11 (GPa)	230.00
	Transverse modulus, Ef22 = Ef33 (GPa)	13.80
	In-plane shear modulus, Gf12 (GPa)	8.97
	Out-of-plane shear modulus, Gf13 (GPa)	8.97
	Out-of-plane shear modulus, Gf23 (GPa)	4.38
	In-plane Poisson’s ratio, νf12	0.20
	Out-of-plane Poisson’s ratio, νf13	0.20
	Out-of-plane Poisson’s ratio, νf23	0.25
	Density, ρf (g/cm3)	1.76
Matrix (Cycom970)	Elastic modulus, Em (GPa)	3.35
	Elastic Poisson’s ratio, νm	0.35
	Density, ρm (g/cm3)	1.24

.

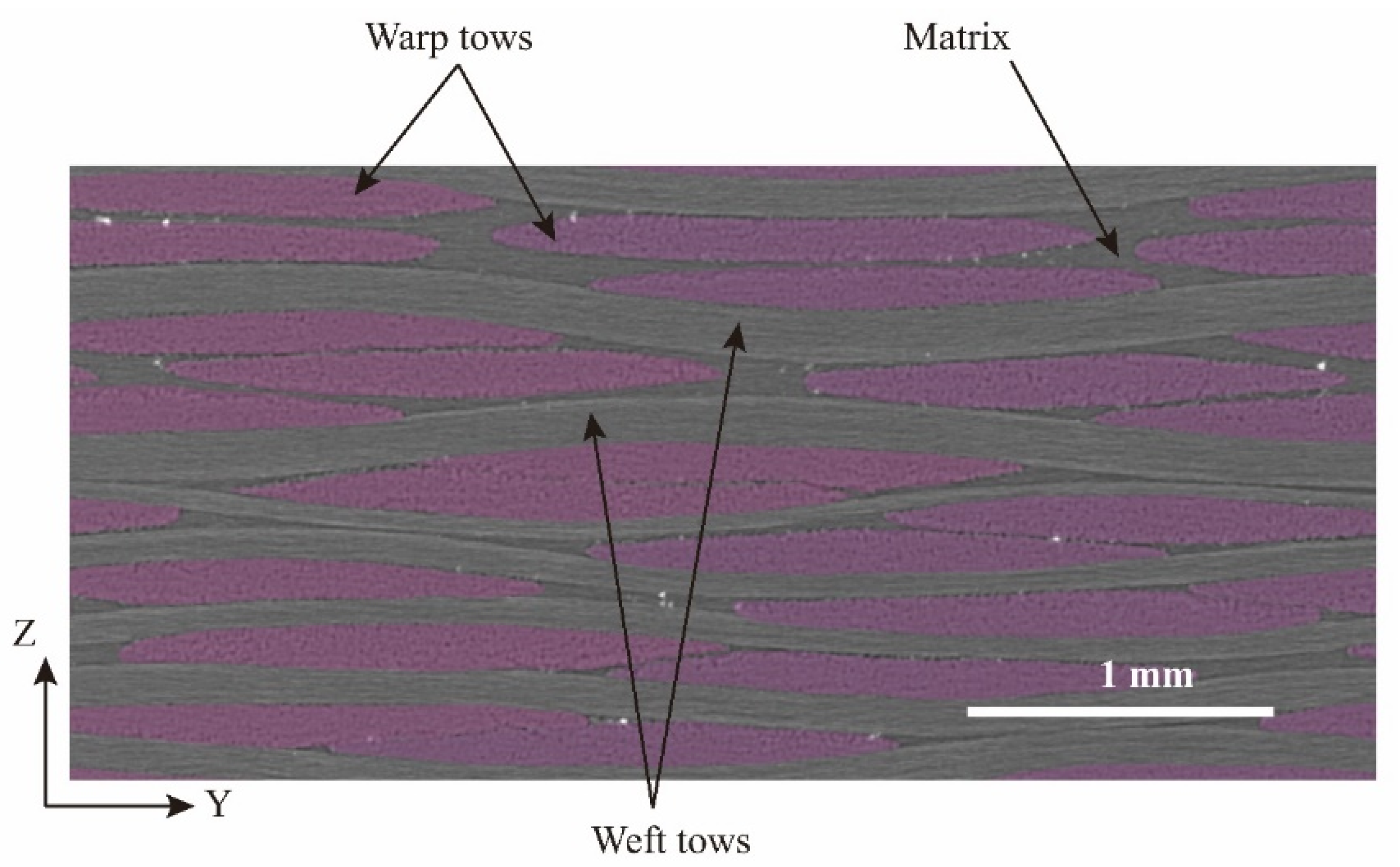
Specimens of T300/Cycom970 laminates with a stacking sequence of [0]₁₆ and dimensions of 25 mm × 25 mm × 3.456 mm are manufactured and scanned first with micro-CT equipment to achieve the necessary geometric parameters. As a carbon fiber/epoxy composite, the similar atomic numbers of the fiber and the matrix in the T300/Cycom970 laminates lead to a small difference in the components’ X-ray absorption rates. In order to solve the blurry imaging problem micro-CT equipment with a high-resolution lens-coupled detector is utilized in the current scanning. A typical Y–Z slice image of the fabric laminate is illustrated in Figure 9 and the statistical average values of a, b, r_U and L_RUC from different samples of sections are presented in

Table 2. Geometric parameters of fiber tows in the T300/Cycom970 plain-woven fabric composite.

Geometric Parameter	Value
Width of the fiber tows’ lenticular cross-section, a (mm)	1.82
Thickness of the fiber tows’ lenticular cross-section, b (mm)	0.13
Radius of the arcs in fiber tows’ undulation path, rU (mm)	7.18
Length of the mesoscale RUC, LRUC (mm)	4.00
Area of the fiber tows’ lenticular cross-section, A (mm2)	0.16
Inertia of the fiber tows’ lenticular cross-section, I (10−4 mm4)	1.67

, together with the corresponding A and I.

Thermal ablation experiments have been conducted on the specimens under the ASTM Standard D3171 [32]-based procedure in order to separate the component of the fiber from the matrix and obtain the total fiber volume fraction of V_fT. The specimens are first weighed with an electronic balance and the initial weight of m₀ for each specimen is achieved. After heating with a chamber furnace under a temperature of 600 °C for four hours, as shown in Figure 10, the epoxy matrix component in the specimens is totally ablated and the residual weight of fibers, m_f, for each specimen is recorded. For each of the specimens, with the densities of the matrix (ρ_m) and the carbon fiber (ρ_f) presented in Table 1, the total fiber volume fraction, V_fT, of the plain-woven fabric composite could be obtained as:

$$V_{fT}=\frac{m_f\cdot {\rho }_m}{m_f\cdot {\rho }_m+(m_0-m_f)\cdot {\rho }_f}$$

(57)

The results of the thermal ablation experiments on the specimens, numbered one–five, are presented in

Table 3. Results of the thermal ablation experiments.

Specimen	Initial Weight ${\mathit{m}}_0$ (g)	Residual Weight ${\mathit{m}}_{\mathit{f}}$ (g)	Total Fiber Volume Fraction ${\mathit{V}}_{\mathit{f}\mathit{T}}$
No. 1	3.21	2.07	0.56
No. 2	3.23	2.09	0.56
No. 3	3.22	2.04	0.55
No. 4	3.20	2.05	0.56
No. 5	3.20	2.05	0.56

. For the studied composite of T300/Cycom970, V_fT is determined as the statistical average value of the experimental results.

In obtaining the fiber volume fraction in tows of V_f, microscopic observations have been conducted on the plain-woven fabric composites. In order to achieve ideal observation results focused ion beam (FIB) polishing has been conducted on the specimen, and the regions of the fiber tows’ cross-sections are then observed with a scanning electron microscope (SEM), as shown in Figure 11. Within a fixed observation area the regions of the fiber sections are distinguished from the adjacent matrix regions through further digital image processing of the observation result. $A_f$ and $A_m$, which represent the area of the fibers and the area of the matrix, respectively, are achieved, and the regional fiber volume fraction, which is equal to the area ratio of $A_f/\left(A_f+A_m\right)$, is then calculated. A typical microscopic observation on the cross-section of the fiber tows and the corresponding digital image processing result are presented in Figure 11, and the value of $V_f$ for the plain-woven fabric composite is determined as the statistical average value of the obtained different regional fiber volume fractions.

According to the Equation (58) the volume fraction of tows, V_t, of the T300/Cycom970 fabric composite could be obtained with V_fT and V_f:

$$V_t=\frac{V_{fT}}{V_f}$$

(58)

The finally determined values of $V_{fT}$, $V_f$ and $V_t$ are listed in

Table 4. Volume fraction parameters of the T300/Cycom970 plain-woven fabric composite.

Parameter	Value
Total fiber volume fraction, VfT	0.56
Fiber volume fraction in tows, Vf	0.78
Volume fraction of tows, Vt	0.72

. Based on the fiber volume fraction in tows of $V_f$ and the constituents’ properties in Table 1, the calculations of the fiber tows’ mechanical properties based on the Chamis equations are presented in

Table 5. Mechanical properties of the fiber tows in the T300/Cycom970 plain-woven fabric composite.

Property	Value
Longitudinal modulus, E11(tow) (GPa)	180.24
Transverse modulus, E22(tow) = E33(tow) (GPa)	10.27
In-plane shear modulus, G12(tow) (GPa)	9.66
Out-of-plane shear modulus, G13(tow) (GPa)	9.66
Out-of-plane shear modulus, G23(tow) (GPa)	3.78

.

With the above inputs the intermediate coefficients of X₁–X₉ are calculated according to the flowchart illustrated in Figure 8, and the result of E₁₁ for the T300/Cycom970 plain-woven fabric composite is predicted as 54.39 MPa.

Tensile experiments have been performed on the laminates made of T300/Cycom970 plain-woven fabrics. The experimental result is compared with the above prediction of E₁₁ in order to validate the proposed analytical model.

Considering the purpose of validation, the manufacturing process of the composite laminates has been intentionally controlled to enhance the specimens’ consistency and reduce the effects of uncertainty. The specimens with a stacking sequence of [0]₁₆ and dimensions of 250 mm × 25 mm × 3.456 mm are shown in Figure 12, which are tested by an electronic universal testing machine with a maximum loading capacity of 100 kN. Six specimens numbered CL-1-01 to CL-1-06 have been tested under the ASTM Standard D3039M-17 [33]-based procedure. Subjected to tensile loading, the stress–strain curves of the specimens have been achieved, with longitudinal strain results obtained from the strain gages. For two different points on the stress–strain curve, the difference in the applied tensile stress is defined as Δσ and the difference between the strains is defined as Δε. Stress–strain data within the lower half of the stress–strain curves are utilized ito calculate the uniaxial tensile modulus of E₁₁:

$$E_{11}=\frac{\Delta \sigma }{\Delta \epsilon }$$

(59)

In

Table 6. Experimental uniaxial tensile modulus of the T300/Cycom970 fabric laminates and comparison with the analytical solution.

Specimen	Experimental E11 (GPa)	Average Value (GPa)	Standard Deviation (GPa)	Coefficient of Dispersion (%)	Analytical Solution of E11 (GPa)	Relative Deviation (%)
CL-1-01	57.35	56.85	0.72	1.27	54.39	−4.33
CL-1-02	57.21
CL-1-03	56.52
CL-1-04	56.21
CL-1-05	55.85
CL-1-06	57.96

the experimental E₁₁ of the specimens is listed, along with the average value, the standard deviation and the coefficient of dispersion. The small values of the standard deviation and the coefficient of dispersion indicate the good repeatability of the experimental results. With neglectable effects of uncertainty, the specimens behave well in the aspect of validation. Compared to the average value of the experimental E₁₁ the calculation result from the analytical model of 54.39 MPa has a deviation of −4.33%. The small deviation validates the effectiveness of the analytical model in predicting the unidirectional tensile modulus of the plain-woven fabric composites and further indicates the rationality of the inputs of the experimentally obtained geometric and mechanical parameters, which could be utilized in the establishment of the composites’ mesoscale RUC.

6. Conclusions

(1) With a solid theoretical foundation and validated by tensile experiments on the laminates, the analytical model based on the energy principles has a small margin of error and a high calculation efficiency. The model provides a new and effective method to predict the uniaxial tensile modulus of plain-woven fabric composites.

(2) The matched experiments were designed to obtain inputs for the analytical model and were conducted to predict the uniaxial tensile modulus of the T300/Cycom970 composite. The experimental procedure provides a reference for the further study of PWF composites’ geometric and mechanical properties.

(3) The proposed analytical model relies heavily on the inputs obtained from experimental methods; the costly experiments limit the wide application of the analytical model to some extent. Besides, the cross-section of fiber tows and the interaction between the warp and weft yarns are simplified in the analytical model for the convenience of the analyses. Although the current margin of error is experimentally validated a more comprehensive and detailed consideration of the fiber tows’ geometric characteristics and internal interactions is still needed in further research.

(4) With the advantages in efficiently validating the choosing of the fiber tows’ geometric and mechanical parameters, the analytical model has good application prospects in guiding the mesoscale modeling of plain-woven fabric composites. In future work the mesoscale RUC will be built on the current basis and multiscale failure analyses could be further carried out on the T300/Cycom970 PWF composite laminates and structures.