A Numerical Study on Aircraft Noise Mitigation Using Porous Stator Concepts
Abstract
:1. Introduction
2. Methods
2.1. Description of Numerical Method
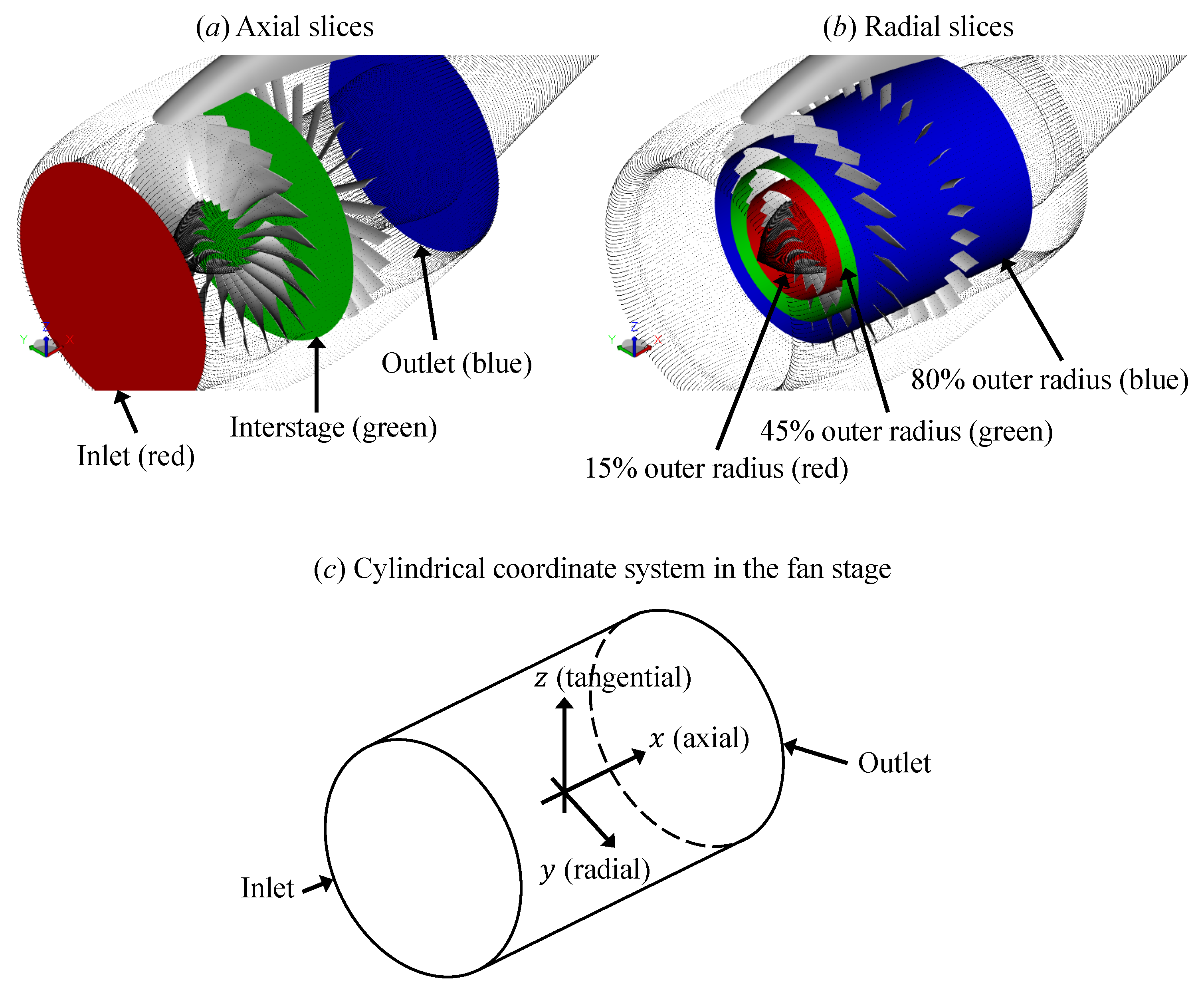
2.2. Simulation Setup
3. Simulation Verifications
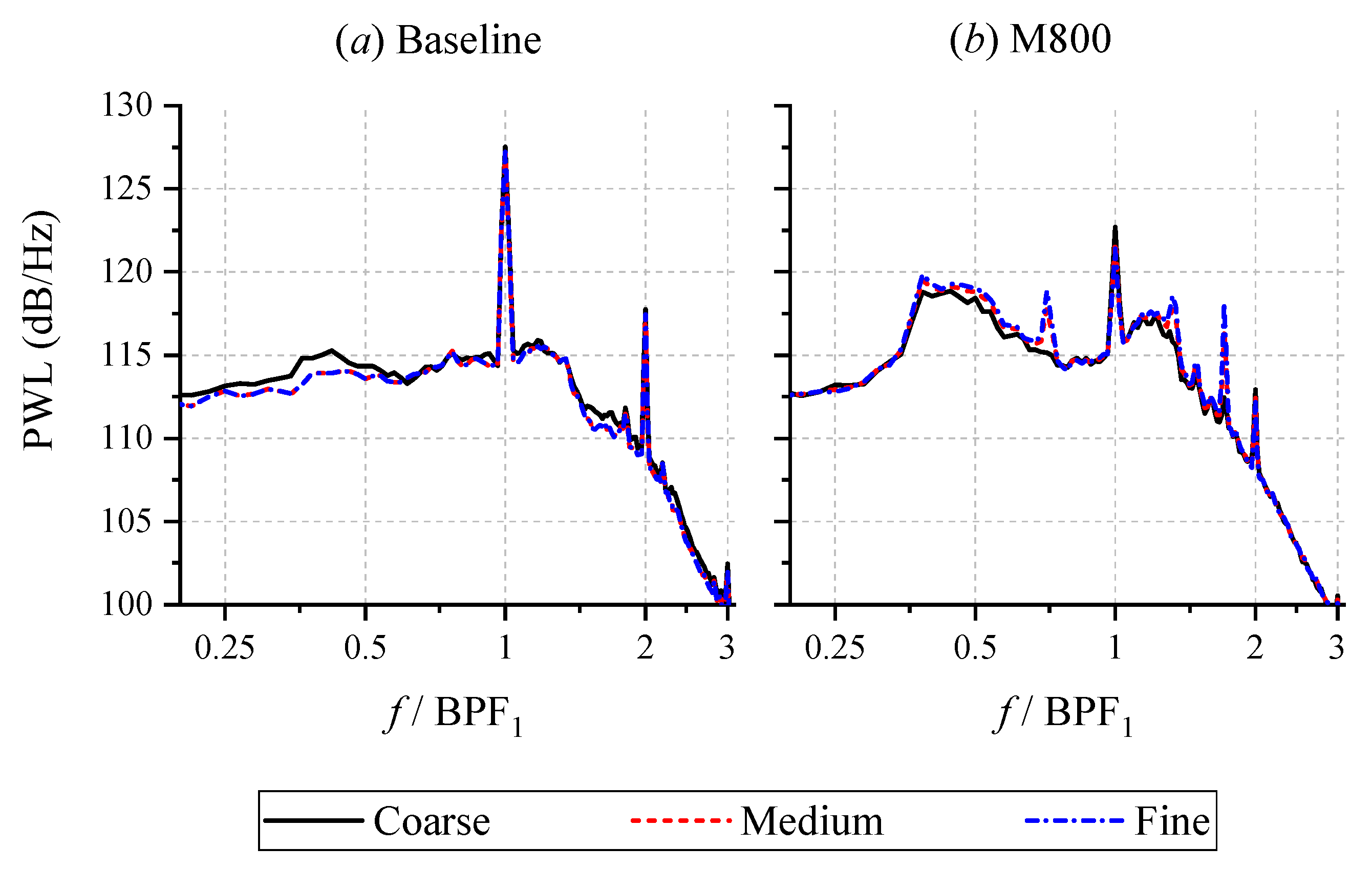
3.1. Grid-Convergence Study
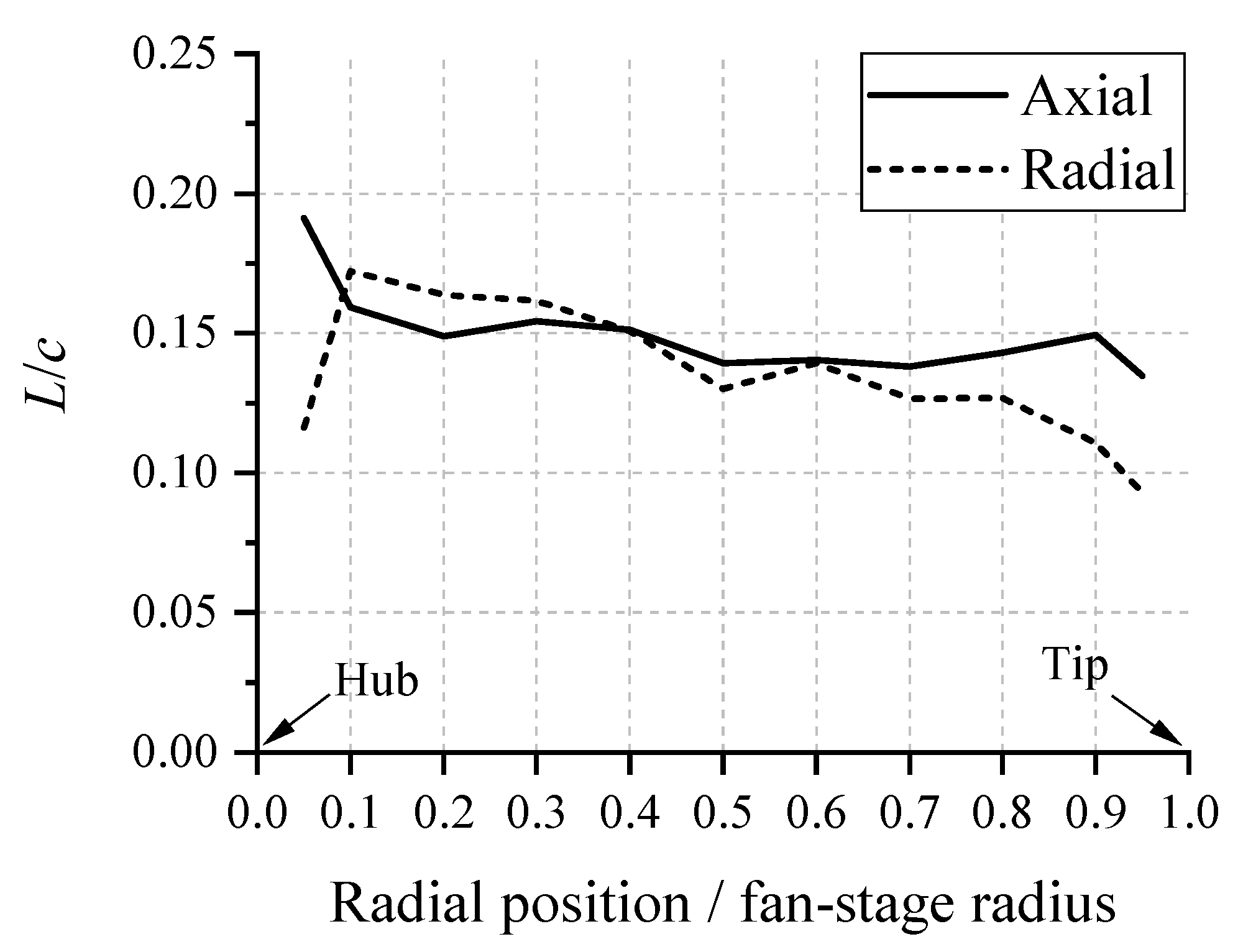
3.2. Integral Length Scales and Serration Design Verification
4. Results
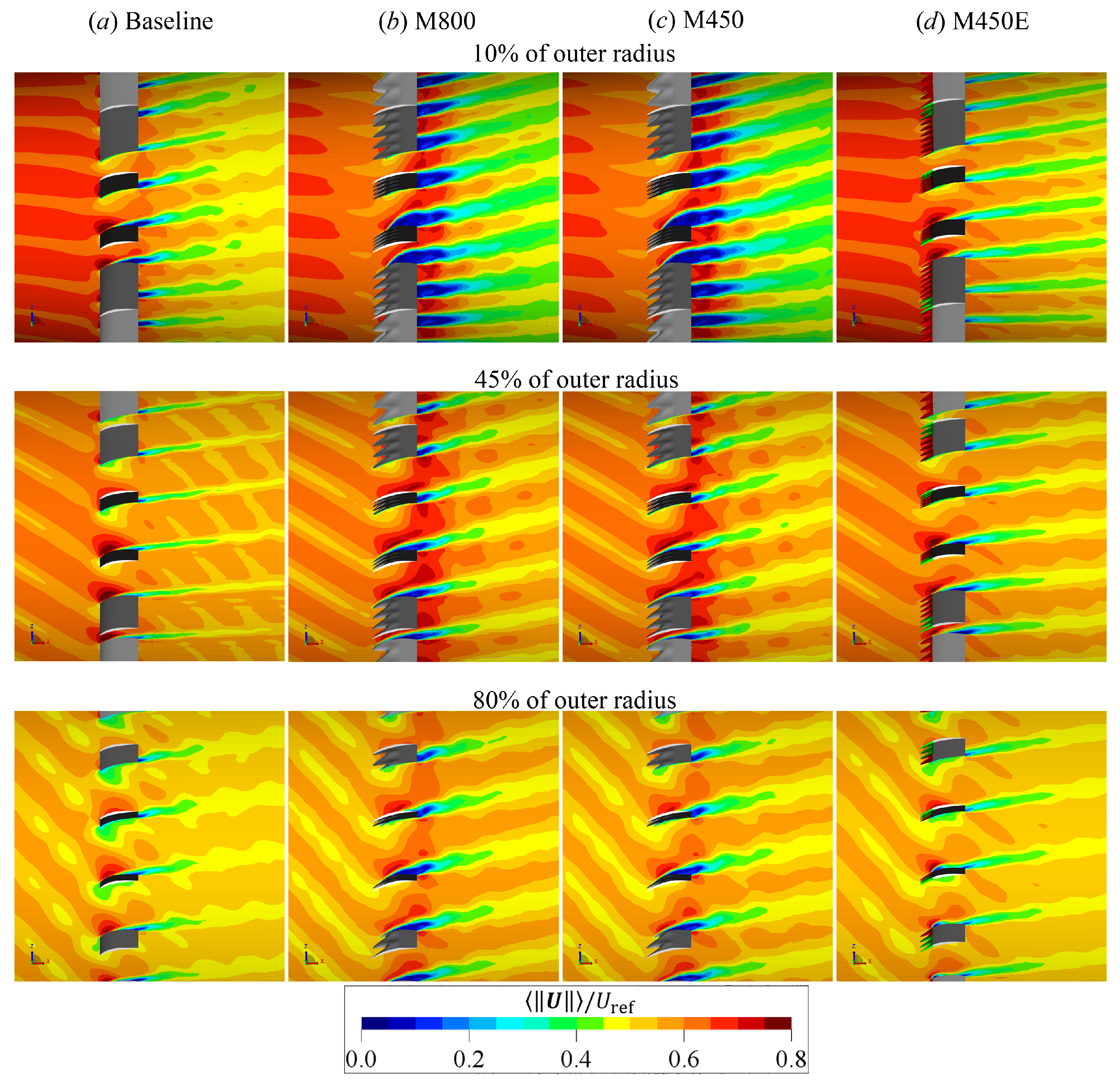
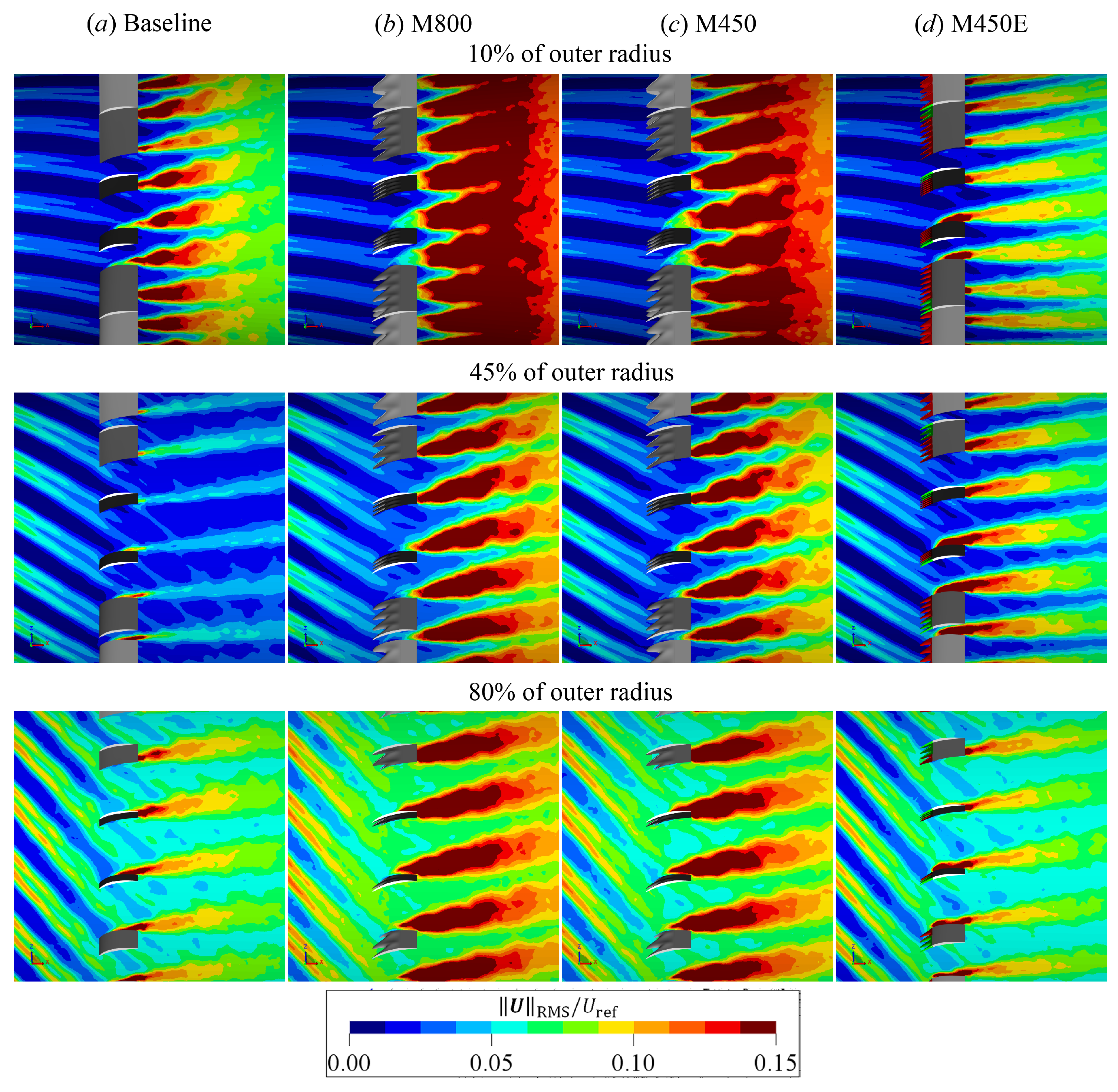
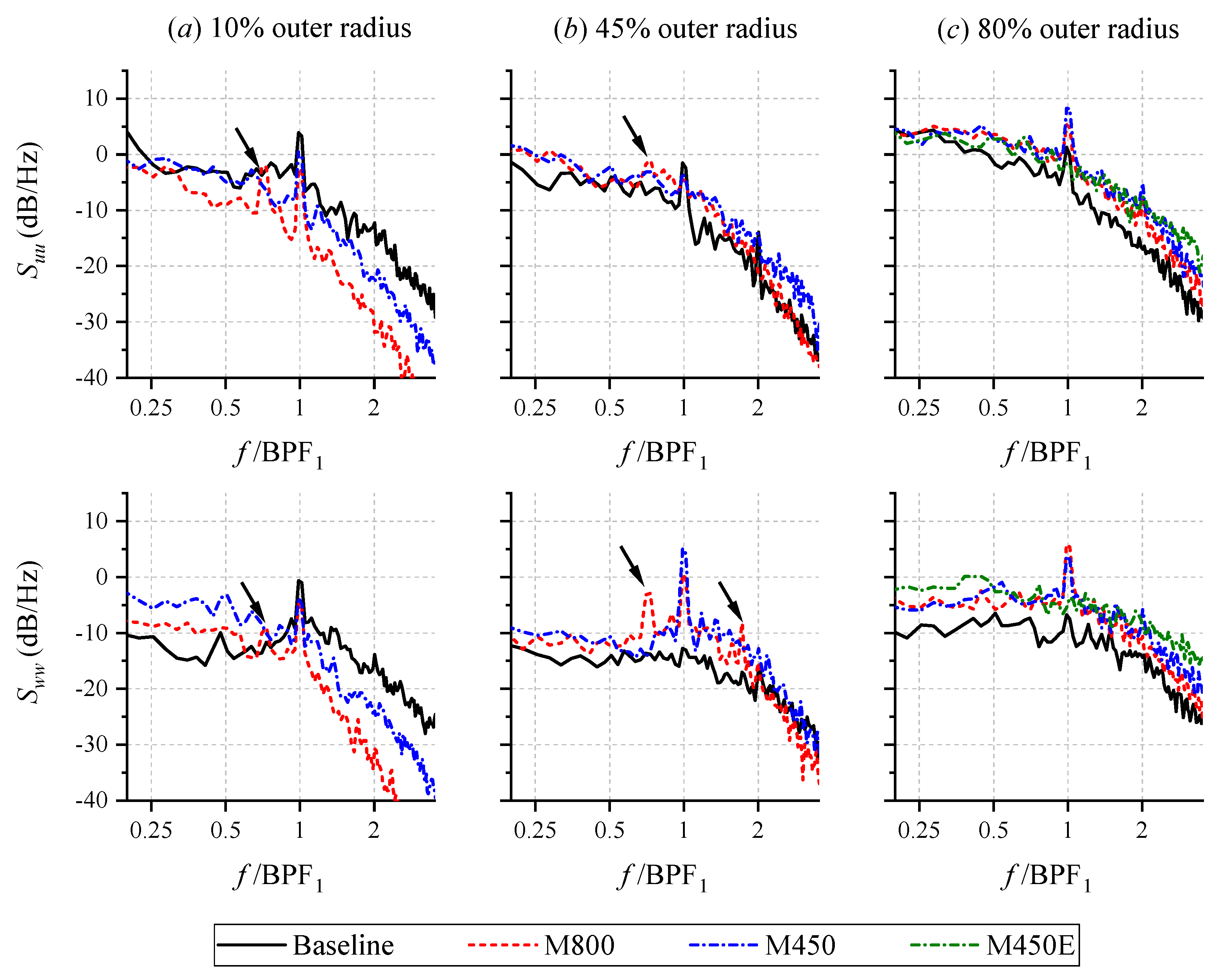
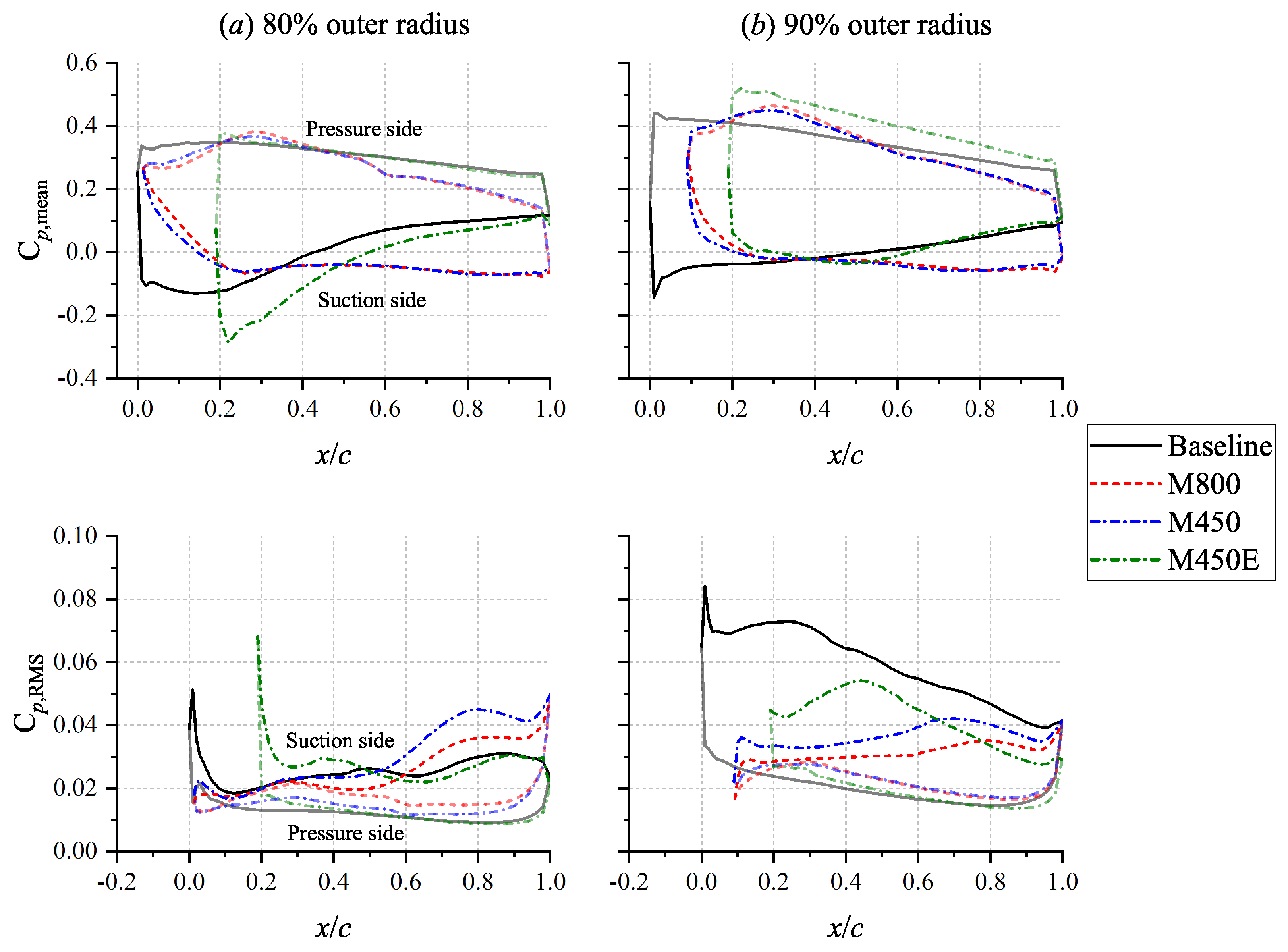
4.1. Aerodynamic Performance and Flow Statistics
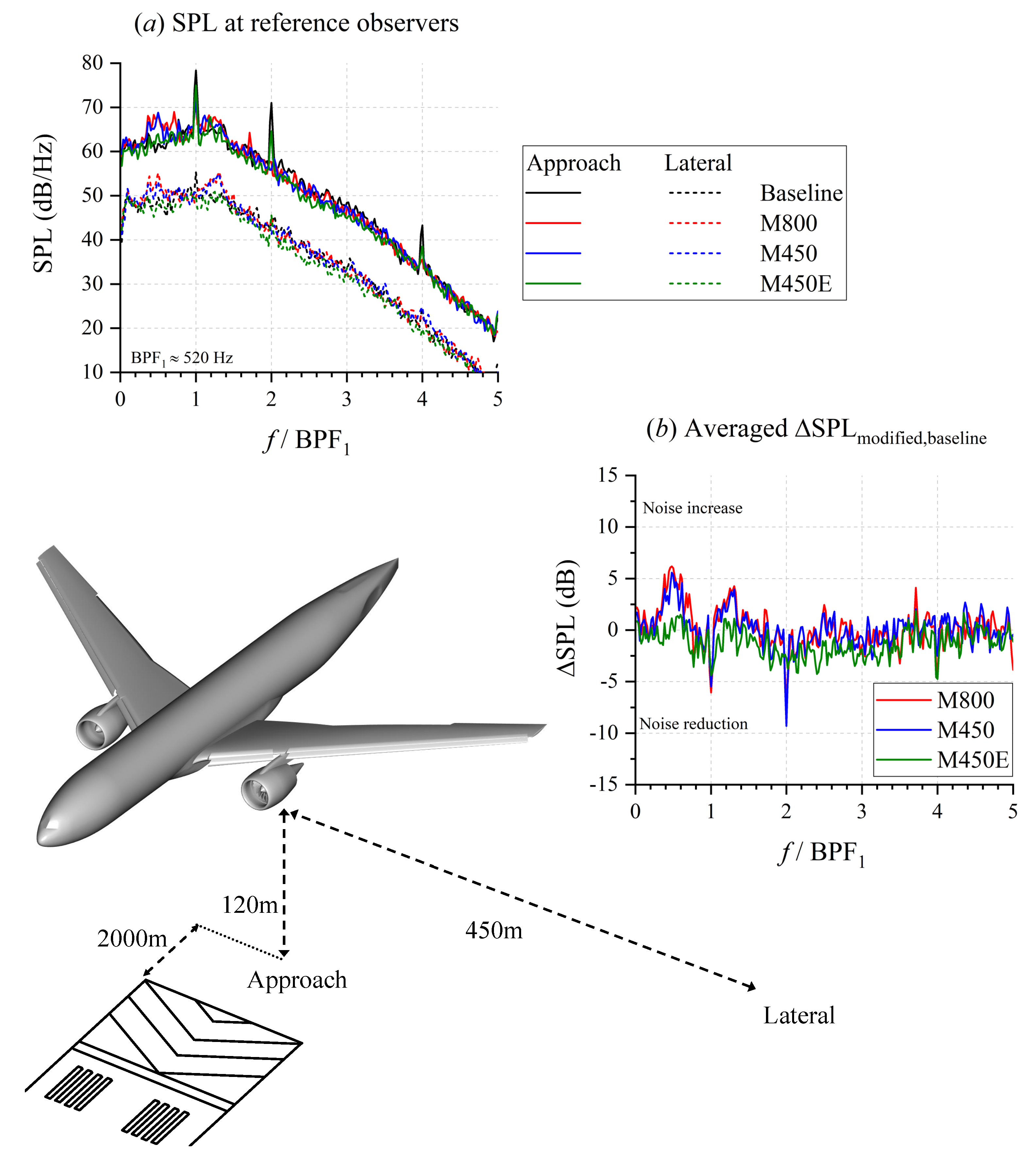
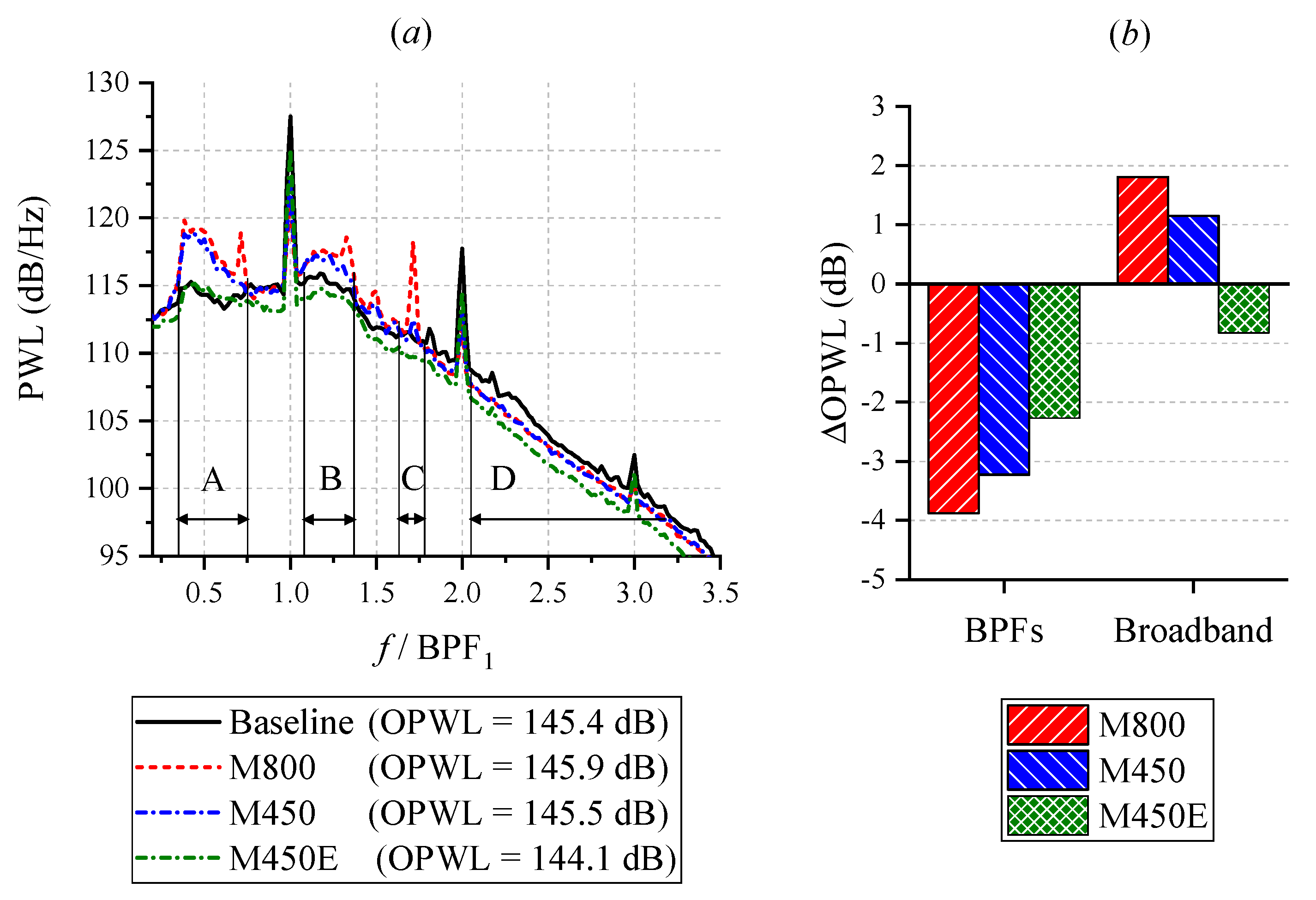
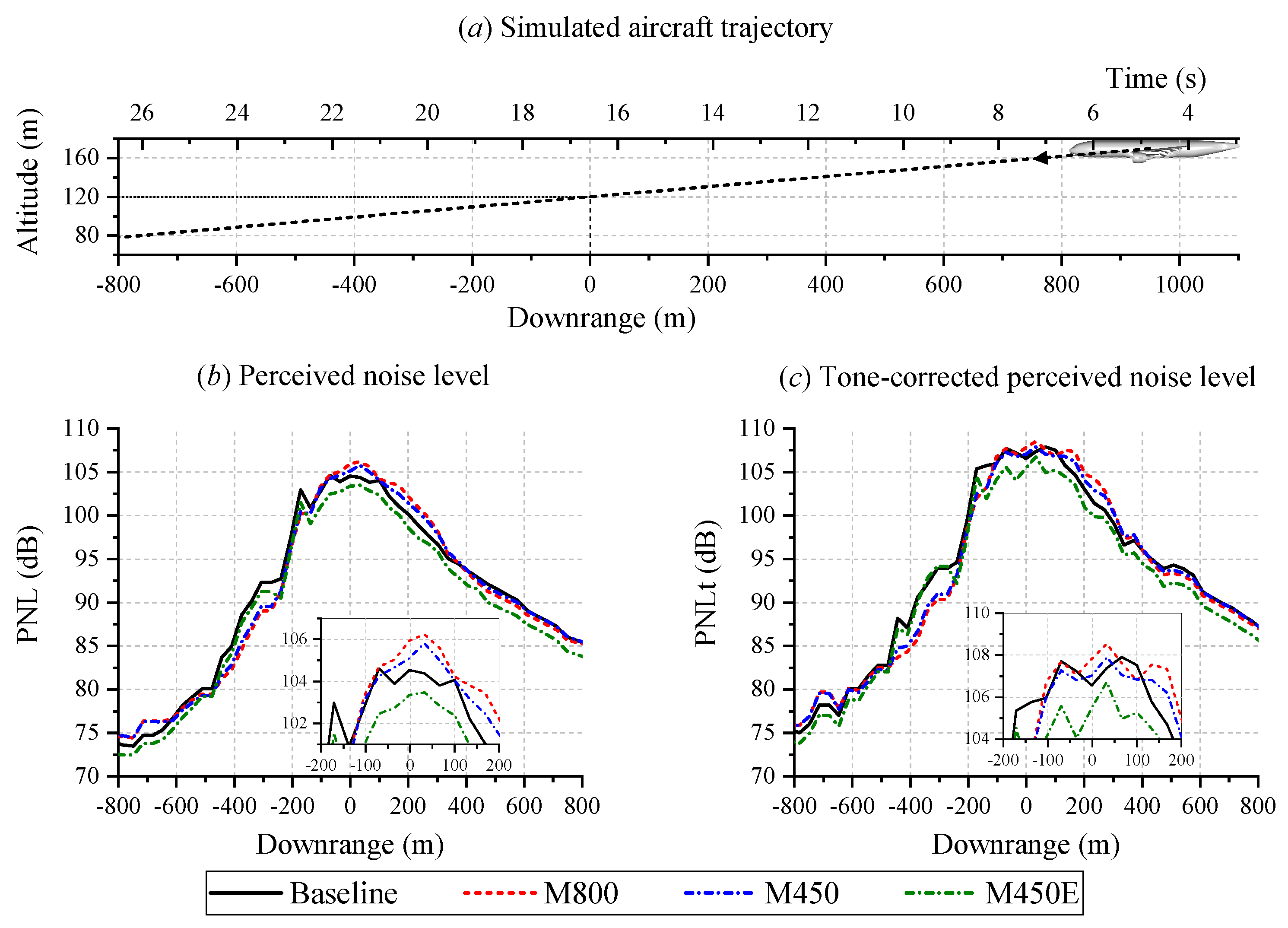
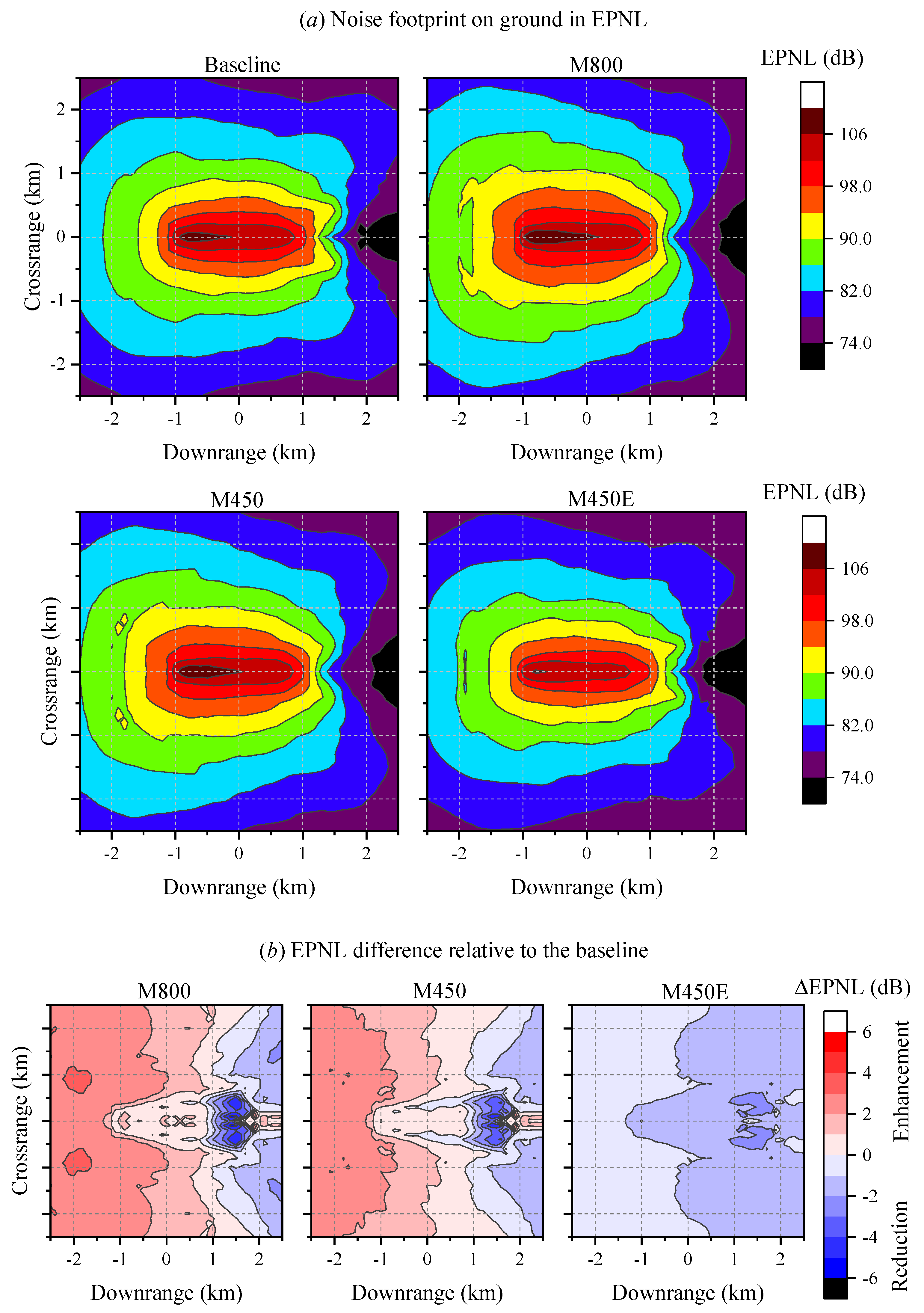
4.2. Far-Field Noise Characteristics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BPF | Blade-passage frequency |
| CRM | Common research model airframe |
| EPNL | Effective perceived noise level |
| FW-H | Ffowcs-Williams and Hawkings analogy |
| LE | Leading edge |
| OGV | Outlet guide vane |
| OPWL | Overall source power level |
| OSPL | Overall sound pressure level |
| PNL | Perceived noise level |
| PNLt | Tone-corrected perceived noise level |
| PWL | Source power level |
| SDT | Source diagnostic test rig |
| SPL | Sound pressure level |
| TE | Trailing edge |
| TIN | Turbulence-impingement noise |
References
- Casalino, D.; Diozzi, F.; Sannino, R.; Paonessa, A. Aircraft noise reduction technologies: A bibliographic review. Aerosp. Sci. Technol. 2008, 12, 1–17. [Google Scholar] [CrossRef]
- Woodward, R.; Hughes, C.; Jeracki, R.; Miller, C. Fan Noise Source Diagnostic Test–Far-field Acoustic Results. In Proceedings of the 8th AIAA/CEAS Aeroacoustics Conference & Exhibit, Breckenridge, CO, USA, 17–19 June 2002; p. 2427. [Google Scholar]
- Zaporozhets, O.; Tokarev, V.; Attenborough, K. Aircraft Noise: Assessment, Prediction and Control; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Casalino, D.; Hazir, A.; Mann, A. Turbofan broadband noise prediction using the Lattice Boltzmann Method. AIAA J. 2018, 56, 609–628. [Google Scholar] [CrossRef]
- Casalino, D.; Avallone, F.; Gonzalez-Martino, I.; Ragni, D. Aeroacoustic study of a wavy stator leading edge in a realistic fan/OGV stage. J. Sound Vib. 2019, 442, 138–154. [Google Scholar] [CrossRef] [Green Version]
- Paterson, R.W.; Amiet, R.K. Noise and surface pressure response of an airfoil to incident turbulence. J. Aircr. 1977, 14, 729–736. [Google Scholar] [CrossRef]
- Hersh, A.S.; Soderman, P.T.; Hayden, R.E. Investigation of acoustic effects of leading-edge serrations on airfoils. J. Aircr. 1974, 11, 197–202. [Google Scholar] [CrossRef]
- Roger, M.; Schram, C.; De Santana, L. Reduction of airfoil turbulence-impingement noise by means of leading-edge serrations and/or porous material. In Proceedings of the 19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany, 27–29 May 2013; p. 2108. [Google Scholar]
- Narayanan, S.; Chaitanya, P.; Haeri, S.; Joseph, P.; Kim, J.; Polacsek, C. Airfoil noise reductions through leading edge serrations. Phys. Fluids 2015, 27, 025109. [Google Scholar] [CrossRef]
- Bampanis, G.; Roger, M.; Ragni, D.; Avallone, F.; Teruna, C. Airfoil-turbulence interaction noise source identification and its reduction by means of leading edge serrations. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019; p. 2741. [Google Scholar]
- Lee, S. Reduction of blade-vortex interaction noise through porous leading edge. AIAA J. 1994, 32, 480–488. [Google Scholar] [CrossRef]
- Sarradj, E.; Geyer, T. Noise generation by porous airfoils. In Proceedings of the 13th AIAA/CEAS Aeroacoustics Conference (28th AIAA Aeroacoustics Conference), Rome, Italy, 21–23 May 2007; p. 3719. [Google Scholar]
- Geyer, T.; Sarradj, E.; Giesler, J.; Hobracht, M. Experimental assessment of the noise generated at the leading edge of porous airfoils using microphone array techniques. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference (32nd AIAA Aeroacoustics Conference), Portland, OR, USA, 5–8 June 2011; p. 2713. [Google Scholar]
- Geyer, T.F.; Lucius, A.; Schrödter, M.; Schneider, M.; Sarradj, E. Reduction of turbulence interaction noise through airfoils with perforated leading edges. Acta Acust. United Acust. 2019, 105, 109–122. [Google Scholar] [CrossRef]
- Teruna, C.; Avallone, F.; Casalino, D.; Ragni, D. Numerical investigation of leading edge noise reduction on a rod-airfoil configuration using porous materials and serrations. J. Sound Vib. 2021, 494, 115880. [Google Scholar] [CrossRef]
- Chen, W.; Qiao, W.; Tong, F.; Wang, L.; Wang, X. Numerical investigation of wavy leading edges on rod–airfoil interaction noise. AIAA J. 2018, 56, 2553–2567. [Google Scholar] [CrossRef]
- Turner, J.M.; Kim, J.W. Aeroacoustic source mechanisms of a wavy leading edge undergoing vortical disturbances. J. Fluid Mech. 2017, 811, 582–611. [Google Scholar] [CrossRef] [Green Version]
- Gea Aguilera, F.; Gill, J.R.; Angland, D.; Zhang, X. Wavy leading edge airfoils interacting with anisotropic turbulence. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–9 June 2017; p. 3370. [Google Scholar]
- Chaitanya, P.; Joseph, P.; Narayanan, S.; Vanderwel, C.; Turner, J.; Kim, J.W.; Ganapathisubramani, B. Performance and mechanism of sinusoidal leading edge serrations for the reduction of turbulence–aerofoil interaction noise. J. Fluid Mech. 2017, 818, 435–464. [Google Scholar] [CrossRef] [Green Version]
- Palleja-Cabre, S.; Paruchuri, C.C.; Joseph, P.; Priddin, M.J.; Ayton, L.J. Downstream Perforations for the Reduction of Turbulence-Aerofoil Interaction Noise: Part I-Experimental Investigation. In Proceedings of the AIAA AVIATION 2021 FORUM, Washington, PA, USA, 2–6 August 2021; p. 2149. [Google Scholar]
- Ayton, L.J.; Colbrook, M.J.; Geyer, T.F.; Chaitanya, P.; Sarradj, E. Reducing aerofoil–turbulence interaction noise through chordwise-varying porosity. J. Fluid Mech. 2021, 906. [Google Scholar] [CrossRef]
- Lockard, D.P.; Choudhari, M.M.; O’Connell, M.D.; Duda, B.M.; Fares, E. Noise simulations of the high-lift common research model. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–9 June 2017; p. 3362. [Google Scholar]
- Ribeiro, A.F.; Ferris, R.; Khorrami, M.R. Aeroacoustic Computations of a Generic Low Boom Concept in Landing Configuration: Part 2-Airframe Noise Simulations. In Proceedings of the AIAA AVIATION 2021 FORUM, Washington, PA, USA, 2–6 August 2021; p. 2196. [Google Scholar]
- König, B.; Fares, E. Exa powerflow simulations for the sixth AIAA drag prediction workshop. J. Aircr. 2018, 55, 1482–1490. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation: For Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Zhang, R.; Fan, H.; Chen, H. A lattice Boltzmann approach for solving scalar transport equations. Philos. Trans. R. Soc. A 2011, 369, 2264–2273. [Google Scholar] [CrossRef] [PubMed]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511. [Google Scholar] [CrossRef]
- Chen, H.; Teixeira, C.; Molvig, K. Realization of fluid boundary conditions via discrete Boltzmann dynamics. Int. J. Mod. Phys. C 1998, 9, 1281–1292. [Google Scholar] [CrossRef]
- Chen, H.; Chen, S.; Matthaeus, W.H. Recovery of the Navier-Stokes equations using a lattice-gas Boltzmann method. Phys. Rev. A 1992, 45, R5339. [Google Scholar] [CrossRef]
- Chen, H.; Orszag, S.A.; Staroselsky, I.; Succi, S. Expanded analogy between Boltzmann kinetic theory of fluids and turbulence. J. Fluid Mech. 2004, 519, 301–314. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Teixeira, C.M. Incorporating turbulence models into the lattice-Boltzmann method. Int. J. Mod. Phys. C 1998, 9, 1159–1175. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Amsterdam, The Netherlands, 1983; pp. 96–116. [Google Scholar]
- Farassat, F.; Succi, G.P. A review of propeller discrete frequency noise prediction technology with emphasis on two current methods for time domain calculations. J. Sound Vib. 1980, 71, 399–419. [Google Scholar] [CrossRef]
- Ffowcs-Williams, J.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Phil. Trans. R. Soc. Lond. A 1969, 264, 321–342. [Google Scholar]
- Casalino, D. An advanced time approach for acoustic analogy predictions. J. Sound Vib. 2003, 261, 583–612. [Google Scholar] [CrossRef]
- Lacy, D.S.; Sclafani, A.J. Development of the high lift common research model (hl-crm): A representative high lift configuration for transonic transports. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 0308. [Google Scholar]
- Rubio Carpio, A.; Merino Martinez, R.; Avallone, F.; Ragni, D.; Snellen, M.; van der Zwaag, S. Broadband Trailing-Edge Noise Reduction Using Permeable Metal Foams. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference, Hong Kong, China, 27–30 August 2017; Volume 255, pp. 2755–2765. [Google Scholar]
- Regulations, F.A. Noise Standards: Aircraft Type and Airworthiness Certification; Technical Report, Technical Report 14 CFR Part 36; United States Federal Aviation Administration: Washington, DC, USA, 2009.
- Podboy, G.; Krupar, M.; Helland, S.; Hughes, C. Steady and unsteady flow field measurements within a NASA 22 inch fan model. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Hampton, VA, USA, 14–17 January 2002; p. 1033. [Google Scholar]
- FAA. Airplane Flying Handbook (FAA-H-8083-3A); Skyhorse Publishing Inc.: New York, NY, USA, 2011. [Google Scholar]
- EASA. Type-Certificate Data Sheet for Trent 1000 Series Engines (EASA.E.036); European Union Aviation Safety Agency: Cologne, Germany, 2019. [Google Scholar]
- Curle, N. The influence of solid boundaries upon aerodynamic sound. Proc. R. Soc. London. Ser. A 1955, 231, 505–514. [Google Scholar]
- Hansen, K.L.; Kelso, R.M.; Dally, B.B. Performance variations of leading-edge tubercles for distinct airfoil profiles. AIAA J. 2011, 49, 185–194. [Google Scholar] [CrossRef]
- Kim, J.W.; Haeri, S.; Joseph, P.F. On the reduction of aerofoil–turbulence interaction noise associated with wavy leading edges. J. Fluid Mech. 2016, 792, 526–552. [Google Scholar] [CrossRef] [Green Version]
- Carpio, A.R.; Avallone, F.; Ragni, D.; Snellen, M.; van der Zwaag, S. Quantitative criteria to design optimal permeable trailing edges for noise abatement. J. Sound Vib. 2020, 485, 115596. [Google Scholar] [CrossRef]
- Brooks, T.F.; Pope, D.S.; Marcolini, M.A. Airfoil Self-Noise and Prediction; NASA Reference Publication, NASA-RP-1218; NASA: Washington, DC, USA, 1989.
- Boettcher, J. Noise Certification Workshop. In Session 2: Aircraft Noise Certification; International Civil Aviation Organization: Montreal, QC, Canada, 2006. [Google Scholar]
- Nöding, M.; Bertsch, L. Application of Noise Certification Regulations within Conceptual Aircraft Design. Aerospace 2021, 8, 210. [Google Scholar] [CrossRef]
- Bertsch, L.; Heinze, W.; Guérin, S.; Lummer, M.; Delfs, J.W. 10 Years of Joint Research at DLR and TU Braunschweig toward Low-Noise Aircraft Design-What Did we Achieve? Aeronaut. Aerosp. Open Access J. 2019, 3, 89–105. [Google Scholar] [CrossRef] [Green Version]
- De La Puente, F.; Guerra Crespo, J.J.; Rodríguez Ahlquist, J.; García Merino, I.; Mancini, S.; Kolb, A. On C295 FWSAR military transport aircraft acoustic certification by CAA. In Proceedings of the AIAA AVIATION 2021 FORUM, Washington, PA, USA, 2–6 August 2021; p. 2202. [Google Scholar]
- Casalino, D.; van der Velden, W.C.; Romani, G. Community noise of urban air transportation vehicles. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 1834. [Google Scholar]
- Michel, U. Correlation of aircraft certification noise levels EPNL with controlling physical parameters. In Proceedings of the 19th AIAA/CEAS Aeroacoustics Conference, Reno, NV, USA, 27–29 May 2013; p. 2014. [Google Scholar]
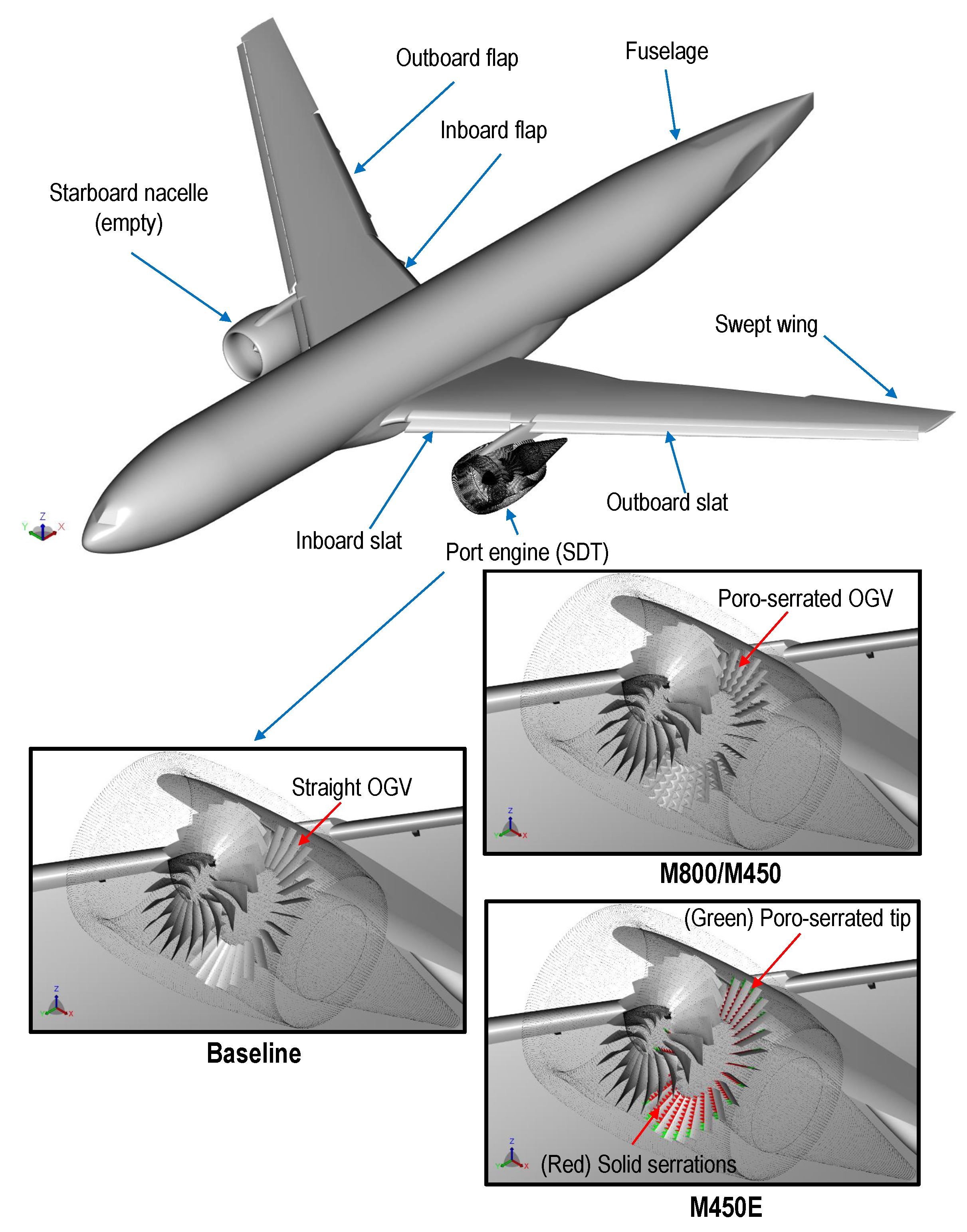
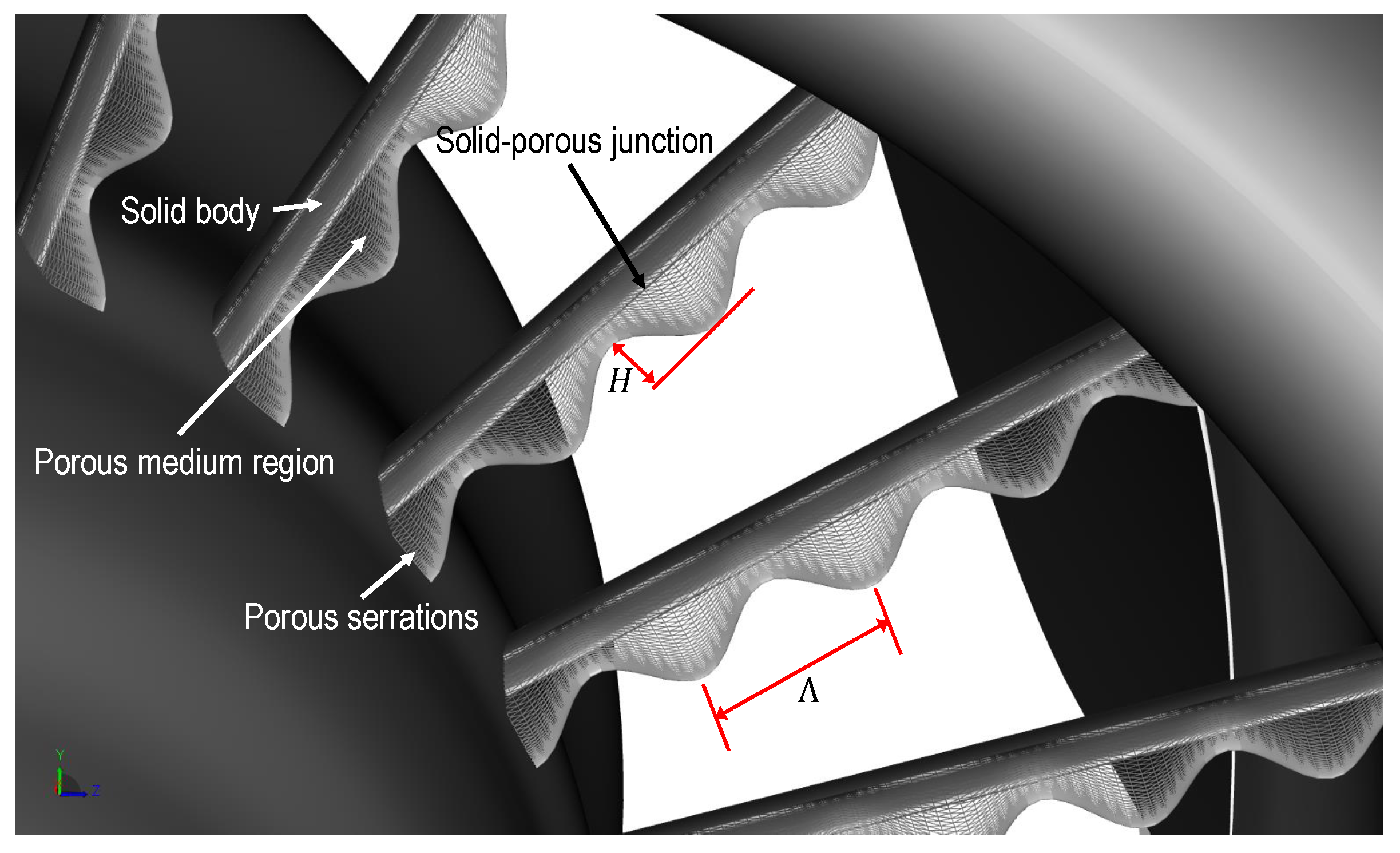
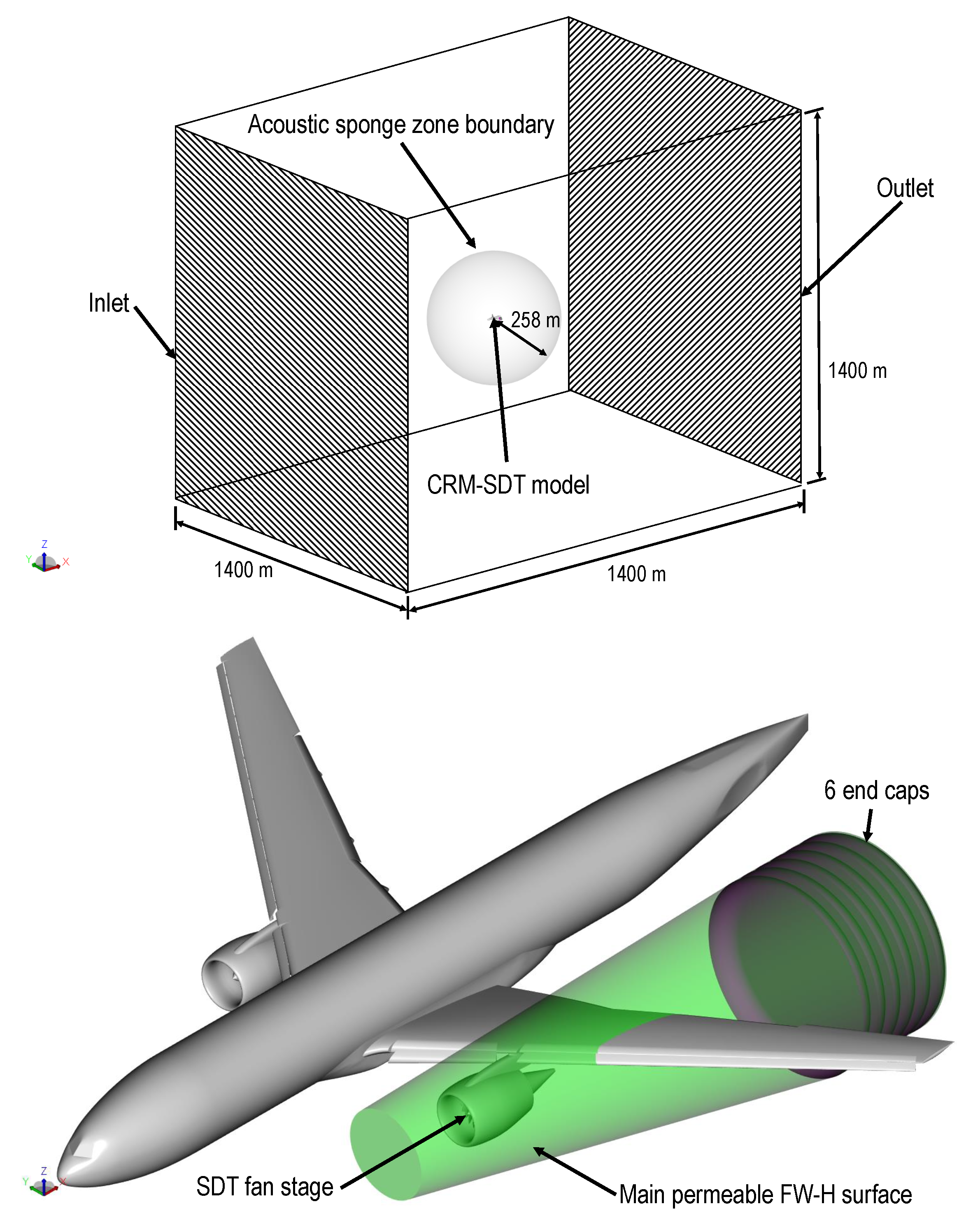






| NASA HL-CRM | Airbus A330-300 | |
|---|---|---|
| Fuselage length (m) | 62.8 | 63.6 |
| Wingspan (m) | 58.7 | 60.3 |
| NASA SDT (5.5:1 scale) | Rolls-Royce Trent 1000 | |
| Fan diameter (m) | 2.93 | 2.85 |
| Bypass ratio | - | 10.8–11.0 |
| Fan blade count | 22 | 20 |
| OGV blade count | 26 | 46 |
| Type | dp (μm) | ϕ (%) | K (m2) | C (m−1) |
|---|---|---|---|---|
| Metal foam (M800) | 800 | 91.65 | 2.7 × 10−9 | 2613 |
| Metal foam (M450/M450E) | 450 | 89.28 | 6.11 × 10−10 | 9758 |
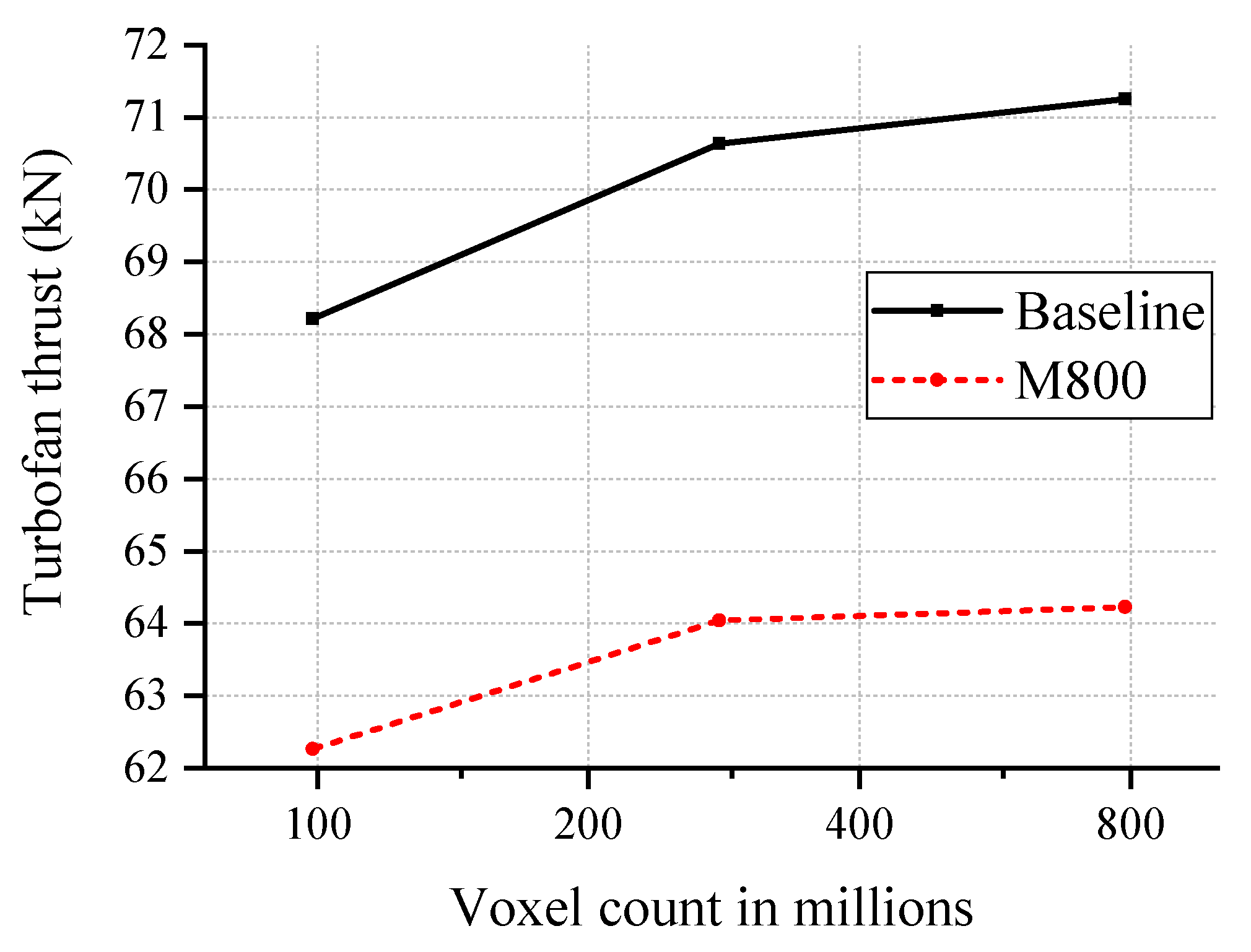
| Grid Type | Resolution (Voxels/c) | Voxel Count (Millions) | |
|---|---|---|---|
| Baseline | M800 | ||
| Coarse | 41 | 104.83 | 104.89 |
| Medium | 61 | 279.28 | 279.44 |
| Fine | 86 | 744.05 | 744.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teruna, C.; Rego, L.; Casalino, D.; Ragni, D.; Avallone, F. A Numerical Study on Aircraft Noise Mitigation Using Porous Stator Concepts. Aerospace 2022, 9, 70. https://doi.org/10.3390/aerospace9020070
Teruna C, Rego L, Casalino D, Ragni D, Avallone F. A Numerical Study on Aircraft Noise Mitigation Using Porous Stator Concepts. Aerospace. 2022; 9(2):70. https://doi.org/10.3390/aerospace9020070
Chicago/Turabian StyleTeruna, Christopher, Leandro Rego, Damiano Casalino, Daniele Ragni, and Francesco Avallone. 2022. "A Numerical Study on Aircraft Noise Mitigation Using Porous Stator Concepts" Aerospace 9, no. 2: 70. https://doi.org/10.3390/aerospace9020070
APA StyleTeruna, C., Rego, L., Casalino, D., Ragni, D., & Avallone, F. (2022). A Numerical Study on Aircraft Noise Mitigation Using Porous Stator Concepts. Aerospace, 9(2), 70. https://doi.org/10.3390/aerospace9020070







