Behavior of Sliding Angle as Function of Temperature Difference between Droplet and Superhydrophobic Coating for Aircraft Ice Protection Systems
Abstract
:1. Introduction
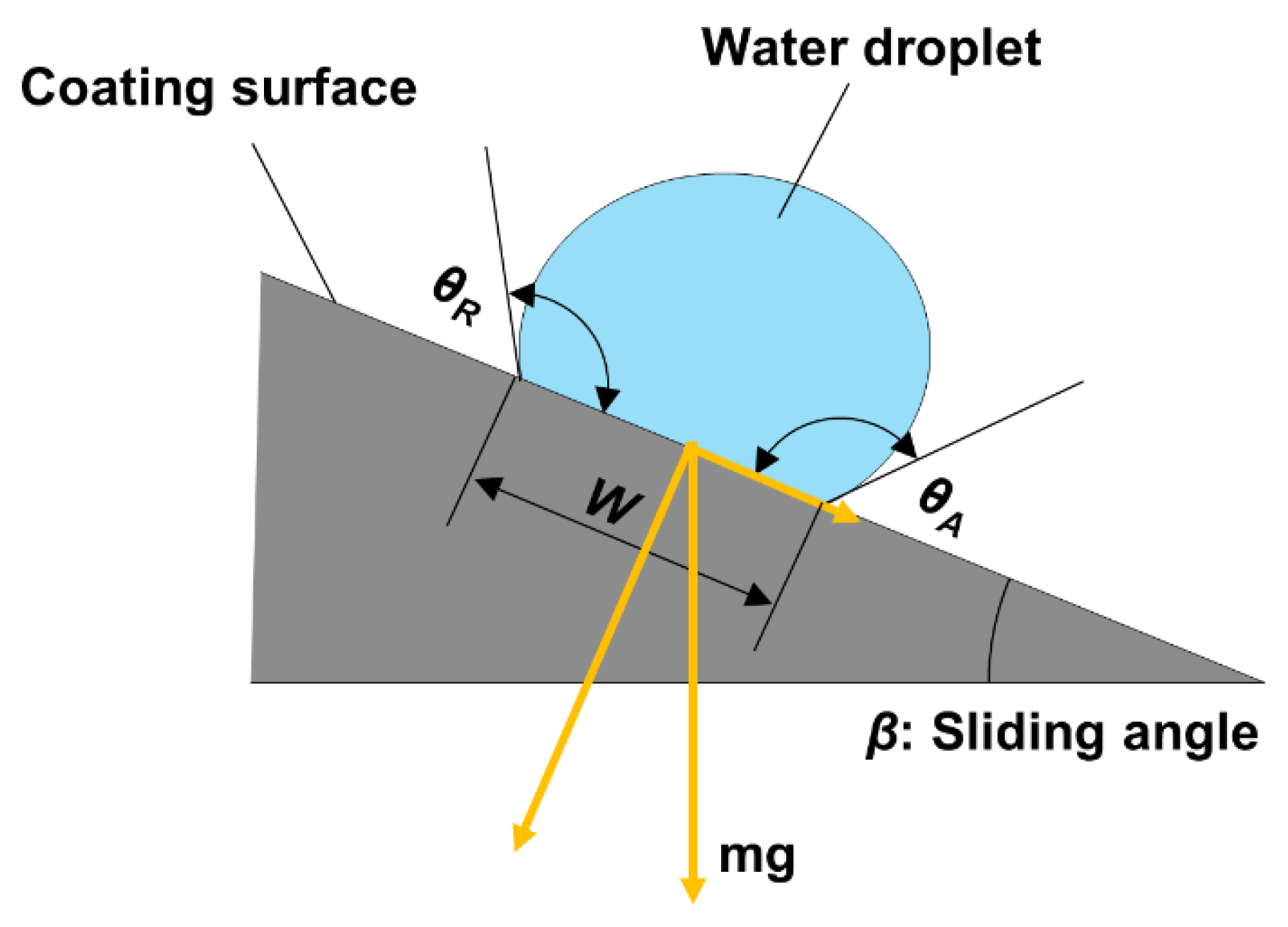
2. Method
3. Experimental Setup
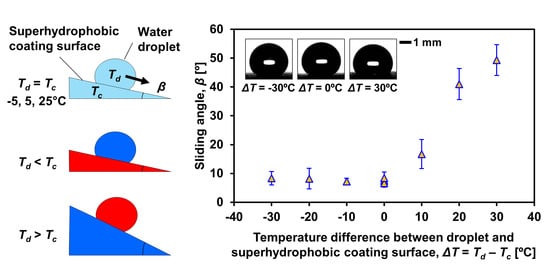
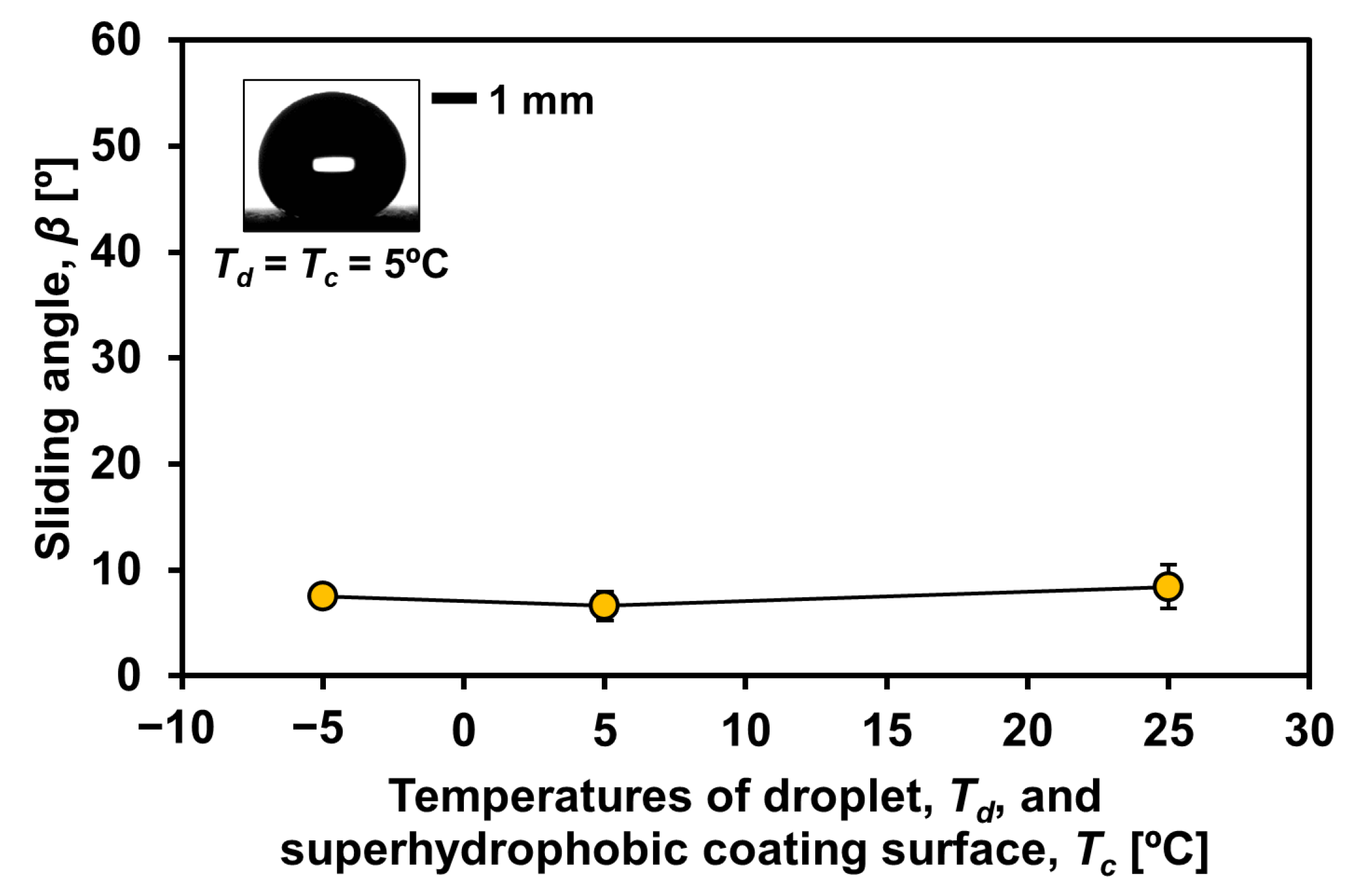
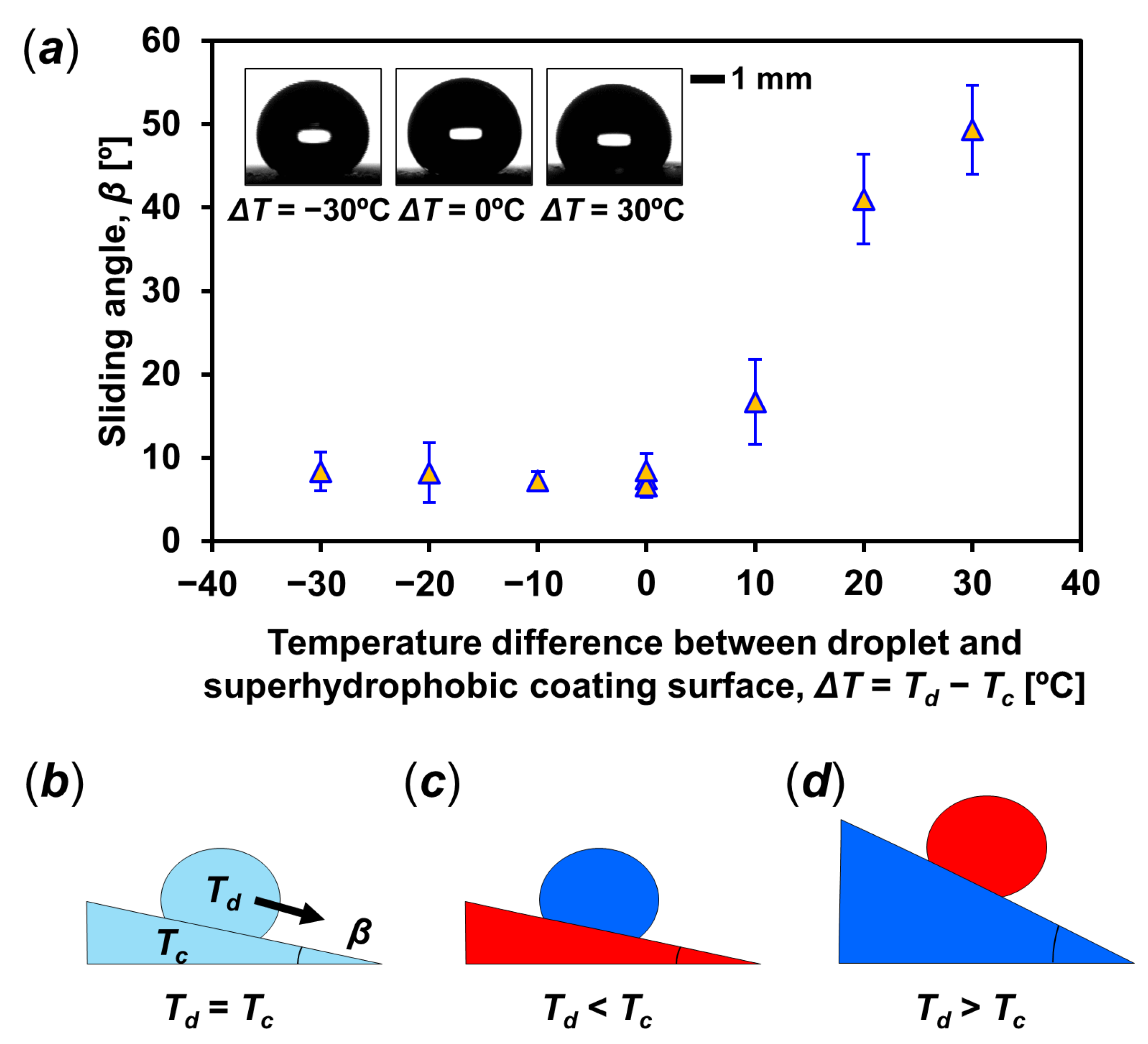
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gent, R.W.; Dart, N.P.; Cansdale, J.T. Aircraft icing. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2000, 358, 2873–2911. [Google Scholar] [CrossRef]
- Bragg, M.B. Aicraft aerodynamic effects due to large droplet ice accretions. In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 1996. [Google Scholar]
- Bragg, M.B.; Perkins, W.R.; Sorter, N.B.; Basar, T.; Voulgaris, P.G.; Gurbacki, H.M.; Melody, J.W.; Mccray, S.A. An interdisciplinary approach to inflight aircraft icing safety. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 1998. [Google Scholar]
- Addy, H.E. Ice Accretions and Icing Effects for Modern Airfoils; NASA/TP-2000-210031 (also DOT/FAA/AR-99/89); NASA: Cleveland, OH, USA, 2000.
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- FAA. Pilot Guid: Flight In Icing Conditions; Advisory Circular AC 91-74B; Federal Aviation Administration: Washington, DC, USA, 2015.
- Meier, O.; Scholz, D. A Handbook Method for the Estimation of Power Requirements for Electrical De-Icing Systems; DLRK: Hamburg, Germany, 2010. [Google Scholar]
- Yeoman, K. Efficiency of a Bleed Air Powered Inlet Icing Protective System; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1994. [Google Scholar]
- Pellissier, M.P.C.; Habashi, W.G.; Pueyo, A. Optimization via FENSAP-ICE of Aircraft Hot-Air Anti-Icing Systems. J. Aircr. 2010, 48, 265–276. [Google Scholar] [CrossRef]
- Kimura, S.; Yamagishi, Y.; Sakabe, A.; Adachi, T.; Shimanuki, M. A new surface coating for prevention of icing on airfoils. In Proceedings of the SAE Technical Papers; SAE International: Warrendale, PA, USA, 2007. [Google Scholar]
- Antonini, C.; Innocenti, M.; Horn, T.; Marengo, M.; Amirfazli, A. Understanding the effect of superhydrophobic coatings on energy reduction in anti-icing systems. Cold Reg. Sci. Technol. 2011, 67, 58–67. [Google Scholar] [CrossRef]
- Morita, K.; Kimura, S.; Sakaue, H. Hybrid system combining ice-phobic coating and electrothermal heating for wing ice protection. Aerospace 2020, 7, 102. [Google Scholar] [CrossRef]
- Hann, R.; Enache, A.; Nielsen, M.C.; Stovner, B.N.; van Beeck, J.; Johansen, T.A.; Borup, K.T. Experimental heat loads for electrothermal anti-icing and de-icing on uavs. Aerospace 2021, 8, 83. [Google Scholar] [CrossRef]
- Neinhuis, C.; Barthlott, W. Characterization and distribution of water-repellent, self-cleaning plant surfaces. Ann. Bot. 1997, 79, 667–677. [Google Scholar] [CrossRef] [Green Version]
- Barthlott, W.; Neinhuis, C. Purity of the sacred lotus, or escape from contamination in biological surfaces. Planta 1997, 202, 1–8. [Google Scholar] [CrossRef]
- Lafuma, A.; Quéré, D. Superhydrophobic states. Nat. Mater. 2003, 2, 457–460. [Google Scholar] [CrossRef] [PubMed]
- Blossey, R. Self-cleaning surfaces—Virtual realities. Nat. Mater. 2003, 2, 301–306. [Google Scholar] [CrossRef]
- Fürstner, R.; Barthlott, W.; Neinhuis, C.; Walzel, P. Wetting and self-cleaning properties of artificial superhydrophobic surfaces. Langmuir 2005, 21, 956–961. [Google Scholar] [CrossRef] [PubMed]
- Milne, A.J.B.; Amirfazli, A. Drop Shedding by Shear Flow for Hydrophilic to Superhydrophobic Surfaces. Langmuir 2009, 25, 14155–14164. [Google Scholar] [CrossRef] [PubMed]
- Mandal, D.K.; Criscione, A.; Tropea, C.; Amirfazli, A. Shedding of Water Drops from a Surface under Icing Conditions. Langmuir 2015, 31, 9340–9347. [Google Scholar] [CrossRef]
- Roisman, I.V.; Criscione, A.; Tropea, C.; Mandal, D.K.; Amirfazli, A. Dislodging a sessile drop by a high-Reynolds-number shear flow at subfreezing temperatures. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2015, 92, 023007. [Google Scholar] [CrossRef]
- Villeneuve, E.; Brassard, J.-D.; Volat, C. Effect of Various Surface Coatings on De-Icing/Anti-Icing Fluids Aerodynamic and Endurance Time Performances. Aerospace 2019, 6, 114. [Google Scholar] [CrossRef] [Green Version]
- Furmidge, C.G.L. Studies at phase interfaces. I. The sliding of liquid drops on solid surfaces and a theory for spray retention. J. Colloid Sci. 1962, 17, 309–324. [Google Scholar] [CrossRef]
- Pierce, E.; Carmona, F.J.; Amirfazli, A. Understanding of sliding and contact angle results in tilted plate experiments. Colloids Surf. A Physicochem. Eng. Asp. 2008, 323, 73–82. [Google Scholar] [CrossRef]
- Milne, A.J.B.; Elliott, J.A.W.; Zabeti, P.; Zhou, J.; Amirfazli, A. Model and experimental studies for contact angles of surfactant solutions on rough and smooth hydrophobic surfaces. Phys. Chem. Chem. Phys. 2011, 13, 16208–16219. [Google Scholar] [CrossRef]
- Wang, Z.; Elimelech, M.; Lin, S. Environmental Applications of Interfacial Materials with Special Wettability. Environ. Sci. Technol. 2016, 50, 2132–2150. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Leong, K.C. Influences of substrate wettability and liquid viscosity on isothermal spreading of liquid droplets on solid surfaces. Exp. Fluids 2002, 33, 728–731. [Google Scholar] [CrossRef]
- Vargaftik, N.B.; Volkov, B.N.; Voljak, L.D. International Tables of the Surface Tension of Water. J. Phys. Chem. Ref. Data 1983, 12, 817–820. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Chen, X.; Xin, J.H. Can superhydrophobic surfaces repel hot water? J. Mater. Chem. 2009, 19, 5602–5611. [Google Scholar] [CrossRef]
- Yu, Z.J.; Yang, J.; Wan, F.; Ge, Q.; Yang, L.L.; Ding, Z.L.; Yang, D.Q.; Sacher, E.; Isimjan, T.T. How to repel hot water from a superhydrophobic surface? J. Mater. Chem. A 2014, 2, 10639–10646. [Google Scholar] [CrossRef]
- Morita, K.; Sakaue, H. Characterization method of hydrophobic anti-icing coatings. Rev. Sci. Instrum. 2015, 86, 115108. [Google Scholar] [CrossRef] [PubMed]
- Morita, K.; Gonzales, J.; Sakaue, H. Effect of PTFE particle size on superhydrophobic coating for supercooled water prevention. Coatings 2018, 8, 426. [Google Scholar] [CrossRef] [Green Version]
- Wier, K.A.; McCarthy, T.J. Condensation on ultrahydrophobic surfaces and its effect on droplet mobility: Ultrahydrophobic surfaces are not always water repellant. Langmuir 2006, 22, 2433–2436. [Google Scholar] [CrossRef]
- Dorrer, C.; Rühe, J. Condensation and wetting transitions on microstructured ultrahydrophobic surfaces. Langmuir 2007, 23, 3820–3824. [Google Scholar] [CrossRef]
- Furuta, T.; Sakai, M.; Isobe, T.; Nakajima, A. Effect of dew condensation on the wettability of rough hydrophobic surfaces coated with two different silanes. Langmuir 2010, 26, 13305–13309. [Google Scholar] [CrossRef]
- Papadopoulos, P.; Mammen, L.; Deng, X.; Vollmer, D.; Butt, H.J. How superhydrophobicity breaks down. Proc. Natl. Acad. Sci. USA 2013, 110, 3254–3258. [Google Scholar] [CrossRef] [Green Version]
- Zhu, P.; Chen, R.; Wang, L. Topography-Directed Hot-Water Super-Repellent Surfaces. Adv. Sci. 2019, 6, 1900798. [Google Scholar] [CrossRef] [Green Version]
- Shiri, S.; Murrizi, A.; Bird, J.C. Trapping a Hot Drop on a Superhydrophobic Surface with Rapid Condensation or Microtexture Melting. Micromachines 2018, 9, 566. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maa, J.R. Drop size distribution and heat flux of dropwise condensation. Chem. Eng. J. 1978, 16, 171–176. [Google Scholar] [CrossRef]
- Kim, S.; Kim, K.J. Dropwise Condensation Modeling Suitable for Superhydrophobic Surfaces. J. Heat Transfer. 2011, 133. [Google Scholar] [CrossRef]

| Temperature Difference, ΔT = Td − Tc (°C) | Temperature of Water Droplet, Td (°C) | |||
|---|---|---|---|---|
| −5 | 5 | 25 | ||
| Temperature of the superhydrophobic coating surface, Tc (°C) | −5 | 0 | 10 | 30 |
| 5 | −10 | 0 | 20 | |
| 25 | −30 | −20 | 0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasegawa, M.; Endo, H.; Morita, K.; Sakaue, H.; Kimura, S. Behavior of Sliding Angle as Function of Temperature Difference between Droplet and Superhydrophobic Coating for Aircraft Ice Protection Systems. Aerospace 2021, 8, 219. https://doi.org/10.3390/aerospace8080219
Hasegawa M, Endo H, Morita K, Sakaue H, Kimura S. Behavior of Sliding Angle as Function of Temperature Difference between Droplet and Superhydrophobic Coating for Aircraft Ice Protection Systems. Aerospace. 2021; 8(8):219. https://doi.org/10.3390/aerospace8080219
Chicago/Turabian StyleHasegawa, Mitsugu, Haruka Endo, Katsuaki Morita, Hirotaka Sakaue, and Shigeo Kimura. 2021. "Behavior of Sliding Angle as Function of Temperature Difference between Droplet and Superhydrophobic Coating for Aircraft Ice Protection Systems" Aerospace 8, no. 8: 219. https://doi.org/10.3390/aerospace8080219
APA StyleHasegawa, M., Endo, H., Morita, K., Sakaue, H., & Kimura, S. (2021). Behavior of Sliding Angle as Function of Temperature Difference between Droplet and Superhydrophobic Coating for Aircraft Ice Protection Systems. Aerospace, 8(8), 219. https://doi.org/10.3390/aerospace8080219