A Review on the Current Status of Icing Physics and Mitigation in Aviation
Abstract
1. Introduction
2. Icing Physics
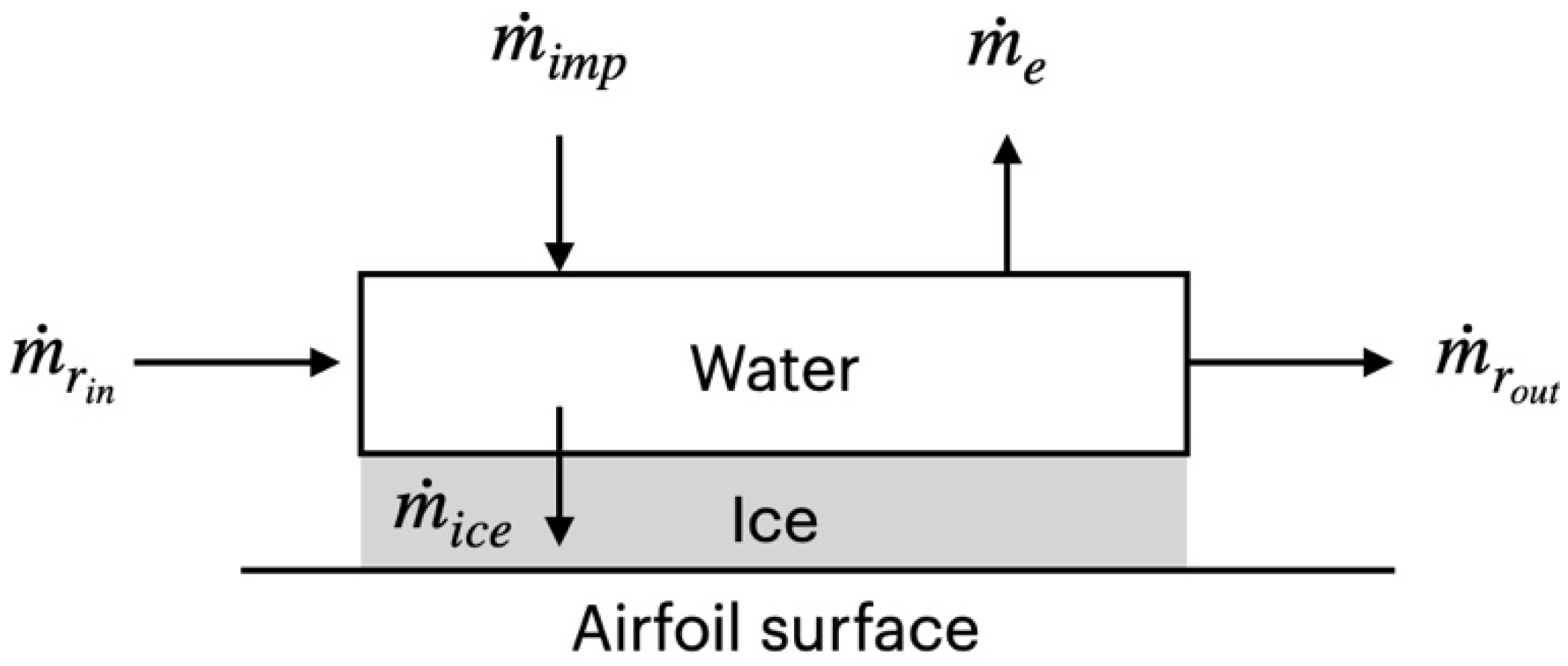
2.1. Fixed Wing Icing
- (1)
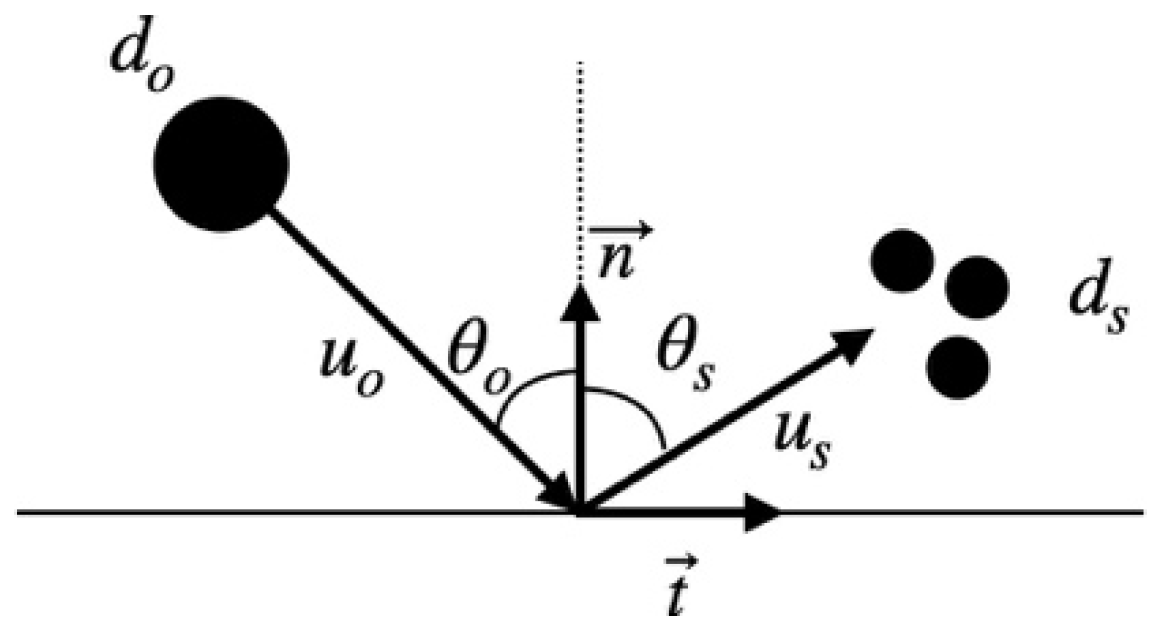
- Droplet Impact
- (2)
- Surface Roughness
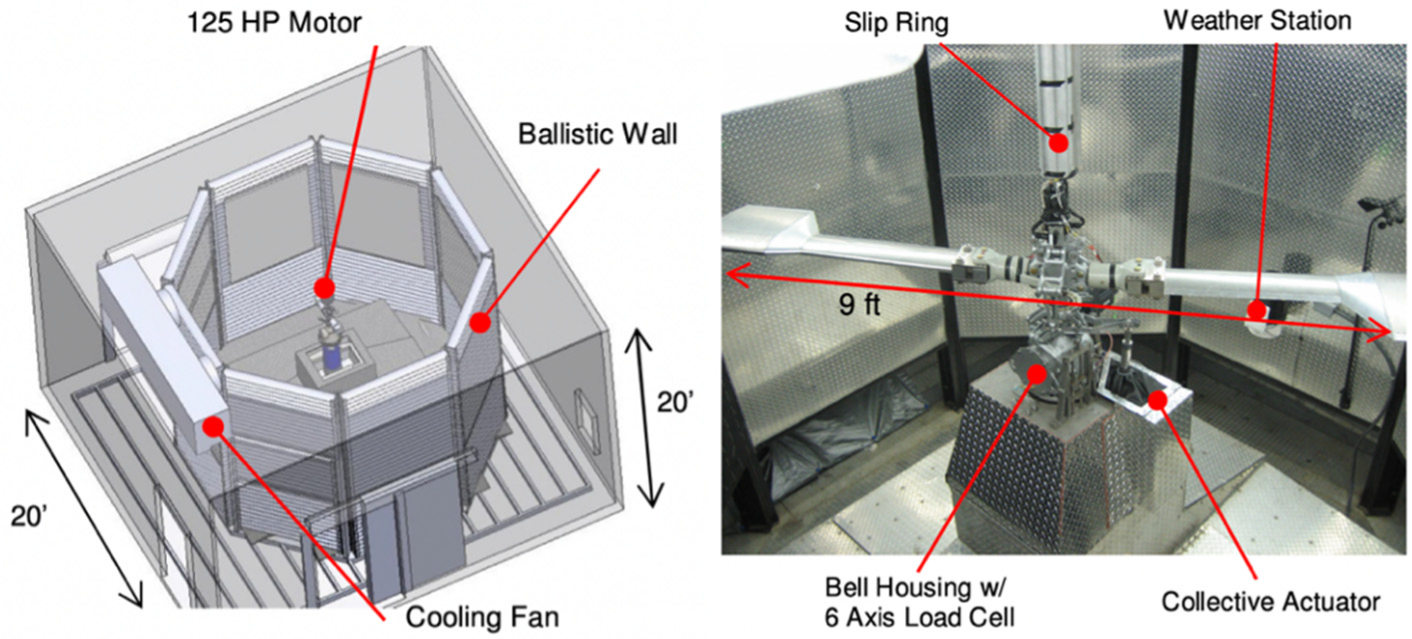
2.2. Rotor Icing
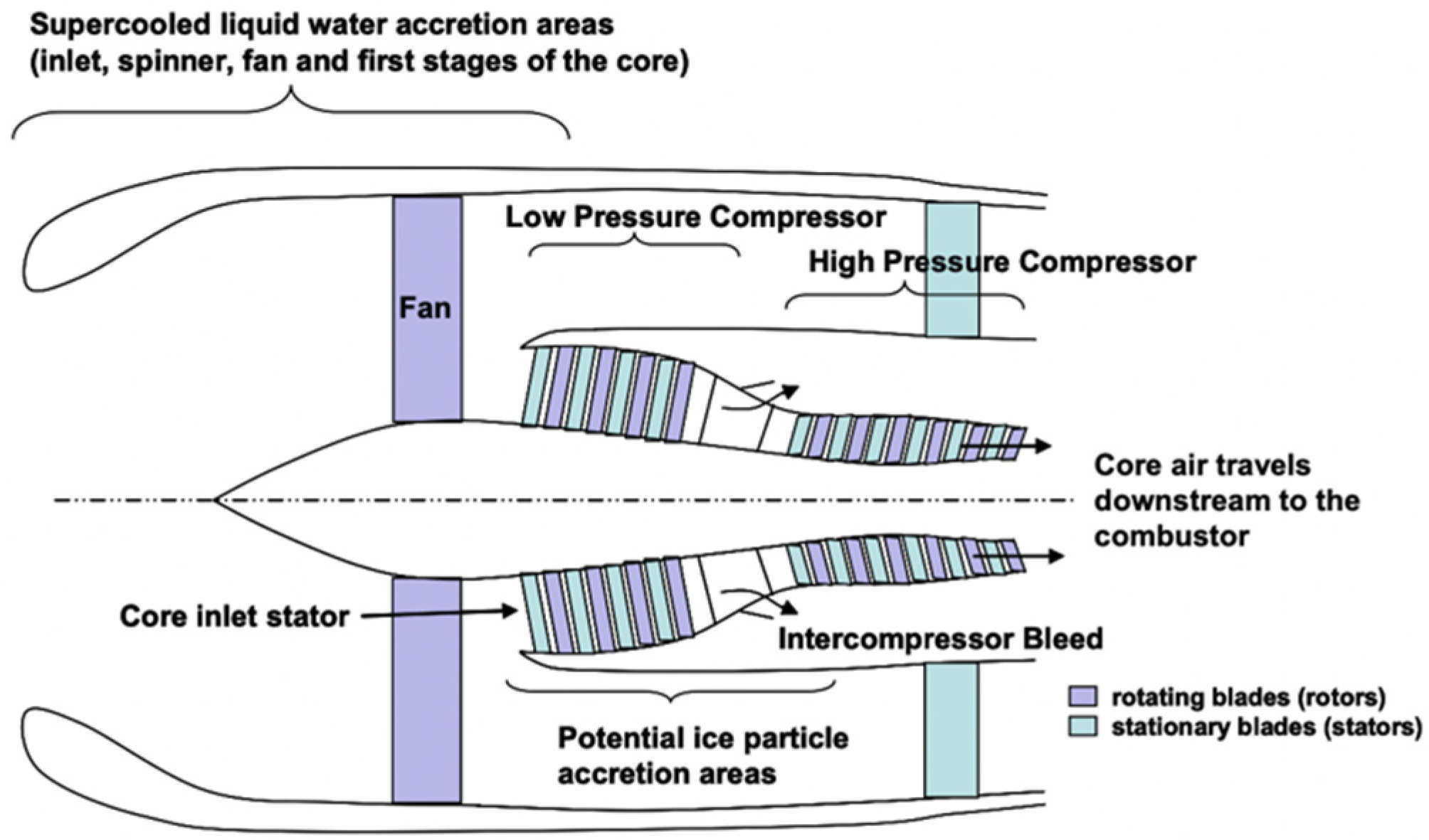
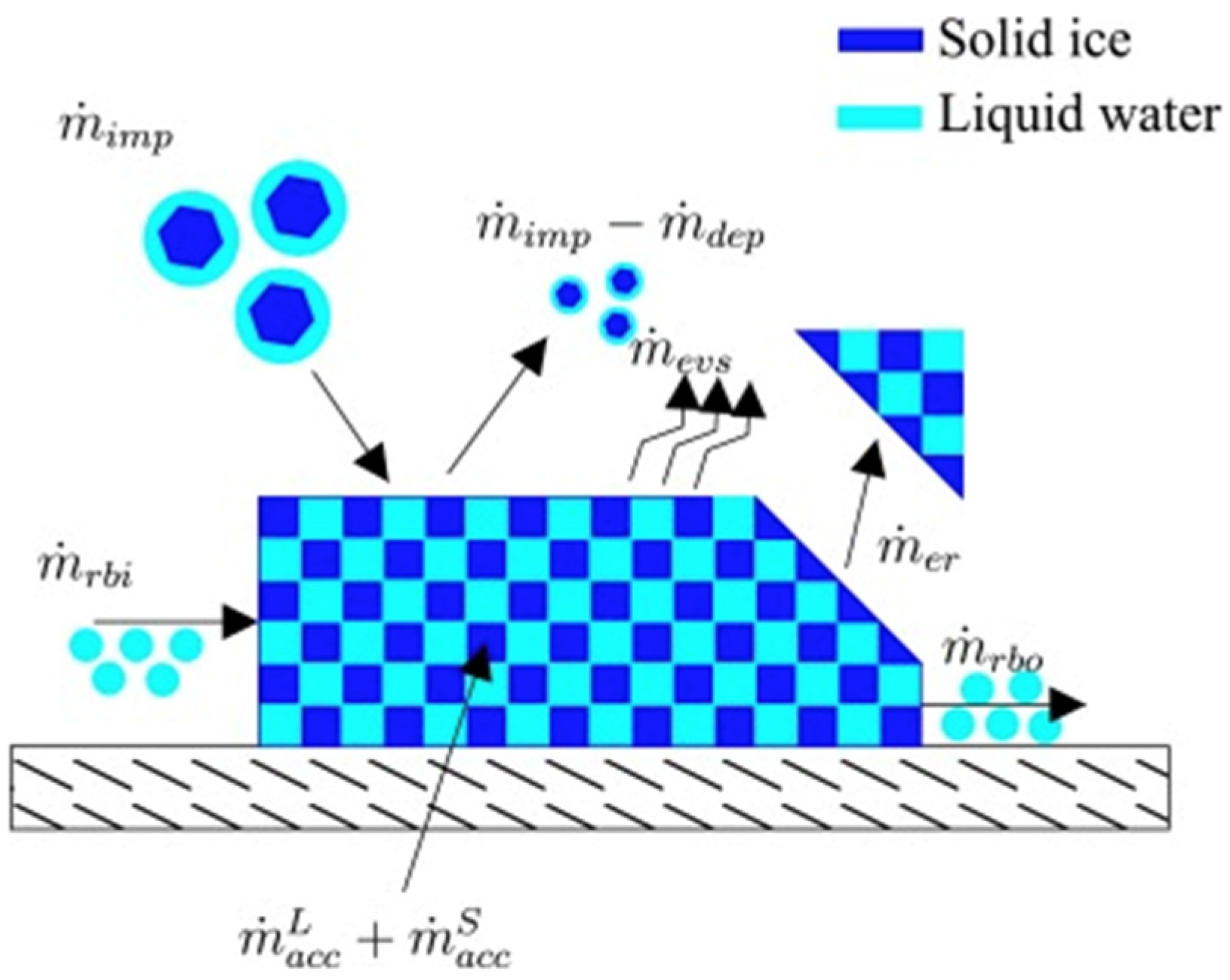
2.3. Engine Icing
- (1)
- Measurement on Ice Crystal Icing
- (2)
- Numerical Models of Ice Crystal Icing Physics
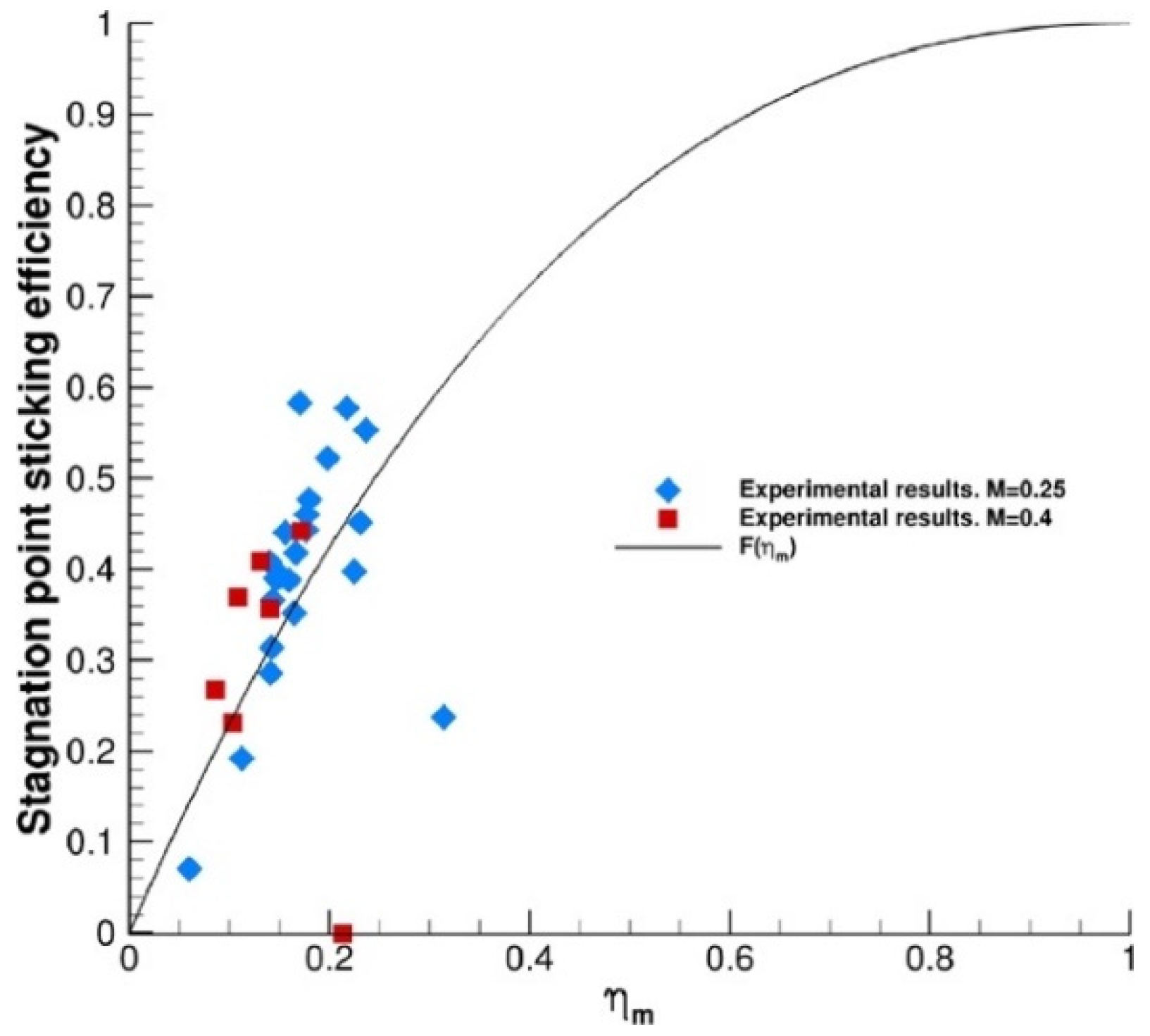
- When only ice crystals exist (), the sticking efficiency becomes 0 since all ice crystals bounce off the wall ().
- When only supercooled water droplets exist (), the sticking efficiency becomes 1 since all impinging droplets stick to the wall.
- In the small region in Figure 8, the function can be considered linear such that where is an adjustable number.
- The function is smooth and increases with the melting ratio.
3. Mitigation Techniques
3.1. Active Mitigation
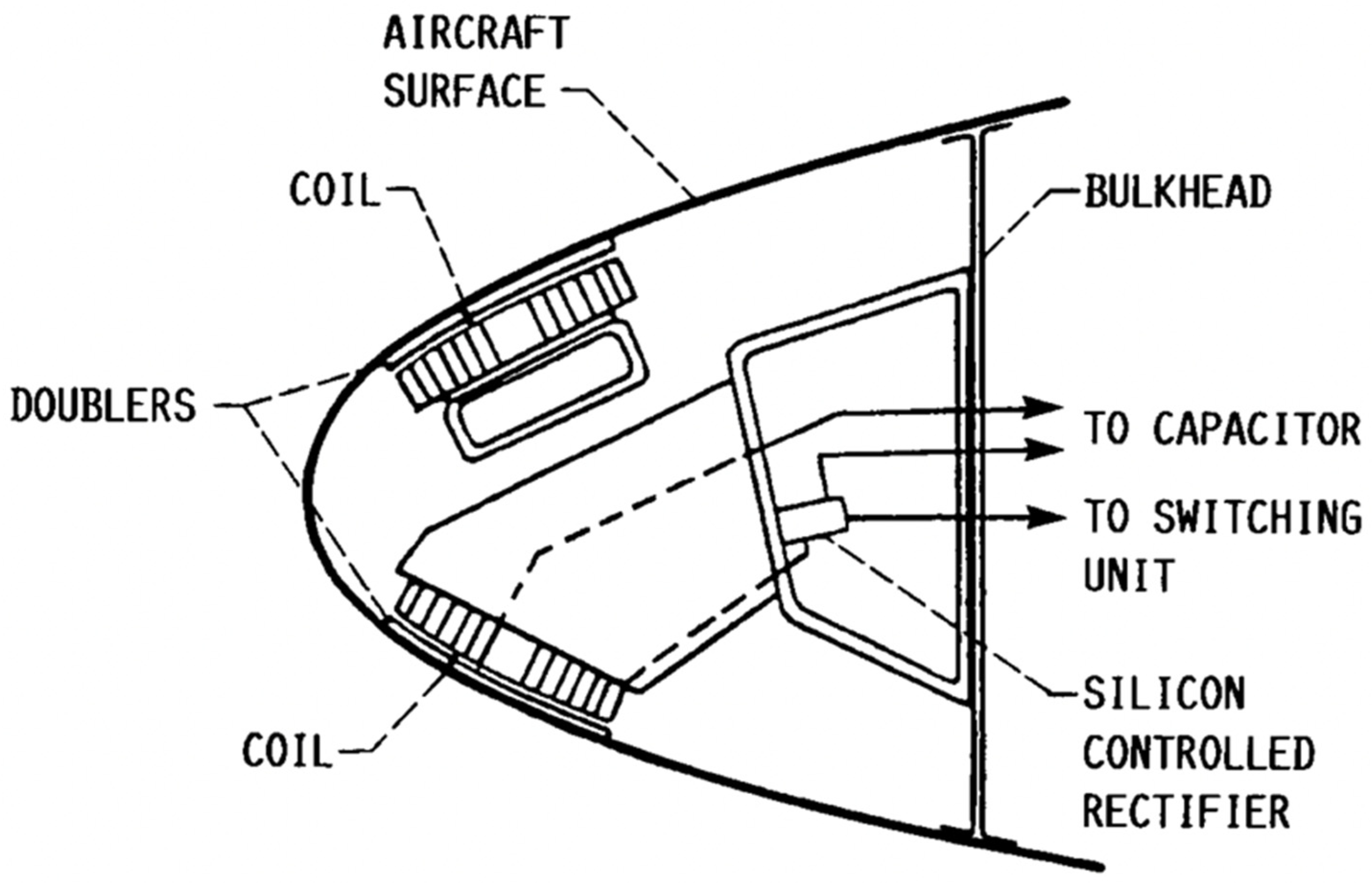
- (1)
- Thermal Method
- Meteorological parameters.
- Ambient temperature, air pressure, air speed, mean volumetric diameter of water droplet (MVD), liquid water content (LWC), etc.
- Structural parameters of the wing.
- Types of materials, wing skin thickness, leading-edge geometry, etc.
- Anti-/deicing system parameters.
- Piccolo tube size, cross-section shape, number of piccolo holes, hole diameter, etc. (hot air).
- Heater placement, power density, etc. (electrothermal).
- (2)
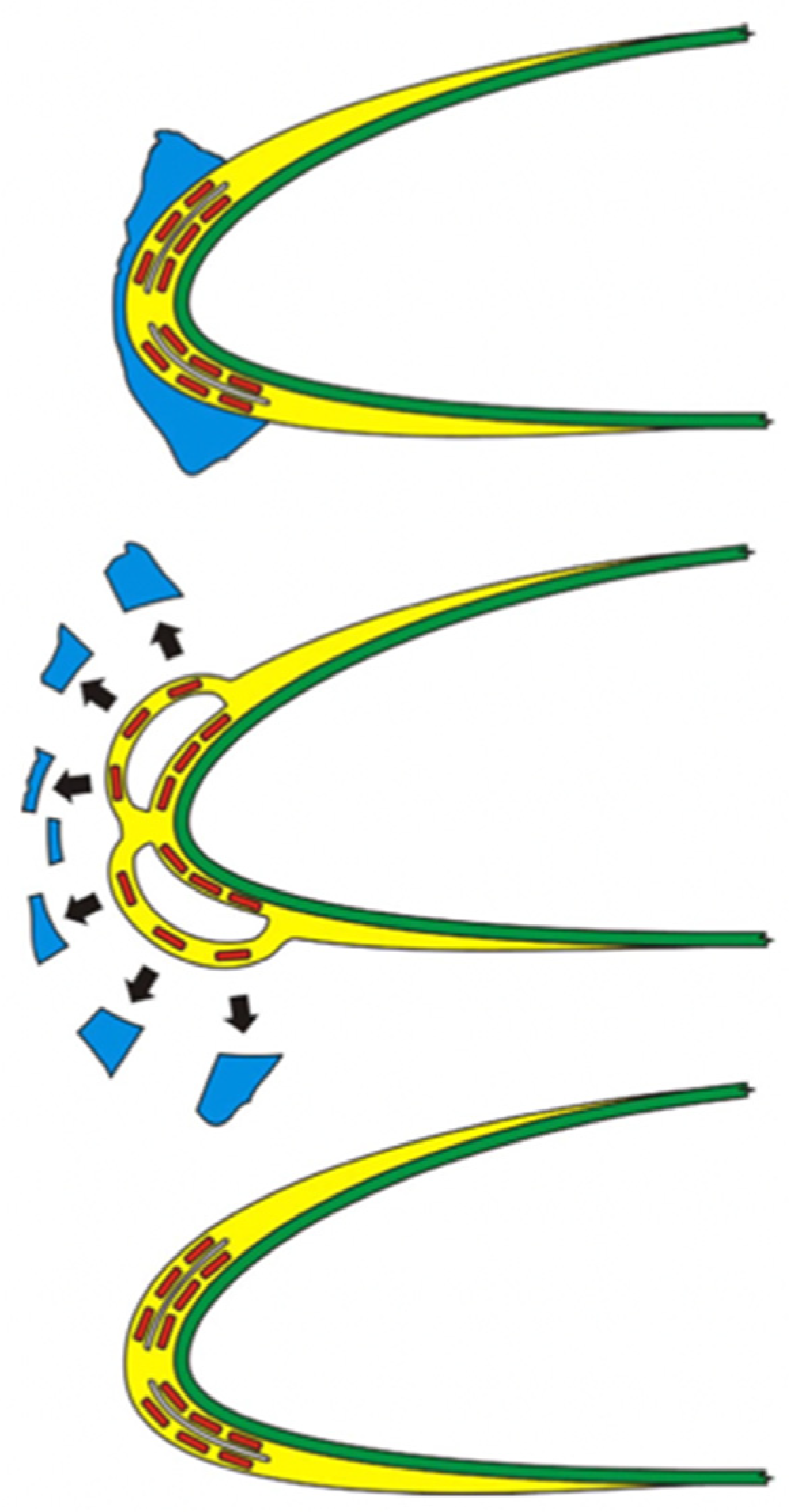
- Mechanical Method
- (3)
- Chemical Method
3.2. Passive Mitigation
- (1)
- Physicochemical Method
3.3. Hybrid Mitigation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Perkins, P.J.; Rieke, W.J. Aircraft icing problems—After 50 years. In Proceedings of the 31st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1993. [Google Scholar]
- Potapczuk, M.G. Aircraft Icing Research at NASA Glenn Research Center. J. Aerosp. Eng. 2013, 26, 260–276. [Google Scholar] [CrossRef]
- Bragg, M.B.; Broeren, A.P.; Blumenthal, L.A. Iced-airfoil aerodynamics. Prog. Aerosp. Sci. 2005, 41, 323–362. [Google Scholar] [CrossRef]
- Thomas, S.K.; Cassoni, R.P.; MacArthur, C.D. Aircraft Anti-Icing and De-Icing Techniques and Modeling. J. Aircr. 1996, 33, 841–854. [Google Scholar] [CrossRef]
- Federal Aviation Administration. Icing Design Envelopes (14 CFR Parts 25 and 29, Appendix C) Converted to a Distance-Based Format; Federal Aviation Administration: Washington, DC, USA, 2002.
- National Transportation Safety Board. In-Flight Icing Encounter and Loss of Control Simmons Airlines, d.b.a. American Eagle Flight 4184 Avions de Transport Regional (ATR) Model 72-212, N401AM, Roselawn, Indiana; Aircraft Accident Report; National Transportation Safety Board: Washington, DC, USA, 1996; Volume 1.
- Mason, J.G.; Strapp, J.W.; Chow, P. The Ice Particle Threat to Engines in Flight. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar] [CrossRef]
- Oliver, M.J. Validation Ice Crystal Icing Engine Test in the Propulsion Systems Laboratory at NASA Glenn Research Center. In Proceedings of the 6th AIAA Atmospheric and Space Environments Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Federal Aviation Administration. 14 CFR Appendix D to Part 33—Mixed Phase and Ice Crystal Icing Envelope (Deep Convective Clouds); Amdt. 33–34, 79 FR 65538, 4 November 2014; Federal Aviation Administration: Washington, DC, USA, 2014.
- European Aviation Safety Agency. Certification Specifications and Acceptable Means of Compliance for Large Aeroplanes CS-25; European Aviation Safety Agency: Cologne, Germany, 2016. [Google Scholar]
- Gent, R.W.; Dart, N.P.; Cansdale, J.T. Aircraft Icing. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2000, 358, 2873–2911. [Google Scholar] [CrossRef]
- Cebeci, T.; Kafyeke, F. Aircraft Icing. Annu. Rev. Fluid Mech. 2003, 35, 11–21. [Google Scholar] [CrossRef]
- Lynch, F.T.; Khodadoust, A. Effects of ice accretion on aircraft aerodynamics. Prog. Aerosp. Sci. 2001, 37, 669–767. [Google Scholar] [CrossRef]
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Mason, J.; Chow, P.; Riley, J. Engine Ice Crystal Icing Technology Plan with Research Needs; Federal Aviation Administration: Washington, DC, USA, 2020.
- Leary, W.M. We Freeze to Please: A History of NASA’s Icing Research Tunnel and the Quest for Flight Safety; NASA: Washington, DC, USA, 2002.
- Shaw, R.J.; Potapczuk, M.G.; Bidwell, C.S. Predictions of Airfoil Aerodynamic Performance Degradation Due to Icing. In Numerical and Physical Aspects of Aerodynamic Flows IV; Cebeci, T., Ed.; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Langmuir, I.; Blodgett, K.B. A Mathematical Investigation of Water Droplet Trajectories; Army Airforce TR No. 5418; US Army Airforces: Washington, DC, USA, 1946. [Google Scholar]
- Messinger, B.L. Equilibrium Temperature of an Unheated Icing Surface as a Function of Air Speed. J. Aeronaut. Sci. 1953, 20, 29–41. [Google Scholar] [CrossRef]
- Cao, Y.; Ma, C.; Zhang, Q.; Sheridan, J. Numerical simulation of ice accretions on an aircraft wing. Aerosp. Sci. Technol. 2012, 23, 296–304. [Google Scholar] [CrossRef]
- Shin, J.; Bond, T.H. Results of an icing test on a NACA 0012 airfoil in the NACA Lewis icing research tunnel. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar]
- Arizmendi, B.; Morelli, M.; Parma, G.; Zocca, M.; Quaranta, G.; Guardone, A. In-flight Icing: Modeling, Prediction, and Uncertainty. In Optimization under Uncertainty with Applications to Aerospace Engineering; Vasile, M., Ed.; Springer: Cham, Switzerland, 2021; pp. 455–506. [Google Scholar]
- Bourgault, Y.; Habashi, W.G.; Dompierre, J.; Baruzzi, G.S. A Finite Element Method Study of Eulerian Droplets Impingement Models. Int. J. Numer. Methods Fluids 1999, 29, 429–449. [Google Scholar] [CrossRef]
- Tan, J.; Papadakis, M.; Sampath, M.K. Computational Study of Large Droplet Breakup in the Vicinity of an Airfoil; Federal Aviation Administration: Washington, DC, USA, 2005.
- Vargas, M.; Feo, A. Experimental Observations on the Deformation and Breakup of Water Droplet near the Leading Edge of an Airfoil; NASA/TM-2011-216946; NASA: Washington, DC, USA, 2010.
- Hsiang, L.P.; Faeth, G.M. Secondary Drop Breakup in the Deformation Regime. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1993. [Google Scholar]
- Pilch, M.; Erdman, C.A. Use of Breakup Time Data and Velocity History Data to Predict the Maximum Size of Stable Fragments for Acceleration-Induced Breakup of a Liquid Drop. Int. J. Multiph. Flow 1987, 13, 741–757. [Google Scholar] [CrossRef]
- Honsek, R.; Habashi, W.G. Eulerian modeling of in-flight icing due to supercooled large droplets. J. Aircr. 2008, 45, 1290–1296. [Google Scholar] [CrossRef]
- ANSYS, Inc. ANSYS FENSAP-ICE User Manual; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Rutkowski, A.; Potapczuk, M. Numerical Study of Droplet Splashing and Re-impingement. In Proceedings of the 41st Aerospace Science Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar]
- Wright, W.B.; Potapczuk, M.G. Semi-empirical modeling of SLD physics. In Proceedings of the 42nd AIAA Aerospace Science Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. [Google Scholar]
- Yarin, A.L. Drop Impact Dynamics: Splashing, Spreading, Receding, Bouncing. Annu. Rev. Fluid Mech. 2006, 38, 159–192. [Google Scholar] [CrossRef]
- Bai, C.; Gosman, A. Development of Methodology for Spray Impingement Simulation. SAE Trans. 1995, 104, 550–568. [Google Scholar]
- Wang, M.; Watkins, A.P. Numerical Modeling of Diesel Spray Wall Impaction Phenomena. Int. J. Heat Fluid Flow 1993, 14, 301–312. [Google Scholar] [CrossRef]
- Stanton, D.; Rutland, C. Modeling Fuel Film Formation and Wall Interaction in Diesel Engines. SAE Trans. 1996, 105, 808–824. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Trapaga, G.; Szekely, J. Mathematical modeling of the isothermal impingement of liquid droplets in spraying processes. Metall. Mater. Trans. B 1991, 22, 901–914. [Google Scholar] [CrossRef]
- Lian, Y. Numerical simulation of supercooled large droplets using the moment of fluid method. In Proceedings of the 53rd Aerospace Science Meeting, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Cao, Y.; Xin, M. Numerical Simulation of Supercooled Large Droplet Icing Phenomenon: A Review. Arch. Comput. Methods Eng. 2020, 27, 1231–1265. [Google Scholar] [CrossRef]
- Mundo, C.; Sommerfeld, M.; Tropea, C. Droplet-wall collisions: Experimental studies of the deformation and breakup process. Int. J. Multiph. Flow 1995, 21, 151–173. [Google Scholar] [CrossRef]
- Cossali, G.E.; Coghe, A.; Marengo, M. The impact of a single drop on a wetted solid surface. Exp. Fluids 1997, 22, 463–472. [Google Scholar] [CrossRef]
- Trujillo, L. Modeling and Experiment of Impingement and atomization of a liquid spray on a wall. J. Engine Res. 2000, 1, 87–105. [Google Scholar] [CrossRef]
- Wright, W.B. Further Refinement of the LEWICE SLD Model. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Honsek, R. Development of a Three Dimensional Eulerian Model of Droplet-Wall Interaction Mechanisms. Master’s Thesis, McGill University, Montreal, QC, Canada, June 2005. [Google Scholar]
- Papadakis, M.; Rachman, A.; Wong, S.C.; Yeong, H.W.; Hung, K.; Bidwell, C. Water Impingement Experiments on a NACA 23012 Airfoil with Simulated Glaze Ice Shapes. In Proceedings of the 42nd AIAA Aerospace Science Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. [Google Scholar]
- Myers, T.G. An extension to the Messinger Model for Aircraft Icing. AIAA J. 2001, 39, 211–218. [Google Scholar] [CrossRef]
- Olsen, W.; Shaw, R.; Newton, J. Ice shapes and the resulting drag increase for a NACA 0012 airfoil. In Proceedings of the 22nd Aerospace Science Meeting, Reno, NV, USA, 9–12 January 1984. [Google Scholar]
- Shin, J. Characteristics of surface roughness associated with leading edge ice accretion. J. Aircr. 1996, 33, 316–321. [Google Scholar] [CrossRef]
- Anderson, D.N.; Shin, J. Characterization of ice roughness from simulated icing encounters. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1997. [Google Scholar]
- Anderson, D.; Hentschel, D.; Ruff, G. Measurement and Correlation of Ice Accretion Roughness. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998. [Google Scholar]
- Han, Y.; Palacios, J. Surface Roughness and Heat Transfer Improved Predictions for Aircraft Ice-Accretion Modeling. AIAA J. 2017, 55, 1318–1331. [Google Scholar] [CrossRef]
- Ignatowicz, K.; Morency, F.; Beaugendre, H. Numerical simulation of ice accretion using Messinger-based approach: Effects of surface roughness. In Proceedings of the CASI Aero 2019—Canadian Aeronautics and Space Institute’s AERO 2019 Conference, Laval, QC, Canada, 14–16 May 2019. [Google Scholar]
- Aupoix, B. Improved heat transfer predictions on rough surfaces. Int. J. Heat Fluid Flow 2015, 56, 160–171. [Google Scholar] [CrossRef]
- Han, Y.; Palacios, J. Surface Roughness and Heat Transfer Prediction for Development of an Improved Aircraft Ice Accretion Modeling Tool. In Proceedings of the 8th AIAA Atmospheric and Space Environments Conference, AIAA AVIATION Forum, Washington, DC, USA, 13–17 January 2016. [Google Scholar]
- McClain, S.; Vargas, M.; Tsao, J.; Broeren, A.; Lee, S. Ice Accretion Roughness Measurements and Modeling. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences, European Conference for AeroSpace Sciences, Milan, Italy, 3–7 July 2017. [Google Scholar]
- Lee, S.; Broeren, A.; Addy, H.; Sills, R.; Pifer, E. Development of 3D Ice Accretion Measurement Method; NASA TM-2012-217702; NASA: Washington, DC, USA, 2012.
- McClain, S.; Tino, T.; Kreeger, R. Ice Shape Characterization Using Self-Organizing Maps. J. Aircr. 2011, 48, 724–730. [Google Scholar] [CrossRef][Green Version]
- McClain, S.T.; Kreeger, R.E. Assessment of Ice Shape Roughness Using a Self-Organizing Map Approach. In Proceedings of the 5th AIAA Atmospheric and Space Environments Conference, San Diego, CA, USA, 24–27 June 2013. [Google Scholar]
- McClain, S.T.; Vargas, M.; Tsao, J.C. Ice Roughness and Thickness Evolution on a Swept NACA0012 Airfoil. In Proceedings of the 9th AIAA Atmospheric and Space Environments Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Wang, Z.; Zhao, N.; Zhu, C. Numerical simulation for three-dimensional rotor icing in forward flight. Adv. Mech. Eng. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Bragg, M.B. Effect of Geometry on Airfoil Icing Characteristics. J. Aircr. 1984, 21, 505–511. [Google Scholar] [CrossRef]
- Peterson, A.A.; Dadone, L.U. Helicopter Icing Review; FAA Contract DOT-FA78WA-4258; US Department of Transportation: Atlantic, NJ, USA, 1980.
- Cao, Y.; Chen, K. Helicopter icing. Aeronaut. J. 2016, 114, 83–90. [Google Scholar] [CrossRef]
- Perkins, P.J. Aircraft Icing; NASA Conference Publication 2086; NASA: Washington, DC, USA, 1978.
- Flemming, R.J.; Britton, R.K.; Bond, T.H. Role of Wind Tunnels and Computer Codes in the Certification and Qualification of Rotorcraft for Flight in Forecast Icing; NASA TM-106747; NASA: Washington, DC, USA, 1994.
- Bell, J. Icing at the McKinley Climatic Laboratory. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar]
- Palacios, J.L.; Han, J.; Brouwers, E.W.; Smith, E.C. Icing Environment Rotor Test Stand Liquid Water Content Measurement Procedures and Ice Shape Correlation. J. Am. Helicopter Soc. 2012, 57, 29–40. [Google Scholar] [CrossRef]
- Palacios, J.L.; Brouwers, E.W.; Han, Y.; Smith, E.C. Adverse Environment Rotor Test Stand Calibration Procedures and Ice Shape Correlation. In Proceedings of the American Helicopter Society 66th Annual Forum, Phoenix, AZ, USA, 11–13 May 2010. [Google Scholar]
- Wright, W.B. User’s Manual for LEWICE Version 3.2; CR-2008-214255; NASA: Cleveland, OH, USA, 2008.
- Beaugendre, H.; Morency, F.; Habashi, W.G. FENSAP-ICE’s Three-Dimensional In-Flight Ice Accretion Module: ICE3D. J. Aircr. 2003, 40, 239–247. [Google Scholar] [CrossRef]
- Hedde, T.; Guffond, D. ONERA Three-Dimensional Icing Model. AIAA J. 1995, 33, 1038–1045. [Google Scholar] [CrossRef]
- Narducci, R.; Kreeger, R. Analysis of a Hovering Rotor in Icing Conditions; NASA TM-217126; NASA: Washington, DC, USA, 2012.
- Lee, J.D.; Harding, R.; Palko, R.L. Documentation of Ice Shapes on the Main Rotor of a UH-1H Helicopter in Hover; NASA CR-168332; Lewis Research Center: Cleveland, OH, USA, 1983.
- Busch, G.; Bragg, M. Computational Prediction of Propeller Performance in Icing Condition. In Proceedings of the AIAA Atmospheric and Space Environments Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Brouwers, E.; Palacios, J.; Smith, E.; Peterson, A. The Experimental Investigation of a Rotor Hover Icing model with Shedding. In Proceedings of the American Helicopter Society 66th Annual Forum, Phoenix, AZ, USA, 11–13 May 2010. [Google Scholar]
- Zhang, S.; El Kerdi, O.; Khurram, R.A.; Habashi, W.G. FEM Analysis of In-flight Ice Break-up. Finite Elem. Anal. Des. 2012, 57, 55–66. [Google Scholar] [CrossRef]
- Zhang, S.; Khurram, R.A.; Fouladi, H.; Habashi, W.G. Computational Modeling of Ice Cracking and Break-up from Helicopter Blades. In Proceedings of the 4th AIAA Atmospheric and Space Environments Conference, New Orleans, LA, USA, 25–28 June 2012. [Google Scholar]
- Zhao, G.; Zhao, Q.; Chen, X. New 3-D ice accretion method of hovering rotor including effects of centrifugal force. Aerosp. Sci. Technol. 2016, 48, 122–130. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, C. Study of the Effect of Centrifugal Force on Rotor Blade Icing Process. Int. J. Aerosp. Eng. 2017, 2017, 8695170. [Google Scholar] [CrossRef]
- Kelly, D.; Habashi, W.G.; Fossati, M. Ice Accretion Effects on Helicopter Rotor Performance, via Multibody and CFD Approached. J. Aircr. 2018, 55, 1165–1176. [Google Scholar] [CrossRef]
- Bucknell, A.; McGilvray, M.; Gillespie, D.R.H.; Jones, G.; Reed, A.; Collier, B. Experimental Studies of Ice Crystal Accretion on Axisymmetric Bodies at Aeroengine Conditions. J. Propuls. Power 2020, 36, 836–850. [Google Scholar] [CrossRef]
- Struk, P.; Currie, T.; Wright, W.B.; Knezevici, D.; Fuleki, D.; Broeren, A.; Vargas, M.; Tsao, J.C. Fundamental Ice Crystal Accretion Physics Studies; NASA TM-2012-217429; NASA: Washington, DC, USA, 2012.
- Currie, T.; Struk, P.; Tsao, J.C.; Fuleki, D.; Knezevici, D. Fundamental Study of Mixed-Phase Icing with Application to Ice Crystal Accretion in Aircraft Jet Engines. In Proceedings of the 4th AIAA Atmospheric and Space Environments Conference, New Orleans, LA, USA, 25–28 June 2012. [Google Scholar]
- Hauk, T. Investigation of the Impact and Melting Process of Ice Particles. Ph.D. Thesis, Technischen Universitat Darmstadt, Darmstadt, Germany, 26 January 2016. [Google Scholar]
- Van Zante, J.F.; Bencic, T.J.; Ratvasky, T.P. Update on the NASA Glenn Propulsion Systems Lab Ice Crystal Cloud Characterization (2015). In Proceedings of the 8th AIAA Atmospheric and Space Environments Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Davison, C.R.; Rutke, T.; Strapp, J.W.; Ratvasky, T.P.; Emery, E.F. Naturally Aspirating Isokinetic Total Water Content Probe: Pre-flight Wind Tunnel Testing and Design Modifications. In Proceedings of the 4th AIAA Atmospheric and Space Environments Conference, New Orleans, LA, USA, 25–28 June 2012. [Google Scholar]
- Davison, C.; Strapp, J.W.; Lilie, L.E.; Ratvasky, T.P.; Dumont, C. Isokinetic TWC Evaporator Probe: Calculations and Systemic Error Analysis. In Proceedings of the 8th AIAA Atmospheric and Space Environments Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Lang, B.; Breitfuss, W.; Schweighart, S.; Breitegger, P.; Pervier, H.; Tramposch, A.; Klug, A.; Hassler, W.; Bergmann, A. Photoacoustic hygrometer for icing wind tunnel water content measurement: Design, analysis, and intercomparison. Atmos. Meas. Tech. 2021, 14, 2477–2500. [Google Scholar] [CrossRef]
- Wright, W.B.; Jorgenson, P.C.E.; Veres, J.P. Mixed Phase Modeling in GlennICE with Application to Engine Icing. In Proceedings of the AIAA Atmospheric and Space Environments Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Trontin, P.; Kontogiannis, A.; Blanchard, G.; Villedieu, P. Description and assessment of the new ONERA2D icing suite IGLOO2D. In Proceedings of the 9th AIAA Atmospheric and Space Environments Conference, AIAA AVIATION Forum, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Nilamdeen, S.; Habashi, W.; Aube, M.; Baruzzi, G. FENSAP-ICE: Modeling of Water Droplets and Ice Crystals. In Proceedings of the 1st AIAA Atmospheric and Space Environments Conference, San Antonio, TX, USA, 22–25 June 2009. [Google Scholar]
- Bucknell, A.; McGilvray, M.; Gillespie, D.; Yang, X.; Jones, G.; Collier, B. ICICLE: A Model for Glaciated & Mixed Phase Icing for Application to Aircraft Engines. SAE Tech. Paper 2019. [Google Scholar] [CrossRef]
- Ganser, G.H. A rational approach to drag prediction of spherical and nonspherical particles. Power Technol. 1993, 77, 143–152. [Google Scholar] [CrossRef]
- Norde, E.; Van der Weide, E.; Hoeijmakers, H. Eulerian Method for Ice Crystal Icing. AIAA J. 2018, 56, 222–234. [Google Scholar] [CrossRef]
- Tsao, J.C.; Struk, P.M.; Oliver, M.J. Possible Mechanisms for Turbofan Engine Ice Crystal Icing at High Altitude. In Proceedings of the 6th AIAA Atmospheric and Space Environments Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Trontin, P.; Villedieu, P. A comprehensive accretion model for glaciated icing conditions. Int. J. Multiph. Flow 2018, 108, 105–123. [Google Scholar] [CrossRef]
- Charlton, V.; Senoner, J.M.; Trontin, P.; Villedieu, P. Semi-empirical Erosion Model with Particle Size and Liquid Water Content Effects for Ice Crystal Icing Simulations. In Proceedings of the AIAA Aviation 2020 Forum, Reno, NV, USA, 15–19 June 2020. [Google Scholar]
- Villedieu, P.; Trontin, P.; Chauvin, R. Glaciated and mixed phase ice accretion modeling using ONERA 2D icing suite. In Proceedings of the 6th AIAA Atmospheric and Space Environments Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Bartkus, T.P.; Tsao, J.C.; Struk, P.M. Analysis of Experimental Ice Accretion Data and Assessment of a Thermodynamic Model During Ice Crystal Icing. SAE Tech. Paper 2019. [Google Scholar] [CrossRef]
- Currie, T.C.; Fuleki, D.M.; Mahallati, A. Experimental studies of mixed-phase sticking efficiency for ice crystal accretion in jet engines. In Proceedings of the 6th AIAA Atmospheric and Space Environments Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Baumert, A.; Bansmer, S.; Trontin, P.; Villedieu, P. Experimental and numerical investigations on aircraft icing at mixed phase conditions. Int. J. Heat Mass Transf. 2018, 123, 957–978. [Google Scholar] [CrossRef]
- Shohag, M.A.S.; Hammel, E.C.; Olawale, D.O.; Okoli, O.I. Damage mitigation techniques in wind turbine blades: A review. Wind Eng. 2017, 41, 185–210. [Google Scholar] [CrossRef]
- Parent, O.; Ilinca, A. Anti-icing and de-icing techniques for wind turbines: Critical review. Cold Reg. Sci. Technol. 2011, 65, 88–96. [Google Scholar] [CrossRef]
- Pellissier, M.P.C.; Habashi, W.G.; Peueyo, A. Optimization via FENSAP-ICE of Aircraft Hot-Air Anti-Icing Systems. J. Aircr. 2011, 48, 265–276. [Google Scholar] [CrossRef]
- Yeoman, K.E. Efficiency of a Bleed Air Powered Inlet Icing Protective System. In Proceedings of the 32nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 1994. [Google Scholar]
- Norris, R.M.; Rumford, K.J.; Youd, D.S. Anti-Icing Valve. U.S. Patent 4,831,819, 7 February 1987. [Google Scholar]
- Ding, L.; Chang, S.; Leng, M. Transient characteristics of an electrothermal anti-icing process based on the improved messinger model. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016. [Google Scholar]
- Pourbagian, M.; Habashi, G.W. Parametric Analysis of Energy Requirements of In-Flight Ice Protection Systems. In Proceedings of the 20th Annual Conference of the CFD Society of Canada (CFD2012), Canmore, AB, Canada, 9–11 May 2012. [Google Scholar]
- Wong, S.H.; Papadakis, M.; Zamora, A. Computational Investigation of a Bleed Air Ice Protection System. In Proceedings of the 1st AIAA Atmospheric and Space Environments Conference, San Antonio, TX, USA, 22–25 June 2009. [Google Scholar]
- Planquart, P.; Vanden Borre, G.; Buchlin, J.M. Experimental and Numerical Optimization of a Wing Leading Edge Hot Air Anti-Icing System. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Wright, W.B. An Evaluation of Jet Impingement Heat Transfer Correlations for Piccolo Tube Application. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. [Google Scholar]
- Brown, J.M.; Raghunathan, S.; Watterson, J.K.; Linton, A.J.; Riordon, D. Heat Transfer Correlation for Anti-Icing Systems. J. Aircr. 2002, 39, 65–70. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, G.; Bu, X.; Mu, Z.; Pan, R.; Ge, Q.; Qiao, X. Temperature and Runback Ice Prediction Method for Three-Dimensional Hot Air Anti-Icing System. In IOP Conference Series: Materials Science and Enginering; IOP Publishing: Bristol, UK, 2017; Volume 187, p. 012017. [Google Scholar]
- Papadakis, M.; Wong, S.H. Parametric investigation of a bleed air ice protection system. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Papadakis, M.; Wong, S.H.; Yeong, H.W.; Wong, S.C.; Vu, G.T. Icing Tests of a Wing Model with a Hot-Air Ice Protection System. In Proceedings of the AIAA Atmospheric and Space Environments Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Zhang, F.; Gao, Y.; Yao, H.; Wang, Y.; Luo, K. Structural Parameter Sensitivity Analysis of an Aircraft Anti-Icing Cavity Based on Thermal Efficiency. Int. J. Aerosp. Eng. 2019, 2019, 7851260. [Google Scholar] [CrossRef]
- Guan, T.; Zhang, J.Z.; Shan, Y. Effect of offset-jets arrangement on leading edge hot-air heating effectiveness of engine inlet guide strut. Appl. Therm. Eng. 2018, 128, 357–372. [Google Scholar] [CrossRef]
- Chen, N.; Hu, Y.; Ji, H.; Zhang, M. Hot-Air Anti-Icing Heat Transfer and Surface Temperature Modeling. AIAA J. 2021, 1–10. [Google Scholar] [CrossRef]
- Li, L.; Liu, Y.; Tian, L.; Hu, H.; Hu, H.; Liu, X.; Hogate, I.; Kohli, A. An experimental study on a hot-air-based anti-/de-icing system for aero-engine inlet guide vanes. Appl. Therm. Eng. 2020, 167, 114778. [Google Scholar] [CrossRef]
- Hui, M.; Dalin, Z. Experiment investigation of hot-air anti-icing structure of engine inlet vane. In Proceedings of the 2016 IEEE/CSAA International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016; pp. 284–289. [Google Scholar]
- Martin, C.; Putt, J. Advanced Pneumatic Impulse Ice Protection System (PIIP) for Aircraft. J. Aircr. 1992, 29, 714–716. [Google Scholar] [CrossRef]
- Reinmann, J.J.; Shaw, R.J.; Ranaudo, R.J. NASA’s Program on Icing Research and Technology; NASA Technical Memorandum 101989; NASA: Cleveland, OH, USA, 1989.
- Jiang, X.; Wang, Y. Studies on the Electro-Impulse De-Icing System of Aircraft. Aerospace 2019, 6, 67. [Google Scholar] [CrossRef]
- Labeas, G.N.; Diamantakos, I.D.; Sunaric, M.M. Simulation of the electroimpulse de-icing process of Aircraft Wings. J. Aircr. 2006, 43, 1876–1885. [Google Scholar] [CrossRef]
- Goraj, Z. An overview of the deicing and anti-icing technologies with prospects for the future. In Proceedings of the 24th International Congress of the Aeronautical Sciences, Yokohama, Japan, 29 August–3 September 2004. [Google Scholar]
- Hill, E.G.; Zierten, T.A. Aerodynamic Effects of Aircraft Ground Deicing/Anti-Icing Fluids. J. Aircr. 1993, 30, 24–34. [Google Scholar] [CrossRef]
- Corsi, S.R.; Mericas, D.; Bowman, G.T. Oxygen Demand of Aircraft and Airfield Pavement Deicers and Alternative Freezing Point Depressants. Water Air Soil Pollut. 2012, 223, 2447–2461. [Google Scholar] [CrossRef]
- Kent, R.A.; Andersen, D.; Caux, P.Y.; Teed, S. Canadian water quality guidelines for glycols—An ecotoxicological review of glycols and associated aircraft anti-icing and deicing fluids. Environ. Toxicol. 1999, 14, 481–522. [Google Scholar] [CrossRef]
- Jaesche, P.; Totsche, K.U.; Kögel-Knabner, I. Transport and anaerobic biodegradation of propylene glycol in gravel-rich soil materials. J. Contam. Hydrol. 2006, 85, 271–286. [Google Scholar] [CrossRef]
- Hartwell, S.I.; Jordahl, D.M.; Evans, J.E.; May, E.B. Toxicity of Aircraft De-Icer and Anti-Icer Solutions to Aquatic Organisms. Environ. Toxicol. Chem. 1995, 14, 1375–1386. [Google Scholar] [CrossRef]
- Pillard, D.A. Comparative Toxicity of Formulated Glycol Deicers and Pure Ethylene and Propylene Glycol to Ceriodaphnia Dubia and Pimephales Promelas. Environ. Toxicol. Chem. 1995, 14, 311–315. [Google Scholar] [CrossRef]
- Cancilla, D.A.; Holtkamp, A.; Matassa, L.; Fang, X. Isolation and Characterization of Microtox-Active Components from Aircraft De-Icing/Anti-Icing Fluids. Environ. Toxicol. Chem. 1997, 16, 430–434. [Google Scholar] [CrossRef]
- Cancilla, D.A.; Martinez, J.; van Aggelen, G.C. Detection of aircraft deicing/antiicing fluid additives in a perched water monitoring well at an international airport. Environ. Sci. Technol. 1998, 32, 3834–3835. [Google Scholar] [CrossRef]
- Wolschke, H.; Xie, Z.; Möller, A.; Sturm, R.; Ebinghaus, R. Occurrence, distribution and fluxes of benzotriazoles along the German large river basins into the North Sea. Water Res. 2011, 45, 6259–6266. [Google Scholar] [CrossRef]
- Giger, W.; Schaffner, C.; Kohler, H.P.E. Benzotriazole and tolyltriazole as aquatic contaminants. 1. Input and occurrence in rivers and lakes. Environ. Sci. Technol. 2006, 40, 7186–7192. [Google Scholar] [CrossRef]
- Liu, Y.S.; Ying, G.G.; Shareef, A.; Kookana, R.S. Biodegradation of three selected benzotriazoles under aerobic and anaerobic conditions. Water Res. 2011, 45, 5005–5014. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, H.; Wang, G.; Liu, A. Recent Progress in Preparation and Anti-Icing Applications of Superhydrophobic Coatings. Coatings 2018, 8, 208. [Google Scholar] [CrossRef]
- Laforte, C.; Carriere, J.C.; Laforte, J.L. How a Solid Coating Can Reduce the Adhesion of Ice on a Structure. In Proceedings of the 10th International Workshop on Atmospheric Icing of Structures IWAIS, Brno, Czech Republic, 17–20 June 2002. [Google Scholar]
- Golovin, K.; Kobaku, S.; Lee, D.; Di Loreto, E.; Mabry, J.; Tuteja, A. Designing durable icephobic surfaces. Sci. Adv. 2016, 2, e1501496. [Google Scholar] [CrossRef] [PubMed]
- Andersson, L.O.; Golander, G.C.; Persson, S. Ice Adhesion to Rubber Material. J. Adhes. Sci. Technol. 1994, 8, 117–132. [Google Scholar] [CrossRef]
- Boinovich, L.B.; Emelyanenko, A.M. Anti-Icing Potential of Superhydrophobic Coatings. Mendeleev Commun. 2013, 23, 3–10. [Google Scholar] [CrossRef]
- Farhadi, S.; Farzaneh, M.; Kulinich, S.A. Anti-icing performance of superhydrophobic surfaces. Appl. Surf. Sci. 2011, 257, 6264–6269. [Google Scholar] [CrossRef]
- Saito, H.; Takai, K.; Yamauchi, G. Water- and ice-repellent coatings. Surf. Coat. Int. 1997, 80, 168–171. [Google Scholar] [CrossRef]
- Kulinich, S.A.; Farzaneh, M. How Wetting Hysteresis Influences Ice Adhesion Strength on Superhydrophobic Surfaces. Langmuir 2009, 25, 8854–8856. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Jones, A.K.; Sikka, V.K.; Wu, J.; Gao, D. Anti-Icing Superhydrophobic Coatings. Langmuir 2009, 25, 12444–12448. [Google Scholar] [CrossRef] [PubMed]
- Meuler, A.J.; Smith, J.D.; Varanasi, K.K.; Mabry, J.M.; McKinley, G.H.; Cohen, R.E. Relationships between Water Wettability and Ice Adhesion. ACS Appl. Mater. Interfaces 2010, 2, 3100–3110. [Google Scholar] [CrossRef]
- Menini, R.; Ghalmi, Z.; Farzaneh, M. Highly resistant icephobic coatings on aluminum alloys. Cold Reg. Sci. Technol. 2011, 65, 65–69. [Google Scholar] [CrossRef]
- Antonini, C.; Innocenti, M.; Horn, T.; Marengo, M.; Amirfazli, A. Understanding the effect of superhydrophobic coatings on energy reduction in anti-icing systems. Cold Reg. Sci. Technol. 2011, 67, 58–67. [Google Scholar] [CrossRef]
- Piscitelli, F.; Chiariello, A.; Dabkowski, D.; Corraro, G.; Marra, F.; Di Palma, L. Superhydrophobic Coatings as Anti-Icing Systems for Small Aircraft. Aerospace 2020, 7, 2. [Google Scholar] [CrossRef]
- Vazirinasab, E.; Maghsoudi, K.; Jafari, R.; Momen, G. A comparative study of the icephobic and self-cleaning properties of Teflon materials having different surface morphologies. J. Mater. Process. Technol. 2020, 276, 116415. [Google Scholar] [CrossRef]
- Wong, T.S.; Kang, S.H.; Tang, S.K.Y.; Smythe, E.J.; Hatton, B.D.; Grinthal, A.; Aizenberg, J. Bioinspired self-repairing slippery surfaces with pressure-stable omniphobicity. Nature 2011, 477, 443–447. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, L.; Gao, Y.; Liu, H.; Hu, H. Bio-Inspired Icephobic Coatings for Aircraft Icing Mitigation: A Critical Review. Rev. Adhes. Adhes. 2020, 8, 2. [Google Scholar]
- Kim, P.; Wong, T.S.; Alvarenga, J.; Kreder, M.J.; Adorno-Martinez, W.E.; Aizenberg, J. Liquid-Infused Nanostructured Surfaces with Extreme Anti-Ice and Anti-Frost Performance. ACS Nano 2012, 6, 6569–6577. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Zhang, Y.; Wang, D.; Liu, Z.; Liu, Y.; Pei, X.; Yu, B.; Zhou, F. Integration of Self-Lubrication and Near-Infrared Photothermogenesis for Excellent Anti-Icing/Deicing Performance. Adv. Funct. Mater. 2015, 25, 4237–4245. [Google Scholar] [CrossRef]
- Shen, Y.; Wu, Y.; Tao, J.; Zhu, C.; Chen, H.; Wu, Z.; Xie, Y. Spraying Fabrication of Durable and Transparent Coatings for Anti-Icing Application: Dynamic Water Repellency, Icing Delay, and Ice Adhesion. ACS Appl. Mater. Interfaces 2019, 11, 3590–3598. [Google Scholar] [CrossRef]
- Zhuo, Y.; Hakonsen, V.; He, Z.; Xiao, S.; He, J.; Zhang, Z. Enhancing the Mechanical Durability of Icephobic Surfaces by Introducing Autonomous Self-Healing Function. ACS Appl. Mater. Interfaces 2018, 10, 11972–11978. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, X.; Wu, S.; Li, Q.; Lv, J.; Wang, J.; Jiang, L. Bioinspired Solid Organogel Materials with a Regenerable Sacrificial Alkane Surface Layer. Adv. Mater. 2017, 29, 170086. [Google Scholar] [CrossRef]
- Shen, Y.; Wu, X.; Tao, J.; Zhu, C.; Lai, Y.; Chen, Z. Icephobic materials: Fundamentals, performance evaluation, and applications. Prog. Mater. Sci. 2019, 103, 509–557. [Google Scholar] [CrossRef]
- Zhuo, Y.; Xiao, S.; Amirfazli, A.; He, J.; Zhang, Z. Polysiloxane as icephobic materials—The past, present and the future. Chem. Eng. J. 2021, 405, 127088. [Google Scholar] [CrossRef]
- Huang, X.; Tepylo, N.; Pommier-Budinger, V.; Budinger, M.; Bonaccurso, E.; Villedieu, P.; Bennani, L. A survey of icephobic coatings and their potential use in a hybrid coating/active ice protection system for aerospace applications. Prog. Aerosp. Sci. 2019, 105, 74–97. [Google Scholar] [CrossRef]
- Morita, K.; Kimura, S.; Sakaue, H. Hybrid System Combining Ice-Phobic Coating and Electrothermal Heating for Wing Ice Protection. Aerospace 2020, 7, 102. [Google Scholar] [CrossRef]
- Pommier-Budinger, V.; Budinger, M.; Tepylo, N.; Huang, X. Analysis of piezoelectric ice protection systems combined with ice-phobic coatings. In Proceedings of the 8th AIAA Atmospheric and Space Environments Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamazaki, M.; Jemcov, A.; Sakaue, H. A Review on the Current Status of Icing Physics and Mitigation in Aviation. Aerospace 2021, 8, 188. https://doi.org/10.3390/aerospace8070188
Yamazaki M, Jemcov A, Sakaue H. A Review on the Current Status of Icing Physics and Mitigation in Aviation. Aerospace. 2021; 8(7):188. https://doi.org/10.3390/aerospace8070188
Chicago/Turabian StyleYamazaki, Masafumi, Aleksandar Jemcov, and Hirotaka Sakaue. 2021. "A Review on the Current Status of Icing Physics and Mitigation in Aviation" Aerospace 8, no. 7: 188. https://doi.org/10.3390/aerospace8070188
APA StyleYamazaki, M., Jemcov, A., & Sakaue, H. (2021). A Review on the Current Status of Icing Physics and Mitigation in Aviation. Aerospace, 8(7), 188. https://doi.org/10.3390/aerospace8070188






