Ion Source—Thermal and Thermomechanical Simulation
Abstract
1. Introduction
2. The Status of the Problem
3. Balance of Particles and Power in the Discharge
- -
- Absorption of HF power by plasma due to plasma electrical conductivity;
- -
- Plasma formation driven by ionization and heating of electrons and leading to an increase in the ionized propellant gas internal energy;
- -
- Carry-over of a portion of plasma power by ions and electrons onto the walls, including ionization energy released during recombination of ions and electrons of the propellant gas, which is also converted into heat.
4. Development of the Ion Source Thermal Model
- -
- Calculate discharge plasma parameters in the GDC;
- -
- Determine heat fluxes from plasma over the surface of the IS structure;
- -
- Solve the problem of heat transfer from the IS structural elements using Equation (5) by numerical methods with account of the boundary conditions (environmental conditions), heat fluxes from the structural elements in view of contact resistances and input heat fluxes from plasma.
- -
- If discrete elements belong to one and the same structural element—by using the finite-difference expression of the Fourier thermal conductivity law, where, instead of the temperature gradient, the temperature difference of adjacent elements attributed to the effective distance between the elements is used [40]:
- -
- If discrete elements belong to different structural elements—this heat flux is software-defined, and the effective value of the thermal conductivity coefficient is used as that is derived from and of the contacting surfaces [49] in the case of an ideal thermal contact; in the case of a real thermal contact, the heat flux is derived from the relation:
5. Thermomechanical Model Development
- -
- The elasticity modulus and thermal linear expansion coefficient depend on temperature in the radial direction only;
- -
- The Kirchhoff—Love’s hypotheses are valid [58] since we consider thin electrodes;
- -
- A rectilinear shell element that is normal to the median surface remains to be rectilinear, normal to the deformed surface and maintains its length after deformation (the straight normal hypothesis);
- -
- Normal stresses in area elements parallel to the median shell surface are low compared to others and can be neglected;
- -
- Tangent stresses are static and drive equilibrium conditions;
- -
- The segments under consideration have an axisymmetric initial deflection.
- -
- Temperature fields in the IES, varying in the radial direction with a temperature differential of tens of degrees between the electrode center and the outer envelope;
- -
- Initially designed deflections of spherical electrodes w0(0) represented as spherical segments that can reach a height of 10–30 mm and more;
- -
- Electrode material linear thermal expansion coefficients;
- -
- Electrode structural orthotropy coefficients kr and kφ depending on the perforation geometry (they are constant over thickness since the electrodes have through holes).
6. The Study of Electrode Thermal Deformation
- -
- By using a well-known powerful resource, such as, for instance, the ANSYS computing system;
- -
- By using the developed simplified algorithm to evaluate the magnitude of additional deflection;
- -
- By determining the manufactured electrode deformation experimentally.
- -
- According to experimental data, AE deformation for a spherical segment was 0.15 mm;
- -
- The deformation numerical simulation with loose AE fixing for a spherical segment without taking the cone height into account resulted in 0.13 mm;
- -
- The total deformation of AE with loose fixing was 0.16 mm;
- -
- The total deformation of AE with elastic fixing was 0.11 mm.
7. Results and Discussion
8. Conclusions
- -
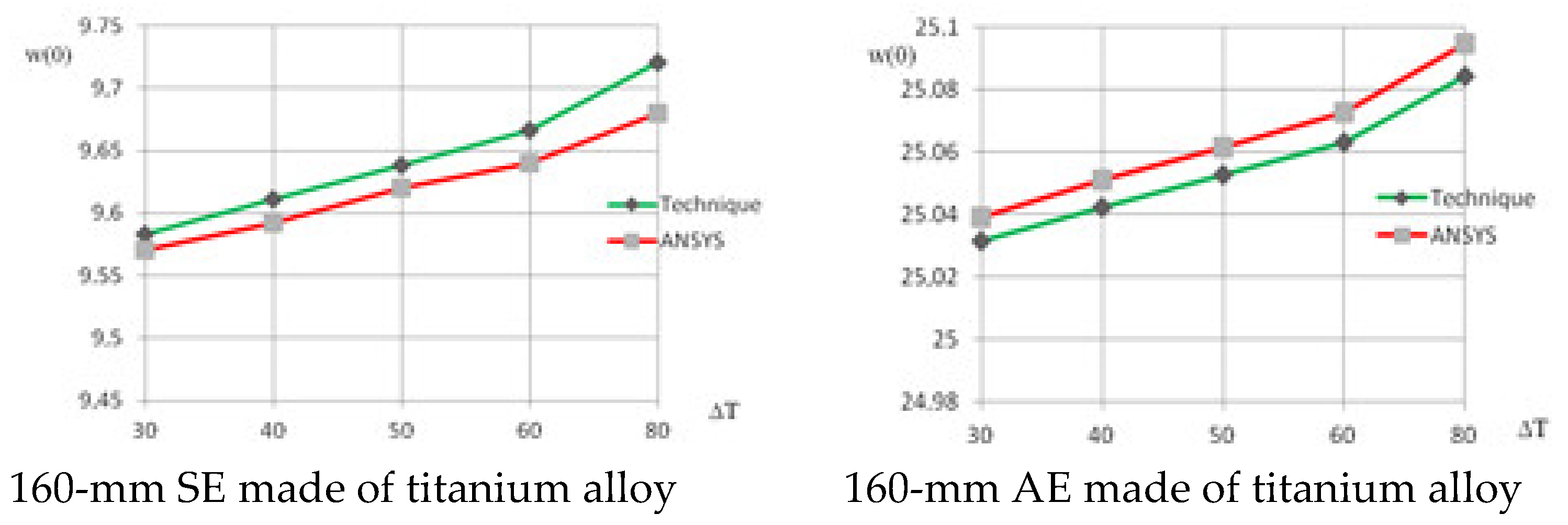
- Correlation between the results obtained through numerical modeling using the ANSYS software system and by the developed algorithm was defined;
- -
- The additional deflection value calculated by the proposed algorithm agrees with the results obtained through the numerical simulation in ANSYS and with the experimental data within 10%;
- -
- The conducted study does not allow us to precisely assess the accuracy of the numerical modeling results, but a fairly good agreement between the calculation results obtained by two independent methods and the experimental data provides more confidence in the reliability of the developed model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AE | accelerating electrode |
| GDC | gas discharge chamber |
| HF | high-frequency |
| IES | ion-extraction system |
| IS | ion source |
| RIT | radio-frequency ion thruster |
| SC | spacecraft |
| SD | space debris |
| SSC | service spacecraft |
| SE | screen electrode |
Nomenclature
| Indexes | |
| AE | index of accelerating electrode parameter |
| EP | index of compensating propulsion system parameter |
| GDC | index of gas discharge chamber parameter |
| IS | index of ion source parameter |
| SC | index of spacecraft parameter |
| SD | index of space debris parameter |
| SE | index of screen electrode parameter |
| Parameters | |
| BHF | induction of high-frequency magnetic field |
| CI | specific power consumption |
| CID | effective energy spent for the production of one ion in the discharge |
| CR | total radiation loss |
| d | distance between service spacecraft and space debris |
| e | electron charge |
| ECP | average energy of the incident charge-exchange ions |
| EIND | intensity of high-frequency electric field |
| Fji | matrix of the element mutual radiation coefficient |
| Fd | force acting on space debris |
| FEP | force acting on the service spacecraft from compensating propulsion system |
| Grad | parameter that determines the input heat flux of the mutual radiative heat exchange between the units of the ion source structure |
| Gpl | parameter that determines the power flux from the discharge plasma |
| Ie | electron current |
| Ii | ion current |
| IiAE | charge-exchange ion current |
| I0 | ion beam current |
| k | ratio between force acting on space debris and force acting on the service spacecraft from compensating propulsion system |
| M | propellant gas atom (ion) mass |
| MSC | mass of service spacecraft |
| MSD | mass of space debris |
| ne | electron density |
| ni | ion density |
| NRF | high-frequency generator power |
| Qi | function of volumetric heat source |
| Qrad | radiative heat |
| RC | numerical value of the contact resistance |
| SGDC | internal area of gas discharge chamber surface |
| SK | area of the screen electrode annular section |
| T | temperature |
| Ta | atom temperature |
| Te | electron temperature |
| Ti | ion temperature |
| Ve | electron velocity |
| Vd | gas discharge chamber plasma volume |
| Vi | first potential of the propellant gas atomionization |
| WEE | thermal power flux onto screen electrode surface facing the gas discharge chamber |
| WiAE | thermal power flux onto accelerating electrode surface facing the screen electrode |
| WGDC | thermal power flux onto the gas discharge chamber wall |
| Wind | thermal power flux from the inductor |
| differential operator | |
| α | ion energy accommodation coefficient |
| δ | L. Kronecker symbol |
| ε | emissivity of the material |
| φe | electronic work function of the screen electrode conductive material |
| φeAE | electronic work function of the accelerating electrode material |
| σ | Stefan-Boltzmann constant |
| σSE | transparency of the screen electrode |
| λ | thermal conductivity coefficient |
| θI | angle between the normal to element I and the axis connecting the centers of elements i and j |
| ω | high-frequency generator frequency |
| ∆U | near-wall plasma potential drop |
| ∆UGDC | plasma potential drop near gas discharge chamber surface |
| ∆USE | plasma potential drop near screen electrode surface |
References
- Kaplan, M.H. Space Debris Realities and Removal. SOSTC Improving Space Operations Workshop Spacecraft Collision Avoidance and Co–Location; The Johns Hopkins University, Applied Physics Laboratory: Baltimore, MD, USA, 2010. [Google Scholar]
- Liou, J.C.; Johnson, N.L.; Hill, N.M. Controlling the Growth of Future LEO Debris Population with Active Debris Removal. Acta Astronaut. 2010, 66, 648–653. [Google Scholar] [CrossRef]
- Debus, T.J.; Dougherty, S.P. Overview and Performance of the Front-end Robotics Enabling Near-Term Demonstration (FREND) Robotic Arm. In Proceedings of the AIAA Infotech@Aerospace Conference, Seattle, WA, USA, 6–9 April 2009. [Google Scholar]
- Kaiser, C.; Sjoberg, F.; Delcura, J.M.; Eilertsen, B. SMART-OLEV—An Orbital Life Extension Vehicle for Servicing Commercial Spacecrafts in GEO. Acta Astronaut. 2008, 63, 400–410. [Google Scholar] [CrossRef]
- Melamed, N.; Griffice, C.P.; Chobotov, V. Survey of GEO Debris Removal Concepts. In Proceedings of the 59th International Astronautical Congress, Glasgow, UK, 29 September–3 October 2008. [Google Scholar]
- Bosse, A.B.; Barnds, W.J.; Brown, M.A.; Creamer, N.G.; Feerst, A.; Hensgaw, C.G.; Hope, A.S.; Kelm, B.E.; Klein, P.A.; Pipitone, F.; et al. SUMO: Spacecraft for the Universal Modification of Orbits. In Proceedings of the International Symposium on Defense and Security, Orlando, FL, USA, 12–16 April 2004. [Google Scholar]
- Norman, T.L.; Gaskin, D. Conceptual Design of an Orbital Debris Defense System; NASA-CR-197211; NASA: Morgantown, WV, USA, 1994.
- Murdoch, N.; Izzo, D.; Bombardelli, C.; Carnelli, I.; Hilgers, A.; Rodgers, D. Electrostatic Tractor for Near Earth Object Deflection. In Proceedings of the 59th International Astronautical Congress, Glasgow, UK, 29 September–3 October 2008. [Google Scholar]
- Bondarenko, S.G.; Lyagushin, S.F.; Shifrin, G.A. Prospects of Using Lasers and Military Space Technology for Space Debris Removal. In Proceedings of the 2nd European Conference on Space Debris, Darmstadt, Germany, 17–19 March 1997. [Google Scholar]
- Nishida, S.-I.; Kawamoto, S.; Okawa, Y.; Terui, F. Space debris removal system using a small satellite. Acta Astronaut. 2009, 65, 95–102. [Google Scholar] [CrossRef]
- Kawamoto, S.; Nishida, S.; Kibe, S. Research on a Space Debris Removal System; NAL Research Progress: Tokyo, Japan, 2003. [Google Scholar]
- Starke, J.; Bischof, B.; Foth, W.-O.; Gunther, J.J. Roger a Potential Orbital Space Debris Removal System. In Proceedings of the 38th COSPAR Scientific Assembly, Bremen, Germany, 15–18 July 2010. [Google Scholar]
- Absalamov, S.K.; Andreev, V.B.; Colbert, T.; Day, M.; Egorov, V.V.; Gnizdor, R.U.; Kaufman, H.; Kim, V.; Koryakin, A.I.; Kozubsky, K.N.; et al. Measurements of Plasma Parameters in the SPT-100 Plume and its effect on Spacecraft Components. In Proceedings of the 28 Joint Propulsion Conference and Exhibit, Nashville, TN, USA, 6–8 July 1992. [Google Scholar]
- Raikunov, G. (Ed.) Prevention of Space Debris Formation/Under the Science; Ed. Doct. Tech. Sciences; FIZMATLIT: Moscow, Russia, 2014; (In Russian). ISBN 9785922115049. [Google Scholar]
- Cherkasova, M.; Mogulkin, A.; Nigmatzyanov, V.; Peysakhovich, O.; Popov, G. Computational and experimental investigation of a weakly diverging ion beam source. In IOP Conference Series: Materials Science and Engineering, Proceedings of the 18th International Conference “Aviation and Cosmonautics” (AviaSpace-2019), Moscow, Russia, 18–22 November 2019; IOP: Bristol, UK, 2020; Volume 868, p. 012019. [Google Scholar]
- Obukhov, V.A.; Mogulkin, A.I.; Peysakhovich, O.D.; Nigmatzyanov, V.V.; Svotina, V.V. Modeling and experimental study of an ion source with a weakly diverging ion beam. In IOP Conference Series: Materials Science and Engineering, Proceedings of the II International Conference «MIP: Engineering-2020: Modernization, Innovations, Progress: Advanced Technologies in Material Science, Mechanical and Automation Engineering», Krasnoyarsk, Russia, 16–18 April 2020; IOP: Bristol, UK, 2020; Volume 862, p. 062082. [Google Scholar]
- Brown, I.; Lane, J.; Youngquist, R. A Lunar-Based Spacecraft Propulsion Concept—The Ion Beam Sail. Acta Astronaut. 2007, 60, 834–845. [Google Scholar] [CrossRef][Green Version]
- Kitamura, S. Large Space Debris Reorbiter Using Ion Beam Irradiation. In Proceedings of the 61th International Astronautical Congress, Prague, Czech Republic, 27 September–1 October 2010. [Google Scholar]
- Bombardelli, C.; Peláez, J. Ion Beam Shepherd for Contactless Space Debris Removal. J. Guid. Control Dyn. 2011, 34, 916–920. [Google Scholar] [CrossRef]
- Bombardelli, C.; Pelaez, J. Universidad Politecnica de Madrid. Sistema de Modificación de la Posicióny Actitud de Cuerpos en Órbita por Medio de Satélites Guía. ES Patent 2365394B2, 3 October 2011. [Google Scholar]
- Edwards, C.H.; Wallace, N.C. The T5 Ion Propulsion Assembly for Drag Compensation on GOCE. In Proceedings of the 2nd International GOCE User Workshop GOCE, The Geoid and Oceanography, Frascati, Italy, 8–10 March 2004. [Google Scholar]
- Löb, H.W. Ein elektrostatisches Raketentriebwerk mit Hochfrequenzionenquelle. Astronaut. Acta VIII 1962, 1, 49. [Google Scholar]
- Loeb, H.W. Principle of Radio-Frequency Ion Thrusters RIT. In Workshop RIT-22 Demonstrator Test at Astrium at Giessen University; Giessen University: Giessen, Germany, 2010. [Google Scholar]
- Groh, K.H.; Loeb, H.W. State-of-the-art of radio-frequency ion thrusters. J. Propuls. Power 1991, 7, 573–579. [Google Scholar] [CrossRef]
- Killinger, R.; Kukies, R.; Surauer, M.; Tomasetto, A.; van Holtz, L. ARTEMIS Orbit Raising In-flight Experience with Ion Propulsion. Acta Astronaut. 2003, 53, 607–621. [Google Scholar] [CrossRef]
- Killinger, R.; Leiter, H.; Kukies, R. RITA Ion Propulsion Systems for Commercial and Scientific Applications. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint PropulsionConference & Exhibit, Cincinnati, OH, USA, 8–11 July 2007. [Google Scholar]
- Muller, H.; Kukies, R.; Bassner, H. EMC Tests on the RITA Ion Propulsion Assembly for the ARTEMIS Satellite. In Proceedings of the 28th AIAA, SAE, ASME, ASEE Joint Propulsion Conference and Exhibit, Nashville, NT, USA, 6–8 July 1992. [Google Scholar]
- Angelo, N.G.; Clark, S.; Wallace, N.; Collingwood, C.; Guarducci, F. Qualification of the T6 Ion Thruster for the BepiColombo Mission to the Planet Mercury. In Proceedings of the 32nd International Electric Propulsion Conference, Wiesbaden, Germany, 11–15 September 2011. [Google Scholar]
- Loeb, H.W.; Feili, D.; Popov, G.A.; Obukhov, V.A.; Balashov, V.V.; Mogulkin, A.I.; Murashko, V.M.; Nesterenko, A.N.; Khartov, S. Design of High-Power High-Specific Impulse RF-Ion Thruster. In Proceedings of the International Electric Propulsion Conference, Wiesbaden, Germany, 11–15 September 2011. [Google Scholar]
- Riaby, V.A.; Masherov, P.E.; Obukhov, V.A.; Savinov, V.P. Effectiveness of Radiofrequency Inductively Coupled Plasma Sources for Space Propulsion. High Volt. Eng. 2013, 39, 2077–2088. [Google Scholar]
- Abgaryan, V.K.; Akhmetzhanov, R.V.; Loeb, H.W.; Obukhov, V.A.; Cherkasova, M.V. High-Frequency Ion Sources of Inert and Chemically Active Gases. J. Surf. Investig. 2012, 6, 693–698. [Google Scholar] [CrossRef]
- Abgaryan, V.K.; Akhmetzhanov, R.V.; Loeb, H.W.; Obukhov, V.A.; Cherkasova, M.V. Numerical Simulation of a High-Perveance Ion-Extraction System with a Plasma Emitter. J. Surf. Investig. 2013, 7, 1092–1099. [Google Scholar] [CrossRef]
- Bombardelli, C.; Merino-Martinez, M.; Galilea, E.A.; Pelaez, J.; Urrutxua, H.; Herrera-Montojo, J.; Iturri-Torrea, A. Ariadna Call for Ideas: Active Removal of Space Debris. Ion Beam Shepherd for Contactless Debris Removal; Advanced Concept Team; Ariadna ID: 10-4611; ESTEC-ESA: Madrid, Spain, 2011. [Google Scholar]
- Godyak, V.A.; Piejak, R.B.; Alexandrovich, B.M. Experimental Setup and Electrical Characteristics of an Inductively Coupled Plasma. J. Appl. Phys. 1999, 85, 703–712. [Google Scholar] [CrossRef]
- Kozhevnikov, V.V.; Khartov, S.A. Investigation of Local Plasma Parameters in the Discharge Chamber of a Low-Power High-Frequency Ion Thruster. Bull. Russ. Acad. Sci. Energy 2017, 3, 13–20. (In Russian) [Google Scholar]
- Kozhevnikov, V.V.; Khartov, S.A. Investigation of Local Plasma Parameters in the Discharge Chamber of a Low-Power High-Frequency Ion Engine with Multi-Electrode Probes. Bull. Russ. Acad. Sci. Energy 2016, 2, 26–33. (In Russian) [Google Scholar]
- Ryabyi, V.A.; Masherov, P.E. Integral and Local Diagnostics of a Model of an Energy-Efficient RF Source of an Ion Beam. Bull. Russ. Acad. Sci. Energy 2016, 2, 46–57. (In Russian) [Google Scholar]
- Riaby, V.A.; Obukhov, V.A.; Masherov, P.E. On the Objectivity of Plasma Diagnostics Using Langmuir Probes. High Volt. Eng. 2012, 38, 790–793. [Google Scholar]
- Obukhov, V.A.; Grigoryan, V.G.; Latyshev, L.A. Sources of Heavy Ions. In Plasma Accelerators and Ion Injectors; Science: Moscow, Russia, 1984. (In Russian) [Google Scholar]
- Kruglov, K.I. Modeling of Thermophysical Processes in a High-Frequency Ion Thruster. Ph.D. Thesis, Moscow Aviation Institute, Moscow, Russia, 2017. (In Russian). [Google Scholar]
- Abgaryan, V.K.; Abgaryan, M.V.; Nadiradze, A.B.; Nigmatzyanov, V.V.; Semenov, A.A. Radiative Heat Flux from Excited Atoms in a Radiofrequency Ion Thruster. Tech. Phys. Lett. 2021, 47, 201–204. [Google Scholar] [CrossRef]
- Bugrov, G.E.; Kralkina, E.A. Calculation of Specific Energy Consumption for Radiation in a Low-Pressure Xenon Discharge. In Proceedings of the VI All-Union Conference on Plasma Accelerators and Ion Injectors, Dnepropetrovsk, Russia, 26–28 September 1986. (In Russian). [Google Scholar]
- Lotz, B. Plasma Physical and Material Physical Aspects of the Application of Atmospheric Gases as a Propellant for Ion-Thruster of the RIT-Type. Ph.D. Thesis, Justus-Liebig Universität, Bunkissen, Germany, 2013. [Google Scholar]
- Abgaryan, V.K.; Kruglov, K.I.; Mogulkin, A.I.; Obukhov, V.A.; Riaby, V.A. On the Cost of Ion Production in Radio-Frequency Ion Thrusters and Technological Ion Sources. J. Surf. Investig. 2017, 11, 1239–1245. [Google Scholar] [CrossRef]
- Abgaryan, V.K.; Riaby, V.A.; Yamashev, G.G. Power Loss to Generating Ion Current in Radio-Frequency Ion Thrusters and Technological Sources of Ions. J. Surf. Investig. 2017, 11, 1008–1013. [Google Scholar] [CrossRef]
- Antipov, E.A.; Balashov, V.V.; Weber, A.V.; Kuftyrev, R.Y.; Mogulkin, A.I.; Nigmatzyanov, V.V.; Pankov, A.I.; Popov, G.A.; Sitnikov, S.A.; Khartov, S.A. The Choice of Structural Materials for High-Frequency Ion Thruster. Electron. J. Proc. MAI 2013, 65. (In Russian) [Google Scholar]
- Abgaryan, V.K.; Akhmetzhanov, R.V.; Loeb, H.W.; Obukhov, V.A.; Cherkasova, M.V. Numerical Modeling of the Primary Ion Beam and Secondary Ion Flux in the Ion-Optical System of the Ion Thruster. Electron. J. Proc. MAI 2013, 71. (In Russian) [Google Scholar]
- Avduevsky, V.S.; Galitseysky, B.M.; Glebovetal, G.A. Basics of Heat Transfer in Aviation and Rocket and Space Technologies; Mashinostroenie: Moscow, Russia, 1992. (In Russian) [Google Scholar]
- Gartner, W.; Lotz, B.; Meyer, B.K. 3D Thermal Simulation of a μN-RIT. In Proceedings of the 33d International Electric Propulsion Conference, The George Washington University, Washington, DC, USA, 6–10 October 2013. [Google Scholar]
- Mogulkin, A.I. Mechanical–Mathematical Model of Deformations of Profiled Electrodes of Ion Thrusters. Ph.D. Thesis, Moscow Aviation Institute, Moscow, Russia, 2015. [Google Scholar]
- Balashov, V.V.; Mogulkin, A.I.; Nigmatzyanov, V.V.; Obukhov, V.A.; Smirnova, M.E.; Khartov, S.A. Ion Source. Russia Patent RU116273U1, 2 December 2011. (In Russian). [Google Scholar]
- Balashov, V.V.; Popov, G.A.; Antipov, E.A.; Ionov, A.V.; Mogulkin, A.I. Method of Manufacturing Electrodes of the Ion-Optical System. Russia Patent RU2543063C1, 9 October 2013. (In Russian). [Google Scholar]
- Birger, I.A. Round Plates and Shells of Rotation; Oborongiz: Moscow, Russia, 1961. (In Russian) [Google Scholar]
- Grigolyuk, E.I.; Filshtinsky, L.A. Perforated Plates and Shells; Nauka: Moscow, Russia, 1970. (In Russian) [Google Scholar]
- Gurov, A.F.; Fedorov, V.A. Investigation of Stability and Bending of Electrodes of Ion-Optical Systems. In Proceedings of the 3rd Interuniversity Conference on the Research and Design of Medium-Power Electric Propulsion Systems, Kharkov, Ukraine, 15–20 June 1975. (In Russian). [Google Scholar]
- Birger, I.A. Some Mathematical Methods for Solving Engineering Problems; Oborongiz: Moscow, Russia, 1956. (In Russian) [Google Scholar]
- Fedorov, V.A. Investigation of Thermal Stability, Supercritical Behavior and Nonlinear Bending of Densely Perforated Annular Plates of Variable Stiffness. Izv. SSSR Rigid Body Mech. 1976, 5, 197. (In Russian) [Google Scholar]
- Besukhov, N.N.; Goldenblat, I.I.; Badjanov, V.L. Calculations for Strength, Stability and Fluctuations in High Temperature Conditions; Mechanical Engineering: Moscow, Russia, 1965. (In Russian) [Google Scholar]



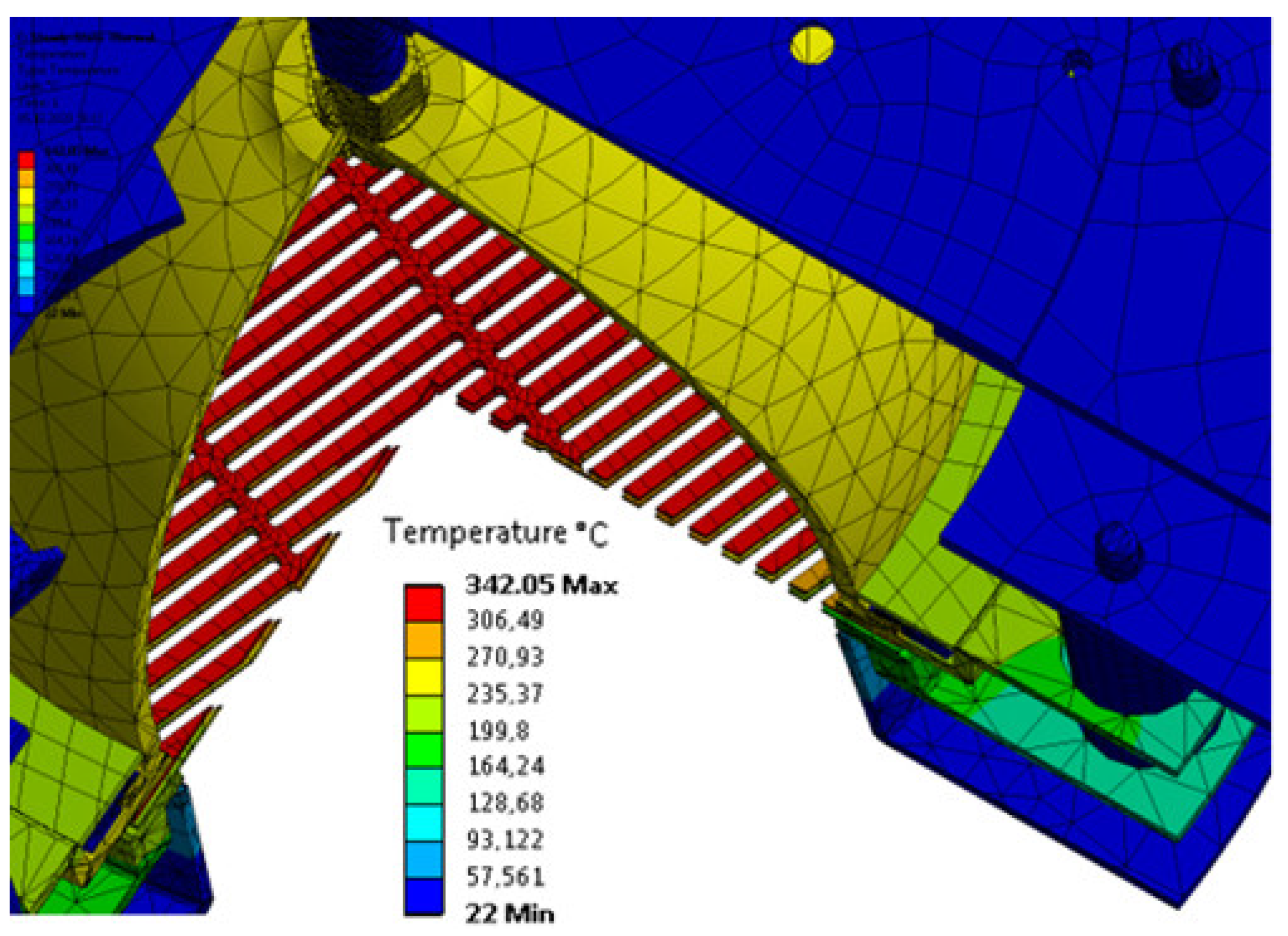
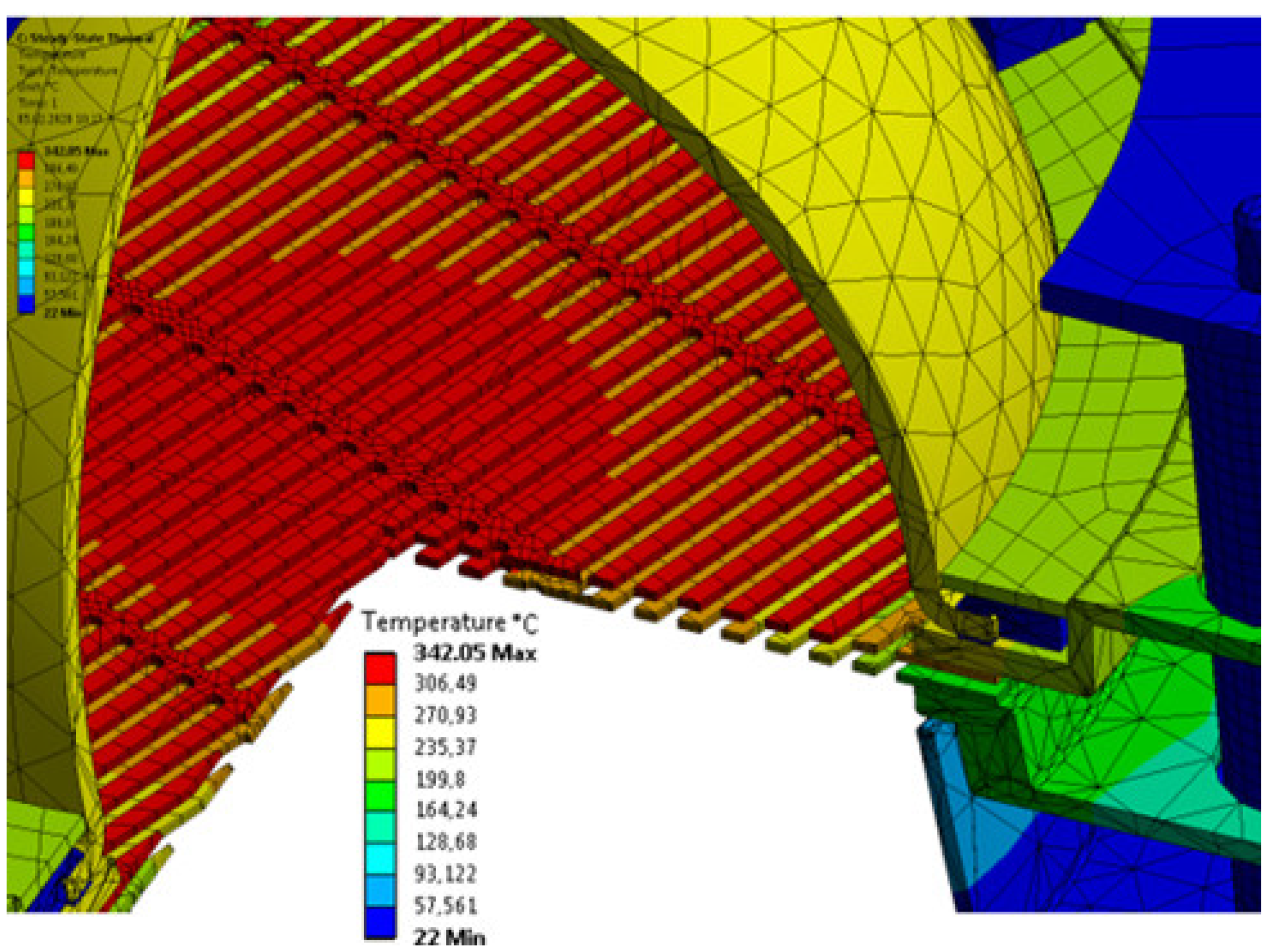

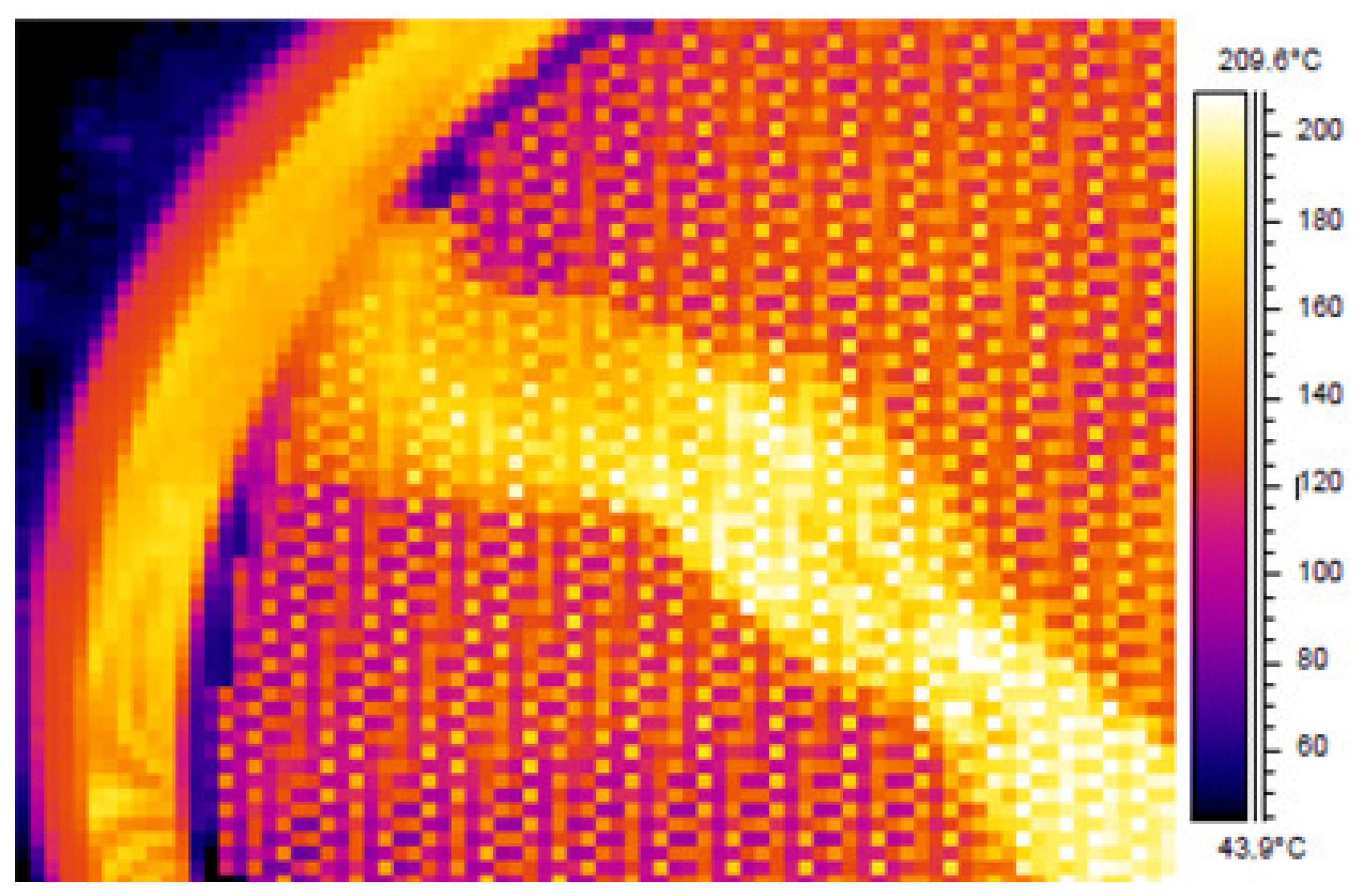
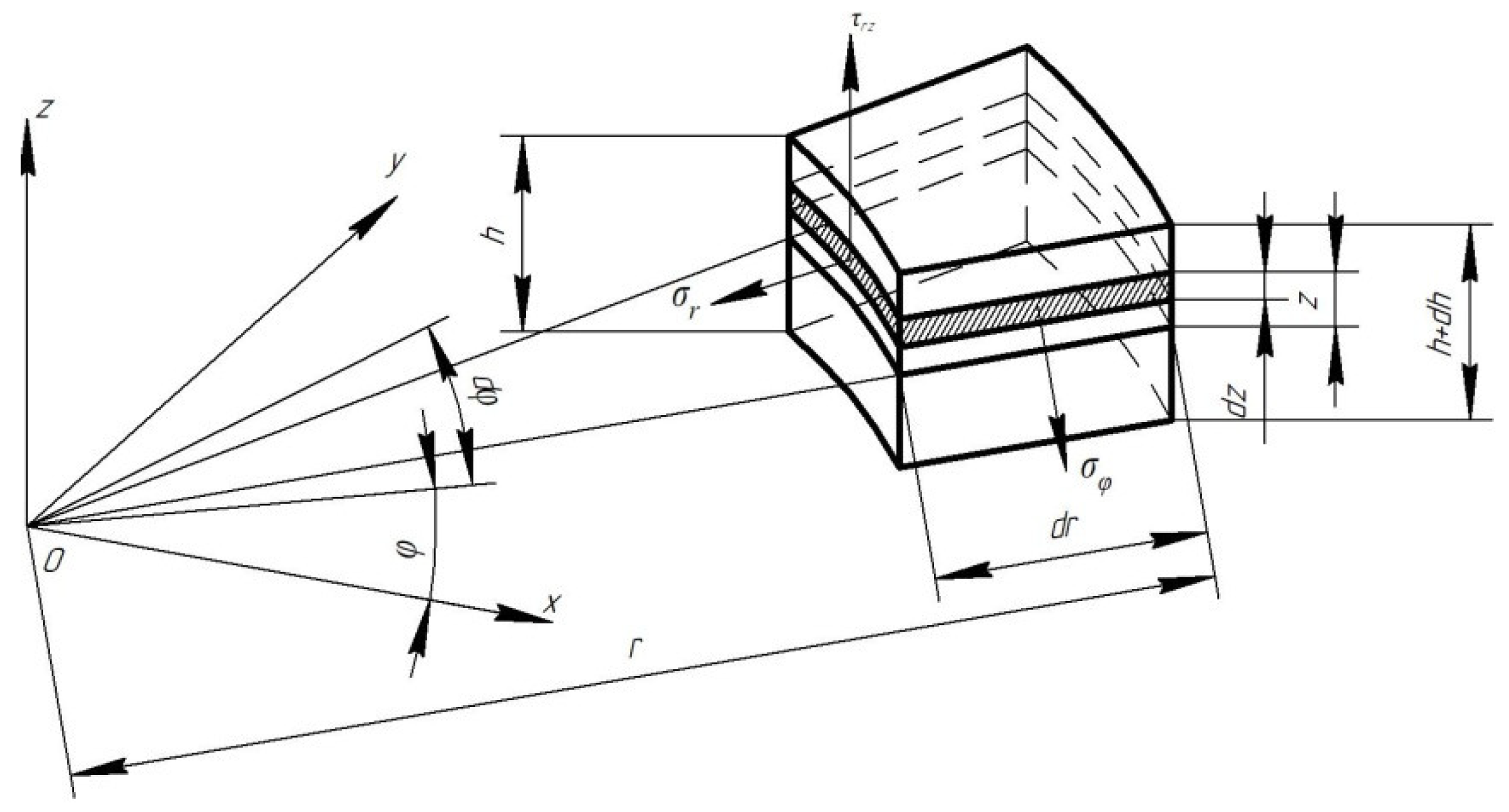
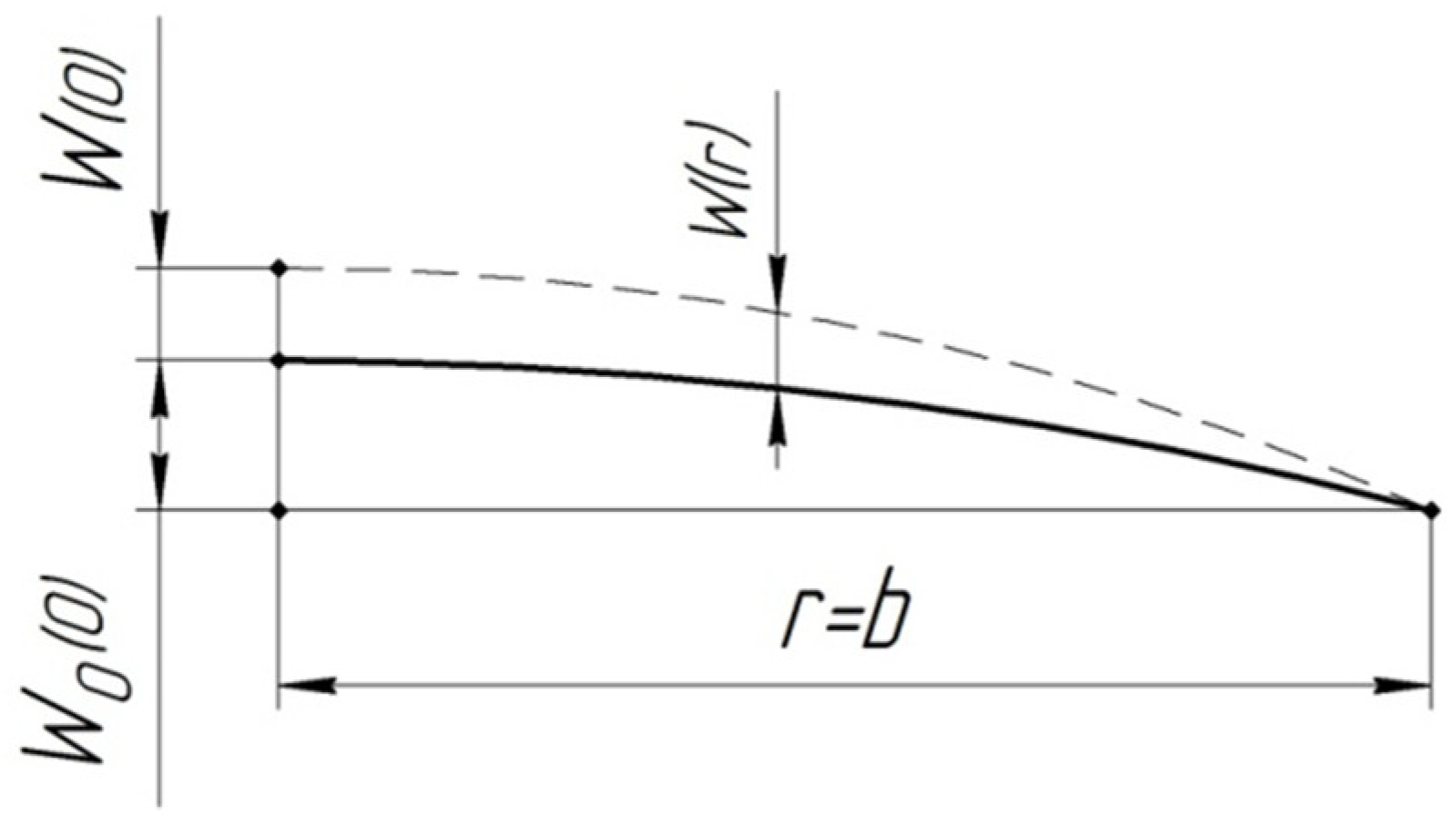
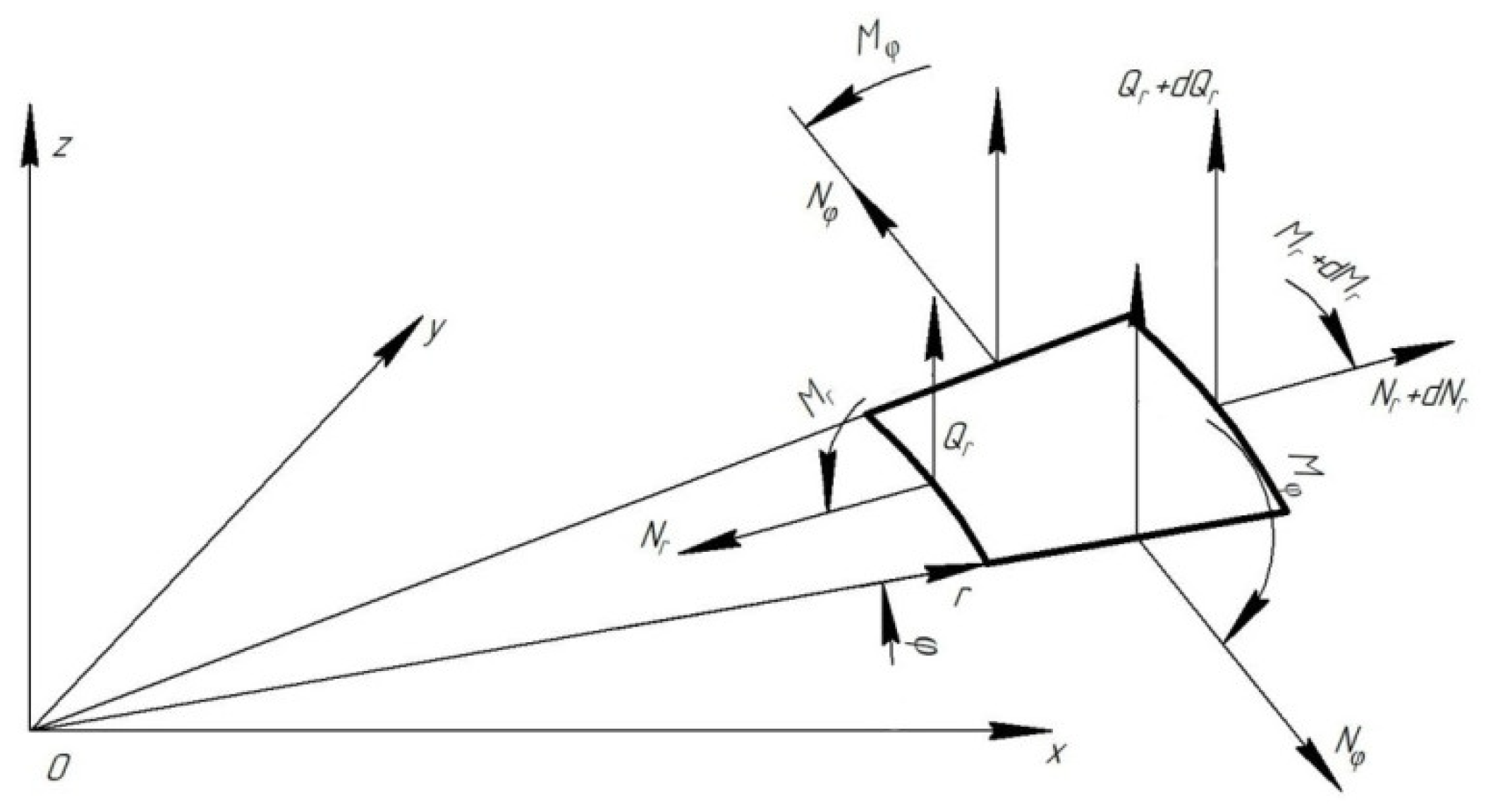
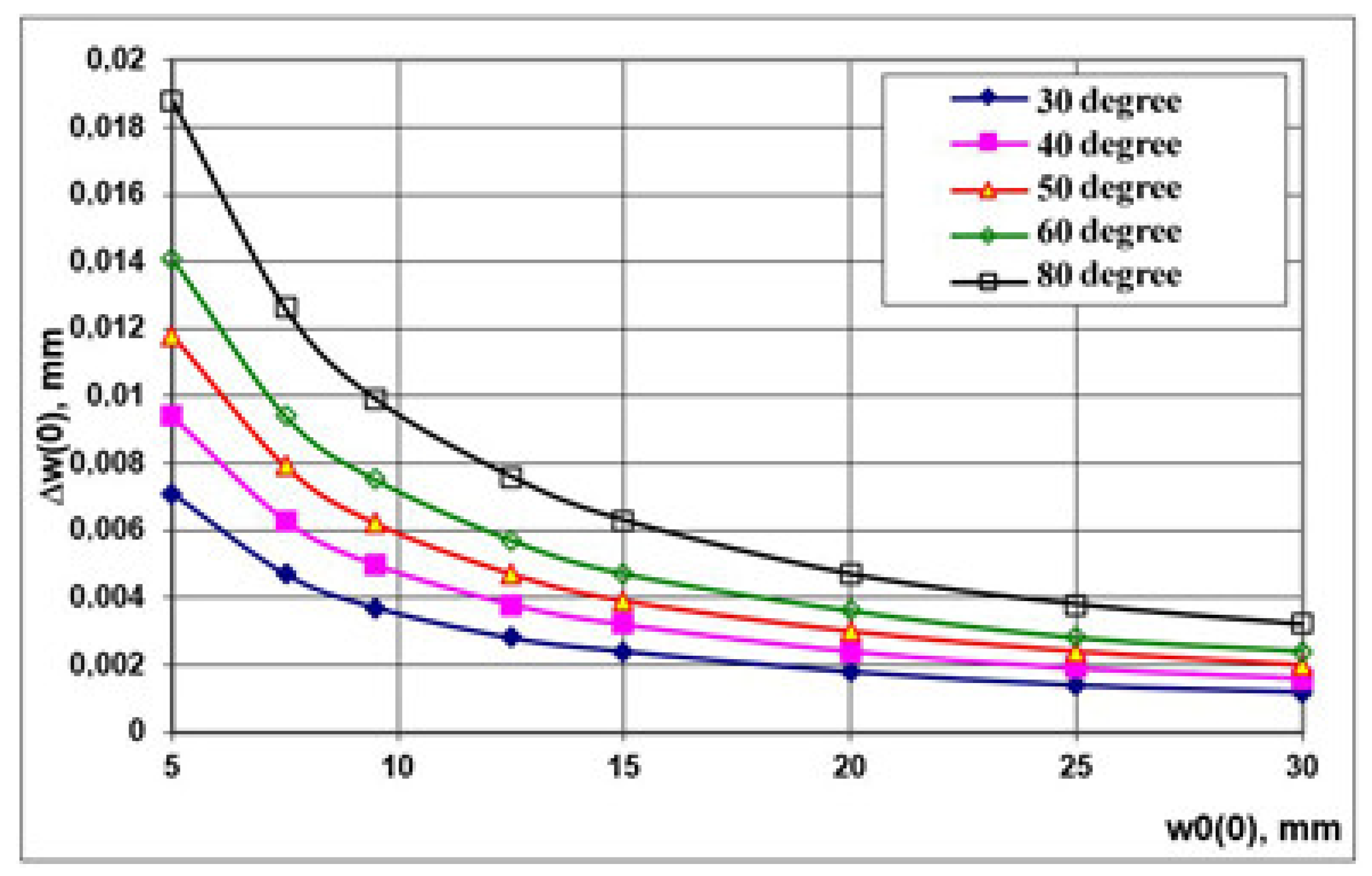
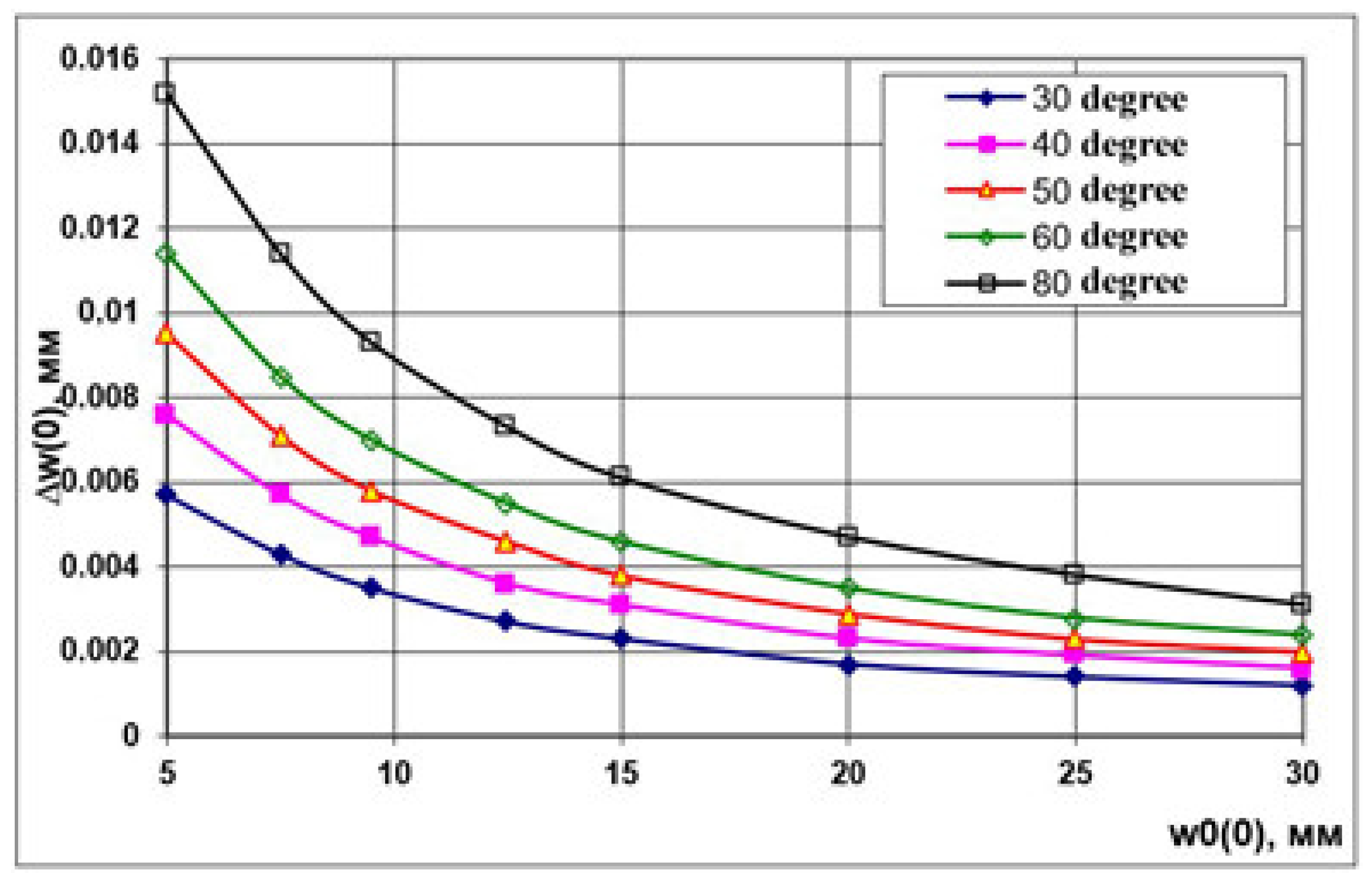

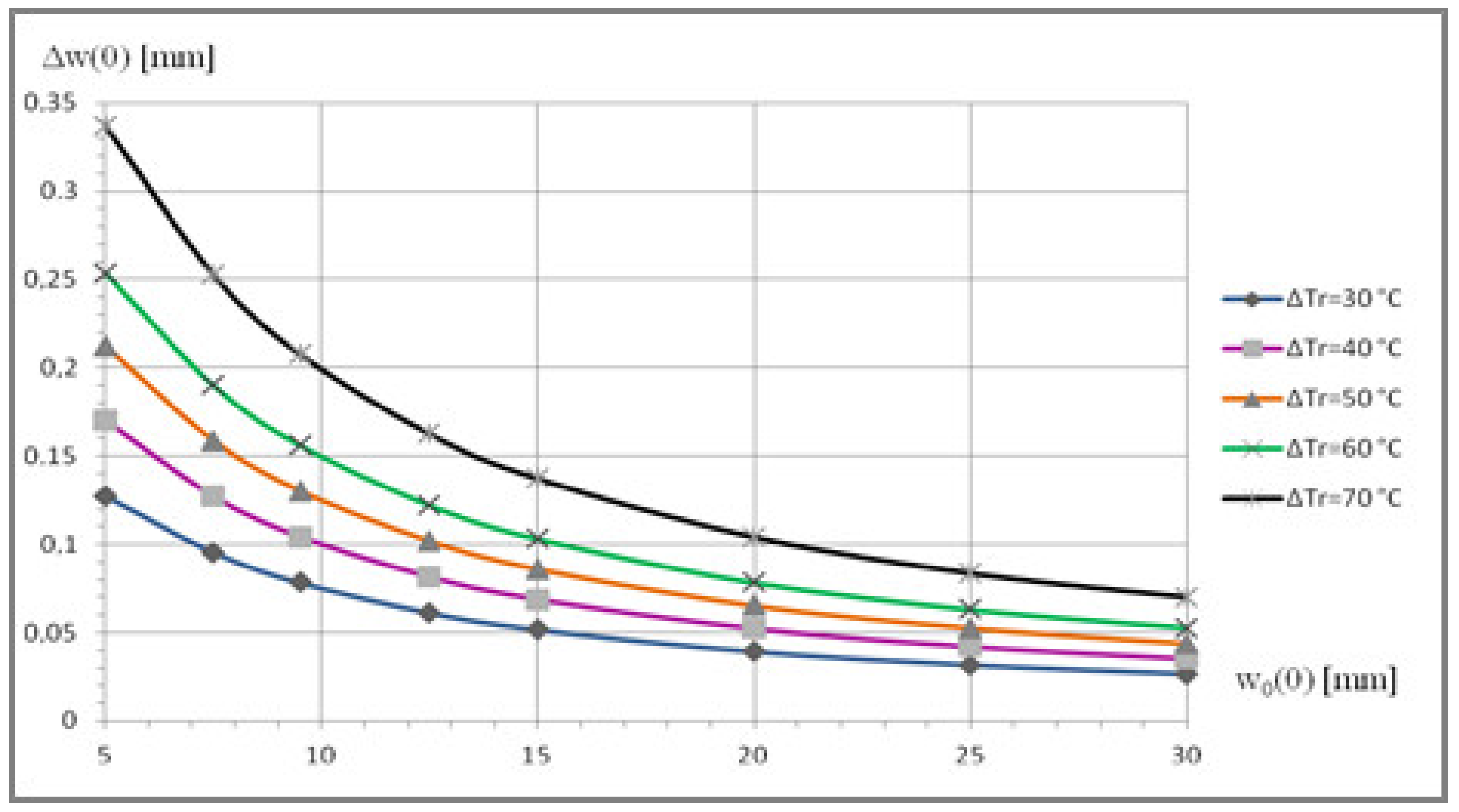
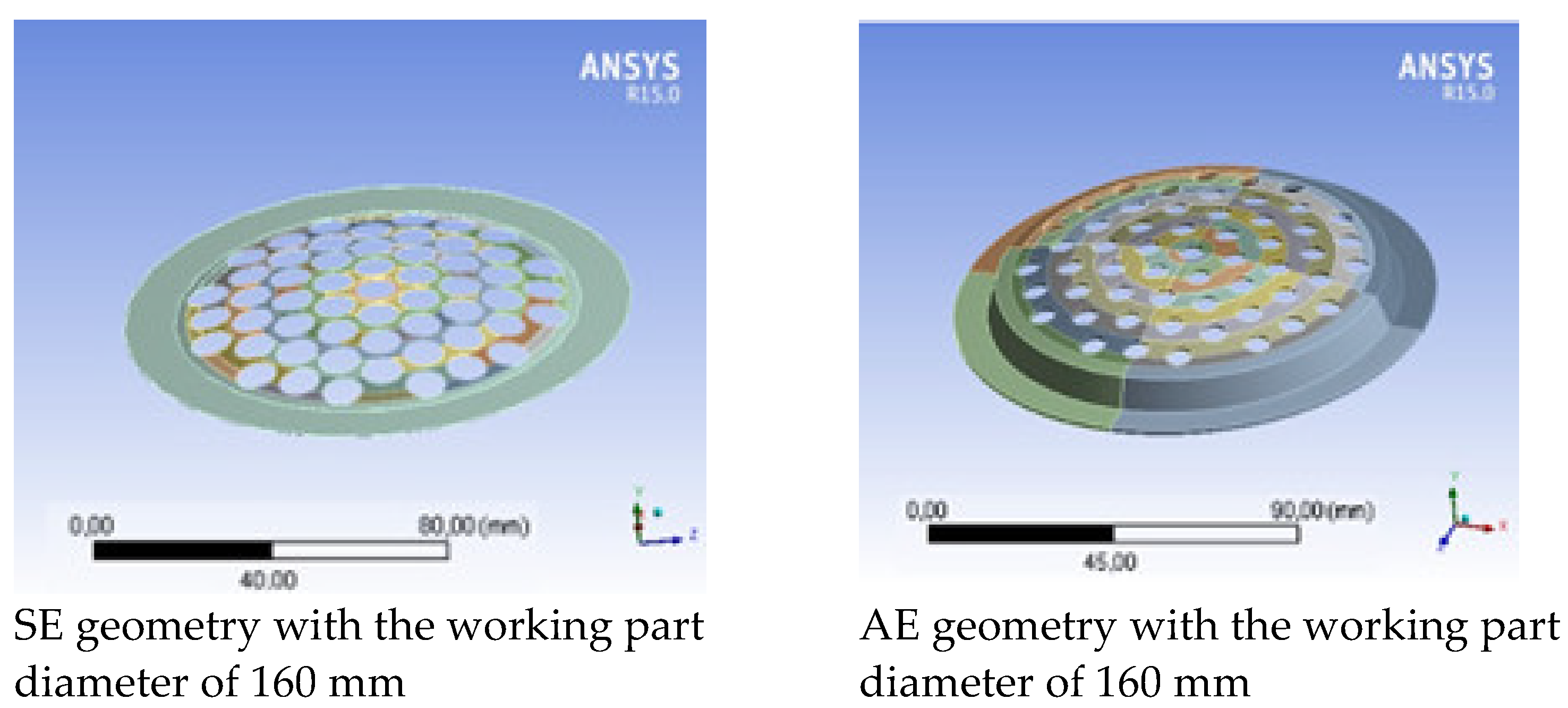



| ΔTr, °C | 30 | 40 | 50 | 60 | 80 |
|---|---|---|---|---|---|
| w0(0), mm | Δw(0), mm | ||||
| Screen electrode | |||||
| 5 | 0.0071 | 0.0094 | 0.0118 | 0.0141 | 0.0188 |
| 7.5 | 0.0047 | 0.0063 | 0.0079 | 0.0094 | 0.0126 |
| 9.5 | 0.0037 | 0.00498 | 0.0062 | 0.0075 | 0.0099 |
| 12.5 | 0.0028 | 0.0038 | 0.0047 | 0.0057 | 0.0076 |
| 15 | 0.0024 | 0.0032 | 0.0039 | 0.0047 | 0.0063 |
| 20 | 0.0018 | 0.0024 | 0.003 | 0.0036 | 0.0047 |
| 25 | 0.0014 | 0.0019 | 0.0024 | 0.0028 | 0.0038 |
| 30 | 0.0012 | 0.0016 | 0.002 | 0.0024 | 0.0032 |
| Acceleration electrode | |||||
| 5 | 0.0057 | 0.0076 | 0.0095 | 0.0114 | 0.0152 |
| 7.5 | 0.0043 | 0.0057 | 0.0071 | 0.0085 | 0.0114 |
| 9.5 | 0.0035 | 0.0047 | 0.0058 | 0.0070 | 0.0093 |
| 12.5 | 0.0027 | 0.0036 | 0.0046 | 0.0055 | 0.0073 |
| 15 | 0.0023 | 0.0031 | 0.0038 | 0.0046 | 0.0061 |
| 20 | 0.0017 | 0.0023 | 0.0029 | 0.0035 | 0.0047 |
| 25 | 0.0014 | 0.0019 | 0.0023 | 0.0028 | 0.0038 |
| 30 | 0.0012 | 0.0016 | 0.0020 | 0.0024 | 0.0031 |
| Mass Flow Rate, mg/s | PRFG, W | USE, V | ISE, A | UAE, V | IAE, A | Isp, s | Ip, A | P, mN | W, keV |
|---|---|---|---|---|---|---|---|---|---|
| 0.771 | 220 | 2500 | 0.190 | 240 | 0.008 | 2083 | 0.18 | 16.0 | 2.50 |
| 0.976 | 310 | 2400 | 0.400 | 220 | 0.001 | 3396 | 0.4 | 33.1 | 2.40 |
| 0.976 | 330 | 2400 | 0.410 | 220 | 0.001 | 3480 | 0.41 | 33.9 | 2.40 |
| 0.488 | 100 | 3000 | 0.100 | 300 | 0.008 | 1896 | 0.09 | 9.28 | 3.00 |
| 0.781 | 150 | 3000 | 0.150 | 300 | 0.009 | 1778 | 0.14 | 13.9 | 3.00 |
| 0.781 | 160 | 3000 | 0.170 | 300 | 0.009 | 2015 | 0.16 | 15.8 | 3.00 |
| 0.781 | 180 | 3000 | 0.190 | 300 | 0.009 | 2252 | 0.18 | 17.6 | 3.00 |
| 0.917 | 220 | 3000 | 0.240 | 300 | 0.010 | 2421 | 0.23 | 22.3 | 3.00 |
| 0.947 | 235 | 3000 | 0.260 | 300 | 0.010 | 2542 | 0.25 | 24.1 | 3.00 |
| 0.947 | 235 | 3000 | 0.280 | 300 | 0.010 | 2737 | 0.27 | 25.97 | 3.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Svotina, V.V.; Mogulkin, A.I.; Kupreeva, A.Y. Ion Source—Thermal and Thermomechanical Simulation. Aerospace 2021, 8, 189. https://doi.org/10.3390/aerospace8070189
Svotina VV, Mogulkin AI, Kupreeva AY. Ion Source—Thermal and Thermomechanical Simulation. Aerospace. 2021; 8(7):189. https://doi.org/10.3390/aerospace8070189
Chicago/Turabian StyleSvotina, Victoria V., Andrey I. Mogulkin, and Alexandra Y. Kupreeva. 2021. "Ion Source—Thermal and Thermomechanical Simulation" Aerospace 8, no. 7: 189. https://doi.org/10.3390/aerospace8070189
APA StyleSvotina, V. V., Mogulkin, A. I., & Kupreeva, A. Y. (2021). Ion Source—Thermal and Thermomechanical Simulation. Aerospace, 8(7), 189. https://doi.org/10.3390/aerospace8070189







