Velocity Obstacle Based Conflict Avoidance in Urban Environment with Variable Speed Limit
Abstract
1. Introduction
2. Urban Setting
2.1. Freedom of Movement
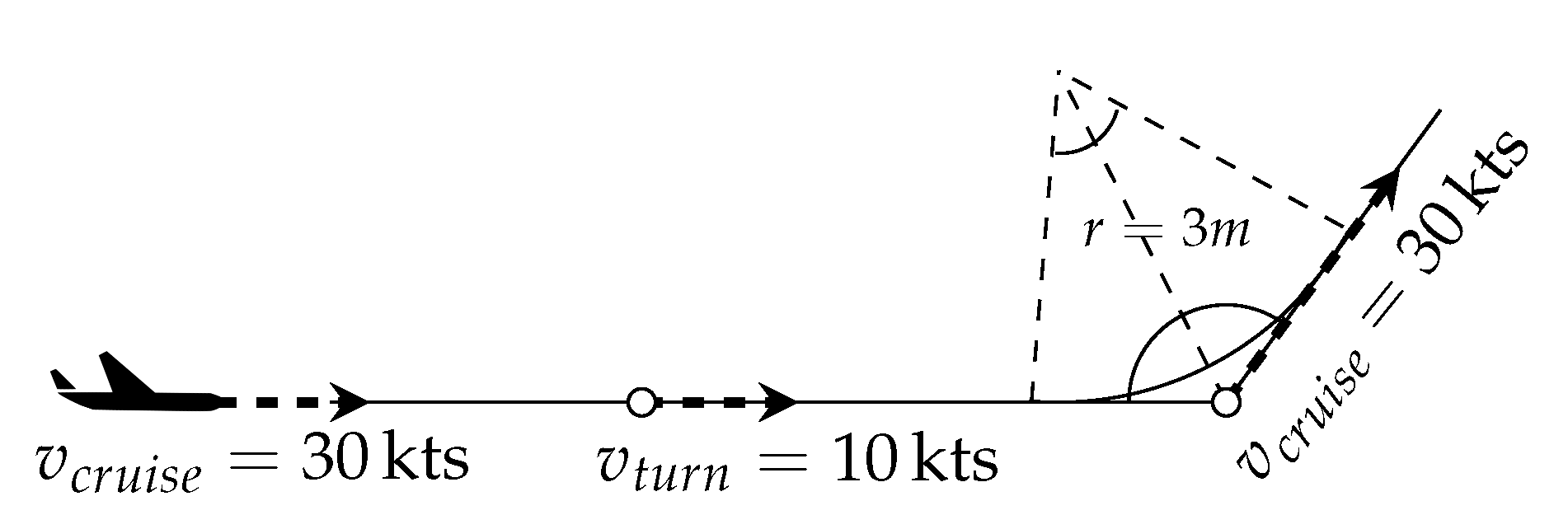
2.2. Turn Estimation
2.3. Speed Changes throughout the Route
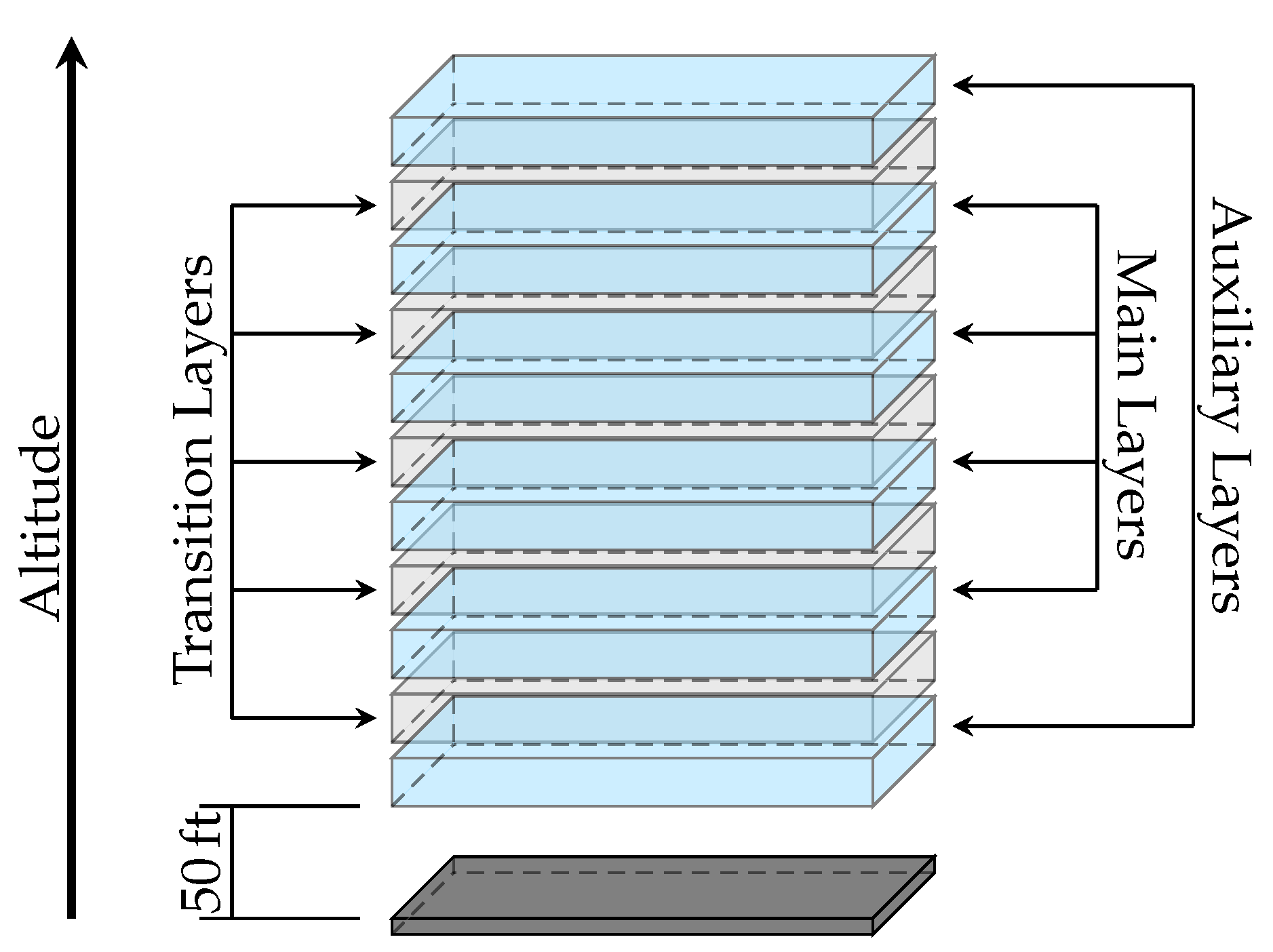
2.4. Heading–Altitude Rules
Transition Layers
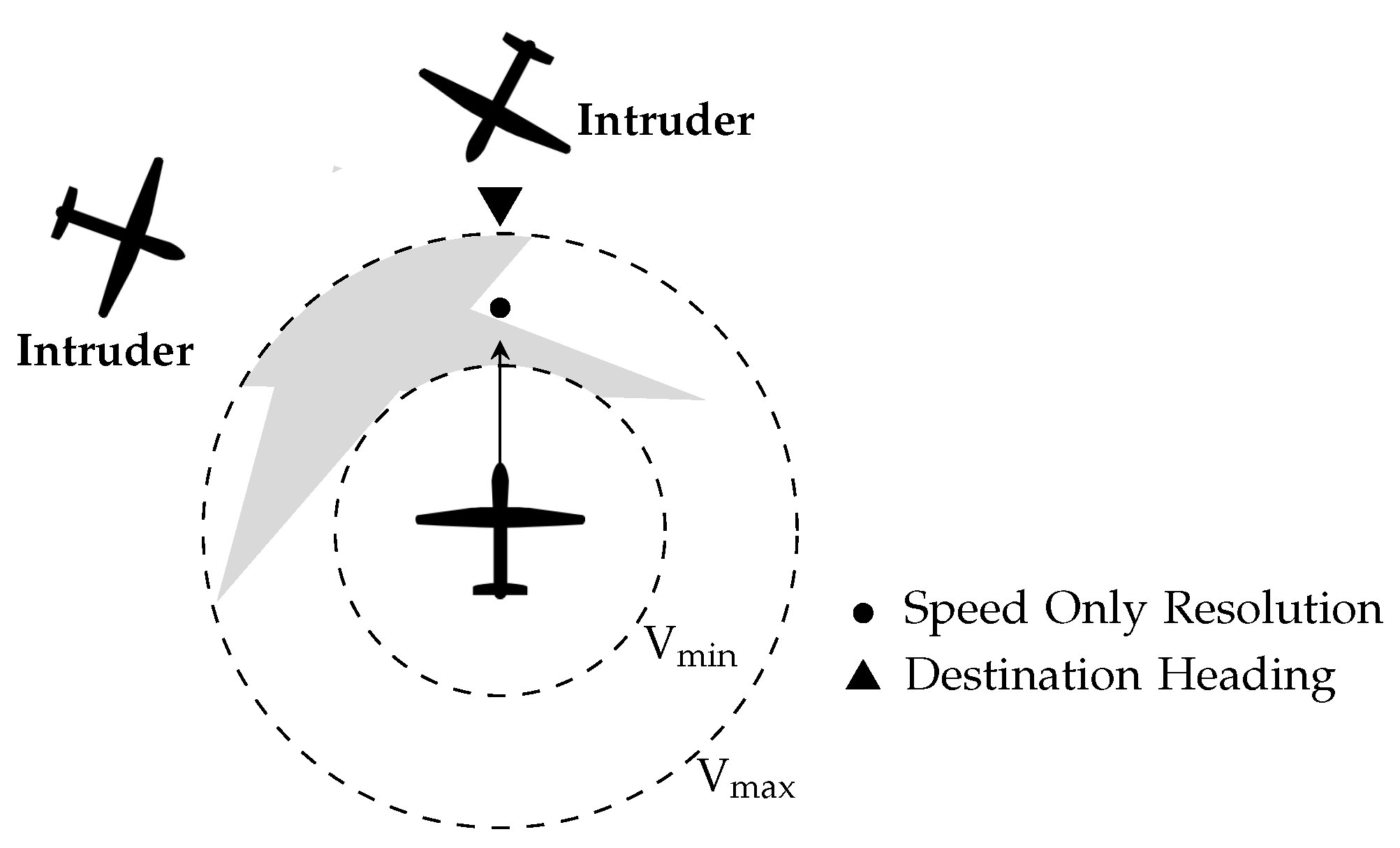
3. Velocity Obstacle Based, Speed-Only Conflict Resolution
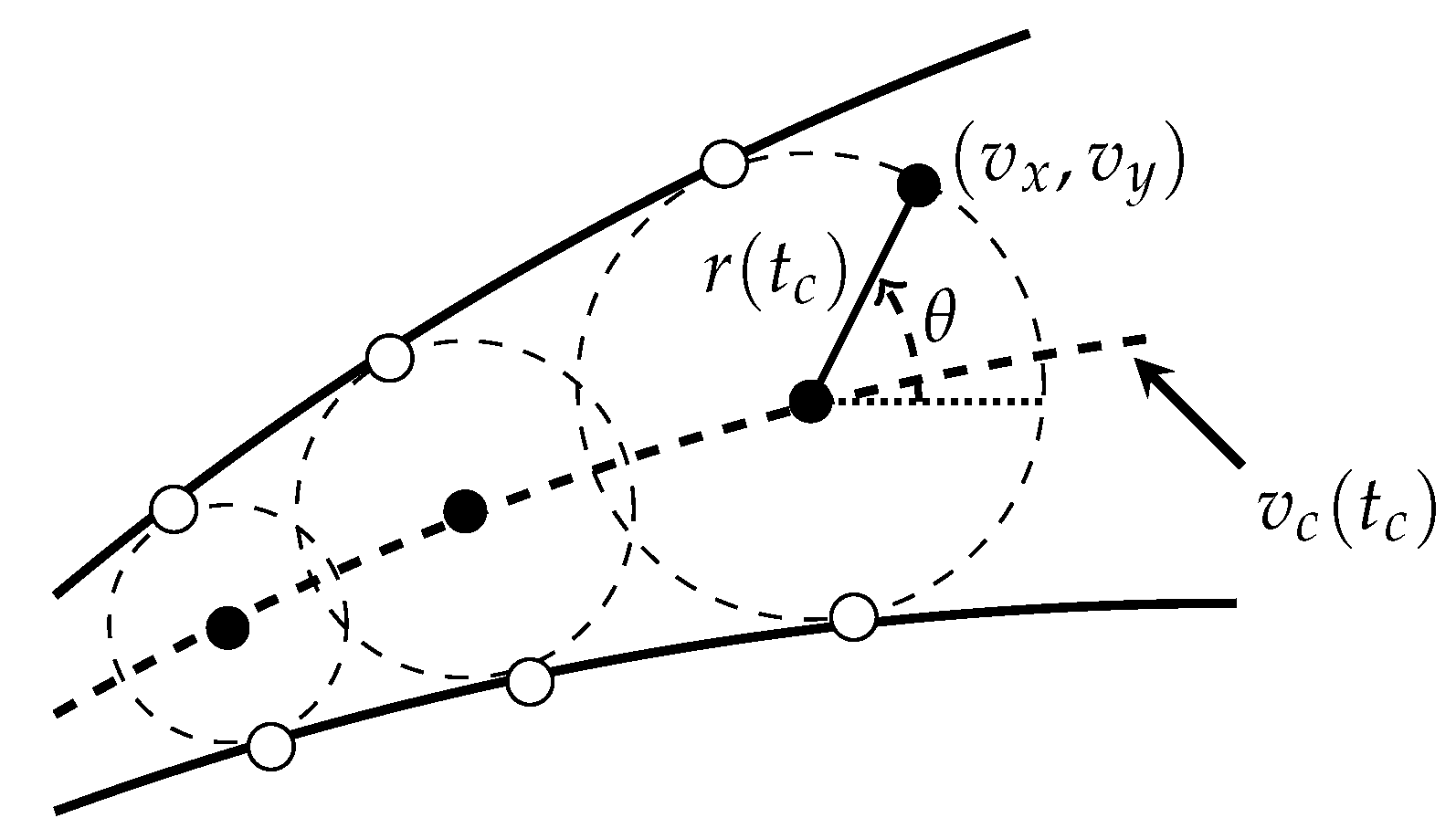
3.1. Velocity Obstacle (VO) Theory
3.2. Solution Space Diagram (SSD) Resolution Model
3.3. Conflict Resolution with Speed Variation
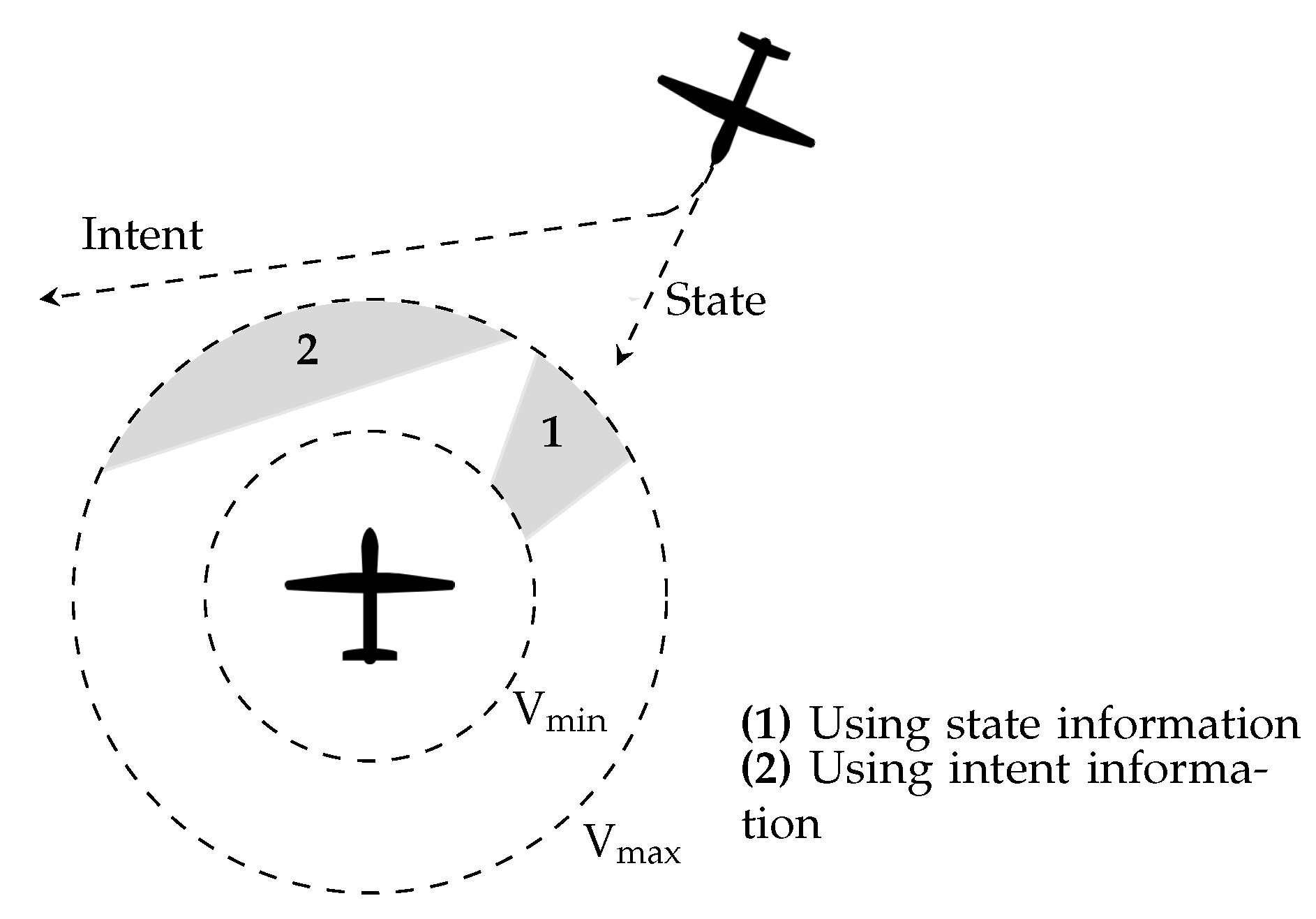
3.4. State-Based vs. Intent-Based Resolution
4. Variable Speed Limit (VSL) with Reinforcement Learning (RL)
4.1. Agent
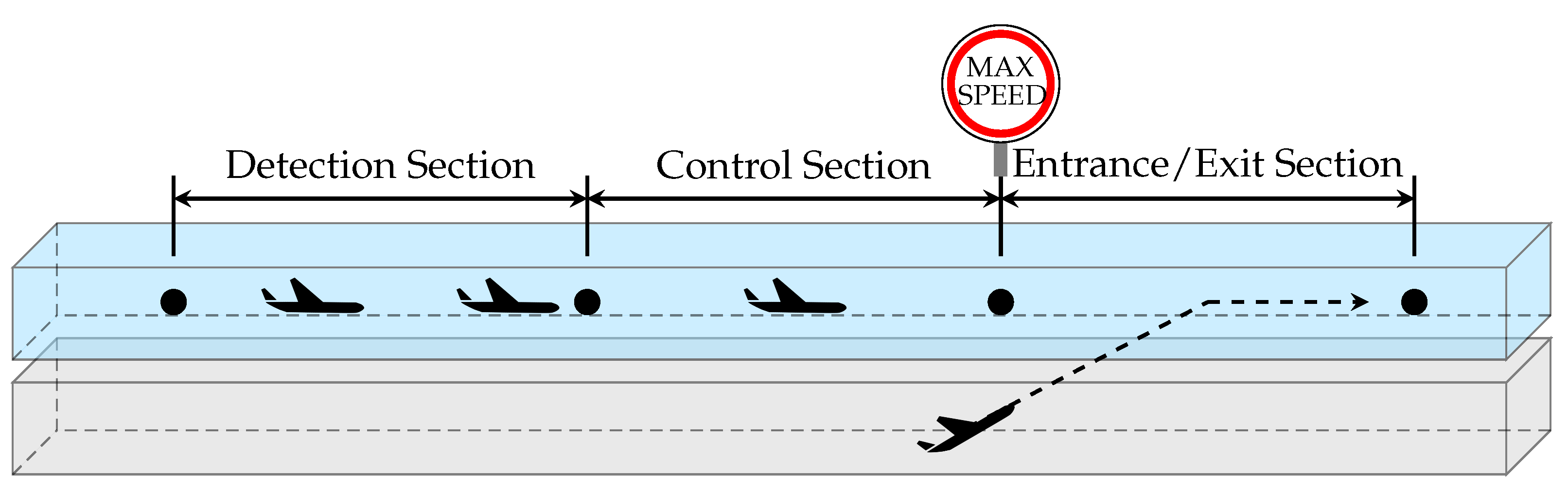
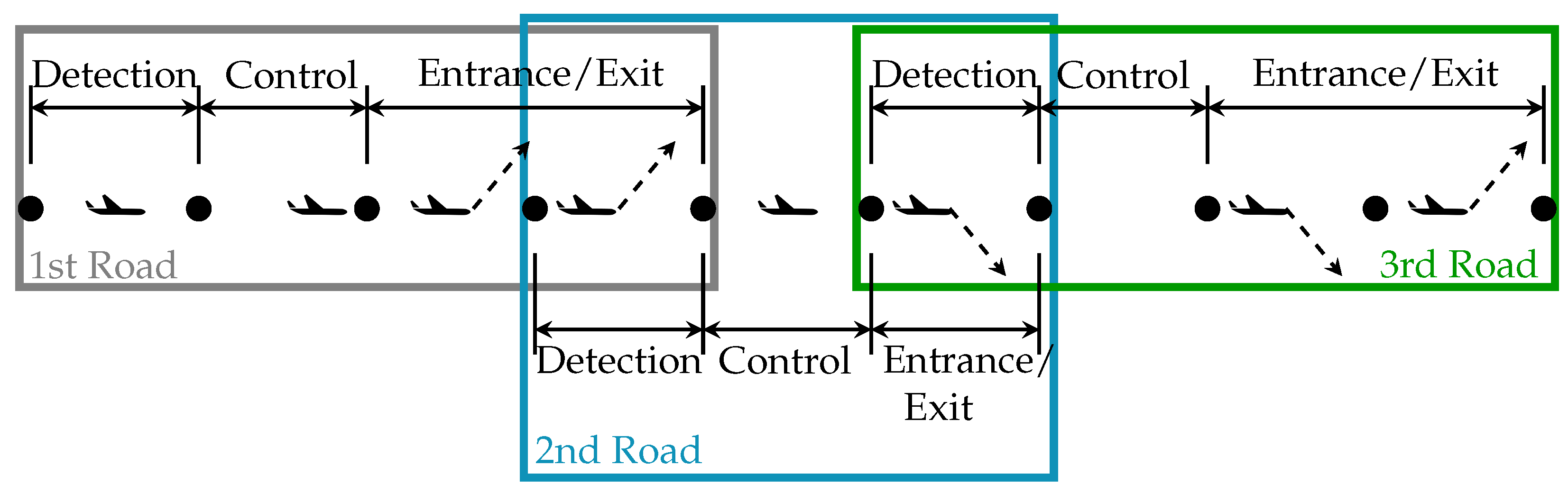
- Detection section: where cruising traffic is detected;
- Control section: in this section, aircraft adjust to the maximum speed set by the VSL agent;
- Entrance/exit section: section where aircraft from adjacent traffic layers are expected to enter the current layer and/or cruising aircraft are expected to exit the current layer. Aircraft are expected to comply with the maximum speed set by the VSL agent.
4.2. Learning Algorithm
| Algorithm 1: Deep Deterministic Policy Gradient |
|
4.3. State
- Number of aircraft expected to transition vertically into the entrance/exit section in the next 60 s;
- Number of aircraft expected to transition vertically out of the entrance/exit section in the next 60 s;
- Cruising aircraft expected to travel from the detection area into the entrance/exit section in the next 60 s;
- Current maximum speed in the detection section.
4.4. Action
4.5. Reward
- A negative reward for a LoS within the road (−10 per LoS);
- A negative reward for near-LoS within the road (−4 when time to Los s; −2 when time to LoS s);
- The difference between the final detected and the expected traffic flow. A higher traffic outflow is rewarded positively (+1 for each extra aircraft that exits the road). An inferior traffic flow is rewarded negatively (−1 for each each aircraft that has not exit the road as it was expected);
- A positive reward for higher maximum speeds (0 for 10 kts; +1 for 15 kts; +2 for 20 kts; +3 for 25 kts; +4 for 30 kts).
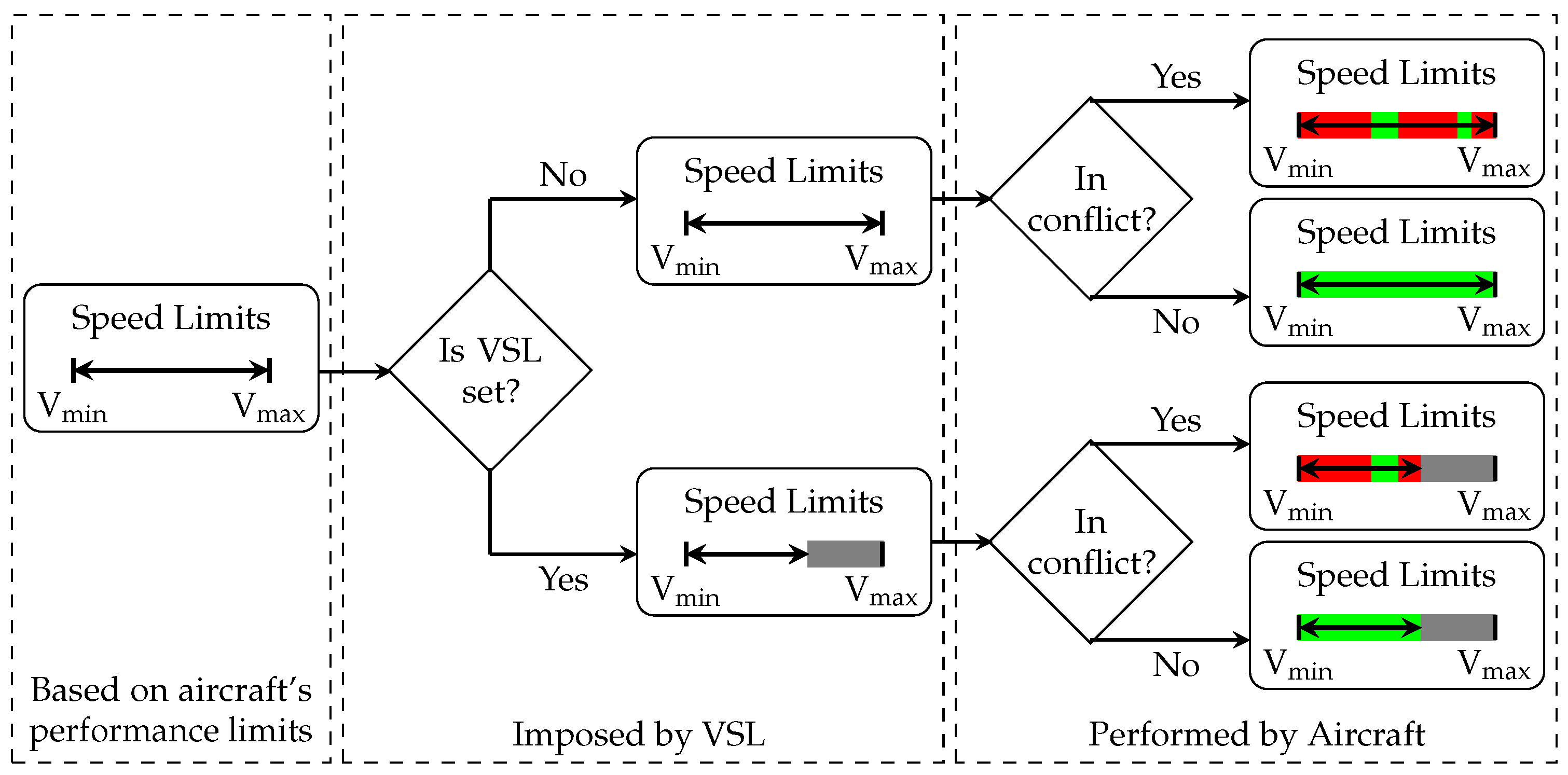
4.6. Aircraft Compliance with the Maximum Speed
5. Experiment: Conflict Resolution in Urban Environment with Variable Speed Limits
5.1. Apparatus and Aircraft Model
5.2. Independent Variables
5.2.1. State/Intent Information Usage
- Only state (S) information: common application which will be used as a performance baseline for comparison;
- State and intent information is used simultaneously (). Conflicts are detected and resolved preparing for both situations: whether intruding aircraft continue in their current state or follow their intent. This is a conservative approach, with aircraft working to prevent all possible risk situations. The disadvantage is that more VOs are included in the solution space and the amount of velocity vectors which can prevent all conflicts becomes smaller; it can potentially even reach a situation where no solution exists.
5.2.2. Heading–Altitude Rules
- All aircraft travel at the same altitude layer, independently of heading. Used for baseline comparison;
- Multiple altitude layers are used. In each layer, aircraft have similar headings.
5.2.3. Variable Speed Limits Compliance
- No variable speed limits are applied, aircraft to follow the maximum cruise speed. Used for baseline comparison;
- Variable speed limits are applied by the RL agent. Aircraft have a compliance rate of 100%;
- Variable speed limits are applied by the RL agent. Aircraft have a compliance rate of 90%.
5.2.4. Traffic Density
6. Experiment: Experimental Design and Procedure
6.1. Minimum Separation
6.2. Conflict Detection
6.3. Simulation Scenarios
- Fewer altitude variations;
- Fewer turns;
- Shortest distance.
6.4. Dependent Variables
6.4.1. Safety Analysis
6.4.2. Stability Analysis
6.4.3. Efficiency Analysis
7. Experiment: Experimental Hypotheses
7.1. Speed-Only Conflict Resolution
7.2. State vs. Intent Information in Conflict Resolution
7.3. Heading–Altitude Rules
7.4. Variable Speed Limits with Reinforcement Learning
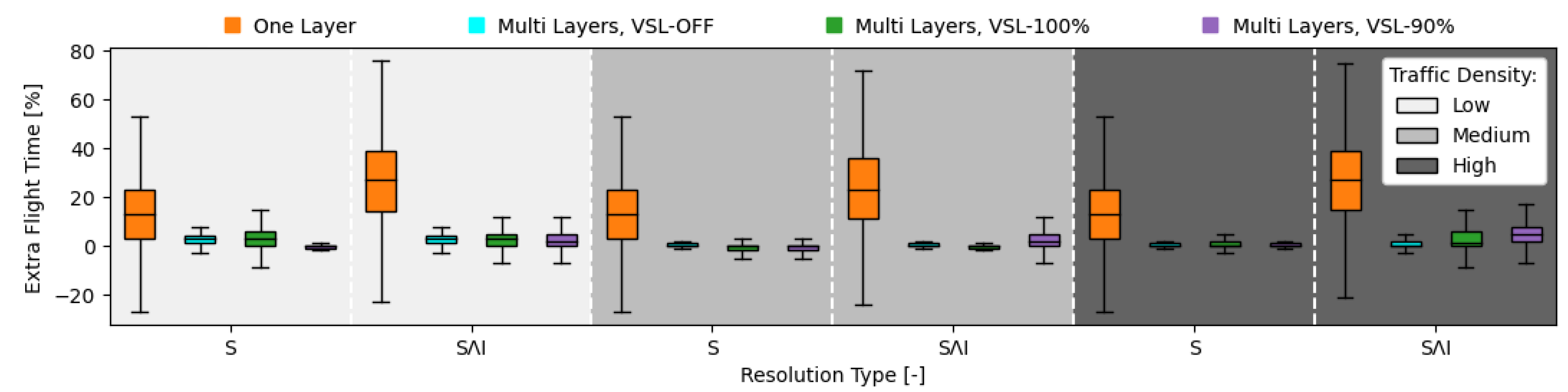
8. Experiment: Results
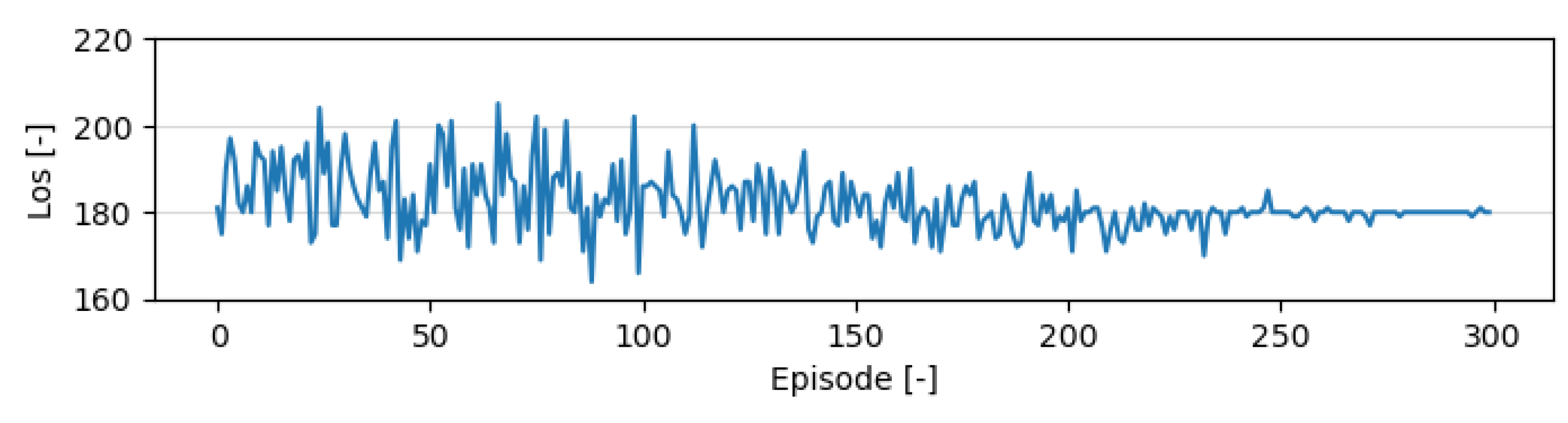
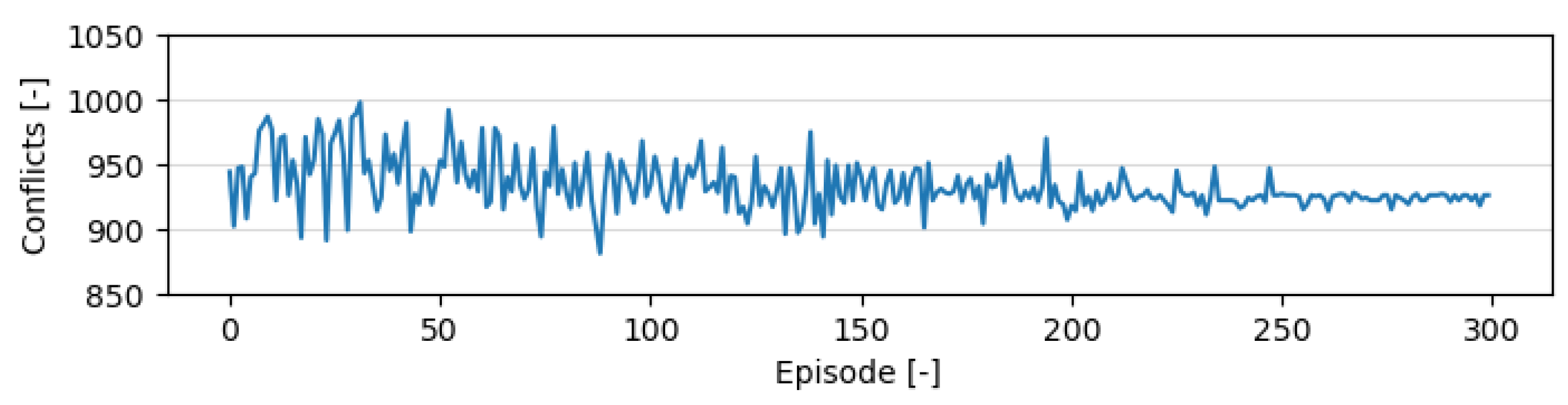
8.1. Training of the RL Agent for Variable Speed Limits
Safety Analysis
8.2. Testing of the RL Agent for Variable Speed Limits
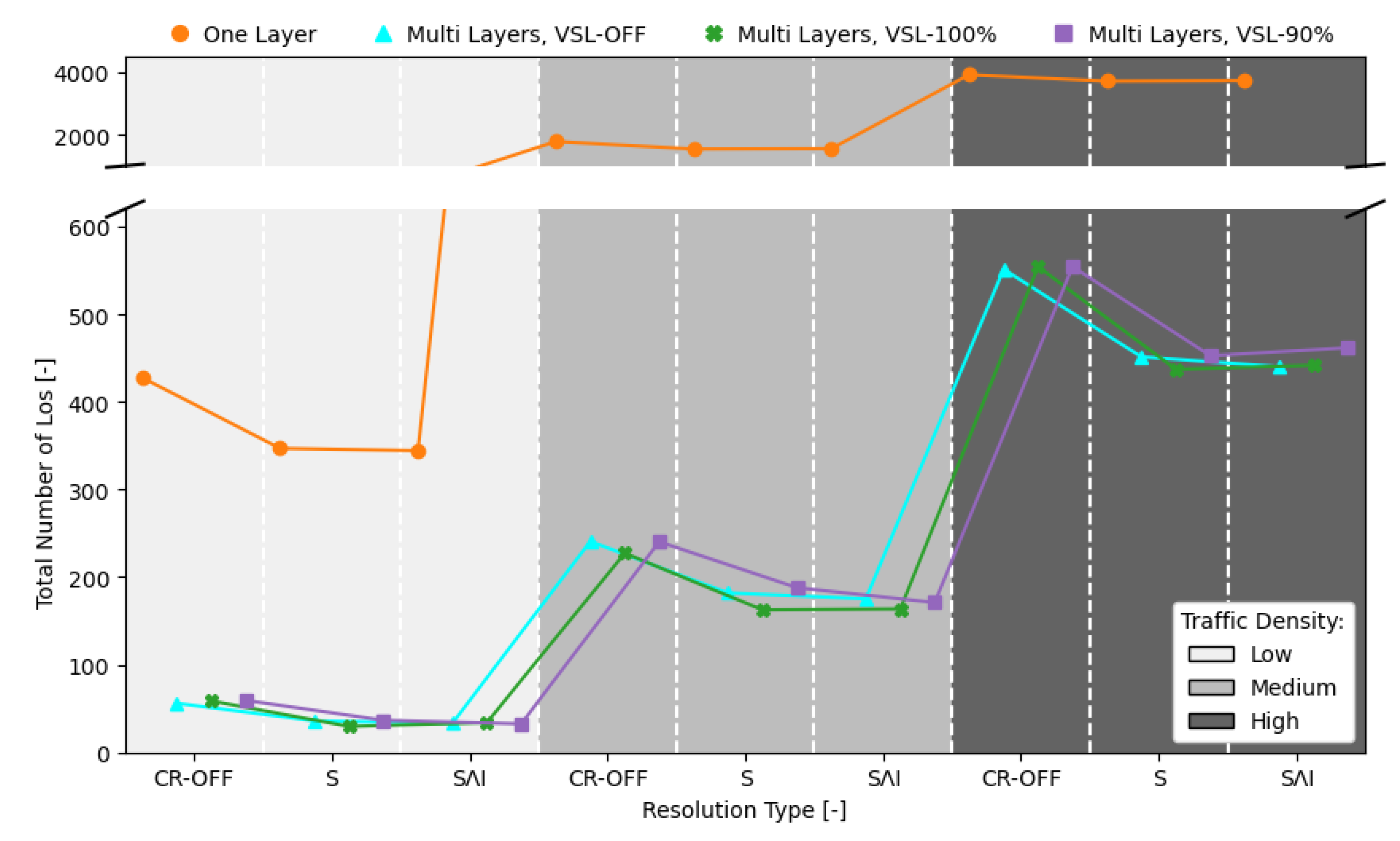
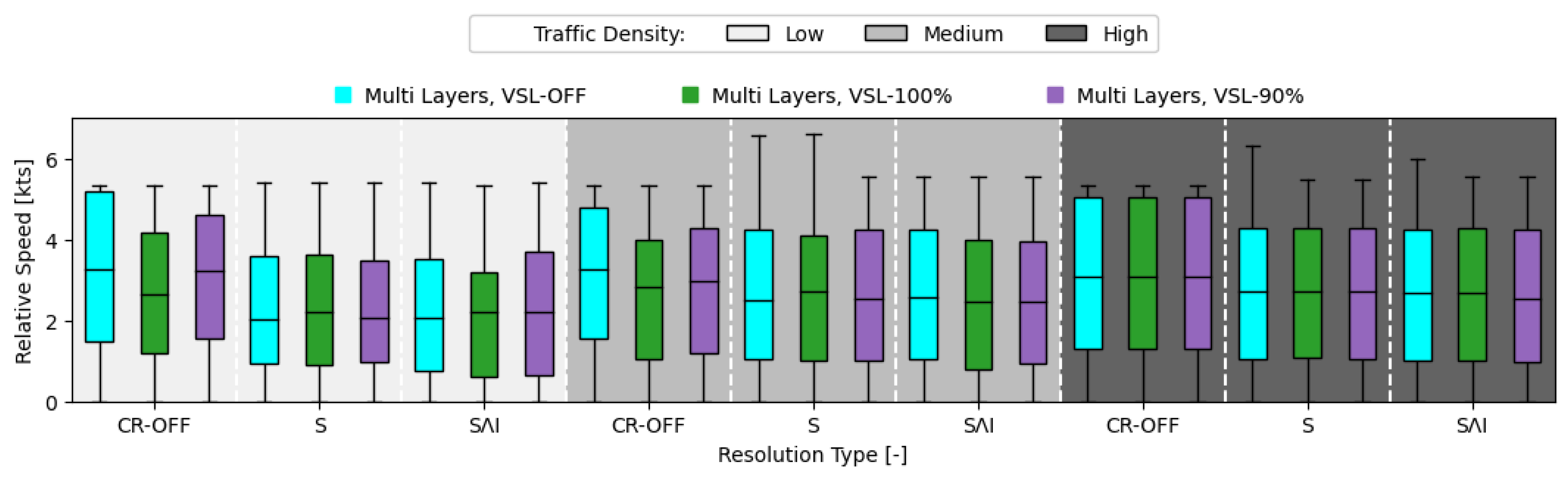
8.2.1. Safety Analysis
8.2.2. Stability Analysis
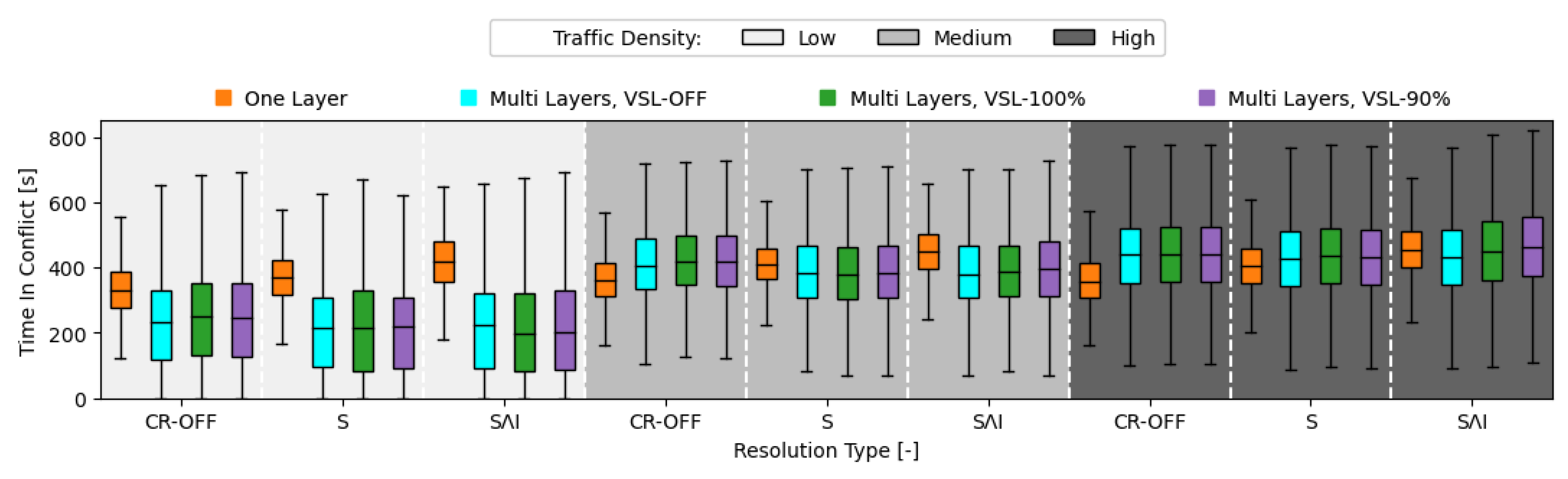
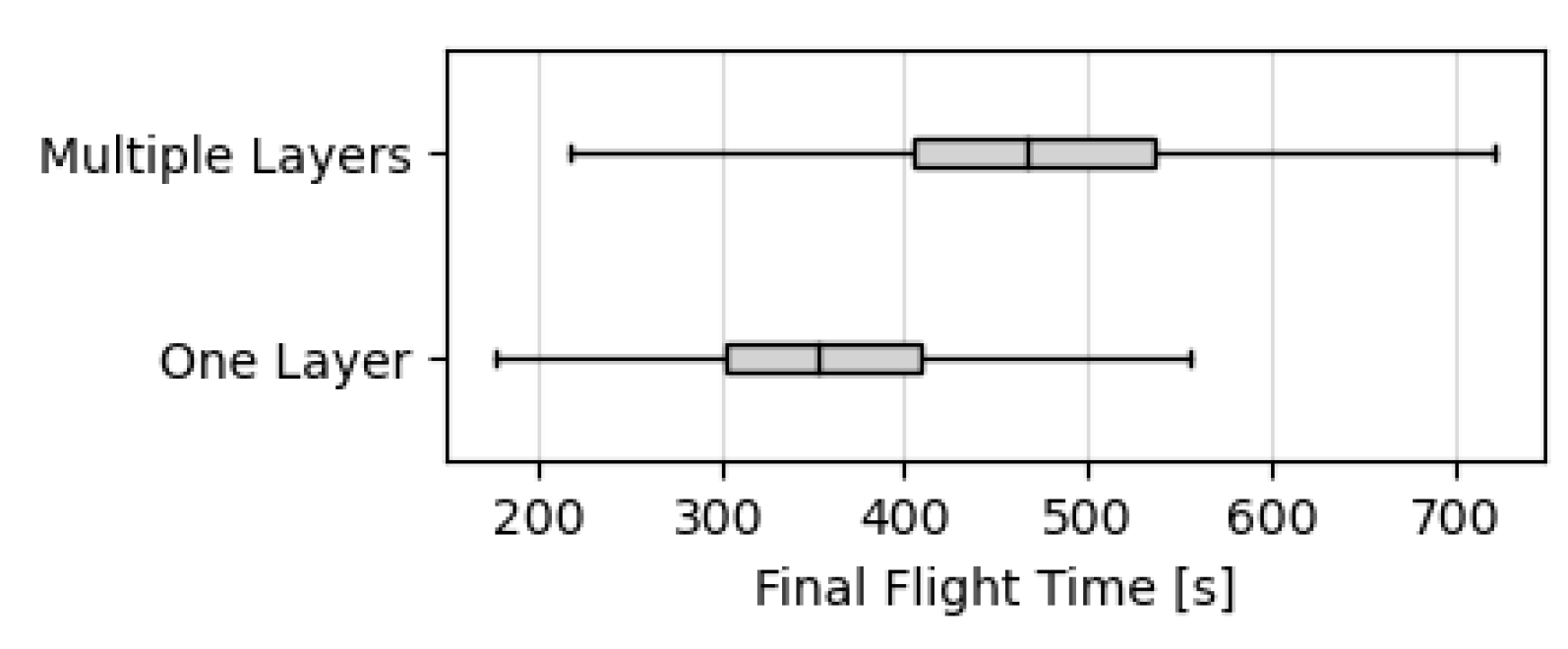
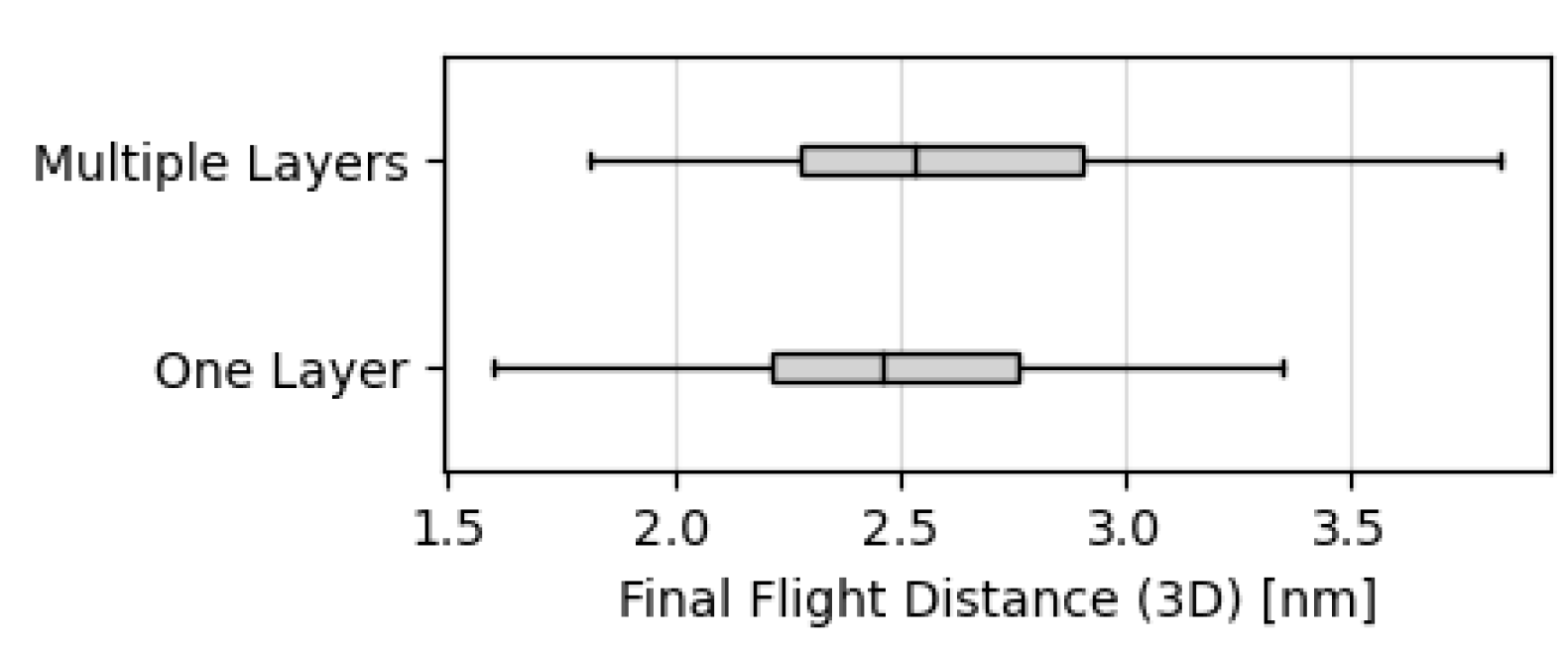
8.2.3. Efficiency Analysis
9. Discussion
9.1. State vs. Intent Information in Conflict Resolution
9.2. Heading–Altitude Rules
9.3. Variable Speed Limit with Reinforcement Learning
- Compliance rate of 90% already cancels out the benefit of employing speed limits. Consequently, the necessary infrastructure should be in place to make sure that aircraft can identify and correctly react to these variable speed limits;
- Training in a specific traffic density proved somewhat inefficient for higher densities. The RL agent should at least be trained at the highest traffic density expected under actual operations. It may also be that different traffic densities require different resolution strategies, as also hypothesised in the Metropolis project [29]. In this case, the RL model must learn different responses per complexity of emergent behaviour resulting from increasing traffic densities.
- Aircraft were able to climb/descend at any point, setting variable speed sections in close proximity. A homogeneous maximum speed value between all sections proved beneficial;
- Reward values were based on the efficiency of conflict resolution. Having aircraft (rapidly) accelerating greatly reduces the efficiency of conflict resolution, as it increases uncertainty regarding the intruders’ trajectory propagation;
- A uniform distribution of the traffic density was favoured to establish a relation between the allowed traffic density and resulting safety level. Throughout one episode, the number of instantaneous aircraft is expected to remain (almost) constant, with variations resulting only from conflict avoidance and/or the randomisation of trajectories.
9.4. Advice for Future Work
- The exploration of more powerful states and reward formulations;
- The exploration of different time periods for the duration of a maximum speed on a section. Duration may be based instead on observable changes of the traffic scenario in the section;
- The current implementation is oblivious to a congestion building up some distance ahead. A greater observability over the environment could be obtained by adding knowledge within a larger surrounding radius to the state formulation. Such a strategy introduces more complexity to the system, but should be considered in favour of a more homogeneous traffic situation throughout the entire environment;
- Further testing with more heterogeneous environments (e.g., different aircraft types, different performance limits, different separation between layers, different climbing/descending rates, different minimum separation).
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sesar Joint Undertaking. European Drones Outlook Study—Unlocking the Value for Europe; Technical Report; Sesar Joint Undertaking: Brussels, Belgium, 2016. [Google Scholar]
- Rakha, T.; Gorodetsky, A. Review of Unmanned Aerial System (UAS) applications in the built environment: Towards automated building inspection procedures using drones. Autom. Constr. 2018, 93, 252–264. [Google Scholar] [CrossRef]
- Besada, J.A.; Campana, I.; Bergesio, L.; Bernardos, A.M.; de Miguel, G. Drone Flight Planning for Safe Urban Operations: UTM Requirements and Tools. In Proceedings of the 2019 IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops), Kyoto, Japan, 11–15 March 2019; pp. 924–930. [Google Scholar] [CrossRef]
- FAA. FAA Modernization and Reform Act of 2012, Conference Report; Technical Report; FAA: Washington, DC, USA, 2012. [Google Scholar]
- ICAO. ICAO Circular 328—Unmanned Aircraft Systems (UAS); Technical Report; ICAO: Montreal, QC, Canada, 2011. [Google Scholar]
- Walraven, E.; Spaan, M.T.; Bakker, B. Traffic flow optimization: A reinforcement learning approach. Eng. Appl. Artif. Intell. 2016, 52, 203–212. [Google Scholar] [CrossRef]
- Li, Z.; Liu, P.; Xu, C.; Duan, H.; Wang, W. Reinforcement Learning-Based Variable Speed Limit Control Strategy to Reduce Traffic Congestion at Freeway Recurrent Bottlenecks. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3204–3217. [Google Scholar] [CrossRef]
- Doole, M.; Ellerbroek, J.; Hoekstra, J. Drone Delivery: Urban airspace traffic density estimation. In Proceedings of the Eighth SESAR Innovation Days, Salzburg, Austria, 3–7 December 2018. [Google Scholar]
- Agogino, A.K.; Tumer, K. A multiagent approach to managing air traffic flow. Auton. Agents Multi-Agent Syst. 2012, 24, 1–25. [Google Scholar] [CrossRef]
- Yang, L.C.; Kuchar, J.K. Using intent information in probabilistic conflict analysis. In Proceedings of the 1998 AIAA Guidance, Navigation, and Control Conference and Exhibit, Boston, MA, USA, 10–12 August 1998; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 1998; pp. 797–806. [Google Scholar] [CrossRef]
- Hwang, I.; Seah, C.E. Intent-Based Probabilistic Conflict Detection for the Next Generation Air Transportation System. Proc. IEEE 2008, 96, 2040–2059. [Google Scholar] [CrossRef]
- Porretta, M.; Schuster, W.; Majumdar, A.; Ochieng, W. Strategic conflict detection and resolution using aircraft intent information. J. Navig. 2010, 63, 61–88. [Google Scholar] [CrossRef]
- Liu, W.; Hwang, I. Probabilistic trajectory prediction and conflict detection for air traffic control. J. Guid. Control Dyn. 2011, 34, 1779–1789. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.R. Intent Based Trajectory Prediction by Multiple Model Prediction and Smoothing. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Dam, S.V.; Mulder, M.; Paassen, R. The Use of Intent Information in an Airborne Self-Separation Assistance Display Design. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2009. [Google Scholar] [CrossRef][Green Version]
- Velasco, G.; Borst, C.; Ellerbroek, J.; van Paassen, M.M.; Mulder, M. The Use of Intent Information in Conflict Detection and Resolution Models Based on Dynamic Velocity Obstacles. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2297–2302. [Google Scholar] [CrossRef]
- d’Engelbronner, J.; Borst, C.; Ellerbroek, J.; Van Paassen, M.; Mulder, M. Solution-space–based analysis of dynamic air traffic controller workload. J. Aircr. 2015, 52, 1146–1160. [Google Scholar] [CrossRef]
- Ribeiro, M.; Ellerbroek, J.; Hoekstra, J. Review of conflict resolution methods for manned and unmanned aviation. Aerospace 2020, 7, 79. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. In Proceedings of the 4th International Conference on Learning Representations (IICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Henderson, P.; Islam, R.; Bachman, P.; Pineau, J.; Precup, D.; Meger, D. Deep Reinforcement Learning that Matters. arXiv 2017, arXiv:1709.06560. [Google Scholar]
- Hoekstra, J.; Ellerbroek, J. BlueSky ATC Simulator Project: An Open Data and Open Source Approach. In Proceedings of the 7th International Conference on Research in Air Transportation, Philadelphia, PA, USA; 2016. [Google Scholar]
- Ellerbroek, J.; ProfHoekstra; MJRibeiroTUDelft. Bluesky Implementation: Underlying the Publication “Velocity Obstacle Based Conflict Avoidance in Urban Environment with Variable Speed Limit”; Zenodo: Geneve, Switzerland, 2021. [Google Scholar]
- Ribeiro, M.; Ellerbroek, J.; Hoekstra, J. Bluesky Data: Underlying the Publication “Velocity Obstacle Based Conflict Avoidance in Urban Environment with Variable Speed Limit”; 4TU.ResearchData: Delft, The Netherlands, 2021. [Google Scholar]
- Boeing, G. OSMnx: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Comput. Environ. Urban Syst. 2017, 65, 126–139. [Google Scholar] [CrossRef]
- Irvine, R. The GEARS Conflict Resolution Algorithm; Technical Report; EUROCONTROL: Paris, France, 1997. [Google Scholar] [CrossRef][Green Version]
- Park, J.; Cho, N. Collision Avoidance of Hexacopter UAV Based on LiDAR Data in Dynamic Environment. Remote Sens. 2020, 12, 975. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, P.; Tan, J.; Li, F. The Obstacle Detection Method of UAV Based on 2D Lidar. IEEE Access 2019, 7, 163437–163448. [Google Scholar] [CrossRef]
- Yang, L.; Han, K.; Borst, C.; Mulder, M. Impact of aircraft speed heterogeneity on contingent flow control in 4D en-route operation. Transp. Res. Part C Emerg. Technol. 2020, 119, 102746. [Google Scholar] [CrossRef]
- Sunil, E.; Hoekstra, J.; Ellerbroek, J.; Bussink, F.; Nieuwenhuisen, D.; Vidosavljevic, A.; Kern, S. Metropolis: Relating Airspace Structure and Capacity for Extreme Traffic Densities. In Proceedings of the 11th USA/EUROPE Air Traffic Management R&D Seminar (ATM Seminar 2015), Lisbon, Portugal, 23–26 June 2015. [Google Scholar]
- Doole, M.; Ellerbroek, J.; Knoop, V.L.; Hoekstra, J.M. Constrained Urban Airspace Design for Large-Scale Drone-Based Delivery Traffic. Aerospace 2021, 8, 38. [Google Scholar] [CrossRef]
- Samir Labib, N.; Danoy, G.; Musial, J.; Brust, M.R.; Bouvry, P. Internet of Unmanned Aerial Vehicles—A Multilayer Low-Altitude Airspace Model for Distributed UAV Traffic Management. Sensors 2019, 19, 4779. [Google Scholar] [CrossRef] [PubMed]
- Cho, J.; Yoon, Y. Extraction and Interpretation of Geometrical and Topological Properties of Urban Airspace for UAS Operations; Korea Advanced Institution of Science and Technology: Daejeon, Korea, 2019. [Google Scholar]
- Tra, M.; Sunil, E.; Ellerbroek, J.; Hoekstra, J. Modeling the Intrinsic Safety of Unstructured and Layered Airspace Designs. In Proceedings of the Twelfth USA/Europe Air Traffic Management Research and Development Seminar, Seattle, WA, USA, 27–30 June 2017. [Google Scholar]
- Fiorini, P.; Shiller, Z. Motion Planning in Dynamic Environments Using Velocity Obstacles. Int. J. Robot. Res. 1998, 17, 760–772. [Google Scholar] [CrossRef]
- Chakravarthy, A.; Ghose, D. Obstacle avoidance in a dynamic environment: A collision cone approach. IEEE Trans. Syst. Man Cybern. Part A Syst. Humans 1998, 28, 562–574. [Google Scholar] [CrossRef]
- Balasooriyan, S. Multi-Aircraft Conflict Resolution Using Velocity Obstacles. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2017. [Google Scholar]
- Haines, E. Point in Polygon Strategies. In Graphics Gems IV; Academic Press Professional, Inc.: Point Pleasant, NJ, USA, 1994; pp. 24–46. [Google Scholar]
- Gawinowski, G.; Garcia, J.L.; Guerreau, R.; Weber, R.; Brochard, M. ERASMUS: A new path for 4D trajectory-based enablers to reduce the traffic complexity. In Proceedings of the 2007 IEEE/AIAA 26th Digital Avionics Systems Conference, Dallas, TX, USA, 21–25 October 2007. [Google Scholar] [CrossRef]
- Chaloulos, G.; Crück, E.; Lygeros, J. A simulation based study of subliminal control for air traffic management. Transp. Res. Part C Emerg. Technol. 2010, 18, 963–974. [Google Scholar] [CrossRef]
- Vela, A.; Solak, S.; Singhose, W.; Clarke, J.P. A Mixed Integer Program for Flight-Level Assignment and Speed Control for Conflict Resolution. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2010; pp. 5219–5226. [Google Scholar] [CrossRef]
- Huang, R.; Liang, H.; Zhao, P.; Yu, B.; Geng, X. Intent-Estimation- and Motion-Model-Based Collision Avoidance Method for Autonomous Vehicles in Urban Environments. Appl. Sci. 2017, 7, 457. [Google Scholar] [CrossRef]
- Lawrence, J.D. A Catalog of Special Plane Curves; Guilford Publications: New York, NY, USA, 2013. [Google Scholar]
- Wu, Y.; Tan, H.; Qin, L.; Ran, B. Differential variable speed limits control for freeway recurrent bottlenecks via deep actor-critic algorithm. Transp. Res. Part C Emerg. Technol. 2020, 117, 102649. [Google Scholar] [CrossRef]
- Brittain, M.; Yang, X.; Wei, P. A Deep Multi-Agent Reinforcement Learning Approach to Autonomous Separation Assurance. arXiv 2020, arXiv:2003.08353. [Google Scholar]
- Li, S.; Egorov, M.; Kochenderfer, M. Optimizing Collision Avoidance in Dense Airspace using Deep Reinforcement Learning. arXiv 2019, arXiv:1912.10146. [Google Scholar]
- Ribeiro, M.; Ellerbroek, J.; Hoekstra, J. Determining Optimal Conflict Avoidance Manoeuvres At High Densities With Reinforcement Learning. In Proceedings of the Tenth SESAR Innovation Days, Virtual Conference, 7–10 December 2020. [Google Scholar]
- Vonk, B. Exploring Reinforcement Learning Methods for Autonomous Sequencing and Spacing of Aircraft. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2019. [Google Scholar]
- Van der Hoff, D. A Multi-Agent Learning Approach to Air Traffic Control. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2020. [Google Scholar]
- Cruciol, L.L.; de Arruda, A.C.; Weigang, L.; Li, L.; Crespo, A.M. Reward functions for learning to control in air traffic flow management. Transp. Res. Part C Emerg. Technol. 2013, 35, 141–155. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Matignon, L.; Laurent, G.J.; Le Fort-Piat, N. Independent reinforcement learners in cooperative Markov games: A survey regarding coordination problems. Knowl. Eng. Rev. 2012, 27, 1–31. [Google Scholar] [CrossRef]
- Duan, Y.; Chen, X.; Edu, C.X.B.; Schulman, J.; Abbeel, P.; Edu, P.B. Benchmarking Deep Reinforcement Learning for Continuous Control. arXiv 2016, arXiv:1604.06778. [Google Scholar]
- Islam, R.; Henderson, P.; Gomrokchi, M.; Precup, D. Reproducibility of Benchmarked Deep Reinforcement Learning Tasks for Continuous Control. arXiv 2017, arXiv:1708.04133. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics (AISTATS), Fort Lauderdale, FL, USA, 11–13 April 2011. [Google Scholar]
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of the Brownian motion. Phys. Rev. 1930, 36, 823–841. [Google Scholar] [CrossRef]
- Papageorgiou, M.; Kosmatopoulos, E.; Papamichail, I. Effects of Variable Speed Limits on Motorway Traffic Flow. Transp. Res. Rec. 2008, 2047, 37–48. [Google Scholar] [CrossRef]
- Golding, R. Metrics to Characterize Dense Airspace Traffic; Technical Report 004; Altiscope: Sunnyvale, CA, USA, 2018. [Google Scholar]
- Alejo, D.; Conde, R.; Cobano, J.; Ollero, A. Multi-UAV collision avoidance with separation assurance under uncertainties. In Proceedings of the 2009 IEEE International Conference on Mechatronics, Malaga, Spain, 14–17 April 2009. [Google Scholar] [CrossRef]
- Bilimoria, K.; Sheth, K.; Lee, H.; Grabbe, S. Performance evaluation of airborne separation assurance for free flight. In Proceedings of the 18th Applied Aerodynamics Conference, Denver, CO, USA, 14–17 August 2000; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2000. [Google Scholar] [CrossRef]
- Ribeiro, M.; Ellerbroek, J.; Hoekstra, J. The Effect of Intent on Conflict Detection and Resolution at High Traffic Densities. In Proceedings of the International Conference on Air Transportation (ICRAT), Virtual Format, 15 September 2020. [Google Scholar]
- Weikl, S.; Bogenberger, K.; Bertini, R.L. Traffic Management Effects of Variable Speed Limit System on a German Autobahn: Empirical Assessment Before and After System Implementation. Transp. Res. Rec. 2013, 2380, 48–60. [Google Scholar] [CrossRef]
- Mott MacDonald. Atm Monitoring and Evaluation, 4-Lane Variable Mandatory Speed Limits 12 Month Report (Primary and Secondary Indicators); Technical Report; European Commission; Directorate General Energy and Transport: London, UK, 2008. [Google Scholar]

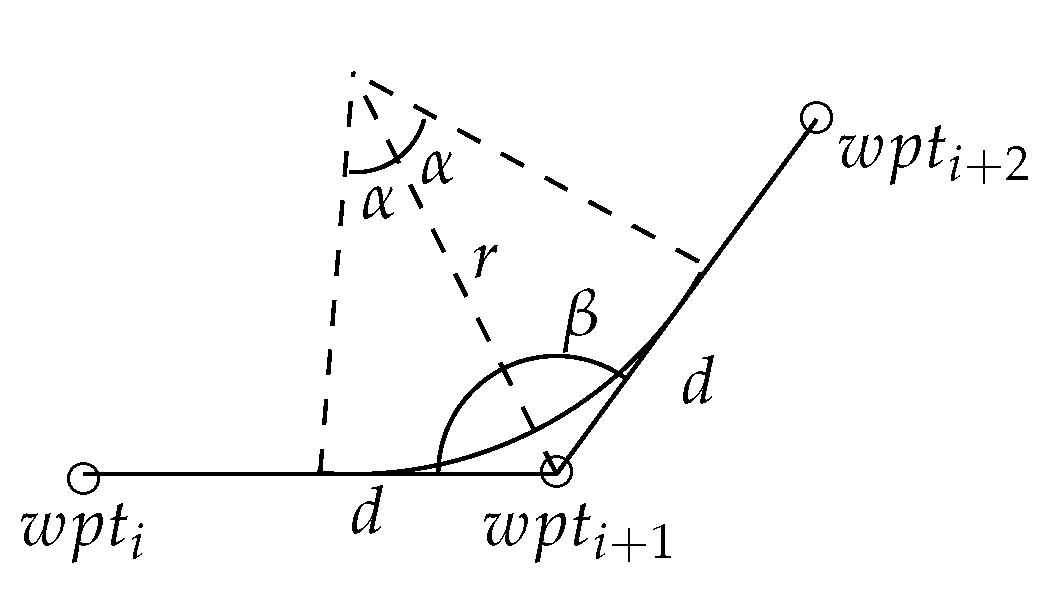









| 1st Layer | 2nd Layer | 3rd Layer | 4th Layer | 5th Layer | 6th Layer |
|---|---|---|---|---|---|
 | 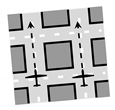 | 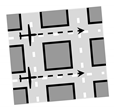 |  |  |  |
| Auxiliary Layer | Main Layers | Auxiliary Layer | |||
 | |||||
| Altitude | |||||
| Parameter | Low | Medium | High |
|---|---|---|---|
| Traffic density [/10,000 NM] | 81,247 | 162,495 | 243,744 |
| Number of instantaneous aircraft [-] | 25 | 50 | 75 |
| Number of spawned aircraft [-] | 453 | 926 | 1366 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ribeiro, M.; Ellerbroek, J.; Hoekstra, J. Velocity Obstacle Based Conflict Avoidance in Urban Environment with Variable Speed Limit. Aerospace 2021, 8, 93. https://doi.org/10.3390/aerospace8040093
Ribeiro M, Ellerbroek J, Hoekstra J. Velocity Obstacle Based Conflict Avoidance in Urban Environment with Variable Speed Limit. Aerospace. 2021; 8(4):93. https://doi.org/10.3390/aerospace8040093
Chicago/Turabian StyleRibeiro, Marta, Joost Ellerbroek, and Jacco Hoekstra. 2021. "Velocity Obstacle Based Conflict Avoidance in Urban Environment with Variable Speed Limit" Aerospace 8, no. 4: 93. https://doi.org/10.3390/aerospace8040093
APA StyleRibeiro, M., Ellerbroek, J., & Hoekstra, J. (2021). Velocity Obstacle Based Conflict Avoidance in Urban Environment with Variable Speed Limit. Aerospace, 8(4), 93. https://doi.org/10.3390/aerospace8040093








