Shape Optimization of Labyrinth Seals to Improve Sealing Performance

Abstract

To reduce gas leakage, shape optimization of a straight labyrinth seal was carried out. The six design parameters included seal clearance, fin width, fin height, fin pitch, fin backward, and forward expansion angle. The CFD (Computational Fluid Dynamics) model was solved to generate the training and testing samples for the surrogate model, which was established by the least square support vector machine. A kind of chaotic optimization algorithm was used to determine the optimal design parameters of the labyrinth seal. As seal clearance, fin width, fin height, fin pitch, fin backward and forward expansion angles are 0.2 mm, 0.1 mm, 7 mm, 9 mm, 0°, and 15°, the discharge coefficient can reach its minimum value in the design space. The chaotic optimization algorithm coupled with least square support vector machine is a promising scheme for labyrinth seal optimization.

1. Introduction

With the increase of operation pressure, leakage in gas turbines has attracted more and more attention. To prevent fluid leakage from high- to low-pressure regions, labyrinth seals, one kind of non-contacting mechanical seal, have been widely used for many decades. Labyrinth seals work by throttling flow through small successive openings in series, each one of which converts pressure into velocity, which ideally is dissipated in the intervening chambers. The main advantages of labyrinth seals are high flow resistance, structural reliability, and simplicity. Due to these advantages, labyrinth seals remain competitive compared with new designs such as brush and finger seals [1,2,3].

To analyze the performance of a labyrinth seal, many numerical and experimental studies have been performed. The influence of fin-shaped parameters on leakage were studied by Du et al. [4] in straight labyrinth seals. Their experimental results showed that increasing the seal clearance, fin width, and fin height all lead to an increase of discharge coefficient, while adding the fin pitch causes the decrease of the discharge coefficient. Anker and Mayer [5] reported that, at realistic clearance, due to negative incidence downstream stator, the flow separation of leakage flow takes place. Pychynski et al. [6] established the prediction model for discharge coefficient with a data mining method. In the model, the discharge coefficient relies on the number of seal fins, fin height, fin pitch, pressure ratio, seal clearance, step shift, honeycomb cell diameter, fin width, groove shift, step height, and groove width. Asok et al. [7] applied an artificial neural network for the prediction and optimization of square cavity labyrinth seals. Kim and Cha [8] indicated that, as the clearance increases, the performance of stepped seals becomes much better compared with straight seals. Labyrinth seals are complex systems under the influence of geometric and flow parameters. To find global optimal solutions for a given set of requirements, researchers need to handle a high-dimensional design space [9,10]. Therefore, an effective optimization tool is necessary to be developed for labyrinth seals.

In the present optimization method, the surrogate model was established by a supervised learning model called a least square support vector machine (LS-SVM). As one kind of SVM, LS-SVM [11,12] is an effective machine learning tool for regression analysis and pattern recognition. Compared with other surrogate models, LS-SVM shows better regression accuracy and lower computation cost. LS-SVM is especially suitable for machine learning with a small-size training sample. Moreover, a kind of chaotic optimization algorithm was applied for global and detail searches. Compared with the random ergodic searches, the chaotic optimization can perform global searches at higher efficiency due to non-repetition of the chaotic system [13,14]

In this paper, the optimization model of straight labyrinth seals was introduced firstly; and then a CFD (Computational Fluid Dynamics) solution was performed to generate the training and testing samples for the surrogate model; finally, the structural optimization was carried out with the chaotic optimization algorithm and LS-SVM surrogate model, and a detailed analysis of optimization results were provided.

2. Objective Function and Design Variables

In current research, the design variables include seal clearance (c), fin pitch (B), fin height (H), fin width (w), fin forward expansion angle (β), and backward expansion angle (α). These parameters were defined in Figure 1, and their lower and upper limits are listed in

Table 1. Design variables and design space.

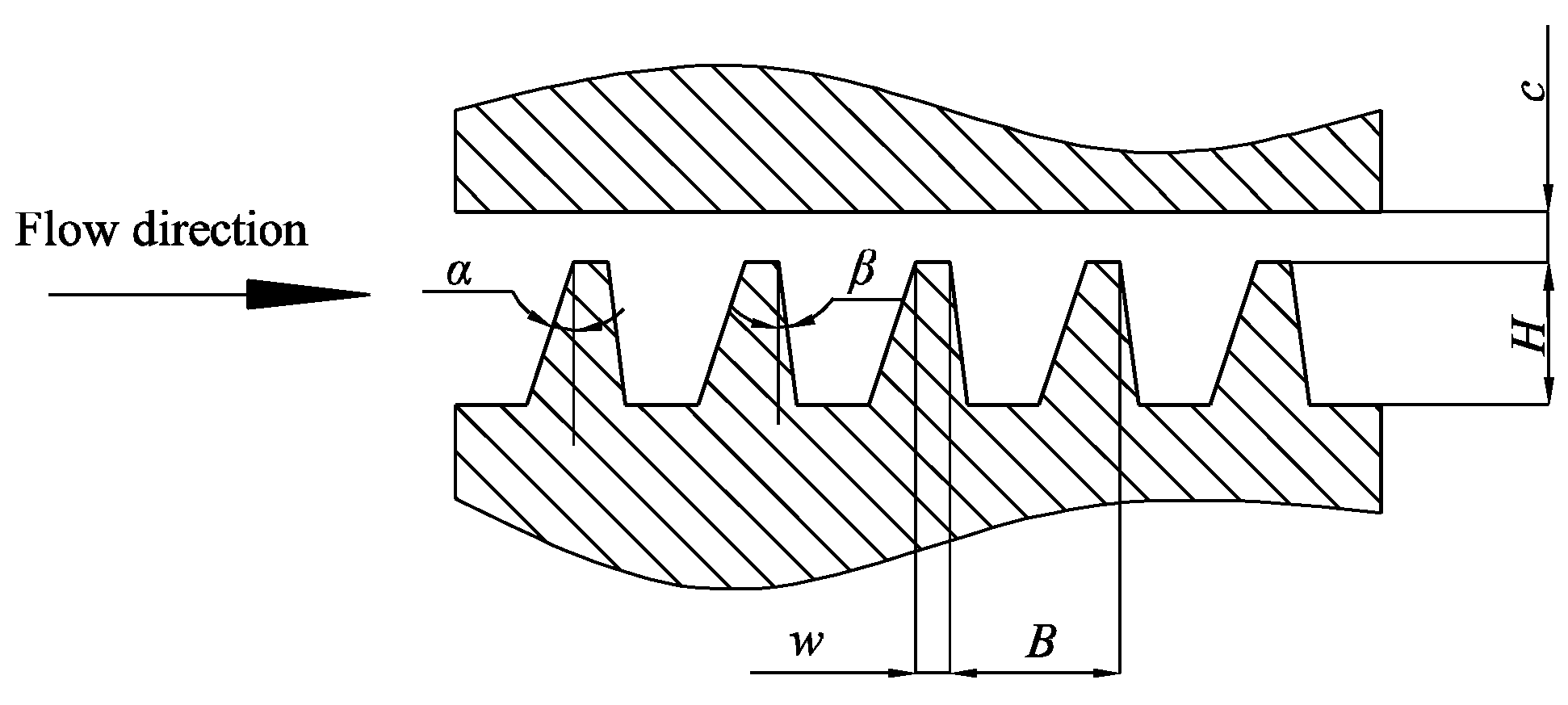
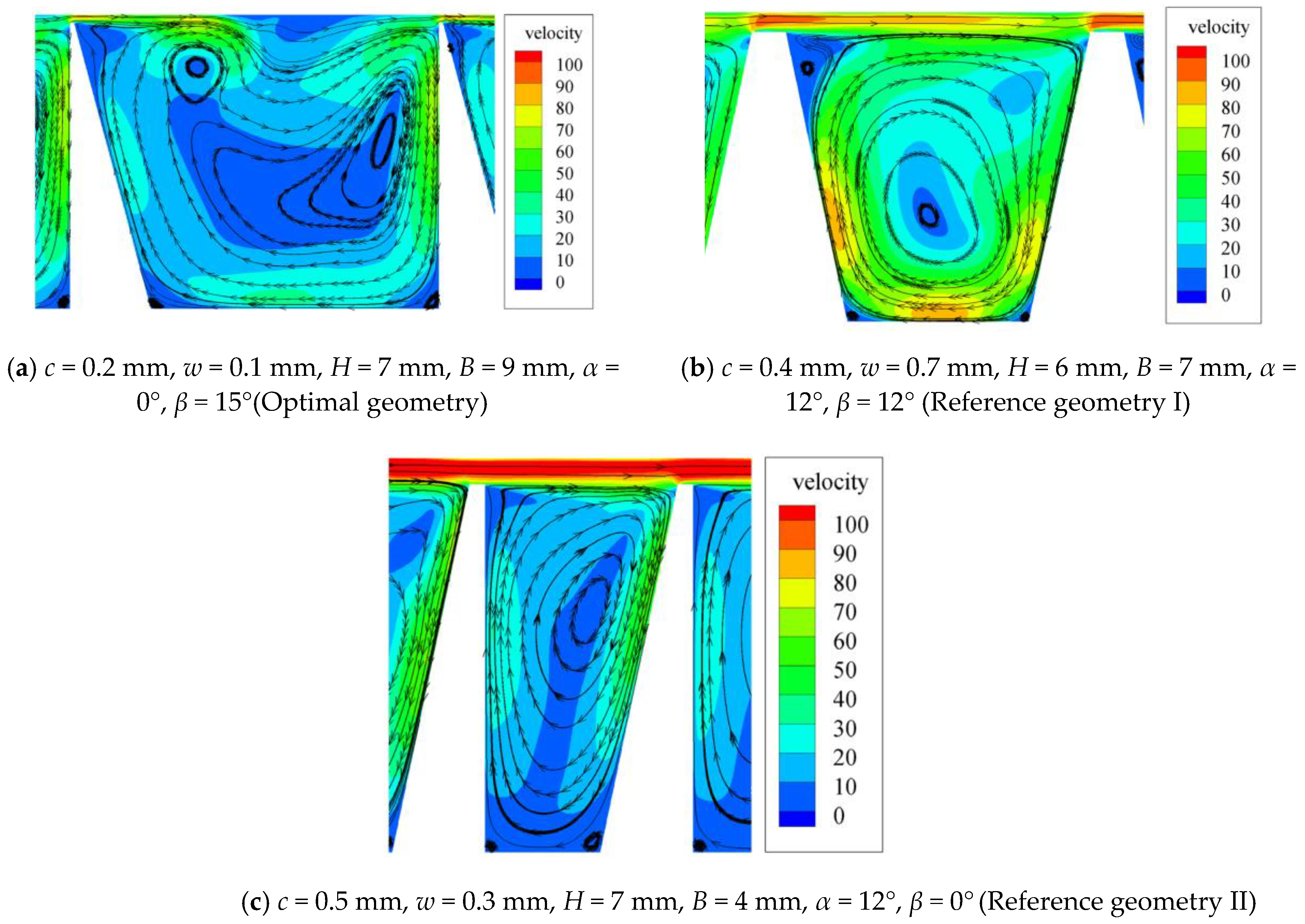
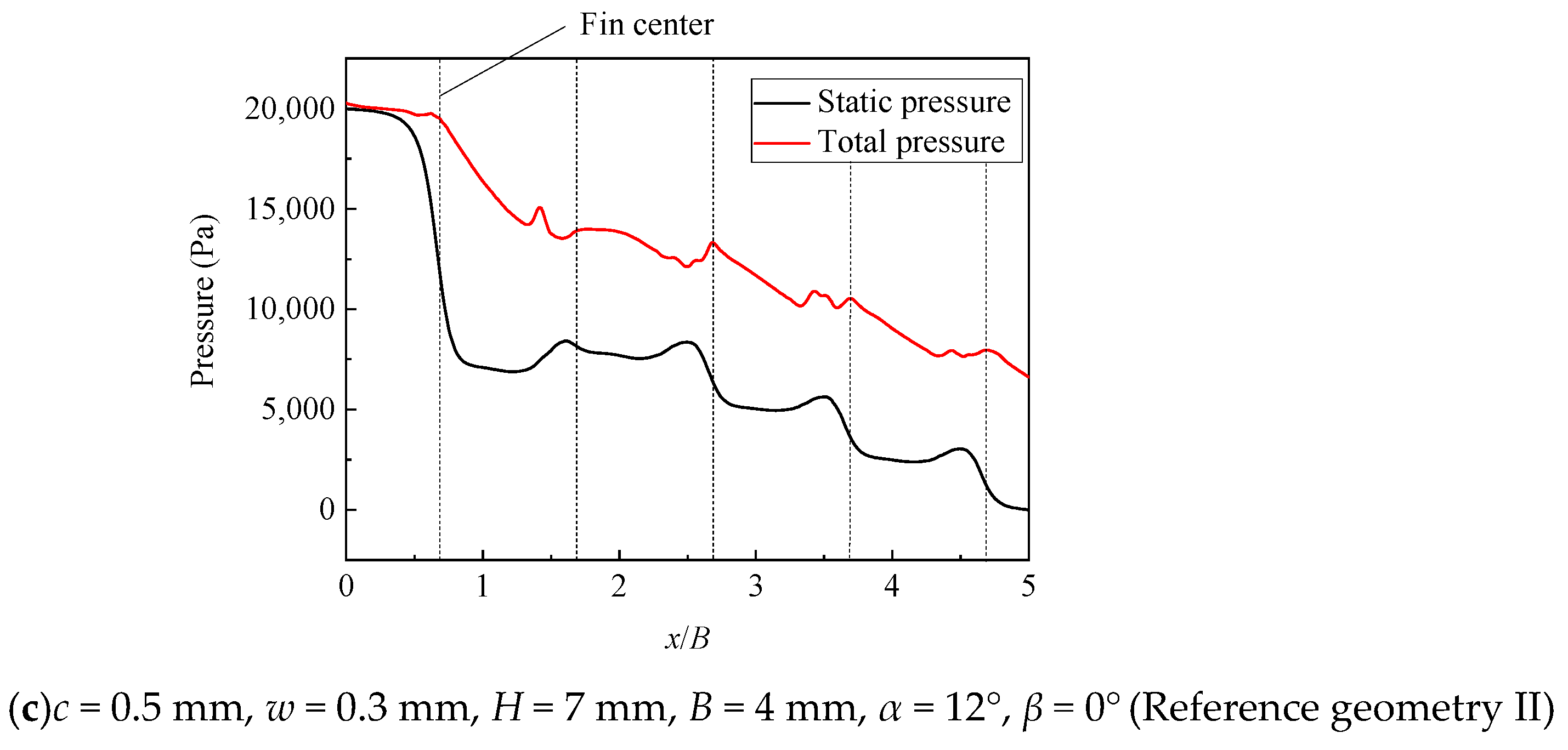
Design Variable	Symbol	Unit	Lower Bound	Upper Bound
Fin clearance	c	mm	0.2	0.6
Fin width	w	mm	0.1	0.7
Fin height	H	mm	3	7
Fin pitch	B	mm	3	9
Fin backward expansion angle	α	°	0	15
Fin forward expansion angle	β	°	0	15

. To meet the high sealing requirement in the outlet region of the high-pressure compressor, the seal in the present model has five fins. The inlet total temperature and pressure are 300 K and 0.12 MPa respectively. The outlet static pressure is 0.1 MPa.

The discharge coefficient is used to evaluate the seal performance quantitatively. C_d is defined as [2,15]:

$$C_d=\frac{m_a}{m_i}$$

(1)

where m_a and m_i denote the actual and ideal mass flow rate through the channel, respectively. m_i can be expressed by:

$$m_i=\frac{p_{0}A}{\sqrt{kR{T}_0}}\sqrt{\frac{2k^2}{k-1}{(\frac{p_n}{p_0})}^{\frac{2}{k}}[1-{(\frac{p_n}{p_0})}^{\frac{k-1}{k}}]}$$

(2)

where k is the isentropic coefficient (k = 1.4). p_n and p₀ denote the static and total pressure at the outlet, respectively. R is the gas constant. A denotes the cross-section area of the channel, and T₀ is the inlet total temperature.

3. Optimization Method

3.1. CFD Method

To study the influences of geometric variables on the discharge coefficient, numerical experiments were carried out by Ansys-Fluent 14.6. Static pressure at the channel outlet, total pressure at the channel inlet, and adiabatic and non-slip condition at the walls are specified. The standard k-ε turbulence model with the enhanced wall function, which has been proven to be suitable for labyrinth-seal flow by Morrison and Al-Ghasem [16], is used for modeling turbulence.

As shown in Figure 2, structured grids are generated by the use of ICEM software. In the clearance region, there are at least 13-layer grids for all the cases. Moreover, 5-layer meshes with the growing ratio of 1.2 were placed in the boundary layer region. The maximum y+ and x+ (flow direction) was less than 10.0 and 40, respectively. To determine the optimal grid number, a grid independent test was performed. Take one case with (c, w, H, B, α, β) = (0.2 mm, 0.1 mm, 7 mm, 7 mm, 8°, 5°) as example. Figure 3 shows the grid independent test results. As the number of computational girds exceeded 117,741, the discharge coefficient kept stable. Therefore, the grid number of 117,741 can be accepted.

Using the Latin hypercube sampling method, 72 groups of data samples were generated for the training samples for the surrogate model, and the other 20 groups generated randomly were used as the testing samples.

3.2. Surrogate Model Based on LS-SVM

It was assumed that there are training points G= {(I_i, O_i), i = 1,…,N} needed to be fitted, where N denotes the total number of training points, which is the input vector, and I_i and O_i denote the input vector and output value, respectively. According to LS-SVM theory, this problem can be expressed by [17,18]:

$$f({\mathit{I}}_j)={\displaystyle \sum _{i=1}^N{O}_i{a}_i\ker ({\mathit{I}}_j,{\mathit{I}}_i)+b}$$

(3)

where f(I_j) is LS-SVM output value, and ker(·) denotes the kernel function. The following equations can be solved to determine a and b:

$$\left[\begin{array}{cc}\begin{array}{l}0\\ {\mathit{A}}_l^T\end{array}& \begin{array}{l}{\mathit{A}}_l\\ \mathit{\Omega }+{\eta }^{-1}\mathit{E}\end{array}\end{array}\right]\left[\begin{array}{l}b\\ \mathit{a}\end{array}\right]=\left[\begin{array}{l}0\\ \mathit{O}\end{array}\right]$$

(4)

where η is the penalty factor, E denotes the unit matrix, a = [a₁,…, a_N]^T, A_l= [1,…, 1], O = [O₁,…, O_Ns]^T, and Ω(i,j) = k(I_i, I_j). Kernel function can be expressed by radial basis function:

$$\ker ({\mathit{I}}_i,{\mathit{I}}_j)=\exp (-\frac{\Vert {\mathit{I}}_i-{\mathit{I}}_j\Vert }{2{\delta }^2})$$

(5)

where δ is the kernel parameter.

3.3. Chaotic Optimization Algorithm

Currently, global optimization schemes including particle swarm algorithm, simulated annealing, evolutionary programming, and genetic algorithm have been widely applied for optimization practice. To escape from the local optimal values, the classical evolutionary (genetic) algorithm accepts some bad solutions under a certain probability. However, in a chaotic optimization scheme, the local optimal value can be avoided directly due to the regularity of chaotic motion [13,14,19]. In the present study, labyrinth seal geometries were optimized by a kind of chaotic algorithm.

The labyrinth seal optimization model can be expressed by:

$$\begin{gathered} \min F(c,w,H,B,\alpha ,\beta ) \\ \mathrm{s}.\mathrm{t}.\{\begin{array}{l}c\in [c_{\min },c_{\max }]\\ w\in [w_{\min },w_{\max }]\\ H\in [H_{\min },H_{\max }]\\ B\in [B_{\min },B_{\max }]\\ \alpha \in [{\alpha }_{\min },{\alpha }_{\max }]\\ \beta \in [{\beta }_{\min },{\beta }_{\max }]\end{array} \end{gathered}$$

(6)

where F(·) denotes the objective function. The chaotic time series is generated by logistic model, which is expressed by:

t_m+1 = λt_m(1 − t_m) λ∈(0, 4.0)

(7)

Adaptive mutative scale chaos optimization can be divided into 9 steps [19]:

Step 1: Give N₁ and N₂ a large positive integer. Set m = 1 and n = 1, where, n and m denote global and detailed searching times.

Step 2: Give t⁽¹⁾ = (t₁⁽¹⁾, t₂⁽¹⁾, …, t₆⁽¹⁾) a 6-dimensional random vector, and generate chaotic series t^(j+1), j = 1,…,N₁ according to the logistic model. Change t_i^(j+1) from the range (0,1) to (t_i,min, t_i,max), i = 1,2,…,6, by:

$$t_i^{\prime (j)}=t_{i,\min }+(t_{i,\max }-t_{i,\min })t_i^{(j)}$$

(8)

Step 3: Assign (t_1′⁽ⁿ⁾, t_2′⁽ⁿ⁾,…, t_6′⁽ⁿ⁾) to (c, w, H, B, α, β), and calculate Fⁿ by LS-SVM. If n equals 1, then assign Fⁿ to F^*.

Step 4: If F^* < Fⁿ, then assign Fⁿ and t_i^’(n) to F^* and t_i^*.

Step 5: Assign n + 1 to n. If n is smaller than N₁, return to Step 3. If n is larger than N₁, then generate (t^’_i,min, t^’_i,max) by:

$$\{\begin{array}{l}{t}_{i,\min }^{/}=t_i^{*}-\phi (t_{i,\max }-t_{i,\min })\\ t_{i,\max }^{/}=t_i^{*}+\phi (t_{i,\max }-t_{i,\min })\end{array}$$

(9)

where φ is in the interval of 0 and 0.5. If t^’_i,min is smaller than t_i,min, then assign t_i,min to t^’_i,min. If t^’_i,max is higher than t_i,max, then assign t_i,max to t^’_i,max.

Step 6: A new chaotic variable t^*_i can be generated by:

$$t_i^{*}=(1-{\beta }_i)\frac{t_i^{*}-t_{i,\min }^{\prime }}{t_{i,\max }^{\prime }-t_{i,\min }^{\prime }}+{\beta }_i\frac{t_i^{N_1}-t_{i,\min }^{}}{t_{i,\max }^{}-t_{i,\min }^{}}$$

(10)

where adaptive adjustment coefficient, β_i can be determined by the following equation:

$${\beta }_i=1-{\left(\frac{m-1}{m}\right)}^l$$

(11)

where l equals 2 in the present stduy.

Step 7: Assign t_i^* to t_i^(m), and give (t₁^(m), t₂^(m), …, t₆^(m)) to (c, w, H, B, α, β). Calculate Fⁿ. If m equals to 1, then assign Fⁿ to F^*.

Step 8: If F^* is smaller than Fⁿ, assign Fⁿ and t_i^(m) to F^* and t_i^*.

Step 9: Assign m + 1 to m. If m is smaller than N₂, then go to 6th step. If m equals to N₂, the optimization processes end.

4. Analysis of Results

4.1. CFD Model Validation

The open-published experimental results from Ref. [4] were used for model validation. The 25 groups of experimental data are shown in

Table 2. Experimental data vs. CFD data.

Number	c (mm)	w (mm)	H (mm)	B (mm)	α(°)	Β(°)	Cd,cal	Cd,exp
1	0.2	0.7	3	3	0	0	0.438	0.450
2	0.3	0.7	4	4	5	5	0.491	0.500
3	0.5	0.7	5	6	8	8	0.530	0.581
4	0.4	0.7	6	7	12	12	0.403	0.389
5	0.6	0.7	7	9	15	15	0.500	0.449
6	0.2	0.5	4	6	12	15	0.322	0.361
7	0.3	0.5	5	7	15	0	0.365	0.426
8	0.5	0.5	6	9	0	5	0.409	0.440
9	0.4	0.5	7	3	5	8	0.573	0.641
10	0.6	0.5	3	4	8	12	0.608	0.551
11	0.2	0.3	5	9	5	12	0.340	0.357
12	0.3	0.3	6	3	8	15	0.472	0.427
13	0.5	0.3	7	4	12	0	0.609	0.595
14	0.4	0.3	3	6	15	5	0.514	0.476
15	0.6	0.3	4	7	0	8	0.511	0.494
16	0.2	0.2	6	4	15	8	0.460	0.516
17	0.3	0.2	7	6	0	12	0.409	0.386
18	0.5	0.2	3	7	5	15	0.342	0.36
19	0.4	0.2	4	9	8	0	0.412	0.369
20	0.6	0.2	5	3	12	5	0.652	0.587
21	0.2	0.1	7	7	8	5	0.363	0.331
22	0.3	0.1	3	9	12	8	0.292	0.274
23	0.5	0.1	4	3	15	12	0.557	0.509
24	0.4	0.1	5	4	0	15	0.373	0.344
25	0.6	0.1	6	6	5	0	0.539	0.497

. Define the calculation error as:

$$error=\left|\frac{C_{d,\mathrm{cal}}-C_{d,\exp }}{C_{d,\exp }}\right|$$

(12)

where C_d,cal is the CFD calculation results and C_d,exp is the experimental results. The mean error is 7.9%, the maximum calculation error is 11.7%, and the minimum error is 1.8%. Overall, CFD calculated results agree with the experimental results well.

4.2. Surrogate Model Validation

The surrogate model is established by the support vector machine toolbox in Matlab software. In the LS-SVM model, the kernel parameter and the penalty factor affect the surrogate accuracy. In current research, these two parameters were determined by the trial-and-error method. The optimal value of the penalty factor and kernel parameter were chosen as 18 and 2.8, respectively, based on 20 groups of testing samples. The calculation error of LS-SVM was 4.31% (shown in Figure 4).

4.3. Analysis of Calculation Results from LS-SVM

The effects of fin width and seal clearance on the discharge coefficient are shown in Figure 5. Adding seal clearance led to the decrease of the jet velocity, which lowered the flow resistance and turbulence induced viscous loss [3]. Therefore, with the increase of seal clearance, the seal performance deteriorated, and the discharge coefficient increased. Adding fin width resulted in the increase of jet penetration length, which mitigated the vortex loss in the downstream cavity [20,21]. Therefore, the discharge coefficient increased with the rise of fin width. Compared with the fin width, the effect of the seal clearance on discharge coefficient is predominant.

(H = 5 mm, B = 6 mm, α = 7.5°, β = 7.5°)

Figure 6 shows the influences of fin height and pitch on the discharge coefficient. The rise of fin pitch resulted in the increase of cavity area; accordingly, vortex loss in the cavity was promoted. Therefore, as fin pitch increased, the discharge coefficient decreased. Adding the fin height promoted the vortex formation and the flow stagnation [21], and thus, the discharge coefficient decreased with the rise of fin height. Compared with the fin height, the effect of fin pitch on discharge coefficient was predominant.

(w = 0.4 mm, c = 0.4 mm, α = 7.5°, β = 7.5°)

Figure 7 shows the influences of fin forward and backward expansion angle on the discharge coefficient. As backward expansion angle increased, the cavity area decreased. Therefore, the discharge coefficient increased as the backward expansion angle increased from 0° to 12°. However, as the backward expansion angle exceeded 12°, the discharge coefficient decreased with the rise of backward expansion angle slightly. Reducing the fin forward expansion angle caused the decrease of jet expansion angle, which mitigated the vortex loss and flow stagnation loss in the subsequent downstream cavity [4]. Therefore, reducing the forward expansion angle caused the increase of discharge coefficient.

(w = 0.4 mm, c = 0.4 mm, H = 5 mm, B = 6 mm)

4.4. Optimization Processes

The labyrinth seal optimization model can be expressed by:

$$\begin{gathered} \min C_d(c,w,H,B,\alpha ,\beta ) \\ \mathrm{s}.\mathrm{t}.\{\begin{array}{l}0.2 \mathrm{mm}\le c\le 0.6 \mathrm{mm}\\ 0.1 \mathrm{mm}\le w\le 0.7 \mathrm{mm}\\ 3 \mathrm{mm}\le H\le 7 \mathrm{mm}\\ 3 \mathrm{mm}\le B\le 9 \mathrm{mm}\\ 0^{°}\le \alpha \le {15}^{°}\\ 0^{°}\le \beta \le {15}^{°}\end{array} \end{gathered}$$

(13)

Set N₁ = 4000 and N₂ = 2000, where N₁ and N₂ denote the maximum global and detailed search step, respectively. Two different optimization processes with different initial design values were performed. In the first optimization process, the initial values of c, w, H, B, α, and β were 0.4 mm, 0.7 mm, 6 mm, 7 mm, 12°, and 12°. As shown in Figure 8a, by optimization, C_d decreased from 0.403 to 0.267, and the optimal design parameters were 0.202 mm, 0.103 mm, 6.950 mm, 8.991 mm, 0.007°, and 14.994°. In the second optimization process, the initial values of c, w, H, B, α, and β were 0.5 mm, 0.3 mm, 7 mm, 4 mm, 12°, and 0°. As shown in Figure 8b, by optimization, C_d decreased from 0.509 to 0.266, and the optimal design parameters were 0.212 mm, 0.105 mm, 6.989 mm, 8.930 mm, 0.009°, and 14.989°). This illustrates that the effects of initial values on optimization results were notobvious.

Gas-velocity distributions in the flow channel are shown in Figure 9. In the cavity, vortexes with different scales were formed. After optimization, the vortex effect was promoted effectively, and this promoted the vortex loss and flow stagnation loss. Moreover, by the optimization, the seal clearance decreased, and the gas leakage was mitigated effectively. The distributions of static and total pressure along the flow direction are shown in Figure 10. The profiles of static pressure show that, as the fluid passed through different seal elements, energy conversion took place. At each throttling location, it showed a gain in kinetic energy and a reduction in static pressure. Conversely, due to the dissipation of kinetic energy, the recovery of static pressure afterwards could also be observed [1]. By the optimization, the dissipation of gas kinetic energy was enhanced and the throttling effect was promoted. The seal performance after optimization was improved effectively.

5. Conclusions

A kind of optimization method was developed for straight labyrinth seals. The discharge coefficient was considered for objective function, which is to be minimized. For the six design variables, namely, seal clearance, fin width, fin height, fin pitch, and fin backward and forward expansion angle, 72 groups of training samples and 20 groups of testing samples were generated by solving a CFD model.

The surrogate model was established by LS-SVM. The prediction of LS-SVM for discharge coefficient agreed well with the experimental data. By analyzing LS-SVM output results, some meaningful conclusions are summarized: adding fin width and seal clearance both lead to the increase of discharge coefficient; the rises of fin forward expansion angle, fin pitch, and height all result in the decrease of discharge coefficient; as the backward expansion angle of fin increases, the discharge coefficient increases firstly, and then decreases slightly.

A chaotic optimization algorithm was used for global searches. By optimization, the sealing performance was improved effectively. The optimal shape of labyrinth seals has a seal clearance of 0.2 mm, fin width of 0.1 mm, fin height of 7 mm, fin pitch of 9 mm, fin backward expansion angle of 0°, and fin forward expansion angle of 15°. It could be found that a chaotic optimization algorithm coupled with LS-SVM suggorate model is an effective tool for labyrinth-seal optimization.

In the present study, only the discharge coefficient was considered an optimization goal. In fact, windage temperature rising performance is also a very important index. THerefore, in the future, muti-goal optimization should be carried out, especially with the condition of small fin number.