Abstract
Predictive maintenance has received considerable attention in the aviation industry where costs, system availability and reliability are major concerns. In spite of recent advances, effective health monitoring and prognostics for the scheduling of condition-based maintenance operations is still very challenging. The increasing availability of maintenance and operational data along with recent progress made in machine learning has boosted the development of data-driven prognostics and health management (PHM) models. In this paper, we describe the data workflow in place at an airline for the maintenance of an aircraft system and highlight the difficulties related to a proper labelling of the health status of such systems, resulting in a poor suitability of supervised learning techniques. We focus on investigating the feasibility and the potential of semi-supervised anomaly detection methods for the health monitoring of a real aircraft system. Proposed methods are evaluated on large volumes of real sensor data from a cooling unit system on a modern wide body aircraft from a major European airline. For the sake of confidentiality, data has been anonymized and only few technical and operational details about the system had been made available. We trained several deep neural network autoencoder architectures on nominal data and used the anomaly scores to calculate a health indicator. Results suggest that high anomaly scores are correlated with identified failures in the maintenance logs. Also, some situations see an increase in the anomaly score for several flights prior to the system’s failure, which paves a natural way for early fault identification.
1. Introduction
Prognostics and health management (PHM) has drawn growing interest from industrial and academic research in the last few years, especially in sectors like aviation where profit margins are small and operational costs are critical. Aircraft availability and system reliability can be improved with effective health monitoring and prognostics. The purpose is the anticipation of system failures before their actual occurrences, as these cause major repair cost and operational disruptions. Condition monitoring is also key for optimising the scheduling of maintenance operations based on the estimated condition or remaining useful life (RUL) of the systems.
The increasing availability of large volumes of sensor data generated daily by aircraft in flight calls for technologies to make the best of recent progresses made in the field of machine learning (ML) and anomaly detection [1]. This data can be exploited by algorithms in order to extract patterns or anomalies to be linked with the degradation of the system. In PHM, data-driven approaches are particularly relevant for complex systems for which appropriate physics-based models may not exist.
In this paper, we investigate the use of anomaly detection to generate system health indicators (HI) for a fleet of a modern wide-body aircraft. We focus our analysis on a specific aircraft system, but claim that the presented methodology is generic enough to be adapted to other use cases. More precisely, our contribution includes:
- a presentation of the different sources of data available at a major airline for the maintenance of an aircraft cooling system unit. We explain the difficulties to exploit such data for health monitoring primarily due to the inherent uncertainties in the maintenance data;
- the introduction of a semi-supervised anomaly detection approach for condition monitoring based on autoencoders to extract meaningful information from a complex dataset with high uncertainty in the labelling. For the sake of confidentiality, data has been anonymized and prior knowledge about the system under study is very limited;
- the experimentation of the proposed approach with three types of autoencoders to compute the anomaly scores: a fully-connected autoencoder, a convolutional autoencoder, and a variant of a long short-term memory (LSTM) autoencoder available in the literature.
- a method to determine a health indicator from the anomaly scores by computing a threshold based on the -score metric.
- the evaluation of the autoencoders with a set of binary classification metrics by using instance weights to account for the uncertainty on the provided failure data.
We explore the feasibility and potential of an approach based on standard anomaly detection techniques and autoencoders for condition monitoring when applied to a real and complex dataset.
The results of the study show that a relatively high anomaly score usually corresponds with the periods where a failure has been expected by maintenance engineers. In some cases, we also observe an upward trend on the anomaly scores a few flights before the failure was actually detected by the maintenance operators. However, the task remains challenging because of the lack of prior system knowledge (confidentiality constraints), sensor data complexity, the lack of guarantee that available signal data are appropriate to detect a given failure and general uncertainties in the sensor and provided failure data.
The paper is organised as follows. Section 2 reviews the classical and more recent anomaly detection methods used in aviation, as well as the data-driven approaches specific to prognostics and their application to health monitoring. Section 3 describes the system under study and the different data sources available as well as the adopted approach to constitute a properly labelled dataset with failure periods. Section 4 overviews the anomaly detection approach to address data labelling uncertainty and compute the health indicator. Section 5 presents the design of the autoencoders used for anomaly detection and the alternative options tested. Section 6 describes the details of the training and testing of the autoencoders. Section 7 provides an analysis of the results and a discussion on the suitability and issues related to the use of such models for health monitoring. Lastly, Section 8 highlights the main points of the study, the implications for health monitoring and suggests some potential ideas for future work.
2. Literature Review and Background
2.1. Anomaly Detection Methods in Aviation
Autoencoder architectures can be considered as part of the recent advances in the field of neural networks and deep learning, which explains why their application to anomaly detection in aviation and PHM are still relatively limited compared to other classical approaches.
In this sub-section, we briefly review progresses made in anomaly detection applied to aviation in general, before focusing in the next subsections on data-driven methods adapted to the PHM field. For more details, the reader may refer to popular surveys in the literature on anomaly detection methods [2,3,4] including the recent advances [5] and their application to aviation [1].
Firstly, it is important to note that aviation data is challenging for several reasons: its large volume, high-dimensionality, heterogeneity (mixed categorical and continuous attributes), multi-modality (multiple modes of nominal and non-nominal operations with different types of aircraft, airports and airspaces) and temporality (long time-series). In addition, the challenge is expected to be even bigger in the future with the continuously growing number of sensor-equipped aviation systems.
Among the classical approaches for anomaly detection in aviation, Multiple Kernel Anomaly Detection (MKAD) [6] developed by NASA is still one of the state-of-the-art methods for the detection of anomalies in flight data. Based on kernel functions and One-Class Support Vector Machine (OC-SVM) [7], its computational complexity is quadratic with respect to the number of training examples. More recently, Puranik et al. [8] propose a framework based on OC-SVM to identify anomalies with the aim of improving the safety of general aviation operations.
Anomaly detection based on clustering methods (ClusterAD) are also widely applied. For instance, Li et al. [9,10] uses ClusterAD methods based on DBSCAN [11] to detect anomalies in the take-off and approach operations with datasets containing from a few hundreds to a few thousands flights. OC-SVM and ClusterAD methods have both performance issues with large datasets. ClusterAD methods have the advantage though that they can identify multiple types of flight operation patterns (different nominal operations) corresponding to the identified clusters.
As far as we know, only a few classical techniques for anomaly detection are scalable to large datasets. For instance, Oehling et al. [12] approach based on Local Outlier Probability (LoOP) [13] was applied to an airline dataset of 1.2 million flights in order to detect anomalies related to safety events.
Classical approaches such as clustering or distance-based methods like k-Nearest Neighbours (kNN) suffer from the curse of dimensionality issue when applied to high-dimensional data. The solution is often the application of a dimensionality reduction technique like principal component analysis (PCA) [14] as a preprocessing step. On the other hand, distance-based methods are computationally expensive even during the prediction phase, which makes them inappropriate for certain applications.
With large-scale high-complex data as the one generally available in aviation, deep-learning approaches are supposed to perform better than traditional machine learning methods [5]. This is because deep-learning algorithms are specifically designed to learn complex patterns in big data. A diversity of neural network models are used in deep-learning, such as the traditional Fully Connected Network (FCN), Convolutional Neural Networks (CNN) or Recurrent Neural Networks (RNN). Deep-learning architectures are based on a sequence of layers combining one or several types of such neural network models. Their goal is to progressively find a representation of the original data features which is more appropriate for tasks like classification or regression.
In the particular case of autoencoders, they are trained to find a lower-dimensional hidden representation (latent space) from which original data can be reconstructed, so they are often used as a technique for non-linear dimensionality reduction. In addition, they are suitable for anomaly detection based on the assumption that anomalies are incompressible and cannot be properly reconstructed from the lower dimensional representation of the latent variables. In the case of time-series data, autoencoders with RNN layers should be particularly adapted to exploit the temporal dependencies related to anomalies. In practice, however, they present significant limitations when applied to long sequences.
2.2. Data-Driven Approaches for Prognostics
PHM has leveraged the increasing availability of sensor data to monitor the health of complex systems. The advantage of data-driven approaches is that they generally do not require any knowledge about the failure mechanisms inherent to these systems.
Depending on the availability of time-to-failure or end-of-life data, data-driven methods for prognostics can have two types of expected outputs [15]: direct failure prediction in the form of remaining useful life (RUL) estimation, or indirect failure prediction through the calculation of health degradation indicators. The first type of output requires availability of enough historical failure cases to train a RUL estimator. In the aerospace domain, failures are very scarce which make RUL prediction challenging. This second type of results need fewer failure cases, but do require the definition of a threshold to decide on the presence of a failure. Anomaly detection for prognostics falls within this second category.
Data-driven approaches for PHM can be divided in two major categories [16,17,18]: statistical approaches (e.g., hidden Markov models, Bayesian networks, Gaussian mixture models) and neural networks approaches (e.g., autoencoders), the latter being more frequently used over the past few years.
As for the statistical approaches, in [19] a mixture of Gaussian Hidden Markov Models is presented for RUL prediction of bearings from a NASA benchmark database. Also, we can cite the work by Zhao et al. [20] to detect early anomalies in an electric generator’s multivariate sensor data, based on Pearson correlation between the sensors and vector quantization clustering.
Concerning the application of neural networks to PHM, as sensor data come naturally in the form of time series, RNN have been widely used. For instance, in [21,22] a RNN is trained for temporal feature extraction and RUL estimation. In both methods, models are trained in a supervised way on run-to-failure time series data, and test on time series data for systems that have not reached failure yet. More recently, Husebø et al. [23] propose a CNN autoencoder for feature extraction to diagnose electrical faults in induction motors.
In PHM, neural networks have also been specifically used for anomaly detection. We can mention hybrid neural network approaches such in [24], where a CNN is combined with a gated recurrent unit (GRU) RNN in order to extract spatio-temporal features from sensor data and detect anomalies in rotating machinery. Hundman et al. [25] propose an approach based on LSTM for anomaly detection in spacecraft systems in real time: the comparison between the values predicted by the LSTM and the actual data gives a reconstruction error, used as a health indicator. Non-parametric dynamic thresholding is then used to determine whether there is a failure or not and alert operations engineers.
2.3. Applications to Aircraft Systems Health Monitoring
The increasing availability of condition monitoring data for aircraft fleets has made data-driven PHM valuable for proactive maintenance of aviation systems. Thus, in [26] a non-parametric modelling technique is described to calculate the health indicator for an aircraft air conditioning system. In [27], a study is made on several feature selection techniques in combination with neural networks for RUL prediction applied to a gas turbine engine dataset.
More recently, Schwartz et al. [28] propose a method using self-organizing maps (SOMs) and kernel density estimation for fault detection and identification in aircraft jet engines. Baptista et al. [29] study the use of hybrid neural networks combining RNN layers with multi-layer perceptron (MLP) layers to estimate the RUL. The hybrid neural network is fed with statistical features computed on time series of two real-world aircraft engine datasets.
Concerning the more specific use of autoencoder-based anomaly detection with flight data, we can mention a few recent efforts. For instance, an approach based on fully-connected deep autoencoders [30] and another one based on convolutional denoising autoencoders [31] have been applied for fault detection, the first on the NASA DASHlink open database [32], and the second on a dataset of customer notification reports sent over aircraft communications addressing and reporting system (ACARS) to airlines for engine fault detection.
However, as far as we know, there is no comparative study in the literature on the use of several kinds of autoencoders for the computation of a health indicator of an aircraft system, which is the purpose of our research.
3. System and Data Description
3.1. System under Study
The aircraft system under study is a cooling unit system belonging to a modern and widely-used airliner. Each aircraft has four units installed. A pump package pumps cooling fluid sequentially through each of the 4 cooling-units. Each cooling unit consists of a compressor, condenser, flash-tank and evaporator. Depending on the required cooling capacity, one or more cooling units may be operational. By changing the priorities of the cooling unit during each flight, the aircraft attempts to spread usage equally over each of the 4 units. For most failure cases, failure starts with clogging of the cooling-units filters, which can ultimately lead to failure of the compressor. When failure on any of the cooling units internals is expected, the entire unit is replaced and sent to the maintenance-shop for repair. Early detection of a fault in the filter could avoid a costly repair of the cooling-unit’s compressor. These cooling units are not safety critical, the aircraft is allowed to depart even with all cooling-units inoperative. However, this would impose an operational limitation to the airline.
3.2. Flight and Sensor Data
The 32 GB dataset provided by the airline contains anonymous sensor and contextual data for 18,294 flights. Contextual flight data is a mix of categorical and continuous variables such as timestamp, flight identification number, tail number, flight phase, altitude, computed airspeed (CAS), airport departure and arrival. Sensitive information such as the names of the airports or the flights and tail numbers have been encrypted, and timestamps do not correspond with the real departure times as they have been shifted.
Sensor data is provided in the form of variable-length (per flight) time series of nine continuous variables sampled at 1 Hz for each of the four cooling units installed. The physical nature of the signals is unknown as the names of the parameters are encrypted. After a discussion with the airline, it was concluded that the four units could be assumed to work independently, so the number of actual samples are four times the number of flights.
Figure 1 shows the nine types of anonymised sensor signals for a healthy cooling unit system during a flight. Each of the nine subplots displays four time series representing the sensor values of the four cooling units installed in the aircraft.
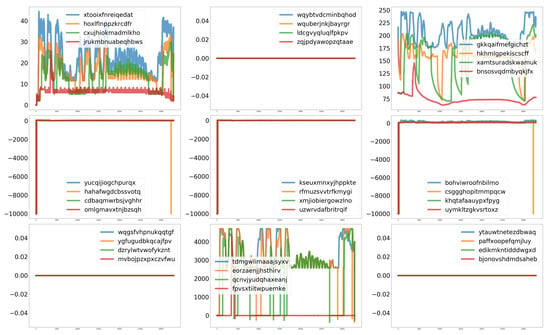
Figure 1.
Anonymous sensor data during a flight for the four healthy cooling units installed in an aircraft.
3.3. Maintenance Data
For the cooling unit, most replacements are triggered by aircraft maintenance messages (MMS). These messages are raised when a suspected deviation from nominal operation is detected by the aircraft. In the ideal case, a failure isolation procedure follows, which identifies the corrective action immediately, resulting in replacement of the cooling unit and disappearance of the MMS. In most cases however, trouble-shooting is less trivial, as these maintenance message are ’noisy’ on its own. For example, faults in various components may result in the same maintenance message, making fault isolation challenging. Furthermore, a simple re-set of a system can make the messages disappear, only to re-occur months later. In practise, the diagnostics of whether a cooling unit is faulty and need replacement comes down to the engineering judgement of the responsible specialist. When the replaced cooling-unit is inspected at the repair-shop the existence of the fault can be confirmed, but no start-date of the fault can be inferred from this inspection. This makes labelling of the data a challenge on its own. To address this problem, we make use of multiple data sources for labelling of the data:
- Removal data: list of removal dates for all replaced cooling units. For non-safety critical components such as the cooling unit, immediate corrective action after expected failure is not mandatory. Hence, removals dates do not correspond to actual failure dates.
- Aircraft technical logbook: Contains potential issues reported by the crew. This textual data is ordered by date, but the fault description is not well structured which makes it difficult to link an issue directly to cooling-unit failure.
- Central maintenance computing function (CMCF) data: system generated messages including flight deck effects (FDE) and MMS.
- Shop reports: List the condition of the internals of the cooling unit upon inspection at the component repair shop.
For labelling the data, the following approach is taken. Firstly, the dates for all unscheduled removals of the cooling unit are collected. Only removals that have resulted in disappearance of the MMS are considered. Subsequently, only those removals that were confirmed in the shop-report were considered. For these failures, the start-date of each of these failures was selected to be the first day prior to the removal, after which maintenance message appeared consistently over multiple flights. Technical specialists and predictive maintenance engineers from the airline were asked to confirm these failure dates (PM). As uncertainty about the actual failure data persisted, each failure in the PM data was tagged by the airline as either TRUE, LIKELY or DUBIOUS.
The final labelling data consists of expected failures of the cooling-unit, including: the aircraft tail number, the position of the failed cooling system unit, dates on which the failure was detected, dates on which the failure was fixed by the removal, the uncertainty tag (TRUE, LIKELY or DUBIOUS) and sometimes associated comments. The tag and comments can provide valuable information concerning the uncertainty on the actual occurrence of fault.
The airline provided the MMS as well, which might help to understand some anomalies identified by the models outside the PM failure data intervals (potential false positives). MMS and PM uncertainty tags are especially exploited when computing the performance metrics on the models (see Section 7.2).
The distribution of faults per aircraft is shown in Table 1.

Table 1.
PM and MMS fault distribution per aircraft tail number.
4. Anomaly Detection Approach
4.1. Semi-Supervised Learning
Models are trained on what we assume to be normal or healthy data, i.e., flights for which a failure has been identified are removed from the training set. Thus, our setting is the most extended variant of semi-supervised anomaly detection known as learning from positive (i.e., normal) and unlabeled examples (LPUE) [33,34].
More precisely, we removed from the training set the flights falling within the PM failure periods. However, we do not exclude the flights for which only a MMS but no confirmation of a fault exists. In addition, we removed from the training set the flights within the 20 days preceding the detection of a PM failure, where the uncertainty on the real health status of the cooling system is higher. In spite of that, the uncertainty on the labelling makes it impossible to ensure that all flights in the training set are actually healthy.
4.2. Anomaly Detection Models
Anomaly detection is based on a variety of neural networks known as autoencoders. The advantage of the autoencoders is their ability to reduce dimensionality, by automatically extracting the most significant features in a lower dimensional latent space.
Three variants of autoencoders are tested: fully-connected, convolutional and RNN autoencoders. RNN-based autoencoders are well adapted to find time-dependent patterns in the signals, which is not the case of the fully-connected and convolutional autoencoders. In addition, RNN autoencoders can accept variable-length sequences as input, whereas the other two types of autoencoders require the use sliding windows to breakdown the sequences into fixed-sized vectors.
Autoencoders output an anomaly score which is the reconstruction loss, i.e., the difference between the predicted and the actual value according to some norm (e.g., MSE, L1). Anomaly scores are assumed to increase with anomalous data “not seen” by the model, since correlations in sensor data should change because of some incipient degradation or fault. In addition, we expect the anomaly scores to present an upward trend a few flights before the system runs into failure in order to prevent its breakdown.
The architecture and characteristics of the three variants of autoencoders are further detailed in Section 5.
4.3. Anomaly Threshold
For each flight and for each cooling unit, a health indicator is produced, which is an anomaly score along with a binary health status (“healthy” or “faulty”). A flight anomaly score is the mean of the anomaly scores calculated at sensor level. For the models requiring a sliding window, we take the average of the scores computed over the sliding windows of a flight.
In order to determine the health status, we need to compute a threshold. Then, we can predict the label (“faulty” or “healthy”) of a flight depending on whether the anomaly score of the system is higher (“faulty”) or lower (“healthy”) than the threshold. The predicted label can then be compared with the real label in order to assess the performance of our model. However, the ground truth as to whether a flight is faulty or not depends on the fault information, which is uncertain for the reasons we mentioned before.
Obviously, there is a trade-off when computing the threshold. If it is set too high, some faults will be missed. If it is too low, the rate of false alarms (false positives) will become unacceptable. Selecting the optimal threshold is case-specific, as it depends on the underlying failure rate of the cooling unit, the performance of the anomaly detector, and the cost of (corrective and preventive) maintenance. After a discussion with the airline, it seems preferable to set a relative high threshold because of several reasons. Firstly, faults are rare in aviation and so they are for this cooling unit. Hence, the distribution between healthy and faulty legs is biased to healthy data. For instance, if we say only 0.1% of the flights are faulty, a model with a 100% of true positives and 1% of false positives will end up triggering 110 alerts every 10,000 flights even though only 10 alerts correspond with a real fault. Secondly, too many false alarms would outweigh the benefit of cheaper preventive repairs, and may require more units to be held in stock. Finally, a low rate of false positives is necessary if we want our prognostic alerts to be trusted and accepted by the maintenance operators. This requires that at least between 65% or 70% of the total alarms are true (precision).
The methodology to determine the threshold is described in Section 7.2.
5. Autoencoder Models
We have implemented three different autoencoders solutions which are described in the following three subsections. Although we did perform some testing with other variants in order to select the presented architectures, the objective was not to find the most optimized one in terms of layers, units per layer, activation functions and so on. The goal was to come up with three reasonable models for comparison, each one representing a different approach to autoencoders: fully-connected, convolutional-based and LSTM-based autoencoders.
5.1. Fully-Connected Autoencoder (FCAE)
The FCAE used in this paper is a multi-layered neural network with an input layer, multiple hidden layers and an output layer (see Figure 2). Each layer can have a different number of neural units and each unit in a layer is connected with every other one in the next layer. For this reason we call it here fully-connected, although in the literature it is usually refer to as autoencoder (AE), or to emphasise the multi-layer architecture aspect, as deep autoencoder (DAE) or stacked autoencoder (SAE). In all cases, an autoencoder performs two functions in a row: encoding and decoding.

Figure 2.
FCAE with multiple stacked layers.
The encoding function maps the input data to a hidden representation where and are respectively the weight matrix and the bias vector and is a non linear activation function such as the sigmoid or ReLU functions. The decoding function maps the hidden representation back to the original input space according to , being most of the time the same activation function.
The objective of the autoencoder model is to minimise the error of the reconstructed result:
where is a loss function determined according to the input range, typically the mean squared error (MSE) loss:
where u is the vector of observation, v the reconstructed vector and n the number of available samples indexed by variable i.
The proposed FCAE architecture is described in Table 2. We use three blocks of layers both in the encoder and decoder, which have a symmetric structure in terms of number of neural units per layer. The output shape refers to the shape of the tensors after the layers have been applied, where , and refers respectively to the the batch size, (sliding) window length and number of features. The layer dimensions are defined as , and .

Table 2.
Fully-Connected Autoencoder (FCAE) architecture.
The encoder Enc1 and Enc2 are blocks made up of pairs of Linear and ReLU activation layers. The input encodings (bottleneck with dimension ) are the result of Enc3. As a mirror of the encoder, the decoder has also two blocks (Dec1 and Dec2) both combining Linear and ReLU layers. The last decoding block (Dec3) is made up of a Linear layer with a Sigmoid activation as FCAE outputs are expected to be in the range of 0 to 1 (features are min-max scaled). A ReLU rather than a Sigmoid activation is used in all the other layers as it presents theoretical advantages such as sparsity and a minor likelihood of vanishing gradient resulting in faster learning.
5.2. Convolutional Autoencoder (CAE)
Table 3 shows the CAE architecture proposed in this paper. It is inspired from the one in [23], which has been applied with good results for anomaly detection in time series data. The proposed CAE is a variant of the FCAE where fully-connected and convolutional layers are mixed in the encoder and decoder. Like the FCAE, the decoder structure is kind of a mirrored version of the encoder.

Table 3.
Convolutional autoencoder (CAE) architecture.
Table 3 shows also the shape of the input and output tensors in each layer, where and refers to batch size and number of features respectively. The input is three-dimensional, where the last dimension is the (sliding) window size (30) and the second dimension is the number of channels which in our case are the features (). Unlike a FCAE, a change in the size of the input window may involve substantial parameter adaptation, because of the symmetric structure of the autoencoder and the nature of convolutional layers.
The first three layers of the encoder (Conv1 to Conv3) and the last three ones of the decoder (ConvTransp1 to ConvTransp3) are convolutional, whereas the innermost layers are fully-connected. Conv1d(ic, oc, k, s, p) (and its transpose Conv1DTransp(ic, oc, k, s, p, op)) denotes a convolutional (deconvolutional) layer with and channels, kernel size k, stride s and padding p and output padding . Please note that dimensionality reduction is achieved by using a rather than by using pooling layers [35].
All convolutional layers are followed by BatchNorm layers [36] to normalise the inputs to the activation layers. ReLU is used as the activation layer everywhere except for the last one in the decoder (ConvTransp3) where a Sigmoid has been used instead for the same reasons stated with the FCAE.
We tested other alternative options for the activation functions, such as using SELU everywhere (with appropriate LeCun normal initialisation of weights), or Sigmoid in the dense layers and ReLU in the convolutional ones as in [23]. However, the results were worse and these options were abandoned.
5.3. LSTM Autoencoder (LSTMAE)
The blocks of the two autoencoders previously introduced are made up of either dense or convolutional layers, which makes necessary the use of sliding windows to provide them with fixed-sized input vectors. In this subsection, we introduce the LSTM autoencoders (LSTMAE), where layers consist of Long Short-Term Memory (LSTM) neural networks allowing for input sequences to be of variable length.
A LSTM is a type of RNN widely used for sequential data processing, since it can learn temporal dependencies over longer sequences than a simple RNN. For our particular purpose, a LSTMAE presents a theoretical advantage: samples can be entire flights instead of sliding windows, and anomaly scores can be calculated for the flight as a whole rather than by aggregating window anomaly scores.
In the literature, there have been a few efforts to implement a LSTMAE. For instance, Malhotra et al. [37] introduced the model in Figure 3 for anomaly detection in time series data.

Figure 3.
LSTM autoencoder by Malhotra et al. [37].
In this architecture, the encoder and the decoder are both LSTM networks. The last hidden state of the encoder is passed as the initial hidden state to the decoder. Then, at every instant t, the decoder takes as input the reconstruction of the previous instant obtained by linear transformation of the hidden state computed by the decoder cell.
Srivastava et al. [38] introduced the LSTMAE architecture shown in Figure 4, which combines input reconstruction with future prediction in order to achieve a better hidden representation. Reconstruction is operated in reversed order as the last hidden state of the input sequence contains better information about the short-term correlations which should improve the reconstruction of the beginning of the sequence in reversed order.

Figure 4.
LSTM autoencoder by Srivastava et al. [38].
The authors reported good results in both papers. However, Malhotra’s LSTMAE is mostly applied to short univariate time series of around 30 points, or several hundred points in the case of periodic series. As for Srivastava’s, good results are also reported with short video sequences (although of very high dimensions) by using high-dimensional hidden state vectors of size 2048 or even 4096.
We tested both LSTMAE architectures with our data and reconstructions were in general of poor quality, even with large latent spaces and after dimensionality reduction with severe signal downsampling and PCA. The intuition is these methods do not scale well when applied to our time series, which can reach several thousand points in long-haul flights. This could be explained by the fact that the hidden representation has not enough capacity to allow for a good reconstruction of a long and multivariate input sequence.
Pereira et al. [39] mentioned this issue with long sequences and propose an attention-based mechanism to help the decoder. The resulting architecture is however highly complex, so we decided instead to work on a variant of the LSTMAE architectures by Malhotra and Srivastava. The goal is to test whether such an architecture could be good enough for our data when combined with appropriate dimensionality reduction.
The proposed LSTMAE architecture is depicted in Figure 5. Two encoders and two decoders are introduced to improve the reconstruction of long sequences, in particular the beginning and the end of the input sequence, where signal variation is very significant.
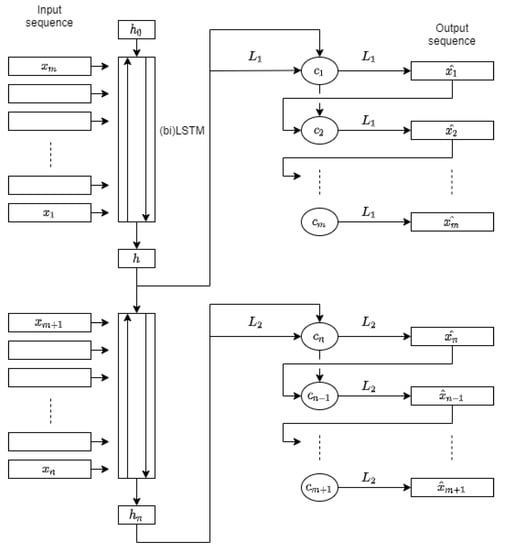
Figure 5.
LSTM autoencoder proposal.
The input sequence of length n is split in half, where each () is a vector of size (the number of features). In Figure 5, each encoder is represented by a rectangular block of multiple LSTM cells, where h and are the last hidden state vectors output respectively by the top and bottom encoder. As for the decoders, they are both represented on the right side. The two sequences of small circles are the LSTM cells of the decoders. Each outputs a hidden state vector computed from the reconstruction and the hidden state of the previous decoder step. The dimensions of all hidden states of the two encoders and decoders have been set to 80.
The top LSTM encoder receives the first half of the input in reversed order and computes latent representation h which is fed to the top decoder. The bottom encoder receives h and the second half of the input sequence in the original order and outputs the hidden representation . The top decoder takes h and linear transformation to feed cell state . The rest of the cell states () hidden states are computed from previous hidden state and reconstruction . The first half of the output sequence is obtained by linear transformation of the cell hidden states.
The inputs of the bottom LSTM encoder block are h and the second half of the input sequence in the original order, and its output the hidden state . The bottom decoder decodes the sequence in reversed order, and takes as inputs and linear transformation to output hidden state. The rest of the cell hidden states for () are computed from hidden state and . The second half of the output sequence is obtained by linear transformation of the cell hidden states and needs to be reversed.
6. Model Training and Testing
6.1. Dataset Preparation
After studying the distribution of flight durations, we excluded from the dataset the flights with a duration of less than two hours (952 flights). These flights correspond to shorter legs in case the aircraft flies multiple legs in a single flight-segment. The goal was to reduce variability on operational conditions and focus the study on medium and long-haul flights, i.e., the main operating mode for the fleet under study. 139 flights with NaN values in sensor data were also removed. The NaN were present in the readings of sensors 2, 7 and 9 for the whole duration of the flights, since these sensors were not operational yet for these flights according to the airline.
Also, we noticed in some cases the presence of −9999 values recorded for practically the whole duration of a flight. These outlier values appeared simultaneously in several sensors and often for the four system units. This occurred independently of the real health status of the concerned cooling units due to a failure in a higher level system upstream of the cooling unit. In total, 207 flights were identified and removed from the dataset.
In order to reduce the dimensionality of sensor data, we generated several datasets by downsampling the original 1 Hz sensor data to lower rates such as Hz, Hz and Hz. The last two sampling rates were tested only with the LSTMAE as a way to mitigate the LSTM limitations with long sequences. Also, like Malhotra et al. [37], we apply an additional linear dimensionality reduction technique (PCA), as an optional pre-processing step when using LSTMAE.
Figure 6 shows the variance ratio explained by the three first components, which reaches 99% no matter the sampling rate used to generate the dataset.

Figure 6.
PCA—Variance ratio explained vs number of features.
Sliding windows were also generated for the FCAE and CAE models which need fixed-length sequences as inputs. After a few preliminary tests were done with different windows lengths and steps, we finally chose to apply 30-point-long and 20-step sliding windows (10 overlapping points).
Following the cleaning and re-sampling, we create a test set () by selecting a subset of six tails with a significant number of failures, which accounts for about 20% of data. The 80% of data left is split into what we assume to be healthy and faulty data. Around 80% of healthy data is used as training set (), and the 20% left as validation set () for early-stopping. A second validation set () is created with the remaining faulty data, which is combined with to set the anomaly threshold (see Section 7.2).
Finally, we calculate the max and min values for each feature in the training set in order to perform feature max-min scaling in all of the datasets.
In Table 4 we show the sample distribution per dataset type as well as in terms of health status (healthy vs faulty). Please note that there are four samples for each flight in the dataset, i.e., one for each system unit. When using sliding windows, the number of samples is much higher (see Table 5) and sample distribution can be slightly different as NaN filtering is performed at window rather than at flight level.

Table 4.
Cooling unit dataset.

Table 5.
Cooling unit dataset with 30-20 sliding windows.
6.2. Model Training
Several runs were planned to test some combinations of models, training datasets and hyper-parameters. In particular, several experiments are defined to test the LSTMAE with different sampling rates as well as with and without PCA.
The batch size is set to 200 samples for LSTMAE and 20,000 samples for the FCAE and CAE. This is to take into account the fact that LSTMAE takes as input long time series corresponding with full flights (it can be several thousand points), whereas the other two models take windows of reduced size (30 points).
LSTM can be hard to train [40], especially with long input sequences of more of a thousand points for a long-haul flight with Hz sampling rate. To avoid the issue of unstable training linked to exploding gradients, we apply gradient norm clipping set to during the training of LSTMAE models. In addition, we use the truncated back-propagation through time (TBTT) technique [41]: input sequences are split into chunks of 200 time-steps for both the forward and backward-pass.
To avoid overfitting, the number of training epochs is controlled via an early-stopping mechanism and the validation dataset. Early-stopping is setup to monitor the validation loss and halts the training process after 10 consecutive training epochs with no improvement of the validation loss.
The model parameters are optimised with Adam algorithm [42] to minimise the MSE loss with a learning rate set to 1 × 10−3.
Table 6 lists the subset of the runs for further analysis in Section 7. Other runs were performed to test a few architectural options (see Section 5), but resulted in overall worse performance in terms of the metrics defined in Section 7.2. Hence, we dropped them to limit the study to the best candidate model found per autoencoder category. In the case of LSTMAE models, we included several runs to test the impact of several pre-processing options (the use of PCA and sampling rate).

Table 6.
Runs performed with the number of epochs.
The name of each run indicates: (1) the model used (fcae, cae, lstmae), (2) whether PCA features (pca) are used instead of the original ones, (3) the length and step used for the sliding windows (30_20) for FCAE and AE models, (4) the resampling rate (e.g., 10 means Hz). The epochs shown are the effective number of epochs as controlled by the early stopping mechanism with the maximum number of epochs set to 120.
6.3. Model Testing
During the testing phase, trained models are used to output the anomaly scores for all the samples. Then, we set an anomaly threshold based on the scores in the validation dataset, which allows for the calculation of the performance metrics on the test set.
Figure 7 plots the anomaly score distribution per dataset type as calculated with a CAE model. You can see as the anomaly scores for the datasets with faulty data are distributed differently from the ones with normal data: faulty data present a higher density for the highest anomaly scores.

Figure 7.
Anomaly score distribution with a LSTMAE obtained with a CAE model.
In order to calculate the metrics commonly used to evaluate the performance of binary classifiers, we need first to set a threshold . A flight is faulty if and healthy otherwise, where is the anomaly score of a system unit.
is calculated by maximizing -score:
According to the parameter and the precision and recall values computed for a set of possible thresholds over the merge of the two validation sets and .
We can observe the trade-off between precision and recall in Figure 8, which plots the precision-recall curve for a run with a LSTMAE. For the reasons explained in Section 4.3, maximising the precision is the priority which means to choose a . For the sake of comparison, we will set to compute the threshold as well as the related performance metrics.

Figure 8.
Precision-Recall curve for threshold setting.
Once the threshold is set, models can be evaluated with the test set by using classical performance metrics such as precision, recall and -score. In addition to the classification performance metrics, we calculate the rate of flights predicted as faulty five days before the fault was actually identified in the maintenance checks (pbfr). This metric is to measure the predictive ability of the models to anticipate a fault, which highly depends on whether a “degradation signature” is actually present or not in the signals.
To take fault data uncertainty into account when calculating the performance metrics, we give a weight between 0 and 1 to each sample based on the level of confidence on its real label. Please note that by sample here we mean a system unit per flight (not a sliding window).
Table 7 describes more precisely the rules for sample allocation of health status label and uncertainty weights. We allocate zero weight to samples for the 20 days prior to the identification of a fault or for which we have an associated MMS, since their real health status is in fact unknown. On the other hand, we set a high weight for the flights where the fault has been labelled as TRUE or LIKELY by the airline. For the vast majority of cases (Rest category in Table 7), we assume they are mostly healthy with a weight of 0.85.

Table 7.
Rules on sample allocation of health status label and weight.
7. Results and Discussion
7.1. Training and Validation Losses
Before analysing the performance metrics in the next section, it is worth looking at what happened during the learning process in terms of the evolution of the reconstruction losses. This should help understand the models ability to learn to reconstruct what we consider normal data. By analysing the training and validation curves, we can also check whether there are cases of models overfitting or underfitting the data.
The x-axis in the loss plots represents the step in the training and validation set (i.e., an iteration with a forward and backward pass of a batch of samples) and y-axis is the MSE loss. The left subplots display the evolution of the loss for the training set () and the right ones for the validation one ().
Figure 9 shows the training and validation curves for the FCAE and CAE models. We can observe that convergence of both losses is reached pretty early by the two models. Loss decreasing is smooth in all cases except for a slight fluctuation of the validation loss of the CAE model. Based on these observations, there is no evidence of either model overfitting or underfitting.

Figure 9.
FCAE and CAE—Reconstruction loss (MSE) for the training (left) and validation (right) sets.
Figure 10 shows the training and validation curves for the LSTMAE models trained with the original nine features. The training loss is very noisy for the three runs, although a downwards trend (orange curve) can still be observed in the three cases. The periodic fluctuations in the training loss is a sign of instability in the batch gradient descent caused by the variety of batches containing each one a different subset of flights. The high volatility is also symptomatic of the difficulty for our LSTMAE models to learn from long-sequences, in spite of our design with a double LSTM encoder/decoder and the application of training techniques such as gradient clipping to avoid gradient vanishing or exploding. A smoother downward trend can be observed in the three validation losses. In conclusion, there is no evidence of overfitting, but we cannot completely rule out a certain degree of model underfitting based on the shape of the training losses.

Figure 10.
LSTMAE trained with the nine original features—Reconstruction loss (MSE) for the training (left) and validation (right) sets.
The losses for the LSTMAE trained with PCA are plotted in Figure 11. The training loss curve is again fluctuating but still headed downwards. However, in the last two plots there is a change of trend with an increase of the training and validation losses towards the end. The increases in the validation losses certainly triggered the early-stopping mechanism to halt the training process in order to avoid overfitting. The validation losses for the two last plots are also far less smooth when compared to the ones for the LSTMAE models trained with the original features. If overfitting has been prevented by early-stopping even in the most evident case of lstmae_pca_30, we cannot rule out by looking at the training curve the possibility of a certain degree of underfitting.
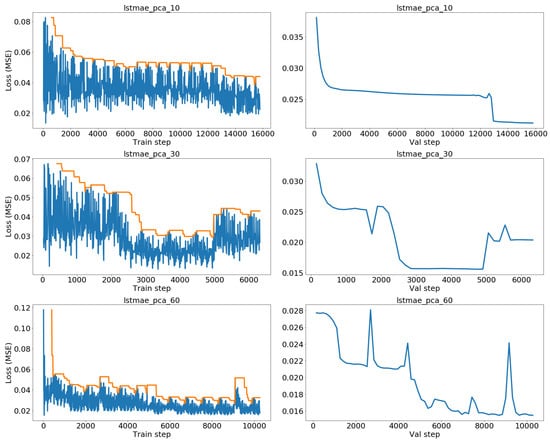
Figure 11.
LSTMAE trained with PCA—Reconstruction loss (MSE) for the training (left) and validation (right) sets.
7.2. Performance Metrics
Table 8 lists the resulting performance metrics for the runs sorted out by the auc_pr (area under precision-recall curve) metric and -score computed with .

Table 8.
Performance metrics.
In terms of -score and precision only, CAE and FCAE models gets the top results. However, when considering other metrics like recall or pbfr, LSTMAE presents a more balanced overall performance in most of the runs, especially in lstmae_pca_10.
LSTMAE performance is highly sensitive to the combination of sampling rate and PCA. The best precision and -score for LSTMAE models is practically always reached with PCA. On the other hand, the higher the sampling rate the better the auc_pr metric is when using PCA.
In general, but particularly with FCAE and CAE models, recall is low, even though it could be increased with a higher by sacrificing part of the precision. Depending on the shape of the precision-recall curve, an increase of recall (even small) is not always possible without a significant drop of precision. In that sense, the relatively low auc_pr of FCAE and CAE models is not a good sign.
The evaluated autoencoders can correctly identify the health status of the flights in the test set with a level of precision higher than the goal of 65% discussed in Section 4.3. Although FCAE and CAE precision is the highest, both models tend to reconstruct some of the anomalies in the test set which results in a high rate of false negatives and low recall (further analysis provided in Section 7.4). The added complexity of a CAE compared to a FCAE does not translate into any performance improvement. LSTMAE models are more balanced in terms of precision and recall and overall superior when considering auc_pr and pbfr. Based on the auc_pr metric, which offers a good comparison between different models on a binary classification problems with an imbalanced dataset as in our case, we recommend using lstmae_pca_10 model.
As for the choice of sensors and features, apart from recommending the use of the PCA features and a sample rate of Hz for the LSTMAE model, the analysis in Section 7.6 points out the relevance of sensors 2, 3 and 9 and the insignificance of the others as fault precursors. It would be interesting to evaluate the models again with only these three sensors. Concerning the parameters of the sliding windows for the FCAE and CAE, more tests are required to assess the sensitivity of the models to their length and step. It is however not straightforward in the case of the CAE to perform such tests as the design needs to be adapted each time we change the sliding window length.
7.3. Signal Reconstruction
The main assumption when using autoencoders for anomaly detection is that after being trained with mostly normal data, they should be able to reconstruct healthy data better than faulty one.
FCAE and CAE models produce reconstructions of similar quality. Figure 12 illustrates this principle with an example of signal reconstruction for 4 sensors by a FCAE of both a healthy (left) and a faulty (right) cooling unit during two flights of aircraft tjyjdtaf. We can see that reconstruction is indeed better for the healthy than the faulty system, which results in a correct identification of their health status.

Figure 12.
Signal reconstruction examples with a FCAE of two flights from tail tjyjdtaf. On the left, good reconstruction for a healthy cooling unit. On the right, bad reconstruction for a faulty cooling unit.
As for the LSTMAE (see Figure 13), in spite of reconstructions following the original signal trend, they are very smooth even with the dataset generated with a sample rate of Hz. As high-frequency components of the signals are ignored, LSTMAE performance is worse than the one of the FCAE and CAE models in terms of -score and precision (see Table 8). However, LSTMAE overall performance is more balanced in general as discussed in Section 7.2, and the HI produced correlates well with some of the failures (see Section 7.5).

Figure 13.
LSTMAE signal reconstruction examples (run lstmae_pca_10) of the same two flights and sensors from Figure 12.
7.4. False Negative and False Positive Analysis
Unfortunately, we have cases where faulty signals are correctly reconstructed (false negatives) and healthy signals are not (false positives). Thus, it can be interesting to look at the loss signatures to analyse which sensor contributes the most to the different cases. The spider plots represent the contribution to the reconstruction loss per sensor for the different cases and models.
Figure 14 shows the average loss per sensor as generated by a FCAE for each of the four cooling units. We plot on top the contribution of each sensor in the true positive cases, and in the bottom those of the false negatives. A first observation is that not all faulty cooling units (true positives) present exactly the same loss signature, so there are some differences in the way they fail. A second observation is that in the false negative cases, the model is able to reconstruct the signals better that it should have done, including sensor 9 (units 1, 3, 4) as well as sensors 5 and 6 (unit 2), which are the main contributors in the case of the true positives.

Figure 14.
FCAE loss signatures per cooling unit for the true positive cases (top) and the false negatives (bottom).
Figure 15 shows the plots for the cases where healthy flights are correctly classified (true negatives) or wrongly classified as faulty (false positives). For the true negatives, sensor 9 signals are the ones being reconstructed the worst, although its loss value is still relatively low enough. For the false positives, the situation is more complex as several sensors contribute to the misclassification. Furthermore, each unit has a different false positive signature, although the ones in unit 1 and 3 are close. Sensor 9 is in all cases the major contributor to false positives.
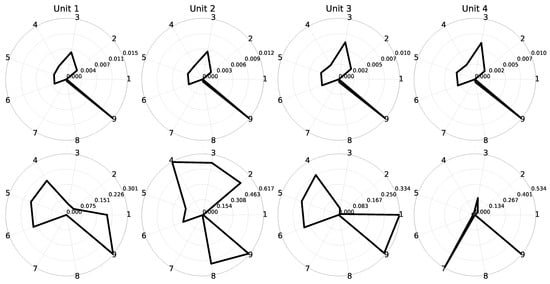
Figure 15.
FCAE loss signatures per cooling unit for the true negative cases (top) and the false positives (bottom).
However, we noticed that loss signatures are model dependent. For instance, we can see in Figure 16 how the false negatives and false positive loss signatures for a LSTMAE (run lstmae_pca_10) can be significantly different from the FCAE ones.

Figure 16.
LSTMAE loss signatures per cooling unit for false negatives (top) and false positives (bottom).
After analysis with the help of the airline, false negatives can be generally explained by weak or short-lived faulty signatures. Even for the airline experts, it was difficult sometimes to detect a clear faulty signature when looking at some of the signal plots. Another explanation could be the uncertainty on the labelling of health status, especially for the flights with incipient faults in the beginning of the failure period. This is however not always the case as it can be observed in the HI plots in Section 7.5. Finally, we noticed false negatives are less frequent for the flights where there is a corresponding MMS.
On the other hand, we have not found an enough degree of similarity in the signatures generated by the different models as to hold a specific subset of sensors responsible for the false positives. Noisy data could have been then a clear cause, such as a malfunction in an external system impacting the operation of the cooling system and changing signal correlations. Whereas noise can still be one of the issues, false positives can also be linked to model shortcomings in discriminating certain cases. Also, a subset of the false positives are repeating in almost every run, which indicates that for some reason correlations in the sensor signals in these cases must be significantly different from the ones found in healthy signals. Finally, some of the false positives are correlated with the presence of MMS (see example in Section 7.5), which indicates the detection of some abnormal behaviour on the system.
7.5. Health Indicator: Correlation with PM Faults and MMS
In this section, we analyse whether high anomaly scores and predicted failure health status correspond well with the periods where a fault has been identified. For that, we plot the HI showing the anomaly score per flight and system unit along with the failure periods. Due to the size of the figures, we present only the plots for two of the tails in the test set. The anomaly scores in the plots has been generated with a LSTMAE model (run lstmae_pca_10).
Figure 17 shows the HI for the tail enwslczm. There are four plots, each one representing one of the four system units. The blue horizontal line is the average HI for healthy data and the red horizontal line is the anomaly threshold . On top of each plot, the coloured bars show the PM failure periods: TRUE faults in red and LIKELY faults in orange. The blue little ticks underneath the bars represent the MMS, whereas the vertical lines represent the anomaly scores for a system unit computed over a flight. Health status is determined from the anomaly scores and threshold: red for the faulty flights () and green otherwise.

Figure 17.
HI computed for the test tail enwslczm.
The long TRUE failure period in unit 1 has many flights properly identified as faulty. However, for the LIKELY failure period that follows, no flights are identified as faulty. In unit 3, only four flights are faulty for the LIKELY fault period. These two LIKELY cases are examples of fault uncertainty, which makes it difficult to ascertain whether the model predictions are correct.
Another observation is that for the long failure period in unit 1, some of the anomaly scores can be high in spite of the lack of an associated MMS. We have noticed this happening for other failure periods in other tails, which drew the attention of the airline as it shows our anomaly detection can be complementary to the one currently implemented in the aircraft.
Figure 18 plots the HI for another tail in the test set (tjyjdtaf). The second fault in unit 4 is well identified, with all corresponding flights in the period being predicted as faulty. Unfortunately, this is not at all the case for the shorter failure periods in units 3 and 4, in spite of the anomaly scores being relatively high and close to the threshold. The shorter LIKELY fault period in unit 1 is also well identified. In unit 2, there are a few MMS and no confirmed PM faults. It can be observed that some of the MMS correlate sometimes with high anomaly scores, which seems to indicates there was some issue with the system identified by the aircraft and reflected in sensor data. Finally, we can see a few isolated red anomaly peaks in units 1, 2 and 3 with no corresponding MMS or fault, which are fault positives.

Figure 18.
HI computed for the test tail tjyjdtaf.
7.6. Fault Anticipation
In addition for our models to be able to properly discriminate healthy from faulty data, we would like them to anticipate the occurrence of a fault. Ideally, any incipient degradation present in the signals should translate into a progressively higher anomaly score for the few flights preceding the start of a failure period. Of course, such capability ultimately depends on whether a degradation signature actually exists in the sensor signals.
Figure 19 shows the evolution of the anomaly scores for the last 40 flights before a cooling unit runs into failure as computed in run lstmae_pca_10. We plot only the subset of faults tagged as TRUE and concerning the tails in the test set. Each plot shows the rolling average of both the anomaly score per sensor and the aggregated mean loss (thick blue line).

Figure 19.
Run-to-failure computed in run lstmae_pca_10 for the test tails.
In general, the average loss is rather flat except for the last plot (fault_id = 28), where the upward trend is the most visible by far. Sensors 2, 3 and sometimes 9 are the main contributors to the increasing trend, whereas the rest of the sensors play a minor role and remain mostly flat except in the last plot. The characteristics of the anomaly score slopes are highly dependent on the fault and seem to indicate different degradation signatures probably corresponding to different failure modes.
Although an upward trend in the anomaly scores of some sensors can be observed for most of the faults, the prediction of a fault occurrence seems difficult as dynamics are different from one case to another. The limited number of faults in the dataset and the lack of knowledge on the failure modes make the task very challenging. However, what these plots do seem to reveal is the importance of sensors 2, 3 and 9 and the insignificance of the others as fault precursors when using a LSTMAE. These same subset of sensors are also the main contributors to the loss signatures of a LSTMAE (see Figure 16).
8. Conclusions
In this study, we illustrated the difficulties in extracting meaningful information for health monitoring, by exploiting real raw sensor and maintenance data provided by an airline. We focused on a specific example with the cooling unit system of a modern wide body aircraft. Determining the ground truth on the real health status of the aircraft systems is an arduous task: the labelling of data is uncertain and the use of supervised ML techniques unfitted.
In this context, we investigated the potential of a semi-supervised anomaly detection framework: we evaluated three different autoencoder architectures to assess whether such approach is viable with a complex system such as the cooling unit system. The training and the proper evaluation of the models have proven to be challenging because of the uncertainty in the ground truth and the lack of prior knowledge on the system. In the end, the proposed approach provided useful insights for condition monitoring in spite of uncertain and noisy data.
High anomaly scores and faulty status detected by our models matched periods where a fault had been identified. Further, our metrics (the health indicator) were able to correctly detect faulty flights which were not identified as such by the on-board detection systems, with a clear upward trend before a failure occurs in some situations. This approach opens promising perspectives, and would be appreciated as a complement to the existing certified aircraft fault detection systems. Alongside other information sources such as MMS, the health indicator can help the airline maintenance team with more efficient diagnostics. Although the different dynamics in the evolution of the anomaly curves do not make their use very straightforward for fault prediction, they can be of great value for monitoring the rate of degradation, anticipating an impending failure and scheduling a preventive replacement at a convenient time-slot.
Future research works include a thorough finetuning of hyper-parameters and autoencoder architectures and a better understanding of the trends in resulting anomaly scores depending on the physics of the system; this would bring the approach to a higher technology readiness level, which falls beyond the scope of our current study. Further, as LSTMAE and RNN-based autoencoders seems unfitted for such long time series, attention-based mechanisms [43] or transformer architectures [44] could be a powerful tool to cope with longer intra-flight or even inter-flight temporal dependencies.
In spite of the mentioned shortcomings pointed out in our study, we have shown the potential of our proposed approach and its value to monitor the health of an aircraft fleet.
Author Contributions
Conceptualization, L.B.; methodology, L.B., P.B. and X.O.; software, L.B., P.B. and X.O.; validation, L.B., X.O. and F.F.; formal analysis, L.B., X.O. and P.B.; investigation, L.B., X.O. and P.B.; resources, L.B., X.O., P.B. and F.F.; data curation, L.B. and F.F.; writing—original draft preparation, L.B.; writing—review and editing, L.B., X.O., P.B. and F.F.; visualization, L.B.; supervision, L.B.; project administration, X.O.; funding acquisition, X.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 769288.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACARS | Aircraft Communications Addressing and Reporting System |
| AE | Autoencoder |
| CAE | Convolutional Autoencoder |
| CMCF | Central Maintenance Computing Function |
| CNN | Convolutional Neural Network |
| FDE | Flight Deck Effects |
| GRU | Gated Recurrent Unit |
| HI | Health Indicator |
| LSTM | Long-Short Term Memory |
| LSTMAE | Long-Short Term Memory Autoencoder |
| MMS | Maintenance Messages |
| MSE | Mean Square Error |
| PCA | Principal Component Analysis |
| PHM | Prognostics and Health Management |
| PM | Predictive Maintenance |
| RNN | Recurrent Neural Networks |
| RUL | Remaining Useful Life |
References
- Basora, L.; Olive, X.; Dubot, T. Recent Advances in Anomaly Detection Methods Applied to Aviation. Aerospace 2019, 6, 117. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41. [Google Scholar] [CrossRef]
- Pimentel, M.A.; Clifton, D.A.; Clifton, L.; Tarassenko, L. A review of novelty detection. Signal Process. 2014, 99, 215–249. [Google Scholar] [CrossRef]
- Agrawal, S.; Agrawal, J. Survey on Anomaly Detection using Data Mining Techniques. Procedia Comput. Sci. 2015, 60, 708–713. [Google Scholar] [CrossRef]
- Chalapathy, R.; Chawla, S. Deep Learning for Anomaly Detection: A Survey. arXiv 2019, arXiv:1901.03407. [Google Scholar]
- Das, S.; Matthews, B.L.; Srivastava, A.N.; Oza, N.C. Multiple kernel learning for heterogeneous anomaly detection: Algorithm and aviation safety case study. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010; pp. 47–56. [Google Scholar]
- Schölkopf, B.; Williamson, R.C.; Smola, A.J.; Shawe-Taylor, J.; Platt, J.C. Support vector method for novelty detection. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 29 November–4 December 1999; pp. 582–588. [Google Scholar]
- Puranik, T.G.; Mavris, D.N. Anomaly Detection in General-Aviation Operations Using Energy Metrics and Flight-Data Records. J. Aerosp. Inf. Syst. 2017, 15, 22–36. [Google Scholar] [CrossRef]
- Li, L.; Gariel, M.; Hansman, R.J.; Palacios, R. Anomaly detection in onboard-recorded flight data using cluster analysis. In Proceedings of the 2011 IEEE/AIAA 30th Digital Avionics Systems Conference, Seattle, WA, USA, 16–20 October 2011. [Google Scholar]
- Li, L.; Das, S.; John Hansman, R.; Palacios, R.; Srivastava, A.N. Analysis of flight data using clustering techniques for detecting abnormal operations. J. Aerosp. Inf. Syst. 2015, 12, 587–598. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Oehling, J.; Barry, D.J. Using machine learning methods in airline flight data monitoring to generate new operational safety knowledge from existing data. Saf. Sci. 2019, 114, 89–104. [Google Scholar] [CrossRef]
- Kriegel, H.P.; Kröger, P.; Schubert, E.; Zimek, A. LoOP: Local outlier probabilities. In Proceedings of the 18th ACM Conference on Information and Knowledge Management, Hong Kong, China, 2–6 November 2009; pp. 1649–1652. [Google Scholar]
- Jolliffe, I.T. Principal Component Analysis; Springer Series in Statistics; Springer: New York, NY, USA, 1986. [Google Scholar] [CrossRef]
- Baptista, M.; de Medeiros, I.P.; Malere, J.P.; Nascimento, C., Jr.; Prendinger, H.; Henriques, E.M. Comparative case study of life usage and data-driven prognostics techniques using aircraft fault messages. Comput. Ind. 2017, 86, 1–14. [Google Scholar] [CrossRef]
- Xiongzi, C.; Jinsong, Y.; Diyin, T.; Yingxun, W. Remaining useful life prognostic estimation for aircraft subsystems or components: A review. In Proceedings of the IEEE 2011 10th International Conference on Electronic Measurement & Instruments, Chengdu, China, 16–19 August 2011; Volume 2, pp. 94–98. [Google Scholar]
- Si, X.S.; Wang, W.; Hu, C.H.; Zhou, D.H. Remaining useful life estimation–a review on the statistical data driven approaches. Eur. J. Oper. Res. 2011, 213, 1–14. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Tobon-Mejia, D.A.; Medjaher, K.; Zerhouni, N.; Tripot, G. A data-driven failure prognostics method based on mixture of Gaussians hidden Markov models. IEEE Trans. Reliab. 2012, 61, 491–503. [Google Scholar] [CrossRef]
- Zhao, P.; Kurihara, M.; Tanaka, J.; Noda, T.; Chikuma, S.; Suzuki, T. Advanced correlation-based anomaly detection method for predictive maintenance. In Proceedings of the 2017 IEEE International Conference on Prognostics and Health Management (ICPHM), Dallas, TX, USA, 19–21 June 2017; pp. 78–83. [Google Scholar]
- Heimes, F.O. Recurrent neural networks for remaining useful life estimation. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–6. [Google Scholar]
- Gugulothu, N.; Tv, V.; Malhotra, P.; Vig, L.; Agarwal, P.; Shroff, G. Predicting remaining useful life using time series embeddings based on recurrent neural networks. arXiv 2017, arXiv:1709.01073. [Google Scholar]
- Husebø, A.B.; Kandukuri, S.T.; Klausen, A.; Robbersmyr, K.G. Rapid Diagnosis of Induction Motor Electrical Faults using Convolutional Autoencoder Feature Extraction. In Proceedings of the PHM Society European Conference, Turin, Italy, 27–31 July 2020; Volume 5, p. 10. [Google Scholar]
- Lee, K.; Kim, J.K.; Kim, J.; Hur, K.; Kim, H. CNN and GRU combination scheme for bearing anomaly detection in rotating machinery health monitoring. In Proceedings of the 2018 1st IEEE International Conference on Knowledge Innovation and Invention (ICKII), Jeju Island, Korea, 23–27 July 2018; pp. 102–105. [Google Scholar]
- Hundman, K.; Constantinou, V.; Laporte, C.; Colwell, I.; Soderstrom, T. Detecting spacecraft anomalies using lstms and nonparametric dynamic thresholding. In Proceedings of the 24th ACM SIGKDD International Conference on knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 387–395. [Google Scholar]
- Jianzhong, S.; Chaoyi, L.; Cui, L.; Ziwei, G.; Ronghui, W. A data-driven health indicator extraction method for aircraft air conditioning system health monitoring. Chin. J. Aeronaut. 2019, 32, 409–416. [Google Scholar]
- Khumprom, P.; Grewell, D.; Yodo, N. Deep Neural Network Feature Selection Approaches for Data-Driven Prognostic Model of Aircraft Engines. Aerospace 2020, 7, 132. [Google Scholar] [CrossRef]
- Schwartz, S.; Jimenez, J.J.M.; Salaün, M.; Vingerhoeds, R. A fault mode identification methodology based on self-organizing map. Neural Comput. Appl. 2020, 32, 13405–13423. [Google Scholar] [CrossRef]
- Baptista, M.; Prendinger, H.; Henriques, E. Prognostics in Aeronautics with Deep Recurrent Neural Networks. In Proceedings of the PHM Society European Conference, online, 27–31 July 2020; Volume 5, p. 11. [Google Scholar]
- Reddy, K.K.; Sarkar, S.; Venugopalan, V.; Giering, M. Anomaly detection and fault disambiguation in large flight data: A multi-modal deep auto-encoder approach. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Fu, X.; Luo, H.; Zhong, S.; Lin, L. Aircraft engine fault detection based on grouped convolutional denoising autoencoders. Chin. J. Aeronaut. 2019, 32, 296–307. [Google Scholar] [CrossRef]
- Balaban, E.; Saxena, A.; Bansal, P.; Goebel, K.F.; Curran, S. Modeling, Detection, and Disambiguation of Sensor Faults for Aerospace Applications. IEEE Sens. J. 2009, 9, 1907–1917. [Google Scholar] [CrossRef]
- Denis, F. PAC learning from positive statistical queries. In Proceedings of the International Conference on Algorithmic Learning Theory, Otzenhausen, Germany, 8–10 October 1998; pp. 112–126. [Google Scholar]
- Zhang, B.; Zuo, W. Learning from positive and unlabeled examples: A survey. In Proceedings of the 2008 International Symposiums on Information Processing, Moscow, Russia, 23–25 May 2008; pp. 650–654. [Google Scholar]
- Springenberg, J.T.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for simplicity: The all convolutional net. arXiv 2014, arXiv:1412.6806. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Malhotra, P.; Ramakrishnan, A.; Anand, G.; Vig, L.; Agarwal, P.; Shroff, G. LSTM-based encoder-decoder for multi-sensor anomaly detection. arXiv 2016, arXiv:1607.00148. [Google Scholar]
- Srivastava, N.; Mansimov, E.; Salakhudinov, R. Unsupervised learning of video representations using lstms. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 843–852. [Google Scholar]
- Pereira, J.; Silveira, M. Unsupervised anomaly detection in energy time series data using variational recurrent autoencoders with attention. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 1275–1282. [Google Scholar]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; pp. 1310–1318. [Google Scholar]
- Williams, R.J.; Peng, J. An efficient gradient-based algorithm for on-line training of recurrent network trajectories. Neural Comput. 1990, 2, 490–501. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Xu, K.; Ba, J.; Kiros, R.; Cho, K.; Courville, A.; Salakhudinov, R.; Zemel, R.; Bengio, Y. Show, attend and tell: Neural image caption generation with visual attention. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2048–2057. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).