Wing Structure of the Next-Generation Civil Tiltrotor: From Concept to Preliminary Design
Abstract
1. Introduction
2. Previous Similar Works
3. Requirements and Design Strategy
3.1. Materials and Methods
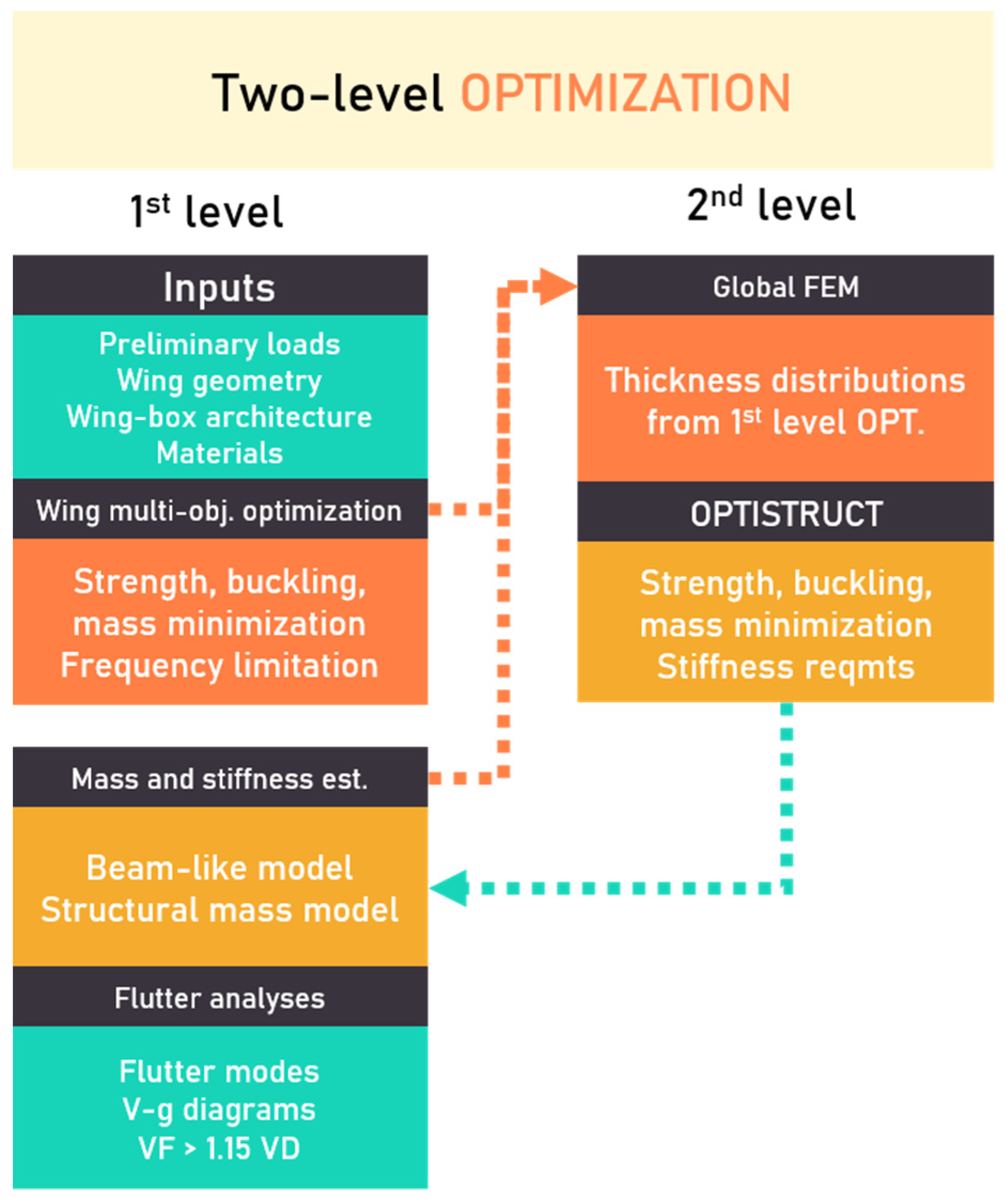
3.1.1. Genetic Algorithm Multi-Objective Optimization Approach (First Phase)
3.1.2. Aeroelastic Model
3.1.3. Size Optimization with FEM (Second Phase)
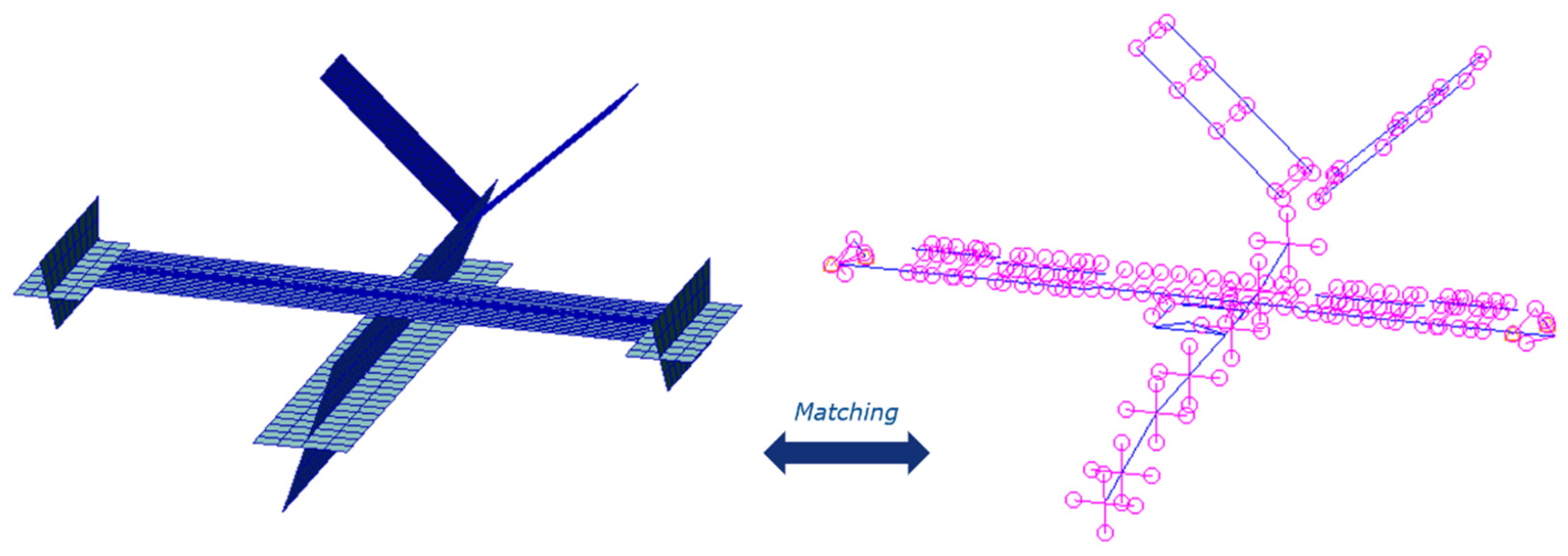
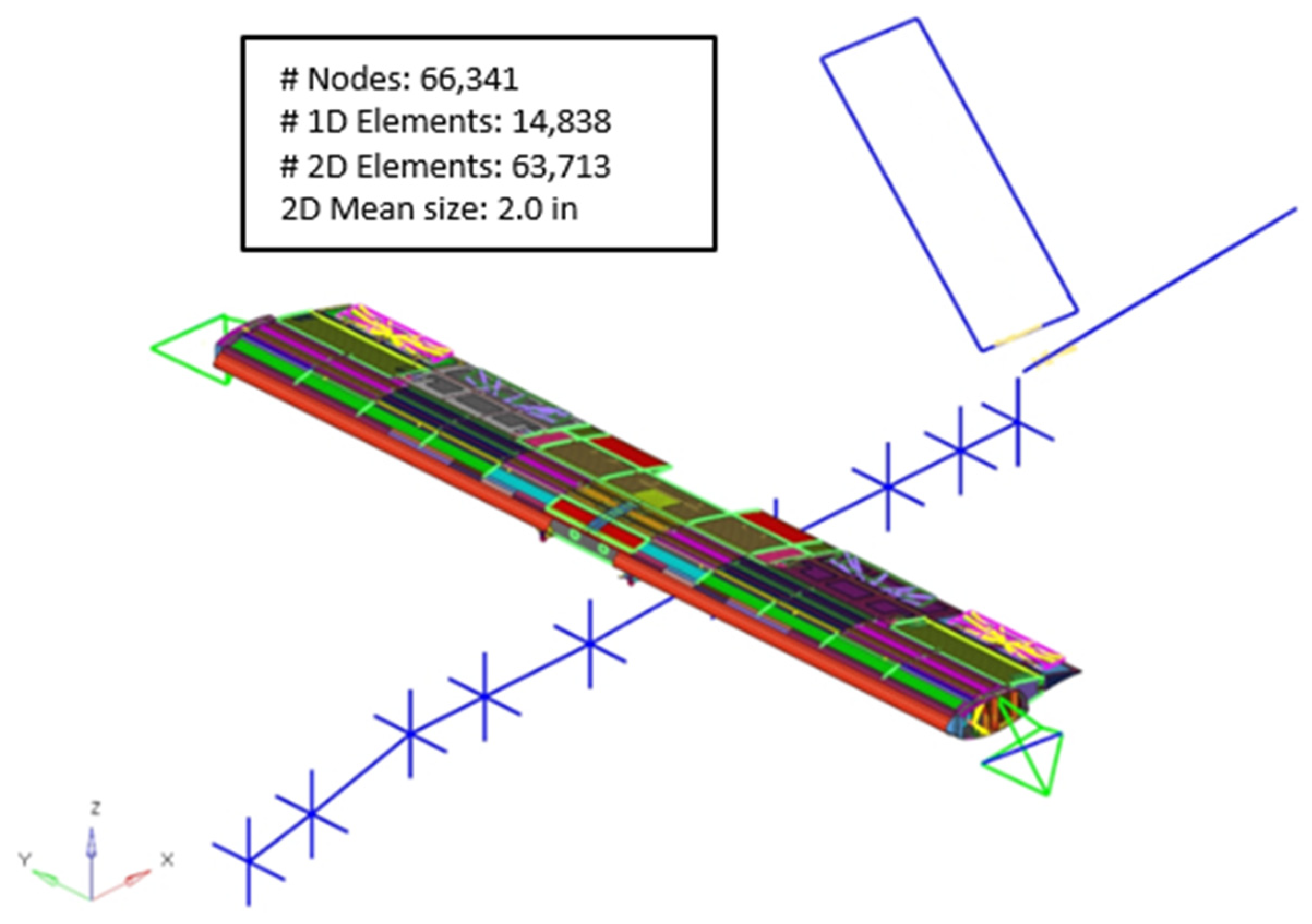
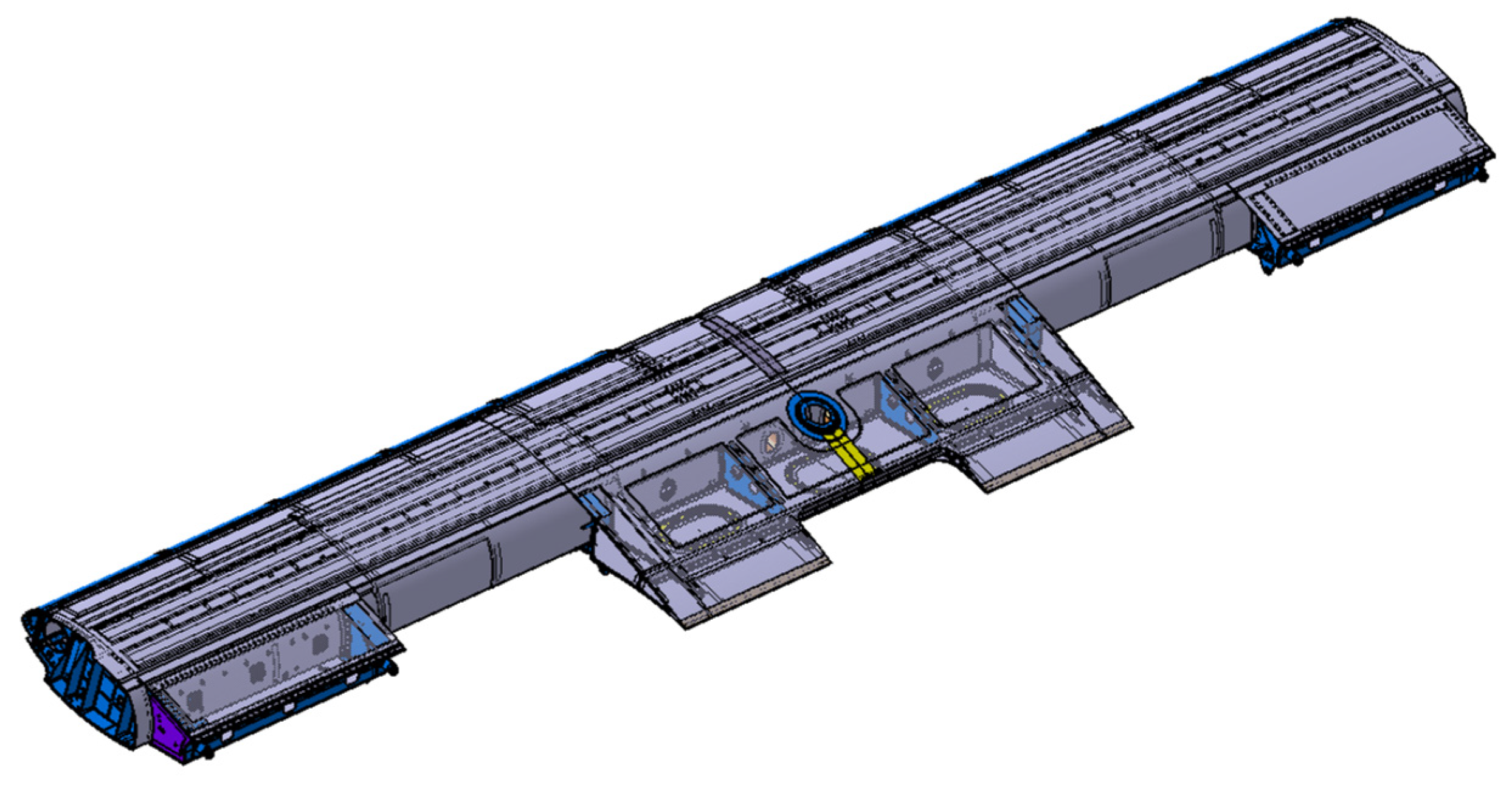
3.1.3.1. Structural Finite Element Model—Starting Model
3.1.3.2. Materials
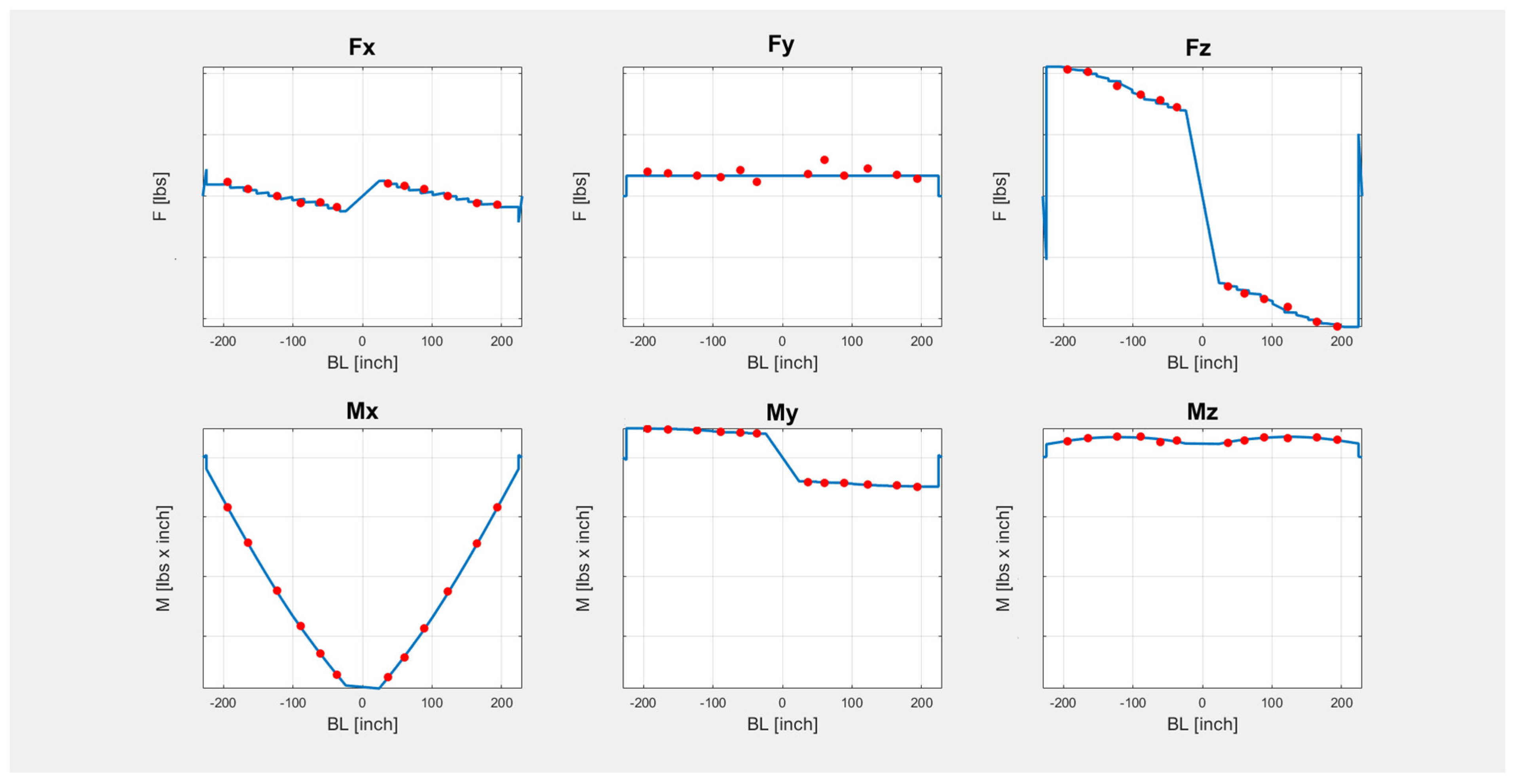
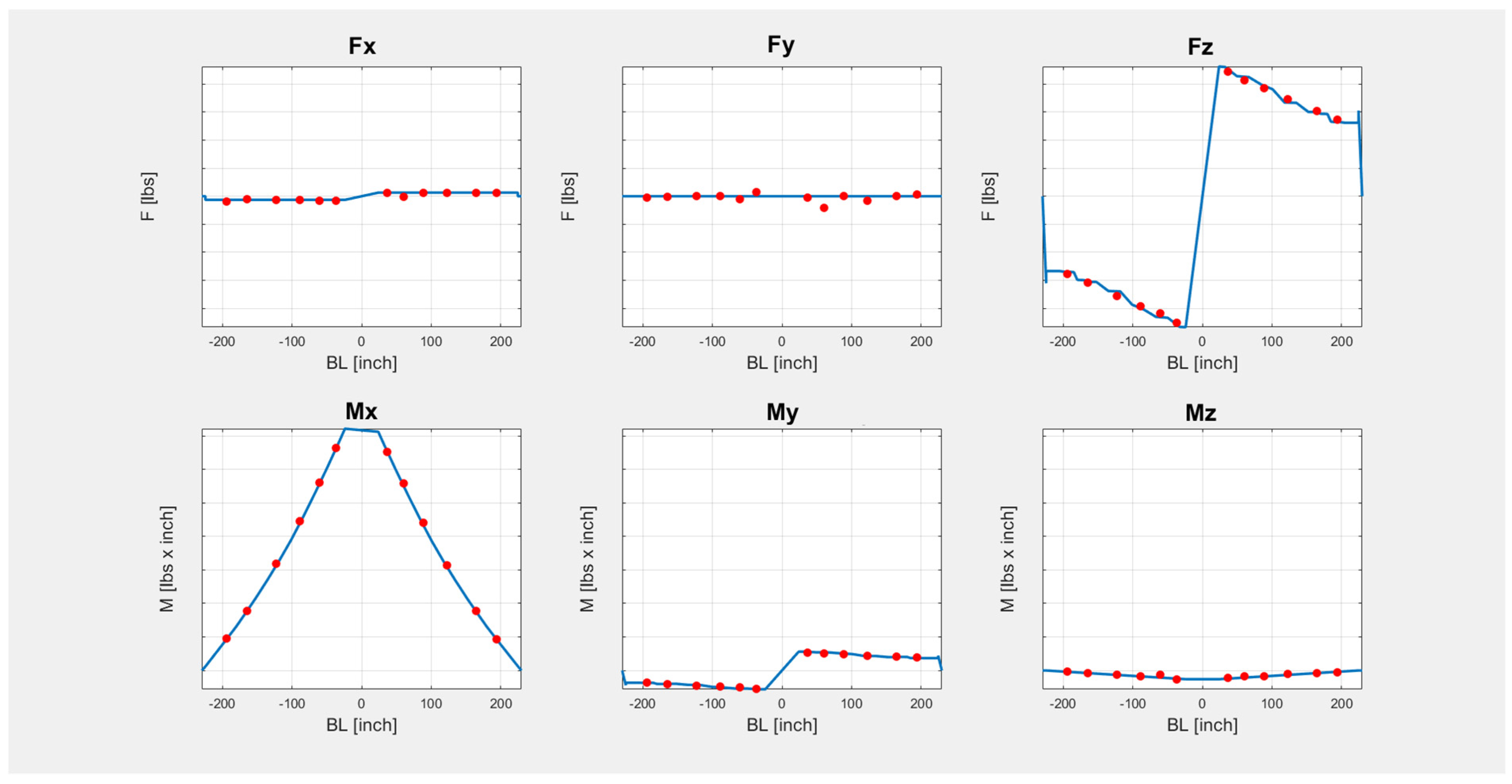
3.1.3.3. Loads
3.1.3.4. Modifications to the Model Loading Strategy
3.1.4. Wing Stiffness Evaluation from FEM (Second Phase)
4. Preliminary Structural Design Results
4.1. Results of the Optimization Process and Flutter Analysis in the First Phase
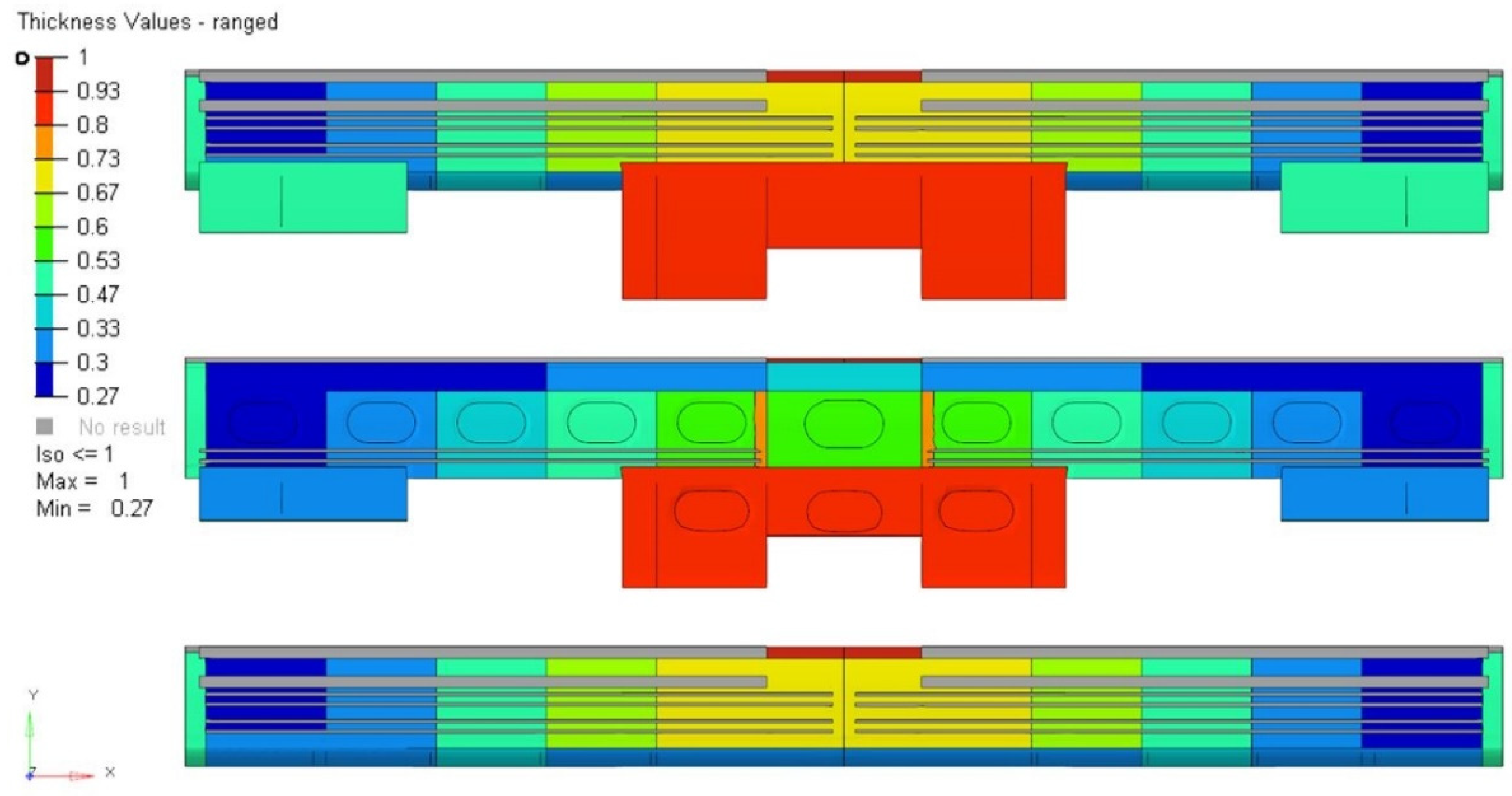
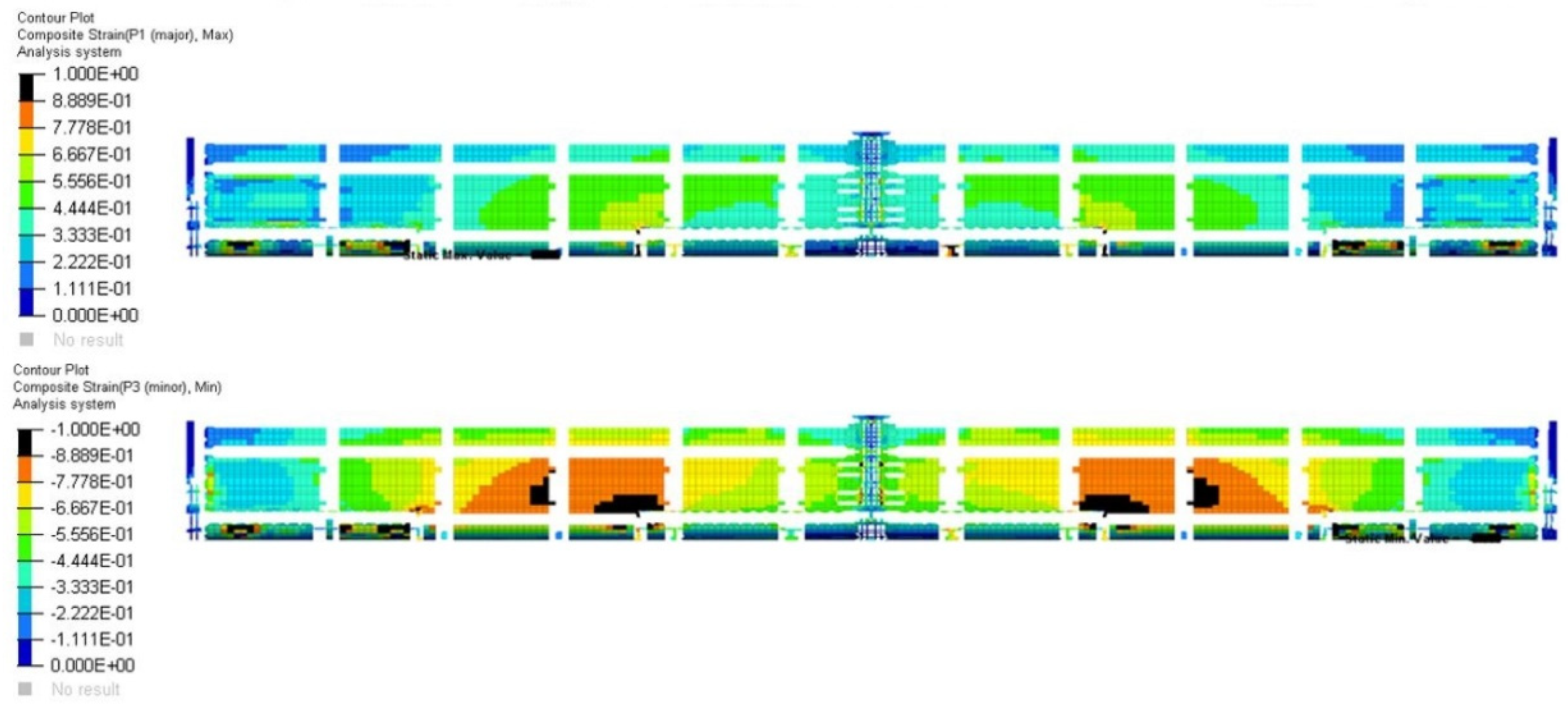
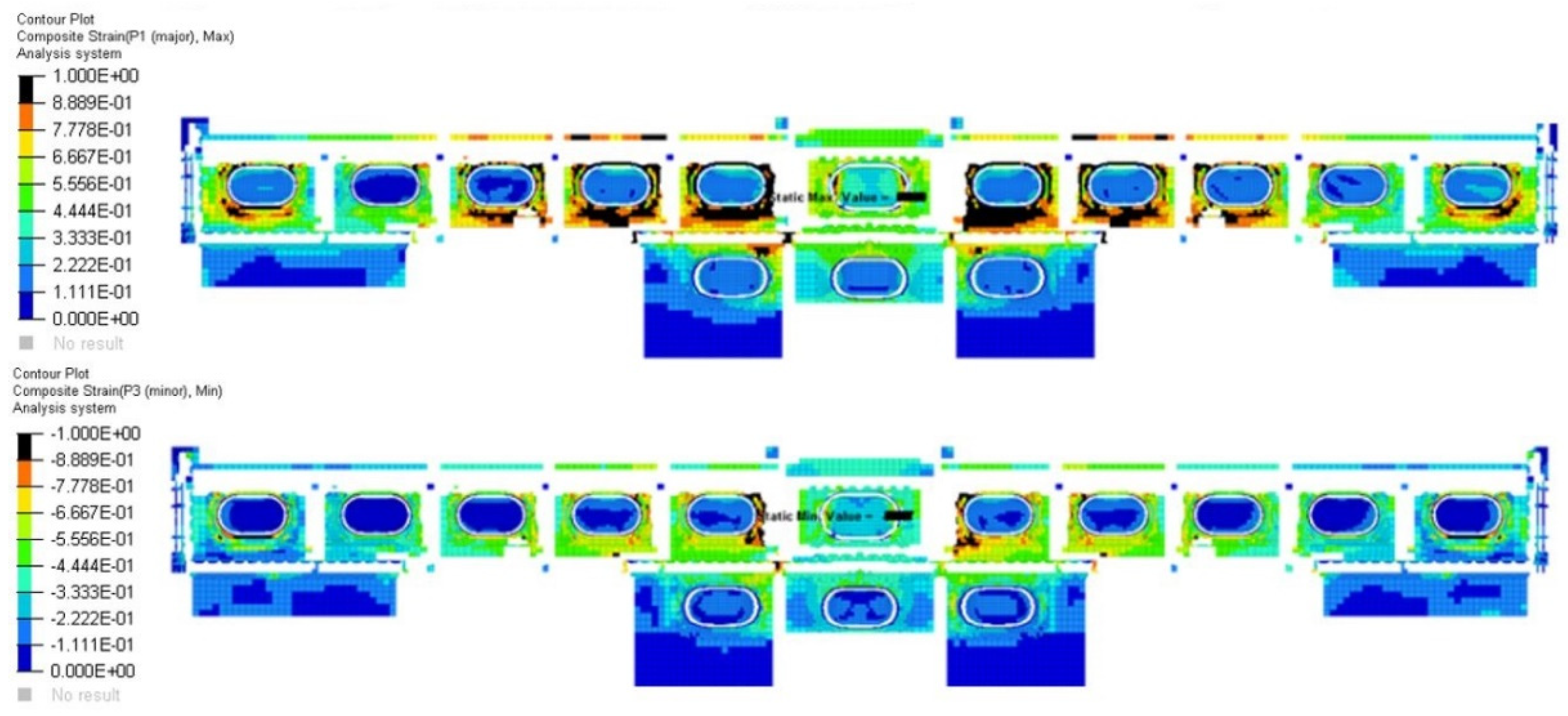
4.2. Results of Finite Element Optimization (Second Phase) and Comparison with Respect to the Base Design
4.3. Wing Stiffness Evaluation
4.4. Flutter Results Comparison
5. Higher Fidelity Models
6. Conclusions
Author Contributions
Funding

Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- CLEAN SKY 2 Joint Undertaking Third Amended Bi-Annual Work Plan and Budget 2018–2019, Annex to decision CS-GB-2019-04-09 Decision Third Amended and Budget 2018–19. Available online: https://ec.europa.eu/research/participants/data/ref/h2020/other/wp/jtis/h2020-wp1819-cleansky_en.pdf (accessed on 1 April 2021).
- Belardo, M.; Beretta, J.; Marano, A.D.; Diodati, G.; Paletta, N.; Di Palma, L. On the preliminary structural design strategy of the wing of the Next Generation Civil Tilt-Rotor Technology Demonstrator. Int. J. Aeronaut. Space Sci. 2020. [Google Scholar] [CrossRef]
- Park, J.-S.; Jung, S.N.; Lee, M.-K.; Kim, J.M. Design optimization framework for tiltrotor composite wings considering whirl flutter stability. Compos. Part B Eng. 2010, 41, 257–267. [Google Scholar] [CrossRef]
- Kim, T.; Lim, J.; Shin, S.J.; Kim, D.-H. Structural Design Optimization of a Tiltrotor Aircraft Composite Wing to Enhance Whirl Flutter Stability. Compos. Struct. 2013, 95, 283–294. [Google Scholar] [CrossRef]
- Belardo, M.; Paletta, N.; Di Palma, L.; Pecora, M. Structural and Aeroelastic Design of a Joined-Wing UAV. J. Aerosp. Eng. 2014, 27, 93–111. [Google Scholar] [CrossRef]
- Paletta, N.; Belardo, M.; Di Palma, L. Non-Linear Dynamic Loads Due to the Landing Impact of a Joined-Wing UAV; SAE Technical Paper Series; SAE: Warrendale, PA, USA, 2011. [Google Scholar] [CrossRef]
- Acree, C.W., Jr.; Johnson, W. Performance, Loads and Stability of Heavy Lift Tiltrotors. In Proceedings of the American Helicopter Society Vertical Lift Aircraft Design Conference, San Francisco, CA, USA, 18–20 January 2006. [Google Scholar]
- Bielawa, R.L. Rotary Wing Structural Dynamics and Aeroelasticity, 2nd ed.; AIAA Publishing: Reston, VA, USA, 2006. [Google Scholar]
- Johnson, W. Dynamics of Tilting Proprotor Aircraft in Cruise Flight; NASA Technical Note D-7677; NASA: Washington, DC, USA, 1974.
- Moore, M.J.; Yablonski, M.J.; Mathew, B.; Liu, J. High Speed Tiltrotors: Dynamics Methodology. In Proceedings of the American Helicopter Society 49th International Annual Forum Proceedings, St. Louis, MO, USA, 19–21 May 1993. [Google Scholar]
- Cecrdle, J. Whirl Flutter of Turboprop Aircraft Structures; Woodhead Publishing: Cambridge, UK, 2015. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhu, N.; O’Connor, I. iMASKO: A Genetic Algorithm Based Optimization Framework for Wireless Sensor Networks. J. Sens. Actuator Netw. 2013, 2, 675–699. [Google Scholar] [CrossRef]
- Bruhn, E.F. Analysis and Design of Flight Vehicle Structures; Tri-State Offset Company: New York, NY, USA, 1973. [Google Scholar]
- Albano, E.; Rodden, W.P. A Doublet-Lattice Method for Calculating Lift Distributions on Oscillating Surfaces in Subsonic Flows. AIAA J. 1969, 7, 279–285. [Google Scholar] [CrossRef]
- Johnson, W. Calculation of Tiltrotor Aeroacoustic Model, Performance, Airloads, and Structural Loads. In Proceedings of the American Helicopter Society Aeromechanics Specialists’s Meeting, Atlanta, GA, USA, 13–15 November 2000. [Google Scholar]
- Harden, R.L.; Desmarais, R.N. Interpolation Using Surface Splines. J. Aircr. 1972, 9, 189–191. [Google Scholar] [CrossRef]
- Loewer, S. Sensitivity of Tiltrotor High Speed Performance to Wing Structural Parameters. Diploma Thesis, Technische Universität Braunschweig, Braunschweig, Germany, 1992. [Google Scholar]
- Altair Engineering. Altair OptiStruct Verification Problems Manual—for NAFEMS, MacNeal-Harder, and Raasch Challenge Models; Altair Engineering: Troy, MI, USA, 2017. [Google Scholar]
- Lange, K. Optimization; Springer: New York, NY, USA, 2013. [Google Scholar]
- Friedlander, M.P.; Macedo, I.; Pong, T.K. Gauge Optimization and Duality. SIAM J. Optim. 2014, 24, 1999–2022. [Google Scholar] [CrossRef][Green Version]
- Chiariello, A.; Orlando, S.; Vitale, P.; Linari, M.; Longobardi, R.; Di Palma, L. Development of smart morphing landing gear composite door for high speed compound rotorcraft. Aerospace 2020, 7, 88. [Google Scholar] [CrossRef]
- Mora, H.; Mora-Pascual, J.M.; García-García, A.; Martínez-González, P. Computational Analysis of Distance Operators for the Iterative Closest Point Algorithm. PLoS ONE 2016, 11, e0164694. [Google Scholar] [CrossRef] [PubMed]
- Drela, M. ASWING 5.99 Technical Description—Steady Formulation; 10 March 2015. Available online: https://web.mit.edu/drela/Public/web/aswing/asw_theory.pdf (accessed on 1 April 2021).
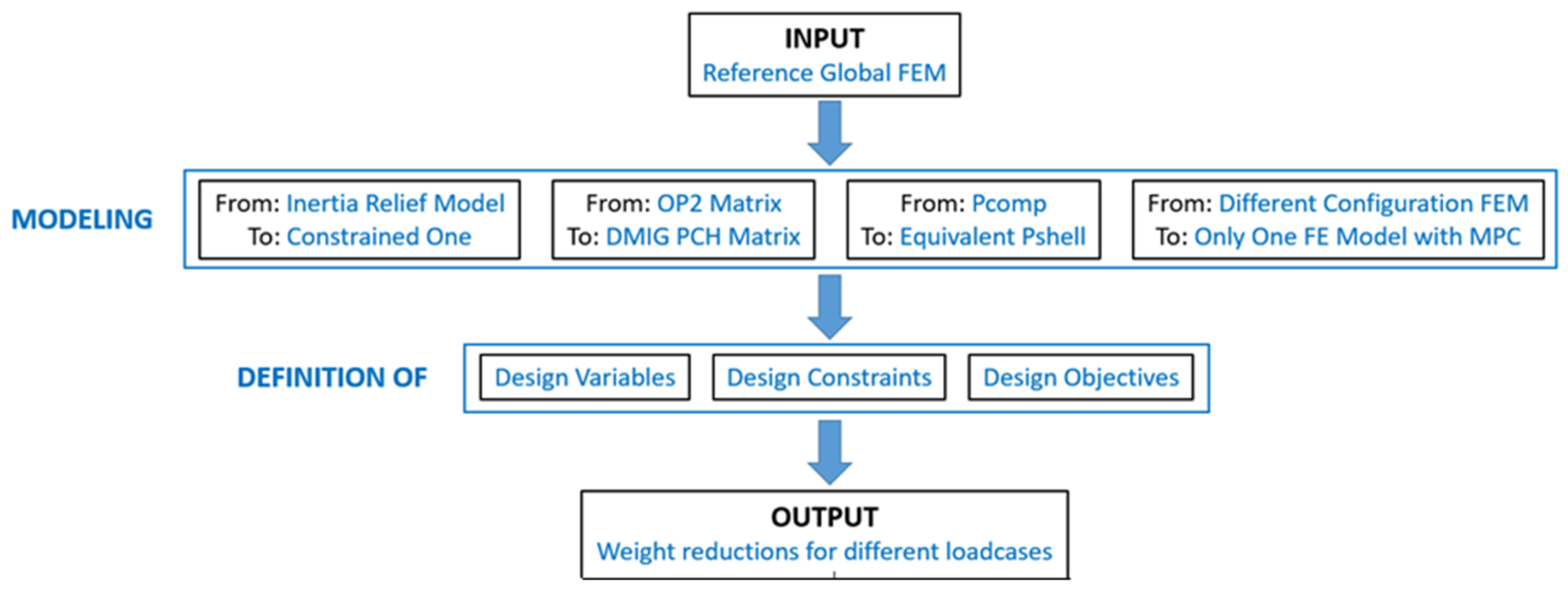


| Mass | Volume | Center of Gravity |
|---|---|---|
| Moment of Inertia | Static Compliance | Static Displacement |
| Natural Frequency | Buckling Factor | Static Stress, Strain, Forces |
| Static Composite Stress, Strain, Failure Index | Frequency Response Displacement, Velocity, Acceleration | Frequency Response Stress, Strain, Forces |
| Weighted Compliance Function | Weighted Frequency | Combined Compliance Index |
| Temperature |
| Properties | Direction | Modulus | RTD Value (MPa) | Density (Kg/m3) | Cured Ply Thickness (mm) |
|---|---|---|---|---|---|
| Tension | 0 | E11 | 59,777 | 1520 | 0.31877 |
| Compression | 0 | −E11 | 55,916 | ||
| Tension | 90 | E22 | 58,053 | ||
| Compression | 90 | −E22 | 55,020 | ||
| Shear | - | G12 | 3930 | ||
| Poisson ratio | - | ν12 | 0.056 |
| Properties | Direction (°) | Modulus (GPa) | Tensile Strength (MPa) | Density (Kg/m3) | Yield Strength (MPa) |
|---|---|---|---|---|---|
| Tension | 0, 90 | 71 | 525 | 2750 | 470 |
| Shear | - | 26.5 | - | ||
| Poisson ratio | - | 0.33 | 0.056 |
| Load Case ID | Description | Wing Mass Condition | Nacelle Angle | Airspeed (V/VD) |
|---|---|---|---|---|
| 9 | Symmetric Pull-up | Zero Fuel | 90 | 0.42 |
| 12 | Taxi | Full Fuel | 95 | 0.00 |
| 13 | Gust Condition | Full Fuel | 0 | 0.43 |
| 15 | Symmetric Pull-up | Full Fuel | 95 | 0.41 |
| 17 | Symmetric Pull-up | Zero Fuel | 90 | 0.99 |
| 25 | Rolling Pull-out | Full Fuel | 30 | 1.06 |
| Optimization | Delta-Weight (%) |
|---|---|
| Buckling | −26% |
| Buckling Stiffness (Out-of-plane flexural and Torsional) | −14% |
| Buckling Strength | −5% |
| Buckling Stiffness (In-plane and Out-of-plane flexural and Torsional) Strength | −3% |
| Case Analyzed | First-Phase Optimized Wing | Second-Phase Optimized Wing |
|---|---|---|
| Full fuel case | 1.52 | 1.67 |
| Zero fuel case | 1.48 | 1.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belardo, M.; Marano, A.D.; Beretta, J.; Diodati, G.; Graziano, M.; Capasso, M.; Ariola, P.; Orlando, S.; Di Caprio, F.; Paletta, N.; et al. Wing Structure of the Next-Generation Civil Tiltrotor: From Concept to Preliminary Design. Aerospace 2021, 8, 102. https://doi.org/10.3390/aerospace8040102
Belardo M, Marano AD, Beretta J, Diodati G, Graziano M, Capasso M, Ariola P, Orlando S, Di Caprio F, Paletta N, et al. Wing Structure of the Next-Generation Civil Tiltrotor: From Concept to Preliminary Design. Aerospace. 2021; 8(4):102. https://doi.org/10.3390/aerospace8040102
Chicago/Turabian StyleBelardo, Marika, Aniello Daniele Marano, Jacopo Beretta, Gianluca Diodati, Mario Graziano, Mariacarmela Capasso, Pierpaolo Ariola, Salvatore Orlando, Francesco Di Caprio, Nicola Paletta, and et al. 2021. "Wing Structure of the Next-Generation Civil Tiltrotor: From Concept to Preliminary Design" Aerospace 8, no. 4: 102. https://doi.org/10.3390/aerospace8040102
APA StyleBelardo, M., Marano, A. D., Beretta, J., Diodati, G., Graziano, M., Capasso, M., Ariola, P., Orlando, S., Di Caprio, F., Paletta, N., & Di Palma, L. (2021). Wing Structure of the Next-Generation Civil Tiltrotor: From Concept to Preliminary Design. Aerospace, 8(4), 102. https://doi.org/10.3390/aerospace8040102









