Numerical Evaluation of Structural Safety of Linear Actuator for Flap Control of Aircraft Based on Airworthiness Standard
Abstract
:1. Introduction
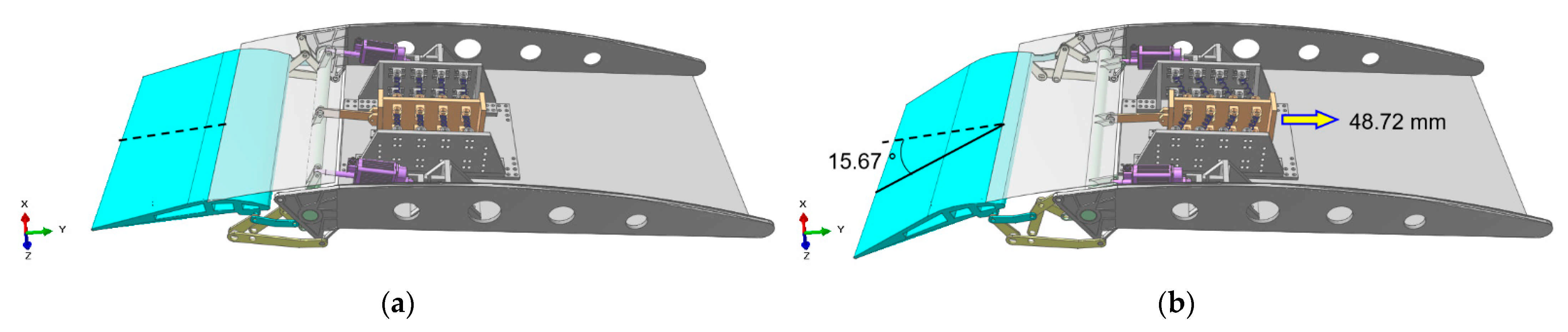
2. Multibody Dynamics Analysis
3. Structural Analysis
3.1. Material Properties
3.2. Static Analysis
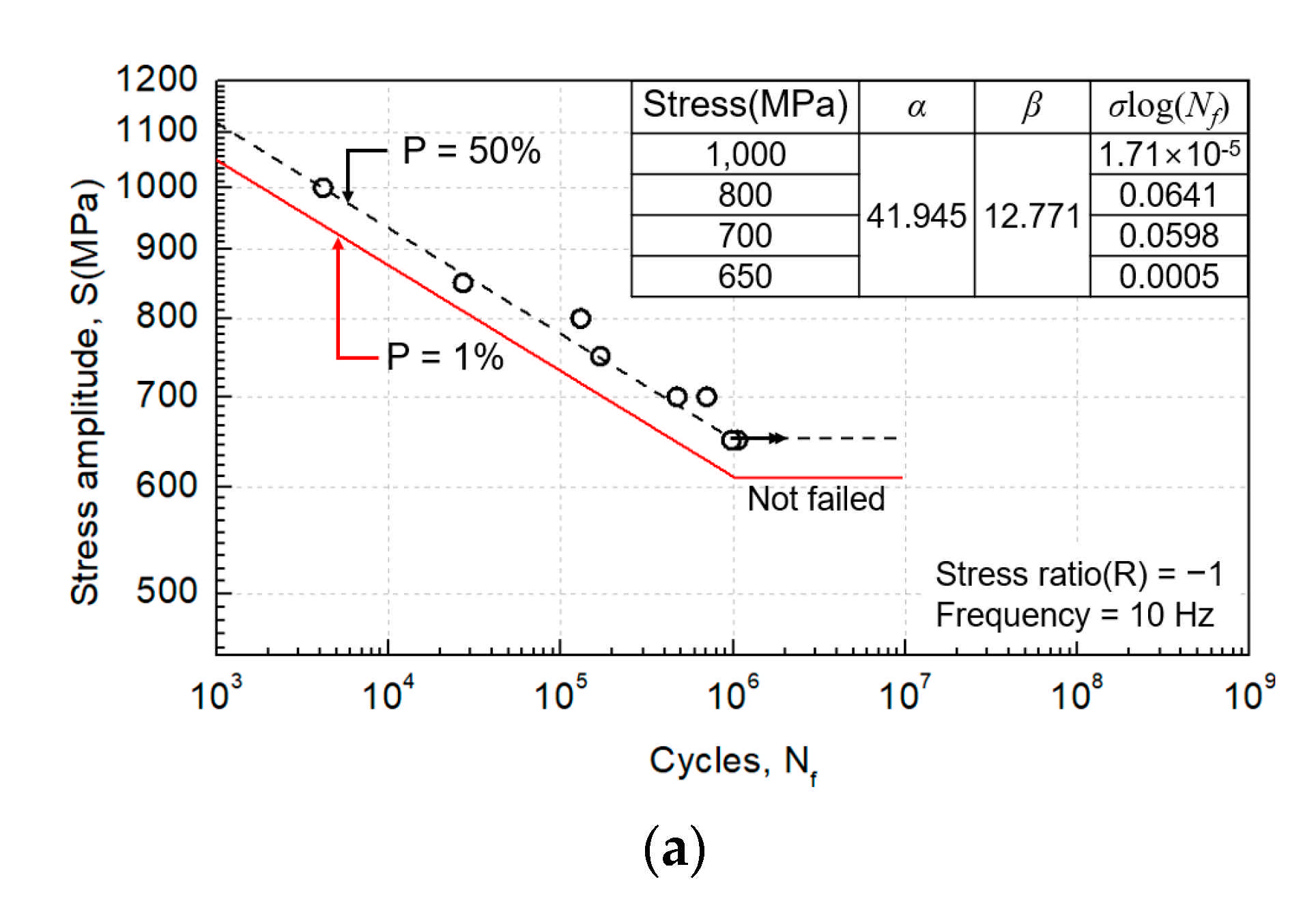
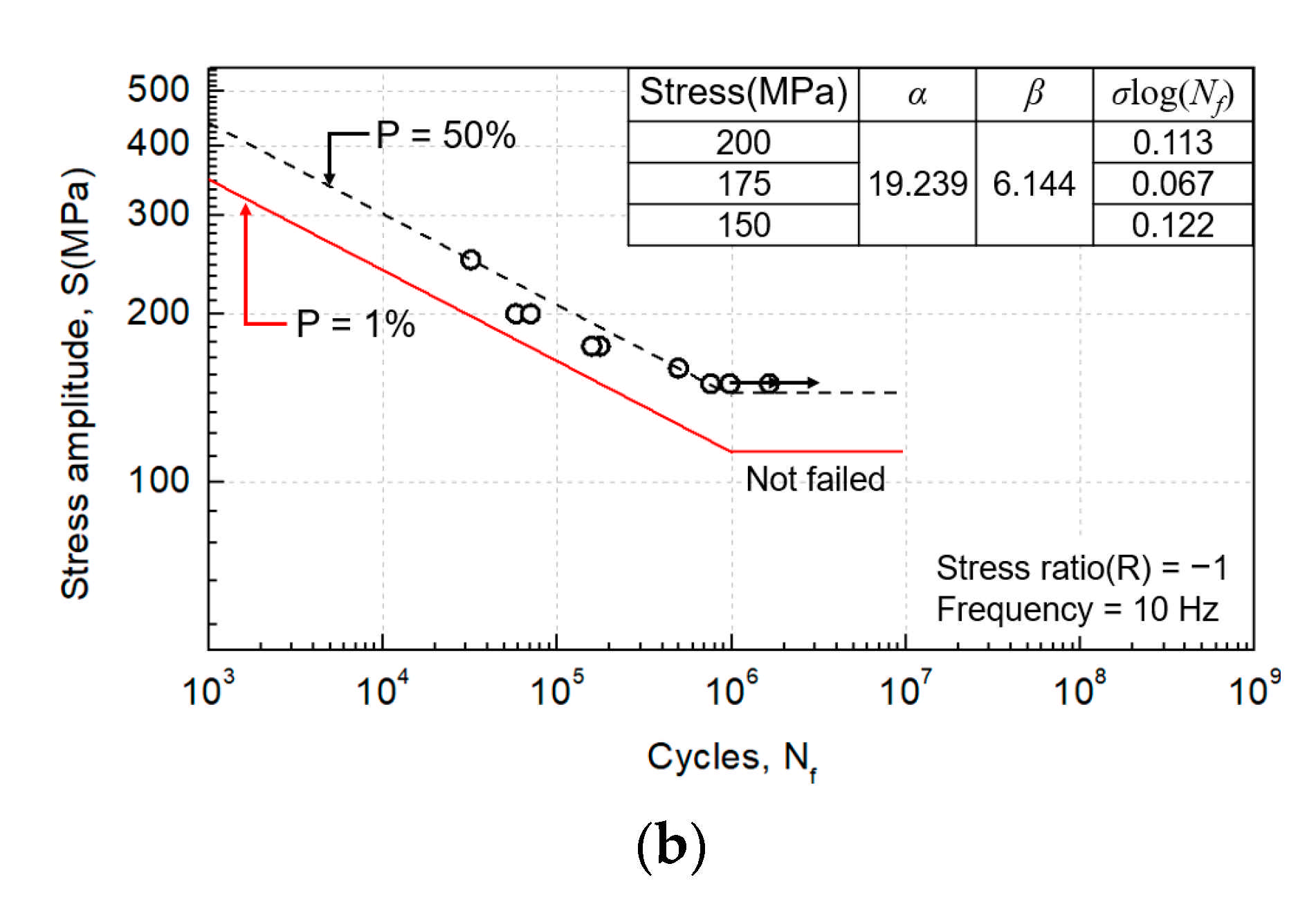
3.3. Fatigue Analysis
4. Results
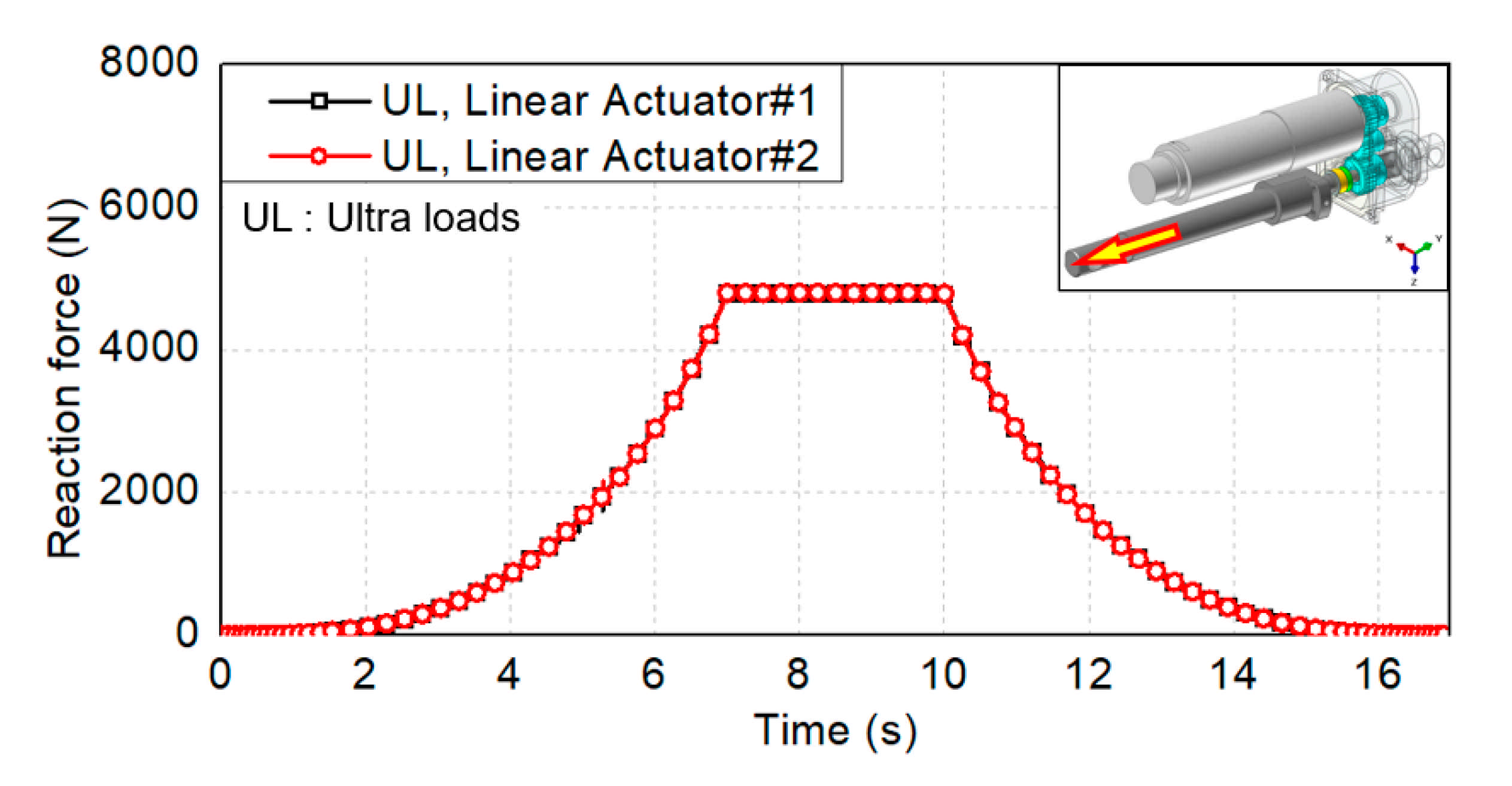
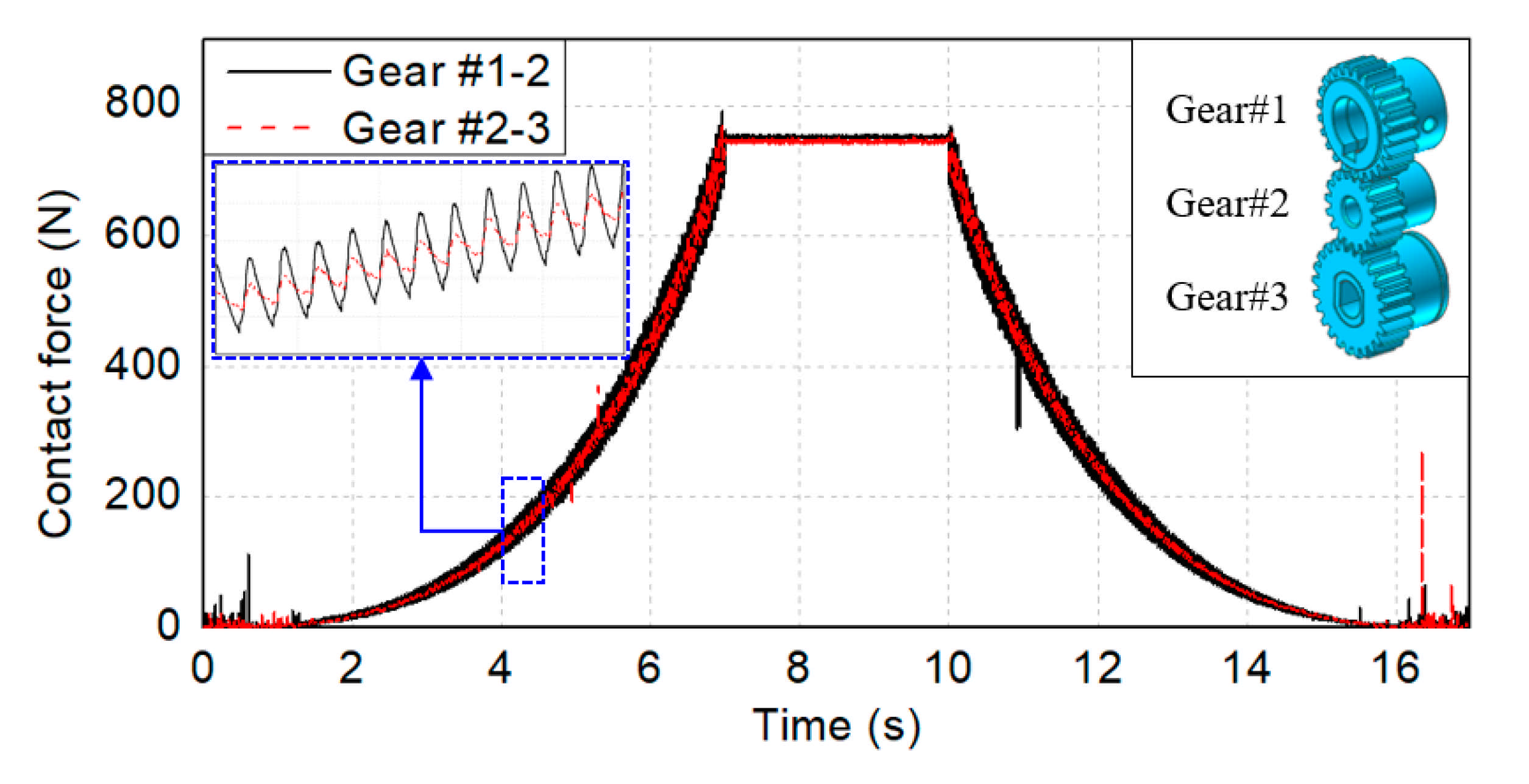
4.1. Multibody Dynamics Analysis
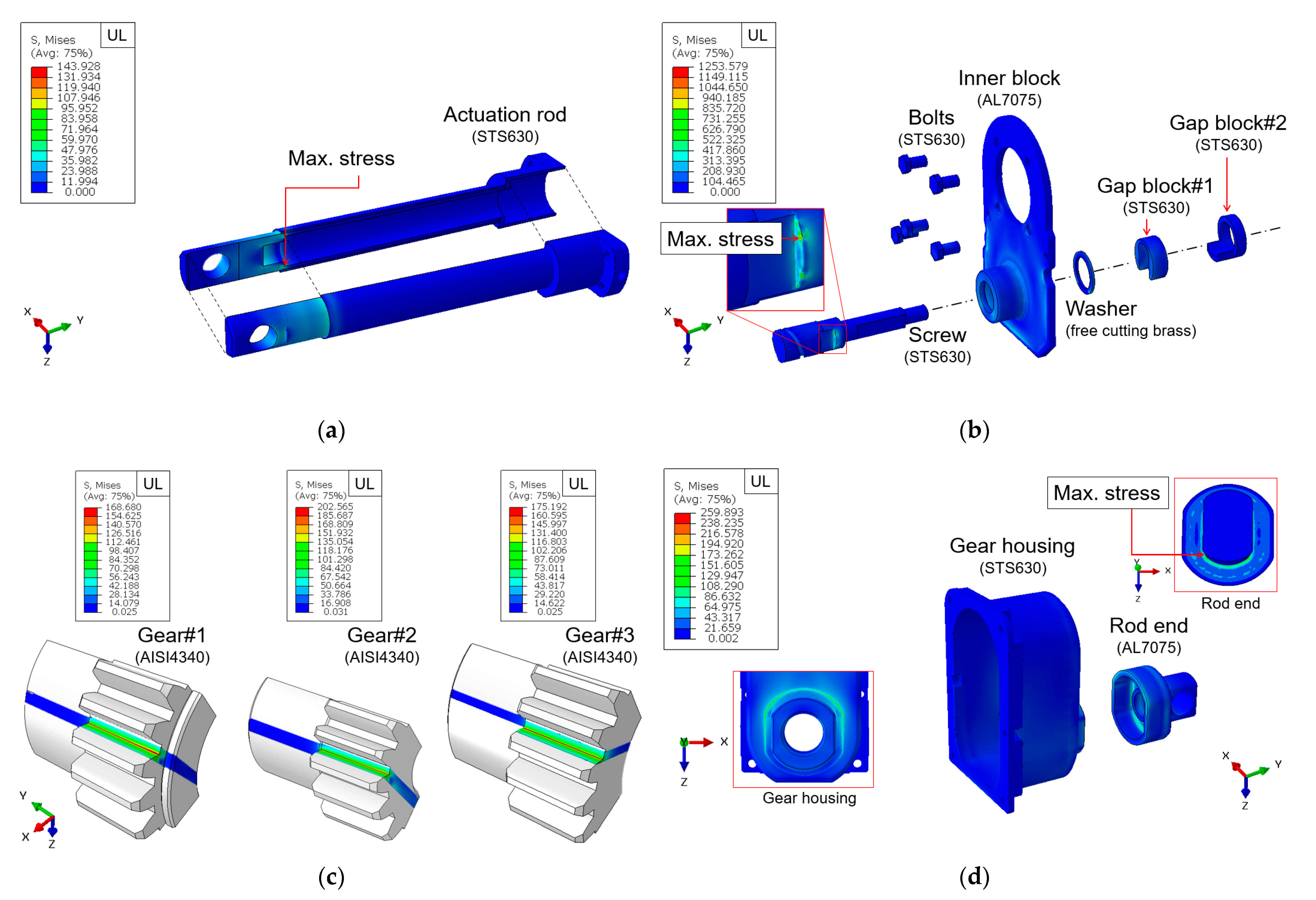
4.2. Static Analysis
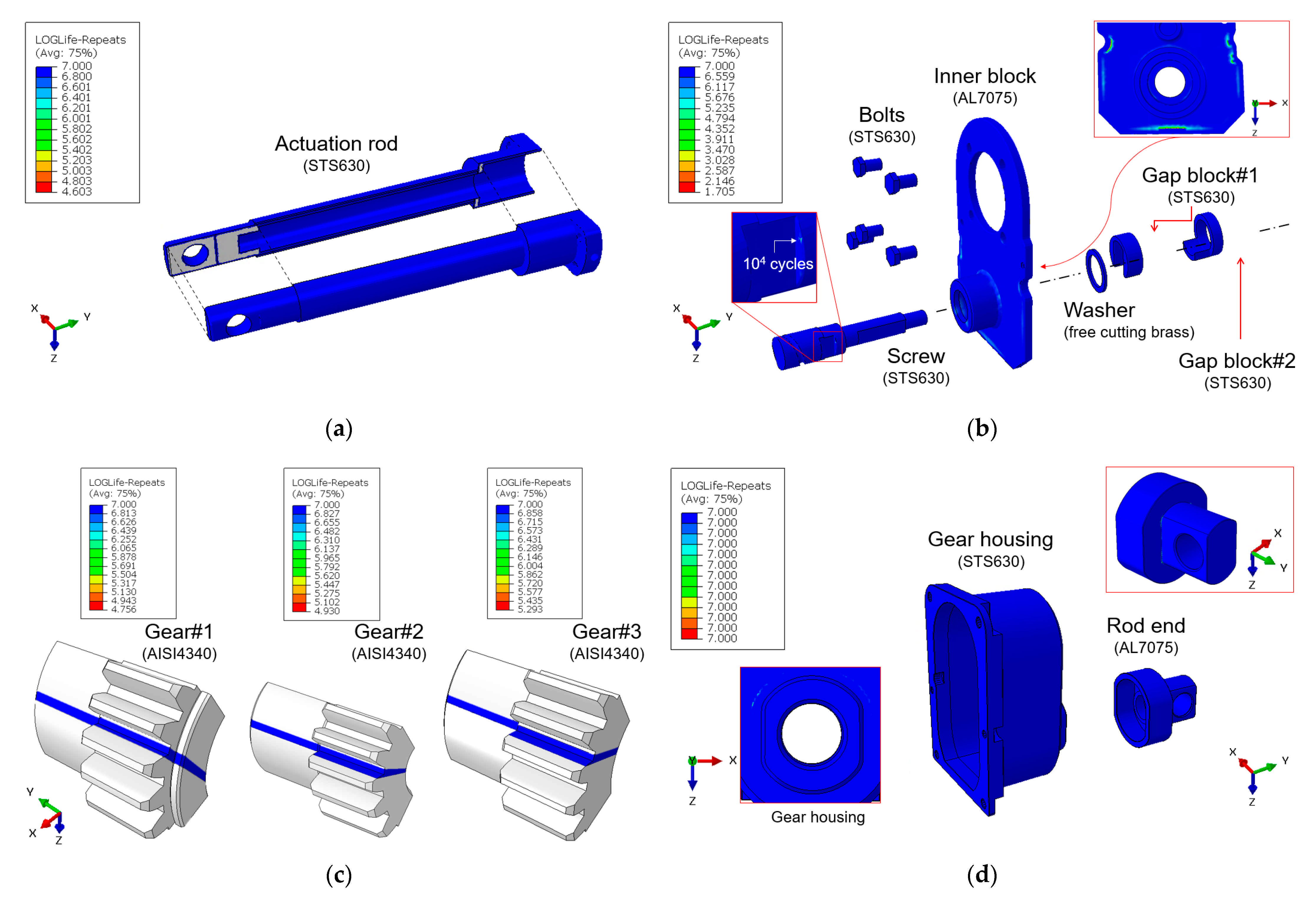
4.3. Fatigue Analysis
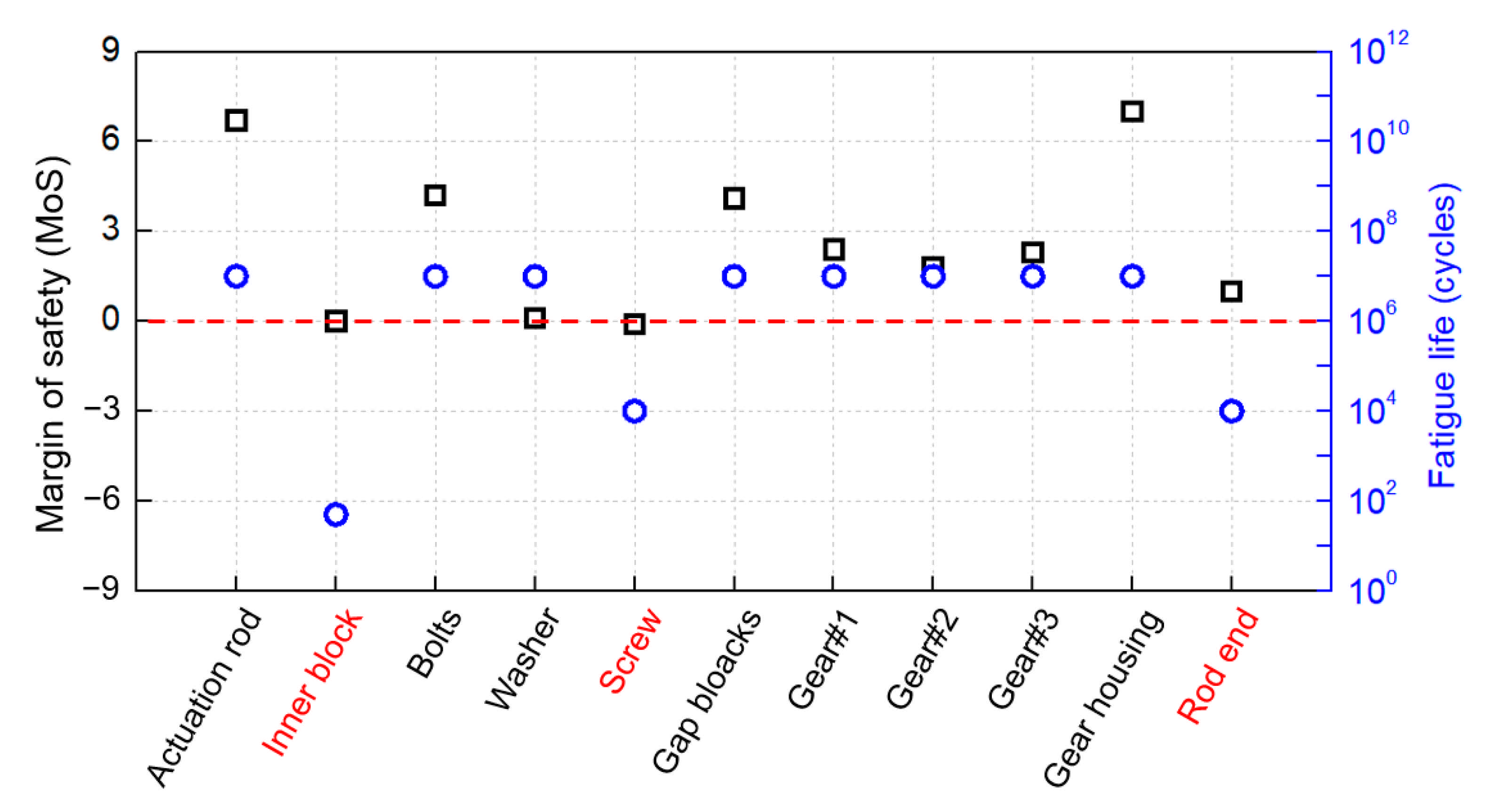
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, Y.; Oh, S. Reliability analysis of aircraft flap. In Proceedings of the Spring Conference of The Korean Society of Mechanical Engineering, Suwon-si, Korea, 4–5 January 1994. [Google Scholar]
- Reports A-032/2008. Accident Involving a McDonnell Douglas DC-9-82 (Aircraft), Registration EC-HFP, Operated by Spanair, at Madrid-Barajas Airport; CIAIAC: Madrid, Spain, 2008. [Google Scholar]
- Aircraft Accident Report. Final Report Mandala PK-Rim 5Sep05; National Transportation Safety Committee: Jakarta, Indonesia, 2009. [Google Scholar]
- Ministry of Land, Infrastructure and Transport. KAS Part 23.697: Wing Flap Controls and Part 23.701: Flap Interconnection. 2013. Available online: http://atis.casa.go.kr/ACS/sub04_3.asp (accessed on 7 March 2021).
- Claeyssen, F.; Janker, P.; LeLetty, R.; Sosniki, O.; Pages, A.; Magnac, G.; Christmann, M.; Dodds, G. New actuators for aircraft, space and military applications. In Proceedings of the 12th International Conference on New Actuators, Bremen, Germany, 14–16 June 2010. [Google Scholar]
- Yoon, G.; Park, H.; Jang, K. The state of the art and application of actuator in aerospace. J. Korean Soc. Propuls. Eng. 2010, 14, 89–102. [Google Scholar]
- Hur, J. Study on fatigue life estimation for aircraft engine support structure. Trans. Korean Soc. Mech. Eng. A 2010, 34, 1667–1674. [Google Scholar] [CrossRef]
- Kim, S.; Kim, T. Study on aircraft fatigue life substantiation method. J. Korean Soc. Aeronaut. Space Sci. 2016, 24, 41–46. [Google Scholar]
- Ministry of Land, Infrastructure and Transport. KAS Part 23.305: Strength and Deformation and Part 23.307: Proof of Structure. 2013. Available online: http://atis.casa.go.kr/ACS/sub04_3.asp (accessed on 7 March 2021).
- Ministry of Land, Infrastructure and Transport. Notice 932: Procedures for Type Certification. 2017. Available online: https://www.molit.go.kr/USR/I0204/m_45/lst.jsp?gubun=1 (accessed on 7 March 2021).
- Kim, D.; Kim, M.; Kim, S. Evaluation of structural safety of critical design model of linear actuator for flap control of aircraft and test rig. Trans. Korean Soc. Mech. Eng. A 2020, 44, 733–744. [Google Scholar] [CrossRef]
- Kim, D.; Kim, S. Evaluation of structural safety of linear actuator for flap control of aircraft. J. Aerosp. Syst. Eng. 2019, 13, 66–73. [Google Scholar]
- Ministry of Land, Infrastructure and Transport. KAS Part 23.301: Loads and Part 23.303: Factor of Safety. 2013. Available online: http://atis.casa.go.kr/ACS/sub04_3.asp (accessed on 7 March 2021).
- Cho, H.; Lee, I.; Kim, S.; Park, S.; Yang, M. No-failure accelerated life test of flap actuating system using Weibull distribution. J. Aerosp. Syst. Eng. 2016, 10, 51–58. [Google Scholar] [CrossRef]
- SAE-AISI 4340 (SNCM439, G43400) Ni-Cr-Mo Steel. Available online: https://www.makeitfrom.com/material-properties/SAE-AISI-4340-SNCM439-G43400-Ni-Cr-Mo-Steel (accessed on 7 March 2021).
- Free Cutting Brass UNS C36000. Available online: https://www.azom.com/article.aspx?ArticleID=6391 (accessed on 7 March 2021).
- ASTM. ASTM E8/E8M-16a Standard Test Methods for Tension Testing of Metallic Materials. 2016. Available online: https://www.astm.org/DATABASE.CART/HISTORICAL/E8E8M-16A.htm (accessed on 7 March 2021).
- ASTM. ASTM B557-15 Standard Test Methods for Tension Testing Wrought and Cast Aluminum-and Magnesium-Alloy Products. 2015. Available online: https://www.astm.org/Standards/B557.htm (accessed on 7 March 2021).
- ASTM. ASTM E466-15 Standard Practice for Conducting Force Controlled Constant Amplitude Axial Fatigue Tests of Metallic Materials. 2015. Available online: https://www.astm.org/Standards/E466 (accessed on 7 March 2021).
- JSME S002. Standard method of statistical fatigue testing. J. Jpn. Soc. Mech. Eng. 1994, 10–42. [Google Scholar]
- Kim, T.; Lee, J.; Hur, S.; Seol, J.; Lee, B. A study on the finite element fatigue analysis of single tooth of reduction gear of aircraft. In Proceedings of the Society for Aerospace System Engineering Fall Conference, Gyeongju-si, Korea, 31 October–2 November 2018. [Google Scholar]
- ISO 6336-3. Calculation of Load Capacity of Spur and Helical Gears—Part 3: Calculation of Tooth Bending Strength, 2nd ed.; ISO: Geneva, Switherland, 2019. [Google Scholar]
- Kim, D.; Kim, G.; Kim, J.; Ahn, B. Fatigue test and analysis of automotive bevel gear. In Proceedings of the Spring Conference of the Korea Society of Mechanical Engineers, Busan, Korea, 26–27 May 2005. [Google Scholar]
- Ministry of Land, Infrastructure and Transport. KAS Part 23.572: Metallic Wing, Empennage, and Associated Structures. 2013. Available online: http://atis.casa.go.kr/ACS/sub04_3.asp (accessed on 7 March 2021).
- Park, Y.; Im, J.; Park, J. Damage tolerant design for the tilt rotor UAV. J. Aerosp. Syst. Eng. 2007, 1, 27–36. [Google Scholar]
- Budynas, R.; Nisbett, J. Shigley’s Mechanical Engineering Design, 9th ed.; McGraw-Hill Book Company: Newyork, NY, USA, 2012. [Google Scholar]
- Kim, S.; Kim, T. Study on fixed wing aircraft fatigue life substantiation method. In Proceedings of the Fall Conference of the Korean Society for Aeronautical and Space Sciences, Jeju-si, Korea, 18–20 November 2015. [Google Scholar]



| Specifications | Values | Units |
|---|---|---|
| Load rating | 3200 | N |
| Maximum velocity | 10 | mm/s |
| Maximum stroke | 70 | mm |
| Life cycles | 1,000,000 | cycles |
| Properties | Materials | Units | |||
|---|---|---|---|---|---|
| STS630-H1025 | AL7075-T651 | Free-Cutting Brass | AISI4340 | ||
| Young’s modulus | 200.4 | 72.0 | 97.0 | 205.0 | GPa |
| Poisson’s ratio | 0.28 | 0.33 | 0.33 | 0.28 | mm/mm |
| Yield strength | 1122.0 | 536.5 | 310.0 | 586.0 | MPa |
| Ultimate strength | 1134.6 | 577.5 | 469.0 | 781.0 | MPa |
| Fatigue strength ( = 106 cycles) | 610.9 | 113.1 | 138.0 | 387.6 | MPa |
| Components | Thicknesses | Widths | Effective Diameters |
|---|---|---|---|
| Gear#1 | 1.50 mm | 8 mm | 24 mm |
| Gear#2 | 1.47 mm | 8 mm | 17 mm |
| Gear#3 | 1.50 mm | 8 mm | 24 mm |
| Components | |||||
|---|---|---|---|---|---|
| Gear#1 | 0.762 | 1.11 | 1 | 1 | 0.85 |
| Gear#2 | 0.762 | 1.14 | 1 | 1 | 0.87 |
| Gear#3 | 0.762 | 1.11 | 1 | 1 | 0.85 |
| Components | UL | Units |
|---|---|---|
| Gear#1–2 | 790.5 | N |
| Gear#2–3 | 769.5 | N |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.-H.; Kim, Y.-C.; Kim, S.-W. Numerical Evaluation of Structural Safety of Linear Actuator for Flap Control of Aircraft Based on Airworthiness Standard. Aerospace 2021, 8, 104. https://doi.org/10.3390/aerospace8040104
Kim D-H, Kim Y-C, Kim S-W. Numerical Evaluation of Structural Safety of Linear Actuator for Flap Control of Aircraft Based on Airworthiness Standard. Aerospace. 2021; 8(4):104. https://doi.org/10.3390/aerospace8040104
Chicago/Turabian StyleKim, Dong-Hyeop, Young-Cheol Kim, and Sang-Woo Kim. 2021. "Numerical Evaluation of Structural Safety of Linear Actuator for Flap Control of Aircraft Based on Airworthiness Standard" Aerospace 8, no. 4: 104. https://doi.org/10.3390/aerospace8040104
APA StyleKim, D.-H., Kim, Y.-C., & Kim, S.-W. (2021). Numerical Evaluation of Structural Safety of Linear Actuator for Flap Control of Aircraft Based on Airworthiness Standard. Aerospace, 8(4), 104. https://doi.org/10.3390/aerospace8040104






