Electrospray Propulsion Engineering Toolkit (ESPET)
Abstract
1. Introduction
2. Overview of ESPET
3. ESPET Components
3.1. Microfluidics Properties Database
3.2. Domain Modeler
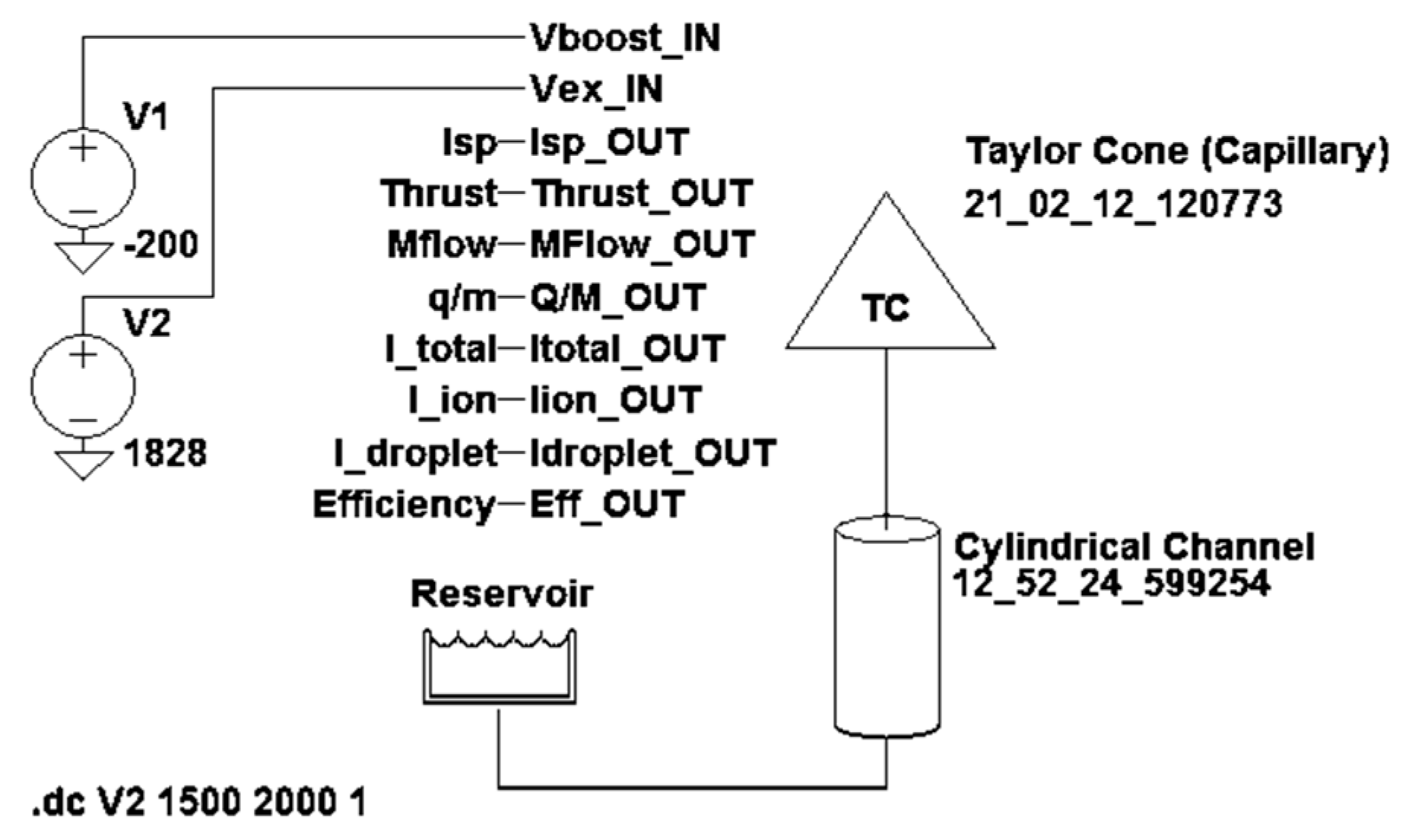
3.2.1. Feed System Models
3.2.2. Emitter Domains
3.3. Network Solver
3.3.1. SPICE Network Solver
3.3.2. QuickSolver
4. Application of ESPET to Examples in the Literature
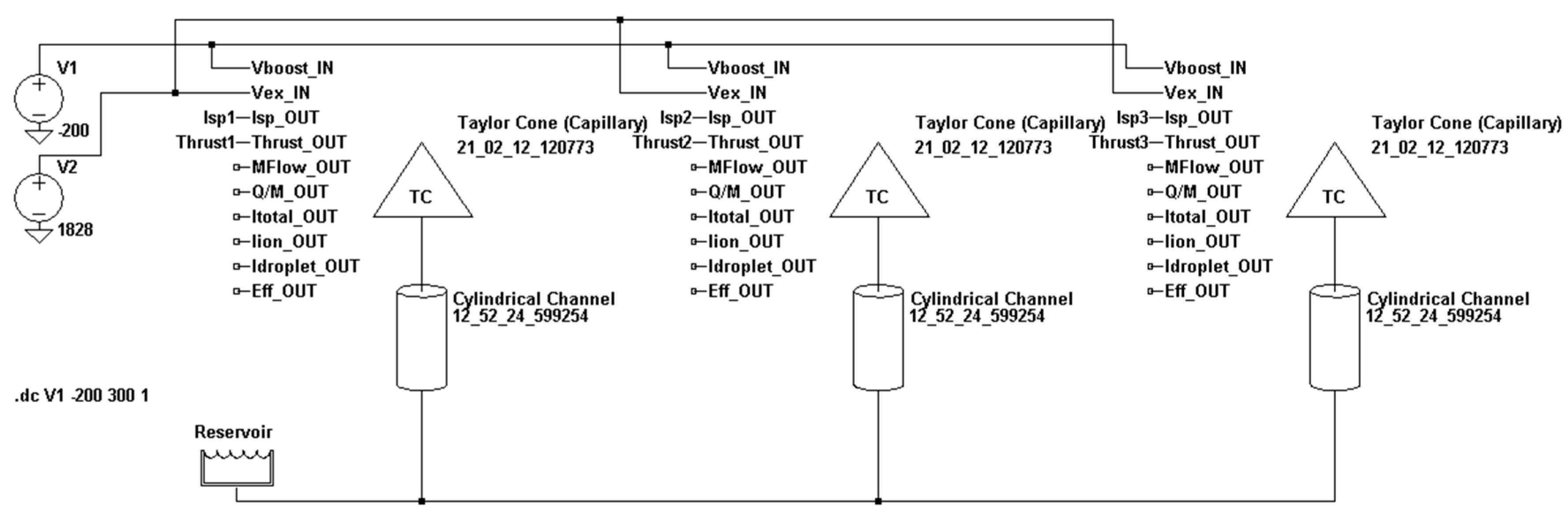
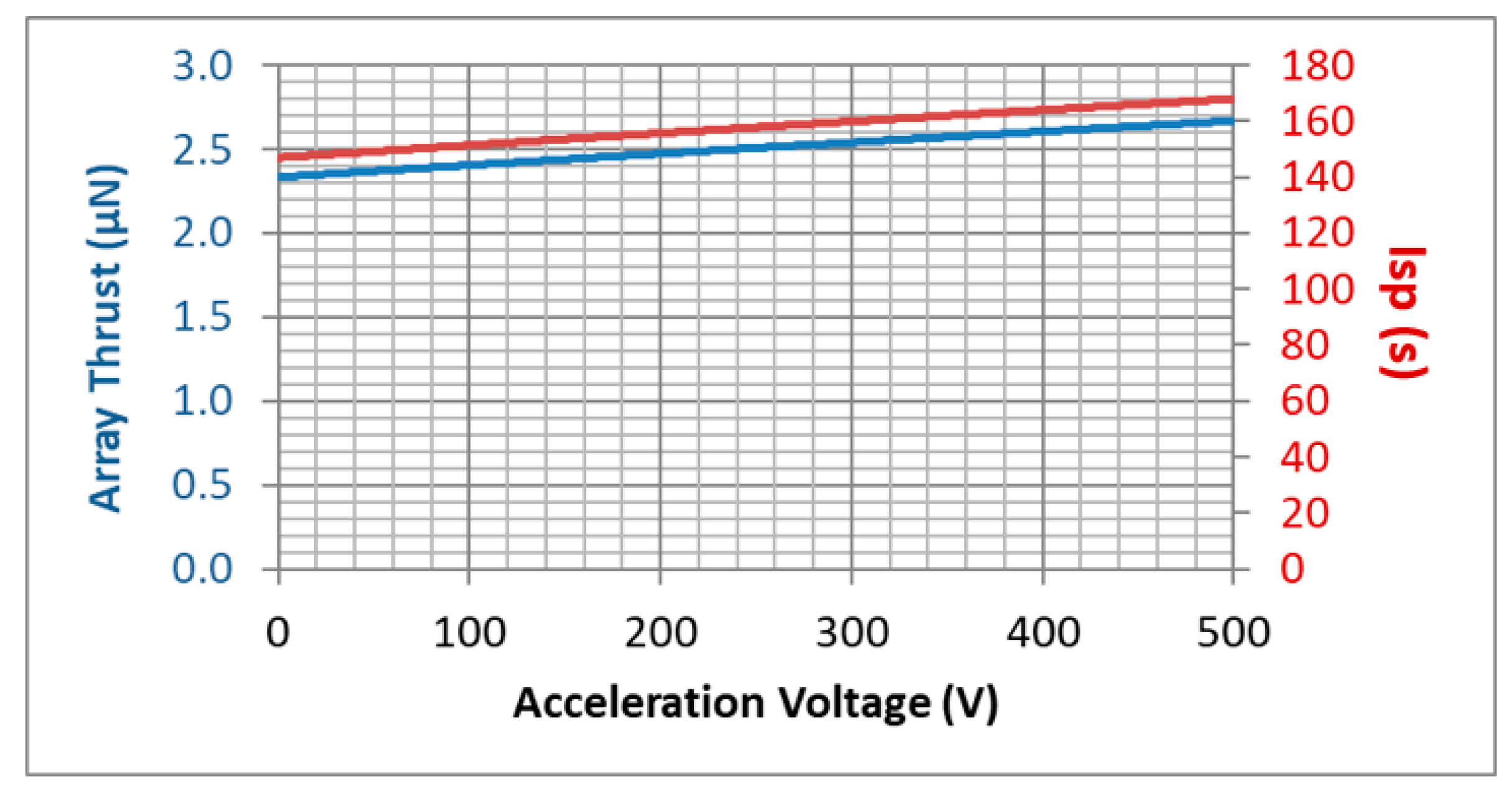
4.1. Actively Pressurized Capillary Emitters Using SPICE Option
4.2. Passively Driven Capillary Emitter Array
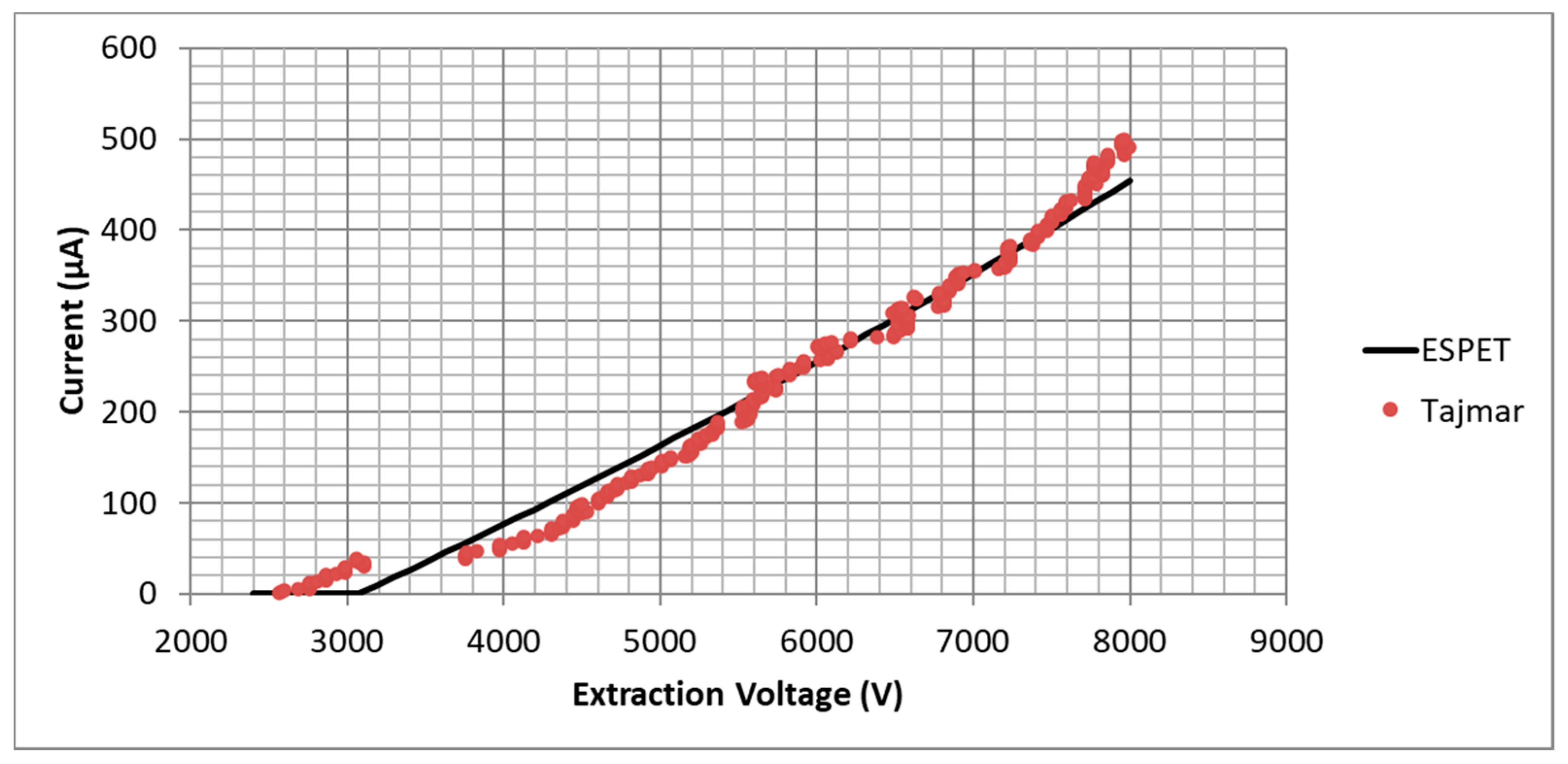
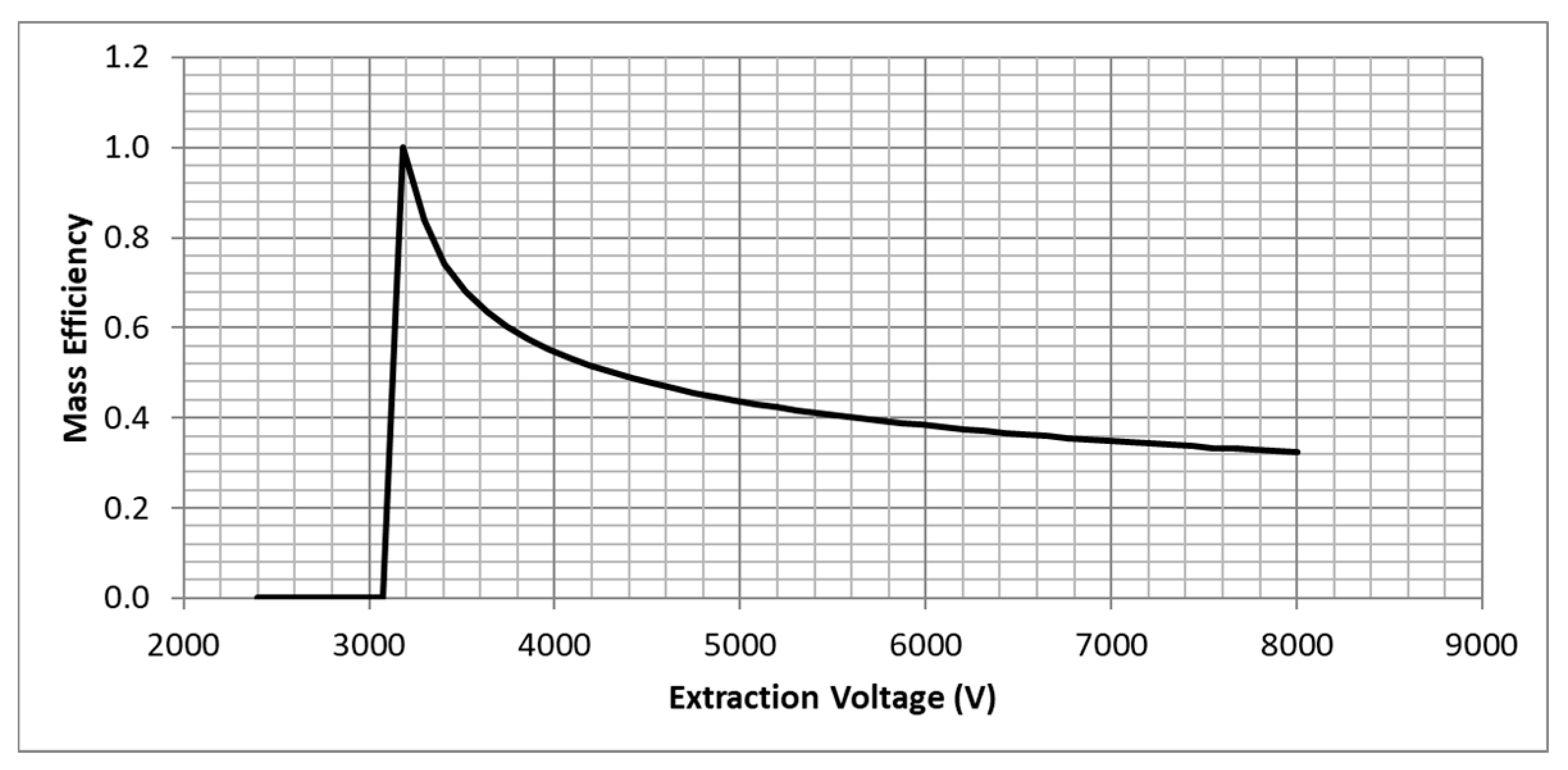
4.3. Externally Wetted Liquid Metal Emitter
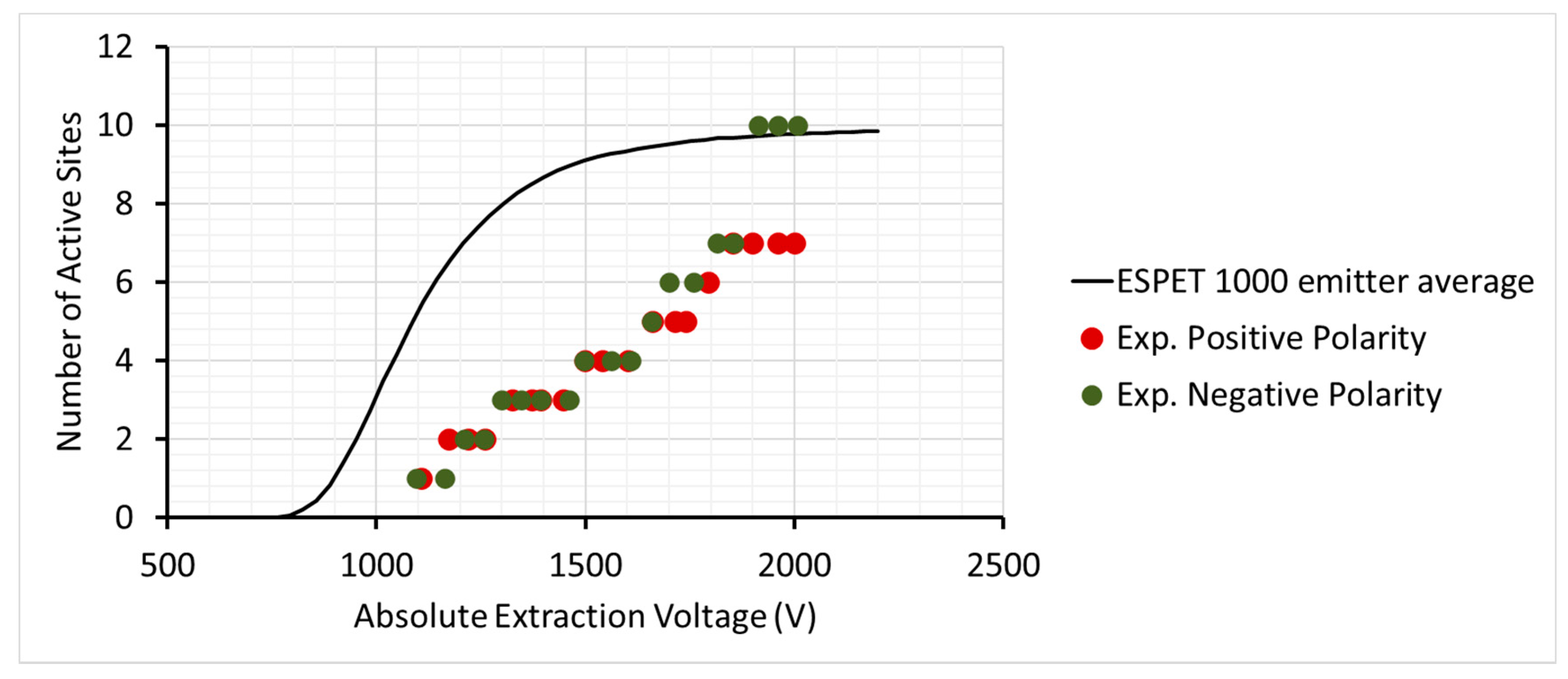
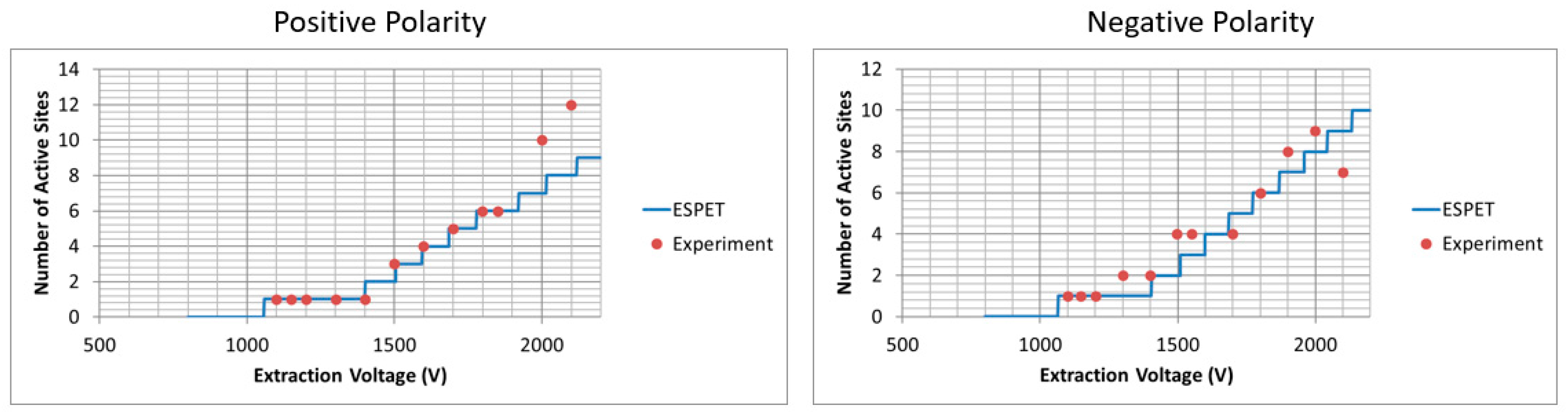
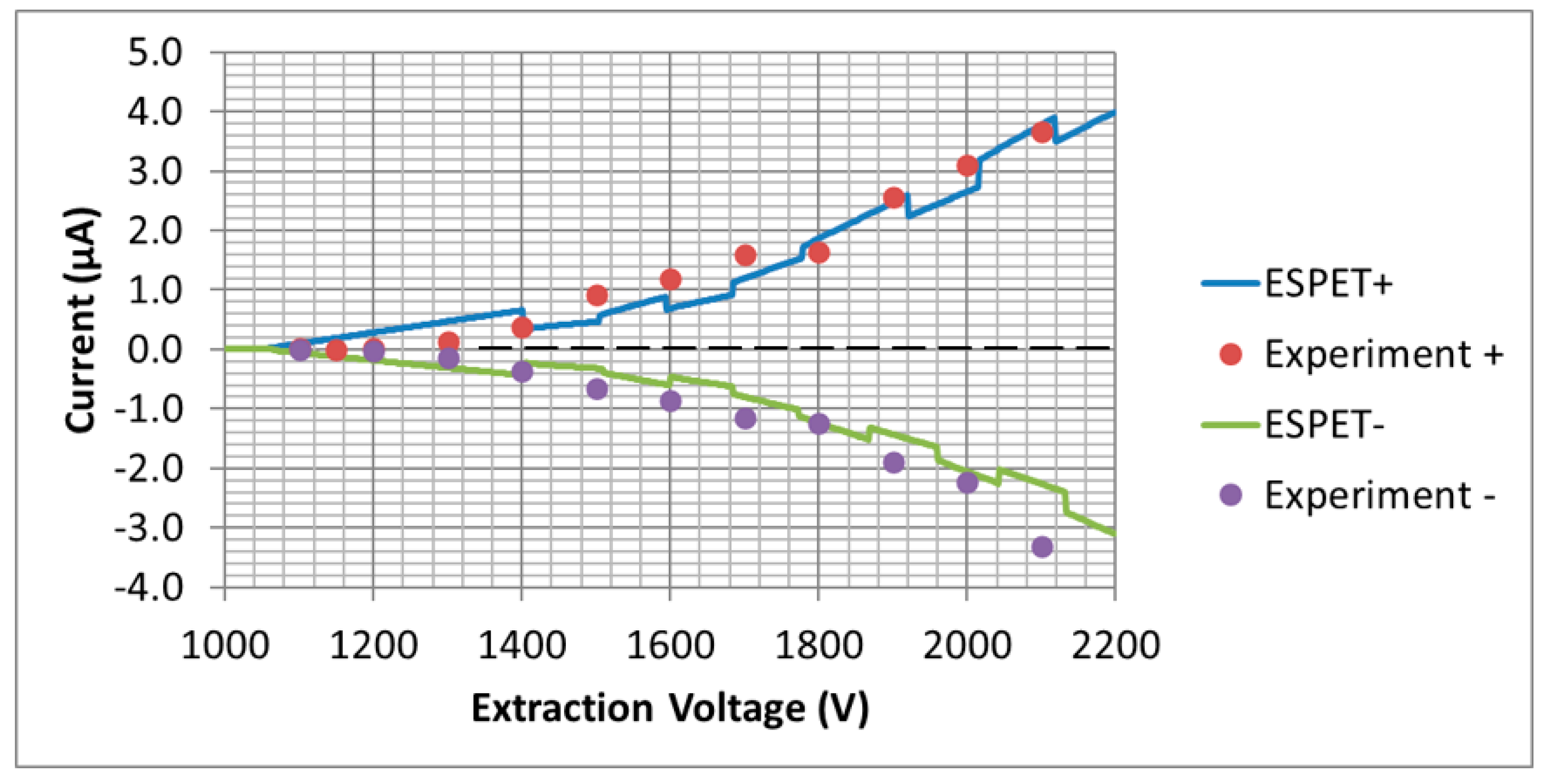
5. The Development of Models for Emitters with Multiple Emission Sites
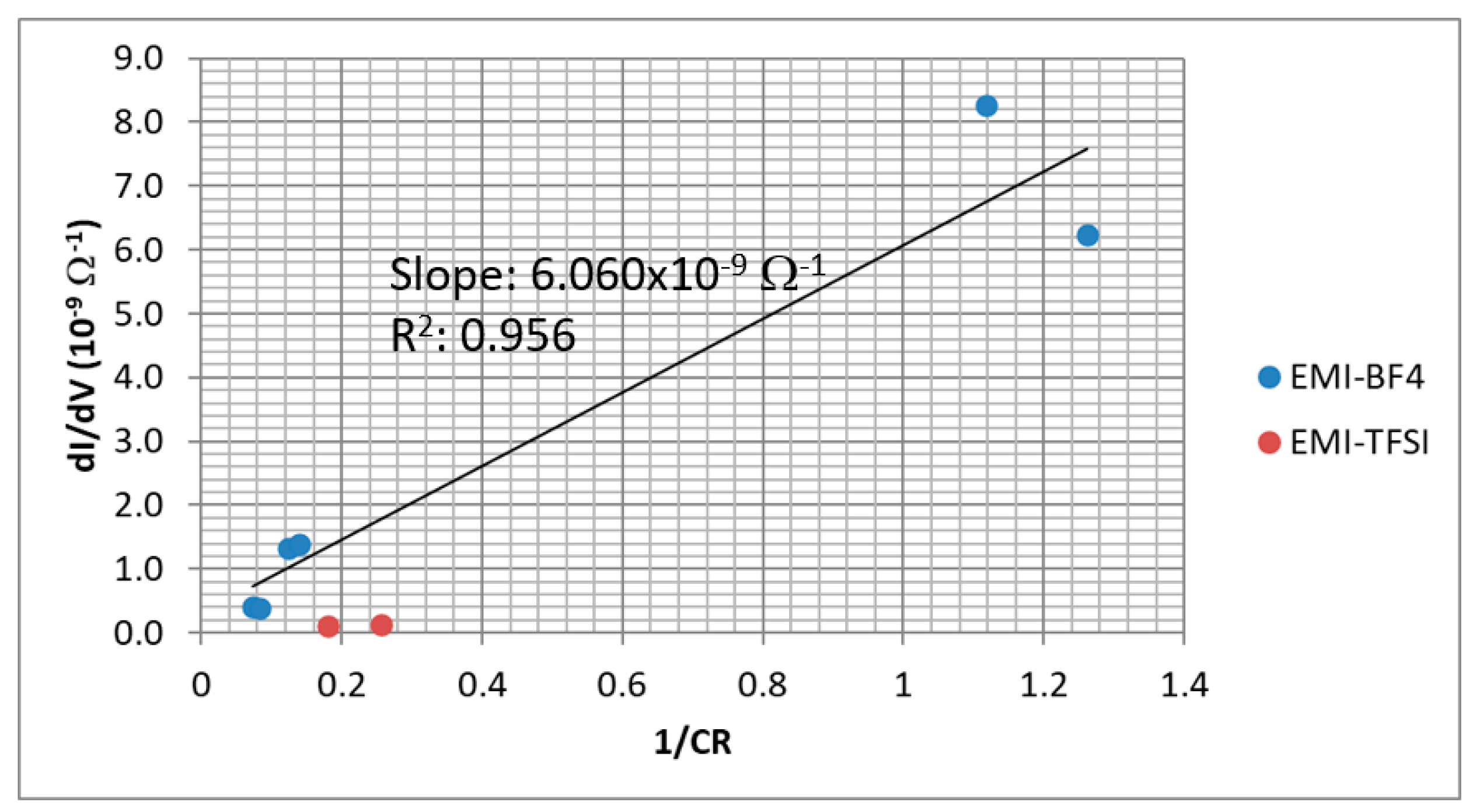
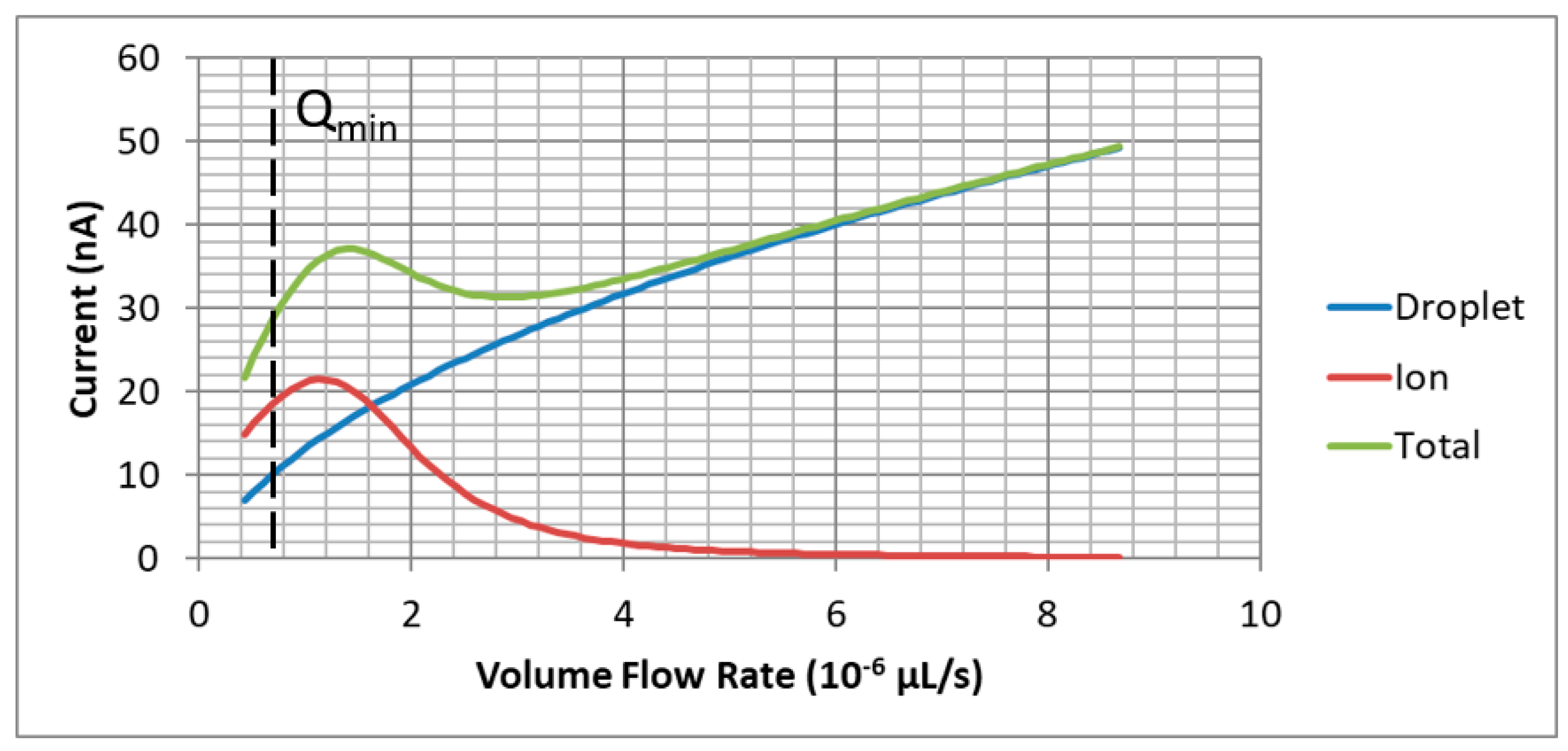
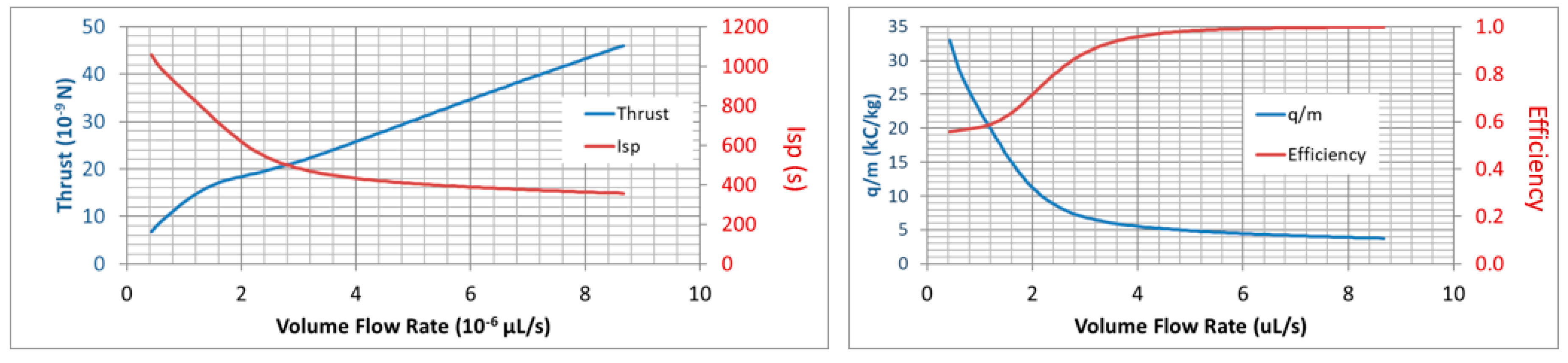
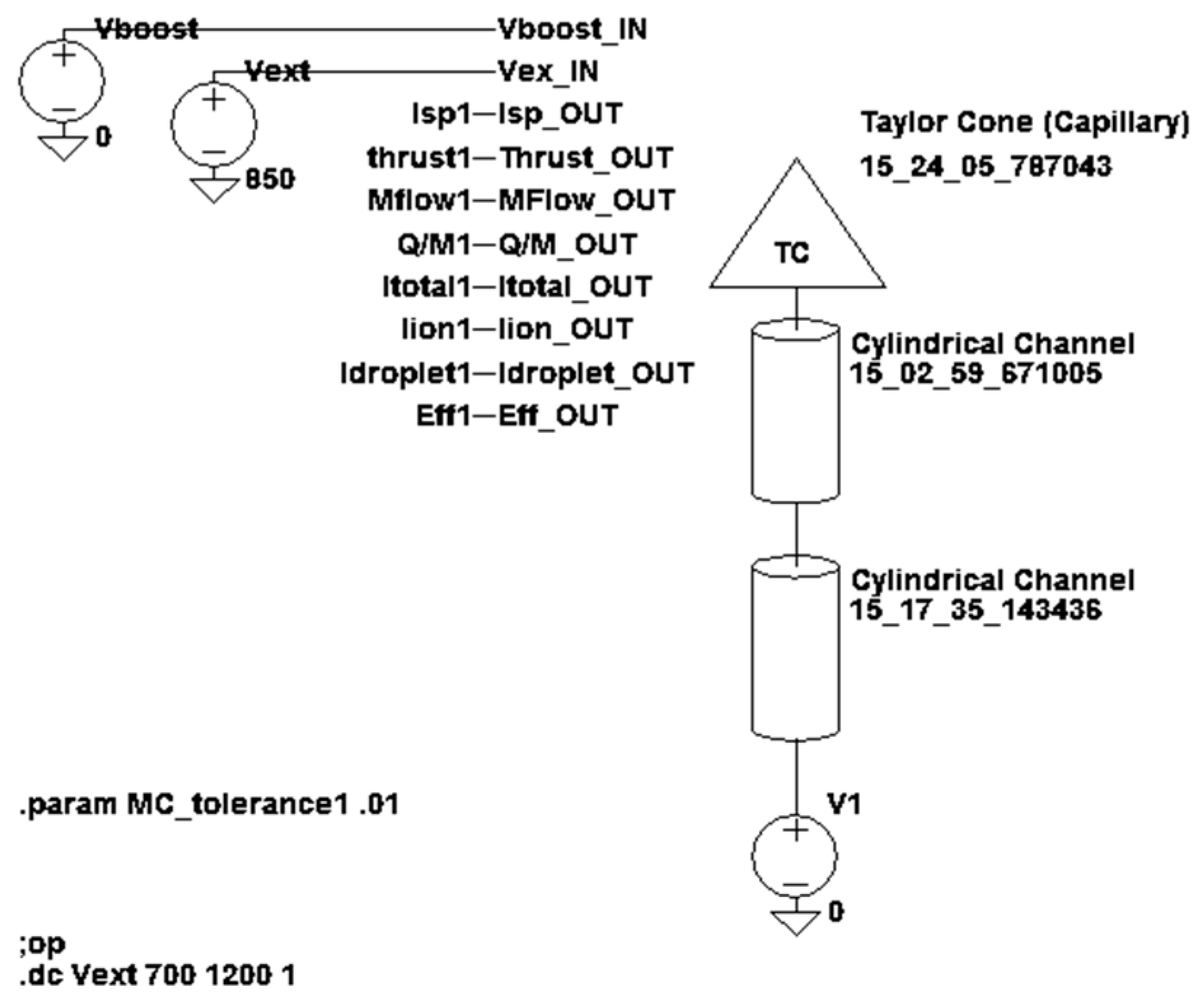
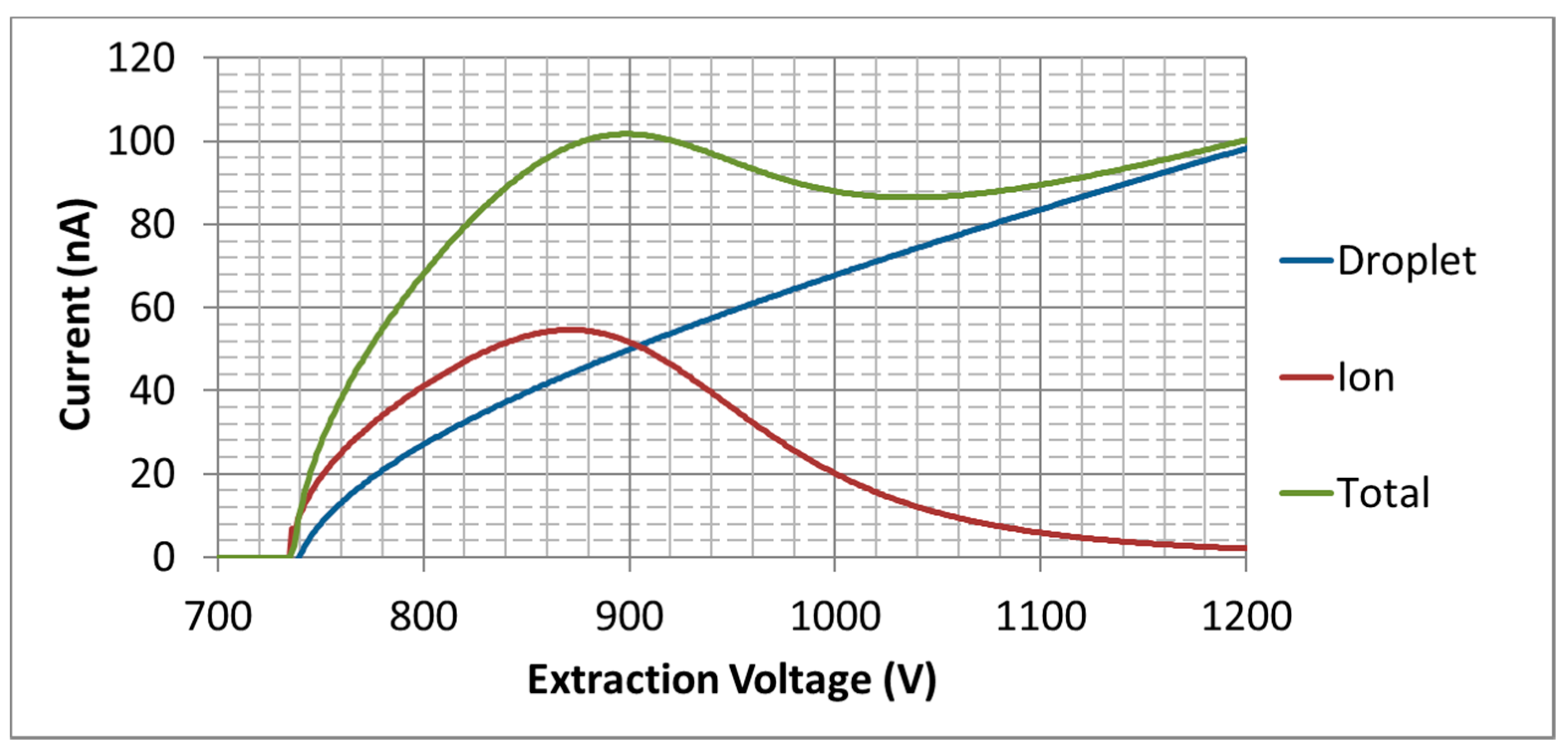
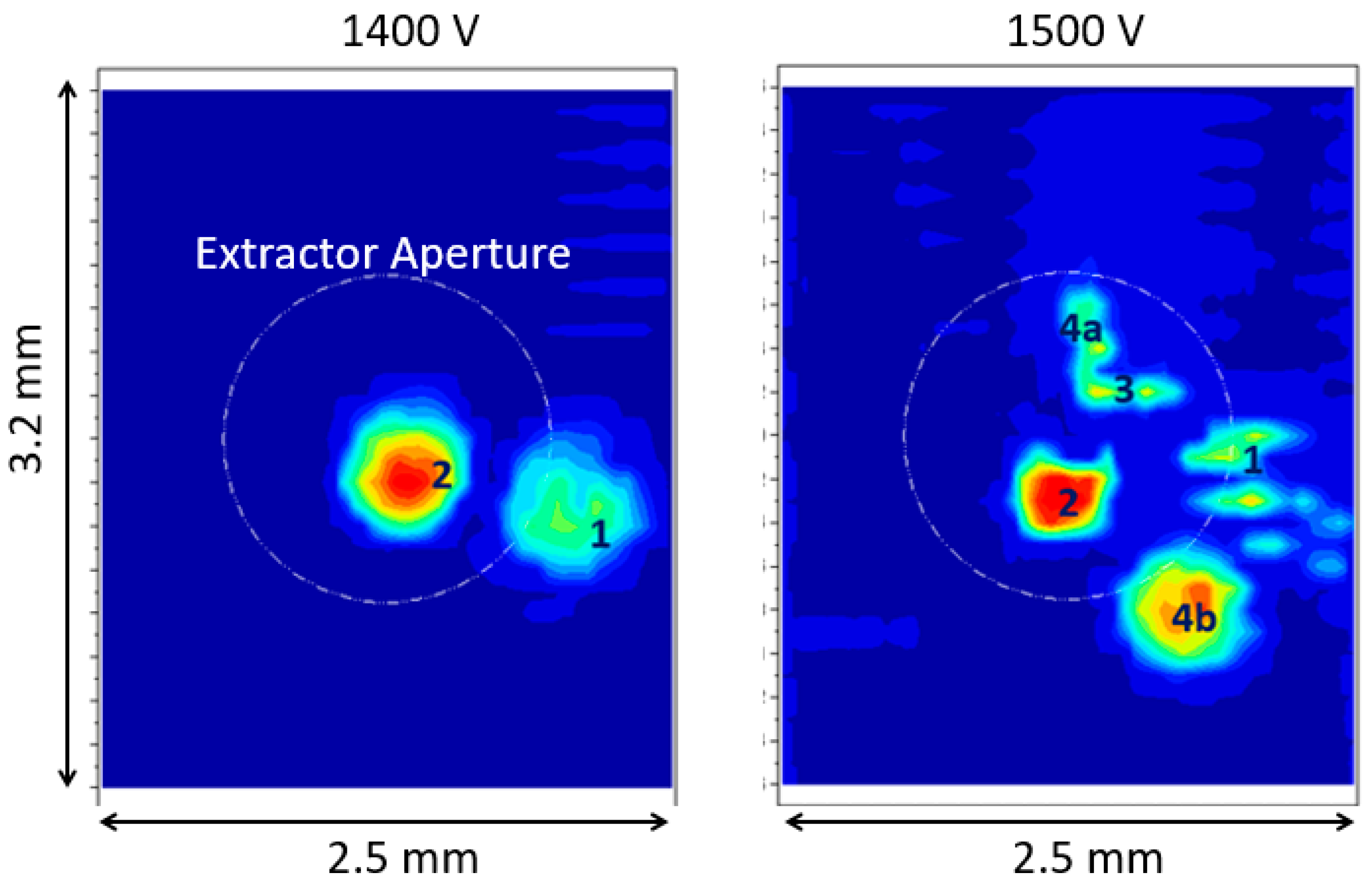
5.1. Externally Wetted Emitter Using Ionic Liquid
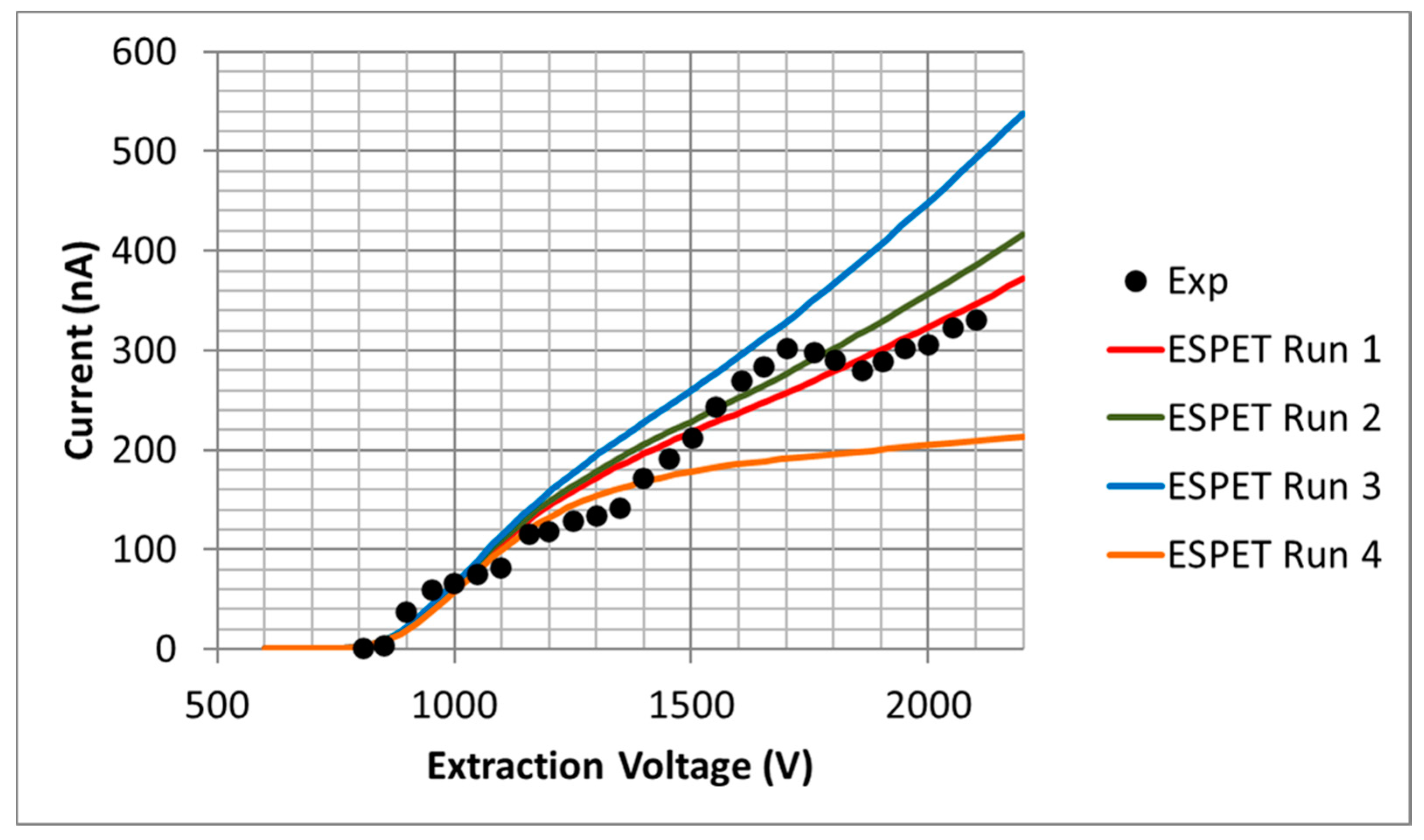
5.2. Conical Porous Glass Emitter Using Ionic Liquid
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dandavino, S.; Ataman, C.; Ryan, C.N.; Chakraborty, S.; Courtney, D.; Stark, J.P.W.; Shea, H. Microfabricated electrospray emitter arrays with integrated extractor and accelerator electrodes for the propulsion of small spacecraft. J. Micromechanics Microengineering 2014, 24, 075011. [Google Scholar] [CrossRef]
- Courtney, D.G.; Li, H.Q.; Lozano, P. Emission measurements from planar arrays of porous ionic liquid ion sources. J. Phys. D Appl. Phys. 2012, 45, 485203. [Google Scholar] [CrossRef]
- Legge, R.S.; Lozano, P.C. Electrospray propulsion based on emitters microfabricated in porous metals. J. Propuls. Power 2011, 27, 485–495. [Google Scholar] [CrossRef]
- Gassend, B.; Velasquez-Garcia, L.F.; Akinwande, A.I.; Martinez-Sanchez, M. A Microfabricated Planar Electrospray Array Ionic Liquid Ion Source With Integrated Extractor. Microelectromechanical Syst. J. 2009, 18, 679–694. [Google Scholar] [CrossRef]
- Velasquez-Garcia, L.F.; Akinwande, A.I.; Martinez-Sanchez, M. A Planar Array of Micro-Fabricated Electrospray Emitters for Thruster Applications. J. Microelectromechanical Syst. 2006, 15, 1272–1280. [Google Scholar] [CrossRef]
- Taylor, G.I. Disintegration of water drops in an electric field. Proc. R. Soc. A 1964, 280, 383–397. [Google Scholar]
- De la Mora, J.F. The effect of charge emission from electrified liquid cones. J. Fluid Mech. 1992, 243, 561–574. [Google Scholar] [CrossRef]
- De la Mora, J.F. The fluid dynamics of Taylor cones. Annu. Rev. Fluid Mech. 2007, 39, 217–243. [Google Scholar] [CrossRef]
- De la Mora, J.F.; Loscertales, I.G. The current emitted by highly conducting Taylor cones. J. Fluid Mech. 1994, 260, 155–184. [Google Scholar] [CrossRef]
- Gamero-Castaño, M.; Aguirre-de-Carcer, I.; De Juan, L.; de la Mora, J.F. On the current emitted by Taylor cone-jets of electrolytes in vacuo: Implications for liquid metal ion sources. J. Appl. Phys. 1998, 83, 2428–2434. [Google Scholar] [CrossRef]
- Gamero-Castaño, M.; de la Mora, J.F. Direct measurement of ion evaporation kinetics from electrified liquid surfaces. J. Chem. Phys. 2000, 113, 815–832. [Google Scholar] [CrossRef]
- Loscertales, I.; de la Mora, J.F. Experiments on the kinetics of field evaporation of small ions from droplets. J. Chem. Phys. 1995, 103, 5041–5060. [Google Scholar] [CrossRef]
- Mair, G. The effects of flow impedance on the current-voltage characteristics of liquid-metal ion sources. J. Phys. D Appl. Phys. 1997, 30, 1945. [Google Scholar] [CrossRef]
- Tajmar, M. Influence of Taylor cone size on droplet generation in an indium liquid metal ion source. Appl. Phys. A 2005, 81, 1447–1450. [Google Scholar] [CrossRef]
- Tajmar, M. Indium capillary liquid-metal-ion-source operation in the flow resistance regime. J. Phys. D Appl. Phys. 2004, 37, 3056. [Google Scholar] [CrossRef]
- Courtney, D.G.; Shea, H. Influences of porous reservoir Laplace pressure on emissions from passively fed ionic liquid electrospray sources. Appl. Phys. Lett. 2015, 107, 103504. [Google Scholar] [CrossRef]
- Coffman, C. Charge Emission from Electrified Ionic Liquid Menisci: Fundamental Phenomena and Applications to Micropropulsion. Ph.D. Thesis, Aeronautics and Astronautics Dept, Massachusetts Institute of Technology, Cambridge, MA, USA, 2016. [Google Scholar]
- Coffman, C.; Martínez-Sánchez, M.; Higuera, F.J.; Lozano, P.C. Structure of the menisci of leaky dielectric liquids during electrically-assisted evaporation of ions. Appl. Phys. Lett. 2016, 109, 231602. [Google Scholar] [CrossRef]
- Cloupeau, M.; Prunet-Foch, B. Electrohydrodynamic spraying functioning modes: A critical review. J. Aerosol Sci. 1994, 25, 1021–1036. [Google Scholar] [CrossRef]
- SPICE. Available online: http://embedded.eecs.berkeley.edu/pubs/downloads/spice/ (accessed on 30 June 2020).
- SQLite. Available online: https://www.sqlite.org/ (accessed on 30 June 2020).
- Fröba, A.P.; Kremer, H.; Leipertz, A. Density, refractive index, interfacial tension, and viscosity of ionic liquids [EMIM][EtSO4], [EMIM][NTf2], [EMIM][N(CN)2], and [OMA][NTf2] in dependence on temperature at atmospheric pressure. J. Phys. Chem. B 2008, 112, 12420–12430. [Google Scholar] [CrossRef]
- Zaitsau, D.H.; Kabo, G.J.; Strechan, A.A.; Paulechka, Y.U.; Tschersich, A.; Verevkin, S.P.; Heintz, A. Experimental vapor pressures of 1-Alkyl-3-methylimidazolium Bis(trifluoromethylsulfonyl)imides and a correlation scheme for estimation of vaporization enthalpies of ionic liquids. J. Phys. Chem. A 2006, 110, 7303–7306. [Google Scholar] [CrossRef]
- Umecky, T.; Saito, Y.; Matsumoto, H. Direct measurements of ionic mobility of ionic liquids using the electric field applying pulsed gradient spin-echo NMR. J. Phys. Chem. B 2009, 113, 8466–8468. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Sun, N.; He, X.; Lu, X.; Zhang, X. Physical properties of ionic liquids: Database and evaluation. J. Phys. Chem. Ref. Data 2006, 35, 1475–1517. [Google Scholar] [CrossRef]
- Kolbeck, C.; Lehmann, J.; Lovelock, K.; Cremer, T.; Paape, N.; Wasserscheid, P.; Froba, A.; Maier, F.; Steinruck, H.-P. Density and surface tension of ionic liquids. J. Phys. Chem. B 2010, 114, 17025–17036. [Google Scholar] [CrossRef] [PubMed]
- McEwen, A.B.; Ngo, H.L.; LeCompte, K.; Goldman, J.L. Electrochemical properties of imidazolium salt electrolytes for electrochemical capacitor applications. J. Electrochem. Soc. 1999, 146, 1687–1695. [Google Scholar] [CrossRef]
- Xu, W.-G.; Li, L.; Ma, X.-X.; Wei, J.; Duan, W.-B.; Guan, W.; Yang, J.-Z. Density, surface tension, and refractive index of ionic liquids homologue of 1-alkyl-3-methylimidazolium tetrafluoroborate [Cn mim][BF4](n= 2, 3, 4, 5, 6). J. Chem. Eng. Data 2012, 57, 2177–2184. [Google Scholar] [CrossRef]
- Wakai, C.; Oleinikova, A.; Ott, M.; Weingärtner, H. How polar are ionic liquids? Determination of the static dielectric constant of an imidazolium-based ionic liquid by microwave dielectric spectroscopy. J. Phys. Chem. B 2005, 109, 17028–17030. [Google Scholar] [CrossRef]
- Yang, J.-Z.; Zhang, Q.-G.; Xue, F. Studies on the properties of EMIGaCl4. J. Mol. Liq. 2006, 128, 81–84. [Google Scholar] [CrossRef]
- Perez-Martinez, C.S. Engineering Ionic Liquid Ion Sources for Ion Beam Applications. Ph.D. Thesis, Aeronautics and Astronautics Dept, Massachusetts Institute of Technology, Cambridge, MA, USA, 2016. [Google Scholar]
- Williams, D.D.; Miller, R.R. Densities of Liquid and Solid Indium. J. Am. Chem. Soc. 1950, 72, 3821. [Google Scholar] [CrossRef]
- Strauss, S. The temperature dependence of the viscosity of liquid metals Nucl. Sci. Eng. 1962, 12, 436–439. [Google Scholar]
- Keene, B. Review of data for the surface tension of pure metals. Int. Mater. Rev. 1993, 38, 157–192. [Google Scholar] [CrossRef]
- Cusack, N.E. The electronic properties of liquid metals. Rep. Prog. Phys. 1963, 26, 361. [Google Scholar] [CrossRef]
- Hardy, S.C. The surface tension of liquid gallium. J. Cryst. Growth 1985, 71, 602–606. [Google Scholar] [CrossRef]
- Lu, H.; Jiang, Q. Surface tension and its temperature coefficient for liquid metals. J. Phys. Chem. B 2005, 109, 15463–15468. [Google Scholar] [CrossRef] [PubMed]
- Dandavino, S.; Ataman, C.; Shea, H.; Ryan, C.; Stark, J. Microfabrication of capillary electrospray emitters and tof characterization of the emitted beam. IEPC-2011-131. In Proceedings of the 32nd International Electric Propulsion Conference, Wiesbaden, Germany, 11–15 September 2011. [Google Scholar]
- Higuera, F.J. Model of the meniscus of an ionic-liquid ion source. Phys. Rev. E 2008, 77, 026308. [Google Scholar] [CrossRef] [PubMed]
- Forbes, R.G. Liquid-Metal ion sources and electrosprays operating in cone-jet mode: Some theoretical comparisons and comments. J. Aerosol Sci. 2000, 31, 97–120. [Google Scholar] [CrossRef]
- Forbes, R.G.; Ljepojevic, N.N. Liquid-metal ion source theory: Electrohydrodynamics and emitter shape. Surf. Sci. 1992, 266, 170–175. [Google Scholar] [CrossRef]
- Tajmar, M.; Genovese, A. Experimental validation of a mass-efficiency model for an indium liquid-metal ion source. Appl. Phys. A 2003, 76, 1003–1006. [Google Scholar] [CrossRef]
- Perez-Martinez, C.; Lozano, P. Ion field-evaporation from ionic liquids infusing carbon xerogel microtips. Appl. Phys. Lett. 2015, 107, 043501. [Google Scholar] [CrossRef]
- Tajmar, M.; Jang, B. New materials and processes for field emission ion and electron emitters. Ceas Space J. 2013, 4, 47–54. [Google Scholar] [CrossRef]
- Reissner, A.; Buldrini, N.; Seifert, B.; Hörbe, T.; Plesescu, F.; del Amo, J.G.; Massotti, L. Testing and Modelling of the mN-FEEP Start-Up Performance. IEPC-2015-123. In Proceedings of the 34th International Electric Propulsion Conference and 6th Nano-satellite Symposium, Hyogo-Kobe, Japan, 4–10 July 2015. [Google Scholar]
- Vasiljevich, I.; Buldrini, N.; Plesescu, F.; Schamiloglu, E. Performance of porous tungsten needle lims for use as indium feep emitters. IEPC-2011-268. In Proceedings of the 32nd International Electric Propulsion Conference, Wiesbaden, Germany, 11–15 September 2011. [Google Scholar]
- Gañán-Calvo, A.M.; Dávila, J.; Barrero, A. Current and droplet size in the electrospraying of liquids. Scaling laws. J. Aerosol Sci. 1997, 28, 249–275. [Google Scholar] [CrossRef]
- Gamero-Castaño, M. Characterization of the electrosprays of 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl) imide in vacuum. Phys. Fluids 2008, 20, 032103. [Google Scholar] [CrossRef]
- Guerra-Garcia, C.; Krejci, D.; Lozano, P. Spatial uniformity of the current emitted by an array of passively fed electrospray porous emitters. J. Phys. D Appl. Phys. 2016, 49, 115503. [Google Scholar] [CrossRef]
- LTspice. Available online: http://www.linear.com/solutions/ltspice. (accessed on 30 June 2020).
- Gamero-Castaño, M.; Hruby, V. Electrospray as a source of nanoparticles for efficient colloid thrusters. J. Propuls. Power 2001, 17, 977–987. [Google Scholar] [CrossRef]
- Gamero-Castaño, M. Characterization of a six-emitter colloid thruster using a torsional balance. J. Propuls. Power 2004, 20, 736–741. [Google Scholar] [CrossRef]
- Jorns, B.A.; Gorodetsky, A.; Lasky, I.; Kimber, A.; Dahl, P.; Peter, B.S.; Dressler, R. Uncertainty Quantification of Electrospray Thruster Array Lifetime. IEPC-2019-317. In Proceedings of the 36th International Electric Propulsion Conference, Vienna, Austria, 15–20 September 2019. [Google Scholar]
- Collins, A.L.; Thuppul, A.; Wright, P.L.; Uchizono, N.M.; Huh, H.; Davis, M.J.; Ziemer, J.K.; Demmons, N.R.; Wirz, R.E. Assessment of grid impingement for electrospray thruster lifetime. IEPC-2019-213. In Proceedings of the 36th International Electric Propulsion Conference, Vienna, Austria, 15–20 September 2019. [Google Scholar]
- Wirz, R.E.; Collins, A.C.; Thuppul, A.; Wright, P.L.; Uchizono, N.M.; Huh, H.; Davis, M.J. Electrospray Thruster Performance and Lifetime Investigation for the LISA Mission. AIAA-2019-3816. In Proceedings of the AIAA Propulsion and Energy Forum, Indianapolis, IN, USA, 16 August 2019. [Google Scholar]
- Thuppul, A.; Wright, P.L.; Wirz, R.E. Lifetime Considerations and Estimation for Electrospray Thrusters. AIAA-2018-4652. In Proceedings of the 54th AIAA/SAE/ASEE Joint Propulsion Conference, Cincinnati, OH, USA, 8 July 2018. [Google Scholar] [CrossRef]
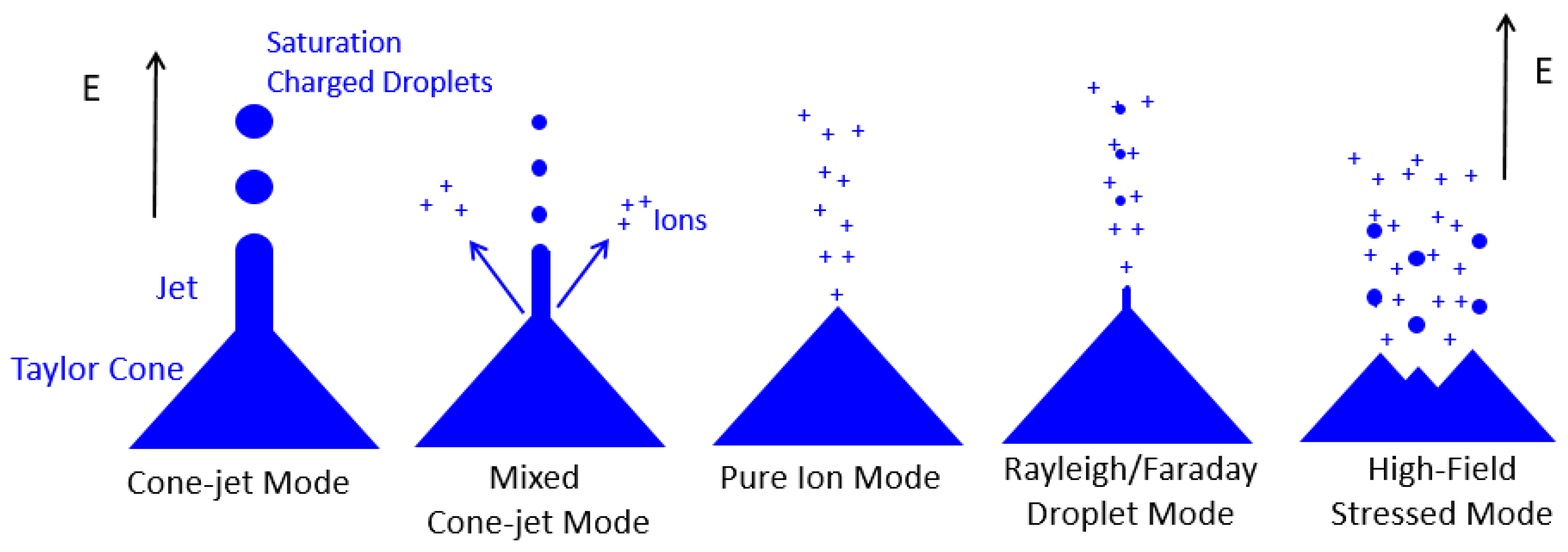
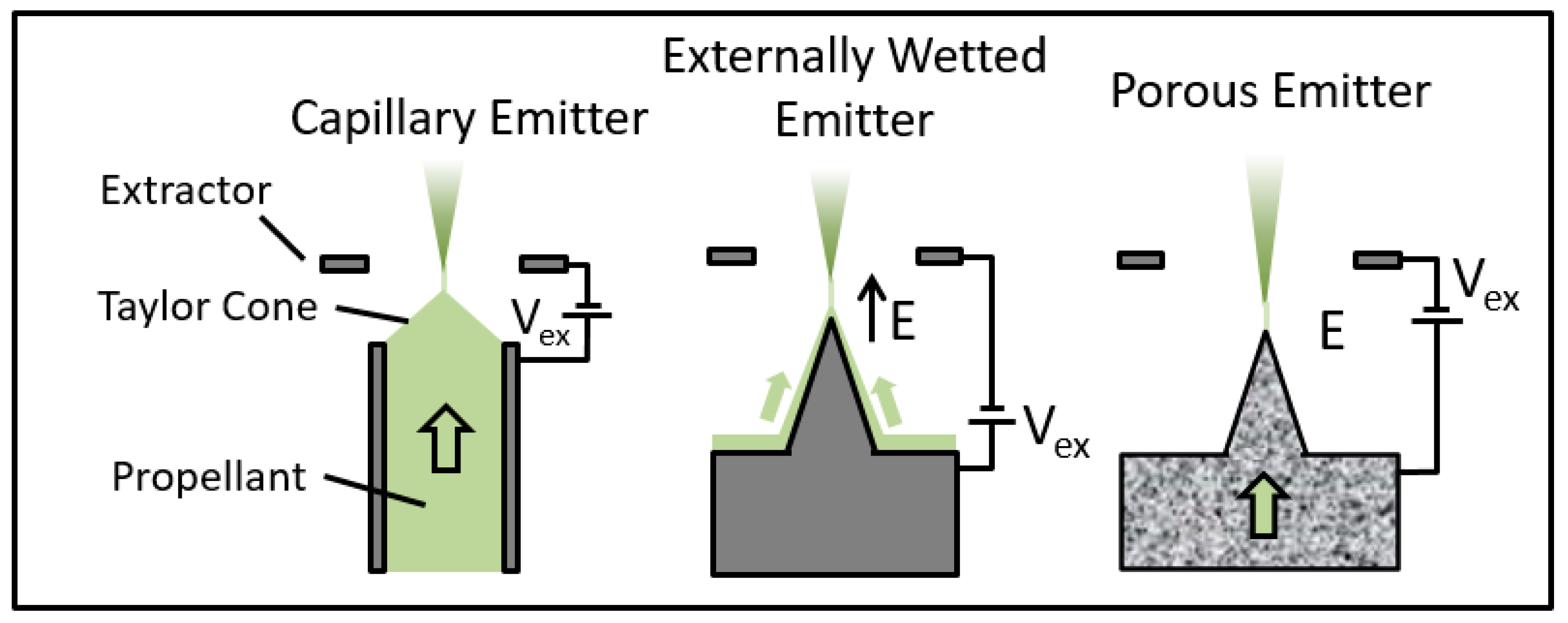
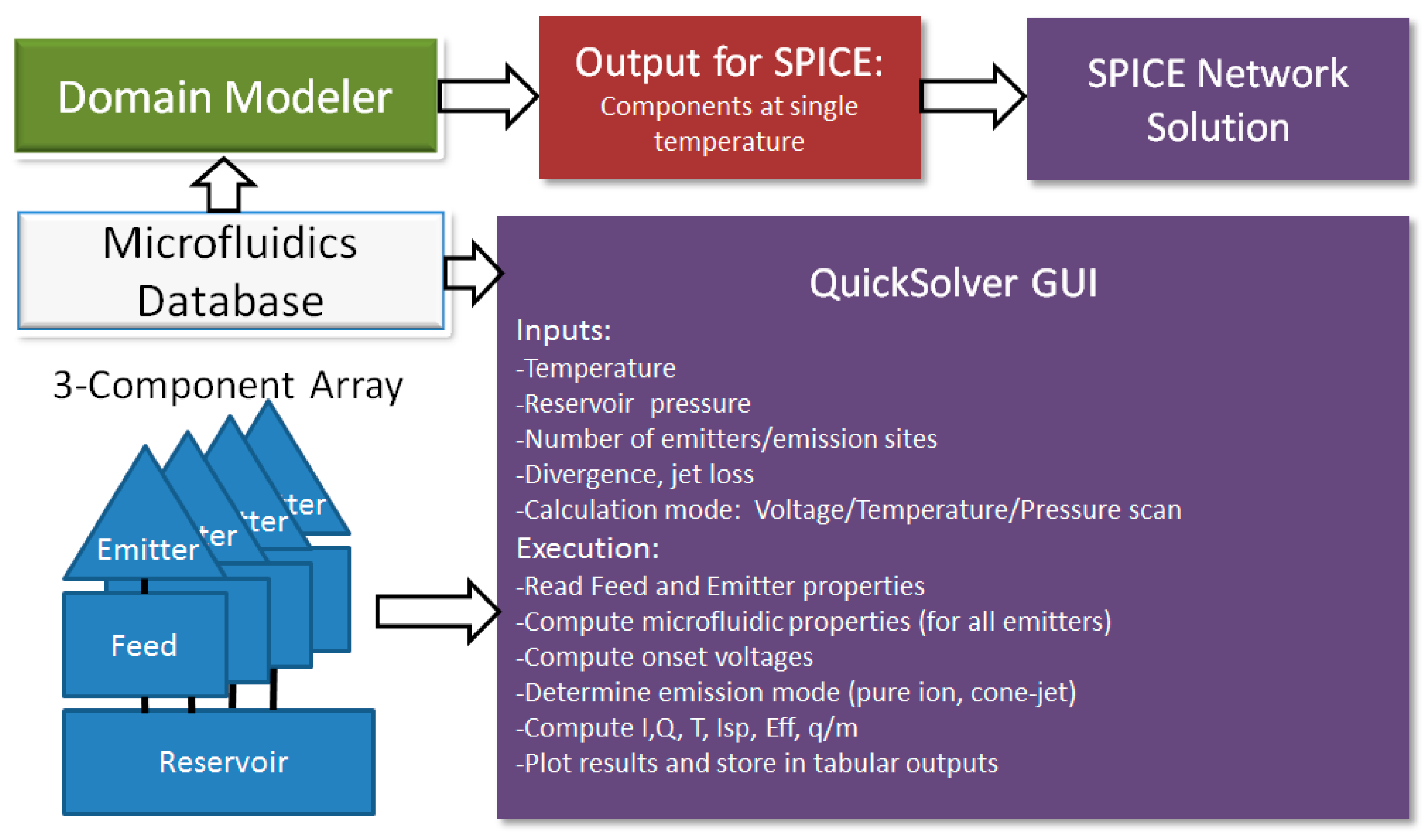
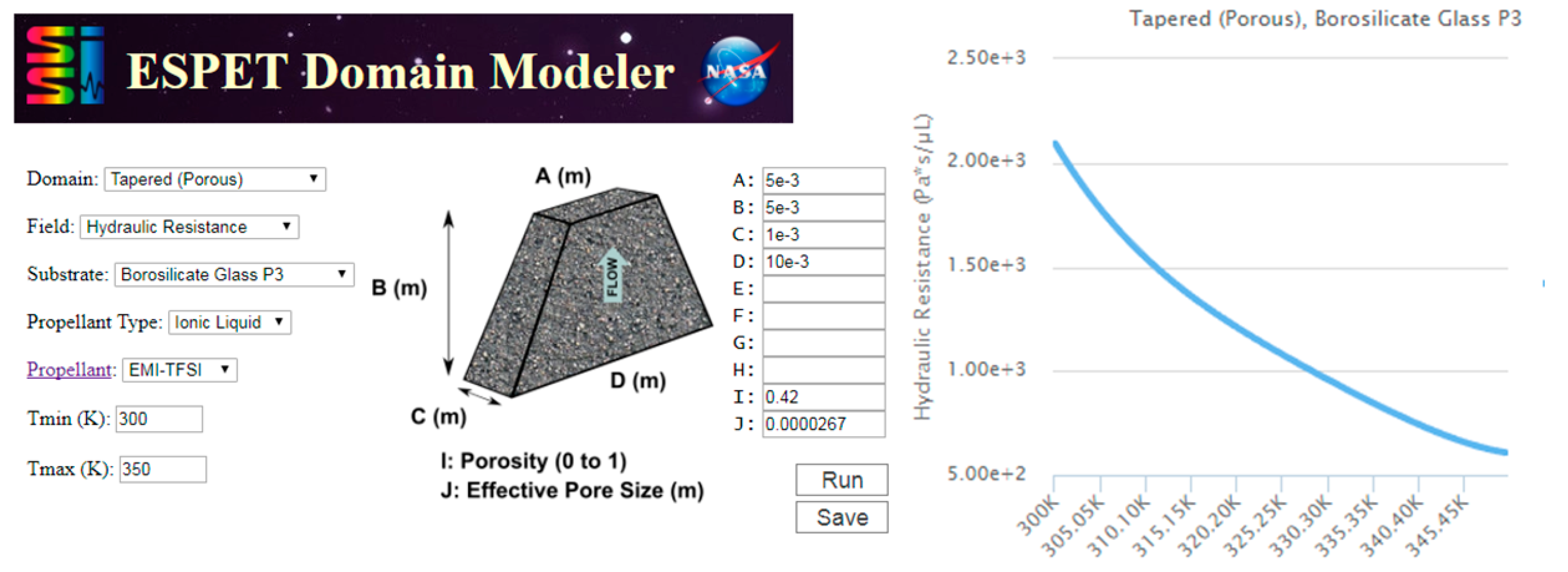




| Propellant | References |
|---|---|
| Ionic Liquids: | |
| EMI-TFSI | [22,23,24,25] |
| EMI-BF4 | [24,25,26,27,28,29] |
| EMI-GaCl4 | [30,31] |
| Liquid Metals: | |
| Indium | [32,33,34,35] |
| Gallium | [33,35,36] |
| Cesium | [33,34,35,37] |
| Substrate | Type | Description |
|---|---|---|
| Stainless Steel Fiber Mat | Porous | Metallic fiber filter |
| Silicon | Channel | Oxidized silicon |
| Borosilicate Glass | Channel | Borosilicate glass channel |
| Tungsten | Porous | |
| Rhenium | Porous | |
| Borosilicate Glass P0 | Porous | Sintered porous glass |
| Borosilicate Glass P1 | Porous | Sintered porous glass |
| Borosilicate Glass P2 | Porous | Sintered porous glass |
| Borosilicate Glass P3 | Porous | Sintered porous glass |
| Borosilicate Glass P4 | Porous | Sintered porous glass |
| Borosilicate Glass P5 | Porous | Sintered porous glass |
| Borosilicate Glass Fiber Mat | Porous | Glass fiber filter |
| Xerogel 1 | Porous | Carbon xerogel |
| Gold | Channel | |
| Platinum | Channel | |
| Aluminum | Channel |
| Propellant Fields | Substrate Fields | Interface Fields |
|---|---|---|
| Molecular Mass | Density | Contact Angle |
| Melting Temp | Conductivity | Effective Pore Size |
| Decomposition Temp | Porosity | |
| Mobility | Roughness | |
| Electrochemical Window | Relative Permittivity | |
| Cathode Limit | ||
| Anode Limit | ||
| Dissociation Energy | ||
| Monomer Cation Solvation Energy | ||
| Monomer Anion Solvation Energy | ||
| Dimer Cation Solvation Energy | ||
| Dimer Anion Solvation Energy | ||
| Density a | ||
| Dynamic Viscosity a | ||
| Surface Tension a | ||
| Conductivity a | ||
| Relative Permittivity a | ||
| Vapor Pressure a |
| Emitter Type | ESPET Domain Name | Status | References |
|---|---|---|---|
| Capillary (internally wetted) | Taylor Cone (Capillary) | Ionic liquid Liquid metal | [12,13,17,18,39,40,41,42] |
| Conical porous tip | Taylor Cone (Porous) | Ionic liquid Liquid metal | [2,3,43] [44,45,46] |
| Porous edge | Taylor Edge (Porous) | Ionic liquid Liquid metal | [16] |
| Conical externally wetted | Taylor Cone (Ext Wetted) | Ionic liquid Liquid metal | [12,13,17,18,39,40,41,42] |
| Edge externally wetted | Taylor Edge (Ext Wetted) | Ionic liquid Liquid metal | [12,13,17,18,39,40,41,42] |
| Property | ESPET | Busek | ESPET | Busek |
|---|---|---|---|---|
| Pressure (Pa) | 4100 | 1600 | ||
| Thrust (μN) | 0.78 | 0.63 | 0.38 | 0.35 |
| Isp (s) | 147 | 126 | 185 | 171 |
| q/m (C/kg) | 636 | 625 | 1008 | 820 |
| Mass flow (μg/s) | 0.54 | 0.54 | 0.21 | 0.21 |
| Current (μA) | 0.34 | 0.31 | 0.21 | 0.22 |
| Extraction voltage (V) | 1828 | 1828 | 1828 | 1828 |
| Efficiency (%) | 89 | 68 | 89 | 68 |
| Property | EPFL | ESPET (SPICE) |
|---|---|---|
| Current (nA) | 250 | 92.7 |
| Thrust (nN) | 16.5 | 23.7 |
| Isp (s) | 474 | 678 |
| (kg/s) | 3.55 × 10−12 | 3.56 × 10−12 |
| q/m (C/kg) | 70,423 | 26,020 |
| Efficiency, η | 0.18 | 0.29 |
| Power, P (µW) | 212 | 79 |
| fion | 0.95 | 0.57 |
| Property | EPFL | ESPET QuickSolver |
|---|---|---|
| I (nA) | 250 | 246 |
| Thrust (nN) | 16.5 | 23.1 |
| Isp (s) | 474 | 520 |
| (kg/s) | 3.55 × 10−12 | 4.54 × 10−12 |
| q/m (C/kg) | 70,423 | 54,185 |
| Efficiency, η | 0.18 | 0.28 |
| Power, P (µW) | 212 | 209 |
| Input Parameters | Value |
|---|---|
| Emitter inner radius (µm) | 3.95 ± 0.25 |
| CR (average) | 3.2 |
| CR mode limit | 3.25 |
| B(Ω-1) | 1.8 × 10−8 |
| pscale | 0.023 |
| Droplet energy loss (V) | 150 |
| Beam divergence | 30° |
| Tip-to-extractor distance (μm) | 175 |
| Output Parameters | Value |
| Fraction of emitters in pure ionic regime (PIR) | 0.46 |
| Parameter | Value |
|---|---|
| Curvature, Rc (μm) | 2.25 |
| Half angle, ϑ (°) | 15 |
| Tip height, H (mm) | 5 |
| Tip-to-extractor distance, D (mm) | 2 |
| Film thickness, δ (μm) | 0.5 |
| Temperature, T (K) | 453 |
| Parameter | Value |
|---|---|
| Cone radius of curvature (μm) | 6 |
| Cone half angle (°) | 15 |
| Roughness (μm) | 2.8 ± 1.0 |
| Number of emission sites | 10 |
| Tip height (m) | 2.0 × 10−3 |
| Number of half-cylindrical grooves | 4 |
| Groove radius (μm) | 2.0 ± 0.4 |
| Feed length (m) | 2.0 × 10−3 |
| Extractor-tip distance (μm) | 200 |
| CR limit (EMI-TFSI propellant) | 20 |
| B (Ω−1) (Equation (10)) | 3.8 × 10−8 |
| Property | Value |
|---|---|
| Propellant | EMI-TFSI |
| Feed | Cylindrical, porous |
| Material | Borosilicate P3 |
| Diameter (m) | 4 × 10−4 |
| Length (m) | 2.5 × 10−4 |
| Pore Size (m) | (28 ± 12) × 10−6 |
| Porosity | 0.42 |
| Emitter | Conical, porous |
| Material | Borosilicate P5 |
| Height (m) | 3.5 × 10−4 |
| Cone half angle (deg) | 30 |
| Radius of curvature (m) | 16 × 10−6 |
| Pore diameter e(m) | (1.3 ± 0.3) × 10−6 |
| Porosity | 0.5 |
| Extractor-to-tip distance (D, m) | 1.2 × 10−4 |
| Polarity | Positive |
| Parameter | Value |
|---|---|
| CR limit | 20 |
| pscale | 0.023 |
| b0 (μm) | 8 |
| Nmax | 20 |
| B (Ω−1) | 5.2 × 10−8 |
| Spray divergence (°) | 30 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peter, B.S.; Dressler, R.A.; Chiu, Y.-h.; Fedkiw, T. Electrospray Propulsion Engineering Toolkit (ESPET). Aerospace 2020, 7, 91. https://doi.org/10.3390/aerospace7070091
Peter BS, Dressler RA, Chiu Y-h, Fedkiw T. Electrospray Propulsion Engineering Toolkit (ESPET). Aerospace. 2020; 7(7):91. https://doi.org/10.3390/aerospace7070091
Chicago/Turabian StylePeter, Benjamin St., Rainer A. Dressler, Yu-hui Chiu, and Timothy Fedkiw. 2020. "Electrospray Propulsion Engineering Toolkit (ESPET)" Aerospace 7, no. 7: 91. https://doi.org/10.3390/aerospace7070091
APA StylePeter, B. S., Dressler, R. A., Chiu, Y.-h., & Fedkiw, T. (2020). Electrospray Propulsion Engineering Toolkit (ESPET). Aerospace, 7(7), 91. https://doi.org/10.3390/aerospace7070091




