Characterization of Vacuum Arc Thruster Performance in Weak Magnetic Nozzle
Abstract
1. Introduction
2. Experimental Setup
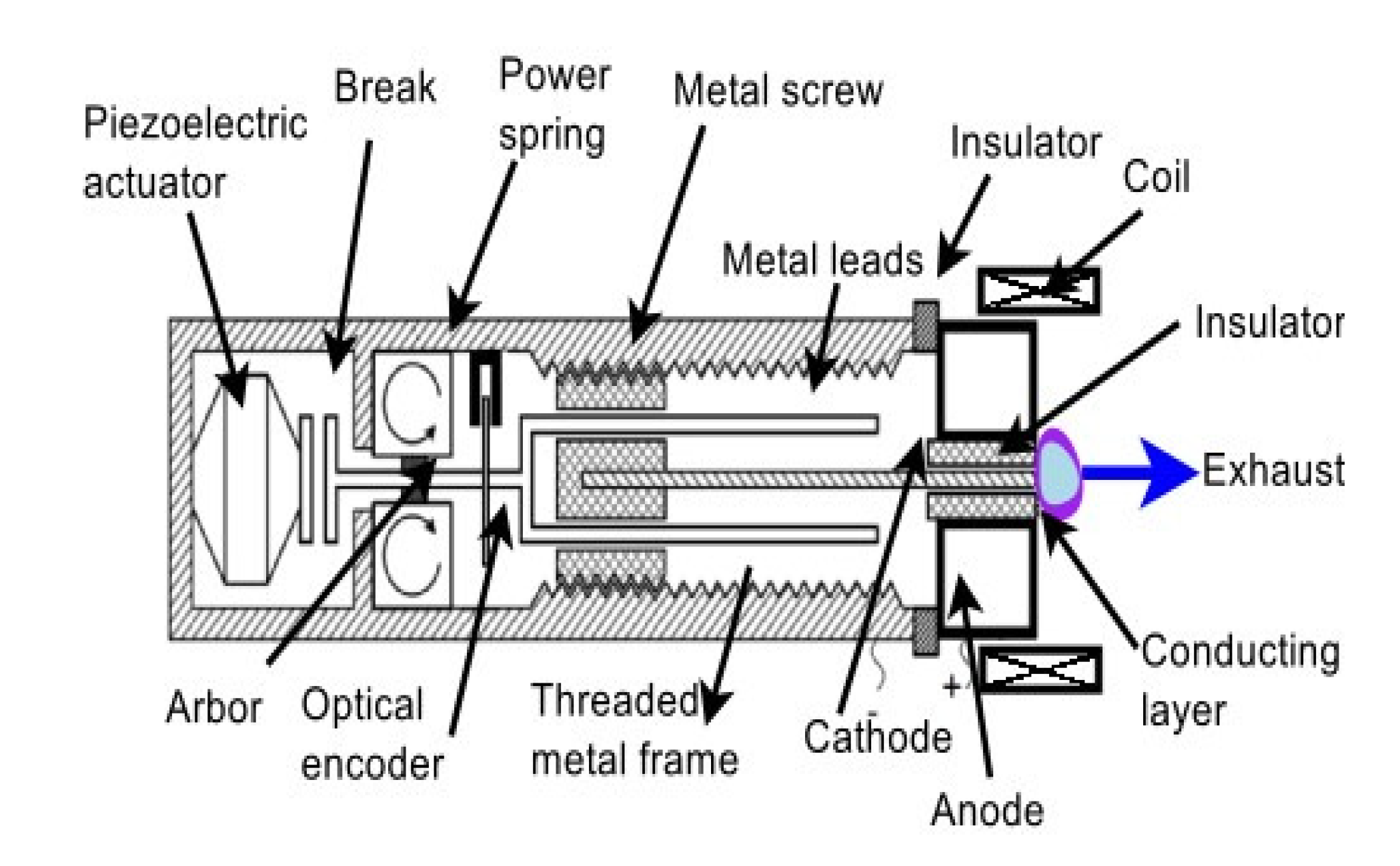
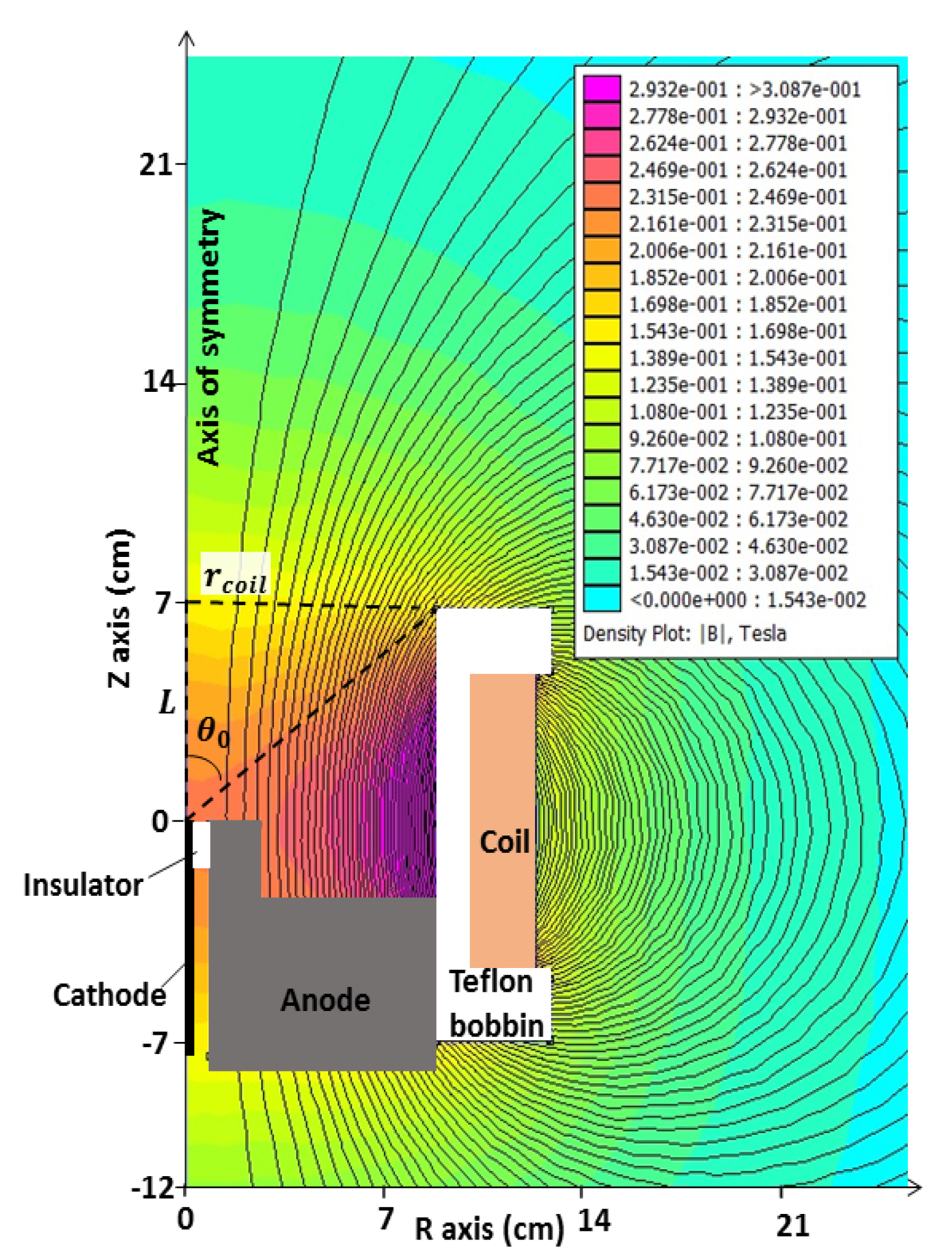
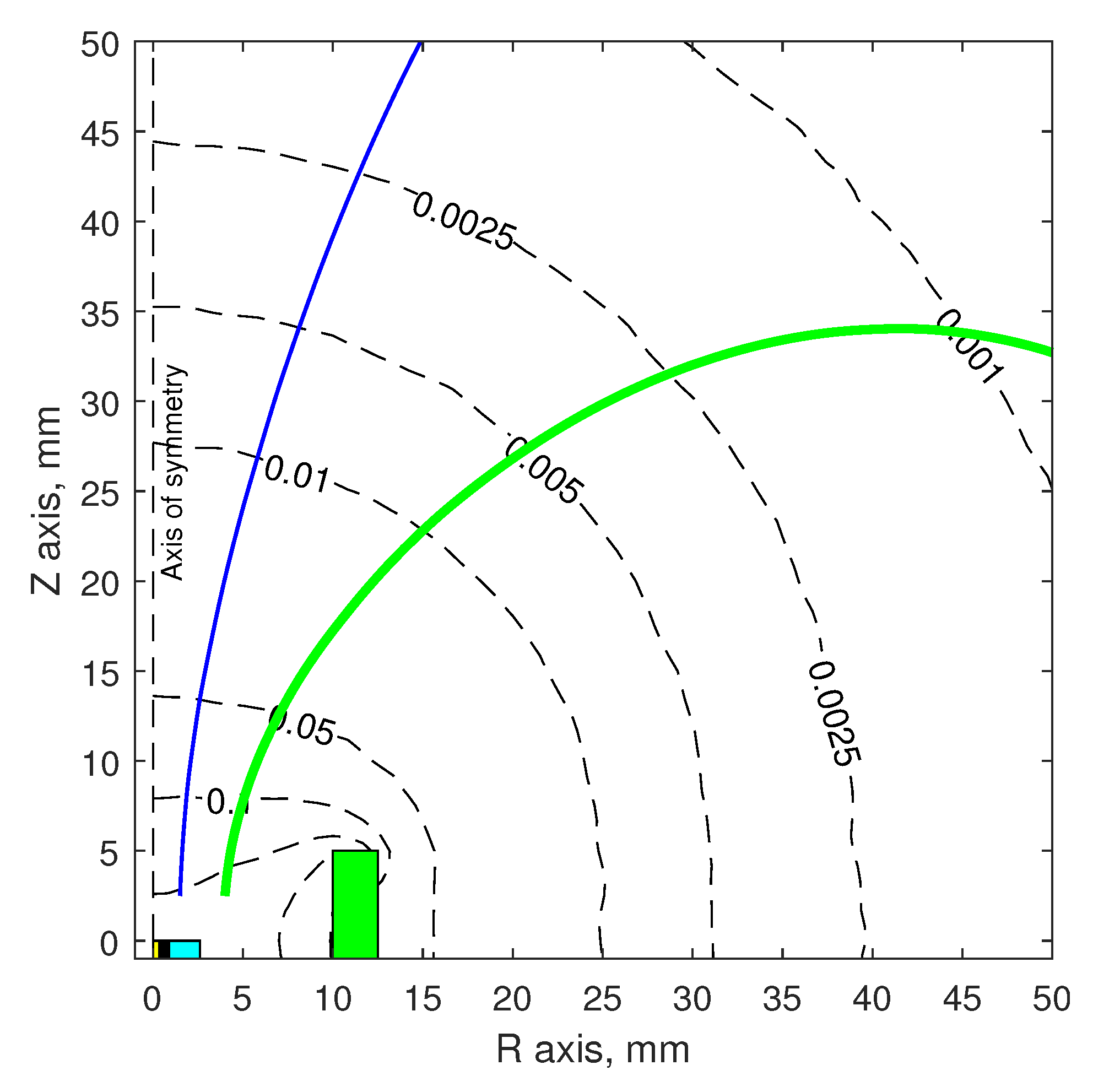
2.1. Thruster and Magnetic Setup
- (a)
- operating the thruster for several minutes with a pre-selected number of firing-pulses.
- (b)
- discharge turned off by switching off the dc/dc converter that powered the main coil and a cool down the PM for few minutes.
- (c)
- cathode is advanced by a predetermined length using the feeding mechanism. Operation takes few seconds.
- (d)
- the dc/dc converter that powers the main coil is turned on for the next discharge. See stage (a).
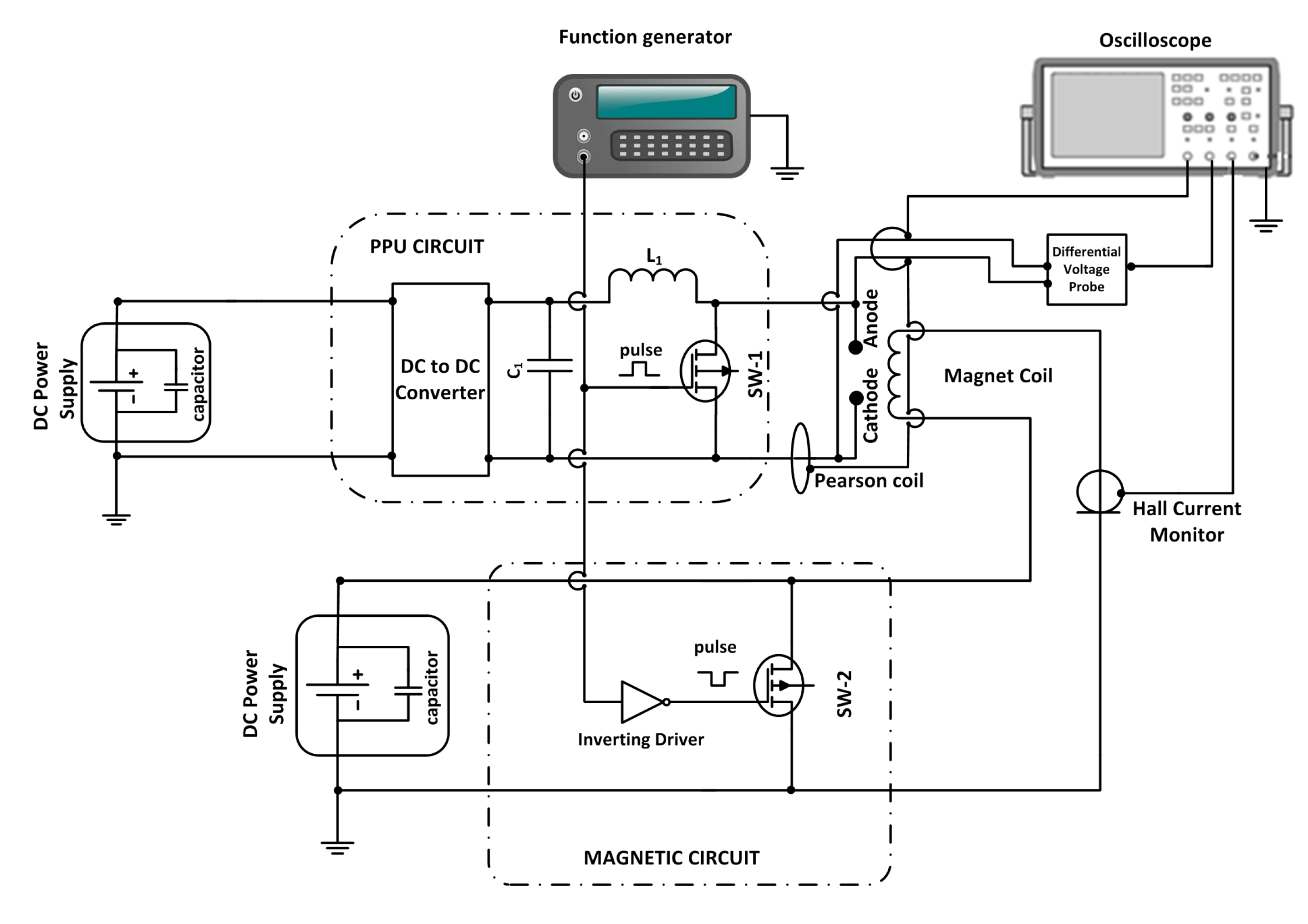
2.2. Experimental Electrical Setup
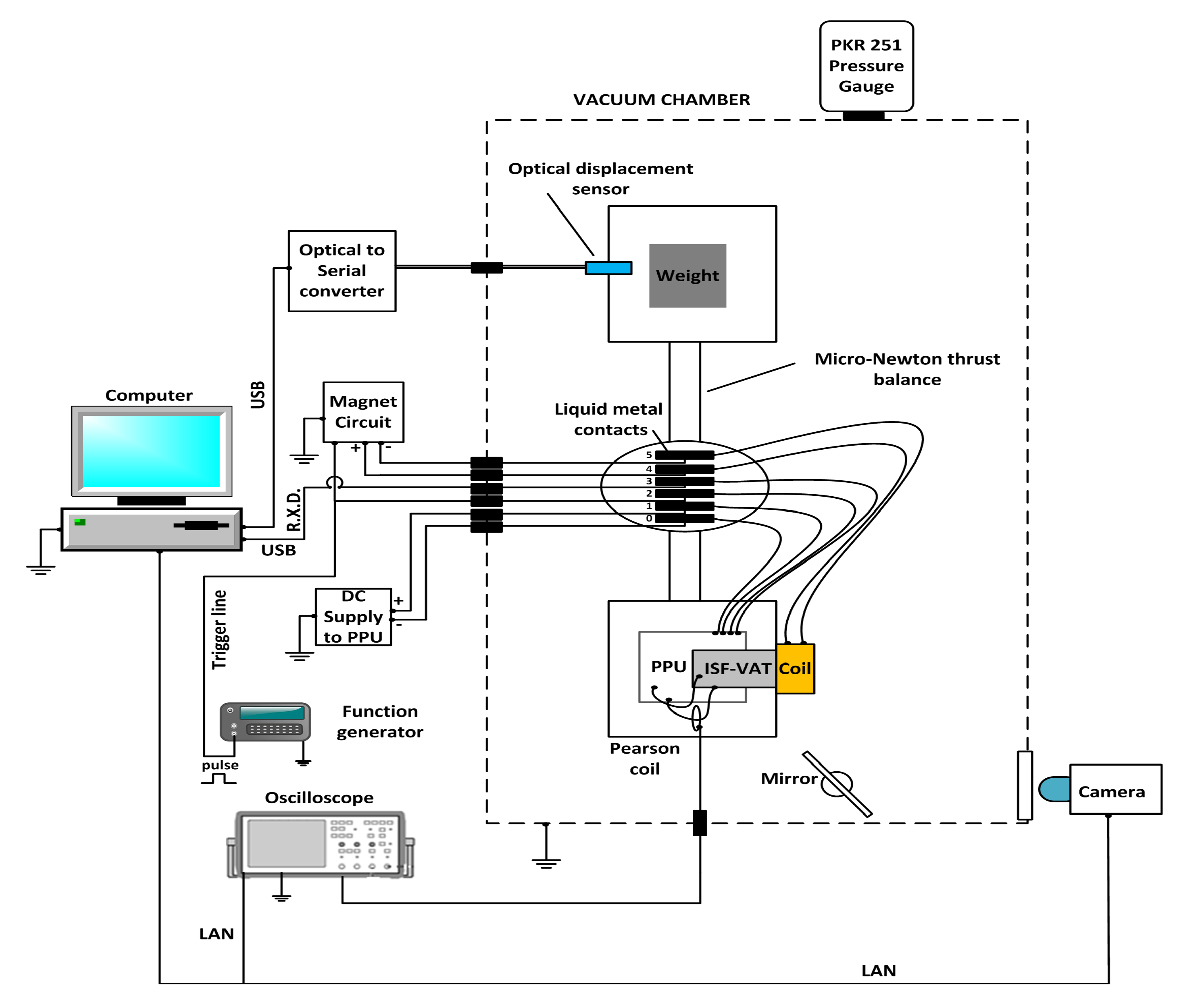
2.3. Experimental Thrust Measurement Setup
3. Experimental Results
3.1. Single Pulse Results
3.2. Single Firing Cycle Results
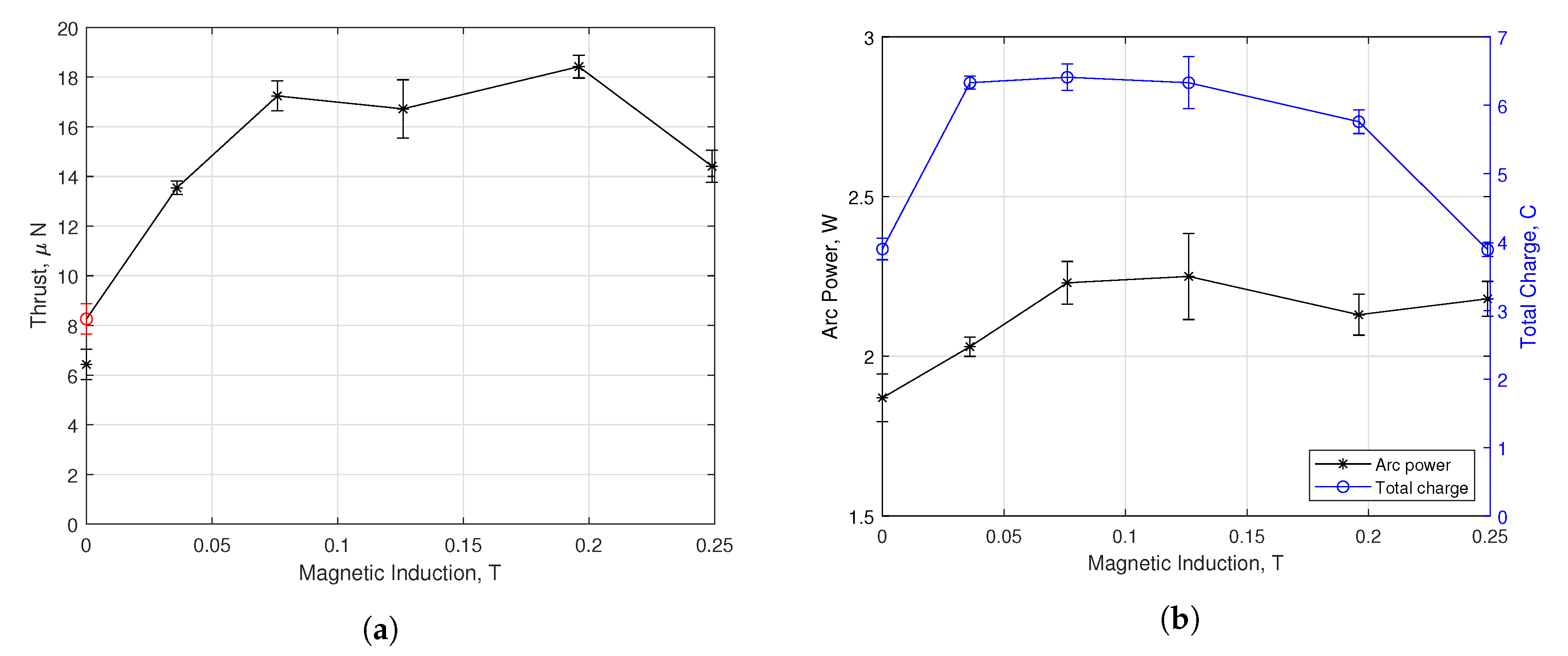
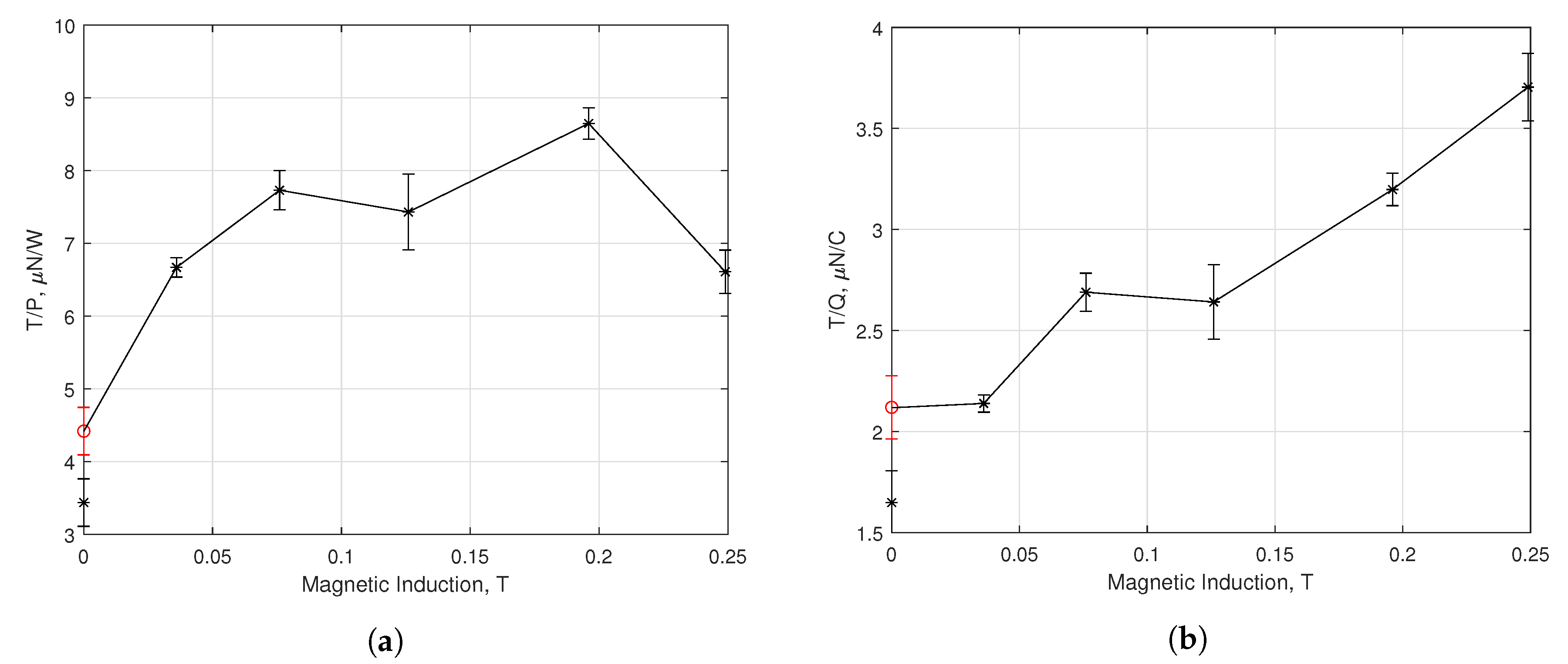
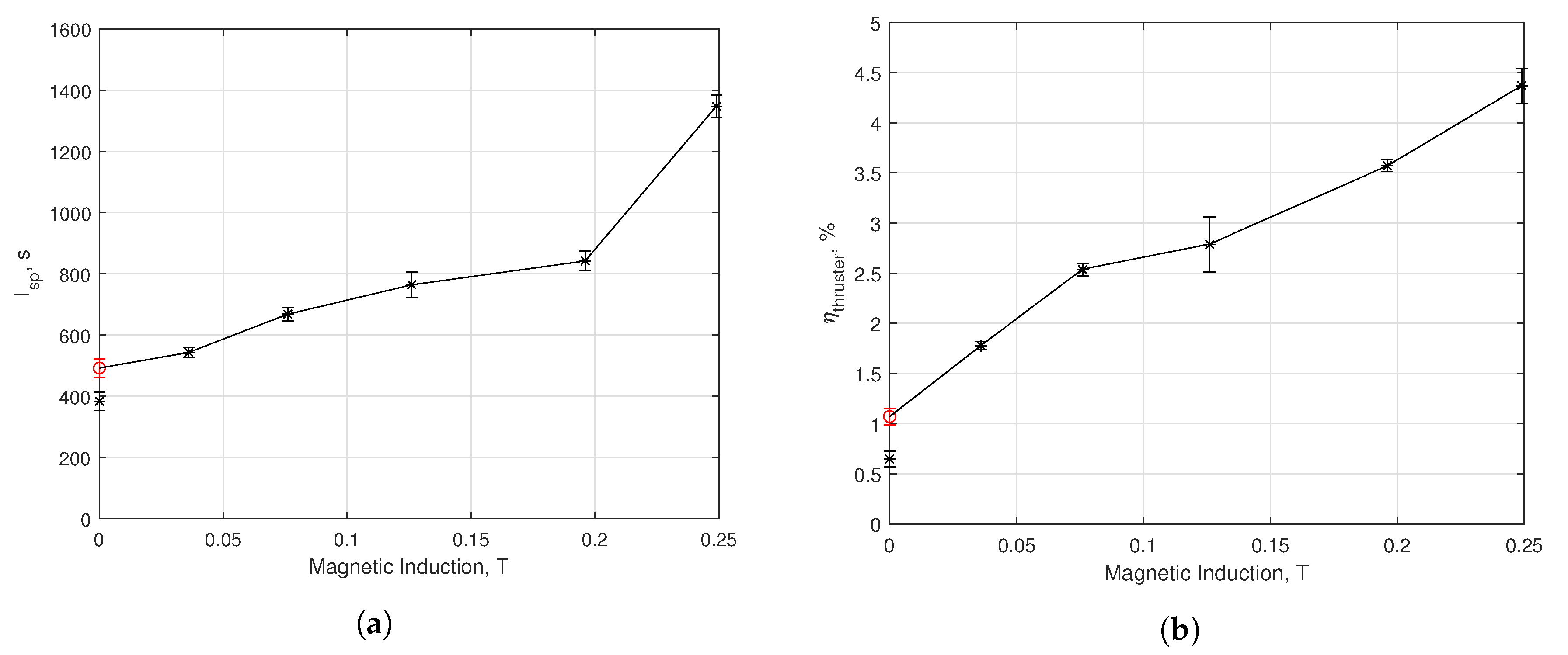
3.3. Multiple Firing Cycle Results
4. Discussion
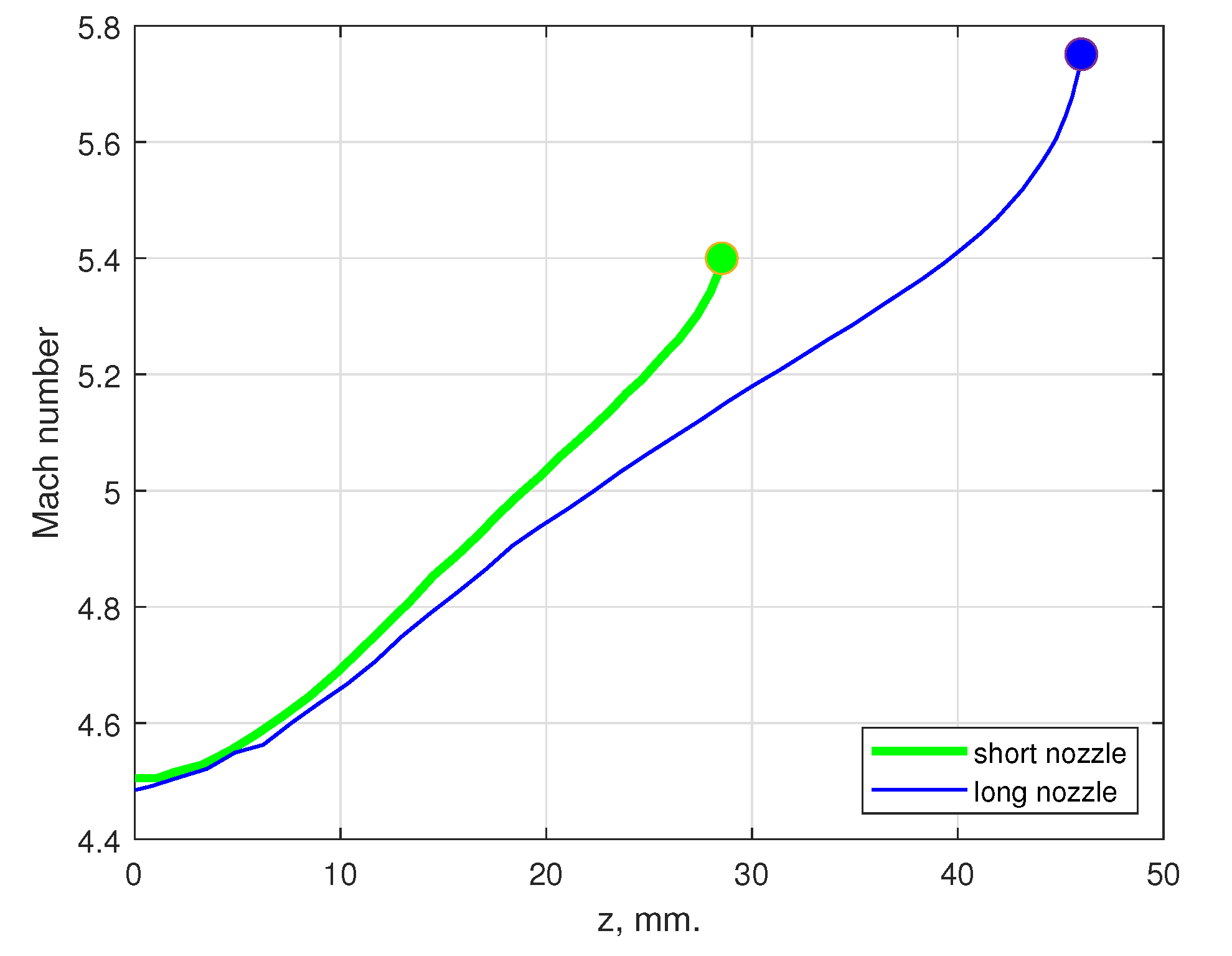
4.1. Performance Enhancement by Beam Collimation
4.2. Performance Enhancement by Magnetic Nozzle Effect
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Levchenko, I.; Bazaka, K.; Ding, Y.; Raitses, Y.; Mazouffre, S.; Henning, T.; Klar, P.J.; Shinohara, S.; Schein, J.; Garrigues, L.; et al. Space micropropulsion systems for Cubesats and small satellites: From proximate targets to furthermost frontiers. Appl. Phys. Rev. 2018, 5, 011104. [Google Scholar] [CrossRef]
- Kronhaus, I.; Schilling, K.; Pietzka, M.; Schein, J. Simple orbit and attitude control using vacuum arc thrusters for picosatellites. J. Spacecr. Rockets 2014, 51, 2008–2015. [Google Scholar] [CrossRef]
- Schein, J.; Qi, N.; Binder, R.; Krishnan, M.; Ziemer, J.; Polk, J.; Anders, A. Low mass vacuum arc thruster system for station keeping missions. In Proceedings of the 27th International Electric Propulsion Conference, Pasadena, CA, USA, 15–19 October 2001. [Google Scholar]
- Anders, A. Cathodic Arcs: From Fractal Spots to Energetic Condensation; Springer Science & Business Media: New York, NY, USA, 2009; Volume 50. [Google Scholar]
- Boxman, R.L.; Sanders, D.M.; Martin, P.J. Handbook of Vacuum Arc Science & Technology: Fundamentals and Applications; Noyes Publication: Park Ridge, NJ, USA, 1996. [Google Scholar]
- Zhuang, T.; Shashurin, A.; Brieda, L.; Keidar, M. Development of micro-vacuum arc thruster with extended lifetime. In Proceedings of the 31st International Electric Propulsion Conference, Ann Arbor, MI, USA, 20–24 September 2009. [Google Scholar]
- Kolbeck, J.; Anders, A.; Beilis, I.I.; Keidar, M. Micro-propulsion based on vacuum arcs. J. Appl. Phys. 2019, 125, 220902. [Google Scholar] [CrossRef]
- Keidar, M.; Schein, J.; Wilson, K.; Gerhan, A.; Au, M.; Tang, B.; Idzkowski, L.; Krishnan, M.; Beilis, I.I. Magnetically enhanced vacuum arc thruster. Plasma Sources Sci. Technol. 2005, 14, 661. [Google Scholar] [CrossRef]
- Baranov, O.O.; Cvelbar, U.; Bazaka, K. Concept of a magnetically enhanced vacuum arc thruster with controlled distribution of ion flux. IEEE Trans. Plasma Sci. 2017, 46, 304–310. [Google Scholar] [CrossRef]
- Keidar, M.; Zhuang, T.; Shashurin, A.; Teel, G.; Chiu, D.; Lukas, J.; Haque, S.; Brieda, L. Electric propulsion for small satellites. Plasma Phys. Control. Fusion 2014, 57, 014005. [Google Scholar] [CrossRef]
- Zhuang, T.; Shashurin, A.; Denz, T.; Keidar, M.; Vail, P.; Pancotti, A. Performance characteristics of micro-cathode arc thruster. J. Propul. Power 2014, 30, 29–34. [Google Scholar] [CrossRef]
- Tang, B.; Idzkowski, L.; Au, M.; Parks, D.; Krishnan, M.; Ziemer, J. Thrust improvement of the magnetically enhanced vacuum arc thruster (MVAT). In Proceedings of the International Electric Propulsion Conference, IEPC, Princeton, NJ, USA, 31 October–4 November 2005; Volume 304, p. 2005. [Google Scholar]
- Kronhaus, I.; Laterza, M.; Maor, Y. Inline screw feeding vacuum arc thruster. Rev. Sci. Instrum. 2017, 88, 043505. [Google Scholar] [CrossRef]
- Kronhaus, I.; Chowdhury, S.; Laterza, M. Axial Magnetic Field Effect on Vacuum Arc Thruster Performance. In Proceedings of the 36th International Electric Propulsion Conference, IEPC-2019-662, Vienna, Austria, 15–20 September 2019. [Google Scholar]
- Kronhaus, I. Inline Screw Feeding Vacuum Arc Thruster. U.S. Patent App. 16/310,175, 31 October 2019. [Google Scholar]
- Meeker, D.C. Finite Element Method Magnetics; Version 4.2. User’s Manual; University of Virginia: Charlattesville, VA, USA, 2009. [Google Scholar]
- Seifert, B.; Reissner, A.; Buldrini, N.; Plesescu, F.; Scharlemann, C.; Bulit, A.; del Amo, J.G. Development and verification of a μN thrust balance for high voltage electric propulsion systems. In Proceedings of the 33rd International Electric Propulsion Conference, Washington, DC, USA, 6–10 October 2013. [Google Scholar]
- Grondona, D.; Kelly, H.; Minotti, F. Hydrodynamic model for a vacuum arc operated with background gas: Theory and experimental validation. J. Appl. Phys. 2006, 99, 043304. [Google Scholar] [CrossRef]
- Brown, I.G. Vacuum arc ion sources. Rev. Sci. Instrum. 1994, 65, 3061–3081. [Google Scholar] [CrossRef]
- Laterza, M.; Kronhaus, I. Analysis of Erosion and Redeposition Processes in Coaxial Vacuum Arc Thrusters. In Proceedings of the 36th International Electric Propulsion Conference, IEPC-2019-661, Vienna, Austria, 15–20 September 2019. [Google Scholar]
- Goebel, D.M.; Katz, I. Fundamentals of Electric Propulsion: Ion and Hall Thrusters; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 1. [Google Scholar]
- Ahedo, E.; Merino, M. Two-dimensional supersonic plasma acceleration in a magnetic nozzle. Phys. Plasmas 2010, 17, 073501. [Google Scholar] [CrossRef]
- Kronhaus, I.; Laterza, M.; Linossier, A.R. Experimental Characterization of the Inline-Screw-Feeding Vacuum-Arc-Thruster Operation. IEEE Trans. Plasma Sci. 2018, 46, 283–288. [Google Scholar] [CrossRef]

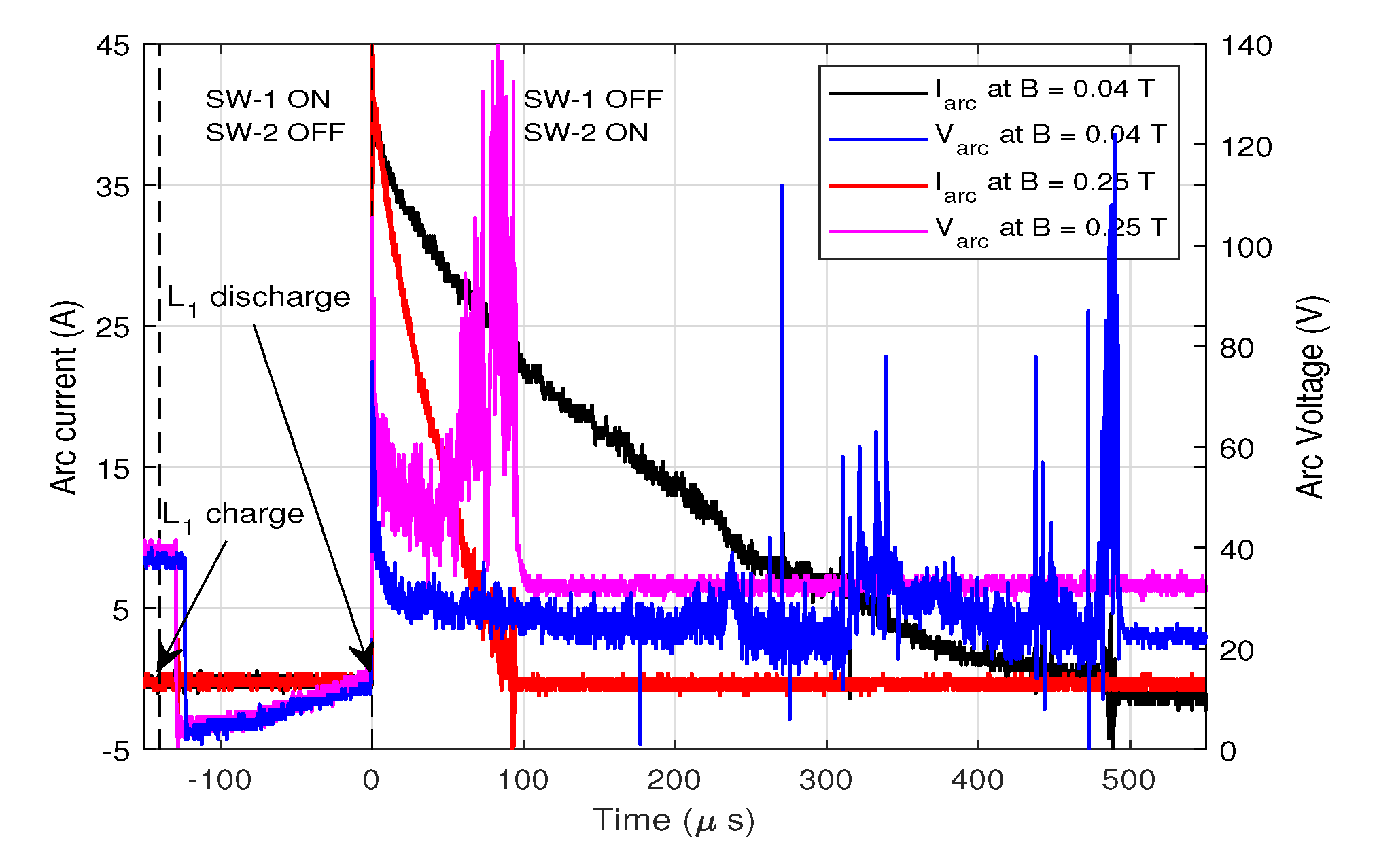
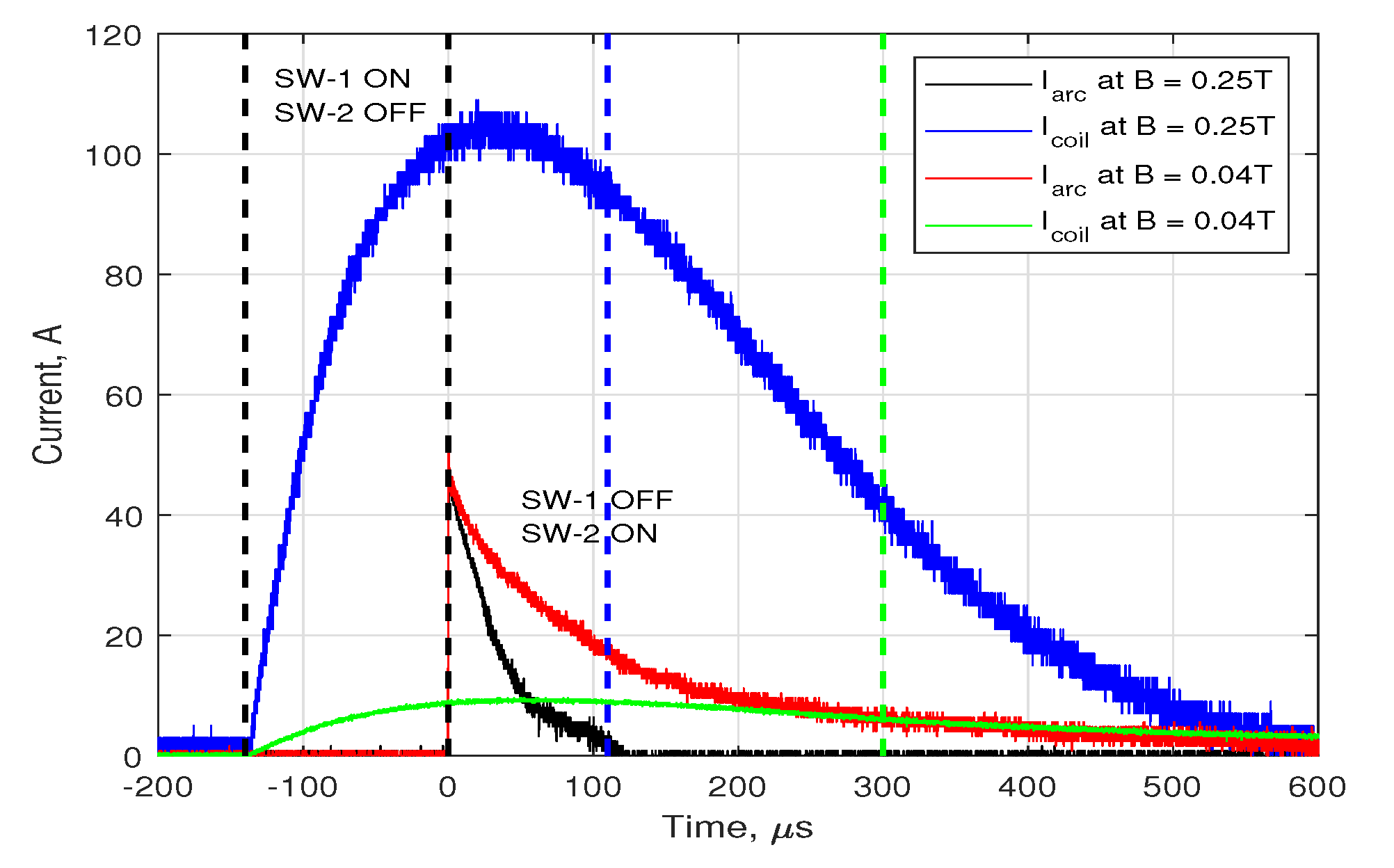


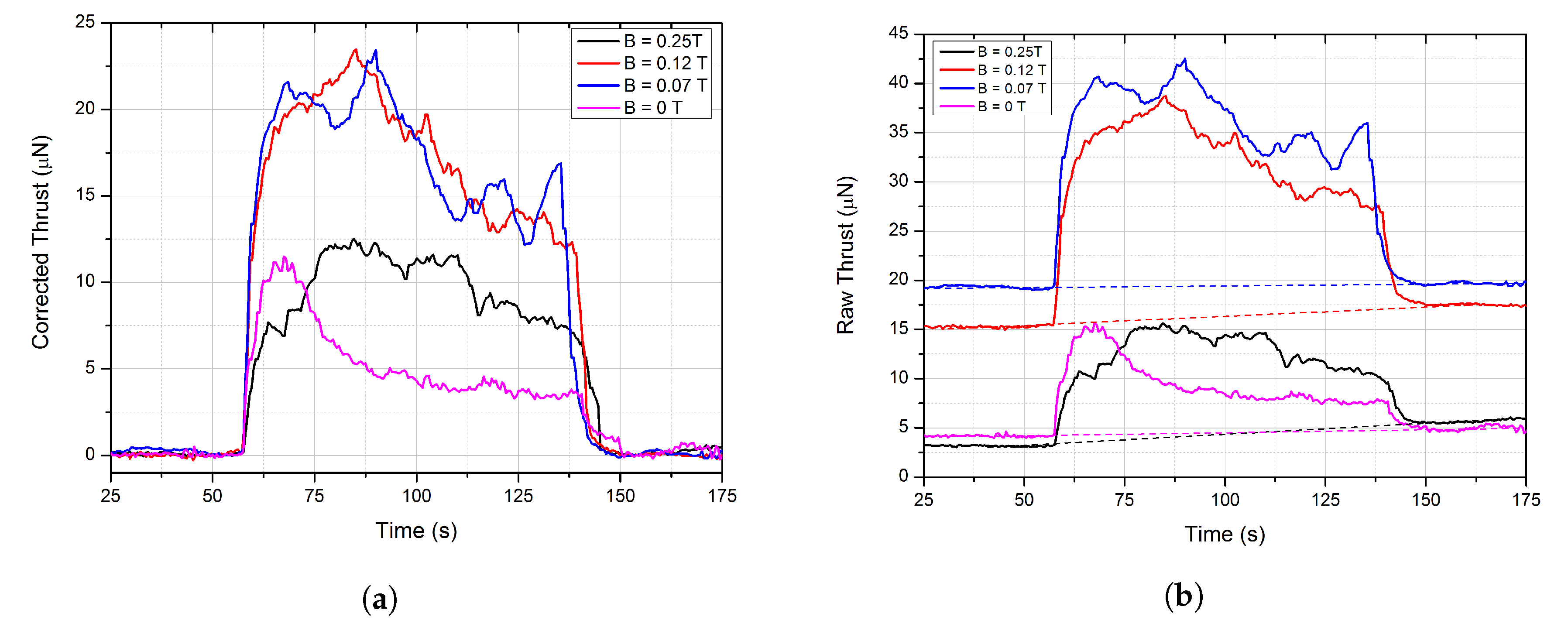
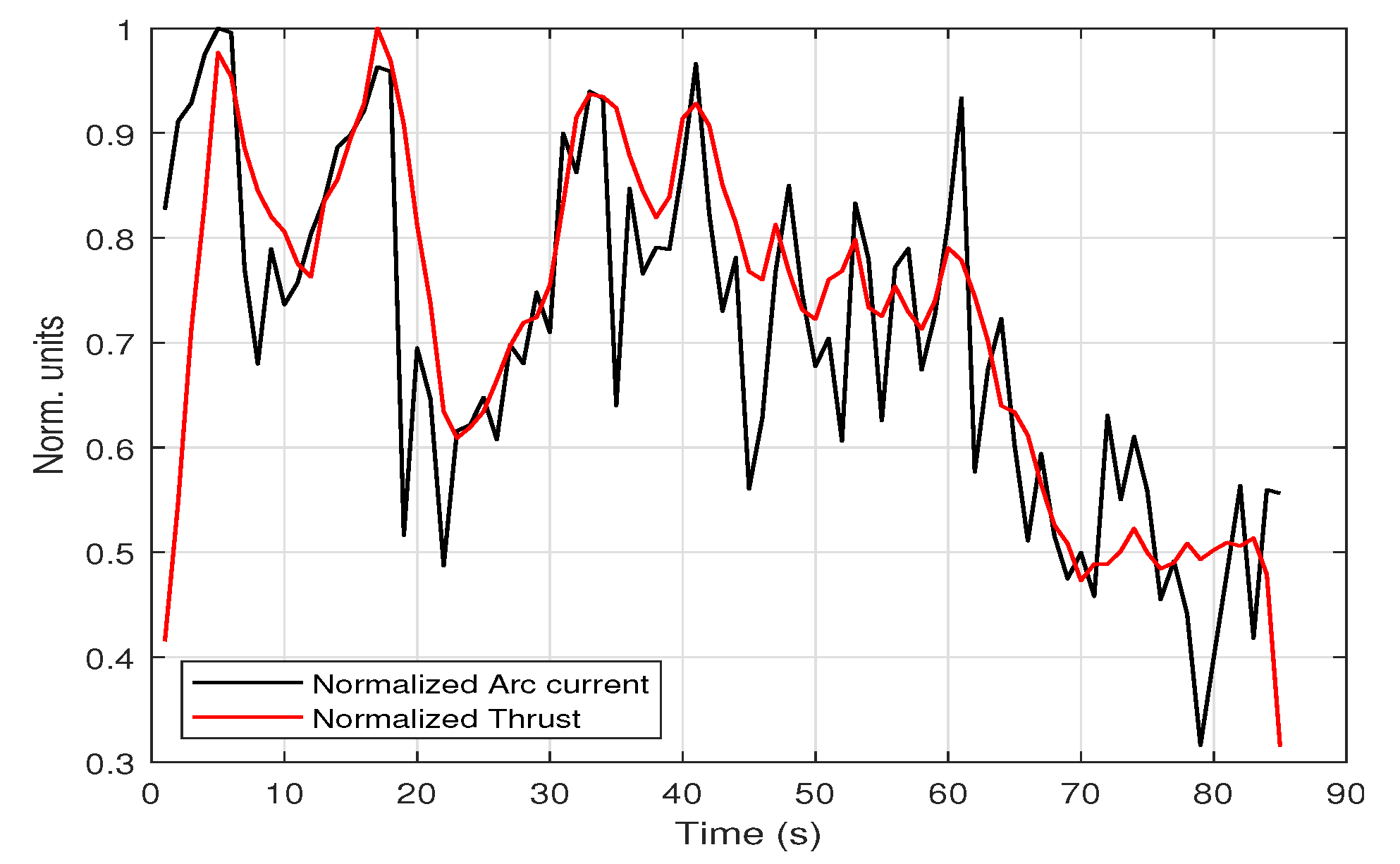
| Icoil,max (A) | Δt10% of Icoil,max (μs) | Bmax (T) | < Varc > (V) | tarc (μs/pulse) | Qi (mC/pulse) | εarc (mJ/pulse) |
|---|---|---|---|---|---|---|
| 0 | N.A. | 0.00 | 41.53 ± 1.63 | 135 ± 79 | 2.70 ± 1.59 | 112.13 ± 66 |
| 9 | 300 | 0.04 | 27.77 ± 0.50 | 217 ± 68 | 4.34 ± 1.36 | 120.52 ± 38 |
| 27 | 250 | 0.07 | 29.03 ± 1.73 | 214 ± 69 | 4.29 ± 1.38 | 124.54 ± 40 |
| 45 | 150 | 0.12 | 34.30 ± 1.01 | 216 ± 58 | 4.32 ± 1.17 | 148.18 ± 40 |
| 70 | 120 | 0.20 | 32.57 ± 0.93 | 192 ± 59 | 3.85 ± 1.19 | 125.39 ± 39 |
| 105 | 110 | 0.25 | 51.23 ± 1.33 | 133 ± 43 | 2.66 ± 0.86 | 136.27 ± 44 |
| B (T) | (g/s) | (g/s) |
|---|---|---|
| 0.00 | 2.11 ± 0.08 | 1.71 ± 0.03 |
| 0.04 | 2.11 ± 0.08 | 2.54 ± 0.11 |
| 0.07 | 2.11 ± 0.08 | 2.63 ± 0.15 |
| 0.12 | 2.11 ± 0.08 | 2.23 ± 0.05 |
| 0.20 | 2.11 ± 0.08 | 2.23 ± 0.12 |
| 0.25 | 2.11 ± 0.08 | 1.09 ± 0.05 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chowdhury, S.; Kronhaus, I. Characterization of Vacuum Arc Thruster Performance in Weak Magnetic Nozzle. Aerospace 2020, 7, 82. https://doi.org/10.3390/aerospace7060082
Chowdhury S, Kronhaus I. Characterization of Vacuum Arc Thruster Performance in Weak Magnetic Nozzle. Aerospace. 2020; 7(6):82. https://doi.org/10.3390/aerospace7060082
Chicago/Turabian StyleChowdhury, Satyajit, and Igal Kronhaus. 2020. "Characterization of Vacuum Arc Thruster Performance in Weak Magnetic Nozzle" Aerospace 7, no. 6: 82. https://doi.org/10.3390/aerospace7060082
APA StyleChowdhury, S., & Kronhaus, I. (2020). Characterization of Vacuum Arc Thruster Performance in Weak Magnetic Nozzle. Aerospace, 7(6), 82. https://doi.org/10.3390/aerospace7060082





