Temperature Effects on Polymer-Ceramic Pressure-Sensitive Paint as a Luminescent Pressure Sensor
Abstract
1. Introduction
2. Experimental Setup and Methods
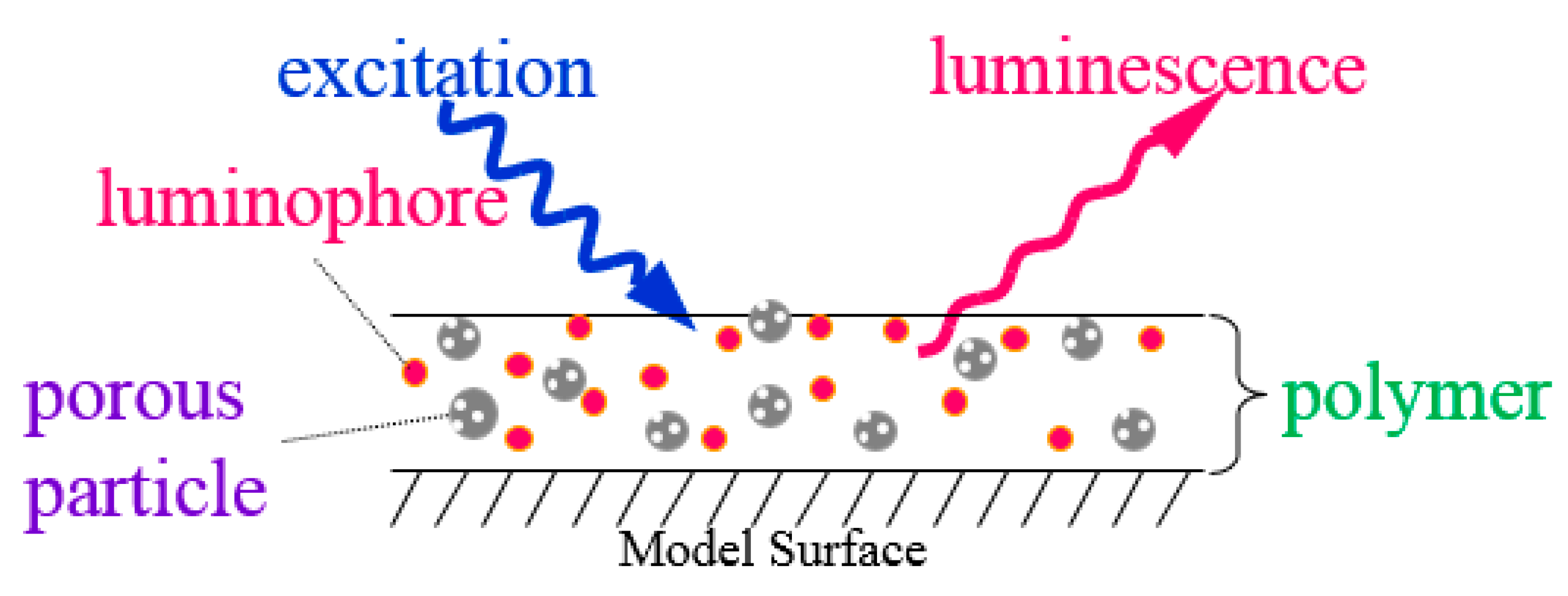
2.1. Materials
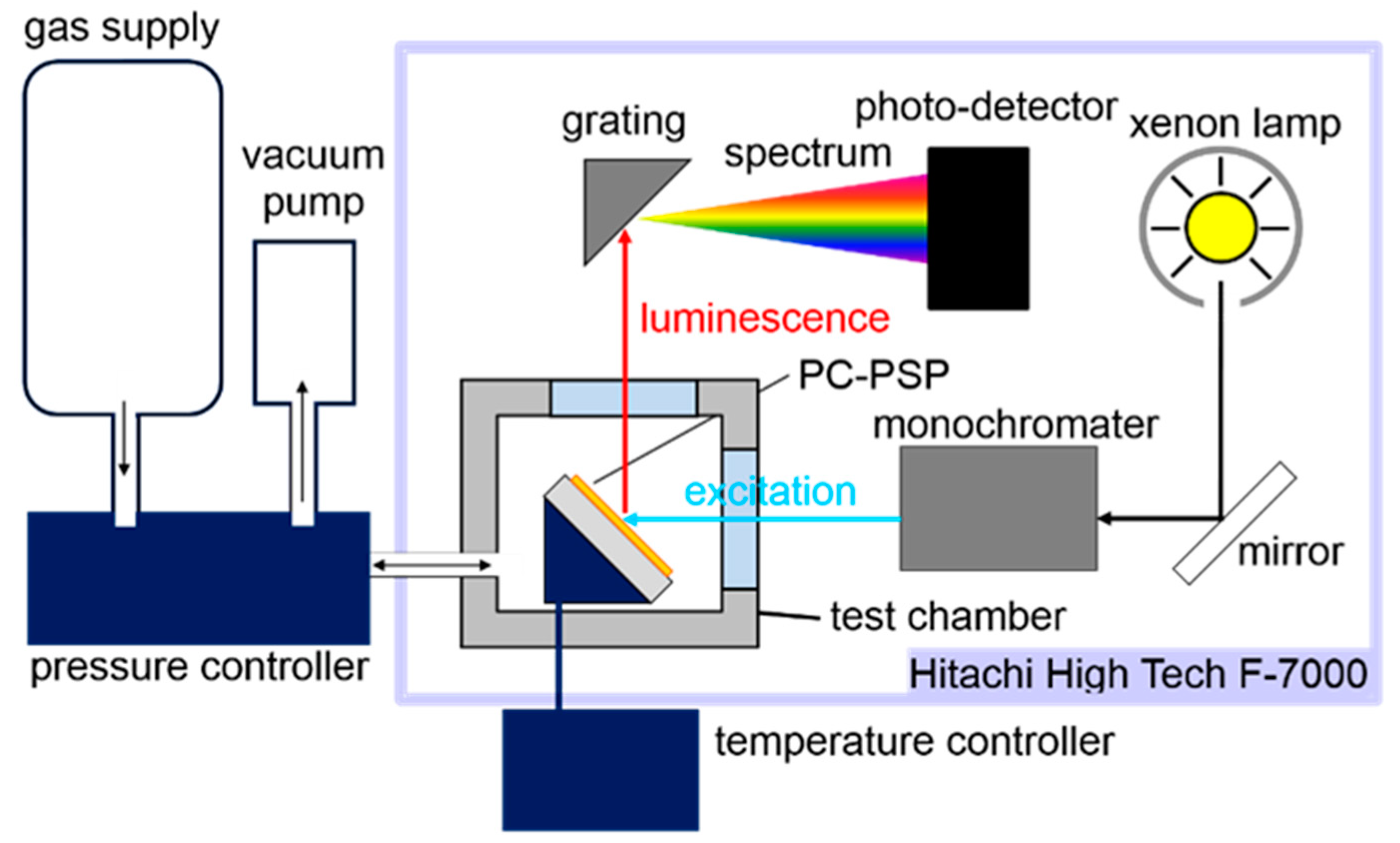
2.2. Static Characterization
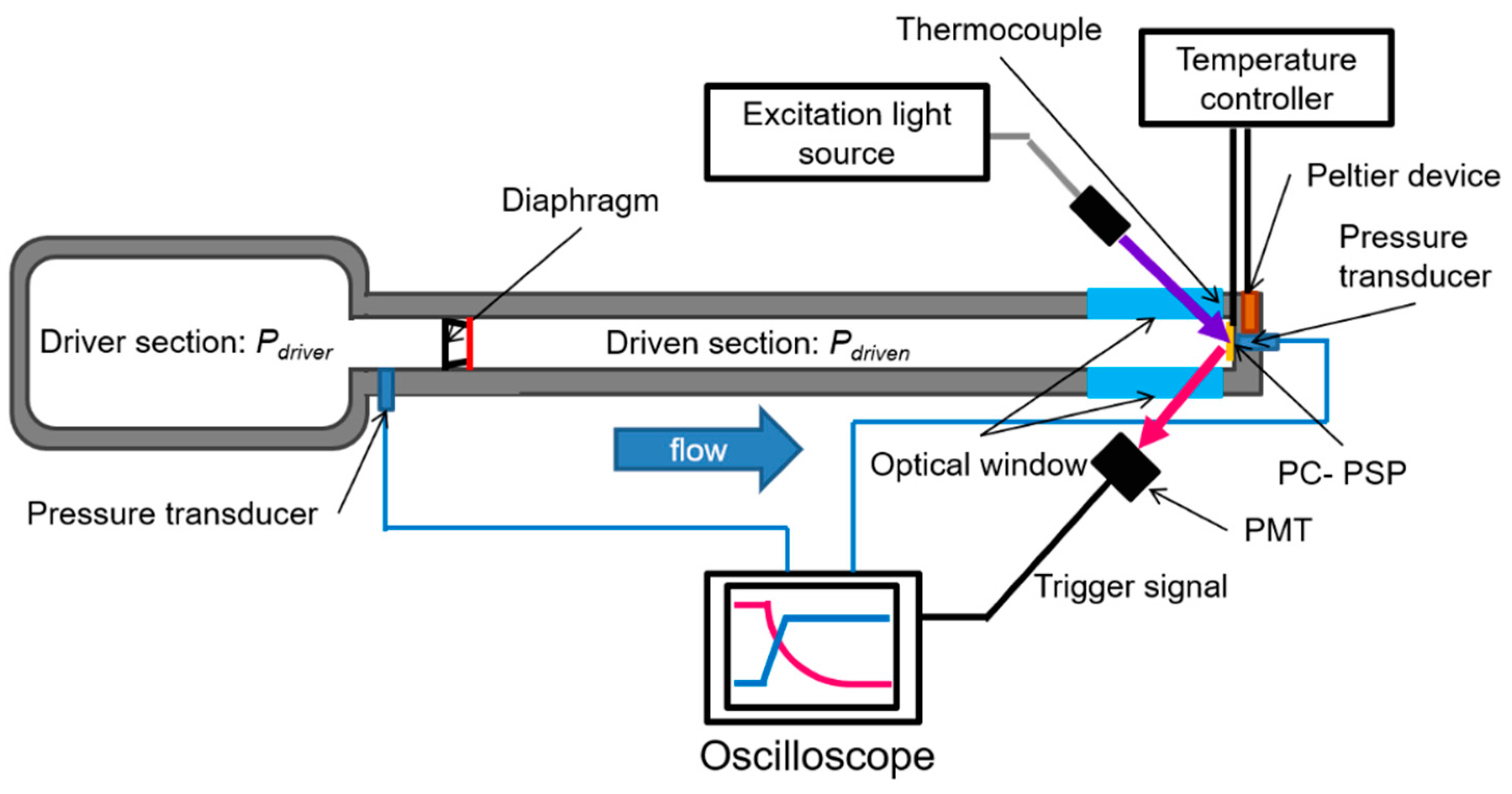
2.3. Dynamic (Dynamic-State) Characterization
3. Results and Discussion
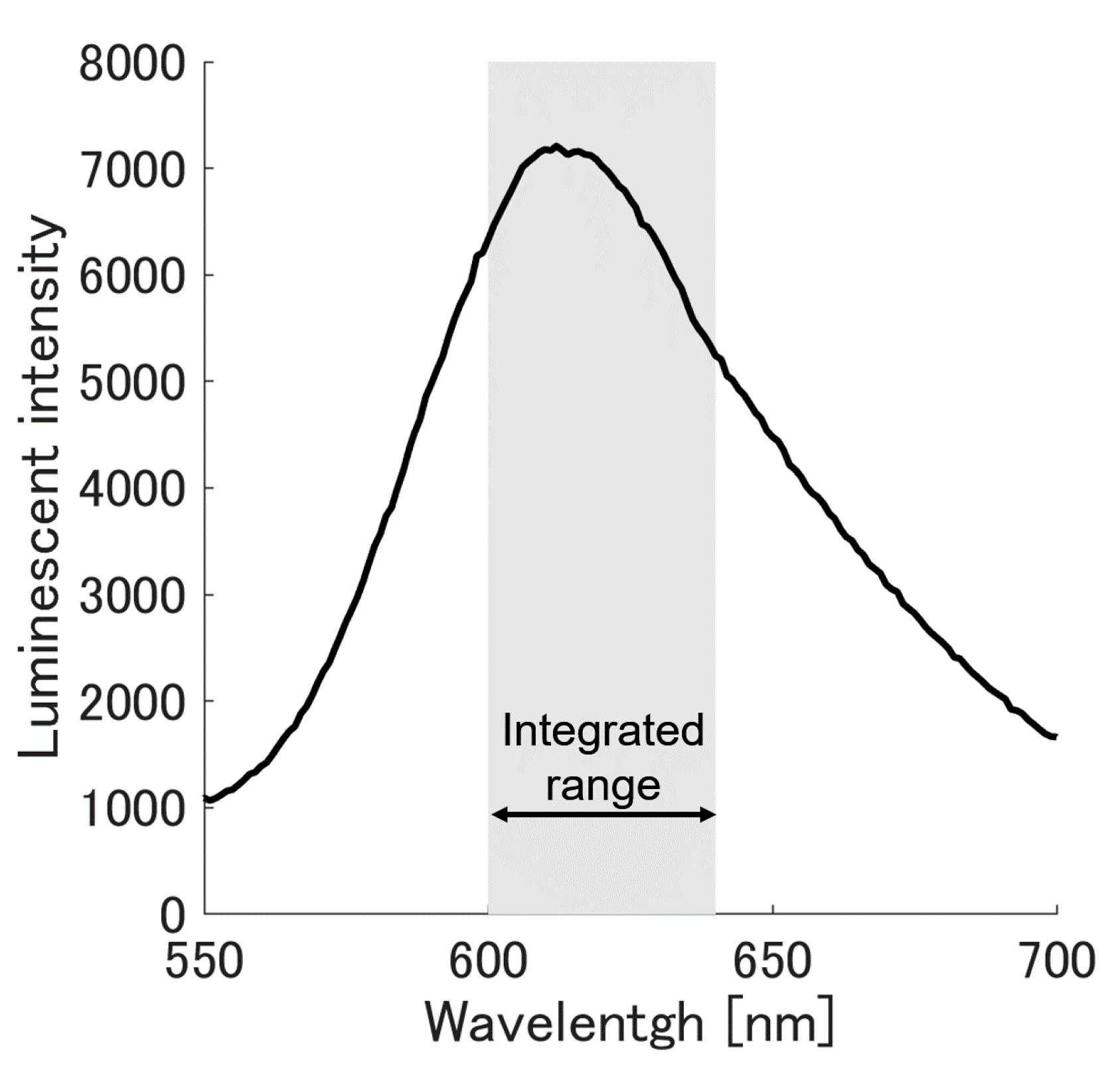
3.1. Luminescent Intensity Change
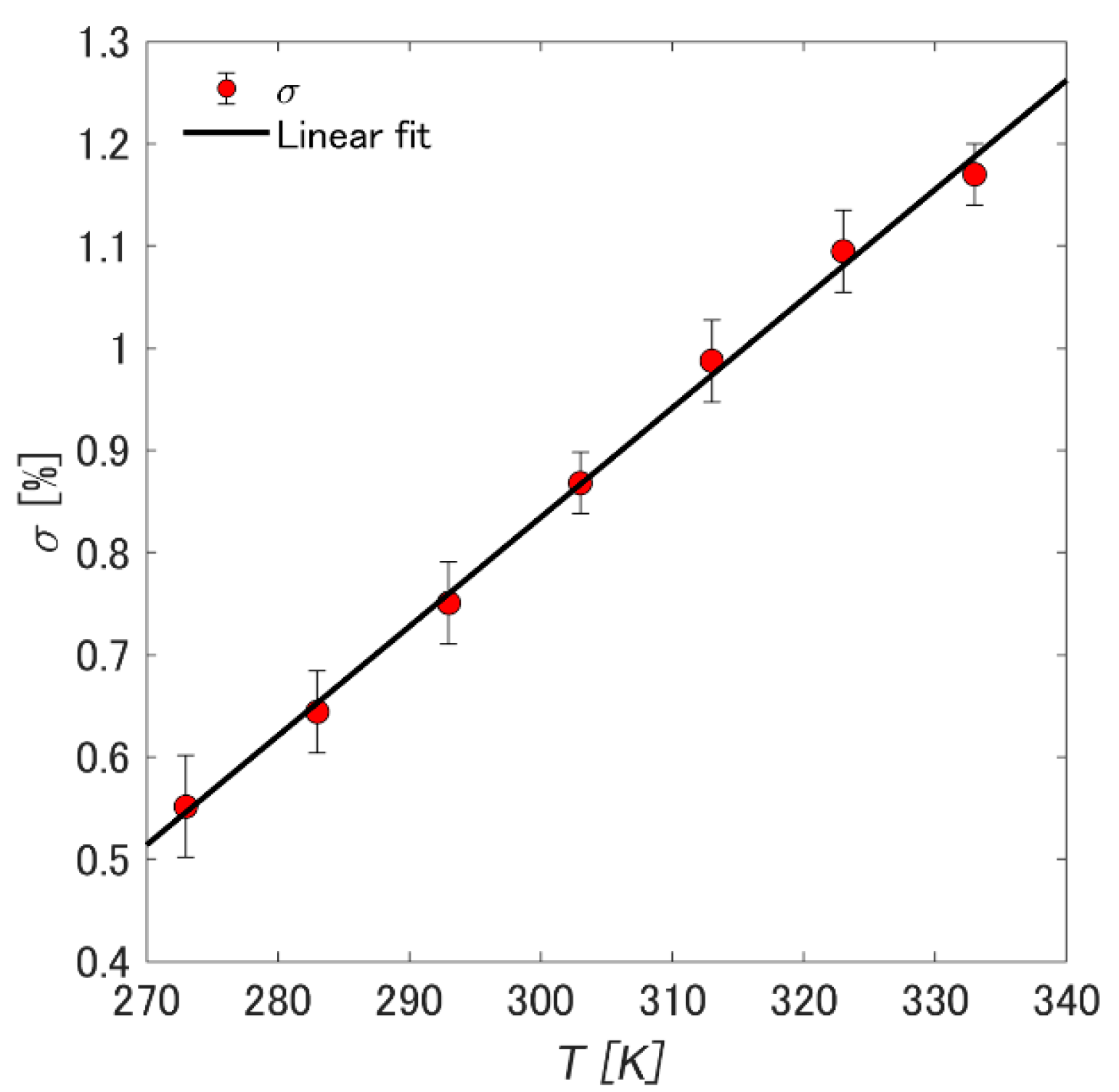
3.2. Pressure Sensitivity
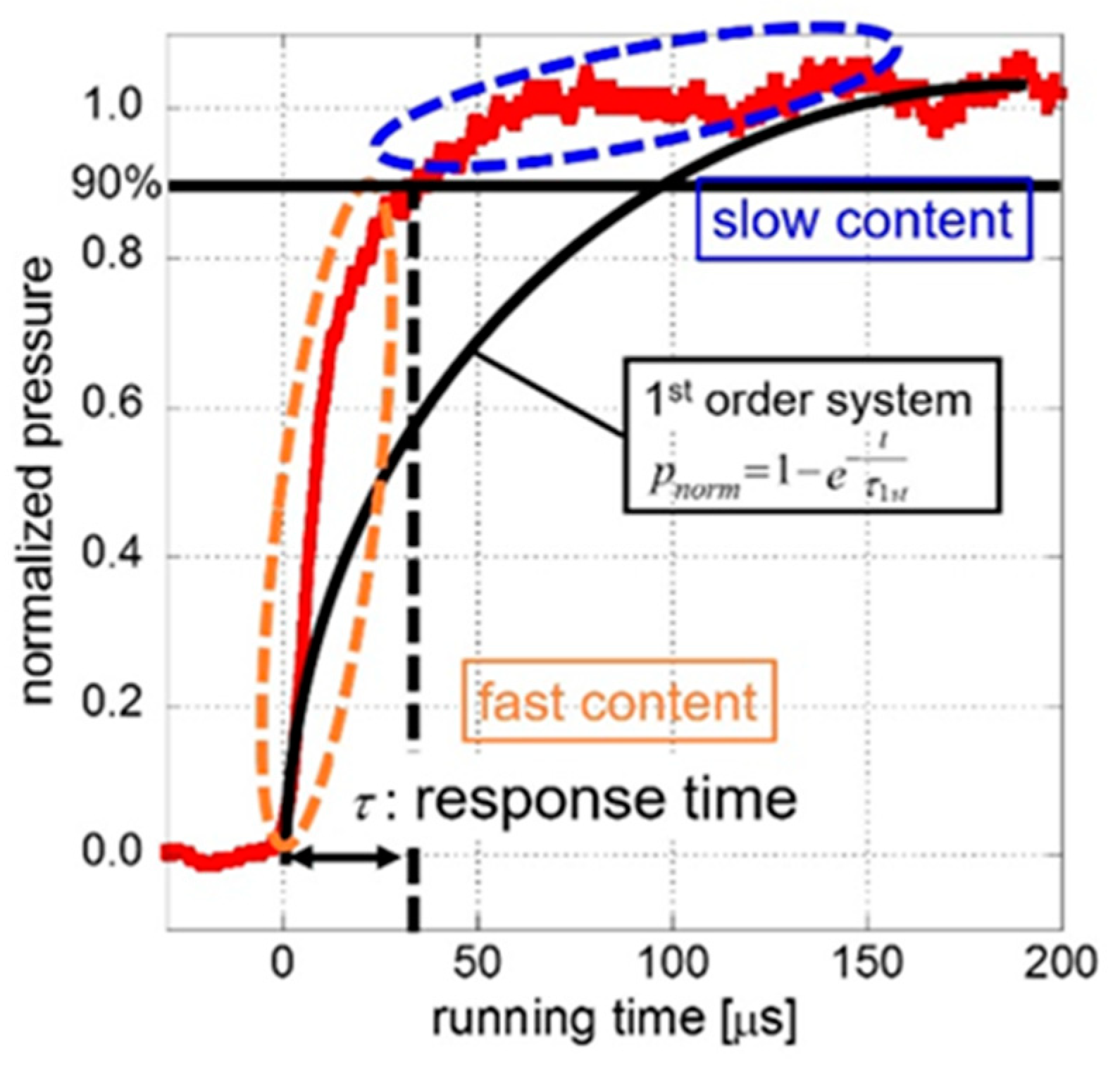
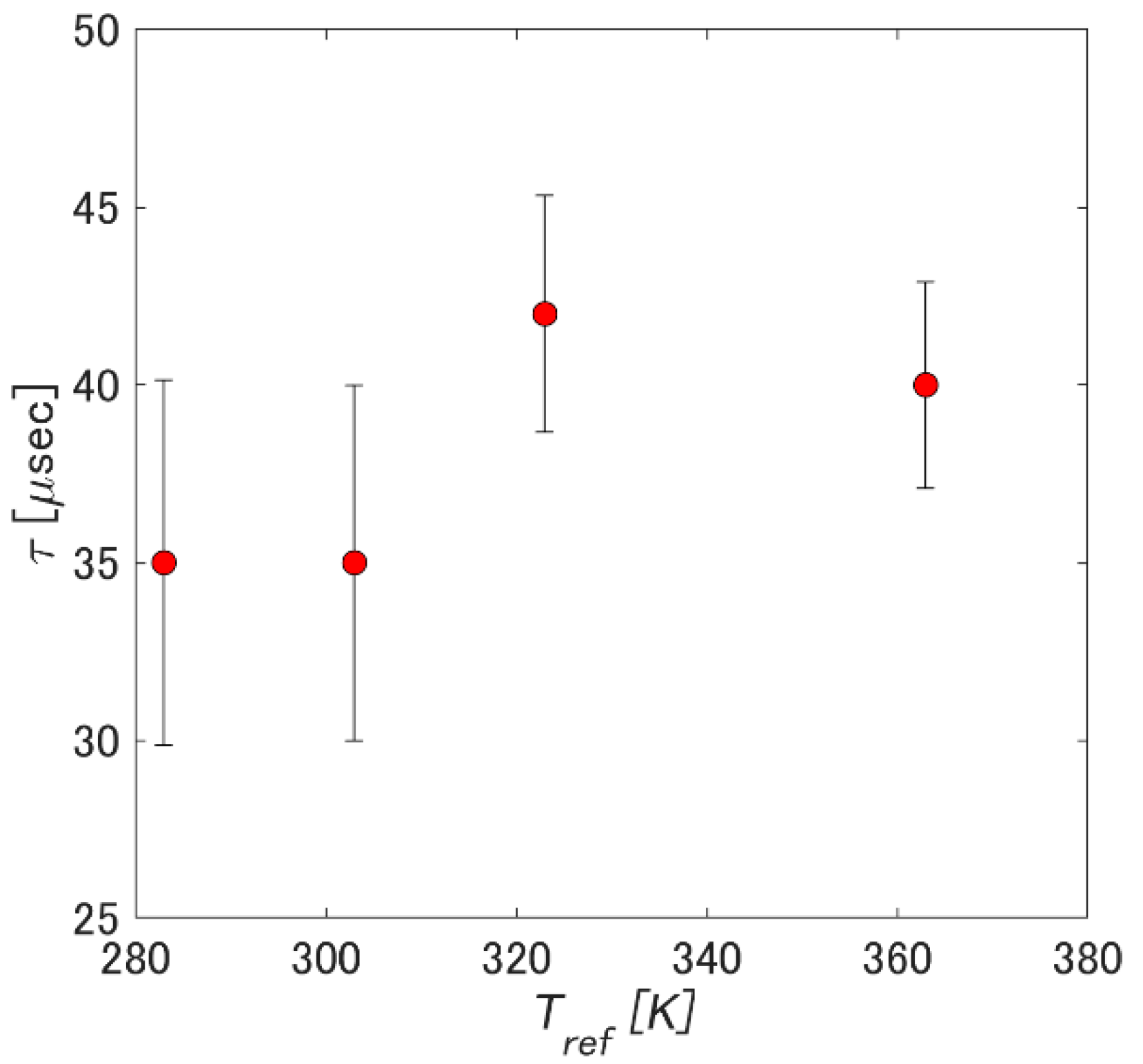
3.3. Time Response
3.4. Discussion: Temperature Effect to Unsteady Pressure Measurement
4. Conclusion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, T.S.; John, P.S. Pressure and Temperature Sensitive Paint; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 3540222413. [Google Scholar]
- Currao, G.M.D.; Neely, A.J.; Kennell, C.M.; Gai, S.L.; Buttsworth, D.R. Hypersonic Fluid–Structure Interaction on a Cantilevered Plate with Shock Impingement. AIAA J. 2019, 57, 4819–4834. [Google Scholar] [CrossRef]
- Coschignano, A.; Babinsky, H. Boundary-Layer Development Downstream of Normal Shock in Transonic Intakes at Incidence. AIAA J. 2019, 57, 5241–5251. [Google Scholar] [CrossRef]
- Panda, J.; Roozeboom, N.H.; Ross, J.C. Wavenumber-Frequency Spectra on a Launch Vehicle Model Measured via Unsteady Pressure-Sensitive Paint. AIAA J. 2019, 57, 1–17. [Google Scholar] [CrossRef]
- Gößling, J.; Ahlefeldt, T.; Hilfer, M. Experimental validation of unsteady pressure-sensitive paint for acoustic applications. Exp. Therm. Fluid Sci. 2020, 112, 1–12. [Google Scholar] [CrossRef]
- Bell, J.H.; Schairer, E.T.; Hand, L.A.; Mehta, R.D. Surface Pressure Measurements Using Luminescent Coatings. Annu. Rev. Fluid Mech. 2001, 33, 155–206. [Google Scholar] [CrossRef]
- Gregory, J.W.; Asai, K.; Kameda, M.; Liu, T.; Sullivan, J.P. A review of pressure-sensitive paint for high-speed and unsteady aerodynamics. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2008, 222, 249–290. [Google Scholar] [CrossRef]
- Quinn, M.K.; Yang, L.; Kontis, K. Pressure-sensitive paint: Effect of substrate. Sensors 2011, 11, 11649–11663. [Google Scholar] [CrossRef]
- Sakaue, H.; Kakisako, T.; Ishikawa, H. Characterization and optimization of polymer-ceramic pressure-sensitive paint by controlling polymer content. Sensors 2011, 11, 6967–6977. [Google Scholar] [CrossRef]
- Sakaue, H.; Hayashi, T.; Ishikawa, H. Luminophore application study of polymer-ceramic pressure-sensitive paint. Sensors 2013, 13, 7053–7064. [Google Scholar] [CrossRef]
- Egami, Y.; Konishi, S.; Sato, Y.; Matsuda, Y. Effects of solvents for luminophore on dynamic and static characteristics of sprayable polymer/ceramic pressure-sensitive paint. Sens. Actuators A Phys. 2019, 286, 188–194. [Google Scholar] [CrossRef]
- Hayashi, T.; Sakaue, H. Dynamic and steady characteristics of polymer-ceramic pressure-sensitive paint with variation in layer thickness. Sensors 2017, 17, 1125. [Google Scholar] [CrossRef]
- Peng, D.; Jiao, L.; Sun, Z.; Gu, Y.; Liu, Y. Simultaneous PSP and TSP measurements of transient flow in a long-duration hypersonic tunnel. Exp. Fluids 2016, 57, 1–16. [Google Scholar] [CrossRef]
- Yamashita, T.; Sugiura, H.; Nagai, H.; Asai, K.; Ishida, K. Pressure-sensitive paint measurement of the flow around a simplified car model. J. Vis. 2007, 10, 289–298. [Google Scholar] [CrossRef]
- Le Sant, Y.; Mérienne, M.C. Surface pressure measurements by using pressure-sensitive paints. Aerosp. Sci. Technol. 2005, 9, 285–299. [Google Scholar] [CrossRef]
- Kameda, M.; Yoshida, M.; Sekiya, T.; Nakakita, K. Humidity effects in the response of a porous pressure-sensitive paint. Sens. Actuators B Chem. 2015, 208, 399–405. [Google Scholar] [CrossRef]
- Liu, T.; Guille, M.; Sullivan, J.P. Accuracy of pressure-sensitive paint. AIAA J. 2001, 39, 103–112. [Google Scholar] [CrossRef]
- Sakaue, H. Luminophore application method of anodized aluminum pressure sensitive paint as a fast responding global pressure sensor. Rev. Sci. Instrum. 2005, 76, 1–6. [Google Scholar] [CrossRef]
- Egami, Y.; Sato, Y.; Konishi, S. Development of Sprayable Pressure-Sensitive Paint with a Response Time of Less Than 10 μs. AIAA J. 2019, 57, 2198–2203. [Google Scholar] [CrossRef]
- Pandey, A.; Gregory, J.W. Step response characteristics of polymer/ceramic pressure-sensitive paint. Sensors (Switzerland) 2015, 15, 22304–22324. [Google Scholar] [CrossRef]
- Carroll, B.; Abbitt, J.D.; Lukas, E.W. Step Response of Pressure-Sensitive Paints. AIAA J. 1996, 34, 521–526. [Google Scholar] [CrossRef]
- Sakaue, H.; Sullivan, J.P. Time response of anodized aluminum pressure-sensitive paint. AIAA J. 2012, 39, 1944–1949. [Google Scholar] [CrossRef]
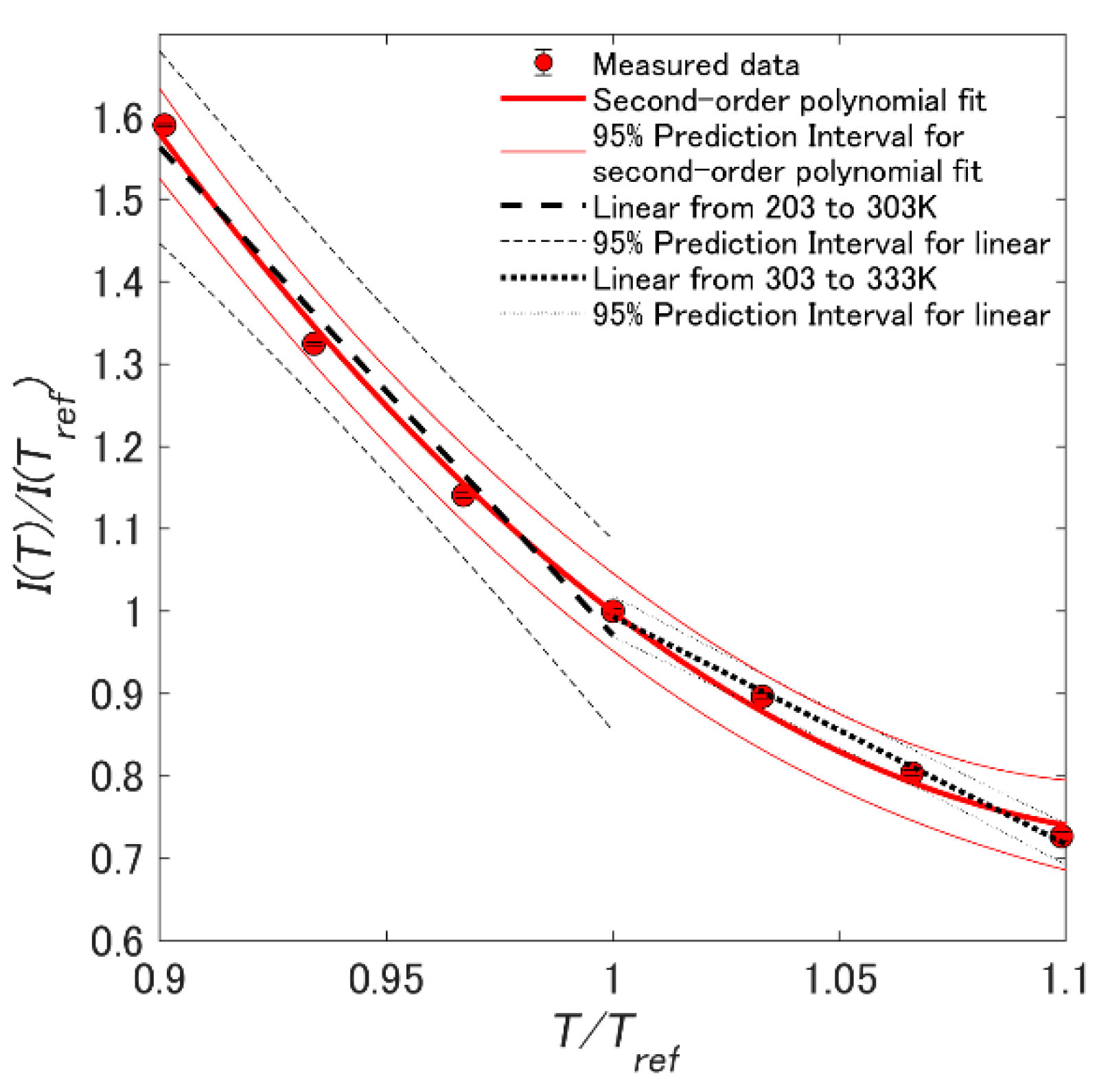
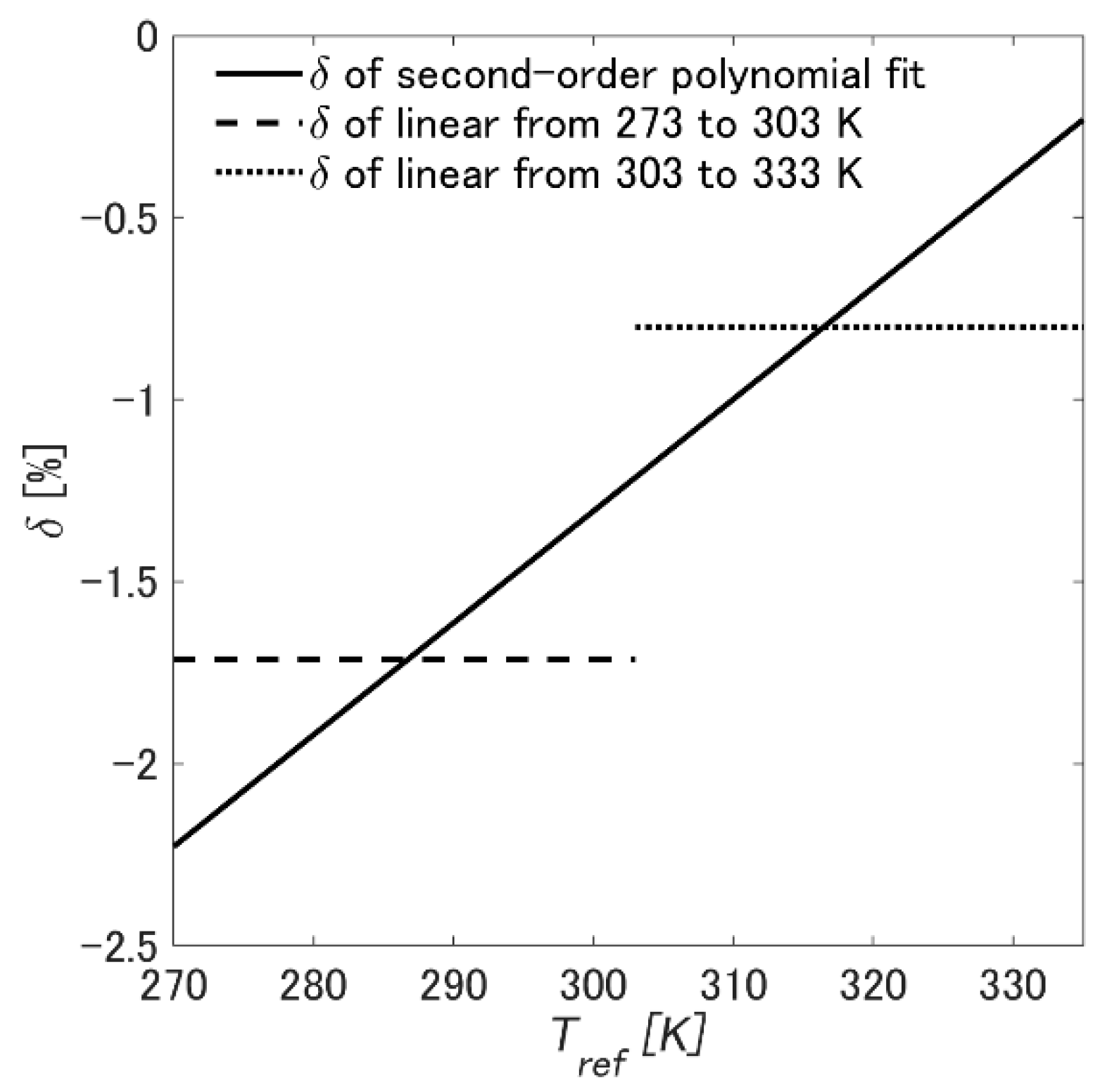
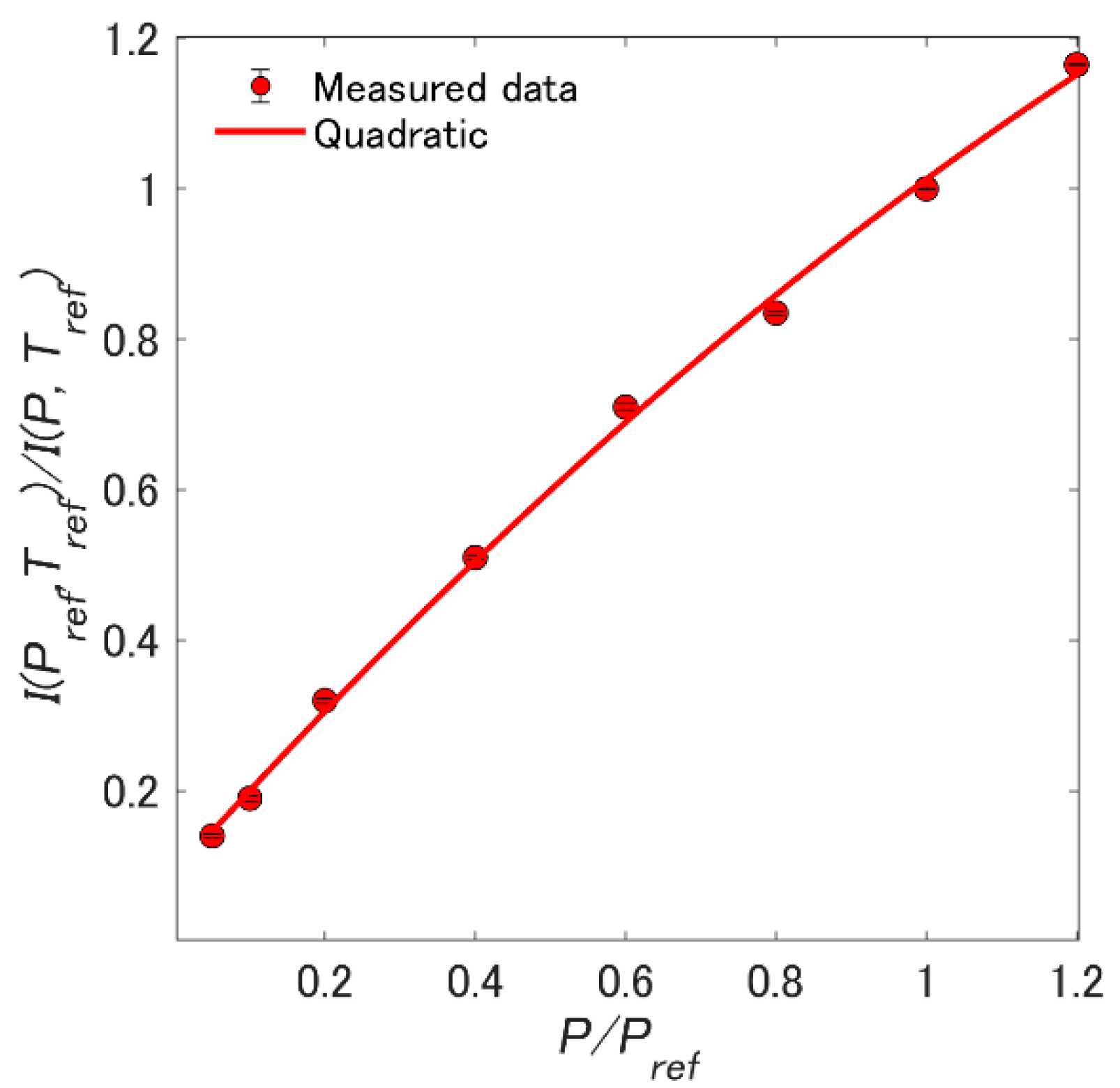
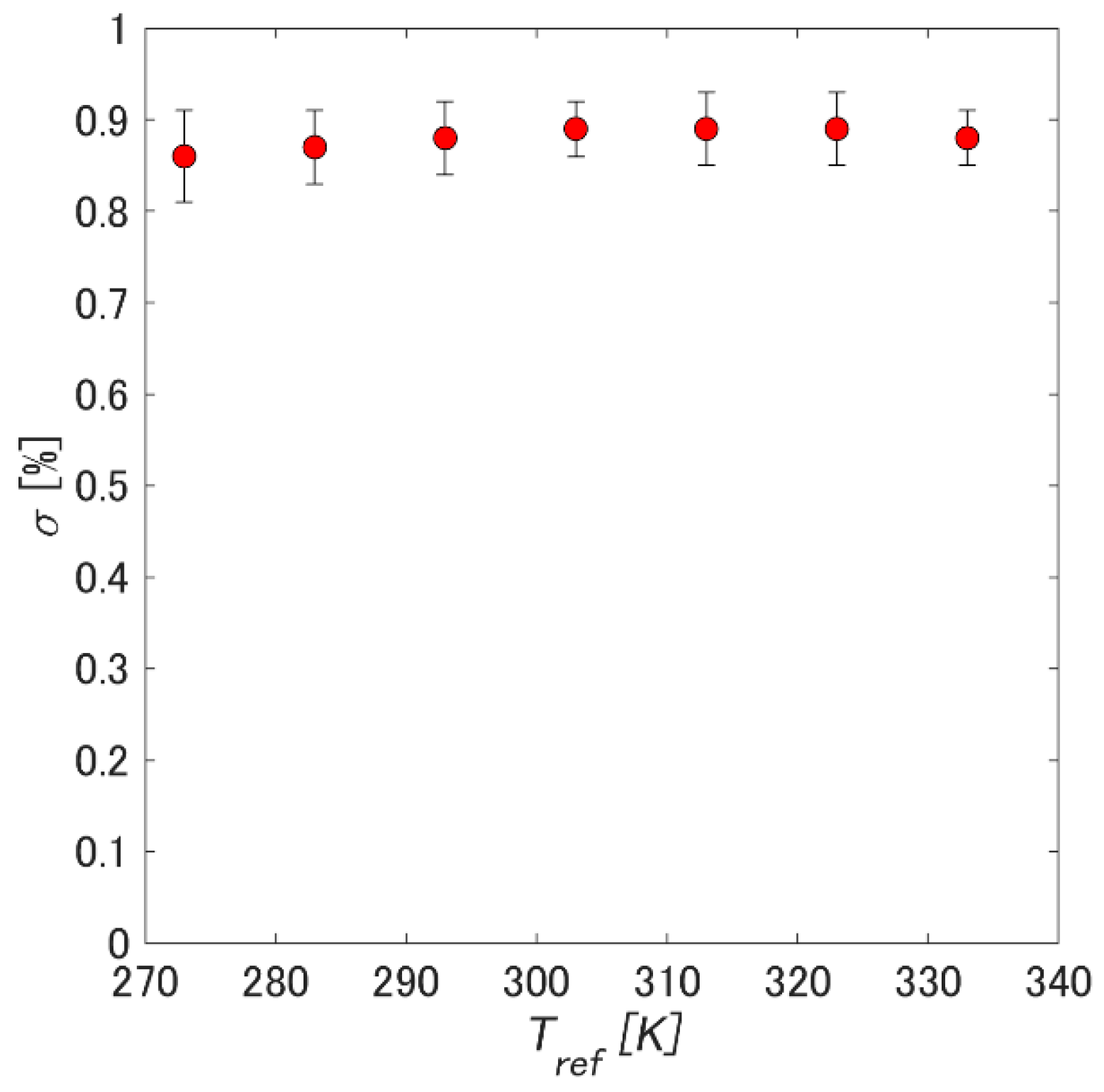
| Test Conditions | Luminescent Intensity Change, δ (%/K) | Pressure Sensitivity, σ (%/K) | Time Response, τ (usec/K) |
|---|---|---|---|
| Case 1: the reference and measurement temperatures can be controlled. | Constant (within uncertainty) | Constant (within uncertainty) | NA |
| Case 2: the reference and measurement temperatures cannot be controlled. | 3.07%/K | 1.06%/K | Constant (within uncertainty) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayashi, T.; Sakaue, H. Temperature Effects on Polymer-Ceramic Pressure-Sensitive Paint as a Luminescent Pressure Sensor. Aerospace 2020, 7, 80. https://doi.org/10.3390/aerospace7060080
Hayashi T, Sakaue H. Temperature Effects on Polymer-Ceramic Pressure-Sensitive Paint as a Luminescent Pressure Sensor. Aerospace. 2020; 7(6):80. https://doi.org/10.3390/aerospace7060080
Chicago/Turabian StyleHayashi, Tatsunori, and Hirotaka Sakaue. 2020. "Temperature Effects on Polymer-Ceramic Pressure-Sensitive Paint as a Luminescent Pressure Sensor" Aerospace 7, no. 6: 80. https://doi.org/10.3390/aerospace7060080
APA StyleHayashi, T., & Sakaue, H. (2020). Temperature Effects on Polymer-Ceramic Pressure-Sensitive Paint as a Luminescent Pressure Sensor. Aerospace, 7(6), 80. https://doi.org/10.3390/aerospace7060080






