Traffic Network Identification Using Trajectory Intersection Clustering
Abstract
1. Introduction
2. Status Quo
3. Materials and Methods
3.1. Clustering Algorithm DBSCAN
3.2. Pathfinding Algorithm
3.3. General Approach
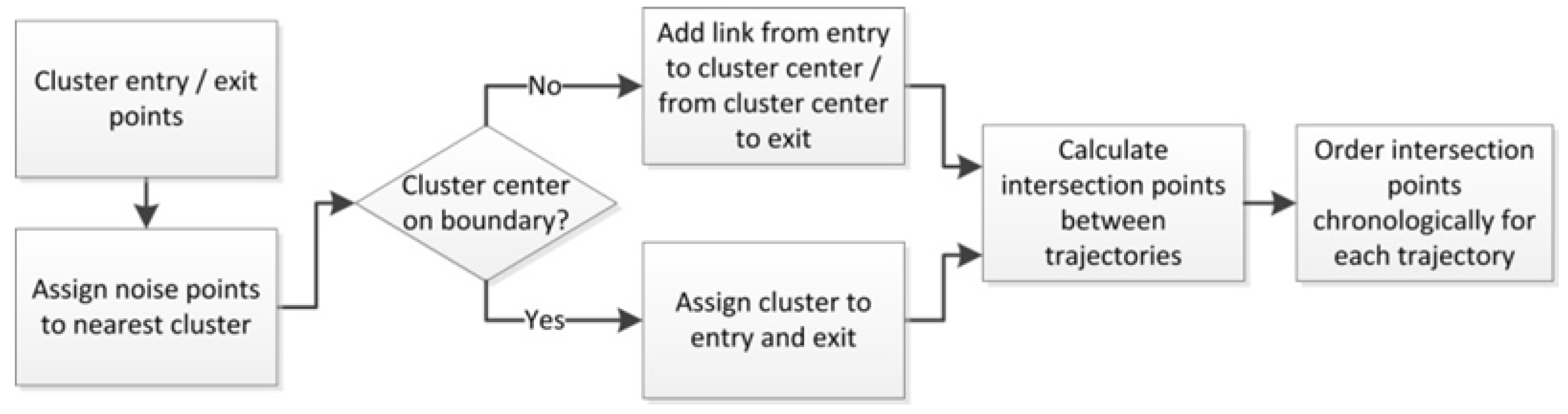
3.3.1. Pre-Processing
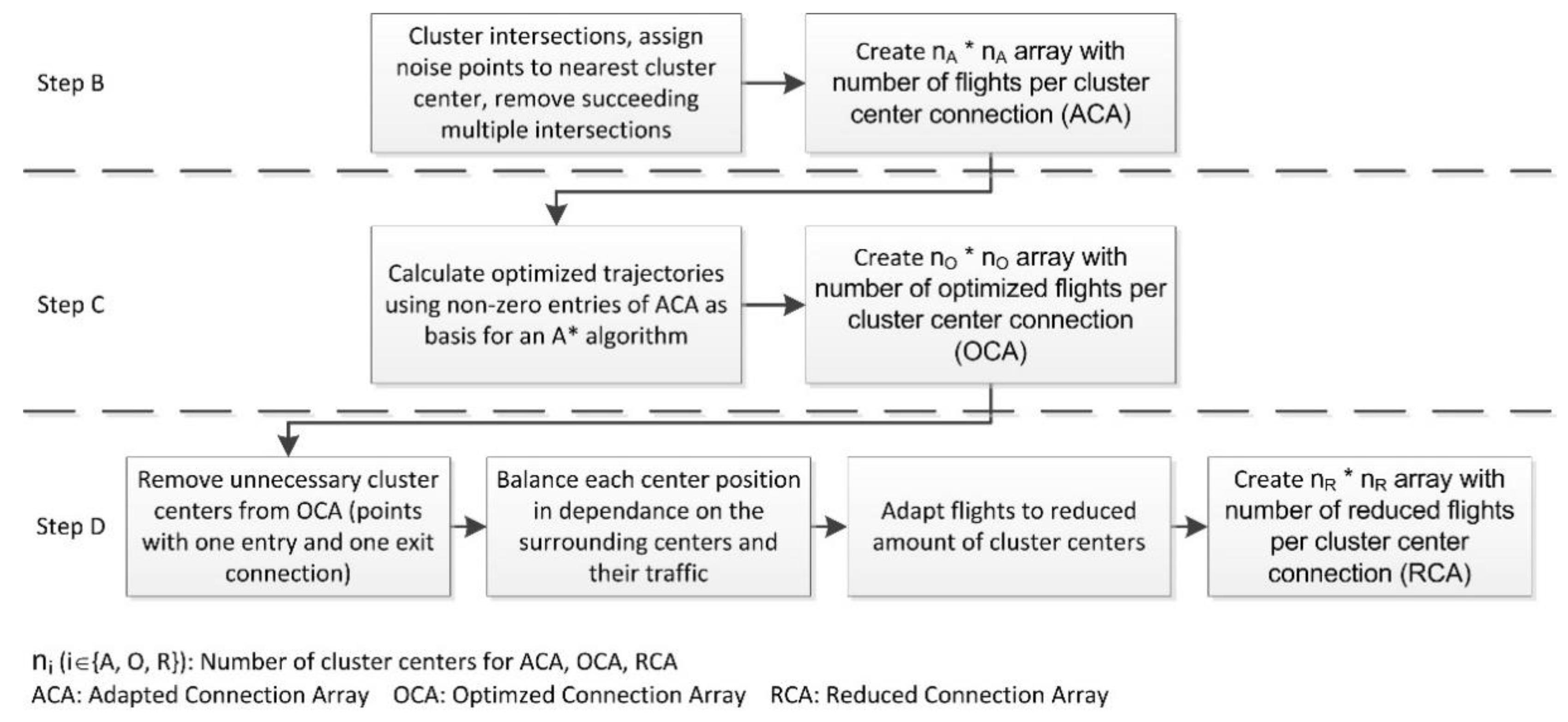
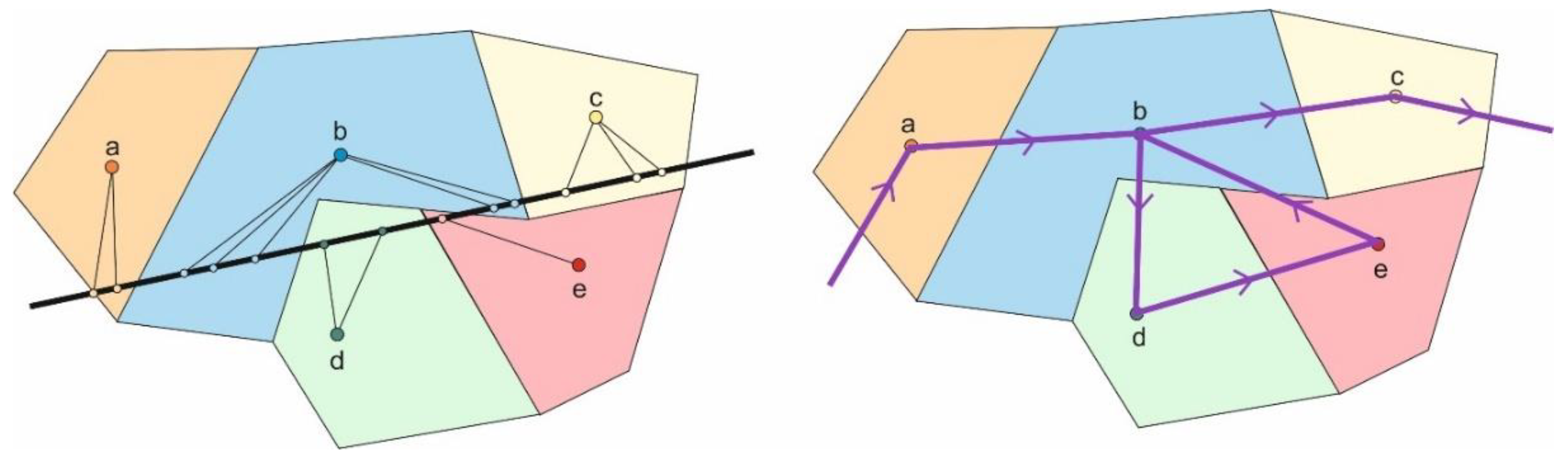
3.3.2. Main-Flow Processing
3.3.3. Calculation of Flight Parameters
4. Experimental Setup
4.1. Assumptions and Limitations
4.2. Assessment Metrics
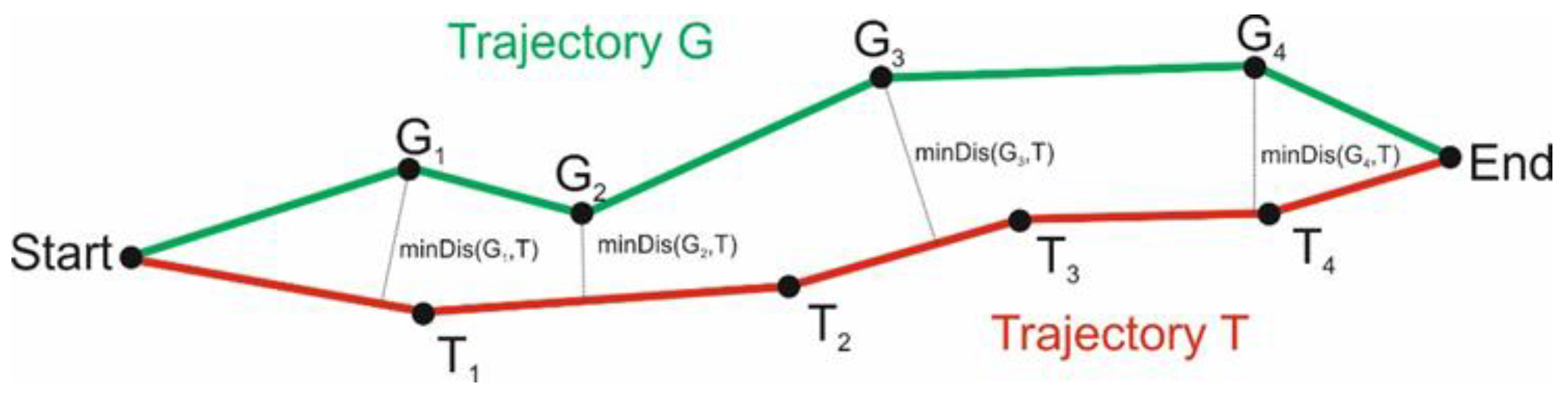
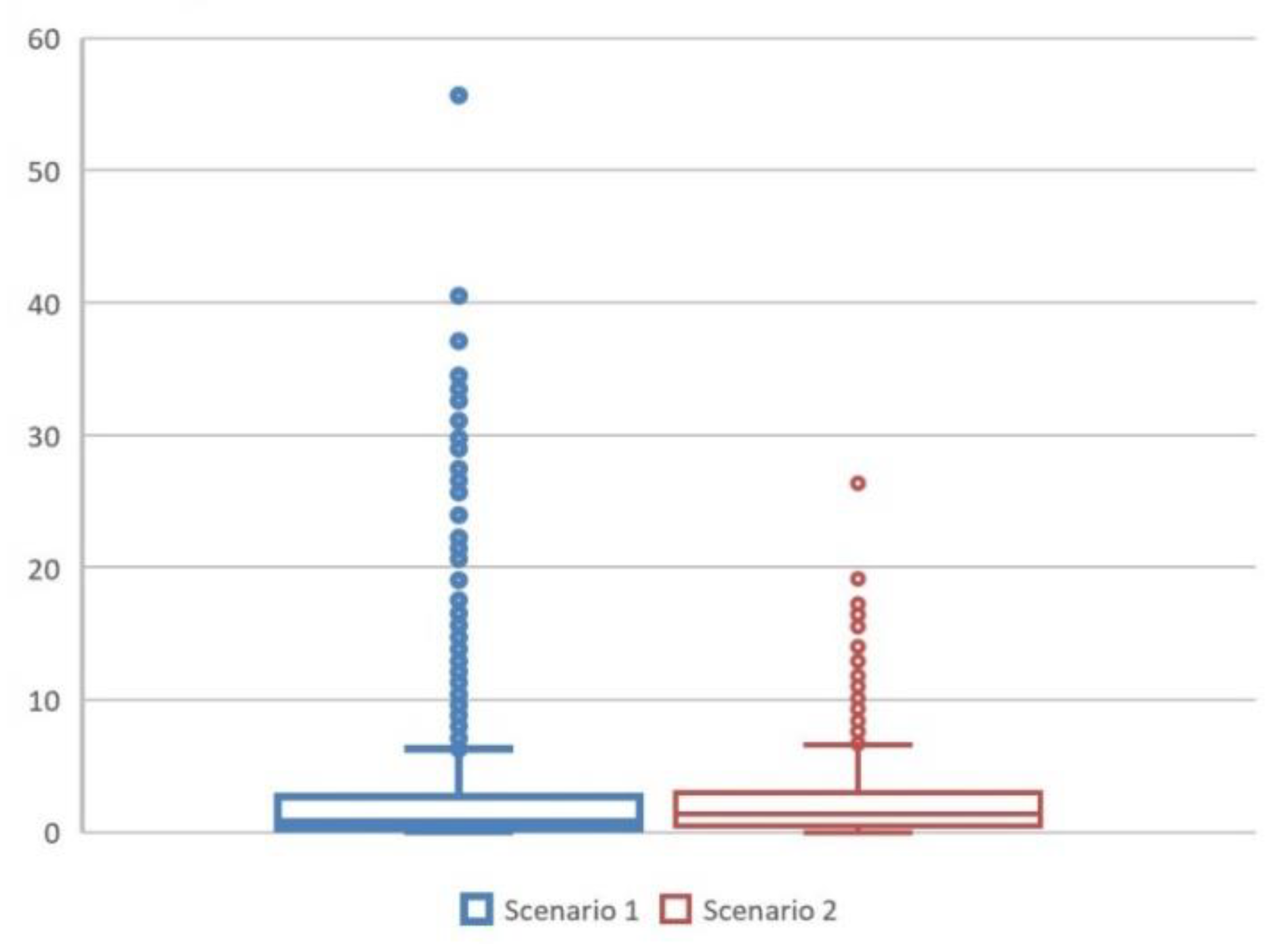
4.2.1. Trajectory Distance
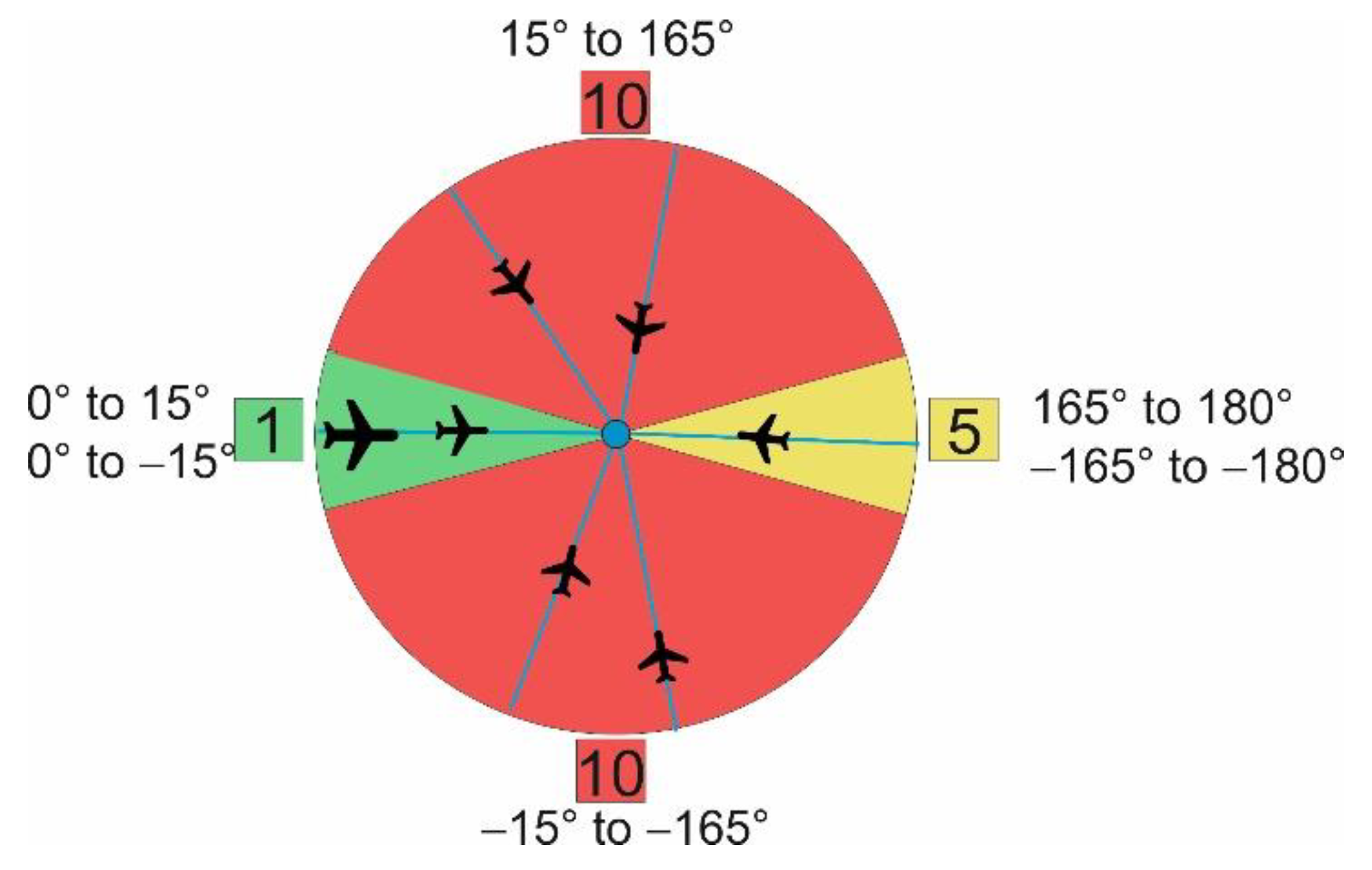
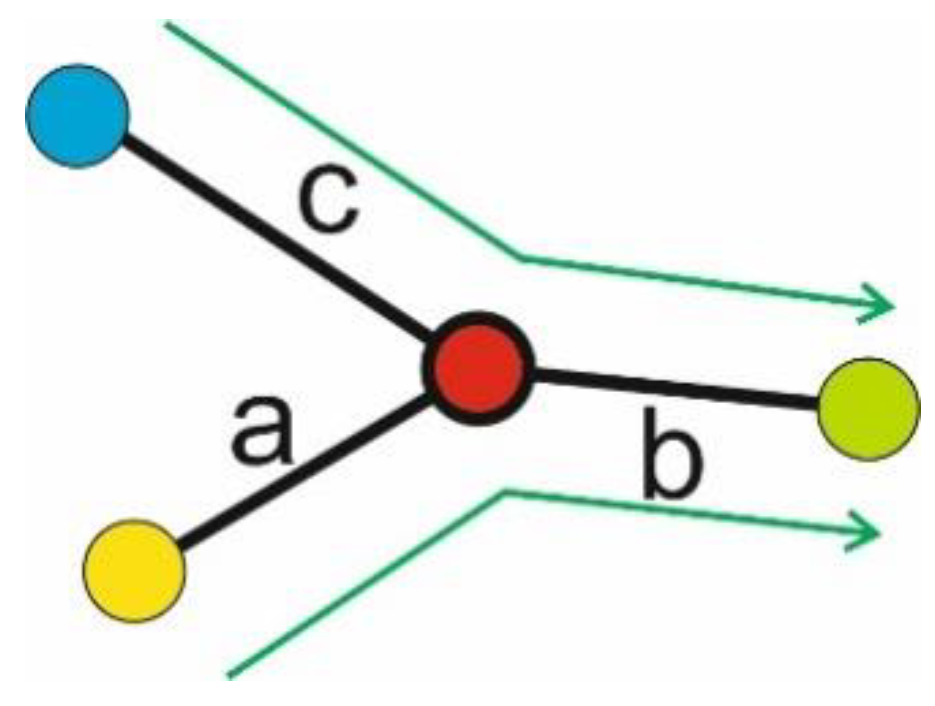
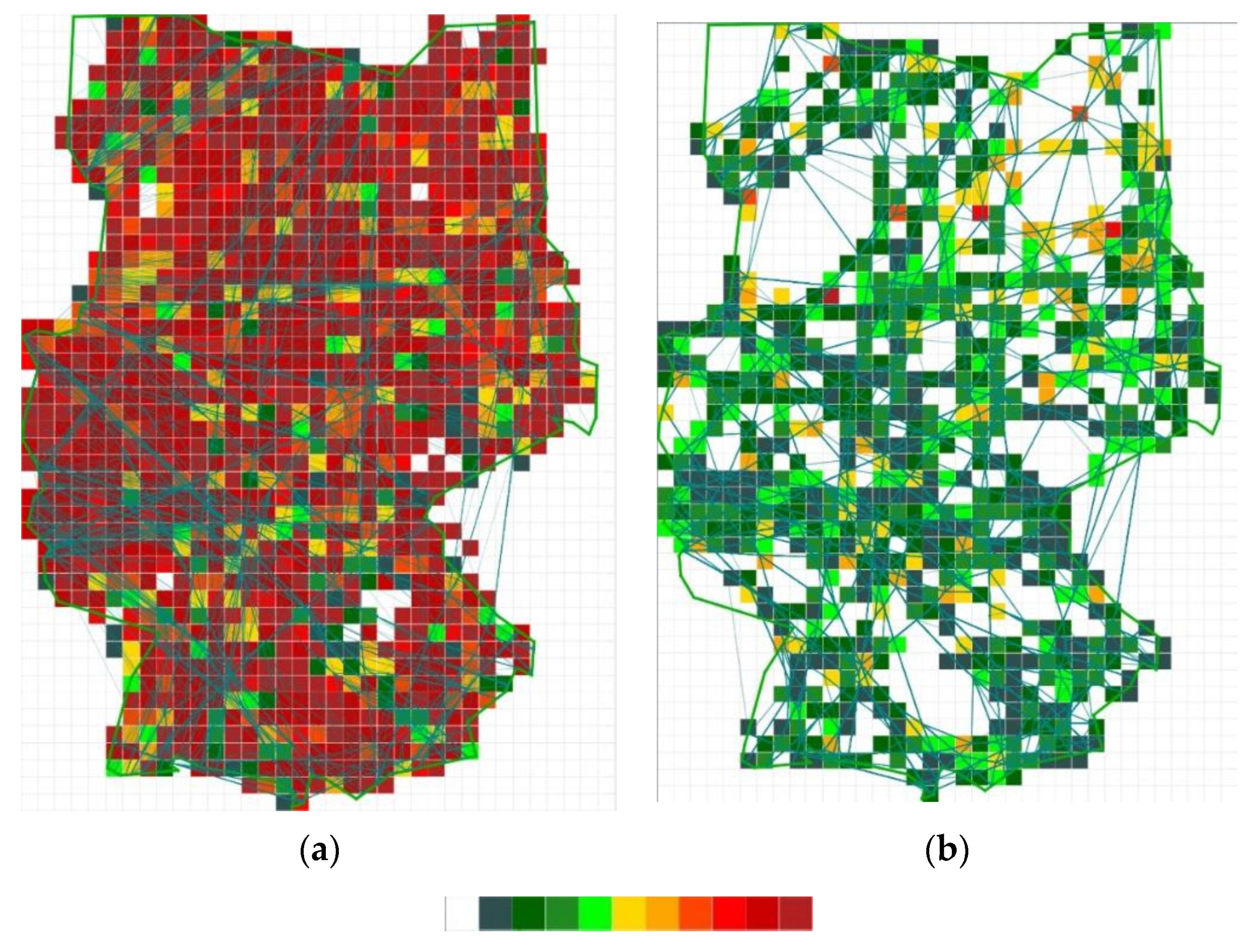
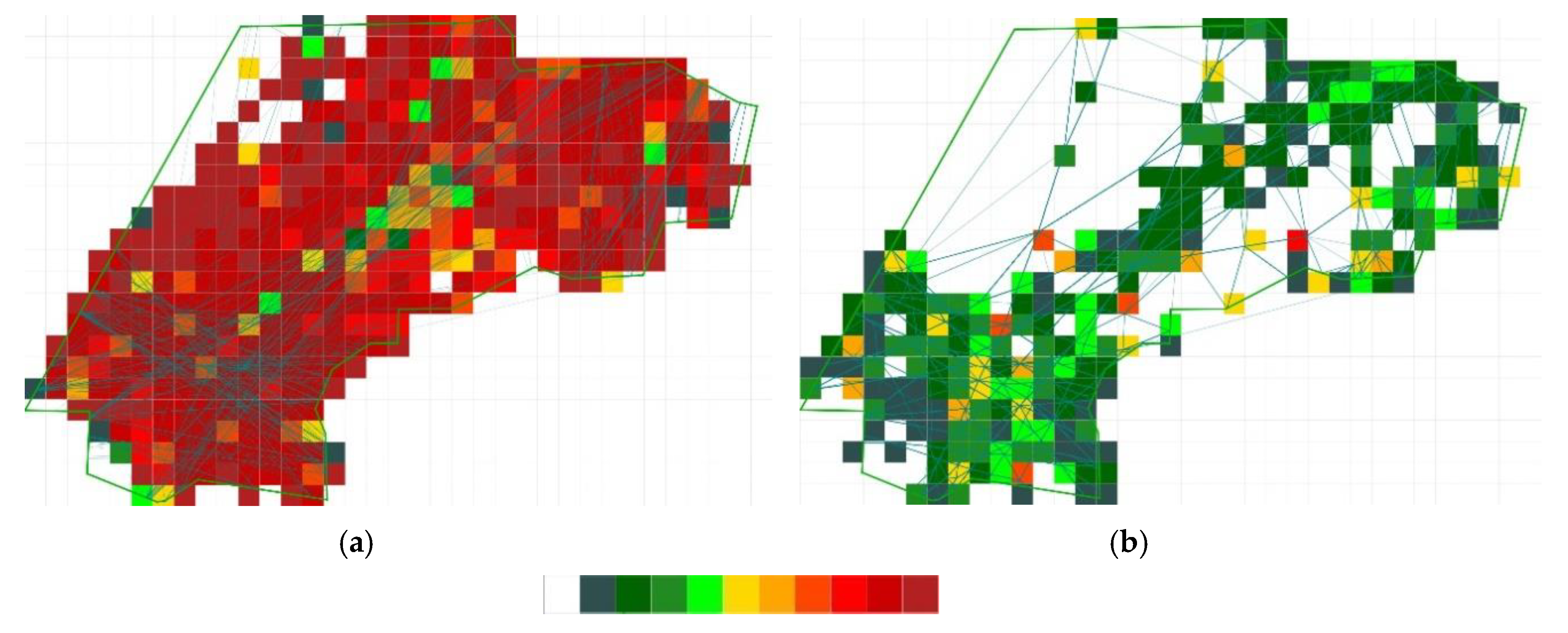
4.2.2. Structural Complexity of the Network
- Dominant flows intersected by less frequented other flows.
- Traffic from various directions with similar intensity.
- Broad variability in usage of intersection points.
4.2.3. Algorithm with Structural Complexity
4.3. Scenario Description and Simulation Parameters
4.4. Simulation Parameters
5. Results
5.1. Computational Efficiency
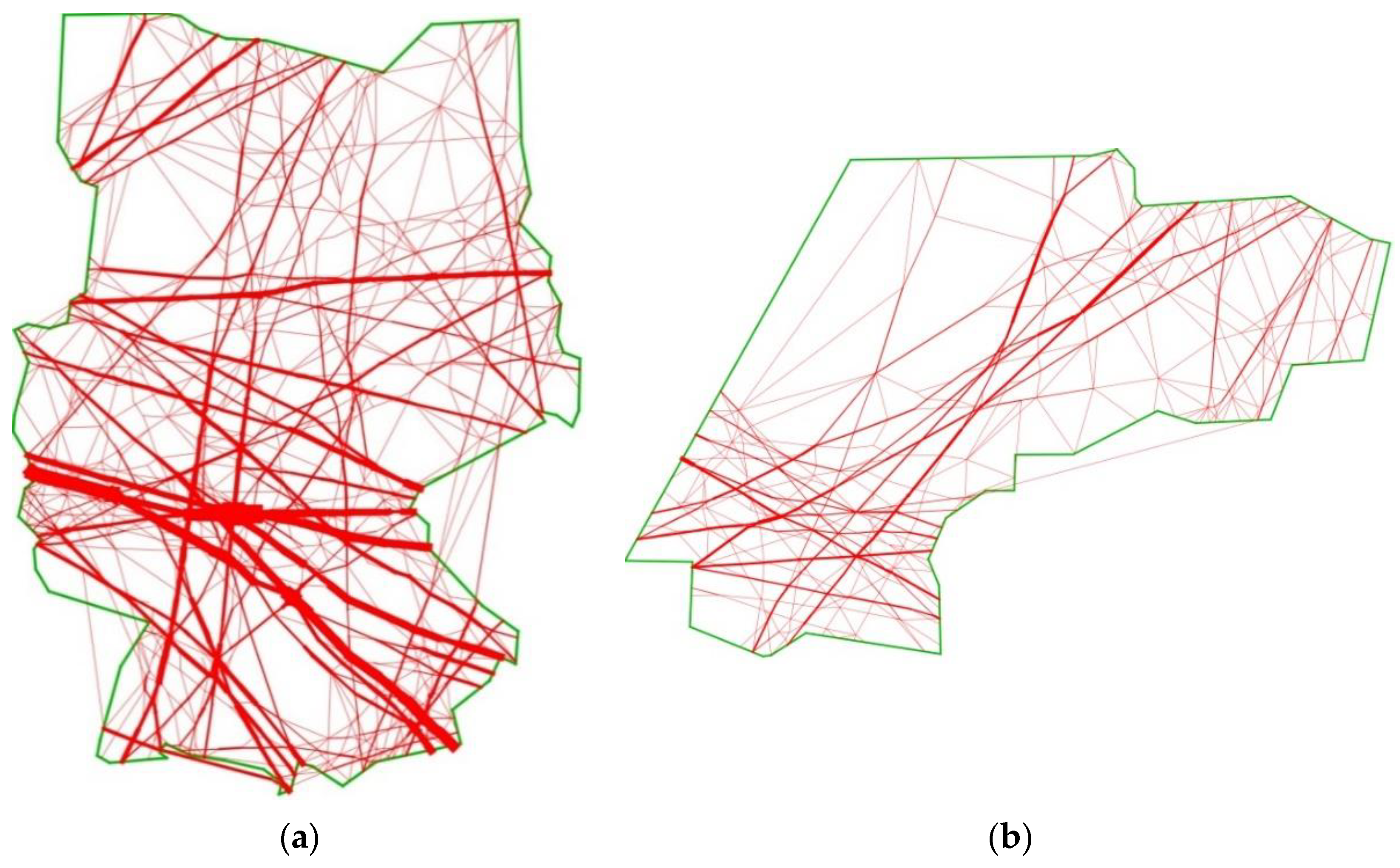
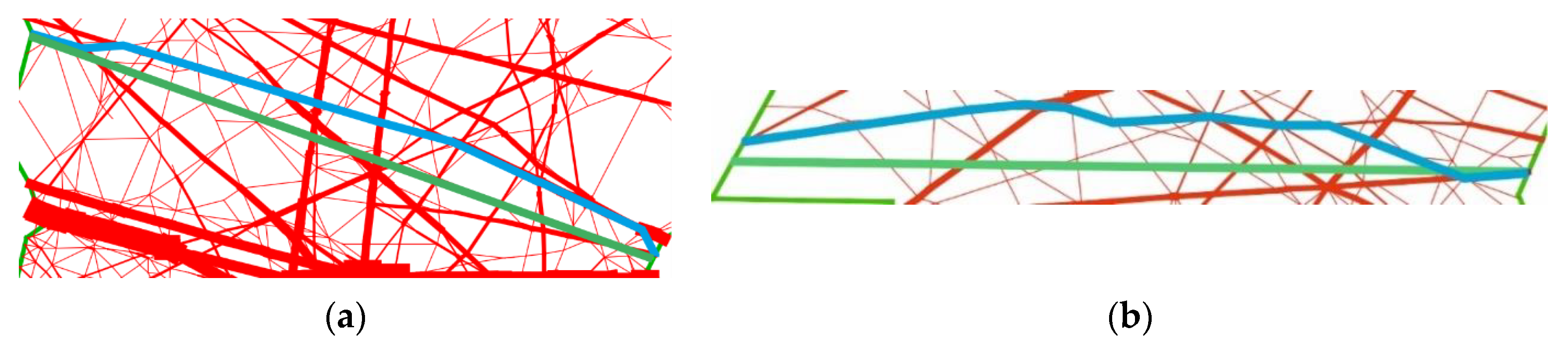
5.2. Main-Flow Network
5.3. Flight Parameters
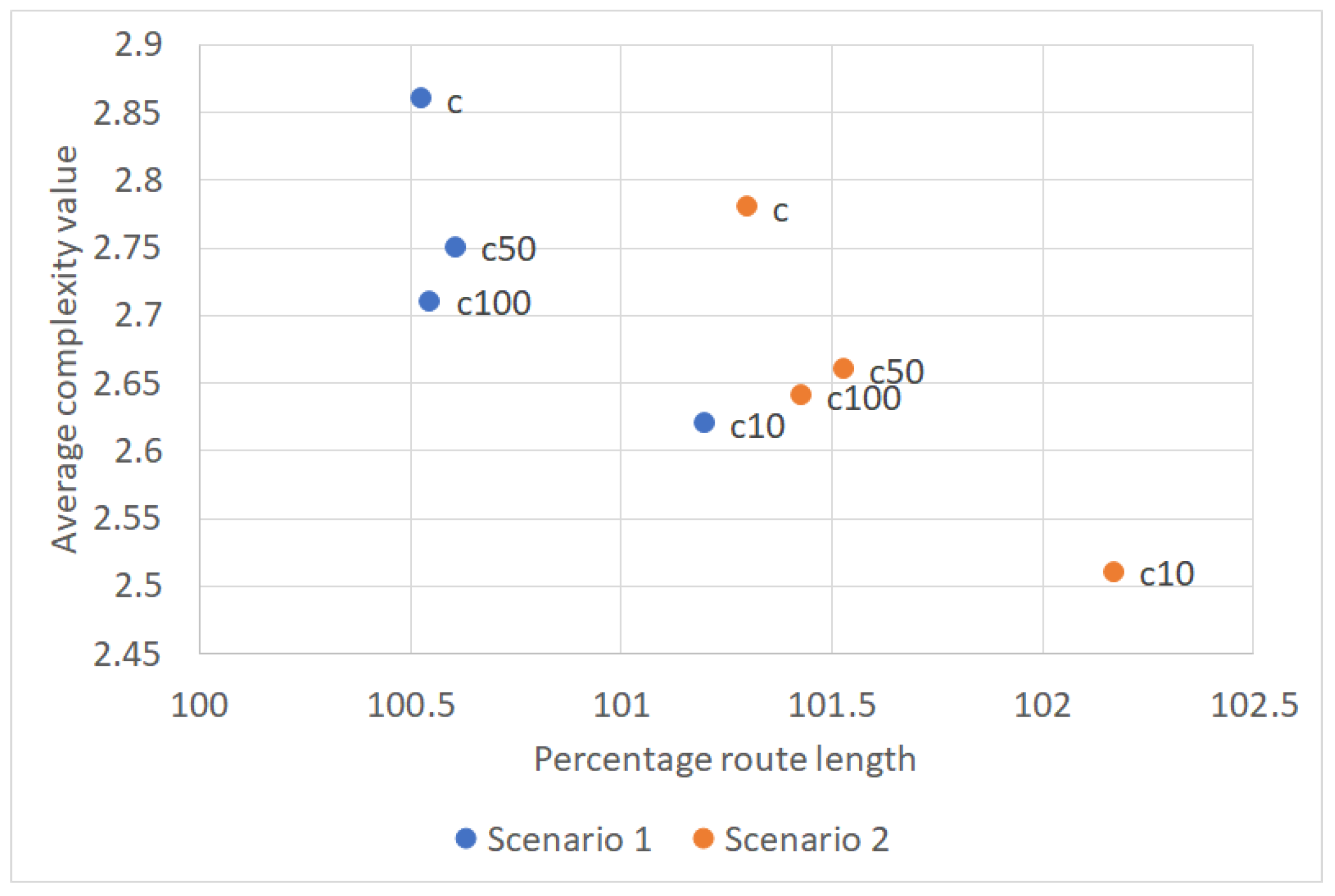
5.4. Adapted Cost Function
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schultz, M.; Olive, X.; Rosenow, J.; Fricke, H.; Alam, S. Analysis of airport ground operations based on ADS-B data. In Proceedings of the 2020 International Conference on Artificial Intelligence and Data Analytics for Air Transportation (AIDA-AT), Singapore, 3–4 February 2020. [Google Scholar] [CrossRef]
- Gariel, M.; Srivastava, A.N.; Feron, E. Trajectory Clustering and an Application to Airspace Monitoring. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1511–1524. [Google Scholar] [CrossRef]
- Gerdes, I.; Temme, A.; Schultz, M. From free-route air traffic to an adapted dynamic main-flow system. Transp. Res. Part C Emerg. Technol. 2020, 115, 102633. [Google Scholar] [CrossRef]
- Yuan, G.; Sun, P.; Zhao, J.; Li, D.; Wang, C. A review of moving object trajectory clustering algorithms. Artif. Intell. Rev. 2016, 47, 123–144. [Google Scholar] [CrossRef]
- Basora, L.; Morio, J.; Mailhot, C. A Trajectory Clustering Framework to Analyse Air Traffic Flows. In Proceedings of the 7th Sesar Innovation Days, Belgrade, Serbia, 28–30 November 2017. [Google Scholar]
- Delahaye, D.; Puechmorel, S.; Alam, S.; Feron, E. Trajectory Mathematical Distance Applied to Airspace Major Flows Extraction. In Lecture Notes in Electrical Engineering, Air Traffic Management and Systems III; Springer: Cham, Switzerland, 2018; pp. 51–66. [Google Scholar]
- Marzuoli, A.; Gariel, M.; Vela, A.; Feron, E. Data-Based Modeling and Optimization of En Route Traffic. J. Guid. Control. Dyn. 2014, 37, 1930–1945. [Google Scholar] [CrossRef]
- Olive, X.; Morio, J. Trajectory clustering of air traffic flows around airports. Aerosp. Sci. Technol. 2018, 84, 776–781. [Google Scholar] [CrossRef]
- Lee, J.-G.; Han, J.; Whang, K.-Y. Trajectory clustering: A partition-and-group framework. In Proceedings of the SIGMOD’07, Beijing, China, 11–14 June 2007. [Google Scholar] [CrossRef]
- Besse, P.C.; Guillouet, B.; Loubes, J.-M.; Royer, F. Review and Perspective for Distance-Based Clustering of Vehicle Trajectories. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3306–3317. [Google Scholar] [CrossRef]
- Vlachos, M.; Kollios, G.; Gunopulos, D. Discovering Similar Multidimensional Trajectories. In Proceedings of the 18th International Conference on Data Engineering, San Jose, CA, USA, 26 February–1 March 2002. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Reddy, C.K. (Eds.) Data Clustering: Algorithms and Applications. In Data Mining and Knowledge Discovery; CRC Press: Boca Raton, FL, USA; Taylor & Francis Inc.: Oxfordshire, UK, 2014; Volume 31, ISBN 978-1466558212. [Google Scholar]
- Mc Innes, L.; Healy, J. Accelerated Hierarchical Density Clustering. In Proceedings of the IEEE International Conference on Data Mining Workshops (ICDMW), New Orleans, LA, USA, 18–21 November 2017. [Google Scholar] [CrossRef]
- Mirkin, B. Mathematical Classification and Clustering; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996; ISBN 978-1-4613-0457-9. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters. In Proceedings of the KDD-96, Portland, OR, USA, 2–4 August 1996. [Google Scholar]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Ankerst, M.; Breunig, M.; Kriegel, H.-P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Philadelphia, PA, USA, 1–3 June 1999. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Sheridan, K.; Puranik, T.; Mangortey, E.; Pinon, O.; Kirby, M.; Mavris, D. An Application of DBSCAN Clustering for Flight Anomaly Detection during the Approach Phase. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- ICAO. Annex 2 to the Convention on International Civil Aviation. Rules of the Air. ICAO, 10th ed.; ICAO: Montreal, QC, Canada, 2005. [Google Scholar]
- Athènes, S.; Averty, P.; Puechmorel, S.; Delahaye, D.; Collet, C. ATC complexity and controller workload: Trying to bridge the gap. In Proceedings of the International Conference on HCI in Aeronautics, Cambridge, MA, USA, 23–25 October 2002. [Google Scholar]
- Prandini, M.; Piroddi, L.; Puechmorel, S.; Brazdilova, S.L. Toward Air Traffic Complexity Assessment in New Generation Air Traffic Management Systems. IEEE Trans. Intell. Transp. Syst. 2011, 12, 809–818. [Google Scholar] [CrossRef]
- EUROCONTROL. Complexity Metrics for ANSP Benchmarking Analysis; ACE Working Group on Complexity: EUROCONTROL: Brussels, Belgium, 2006. [Google Scholar]
- Gianazza, D. Airspace configuration using air traffic complexity metrics. In Proceedings of the 7th USA/Europe Air Traffic Management R&D Seminar, Barcelona, Spain, 2–5 July 2007. [Google Scholar]
- EUROCONTROL. DDR2 Reference Manual 2.9.5; EUROCONTROL: Brussels, Belgium, 2018. [Google Scholar]



| Objects Clustered | Scenario | [NM] | [# Points] |
|---|---|---|---|
| Common Points | 1 | 0.7 | 30 |
| 2 | 0.6 | 20 | |
| Entry/Exit | 1 | 2.0 | 5 |
| 2 | 2.0 | 3 |
| Scenario | Step A | Step B | Step C | Step Cadv | Step D | |
|---|---|---|---|---|---|---|
| 1 | German Airspace [s] | 45 | 32 | 225 | 1040 | 2 |
| 2 | EDYYDUTA [s] | 2 | 2 | 7 | 136 | 1 |
| Common Points | Cluster Centers | |||||
|---|---|---|---|---|---|---|
| Scenario | # Flights | Total | Different | Adapted | Reduced | Noise [%] |
| 1 | 4027 | 4,048,686 | 53,449 | 3698 | 1866 | 2.6 |
| 2 | 1183 | 310,704 | 23,897 | 1538 | 642 | 11.8 |
| Scenario | Entry | Exit | Combined |
|---|---|---|---|
| 1 | 54 | 55 | 25 |
| 2 | 36 | 45 | 7 |
| Scenario | SSPD [NM] | Route Length Relative to Original Routes [%] | SC Intersections | SC Cluster Centers | Trajectories per Cluster Center [#] | |
|---|---|---|---|---|---|---|
| 1 | Median | 0.8 | 100.2 | 7.1 | 2.9 | 48 |
| 1. Quartile | 0.2 | 99.9 | 5.6 | 1.8 | 25 | |
| 3. Quartile | 2.6 | 101.2 | 7.5 | 4.4 | 84 | |
| 2 | Median | 1.4 | 100.5 | 8.8 | 2.80 | 38 |
| 1. Quartile | 0.5 | 100. | 9.6 | 1.9 | 14 | |
| 3.Quartile | 2.9 | 101.5 | 11.7 | 4.3 | 58 |
| Flight Level | Track 0–179° | Track 180–359° | ||||
|---|---|---|---|---|---|---|
| H | M | L | H | M | L | |
| Scenario 1 | 356 | 351 | 350 | 364 | 358 | 355 |
| Scenario 2 | 330 | 344 | 330 | 345 | 345 | 356 |
| Speed | Track 0–179° | Track 180–359° | ||||
|---|---|---|---|---|---|---|
| H | M | L | H | M | L | |
| Scenario 1 | 510 | 493 | 309 | 422 | 412 | 309 |
| Scenario 2 | 506 | 483 | 370 | 428 | 418 | 327 |
| Scenario | Route Length Relative to Original Routes [%] | SC of Cluster Centers | Number of Links | Length of Main-flow System | SSPD | Node Number per Trajectory |
|---|---|---|---|---|---|---|
| 100.5 | 2.9 | 4942 | 29,159 | 0.78 | 43 | |
| 1 with | 100.6 | 2.7 | 5329 | 31,641 | 0.78 | 43 |
| 2 with | 100.3 | 2.8 | 1780 | 10,089 | 1.35 | 36 |
| 2 with | 101.4 | 2.6 | 2060 | 11,437 | 1.49 | 35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerdes, I.; Temme, A. Traffic Network Identification Using Trajectory Intersection Clustering. Aerospace 2020, 7, 175. https://doi.org/10.3390/aerospace7120175
Gerdes I, Temme A. Traffic Network Identification Using Trajectory Intersection Clustering. Aerospace. 2020; 7(12):175. https://doi.org/10.3390/aerospace7120175
Chicago/Turabian StyleGerdes, Ingrid, and Annette Temme. 2020. "Traffic Network Identification Using Trajectory Intersection Clustering" Aerospace 7, no. 12: 175. https://doi.org/10.3390/aerospace7120175
APA StyleGerdes, I., & Temme, A. (2020). Traffic Network Identification Using Trajectory Intersection Clustering. Aerospace, 7(12), 175. https://doi.org/10.3390/aerospace7120175






