Assessment of a Turbo-Electric Aircraft Configuration with Aft-Propulsion Using Boundary Layer Ingestion
Abstract
1. Introduction
- Improved operability of the gas generator (e.g., by minimizing cooling requirements or enhancing component performance in terms of stall margins, resulting in reduced required variability),
- possible re-(down-)sizing and optimization of the gas generator (e.g., by relieving the core engine requirements by additional power input from an electrical source at the most demanding, and hence, sizing relevant mission points), and
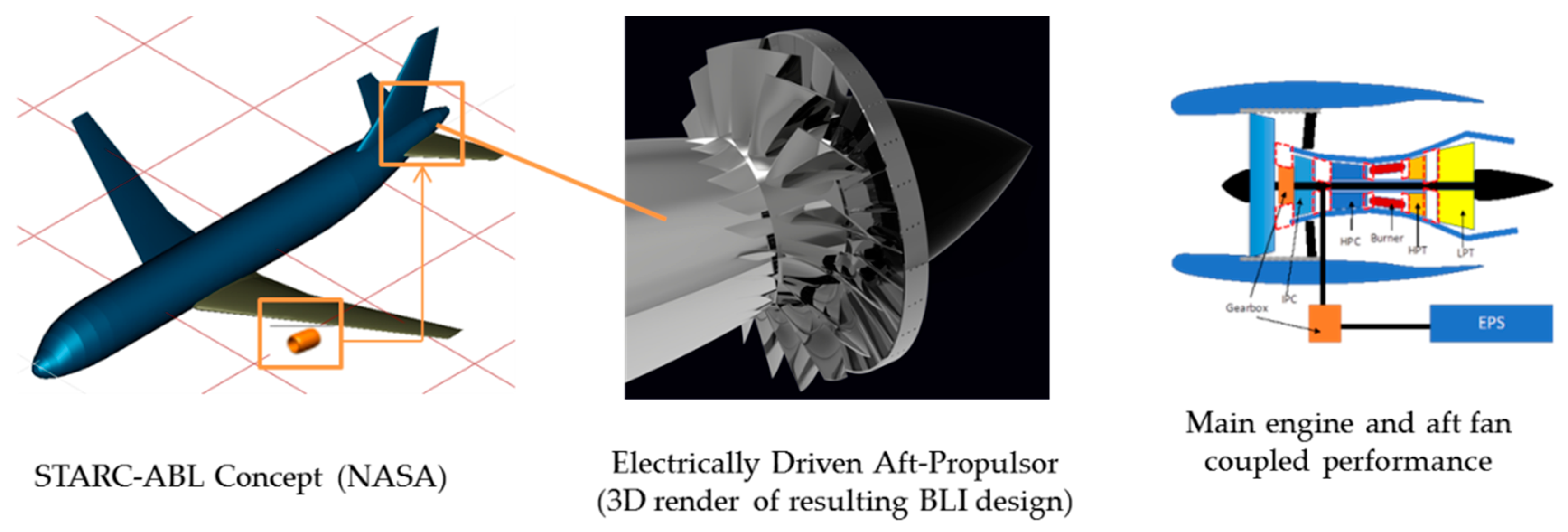
- decouple the location of thrust induction from power generation and thereby further opening the entire design space and allowing for novel aircraft configurations with improved engine integration (e.g., by ingesting the fuselage boundary layer).
2. Research Objectives and Layout of the Present Study
- The amount of boundary layer captured by the aft-propulsor and hence, the level of achievable propulsive efficiency;
- The performance and design of the aft-fan;
- The performance of the main engine and its components, in particular considering that power is being extracted and transferred to drive the aft propulsor;
- The performance and weight of the electrical system.
- (1)
- What is the sensitivity of the system top-level parameters, here mainly being the power extraction from the main engine low speed shaft (PWX46) to the aft-fan (PWX48), as well as the aft-fan FPR, on the overall performance metrics (downselection)?
- (2)
- What implications and challenges do those choices impose on the conceptual design of the aft-fan and to what extent do they affect the gas turbine/main engine performance?
3. Assumptions and Methodology
3.1. Aircraft and Mission Profile
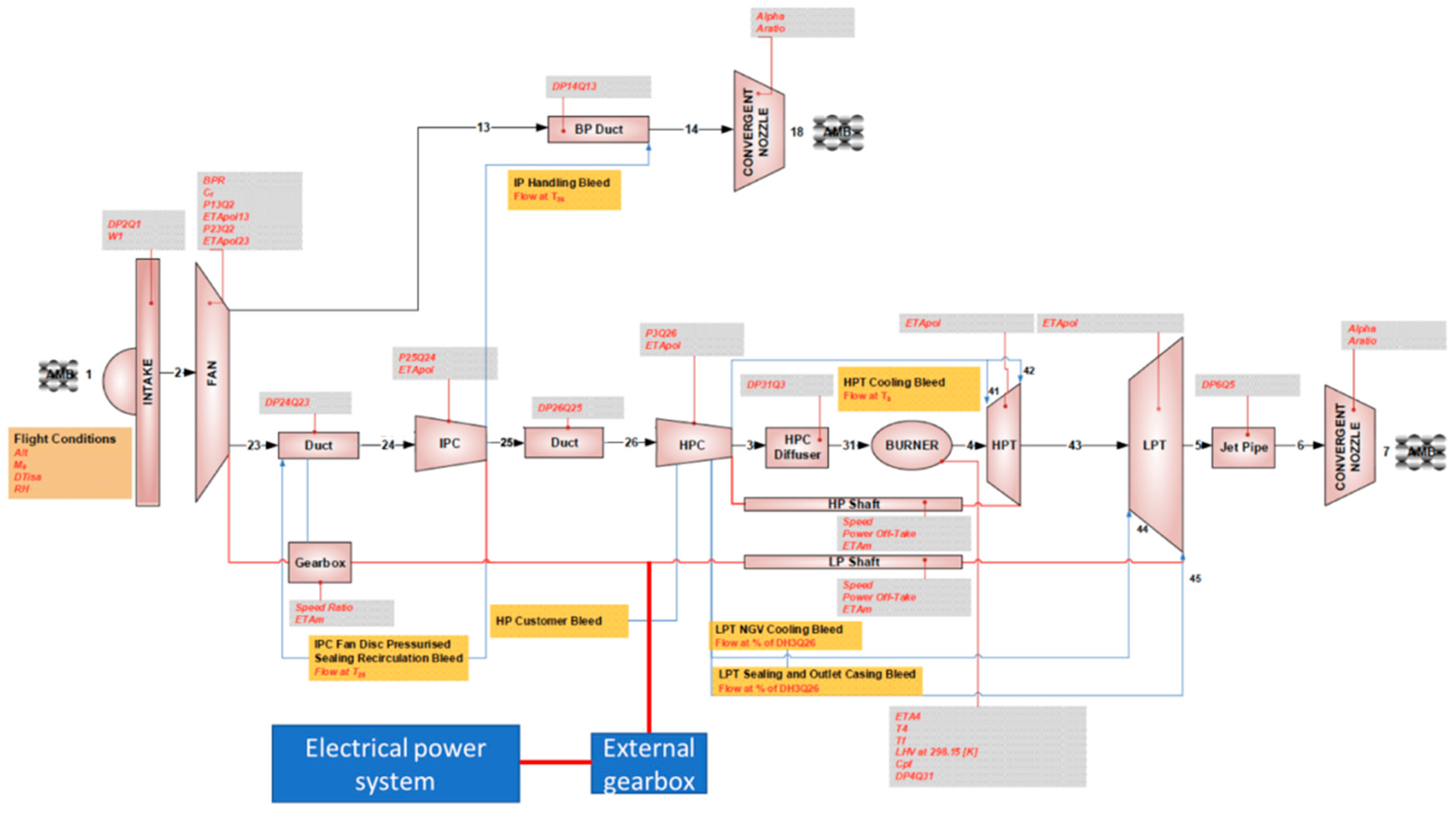
3.2. Main Engine Gas Turbine Cycle
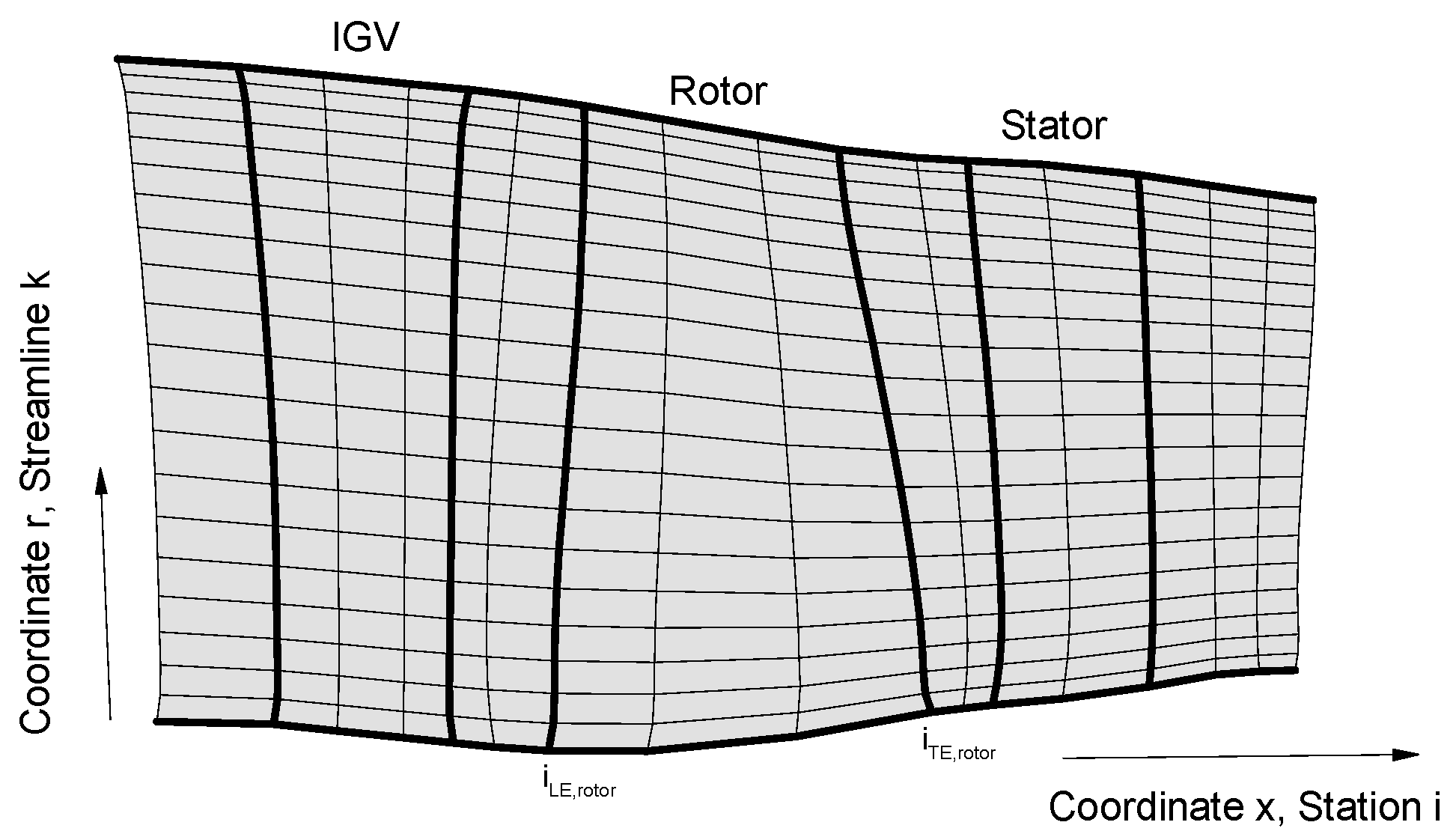
3.3. Propulsor Conceptual Design
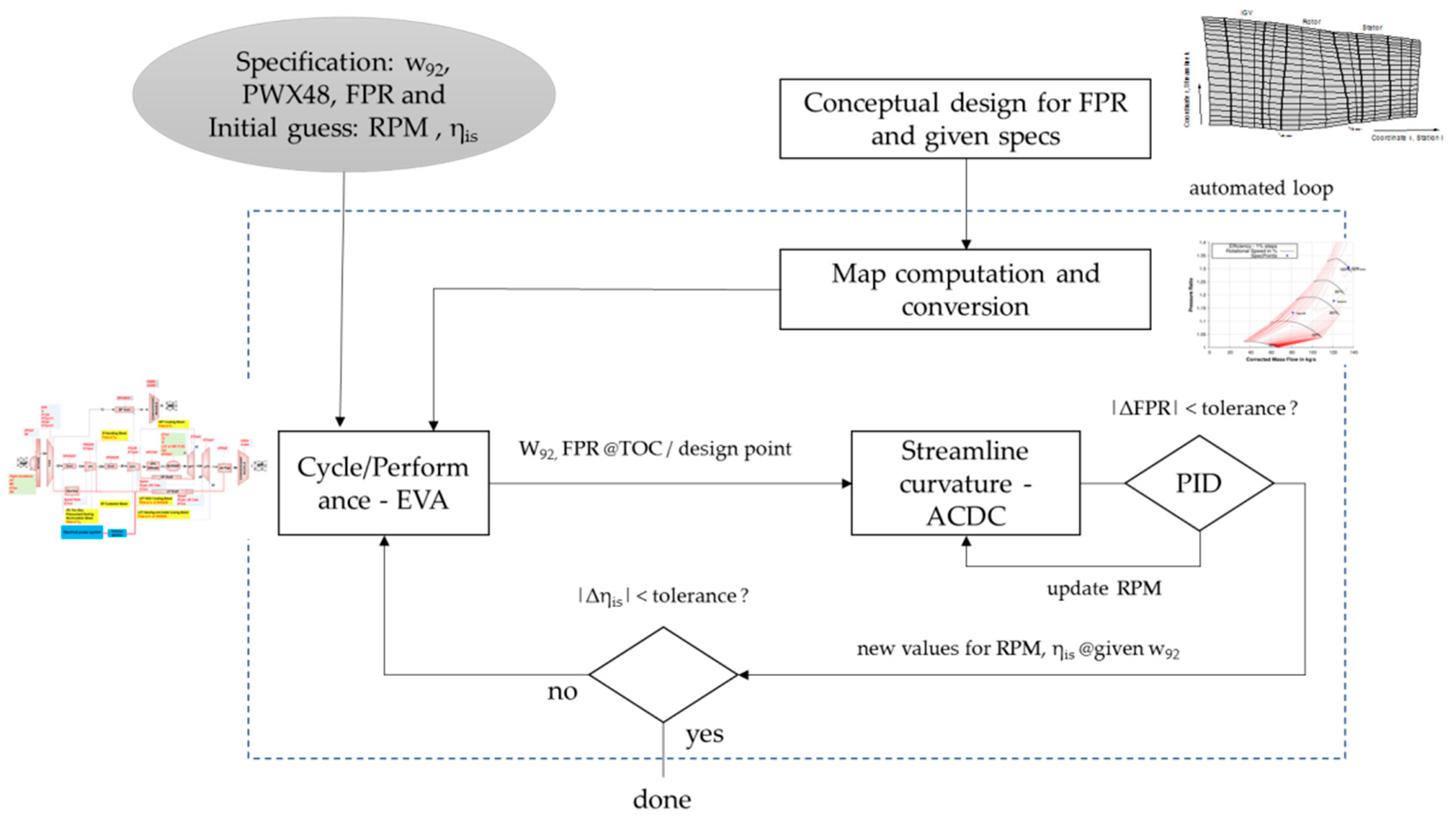
3.4. Method Coupling Procedure and Performance Characteristics Sensitivity
- Use and scaling of a standard component map (either from open literature or from an internal database, depending on the level of knowledge);
- The scaling of a more tailored map (e.g., stemming from initial design considerations of the respective module);
- Direct use of the unscaled map, e.g., from more advanced conceptual design iterations of the module; or
- A direct coupling between the cycle performance and the component design, typically realized in an iterative manner for each mission point (a zooming-like approach).
4. Results and Discussion
4.1. Sensitivity Studies
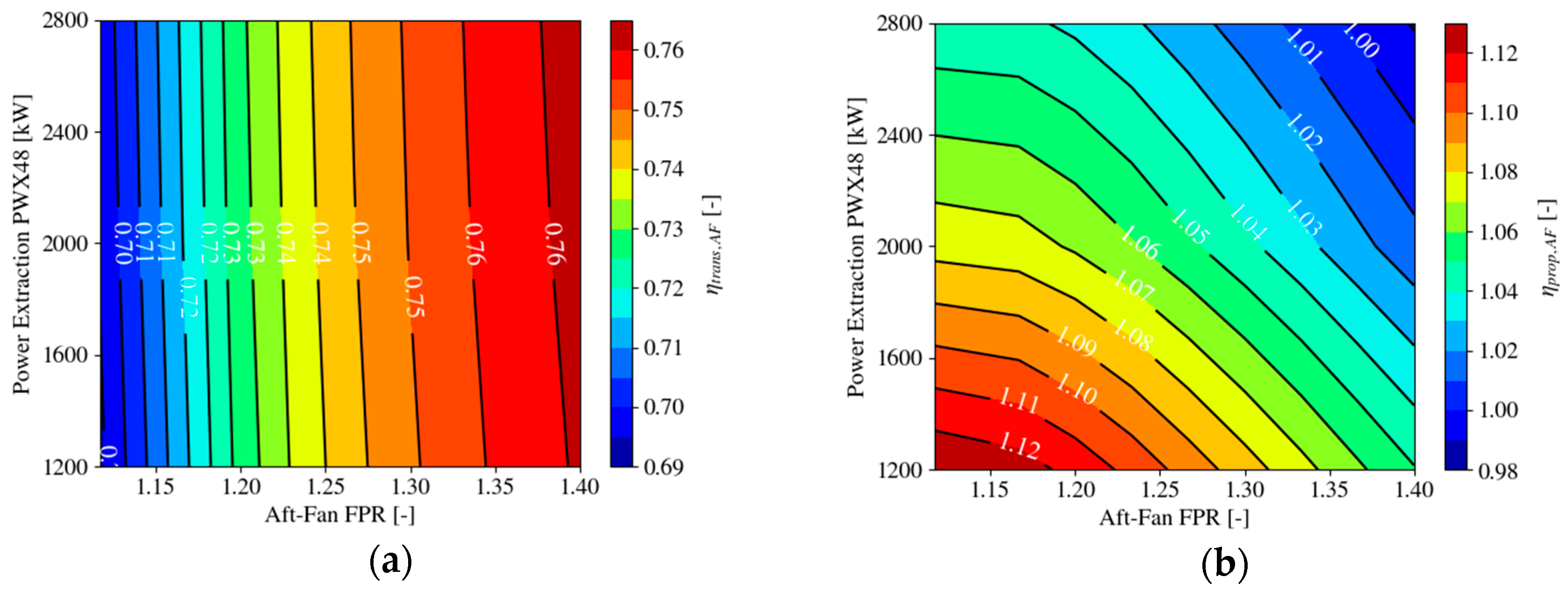
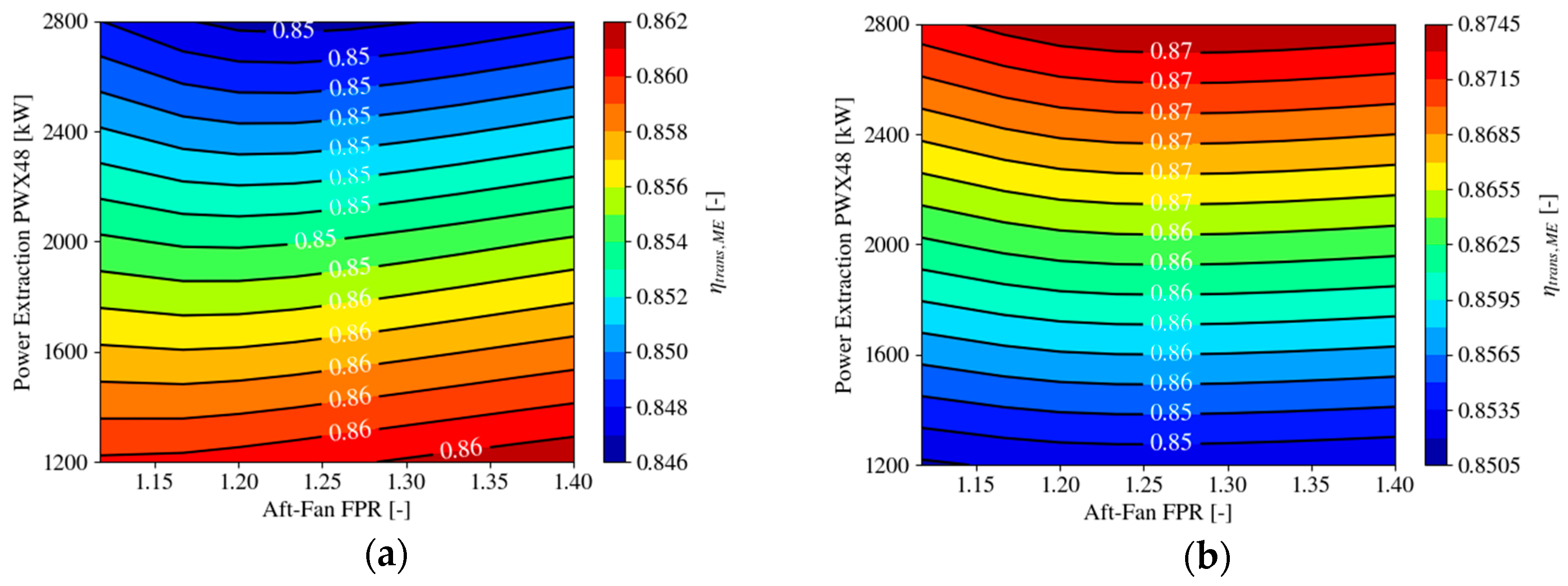
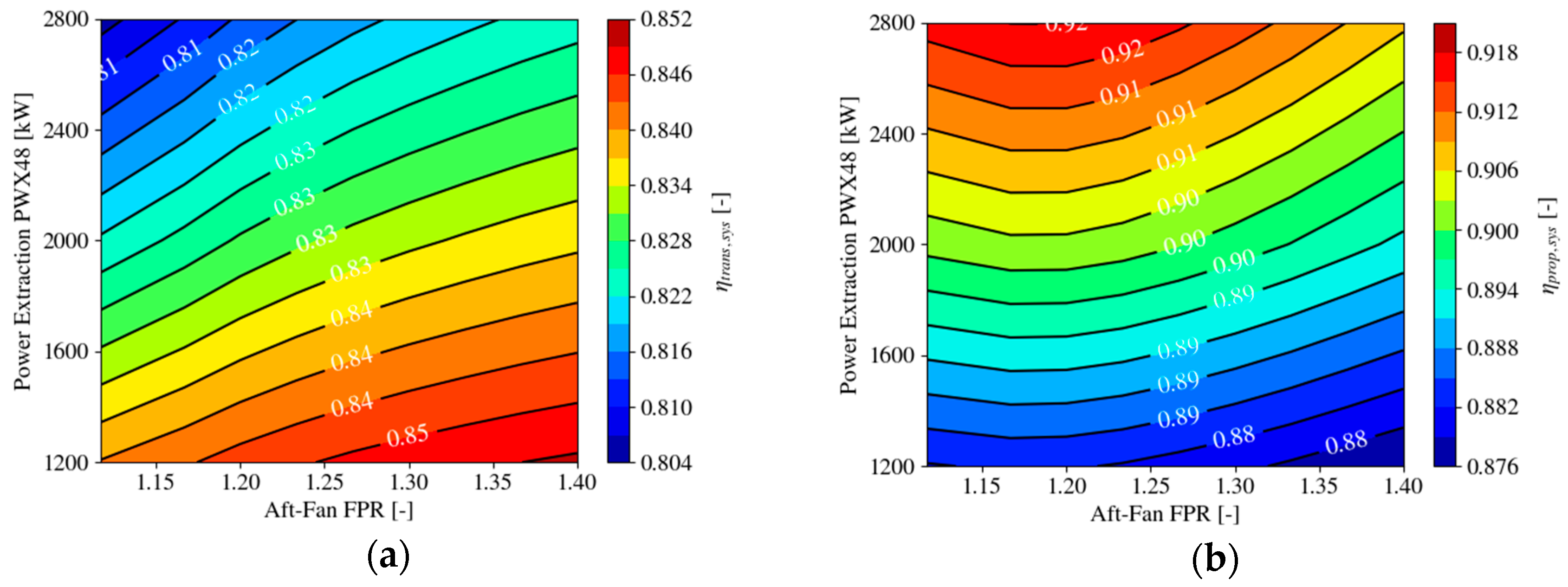
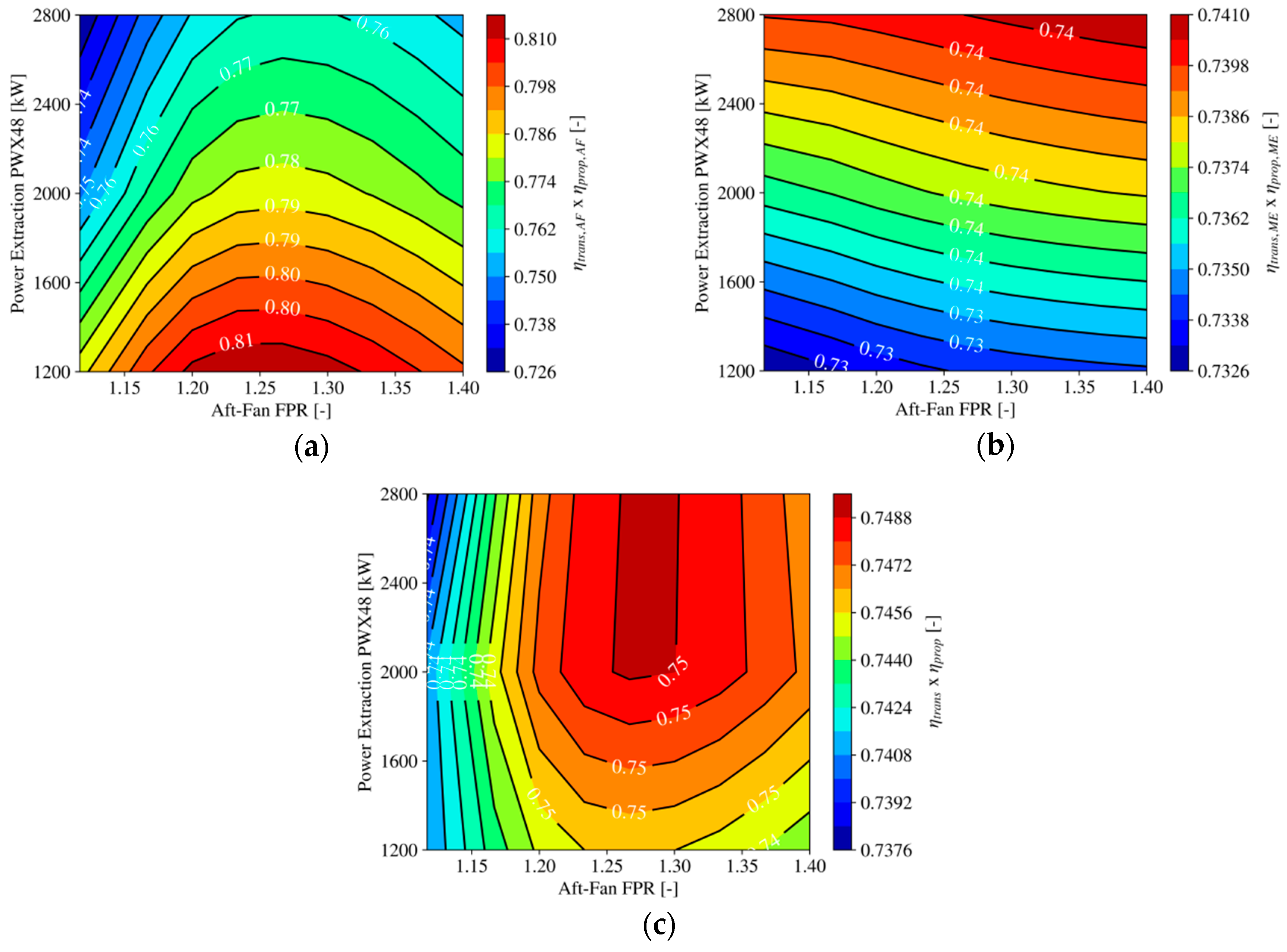
4.1.1. Efficiency Definitions and Figures of Merit
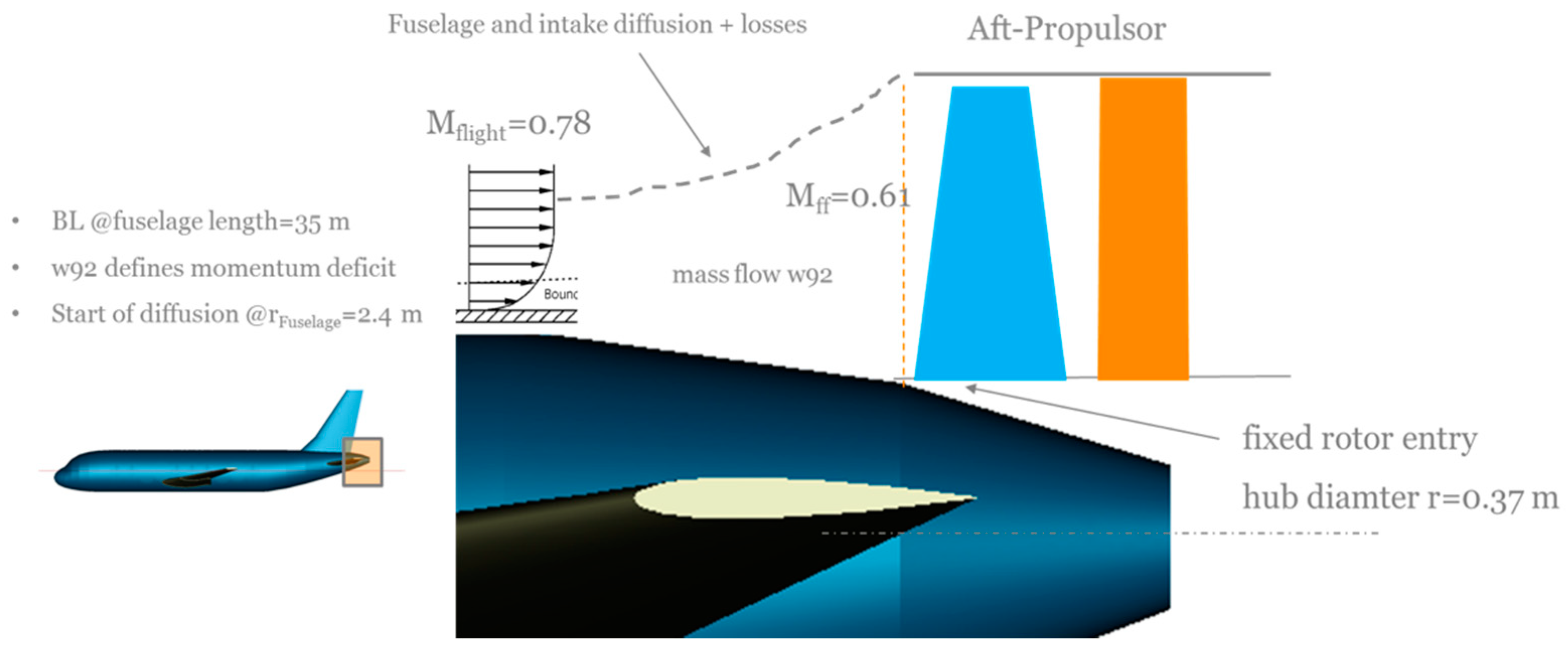
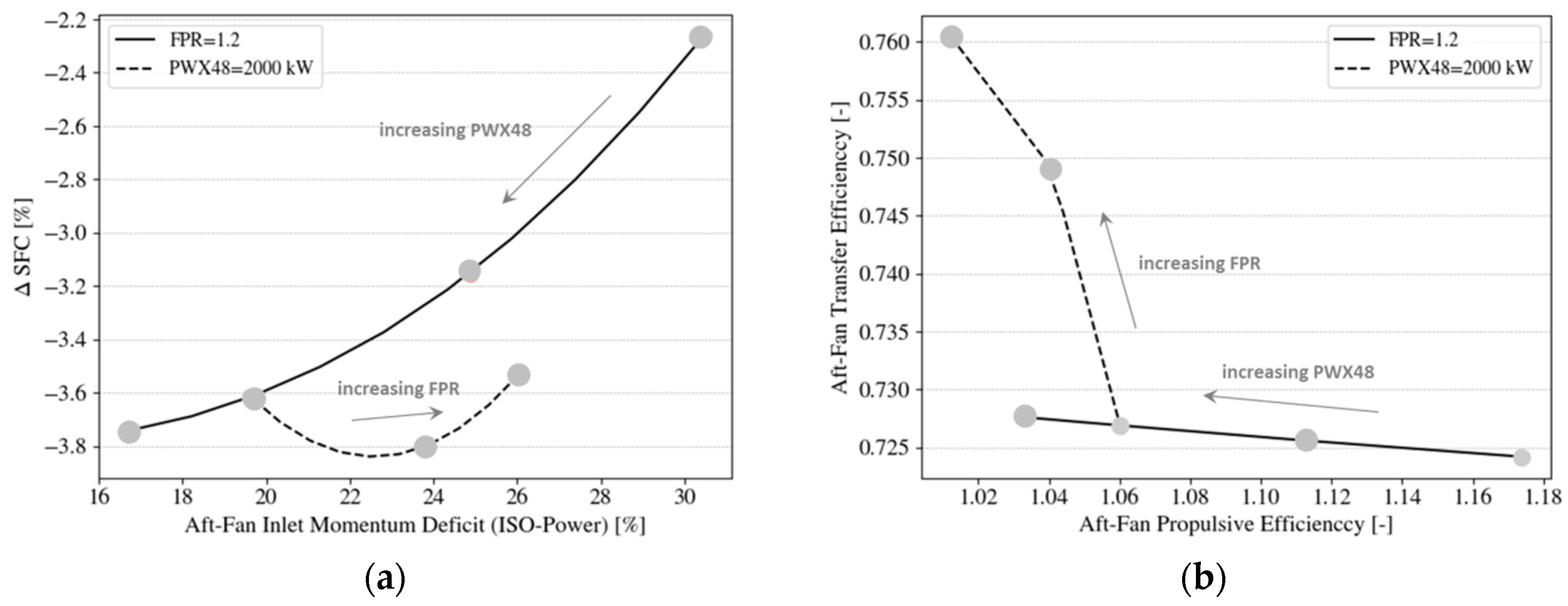
4.1.2. Power, Thrust Split and Aft-Fan Inlet Momentum Deficit/BLI Impact
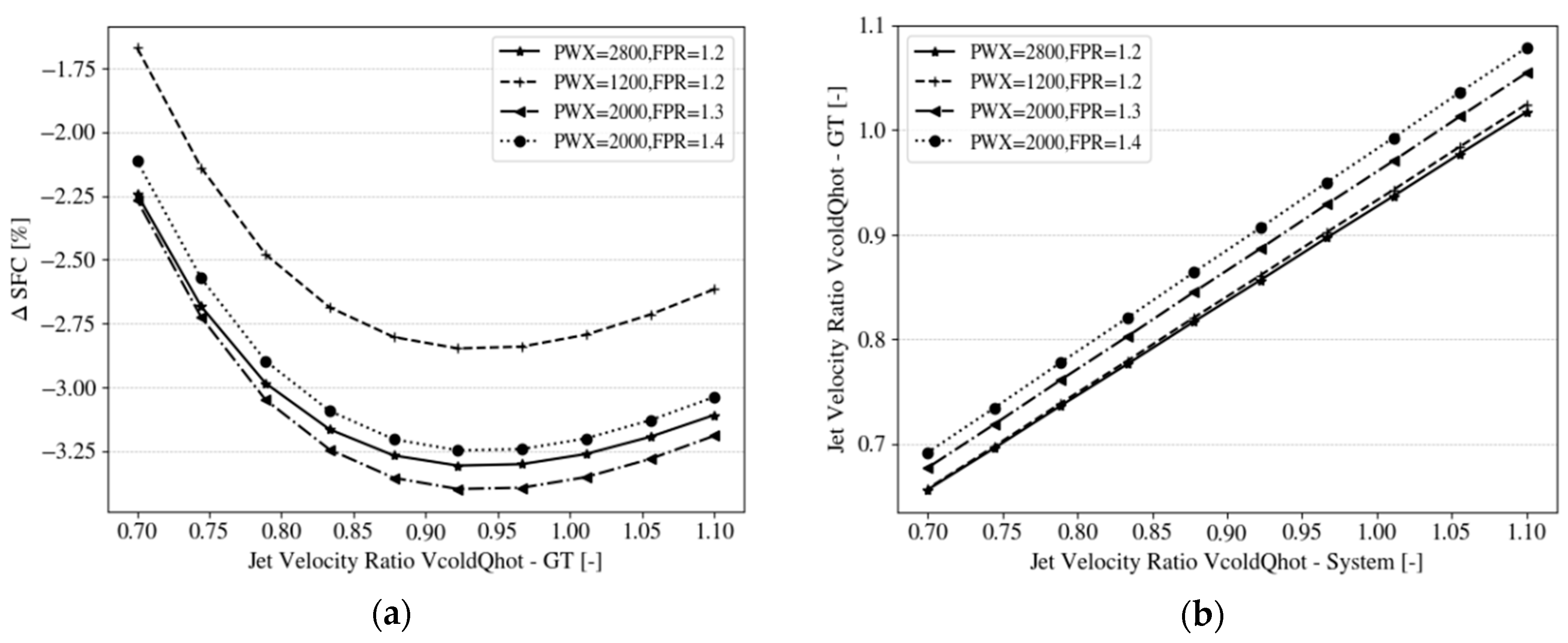
4.1.3. Gas Turbine and Aft-Propulsor Jet Velocity Ratio Impact
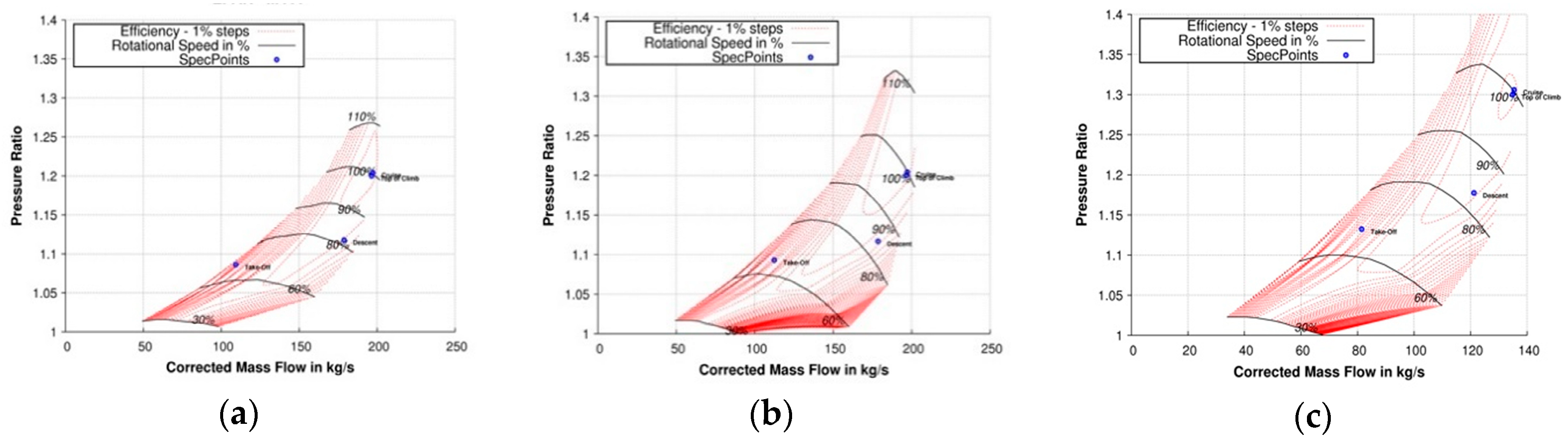
4.2. Cases Downselection
- FPR = 1.2 and PWX48 = 1200 kW,
- FPR = 1.2 and PWX48 = 2800 kW,
- FPR = 1.3 and PWX48 = 2000 kW and
- FPR = 1.4 and PWX48 = 2000 kW.
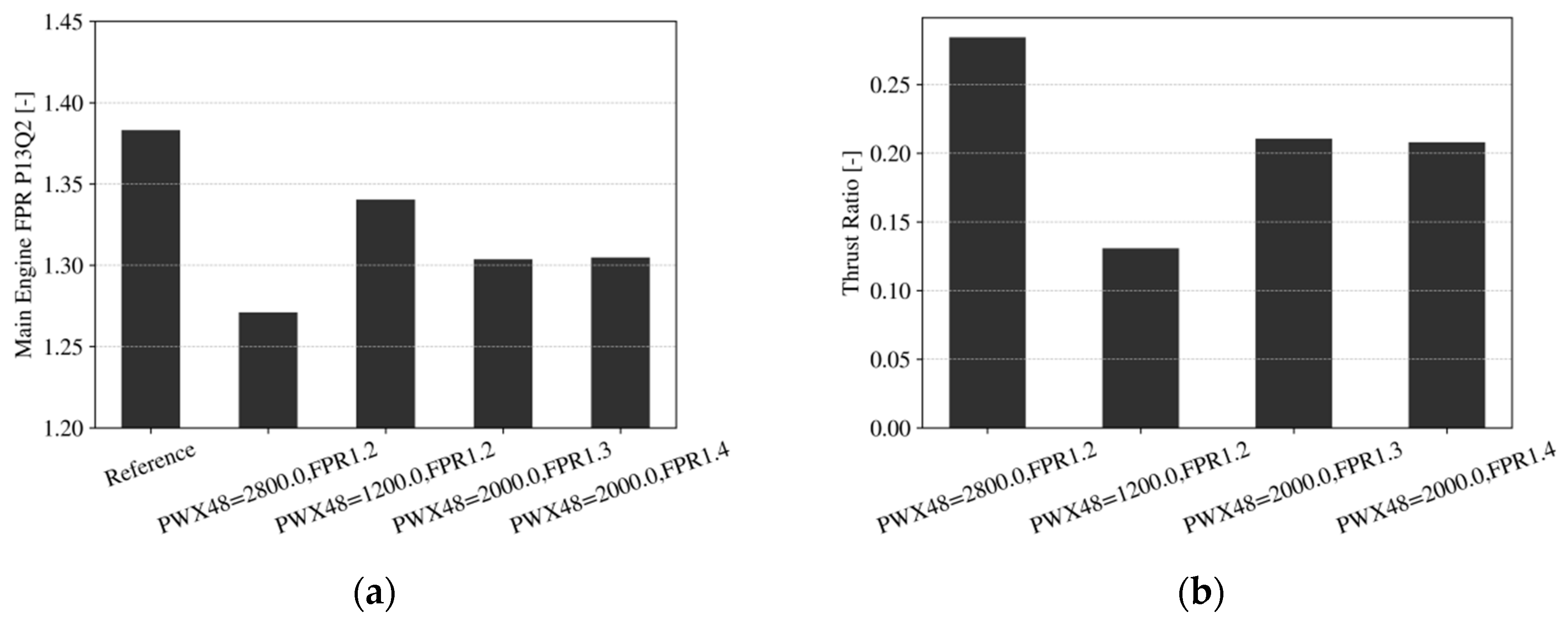
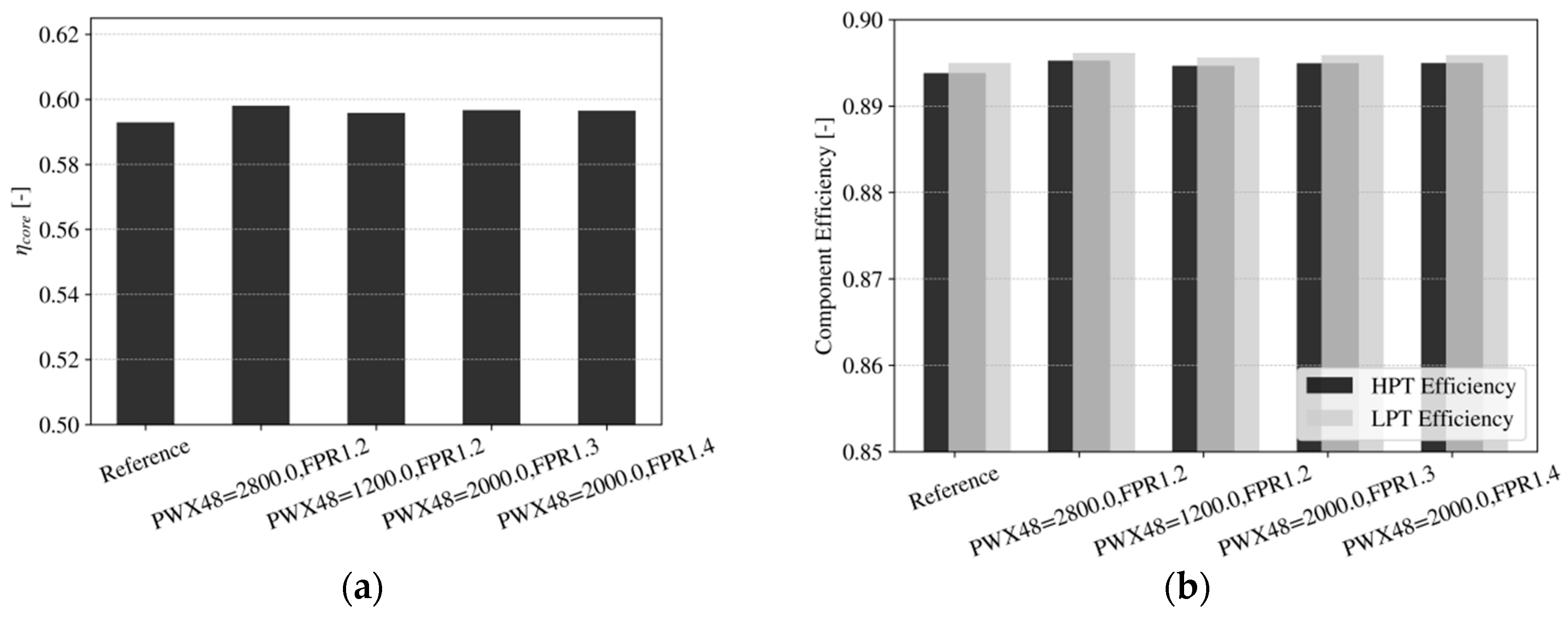
4.2.1. Choice of Main Gas Turbine Cycle and Resulting Engine Performance
4.2.2. Aft-Propulsor Design Rationale and Top-Level Design Parameters for Downselected Cases
- Constant meridional Mach number at fan face: Maff = 0.61 (this value is based on experience, reflecting trends in both, current and future engine designs, and was chosen in order to allow for high fan efficiency levels, sufficient flow capacity and compactness of the engine, see Reference [24] or Reference [25]). For the BLI-cases, where the resulting Mach number at fan entry at a given mass flow rate is inherently not constant over the span, an average value of Maff = 0.61 was targeted when sizing the aft-fan in order to ensure a certain coherence in the design strategies. Further design assumptions were:
- Swirl free outflow from the OGV;
- A loss-driven limitation of the mean OGV exit Mach number (Ma < 0.65);
- Fixed hub radius at the rotor leading edge: r = 0.37 m.
- Corrected tip speed (or respective work coefficient Ψ);
- Hub-to-tip ratio;
- Different radial total pressure profiles of the rotor (quasi free-vortex and bound-vortex);
- Major annulus design parameters/contraction.
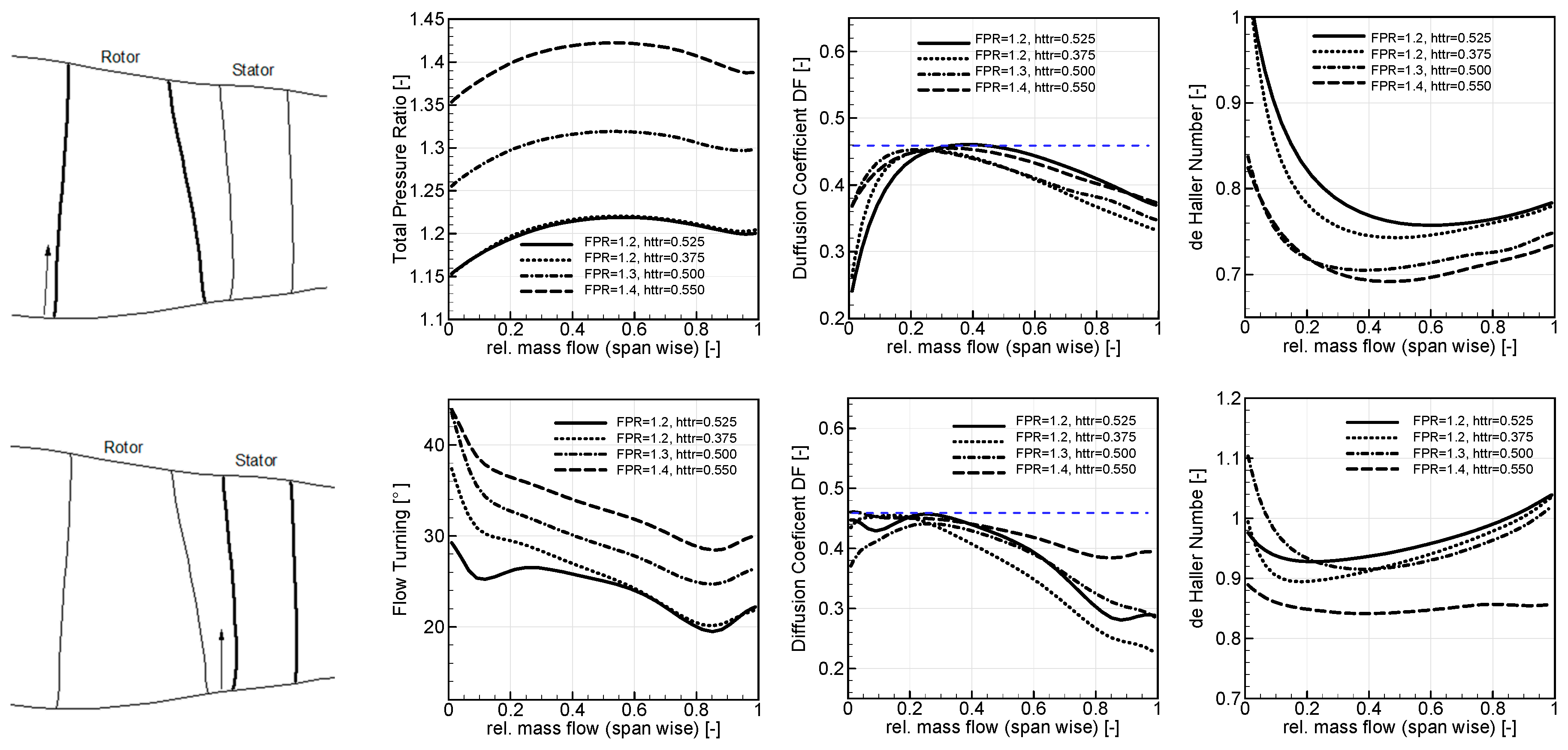
4.2.3. Aft-Propulsor Baseline Designs and Non-BLI Performance (Dfan for BLI Cases Adapted to Meet Target Fan-Face Axial Mach Number at Given Mass Flow Rate)
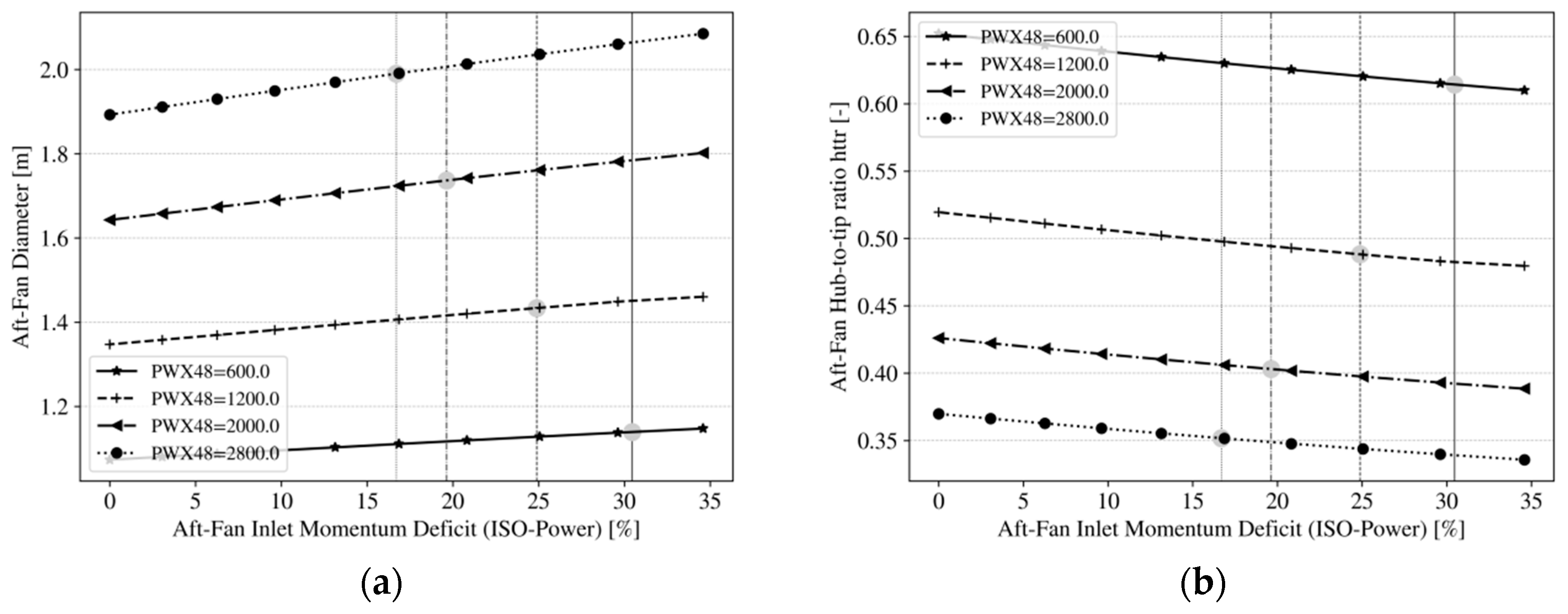
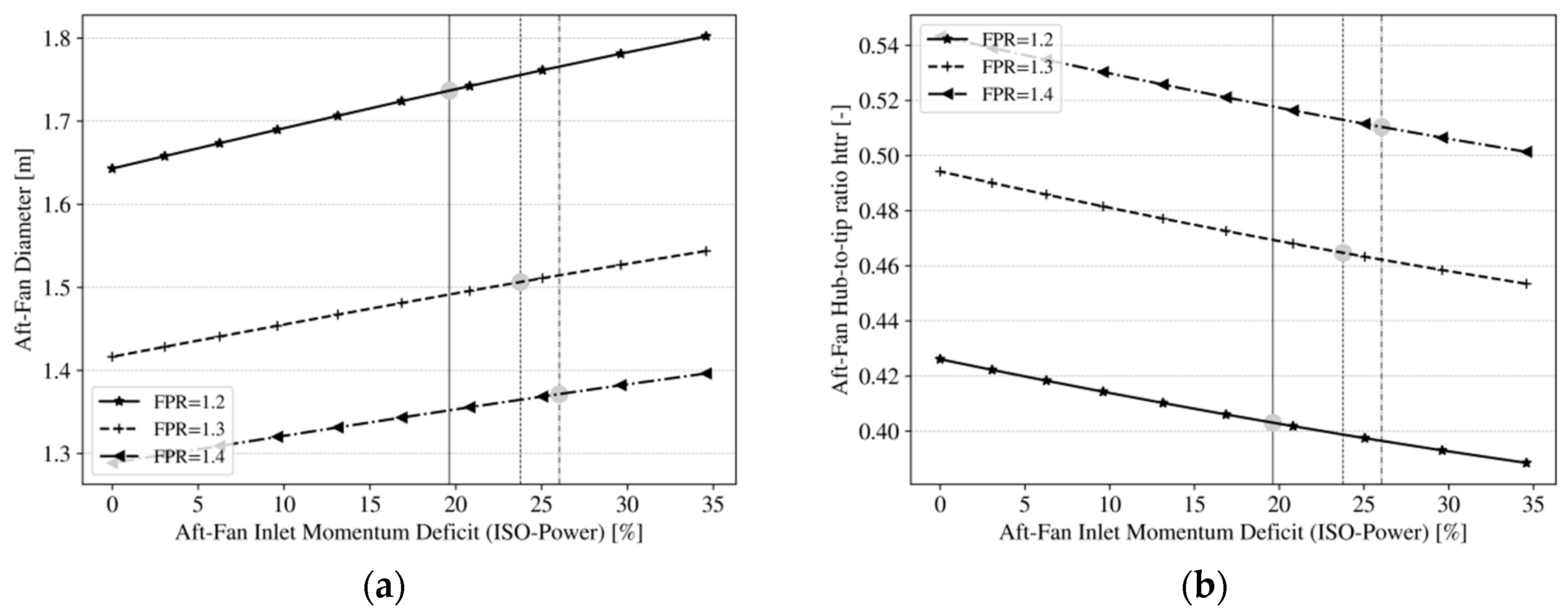
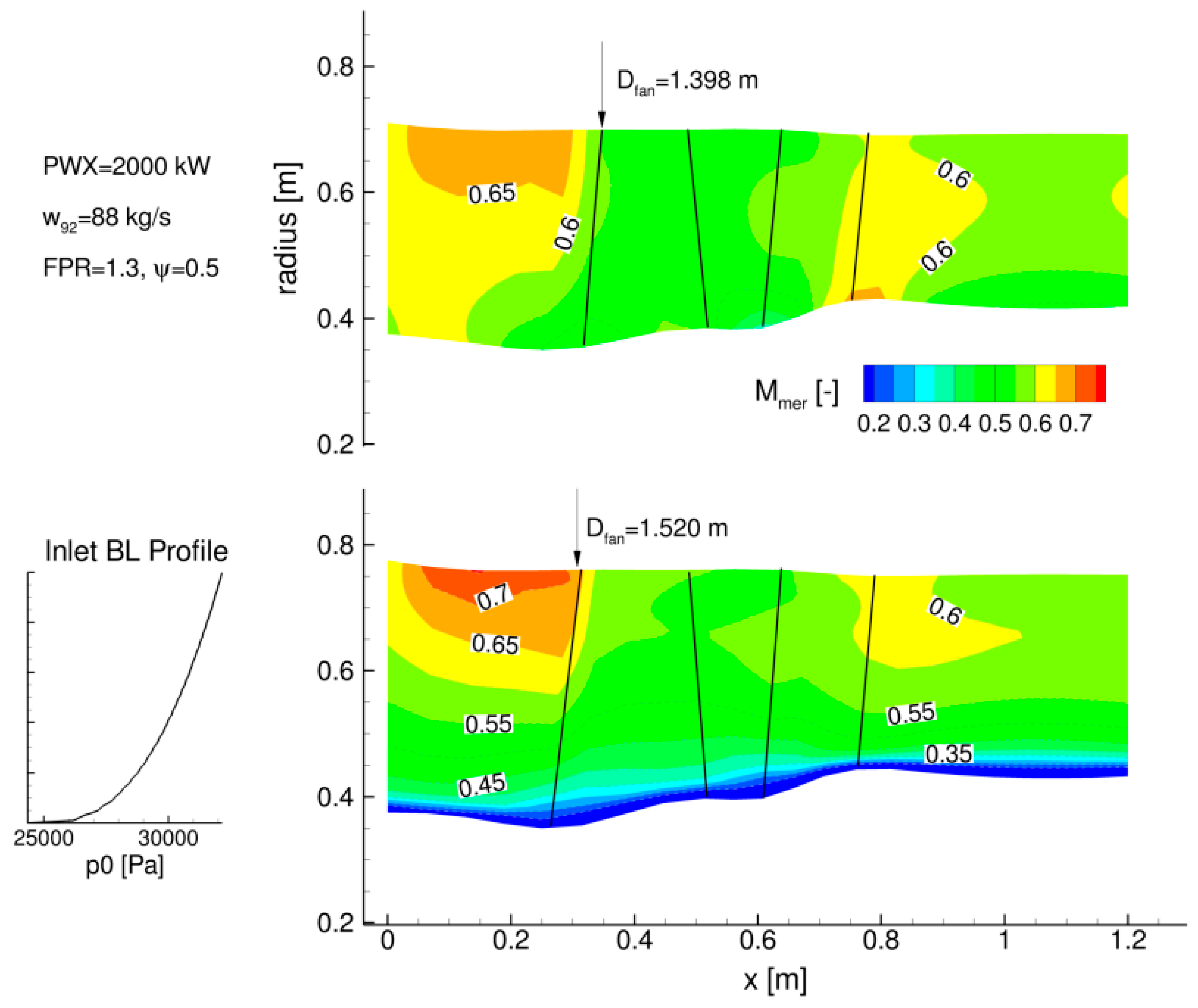
4.2.4. BLI Effect on Aft-Fan Performance and Design Update of Selected Cases
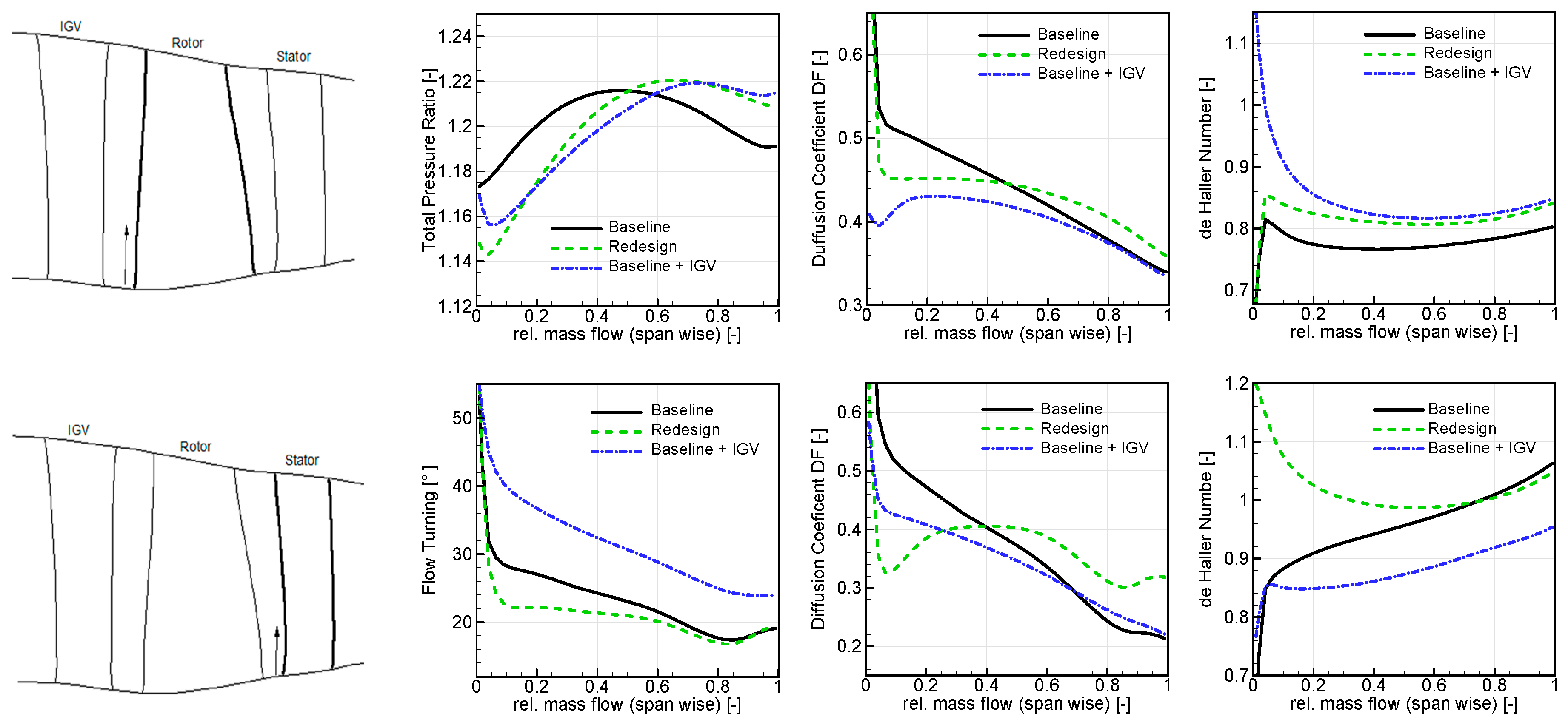
BLI Effect on Baseline Design
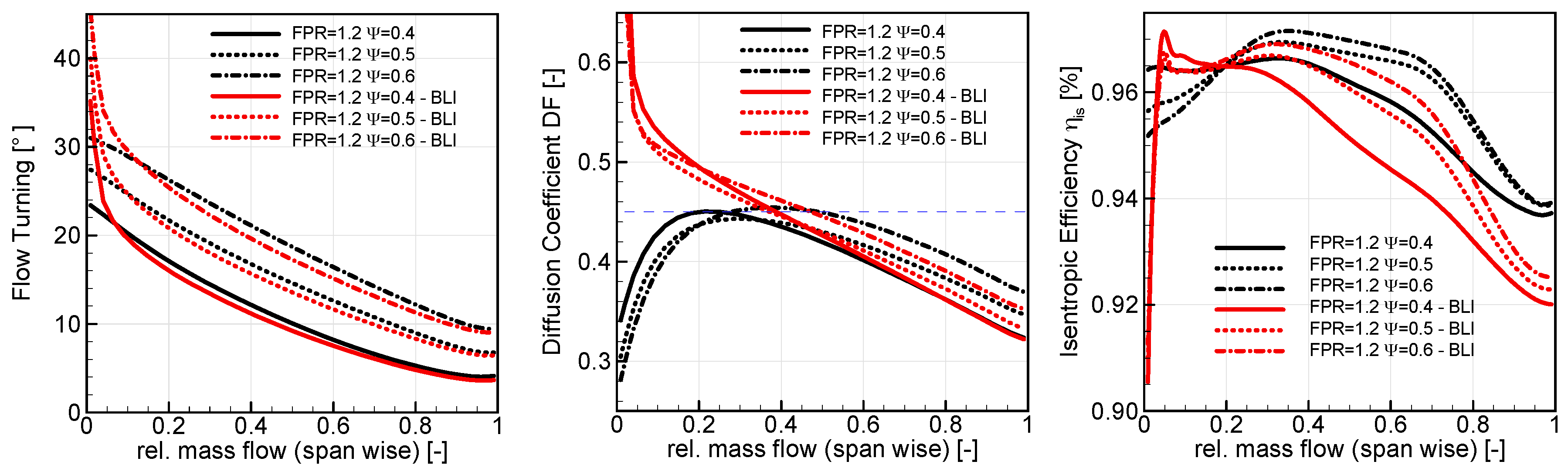
Influence of Corrected Tip Speed on BLI Performance
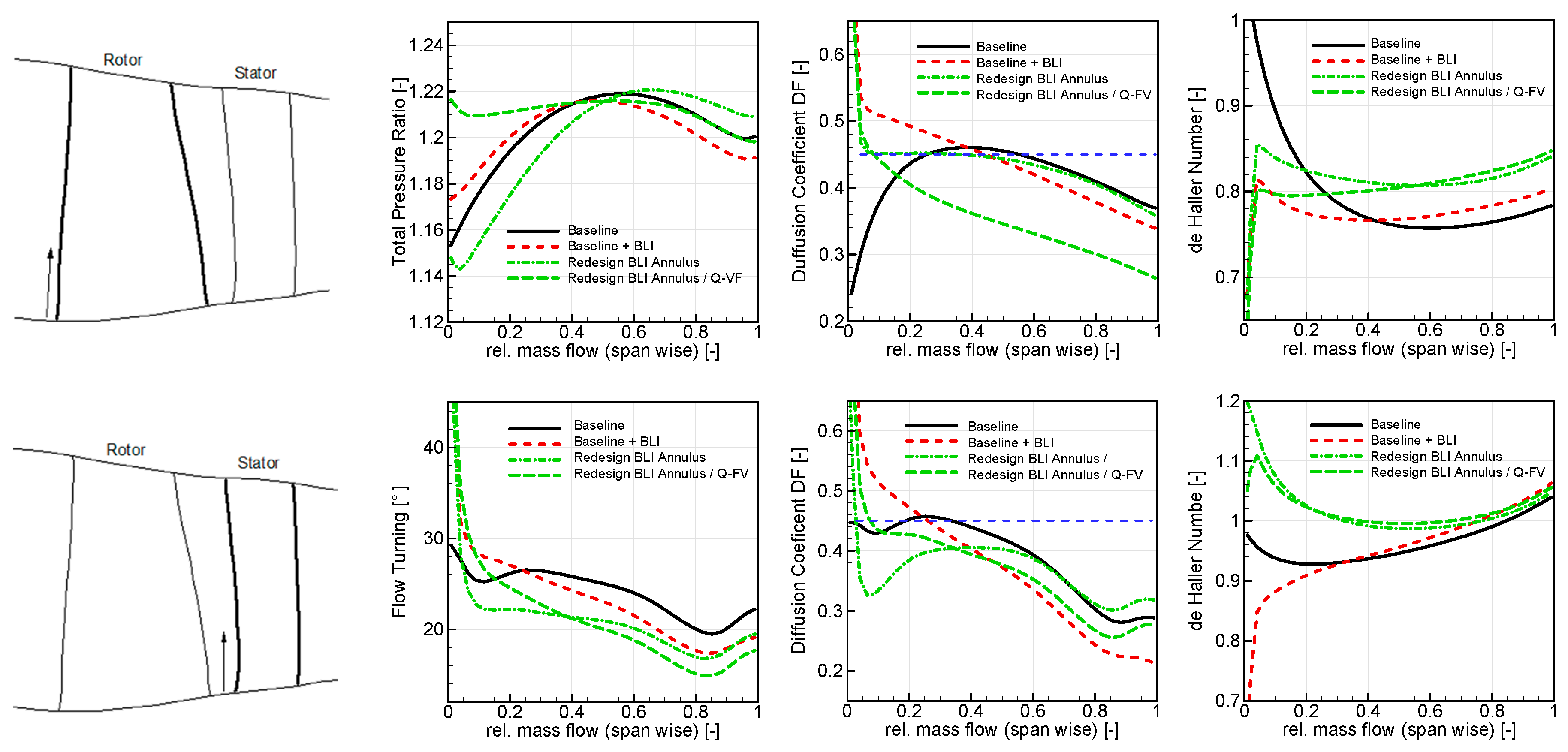
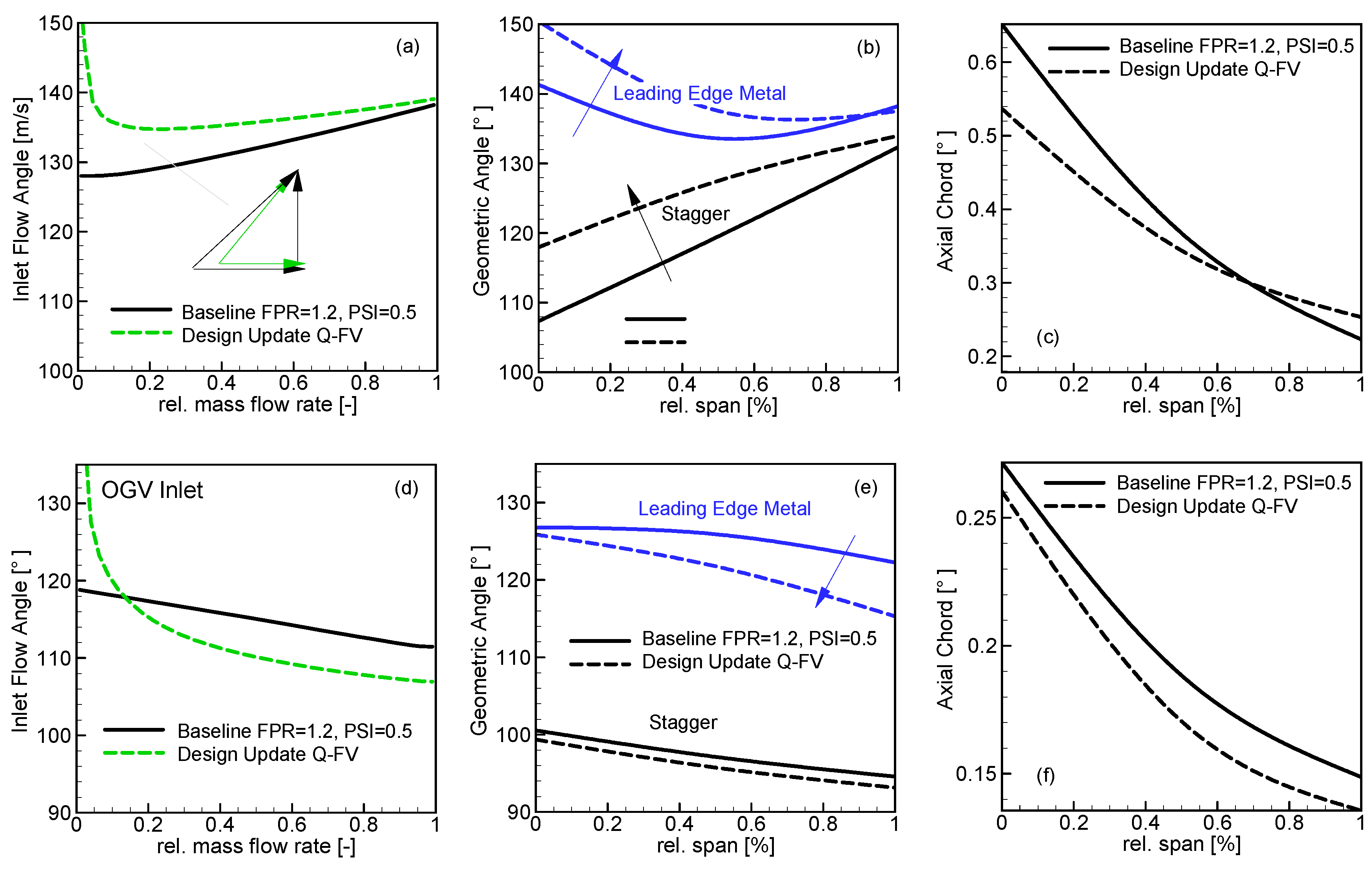
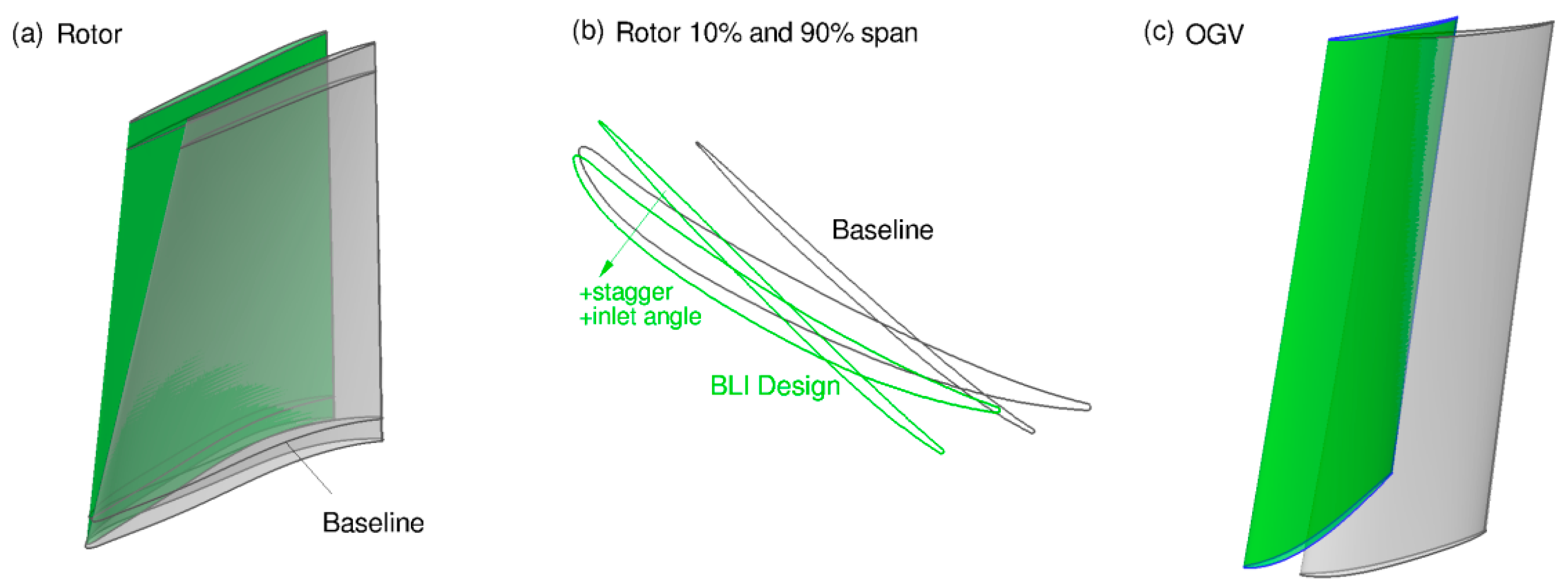
BLI Design Update (Conceptual)
BLI Design Update—Resulting Geometric Changes
BLI Design Update—Introduction of an Inlet Guide Vane (IGV)
4.3. Overall Configuration Potential
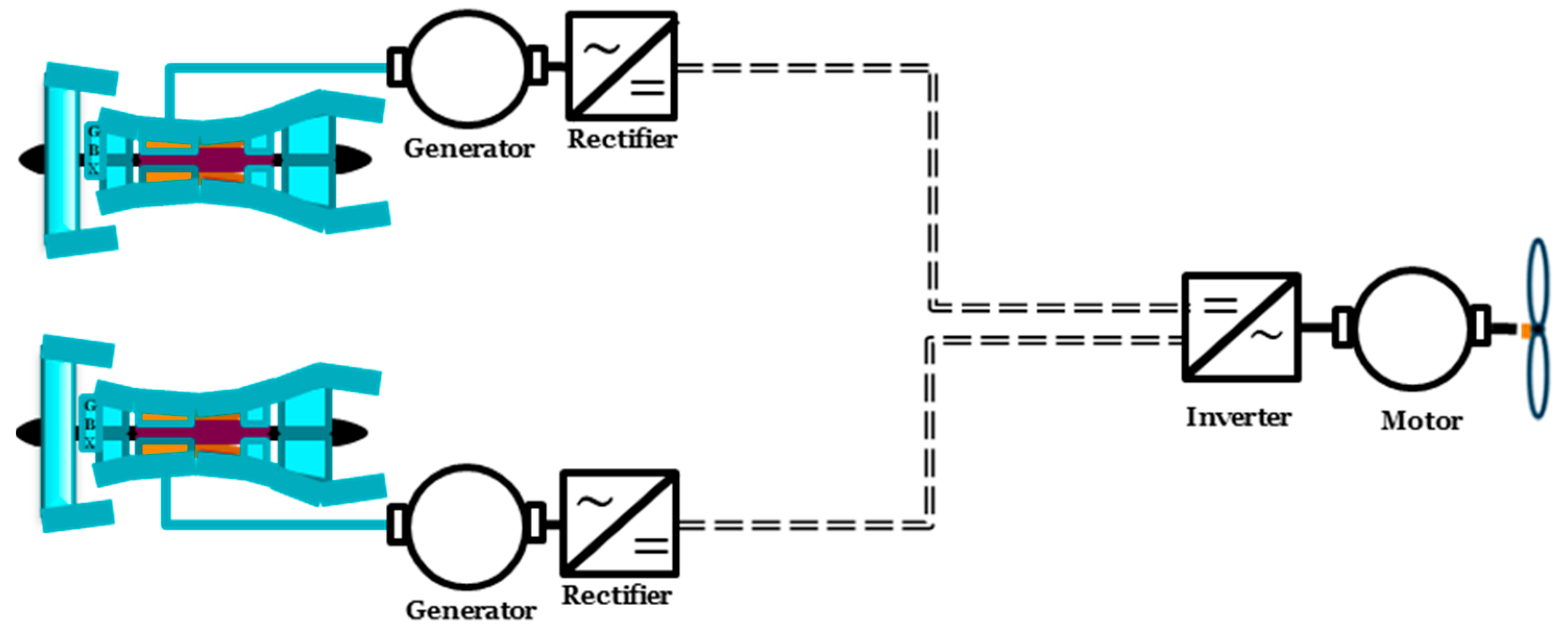
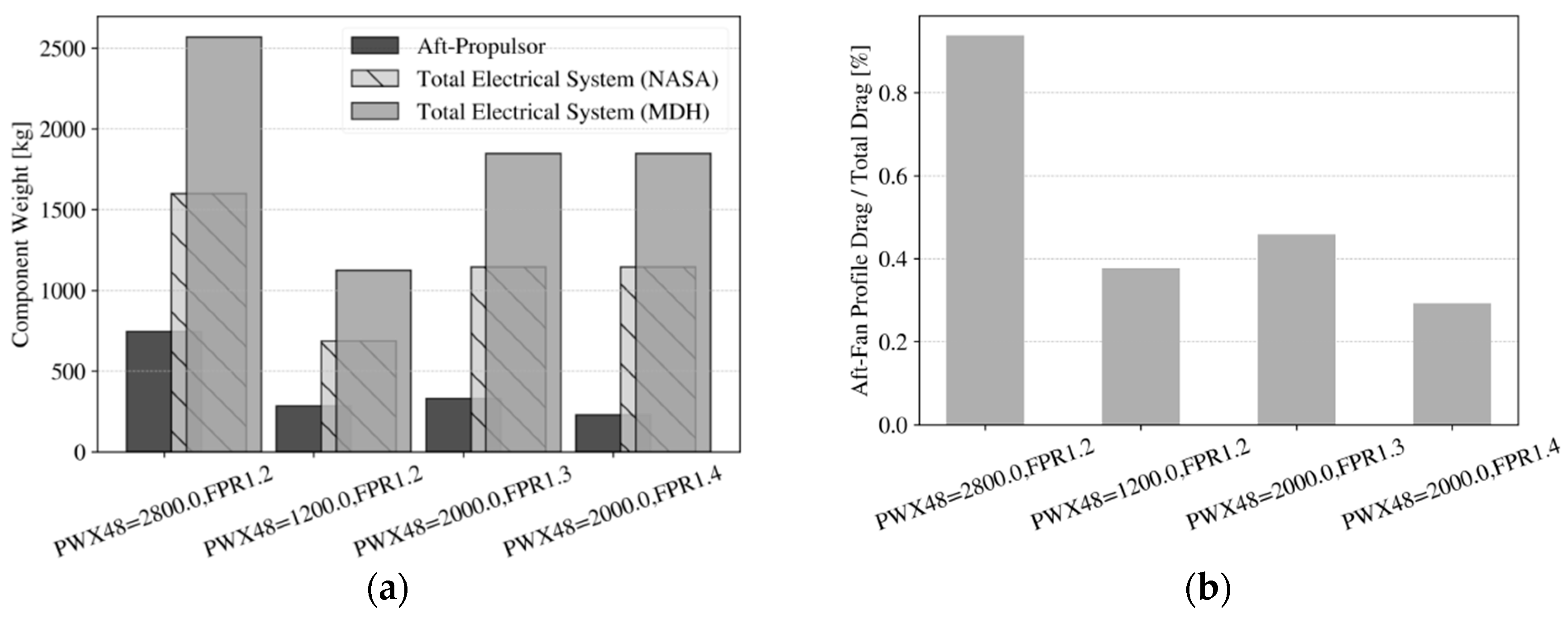
4.3.1. Electrical System Dimensioning
4.3.2. Block Fuel Exchange Rates and Weight/Drag Sensitivity
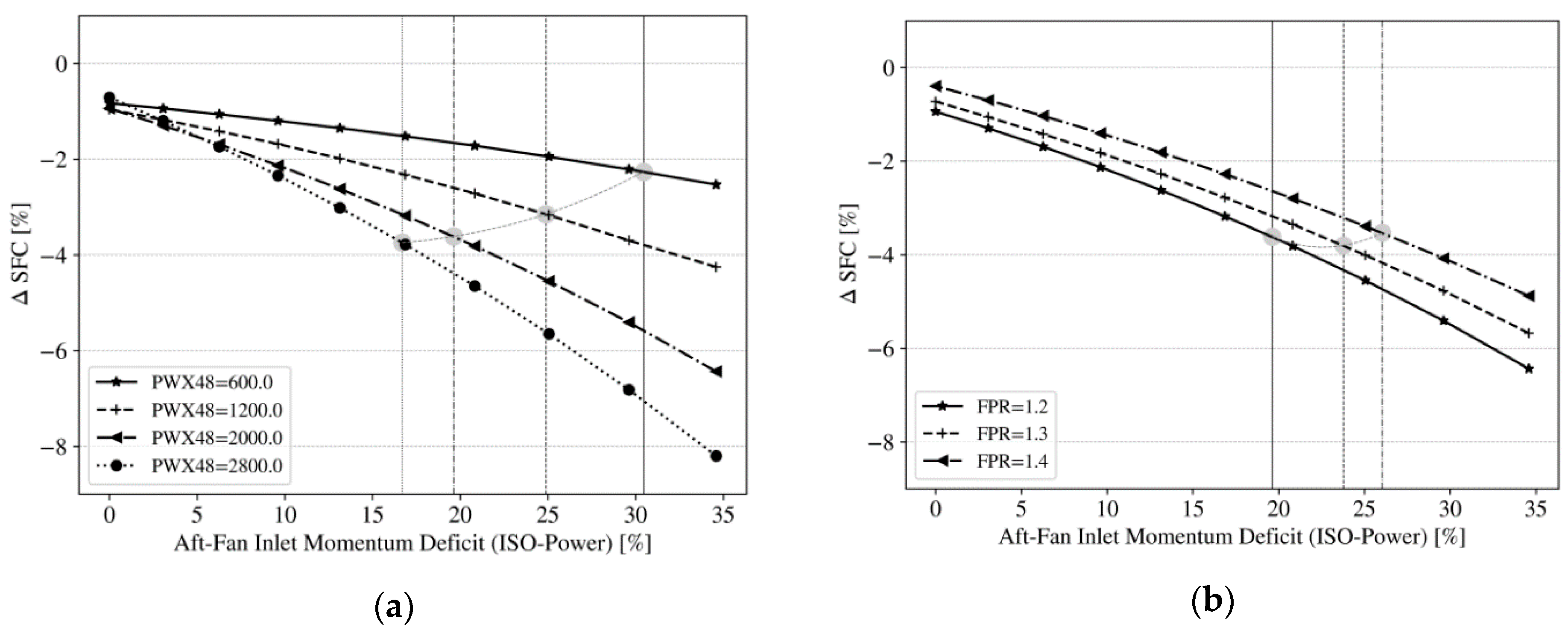
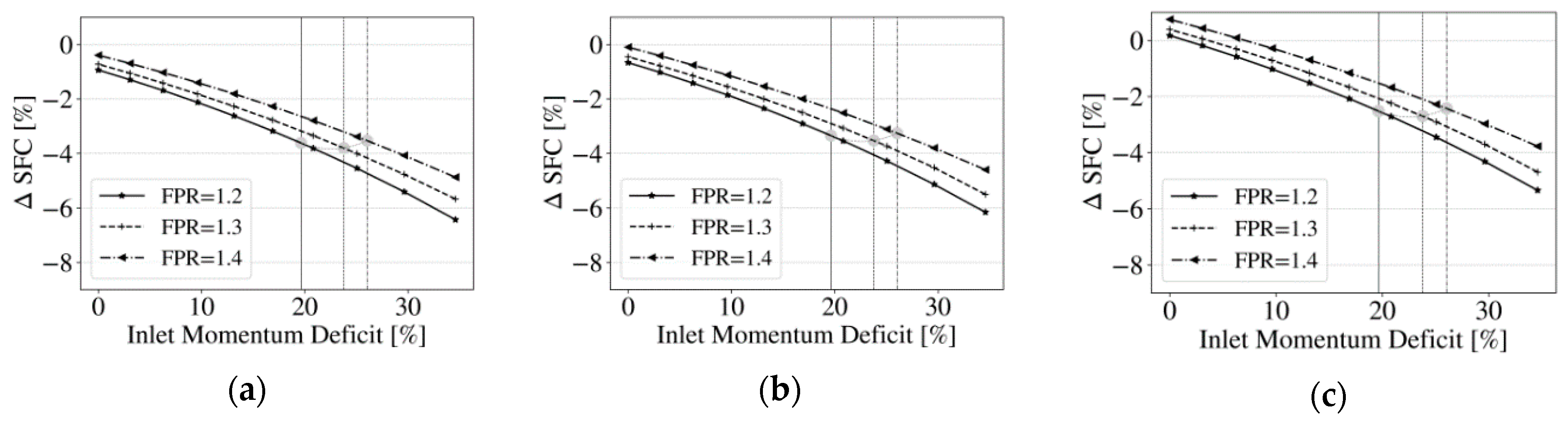
4.3.3. Inlet Momentum Deficit Sensitivity
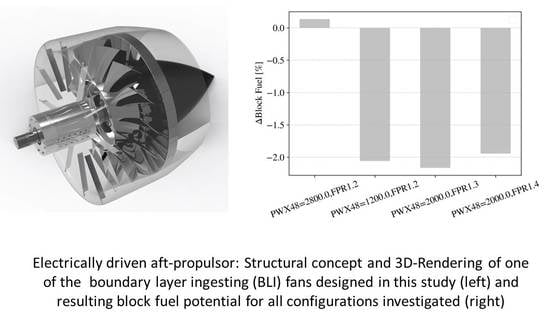
4.3.4. Block-Fuel Estimation of Selected Configurations
5. Summary and Conclusions
- Firstly, a sensitivity study was carried out in order to account for the uncertainty in predicting the incoming momentum deficit as induced by the fuselage boundary layer. Those sensitivities were quantified, allowing for a correction of the results if more detailed knowledge of the actual flow characteristics is available.
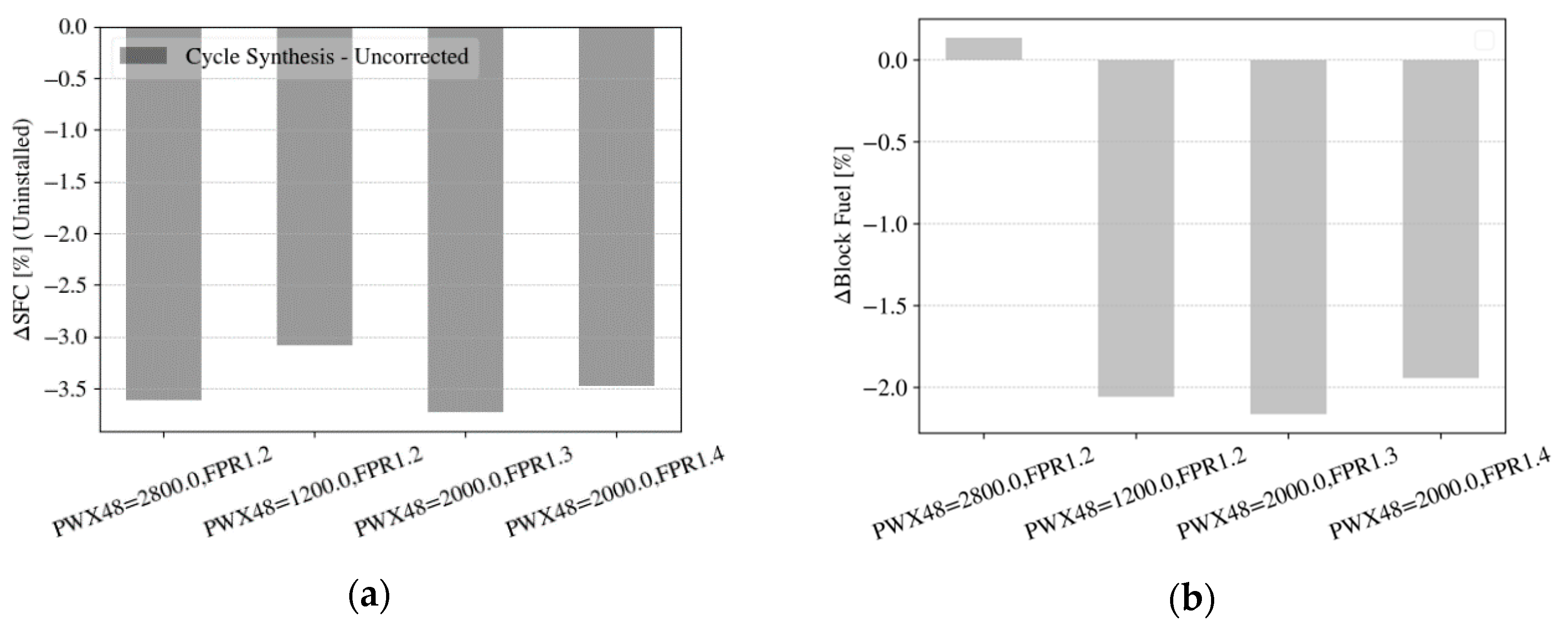
- The optimal fan pressure ratio and power off-take were determined for a minimal uninstalled SFC benefit based on results from multi-point cycle synthesis. The results suggest that an optimal value of approximately FPR ≈ 1.27 for the aft-fan leads to an uninstalled SFC benefit of 3.9%, however, the ranges in SFC between the identified possible values of momentum deficit are on the same order as the total savings. In this context, the special role of transfer and propulsive efficiency was analyzed and discussed. At a certain level of PWX48, no further reduction in SFC was observed, due to a diminishing BLI effect and opposite trends in transfer efficiency levels between the main engine and the aft-fan. The main engine essentially traded propulsive efficiency for transfer efficiency and the benefit at the system level came from the aft-propulsor’s gain in propulsive efficiency at sufficient levels of power extraction. Further studies might involve a different strategy for designing the main engine by retaining the fan pressure ratio and allowing for a reduction in engine diameter and bypass ratio (as discussed in Reference [10]).
- It was also discussed how this optimal SFC was translated to mission fuel burn based on derived exchange rates and how it was compromised by a number of factors, such as additional weight and drag. This also changed the ranking of the selected configurations, substantially penalizing larger power-off takes and smaller aft-fan FPR.
- The average achievable benefit in terms of block fuel for the given configuration was estimated to be up to 2.2% compared with the baseline scenario under the given (optimistic) assumptions.
- Under the given assumptions, the fan rotor hub-to-tip ratio varies with increasing fan diameter and power off-take, which requires a dedicated design effort for given top-level parameters.
- The impact of BLI on fan stage performance was firstly assessed by following a conventional design approach and then by applying the incoming boundary layer. This was done for four downselected cases based on conceptual design studies involving a streamline-curvature method.
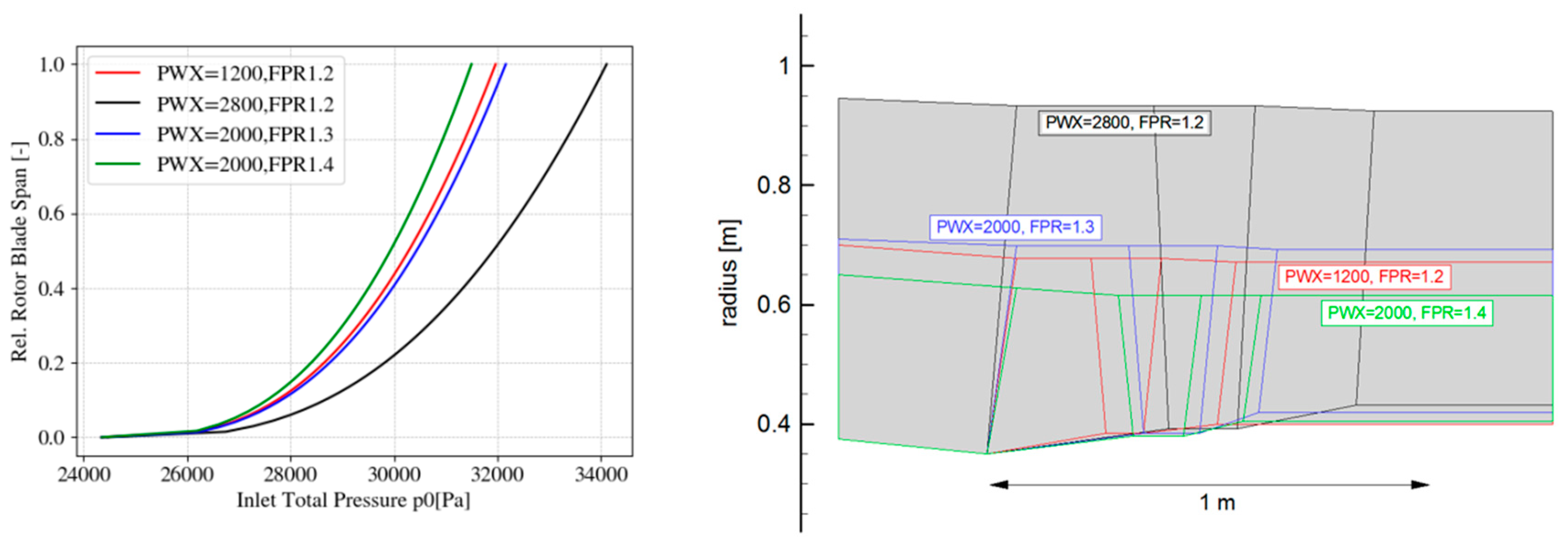
- The baseline results suggest that the hub sections are likely to fail under the influence of the BLI, due to the massively increase turning requirements to meet an imposed fan pressure ratio distribution.
- Several rotor design strategies were investigated to mitigate the effect of the BLI and allow for the design of an operational fan. In that context, the role of rotor tip speed was discussed, suggesting that higher Ψ-values be beneficial in terms of maintaining efficiency levels. This needs further confirmation with CFD-based design optimization studies. Furthermore, an increase in the total pressure ratio near the hub, leading to a quasi free-vortex design, was discussed and seemed beneficial in order to balance the flow radially. Further increasing the total pressure ratio to realize a descending pressure ratio profile was not investigated, but might help to homogenize the OGV outflow. This would require a higher value of the hub radius or respective hub-to-tip ratio in order to accommodate the high flow turning requirements at given tip speed.
- Further design updates of the fan stage were realized by introducing local contraction by an increased hub line curvature and associated pressure gradient in order to unload the rotor and the OGV and hence, limit DF values for a given low turning under BLI.
- Based on the results, it is believed that high levels of efficiency can be retained, at least for the given axisymmetric pressure profile. Off-design performance, however, needs to be further addressed, in particular considering the location of the Take-Off point at constant power extraction levels, which was located close to the stability limit for almost all designs. This either promotes the use of variability, or the decision to go for higher levels of aft-fan FPR.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| A/C | Aircraft |
| ACDC | Advanced Compressor Design Code (Streamline Curvature Method as used in this study) |
| ACARE | Advisory Council for Aeronautical Research in Europe |
| AF | Aft-Fan |
| BLI | Boundary Layer Ingesting |
| BF | Block Fuel |
| CFD | Computational Fluid Dynamics |
| CeRAS | Central Reference Aircraft Data System |
| CPACS | Common Parametric Aircraft Configuration Schema |
| DLR | Deutsches Zentrum fuer Luft- und Raumfahrt/German Aerospace Center |
| EVA | EnVironmental Assessment Framework |
| FPR | Fan (total) pressure ratio |
| GT | Gas Turbine (=Main Engine) |
| IGV | Inlet Guide Vane |
| LE | Blade Row Leading Edge |
| LPC/HPC | Low/High-Pressure Compressor |
| LPT/HPT | Low/High-Pressure Turbine |
| ME | Main Engine |
| MDH | Mälardalen Högskola |
| OGV | Outlet Guide Vane |
| OPR | Overall Pressure Ratio |
| PID | Controller with Proportional, Integral and Differential Terms |
| SLC | Streamline-Curvature Method (also referred to as Throughflow-Method). The method applied here is ACDC (DLR in-house code). |
| STARC-ABL | Single-aisle Turboelectric Aircraft with an Aft Boundary Layer Propulsor |
| TOC | Top-of-Climb |
| TE | Blade Row Trailing Edge |
Nomenclature and Performance Metrics Definition
| cu2,mean | Velocity | [m/s] | Mean circumferential velocity at rotor outlet. Mean here meaning at a radial position dividing the total mass flow in half. | Definition according to Reference [25] |
| ΔI | Momentum Deficit (Intergal) | [%] | Aft-fan incoming momentum deficit with respect to ram momentum at given fligh speed v0 | [v0,BLI * w92,BLI − v0 * w92]/(v0 * w92) |
| de-Haller | [-] | Blade row flow acceleration/diffusion: Velocity ratio at blade row outlet over inlet in relative system | ||
| D | Diameter | [m] | (Fan) outer diameter | |
| DF | Diffusion coefficient | [-] | Rotor or OGV blade loading resulting from flow diffusion and flow turning | Definition according to Lieblein as, e.g., in References [24] or [25] |
| Ecore | Energy per time unit | [W] | Core exit potential power; the core exit is where the fan core and LPC power requirements are satisfied in the LPT expansion | |
| Ep,core | Energy potential per time unit | [W] | Power available after all power requirements of the core compression processes (including power off-take) are satisfied | |
| Efuel | Energy per time unit | [W] | Power as introduced by the fuel | Efuel = wf × FHV |
| ΔEkin,jets | Energy per time unit | [W] | Change in jet kinetic power | |
| FN | Net Thrust | [N] | Engine net thrust | |
| FHV | Fuel heat value | [J/kg] | ||
| Δht | Enthalpy | [J/kg] | Enthalpy change over the fan stage | |
| Ma | Mach number | [-] | ||
| Maff | Fan-face Mach Number | [-] | (Meridional or axial) Mach number at fan entry | |
| N48 | Rotational Speed | [1/min] | Aft-fan rotational speed | |
| p0 | Total pressure | [Pa] | Average Inlet Total Pressure | |
| P13Q2 | Main engine fan total pressure ratio | [-] | Bypass section of the fan | |
| P23Q2 | Main engine fan total pressure ratio | [-] | Core section of the fan | |
| PRn | Pressure ratio split | [-] | (Logarithmic) Pressure ratio split between LPC and HPC | Definition as in Reference [6] |
| PWX48 | Power Extraction | [kW] | Power input to the aft-fan | PWX48 = PWX46 * ηmech * ηel |
| PWX46 | Power Extraction | [kW] | PWX46 extraction from the LP shaft | |
| RPM | Rotational speed | [1/min] | ||
| Re | [-] | Reynolds Number | ||
| r | Radius | [m] | ||
| SFN | Specific Thrust | [m/s] | ||
| SFC | Specific Fuel Consumption | [g/(kN*s)] | ||
| Tt | Total Temperature | [K] | Total Temperature at component inlet 1 or outlet 2 | |
| utip(,c) | Circumferential velocity | [m/s] | Rotor blade (corrected) tip speed | |
| v0 | Velocity | [m/s] | Flight velocity | |
| v0,BLI | Velocity | [m/s] | Velocity at fan entry due to BLI | |
| vid,95 | Velocity | [m/s] | Aft-fan nozzle exit velocity (ideally expanded) | |
| vid,18 | Velocity | [m/s] | Main engine bypass nozzle exit velocity (ideally expanded) | |
| v‘18 | Velocity | [m/s] | Mixed out jet velocity comprising of the cold jet in the main engine bypass and the hot jet after the core nozzle | |
| vid,7 | Velocity | [m/s] | Main engine core nozzle exit velocity (ideally expanded) | |
| VcoldQhot | Jet Velocity Ratio | [-] | Ratio of the velocity of cold (bypass) jet over the core nozzle velocity | |
| w18 | Mass flow rate | [kg/s] | Mass flow through the fan bypass | |
| w2 | Mass flow rate | [kg/s] | Engine inlet mass flow | |
| w92 | Mass flow rate | [kg/s] | Aft-fan mass flow rate | |
| w7 | Mass flow rate | [kg/s] | Core mass flow rate | |
| wf | Mass flow rate | [kg/s] | Fuel mass flow rate flow | |
| ηel | Efficiency | [%] | Transfer efficiency of the electrical system | |
| ηmech | Efficiency | [%] | Efficiency of the mechanical system (e.g., bearing losses etc.) | |
| ηth | Thermal Efficiency | [%] | Increase of the kinetic energy of the gas stream over the amount of heat employed | ηth = ηcore * ηtrans |
| ηcore | Core Efficiency | [%] | Ratio of energy available after all the power requirements of the core compression processes are satisfied and the fuel energy | Definitions for the main engine, aft-fan and system according to Equations (4) and (9) |
| ηtrans | Transmission Efficiency | [%] | Quality of the energy transfer from the core stream to the bypass stream | Definitions for the main engine, aft-fan and system according to Equations (5) and (7), (11) and (15) |
| ηprop | Propulsive Efficiency | [%] | Useful propulsive energy over the kinetic energy loss of the jet | Definitions for the main engine, aft-fan and system according to Equations (6), (8), (10) and (14) |
| ηov | Overall Efficiency | [%] | Resulting propulsive power to the energy content of the fuel | Definitions for the main engine, aft-fan and system according to Equation (17) |
| ηis | Isentropic Efficiency | [%] | Component isentropic efficiency | |
| ηpol | Polytropic Efficiency | [%] | Component polytropic efficiency | |
| ν | Hub-to-tip ratio | [-] | Rotor leading edge hub to tip radius | |
| Total Pressure Ratio | [-] | Fan stage total pressure ratio | ||
| Ψ | Fan Rotor Work Coefficient | [-] | More details, e.g., in References [24] or [25] |
Appendix A
| EIS 2035 Assumptions | Unit | Value |
| Gear Box Speed Ratio | - | 3.0 |
| Fan bypass/core polytropic efficiency | - | 0.946/0.956 |
| Low pressure compressor polytropic efficiency | - | 0.923 |
| High pressure compressor polytropic efficiency | - | 0.925 |
| High pressure turbine polytropic efficiency | - | 0.897 |
| Low pressure turbine polytropic efficiency | - | 0.929 |
| Combustor Outlet Ttemperature @ hot day TOC (ISA + 10 K) | K | 1900 |
| Turbine metal temperature @ hot day T/O (ISA + 15 K) | K | 1240 |
| Baseline Parameters | Unit | Value |
| Cruise Specific Thrust SFN | m/s | 91 |
| Cruise OPR | - | 55 |
| Cruise VcoldQhot | - | 0.77 1 |
| Cruise PRn | - | 0.402 |
| TOC Bypass Ratio BPR | - | 15.2 |
| TOC Fan Pressure Ratio FPR | - | 1.48 |
| TOC LPC Pressure Ratio | - | 3.68 |
| TOC HPC Pressure Ratio | - | 12.32 |
| TOC HPC Exit Temperature | K | 979 |
| HPT Cooling flow fraction | % | 21.2 |
| LPT Cooling flow fraction | % | 1.1 |
| Key Engine Parameters | Units | Hot-Day Top-of-Climb Conditions (ISA+10, FL350, Mach 0.78) | Hot-Day End-of-Runway Take-Off Conditions (ISA+15, FL0, Mach 0.25) | Cruise Conditions (ISA, FL350, Mach 0.78) |
|---|---|---|---|---|
| Specific thrust | m/s | Solved for in the analysis | Solved for in the analysis | Solved for in the analysis |
| Jet velocity ratio | - | Solved for in the analysis | Solved for in the analysis | Synthesis Target 2 |
| Pressure ratio split exponent | - | Solved for in the analysis | Solved for in the analysis | Synthesis Target 3 |
| Fan tip over hub pressure rise ratio | - | Target | Solved for in the analysis | Solved for in the analysis |
| Overall pressure ratio | - | Solved for in the analysis | Solved for in the analysis | Synthesis Target 4 |
| HPC outlet temperature | K | Solved for in the analysis | Solved for in the analysis | Solved for in the analysis |
| HPT 1st vane metal temperature | K | Solved for in the analysis | Synthesis Target 5 | Solved for in the analysis |
| HPT 1st rotor metal temperature | K | Solved for in the analysis | Synthesis Target 6 | Solved for in the analysis |
| HPT 2nd vane metal temperature | K | Solved for in the analysis | Synthesis Target 7 | Solved for in the analysis |
| HPT 2nd rotor metal temperature | K | Solved for in the analysis | Synthesis Target 8 | Solved for in the analysis |
| LPT 1st vane metal temperature | K | Solved for in the analysis | Synthesis Target 9 | Solved for in the analysis |
| LPT 1st rotor metal temperature | K | Solved for in the analysis | Synthesis Target 10 | Solved for in the analysis |
| BLI Fan shaft power | kW | Target | Target/Solved for in the analysis | Target/Solved for in the analysis |
| Thrust | kN | Target | Target | Target |
| BLI Fan pressure ratio | - | Fixed | Solved for in the analysis | Solved for in the analysis |
| BLI Fan inlet mass flow | kg/s | Variable | Solved for in the analysis † | Solved for in the analysis † |
| Engine inlet mass flow | kg/s | Fixed | Solved for in the analysis | Solved for in the analysis |
| Fan tip pressure ratio | - | Synthesis Variable 1 | Solved for in the analysis | Solved for in the analysis † |
| Bypass ratio | - | Synthesis Variable 2 | Solved for in the analysis | Solved for in the analysis † |
| Fan root pressure ratio | - | Variable | Solved for in the analysis | Solved for in the analysis |
| LPC pressure ratio | - | Synthesis Variable 3 | Solved for in the analysis | Solved for in the analysis † |
| HPC pressure ratio | - | Synthesis Variable 4 | Solved for in the analysis | Solved for in the analysis † |
| HPT 1st stage vane cooling flow (% HPC flow) | % | Synthesis Variable 5 | same as @ToC † | same as @ToC |
| HPT 1st stage rotor cooling flow (% HPC flow) | % | Synthesis Variable 6 | same as @ToC † | same as @ToC |
| HPT 2nd stage vane cooling flow (% HPC flow) | % | Synthesis Variable 7 | same as @ToC † | same as @ToC |
| HPT 2nd stage rotor cooling flow (% HPC flow) | % | Synthesis Variable 8 | same as @ToC † | same as @ToC |
| HPT 2nd stage cooling flow extraction point | % | Fixed | same as @ToC | same as @ToC |
| LPT 1st stage vane cooling flow (% HPC flow) | % | Synthesis Variable 9 | same as @ToC † | same as @ToC |
| LPT 1st stage rotor cooling flow (% HPC flow) | % | Synthesis Variable 10 | same as @ToC † | same as @ToC |
| LPT cooling flow extraction point | % | Fixed | same as @ToC | same as @ToC |
| Combustor outlet temperature | K | Variable | Variable | Synthesis Target 1 |
| Core nozzle area | m2 | Solved for in the analysis | Solved for in the analysis | Solved for in the analysis |
| Bypass nozzle area | m2 | Solved for in the analysis | Solved for in the analysis | Solved for in the analysis |
| Core inlet mass flow | kg/s | Solved for in the analysis | Solved for in the analysis | Solved for in the analysis |
| High pressure turbine rotor inlet temperature | K | Solved for in the analysis | Solved for in the analysis | Solved for in the analysis |
| Turbomachines polytropic efficiency | % | Fixed | Solved for in the analysis | Solved for in the analysis |
| Engine intake pressure loss dP/P | % | Fixed | Solved for in the analysis | Solved for in the analysis |
| Combustor pressure loss dP/P | % | Fixed | Solved for in the analysis | Solved for in the analysis |
| Ducts pressure loss dP/P | % | Fixed | Solved for in the analysis | Solved for in the analysis |
| Nozzles thrust coefficient | % | Fixed | Solved for in the analysis | Solved for in the analysis |
| Shafts mechanical efficiency | % | Fixed | Solved for in the analysis | Solved for in the analysis |
| Gearbox speed ratio | % | Fixed | same as @ToC | same as @ToC |
| Gearbox mechanical efficiency | % | Fixed | Solved for in the analysis | Solved for in the analysis |
| Component | Efficiency | Specific Power | Case 1 | Case 2 | Case 3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [%] | [kW/kg] | Power | Loss | Weight | Power | Loss | Weight | Power | Loss | Weight | ||||||
| *[A/(kg/m)] | [kW] | [kg] | [kW] | [kg] | [kW] | [kg] | ||||||||||
| Pess. | Opt. | Pess. | Opt. | Pess. | Opt. | Pess. | Opt. | |||||||||
| Motor | 1 | 96.0 | 13 | 16 | 1200 | 48 | 92 | 75 | 2800 | 112 | 215 | 175 | 2000 | 80 | 154 | 125 |
| Inverter | 1 | 99.0 | 10 | 19 | 1250 | 13 | 125 | 66 | 2917 | 29 | 292 | 154 | 2083 | 21 | 208 | 110 |
| Circ. Protection | 4 | 99.5 | 200 | 200 | 631 | 13 | 13 | 13 | 1473 | 29 | 29 | 29 | 1052 | 21 | 21 | 21 |
| Cable | 2 | 99.6 | 170* | 170* | 634 | 5 | 290 | 290 | 1480 | 12 | 677 | 677 | 1057 | 8 | 484 | 484 |
| Rectifier | 2 | 99.0 | 10 | 19 | 637 | 13 | 127 | 67 | 1486 | 30 | 297 | 156 | 1062 | 21 | 212 | 112 |
| Generator | 2 | 96.0 | 13 | 16 | 643 | 51 | 99 | 80 | 1501 | 120 | 231 | 188 | 1072 | 86 | 165 | 134 |
| Thermal System | 0.68 | 1.6 | 202 | 86 | 471 | 200 | 1117 | 337 | 143 | |||||||
| Total System | 137 | 948 | 677 | 320 | 2213 | 1579 | 229 | 1581 | 1128 | |||||||
References
- International Cival Aviation Organization: On Board a Sustainable Future, ICAO Environmental Report. Available online: https://www.icao.int/environmental-protection/Pages/env2016.aspx (accessed on 13 October 2019).
- ACARE Strategic Research & Innovation Agenda. Advisory Council for Aviation Research and Innovation in Europe, 2017; Volume 1. Available online: https://www.acare4europe.org/sites/acare4europe.org/files/document/ACARE-Strategic-Research-Innovation-Volume-1.pdf (accessed on 13 October 2019).
- Lents, C.E.; Hard, L.; Rheaume, J.; Kohlman, L. Parallel Hybrid Gas-Electric Geared Turbofan Engine Conceptual Design and Benefits Analysis. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar]
- Freeh, J.E.; Steffen, C.J.; Larosiliere, L.M. Off-design performance analysis of a solid-oxide fuel cell/gas turbine hybrid for auxiliary aerospace power. In Proceedings of the ASME 2005 3rd International Conference on Fuel Cell Science, Engineering and Technology, Ypsilanti, MI, USA, 23–25 May 2005. [Google Scholar]
- Lupelli, L.; Geis, T. A Study on the Integration of the IP Power Offtake System within the Trent 1000 Turbofan Engine. Available online: https://core.ac.uk/reader/14703878 (accessed on 13 October 2019).
- Zhao, X.; Sahoo, S.; Kyprianidis, K.; Rantzer, J.; Sielemann, M. Off-design performance analysis of hybridised aircraft gas turbine. Aeronaut. J. 2019, 123, 1999–2018. [Google Scholar] [CrossRef]
- Smith, A.M.O.; Roberts, H.E. The Jet Airplane Utilizing Boundary Layer Ingestion for Propulsion. J. Aeronaut. Sci. 1947, 14, 97–109. [Google Scholar] [CrossRef]
- Smith, L.H. Wake Ingesting Propulsion Benefit. J. Propuls. Power 1993, 9, 74–82. [Google Scholar] [CrossRef]
- Plas, A.P.; Sargeant, M.A.; Madani, V.; Chrichton, D.; Greitzer, E.M.; Hynes, T.P.; Hall, C.A. Performance of a Boundary Layer Ingesting (BLI) Propulsion System. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. AIAA 2007-450. [Google Scholar]
- Welstead, J.R.; Felder, J.L. Conceptual Design of a Single-Aisle Turboelectric Commercial Transport with Fuselage Boundary Layer Ingestion. In Proceedings of the 54th AIAA Aerospace Sciences Meeting/Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Yildirim, A.; Gray, J.S.; Mader, C.A.; Martins, J. Aeropropulsive Design Optimization of a Boundary Layer Ingestion System. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar]
- Gray, J.S.; Kenway, G.K.; Mader, C.A.; Martins, J. Aero-propulsive Design Optimization of a Turboelectric Boundary Layer Ingestion Propulsion System. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Kenway, G.K.; Kiris, C.C. Aerodynamic Shape Optimization of the STARC-ABL Concept for Minimal Inlet Distortion. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Seitz, A.; Isikveren, A.T.; Hornung, M. Pre-concept performance investigation of electrically powered aero-propulsion systems. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 14–17 July 2013; p. 3608. [Google Scholar]
- Isikveren, A.T.; Pornet, C.; Vratny, P.C.; Schmidt, M. Conceptual studies of future hybrid-electric regional aircraft. In Proceedings of the 22nd International Symposium on Air Breathing Engines, Phoenix, AZ, USA, 22–25 October 2015. [Google Scholar]
- CeRAS Central Reference Aircraft Data System. Available online: https://ceras.ilr.rwth-aachen.de/ (accessed on 13 December 2019).
- Kyprianidis, K.G.; Quintero, R.F.C.; Pascovici, D.S.; Ogaji, S.O.T.; Pilidis, P.; Kalfas, A.I. EVA: A Tool for EnVironmental Assessment of Novel Propulsion Cycles. In Proceedings of the ASME Turbo Expo: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; pp. 547–556. [Google Scholar]
- Schlichting, H. Boundary Layer Theory (Grenzschicht-Theorie); Springer: Karlsruhe, Germany, 1964. [Google Scholar]
- Klabes, A.; Appely, C.; Herr, M. Fuselage Excitation During Cruise Flight Conditions: Measurement and Prediction of Pressure Point Spectra. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015. AIAA Paper 2015-3115. [Google Scholar]
- Schnös, M.; Nicke, E. Exploring a Database of Optimal Airfoils for Axial Compressor Design. In Proceedings of the 23rd International Symposium on Air Breathing Engines, Manchester, UK, 3–8 September 2017. ISABE Paper 2017-21493. [Google Scholar]
- Schnös, M.; Voß, C.; Nicke, E. Design Optimization of a Multi-Stage Axial Compressor Using Throughflow and a Database of Optimal Airfoils. In Proceedings of the GPPS Montreal 18 Conference, Montreal, QC, Canada, 7–9 May 2018. [Google Scholar]
- Kavvalos, M.; Zhao, X.; Schnell, R.; Aslanidou, I.; Kalfas, A.; Kyprianidis, K. A Modelling Approach of Variable Geometry for Low Pressure Ratio Fans. In Proceedings of the International Society of Air Breathing Engines, Canberra, Australia, 23–27 September 2019. ISABE Paper 2019-24382. [Google Scholar]
- Kyprianidis, K.G. Future Aero Engine Designs: An Evolving Vision. In Advances in Gas Turbine Technology; Benini, E., Ed.; IntechOpen: London, UK; Available online: https://www.intechopen.com/books/advances-in-gas-turbine-technology/future-aero-engine-designs-an-evolving-vision (accessed on 4 November 2011). [CrossRef]
- Schnell, R.; Goldhahn, E.; Julain, M. Design and Performance of a Low Fan-Pressure-Ratio Propulsion System. In Proceedings of the International Society of Air Breathing Engines, Canberra, Australia, 23–27 September 2019. ISABE Paper 2019-24017. [Google Scholar]
- Crichton, D.; Xu, L.; Hall, C.A. Preliminary Fan Design for a Silent Aircraft. J. Turbomach. 2017, 129, 184–191. [Google Scholar] [CrossRef]
- Kurzke, J. Preliminary Engine Design. In Aero Engine Design: From State of the Art Turbofans Towards Innovative Architectures; Lecture Series 2008-03; Von Karman Institute (VKI): Brussels, Belgium, 2008. [Google Scholar]
- Cumpsty, N.A. Compressor Aerodynamics; Krieger Publishing Company: Malabar, FL, USA, 2004. [Google Scholar]
- Grieb, H. Verdichter Für Turbo-Flugtriebwerke/Aero Engine Compressors; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-34374-5. [Google Scholar]
- Lee, B.J.; Liou, M.F. Aerodynamic Design and Optimization of Fan Stage for Boundary Layer Ingestion Propulsion System. In Proceedings of the 10th International Conference on Computational Fluid Dynamics (ICCFD10), Barcelona, Spain, 9–13 July 2018. ICCFD10-091. [Google Scholar]
- Mennicken, M.; Schönweitz, D.; Schnoes, M.; Schnell, R. Conceptual Fan Design for Boundary Layer Ingestion. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. ASME Paper GT2019-90257. [Google Scholar]
- Dever, T.P. Assessment of Technologies for Noncryogenic Electric Propulsion; Report NASA/TP—2015-216588; NASA: Cleveland, OH, USA, 2015.
- Duffy, K.P. Electric Motors for Non-Cryogenic Hybrid Electric Propulsion. In Proceedings of the 51st AIAA/SAE/ASEE Joint Prpulsion Conference, Orlando, FL, USA, 27–29 July 2015. [Google Scholar]
- Jansen, R.; Bowman, C.; Jankovysky, A.; Dyson, R.; Felder, J. Overview of NASA Electrified Aircraft Prpulsion (EAP) Research for Large Subsonic Transports. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017. [Google Scholar]
- National Academies of Sciences and Medicine. Commercial Aircraft Propulsion and Energy Systems Research: Reducing Global Carbon Emission; National Academies Press: Washington, DC, USA, 2016. [Google Scholar]
- Lee, B.J.; Liou, M.-F. Aerodynamic Conceptual Design of Boundary Layer Ingestion Propulsor Systems: A Quasi-2d Through Flow Analysis Method and Multi-Fidelity Propulsor Design Framework. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Lillestrom (Oslo), Norway, 11–25 June 2018. ASME Paper GT2018-75861. [Google Scholar]
- Sahoo, S.; Zhao, X.; Kyprianidis, K. Performance Assessment of an Integrated Parallel Hybrid-Electric Propulsion System Architecture. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. ASME Paper GT2019-91459. [Google Scholar]
- Lengyel-Kampmann, T.; Voß, C.; Nicke, E.; Rud, K.-P.; Schaber, R. Generalized Optimization of Counter-Rotating and Single-Rotating Fans. In Proceedings of the ASME Turbo Expo, Duesseldorf, Germany, 16–20 June 2014. ASME Paper 2014-26008. [Google Scholar]
- Kyprianidis, K.; Rolt, A.M. On the Optimization of a Geared Fan Intercooled Core Engine Design. J. Eng. Gas Turbines Power 2015, 137, 041201. [Google Scholar] [CrossRef]
- Jenkinson, L.; Simkin, P.; Rhodes, D. Civil Jet Aircraft Design; Arnold: London, UK, 1999; ISBN 0-340-74152-X. [Google Scholar]
- Gray, S.; Mader, C.A.; Kenway, G.K.W.; Martins, J.R.R.A. Modeling Boundary Layer Ingestion Using a Coupled Aeropropulsive Analysis. J. Aircr. 2017, 55, 1191–1999. [Google Scholar] [CrossRef]



| Take-Off | Top-of-Climb | Cruise | |
|---|---|---|---|
| Thrust (kN) | 92.5 | 24.0 | 18.0 |
| Altitude (m) | 0 | 10,668 | 10,668 |
| Flight Mach (-) | 0.25 | 0.78 | 0.78 |
| ΔTISA (K) | +15 | +10 | +0 |
| Aircraft and Mission | Unit | Value |
|---|---|---|
| Design Range | km | 4800 |
| Business Case Range | km | 925 |
| Passenger Capability | - | 150 |
| Wing Area | m2 | 122.4 |
| Wing Span | m | 33.91 |
| Tailplane Area | m2 | 31.0 |
| Tailplane Span | m | 12.45 |
| Fin Area | m2 | 21.5 |
| Fin Span | m | 6.26 |
| Fuselage Length | m | 37 |
| Case | FPR | Ψ | httr | w92 | RPM | utip,c | Dfan | PWX48 | Objective |
|---|---|---|---|---|---|---|---|---|---|
| (-) | (-) | (-) | (kg/s) | (1/min) | (m/s) | (m) | (kW) | ||
| non-BLI and BLI | 1.2 | 0.4 | 0.5 | 80 | 3551 | 263 | 1.331 | 1200 | Study Ψ/tip-speed effect |
| 0.5 | 3176 | 234 | |||||||
| 0.6 | 2899 | 215 | |||||||
| (1) BLI | 1.2 | 0.5 | 0.525 | 80 | 3090 | 233 | 1.357 | 1200 | Study four selected cases:
|
| 0.500 | 3024 | 1.460 | |||||||
| (2) BLI | 1.2 | 0.5 | 0.375 | 180 | 2373 | 246 | 1.868 | 2800 | |
| 0.350 | 2234 | 2.000 | |||||||
| (3) BLI | 1.3 | 0.5 | 0.500 | 88 | 3656 | 284 | 1.398 | 2000 | |
| 0.475 | 3552 | 1.520 | |||||||
| (4) BLI | 1.4 | 0.6 | 0.550 | 66 | 4148 | 289 | 1.256 | 2000 | |
| 0.525 | 3841 | 1.370 |
| Perturbation | Exchange Rate/Change in Block Fuel |
|---|---|
| +1% SFC | 1.06% |
| +1% total drag | 0.78% |
| 1000 kg weight penalty | 1.30% |
| ΔSFC | ||||
|---|---|---|---|---|
| Case 1: PWX = 2800 kW FPR = 1.2 | Case 2: PWX = 1200 kW FPR = 1.2 | Case 3: PWX = 2000 kW FPR = 1.3 | Case 4: PWX = 2000 kW FPR = 1.4 | |
| +/−25% uncertainty in aft-fan incoming momentum deficit ΔI | +/−0.8% | +/−0.625% | +/−0.9% | +/−0.975% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schnell, R.; Zhao, X.; Rallis, E.; Kavvalos, M.; Sahoo, S.; Schnoes, M.; Kyprianidis, K. Assessment of a Turbo-Electric Aircraft Configuration with Aft-Propulsion Using Boundary Layer Ingestion. Aerospace 2019, 6, 134. https://doi.org/10.3390/aerospace6120134
Schnell R, Zhao X, Rallis E, Kavvalos M, Sahoo S, Schnoes M, Kyprianidis K. Assessment of a Turbo-Electric Aircraft Configuration with Aft-Propulsion Using Boundary Layer Ingestion. Aerospace. 2019; 6(12):134. https://doi.org/10.3390/aerospace6120134
Chicago/Turabian StyleSchnell, Rainer, Xin Zhao, Efthymios Rallis, Mavroudis Kavvalos, Smruti Sahoo, Markus Schnoes, and Konstantinos Kyprianidis. 2019. "Assessment of a Turbo-Electric Aircraft Configuration with Aft-Propulsion Using Boundary Layer Ingestion" Aerospace 6, no. 12: 134. https://doi.org/10.3390/aerospace6120134
APA StyleSchnell, R., Zhao, X., Rallis, E., Kavvalos, M., Sahoo, S., Schnoes, M., & Kyprianidis, K. (2019). Assessment of a Turbo-Electric Aircraft Configuration with Aft-Propulsion Using Boundary Layer Ingestion. Aerospace, 6(12), 134. https://doi.org/10.3390/aerospace6120134