Impact of Energy Dependence on Ground Level and Avionic SEE Rate Prediction When Applying Standard Test Procedures
Abstract
1. Introduction
2. SEE Qualification Approaches
- Method 1 (M1): Spallation neutron source. The source provides a neutron spectrum over a wide energy range, from thermal up to high energy neutrons. Among the neutron sources, it has the closest shape to the atmospheric spectrum. Although energies in the atmospheric spectrum can be as high as 100 GeV, these facilities can normally provide energies only up to 1 GeV. However, the atmospheric flux at such high energies is several orders of magnitude lower than that at 100 MeV and therefore its impact is considered to be negligible. The SEU and SEL cross section measured in such facilities encompasses the information of a very wide spectrum in a single value. Thus, it is not possible to extract the energy contributions separately, such as the thermal neutron and high energy hadron (HEH) cross sections. The most well-known facilities are WNR in Los Alamos, TRIUMF in Vancouver and ChipIr in Didcot (UK).
- Method 2 (M2): Monoenergetic beams up to 200 MeV. The JEDEC standard [5] suggests performing the characterization with at least four different energies: 14, 50, 100 and 200 MeV. Then, from these experimental points, calculating the memory response through the Weibull fit. Tests with 14 MeV should be carried out with a neutron beam, whereas above 50 MeV both neutron and proton beams can be used, as their nuclear cross sections are similar. The SEE rate is calculated through the integral of the operational spectrum folded with the memory response, which is also valid for avionic applications [1].
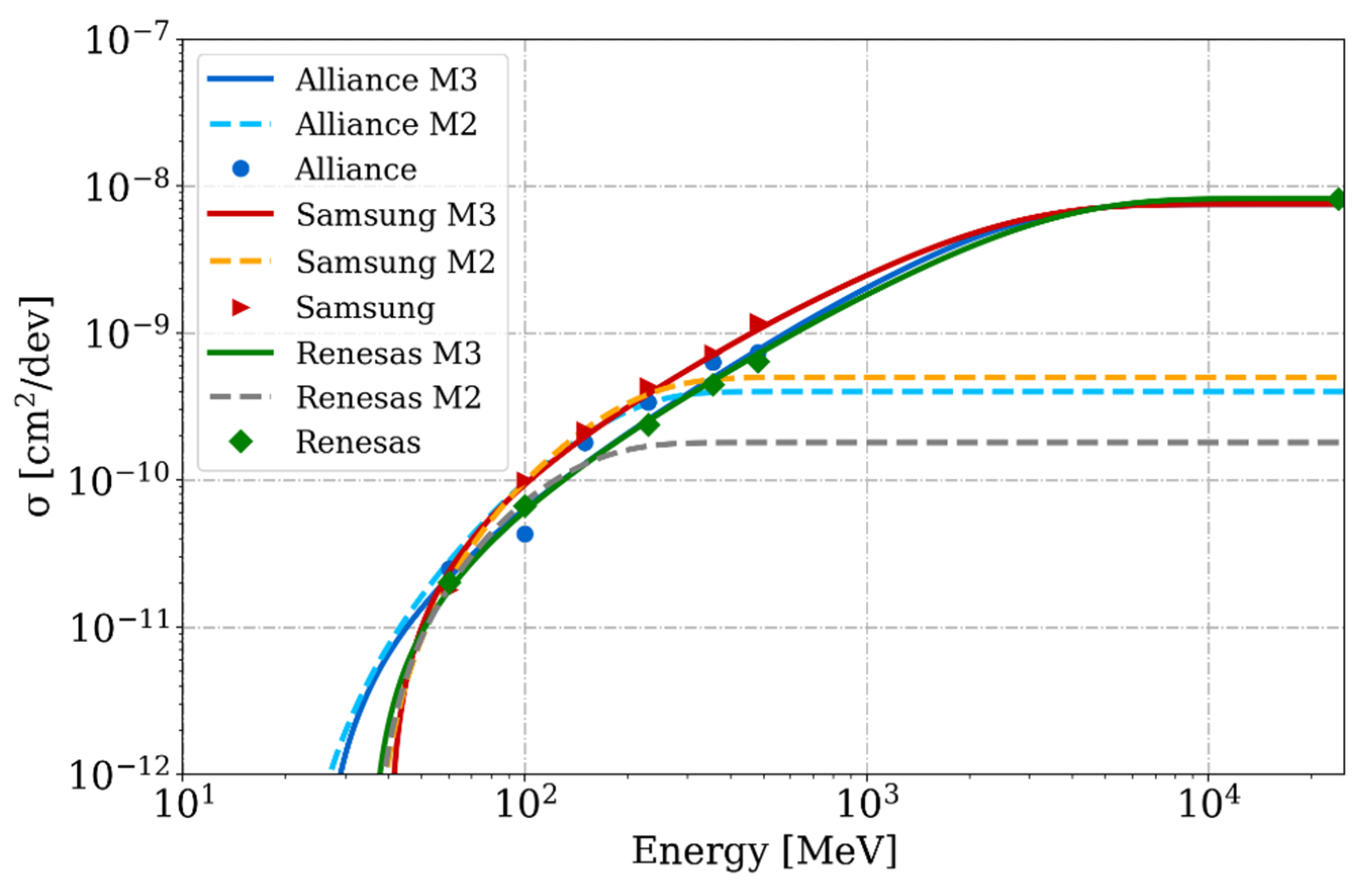
- Method 3 (M3): Monoenergetic beams/simulations up to several GeV. This method is not outlined in the standards and it overcomes some limitations of M2. M2 makes the large assumption that the memory cross section is saturated after 200 MeV. However, as shown in References [13,14,15], some devices with a strong energy dependence—due to the presence of tungsten near the sensitive volume—show an increasing SEE cross section above 200 MeV, and up to several GeV before saturation. Therefore, the characterization should be performed up to GeV energies in order to assess the SEE impact from high energy particles in the atmosphere. Despite their fluxes being an order of magnitude lower than those around 100 MeV, the fact that the SEE cross section is still increasing after 200 MeV plays an important role, as will be detailed in this paper. Tests with such high energies can be performed for example in the CERN high energy accelerator mixed field facility (CHARM) at CERN, which provides a 24 GeV proton beam extracted from the Proton Synchrotron (PS). Otherwise, the memory cross section can be calculated through simulations with a FLUKA model. FLUKA is a Monte Carlo tool [9,16] for studying the interactions of particles and matter. The model is employed to calculate the deposited energy inside the memory’s sensitive volume needed to trigger an SEE, and it has been validated for protons [13] and neutrons [2]. It requires input of the following information:-The geometrical parameters of the memory structure.-The layers of materials, especially the amount of possible tungsten, which is the direct cause of the SEE cross section increase.-The experimental heavy ion SEE response of the component.
- Other methods. In addition to the previous methods, the standards mention real time and quasi monoenergetic neutron measurements. The real time method consists of observing SEEs under nominal conditions without accelerated tests, but it is impractical since it would take years (or the testing of a vast number of components) to obtain meaningful statistics. The quasi monoenergetic neutron beam is characterized by a main peak at nominal energy and a tail at lower energies ranging over more than 100 MeV. The difficulty lies in distinguishing between the SEEs induced by the neutron peak and the tail [17]. Due to the aforementioned complications, these two methods were not taken into account in this work.
3. Atmospheric Radiation Environments
4. SEE Calculation and Results
5. Conclusions
Materials and Methods
Author Contributions
Funding
Conflicts of Interest
References
- Process Management for Avionics—Atmospheric Radiation Effects. Accommodation of Atmospheric Radiation Effects via Single Event Effects within Avionics Electronic Equipment; IEC Standard 62396-1; International Electrotechnical Commission: Geneva, Switzerland, 2016.
- Cecchetto, M.; Fernández-Martínez, P.; Alía, R.G.; Ferraro, R.; Danzeca, S.; Wrobel, F.; Cazzaniga, C.; Frost, C.D. SEE Flux and Spectral Hardness Calibration of Neutron Spallation and Mixed-Field Facilities. IEEE Trans. Nucl. Sci. 2019, 66, 1532–1540. [Google Scholar] [CrossRef]
- Lambert, D.; Desnoyers, F.; Thouvenot, D.; Riant, O.; Galinat, J.; Azaïs, B.; Colladant, T. Single event upsets induced by a few MeV neutrons in SRAMs and FPGAs. In Proceedings of the 2017 IEEE Radiation Effects Data Workshop (REDW), New Orleans, LA, USA, 17–21 July 2017; pp. 114–118. [Google Scholar]
- Quinn, H.; Watkins, A.; Dominik, L.; Slayman, C. The Effect of 1–10-MeV Neutrons on the JESD89 Test Standard. IEEE Trans. Nucl. Sci. 2019, 66, 140–147. [Google Scholar] [CrossRef]
- Process Management for Avionics—Atmospheric Radiation Effects. Guidelines for Single Event Effects Testing for Avionics Systems; IEC Standard 62396-2; International Electrotechnical Commission: Geneva, Switzerland, 2017.
- Sierawski, B.D.; Pellish, J.A.; Reed, R.A.; Schrimpf, R.D.; Warren, K.M.; Weller, R.A.; Mendenhall, M.H.; Black, J.D.; Tipton, A.D.; Xapsos, M.A.; et al. Impact of low-energy proton induced upsets on test methods and rate predictions. IEEE Trans. Nucl. Sci. 2009, 56, 3085–3092. [Google Scholar] [CrossRef]
- Sierawski, B.D.; Mendenhall, M.H.; Reed, R.A.; Clemens, M.A.; Weller, R.A.; Schrimpf, R.D.; Blackmore, E.W.; Trinczek, M.; Hitti, B.; Pellish, J.A.; et al. Muon-induced single event upsets in deep-submicron technology. IEEE Trans. Nucl. Sci. 2010, 57, 3273–3278. [Google Scholar] [CrossRef]
- “MAIRE,” RadMod Research. Available online: https://www.radmod.co.uk/maire (accessed on 24 August 2019).
- Fasso, A.; Ferrari, A.; Ranft, J.; Sala, P.R. FLUKA: A Multi-Particle Transport Code; SLAC-R-773, 877507; CERN: Meyrin, Switzerland, 2005. [Google Scholar] [CrossRef]
- Schwank, J.R.; Shaneyfelt, M.R.; Baggio, J.; Dodd, P.E.; Felix, J.A.; Ferlet-Cavrois, V.; Paillet, P.; Lambert, D.; Sexton, F.W.; Hash, G.L.; et al. Effects of particle energy on proton-induced single-event latchup. IEEE Trans. Nucl. Sci. 2005, 52, 2622–2629. [Google Scholar] [CrossRef]
- Turflinger, T.L.; Clymer, D.A.; Mason, L.W.; Stone, S.; George, J.S.; Savage, M.; Koga, R.; Beach, E.; Huntington, K. RHA Implications of Proton on Gold-Plated Package Structures in SEE Evaluations. IEEE Trans. Nucl. Sci. 2015, 62, 2468–2475. [Google Scholar] [CrossRef]
- Measurement and Reporting of Alpha Particle and Terrestrial Cosmic Ray-Induced Soft Errors in Semiconductor Devices. JEDEC Standard 89A (JESD89A). Available online: https://www.jedec.org/standards-documents/docs/jesd- (accessed on 30 October 2019).
- Alía, R.G.; Brugger, M.; Danzeca, S.; Ferlet-Cavrois, V.; Poivey, C.; Røed, K.; Saigné, F.; Spiezia, G.; Uznanski, S.; Wrobel, F. Energy Dependence of Tungsten-Dominated SEL Cross Sections. IEEE Trans. Nucl. Sci. 2014, 61, 2718–2726. [Google Scholar] [CrossRef]
- Alía, R.G.; Blackmore, E.W.; Brugger, M.; Danzeca, S.; Ferlet-Cavrois, V.; Gaillard, R.; Mekki, J.; Poivey, C.; Røed, K.; Saigné, F.; et al. SEL Cross Section Energy Dependence Impact on the High Energy Accelerator Failure Rate. IEEE Trans. Nucl. Sci. 2014, 61, 2936–2944. [Google Scholar] [CrossRef]
- García Alía, R.; Brugger, M.; Danzeca, S.; Ferlet-Cavrois, V.; Frost, C.; Gaillard, R.; Mekki, J.; Saigné, F.; Thornton, A.; Uznanski, S.; et al. SEL Hardness Assurance in a Mixed Radiation Field. IEEE Trans. Nucl. Sci. 2015, 62, 2555–2562. [Google Scholar] [CrossRef]
- Battistoni, G.; Cerutti, F.; Fassò, A.; Ferrari, A.; Muraro, S.; Ranft, J.; Roesler, S.; Sala, P.R. The FLUKA code: Description and benchmarking. In Proceedings of the AIP Conference Proceedings, Batavia, IL, USA, 6–8 September 2007; Volume 896, pp. 31–49. [Google Scholar]
- Alía, R.G.; Brugger, M.; Danzeca, S.; Mekki, J.; Thornton, A. SEE cross section calibration and application to quasi-monoenergetic and spallation facilities. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2017; Volume 153, p. 08015. [Google Scholar]
- Alía, R.G.; Brugger, M.; Danzeca, S.; Cerutti, F.; de Carvalho Saraiva, J.P.; Denz, R.; Ferrari, A.; Foro, L.L.; Peronnard, P.; Røed, K.; et al. Single event effects in high-energy accelerators. Semicond. Sci. Technol. 2017, 32, 034003. [Google Scholar] [CrossRef]
- Uznanski, S.; Alia, R.G.; Blackmore, E.; Brugger, M.; Gaillard, R.; Mekki, J.; Todd, B.; Trinczek, M.; Villanueva, A.V. The Effect of Proton Energy on SEU Cross Section of a 16 Mbit TFT PMOS SRAM with DRAM Capacitors. IEEE Trans. Nucl. Sci. 2014, 61, 3074–3079. [Google Scholar] [CrossRef]
- Alía, R.G.; Brugger, M.; Cecchetto, M.; Cerutti, F.; Danzeca, S.; Delrieux, M.; Kastriotou, M.; Tali, M.; Uznanski, S. SEE Testing in the 24-GeV Proton Beam at the CHARM Facility. IEEE Trans. Nucl. Sci. 2018, 65, 1750–1758. [Google Scholar] [CrossRef]
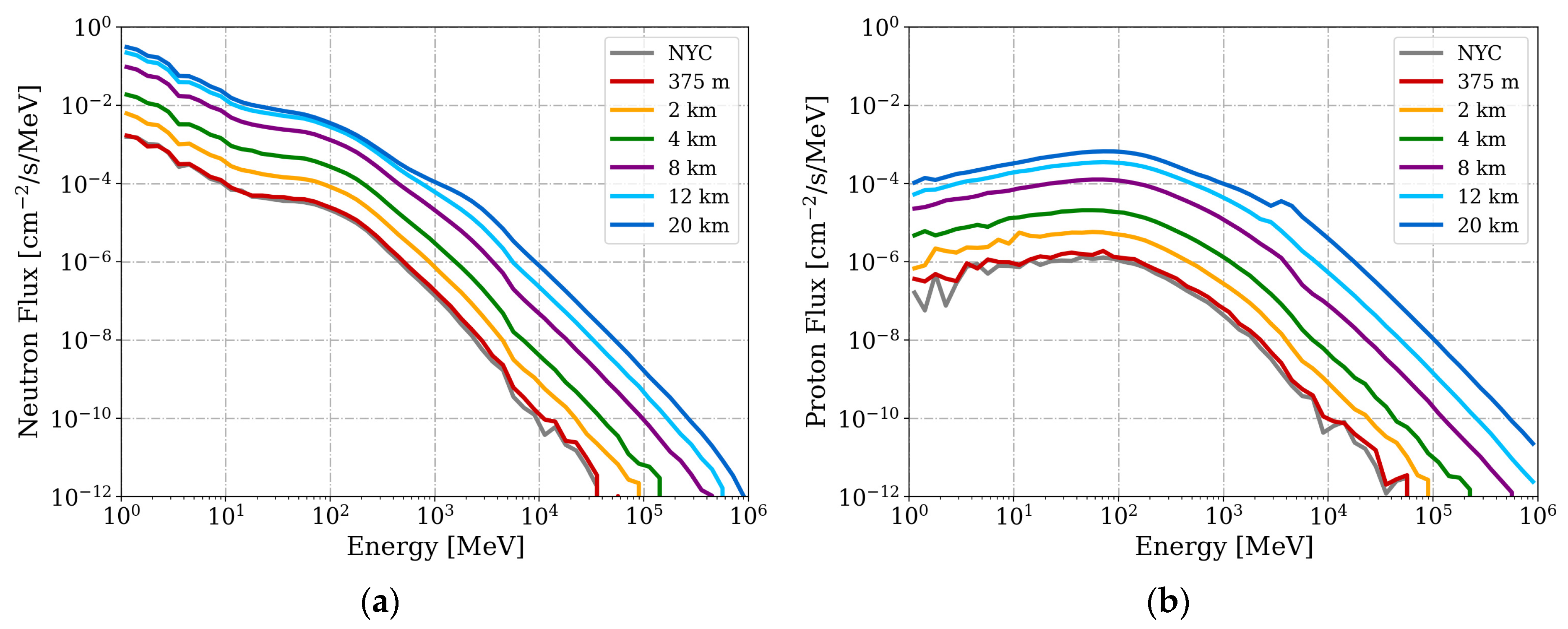
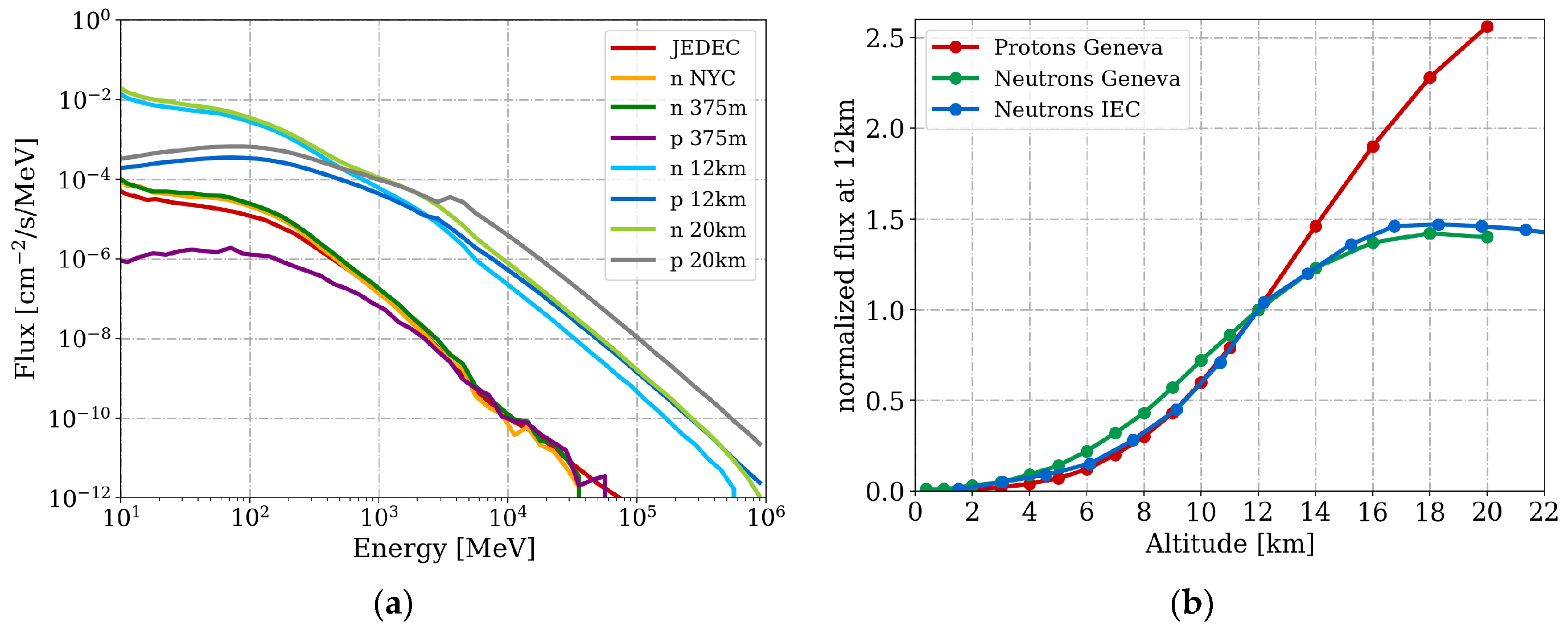
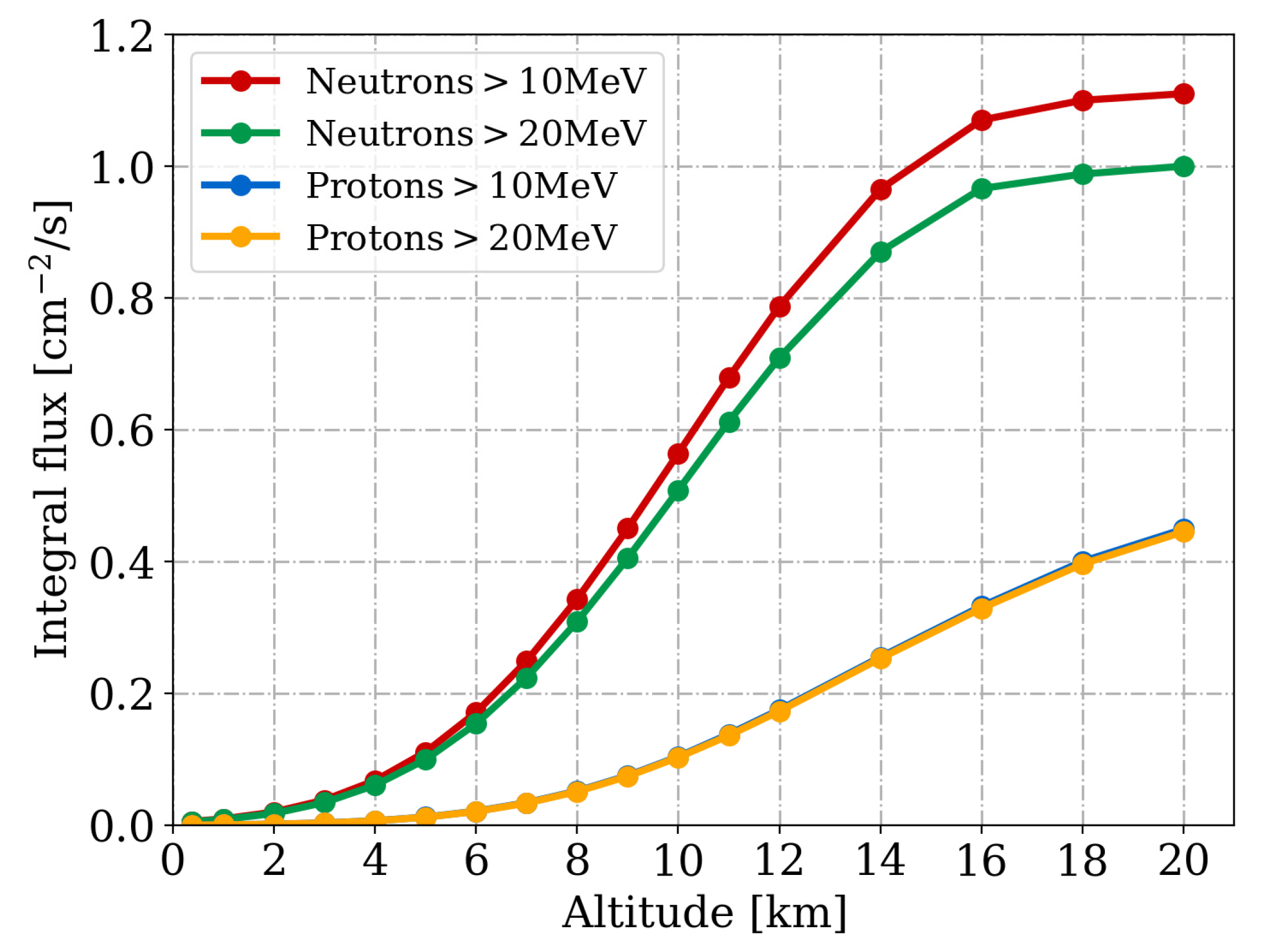
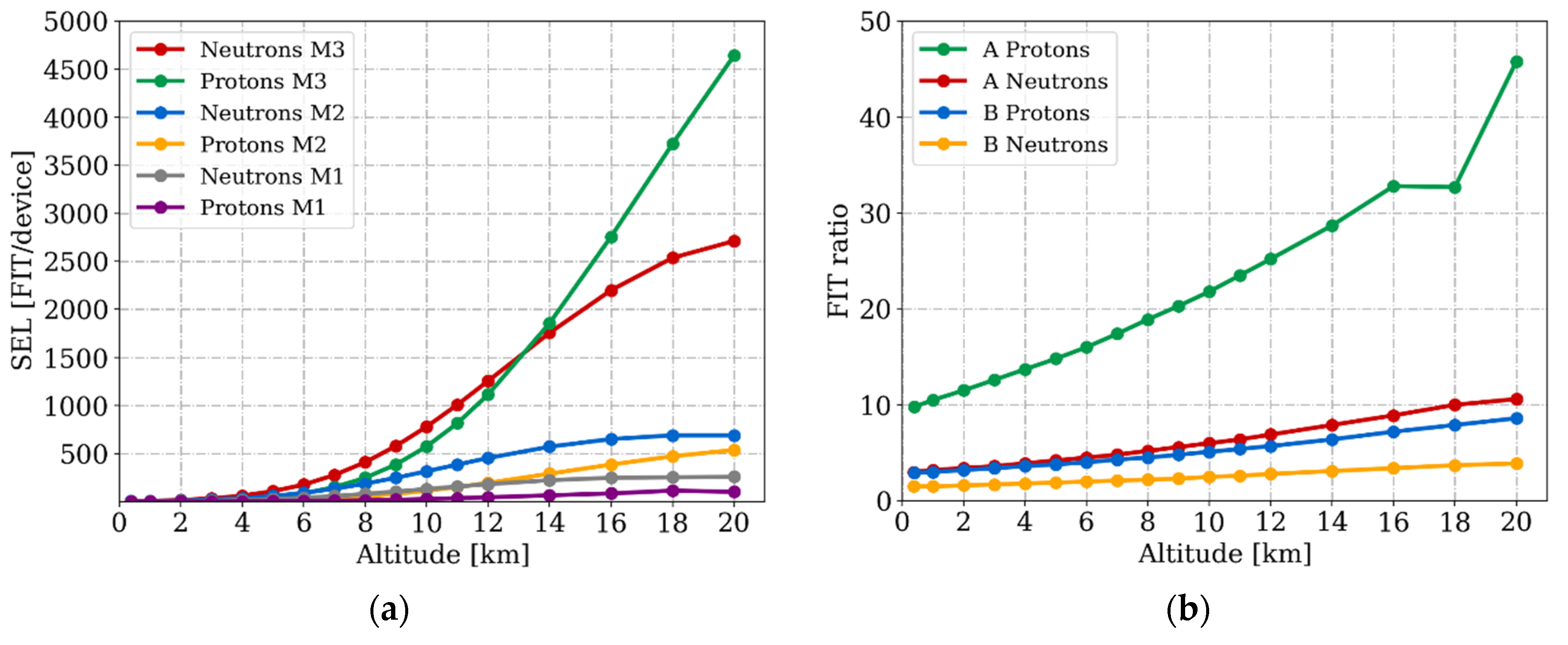
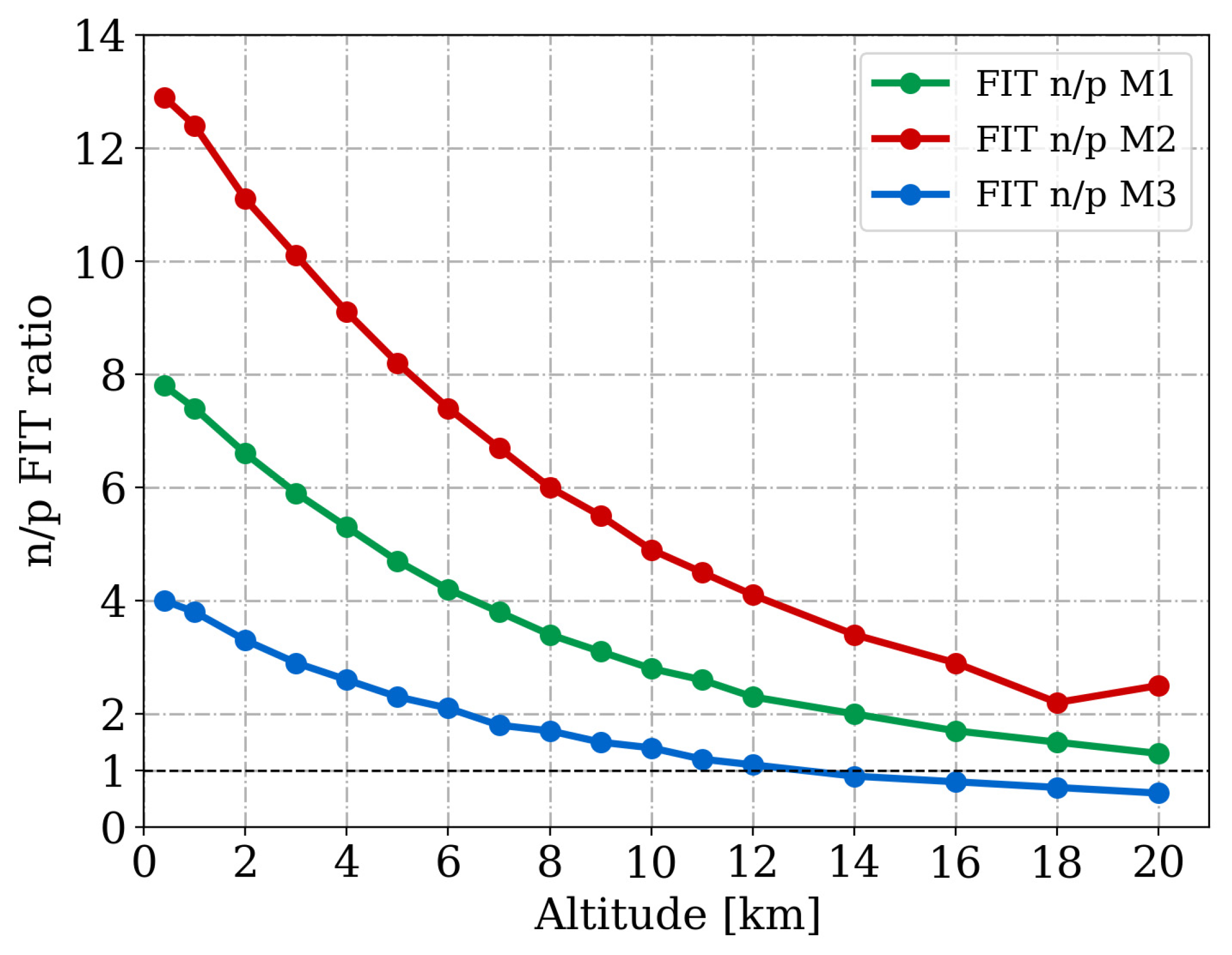
| Altitude (km) | JEDEC | 0.356 | 4 | 8 | 12 | 12 (Equator) | 12 (Pole) | 20 |
|---|---|---|---|---|---|---|---|---|
| H10% (MeV) | 525 | 450 | 566 | 805 | 1275 | 1420 | 1014 | 1790 |
| Memory | Tech (nm) | Size | SEE | Weibull | σsat (cm2/dev) | Eth | W | s |
|---|---|---|---|---|---|---|---|---|
| Alliance | 200 | 4 Mbit | SEL | M2 | 4.0 × 10−10 | 20 | 156 | 1.93 |
| M3 | 7.5 × 10−9 | 25 | 2210 | 1.41 | ||||
| Samsung | 180 | 4 Mbit | SEL | M2 | 5.0 × 10−10 | 35 | 157 | 1.74 |
| M3 | 7.5 × 10−9 | 40 | 2000 | 1.25 | ||||
| Renesas | 150 | 16 Mbit | SEU | M2 | 1.8 × 10−10 | 35 | 100 | 1.6 |
| M3 | 8.2 × 10−9 | 35 | 2800 | 1.3 |
| Memory | FIT for E < 230 MeV | FIT for E > 230 MeV | ||||||
|---|---|---|---|---|---|---|---|---|
| Neutrons | Protons | Neutrons | Protons | |||||
| M2 | M3 | M2 | M3 | M2 | M3 | M2 | M3 | |
| Alliance | 193 | 134 | 34 | 24 | 260 | 1121 | 161 | 1090 |
| Samsung | 205 | 169 | 37 | 30 | 321 | 1273 | 200 | 1187 |
| Renesas | 121 | 128 | 21 | 23 | 121 | 1040 | 75 | 1032 |
| Memory | SEE | Altitude | M1 | M2 | M3 | A | B |
|---|---|---|---|---|---|---|---|
| Alliance | SEL | Ground | 1.4 | 3.1 | 5.1 | 3.5 | 1.6 |
| 12 | 225 | 647 | 2368 | 11 | 3.7 | ||
| 20 | 358 | 1226 | 7351 | 21 | 6.0 | ||
| Samsung | SEL | Ground | 1.4 | 3.6 | 6.1 | 4.4 | 1.7 |
| 12 | 216 | 762 | 2660 | 12.3 | 3.5 | ||
| 20 | 343 | 1468 | 7918 | 23 | 5.4 | ||
| Renesas | SEU | Ground | 1.8 | 4.7 | 2.7 | ||
| 12 | 338 | 2223 | 6.6 | ||||
| 20 | 618 | 7075 | 11.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cecchetto, M.; García Alía, R.; Wrobel, F. Impact of Energy Dependence on Ground Level and Avionic SEE Rate Prediction When Applying Standard Test Procedures. Aerospace 2019, 6, 119. https://doi.org/10.3390/aerospace6110119
Cecchetto M, García Alía R, Wrobel F. Impact of Energy Dependence on Ground Level and Avionic SEE Rate Prediction When Applying Standard Test Procedures. Aerospace. 2019; 6(11):119. https://doi.org/10.3390/aerospace6110119
Chicago/Turabian StyleCecchetto, Matteo, Rubén García Alía, and Frédéric Wrobel. 2019. "Impact of Energy Dependence on Ground Level and Avionic SEE Rate Prediction When Applying Standard Test Procedures" Aerospace 6, no. 11: 119. https://doi.org/10.3390/aerospace6110119
APA StyleCecchetto, M., García Alía, R., & Wrobel, F. (2019). Impact of Energy Dependence on Ground Level and Avionic SEE Rate Prediction When Applying Standard Test Procedures. Aerospace, 6(11), 119. https://doi.org/10.3390/aerospace6110119





